Understanding the effect of carbon status on stem diameter variations

Abstract

Background

Carbon assimilation and leaf-to-fruit sugar transport are, along with plant water status, the driving mechanisms for fruit growth. An integrated comprehension of the plant water and carbon relationships is therefore essential to better understand water and dry matter accumulation. Variations in stem diameter result from an integrated response to plant water and carbon status and are as such a valuable source of information.

Methods

A mechanistic water flow and storage model was used to relate variations in stem diameter to phloem sugar loading and sugar concentration dynamics in tomato. The simulation results were compared with an independent model, simulating phloem sucrose loading at the leaf level based on photosynthesis and sugar metabolism kinetics and enabled a mechanistic interpretation of the ‘one common assimilate pool’ concept for tomato.

Key Results

Combining stem diameter variation measurements and mechanistic modelling allowed us to distinguish instantaneous dynamics in the plant water relations and gradual variations in plant carbon status. Additionally, the model combined with stem diameter measurements enabled prediction of dynamic variables which are difficult to measure in a continuous and non-destructive way, such as xylem water potential and phloem hydrostatic potential. Finally, dynamics in phloem sugar loading and sugar concentration were distilled from stem diameter variations.

Conclusions

Stem diameter variations, when used in mechanistic models, have great potential to continuously monitor and interpret plant water and carbon relations under natural growing conditions.

INTRODUCTION

Fruit production and quality of tomato (Solanum lycopersicum) are substantially affected by physiological processes related to whole-plant water and carbon relations (e.g. Johnson et al., 1992). To enhance the understanding of water and dry matter accumulation in tomato fruit, it is therefore essential to assess quantitatively the link with plant water and carbon status. In recent years, some effort has already been done to unravel and interpret variations in stem diameter (D_stem) of trees with respect to the tree water and carbon status (e.g. Sevanto et al., 2003; Daudet et al., 2005; De Schepper et al., 2010; De Schepper and Steppe, 2011). These studies highlighted the considerable potential of interpreting variations in D_stem in assessment of plant water and carbon status.

The effect of plant water status on variations in D_stem and the potential of plant water status indicators deduced from D_stem measurements have received extensive attention as a tool in plant-based irrigation scheduling (e.g. Jones, 2004; Steppe et al., 2008; De Swaef et al., 2009, 2012; Fernandez and Cuevas, 2010; Ortuño et al., 2010). Recorded variations in D_stem are an overall result of several distinct mechanisms: irreversible radial growth, reversible shrinking and swelling (in relation to varying levels of hydration) of living cells and expansion or contraction of dead conducting xylem elements due to the increase or relaxation of internal tensions (Daudet et al., 2005). In this respect, contributions of the phloem and cambium tissues have been estimated to account for ∼90 % of the diurnal D_stem variations in deciduous trees, whereas dead xylem tissue accounted for a much smaller fraction (Irvine and Grace, 1997; De Schepper and Steppe, 2010; De Schepper et al., 2012).

Fluctuations in hydration of phloem and cambium tissues result from radial water transport between these tissues and the xylem, which is proportional to the gradient in total water potential and radial hydraulic conductance (Steppe et al., 2012). The main drivers of variations in this radial water transport are the variations in xylem water potential resulting from transpiration and root water availability. As such, xylem water potential and consequently plant water status dominate short-term variations in D_stem.

The effects of plant carbon status on D_stem are somewhat slower than the effects of water status. Because plants seem to maintain a rather steady supply of carbon to the sinks during the night, under low light, low CO₂ conditions or drought stress, loading rates of sucrose into the phloem are thought to be less variable than transpiration rates (Geiger et al., 2000; Komor, 2000). Furthermore, peach fruit growth has been shown to be rather independent of drought stress (Berman and DeJong, 1996). Such a steady supply could be achieved because of the temporary storage of transitional starch or vacuolar glucose and fructose under light conditions, and the mobilization of starch under conditions of low or absent photosynthesis. As such, diurnal phloem loading dynamics are attenuated compared with photosynthesis (or transpiration) rates, with (slightly) higher loading rates during the day than during the night. Furthermore, research in tomato has indicated that mature leaves aim to achieve an equilibrium of carbon gain by photosynthesis and carbon export, by regulating the rate of carbon loading in proportion to the concurrent carbon fixation (Ho, 1978). As such, a mature leaf can maintain a carbon output equal to carbon input. Under variable conditions, a temporary slight loss or gain of carbon in the leaf may occur. However, when a new environmental condition persists, which is different from the condition the leaf was adapted to, acclimation occurs. During acclimation, the rate of carbon is regulated not in proportion to concurrent carbon fixation but in proportion to the amount of carbon reserves in the leaf (Ho, 1978). A new carbon balance could then be achieved within 2–10 d after the start of the new environmental conditions (Ho, 1978). As such, leaves can maintain higher loading rates under conditions that are favourable for photosynthesis and limit export rates when these conditions are unfavourable (Ho, 1978).

Recently, it has been demonstrated for trees that an accumulation of sucrose in the stem phloem affects D_stem in two ways: an effect on overall growth rate and an effect on the time lag between xylem and phloem diameter variations (Sevanto et al., 2003, 2011; Daudet et al., 2005; De Schepper et al., 2010; De Schepper and Steppe, 2011). For herbaceous crops such as tomato, distinction between xylem and stem diameter variations is very difficult to measure, leaving overall D_stem variations as the only option to unravel plant carbon status. The effect of varying plant carbon status on D_stem could be produced by two different mechanisms. First, accumulation of carbohydrates in the stem could serve as a substrate for metabolic energy and consequently enhanced structural radial growth (Daudet et al., 2005). A second effect of a higher sugar concentration is a more negative osmotic potential in stem phloem cells, by which more water is attracted. Consequently, a higher turgor potential could be achieved and thus cell enlargement could be enhanced (De Schepper et al., 2010; De Schepper and Steppe, 2011).

Small variations in D_stem are relatively easy to record using point dendrometers or linear variable displacement transducers (LVDTs) and have been shown to be highly responsive to water and carbon status variations. However, because of this double responsiveness, an unambiguous interpretation of variations in D_stem is not straightforward and requires mechanistic modelling (Sevanto et al., 2011). The effect of carbon status on D_stem has indirectly been assessed by identifying plant fruit load to interact with D_stem and D_stem-derived plant water status indicators such as maximum daily shrinkage (MDS) (Intrigliolo and Castel, 2007; De Swaef and Steppe, 2010). Because plant fruit load affects the phloem sugar unloading rates, it consequently affects the stem carbon status. To allow the use of D_stem-derived plant water status indicators in irrigation scheduling, distinction must be made between water and carbon status effects when interpreting D_stem data.

The present experiment aimed at dividing the overall D_stem response of tomato plants, growing under natural conditions, into its two main effectors: plant water and carbon relations. Therefore, we compared two independent modelling approaches to investigate the dynamics of sucrose loading and the carbon status of the tomato plant in relation to variations in D_stem. One approach consisted of simulating concentrations of sucrose and storage of carbohydrates and sucrose export from tomato leaves based on photosynthesis and sugar metabolism kinetics previously described. The second approach involved simulation of variables that are difficult to measure continuously such as phloem sucrose concentration and hydrostatic potential based on stem diameter variations and sap flow rates using mechanistic flow-resistance model equations. As such, the hypothesis of the ‘one common assimilate pool’ for tomato was tested.

MATERIALS AND METHODS

To validate the results of the experiment described below, an additional experiment was carried using a different variety, details of which are given in the Supplementary Data.

Plant material and experimental set-up

Tomato plants (Solanum lycopersicum ‘Cappricia’) were grown in a greenhouse compartment (96 m²) at the Wageningen UR Greenhouse Horticulture experimental station Bleiswijk, the Netherlands. Plants were sown on 1 July 2010, grafted on the rootstock ‘Maxifort’ and transplanted into rockwool slabs on 29 July 2010 at a plant density of 2·5 m⁻². Leaves under the lowest ripe truss were removed and the lowest part of the stem was horizontal, as is common practice in tomato. The leaf area index (LAI) was on average 2·2, resulting from an average plant leaf area of 0·87 m². Two plants were selected to be continuously monitored, both located at the centre of the compartment.

Micrometeorological measurements

Photosynthetically active radiation (PAR) was measured with a quantum sensor (Li-190S, Li-COR, Lincoln, NE, USA) in the greenhouse above the plant tops. Relative air humidity (RH) and air temperature (T) were measured using an integrated relative humidity sensor (Type HIH-3605-A, Honeywell, Morristown, NJ, USA), inserted in a radiation shield at approx. 1·5 m above the ground. Vapour pressure deficit (VPD) of the air was calculated based on measurements of T and RH, as the difference between the air's potential saturated vapour pressure value and actual value (Jones, 1992). Furthermore, ambient CO₂ concentration (C_a) in the greenhouse was measured (Model GMM-221, Vaisala, Helsinki, Finland). C_a in the greenhouse ranged between 600 p.p.m. at night and 800 p.p.m. during the day (data not shown).

Plant physiological measurements

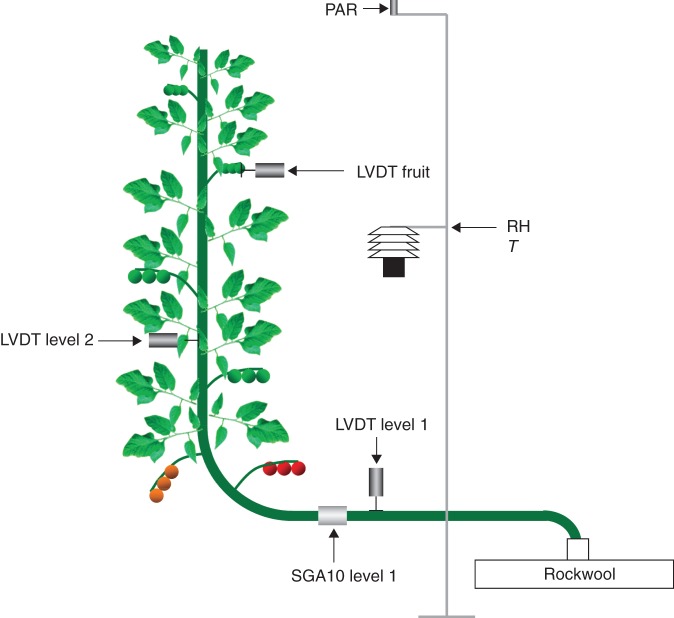
Sap flow rates (F_stem) were continuously measured using heat balance sap flow sensors (SGA10-WS, Dynamax Inc., Houston, TX, USA) installed below the lowest leaf. Sensors were wrapped in aluminium and bubble foil according to the installation manual to avoid interference from external temperature variations and radiation with the heat-based measurements (van Bavel and van Bavel, 1990). Stem diameter (D_stem) variations were recorded using LVDTs (2·5 DF, Solartron Metrology, Bognor Regis, UK) that were positioned just below or above the sap flow sensors as was practically feasible. Variations in D_stem were additionally measured four leaves higher up the plant and variations in fruit diameter (D_fruit) were measured on one fruit at a distance of approx. 1 m from the lowest leaf. The LVDT sensors were installed on the stem and the fruit by using custom-made stainless steel holders and were tested for temperature effects by installing them on a 12-mm-thick aluminium rod over a temperature range of 15–40 °C. This test showed that temperature effects were small (approx. 0·2 µm °C⁻¹) and therefore no temperature correction was applied. The initial values of D_stem and D_fruit were measured using an electronic calliper (Table 1). A summary of the sensor installation is given in Fig. 1.

Table 1.

Parameter values and initial conditions of the flow and storage model for two levels of two plants: level 1, below the canopy; level 2, within the canopy (four leaves higher)

	Plant 1		Plant 2
Parameter	Level 1	Level 2	Level 1	Level 2
Dstem(0) (mm)	12·67	17·07	14·81	13·90
Dfruit(0) (mm)	42·61		41·23
kphloem (h−1)	8·6 × 10−3
ɛ0 (m−1)	787	1231	1043	1016
φphloem(0) (MPa−1 h−1)	56·86 × 10−5	123·90 × 10−5	6·40 × 10−5	237·50 × 10−5
Rxylem (MPa h g−1)	0·003	0·004	0·003	0·004
L (m)	2·1
b (dimensionless)	0·9
r (MPa h g−1)	0·1
Γphloem (MPa)	0·3
Ψtotmedium (MPa)	–0·1
Cphloem(0) (g g−1)	0·08873
kfruit (h−1)	0·0035

D_stem(0): initial stem diameter; D_fruit(0): initial fruit diameter; k_phloem: parameter describing time dependency of phloem cell-wall extensibility; ɛ₀: proportionality constant for the bulk elastic modulus; φ_phloem(0): parameter describing the time dependency of the cell-wall extensibility; R_xylem: hydraulic resistance in the xylem; L: length of the considered stem compartment; b: proportion of inelastic tissue; r: radial hydraulic resistance between the xylem and the phloem tissue; Γ_phloem: threshold hydrostatic potential at which wall yielding occurs; Ψ^tot_medium: water potential in the rooting medium; C_phloem(0): sucrose concentration at the start of the simulation; k_fruit: parameter describing the time dependency of fruit cell-wall extensibility. D_stem(0) and D_fruit(0) and parameter values L and b were defined based on measurements; R^x, r, Γ_phloem and Ψ^tot_medium were adopted from earlier studies (De Swaef and Steppe, 2010; De Swaef, 2011) whereas the other parameters were estimated via automatic calibration.

Fig. 1.

Schematic overview of the sensor installation on the plant: linear variable displacement transducers (LVDT) to measure stem and fruit diameter, heat balance sap flow sensor (SGA10) to measure plant water uptake rates, relative humidity (RH), temperature (T) and photosynthetically active radiation above the canopy (PAR).

All sensor signals were logged (CR1000, Campbell Scientific Inc., Logan, Utah, USA) at 30-s intervals and averaged every 5 min.

Sugar and starch analyses

Leaf samples for sugar and starch analysis were collected at a height of approx. 1 m above the lowest leaf from surrounding plants at several times during the day and night on 13, 14, 21 and 22 October 2010. Four samples were taken in each sampling period and all samples were immediately frozen in liquid nitrogen and stored at –80 °C. Soluble sugars were extracted from the ground leaf samples with 80 % ethanol at 45 °C for 3 h, followed by centrifugation at 5000 g for 5 min. Glucose, fructose and sucrose were quantified using an Agilent 1100 high-performance liquid chromatography (Santa Clara, CA, USA) system coupled to an Alltech 3300 electrochemical light scattering detector (IL, USA) using acetonitrile/water (75 : 25) as eluents (Pollet et al., 2011). The remaining ethanol-insoluble material was washed twice with 80 % ethanol and the residual pellet was treated with 1 m HCl for 2 h at 95 °C to achieve starch hydrolysis. Starch content, expressed as glucose equivalents, was determined spectrophotometrically (Genesys 10UV, Spectronic Analytical Instruments, Leeds, UK) at 340 nm by the enzymatic reduction of NADP⁺.

At the end of the experiment total plant leaf area, stem length, leaf dry and fresh weight were destructively measured.

MODEL DESCRIPTION

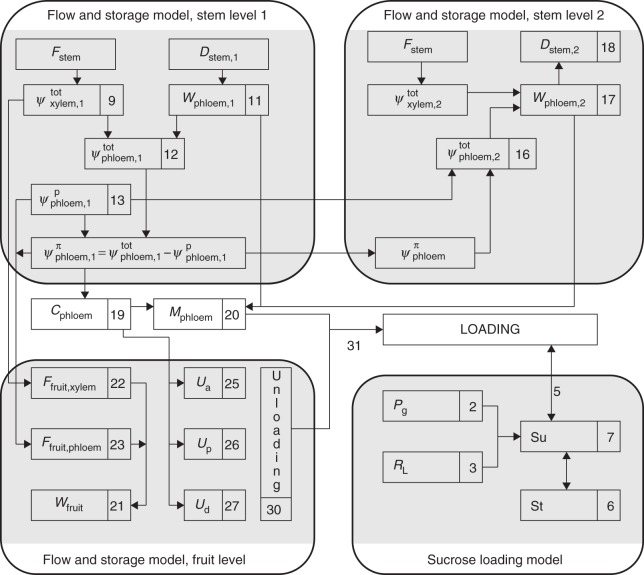
In the present research we used two independent models, hereafter referred to as the sucrose loading and the flow and storage models (Fig. 2). The sucrose loading model uses microclimatic data to calculate photosynthesis rates and the distribution of carbon for export and (temporary) storage. The flow and storage model uses sap flow and stem diameter variations as input variables and calculates the total, hydrostatic and osmotic water potential in different stem compartments. Based on the sugar content of the phloem, derived from the osmotic potential, and the sugar unloading rate, derived from the fruit sub-model (Liu et al., 2007), the loading rate of sugar into the phloem is calculated.

Fig. 2.

Scheme of the different components in the flow and storage model and the sucrose loading model. Numbers refer to the equations in the text, and arrows indicate connections between different equations and sub-models. Parameter explanations are given in the ‘Model description’ section of the text.

Sucrose loading model

To calculate the overall plant photosynthesis rate, the vertical profile of PAR was taken into account. Therefore, the plant canopy was virtually divided into three leaf layers (i = 1, 2, 3), each of them accounting for one-third of the total leaf area. LAI_i was then the leaf area index above the middle of leaf layer i (m² m⁻²): LAI₁ equalled 5/6 of the total LAI, whereas LAI₂ and LAI₃ equalled 3/6 and 1/6 of the total LAI, respectively. PAR was then calculated for the three layers assuming exponential light extinction (Monsi and Saeki, 2005):

(1)

where PAR₀ is the PAR (mmol m⁻² h⁻¹) measured above the canopy and k_L the light extinction coefficient. Based on the calculated PAR_i and the measured ambient CO₂ concentration (C_a in p.p.m.) gross photosynthesis rates (P_g in mmol CO₂ m⁻² h⁻¹) were calculated per leaf layer using the rectangular hyperbola describing single leaf photosynthesis (Acock et al., 1978; Jones et al., 1991; Bertin and Heuvelink, 1993):

(2)

where α is the leaf photochemical efficiency (mmol CO₂ mmol⁻¹ PAR) and β is the CO₂ use efficiency (mmol CO₂ m⁻² h⁻¹ p.p.m.⁻¹).

Leaf respiration (R_L in mmol m⁻² h⁻¹) was calculated as described by Gary (1988a, b) to account for the effect of changes in carbon availability and temperature:

(3)

and

(4)

where R_L,max is the maximum leaf respiration rate (mmol CO₂ m⁻² h⁻¹), Su the leaf sucrose concentration (mmol m⁻²), St the concentration of storage carbohydrates (i.e. starch and hexoses; mmol sucrose equivalents m⁻²), K_0·5 the total carbon concentration at which R_L equals half of R_L,max (mmol sucrose equivalents m⁻²) and T the temperature (°C).

Net photosynthesis rates (P_n) per leaf layer were calculated as the difference between P_g and R_L. The overall plant photosynthesis rate was then the weighted average of P_n in the different leaf layers.

As sucrose is known to be the main transport sugar in tomato and in many other plant species (Ho, 1976; Komor, 2000; Geiger et al., 2000), we only considered loading of sucrose. Consequently, all of the following variables are expressed in sucrose equivalents. Because tomato is an apoplastic loader (van Bel, 1993; Kingston-Smith et al., 1998), loading of the phloem (Load, in mmol m⁻² h⁻¹) is dependent of enzyme activity. To describe loading rate we opted to use a saturable Michaelis–Menten component in combination with an unsaturable component obeying first-order kinetics (Lalonde et al., 2003):

(5)

where V_max,L and K_M,L are the Michaelis–Menten constants (mmol m⁻² h⁻¹ and mmol m⁻², respectively) and k₁ is the first-order rate constant (h⁻¹).

To include the contribution of starch metabolism into the loading dynamics a general formula was used, which allowed simulation of different dynamics such as the Michaelis–Menten kinetics for starch synthesis from a sucrose substrate, sucrose concentration-dependent inter-conversion between starch and sucrose with a target sucrose concentration (Su₀ in mmol m⁻²) and starch concentration-dependent hydrolysis (Lacointe and Minchin, 2008):

(6)

where V_max,St and K_M,St are the Michaelis–Menten constants, k₂ the inter-conversion constant (h⁻¹) and k₃ the hydrolysis constant (h⁻¹).

The resulting rate of change in Su is then given by (Lacointe and Minchin, 2008):

(7)

where P_n was divided by 12 because the expression of Su was in mmol sucrose equivalents m⁻² h⁻¹, whereas P_n was in mmol CO₂ m⁻² h⁻¹.

These equations ultimately describe the overall gain or loss in leaf carbon as:

(8)

Flow and storage model

The stem of the tomato plant was divided into two compartments, corresponding to the installation of the D_stem sensors: level 1 was the lower (older) stem part and the overall response was described by the sensor installed below the canopy, whereas level 2 was the upper (younger) stem part and was described by the sensor installed at a height of approx. 1·5 m.

The model equations were arranged in such a way that both F_stem and D_stem measured at level 1 could be used as input variables. Subscripts were added to the notation if the variables or parameters were specific for level 1 (subscript 1) or level 2 (subscript 2).

F_stem was used to simulate the diurnal dynamics in stem xylem water potential (Ψ^tot_xylem):

(9)

where Ψ^tot_medium is the total water potential of the rooting medium (MPa) and R_xylem,1 the hydraulic resistance between the rooting medium and the stem at level 1 (MPa h g⁻¹). As the plants were well-watered, Ψ^tot_medium could be assumed constant for the rockwool-growing medium and effects of cavitation or root uptake capacity on R_xylem,1 are not accounted for (Table 1).

When assuming a round tomato stem, the relationship between initial water content of the phloem [W_phloem,1(0) in g] and the initial D_stem,1 [D_stem,1(0)] can be expressed as:

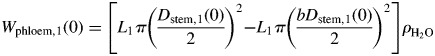(10)

where L₁ is the length of the considered stem compartment, b is the proportion of the inelastic tissue for D_stem,1 and ρ_H2O is the density of water (10⁶ g m⁻³). Assuming that the inelastic tissue shows no growth nor variation for the simulation period, the variations of W_phloem,1 can be expressed as:

(11)

Because we assume that phloem water transport to the fruits is compensated for by phloem water coming from the leaves, dW_phloem,1/dt corresponds to the flow of water between xylem and phloem at stem level. The total water potential of the phloem tissue (Ψ^tot_phloem,1) can thus be calculated in analogy with eqn (9):

(12)

where r was the hydraulic resistance between the xylem and the phloem tissue (MPa h g⁻¹).

The hydrostatic potential of the phloem tissue (Ψ^p_phloem,1) could be derived from W_phloem,1 based on the combination of plastic and elastic deformation when Ψ^p_phloem,1 exceeds the threshold at which wall yielding occurs (Γ_phloem) (Lockhart, 1965; Ortega, 1985; Proseus et al., 1999; Steppe et al., 2006):

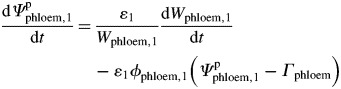(13a)

or based on only elastic deformation when Ψ^p_phloem,1 is lower than Γ_phloem:

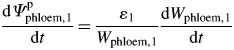(13b)

where ɛ₁ is the bulk elastic modulus of the phloem tissue (MPa), ϕ_phloem,1 the cell-wall extensibility (MPa⁻¹ h⁻¹) and Γ_phloem the threshold Ψ^p_phloem at which wall yielding occurs (MPa).

ɛ has been suggested to be proportional to Ψ^p_phloem and D_stem (Génard et al., 2001; Steppe et al., 2006; De Schepper and Steppe, 2010; De Swaef and Steppe, 2010):

(14)

where ɛ_0,1 is a proportionality constant (m⁻¹).

Because the current research aims at describing D_stem over a longer period, the effect of stem age was taken into account in the calculation of φ_phloem,1, which has already been suggested for tomato and mango fruit (Léchaudel et al., 2007; Liu et al., 2007):

(15)

where ϕ_phloem,1(0) (MPa⁻¹ h⁻¹) and k_phloem (h⁻¹) are parameters describing the time dependency.

The osmotic potential of the phloem tissue (Ψ^π_phloem,1) was calculated as the difference between Ψ^tot_phloem,1 and Ψ^p_phloem,1.

Ψ^tot_xylem,2 was calculated with eqn (9), again using the F_stem data measured below the lowest leaf, but with a different R_xylem. Although it is possible that the actual F_stem above the fourth leaf differed slightly from F_stem measured at level 1, the magnitude of this error is expected to be small, as the leaves located between both levels were the oldest and most shaded ones. Consequently, their contribution to the total plant transpiration was assumed to be small.

Based on the ‘one common assimilate pool’ concept of Heuvelink (1995), Ψ^π_phloem was assumed to be equal for the entire stem (Ψ^π_phloem = Ψ^π_phloem,1) and could therefore be used to calculate Ψ^tot_phloem,2:

(16)

Subsequently, W_phloem for the second stem level was calculated by rearranging eqn (12):

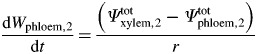(17)

Rearranging eqn (11) allows us to calculate D_stem,2:

(18)

ɛ₂, ϕ_phloem,2 and Ψ^p_phloem,2 for the second stem level were calculated using eqns (14), (15) and (13), respectively.

Based on Ψ^π_phloem, the sucrose concentration (C_phloem in g g⁻¹) and the sucrose content (M_phloem in g) were calculated:

(19)

and

(20)

where 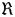is the universal gas constant (8·31 MPa g mol⁻¹ K⁻¹), T temperature (°C), MM_su the molar mass of sucrose (342·3 g mol⁻¹) and ΣW_phloem the sum of W_phloem of level 1 and 2.

In the reproductive stage of a tomato plant, fruits can be considered to be the dominating sinks for assimilates (e.g. Ho et al., 1989). To estimate the amount of sucrose that was unloaded from the phloem, the model of Liu et al. (2007) was coupled to the flow and storage model. This biophysical model mechanistically describes the water and carbon import in the fruits during the period of cell elongation [after approx. 10 days after anthesis (DAA)] and was originally developed for peach (Fishman and Génard, 1998). The model presents the fluxes of water and carbon between the plant and the fruit via xylem and phloem transport, and the loss of water and carbon to the atmosphere through fruit transpiration and respiration. Consequently, the accumulation of water in fruits is calculated as:

(21)

where W_fruit is the fruit water content (g), F_fruit,xylem and F_fruit,phloem are the water import via the xylem and the phloem, respectively (g h⁻¹), and T_fruit is fruit transpiration (g h⁻¹).

F_fruit,xylem and F_fruit,phloem are calculated based on flow resistance concepts:

(22)

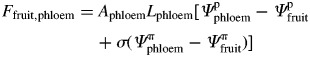(23)

A_xylem and A_phloem are the surface (cm²) of exchange between the vascular networks entering the fruit and the fruit compartment, and are assumed to be proportional to the fruit surface area according to a coefficient (a). σ is the reflection coefficient of the membrane separating the fruit from the phloem conductive tissue and is assumed to be time-dependent:

(24)

where τ is a constant parameter (h⁻²) and t is the time (h) since the start of the cell elongation phase at 10 DAA.

Sucrose import in the fruits was calculated as the sum of active (U_a, g h⁻¹), passive mass-flow (U_p, g h⁻¹) and diffusion (U_d, g h⁻¹) transport:

(25)

(26)

(27)

where M_fruit is the fruit dry matter content (g), v_m is a kinetic constant (g sucrose g⁻¹ dry matter h⁻¹) and K_M is the Michaelis–Menten constant (g g⁻¹). Additionally, an effect of fruit age was included and was described by the constants δ and f and the initial fruit dry weight M_fruit(0) (g). Furthermore, C_fruit is the fruit sugar concentration (g g⁻¹ fresh weight) and p_s is the solute permeability coefficient (g cm⁻² h⁻¹).

The accumulation of carbon was calculated as the difference between the import of sucrose and respiration.

Finally, Lockhart's equation (1965) is then used to assess the relationship between the fruit hydrostatic water potential (Ψ^p_fruit, MPa) and the accumulation of water:

(28)

where ϕ_fruit is the fruit cell-wall extensibility (MPa⁻¹ h⁻¹) and Γ_fruit is the threshold Ψ^p_fruit at which wall yielding occurs (MPa).

In addition to eqns (24) and (25), fruit age is taken into account in a third way by assuming an exponential decrease of ϕ_fruit during tomato fruit growth:

(29)

where ϕ^max is the double of the maximum cell-wall extensibility (MPa⁻¹ h⁻¹) at t = 0 (i.e. at 10 DAA) and k_fruit is a time constant (h⁻¹).

Because the plants carried on average six trusses of different age with three fruits per truss, this was represented in the model by 18 fruits in total, divided in six groups in which the fruits had the same age. The six fruit ages used at the start of the experiment were 10, 18, 26, 34, 42 and 50 DAA in order to attain a rather continuous distribution between setting fruits and ripe fruits. The total amount of sucrose that was unloaded from the phloem was then calculated as the sum of the sucrose accumulation in the 18 fruits:

(30)

The loading rate (g h⁻¹) could then be calculated based on the mass balance of the stem:

(31)

Model simulation and calibration

A fourth-order Runge–Kutta numerical integrator with a fixed time step (0·01 h) was used for solving the model differential equations. Automatic model calibration was done using the simplex method, originally developed by Nelder and Mead (1965), to minimize the sum of squared errors between the measured and simulated D_stem,2 and the measured and simulated D_fruit. Measurements of D_fruit were done on the second truss (DAA = 18) and used to estimate the parameter value of k_fruit, to which modelled D_fruit had proven to be the most sensitive (data not shown). Other parameters from the fruit sub-model were adopted from Liu et al. (2007). Parameters ɛ_0,1, ɛ_0,2, ϕ_phloem,1(0), ϕ_phloem,2(0), k_phloem and C_phloem(0) were automatically calibrated, taking into account the physically acceptable boundaries. To comply with the identifiability criteria, R^x was given a representative value based on earlier measurements of Ψ^tot_xylem in tomato (De Pauw et al., 2008; De Swaef and Steppe, 2010). For the sucrose loading model, parameter values were estimated by minimizing the sum of squared errors between measured and simulated leaf sucrose and starch concentrations. Parameter values that were measured, adopted from the literature or obtained by automatic calibration, are given in Table 1 and 2.

Table 2.

Symbols, definition and estimated or literature value of the sucrose loading model parameters

Parameter (unit)	Definition	Value
α (mol CO2 mol−1 PAR)	Leaf photochemical efficiency	0·0645
β (mmol CO2 m−2 h−1 p.p.m.−1)	CO2 use efficiency	0·252
kL (dimensionless)	Light extinction coefficient	0·58
LAI1 (m2 m−2)	Leaf area index above level 1	1·6667
LAI2 (m2 m−2)	Leaf area index above level 2	1·1
LAI3 (m2 m−2)	Leaf area index above level 3	0·3333
K0·5 (mmol sucrose eq. m−2 h−1)	Total leaf carbon concentration at which RL = RL,max/2	11·68
k1 (h−1)	First-order rate constant for phloem loading	3·31 × 10−8
k2 (h−1)	Kinetic parameter for inter-conversion of sucrose and storage carbohydrates	1·2895
k3 (h−1)	Kinetic parameter for hydrolysis	0·1555
Su0 (mmol sucrose eq. m−2)	Target sucrose concentration	0·388
Vmax,L (mmol sucrose eq. m−2 h−1)	Michaelis–Menten constant for phloem loading	2·95
KM,L (mmol sucrose eq. m−2)	Michaelis–Menten constant for phloem loading	11·2
Vmax,St (mmol sucrose eq. m−2 h−1)	Michaelis–Menten constant for starch synthesis	3·16 × 10−2
KM,St (mmol sucrose eq. m−2)	Michaelis–Menten constant for starch synthesis	37·5

Parameter values for α, β and k_L were adopted from Bertin and Heuvelink (1993), K_0·5 from Gary (1988b), K_M,L from Sovonick et al. (1974) and values for LAI were assessed by definition. Other parameters were estimated via automatic calibration using measurements of sucrose, starch and hexose concentrations.

Model implementation

The model, consisting of a set of algebraic and differential equations, was implemented and solved numerically using the modelling and simulation software package PhytoSim (Phyto-IT BVBA, Mariakerke, Belgium). This environment allows model implementation, simulation, calibration, sensitivity analysis, identifiability analysis and data acquisition.

RESULTS

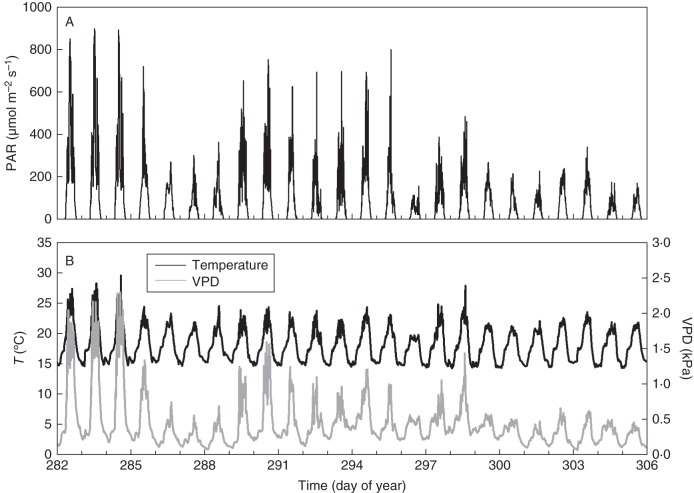
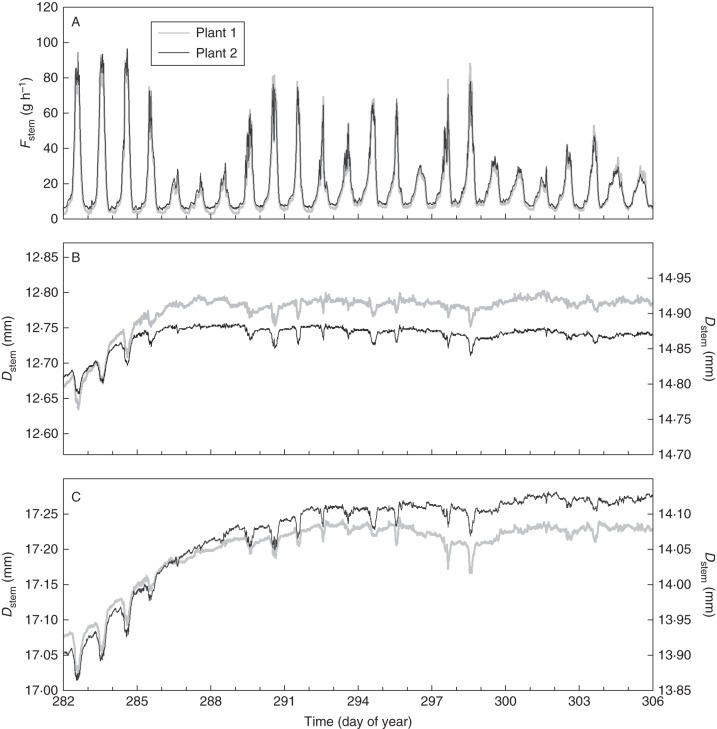
Alternating periods of relatively high and very low PAR during the 24-d experiment (9 October to 1 November 2010) are shown in Fig. 3A. Consequently, VPD and air temperature (T) showed similar variations to PAR, although variations in T were less pronounced (Fig. 3B). F_stem was very similar for both selected plants for the entire study period (Fig. 4A). D_stem measured in the canopy (Fig. 4C) showed a moderately higher overall growth compared with D_stem measured below the canopy for both plants (Fig. 4B): on average 0·19 mm vs. 0·09 mm, respectively. Absolute values of D_stem differed between plants as well as within each plant. However, because the plant physiological information is in D_stem variations instead of in absolute values, this variability is not important. All of the measured stems showed a markedly faster growth rate during the first 4 d compared with the rest of the period. Moreover, periods of faster and slower stem growth rates of plant 1 corresponded remarkably well with those of plant 2.

Fig. 3.

(A) Photosynthetically active radiation (PAR) and (B) temperature (T) and vapour pressure deficit (VPD) for a 24-d period from 9 October to 1 November 2010.

Fig. 4.

(A) Sap flow rates (F_stem), (B) stem diameter (D_stem) at level 1 (below the canopy) and (C) at level 2 (above the oldest four leaves) for plant 1 and plant 2 over time. In (B) and (C) data for plant 1 corresponds to the left y-axis, plant 2 to the right.

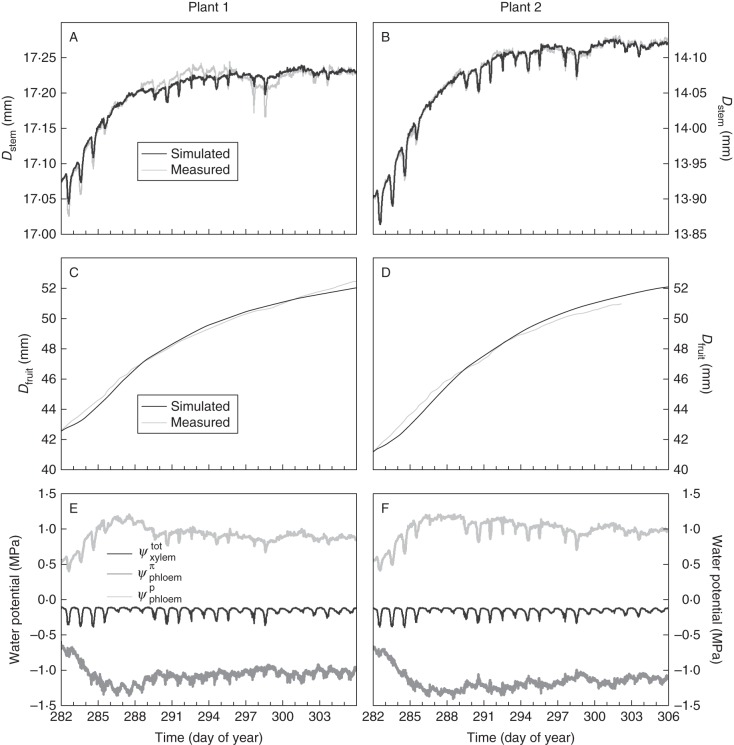
Measured and simulated D_stem on level 2, using the flow and storage model, corresponded very well (Fig. 5A, B, Fig. S2A, B). The model allowed us to describe the decrease in fruit growth rate with increasing age quite adequately (Fig. 5C, D, Fig. S2C, D). The simulations of Ψ^tot_xylem showed a strong correspondence between both plants as a result of the very similar F_stem measurements for both plants. Additionally, the simulation results for Ψ^p_phloem and Ψ^π_phloem showed a strong correspondence between both plants, with a clear increase in Ψ^p_phloem during the first 4 d, followed by a slight overall decrease for the remainder of the period. For Ψ^π_phloem, an opposite pattern resulted from the simulation. Simulated values of Ψ^p_phloem, Ψ^π_phloem and Ψ^tot_xylem are well within the range of values reported previously (Nobel, 1999; Pritchard, 2007; De Swaef and Steppe, 2010).

Fig. 5.

(A, B) Simulated and measured stem diameter (D_stem) for level 2 (above the oldest four leaves), (C, D) simulated and measured fruit diameter on the second truss (D_fruit) and (E, F) simulated xylem water potential (Ψ^tot_xylem), phloem osmotic potential (Ψ^π_phloem) and phloem hydrostatic potential (Ψ^p_phloem) for plant 1 and plant 2 plotted against time.

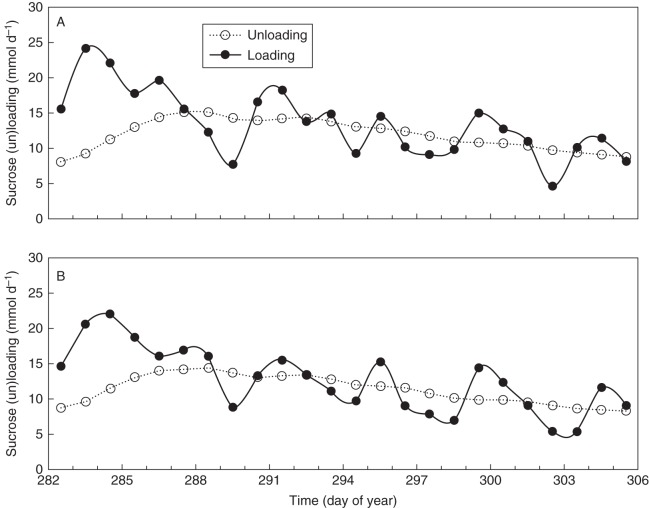
Additionally, the daily loading and unloading rates were simulated with the flow and storage model (Fig. 6, Fig. S3). For plants 1 and 2, the loading rates were consistently higher than the unloading rates during the first 6 d, whereas for the remainder of the period the values for the loading rate oscillated around the values of the unloading rate and showed a decreasing trend (Fig. 6). The unloading rates increased slightly during the first 6 d and continuously decreased for the remainder of the period.

Fig. 6.

Simulated daily loading and unloading rates using the flow and storage model for (A) plant 1 (B) and plant 2, plotted against time.

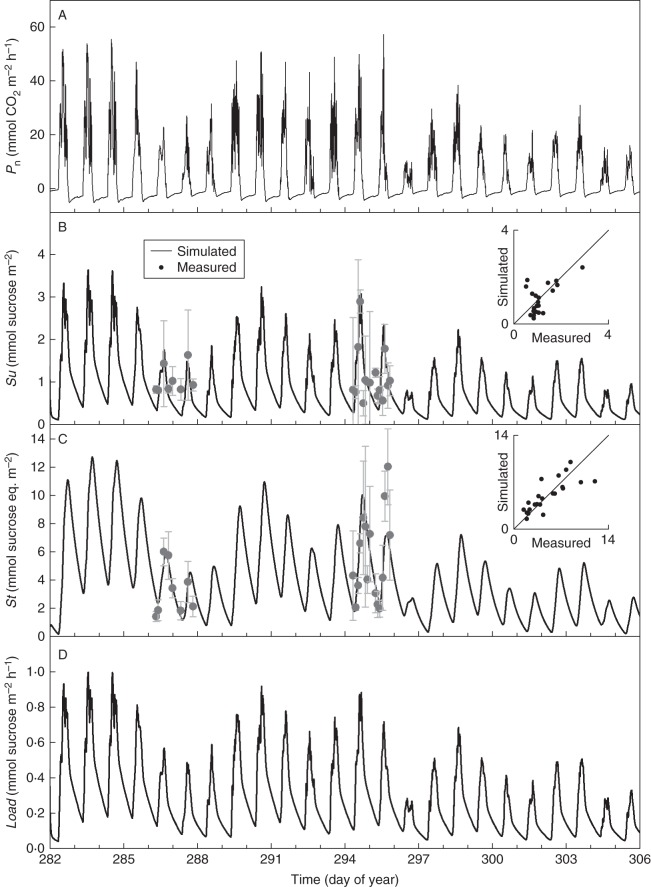
Figure 7 shows dynamics at the leaf level of net photosynthesis (P_n, Fig. 7A), sugar concentration (Su, Fig. 7B), starch concentration (St, Fig. 7C) and phloem loading rate of sucrose (Load, Fig. 7D) simulated using the sucrose loading model for the second leaf layer. Diurnal dynamics in sugar and starch concentration were measured on mature leaves on 13, 14, 21 and 22 October (DOY 286, 287, 294 and 295; Fig. 7B, C). As these leaf samples were taken from neighbouring plants, the model simulations were considered to be representative for all plants in the greenhouse compartment, and consequently the simulations were identical for plants 1 and 2. The insets to Fig. 7B and C depict the correspondence between measured and simulated sucrose and starch concentrations.

Fig. 7.

Simulated net photosynthesis rates (P_n), simulated and measured concentrations of sucrose (Su), simulated and measured concentrations of storage carbohydrates including starch and hexoses (St) and phloem loading rates (Load) for leaves in the second leaf layer, plotted against time. Error bars indicate the standard deviation on four samples.

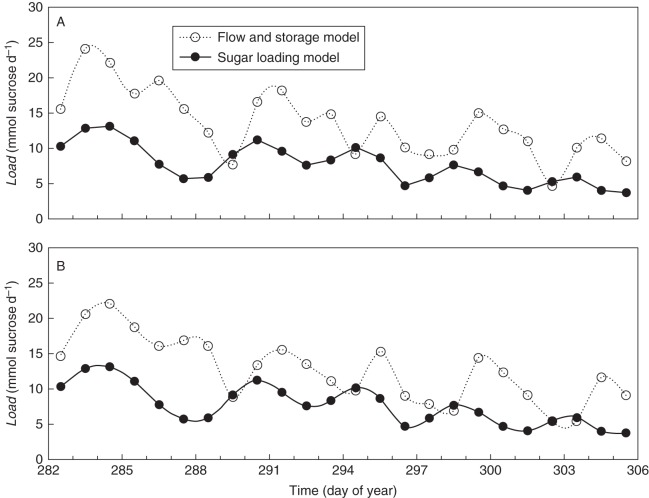
The simulated data for the daily loading rate obtained with the flow and storage model (Fig. 6) were compared with the daily loading rate calculated via the sucrose loading model (Fig. 7D) (Fig. 8). Overall, a similar pattern was found for the stem and the leaf approach for both plants, with alternating periods of increasing and decreasing loading rates (Fig. 8). Moreover, considering the average leaf area of 0·87 m² per plant, simulation results from both models are quantitatively in the same order of magnitude. However, it is worth noting that simulations based on the sucrose loading model appeared to precede the simulations of the flow and storage model by 1 or 2 d.

Fig. 8.

Comparison between daily loading rates simulated with the flow and storage model and the sucrose loading model for (A) plant 1 and (B) plant 2, plotted against time. For calculation of the loading rate via the sucrose loading model the total leaf area of 0·87 m² was taken into account.

DISCUSSION

The immediate changes in water status are well reflected in the D_stem data presented in Fig. 4 and Fig. S1. On days with higher sap flow rates, such as DOY 282–284, 290 and 298, the corresponding D_stem shows markedly deeper diurnal shrinkage compared with days with low sap flow rates, such as DOY 286–288, 297 and 299–306. Besides evaporative atmospheric demand, root water availability has been demonstrated to affect xylem water tension and consequently D_stem (De Pauw et al., 2008; Fernandez and Cuevas, 2010; Ortuño et al., 2010). In our experiment, the plants could be expected to be well watered, allowing us to assume that the direct effect of root water availability on the growth rate was limited or even absent. Consequently, refilling of the phloem tissue during the night was not hampered by the water status throughout the studied period.

On the other hand, the correspondence between variations in PAR during the studied period (Fig. 3) and the variations in growth rate (Fig. 4) highlighted the possibility of varying plant carbon status as an additional driver on top of the water relations. The effect of sugar accumulation in the phloem on D_stem variations has recently been investigated in trees by girdling studies and these studies report on an artificially induced manipulation of stem carbon status (De Schepper et al., 2010; De Schepper and Steppe, 2011). To our knowledge, the present research is the first attempt to thoroughly investigate the relationship between D_stem and carbon status under natural growing conditions. Girdling studies on trees have indicated that enhanced stem growth is supported by an increased osmotic potential in the phloem (De Schepper et al., 2010; De Schepper and Steppe, 2011) and potentially an increased starch content in the stem which could serve as a pool for metabolic energy for cell growth (Daudet et al., 2005). Because in tomato the majority of the carbohydrates stored in the stem pool are soluble carbohydrates (Hewitt and Marrush, 1986; Gary et al., 2003), it could be expected that variations in D_stem were largely due to osmotic variations in the phloem. For our model calculations, we assumed that the carbon-related variations in D_stem were solely attributed to osmotic variations in the phloem.

One common assimilate pool?

The D_stem data showed that the older stem parts (level 1) had a slower growth rate than the younger stem parts (level 2) (Fig. 4, Fig. S1), probably due to a reduced ϕ_phloem (Table 1), which agrees with previous results (De Swaef and Steppe, 2010). However, despite their different growth rate, these data profiles showed a marked correspondence between both stem levels within a plant, indicating that the variations in phloem sugar concentration occurred equally at both levels. Consequently, we assumed that the stem phloem tissue acted as one common assimilate pool in accordance with Heuvelink (1995) and that the osmotic potential was constant throughout the entire stem phloem. The striking agreement between measured and simulated D_stem on level 2 (Fig. 5, Fig. S2) indicated that the variations in Ψ^π_phloem simulated at level 1 were able to account for the variations in D_stem at level 2. Differences between D_stem at level 1 and 2 within a plant could thus entirely be attributed to differences in R^x, ϕ_phloem and ɛ. Furthermore, altering these parameters in a sensitivity analysis showed changes in either diurnal shrinkage or overall growth rate, but could not account for differences in D_stem growth rate between different days (data not shown). Consequently, this appears to justify our assumption that the osmotic potentials at level 1 and 2 were similar as well as the hypothesis of Heuvelink (1995).

Unloading versus loading rates

Sucrose unloading rates roughly varied between 0·08 and 0·15 g h⁻¹, corresponding to an average of 4·44 and 8·33 mg h⁻¹ per fruit, which is acceptable when comparing with previously reported maximum fruit growth rates for round-fruited cultivars (8·3–15·4 mg dry matter h⁻¹; Ho et al., 1983; Heuvelink and Marcelis, 1989; Jones et al., 1991). During the first 4–5 d (DOY 282–286), the calculated phloem loading rates continuously exceeded the phloem unloading rates, whereas for the remainder of the period sucrose loading oscillated around the unloading rate (Fig. 6). As such, variations in phloem loading rate over several days are less visible in the phloem unloading rate towards the fruits (see also Fig. S3). Thus, the plant seems to achieve a rather constant supply of carbon towards the fruits as a result of two attenuation processes: at the loading level by temporary storage of carbon in starch, and at the unloading level.

The order of magnitude of stem respiration was calculated based on observations of Xu et al. (1997) who measured rates of tomato stem respiration of 0·42 × 10⁻² μmol kg⁻¹ s⁻¹. This corresponds to 0·33 mg sucrose h⁻¹ for a stem of approx. 4·2 m, as was the case in our experiment. As these stem respiration rates are about 1000-fold smaller than the loading and unloading rates, these were not taken into account in the model analysis.

To estimate phloem loading rates using the sucrose loading model, we opted to use a saturable component obeying Michaelis–Menten kinetics in combination with an unsaturable component obeying first-order kinetics as was suggested to describe apoplastic loading by Lalonde et al. (2003) (eqn 5). Because the Michaelis–Menten kinetic parameters (V_max,L and K_M,L) appeared to be highly correlated, we opted to assign a fixed value to K_M,L (11·2 mmol m⁻², calculated from Sovonick et al., 1974) and to estimate V_max,L by automatic calibration based on measurements of sugar and starch concentration along with the other sucrose loading model parameters. Because the estimated first-order rate constant was small (6 × 10⁻⁵), the loading rate was predominantly described by the saturable Michaelis–Menten component. However, the simulated loading rate was approximately linearly related to the leaf sugar concentration (Fig. 7), indicating that the sugar concentration was too low to reach the saturation phase of Michaelis–Menten kinetics (eqn 5). This can be explained by the relatively low measured PAR above the canopy (Fig. 3A) and decreasing photoperiods, as this experiment was carried out during October at a latitude of 52 °N. Moreover, the measured concentrations of starch were low compared with similar measurements done during summer (0·1–2·7 mg g⁻¹ vs. 3·7 – 13·1 mg g⁻¹ f. wt). Consequently, starch reserves were insufficient to maintain the same sucrose loading rate of the first 4 d (DOY 282–285) during the three subsequent days (DOY 286–288), resulting in a reduced growth rate of D_stem (Fig. 4B, C). Because of the limited starch reserves, phloem loading rate and thus variations in D_stem were closely related to actual rates of P_n. Extending this hypothesis towards periods of large starch reserves, it could be expected that variations in daily sums of PAR would be less visible in D_stem. This finding could also be important on a broader scale, as the interpretation of D_stem data could consequently be used as a tool to detect carbon starvation. This is a topic that is of great interest in relation to drought (McDowell, 2011).

Comparison of two models

Variations in D_stem are known to respond at very short notice (i.e. minutes) to changes in plant water status (e.g. Steppe et al., 2006), whereas plant carbon status affects D_stem in its overall growth rate and shows a slower response because of attenuating processes such as temporary storage of starch in the leaves (Geiger et al., 2000; Komor, 2000).

In the past decade, several dynamic models describing plant water relationships have been developed and tested, resulting in detailed equations describing the relationship between water potential, water transport and variations in D_stem (e.g. Génard et al., 2001; Daudet et al., 2005; Steppe et al., 2006; De Pauw et al., 2008; De Schepper and Steppe, 2010). In contrast, phenomena related to carbon loading have as yet not been described in similar detail. This difference in knowledge between plant water and carbon relationships prevented us from using more detailed equations (and fewer assumptions) with respect to carbon relations: i.e. the sucrose loading model and the ‘one common assimilate pool’ assumption. This approach is justified, because D_stem responds much faster to changes in water relations than to changes in carbon relations and because the ‘one common assimilate pool’ hypothesis could not be rejected.

Daily loading rates obtained by both the flow and storage model and the sugar loading model showed a decreasing pattern over the measurement period (Fig. 8), as day length and light intensity decreased (Fig. 3). Furthermore, within this decreasing trend, local maxima and minima were noticeable for both approaches. Strikingly, the maxima and minima of the sucrose loading model preceded the flow and storage model by 1 or 2 d. Although temporal storage of carbohydrates was taken into account, loading rates simulated by the sucrose loading model closely followed the measured PAR (Fig. 3), whereas loading rates calculated via D_stem showed a delayed response. Possibly, detailed processes such as up- or downscaling loading under variable conditions were missing in the sucrose loading model. As such, including a dependency of parameters such as V_max,L, K_M,L or Su₀ to the amount of stored carbohydrates in the leaf might improve the sucrose loading model performance under different environmental conditions. Additional knowledge of the mechanisms and kinetics of carbon loading is therefore required to further extend this model and include more detailed underlying mechanisms.

On the other hand, the relatively low level of anatomical detail in the flow and storage model might have contributed to the observed differences between both models as the contribution of different stem tissues to the variations in D_stem are not well understood. Specific experiments combining novel imaging techniques such as magnetic resonance imaging with continuous measurements of D_stem will overcome these current uncertainties (De Schepper et al., 2012).

Perspectives

Continuous, sensitive measurements of variations in D_stem do not require very expensive or highly sophisticated equipment and have proven to be a valuable source of information about the carbon and water status in trees and in herbaceous plants such as tomato (e.g. Steppe et al., 2008; Villez et al., 2009; De Schepper and Steppe, 2011; Sevanto et al., 2011). The present research has demonstrated the response of D_stem under natural occurring variations in plant carbon status and the possibility of extracting this valuable information via mechanistic modelling. Besides the relatively low sensor cost and the applicability in the field, our approach allows continuous simulation of variables such as phloem sap concentration and hydrostatic potential, which are difficult to measure in a continuous and non-destructive manner (e.g. Najla et al., 2010).

Furthermore, as D_stem represents a structural response to plant functioning and provides an integrated interpretation of plant water and carbon status, it can serve functional–structural plant models that predict whole-plant photosynthesis and transpiration (Sarlikioti et al., 2011). As such we believe that this would contribute to an improved understanding of plant functioning as an individual in a crop.

D_stem in combination with mechanistic modelling of the tomato stem water and carbon relations is perfectly compatible with the virtual fruit approach suggested by Génard et al. (2007), and is therefore a valuable tool to understand the relationship between plant behaviour and fruit growth.

Finally, our approach could help to provide unambiguous plant water status information for irrigation scheduling purposes (even in many other fruit-bearing crops) as it has been shown that effects of crop load (and thus carbon status) on D_stem cause difficulties in introducing D_stem-derived variables in plant-based irrigation strategies (Intrigliolo and Castel, 2007). Comparing the mathematical prediction of D_stem, including the plant carbon relations, with the actual measured D_stem could provide the information needed to effectively control irrigation in a plant-based manner.

Conclusions

The present research has highlighted the potential of using D_stem variations to continuously monitor and interpret plant water and carbon relations under natural growing conditions. The research provided a mechanistic interpretation of the one common assimilate carbon pool in tomato as was suggested by Heuvelink (1995), by interpreting variations in D_stem recorded at different stem heights. Furthermore, the combination of measured D_stem variations and mechanistic modelling allowed us to distinguish the effects of plant carbon status on D_stem, by comparison via an independent model describing sucrose loading rates at the leaf level. Furthermore, our approach enabled prediction of dynamic variables which are difficult to measure in a continuous and non-destructive way, such as stem water potential, phloem hydrostatic pressure and phloem osmotic potential. Finally, our flow and storage model allowed simulation of dynamics in phloem sugar loading and sugar concentration.

SUPPLEMENTARY DATA

Supplementary data are available online at www.aob.oxfordjournals.org and consist of the details of an additional experiment that was carried out to validate the results obtained in the main experiment.