Dynamics of Functionalized Surface Molecular Monolayers Studied with Ultrafast Infrared Vibrational Spectroscopy

Abstract

The structural dynamics of thin films consisting of tricarbonyl (1,10-phenanthroline)rhenium chloride (RePhen(CO)₃Cl) linked to an alkyl silane monolayer through a triazole linker synthesized on silica-on-calcium-fluoride substrates are investigated using ultrafast infrared (IR) techniques. Ultrafast 2D IR vibrational echo experiments and polarization selective heterodyne detected transient grating (HDTG) measurements, as well as polarization dependent FT-IR and AFM experiments are employed to study the samples. The vibrational echo experiments measure spectral diffusion, while the HDTG experiments measure the vibrational excited state population relaxation and investigate the vibrational transition dipole orientational anisotropy decay. To investigate the anticipated impact of vibrational excitation transfer, which can be caused by the high concentration of RePhen(CO)₃Cl in the monolayer, a concentration dependence of the spectral diffusion is measured. To generate a range of concentrations, mixed monolayers consisting of both hydrogen terminated and triazole/RePhen(CO)₃Cl terminated alkyl silanes are synthesized. It is found that the measured rate of spectral diffusion is independent of concentration, with all samples showing spectral diffusion of 37 ± 6 ps. To definitively test for vibrational excitation transfer, polarization selective HDTG experiments are conducted. Excitation transfer will cause anisotropy decay. Polarization resolved heterodyne detected transient grating spectroscopy is sensitive to anisotropy decay (depolarization) caused by excitation transfer and molecular reorientation. The HDTG experiments show no evidence of anisotropy decay on the appropriate time scale, demonstrating the absence of excitation transfer the RePhen(CO)₃Cl. Therefore the influence of excitation transfer on spectral diffusion is inconsequential in these samples, and the vibrational echo measurements of spectral diffusion report solely on structural dynamics. A small amount of very fast (~2 ps time scale) anisotropy decay is observed. The decay is concentration independent, and is assigned to wobbling-in-a-cone orientational motions of the RePhen(CO)₃Cl. Theoretical calculations reported previously for experiments on a single concentration of the same type of sample suggested the presence of some vibrational excitation transfer and excitation transfer induced spectral diffusion. Possible reasons for the experimentally observed lack of excitation transfer in these high concentration samples are discussed.

I. Introduction

Thin films and molecular monolayers are of fundamental interest and they have substantial technological importance as they allow for the tuning of surface and interfacial properties in systems as varied as microelectronics,^1,2 chemical sensors,³ and catalysis.^4-7 The properties of molecular monolayers depend on the structure and dynamics of the surface attached molecules. New tools for the study of such systems are making it possible to examine their complex and varied molecular dynamics. Advances in time-resolved infrared spectroscopy permit the direct observation of ambient condition picosecond timescale dynamics of molecular functionalized surfaces.^8-14 Recently, ultrafast two-dimensional infrared (2D IR) vibrational echo spectroscopy was applied to a functionalized monolayer of catalyst molecules and observed picosecond timescale structural dynamics.⁹

Here we expand on the earlier measurements of tricarbonyl (1,10)phenanthroline rhenium chloride (RePhen(CO)₃Cl) immobilized on silica. The immobilized Re complex is a photocatalyst for the reduction of CO₂ to CO, an important reaction in closing the carbon cycle.^15-19 Due to the large IR extinction coefficient of its carbonyl modes, RePhen(CO)₃Cl is also an important model system for studying the structural dynamics of molecular monolayers and thin films through non-linear optical spectroscopy. Monolayers are extremely difficult to study spectroscopically because of their low absorptivity and correspondingly weak non-linear response functions. The large transition dipole moments of the carbonyl stretches of the Re carbonyl complex and advances in experimental methodology help overcome this limitation.

The structure and dynamics of molecular monolayers and thin films have been traditionally studied using linear infrared spectroscopy²⁰ (or electron-energy loss spectroscopy²¹), sum-frequency generation spectroscopy,²² X-ray photoelectron spectroscopy,²³ atomic force microscopy,^24,25 and scanning tunneling microscopy.²⁶ None of these techniques are inherently sensitive to the microscopic molecular dynamics of a molecular monolayer. IR and SFG methods are only sensitive to molecular dynamics through complex line shape functions which are exceedingly difficult to interpret quantitatively.²⁷ Recently, there have been advances in time-resolved SFG methods and also directly applying third-order non-linear spectroscopy, like 2D IR, to carefully designed interfaces.^8-12,28 Time resolved SFG is influenced by orientational dynamics, although the interpretation of the data can be complex.²⁹ Using 2D IR vibrational echoes and heterodyne detected transient grating (HDTG) experiments directly on interfaces has distinct experimental advantages such as inherently higher sensitivity because these techniques use lower order non-linear optical processes than SFG, although they are not specifically interface selective. HDTG can measure both vibrational lifetimes and orientational relaxation, while the vibrational echo experiments measure spectral diffusion.

Experimental methods that are sensitive to dynamics will be extremely important in the development of a molecular level understanding of immobilized homogeneous catalysts. Homogeneous catalysts that have been immobilized are an important class of catalytic systems that combine the molecular selectivity and specificity of homogeneous catalysts with the practical advantages of heterogeneous catalysts.^4-7,30 The catalytic efficacy should depend on the detailed structure and dynamics of the interfacial system.³⁰ The kinetic and thermodynamic properties governing reactive intermediate formation are determined by the interfacial structure and dynamics. Formation of reactive intermediates depends on the catalyst geometries and the dynamics that govern the transitions between reactive and un-reactive structural states. Understanding the timescales of motion in a surface functionalized monolayer of molecules with complicated structure is a challenging problem that has not been studied to any extent. Here, we will demonstrate that thin films of immobilized metal complexes undergo structural fluctuations on a timescale of tens of picoseconds.

In the present study, we measure the pure structural dynamics of RePhen(CO)₃Cl immobilized on silica through a triazole-alkane linker. The structural dynamics are studied through the time-dependence of the frequency-frequency correlation function (FFCF), a spectroscopic observable that can be obtained with 2D IR vibrational echo spectroscopy.^27,31,32 2D IR spectroscopy can measure the time-dependent correlation of the vibrational frequency.^32,33 The correlation decays due to microscopic fluctuations of the molecular system’s structure, which randomizes the frequency as the system samples all accessible structures. The timescale of the frequency fluctuations reports on the timescale of changes between structural microstates.^34,35

The FFCF can also decay due to excitation transfer between nearby molecules.^9,13,36-38 Excitation transfer most typically occurs due to dipole-dipole coupling between chromophores through the Förster mechanism.^37-40 The theory of excitation transfer induced spectral diffusion (ETISD) has recently been developed by Rosenfeld and Fayer, and a preliminary version of this theory was used to interpret the first 2D IR measurements of the RePhen(CO)₃Cl system.⁹ The theory suggested that ETISD made a non-negligible contribution to observed spectral diffusion, which had to be accounted for to obtain the structural spectral diffusion in the molecular monolayers. Although the predicted ETISD curves relied on quantitative IR spectroscopic data, several assumptions result in significant uncertainty in the predicted FFCF decays. Excitation transfer is also well known to be extremely difficult to predict accurately. Even, in the case of electronic excitation transfer, uncertainties over a factor of two can be present when the index of refraction is unknown and the impact of the local field is not accounted for.⁴¹ Given the uncertainties in the calculation of vibrational excitation transfer, a concentration study is important to determine the extent of excitation transfer in the dense two-dimensional systems studied here. A concentration study presents considerable experimental difficulty as the number of molecules probed in a monolayer is very small, orders of magnitude smaller than the number in a typical bulk solution experiment. Lower sub-monolayer concentrations further reduce the signal in the experiment.

Excitation transfer is sensitive to changes in surface density (concentration) through the r⁻⁶ dependence of the Förster excitation transfer mechanism.^39,40,42,43 Changing the surface density of the RePhen(CO)₃Cl will change the ETISD timescale through the reduced concentration parameter as described in the theories of Rosenfeld and Fayer and Baumann and Fayer.^38,44 A change in the concentration by a factor of two will result in a slowing down of the timescale of the transfer by a factor of two, which will be readily observable if there is excitation transfer. We therefore synthesize six different molecular monolayers which vary in density across a range from 1 to 2.5 × 10¹⁴ cm⁻². The 2D IR measurements of spectral diffusion show no change with concentration, which demonstrates that the observed spectral diffusion occurs solely from structural evolution of the systems. A very sensitive test for excitation transfer is ET induced anisotropy decay.⁴⁵ As an excitation jumps from one molecule to another, which in general have transition dipoles pointing in different directions, the vibrational excitation anisotropy will decay. The decay of the anisotropy is directly related to G_s(t) (the self part of the Green Functions) that gives the probability that the excitation is still on the initially excited molecule because it has not transferred to other molecules.^43-45 Polarization selective HDTG is used to measure the polarization anisotropy as a function of time. The HDTG experiments confirm that excitation transfer does not occur in the RePhen(CO)₃Cl monolayers. Therefore, the observed spectral diffusion can be assigned to structural evolution of the monolayer.

II. Experimental Procedures

A. Preparation and Synthesis of Mixed Monolayers on Silicon

Silicon substrates (University Wafer; intrinsic Si, 400 μm thickness, double side polished) were sonicated in detergent and water for 20 minutes, rinsed with de-ionized water, and sonicated in ethanol (ACROS; 99.5+%; 200 proof) for 5 minutes. The substrates were subsequently cleaned under Argon plasma and stored under de-ionized water before use.

Mixed monolayers on the Si substrates were prepared by deposition of 11-bromoundecyltrichlorosilane (ACBR GmBH; 95%) and undecyltrichlorosilane (Gelest, Inc.) from the same solution. Relative surface concentration (10%, 20%, 50%, 80%, 100% Br) was controlled by relative volumetric concentration of the solution trichlorosilane precursors. Volume ratios and mole ratios are within 0.5% of each other. Deposition was performed for 1 hour at room temperature in bicyclohexyl (Sigma-Aldrich, 99%; used as received; 11 ppm water content measured by coulometric Karl-Fischer titration) using 10 μL total trichlorosilane. After deposition the silicon substrate was sonicated in p-xylene (Sigma-Aldrich) for 30 seconds and ethanol (Sigma-Aldrich) for 30 seconds to remove un-reacted precursor. The wafers were dried by the flow of clean, dry nitrogen gas.

Nucleophilic substitution of an azide ion for the terminal bromine in the above monolayers was performed by immersion in a saturated solution of sodium azide in dimethylformamide for 24 hours. Verification of substitution was performed by observation of the azide stretch at ~2100 cm⁻¹ by infrared spectroscopy.

fac-Re(phenC≡CH)(CO₃)Cl (synthesized by standard methods)⁴⁶ was immobilized at the terminal azide sites through a copper catalyzed azide-alkyne cycloaddition (CuAAC).⁴⁷ A 2:1 DMSO:water solution of the Re metal complex (0.3 mM), Cu(SO₄)·5H₂O (0.3 mM) and TTMA (triethyl 2,2′,2″-(4,4′,4″-(nitrilotris(methylene))tris(1H-1,2,3-triazole-4,1-diyl))triacetate; 0.3 mM, synthesized by standard methods⁴⁸) was prepared and purged with N₂ for 10 minutes. The azide functionalized substrates were submerged, followed by addition of sodium ascorbate (15 mM aq., 10 equiv. per Cu). The solutions were capped for 2 days at room temperature. The substrates were removed and sonicated in 2:1 DMSO:H₂O for 10 minutes and further rinsed with DMSO and water. Verification of the success of the alkyne-azide cyclic addition reaction was performed by FT-IR.

B. Preparation and Synthesis of Mixed Monolayers on Silica-on-Calcium-Fluoride

Silica-on-calcium-fluoride substrates were prepared from 3 mm thick CaF₂ optical windows (Red Optronics, Inc.) using a Surface Technology Systems Plasma Enhanced Chemical Vapor Deposition chamber. 40 nm silica films were grown on the CaF₂ substrates in a low frequency plasma under a flow of nitrous oxide gas and silane gas at a temperature of 350 °C and a system pressure of 650 mTorr. The substrates were used after PECVD with no additional processing.

The SiO₂ coated CaF₂ windows were alkylated using trichloroalkylsilanes in the same manner as the Si substrates. The terminal bromines in the monolayers were substituted for with azide by the same protocol as for the Si substrates. The terminal metal complexes were linked to the azide functionalized monolayers by the same method as for the Si wafer. Unlike the Si wafers, as a final step to make sure all excess un-reacted metal complex is removed from the surface, the substrates are soaked in chloroform for one hour, rinsed with ethanol, and dried under a flow of dry nitrogen.

C. Infrared Absorption Spectroscopy

Absorption FT-IR spectroscopy was performed on the samples prepared by the above methods. To determine the absorptivity and estimate the surface coverage of the samples in the experimental conditions used for the non-linear optical experiments, the IR absorption spectrum was measured at zero degrees incident angle with unpolarized light. To measure the orientation of the chromophores relative to the surface, two polarization resolved measurements at s and p polarization were also made with the sample tilted at Brewster’s angle relative to the beam propagation direction. By combining the two measurements, the surface coverage can be estimated quantitatively.⁹

The two absorption spectra from the polarization resolved FT-IR measurement are base lined to remove the impact of reflection induced loss, and the absorption due to the highest frequency carbonyl band in the surface attached metal complex is extracted. The peak height in each spectrum is obtained by Gaussian fitting and the dichroic ratio, A_s/A_p, is calculated, where A is the absorptivity and s or p denotes the setting of the polarizer during the measurement. Assuming uniaxial symmetry (macroscopic effective C_∞ symmetry), the dichroic ratio is then related to the orientational order parameter 〈 S 〉 = 〈 P₂ (cos θ)〉 = 1/2 (3〈 cos² θ〉 - 1) by the following relation,^49-51

$$\frac{A_s}{A_p}={\left(1+3\left({\sin }^2\alpha \right)\left(\frac{\langle S\rangle }{1-\langle S\rangle }\right)\right)}^{-1}$$ (1)

P₂ is the second-order Legendre polynomial, α is the angle of incidence of the infrared light, θ is the polar angle between the transition dipole moment of a surface attached chromophore and the surface normal. By inversion of this relation and the assumption that the orientational distribution function is narrowly peaked, an estimate of the “average” angle can be extracted. It is important to recognize that this “average” angle is dependent on both the mean, variance and higher order moments (due to the cosine function) of the orientational distribution function.⁵⁰

Given the measurement of the orientation of the chromophores on the surface, it is possible to determine the surface coverage using the bulk extinction coefficient. The orientational information is used to account for the anisotropy of the thin film relative to the isotropic nature of bulk solution. Explicitly, from the Beer-Lambert law the surface coverage (Γ_surf) is,

$$\begin{array}{cc}\hfill {\Gamma }_{\text{surf}}& =c\times l=\frac{A_{\text{integrated}}^{\left(\text{surf}\right)}}{{\tilde{\epsilon }}_{\text{integrated}}^{\left(\text{surf}\right)}}=\frac{A_{\text{integrated}}^{\left(\text{surf}\right)}}{R{\tilde{\epsilon }}_{\text{integrated}}^{\left(\text{bulk}\right)}}\hfill \\ \hfill {\tilde{\epsilon }}_{\text{integrated}}^{\left(\text{bulk}\right)}& =\int {\tilde{\epsilon }}^{\left(\text{bulk}\right)}d\tilde{\upsilon }=\int \frac{1000{\epsilon }^{\left(\text{bulk}\right)}}{N_A}d\tilde{\upsilon }\hfill \end{array}$$ (2)

where c is molar concentration, l is path length, A denotes absorption, ${\tilde{\epsilon }}_{\text{integrated}}^{\left(\text{bulk}\right)}$ is the bulk integrated extinction coefficient expressed in terms of molecules/cm², $\tilde{\upsilon }$ is frequency in wave numbers, N_A is Avogadro’s number and R is a correction factor for the difference between isotropic and anisotropic absorption. Because the bulk extinction coefficient is known, and it is not anticipated to change significantly upon immobilization, the surface coverage can be obtained from the infrared absorption. At normal incidence the ratio of the interfacial molecular absorbance to the bulk absorbance can be derived from the square law for absorption, and is,

$$R=\frac{A_{\text{integrated}}^{\left(\text{surf}\right)}}{A_{\text{integrated}}^{\left(\text{bulk}\right)}}=1-\langle S\rangle ,$$ (3)

where S is the order parameter as above. The above method has previously yielded accurate surface coverage values as verified by inductively coupled plasma mass spectrometry (ICP-MS).⁹ It is important to note that the choice of bulk solvent for the extinction coefficient measurement makes a difference in the calculated surface density due to both chemical and electromagnetic effects of the solvent on the infrared absorption cross-section.^52,53 The ICP-MS calibration of this method agreed well with the measurement of the extinction coefficient of the symmetric carbonyl stretch of the RePhen(CO)₃Cl measured in dichloromethane.⁹ The integrated bulk extinction coefficient used was 3.06 × 10² L mol⁻¹ cm⁻², where the integration has been performed in wave numbers.

D. Atomic Force Microscopy

Atomic Force Microscopy (AFM) measurements were performed on each thin film sample prepared on SiO₂-on-CaF₂ substrates using a Park Systems XE-70 AFM in non-contact mode. Surface roughness was characterized by three different parameters,^54,55 R_q, L_c and S_dr, in several 4×4 μm patches for each sample. R_q is the r.m.s. surface height variation, L_c is the correlation length based on an estimator of the autocovariance function of the sample surface, and S_dr is the developed surface area ratio – the ratio of the actual surface area of the sample as calculated by numerical integration vs. the geometric area of the planar substrate.

E. Ultrafast Two-Dimensional Infrared Vibrational Echo Spectroscopy

Ultrafast two-dimensional infrared vibrational echo spectroscopy is a third-order non-linear optical technique that probes the structure and dynamics of vibrational resonances in the mid-infrared.⁵⁶ The theory and experimental design have been described in detail in other publications, but a brief summary is given here.³² Ultrafast mid-infrared laser pulses are generated by difference frequency mixing the output of an optical parametric amplifier that is pumped by a regeneratively amplified Ti:Sapphire laser system. Using 640 μJ of 800 nm light with a bandwidth of 15 nm, 5 μJ pulses at 2025 cm⁻¹ with a 90 cm⁻¹ bandwidth were generated. The pulses were compressed through GVD compensation to a nearly transform limited 170 fs. The 90 cm⁻¹ bandwidth enables selective pumping of the symmetric CO stretch without exciting the other two CO modes or residual azide that may remain on the surface.

The mid-IR laser pulse is split to create four laser pulses using coated ZnSe wedges. The first three are as close to 1/3 of the total laser power as possible, while the fourth is a weak local oscillator. The three beams are overlapped in time and space at the sample in a BOXCARS geometry. To enhance the signal, the third beam is focused tighter than the first two, resulting in better spatial overlap between the polarization induced by the first two laser pulses and the electric field of the third laser pulse. The three laser pulses result in a phase-matched non-linear optical signal, the vibrational echo pulse that is combined with the local oscillator pulse, which is coincident in time with the third excitation pulse, and passed through a monochromator used as a spectrograph. The frequency dependent interference between the local oscillator and non-linear optical signal is monitored through the use of a 32 element HgCdTe array. The time delays between the three incident pulses are controlled using precision mechanical delay lines. The pulse 1 and pulse 2 time delay is automatically re-timed under computer control by performing a non-resonant three pulse cross-correlation. The pulse 3 and local oscillator timing is automatically controlled by finding the maximum interference fringe in a time-domain interferometric cross-correlation measured using the square-law response of a single element HgCdTe detector. These methods produce a reduction in the timing deviation of pulses 1 and 2 to ~1 fs during all experiments, and sub-fs timing error between pulse 3 and the local oscillator. As a cycle of light at a wavelength of 5 μm is ~17 fs, these timing errors are small enough not to destroy the interference fringes being measured.

The three incident laser pulses interact with the vibrational resonance (the symmetric CO stretching mode of RePhen(CO)₃Cl) to generate a vibrational echo. The first pulse induces a vibrational coherence between the ground state and the first vibrationally excited state. A time, τ, later the second pulse drives the coherence into a population state. A waiting period of length T_w is then initiated during which the molecules undergo time evolution due to the microscopic dynamics of the molecular system. The waiting period is terminated by the arrival of the third intense infrared pulse which drives the vibrational system into a coherence which gives rise to the emitted vibrational echo pulse. The vibrational echo pulse encodes the underlying information about the molecular dynamics experienced during the waiting period. As discussed above, the vibrational echo pulse is overlapped with the local oscillator and the combined beams are dispersed and the intensity at each frequency is measured. The frequencies measured by the monochromator are denoted ω_m (the vertical axis in the 2D spectra). The amplitude of the vibrational echo signal at each ω_m is extracted and measured as a function of the duration of the coherence period τ. At each ω_m a time-domain interferogram is generated by this method. Fourier transformation at each ω_m as a function of τ results in a spectrum along the ω_τ (the horizontal axis in the 2D spectra). Plotting these spectra as a function of both ω_τ and ω_m results in a 2D IR spectrum. The ω_τ axis is the initial excitation frequency of molecular vibrations and the ω_m axis is the vibrational echo emission frequency of the same vibrations after a time T_w.

A series of 2D IR spectra recorded at different T_w’s report on the time-dependent correlation of vibrational frequencies in an ensemble of molecules. The time dependent information is contained in the change of shape of the 2D spectrum with T_w. The method yields quantitative measurements of the homogeneous broadening, spectral diffusion, and inhomogeneous broadening of the vibration under study. Homogeneous broadening is caused by ultrafast dynamics that result in motional narrowing as well as contributions from vibrational relaxation and orientational relaxation. Spectral diffusion is the time-dependent stochastic fluctuation in vibrational frequency induced by microscopic changes in the structural environment. It is characterized by a statistical autocorrelation function, the frequency-frequency correlation function (FFCF). Spectral diffusion can also be caused by vibrational excitation transfer among molecules of different frequencies.^37,38 The 2D IR spectra acquired as a function of T_w can be analyzed using the center-line-slope (CLS) method, which extracts the normalized FFCF.^27,31 Using this method, the series of 2D IR spectra are transformed into a single decay curve. The decay of the CLS gives the spectral diffusion decay time(s). The difference of the CLS from 1 at T_w = 0 gives the extent of homogeneous broadening.³¹ By combining the CLS and the linear IR absorption spectrum, the full FFCF, including the spectral diffusion and the homogeneous component, is obtained. The time span of the measurement is limited by the vibrational lifetime and the very low concentrations of the samples.

F. Polarization Resolved Heterodyne Detected Transient Grating Spectroscopy

Transient grating spectroscopy is the basis of many non-linear optical methods.^57-60 In transient grating spectroscopy, two short laser pulses are crossed in the sample. The spatial constructive and destructive interference of the two laser beams during the laser pulses creates spatially sinusoidal bleaching in the sample as more chromophores are excited in the “light” regions than in the “dark” regions. The sinusoidal spatial grating of vibrational excitations can induce diffraction in any beams that subsequently illuminate the sample as long as the bleaching lasts.⁶⁰ For vibrational transient gratings, the grating survives until vibrational relaxation has destroyed all of the contrast between the light and dark fringes. The spatial period of the grating is set by the crossing angle and wavelength. The spatial period also determines the Bragg condition for the grating. When a third beam is allowed to illuminate the sample at the Bragg angle (phase matching condition), a first order diffracted beam is generated. The sensitivity of the technique is limited by the minimal amount of diffracted light that can be detected and the amount of scattered radiation due to defects in the sample. The diffracted beam intensity is related to the modulation depth of the absorption or index of refraction of the laser induced grating;⁵⁷ when there is a miniscule absorption, there is little diffraction.

The sensitivity of the transient grating method can be improved by optical heterodyne detection,⁶¹ which is the same method used to gain phase information and signal amplification in 2D IR spectroscopy. However, in heterodyne detected transient grating spectroscopy (HDTG), the signal amplification is all that is desired, and the phase information is a confounding variable because changes in the relative diffracted beam/local oscillator phase can make the signal positive, negative, zero or any value in between. The amplitude of the HDTG signal can be recovered ignoring phase information by measuring the HDTG signal as a function of a small delay between the pulses that create the grating (or by small changes in the heterodyne timing). These changes induce an extra linear phase term at each detection frequency which modulates the output signal. By fitting the output signal at each detection frequency to a sinusoidal term plus an offset, the amplitude of the modulation can be determined. In practice, pulses 1 and 2 are fixed at τ = 0. These are the pulses that make the grating. At each delay of the third pulse (T_w) a small number of femtosecond steps are taken about this point. The maximum signal from these points, which vary sinusoidally, is the desired value of the signal at T_w. This method eliminates the unknown phase of the interference of the signal with the local oscillator that would result if T_w is just stepped out in time to sample widely space time points. Each scan is fit independently and the results are averaged, which produces the high fidelity signals presented later in the paper. Scatter is suppressed by a combination of chopping and phase cycling. The diffracted beam is chopped, suppressing scatter due to the excitation beams. Furthermore, the scatter due to the diffracted beam is suppressed by averaging repeated (once at the nominal delay and once at a half-wavelength delay further) measurements of the signal at each delay. The τ = 0 vibrational echo signal (pulses 1 and 2 at the same time), detected in the same way as a 2D IR signal, is a heterodyne detected transient grating and directly monitors vibrational dynamics excluding spectral diffusion if the laser pulse bandwidth is broader than the vibrational resonance. The τ = 0 vibrational echo signal is an HDTG signal because at this time, the first two pulses are overlapped in time and create a transient diffraction grating. By examining the Fourier transform relationships between the 2D IR signal and the HDTG signal (in the same way as is done in the projection-slice theorem), it is clear that the HDTG signal is equivalent to the transient absorption signal. The data processing routine discussed above is a way to estimate the τ = 0 signal. For resonances with anharmonicities at least as large as the linewidth (which is the case here) there is little or no interference between the 0-1 and 1-2 transitions. Therefore, using a standard 2D IR spectrometer apparatus with BOXCARS geometry it is possible to perform HDTG spectroscopy for ultra-sensitive measurement of vibrational dynamics (vibrational lifetime, excitation transfer, orientational relaxation) excluding spectral diffusion.

III. Results and Discussion

A. Characterization of RePhen(CO)₃Cl Concentration in Mixed Monolayers

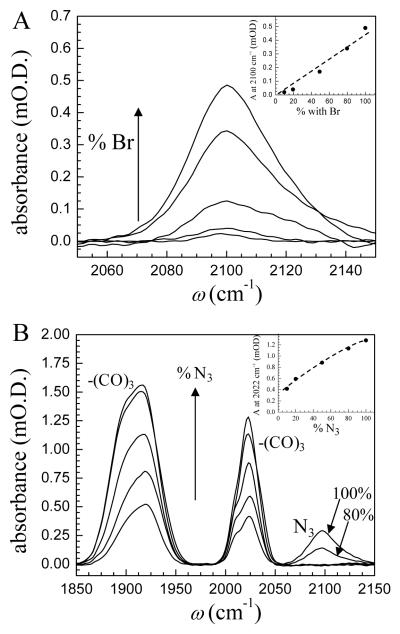
Mixed azide and hydrogen terminated undecane silane monolayers were synthesized by the methods discussed above on the native oxide of undoped silicon wafers. By varying the relative concentration of bromo-alkyl-trichlorosilanes and alkyl-trichlorosilanes, the azide concentration of the surface after nucleophilic substitution was controlled. The process was developed initially on silicon due to the simplified substrate processing. Also, since the wafer is polished on both sides (doubling the probed concentration), and the IR absorption measurement is made at Brewster’s angle (~74°; increases the effective path length) the weak azide signal is easier to measure even at low concentration on silicon native oxide. Figure 1A shows the absorption spectra of five wafers processed with different brominated/unbrominated alkyl-silane ratios ranging from 10-100%. A nearly linear trend in peak absorption is shown indicating the ability of controlling the azide concentration on the surface. Due to the difficulty in measuring the weak azide absorption, the peak intensity is used, where the signal-to-noise-plus-interference ratio is highest. The line shape is not quantitatively studied (nor is it integrated) due to the distortions from the small amount of etalon effects (which result in interference) that remain even at Brewster’s angle.

Figure 1.

(A) Absorbance spectra of 11-azido-undecyl-silane modified silicon native oxide. The 2100 cm⁻¹ absorption peak, due to the azide stretch, increases as the amount of 11-bromo-undecyl-trichlorosilane is increased in the initial deposition reaction mixture. (A - inset) Peak height of the azide stretch as a function of 11-bromo-undecyl-trichlorosilane. The trend is seen to be approximately linear, indicating that control over the azide content of the surface is achieved by simply changing the relative concentration of the functionalized and un-functionalized alkyl-trichlorosilane reagents. (B, B - inset) Absorbance spectra of the RePhen(CO)₃Cl monolayers on silicon native oxide. There are three peaks in the spectrum due to the Re complex carbonyl stretching modes. The ~2025 cm⁻¹ stretch is the tricarbonyl symmetric stretching mode. The modes at ~1895 and ~1920 cm⁻¹ are the antisymmetric modes which are nearly degenerate. Residual azide after cycloaddition is visible due to the stretch at 2100 cm⁻¹. The monolayers are synthesized with different amounts of azide as controlled by the relative concentration of the brominated precursor silane. A sub-linear trend in Re metal complex concentration is seen in the inset, indicating that there are other factors that influence the concentration of Re metal complex achieved after cycloaddition. Below 50% azide concentration on the surface, the residual azide remaining after cycloaddition is undetectable.

Subsequently the RePhen(CO)₃Cl terminated monolayers on silicon native oxide were synthesized by the methods discussed above. The wafers were studied by IR absorption spectroscopy, and the IR absorption spectra in the azide and carbonyl region are shown in Figure 1B. The RePhen(CO)₃Cl carbonyl absorptions (labeled –(CO)₃) track the trend in the azide (labeled N₃). As the percentage of azide is increased, the carbonyl absorptions increase. However, the trend in Re complex attachment is not one-to-one. As can be seen in Figure 1B, for 100% and 80% relative azide loadings, there is remaining azide absorption following the reactions to attach the Re complex. The azide is completely depleted at 50% and lower azide loadings, as shown by the absence of residual azide peaks. There are several possible reasons for the observed behavior. One very likely reason is that steric hindrance can limit the RePhen(CO)₃Cl loading on the surface because of the size of the complex. The presence of azide absorption for greater than 50% relative azide concentration before the RePhen(CO)₃Cl is added is consistent with the role of steric limitations in Re complex surface attachment.⁶² Another reason could be that a limited number of adsorption sites affects the rate of the cycloaddition reaction. The reaction is run for two days to allow for the reaction to run to completion, but the limited amount of reductant (ascorbate) available combined with the slower adsorption kinetics could hinder the completion of the reaction.

The narrowest and most isolated carbonyl absorption peak occurs at ~2022 cm⁻¹. This mode is essentially the symmetric stretch of the COs. There are two other lower frequency modes at 1896 and 1920 cm⁻¹. These modes are broader and also overlapping. Therefore, the higher frequency mode is chosen for non-linear optical study. Inspection of the line shape of the 2022 cm⁻¹ CO band shows a shoulder at ~2010 cm⁻¹. This shoulder is removed when the wafers are soaked in chloroform for one hour (see Figure 2A). The increased extent of the cycloaddition reaction, as controlled by azide coverage, primarily impacts the growth of the high frequency main band, and the low frequency band is still clearly evident in Figure 1B at low azide concentration. The lack of correlation of the shoulder intensity with the azide content suggests that the band is not due to multiple types of cycloaddition sites. The shoulder is more likely caused by un-attached Re complex trapped in the thin film. Chloroform is a good solvent of the Re complex, which is insoluble in water and ethanol (although it is soluble in DMSO and 2:1 DMSO:water, the reaction solvent), which might indicate why it is well suited for removing un-attached material. A control cycloaddition reaction was run without the presence of an alkane monolayer, and carbonyl peaks were not seen in the IR absorbance spectrum proving that precipitation or physisorption is not possible on silica only. Some RePhen(CO)₃Cl could dissolve into the alkane monolayer though, which is what we believe was removed by washes in various solvents. Cycloaddition was proven by the strong decrease in azide stretch coincident with the rise in CO stretch intensities.

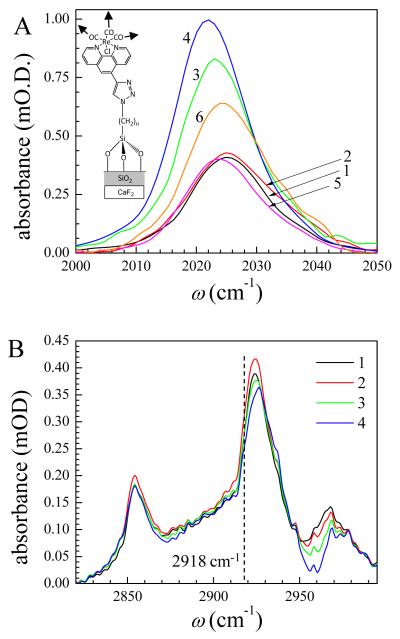
Figure 2.

(A) Symmetric stretching region of the carbonyl modes of the immobilized RePhen(CO)₃Cl on SiO₂-on-CaF₂ substrates. Sample numbers are as in Table 1. Increasing integrated peak area is due to increased Re metal complex surface density. The figure demonstrates that a significant variation in surface density is achieved through changes in the azide surface density and also variation in total immobilization process yield, as discussed in the text. (B) CH stretching region of the 11-bromo-undecyl-trichlorosilane monolayers formed as precursors for Re metal complex cycloaddition on monolayers #1-4. The layers are measured directly after deposition to prevent alkane contamination. The peak shapes and heights are comparable and the peak heights for the CH₂ antisymmetric stretch (~2925 cm⁻¹) are within ±7% of the peak height for monolayer #1, indicating there is not a significant difference in alkane monolayer surface density for the synthesized monolayers. The shift to higher frequency of the CH₂ antisymmetric stretch from the all-trans value (2918 cm⁻¹; dashed vertical line) indicates the presence of gauche defects and disorder in the monolayer.

For both linear and non-linear optical study, RePhen(CO)₃Cl was attached to SiO₂-on-CaF₂ substrates by the methods described above. Six different substrates were prepared with 10%, 20%, 50% and 100% relative azide concentrations. One of the 100% azide samples used propyl trichlorosilane as the underlying alkane layer while the rest used undecane trichlorosilane for the underlying alkane. The IR spectra in the carbonyl stretch region for the six SiO₂-on-CaF₂ samples are shown in Figure 2A. Parameters that describe the spectra are reported in Table 1. Control over the RePhen(CO)₃Cl surface density is comparable to that achieved on the Si native oxide substrates. For samples #1-4 the Re complexes were attached to the four samples at the same time in the same solutions. These samples show increasing carbonyl stretch absorbance as the initial azide concentration is increased (see Figure 2A). The surface coverage of each sample (see Table 1), as measured by the IR absorbance method discussed above, shows a sub-linear trend as was observed for the Si native oxide substrates. A second synthesis of a monolayer (sample #5) with 50% relative azide loading yielded even lower concentration of surface attached RePhen(CO)₃Cl than found on sample #1 (10% relative azide concentration). Variation in the Re complex loading of the surface can occur during the silanation step, the azidification step, or the cycloaddition reaction.

Table 1.

Parameters from linear IR spectroscopy describing the mixed monolayers synthesized for study by ultrafast infrared spectroscopy.

#	% N3	υ0 (cm−1)	max A (mOD)	<S>	θ avg.	Γ (1014 cm−2)	Δ (cm−1)
1	10	2025.1	0.41	−0.169	62°	1.23	14.9
2	20	2025.1	0.43	−0.191	63°	1.5	17.3
3	50	2023.0	0.83	−0.232	65°	2.32	14.1
4	100	2022.0	0.97	−0.232	65°	2.50	14.0
5	50	2023.8	0.40	−0.232	65°	1.08	14.9
6	100 (C3)	2024.3	0.64	−0.169	62°	1.90	15.8

υ₀ – Peak frequency of symmetric carbonyl stretch

max A – Peak absorbance of symmetric carbonyl band

<S> – Orientational order parameter

θ_avg. – Average angle assuming only a single polar angle in orientational distribution function

Γ – Surface density

Δ – Empirical FWHM found by numerical integration

The most concentrated RePhen(CO)₃Cl sample is ~2.5 times that of the lowest concentration sample. This change in concentration is more than sufficient to test whether there is vibrational excitation transfer among the Re complexes on the surface.

Samples #1-4 were prepared with bromoalkylsilane on the same day, and the CH stretching region of the IR absorption spectrum investigated immediately after the bromoalkylsilane deposition (to prevent significant alkane contamination from air or during subsequent solution phase processing). The CH IR absorption bands of these samples are shown in Figure 2B. It is apparent that the peak intensities and lineshapes are very similar. The peak heights of the CH₂ antisymmetric stretch (~2925 cm⁻¹, which is consistent with literature values for this monolayer⁶³) are all within ±7% of the peak height for sample number 1. The similarity in the peak heights suggests that the initial silanation yield is almost the same for samples #1-4. Many researchers have found that water content in the silane deposition reaction solvent can change the rate and structure of the resulting monolayer^1,64-66 We saw no evidence of island formation by AFM, and our water content was controlled by the water content of the bicyclohexyl reaction solvent which was stable. This suggests that the variation in surface coverage is either due to differing amounts of azide substitution or changes in the extent of the cycloaddition reaction. The quantitative substitution of N₃ for Br, even at surfaces, is well documented in the literature,^63,67 but future studies of these processes will be needed to fully understand the variation in yield.

The frequency of absorption of the CH₂ antisymmetric stretch has been correlated in the literature with the number of gauche defects in alkane molecular monolayers. Shifts to higher frequency from the all-trans frequency of 2918 cm⁻¹ indicate disorder and the presence of gauche defects.^20,68,69 Therefore, based on the literature CH₂ antisymmetric stretching frequency criterion, the monolayers measured here, have significant gauche defects, indicating that the monolayer has significant disorder.

Examining the table of spectroscopic parameters (Table 1) derived from the spectra shown in Figure 2A several trends are evident. First there is a weak correlation between surface coverage and transition frequency of the highest frequency carbonyl band (denoted υ₀). At high coverage, the band absorbs at lower frequency, although the shift is minor and the correlation is not perfect. This suggests that as the surface density increases changes in the structure and properties of the thin films occur. The changes in the frequency could be due to changes in the dispersive force, as the density of the layer most likely increases upon cycloaddition.⁵² The width of the bands does not change much with surface coverage, with the notable exception of sample 2 which is 3 cm⁻¹ wider. All of the thin films show substantial anisotropy as indicated by the order parameter. The order parameter can be turned into an “average” orientation angle relative to the polar axis by assuming the polar distribution is narrowly peaked as discussed in the methods section above. When this is done for each sample, the angles range from 62°-65° (see Table 1). This range is probably within experimental error.

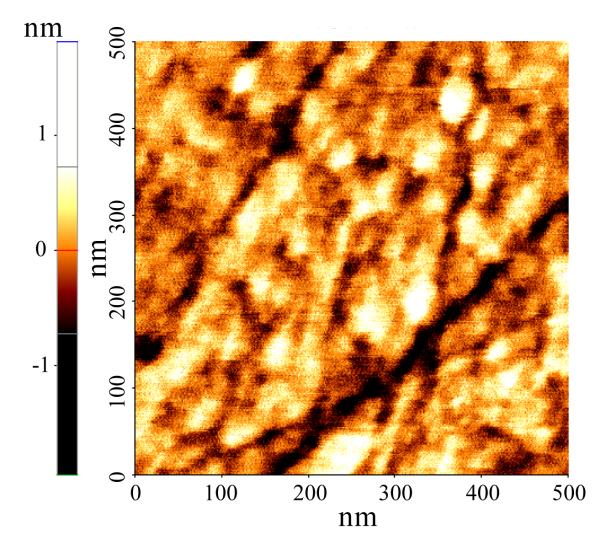
AFM was performed on all six monolayer samples and a control slide of SiO₂-on-CaF₂ prepared for this study. Figure 3 shows an example of an AFM micrograph for monolayer #4. The height variations are sub-nanometer over 500 nm, and there is significant correlation of the height for >10nm. The parameters R_q, L_c and S_dr were found to be somewhat position dependent (as is expected), so only general remarks can be made about the surfaces. The surfaces are smooth; R_q (r.m.s. surface height variation) ranges between 0.28 nm (smallest observed) to 1.6 nm (largest observed) and there is no obvious correlation with coverage or sample. The correlation lengths (L_c) are long (even for the rougher regions), and always exceed 10 nm and often exceed 20 nm. Due to the long range correlation in topographical height, the developed surface area ratio S_dr is close to 1 for all samples. Deviations from 1 are always under 1% indicating that the molecular surface layers are smooth. This also indicates that the surface loadings as estimated are expected to be the true local surface loadings. For the SiO₂-on-CaF₂ substrate (no molecular layer), the R_q value was 0.26 nm and the correlation length was ~20 nm. The excess surface area was only 0.05%.

Figure 3.

Example AFM micrograph of monolayer #4 which has a surface density of 2.50×10¹⁴ cm⁻². The color range used in the image shows variations in the range of about ±7 Å. The R_q for this image is 0.42 nm and the autocorrelation function decays on a ~10 nm length scale. Significant correlation in peak heights is visible on the 10 nm length scale in the image. No evidence of island formation is seen in this image or larger scale images.

B. Polarization Resolved Heterodyne Detected Transient Grating Spectroscopy

Heterodyne detected transient gratings with parallel polarization (just due to the laser system’s inherent polarization) were measured for each sample. The decay curves were fit with exponential decays with no offsets and the time constants, τ_VR, are reported in Table 2. With the exception of sample number 2, all of the values are within the error bars of each other. Sample 2 had a decay that was slightly faster than the rest. The vibrational lifetime is 18.6 ± 0.8 ps. Vibrational lifetimes are very sensitive to the local environment, which provides a bath of low frequency modes that aids in the vibrational relaxation, which is an energy conserving process.⁷⁰ The lack of any trend with concentration of the HDTG decay time constants indicates no significant change in the local environment of the RePhen(CO)₃Cl moiety. These measurements with parallel polarization can have contributions from both the vibrational lifetime and orientation relaxation, if any. The lack of a trend with concentration means that there is no change in the vibrational or orientational relaxation and no change in any vibrational excitation transfer processes as a function of concentration. A change in any of these processes would cause a trend in the measured time constant or the appearance of a bi-exponential decay.

Table 2.

Parameters from linear IR spectroscopy describing the mixed monolayers synthesized for study by ultrafast infrared spectroscopy.

#	Δh (cm−1)	ΔSD (cm−1)	τSD (ps)	τVR (ps)
1	1.8	14.0	30 ± 5	18.8 ± 0.6
2	2.2	16.2	43 ± 5	17.1 ± 0.6
3	1.6	13.4	30 ± 4	19.4 ± 0.6
4	1.55	13.3	35 ± 6	19.1 ± 0.4
5	1.1	14.4	42 ± 11	18.6 ± 0.4
6	1.9	14.9	50 ± 10	18.6 ± 0.4
avg.	1.7	14.4	37 ± 5	18.6 ± 0.8

Δ_h – Homogeneous linewidth (FWHM) found by simultaneous analysis of initial CLS and absorption linewidth

Δ_SD –Inhomogeneous spectrally diffusing linewidth (FWHM) found by simultaneous analysis of initial CLS and absorption linewidth

τ_VR – Vibrational lifetime measured by heterodyne detected transient grating spectroscopy

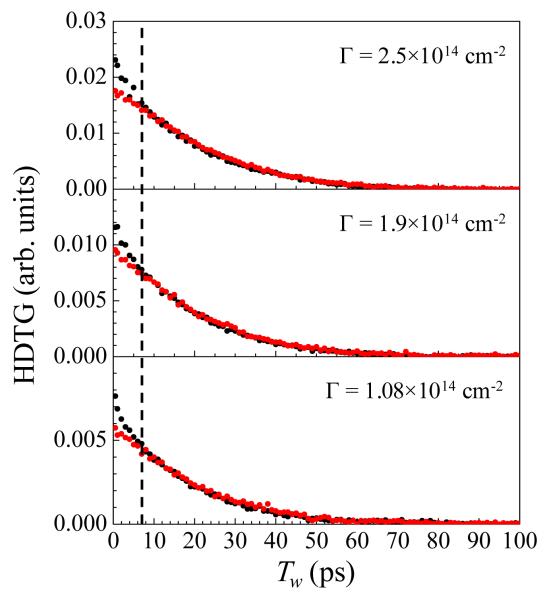
Polarization resolved HDTG experiments with both parallel and perpendicular polarizations were carried out for three of the six monolayers studied. Monolayers #4,#5 and #6 span the range of the surface densities. The decay curves of both parallel (black circles) and perpendicular (red circles) experimental decay curves are shown in Figure 4. The perpendicular decays have been scaled by a factor determined by least squares analysis such that the mean square differences between the parallel and perpendicular curves are minimized after 7 ps to permit comparison of the decays. The dashed vertical line in Figure 4 is at 7 ps. After ~7 ps (see below), in each panel the perpendicular and parallel excitation HDTG signals decay identically. There is no concentration dependence to the decays either before or after 7 ps, and as discussed above, the single exponential decay constants (>7 ps) are independent of concentration, and from the data, also independent of polarization.

Figure 4.

Polarization resolved heterodyne detected transient grating data for three different surface densities. Black circles are parallel polarization, and red circles are perpendicular polarization. A least squares fit has been performed to set the amplitudes to comparable scales, as the experiments are done with different absolute sensitivities. The curves are seen to decay with exactly the same functional form after about 7 ps (dashed vertical line). The early time discrepancy is most likely due to wobbling motions of the RePhen(CO)₃Cl head groups (see text for discussion). No change in the agreement between parallel and perpendicular decays is seen as a function of concentration.

The polarization resolved HDTG experiments demonstrate the absence of vibrational excitation transfer in these systems. The decays show no change in timescale or change in the functional form of the decays when the excitation polarization is varied for times >7 ps. Even for times less than 7 ps (discussed below), there is no concentration dependence. If there were excitation transfer, either the perpendicular polarization and parallel polarization decays would appear bi-exponential, or if the bi-exponential is not clearly resolved, would differ in time constant. The decays would be polarization dependent because the pump beams create an initial alignment in the excited transition dipoles along the laser polarization direction. This alignment causes the transient grating diffraction efficiency to be strongly polarization dependent. If an excitation jumps from one molecule to another depolarization will occur because in general the transition dipoles of the two molecules will point in different directions. As the initial transition dipole alignment decays by some dynamic process (excitation transfer or reorientation) the change in transient grating diffraction efficiency decays.⁷¹ For re-orientation, the gratings have a polarization dependent term proportional to the second-order Legendre polynomial correlation function.⁷² For excitation transfer the gratings have a polarization dependent term proportional to the self-part of the Green’s function, G_s(t), (the probability that the initially excited chromophore is still excited at a time t after excitation).⁴⁴ The amount of decay amplitude is dependent on the orientational distribution function model, but for typical models, around 30-40% of the decay amplitude in the parallel grating is due to depolarization.⁷² For orientational relaxation, the time constant depends on the model and the orientational diffusion constant,^29,72,73 whereas for excitation transfer the decay is equal to the G_s(t).^44,45 The data in Figure 4 clearly shows that after 7 ps there is no difference in the decays. Not only are the time constants the same, but the decays are indistinguishable. Prior to 7 ps, the parallel and perpendicular decays differ but show no concentration dependence. Excitation transfer is highly concentration dependent due to the r⁻⁶ dependence of the rate.^38,39,44 Previous calculation show that if vibrational excitation transfer did occur in the type of system studied here, it would take place on a 100 ps time scale.⁹ The lack of a concentration dependence and the identical decays of the parallel and perpendicular curves on the time scale on which excitation transfer might happen shows that there is no significant vibrational excitation transport. These HDTG results are confirmed by the lack of a concentration dependence in the 2D IR experiments presented below.

Because the parallel and perpendicular curves become identical at 7 ps, the process giving rise to the short time depolarization dynamics occur on an ~2 ps time scale. The lack of concentration dependence indicates that the first 2 ps small extent of depolarization that does take place is caused by orientational relaxation. The time scale is far too fast for full orientational randomization of the RePhen(CO)₃Cl head group. Given the attachment to the surface, full orientational relaxation is virtually impossible in this system, and large scale reorientation will occur on a nanosecond rather than picosecond time scale. Therefore, the small extent of time dependent depolarization is most likely caused by “wobbling-in-a-cone”^74,75 of the Re complex. Wobbling-in-a-cone is restricted incomplete orientational relaxation. Because of physical restrictions, a chromophore can only sample a limited range of angles, a cone of angles. Wobbling has been observed for vibrational excitations in highly confined systems previously.⁷⁶ Here, the fast and small extent of depolarization will occur if the RePhen(CO)₃Cl can rapidly sample a very limited range of angles.

C. 2D IR Vibrational Echo Experiments

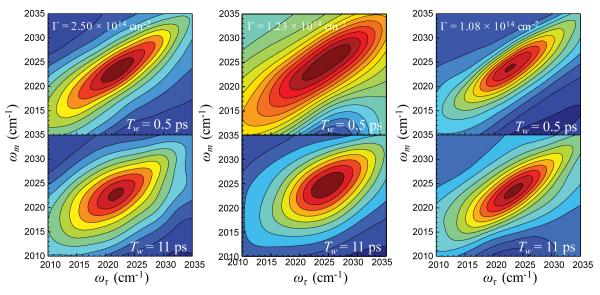
2D IR vibrational echo experiments were performed on each of the six samples with RePhen(CO)₃Cl bound to them. Figure 5 displays 2D IR spectra showing the symmetric stretch 0→1 vibrational transition region around 2024 cm⁻¹ for three of the six monolayers samples. Spectra are shown for samples #4, #1 and #5 from left to right in Figure 5. The top row is for a short waiting time, T_w = 0.5 ps, and the bottom row is for a longer T_w = 11 ps. All spectra show significant spectral diffusion by T_w = 11 ps, as indicated by the change in shape of the contours of the 2D IR spectra.

Figure 5.

Purely absorptive 2D IR contour plots for the 0→1 region of the symmetric carbonyl stretch of RePhen(CO)₃Cl as a function of surface density. Three densities are shown from left to right corresponding to samples 4, 1 and 5 in Table 1. For each density, two spectra are shown, one for the earliest waiting time, 0.5 ps, and one for the longest, 11 ps. Significant spectral diffusion relative to the early time spectra is evident for each sample.

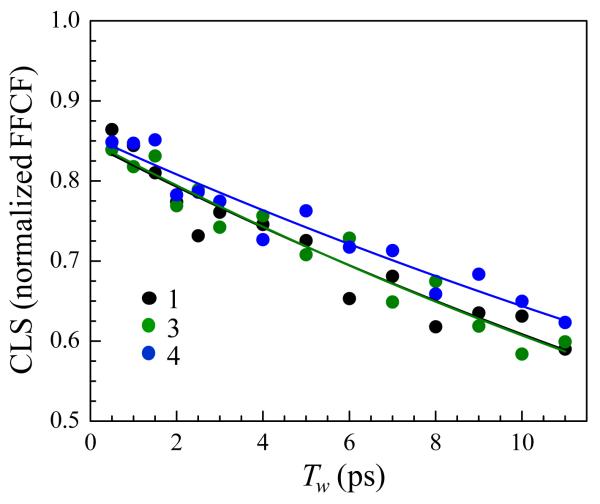
The CLS has been calculated using 2D IR spectra like those shown in Figure 5 for all six monolayers studied. As mentioned above, the CLS is a method for obtaining the FFCF from the 2D IR spectra.^27,31 The CLS is the normalized FFCF. The CLS are plotted for three of the 6 samples in Figure 6. These samples range from the highest concentration to almost the lowest concentration. The CLS are essentially the same within experimental error. Similar results are obtained for all 6 samples with the possible exception of sample #6 (see below) indicating that spectral diffusion occurs on the same timescale in all samples. Quantitative analysis of each CLS decay curve yields the FFCF, which gives the time constants and homogeneous linewidths. The FFCF results are presented in Table 1. The time constant for the pooled data is 37 ± 6 ps.

Figure 6.

The measured CLS decays for monolayers #1,#3 and #4. The points are experimental data and the solid lines are single exponential fits. The time constants and homogeneous linewidths extracted from the fits are reported in Table 1. It is evident that it is not possible to distinguish the decays, despite the large changes in surface density across the monolayers studied.

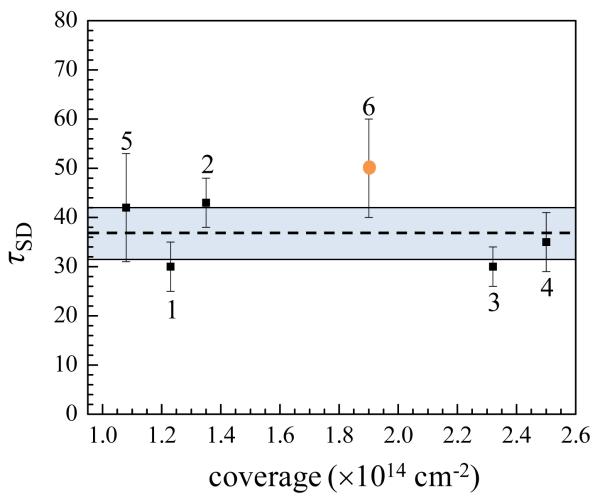
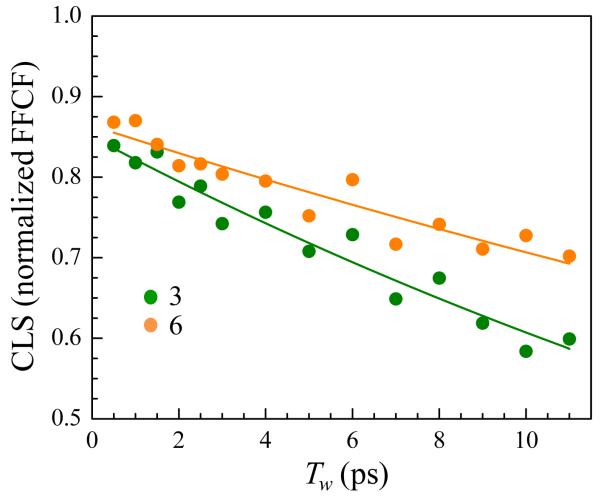
An important question is whether there is a contribution to the spectral diffusion from vibrational excitation transfer.⁹ The HDTG experiments presented above establish that there is no excitation transfer in the system, but any presence of excitation transfer can be further tested with the 2D IR measurements. An excitation transfer contribution to spectral diffusion would manifest itself as a concentration dependent spectral diffusion time constant. Figure 7 plots each measured time constant with 95% confidence intervals as a function of coverage. The sample number is given by each point, and the coverage values are given in Table 1. The dashed line is the average value, and the shaded region is the 95% confidence region for the pooled data. While there is spread in the values obtained from the different samples, given the difficulty of the measurements, the agreement in the τ_SD values for the various samples is reasonably good. Clearly there is no concentration dependence to the spectral diffusion time constant, which is consistent with the HDTG experiments that show there is no significant vibrational excitation transfer in these systems. Sample #6 (orange circle) is different from the rest in that it has a three carbon chain rather than an eleven carbon chain linking the head group to the surface. Sample #6 is the furthest from the average value. Figure 8 shows the CLS curves for sample #3 (undecyl linker) and sample #6 (propyl linker). The slopes of the two CLS curves are clearly different. It is possible that the shorter alkyl chain of sample #6 results is somewhat slower dynamics than the samples with the longer chains. However, the difference of sample #6 from the other samples is within the errors in the measurements. It is possible that future measurements may be able to determine if the difference in the dynamics with chain length is real.

Figure 7.

Spectral diffusion time constants plotted as a function of surface density. The error bars are ±2σ, i.e. about 95% confidence intervals and are the same as shown in Table 1. None of the time constants are statistically different from each other or the pooled data (shown as a light blue shaded region, the mean is the dashed central line). Sample #6, denoted by the orange dot was made from a C3 alkane linker, all other samples were made with C11 alkane linkers.

Figure 8.

The measured CLS decays for monolayers #3 (green) and #6 (orange). Symbols are experimental data, and solid lines are exponential fits. Monolayer #3 is synthesized from a C11 alkane linker, and monolayer #6 from a C3 alkane linker. The shorter linker chain sample appears to undergo spectral diffusion at a slower rate, although the difference may not be statistically significant.

That the spectral diffusion decay is independent of concentration also strongly suggests that spectral diffusion of the CO symmetric stretch in RePhen(CO)₃Cl functionalized monolayers is not driven by headgroup-headgroup interactions. As the number of headgroups decreases, the average number of nearest neighbor headgroups decreases. If the spectral diffusion were caused by fluctuations of the nearby metal complexes, then the spectral diffusion would be strongly dependent on the concentration. The lack of observed concentration dependence suggests that the structural dynamics are related to the overall environment of the thin film which solvates each headgroup. This indicates that spectral diffusion is a sensitive probe for investigating structural and dynamical changes in perturbed thin films.

D. On the Absence of Vibrational Excitation Transfer

The first 2D IR experiments on a surface bound monolayer were performed on a sample that was very similar to the ones studied here.⁹ In that report, concern about the possibility of vibrational excitation transfer was addressed theoretically. The results suggested that vibrational excitation transfer in the RePhen(CO)₃Cl vibrational chromophore linked to the SiO₂ surface could have vibrational excitation transfer occurring on a 100 ps time scale. Although it is the structural dynamics that influence many chemical and physical processes at surfaces, the nature of vibrational excitation transfer is also important as it can influence experimental observables. Structural evolution produces structural spectral diffusion. However, in the presence of excitation transfer induced spectral diffusion, it is necessary to separate the two contributions to the 2D IR observables. Calculation of the vibrational excitation transfer induced spectral diffusion is fraught with difficulties. The results presented here show that there is no vibrational excitation transfer. Some of the physical features that were not included in the excitation transfer induced spectral diffusion theoretical calculations that could result in overestimating excitation transfer are discussed here.

Alkane molecular thin films linked to RePhen(CO)₃Cl synthesized for this study are smooth, as verified by AFM. However, the films have a disordered alkane layer with significant gauche defects as verified by IR spectroscopy. The gauche defects are consistent with the literature, where C11 monolayers also showed higher CH anti-symmetric stretching frequencies than defect free monolayers.^63,68 The presence of gauche defects suggests that the monolayer could have a complex structure where the metal complexes are not necessarily ordered in a plane on top of the alkane under layer. In the theoretical calculations presented in the first study of this system, it was assumed that all of the RePhen(CO)₃Cl groups were in a plane. A thin disordered film may be a more accurate description of the thin layer.

Excitation transfer is not slowed down by surface roughness, as the samples are smooth. Surface roughness could slow down the excitation transfer because the measured surface coverage of a rough sample is much higher than the local surface coverage which is of physical relevance to the excitation transfer problem. The parameter which describes the effective local concentration is the developed surface area ratio, and this factor is essentially 1 for every sample studied here, indicating that the local concentration is equal to the macroscopically measured concentration. Furthermore, the density of the alkane films on the SiO₂-on-CaF₂ substrates are comparable as verified by IR spectroscopy, indicating the comparability across samples.

The presence of gauche defects in the alkyl chains suggests that the distribution of the chromophores in the sample is non-planar. Out of plane density of chromophores would slow down excitation transfer as the distance between chromophores would be increased over a planar sample. To examine the magnitude of this effect we have performed model excitation transfer calculations. The details of this type of calculation can be found in References 9 and 36. The input parameters are the molecular diameter, density, extinction coefficient, lifetime and quantum yield.^9,38 We have simulated the smallest possible molecular diameter (6.5 Å) for the most dense monolayer and the characteristic decay time of the excitation transfer induced spectral diffusion is about 40 ps, which would basically explain the full spectral diffusion measured. Although physically unreasonable (as other sources of spectral diffusion must also exist), this is the starting point for simulating excitation transfer in the non-planar thin film. As the thickness of the layer is increased, the excitation transfer induced spectral diffusion slows down. At 20 Å using the estimated molecular diameter of 7.75Å, the timescale is ~140 ps. Thus, it is reasonable that a non-planar distribution of chromophores could suppress the excitation transfer sufficiently to be immeasurable in the concentration dependent spectral diffusion measurements. However, we also performed the polarization resolved HDTG experiments. The transient grating experiments are sensitive to the self-part of the excitation transfer Green’s function, which decays faster than the excitation transfer induced spectral diffusion.³⁸ Even for the 20 Å thick layer, the self part of the Green’s function, which is formally a stretched exponential, decays on a characteristic 20-40 ps timescale. This would suggest that there should be a second component in the parallel and perpendicular HDTG decays, or that the decays should differ significantly over the 20-40 ps timescale, neither of which is true. Therefore it is plausible that additional mechanisms that suppress excitation transfer are also at play. The recent theoretical work of Rosenfeld and Fayer has shown that changes to the orientational distribution function can cause large changes (factors of 0.5 – 2 depending on the model) in the excitation transfer rate.³⁸ Since, we only measure the orientational order parameter, the form of the orientational distribution function is unknown. In the theoretical calculations presented previously⁹ and the calculations performed for the results described above, we assumed that all of the transition dipoles have the same angle relative to the plane of the surface, and they are random in a conical surface with this angle. A different angular distribution can have a drastic effect on the excitation transfer process with the possibility of greatly reducing it.

Another uncertainty that is unrelated to geometry in determining the excitation transfer is the presence of two coupled vibrational modes at 1896 and 1920 cm⁻¹. The possible influence of these modes was not included in calculations. These modes are antisymmetric stretching modes of the three carbonyl modes on the Re complex headgroup.^9,77 Coupled normal modes can undergo rapid equilibration (intramolecular vibrational excitation transfer) on a picosecond timescale. Equilibration of population between the vibrational modes would result in bi-exponential decays. As single exponential decays fit the HDTG curves well, there is no direct observation of equilibration. However, because the resonant signal is very weak, the equilibration can occur very rapidly and be obscured by the coherent artifact that limits the observation at short time. Since the modes are only separated by 100 cm⁻¹, it is expected that the energy deposited by the infrared laser pulse into the carbonyl vibrations spends ~2/3 of the time in the lower energy modes. If this equilibration happens on the surface, which has yet to be investigated, then the excitation transfer theory would have to be modified to include intermolecular excitation transfer for the lower frequency modes. If the lower frequency modes have slow excitation transfer, then the absence of excitation transfer shown here would be explained. It is highly plausible that the lower frequency modes have slower excitation transfer. Their linewidths are significantly broader as determined by Gaussian fitting (26.5 cm⁻¹ for the low frequency peaks vs. 15.2 cm⁻¹ for the high frequency peak). If the homogeneous linewidths are about the same as the high frequency symmetric stretching mode studied, the increase in the inhomogeneous linewidth would slow down the excitation transfer significantly.^9,38 Further ultrafast infrared spectroscopic studies are needed to fully understand the couplings in this molecule and the impact of surface attachment on intramolecular couplings among the modes. Once the intermolecular couplings are known, the intramolecular vibrational excitation transfer can be incorporated into the intermolecular energy transfer model. All three modes would exchange energy among each other while simultaneously exchanging energy with nearby molecules through resonant excitation transfer. As we are not yet able to measure fully the intramolecular vibrational dynamics at the surface, this portion of the energy transfer model cannot be investigated yet.

Above we have focused on the uncertainty in excitation transfer calculations due to geometric and molecular effects. There is also significant debate over the impact of the effects of the medium. Local field and index of refraction effects can cause large changes in excitation transfer rates.^41,53 Investigating the places where the index of refraction occurs in the theory and considering the range of possible values can easily change the excitation transfer rate by a factor of 2.⁴¹ Further complications are added when the quantum yield is calculated only from spectroscopic data; a task which is extremely difficult.⁴¹ In the infrared vibrational experiments, there is no method of measuring directly the quantum yield, as there is with fluorescent molecules. Also, the quantum yield depends on the local medium, and the boundary conditions of the associated electromagnetic problem,⁴¹ all of which are extremely difficult to account for and for which there is little empirical data in the infrared. For the above reasons theoretical calculation of vibrational excitation transfer have a great deal of uncertainty. The initial calculations⁹ did not consider a number of aspects of the problem that can reduce the calculated rate of excitation transfer.

Despite the uncertainty of the theoretical treatment of vibrational excitation transfer on a surface, we have experimentally unambiguously determined that it does not happen for the immobilized molecular system studied here. This means that we have also measured the true bare surface (no liquid solvent) structural spectral diffusion time constant to be 37 ± 6 ps. The amount of data we have collected is about 20 times greater than those that comprised the first report of surface 2D IR experiments. In addition, the preparation and characterization of the surfaces and samples used in the current experiments is far superior to the initial experiments. Therefore, the results presented her are a better determination of the surface structural spectral diffusion time constant.

IV. Concluding Remarks

The structural dynamics of thin films consisting of tricarbonyl (1,10-phenanthroline)rhenium chloride (RePhen(CO)₃Cl) linked to an alkyl silane monolayer through a triazole linker synthesized on silica-on-calcium-fluoride substrates were studied using 2D IR vibrational echo spectroscopy and infrared optical heterodyne detected transient grating experiments. In addition, FT-IR absorption spectroscopy and AFM experiments were used to characterize the samples. The experiments were conducted for a range of surface concentrations of RePhen(CO)₃Cl. Both the HDTG and vibrational echo experiments demonstrate conclusively that vibrational excitation transfer does not occur in this system. Vibrational excitation transfer will contribute to spectral diffusion observed with the vibrational echo experiments. Because the information of interest is structural spectral diffusion, which provides information on the structural dynamics of the monolayer, ruling out a vibrational excitation transfer contribution to spectral diffusion is extremely advantageous for future studies of monolayers of this type. Future measurements of spectral diffusion and HDTG studies can be safely taken to be uncontaminated by excitation transfer. The polarization selective HDTG studies presented here demonstrate a useful method for detecting the presence of excitation transfer if it reaches an appreciable rate.

The measurement of the picosecond timescale pure structural dynamics of the Re complex monolayers demonstrates that the Re complexes are able to sample the accessible structural microstates on a rapid timescale. In addition to ultrafast time scale dynamics that give rise to the homogeneous component (motionally narrowed), we observe structural spectral diffusion takes place with a time constant of 37 ± 6 ps. We have taken data to 20 ps (data not shown). Out to this time, spectral diffusion is not complete, that is, the CLS has not decayed to zero. Therefore, it is possible that there are slower time scales not yet observed in these experiments. However, the current study suggests that the Re complexes can access their full conformational space on a sub-nanosecond timescale. One of the directions of this research is the effect of the solvent on the interface.⁹ Future studies will be able to investigate how the surface dynamics are influenced by a variety of solvents.