The rational design of allosteric inhibitors and activators using the population-shift model: in vitro validation and application to an artificial biosensor

Abstract

The population-shift mechanism can be used to rationally re-engineer structure-switching biosensors to enable their allosteric inhibition and activation. As a proof-of-principle example of this we have introduced distal allosteric sites into molecular beacons, an optical sensor for the detection of specific nucleic acid sequences. The binding of inhibitors and activators to these sites enables the rational modulation of the sensor's target affinity –and thus its useful dynamic range– over three orders of magnitude. The convenience with which this was done suggests that the population-shift mechanism may prove a useful method by which allosteric regulation can be introduced into biosensors, “smart” biomaterials and other artificial biotechnologies.

Allostery, referred to by Perutz as the second secret of life [1], is the primary strategy employed in nature to regulate the affinities of biomolecules and, through this, to control cellular processes and pathways [2]. The ubiquity with which nature employs this mechanism suggests that the ability to engineer allostery into artificial systems could improve the functionality of biomolecules employed in biotechnologies, including synthetic biology [3], “smart” biomaterials [4], and biosensors [5]. Motivated by the above arguments, recent years have seen numerous examples in which rational design or directed evolution have been employed to introduce allosteric regulation into normally unregulated enzymes and nucleic acid catalysts [e.g., 6-9]. To date, however, the literature has seen little exploration regarding the use of allostery to “tune” the useful dynamic range –the range over which measurement precision and specificity are optimal– of the receptors used in biosensing applications. In response, we demonstrate here the utility of employing allostery to control the affinity (and thus dynamic range) of receptors that employ binding-induced conformational changes as a signal transduction mechanism.

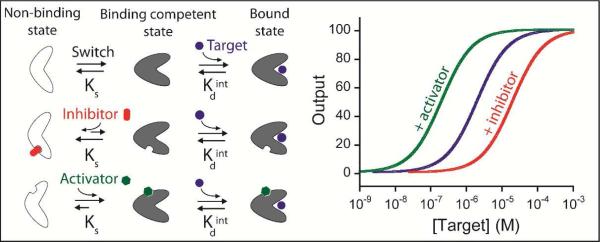
A fundamental problem in the fabrication of useful biosensors has been the limited number of biomolecules that produce any readily detectable physical event (e.g., emission of photons or electrons) upon binding to their target. A recent solution to this problem has been the development of a broad class of biosensors in which target binding is coupled with a large-scale conformational change in the receptor that, in turn, is transduced into an easily measurable optical, catalytic or electrochemical output [reviewed in 10]. Because these sensors are not “spoofed” by the non-specific adsorption of interfering proteins, they tend to work well even in complex sample matrices, such as undiluted blood serum. And because, in many formats, they are reagentless and rapidly reversible, they support continuous, real-time monitoring [reviewed in 11]. Finally, because the binding of these receptors is coupled with an unfavourable conformational change it is possible to tune their affinity by altering the equilibrium constant for this conformational switch [12]. Indeed, we have previously exploited this “population-shift mechanism” [13] to tune the affinity of optical biosensors over as much as five orders of magnitude via mutations that affect their switching equilibrium but leave their specificity unchanged [14]. Here, in contrast, we demonstrate the utility of perturbing the conformational switching equilibrium constant -and thus tuning the useful dynamic range- of a structure-switching biosensor via allosteric regulation, which, unlike mutational approaches, renders it possible to modulate dynamic range “on the fly”, long after its design and fabrication (Figure 1).

Figure 1.

Schematic representations of allosterically regulated receptors employing the population-shift mechanism. (Top) In this mechanism target binding shifts a pre-extisting equilibrium between a binding competent state and a non-binding state [12-13]. Because of this, the overall affinity of the receptor for its target is a function of both the intrinsic affinity of the binding-competent state $\left(K_d^{int}\right)$ and the switching equilibrium constant, K_s. (Middle) The binding of an allosteric inhibitor stabilizes the non-binding state, reducing K_s and thus raising the observed dissociation constant. (Bottom) The binding of an activator, in contrast, stabilizes the binding-competent state, increasing target affinity and pushing the dynamic range to lower target concentrations.

As a proof-of-principle demonstration of the allosteric “tuning” of structure-switching biosensors we have engineered this property into molecular beacons, an optical approach to the detection of specific nucleic acid sequences that is broadly representative of sensors in this class [12, 15]. Molecular beacons comprise a single-stranded fluorophoreand-quencher modified DNA sequence with self-complementary ends. In the absence of target the molecular beacon adopts a stem-loop configuration that holds its fluorophore/quencher pair in proximity, suppressing emission. The hybridization of a specific target DNA to the loop breaks the stem, segregating the fluorophore/quencher pair, increasing fluorescence. Previously we have shown that, as described by the population-shift model [13], the affinity with which a molecular beacon binds its target depends quantitatively on both the intrinsic affinity with which the “open” (linear, stem-broken) state binds its cognate target and on the equilibrium constant for the formation of this state from the “closed,” non-binding stem-loop configuration [12]. In keeping with this, mutations that affect the stability of the stem, and thus alter this conformational equilibrium constant, can be used to rationally vary the beacon's affinity for its target by many orders of magnitude.

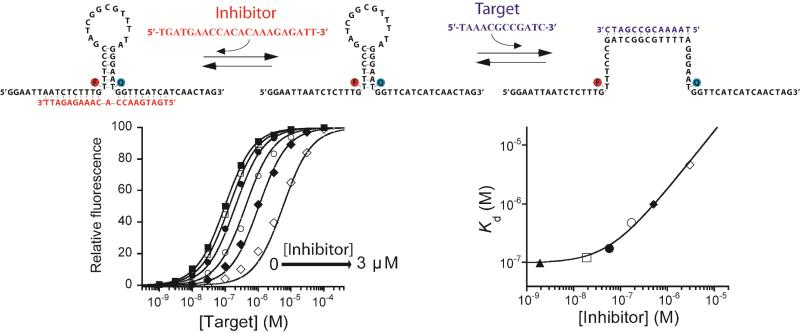
The correlation between a switch-based sensor's conformational equilibrium constant, K_s, and the overall affinity with which it binds its target provides a ready route to their allosteric inhibition. To achieve this we have modified a traditional, stem-loop molecular beacon by introducing two single-stranded “tails” acting together as a single allosteric binding site (Figure 2, top). The inhibitor, a single-stranded DNA binding both tails simultaneously, spans the junction and thus hinders stem opening. The resultant stabilization of the closed, stem-loop configuration reduces the switching equilibrium constant (K_s), in turn reducing the beacon's affinity for its target. Consistent with this, as we increase the concentration of the inhibitor from 0 to 3 μM the affinity of our test-bed molecular beacon rises monotonically from a dissociation constant of 0.097 μM to one of 4.6 μM (Figure 2, bottom).

Figure 2. Rational design of an allosterically inhibited biosensor.

(Top) We have engineered allosteric inhibition into a molecular beacon by adding two single-stranded “tails” that, together, serve as the allosteric binding site. The binding of an inhibitor that bridges across these tails stabilizes the non-binding state of the beacon, consequently reducing target affinity and pushing the useful dynamic range to higher target concentrations. (Bottom) As expected, the extent to which this allosteric inhibition shifts the dynamic range of the beacon (here and in all the experiments at 10 nM concentration) can be fine-tuned by varying the inhibitor concentration. Here we have employed inhibitor concentrations producing (from left to right) 0, 5, 25, 50, 75, 90 and 98% occupancy of the allosteric site. Using the population-shift model (Eqs. 1 and 4) and the independently determined target and inhibitor affinities (Figure S1), we can simulate this allosteric behaviour (solid lines, bottom left and right) with high precision without the use of any floating parameters (see Figure S2 for details about correlation between estimated and experimentally observed values).

The behavior of the inhibited molecular beacon is well described by the population-shift model [13]. To demonstrate this, we start with the Langmuir isotherm, which defines the target concentration/receptor occupancy curve for single-site binding at equilibrium:

$$F_{\left[T\right]}=F_0+\left(\frac{\left[\mathrm{T}\right](F_B-F_0}{\left[\mathrm{T}\right]+K_d}\right)$$ Eq. 1

Here F_[T] represents the output of the molecular beacon as a function of [T], the target concentration, F₀ and F_B represent the fluorescence of the unbound and target-bound states respectively, and K_d is the dissociation constant of the beacon/target duplex. Because of the binding-induced conformational change mechanism of molecular beacons, their affinity, K_d, is described by the population-shift model [12], in which:

$$K_{\mathrm{d}}=K_{\mathrm{d}}^{\text{int}}\left(\frac{1+K_{\mathrm{S}}}{K_{\mathrm{S}}}\right)$$ Eq. 2

Here K_s is the equilibrium constant for the switch between the receptor's non-binding and binding-competent states and $K_d^{int}$ is the intrinsic affinity of the target for the binding competent, open (linear) state. Previously we have fabricated molecular beacons with variant stem sequences, thus altering K_s and, in turn, tuning the sensor's useful dynamic range [12]. Here, where we instead modulate the conformational equilibrium via the binding of an allosteric inhibitor, K_s is given by:

$$K_{\mathrm{S}}\left(\text{inhib}\right)=K_{\mathrm{s}}^0\left(\frac{K_{\mathrm{i}}}{K_{\mathrm{i}}+\left[\mathrm{I}\right]}\right)$$ Eq. 3

where $K_s^o$ is the switching equilibrium constant in the absence of inhibitor, K_i is the dissociation constant for the inhibitor binding to the allosteric site of our modified molecular beacon and [I] is the inhibitor concentration. The overall affinity of the molecular beacon thus becomes:

$$K_{\mathrm{d}}\left(\text{inhib}\right)=K_d^{\text{int}}\left(\frac{1+K_{\mathrm{S}}^0\left(\frac{K_{\mathrm{i}}}{K_{\mathrm{i}}+\left[\mathrm{I}\right]}\right)}{K_{\mathrm{S}}^0\left(\frac{K_{\mathrm{i}}}{K_{\mathrm{i}}+\left[\mathrm{I}\right]}\right)}\right)$$ Eq. 4

We have used previously employed methods [12] to determine $K_d^{int}$ and $K_s^o$ for this modified beacon. A small, but detectable, decrease in the beacon's output associated with inhibitor binding (which brings the fluorophore and quencher into closer proximity) likewise provides an independent means of measuring K_i (Figure S1). Using these values in Eqs. 1, 2 and 4 we can simulate quantitatively the output of our molecular beacon over a range of target and inhibitor concentrations without the use of any fitted parameters (solid lines, Figure 2, bottom), highlighting the ability of the population-shift model to account for the behavior of this simple allosteric system at the equilibrium (Figure S3).

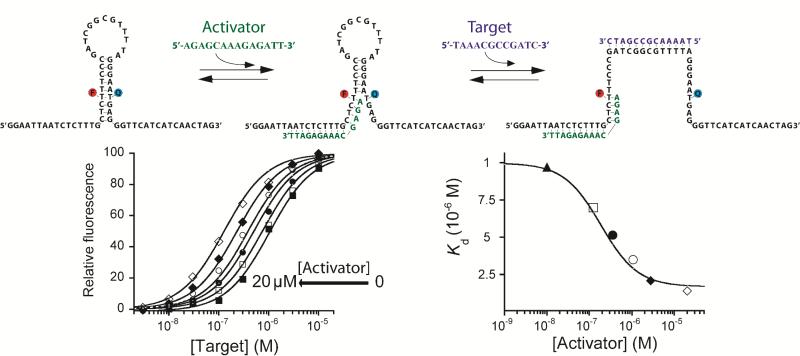
The population-shift mechanism likewise provides a route to the design of allosterically-activatable sensors using activators that destabilize the beacon's non-binding conformation, increasing K_s. We have done so using an oligonucleotide that binds to one tail of a “two-tailed” beacon so as to partially invade the double-stranded stem, reducing its stability (Figure 3, top). An important distinction between activation and inhibition, however, is that activation cannot be carried out ad infinitum. Specifically, because the non-binding conformation of the molecular beacon is dark, inhibitor binding can stabilize this state arbitrarily without increasing the background fluorescence. Activators, in contrast, stabilize the emissive, binding-competent state, thus increasing this background. For this reason the extent to which an activator can improve the affinity of a receptor is limited, as excessive background fluorescence ultimately reduces the sensor's gain (Figure S5). For this same reason the “activatable” receptor we have designed varies slightly from the receptor employed in the above inhibition studies. Specifically, we placed this construct's fluorophore and quencher pair in the middle of a 9-base pair stem and designed an activator that disrupts only 4 of these nine base pairs (Figure 3) [16].

Figure 3. Rational design of an allosterically activated biosensor.

(Top) We have engineered allosteric activation into a molecular beacon by using one single-stranded “tail” as an allosteric binding site. An activator sequence binding to this tail partially “invades” the stem, destabilizes the non-binding state and thus improves target affinity. (Bottom) The extent of this activation can be fine-tuned by changing activator concentration. Here we have used concentrations producing (from right to left) 0, 2, 10, 25, 50, 75 and 95% occupancy of the allosteric site. Using the population-shift model (Eqs. 1 and 5) and the dissociation constants of the beacon for its target and the activator (Figure S4), we can simulate this allosteric behaviour (solid lines, bottom) with high precision without the use of any floating parameters (see Figure S2 for details about correlation between simulated and experimentally observed values).

The allosterically activated molecular beacon performs as expected. In the absence of its activator the dose-response curve of the modified molecular beacon is well described by the expected hyperbolic binding curve (Eq. 1) with a dissociation constant of 1.06 μM (Figure 3). Upon the addition of activator the sensor's dissociation constant falls monotonically, reaching 0.12 μM at 20 μM activator. Confirming the validity of the population-shift model, the observed affinity is well modeled (Figure S2) by Eq. 2, save with a conformational equilibrium constant given by:

$$K_d\left(\text{act}\right)=K_d^{\text{int}}\left(\frac{1+{K^o}_S}{{K^o}_S}\right)\left(\frac{1+\frac{\left[A\right]}{K_{act}}}{1+\frac{\left[A\right]}{\alpha K_{act}}}\right)$$ Eq. 5

where K_act is the dissociation constant of the beacon-activator complex and α is the ratio between the dissociation constants in the presence of saturating activator and in the absence of activator.

A final, important consideration is that the allosteric control presented here does not alter target specificity. That is, because the allosteric binding site is separated from the target-binding element, our allosterically activated molecular beacon retains the same discrimination power (perfect target versus a 1-base mismatch) as the unmodified parent beacon (Figure S7).

Here we have employed the population-shift model to rationally engineer allosteric regulation into a representative structure-switching biosensor over three orders of magnitude via the introduction of the appropriate concentration of allosteric inhibitor or activator. Consistent with the design principles we have employed, the input-output curves of both the inhibited and activated sensors are quantitatively described by the population-shift model, supporting our argument that this mechanism provides a convenient method by which finely tuned allostery can be introduced into structure-switching biosensors.

Due to their simple structure and easy “designability”, DNA molecular beacons are particularly amenable to the engineering approaches demonstrated here. This said, we believe these approaches provide a route by which allosteric regulation can be introduced into many conformation-switching biosensors. Aptamer-based sensors, for example, can be inhibited via complementary sequences stabilizing a double-stranded, non-target-binding state [17] and can likely be activated by sequences that suppress this effect (by sequestering the inhibitor). Even protein-based switches can be modulated via the population-shift mechanism. For example, we have previously demonstrated the ease with which single-domain proteins can be re-engineered to support binding-induced folding [18]. We speculate that antibodies that bind a conformational epitope will stabilize the native state of such a protein, thus activating it, while antibodies directed against epitopes exposed only in the unfolded state would, conversely, produce inhibition.

The availability of tunable biomolecules could prove of value in many biotechnologies. An obvious application, of course, is, as shown here, the development of sensors that circumvent the fixed dynamic ranges associated with traditional biomolecular recognition elements. More speculatively, the availability of tunable bio-receptors may be useful in the field of synthetic biology. The re-engineering of new cellular functions through the design of synthetic gene networks that can be fine-tuned through the use of allosteric effectors could provide a powerful tool to precisely modulate genetic regulatory networks thus allowing their application in biomanufacturing [19].