Abstract
Nickel-containing hydrogenases, the biological catalysts of 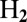 oxidation and production, reversibly inactivate under anaerobic, oxidizing conditions. We aim at understanding the mechanism of (in)activation and what determines its kinetics, because there is a correlation between fast reductive reactivation and oxygen tolerance, a property of some hydrogenases that is very desirable from the point of view of biotechnology. Direct electrochemistry is potentially very useful for learning about the redox-dependent conversions between active and inactive forms of hydrogenase, but the voltammetric signals are complex and often misread. Here we describe simple analytical models that we used to characterize and compare 16 mutants, obtained by substituting the position-74 valine of the
oxidation and production, reversibly inactivate under anaerobic, oxidizing conditions. We aim at understanding the mechanism of (in)activation and what determines its kinetics, because there is a correlation between fast reductive reactivation and oxygen tolerance, a property of some hydrogenases that is very desirable from the point of view of biotechnology. Direct electrochemistry is potentially very useful for learning about the redox-dependent conversions between active and inactive forms of hydrogenase, but the voltammetric signals are complex and often misread. Here we describe simple analytical models that we used to characterize and compare 16 mutants, obtained by substituting the position-74 valine of the 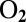 -sensitive NiFe hydrogenase from Desulfovibrio fructosovorans. We observed that this substitution can accelerate reactivation up to 1,000-fold, depending on the polarity of the position 74 amino acid side chain. In terms of kinetics of anaerobic (in)activation and oxygen tolerance, the valine-to-histidine mutation has the most spectacular effect: The V74H mutant compares favorably with the
-sensitive NiFe hydrogenase from Desulfovibrio fructosovorans. We observed that this substitution can accelerate reactivation up to 1,000-fold, depending on the polarity of the position 74 amino acid side chain. In terms of kinetics of anaerobic (in)activation and oxygen tolerance, the valine-to-histidine mutation has the most spectacular effect: The V74H mutant compares favorably with the 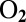 -tolerant hydrogenase from Aquifex aeolicus, which we use here as a benchmark.
-tolerant hydrogenase from Aquifex aeolicus, which we use here as a benchmark.
Keywords: electrocatalysis, direct electron transfer, protein film voltammetry, hydrogen
The nickel–iron hydrogenases that have been crystallized and/or thoroughly studied so far are very similar from a structural point of view: They all are either soluble heterodimers or heterodimers isolated from a membrane-associated complex. The amino acids that surround the NiFe active site are conserved (1) and yet the kinetic properties of these enzymes are diverse. For example, some NiFe hydrogenases can oxidize and produce 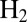 , whereas others preferentially catalyze one direction of the reaction (2
–4). Another property of some hydrogenases that has attracted considerable interest is their sensitivity (and sometimes their resistance) to
, whereas others preferentially catalyze one direction of the reaction (2
–4). Another property of some hydrogenases that has attracted considerable interest is their sensitivity (and sometimes their resistance) to 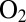 . This interest stems from the fact that hydrogenases could be used for
. This interest stems from the fact that hydrogenases could be used for 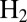 oxidation in fuel cells or
oxidation in fuel cells or 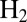 production in photo-electrochemical cells if they were functional under aerobic conditions (5).
production in photo-electrochemical cells if they were functional under aerobic conditions (5).
The NiFe hydrogenases that have been studied first, referred to as “standard,” were purified from Allochromatium vinosum or Desulfovibrio species. Upon exposure to 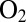 , they convert into two inactive forms called NiA and NiB, where an oxygenated ligand bridges the Ni and the Fe. The NiB and NiA states can be reactivated by reduction, the former more quickly than the latter (6). The membrane-bound NiFe hydrogenases from, e.g., Ralstonia eutropha or Aquifex aeolicus are reversibly inhibited by
, they convert into two inactive forms called NiA and NiB, where an oxygenated ligand bridges the Ni and the Fe. The NiB and NiA states can be reactivated by reduction, the former more quickly than the latter (6). The membrane-bound NiFe hydrogenases from, e.g., Ralstonia eutropha or Aquifex aeolicus are reversibly inhibited by 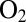 and termed “
and termed “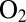 resistant.” Apparently, this resistance results from (i) the enzyme reacting with
resistant.” Apparently, this resistance results from (i) the enzyme reacting with 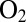 to form only the NiB state and (ii) this NiB state reactivating much more quickly than in standard hydrogenases (4, 7). The most patent differences between
to form only the NiB state and (ii) this NiB state reactivating much more quickly than in standard hydrogenases (4, 7). The most patent differences between 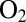 -resistant and
-resistant and 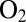 -sensitive hydrogenases are the structures and redox properties of the FeS cluster that is proximal to the active site. Recent structural and spectroscopic investigations have shown that in
-sensitive hydrogenases are the structures and redox properties of the FeS cluster that is proximal to the active site. Recent structural and spectroscopic investigations have shown that in 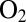 -resistant enzymes, it is an unprecedented 4Fe3S cluster (8
–10) that has a high reduction potential and the ability to cycle through three redox states in a narrow range of potential (11).
-resistant enzymes, it is an unprecedented 4Fe3S cluster (8
–10) that has a high reduction potential and the ability to cycle through three redox states in a narrow range of potential (11).
The rate of reactivation of NiB partly determines 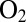 tolerance, but the reason this reaction is orders of magnitude faster in oxygen-resistant hydrogenases than in standard hydrogenases has not been investigated. The hypothesis that fast reactivation may result from a thermodynamic advantage (that is, NiB having a higher reduction potential) (7) has found no experimental support: The redox potential of the NiB state in the NiFe hydrogenase from A. aeolicus is not significantly greater than in standard hydrogenases (4), and the V74C mutation in Desulfovibrio fructosovorans has no effect on the spectral and redox properties of the NiB state, whereas it does increase significantly its rate of reduction (12).
tolerance, but the reason this reaction is orders of magnitude faster in oxygen-resistant hydrogenases than in standard hydrogenases has not been investigated. The hypothesis that fast reactivation may result from a thermodynamic advantage (that is, NiB having a higher reduction potential) (7) has found no experimental support: The redox potential of the NiB state in the NiFe hydrogenase from A. aeolicus is not significantly greater than in standard hydrogenases (4), and the V74C mutation in Desulfovibrio fructosovorans has no effect on the spectral and redox properties of the NiB state, whereas it does increase significantly its rate of reduction (12).
The anaerobic conversion between active enzyme and the NiB state is often studied in protein film voltammetry experiments, where the enzyme is adsorbed or attached to a rotating-disk electrode and electron transfer is direct. The value of the electrode potential (E) is set to drive the catalytic reaction while the turnover rate (the activity) is simultaneously measured as a current (13). Changing the electrode potential also triggers the conversion between active and inactive states. In chronoamperometry (CA) experiments, the (in)activation is seen as current transients following potential steps (14, 15). In cyclic voltammetry (CV) experiments, the oxidative inactivation gives the electrochemical response the complex shape that is shown in Fig. 1A
(14
–16). Starting from the low potential limit, the current initially increases as the electrode potential increases (and so does the driving force for 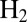 oxidation) and then bends down or even decreases at high potential, as a result of the oxidative formation of the inactive state. As the potential is lowered back on the reverse scan, the reactivation produces an increase in current, which is eventually outcompeted by the decrease in steady-state activity that results from the potential being less oxidizing. Hysteresis occurs because the conversion between (in)active states is slow on the voltammetric timescale (16), irrespective of scan rate in the experimentally accessible range of scan rate (
oxidation) and then bends down or even decreases at high potential, as a result of the oxidative formation of the inactive state. As the potential is lowered back on the reverse scan, the reactivation produces an increase in current, which is eventually outcompeted by the decrease in steady-state activity that results from the potential being less oxidizing. Hysteresis occurs because the conversion between (in)active states is slow on the voltammetric timescale (16), irrespective of scan rate in the experimentally accessible range of scan rate (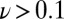 mV/s). The wave shape is defined by the steady-state electrochemical response of the active enzyme (17) and the potential-dependent kinetics of conversion between active and inactive states, but the latter, crucial information is not easily disclosed. In particular, the position of the first inflection point on the reverse scan (the so-called “switch potential,”
mV/s). The wave shape is defined by the steady-state electrochemical response of the active enzyme (17) and the potential-dependent kinetics of conversion between active and inactive states, but the latter, crucial information is not easily disclosed. In particular, the position of the first inflection point on the reverse scan (the so-called “switch potential,” 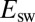 , shown as vertical segments in Fig. 1A
) is very dependent on scan rate
†
and should therefore not be interpreted as a thermodynamic quantity. Considering that voltammetry is now used in several research groups to characterize hydrogenases isolated from various organisms (e.g., refs. 3, 18
–21), there is a crucial need for simple theoretical models that will ease quantitative investigations.
, shown as vertical segments in Fig. 1A
) is very dependent on scan rate
†
and should therefore not be interpreted as a thermodynamic quantity. Considering that voltammetry is now used in several research groups to characterize hydrogenases isolated from various organisms (e.g., refs. 3, 18
–21), there is a crucial need for simple theoretical models that will ease quantitative investigations.
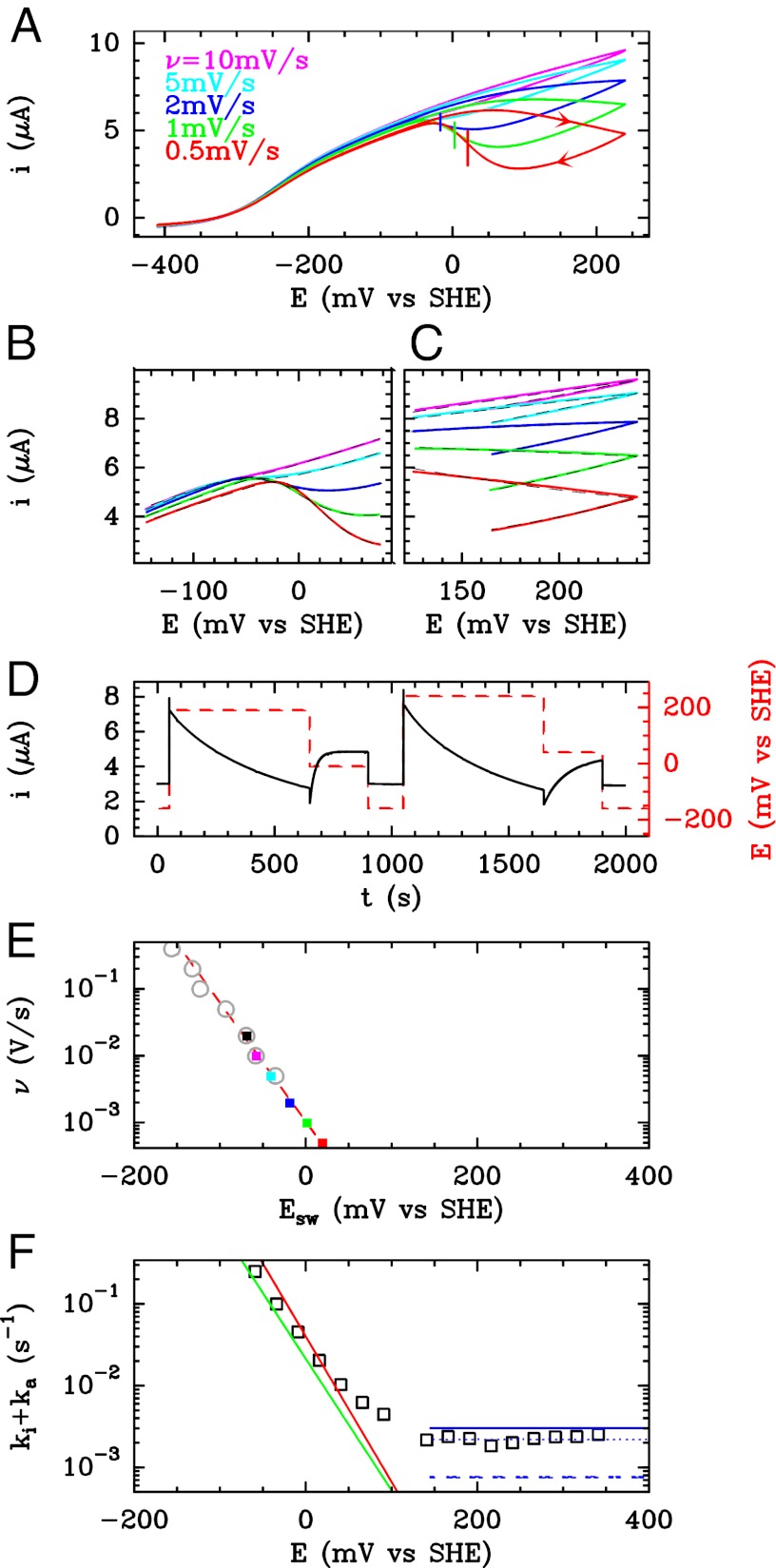
Fig. 1.
Electrochemical characterization of the D. fructosovorans V74N mutant. (A) CVs recorded with the enzyme attached to a rotating-disk graphite electrode. Potentials are quoted versus the standard hydrogen electrode (SHE). One atmosphere 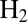 , pH 5.5, 40 °C, electrode rotation rate ω = 3,000 rpm. The vertical lines mark the “switch” potentials. (B and C) Solid lines show portions of the voltammograms in A. The dashed lines are the best fits to Eq. 5
(C) and Eq. 7
(B). (D) Current response (after subtraction of the capacitive current recorded in a control experiment with no adsorbed enzyme) when the potential was stepped according to the sequence
, pH 5.5, 40 °C, electrode rotation rate ω = 3,000 rpm. The vertical lines mark the “switch” potentials. (B and C) Solid lines show portions of the voltammograms in A. The dashed lines are the best fits to Eq. 5
(C) and Eq. 7
(B). (D) Current response (after subtraction of the capacitive current recorded in a control experiment with no adsorbed enzyme) when the potential was stepped according to the sequence 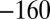 , 190,
, 190, 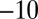 ,
, 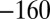 , 240, 40,
, 240, 40, 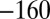 mV, as shown using the dashed line and the Y-right axis. (E) The relation between
mV, as shown using the dashed line and the Y-right axis. (E) The relation between 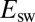 and scan rate. The straight dashed red line is a fit to Eq. 10
. F shows as open squares the time constants determined by fitting exponential functions to the current transients. The blue horizontal lines indicate the values of
and scan rate. The straight dashed red line is a fit to Eq. 10
. F shows as open squares the time constants determined by fitting exponential functions to the current transients. The blue horizontal lines indicate the values of 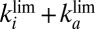 (solid line)
(solid line) 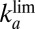 (dashed line), and
(dashed line), and 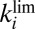 (dotted line) determined by fitting the portions of CVs shown in C. The green line shows the rate of reactivation
(dotted line) determined by fitting the portions of CVs shown in C. The green line shows the rate of reactivation 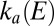 at low potential, determined by fitting the data in B. The red line shows the rate of reactivation
at low potential, determined by fitting the data in B. The red line shows the rate of reactivation 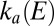 at low potential, determined by fitting the change in switch potential against scan rate.
at low potential, determined by fitting the change in switch potential against scan rate.
Valine 74 shapes a bottleneck in the channel that guides 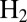 from solvent to the active site of D. fructosovorans NiFe hydrogenase (22). Substitutions of this amino acid have a strong effect on the rates of intramolecular diffusion (23, 24) and, consequently, on the Michaelis constant for
from solvent to the active site of D. fructosovorans NiFe hydrogenase (22). Substitutions of this amino acid have a strong effect on the rates of intramolecular diffusion (23, 24) and, consequently, on the Michaelis constant for 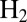 (24), on the catalytic bias of the enzyme (2), and on the rates of inhibition by CO and
(24), on the catalytic bias of the enzyme (2), and on the rates of inhibition by CO and 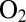 (23, 24). For example, the V74Q, V74M, and V74E mutants are inhibited by
(23, 24). For example, the V74Q, V74M, and V74E mutants are inhibited by 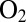 more slowly than the wild-type (WT) enzyme, but this effect on the rate of inhibition is not strong enough to make the enzyme oxygen resistant. Indeed, in contrast to standard hydrogenases, those that are naturally
more slowly than the wild-type (WT) enzyme, but this effect on the rate of inhibition is not strong enough to make the enzyme oxygen resistant. Indeed, in contrast to standard hydrogenases, those that are naturally 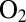 resistant reactivate after they have been transiently exposed to
resistant reactivate after they have been transiently exposed to 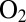 even under oxidizing conditions. A high rate of reactivation is therefore more beneficial than a slow rate of reaction with
even under oxidizing conditions. A high rate of reactivation is therefore more beneficial than a slow rate of reaction with 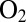 , and oxygen resistance cannot be achieved only by obstructing the gas channel (24). The V74M (25) and V74C (12) mutations significantly increase the resistance to
, and oxygen resistance cannot be achieved only by obstructing the gas channel (24). The V74M (25) and V74C (12) mutations significantly increase the resistance to 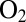 because they modify the way
because they modify the way 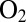 reacts at the active site, independently of the effect of the rate of diffusion toward the active site. The V74M variant can oxidize
reacts at the active site, independently of the effect of the rate of diffusion toward the active site. The V74M variant can oxidize 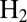 over extended periods of time in the presence of
over extended periods of time in the presence of 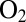 (25) and the V74C mutant reacts with
(25) and the V74C mutant reacts with 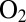 to form preferentially a NiB state that has the same thermodynamic and spectral properties as in the WT enzyme, but reactivates much more quickly (12): These are precisely the properties one seeks if the goal is to mimic
to form preferentially a NiB state that has the same thermodynamic and spectral properties as in the WT enzyme, but reactivates much more quickly (12): These are precisely the properties one seeks if the goal is to mimic 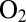 -tolerant hydrogenases.
-tolerant hydrogenases.
Suspecting that V74 mutants other than V74M and V74C may have interesting properties, and aiming at understanding the reason these substitutions affect 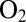 tolerance, we developed electrochemical methods and used them for screening in a quantitative manner 16 position-74 mutants. We discuss the interpretation of the electrochemical data and the relation between kinetics of anaerobic inactivation and oxygen tolerance, and we identify a mutation (V to H) that results in a spectacular improvement.
tolerance, we developed electrochemical methods and used them for screening in a quantitative manner 16 position-74 mutants. We discuss the interpretation of the electrochemical data and the relation between kinetics of anaerobic inactivation and oxygen tolerance, and we identify a mutation (V to H) that results in a spectacular improvement.
Results and Discussion
We interpret the electrochemical data by considering the anaerobic, redox-dependent transformation between active and inactive enzyme:
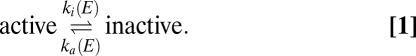 |
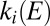 and
and 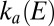 are the first-order rate constants of inactivation and reactivation, respectively. The change in concentration of active enzyme,
are the first-order rate constants of inactivation and reactivation, respectively. The change in concentration of active enzyme, 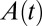 , is obtained by solving
, is obtained by solving
The enzyme activates or reactivates when the electrode potential is changed because 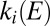 and/or
and/or 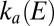 depend on E.
depend on E.
Fitting Chronoamperograms Returns k i(E)+k a(E) at Every Potential.
The (in)activation is clearly detected in CA experiments where the hydrogenase is attached to a rotating-disk graphite electrode and the potential is changed stepwise. Fig. 1D
shows a sequence of potential steps and the corresponding current response of the V74N mutant of D. fructosovorans NiFe hydrogenase. The  -oxidation current instantly increases each time the potential is stepped up as a result of the increase in driving force and then decreases slowly as the enzyme inactivates. After each step down, the catalytic current immediately drops and then slowly increases as activity is recovered.
-oxidation current instantly increases each time the potential is stepped up as a result of the increase in driving force and then decreases slowly as the enzyme inactivates. After each step down, the catalytic current immediately drops and then slowly increases as activity is recovered.
A straightforward analysis of these experiments consists of fitting each current transient to an exponential function to measure the time constant 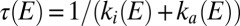 at any potential (4, 15); the results are shown as squares in Fig. 1F
.
at any potential (4, 15); the results are shown as squares in Fig. 1F
.
Whether the enzyme will activate or inactivate after a certain potential step can be predicted only if one knows the variations of both 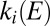 and
and 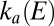 . For example, if the ratio
. For example, if the ratio 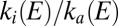 increases as the electrode potential increases, the enzyme inactivates after a step up. We have shown that, to independently determine the two rate constants from CA experiments, one must simultaneously interpret the time constant and the magnitude of the transients (15). The result of such detailed investigation of the oxygen-tolerant hydrogenase from A. aeolicus in ref. 15 is summarized by the following empirical equations (plotted in Fig. S1A), which can be used to simulate the whole voltammogram (15):
increases as the electrode potential increases, the enzyme inactivates after a step up. We have shown that, to independently determine the two rate constants from CA experiments, one must simultaneously interpret the time constant and the magnitude of the transients (15). The result of such detailed investigation of the oxygen-tolerant hydrogenase from A. aeolicus in ref. 15 is summarized by the following empirical equations (plotted in Fig. S1A), which can be used to simulate the whole voltammogram (15):
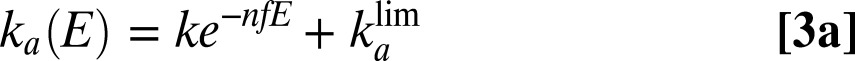 |
 |
The prefactor k is a rate constant whose meaning is discussed below. We note 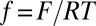 .
.
Eq. 3
appears to be general: It is consistent with the results of CA experiments carried out with A. vinosum (14) and A. aeolicus (4, 15) WT NiFe hydrogenases and also with the V74N D. fructosovorans mutant (Fig. 1F
): The rate of interconversion between active and inactive states (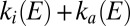 ) levels off at high potential and increases exponentially with
) levels off at high potential and increases exponentially with 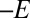 at low potential. The voltammetric traces are also consistent with Eq. 3
. Indeed, the oxidative inactivation proceeds gradually because both
at low potential. The voltammetric traces are also consistent with Eq. 3
. Indeed, the oxidative inactivation proceeds gradually because both 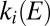 and
and 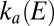 are independent of E at high potential (Eq. 3
and Fig. S1A). On the reverse scan, as the electrode potential is lowered,
are independent of E at high potential (Eq. 3
and Fig. S1A). On the reverse scan, as the electrode potential is lowered, 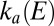 increases whereas
increases whereas 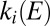 does not, and the enzyme therefore reactivates; the increase in current is very sudden around the so-called switch potential because the exponential increase in rate of reactivation (Eq. 3a
) produces a sharp voltammetric feature.
does not, and the enzyme therefore reactivates; the increase in current is very sudden around the so-called switch potential because the exponential increase in rate of reactivation (Eq. 3a
) produces a sharp voltammetric feature.
We now assume that Eq. 3
also applies in the case of all other V74 mutants of D. fructosovorans NiFe hydrogenase and we derive models that can be used to determine the parameters in Eq. 3
(k, n, 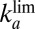 , and
, and 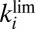 ) from voltammetric experiments. Fitting the entire voltammogram recorded at slow scan rate is not straightforward because Eq. 2
must be numerically solved to obtain the time-dependent fraction of enzyme that is in the active form,
) from voltammetric experiments. Fitting the entire voltammogram recorded at slow scan rate is not straightforward because Eq. 2
must be numerically solved to obtain the time-dependent fraction of enzyme that is in the active form, 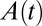 (15). However, we show hereafter that there are potential ranges where the equations for
(15). However, we show hereafter that there are potential ranges where the equations for 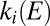 and
and 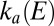 are simple enough that closed-form expressions can be derived and used to fit fragments of the cyclic voltammograms (CVs) that embed the relevant information. The dependence of the switch potential on scan rate can also be rigorously interpreted.
are simple enough that closed-form expressions can be derived and used to fit fragments of the cyclic voltammograms (CVs) that embed the relevant information. The dependence of the switch potential on scan rate can also be rigorously interpreted.
Wave Shape at High Potential Depends on 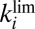 and
and 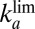 .
.
If E is high enough that 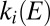 and
and 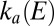 are constant, then the fraction of active enzyme decreases exponentially with time, with a time constant
are constant, then the fraction of active enzyme decreases exponentially with time, with a time constant 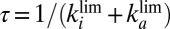 that depends mainly on
that depends mainly on 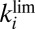 , toward a limiting value
, toward a limiting value 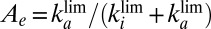 ,
,
where 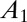 is the fraction of active enzyme at
is the fraction of active enzyme at 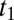 (herein, subscript “1” is used to denote an initial condition that will be treated as an adjustable parameter in a fitting procedure). The current is obtained by multiplying the time-dependent fraction of active enzyme by the steady-state current response of the active enzyme (15), which, in the potential range of interest, is a linear function of E (cf. equation 9 in ref. 17),
(herein, subscript “1” is used to denote an initial condition that will be treated as an adjustable parameter in a fitting procedure). The current is obtained by multiplying the time-dependent fraction of active enzyme by the steady-state current response of the active enzyme (15), which, in the potential range of interest, is a linear function of E (cf. equation 9 in ref. 17),
where 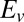 is the vertex potential and the scan rate v is counted as positive in both directions. The linear steady-state contribution results from the fact that enzyme molecules that are weakly coupled to the electrode contribute to the current only at high driving force. Eq. 5
is defined by five independent parameters: a and b (which can be measured from the slope of the voltammogram in the potential range where there is no inactivation),
is the vertex potential and the scan rate v is counted as positive in both directions. The linear steady-state contribution results from the fact that enzyme molecules that are weakly coupled to the electrode contribute to the current only at high driving force. Eq. 5
is defined by five independent parameters: a and b (which can be measured from the slope of the voltammogram in the potential range where there is no inactivation), 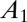 and
and 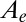 (both in the range [0–1]), and τ. The initial potential (
(both in the range [0–1]), and τ. The initial potential (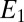 ), vertex potential (
), vertex potential (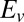 ), and scan rate (v) are known.
), and scan rate (v) are known.
The solid lines in Fig. 1C
are the high-potential parts of the CVs shown in Fig. 1A
. The dashed lines are the fits to Eq. 5
obtained with a single pair of values for the parameters 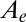 and τ. The blue, solid, horizontal line in Fig. 1F
indicates the values of
and τ. The blue, solid, horizontal line in Fig. 1F
indicates the values of 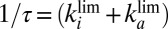 : It agrees with the results of the CA measurements. The dashed and dotted horizontal blue lines mark the values of
: It agrees with the results of the CA measurements. The dashed and dotted horizontal blue lines mark the values of 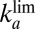 and
and 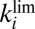 , respectively.
, respectively.
Wave Shape on the Reverse Scan Gives k and n, Which Define 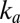 (E) at Low Potential.
(E) at Low Potential.
On the reverse scan, when the electrode potential becomes low, 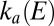 starts to increase and so does
starts to increase and so does 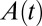 . Here we assume that (i) the potential is low enough (lower than a certain potential
. Here we assume that (i) the potential is low enough (lower than a certain potential 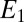 ) that
) that 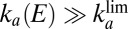 and (ii) the reactivation is irreversible (that is, the second term in the right-hand side of Eq. 2
dominates). If
and (ii) the reactivation is irreversible (that is, the second term in the right-hand side of Eq. 2
dominates). If 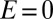 when
when 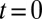 ,
, 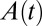 obeys
obeys
This equation is solved using the initial condition that 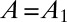 at
at 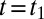 , and the current equation for the reverse sweep is obtained by multiplying
, and the current equation for the reverse sweep is obtained by multiplying 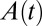 by the linear current response of the active enzyme,
by the linear current response of the active enzyme,
Five parameters must be adjusted to fit the data: a and b, 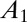 (the initial fraction of active enzyme at
(the initial fraction of active enzyme at 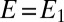 ), n, and k.
), n, and k.
The solid lines in Fig. 1B
show the fragments of the CVs shown in Fig. 1A
that can be described by Eq. 7
. The best fit (dashed lines) has been obtained with a single pair of parameters for k and n. Using these values, Eq. 3a
was used to recalculate the low-potential part of 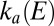 , shown as a green line in Fig. 1F
: Again the agreement with the results of the CA measurements is very good.
, shown as a green line in Fig. 1F
: Again the agreement with the results of the CA measurements is very good.
Switch Potential Is a Kinetic, Rather than Thermodynamic, Parameter.
We demonstrate in SI Text that if the reactivation is irreversible [condition (ii) in the previous section], then 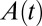 passes through an inflection point when
passes through an inflection point when
 |
The physical meaning of Eq. 8
is that reactivation depends on two different timescales: the rate of reactivation, 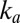 , and the rate at which
, and the rate at which 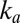 increases,
increases, 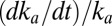 . On the high-potential part of the return sweep,
. On the high-potential part of the return sweep, 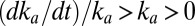 , and the fast increase in
, and the fast increase in 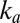 makes the current increase faster and faster. On the low-potential part of the return sweep, the process slows down before reaching completion because
makes the current increase faster and faster. On the low-potential part of the return sweep, the process slows down before reaching completion because 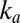 is large enough that the decrease in the amount of inactive species counteracts the increase in
is large enough that the decrease in the amount of inactive species counteracts the increase in 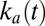 . The switch potential marks the transition between the two regimes.
. The switch potential marks the transition between the two regimes.
Using the Change in 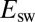 Against v to Measure k and n.
Against v to Measure k and n.
Substituting 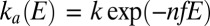 in Eq. 8
gives
in Eq. 8
gives
and after rearrangement
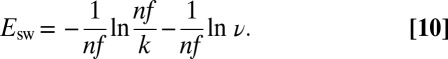 |
Eq. 10
predicts the value of 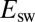 and explains the linear relation between
and explains the linear relation between 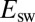 and
and 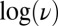 that has been observed every time the effect of scan rate has been examined.† Because Eq. 10
predicts a
that has been observed every time the effect of scan rate has been examined.† Because Eq. 10
predicts a 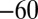 mV
mV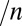 change in
change in 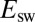 per decade of scan rate, a switch potential should always be quoted along with the value of the scan rate.
per decade of scan rate, a switch potential should always be quoted along with the value of the scan rate.
We analyzed the data in Fig. 1A
by determining the values of 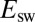 from the position of the minimum on the first derivative of each reverse sweep (Fig. S2). The relation between
from the position of the minimum on the first derivative of each reverse sweep (Fig. S2). The relation between 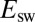 and
and 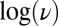 is shown as squares in Fig. 1E
. Fitting a straight line to these data (Eq. 10
) returned the values of k and n that we used to calculate the low-potential part of
is shown as squares in Fig. 1E
. Fitting a straight line to these data (Eq. 10
) returned the values of k and n that we used to calculate the low-potential part of  shown in red in Fig. 1F
.
shown in red in Fig. 1F
.
At fast scan rates, the switch is not detected on the reverse scan because the enzyme has had no time to inactivate on the forward scan (e.g., purple line in Fig. 1A
). We carried out experiments (Fig. S3) where the electrode potential is poised at 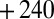 mV for about 15 min (to let the enzyme inactivate) before quickly sweeping the potential down. We used these data to determine the switch potentials whose values are shown as open circles in Fig. 1E
. There is no deviation from the linear relationship between
mV for about 15 min (to let the enzyme inactivate) before quickly sweeping the potential down. We used these data to determine the switch potentials whose values are shown as open circles in Fig. 1E
. There is no deviation from the linear relationship between 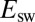 and
and 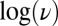 that is observed at a slower scan rate. The switch potential decreases by about 200 mV when the scan rate is increased from 0.5 mV/s to 0.4 V/s.
that is observed at a slower scan rate. The switch potential decreases by about 200 mV when the scan rate is increased from 0.5 mV/s to 0.4 V/s.
Relation Between the Switch Potential and the Result of Equilibrium Titrations.
As activation proceeds, the fully oxidized inactive state NiB is first one-electron reduced (with a reduction potential 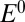 ), into an inactive “NiSIr” state, before it gives the active form NiSIa that binds
), into an inactive “NiSIr” state, before it gives the active form NiSIa that binds 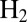 as part of the catalytic cycle (scheme 1 in ref. 4):
as part of the catalytic cycle (scheme 1 in ref. 4):
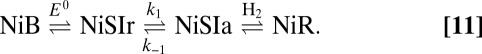 |
The above mechanism is consistent with the kinetics of reactivation. Indeed, in the case of all mutants analyzed here, the changes in 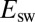 against
against 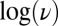 and the fits of the CVs to Eq. 7
returned values of n close to unity (in the range 0.8–1.1)
‡
, suggesting that the low potential increase in
and the fits of the CVs to Eq. 7
returned values of n close to unity (in the range 0.8–1.1)
‡
, suggesting that the low potential increase in 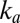 , which determines
, which determines 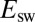 , is the onset of the one-electron sigmoid plotted in Fig. S1B:
, is the onset of the one-electron sigmoid plotted in Fig. S1B: 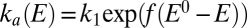 . Hence k in Eq. 3a
equates to
. Hence k in Eq. 3a
equates to 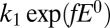 . The rate of reactivation is independent of
. The rate of reactivation is independent of  , consistent with the earlier observation that
, consistent with the earlier observation that 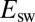 and
and 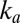 are independent of
are independent of 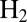 concentration (14, 15). The low-potential plateau at
concentration (14, 15). The low-potential plateau at 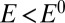 was not approached in our experiments, suggesting that
was not approached in our experiments, suggesting that 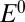 is, in each case, lower than the lowest potential probed in the CA experiments and lower than the switch potential measured even at the fastest scan rates.
is, in each case, lower than the lowest potential probed in the CA experiments and lower than the switch potential measured even at the fastest scan rates.
When the scan rate is decreased, the value of 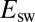 increases and drifts away from
increases and drifts away from 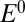 . At an infinitely low scan rate,
. At an infinitely low scan rate, 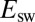 tends to the potential where
tends to the potential where 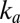 and
and 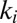 intersect;
§
this value depends on
intersect;
§
this value depends on 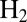 concentration because
concentration because 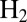 binding prevents inactivation. We have indeed observed that
binding prevents inactivation. We have indeed observed that 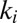 decreases when the concentration of
decreases when the concentration of 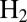 increases (figure 4 in ref. 15).
increases (figure 4 in ref. 15).
In redox titrations (in the absence of  ), NiSIr and NiSIa are in equilibrium and the measured potential is more positive than
), NiSIr and NiSIa are in equilibrium and the measured potential is more positive than 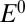 by an amount
by an amount 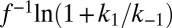 .
.
Summary About the Switch Potential.
The value of this parameter is determined by the rate of reactivation. It is not the reduction potential of the inactive state. It is independent of [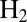 ], dependent on scan rate (Fig. 1E
), and always greater than
], dependent on scan rate (Fig. 1E
), and always greater than 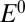 (defined by Eq. 11
). Its pH dependence should be the same as that of
(defined by Eq. 11
). Its pH dependence should be the same as that of 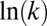 (Eq. 10
). Redox titrations return an equilibrium potential that is also greater than
(Eq. 10
). Redox titrations return an equilibrium potential that is also greater than 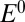 and may, accidently, match
and may, accidently, match 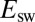 .
.
Histidine Variant Exhibits the Fastest (In)activation Rates and a Slightly Biphasic Behavior.
Fig. S4 and Fig. 2 summarize the results obtained with the V74H mutant, which exhibits the fastest rates of equilibration between active and inactive states. Fig. S4 shows that the hypothesis that a single inactive state is reversibly formed at high potential in a redox-dependent process that is defined by Eq. 3 leads to a satisfactory description of the CV data.
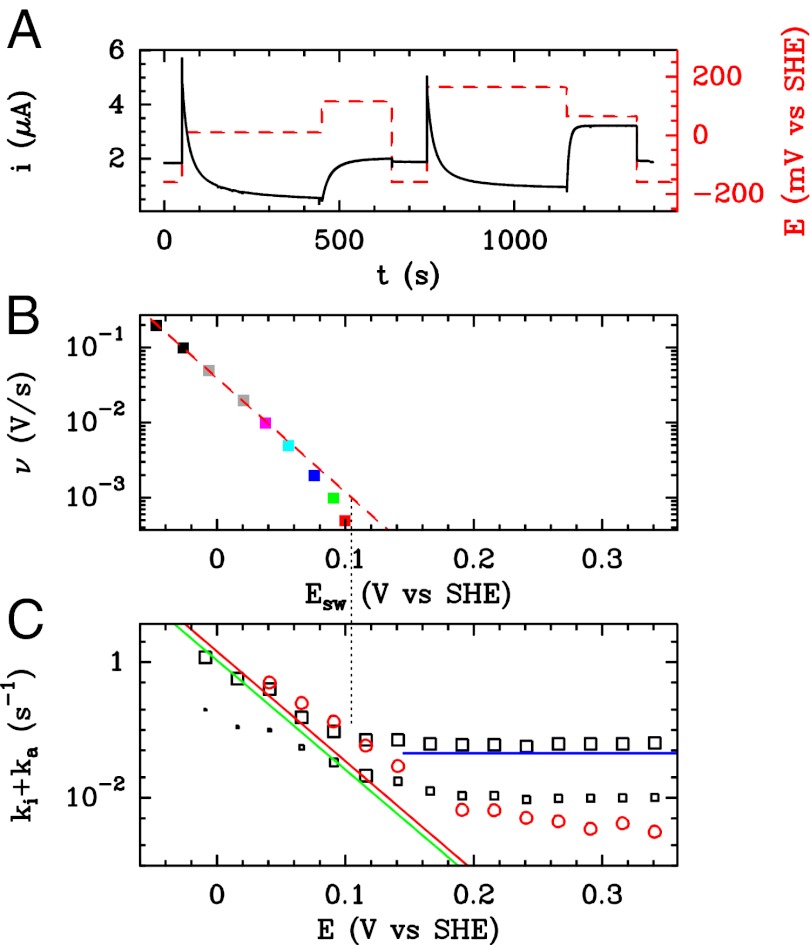
Fig. 2.
Characterization of the V74H mutant and comparison with the enzyme from A. aeolicus. (A) The result of a CA experiment performed with the V74H mutant. The electrode potential was stepped according to the sequence 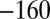 ,
, 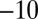 ,
, 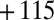 ,
, 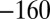 ,
, 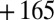 ,
, 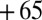 ,
, 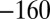 mV vs. SHE. (B) Change in
mV vs. SHE. (B) Change in 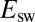 against scan rate, for V74H, fitted to Eq. 10
. (C) Open squares show the time constants for V74H, determined by fitting the sum of two exponential functions to CA traces like those in A; the symbols that mark the slower time constant have a surface that is proportional to the relative amplitude of the slow phase. The blue line in C indicates the value of
against scan rate, for V74H, fitted to Eq. 10
. (C) Open squares show the time constants for V74H, determined by fitting the sum of two exponential functions to CA traces like those in A; the symbols that mark the slower time constant have a surface that is proportional to the relative amplitude of the slow phase. The blue line in C indicates the value of 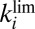 determined by fitting portions of CVs recorded in the high-potential range (Fig. S4C and Eq. 5
). The green line in C shows the rate of reactivation
determined by fitting portions of CVs recorded in the high-potential range (Fig. S4C and Eq. 5
). The green line in C shows the rate of reactivation 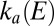 determined by fitting portions of CVs recorded in the intermediate range of potential (Fig. S4B and Eq. 7
). The red line shows the rate of reactivation
determined by fitting portions of CVs recorded in the intermediate range of potential (Fig. S4B and Eq. 7
). The red line shows the rate of reactivation 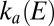 at low potential, determined by fitting the change in switch potential against scan rate (B and Eq. 10
). The open red circles in C show the time constants measured by fitting CA traces recorded with the
at low potential, determined by fitting the change in switch potential against scan rate (B and Eq. 10
). The open red circles in C show the time constants measured by fitting CA traces recorded with the 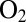 -resistant enzyme from A. aeolicus under the same conditions, 40 °C, pH 5.5, 1 atm of
-resistant enzyme from A. aeolicus under the same conditions, 40 °C, pH 5.5, 1 atm of 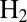 ,
, 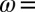 3,000 rpm.
3,000 rpm.
However, the CA data obtained with the V74H mutant attest to the formation of more than one inactive state. Indeed, the current transients are better described by a sum of two exponentials than by a single exponential function. The deviation from a clean exponential decay is clear, for example, on the current traces shown in Fig. 2A . Fitting a sum of two exponential functions to these data returned the time constants shown as open black squares in Fig. 2C ; the symbols that mark the slower time constant have a surface that is proportional to the relative amplitude of the slow phase, ranging from 1/2.5 at high potential to about 1/45 at low potential. The correspondence between the rates of the largest-amplitude transients and the lines in Fig. 2C (deduced from the interpretation of the voltammetry) shows that analyzing the voltammetric data with a model that assumes the formation of a single inactive state returns the rate of (in)activation that corresponds to the major species.
Fig. 2C
compares the time constants of (in)activation determined in CA experiments carried out with the V74H mutant (open black squares) and the 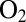 -resistant enzyme from A. aeolicus (open red circles) under the same conditions. The fast reactivation phase that dominates the V74H transients is faster than in A. aeolicus (the latter exhibits monophasic transients) (15). The slow phase of V74H has about the same rate as the unique phase of A. aeolicus NiFe hydrogenase.
-resistant enzyme from A. aeolicus (open red circles) under the same conditions. The fast reactivation phase that dominates the V74H transients is faster than in A. aeolicus (the latter exhibits monophasic transients) (15). The slow phase of V74H has about the same rate as the unique phase of A. aeolicus NiFe hydrogenase.
We repeated the above electrochemical characterization of the V74N and V74H mutants with 14 other V74 mutants, and we found that the above conclusions are always true: The model that assumes the formation of a single inactive state describes well the CV data, showing (i) that this reversible (in)activation is responsible for the major voltammetric features in all cases and (ii) that the mutation of the position-74 valine affects the rate but not the mechanism of this process. However, many mutants, like V74H, exhibit nonideal (biphasic) behavior in CA experiments. When the CA traces reveal that two inactive states are formed and/or reactivated on the timescale of the electrochemical experiments, the CVs inform on the inactive state whose formation or activation dominates the chronoamperometric transients.
Hydrophilic Position-74 Side Chains Accelerate Anaerobic (In)activation.
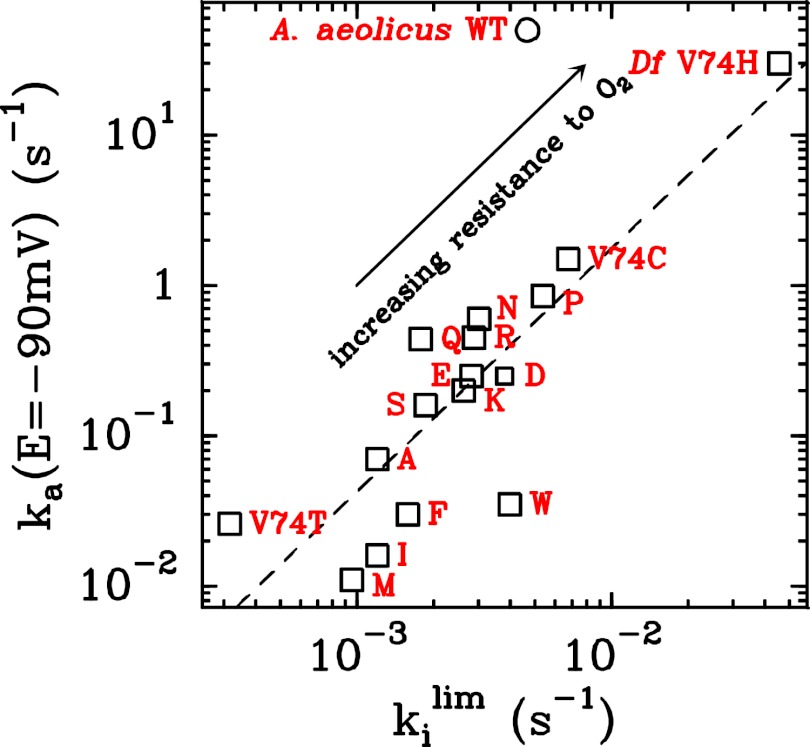
We analyzed the data obtained with all mutants and collected the results in Fig. 3, which shows the rate of reactivation 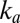 at −90 mV (an arbitrary value) against the limiting value of
at −90 mV (an arbitrary value) against the limiting value of 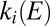 at high potential (compare Eqs. 3
).
at high potential (compare Eqs. 3
).
Fig. 3.
The rate of reactivation 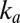 at
at 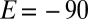 mV plotted against the rate of inactivation at high potential for all D. fructosovorans NiFe hydrogenase mutants (squares; the red letter indicates the position-74 residue) and the
mV plotted against the rate of inactivation at high potential for all D. fructosovorans NiFe hydrogenase mutants (squares; the red letter indicates the position-74 residue) and the 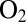 -resistant enzyme from A. aeolicus (open circle).
-resistant enzyme from A. aeolicus (open circle).
Fig. 3 and Table S1 show that substituting V74 may change the rate of reactivation by more than three orders of magnitude, from 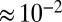 s for V74M to
s for V74M to 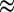 30 s−1 for V74H (at −90 mV, pH 5.5, 40 °C). The rate of reactivation of the histidine mutant is 20 times that of the V74C mutant, and close to that observed with the O2-tolerant enzyme from A. aeolicus (4, 15).
30 s−1 for V74H (at −90 mV, pH 5.5, 40 °C). The rate of reactivation of the histidine mutant is 20 times that of the V74C mutant, and close to that observed with the O2-tolerant enzyme from A. aeolicus (4, 15).
The mutants that show the fastest reactivation rates are those where valine is replaced by a polar amino acid (threonine is an exception). The pKa of the position-74 side chain does not seem be determining, because, for example, the V74K and V74E mutants reactivate at about the same rate. Therefore, the rates k i and k a are not dependent on a proton transfer mediated by the position-74 side chain.
Fig. 3 shows that there is a strong positive correlation between the rate of reactivation at a low potential, k
a(E = −90 mV), and the rate of inactivation at high potential, 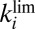 . The CVs shown in this paper illustrate this correlation: The V74N mutant inactivates more slowly at high potential and reactivates more slowly (hence at a lower potential) than the V74H mutant (compare Fig. 1A
and Fig. S4A). The relation between
. The CVs shown in this paper illustrate this correlation: The V74N mutant inactivates more slowly at high potential and reactivates more slowly (hence at a lower potential) than the V74H mutant (compare Fig. 1A
and Fig. S4A). The relation between 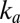 and
and 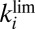 shows that, unexpectedly, the mutations affect the rate of a step that is common to both processes.
shows that, unexpectedly, the mutations affect the rate of a step that is common to both processes.
Mutants That (In)activate More Quickly Under Anaerobic Conditions Resist Better.
We tested the O2 sensitivity of all mutants, and we found that the mutants that exhibit the fastest rates of (in)activation are also those that exhibit the greatest resistance to O2.
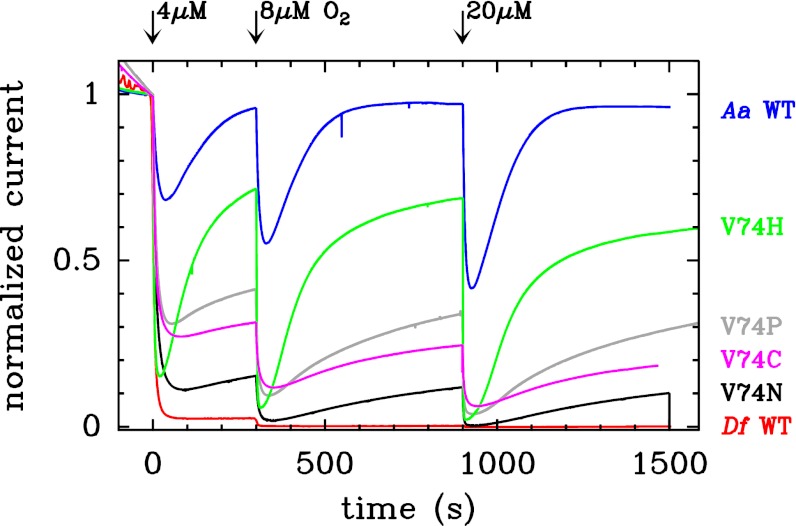
Fig. 4 shows how transient expositions to 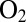 affect the activity of the most resistant mutants (additional results in Fig. S5). The experiments were carried out by poising the electrode potential at
affect the activity of the most resistant mutants (additional results in Fig. S5). The experiments were carried out by poising the electrode potential at 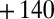 mV vs. SHE, under an atmosphere of
mV vs. SHE, under an atmosphere of  , and repeatedly injecting in the cell solution small amounts of an
, and repeatedly injecting in the cell solution small amounts of an  -saturated buffer, reaching concentrations of 4, 8 and 20 μM. After each injection,
-saturated buffer, reaching concentrations of 4, 8 and 20 μM. After each injection,  is flushed away by the stream of
is flushed away by the stream of  , and its concentration decreases exponentially with time, with a time constant of about 20 s (26). The red and blue traces in Fig. 4 can be used to benchmark the
, and its concentration decreases exponentially with time, with a time constant of about 20 s (26). The red and blue traces in Fig. 4 can be used to benchmark the 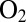 tolerance of the mutants. WT D. fructosovorans NiFe hydrogenase quickly loses nearly all activity after the first exposure to
tolerance of the mutants. WT D. fructosovorans NiFe hydrogenase quickly loses nearly all activity after the first exposure to 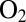 (red trace), whereas the enzyme from A. aeolicus (blue trace) recovers activity after each injection. The time constant of the reactivation after the enzyme has been exposed to
(red trace), whereas the enzyme from A. aeolicus (blue trace) recovers activity after each injection. The time constant of the reactivation after the enzyme has been exposed to 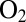 (
(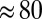 s) is equal to the time constant of anaerobic equilibration between the active and the inactive state [
s) is equal to the time constant of anaerobic equilibration between the active and the inactive state [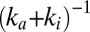 , open red circles in Fig. 2C
], which implies that anaerobic oxidation and reaction with
, open red circles in Fig. 2C
], which implies that anaerobic oxidation and reaction with 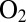 form the same inactive state (see discussion of figure 7 in ref. 4).
form the same inactive state (see discussion of figure 7 in ref. 4).
Fig. 4.
Effect of transient exposure to 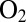 on the turnover rate of WT D. fructosovorans NiFe hydrogenase (red); the V74H (green), V74P (gray), V74N (black), and V74C (purple) mutants; and the WT enzyme from A. aeolicus (blue). All experiments were performed at 40 °C,
on the turnover rate of WT D. fructosovorans NiFe hydrogenase (red); the V74H (green), V74P (gray), V74N (black), and V74C (purple) mutants; and the WT enzyme from A. aeolicus (blue). All experiments were performed at 40 °C, 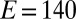 mV vs. SHE, pH 5.5, under 1 atm of
mV vs. SHE, pH 5.5, under 1 atm of 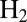 ,
, 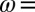 3,000 rpm.
3,000 rpm.
Regarding the hydrogenases from D. fructosovorans, we observed that the V74 mutations have little effect on the bimolecular rate of reaction with 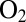 (the parameter we called
(the parameter we called 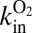 in ref. 24) unless diffusion along the channel is so slow that the diffusion step limits the rate of inactivation, as is the case for V74Q, V74E, and V74M (24). For all other mutants, the rate-limiting step for the reaction with
in ref. 24) unless diffusion along the channel is so slow that the diffusion step limits the rate of inactivation, as is the case for V74Q, V74E, and V74M (24). For all other mutants, the rate-limiting step for the reaction with 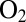 is the reaction at the active site (24), and substituting V74 results in a smaller than twofold effect on the rate of reaction with
is the reaction at the active site (24), and substituting V74 results in a smaller than twofold effect on the rate of reaction with 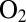 : This rate appears to be independent of the nature of the position-74 side chain.
: This rate appears to be independent of the nature of the position-74 side chain.
The purple, gray, and green traces in Fig. 4 show the response of the V74H, V74P, and V74C mutants to transient exposures to  . The histidine variant reactivates as quickly as the enzymes from A. aeolicus, consistent with the observation in Fig. 2C
that the sum
. The histidine variant reactivates as quickly as the enzymes from A. aeolicus, consistent with the observation in Fig. 2C
that the sum 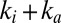 takes the same value for the two enzymes at the potential used in the experiment in Fig. 4 (
takes the same value for the two enzymes at the potential used in the experiment in Fig. 4 (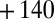 mV vs. SHE). The experiment in Fig. 4 clearly shows that the reactivation after exposure to
mV vs. SHE). The experiment in Fig. 4 clearly shows that the reactivation after exposure to 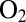 is not complete, but full activity was recovered after a 800-s poise at
is not complete, but full activity was recovered after a 800-s poise at 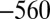 mV (Fig. S6), suggesting that at least two inactive states have been formed and that they reactivate at different rates. This conclusion was confirmed by FTIR experiments carried out in the absence of potential control (Fig. S7). After aerobic purification, the V74H mutant is mostly in the NiA state. After reduction and reoxidation with air, the FTIR signal shows that two major species have been formed: One has a typical NiB FTIR signature, and the other (with a CO band at 1,943 cm) is unprecedented.
mV (Fig. S6), suggesting that at least two inactive states have been formed and that they reactivate at different rates. This conclusion was confirmed by FTIR experiments carried out in the absence of potential control (Fig. S7). After aerobic purification, the V74H mutant is mostly in the NiA state. After reduction and reoxidation with air, the FTIR signal shows that two major species have been formed: One has a typical NiB FTIR signature, and the other (with a CO band at 1,943 cm) is unprecedented.
Kinetic Determinants of 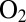 Tolerance Are
Tolerance Are 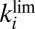 and
and 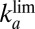 , Not
, Not 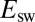 or the Low-Potential Part of
or the Low-Potential Part of 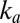 (E).
(E).
Certain NiFe hydrogenases are 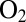 resistant because they react with
resistant because they react with 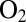 to form a single inactive state, NiB, that reactivates more quickly than the NiB state of standard hydrogenases. So far, this kinetic property has been related only to the rate of reactivation at low potential or, equivalently, to the value of the switch potential (and indeed, the two are related to each other by Eq. 10
).
to form a single inactive state, NiB, that reactivates more quickly than the NiB state of standard hydrogenases. So far, this kinetic property has been related only to the rate of reactivation at low potential or, equivalently, to the value of the switch potential (and indeed, the two are related to each other by Eq. 10
).
The experiments reported here illustrate this relation: The mutants that exhibit the fastest reactivation rates (at low potential under anaerobic conditions) are also those that reactivate quickly, at high potential, after exposure to 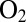 . However, it is important to realize that it is the large value of the inactivation rate constant (
. However, it is important to realize that it is the large value of the inactivation rate constant (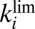 in Eq. 3
, Fig. S1A) that is beneficial. Indeed, if the same inactive state is formed under aerobic and anaerobic conditions, then the recovery of activity after the enzyme has been inhibited by
in Eq. 3
, Fig. S1A) that is beneficial. Indeed, if the same inactive state is formed under aerobic and anaerobic conditions, then the recovery of activity after the enzyme has been inhibited by 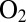 occurs with a time constant
occurs with a time constant 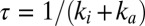 , which, at high potential, depends mainly on
, which, at high potential, depends mainly on 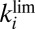 ; a fast rate of anaerobic inactivation at high potential is therefore synonymous with fast recovery of activity after the enzyme has been exposed to
; a fast rate of anaerobic inactivation at high potential is therefore synonymous with fast recovery of activity after the enzyme has been exposed to 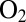 . The fact that
. The fact that 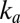 at low potential and
at low potential and 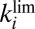 are correlated (Fig. 3) is the only reason
are correlated (Fig. 3) is the only reason 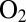 tolerance seems to relate to
tolerance seems to relate to 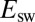 .
.
Future Directions.
It has recently been suggested that certain enzymes are 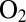 tolerant because a 4Fe3S cluster that is proximal from the active site prevents the formation of NiA. However, the fact that this cluster has a very high reduction potential (11) should not favor fast electron transfer toward the active site and fast reduction of NiB. Recent results show that modifying the proximal cluster has no effect on the switch potential (27) and, therefore, on the rate of reactivation. The reason the inactive state reactivates quickly in
tolerant because a 4Fe3S cluster that is proximal from the active site prevents the formation of NiA. However, the fact that this cluster has a very high reduction potential (11) should not favor fast electron transfer toward the active site and fast reduction of NiB. Recent results show that modifying the proximal cluster has no effect on the switch potential (27) and, therefore, on the rate of reactivation. The reason the inactive state reactivates quickly in 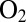 -tolerant NiFe hydrogenases has yet to be understood.
-tolerant NiFe hydrogenases has yet to be understood.
The observation herein that hydrophilic position-74 residues accelerate the reactivation of the enzyme from D. fructosovorans is reminiscent of the recent finding that water-filled cavities are present in the environment of the NiFe active site of the 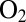 -tolerant membrane-bound hydrogenase from R. eutropha (8). It has been suggested that they are part of a hydrophilic channel that guides away from the active site the water molecules that are constantly produced upon complete reduction of the attacking
-tolerant membrane-bound hydrogenase from R. eutropha (8). It has been suggested that they are part of a hydrophilic channel that guides away from the active site the water molecules that are constantly produced upon complete reduction of the attacking 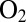 (8). This has not been supported yet by the results of mutagenesis experiments. In R. eutropha, mutating amino acids that shape this hydrophilic cavity (G80 and C81) have no effect on the inhibition constant relative to
(8). This has not been supported yet by the results of mutagenesis experiments. In R. eutropha, mutating amino acids that shape this hydrophilic cavity (G80 and C81) have no effect on the inhibition constant relative to 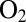 (1), and in D. fructosovorans, the reverse mutations (Y77G and V78C) have no effect on the bimolecular rate of inhibition by
(1), and in D. fructosovorans, the reverse mutations (Y77G and V78C) have no effect on the bimolecular rate of inhibition by 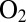 (28). Whether these amino acids affect the rates of anaerobic (in)activation now deserves investigation.
(28). Whether these amino acids affect the rates of anaerobic (in)activation now deserves investigation.
Materials and Methods
The D. fructosovorans NiFe hydrogenase mutants were purified as described previously (12). Table S1 lists their purification yields, specific activities, and Michaelis constants for 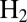 . The purification of the enzyme from A. aeolicus is described in ref. 15. All voltammetric experiments were carried out with the enzyme molecules covalently attached (29) to a rotating-disk pyrolytic graphite edge electrode, in a glove box filled with nitrogen, using the equipment described previously (12). We analyzed the electrochemical data using the in-house programs SOAS and Qsoas. The former is available free and free of charge on our Web site at http://bip.cnrs-mrs.fr/bip06/software.html (30). Qsoas can be used to simultaneously fit a series of datasets by forcing certain parameters to have the same values for all datasets: This was useful for finding the best values of
. The purification of the enzyme from A. aeolicus is described in ref. 15. All voltammetric experiments were carried out with the enzyme molecules covalently attached (29) to a rotating-disk pyrolytic graphite edge electrode, in a glove box filled with nitrogen, using the equipment described previously (12). We analyzed the electrochemical data using the in-house programs SOAS and Qsoas. The former is available free and free of charge on our Web site at http://bip.cnrs-mrs.fr/bip06/software.html (30). Qsoas can be used to simultaneously fit a series of datasets by forcing certain parameters to have the same values for all datasets: This was useful for finding the best values of 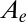 and τ defined in Eq. 5
or k and n in Eq. 7
, by fitting a series of CVs recorded over a range of scan rates.
and τ defined in Eq. 5
or k and n in Eq. 7
, by fitting a series of CVs recorded over a range of scan rates.
Supplementary Material
Acknowledgments
Our work is funded by the Centre National de la Recherche Scientifique, Aix-Marseille Université, Agence Nationale de la Recherche, City of Marseilles, Région Provence Alpes Côte d’Azur, and the Spanish Ministerio de Ciencia (Project CTQ2009-12649).
Footnotes
The authors declare no conflict of interest.
*This Direct Submission article had a prearranged editor.
†See, e.g., the experiments with D. fructosovorans NiFe hydrogenase, figure S4 in ref. 15; Aa NiFe hydrogenase, figure 6 in ref. 15; and D. vulgaris MF NiFe hydrogenase, figure SI4 in ref. 18.
‡For the enzyme from A. aeolicus, 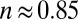 under the same conditions (pH 5.5). This value is lower at a greater pH: We determined
under the same conditions (pH 5.5). This value is lower at a greater pH: We determined 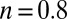 at pH 6 and n = 0.66 at pH 7 and 8 (15).
at pH 6 and n = 0.66 at pH 7 and 8 (15).
§The interconversion between active and inactive forms is so fast in the V74H mutant that the voltammetric trace approaches steady state at 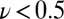 mV/s (red trace in Fig. S4A). Fig. 2B
shows that at very low scan rate, the change in
mV/s (red trace in Fig. S4A). Fig. 2B
shows that at very low scan rate, the change in 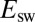 against
against 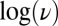 deviates from the red dashed line and tends to the potential where
deviates from the red dashed line and tends to the potential where 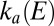 and
and 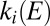 intersect (as indicated by the dotted line that connects Fig. 2B
and 2C
). This steady-state limit (the near lack of hysteresis observed in the
intersect (as indicated by the dotted line that connects Fig. 2B
and 2C
). This steady-state limit (the near lack of hysteresis observed in the 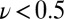 mV/s scan rate trace in Fig. S4A) has not been achieved with any other hydrogenase. Therefore, for all enzymes but the V74H mutant, the switch potential is always lower (possibly much lower) than the value that would be obtained in the low scan-rate limit.
mV/s scan rate trace in Fig. S4A) has not been achieved with any other hydrogenase. Therefore, for all enzymes but the V74H mutant, the switch potential is always lower (possibly much lower) than the value that would be obtained in the low scan-rate limit.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1212258109/-/DCSupplemental.
References
- 1.Ludwig M, Cracknell JA, Vincent KA, Armstrong FA, Lenz O. Oxygen-tolerant H2 oxidation by membrane-bound [NiFe] hydrogenases of ralstonia species. Coping with low level H2 in air. J Biol Chem. 2009;284(1):465–477. doi: 10.1074/jbc.M803676200. [DOI] [PubMed] [Google Scholar]
- 2.Abou Hamdan A, et al. Understanding and tuning the catalytic bias of hydrogenase. J Am Chem Soc. 2012;134(20):8368–8371. doi: 10.1021/ja301802r. [DOI] [PubMed] [Google Scholar]
- 3.McIntosh CL, Germer F, Schulz R, Appel J, Jones AK. The [NiFe]-hydrogenase of the cyanobacterium Synechocystis sp. PCC 6803 works bidirectionally with a bias to H2 production. J Am Chem Soc. 2011;133(29):11308–11319. doi: 10.1021/ja203376y. [DOI] [PubMed] [Google Scholar]
- 4.Pandelia ME, et al. Membrane-bound hydrogenase I from the hyperthermophilic bacterium Aquifex aeolicus: Enzyme activation, redox intermediates and oxygen tolerance. J Am Chem Soc. 2010;132(20):6991–7004. doi: 10.1021/ja910838d. [DOI] [PubMed] [Google Scholar]
- 5.Cracknell JA, Vincent KA, Armstrong FA. Enzymes as working or inspirational electrocatalysts for fuel cells and electrolysis. Chem Rev. 2008;108(7):2439–2461. doi: 10.1021/cr0680639. [DOI] [PubMed] [Google Scholar]
- 6.Fernandez VM, Hatchikian EC, Cammack R. Properties and reactivation of two different deactivated forms of Desulfovibrio gigas hydrogenase. Biochim Biophys Acta. 1985;832:69–79. [Google Scholar]
- 7.Cracknell JA, Wait AF, Lenz O, Friedrich B, Armstrong FA. A kinetic and thermodynamic understanding of O2 tolerance in [NiFe]-hydrogenases. Proc Natl Acad Sci USA. 2009;106(49):20681–20686. doi: 10.1073/pnas.0905959106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Fritsch J, et al. The crystal structure of an oxygen-tolerant hydrogenase uncovers a novel iron-sulphur centre. Nature. 2011;479(7372):249–252. doi: 10.1038/nature10505. [DOI] [PubMed] [Google Scholar]
- 9.Shomura Y, Yoon KSS, Nishihara H, Higuchi Y. Structural basis for a [4Fe-3S] cluster in the oxygen-tolerant membrane-bound [NiFe]-hydrogenase. Nature. 2011;479(7372):253–256. doi: 10.1038/nature10504. [DOI] [PubMed] [Google Scholar]
- 10.Volbeda A, et al. X-ray crystallographic and computational studies of the O2-tolerant [NiFe]-hydrogenase 1 from Escherichia coli. Proc Natl Acad Sci USA. 2012;109(14):5305–5310. doi: 10.1073/pnas.1119806109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Pandelia ME, et al. Characterization of a unique [FeS] cluster in the electron transfer chain of the oxygen tolerant [NiFe] hydrogenase from Aquifex aeolicus . Proc Natl Acad Sci USA. 2011;108(15):6097–6102. doi: 10.1073/pnas.1100610108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Liebgott PP, et al. Original design of an oxygen-tolerant [NiFe] hydrogenase: Major effect of a valine-to-cysteine mutation near the active site. J Am Chem Soc. 2011;133(4):986–997. doi: 10.1021/ja108787s. [DOI] [PubMed] [Google Scholar]
- 13.Léger C, Bertrand P. Direct electrochemistry of redox enzymes as a tool for mechanistic studies. Chem Rev. 2008;108(7):2379–2438. doi: 10.1021/cr0680742. [DOI] [PubMed] [Google Scholar]
- 14.Jones AK, et al. Enzyme electrokinetics: Electrochemical studies of the anaerobic interconversions between active and inactive states of Allochromatium vinosum [NiFe]-hydrogenase. J Am Chem Soc. 2003;125(28):8505–8514. doi: 10.1021/ja035296y. [DOI] [PubMed] [Google Scholar]
- 15.Fourmond V, Infossi P, Giudici-Orticoni MT, Bertrand P, Léger C. “Two-step” chronoamperometric method for studying the anaerobic inactivation of an oxygen tolerant NiFe hydrogenase. J Am Chem Soc. 2010;132(13):4848–4857. doi: 10.1021/ja910685j. [DOI] [PubMed] [Google Scholar]
- 16.Limoges B, Savéant JM. Catalysis by immobilized redox enzymes. Diagnosis of inactivation and reactivation effects through odd cyclic voltammetric responses. J Electroanal Chem. 2004;562:43–52. [Google Scholar]
- 17.Léger C, Jones AK, Albracht SPJ, Armstrong FA. Effect of a dispersion of interfacial electron transfer rates on steady state catalytic electron transport in [NiFe]-hydrogenase and other enzymes. J Phys Chem B. 2002;106:13058–13063. [Google Scholar]
- 18.Millo D, Hildebrandt P, Pandelia ME, Lubitz W, Zebger I. SEIRA spectroscopy of the electrochemical activation of an immobilized [NiFe] hydrogenase under turnover and non-turnover conditions. Angew Chem Int Ed Engl. 2011;50(11):2632–2634. doi: 10.1002/anie.201006646. [DOI] [PubMed] [Google Scholar]
- 19.Vincent KA, et al. Electrochemical definitions of O2 sensitivity and oxidative inactivation in hydrogenases. J Am Chem Soc. 2005;127(51):18179–18189. doi: 10.1021/ja055160v. [DOI] [PubMed] [Google Scholar]
- 20.Lukey MJ, et al. How Escherichia coli is equipped to oxidize hydrogen under different redox conditions. J Biol Chem. 2010;285(6):3928–3938. doi: 10.1074/jbc.M109.067751. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Lauterbach L, et al. The hydrogenase subcomplex of the NAD+-reducing [NiFe] hydrogenase from Ralstonia eutropha - Insights into catalysis and redox interconversions. Eur J Inorg Chem. 2011;2011:1067–1079. [Google Scholar]
- 22.Wang PH, Blumberger J. Mechanistic insight into the blocking of CO diffusion in [NiFe]-hydrogenase mutants through multiscale simulation. Proc Natl Acad Sci USA. 2012;109(17):6399–6404. doi: 10.1073/pnas.1121176109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Leroux F, et al. Experimental approaches to kinetics of gas diffusion in hydrogenase. Proc Natl Acad Sci USA. 2008;105(32):11188–11193. doi: 10.1073/pnas.0803689105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Liebgott PP, et al. Relating diffusion along the substrate tunnel and oxygen sensitivity in hydrogenase. Nat Chem Biol. 2010;6(1):63–70. doi: 10.1038/nchembio.276. [DOI] [PubMed] [Google Scholar]
- 25.Dementin S, et al. Introduction of methionines in the gas channel makes [NiFe] hydrogenase aero-tolerant. J Am Chem Soc. 2009;131(29):10156–10164. doi: 10.1021/ja9018258. [DOI] [PubMed] [Google Scholar]
- 26.Léger C, Dementin S, Bertrand P, Rousset M, Guigliarelli B. Inhibition and aerobic inactivation kinetics of Desulfovibrio fructosovorans NiFe hydrogenase studied by protein film voltammetry. J Am Chem Soc. 2004;126(38):12162–12172. doi: 10.1021/ja046548d. [DOI] [PubMed] [Google Scholar]
- 27.Lukey MJ, et al. Oxygen-tolerant [NiFe]-hydrogenases: The individual and collective importance of supernumerary cysteines at the proximal Fe-S cluster. J Am Chem Soc. 2011;133(42):16881–16892. doi: 10.1021/ja205393w. [DOI] [PubMed] [Google Scholar]
- 28.Leroux F, et al. Is engineering O2-tolerant hydrogenases just a matter of reproducing the active sites of the naturally occurring O2-resistant enzymes? Int J Hydrogen Energy. 2010;35:10770–10777. [Google Scholar]
- 29.Rüdiger O, Abad JM, Hatchikian EC, Fernandez VM, De Lacey AL. Oriented immobilization of Desulfovibrio gigas hydrogenase onto carbon electrodes by covalent bonds for nonmediated oxidation of H2 . J Am Chem Soc. 2005;127(46):16008–16009. doi: 10.1021/ja0554312. [DOI] [PubMed] [Google Scholar]
- 30.Fourmond V, et al. Soas: A free software to analyse electrochemical data and other one-dimensional signals. Bioelectrochemistry. 2009;76:141–147. doi: 10.1016/j.bioelechem.2009.02.010. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.