Mechanism for adaptive remodeling of the bacterial flagellar switch

Abstract

The bacterial flagellar motor has been shown in previous work to adapt to changes in the steady-state concentration of the chemotaxis signaling molecule, CheY-P, by changing the FliM content. We show here that the number of FliM molecules in the motor and the fraction of FliM molecules that exchange depend on the direction of flagellar rotation, not on CheY-P binding per se. Our results are consistent with a model in which the structural differences associated with the direction of rotation modulate the strength of FliM binding. When the motor spins counterclockwise, FliM binding strengthens, the fraction of FliM molecules that exchanges decreases, and the ring content increases. The larger number of CheY-P binding sites enhances the motor’s sensitivity, i.e., the motor adapts. An interesting unresolved question is how additional copies of FliM might be accommodated.

Motile Escherichia coli swim by rotating helical flagellar filaments with tiny, reversible, ion-driven motors (1). Each motor switches between clockwise (CW) and counterclockwise (CCW) states. Modulation of reversal frequency allows the bacterium to swim toward attractants or away from repellents (chemotaxis). CW rotation is promoted by the binding of an activated cytoplasmic response regulator, CheY-P, to the C-ring component FliM. CheY-P binds to FliM and then to FliN (2), triggering a change in the conformation of FliG, a component at the periphery of the C-ring engaged by the stator element MotA.

CheY-P serves to link the input of the chemotaxis network (the receptors) to the output (the flagellar motors). An important feature of the chemotaxis network is precise adaptation to chemical stimuli, which involves resetting of the motor output to the prestimulus output, measured in terms of the probability of CW rotation (CW_bias). Adaptation regulates the chemotactic sensitivity and extends the range of signal detection, enhancing chances of survival. Until recently, adaptation was believed to occur only at the level of chemoreceptors (3). Recent experiments revealed that the motor itself has the ability to adapt to varying CheY-P levels by dynamically increasing the content of FliM, a process that is independent of receptor methylation and demethylation (4). This helps the cell match the motor’s operating point to the levels of CheY-P set by the chemotaxis signaling pathway. However, the mechanism by which the motor detects CheY-P levels and remodels the FliM ring is unknown (5). Here, we dissect this mechanism.

Results and Discussion

Effect of Direction of Rotation on FliM Numbers.

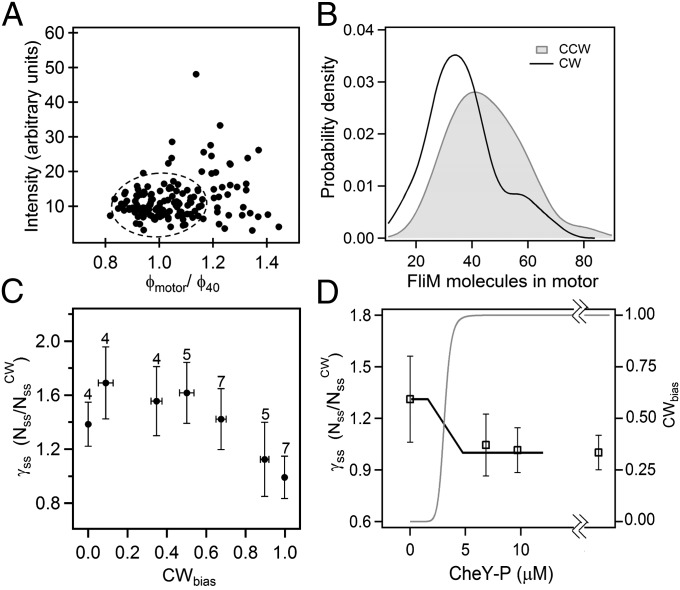
We used total internal reflection fluorescence (TIRF) microscopy to visualize the numbers of molecules of FliM-eYFP (FliM fused to yellow fluorescence protein) in individual motors of tethered cells of E. coli spinning exclusively CW or CCW. The CW cells either contained large amounts of CheY-P or were deleted for cheY and expressed a FliG varient locked in the CW state, which does not affect other motor properties (6, 7). CCW cells were simply deleted for cheY. The TIRF measurements were conducted under identical laser power and focusing conditions and motor intensities were calculated by summing over pixel intensity values within a 450-nm diameter circular mask around the motor (Materials and Methods and SI Text). Studies have shown that there are multiple FliM assemblies diffusing in the cell body that are probably prototypical motors (8). The limited resolution of wide-field fluorescence microscopy means that it is not possible to resolve such a diffusing FliM spot that is in close proximity to the motor under observation, leading to spuriously high intensities within the motor mask. However, because the tethered cell body rotates a full turn in a single-image capture, the convoluted intensity distribution would have a larger width than that of a single motor. To exclude such instances, we applied the following criterion for selection of suitable motors for further analysis. From TIRF images of 40-nm fluorescent beads (comparable to the known motor diameter of ∼45 nm), we found the apparent mean diameter (φ₄₀, SI Text) and normalized all of the motor diameters (φ_motor) by this number. A plot of motor intensity vs. normalized diameter is shown in Fig. 1A. Candidate motors were selected if their diameters were within the full width at half maximum of the distribution for the beads. To exclude cases where the separation between diffusing and fixed motors might be too low to make a measurable difference in the width, we imposed a cutoff on intensities (less than two times mean intensity), as indicated in Fig. 1A. The selected region includes about 75% of our total data (72 CW motors and 89 CCW motors).

Fig. 1.

TIRF measurements. (A) Variations in motor intensities (arbitrary units) over a range of apparent motor diameters (φ_motor) normalized by the mean apparent diameter of 40-nm fluorescent beads (φ₄₀). The encircled region indicates the data points selected for further analysis. (B) FliM population distribution inferred from intensity measurements for CCW motors (shaded curve, 63 motors) and CW fliG mutant motors (solid curve, 57 motors), both strains deleted for cheY. Gaussian fits to the data: μ = 43.7, σ = 22.9 (CCW) and μ = 34, σ = 12 (CW), where μ is mean and σ is SD. (C) CW_bias values (0 < CW_bias < 1) for wild-type cells expressing different levels of CheY binned in six bins of equal width. The averages of relative FliM numbers (γ_ss) and the CW_bias values for each bin are shown. SEs are indicated and numbers on error bars are sample sizes. (D) Relative motor FliM numbers as a function of CheY level plotted with respective SEs. The last point is the population found for the CW fliG mutant. Solid curve is a guide to the eye. Shaded curve is the sensitivity curve obtained by Cluzel and coworkers (11).

Previous cryo-EM studies of basal bodies in Salmonella of the CW fliG mutation studied here have shown that the C-ring has an average 34-fold symmetry (9). The average intensity obtained from fitting a Gaussian curve to the mutant CW motor intensity distribution was normalized such that the FliM molecules corresponded to 34, yielding the average fluorescence intensity of a single FliM-YFP molecule, I_mol, in our setup. Motor intensity data from all other strains were normalized by I_mol to obtain the number of FliM molecules in their motors. The unbiased kernel density estimations of the data from the CW (fliG mutant) and CCW cells are shown in Fig. 1B (raw data shown in Fig. S1). The ratio of the means obtained from fits to the peaks in these distributions showed that the number of FliM subunits in the CCW state was on average 1.29 times larger than the number of FliM subunits in the CW state, indicating ∼44 molecules in the CCW state. This ratio was unaffected by the selection criterion applied in Fig. 1A. An independent two-sample t test indicated that this difference was significant (P < 0.001). We did not observe significant correlation between FliM numbers and rotational velocities over a range of speeds typical for tethered cells (1–8 Hz).

Because the results of the cryo-EM studies might have been biased, we consider the ratio of the average number of FliM subunits in a given motor to that observed for motors in the CW state to be more significant than the absolute number, based on the assumption that 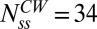. We define this ratio as 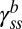, where the subscript ss refers to steady state and superscript b refers to the CW_bias.

To learn how FliM content depends upon CW bias in cells that do not spin exclusively CW or CCW, we measured motor intensities in strains wild type for fliG that expressed varying levels of CheY-P. CW_bias was calculated for each cell by analyzing recorded phase-contrast videos of tethered cell rotation for about 1 min before and also 1 min after the TIRF measurement. 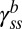decreased with increasing CW_bias, as shown in Fig. 1C. It varied gradually near CW_bias = 0.5, which is the region over which switching frequency peaks (10, 11), so the number of FliM molecules in the ring is not correlated with switching frequency.

Effect of CheY-P Concentration on FliM Numbers.

To further explore the dependence of FliM numbers on CheY-P levels, we overexpressed CheY from a pTrc-based plasmid at two different inducer concentrations: isopropyl β-D-1-thiogalactopyranoside (IPTG) = 30 μM and 50 μM. The CheY-P levels were estimated from previous calibrations of CheY-YFP expression levels for the same pTrc99A vector (12). These motors rotated exclusively CW and contained comparable FliM numbers to those in cells locked in the CW state (Fig. 1D). Given this constancy in 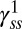at higher CheY-P levels, it is unlikely that CheY-P plays a direct role in controlling FliM content in the motor. Clearly, it plays no role in cells deleted for cheY.

Variations in Exchanging Fractions and Kinetics.

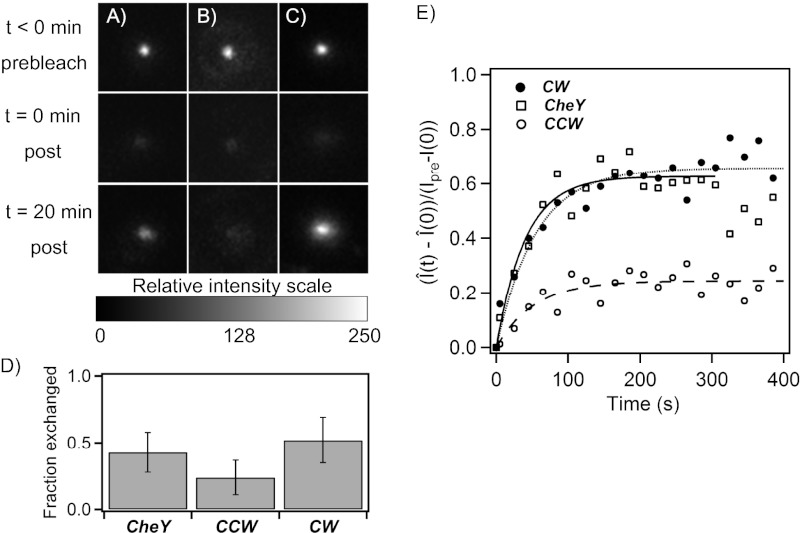
Fluorescence recovery after photobleaching (FRAP) experiments have shown that FliM molecules in the C-ring continuously exchange with a pool of FliM molecules present elsewhere in the cell body, provided that the cells contain active CheY (13–15). The dependence on CheY was not understood (16). To learn whether FliM exchange depends on CheY-P or on direction of rotation, we used FRAP to study the same kind of cells whose motor intensities were determined by TIRF. Motors were imaged before photobleaching, after photobleaching, and then again after 20 min. Photobleaching was achieved with a 7-s pulse applied with the evanescent laser field (SI Text). Fig. 2A shows the motor of a cell expressing a large amount of CheY that recovered nearly all of its initial fluorescence intensity after 20 min, due to continuous replacement of photobleached FliM molecules with unbleached molecules. Previous experiments over similar timescales have ruled out synthesis of new fluorescent molecules as reasons for exchange (13). We carried out similar experiments with cells deleted for cheY that rotated exclusively CCW. Fig. 2B shows one such motor with less recovery. To determine whether CheY was indeed responsible for the FliM exchange, we studied cells lacking CheY that expressed the clockwise FliG mutation. Fig. 2C shows one such motor that recovered nearly all of its initial fluorescence intensity after 20 min. The average fractions of FliM molecules that exchanged in the three kinds of cells are shown in Fig. 2D. These data have been corrected for the partial photobleaching of the unbound fluorescent molecules that occurs during the long bleaching pulse. When, after this pulse, some of the bleached bound molecules happen to exchange with the bleached unbound molecules, the exchange cannot be visualized, resulting in lower recoveries. However, direct epifluorescence measurements of the total fluorescence of a cell before and after the evanescent field bleaching provide information about the average reduction in total cell fluorescence during bleaching (Fig. S2). Knowing the extent of reduction (30% in our setup), one can then correct for this effect, using the mathematical model derived in SI Text. As evident in Fig. 2D a higher exchanging fraction is present in motors in CW rotation than in CCW rotation. We did not observe any significant dependence of these fractions on rotational speeds or switching frequency.

Fig. 2.

FRAP measurements. (A–C) Comparisons between motor intensities before and after recovery for (A) cells expressing large amounts of CheY with CW bias = 1 (CheY), (B) cells deleted for cheY with CW bias = 0 (CCW), and (C) cells expressing FliG locked in the CW state, with CW bias = 1 (CW). Images were taken at time points t < 0, before bleaching; t = 0, immediately after bleaching; and t > 20 min after bleaching. (D) The fraction of FliM that exchanged, corrected for bleaching of unbound molecules, is plotted for the three cases, for CheY (0.43, n = 5), CCW (0.26, n = 6), and CW (0.52, n = 6) motors, with SE bars. (E) Fluorescence recovery curves for FliM after photobleaching, corrected for bleaching of unbound molecules. The values of k_off obtained from the fits were CheY = 0.024 ± 0.003 s⁻¹, n = 8; CCW = 0.019 ± 0.005 s⁻¹, n = 13; and CW = 0.018 ± 0.002 s⁻¹, n = 28. The values for C_ss/N_ss were 0.63 ± 0.02, 0.24 ± 0.01, and 0.66 ± 0.018, respectively. The average SEs were ±0.10, ±0.04, and ±0.06, respectively.

To determine the kinetics of recovery, we measured motor intensities, I(t), every 20 s for 400 s after photobleaching (completed at t = 0). In separate experiments (Fig. S3), we determined that 400 s was adequate for fluorescence recoveries to reach a steady state in our strains. Measurements of increases in intensity following photobleaching, 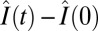, were normalized by the increment, I(t < 0) − I(0). Here I(t < 0) was the motor intensity before photobleaching and 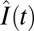was the motor intensity at any time t after photobleaching, corrected for bleaching of the unbound FliM population. Averages of such normalized FRAP recovery curves are shown in Fig. 2E. In all cases, the FliM numbers in motors were at steady state (ss) with regard to CheY-P levels, which were fixed. If 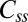is the population of fluorescent molecules in the FliM ring that exchange, and 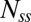is the total population of fluorescent molecules in the FliM ring, then the FRAP data can be fit by 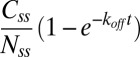, which yields the fraction of molecules that exchange, 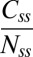, and the rate constant, k_off. The values of fractions were similar to those shown in Fig. 2D, and the values for k_off were about the same for the different strains and are given in the Fig. 2 legend. The values of k_off are in close agreement with those found in previous investigations (13); hence we did not consider more complicated FRAP models (17, 18). Knowing the FliM numbers in respective rings and the exchanging fractions, we conclude for the CW state that about 22 FliM molecules exchange 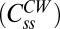and about 12 molecules do not exchange 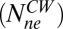. Similarly, for the CCW state, about 11 FliM molecules exchange 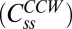and about 33 molecules do not exchange .

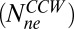Mechanism for Remodeling of FliM Ring.

A previous model for predicting the increase in FliM ring content following the addition of attractants considered only one kind of FliM binding and assumed that the dissociation kinetics for FliM exchange varied with levels of CheY-P (4). Our results reproduce previous observations of CheY affecting FliM exchange (13), but reveal that the total number of FliM molecules in the motor and the fraction of FliM molecules that exchange depend on the direction of rotation and not on CheY per se. However, the rates of FliM exchange do not depend on the direction of rotation. These observations point toward a different kind of mechanism for remodeling of the FliM ring, as explained below.

Because the timescale for FliM exchange (1/k_off ∼ 50 s) is, within a factor of 2, the same as the timescale for the remodeling of the FliM ring (∼25 s) (4), it is likely that this remodeling is effected by the exchanging FliM population. We suggest that changes in rotor conformation affect the number of sites to which FliM is tightly bound. Previous studies have suggested that a FliG molecule contains two FliM binding sites, a lower-affinity outer and a higher-affinity inner binding site (19). A recent model also suggests that FliM molecules bound to the inner sites form a stable, nonexchanging complex (20). We explored quantitatively how a change in the number of sites to which FliM is tightly bound might lead to a change in the total number of FliM molecules bound.

The equation describing the time rate of change of the number of FliM molecules in a motor, N, is

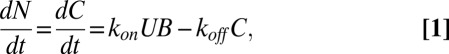where C is the number of molecules in a motor that are weakly bound and free to exchange, U is the number of unbound FliM molecules in the cell, B is the number of vacant sites, and k_on and k_off are the rate constants. At steady state (ss),

and

where N_ne is the number of molecules in a motor that are tightly bound and not able to exchange. The total number of vacant sites (B) plus the occupied sites (C and N_ne) make up the maximum binding sites available for FliM molecules in the C-ring:

With B_ss specified by Eq. 2, we can write the total number of molecules in the motor at steady state in terms of the fraction of molecules that exchange, C_ss/N_ss, as

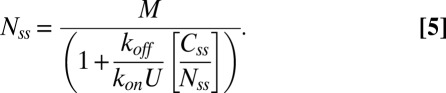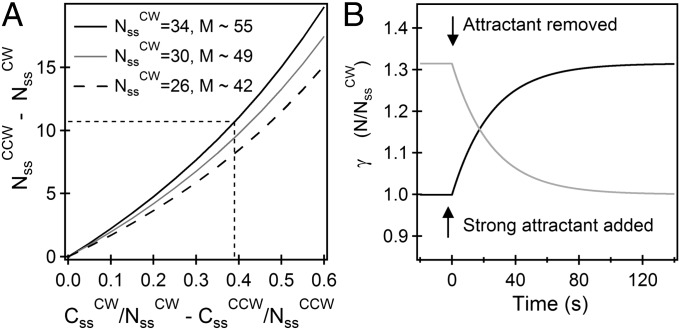
For the CCW state, we know from the FRAP experiments that k_off ∼ 0.02 s⁻¹ and from the measurements of Yuan et al. (4) that k_onU + k_off ∼ 0.04 s⁻¹, yielding k_onU ∼ 0.02 s⁻¹. We assume for the CW state that k_onU ∼ 0.02 s⁻¹, which is reasonable given that the change in conformation does not affect the off rates. The values of exchanging fractions are known experimentally. If we assume, further, that the total number of sites, M, is the same in either state, we find from Eq. 5, 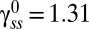(independent of M), in good agreement with the measurements of relative motor intensities made by TIRF (Fig. 1B). Thus, by two independent sets of measurements (made by TIRF and FRAP) we obtain the same ratio for FliM molecules in the CCW vs. the CW states. In Fig. 3A, the difference in the contents of the FliM rings in the two states is plotted against the difference in the exchanging fractions in the two states, which demonstrates how FliM exchange controls the ring content. The three curves correspond to different numbers of FliM molecules in the CW motor at steady state, with the black curve representing the number based on the previous EM work (9). Evidently, for the values of the exchanging fractions found in our work, the exact value of 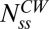does not significantly alter the difference in the numbers in the two states. As can be seen, the larger the difference is in the exchanging fractions, the larger the number of FliM molecules in the CCW motor compared with the CW motor.

Fig. 3.

FliM populations. (A) Variation in the difference between the steady-state numbers of FliM molecules in the CCW and CW states with the difference in the exchanging fractions (for the experimentally observed 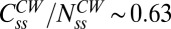). The different curves correspond to the assumed numbers of FliM molecules in the CW ring 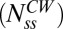, from which M is calculated (Eq. 5). For 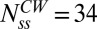and the experimentally observed difference in exchanging fractions (indicated by straight lines), there are ∼11 more FliM molecules in the CCW state, in good agreement with Fig. 1B. (B) Variations in normalized FliM populations calculated for the case of a CW cheR cheB motor subjected to the addition of a strong attractant just before t = 0 s (solid curve) or a CCW motor subjected to a repellent (shaded curve). For the solid curve, k_off = 0.02 s⁻¹, M ∼ 55, C(0)/N_ss = 0. For the shaded curve, k_off = 0.02 s⁻¹, M ∼ 55, C(0)/N_ss = 0.72.

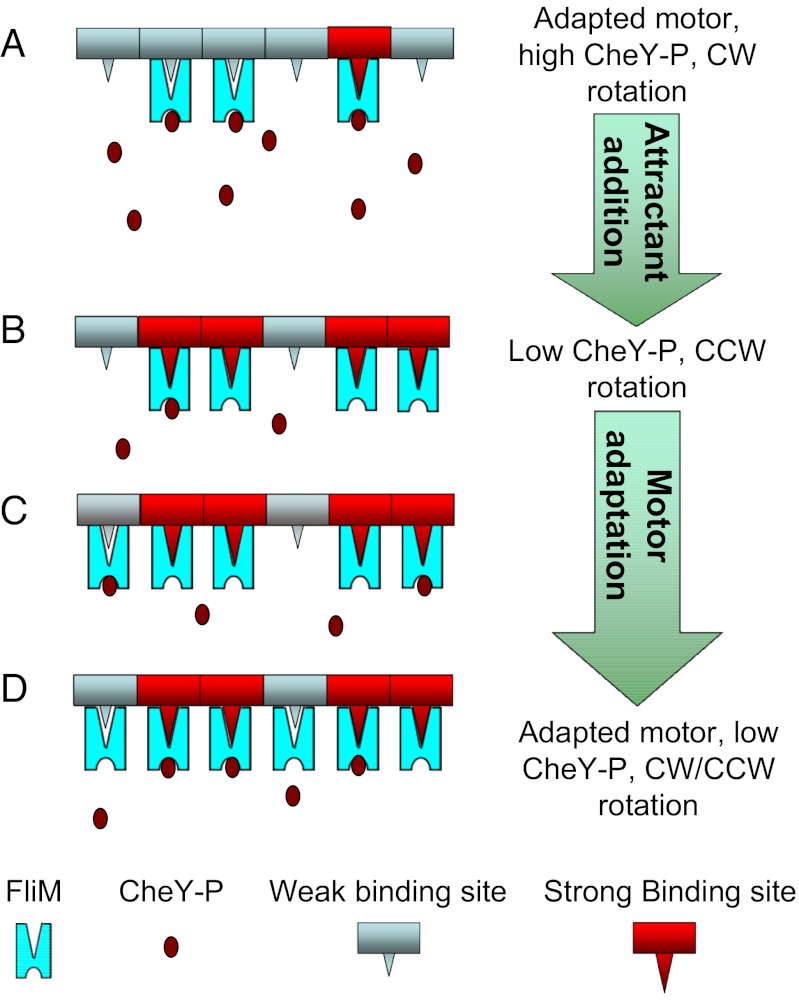
Consider the cartoon shown in Fig. 4. We start with a cheR cheB cell containing a high concentration of CheY-P that spins exclusively CW and add a weak attractant that reduces the CheY-P concentration and causes the motor to switch from CW to CCW. As a result, the number of nonexchanging FliM molecules (the number bound to strong binding sites) jumps from 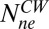to a larger value 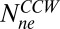. Because most of the FliM molecules initially bound to the motor now bind more strongly, very few of the remaining weak sites are occupied. Over time, the exchanging population evolves to a new steady state as the process of binding and unbinding to the weak sites continues, causing the total number of FliM molecules in the motor to increase. Note that the model assumes fast binding to the strong sites with a very low dissociation constant, consistent with the observations of a nonexchanging population in FRAP experiments.

Fig. 4.

Motor-remodeling cartoon. (A) Binding sites in a motor of a cheR cheB cell are shown. At high CheY-P levels, a large number of CheY-P molecules bind, and the motor rotates CW. The motor contains a small steady-state FliM population, and the exchanging fraction of FliM is in the majority. (B) Upon addition of attractant, CheY-P levels fall, so fewer CheY-P molecules bind, and the motor switches to CCW. Most of the FliM molecules initially bound to the motor now bind more strongly, due to structural changes accompanying the switch to CCW rotation. (C) The exchanging population evolves to a new steady state, leading to a growth in the total FliM content. This growth enhances the probability of CheY-P binding to the motor. (D) The motor now contains a larger steady-state FliM population: The motor has partially adapted and is able to switch.

The evolution is easier to treat analytically when one adds a strong attractant, and the motor continues to spin CCW. The fraction of molecules that exchange suddenly decreases to 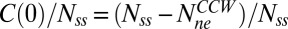. This initial condition is based on a simplifying assumption that change in binding strength and occupancy following a conformational change occurs so rapidly that all strongly binding sites are occupied by the time one has to worry about slow FliM exchange. However, this is not a necessary assumption: A more complex analysis would include the dynamics of both the weak and the strong binding sites but with essentially the same predictions and conclusions. Whereas the simple model presented here does not have any free parameters, the complex model would include the on-rate constant for the strong sites as a free parameter. With this initial condition, Eq. 1 has the solution 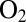. Thus, gradually increases, as shown in Fig. 3B (solid curve). Note that the predicted timescale for motor remodeling and the timescale observed experimentally in previous work are the same, 1/(2k_off) ∼ 25 s. The reverse process for the addition of repellent (or removal of attractant) to an exclusively CCW-rotating cheR cheB motor can be similarly predicted (Fig. 3B, shaded curve), even though the kinetics of exchange remain unchanged, in agreement with our FRAP measurements. The relative FliM ring content and the exchanging fractions at the new steady state (reached several seconds later) reproduce our FRAP and TIRF measurements for the CCW case and the CW case.

Our results offer an explanation for how the motor first detects changes in CheY-P levels and then responds by altering the FliM population (Fig. 4). Because CheY-P regulates the output of the motor by influencing the probabilities of CW rotation, it indirectly modulates the FliM exchange through the above mechanism. This explains the previous observations of signal-dependent FliM turnover.

An interesting feature of the FliM distributions is the presence of large motors (∼50–80 molecules), seen in Fig. 1B. It is unclear at present how the C-ring could accommodate such large numbers of FliM molecules. Does a second FliM-ring form? Does the ring expand or pucker? A previous study showed that higher symmetries in the C-ring lead to an increase in the C-ring diameter (21). This is a problem tailor made for cryo-EM tomography.

Our measurements of FliM populations over a range of values of CW_bias (Fig. 1C) suggest that models of switching that assume fixed FliM stoichiometry (22, 23) should be modified to accurately predict the behavior of the switch over a range of CheY-P values (10, 11). The conformational spread (CS) model (24), in which the rotor is made up of 34 bistable protomers, each protomer made up of one FliM, approximately one FliG molecule, and a tetramer of FliN (25, 26), assumes that the activation energies of all of the three proteins in a protomer can be lumped together in a single activation energy term, Ea ∼ 0.65 k_BT (22). The addition of n FliM molecules would then increase the energy barrier for the protomer ring to cross over from the low-energy state (CCW) to the high-energy state (CW) by ∼0.65n k_BT. This decreases the likelihood of a switch from CCW to CW, countering an increase in the probability of CW rotation due to more CheY-P binding. Quantification using allosteric models such as the Monod, Wyman, Changeux (MWC) model (27, 28) or the CS model suggests that these opposing factors nullify the effect of FliM addition such that little or no motor adaptation will ever occur (Fig. S4). This problem can be overcome by decoupling the energetics of the different rings in the switch complex. It is possible that either the FliG molecule or the FliN tetramer, which has been identified as the most likely bistable element in the protomer (25), dictates the activation energies of the ring. Also, studies of the mismatch between the numbers of FliM and FliG molecules in the motor (29) need to address the issue of variable numbers of FliM molecules. How do FliM and FliG communicate over a range of FliM numbers?

Conclusions

Adaptive remodeling of the FliM ring was previously modeled by assuming that the FliM dissociation rate decreases when the steady-state concentration of CheY-P decreases (4). In the present work, we used TIRF and FRAP with individual motors to dissect the mechanism for adaptive remodeling, finding that it is not CheY-P binding that matters, but rather the direction of rotation, and it is not the rate of FliM exchange that matters, but rather the fraction of FliM strongly bound. Thus, the remodeling is effected by direction-dependent changes in the strength of FliM binding. The changes are dramatic: Assuming that there are ∼34 molecules of FliM in a motor that rotates exclusively clockwise, there are ∼44 molecules in a motor that rotates exclusively counterclockwise. So, bacterial chemotaxis, probably the best-understood signal-transduction system in biology, continues to amaze.

Materials and Methods

Strains and Plasmids.

For the measurement of FRAP curves, we used strain HCB1697: ΔcheB, ΔcheY, ΔcheZ, ΔflgE, fliM-eyfp(A206K) with pTrc99A- flgE (pVN32), which rotates exclusively counterclockwise (CCW strain). To study the effect of switching and the direction of rotation, we transformed the CCW strain with pBAD34-cheY (pPL4), yielding the CheY strain. A DNA cross of flgE into the HCB1697 genome (yielding strain PL37) allowed genomic expression of flgE. This strain was transformed with pTrc99a-cheY (pWB5) to achieve higher levels of CheY-P in a CheY strain, beyond the levels needed to generate CW rotating motors. To generate 100% clockwise motors in the absence of CheY (CW strain), we exchanged the fliG^WT allele with the fliG^CW (ΔPAA) allele (6) in the CCW strain, using the Lambda-red protocol (30). All strains were grown in tryptone broth at 33 °C to OD₆₀₀ = 0.5, and induction levels of plasmid-encoded proteins were controlled with IPTG (0–50 μM) and arabinose (0–0.01%). Cells were washed twice with motility buffer [0.01 M potassium phosphate (pH 7.0), 10⁻⁴ M EDTA, 0.067 M NaCl], and motors were tethered using anti-flgE antibody (31).

Fluorescence Microscopy.

We used a Nikon TIRF microscope (Nikon Eclipse Ti-U) with a 25-mW 515-nm laser (Cobolt Fandango) focused in the back focal plane of a 60× TIRF objective to generate an evanescent laser field with a characteristic decay length of 100 nm. Images of motors tethered by hooks were recorded with a back-illuminated, cooled (−55 °C), electron-multiplying CCD camera (DV887ECS-BV; Andor Technology). Details of FRAP and FliM population measurements are described in SI Text.

Motor Switching and Speed Measurements.

During FRAP measurements, phase-contrast images of tethered cells were obtained in bursts of 20 s (60 fps) at random intervals, using a digital camera (Thorlabs DCC1240M). These images were analyzed to obtain cell rotation and switching statistics, using a digital equivalent of the crossed-slit laser dark-field method (32).

z-Axis Focusing with Phase Contrast.

As detailed in SI Text, we used online particle detection and continuous measurements of the total brightness of latex beads stuck to the coverglass in the vicinity of tethered motors of interest. This allowed us to repeatedly focus at the motors during fluorescence imaging, for each measurement. Drift along the z axis was corrected by manually adjusting the focus to maintain the bead brightness at a constant value.