Mapping Greenland’s mass loss in space and time

Abstract

The melting of polar ice sheets is a major contributor to global sea-level rise. Early estimates of the mass lost from the Greenland ice cap, based on satellite gravity data collected by the Gravity Recovery and Climate Experiment, have widely varied. Although the continentally and decadally averaged estimated trends have now more or less converged, to this date, there has been little clarity on the detailed spatial distribution of Greenland’s mass loss and how the geographical pattern has varied on relatively shorter time scales. Here, we present a spatially and temporally resolved estimation of the ice mass change over Greenland between April of 2002 and August of 2011. Although the total mass loss trend has remained linear, actively changing areas of mass loss were concentrated on the southeastern and northwestern coasts, with ice mass in the center of Greenland steadily increasing over the decade.

The contribution to global sea-level rise from the melting of polar ice sheets has been a focus of intense study over the past several decades. Earth’s second-largest ice sheet, Greenland, has been surveyed by a multitude of techniques. Remote-sensing observations by laser and radar altimetry and interferometric synthetic aperture radar have constrained both the overall variability in Greenland’s mass balance over time (1–7) and the local mass flux of its peripheral western and eastern outlet glaciers (8–11). These measurements have shown both strong variations among seasons and strong decadal variations in the inferred mass change rates (6, 12).

Coincident with these observations since 2002, the Gravity Recovery and Climate Experiment (GRACE) dual-satellite mission has been sensing the Earth’s geopotential field continuously. Many studies have used monthly averaged snapshots of the field to estimate Greenland’s total mass change over the years (13–18). Such estimates of the total have varied from −100 to −250 Gt/y, although as additional data have been added, the range has tightened around an average value close to −220 Gt/y (19, 20) in the last decade. One study (18) with data to 2009 has reported accelerations in the annual mass loss of Greenland of about −30 Gt/y².

The spatial pattern of mass loss that can be estimated from GRACE data is much less well-constrained than its average value over large areas. Whereas traditional remote-sensing techniques actively sample discrete areas on the surface, the geopotential measurement made by GRACE at altitude integrates the signal over a broad region several hundred kilometers in diameter. In addition, because of the character of the errors in the data, it is commonly deemed necessary to employ spatial smoothing (21), which further reduces the spatial resolution. GRACE results from the first half of the 2000s showed broad mass loss along the eastern half of Greenland (13–15). Later work indicated that mass loss increased along the northwest coast of Greenland later in the decade (17, 19, 20, 22). These studies shared the technique of fitting a single linear slope to several years (usually 4–5 y) of geopotential data to examine any temporal changes in the mass flux between these intervals of time.

In this paper, we determine the spatial distribution of mass loss in Greenland over time. Our inversion method relies on a spherical basis of spatiospectrally concentrated Slepian functions (23, 24). We show its ability to resolve unprecedented geographical and temporal detail in the mass flux using gravity data alone. Extracting more of the signal contained within the noisy GRACE data products, we resolve the spatial changes in mass loss on a yearly basis with robust uncertainty estimates. With our results, we aim to settle the controversies surrounding the geographical pattern of Greenland’s ice loss and establish the presence or absence of significant accelerations in the ongoing trends.

The venerable spherical harmonics constitute an orthogonal function basis for the entire sphere, making the distribution of Stokes expansion coefficients for the global gravitational geopotential the standard format for the release of the GRACE level 2 data products. These (monthly) models are currently band-limited, complete to spherical harmonic degree and order 60. When examining a restricted region, such as Greenland, the use of spherical harmonics is no longer ideal or practical: their orthogonality is lost when mere portions of the sphere are being considered. Without orthogonality of the function basis over the area of interest, estimating a regional signal becomes quite a complex operation. In addition, the unfavorable error structure of the results (24–26) renders significance testing of detailed interpretations all but impossible. To obviate these difficulties, some studies gave up intracontinental spatial resolution altogether, using averaging functions over the landmass to determine the broad total rate of mass change over time (15, 27). Other works expanded the GRACE coefficients into the space domain to estimate trends on a latitude–longitude grid and compared forward models of mass anomalies (13, 19). Still other works parameterized either the direct intersatellite range measurements (14) or the global level 2 solutions (20) into basin-scale local mass variations.

By using predefined basin shapes, basis functions that are not orthogonal, smoothing and postprocessing for error reduction, or outright spatial averaging, these now common methods make assumptions about the data or the models that limit their spatial sensitivity and potentially confuse signal and noise. We postulate that the historical lack of agreement between GRACE-based models of Greenland’s mass loss is at least partly because of the failure to fully characterize the tradeoffs and uncertainties that accompany these various choices of averaging, filtering, and parameterization. The differences between estimates from various groups have dwarfed the uncertainties on the instantaneous elastic response of the substrate or the relative magnitude of viscous postglacial rebound corrections, both of which are needed to convert mass anomalies to estimates of ice mass lost due to melting. However, with poorly known portions of signal lost and noise spread to lower spherical harmonic degrees by the analysis procedures, proper accounting for the effects of data processing choices is rarely at the surface of the discussion.

Here, we bypass the commonly used filtering and averaging procedures altogether, and we use a simple estimation method based on an analysis in the spherical Slepian basis explained in Model and Methods. Our methodology involves a small number of assumptions of a statistical and computational nature. Our own choices of the kind were informed by extensive simulation, and their validity was tested on numerous synthetic examples. SI Text has an exhaustive description of the details.

Model and Methods

The spherical Slepian basis (23) is formed by optimization to constitute a fully orthogonal, band-limited basis optimally concentrated to a region of interest (in our case, Greenland). Each Slepian function is a separate solution to an eigenvalue equation that maximizes the concentration of function energy within the specific region, and each different eigenvalue 0 ≤ λ ≤ 1 is a measure of concentration within that region of the corresponding function. Using only those functions in the basis that have the majority of their energy concentrated within the region of interest (for example, λ > 0.5) dramatically improves the signal-to-noise ratio (24). The results experience very little influence caused by the signal originating outside the region of interest. Indeed, minimization of the well-known leakage problem is the explicit optimization objective in the construction of the Slepian basis, as it has been used in 1D signal processing for many decades (28) and in a growing number of applications in geodesy, geomagnetism, astrophysics, cosmology, and the planetary sciences. Extracting information over the full bandwidth of the solution without filtering, the spherical Slepian basis provides spatial sensitivity that is superior to the sensitivity of many other modeling methods.

We used 108 monthly GRACE Release 4 geopotential fields from the Center for Space Research, University of Texas at Austin, covering the time span from April of 2002 to August of 2011, including 5 months with data gaps. The highly variable degree-two, order-zero spherical harmonic coefficients are replaced with values from satellite laser ranging (29), and for the missing degree-one coefficients, replacement values (30) are substituted, as is by now customary. The GRACE geopotential models are transformed into surface mass density using the classical method by Wahr et al. (31); the instantaneous elastic deformation caused by current mass changes is represented and removed with degree-dependent loading Love numbers (32). The surface mass density is subsequently projected onto a Slepian basis designed to capture the region within Greenland’s coastlines with the inclusion of a small buffer zone of 0.5°. We settled on the value of this buffer zone based on the simulations described in SI Text.

The bandwidth of the Slepian basis, L = 60, matches the bandwidth of the GRACE data products. We truncate the expansion at the effective dimension of the combined spatiospectral space (Greenland in space, band-limited spectrally), known as the Shannon number (23, 33). This truncation leaves only 20 target functions, each of which is an eigenmap that has its energy highly concentrated over Greenland. This sparse model space represents a significant reduction of the original spherical harmonic dimension, comprising (L + 1)² = 3,721 functions with expansion coefficients that are substantially influenced by noise and required estimating—or were discarded—by the alternative methods. As described, our method involves only the selection of the size of the buffer zone, the choice of bandwidth, and the number of terms in the Slepian expansion. The rationale behind our selections was validated by extensive simulation (SI Text), and the computer code that accompanies this paper allows the reader to reproduce the results, with modified parameter settings if such modification should be desirable.

The viscous, long-term, geopotential response of the solid Earth caused by past loading by ice caps is accounted for by subtracting from the results the postglacial rebound model by Paulson et al. (34) after projecting the latter onto the same Slepian basis as used for the GRACE-derived geopotential coefficients. The total mass over the region, relative to a 9-y mean (Fig. 1), is then calculated by integrating each function over the region, scaling by its corresponding expansion coefficient and summing over the 20 functions in the basis set. We estimate measurement error by fitting a linear trend and a harmonic with a period of 1 y to each of the Slepian coefficient time series and generating a covariance matrix from the residuals. This result gives a comprehensive measure of the variance of each coefficient and their dependencies, which we extend to the uncertainty of their sum by linear error propagation. In SI Text, we illustrate how critical the knowledge of the covariance is for the interpretation and how different the fully nondiagonal covariance matrix is from the calibrated errors distributed as part of the GRACE data products and from errors approximately estimated using uncorrelated assumptions.

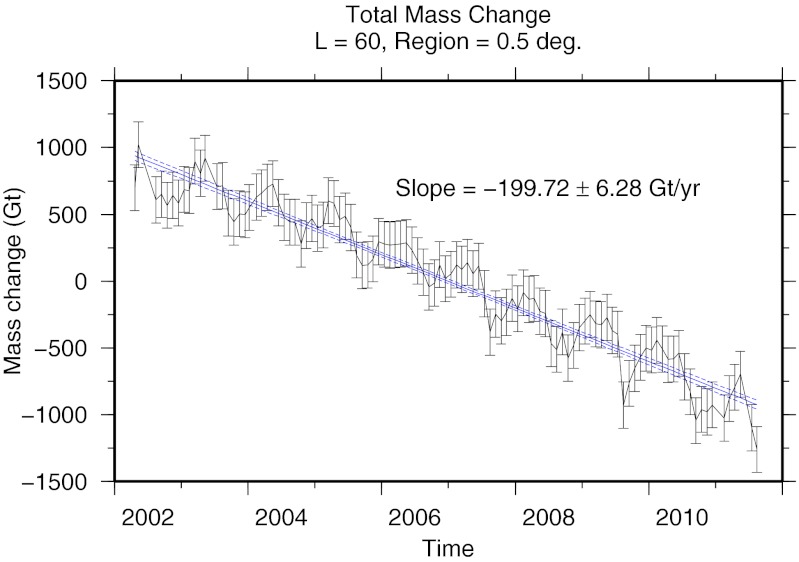
Fig. 1.

Total ice mass change trend for Greenland. The solid black line is the raw GRACE monthly solution projected into the 20-term Slepian basis optimized to capture the interior of the coastlines of Greenland plus a 0.5° buffer region for a bandwidth L = 60 (in spherical harmonic degrees). The solid blue line is the best-fitting linear trend. The dashed blue lines represent the 2σ error envelope of this fit calculated using full covariance information estimated from the data themselves.

Results and Discussion

The total ice mass change (Fig. 1) shows a clear trend as well as an annual variation. The error envelope for the fit is shown with dashed lines. The overall trend is very well-determined, because with almost a decade of data, the analysis covers many seasonal cycles, which can vary strongly between years. The best-fitting linear trend covering all 108 months finds the ice mass change rate over our whole region to be −199.7 ± 6.3 Gt/y. The 2σ uncertainty on the trend derives from the covariance matrix that we estimated by the procedure described in Model and Methods. The uncertainty quoted does not include the uncertainty in the postglacial rebound correction, but this uncertainty could be added to the uncertainty of the trend if so desired. Many of the GRACE-based studies of Greenland use the rebound model (34), and therefore, comparisons remain straightforward. Fitting an additional quadratic (and potentially, higher-order terms, as explained in SI Text), we find the acceleration of mass loss to be a modest −8.68 ± 4.1 Gt/y².

Several recent results of the average mass trend measured from GRACE data have been near −220 Gt/y (18–20), although estimates have ranged as low as −161 ± 35 Gt/y (35). Estimates from other measurement techniques have recently been higher [e.g., −260 ± 53 Gt/y derived from surface mass balance calculations (36) or −237 ± 25 Gt/y from altimetry data (37)]. On this subject, our results are in general agreement with the most recent GRACE studies, but in obtaining them, we have relied on fewer processing steps by the judicious choice of basis, as described above. A reestimation of the trends up to the year 2006, in which three studies appeared with much variability in the conclusions (13–15), reconciles the results as nearly falling within each other’s uncertainties when evaluated according to our method. We conclude that the discrepancies in the early literature were more a matter of statistics rather than physics or data selection.

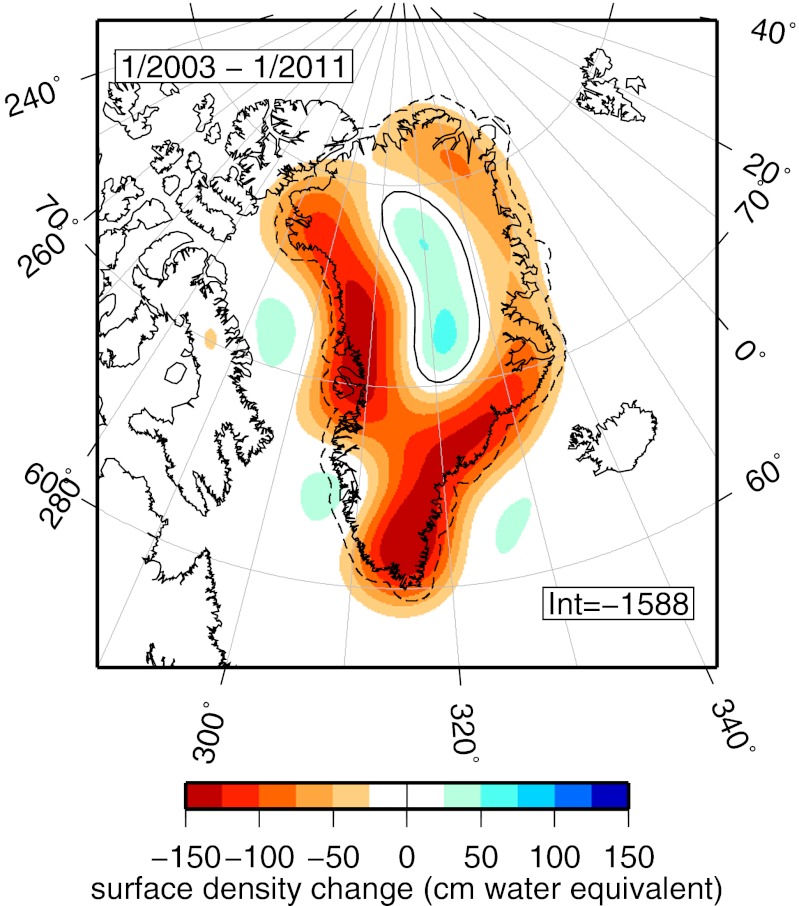
Using an extension of our approach to estimate the average mass trend, we are able to measure the spatial pattern of mass change and how it changes with time. To each of our 20 Slepian function expansion coefficient time series, we have fit a first-, second-, or third-order polynomial, depending on whether each additional term passed an F test for significance. This fit then becomes our new estimate for the signal. These fits embody the gradual changes over time spans of several years, and they ignore much of the variability within each year. Fig. 2 displays a map of the total mass change of the estimated signal over the 8-y period from January of 2003 to January of 2011. Because data for the month of January of 2011 are unavailable, we used a value for January 15th, 2011 interpolated from our estimated signal for this analysis, and subsequent analyses.

Fig. 2.

Geographical pattern of the ice mass change over Greenland averaged for the period between January of 2003 and January of 2011. The map is the result of the combination of signal estimates conducted on individual time series of Slepian function expansion coefficients. The integral value (Int) for the entire epoch is shown in gigatons. The 0-cm water contour is shown in black.

Two other recent GRACE studies (20, 22) have presented results of Greenland’s mass loss in map form, which are in broad agreement with what we show here. Although this convergence of the literature is a tribute to the quality and longevity of the data, the degree of spatial localization that we derive from the Slepian basis methodology significantly shrinks the geographical footprint that can now be robustly modeled routinely. For instance, the clear concentration of mass loss along the coasts, mainly in the southeast and northwest, coincides with where detailed radar interferometry studies (4) have reported large ice flow speeds associated with outlet glaciers.

In the central high-elevation portions of Greenland, there is evidence for significant accumulation of ice mass, a result that was not clearly imaged by previous GRACE studies (17, 19, 22). However, in a combined inversion of GRACE and Global Positioning System data, the work by Wu et al. (35) did show some mass accumulation in central Greenland. Accumulation in the continental interior is expected in a warming climate (3), and it has been observed also by satellite altimetry (1, 4, 5, 38). Recent modeling of Greenland’s climate over the past 50 y (7) reveals that precipitation and runoff increased significantly beginning in 1996. Although the precise locations are unclear from these studies, between 2003 and 2008, large areas of Greenland’s interior are thought to have gained mass (between 0 and 10 cm water equivalent per year, which is near the maximum that we recovered). Our observation of the interior mass accumulation is spatially very well-resolved, and this finding also represents a significant improvement over earlier attempts to localize this anticipated pattern from GRACE data alone.

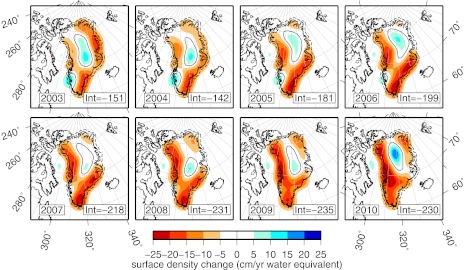
The spatially well-resolved maps of Greenland’s mass loss give us confidence to attempt extracting higher-resolution temporal variations of the geographic signal. When each year is examined in more detail (Fig. 3), the loci of largest mass loss move around Greenland with time. In 2003 and 2004, mass loss was concentrated along the entire eastern coast of Greenland. In 2005 and 2006, mass loss was reduced in the northeast but increased in the southeast. Meanwhile, mass loss began to increase along the northwest coast. From 2007 to 2010, mass loss further increased in northwest Greenland, whereas mass loss diminished in the southeast coast areas after 2008. Each year displays a region in the interior of Greenland with mass increases exceeding 5 cm/y (light blue), shifting slightly geographically from year to year.

Fig. 3.

Yearly resolved maps of ice mass change over Greenland from 2003 to 2010. The sum of these maps was shown in Fig. 2. For every year, we show the difference of the signal estimated between January of that year and January of the next year. The integral values (Int) of the mass change per year are shown expressed in gigatons. The 0-cm/y water contours are shown in black.

Overall, the spatially shifting mass changes recovered by our method match well to remote-sensing observations. The increased mass loss in southeast Greenland first seen in 2005 coincides with accelerated flow observed in eastern outlet glaciers during that time (10). Increasing mass losses in northwest Greenland since 2006 are also seen in observations by radar interferometry and Global Positioning System (6, 22). The observed deceleration in mass loss in the southeast in 2009 and 2010 may be related to decreased glacier velocities in that region (39), although continued study is needed to substantiate this claim.

In addition, our results confirm the two large zones of melting (southeast and northwest coasts) seen in previous GRACE studies (17, 19, 20, 22). With our additional spatial detail, however, we observe more clearly the separation between these regions and their different mass changes over time. In our results, we observe larger magnitudes of surface density change than other GRACE studies, because the mass losses are concentrated on the coasts instead of being smoothed over larger areas. For this same reason, we observe fluctuating mass changes on Greenland’s northeast coast, where other studies have not detected much variability. We also more clearly show the waxing and waning of mass in the southeast over the span of 8 individual years, with 2005 and 2006 exhibiting the largest mass losses compared with the others in the decade.

All together, our results show both the power of spatiospectrally concentrated Slepian localization methods in enhancing the signal-to-noise ratio for regional modeling, and of course, the benefits of long time series of time-variable gravimetry to examine the long-term mass flux over glaciated areas. As this kind of data (e.g., from the Gravity Recovery and Interior Laboratory (GRAIL) mission orbiting the moon or GRACE follow-on missions) continues to evolve with technology, so do the methods to study them. Pushing the envelope of the analysis will ensure that satellite gravity, even when other more direct observations should be lacking, will continue to play a major role in studying terrestrial, lunar, and planetary systems in the future.