Self-boosting vaccines and their implications for herd immunity

Abstract

Advances in vaccine technology over the past two centuries have facilitated far-reaching impact in the control of many infections, and today’s emerging vaccines could likewise open new opportunities in the control of several diseases. Here we consider the potential, population-level effects of a particular class of emerging vaccines that use specific viral vectors to establish long-term, intermittent antigen presentation within a vaccinated host: in essence, “self-boosting” vaccines. In particular, we use mathematical models to explore the potential role of such vaccines in situations where current immunization raises only relatively short-lived protection. Vaccination programs in such cases are generally limited in their ability to raise lasting herd immunity. Moreover, in certain cases mass vaccination can have the counterproductive effect of allowing an increase in severe disease, through reducing opportunities for immunity to be boosted through natural exposure to infection. Such dynamics have been proposed, for example, in relation to pertussis and varicella-zoster virus. In this context we show how self-boosting vaccines could open qualitatively new opportunities, for example by broadening the effective duration of herd immunity that can be achieved with currently used immunogens. At intermediate rates of self-boosting, these vaccines also alleviate the potential counterproductive effects of mass vaccination, through compensating for losses in natural boosting. Importantly, however, we also show how sufficiently high boosting rates may introduce a new regime of unintended consequences, wherein the unvaccinated bear an increased disease burden. Finally, we discuss important caveats and data needs arising from this work.

Vaccination has long played a central role in the control and eradication of infectious diseases. For childhood infections such as measles and mumps, mass immunization programs have allowed for major impact (1), including the potential for local interruption of transmission, through raising lasting “herd immunity” (2), or indirect protection for the unvaccinated. However, such impact has so far proved more elusive for pathogens such as Bordetella pertussis and Vibrio cholerae (3, 4), largely because these infections do not elicit lifelong, sterilizing immunity.

Current vaccination schedules for many such infections incorporate supplemental “booster” vaccines, aimed at prolonging protection (5). Such programs can be limited by the impracticality of delivering frequent booster doses throughout life, particularly given notorious difficulties in providing high vaccine coverage in adult populations (6–8). Consequently, even booster schedules do not offer a reliable means of maintaining herd immunity. On the other hand, boosting may instead be supplied through natural exposure to infection, in which case vaccination may in fact reduce existing herd immunity. In the context of B. pertussis, for example, it has recently been proposed that mass immunization, eliciting waning immunity, may have reduced opportunities for natural boosting to occur, thus permitting an increase in overall disease incidence (9). In the 1990s, similar dynamics were proposed when assessing the potential effect of vaccination against varicella-zoster virus (10).

Emerging vaccine technologies could offer qualitatively new opportunities to address such issues. Here we consider the potential impact of emerging vaccines for which attenuated viral vectors act as vehicles for the expression of recombinant, target antigens. Suitably chosen, these vectors could in essence provide the foundation for novel “self-boosting” vaccines, capable of recurring antigen presentation throughout a recipient’s lifetime, with potentially novel, far-reaching implications for herd immunity. In what follows we present a brief overview of the biology underpinning these vaccines; we then use simple mathematical models to explore the potential impact of these vaccines on herd immunity against infections such as those described above. We next consider how such vaccines may interact with natural boosting, potentially to mitigate the adverse population-level effects associated with “conventional” (non–self-boosting) vaccines. Finally, we discuss important caveats and data needs arising from this work.

Basis for Self-Boosting Vaccines

Several vaccines currently in development take advantage of attenuated viruses as expression vectors for antigens of interest (11). Vectors such as Modified Vaccinia Ankara and adenovirus-5 show efficient antigen expression (12), but their long-term action is limited by host immunity against the vector itself. However, cytomegalovirus (CMV) (13) and herpes simplex virus type 1 (HSV-1) (14) have been recently proposed as potential vectors with a capacity for long-term antigen expression.

Ubiquitous herpes viruses, CMV and HSV typically establish long-term, subclinical infection in otherwise healthy adults. As members of the family Herpesviridae, they exhibit true latency. Their within-host dynamics are therefore characterized by periods of quiescence, during which most viral genes are silent, punctuated by episodes of viral reactivation (15), leading to intermittent replication and antigen production (e.g., ref. 16). Moreover, they both have comparatively large genomes (17, 18), potentially allowing the expression of a range of recombinant antigens. Recent experiments on nonhuman primates (19) illustrate the potential of CMV and HSV for maintaining long-term immunity against select antigens.

The reactivation kinetics of herpesviruses vary widely both within and among the virus subfamilies. Both anecdotal (20) and experimental (21) evidence suggests that herpesviruses reactivate in response to their immune milieu. However, the durations between HSV reactivations are strikingly variable; some episodes are only days apart and others are separated by months (16, 22). The reasons for this variability remain a puzzle. One recently postulated explanation is that reactivation occurs constantly, but virus populations may or may not expand, depending on stochastic and highly localized levels of immunity (23). For CMV, there is evidence that viral reactivation is linked to the differentiation status of myeloid cells, where the latent-phase virus appears to localize (24, 25).

These and other issues, described in further detail in Discussion, are important considerations in the continued development of such vaccines. In the present work, however, we aim to look beyond such complexities to address potential population-level implications, essentially by exploring the dynamics that could arise from a boosting regime considerably more frequent than what is practically achievable today. As described in more detail below, a key uncertainty is the implication of vector reactivation dynamics for maintenance of immune memory: For example, would vaccine-induced immunity be lifelong and persistent or only intermittent and recurring? Our parsimonious framework allows for either possibility.

Model

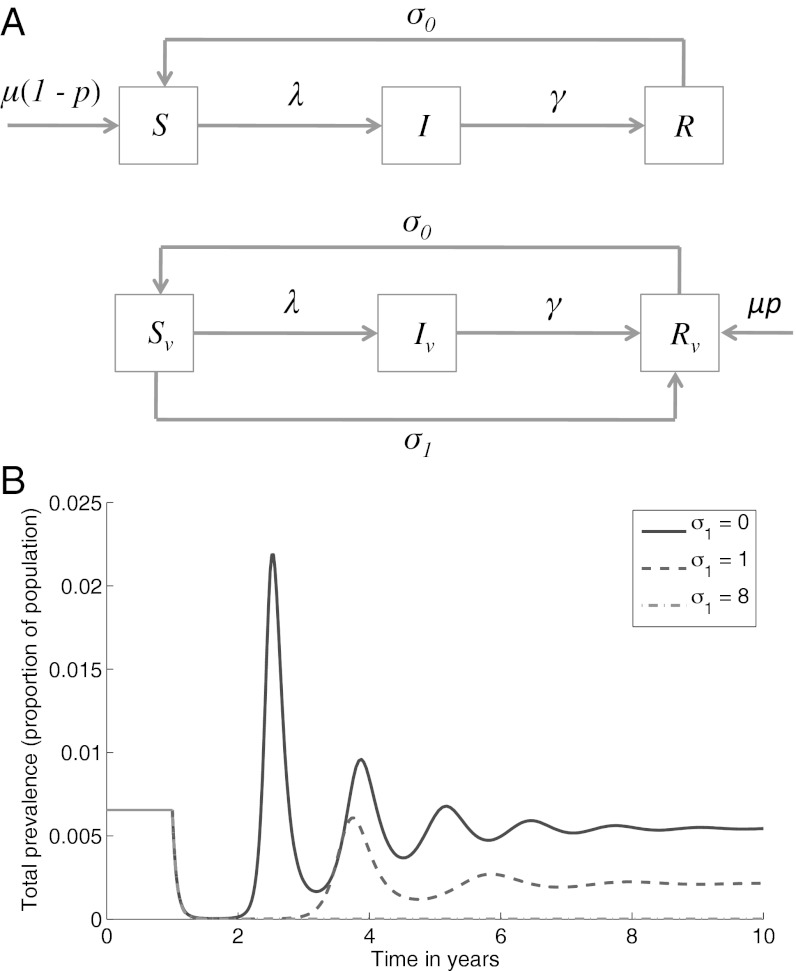
We use the classic, deterministic SIRS framework (26) to represent the dynamics of a given infection that engenders waning immunity as illustrated by Fig. 1A; in the absence of vaccination we partition a well-mixed, homogeneous population into those who are susceptible (a proportion S), infected and infectious (I), and recovered and immune (R), allowing a per-capita rate σ₀ of transition from R to S (waning immunity).

Fig. 1.

The basic model of waning immunity and self-boosting vaccination. (A) Schematic illustrating the model structure. All individuals die at a per-capita death rate μ, not shown in the diagram for clarity. (B) Dynamical behavior for a range of self-boosting rates, σ₁, assuming that mass vaccination acts from t = 1 onward. Although shown for a specific set of parameters (R₀ = 15, μ = 1/50, σ₀ = 0.1, γ = 17, P = 0.95), these curves illustrate the general, qualitative dynamics arising from the model shown in A.

We now include self-boosting vaccination by assuming that a random fraction p of individuals receive effective vaccination before their first infection. These individuals subsequently maintain “vaccinated” status throughout their lifetimes (due to long-term persistence of the viral vector), although they cycle between susceptible and immune status. We can thus also partition vaccinated individuals into susceptible, infected, and recovered classes, distinguished with a subscript v as in Fig. 1A, Lower.

We assume that vaccinated individuals undergo repeated, endogenous vector reactivation throughout their lifetimes, each reactivation synonymous with a “boosting” event. As described above, there is considerable variability in reactivation rates associated with natural herpesvirus infection. A simple way of representing this variability in vaccinated individuals is to assume a “hazard” of reactivation that is constant in time, corresponding formally (27) to an exponentially distributed interepisode duration. In the present deterministic context, we represent these dynamics with a per-capita rate σ₁ of reactivation among vaccinated individuals. This yields a mean duration of 1/σ₁ y between endogenous boosting events, which we interpret here as arising from the vector “sensitivity” to reactivation stimuli, potentially a target for future, rational vaccine design. Accordingly we present results for a range of σ₁, with σ₁ = 0 representing a conventional (non–self-boosting) vaccine. For simplicity we assume that after each boosting event, vaccine-induced immunity wanes at the same rate σ₀ as infection-induced immunity. Thus, the case σ₀ << σ₁ corresponds to a self-boosting vaccine providing continuous, lifelong immunity. We may, however, also allow for the possibility that immune memory lasts for a shorter timescale than the typical interval between boosting events. In the present framework this corresponds to the regime σ₀ >> σ₁, under which vaccinated individuals undergo repeated, but intermittent phases of immunity throughout their lives. Further details, including model equations, are provided in Materials and Methods.

The “basic reproduction number” R₀ is defined as the mean number of secondary cases arising from a single infected case, in a population with no prior immunity. It is straightforward to show that, in the absence of vaccination, 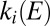. In the presence of prior immunity, and in particular where a proportion p of the population has vaccine-induced immunity, we refer instead to the effective reproduction number R_eff, where R_eff = R₀(1 − p).

Implications for Herd Immunity

A classic result from mathematical epidemiology is the “critical vaccination threshold” p_c (28), denoting the minimum vaccination coverage required to prevent the spread of a given infection. For a disease with given R₀, and lifelong vaccinal immunity, we have p_c = 1 − 1/R₀, as a proportion of the population (28). This is a powerful result because it implies that we need not vaccinate the entire host population to interrupt transmission. For example, to eradicate an acute, lifetime immunizing infection with R₀ = 8, we need only vaccinate at least 88% of the population.

The waning of vaccinal immunity weakens this effect, as the susceptible population is replenished not only by births [Fig. 1A, μ(1 – p)] but also by previously immunized individuals who lose their immunity (Fig. 1A, σ₀). Once infected, such individuals also compound the force of infection, λ. From the governing equations (Materials and Methods), the combined effects of waning immunity (through σ₀) and a self-boosting vaccine (through σ₁) can be summarized through a modified expression for the vaccination threshold,

expressed as a function of σ₀, σ₁ to emphasize their respective roles in shaping the vaccination threshold: Whereas waning immunity (σ₀) tends to raise the critical proportion to be vaccinated, vaccine reactivation (σ₁) acts to counter this effect (see Materials and Methods for further details on derivation). An implication is that, for given vaccination coverage with a conventional vaccine that is below the critical threshold [i.e., p < p_c(σ₀, 0)], increasing σ₁ may engender a situation where p > p_c(σ₀, σ₁), thus opening the way for elimination with the use of existing antigens.

Potential dynamical outcomes are illustrated in Fig. 1B. For illustration of the qualitative dynamics, results are shown for parameter values consistent with B. pertussis; we later incorporate more immunological structure in these dynamics. The black curve in Fig. 1B illustrates the results of mass immunization, using a conventional vaccine (σ₁ = 0). Despite 95% vaccine coverage, herd immunity is impermanent and there is ultimately a resurgence of infection as vaccinated individuals eventually rejoin the susceptible pool. The remaining curves demonstrate two distinct possibilities from the long-term use of novel vaccines: (i) A sufficiently high self-boosting rate can bring p > p_c, thus eliminating infection (Fig. 1B, dot-dashed curve, lying partly on top of the x-axis), and (ii) a subthreshold scenario (p < p_c) where even continuous vaccination permits eventual disease resurgence, but yields a reduced peak of infection, as well as lowered prevalence in the long-term (Fig. 1B, dashed curve). We briefly consider each of these in turn.

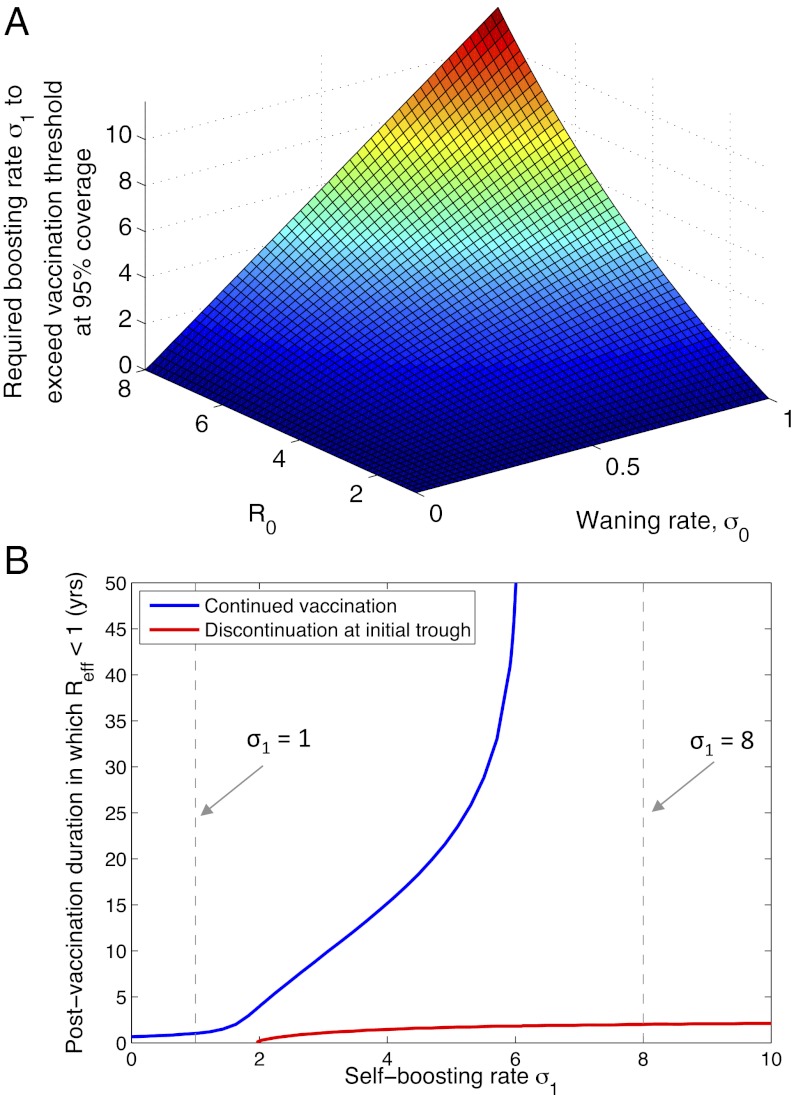
First, what is the requirement for σ₁ to exclude infection indefinitely (i.e., to bring p_c < p)? Fig. 2A illustrates the minimum required boosting rate, for a vaccination coverage of 95% and for a range of infection parameters. It illustrates, for example, that even an infection such as diphtheria with low R₀ and low σ₀ would require boosting at least once every 6 y, to maintain R_eff < 1. Although such rates may be impracticable with currently used booster schedules, they could well be achievable through self-boosting vaccines.

Fig. 2.

Implications of boosting rate σ₁ for herd immunity. As in Fig. 1B, we assume a vaccination coverage of 95%. (A) The minimal boosting rate required to exclude infection (R_eff < 1) indefinitely. (B) Duration of herd immunity, measured as the period during which R_eff < 1 following initiation of a vaccination program. The blue curve represents a vaccination program that continues indefinitely, whereas the red curve represents a program that is discontinued once local elimination of infection is first achieved (the latter measured here as a prevalence lower than 10⁻⁵). All other parameters are as in Fig. 1B. The blue curve has an asymptote at a threshold reactivation rate of σ₁ ∼ 6.1, below which even indefinite vaccination will not maintain herd immunity. Vertical, dashed black lines correspond to the reactivation rates illustrated in Fig. 1B.

Second, in the event that the critical vaccination threshold is not reached (p_c > p), there is a finite “window” of herd immunity (e.g., as in the dashed curve in Fig. 1B). Interpreting herd immunity here in its strongest sense, that is, where infection is excluded altogether from the population (2), Fig. 2B measures the “duration” of herd immunity as the period, following initiation of vaccination, in which R_eff < 1. The blue curve in Fig. 2B shows how this duration increases steeply with vaccine reactivation rate and asymptotes at the critical reactivation threshold, at approximately σ₁ = 6.1. Below this point resurgence will occur, even if vaccination is continued indefinitely. The red curve in Fig. 2B corresponds to the case where vaccination is discontinued upon local elimination of infection. In particular, more frequently reactivating vaccines provide a few additional years of herd immunity after the end of a successful but temporary vaccine campaign: This is due to the continued presence in the population of individuals with vaccine-induced immunity.

Interactions Between Vaccine-Induced and Natural Boosting

We next consider cases where immunity wanes and boosting may be supplied not only by vaccination, but also through sufficiently regular, natural exposure to infection. In such cases, efforts to reduce transmission—whether through conventional vaccination or otherwise—may in fact contribute to an increase in disease, through reducing opportunities for hosts to sustain protective immunity.

For example, it has recently been proposed that such dynamics may have played a role in the resurgence of B. pertussis (9, 29), since the introduction of vaccination in the 1940s. Could self-boosting vaccines “rescue” this effect by replacing the natural boosting that individuals may otherwise lose? In so doing, could they restore the capacity for vaccination programs to eliminate severe disease? As an illustrative case, here we incorporate such vaccines in a recent model of B. pertussis (9), although we discuss other contexts in which these dynamics may also apply.

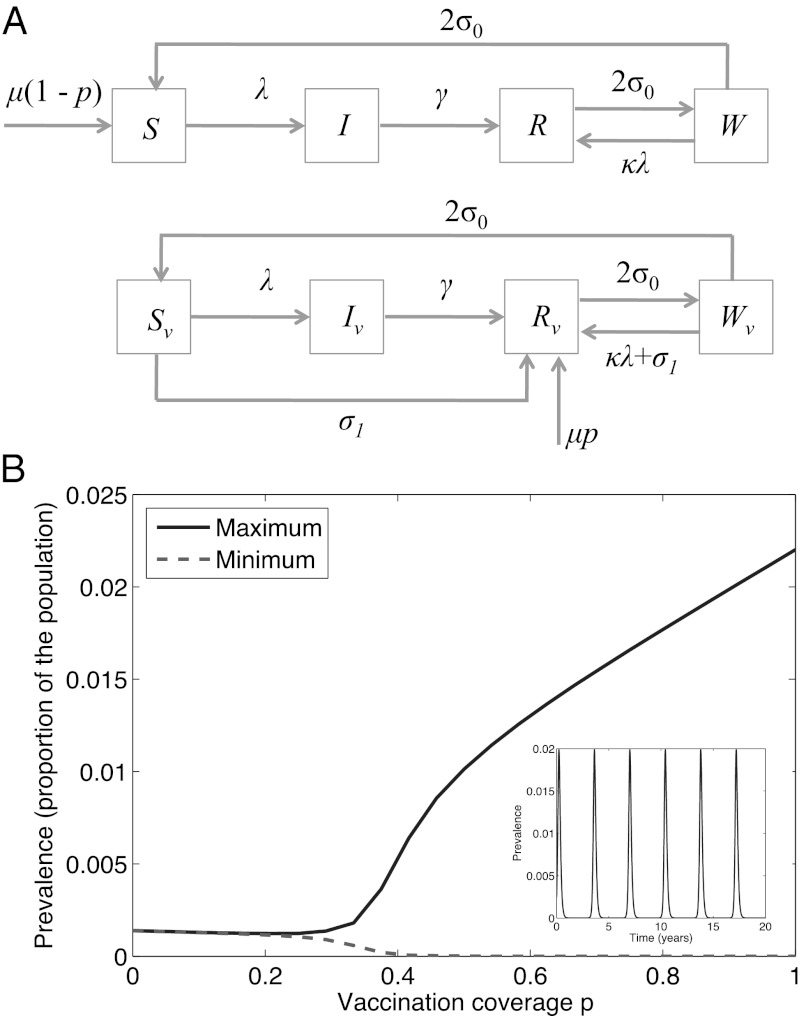
Fig. 3A illustrates the model structure, incorporating self-boosting vaccination. The key development from the “basic” model, discussed above, is the inclusion of an intermediate class of immunity, W. In the absence of reexposure, the immunity of individuals in this class eventually wanes. Where individuals in W encounter reexposure, however, this has the potential of boosting their immunity, such that they revert to the recovered class, R. This effect, dependent on natural circulation of infection, is represented by the term κλ; in the presence of self-boosting vaccination, we assume that this rate is supplemented through the endogenous antigen presentation on the part of the vaccine vector. See Materials and Methods for further details, including model equations. Setting σ₁ = 0 (a conventional vaccine), Fig. 3B recapitulates relevant results in ref. 9, where beyond a certain point, increasing vaccination coverage can be seen to increase overall disease in the population. As illustrated by Fig. 3B, Inset, this behavior arises from the onset of epidemic cycles. In turn, these cycles emerge where vaccination reduces the force of infection (λ in Fig. 3A) to such an extent as to compromise the potential for natural boosting to occur.

Fig. 3.

A model for natural boosting. (A) Schematic illustration of a simple extension of the model presented in ref. 9, to incorporate self-boosting vaccines (Lower). (B) Diagram illustrating the phase transition occurring in this model (9), when σ₁ = 0 and with increasing coverage of conventional vaccination. Parameters are as in Fig. 1B and as in ref. 9. Inset shows the time course of prevalence at 95% coverage (P = 0.95), illustrating epidemic cycles in this regime.

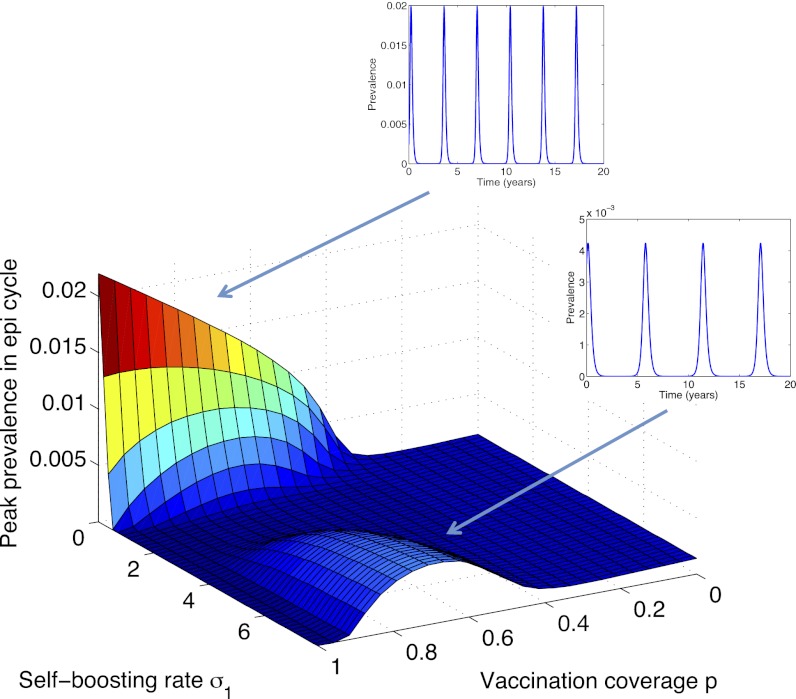
Fig. 4 extends this picture by incorporating self-boosting (σ₁ > 0). It illustrates that such vaccines could in fact rescue the effect shown in Fig. 3B, by compensating for potentially weakened natural boosting. However, self-boosting can come at a cost: At incomplete vaccine coverage and sufficiently high rates of boosting, a different set of cycles may be induced altogether.

Fig. 4.

Simulated peak proportion of the population infected as a function of self-boosting rate σ₁ and vaccination coverage p (an extension of Fig. 3, for σ₁ > 0). Also shown are time courses at two parameter regimes.

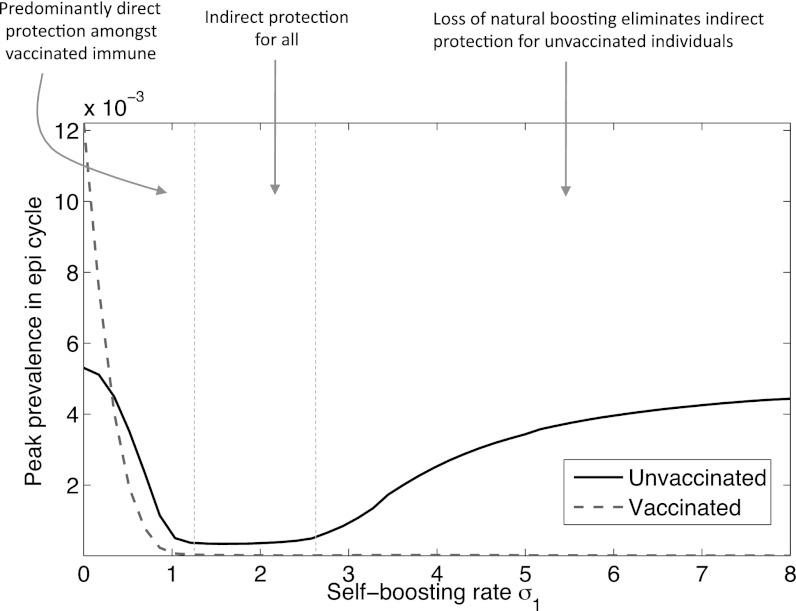
To explore this transition further, Fig. 5 takes a cross-section at 80% vaccine coverage (p = 0.8). It illustrates that the induction of epidemic cycles, by sufficiently high boosting rates, is concentrated solely among nonvaccinated individuals. Intuitively, this effect arises because the beneficial effect of self-boosting vaccine, lifelong mitigation against the loss of natural boosting, is felt only by those receiving vaccination. On a population level, these effects must be balanced against the concomitant, indirect effects of mass immunization on those unvaccinated. In particular, successful control of infection among the vaccinated (σ₁ > 2 in Fig. 5) can expose the unvaccinated to a loss in natural boosting, in direct analogy to Fig. 3B. Annotations in Fig. 5 show how this can be viewed in terms of relative weights of direct and indirect protection, illustrating the potentially complex interactions between natural and vaccine-induced boosting.

Fig. 5.

A cross-section through the surface shown in Fig. 4, at p = 0.8, and disaggregating dynamics among vaccinated and nonvaccinated individuals. Annotations indicate how the different regimes can viewed in terms of direct and indirect protection, for both segments of the population, illustrating the complex relationship between vaccination and herd immunity in this model.

Additional results, shown in SI Materials and Methods, compare these outcomes with what might be achieved through existing, conventional boosting programs, where booster doses are administered through repeated visits to a healthcare professional: Results suggest that the rescue effect shown in Fig. 4 would be possible only with infeasibly high levels of follow-up coverage, among vaccinated individuals, throughout their lifetimes.

Discussion

The waning of natural and vaccine-induced immunity poses substantial barriers in the control of many infections, in particular by compromising the buildup of herd immunity in the population. In some cases the scientific challenge may be partly immunological: to identify new antigens, or perhaps adjuvants, capable of raising more durable immune responses than those used at present. However, emerging vaccine technologies could offer an alternative approach, involving currently used immunogens. In particular, novel vaccines could raise and maintain herd immunity indefinitely (Fig. 2A). Even where they fail to do so, however, they can considerably extend the duration of herd immunity (Fig. 2B). Overall, such effects open the door for local elimination of infections that have hitherto been vaccinated against only for direct protection.

In the longer term these results highlight the potential utility of self-boosting vaccines in “end games” associated with global eradication of an infectious disease. Recent work has illustrated how local elimination of infection can be transitory if control is not concomitantly implemented in neighboring regions as well (30). In this context, by substantially broadening the window during which infection cannot reestablish in a given host population, self-boosting vaccines afford more valuable time for coordinating eradication efforts across political boundaries, particularly when coupled with strategies such as ring vaccination (31). As we enter an era of renewed prospects for global eradication of infectious diseases such as malaria (32, 33) and polio (34), novel vaccine technologies may thus become increasingly important.

Our results also illustrate complex interactions that may arise between natural and vaccine-associated boosting (Fig. 4). These dynamics need not be limited to B. pertussis: In the context of malaria, for example, although acquired immunity is incompletely understood (35, 36), it is likely to have complex interactions with exposure (37–39). Indeed, waning immunity means that individuals tend to lose their protective immunity when spending time away from malaria-endemic regions (33). On the other hand, vaccination technology against malaria continues to develop (40, 41). Certain clinical caveats notwithstanding (see below), self-boosting vaccines could well contribute to the deployment of these and other technologies in the future.

The models we present here also offer a cautionary tale: When reexposure is necessary to maintain immunity, a reactivating vaccine that offers virtually life-long individual-level protection can cause unvaccinated individuals to suffer increased disease incidence. This raises ethical concerns in situations where a subset of the population is unable to receive successful vaccination, whether due to genetics, cultural practices, or access to health-care services. Key questions therefore arise regarding the causes and consequences of population-level heterogeneity in immunity: Do vaccines provide partial protection to everyone (leaky) or full protection to a subset of the population (all or none) (42)? How is R_eff affected by assortative mixing based on vaccination status (43) or age structure (44)?

On the individual level, much as self-boosting vaccines may introduce unique opportunities, the prospect of their clinical development also raises unique challenges. Prominent among the latter are the safety issues associated with herpesvirus vectors. For example, our models neglect the potential for immune senescence of the immune system. However, long-term infection with CMV can reduce the immune system’s ability to fight other infections as, across decades, CMV-specific T cells may overburden the memory repertoire (45–47). Other safety concerns include the potential for complications such as retinitis, from CMV infection (see, e.g., ref. 48). Whereas such risks are typically most significant in immunocompromised individuals, an important question is to what extent these and other issues may be controlled, or even eliminated, by the use of a sufficiently attenuated viral vector.

Equally varied are the potential scientific challenges. In describing the basis for self-boosting vaccines above, we outlined uncertainties relating to the determinants and kinetics of viral reactivation. In addition to these, the consequences of our underlying model assumptions about immunity underscore the need for quantitative studies on the induction, maintenance, and function of immune memory. A prominent example is in the relative roles of antigen stimulation and long-lived memory cells, in the maintenance of immune memory. Recent work suggests a dichotomy, in this respect, between acute and chronic viral infections, with the former stimulating long-lived, antigen-independent memory cells (49, 50) and the latter resulting in the converse: memory cells with diminished persistence in the absence of antigen stimulation (51, 52). Such effects would clearly have significant impacts on the effectiveness of the vaccines proposed here. Herpesviruses such as HSV fall somewhere in between acute and chronic; the infection is not cleared but most antigens are expressed only intermittently (16). More research on herpesvirus-induced immune memory is therefore a key avenue of future research to more fully understand this vaccine technology’s potential.

Another key, clinical question is the potential utility of self-boosting vaccines in maintaining mucosal vs. systemic immunity. A recent experimental study, demonstrating effective protection against mucosal challenge with simian immunodeficiency virus (SIV) (19), raises the possibility of analogous protection against other infections transmitted through mucosal tissue: that is, most respiratory and sexually transmitted pathogens. However, yet another study showed only modest protection against i.v. challenge of SIV (53), and an important question is to what extent such results may extend also to infections such as malaria.

Additionally, as we have shown in this work, the rate of endogenous reactivation (and thereby boosting) is key in determining the population-level success of the proposed vaccine technology. Elucidating the biological determinants of herpes virus reactivation may even open the way for vaccines whose self-boosting rate can be “engineered” or rendered sensitive to stimuli such as exposure to specific antigens. Finally, the development of methods for estimating the duration of transmission-blocking immunity from both vaccine trials and long-term surveillance data is a key avenue of future research.

In conclusion, past advances in vaccine design have facilitated qualitative shifts in the control of infectious diseases. Likewise, our work illustrates how today’s emerging vaccine technologies could offer new opportunities for overcoming the remaining barriers to achieving true herd immunity.

Materials and Methods

Basic Model.

Governing equations for the basic model of self-boosting vaccination, illustrated in Fig. 1A, are

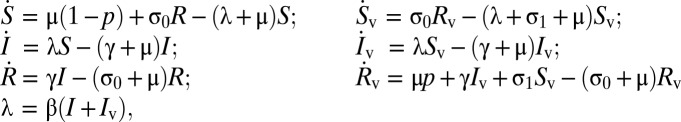where, as described in the main text, S is the proportion of the population unvaccinated and susceptible to infection; I is the proportion unvaccinated and infected; R is the proportion unvaccinated and recovered; and S_v, I_v, and R_v are the respective counterparts among those vaccinated in the population. In the equations above, a dot represents a time derivative, μ is the per-capita birth and death rate, β is the rate of infection, and 1/γ is the mean infectious period.

For given R₀, we find equilibrium S, I, R (i.e., where all time derivatives are zero) in the above equations. As the initial condition for a vaccination program with specified p, we translate a proportion p of these compartments (S, I, R) to their vaccinated counterparts (S_v, I_v, R_v). We then simulate the governing equations in the presence of vaccination.

To find the critical vaccination threshold p_c in this model, we note that in the absence of infection (I = I_v = 0), S, S_v take equilibrium values: S = 1 – p; S_v = pσ₀/(σ₀ + σ₁ + μ). For the effective reproduction number, we have by definition that R_eff = R₀(S + S_v). Taking p_c as the value of p at which R_eff = 1, we arrive at the vaccination threshold given in Eq. 1 in the main text.

Extension of the Basic Model to Include Natural Boosting.

The extended model, illustrated schematically in Fig. 3A, has governing equations

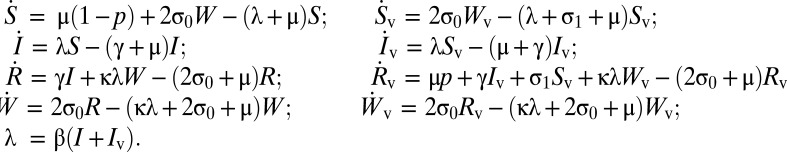Here W is the class of immunity that is waning, but could be boosted by reexposure to antigen, and κ represents the sensitivity of boosting, to reexposure. Following ref. 9 we take κ = 20. Once again, we simulate vaccination-free dynamics (p = 0) to endemic equilibrium and then use this to supply the initial conditions in the presence of vaccination, for a given p.