Abstract
Last few decades theoretical/computational studies of structure, function and reactivity of molecules have been contributing significantly in chemistry by explanation of experimental results, better understanding of underlying principles and prediction of the unknown experimental outcome. Accuracy needed in chemistry has long been established, but due to high power dependency of such accurate methods on the molecular size, it has been a major challenge to apply theoretical methods to large molecular systems. In the present article we will review some examples of such applications. One is theoretical study of growth/formation of carbon nanostructures such as fullerenes and carbon nanotubes, using quantum mechanical molecular dynamics method. For growth of single walled carbon nanotube from transition metal cluster, we have demonstrated continued growth of attached nanotube, cap formation and growth from small carbon fragments. For homogeneous catalysis we presented results of studies on N2 activation by Zr complexes. For biomolecular reactions we use active site and protein models and show that in some catalyses the protein environment is involved in reactions and changes the preferred pathway, and in some other case the effect is modest. The review is concluded with a perspective.
Keywords: theoretical chemistry, computational chemistry, nano structures, catalysis, enzymatic reactions, the ONIOM method
1. Introduction
Theoretical studies of structure, function and reactivity of molecules have fascinated and occupied my interest for the last fifty years. These essential properties of molecules have been studied by experimental chemists for many years and numerous empirical rules have been derived. Based on developments of various sophisticated theoretical methods to deal with complex electronic structure problems and obviously aided by the availability of fast computers as well as efficient computational programs, theoretical/computational studies in the last few decades have been contributing significantly in chemistry by explanation of experimental results, better understanding of underlying principles and prediction of the unknown experimental outcome. Acquiring chemical accuracy (0.1eV or 10kJ/mol) in evaluation of binding energy has long been accomplished for small molecules. However because of high power dependency (~N6) on the size N of molecule, it has not been easy to apply such high accuracy methods to studies of large and complex molecular systems. Therefore, more approximate theoretical methods have been applied to large systems. Density functional theory (DFT) methods give mid-level (~20 kJ/mol) accuracy at mid-level cost and size-dependency and have been the most popular theoretical methods for routine calculations. Semiempirical methods, such as the density functional tight binding (DFTB) method we used in a later section, are low cost alternatives with lower reliability. Classical molecular mechanics (MM) force field is very fast and can be applied to very large (>106 molecules) systems; however, its reliability is limited and cannot usually handle bond-breaking or formation. It is therefore impossible to simulate reactions of a complex molecular system (say 104 atoms) accurately for long periods of time (say 10−9 sec) using a single level of method.
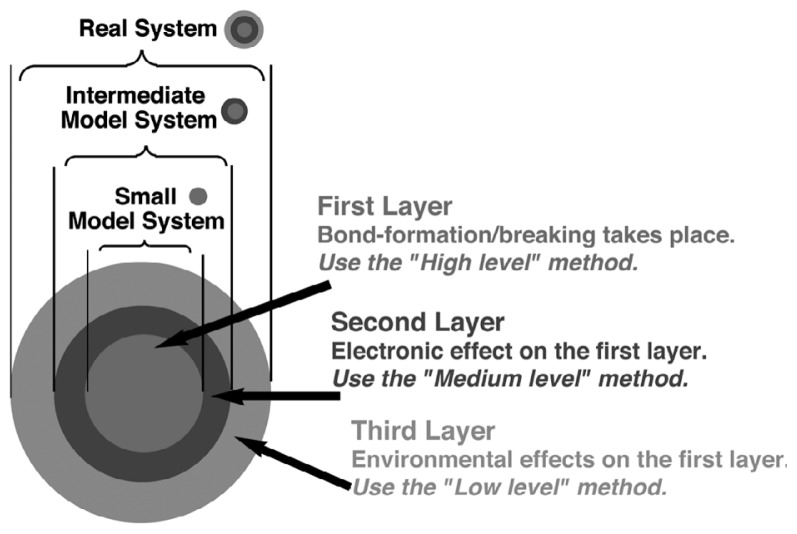
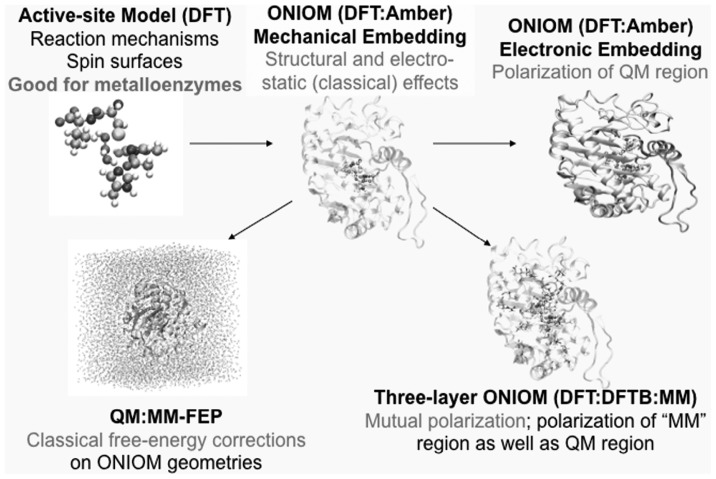
In order to solve such a demanding problem, it is almost mandatory to adopt a combination of these methods or a hybrid method; for instance a highly accurate but costly method for the most important part (say where the reaction is taking place), a medium-accuracy medium-cost method for the immediate neighborhood and an even less accurate and less costly method for the environment. The most popular hybrid method is what is called QM/MM method, in which a quantum mechanical method (QM) is combined with the MM method. The ONIOM (our own N-layered integrated molecular orbital and molecular mechanics) method developed by us allows combination of various levels of theory in multiple layers, as illustrated in Fig. 1, including QM:MM, QM:QM and QM:QM:MM.1)–7) The ONIOM method is being used for a variety of problems all over the world. We will use this method in a later section to discuss the effects of protein environment on the enzymatic reaction, the chemical reaction in protein.
Fig. 1.
The schematic representation of multi-layered ONIOM method.
Although many problems of structure, function and reaction of molecules have been solved or can nowadays be answered by existing theoretical methods, there are also many challenges that need to be resolved by theoretical studies. With all the above background in mind, in the present article we will briefly review some of our own recent studies toward these challenges of theoretical studies of chemical reactions.
2. Formation and growth of carbon nanostructures
2.1. “Shrinking hot giant” road of fullerene formation
Fullerenes are fascinating caged structures consisting only of carbon atoms. However, the mechanism how fullerenes are formed from small carbon fragments is not known. Many hypothetical models have been proposed, but none of them has any solid foundation.8) Moreover, these mechanisms assume a principle that the highly symmetric fullerene cage is built from smaller units in a systematic, step-wise manner. However, fullerenes are formed at high temperature (several thousand degrees in the early stage of graphite arc process and around 1500 K in hydrocarbon combustion process) in a condition far away from thermodynamic equilibrium, and such systems often give rise to auto-catalysis and self-assembly processes associated with irreversible processes.9),10)
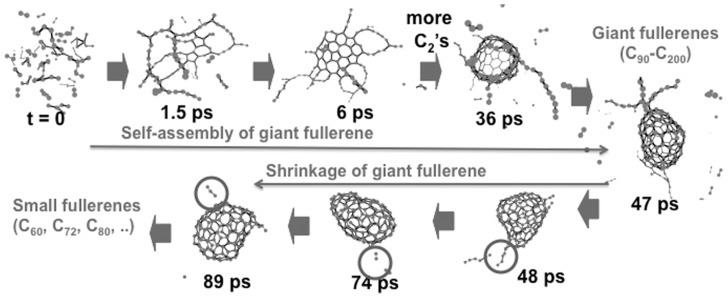
We have performed extensive quantum mechanical/molecular dynamics (QM/MD) simulation of the formation of fullerenes.11)–17) One needs to use QM to calculate the potential energy for nuclear motion on the fly, because molecular mechanics (MM), typically used for long time simulation of molecular systems, is unable to treat the conjugation of π electrons which is essential to the reactivity of trivalent carbon systems. In our simulations we used a semi-empirical QM method called density functional tight binding (DFTB) method. This method is about 100–1000 times faster than the standard DFT method, and allows us to perform simulations up to a few hundred pico second (ps) required to realize self-assembly processes. One needs MD because there are many possible reaction paths that cannot be explored by traditional path optimization approach. Based on the result of DFTB/MD, we have proposed a new mechanism of fullerene formation, called “Shrinking Hot Giant” road, as illustrated in Fig. 2.15) In this mechanism, giant fullerenes are formed by self-assembly of small carbon clusters in three stages: 1. nucleation of polycyclic structures from entangled polyyne chains (irreversible carbon sp2 re-hybridization from sp-hybridized polyynes), 2. repeated growth via “octopus-on-the-rock” structures, consisting of ring condensation of carbon chains and rings attached to the hexagon and pentagon containing nucleus as well as the chain-growth by addition of more C2 fragments to the peripherals, and finally 3. cage closure where polyyne chains reach over the opening and “zip” them closed, which is likewise irreversible due to the gain of energy in eliminating all dangling bonds. The entire self-assembly took less than 100ps if enough supply of carbon source is provided. Resultant fullerenes are “giant fullerenes” containing 100 to over 200 carbon atoms in the cage; no fullerenes with 60 to 80 carbons found commonly in experiment were formed. Continued heating of giant fullerenes led to C2 “pop out” events from the vibrationally hot cage very slowly (roughly one C2 fragment per few hundred ps). As giant fullerenes shrink and become more spherical, such pop-out events occur less frequently. We proposed that this slow but long “size-down” process eventually results in thermal distribution of a variety of fullerenes.
Fig. 2.
“Shrinking Hot Giant” mechanism of fullerene formation from small carbon fragments. The self-assembly (size-up) process took place through different stages: nucleation of polycyclic structures from entangled polyyne chains, 2. repeated growth via “octopus-on-the-rock” structures, consisting of the familiar ring condensation of carbon chains and rings attached to the hexagon and pentagon containing nucleus as well as the chain-growth by addition of more C2 fragments to the peripherals, and finally 3. cage closure where polyyne chains reach over the opening and “zip” them closed. Only giant fullerenes are formed. The size-down or shrinking process very slowly loses C2 fragments from giant fullerenes by “pop-out” events to produce smaller fullerenes.
2.2. Growth of carbon nanotube from transition metal cluster
Carbon nanotubes (CNTs), another form of pure carbon structure, are grown using a variety of techniques such as arc discharge or laser vaporization of graphite.18)–20) Most commonly the single-walled carbon nanotubes (SWNTs) are grown with the presence of transition metal catalysts. The growth mechanism of carbon nanotubes has been a subject of active studies but has not been well established. Theoretical/computational studies for the growth of SWNT on transition metal cluster were in the past performed either using MM/MD method (inability of the MM method to describe π electrons of carbons or the open-shell nature of transition metal cluster makes such calculations unreliable) or using DFT under very unrealistic condition and only for short time (where no real growth has been seen). Obviously better simulations are needed.
In an exceptional case, carbon nanotubes can be grown on the SiC surface by high temperature thermal decomposition.21)–25) We used the DFTB/MD method to show that growth can take place in tens of ps from the carbon-rich surface of SiC.26),27)
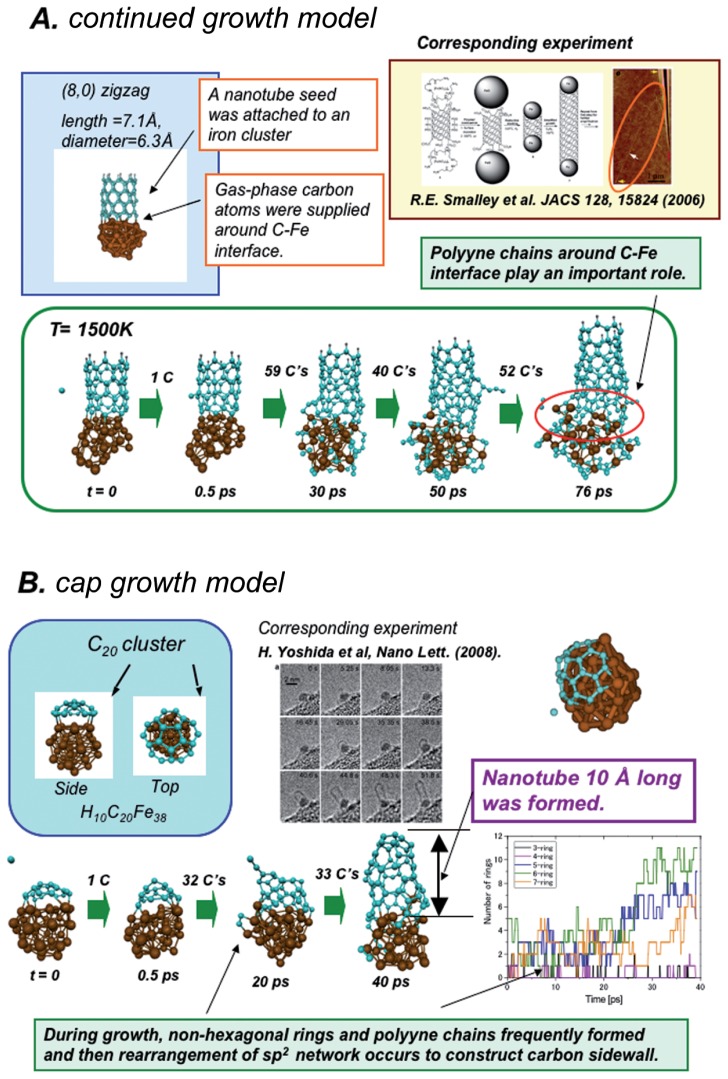
We have also recently succeeded in demonstrating for the first time efficient growth of SWNT from transition metal cluster in the DFTB/MD simulation.28)–30)Figure 3 shows some results of such simulations. The first model system we have adopted is the “continued growth” model, as shown in Fig. 3(A), in which a seed of (8,0)-zigzag or (5,5)-arm-chair SWNT was attached to an Fe38 cluster and carbon atoms were continuously supplied around the C–Fe interface. In the simulation at 1500 K for both seeds, growth of the SWNT up to 8Å has been observed in 80 ps in several of 10 trajectories if enough carbon supply is provided. In this simulation the effect of near-degeneracy of d orbitals of Fe atoms as well as the p orbitals of carbon atoms was taken into account by an electronic temperature which changes the occupancy of frontier orbitals smoothly from 1 to 0 as their orbital energies increase; it turned out that without electronic temperature the Fe cluster is not reactive and thus the open-shell nature of the metal cluster is vital for its catalytic activity. The growth essentially takes place by facile insertion of carbon atoms to the C–Fe bond in the metal-SWNT interface to form C, C2 and longer polyyne chains. These bridging sp-hybridized carbon fragments are vibrationally hot and highly mobile, and therefore become engaged in frequent bond formation and breaking processes between their constituent C and Fe atoms to form 5-, 6-, and 7-membered carbon rings extending the tube sidewall, resulting in overall continued growth of the nanotube on the Fe cluster. The growing SWNT has a large number of defects, and the chirality of the seed SWNT does not seem to be maintained in the growth process. However, we also observed that defects are slowly repaired during the process. In the present simulation, we supply carbon atoms at the rate of 2 carbon atoms/ps, much faster than the corresponding experimental rate. With slower carbon supply rate, more repair will take place during the growth and more regular SWNT will grow, possibly maintaining the chirality of the seed SWNT. We also found modest temperature dependency of the growth process. While 1500 K is the optimum for the growth in the present simulation, at 1000 K, the SWNT growth is suppressed despite the fact that the total number of created rings in the nanotube is comparable to that at 1500 K. In addition, relatively long polyyne chains tend to form extensions from the carbon sidewall to the metal cluster at 1000 K, whereas at 2000 K, deformation of the nanotube becomes more pronounced and diameter narrowing sets in, and polyyne chains at the rim of the nanotube easily dissociate at this high temperature.
Fig. 3.
DFTB/MD simulations of growth of SWNT from Fe38 cluster. (A) Continued growth model. (B) Cap growth model.
In the present simulation we supplied carbon atoms to the C–Fe boundary where they are incorporated almost directly into the growing SWNT. However, in reality we expect that most feed carbon atoms become adsorbed on the metal surface, since the surface area of metal cluster is likely to be much larger than the C–Fe boundary area. These adsorbed carbon atoms, whether as atoms or polyynes, have to migrate or diffuse on the metal surface or through inside of the metal cluster to the C–Fe boundary whether they are incorporated into the SWNT. We have been performing simulations with adsorbed carbons on Fe38 cluster and found that surface migration is dominant (although a few cases subsurface migrations have been recognized) but is slow compared to the growth (and could be rate-determining).
We envision that the actual SWNT formation process on metal catalysts takes place in three stages: nucleation or formation of carbon fragment (a few tens of carbon atoms) on the metal surface, cap formation or formation of organized half-domed carbon cap from the carbon fragment, and growth of tube from the cap by direct or migratory reaction of carbon feed. The reason why the “continued growth” model was chosen above is because we felt that the growth stage must be faster than the other two stages. In Figure 3(B) we show the results of our first simulations starting from cap formation. Here we put a C20 fragment on Fe38 cluster. This fragment reacts very easily with supplied carbon atoms and becomes larger, and the center part of the fragment soon lifts off from the metal surface into a dome-like structure, Then, the C–Fe boundary of the dome reacts efficiently with further supplied carbon atoms, as in the continued growth case above, to form a SWNT as long as 10Å. During growth, non-hexagonal rings and polyyne chains are frequently formed and then rearrangement of sp2 network occurs to construct carbon sidewall.
These theoretical/computational findings are only a few scattered evidences on how SWNT is formed on metal cluster. Much more work is required in order to understand the entire complex mechanism of growth of carbon nanotubes and their variations (nanohorns etc.).
3. Homogeneous catalyses and reactions of transition metal complexes
3.1. History and challenges
A little over twenty five years ago we started working on the mechanism of reactions of transition metal complexes and homogeneous catalytic reactions through calculation of structures and energies of transition states and intermediates of many elementary steps. At that time we encountered a substantial resistance from experimentalists who said that such information does not help to understand complex catalytic processes. In the last decades or so theoretical studies of catalytic processes have gained substantial acceptance as providing insight not obtainable from experiments alone, making it very hard to find a paper without theoretical/computational consideration. Reaction pathways of many elementary reactions such as oxidative addition, reductive elimination, olefin insertion, metathesis and bond activation, are now well understood theoretically.31) Computational approaches in catalyst design have been successfully utilized in industries as well.
However there are several challenges in this field. The most important is the use of realistic models. In early days, mainly because of computational cost, computations were carried out for simplified model systems. As an extreme case, sophisticatedly substituted phosphines PR3 are used in experiments while the simplest model phosphine PH3 was used in calculation; by doing so, many essential features of the proper choice of sophisticated ligands were lost. In order to tackle intricate effects of different ligands on the mechanism and chemo- and stereo-selectivities, one has to adopt real or realistic models. Nowadays systems containing around hundred or more atoms can be treated by density functional methods or hybrid methods such as ONIOM and OM/MM, allowing to include real ligands as well as some solvent molecules or counter ions, if needed, in the calculation.
The second challenge is describing correct spin state during reactions. It is becoming clear that especially for the first raw transition metals such as Fe, Co and Ni, the ground state often changes the spin state by the number and the strength of coordinating ligands, with high spin in low coordination complexes and low spin in high coordination complexes. Thus during the reaction the change of spin state, as well as the change of oxidation state, takes place and the spin cross over sometimes controls the reaction barrier. Unfortunately DFT, the most popular theoretical method, is unable to describe dependably the energy difference between different spin states, and this has to be calibrated by more expensive but more reliable theoretical methods such as the coupled cluster method.
3.2. Activation of nitrogen molecule by Zr complexes—Subtle ligand effects
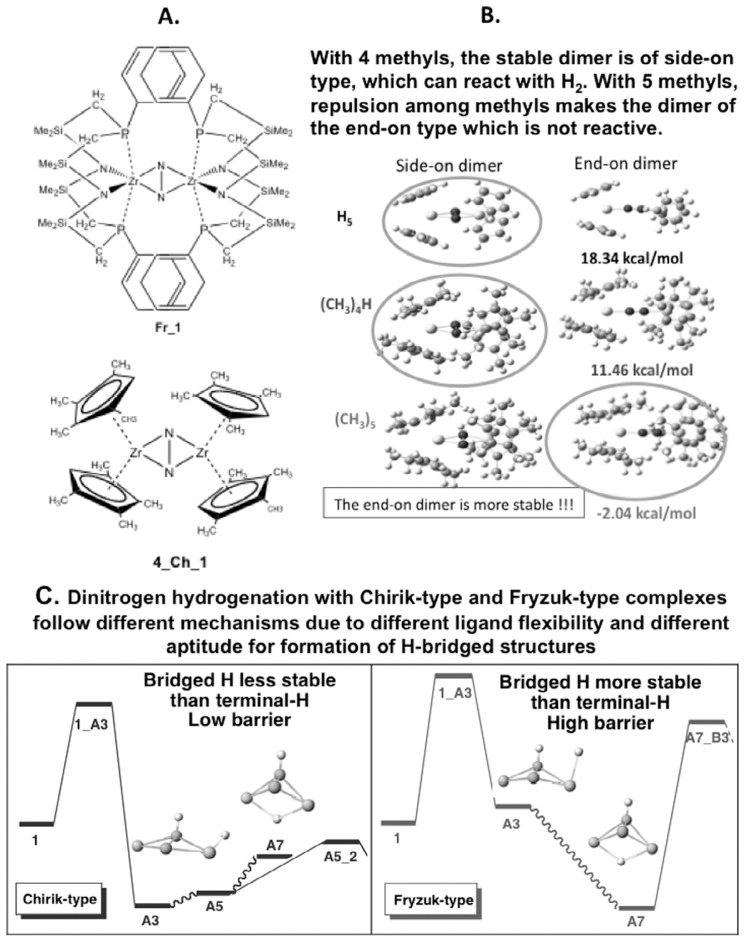
As an example of the effects of subtle difference in the ligand of a catalyst, here we discuss the activation of nitrogen molecule, still very important reaction with economical significance.32)–40) Recent experimental studies41),42) have shown that zirconocene with four methyl groups on each cyclopentadienyl (C5Me4H, structure 4_Ch_1 in Fig. 4(A)) activates N2 molecule to react with three hydrogen molecules, while zirconocene with pentamethyl-cyclopentadienyl (C5Me5) cannot make N2 react with any H2. We have answered by computational studies several questions concerning the N2 activation by this and related complexes.43)–46) In this section, we perrmed all QM calculations.
Fig. 4.
Activation of N2 using two zirconium complexes. (A) Structure of the Fryzuk complex Fr_1 and the Chirik complex 4_Ch_1. (B) The relative energy of the Chirik end-on dimer complex relative to the side-on dimer complex, for different number of methyl groups on the cyclopentadienyl ligand. (C) Comparison of potential energy profile for the activation of the first two hydrogen molecules by Chirik and Fryzuk complexes. (Adapted from Bobadova-Parvanova et al., Ref. 45. Reprinted with permission. Copyright 2006 American Chemical Society.)
Why can the zirconocene with four methyl groups (C5Me4H) activate N2 while that with five methyl groups (C5Me5) cannot? These zirconocenes at first form a dimeric N2 complex, (Cp2Zr)(N2) (ZrCp2), where Cp = C5Me4H, C5Me5. Our theoretical calculations have showed that there are two forms of dimeric N2 complexes, end-on and side-on. The side-on complexes with strong interactions of metal d orbitals with two sets of N2π orbitals activate the N2 molecule to have a long NN distance, so that hydrogen molecule can react easily with this activated N2. On the other hand, the end-on N2 complex has rather weak metal-N2 interaction and the unactivated N2 in this complex cannot react with any H2 molecule. As shown in Fig. 3(B), the most stable form of the dimeric N2 complex for Cp = C5Me4H is a side-on complex that reacts with H2 easily. On the other hand, for Cp = C5Me5 because of steric repulsion between methyl groups on different Zr centers, the side-on complex is less stable, and only the end-on complex is formed and does not react with any H2 molecule.
Why does the present zirconocene N2 complex (called Chirik complex) reacts with three H2 molecules, while another complex, zirconium diimine N2 complex, (called Fryzuk complex, structure Fr_1 in Fig. 4(A))32)–40) reacts with only one H2 molecule? Our calculated potential energy profiles for the reaction of the first two H2 molecules for both complexes are shown in Fig. 3(C). The barrier for the first H2 reaction at the TS 1_A3 is about the same for both complexes, both of them should react easily. However, there is a large difference between the two complexes for the second H2 reaction. For the Chirikcomplex, the most stable form of the H2-adduct (A3) has one H atom on N and the other on Zr. Addition of the second H2 molecule to this complex takes place with a reasonable barrier at TS A5_2. On the other hand, although the nascent form of the adduct for the Fryzuk complex is also A3, this complex bends the Z-N2-Zr angle and moves a hydrogen atom to the bridge position between two Zr’s (A7). This is about 10 kcal/mol more stable than A3 and is a trap. The second H2 addition from A7 has a very high barrier at A7_B3 and cannot take place. The Fryzuk ligand is too flexible, allowing the formation of a stable trapping intermediate. These theoretical calculations have provided insights and guiding principles into intricate effects of substituents and ligands that would not be available easily from experimental studies.
4. Structure and reactions of biomolecular systems—Active site model and effects of protein environment
Understanding of the mechanism of enzymatic reaction, chemical reaction inside protein, is a largest challenge of theoretical/computational studies of mechanisms of chemical reactions. Enzyme is a large complex collection of amino acid residues with some metals, ligands and water and other molecules, and theoretical approaches require a substantial approximation. Three different levels of approaches are being carried out, as shown in Fig. 5.
Fig. 5.
Schematic representation of strategy of ONIOM approaches to effects of protein environments on enzymatic reactions.
The active site model (Fig. 5, top left) In this approach one considers only atoms of the active site (including ligands in the first coordination shell around the central metals or other active centers), substrates and water molecules directly involved in the reaction. Nowadays active site models typically contain around 100 atoms, and the structures of reactants, intermediates and transition states are optimized with an appropriate QM method (nowadays mostly at a DFT level), activation barriers are evaluated and the reaction mechanisms are discussed. The active site approach should work well for metalloenzymes where reactions tend to occur localized in the vicinity of metals. In this approach any explicit effect of protein environment is completely neglected or approximated by a homogenous dielectric medium.
Protein model with geometry optimization (Fig. 5, top center and top right). Here typically starting with an X-ray structure of the protein, atoms within a certain range from the metal centers are selected and supplemented with hydrogen atoms and substrates, if not included in X-ray structure, to construct a protein model typically containing thousands of atoms. Geometry optimization (full or under certain constraints) is performed for complexes, intermediates and transition states to calculate barriers. Since it is impossible to perform QM calculations for such a large system, ONIOM or another hybrid method is usually adopted. There are different ways of including the effect of protein environment in the ONIOM scheme (Fig. 5); the mechanical embedding (ME, Fig. 5 top center) where the environmental electrostatic effect is included classically, the electronic embedding (EE, Fig. 5 top right) where polarization of the QM part by the environment is included or a multi-layered ONIOM method (such as a three-layered method as shown in Fig. 5 bottom right). Since the conformational space of the protein is very extensive, care must be taken so that changes in protein structure are directly coupled to the reaction coordinate, and not to arbitrary conformational changes during the optimization. A conservative solution is to use similar structures for reactant and product, but even this is technically very difficult to achieve and often requires improved optimization algorithms47),48) to stay in the same local MM minima during a reaction step. Comparison of the results of the protein model with those of the active-site model reveals the role of protein environment in the reaction.
Statistical average of protein motion/conformations and free energy calculation (Fig. 5, bottom left). In order to consider a large conformational space of protein, it is desirable to take its statistical average and obtain a “free energy” reaction profile. The DFT/MM method is still very expensive for statistical averaging and various approximations are being explored. Accurate description of statistics and dynamics of reactions of large molecular systems like enzymes is a major challenge at present and great activities are expected in the near future in this area.
In the rest of the section, we will show some examples of application of the active site and protein models to specific enzymatic reactions.
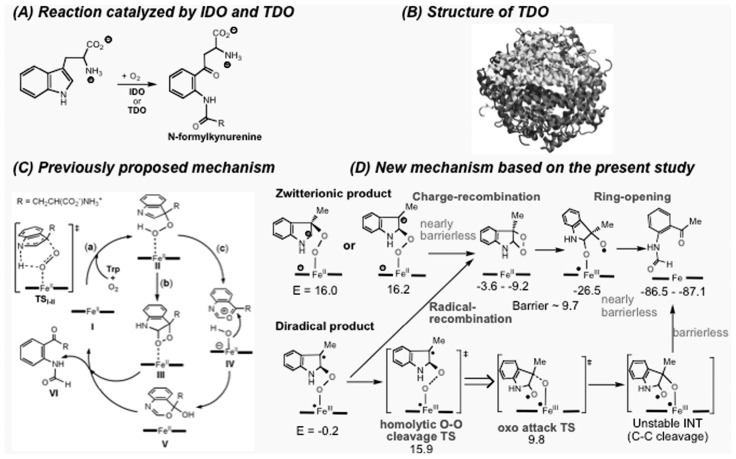
4.1. Indoleamine 2,3-dioxygenase (IDO) and tryptophan 2,3-dioxygenase (TDO)—an active site model study
IDO and TDO are heme-containing dioxygenases and catalyze oxidative cleavage of the pyrrole ring of L-tryptophan (Fig. 6(A)). Based on recent crystal structures (Fig. 6(B)), two mechanistic pathways were proposed. Both pathways start with electrophilic addition of the Fe(II)-bound dioxygen concerted with proton transfer (oxygen ene-type reaction), followed by either formation of a dioxetane intermediate or Criegee-type rearrangement (Fig. 6(C)). We studied the mechanism of this reaction using an active site model,49) and found that these proposed concerted oxygen ene-type and Criegee-type rearrangement pathways have high activation energies and cannot take place. We proposed a new mechanism for dioxygen activation in these heme systems, as shown in Fig. 6(D)), involving (a) direct electrophilic addition of the Fe(II)-bound oxygen to C2 (to give a zwitterionic species with E = −16.0 kcal/mol) or C3 position (to give another zwitterionic species with E = −16,2) of the indole in a closed-shell singlet state or (b) direct radical addition of the Fe(III)-superoxide to C2 position of the indole in a triplet (or open-shell singlet) state (to give a species with E = −0.2). Then, as shown in the top pathway in Fig. 6(D), radical-recombination or nearly-barrierless charge-recombination step from the resultant diradical or zwitterionic intermediates, respectively, proceeds to give metastable dioxetane intermediates (E = −3.6 ~ −9.2), followed by ring-opening of the dioxetanes (E = −26.5). Alternatively, homolytic O–O bond cleavage (bottom path in Fig. 6(D)) from the diradical intermediate (to give a species with E = 15.9), followed by oxo attack and facile C2–C3 bond cleavage may compete with the dioxetane formation pathway.
Fig. 6.
Mechanism of enzymatic reaction of indole 2,3-dioxygenase (IDO) and tryptophan 2,3-dioxygenase (TDO). (A) the reaction catalyzed by IDO and TDO. (B) X-ray structure of TDO. (C) Previously proposed mechanism of the enzymatic reaction, (D) The new mechanism based on the present study. (Adapted from Chung et al., Ref. 49. Reprinted with permission. Copyright 2008 American Chemical Society.)
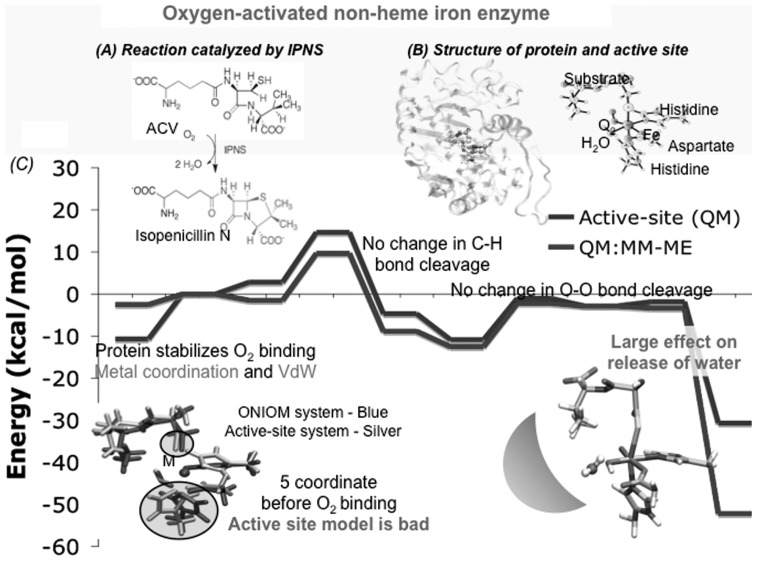
4.2. Isopenicillin N-synthase (IPNS)— Substantial effects of protein environment on energetics
The effects of protein environment have been studied in detail for the conversion of the linear tripeptide substrate δ-(L-α-aminoadi-poyl)-L-cysteinyl-D-valine (ACV) to isopenicillin N by a molecular oxygen catalyzed by IPNS, a non-heme iron enzyme (Fig. 7(A)).50),51) Here the ONIOM(DFT:MM) system we adopted contains 5386 atoms, while the active site QM model consists of 65 atoms (Fig. 7(B)).52)–54)Figure 7(C) shows the potential energy profiles of the first several steps of the entire reaction. Although not shown for brevity, the potential profile of all the reaction steps using the protein model is qualitatively similar to that obtained with the active site model. However the largest difference of 10 kcal/mol was found in the rate-determining first O2 coordination and activation step. This difference makes the reaction easy to occur in protein from difficult to occur without protein, a typical role of a catalyst in catalytic reaction. As shown at the left bottom of Fig. 7(C), this comes from the coordination of molecular oxygen becoming from endothermic (black line) to thermoneutral (blue) in the presence of protein environment, due to the van der Waals interaction between the oxygen molecule and near-by protein residues that are neglected in the active-site-only model.
Fig. 7.
Mechanism of biosynthesis of antibiotics in isopenicillin N synthase (IPNS). (A) The reaction catalyzed by IPNS. (B) Structure of IPNS protein and active site. (C) Potential energy profiles of oxidation of ACV substrate by IPNS, using the active site model (DFT, black) and the protein model (DTF:MM, blue), with some detailed explanation of the effects of protein environments.
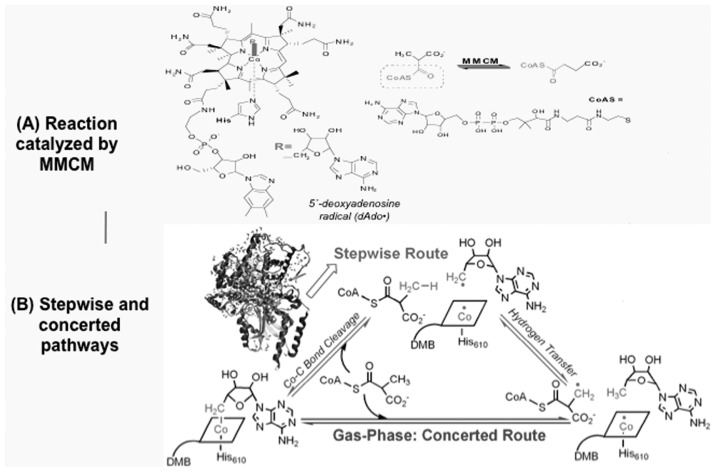
4.3. Mechanism of reaction of B12-dependent methylmalonyl-CoA mutase (MMCM)— Positive participation of protein environments in reaction coordinate
B12-dependent MMCM catalyzes a radical-based transformation of methyl-malonyl-coenzyme A (CoA) to succinyl-CoA.55),56) The cofactor adenosylcobalamin (AdoCbl) serves as a radical reservoir that generates the 5′-deoxyadeno-sine radical (dAdo•, see inset R in Fig. 8(A)) via homolysis of the Co–C5′ bond (thick green line in Fig. 8(A)). The mechanism by which the enzyme stabilizes the homolysis products and achieve an observed ~1012-fold rate acceleration is not yet fully understood. Using the active site model and the protein model containing over 12000 atoms in the ONIOM(DFT:MM) calculation of which up to 100 atoms are treated by the DFT method, we have studied mainly the first and rate-determining stage of the enzymatic reaction, the homolytic Co–C bond cleavage to form 5′-deoxyadenosyl (Ado) radical and cob(II)alamin, and the subsequent hydrogen transfer from the methylmalonyl-CoA substrate to the Ado radical in MMCM.57),58) We found two very important effects of protein environment that completely changed the conclusions derived from the active site model.
Fig. 8.
Mechanism of radical carbon skeleton rearrangement catalyzed by B12-dependent methylmalonyl-CoA mutase (MMCM). (A) The reaction catalyzed by MMCM. (B) Stepwise and concerted pathways for the Co–C bond cleavage and hydrogen transfer stages of the reaction.
At first we found that the Co–C bond dissociation energy is very much reduced in the protein, compared to that in the gas phase. Comparison of the optimized structures of initial enzyme and the intermediate indicates that a dramatic change in the conformational features of the dAdo moiety has taken place. Thus in the present enzyme, change in the protein environment around the active site is a part of the reaction coordinate, and it is essential to include this protein environment for calculating the energy profile of cobalt-carbon bond homolysis. This conformational change caused slight Co–C5′ bond elongation, which is connected to a destabilization of the AdoCbl. The large protein effect on the Co–C bond dissociation energy can be divided into the cage effect, the effect of coenzyme geometrical distortion, and the protein field effect. The largest contributor is the protein field effect; several protein residues including Glu370 play the key role in the Co–C bond cleavage process by stabilizing the Co–C bond cleaved state in the protein by hydrogen bonding and van der Waals interactions.
Secondly in protein the initial Co–C bond cleavage and the subsequent hydrogen transfer were found to occur in a stepwise manner (See Fig. 8(B)). This is in stark contrast with the same reaction in the gas phase, where the transition state for the concerted pathway was found to be lower in energy than for the stepwise pathway. In protein the stepwise transition state is stabilized by the protein environment and become lower in energy than the concerted transition state that is not much stabilized by the protein environment.
Summarizing the effect of protein environment on enzymatic reactions we have studied, we found three different situations.
The effect of protein environment is rather small in the reaction pathway as well as in the potential energy profile. In this situation the active site model without explicit consideration of protein environment give correct description of the reaction mechanism. We found this kind of situation tends to occur when the active site is on the surface of protein.
The effect of protein environment does not change reaction pathways but changes their energies. This situation illustrates the catalytic effect of the protein environment. IPNS belongs to this case. In this situation reaction pathways can be determined with the active site model but the effect of the environment has to be treated properly for energetics.
The protein environment is involved in the reaction coordinate, i.e. changes in protein structure take place and sometimes provide a driving force for the reaction. We have seen this in MMCM, In this situation an active site model is not enough and an extended model include the part of protein environment has been treated for search of reaction pathways.
The task is just started to learn more about the reaction of enzymes from computational studies. More realistic models, more reliable calculations, more statistical averaging and long time dynamics —with all these, in the future we hope to understand enzymatic reactions much better than we do now.
4.4. Mechanism of efficient firefly bioluminescence
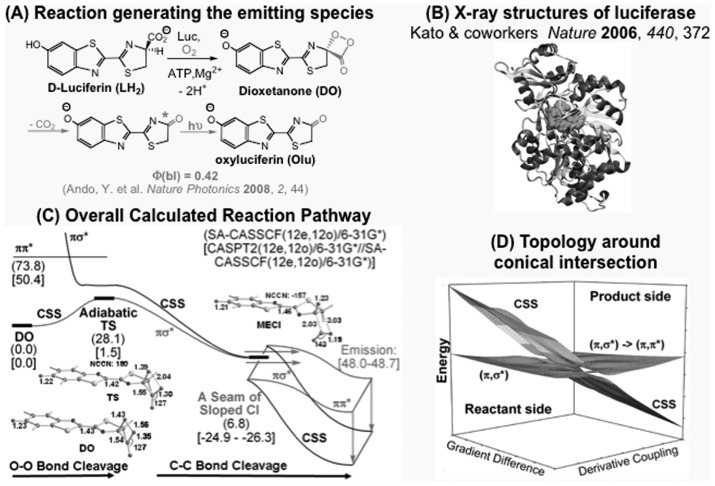
The firefly emission is well-known bioluminescence, in which oxyluciferin (OLu) is produced with high yield in an excited electronic state in the luciferase protein from D-luciferin, ATP and O2 molecule, as shown in Fig. 9(A). A high-resolution X-ray structure has recently been published based on data collected with the SPring-8 Synchrotron radiation facility. However the mechanism of this bioluminescence, in particular how the oxylucuferin is produced in an excited electronic state from a dioxetanone intermediate (DO) in the ground electronic state, has not been known. Since the reactant in the ground state usually produces a product in the ground state, in the present case there must exist a conical intersection, a cone-like crossing between the ground and excited potential energy surfaces that efficiently funnels the ground state reactant to an excited state product. We have recently calculated the potential energy surfaces of various electronic configurations of an active site model from DO to OLu and found for the first time the pathway in which the ground state DO is converted efficiently to the excited state OLu.59) As shown in Fig. 9(C), the DO in the ground state at first goes over a transition state TS with a relatively small barrier while changing its nature from closed-shell singlet (CSS) to πσ* singlet. We located for the first time the structure and energy of a minimum on the seam of crossing MECI between the ground and first excited potential surfaces. The topology of two potential energy surfaces around the conical intersection suggests that the system will travel very efficiently along the red arrows in Fig. 9(D), finding itself in the excited state after the conical intersection, leading to the excited state OLu product. Although this finding itself is a great breakthrough, consideration of the effects of protein environment will further enhance understanding of this important bioluminescence reaction mechanism.
Fig. 9.
The mechanism of efficient firefly bioluminescence via adiabatic transition state and seam of sloped conical intersection. (A) The reaction that generate the excited state of oxyluciferin that emit the light. (B) X-ray structure of luciferase. (C) The calculated overall reaction pathway, shown in red. (D) Topology of two potential energy surfaces in the vicinity of minimum energy conical intersection, MECI. (Adapted from Chung et al., Ref. 58. Reprinted with permission. Copyright 2008 American Chemical Society.)
5. Perspective
The theoretical/computational study of structure, function and reactivity of molecules is a very exciting field of chemistry. Theoretical computation provides insight into the detailed mechanism, pathways, energetics, dynamics of complex reactions mechanism, the information that is not easily available from experiments and complementary to experiments.
For accurate long time simulation of complex molecular systems, the present computing power is insufficient. For instance it is not easy to run DFT/ MM dynamics for ns for an enzymatic reactions. Arrival of faster computers, including “next-generation supercomputer” of 10 peta flop speed scheduled to be in operation in 2012 in Japan, is anxiously waited for. Such new computers will make it possible to carry out such demanding calculations and will give a great opportunity to theoretical/computational chemistry to make a profound impact in the progress of chemical research.
In the coming few decades, understanding and designing structure, function and reactivity of complex molecular systems will remain to be the central issue of theoretical/computational chemistry. In order to accomplish this goal, we have to use all the theoretical/computational methodologies available to us: quantum chemistry, classical and quantum molecular dynamics, long time simulation and statistical averaging. After fifty years of my career, I find this field still very fascinating and believe that it will remain exciting for the foreseeable future. I hope that younger generations also find this field very exciting and take leadership in promoting this endeavor.
Acknowledgements
Acknowledgement is made to all my students, postdocs and collaborators. Particular thanks go Drs. Stephan Irle, Guishan Zheng, Zhi Wang, Yasuhito Ohta, Yoshiko Okamoto, Petia Bobadova-Parvanova, Jamal Musaev, Marcus Lundberg, Lung Wa Chung and Xin Li, whose studies are discussed in this article. The work is supported in part by the Fukui Institute for Fundamental Chemistry and in part by a CREST (Core Research for Evolutional Science and Technology) grant in the area of High Performance Computing for Multi-Scale and Multi-Physics Phenomena from of JST (Japan Science and Technology Agency).
Profile
Keiji Morokuma graduated from Kyoto University in 1957, and finished his Ph.D. in 1963 at Kyoto University with Prof. Kenichi Fukui as adviser. After being junior faculty at Kyoto University for a few years, he was Visiting Research Assistant Professor at Department of Chemistry, Columbia University and Postdoctoral Research Fellow at Department of Chemistry, Harvard University under Prof. Martin Karplus. From 1967 he was Assistant Professor at Department of Chemistry, University of Rochester, and was promoted to Professor in 1971. In 1976 he came back to Japan to spearhead the establishment of Division of Theoretical Studies, Institute for Molecular Science, Okazaki, Japan as Professor, Division Director and Director of Computer Center. In 1993 he moved back to US to become William H. Emerson Professor of Chemistry and Director of Cherry L. Emerson Center for Scientific Computation at Emory University, Atlanta, GA. After becoming Professor Emeritus there, since 2006 he is Research Leader, Fukui Institute for Fundamental Chemistry, Kyoto University. He received the International Academy of Quantum Molecular Science Annual Award (1978), the Chemical Society of Japan Award (1992), the Schrödinger Medal of World Association of Theoretical Organic Chemists (1993), the Fukui Medal of Asian Pacific Association of Theoretical & Computational Chemists (2005), and the Imperial Prize and the Japan Academy Prize (2008). He has been a member (1985–) and President (2000–2006) of the International Academy of Quantum Molecular Science. He published more than 640 papers.

References
- 1).Maseras F., Morokuma K. (1995) IMOMM: A new integrated ab initio + molecular mechanics geometry optimization scheme of equilibrium structures and transition states. J. Comp. Chem. 16, 1170–1179 [Google Scholar]
- 2).Svensson M., Humbel S., Froese R. D. J., Matsubara T., Sieber A., Morokuma K. (1996) ONIOM: A multilayered Integrated MO + MM method for geometry optimizations and single point energy predictions. A test for Diels–Alder re- actions and Pt(P(t-Bu)3)2 + H2 oxidative addition. J. Phys. Chem. 100, 19357–19363 [Google Scholar]
- 3).Dapprich S., Komaromi I., Byun K. S., Morokuma K., Frisch M. J. (1999) A new ONIOM implementation in Gaussian98. Part I. The calculation of energies, gradients, vibrational frequencies and electric field derivatives. J. Mol. Str. (Theochem) 461–462, 1–21 [Google Scholar]
- 4).Vreven T., Morokuma K. (2000) On the application of the IMOMO (integrated molecular orbital + molecular orbital) method. J. Comp. Chem. 21, 1419–1432 [Google Scholar]
- 5).Morokuma K. (2003) ONIOM and its applications to material chemistry and catalyses. Bull. Kor. Chem. Soc. 24, 797–801 [Google Scholar]
- 6).Vreven T., Morokuma K. (2006) Hybrid methods: ONIOM(QM:MM) and QM/MM. Ann. Rep. Comp. Chem. 2, 35–52 [Google Scholar]
- 7).Vreven T., Byun K. S., Komaromi I., Dapprich S., Montgomery J. A., Jr, Morokuma K., et al. (2006) Combining quantum mechanics methods with molecular mechanics methods in ONIOM. J. Chem. Theo. Comp. 2, 815–826 [DOI] [PubMed] [Google Scholar]
- 8).For a review, see for instance, Yamaguchi Y., Maruyama S. (1997) Molecular dynamics of the formation process of fullerene (1 Report, The formation of a caged structure and controlled temperature). JSME 63-611B, 2398–2404 [Google Scholar]
- 9).Nicolis G., Prigogine I. (1997) Self-Organization in Nonequilibrium Systems: From Dissipative Structures to Order Through Fluctuations, Wiley, New York [Google Scholar]
- 10).Prigogine I. (1997) The End of Certainty—Time, Chaos, and the New Laws of Nature. The Free Press, New York [Google Scholar]
- 11).Irle S., Zheng G., Elstner M., Morokuma K. (2003) Formation of fullerene molecules from carbon nanotubes: A quantum chemical molecular dynamics study. Nano Lett. 3, 465–470 [Google Scholar]
- 12).Irle S., Zheng G., Elstner M., Morokuma K. (2003) From C2 molecules to self-assembled fullerenes in quantum chemical molecular dynamics. Nano Lett. 3, 1657–1664 [Google Scholar]
- 13).Zheng G., Irle S., Elstner M., Morokuma K. (2004) Quantum chemical molecular dynamics model study of fullerene formation from open-ended carbon nanotubes. J. Phys. Chem. A 108, 3182–3194 [Google Scholar]
- 14).Zheng G., Irle S., Elstner M., Morokuma K. (2005) Towards formation of buckminsterfullerene C60 in quantum chemical molecular dynamics. J. Chem. Phys. 122, 014708. [DOI] [PubMed] [Google Scholar]
- 15).Irle S., Zheng G., Wang Z., Morokuma K. (2006) The C60 formation puzzle “solved”: QM/ MD simulations reveal the shrinking hot giant road of the dynamic fullerene self-assembly mechanism. J. Phys. Chem. B 110, 14531–14545 [DOI] [PubMed] [Google Scholar]
- 16).Zheng G., Wang Z., Irle S., Morokuma K. (2007) Quantum chemical molecular dynamics study of “shrinking” of hot giant fullerenes. J. Nanosci. Nanotech. 7, 1662–1669 [DOI] [PubMed] [Google Scholar]
- 17).Irle S., Zheng G., Wang Z., Morokuma K. (2007) Theory-experiment relationship of the “shrinking hot giant” road of dynamic fullerene self-assembly in hot carbon vapor. Nano 2, 21– 30 [Google Scholar]
- 18).Iijima S., Ishihashi T. (1993) Single-shell carbon nanotubes of 1-nm diameter. Nature 363, 603–605 [Google Scholar]
- 19).Bethune D. S., Kiang C., DeVries M. S., Gorman G., Savoy R., Beyers R. (1993) Cobalt-catalysed growth of carbon nanotubes with single-atomic-layer walls. Nature 363, 605–607 [Google Scholar]
- 20).Thess A., Lee R., Nikolaev P., Dai H. J., Petit P., Robert J., et al. (1996) Crystalline ropes of metallic carbon nanotubes. Science 273, 483–487 [DOI] [PubMed] [Google Scholar]
- 21).Kusunoki M., Suzuki T., Hirayama T., Shibata N., Kaneko K. (2000) A formation mechanism of carbon nanotube films on SiC(0001). Appl. Phys. Lett. 77, 531–533 [Google Scholar]
- 22).Kusunoki M., Suzuki T., Kaneko K., Ito M. (1999) Formation of self-aligned carbon nanotube films by surface decomposition of silicon carbide. Phil. Mag. Lett. 79, 153–161 [Google Scholar]
- 23).Kusunoki M., Suzuki T., Honjo C., Hirayama T., Shibata N. (2002) Selective synthesis of zigzag-type aligned carbon nanotubes on SiC (0 0 0 − 1) wafers. Chem. Phys. Lett. 366, 458–462 [Google Scholar]
- 24).Kusunoki M., Honjo C., Suzuki T., Hirayama T. (2005) Growth process of close-packed aligned carbon nanotubes on SiC. Appl. Phys. Lett. 87, 103105 [Google Scholar]
- 25).Derycke V., Martel R., Radosvljevic M., Ross F. M. R., Avouris P. (2002) Catalyst-free growth of ordered single-walled carbon nanotube networks. Nano Lett. 2, 1043–1046 [Google Scholar]
- 26).Irle S., Wang Z., Zheng G., Morokuma K., Kusunoki M. (2006) Theory and experiment agree: Single-walled carbon nanotube caps grow catalyst-free with chirality preference on a SiC surface. J. Chem. Phys. 125, 044702. [DOI] [PubMed] [Google Scholar]
- 27).Wang Z., Irle S., Zheng G., Kusunoki M., Morokuma K. (2007) Carbon nanotubes grow on the C face of SiC (000-1) during sublimation decomposition: quantum chemical molecular dynamics simulations. J. Phys. Chem. C 111, 12960– 12972 [Google Scholar]
- 28).Ohta Y., Okamoto Y., Irle S., Morokuma K. K. (2008) Rapid growth of a single-walled carbon nanotube on an iron cluster: density-functional tight-binding molecular dynamics simulations. ACS nano 2, 1437–1444 [DOI] [PubMed] [Google Scholar]
- 29).Ohta Y., Okamoto Y., Irle S., Morokuma K. (2009) Temperature dependence of SWNT growth process on an iron cluster: density functional tight-binding molecular dynamics. J. Phys. Chem. C 113, 159–169 [Google Scholar]
- 30).Ohta Y., Okamoto Y., Irle S., Morokuma K. (2009) SWNT Growth through surface diffusion of carbons on an iron cluster: Density-functional tight-binding molecular dynamics simulations. Carbon 47, 1270–1275 [DOI] [PubMed] [Google Scholar]
- 31).For reviews, for instance, Morokuma K., Musaev D.G. (eds.) (2007) Computational Modeling of Principles and Mechanisms of Transition Metal-Based Homogenous Catalytic Processes. Wiley-VCH, Weinheim [Google Scholar]
- 32).Fryzuk M.D., Johnson D.G. (2000) The continuing story of dinitrogen activation. Coord. Chem. Rev. 200–202, 379–409 [Google Scholar]
- 33).Jennings J.R. (ed.) (1991) Catalytic Ammonia Synthesis. Plenum, New York [Google Scholar]
- 34).Fryzuk M. D. (2004) Inorganic chemistry: Ammonia transformed. Nature 427, 498–499 [DOI] [PubMed] [Google Scholar]
- 35).Schlögl R. (2003) Catalytic synthesis of ammonia —A “never-ending story”? Angew. Chem. Int. Ed. 42, 2004–2008 [DOI] [PubMed] [Google Scholar]
- 36).Mori M. (2004) Activation of nitrogen for organic synthesis. J. Organomet. Chem. 689, 4210–4227 [Google Scholar]
- 37).Yandulov D. V., Schrock R. R. (2003) Catalytic reduction of dinitrogen to ammonia at a single molybdenum center. Science 301, 76–78 [DOI] [PubMed] [Google Scholar]
- 38).Schrock R. R. (2005) Catalytic reduction of dinitrogen to ammonia at a single molybdenum center. Acc. Chem. Res. 38, 955–962 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39).MacKay B. A., Fryzuk M. D. (2004) Dinitrogen coordination chemistry: on the biomimetic borderlands. Chem. Rev. 104, 385–402 [DOI] [PubMed] [Google Scholar]
- 40).Gambarotta S., Scott J. (2004) Multimetallic co- operative activation of N2. Angew. Chem. Intl. Ed. 43, 5298–5308 [DOI] [PubMed] [Google Scholar]
- 41).Pool J. A., Lobkovsky E., Chirik P. J. (2004) Hydrogenation and cleavage of dinitrogen to ammonia with a zirconium complex. Nature 427, 527–530 [DOI] [PubMed] [Google Scholar]
- 42).Bernskoetter W. H., Lobkovsky E., Chirik P. J. (2005) Kinetics and mechanism of N2 hydrogenation in Bis(cyclopentadienyl) zirconium complexes and dinitrogen functionalization by 1,2-addition of a saturated C–H bond. J. Am. Chem. Soc. 127, 14051–14061 [DOI] [PubMed] [Google Scholar]
- 43).Bobadova-Parvanova P., Wang Q., Morokuma K., Musaev D. G. (2005) How many methyl groups in [{(η5-C5MenH5-n)2Zr}2(μ2,η2,η2-N2)] are needed for dinitrogen hydrogenation? A theoretical study. Angew. Chem. Int. Ed. 44, 7101–7103 [DOI] [PubMed] [Google Scholar]
- 44).Bobadova-Parvanova P., Quinonero D., Morokuma K., Musaev D. G. (2006) Theoretical study of the structure and properties of [(η5- C5Me4H)2Zr]2(μ2,η2,η2-N2). J. Chem. Theo. Comp. 2, 336–341 [DOI] [PubMed] [Google Scholar]
- 45).Bobadova-Parvanova P., Wang Q., Quinonero D., Morokuma K., Musaev D. G. (2006) Does dinitrogen hydrogenation follow different me- chanisms for [(η5-C5Me4H)2Zr]2(μ2,η2,η2-N2) and {[PhP(CH2SiMe2NSiMe2CH2)PPh]Zr}2(μ2,η2,η2-N2) complexes? A computational study. J. Am. Chem. Soc. 128, 11391–11403 [DOI] [PubMed] [Google Scholar]
- 46).Musaev D. G., Bobadova-Parvanova P., Morokuma M. (2007) Why [(η5-C5MenH5-n)2Ti]2(μ2, η2,η2-N2) can not add a H2 molecule to the side-on-coordinated N2 while its Zr and Hf analogues can? Insights from computational studies. Inorg. Chem. 46, 2709–2715 [DOI] [PubMed] [Google Scholar]
- 47).Vreven T., Morokuma K., Farkas Ö., Schlegel H. B., Frisch M. J. (2003) Geometry optimization with QM/MM, ONIOM, and other combined methods. I. Microiterations and constraints. J. Comp. Chem. 24, 760–769 [DOI] [PubMed] [Google Scholar]
- 48).Vreven T., Frisch M. J., Kudin K. N., Schlegel H. B., Morokuma K. (2006) Geometry optimization with QM/MM methods II: Explicit quadratic coupling. Mol. Phys. 104, 701–714 [Google Scholar]
- 49).Chung L. W., Li X., Sugimoto H., Shiro Y., Morokuma K. (2008) Density functional theory study on a missing piece in understanding of heme chemistry: The reaction mechanism for indoleamine 2,3-dioxygenase and tryptophan 2,3-dioxygenase. J. Am. Chem. Soc. 130, 12299–12309 [DOI] [PubMed] [Google Scholar]
- 50).Roach L., Clifton I. J., Hensgens C. M. H., Shibata N., Schofield C. J., Baldwin J. E. (1997) Structure of isopenicillin N synthase complexed with substrate and the mechanism of penicillin formation. Nature 387, 827–830 [DOI] [PubMed] [Google Scholar]
- 51).Burzlaff N. I., Rutledge P. J., Clifton I. J., Hensgens C. M. H., Pickford M., Adlington R. M., et al. (1999) The reaction cycle of isopenicillin N synthase observed by X-ray diffraction. Nature 401, 721–724 [DOI] [PubMed] [Google Scholar]
- 52).Lundberg M., Morokuma K. (2007) Protein environment facilitates O2 binding in non-heme iron enzyme. An insight from ONIOM calculations on isopenicillin N synthase (IPNS). J. Phys. Chem. B 111, 9380–9389 [DOI] [PubMed] [Google Scholar]
- 53).Lundberg M., Siegbahn P. E. E., Morokuma K. (2008) The mechanism for isopenicillin N synthase from density-functional modeling highlights the similarities with other enzymes in the 2-His-1-carboxylate family. Biochemistry 47, 1031–1042 [DOI] [PubMed] [Google Scholar]
- 54).Lundberg M., Kawatsu T., Vreven T., Frisch M. J., Morokuma K. (2009) Transition states in the protein environment in isopenicillin N biosynthesis from ONIOM QM:MM modeling. J. Chem. Theo. Comp. 15, 222–234 [DOI] [PubMed] [Google Scholar]
- 55).Mancia F., Evans P. R. (1998) Conformational changes on substrate binding to methylmalonyl CoA mutase and new insights into the free radical mechanism. Structure 6, 711–720 [DOI] [PubMed] [Google Scholar]
- 56).Banerjee R. (2003) Introduction: radical enzymology. Chem. Rev. 103, 2081–2082 [Google Scholar]
- 57).Kwiecien R. A., Khavrutskii I. V., Musaev D. G., Morokuma K., Banerjee R., Paneth P. (2006) Computational insights into the mechanism of radical generation in B12-dependent methyl- malonyl-CoA mutase. J. Am. Chem. Soc. 128, 1287–1292 [DOI] [PubMed] [Google Scholar]
- 58).Li X., Chung L. W., Paneth P., Morokuma K. (2009) DFT and ONIOM(DFT:MM) Studies on the Co–C bond cleavage and the hydrogen transfer in B12-dependent methylmalonyl-CoA mutase. A stepwise or concerted mechanism? J. Am. Chem. Soc. 131, 5115–5125 [DOI] [PubMed] [Google Scholar]
- 59).Chung L. W., Hayashi S., Lundberg M., Nakatsu T., Kato H., Morokuma K. (2008) Mechanism of efficient firefly bioluminescence via adiabatic transition state and seam of sloped conical intersection. J. Am. Chem. Soc. 130, 12880–12881 [DOI] [PubMed] [Google Scholar]