Analyzing social experiments as implemented: A reexamination of the evidence from the HighScope Perry Preschool Program

Abstract

Social experiments are powerful sources of information about the effectiveness of interventions. In practice, initial randomization plans are almost always compromised. Multiple hypotheses are frequently tested. “Significant” effects are often reported with p-values that do not account for preliminary screening from a large candidate pool of possible effects. This paper develops tools for analyzing data from experiments as they are actually implemented.

We apply these tools to analyze the influential HighScope Perry Preschool Program. The Perry program was a social experiment that provided preschool education and home visits to disadvantaged children during their preschool years. It was evaluated by the method of random assignment. Both treatments and controls have been followed from age 3 through age 40.

Previous analyses of the Perry data assume that the planned randomization protocol was implemented. In fact, as in many social experiments, the intended randomization protocol was compromised. Accounting for compromised randomization, multiple-hypothesis testing, and small sample sizes, we find statistically significant and economically important program effects for both males and females. We also examine the representativeness of the Perry study.

1. Introduction

Social experiments can produce valuable information about the effectiveness of interventions. However, many social experiments are compromised by departures from initial randomization plans.¹ Many have small sample sizes. Applications of large sample statistical procedures may produce misleading inferences. In addition, most social experiments have multiple outcomes. This creates the danger of selective reporting of “significant” effects from a large pool of possible effects, biasing downward reported p-values. This paper develops tools for analyzing the evidence from experiments with multiple outcomes as they are implemented rather than as they are planned. We apply these tools to reanalyze an influential social experiment.

The HighScope Perry Preschool Program, conducted in the 1960s, was an early childhood intervention that provided preschool education to low-IQ, disadvantaged African- American children living in Ypsilanti, Michigan. The study was evaluated by the method of random assignment. Participants were followed through age 40 and plans are under way for an age-50 followup. The beneficial long-term effects reported for the Perry program constitute a cornerstone of the argument for early childhood intervention efforts throughout the world.

Many analysts discount the reliability of the Perry study. For example, Hanushek and Lindseth (2009), among others, claim that the sample size of the study is too small to make valid inferences about the program. Herrnstein and Murray (1994) claim that estimated effects of the program are small and that many are not statistically significant. Others express the concern that previous analyses selectively report statistically significant estimates, biasing the inference about the program (Anderson (2008)).

There is a potentially more devastating critique. As happens in many social experiments, the proposed randomization protocol for the Perry study was compromised. This compromise casts doubt on the validity of evaluation methods that do not account for the compromised randomization and calls into question the validity of the simple statistical procedures previously applied to analyze the Perry study.²

In addition, there is the question of how representative the Perry population is of the general African-American population. Those who advocate access to universal early childhood programs often appeal to the evidence from the Perry study, even though the project only targeted a disadvantaged segment of the population.³

This paper develops and applies small-sample permutation procedures that are tailored to test hypotheses on samples generated from the less-than-ideal randomizations conducted in many social experiments. We apply these tools to the data from the Perry experiment. We correct estimated treatment effects for imbalances that arose in implementing the randomization protocol and from post-randomization reassignment. We address the potential problem that arises from arbitrarily selecting “significant” hypotheses from a set of possible hypotheses using recently developed stepdown multiple-hypothesis testing procedures. The procedures we use minimize the probability of falsely rejecting any true null hypotheses.

Using these tools, this paper demonstrates the following points: (a) Statistically significant Perry treatment effects survive analyses that account for the small sample size of the study. (b) Correcting for the effect of selectively reporting statistically significant responses, there are substantial impacts of the program on males and females. Results are stronger for females at younger adult ages and for males at older adult ages. (c) Accounting for the compromised randomization of the program strengthens the evidence for important program effects compared to the evidence reported in the previous literature that neglects the imbalances created by compromised randomization. (d) Perry participants are representative of a low-ability, disadvantaged African-American population.

This paper proceeds as follows. Section 2 describes the Perry experiment. Section 3 discusses the statistical challenges confronted in analyzing the Perry experiment. Section 4 presents our methodology. Our main empirical analysis is presented in Section 5. Section 6 examines the representativeness of the Perry sample. Section 7 compares our analysis to previous analyses of Perry. Section 8 concludes. Supplementary material is placed in the Web Appendix.⁴

2. Perry: Experimental design and background

The HighScope Perry Program was conducted during the early- to mid-1960’s in the district of the Perry Elementary School, a public school in Ypsilanti, Michigan, a town near Detroit. The sample size was small: 123 children allocated over five entry cohorts. Data were collected at age 3, the entry age, and through annual surveys until age 15, with additional follow-ups conducted at ages 19, 27, and 40. Program attrition remained low through age 40, with over 91% of the original subjects interviewed. Two-thirds of the attrited were dead. The rest were missing.⁵ Numerous measures were collected on economic, criminal, and educational outcomes over this span as well as on cognition and personality. Program intensity was low compared to that in many subsequent early childhood development programs.⁶ Beginning at age 3, and lasting 2 years, treatment consisted of a 2.5-hour educational preschool on weekdays during the school year, supplemented by weekly home visits by teachers.⁷ HighScope’s innovative curriculum, developed over the course of the Perry experiment, was based on the principle of active learning, guiding students through the formation of key developmental factors using intensive child–teacher interactions (Schweinhart, Barnes, and Weikart (1993, pp. 34–36), Weikart, Bond, and McNeil (1978, pp. 5–6, 21–23)). A more complete description of the Perry programcurriculum is given inWeb Appendix A.⁸

Eligibility criteria

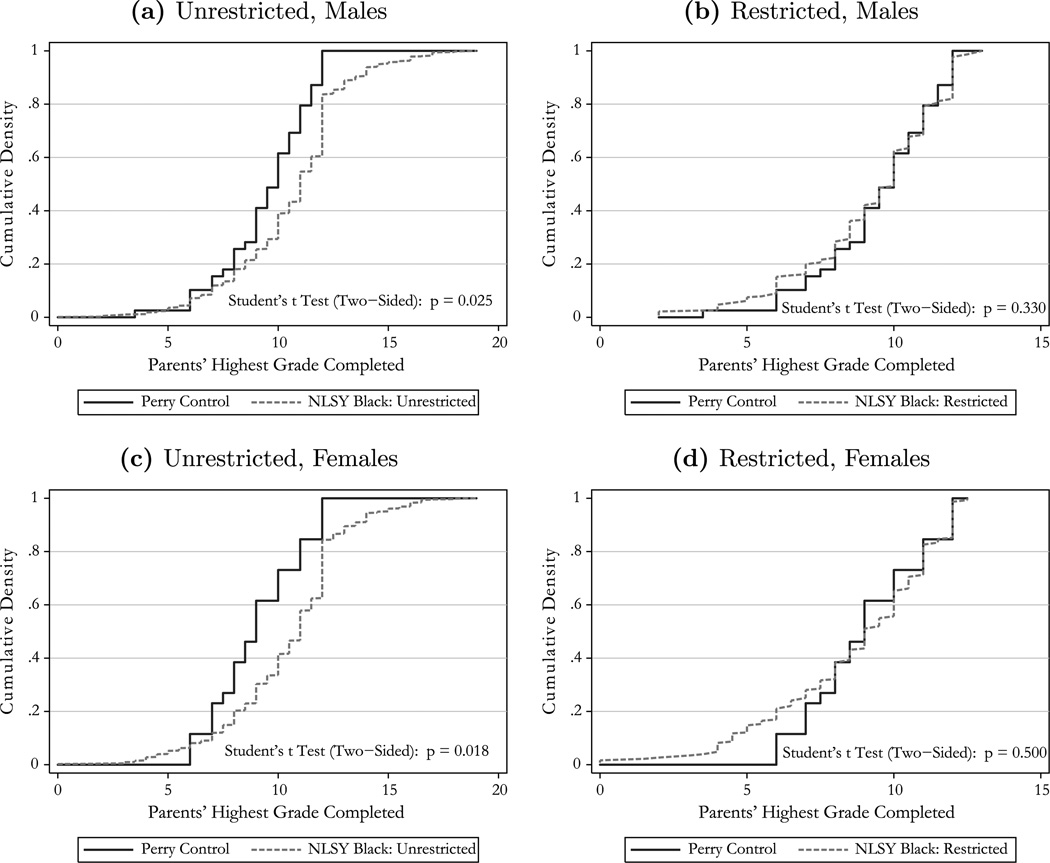
The program admitted five entry cohorts in the early 1960’s, drawn from the population surrounding the Perry Elementary School. Candidate families for the study were identified from a survey of the families of the students attending the elementary school, by neighborhood group referrals, and through door-to-door canvassing. The eligibility rules for participation were that the participants should (i) be African-American; (ii) have a low IQ (between 70 and 85) at study entry,⁹ and (iii) be disadvantaged as measured by parental employment level, parental education, and housing density (persons per room). The Perry study targeted families who were more disadvantaged than most other African-American families in the United States but were representative of a large segment of the disadvantaged African-American population. We discuss the issue of the representativeness of the program compared to the general African-American population in Section⁶.

Among children in the Perry Elementary School neighborhood, Perry study families were particularly disadvantaged. Table 1 shows that compared to other families with children in the Perry School catchment area, Perry study families were younger, had lower levels of parental education, and had fewer working mothers. Further, Perry program families had fewer educational resources, larger families, and greater participation in welfare, compared to the families with children in another neighborhood elementary school in Ypsilanti, the Erickson school, situated in a predominantly middle-class white neighborhood.

Table 1.

Comparing families of participants with other families with children in the Perry Elementary School catchment and a nearby school in Ypsilanti, Michigan.

	Perry School (Overall)a	Perry Preschoolb	Erickson Schoolc
Mother
Average Age	35	31	32
Mean Years of Education	10.1	9.2	12.4
% Working	60%	20%	15%
Mean Occupational Leveld	1.4	1.0	2.8
% Born in South	77%	80%	22%
% Educated in South	53%	48%	17%
Father
% Fathers Living in the Home	63%	48%	100%
Mean Age	40	35	35
Mean Years of Education	9.4	8.3	13.4
Mean Occupational Leveld	1.6	1.1	3.3
Family & Home
Mean SESe	11.5	4.2	16.4
Mean # of Children	3.9	4.5	3.1
Mean # of Rooms	5.9	4.8	6.9
Mean # of Others in Home	0.4	0.3	0.1
% on Welfare	30%	58%	0%
% Home Ownership	33%	5%	85%
% Car Ownership	64%	39%	98%
% Members of Libraryf	25%	10%	35%
% With Dictionary in Home	65%	24%	91%
% With Magazines in Home	51%	43%	86%
% With Major Health Problems	16%	13%	9%
% Who Had Visited a Museum	20%	2%	42%
% Who Had Visited a Zoo	49%	26%	72%
N	277	45	148

Source: Weikart, Bond, and McNeil (1978).

^aThese are data on parents who attended parent–teacher meetings at the Perry school or who were tracked down at their homes by Perry personnel (Weikart, Bond, and McNeil (1978, pp. 12–15)).

^bThe Perry Preschool subsample consists of the full sample (treatment and control) from the first two waves.

^cThe Erickson School was an “all-white school located in a middle-class residential section of the Ypsilanti public school district” (Weikart, Bond, and McNeil (1978, p.14)).

^dOccupation level: 1 = unskilled; 2 = semiskilled; 3 = skilled; 4 = professional.

^eSee the notes at the base ofFigure 3 for the definition of socioeconomic status (SES) index.

^fAny member of the family.

We do not know whether, among eligible families in the Perry catchment, those who volunteered to participate in the program were more motivated than other families and whether this greater motivation would have translated into better child outcomes. However, according to Weikart, Bond, andMcNeil (1978, p.16), “virtually all eligible children were enrolled in the project,” so this potential concern appears to be unimportant.

Randomization protocol

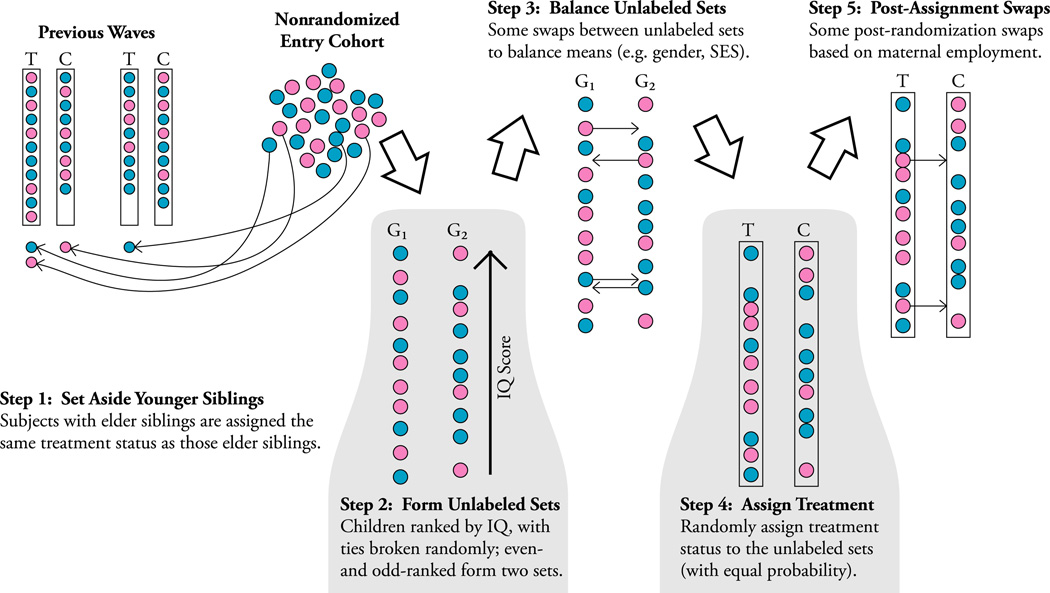
The randomization protocol used in the Perry study was complex. According to Weikart, Bond, and McNeil (1978, p.16), for each designated eligible entry cohort, children were assigned to treatment and control groups in the following way, which is graphically illustrated in Figure 1:

Figure 1.

Perry randomization protocol. This figure is a visual representation of the Perry Randomization Protocol. T and C refer to treatment and control groups respectively. Shaded circles represent males. Light circles represent females. G₁ and G₂ are unlabeled groups of participants.

Step 1. In any entering cohort, younger siblings of previously enrolled families were assigned the same treatment status as their older siblings.¹⁰

Step 2. Those remaining were ranked by their entry IQ scores.¹¹ Odd- and even-ranked subjects were assigned to two separate unlabeled groups.

Balancing on IQ produced an imbalance on family background measures. This was corrected in a second, “balancing,” stage of the protocol.

Step 3. Some individuals initially assigned to one group were swapped between the unlabeled groups to balance gender and mean socioeconomic (SES) status, “with Stanford–Binet scores held more or less constant.”

Step 4. A flip of a coin (a single toss) labeled one group as “treatment” and the other as “control.”

Step 5. Some individuals provisionally assigned to treatment, whose mothers were employed at the time of the assignment, were swapped with control individuals whose mothers were not employed. The rationale for these swaps was that it was difficult for working mothers to participate in home visits assigned to the treatment group and because of transportation difficulties.¹² A total of five children of working mothers initially assigned to treatment were reassigned to control.

Even after the swaps at stage 3 were made, preprogram measures were still somewhat imbalanced between treatment and control groups. See Figure 2 for IQ and Figure 3 for SES index.

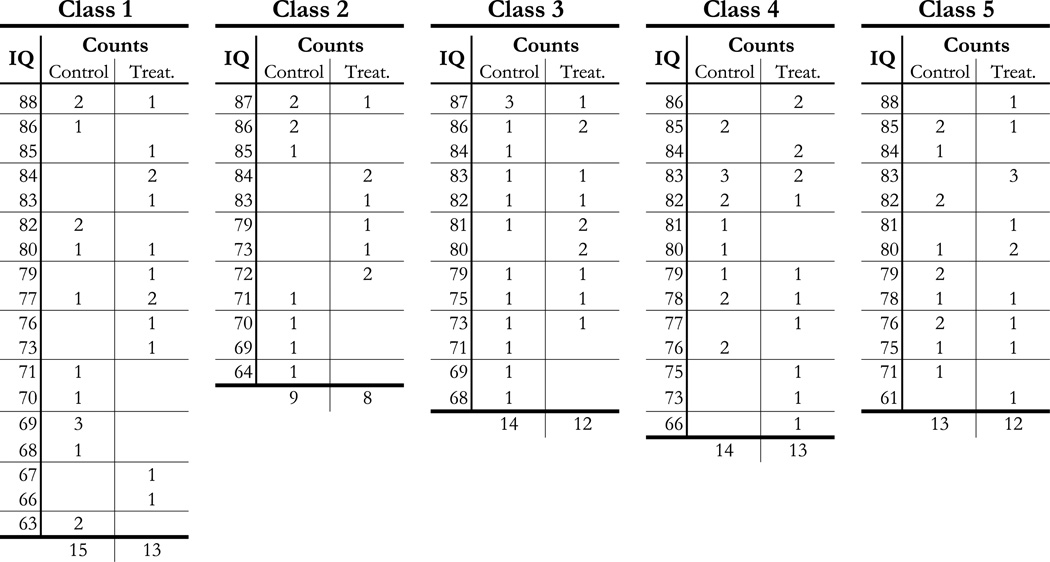
Figure 2.

IQ at entry by entry cohort and treatment status. Stanford–Binet IQ at study entry (age 3) was used to measure the baseline IQ.

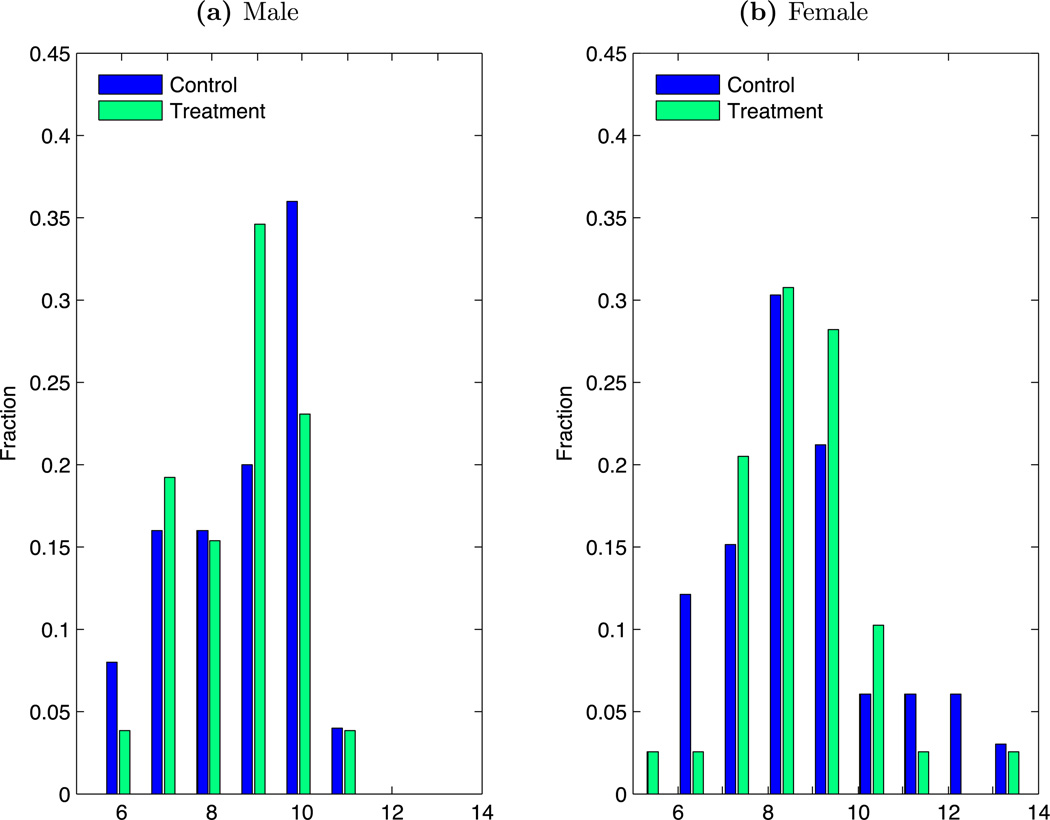
Figure 3.

SES index by gender and treatment status. The socioeconomic status (SES) index is a weighted linear combination of three variables: (a) average highest grade completed by whichever parent(s) was present, with a coefficient 0.5; (b) father’s employment status (or mother’s, if the father was absent): 3 for skilled, 2 for semiskilled, and 1 for unskilled or none, all with a coefficient 2; (c) number of rooms in the house divided by number of people living in the household, with a coefficient 2. The skill level of the parent’s job is rated by the study coordinators and is not clearly defined. An SES index of 11 or lower was the intended requirement for entry into the study (Weikart, Bond, and McNeil (1978, p.14)). This criterion was not always adhered to: out of the full sample, 7 individuals had an SES index above the cutoff (6 out of 7were in the treatment group, and 6 out of 7 were in the last two waves).

3. Statistical challenges in analyzing the Perry Program

Drawing valid inference from the Perry study requires meeting three statistical challenges: (i) small sample size, (ii) compromise in the randomization protocol, and (iii) the large number of outcomes and associated hypotheses, which creates the danger of selectively reporting “significant” estimates out of a large candidate pool of estimates, thereby biasing downward reported p-values.

Small sample size

The small sample size of the Perry study and the nonnormality of many outcome measures call into question the validity of classical tests, such as those based on the t-, F-, and χ²-statistics.¹³ Classical statistical tests rely on central limit theorems and produce inferences based on p-values that are only asymptotically valid.

A substantial literature demonstrates that classical testing procedures can be unreliable when sample sizes are small and the data are nonnormal.¹⁴ Both features characterize the Perry study. There are approximately 25 observations per gender in each treatment assignment group and the distribution of observed measures is often highly skewed.¹⁵ Our paper addresses the problem of small sample size by using permutation-based inference procedures that are valid in small samples.

The treatment assignment protocol

The randomization protocol implemented in the Perry study diverged from the original design. Treatment and control statuses were reassigned for a subset of persons after an initial random assignment. This creates two potential problems.

First, such reassignments can induce correlation between treatment assignment and baseline characteristics of participants. If the baseline measures affect outcomes, treatment assignment can become correlated with outcomes through an induced common dependence. Such a relationship between outcomes and treatment assignment violates the assumption of independence between treatment assignment and outcomes in the absence of treatment effects. Moreover, reassignment produces an imbalance in the covariates between the treated and the controlled, as documented in Figures 2 and 3. For example, the working status of the mother was one basis for reassignment to the control group. Weikart, Bond, and McNeil (1978, p.18) note that at baseline, children of working mothers had higher test scores. Not controlling for mother’s working status would bias downward estimated treatment effects for schooling and other ability-dependent outcomes. We control for imbalances by conditioning on such covariates.

Second, even if treatment assignment is statistically independent of the baseline variables, compromised randomization can still produce biased inference. A compromised randomization protocol can generate treatment assignment distributions that differ from those that would result from implementation of the intended randomization protocol. As a consequence, incorrect inference can occur if the data are analyzed under the assumption that no compromise in randomization has occurred.

More specifically, analyzing the Perry study under the assumption that a fair coin decides the treatment assignment of each participant—as if an idealized, non-compromised randomization had occurred—mischaracterizes the actual treatment assignment mechanism and hence the probability of assignment to treatment. This can produce incorrect critical values and improper control of Type-I error. Section 4.5 presents a procedure that accounts for the compromised randomization using permutation- based inference conditioned on baseline background measures.

Multiple hypotheses

There are numerous outcomes reported in the Perry experiment. One has to be careful in conducting analyses to avoid selective reporting of statistically significant outcomes, as determined by single-hypothesis tests, without correcting for the effects of such preliminary screening on actual p-values. This practice is sometimes termed “cherry picking.”

Multiple-hypothesis testing procedures avoid bias in inference arising from selectively reporting statistically significant results by adjusting inference to take into account the overall set of outcomes from which the “significant” results are drawn.

The traditional approach to testing based on overall F-statistics involves testing the null hypothesis that any element of a block of hypotheses is rejected. We test that hypothesis as part of a general stepdown procedure, which also tests which hypotheses within the block of hypotheses are rejected.

Simple calculations suggest that concerns about the overall statistical significance of treatment effects for the Perry study may have been overstated. Table 2 summarizes the inference for 715 Perry study outcomes by reporting the percentage of hypotheses rejected at various significance levels.¹⁶ If outcomes were statistically independent and there was no experimental treatment effect, we would expect only 1% of the hypotheses to be rejected at the 1% level, but instead 7% are rejected overall (3% for males and 7% for females). At the 5% significance level, we obtain a 23% overall rejection rate (13% for males and 22% for females). Far more than 10% of the hypotheses are statistically significant when the 10% level is used. These results suggest that treatment effects are present for each gender and for the full sample.

Table 2.

Percentage of test statistics exceeding various significance levels.^a

	All Data	Male Subsample	Female Subsample
Percentage of p-values smaller than 1%	7%	3%	7%
Percentage of p-values smaller than 5%	23%	13%	22%
Percentage of p-values smaller than 10%	34%	21%	31%

^aBased on 715 outcomes in the Perry study. (See Schweinhart, Montie, Xiang, Barnett, Belfield, and Nores (2005) for a description of the data.) 269 outcomes are from the period before the age-19 interview; 269 are from the age-19 interview; 95 are outcomes from the age-27 interview; 55 are outcomes from the age-40 interview.

However, the assumption of independence among the outcomes used to make these calculations is quite strong. In our analysis, we use modern methods for testing multiple hypotheses that account for possible dependencies among outcomes. We use a stepdown multiple-hypothesis testing procedure that controls for the family-wise error rate—the probability of rejecting at least one true null hypothesis among a set of hypotheses we seek to test jointly. This procedure is discussed below in Section 4.6.

4. Methods

This section presents a framework for inference that addresses the problems raised in Section 3, namely, small samples, compromised randomization, and cherry picking. We first establish notation, discuss the benefits of a valid randomization, and consider the consequences of compromised randomization. We then introduce a general framework for representing randomized experiments. Using this framework, we develop a statistical framework for characterizing the conditions under which permutation-based inference produces valid small-sample inference when there is corruption of the intended randomization protocol. Finally, we discuss the multiple-hypothesis testing procedure used in this paper.

4.1 Randomized experiments

The standard model of program evaluation describes the observed outcome for participant i, Y_i, by Y_i = D_iY_i,1 + (1 − D_i)Y_i,0, where (Y_i,0, Y_i,1) are potential outcomes corresponding to control and treatment status for participant i, respectively, and D_i is the assignment indicator: D_i = 1 if treatment occurs, D_i = 0 otherwise.

An evaluation problem arises because either Y_i,0 or Y_i,1 is observed, but not both. Selection bias can arise from participant self-selection into treatment and control groups so that sampled distributions of Y_i,0 and Y_i,1 are biased estimators of the population distributions. Properly implemented randomized experiments eliminate selection bias because they produce independence between (Y_i,0 Y_i,1) and D_i.¹⁷ Notationally, (Y₀, Y₁) ⫫ D, where Y₀, Y₁, and D are vectors of variables across participants, and ⫫ denotes independence.

Selection bias can arise when experimenters fail to generate treatment groups that are comparable on unobserved background variables that affect outcomes. A properly conducted randomization avoids the problem of selection bias by inducing independence between unobserved variables and treatment assignments.

Compromised randomization can invalidate the assumption that (Y₀, Y₁) ⫫ D. The treatments and controls can have imbalanced covariate distributions.¹⁸ The following notational framework helps to clarify the basis for inference under compromised randomization that characterizes the Perry study.

4.2 Setup and notation

Denote the set of participants by ℐ = {1,…, I}, where I = 123 is the total number of Perry study participants. We denote the random vector representing treatment assignments by D = (D_i; i ∈ ℐ). The set 𝒟 is the support of the vector of random assignments, namely 𝒟 = [0, 1] × ⋯ × [0, 1], 123 times, so 𝒟 = [0, 1]¹²³. Define the preprogram variables used in the randomization protocol by X = (X_i;i ∈ ℐ). For the Perry study, baseline variables X consist of data on the following measures: IQ, enrollment cohort, socioeconomic status (SES) index, family structure, gender, and maternal employment status, all measured at study entry.

Assignment to treatment is characterized by a function M. The arguments of M are variables that affect treatment assignment. Define R as a random vector that describes the outcome of a randomization device (e.g., a flip of a coin to assign treatment status). Prior to determining the realization of R, two groups are formed on the basis of preprogram variables X. Then R is realized and its value is used to assign treatment status. R does not depend on the composition of the two groups. After the initial treatment assignment, individuals are swapped across assigned treatment groups based on some observed background characteristics X (e.g., mother’s working status). M captures all three aspects of the treatment assignment mechanism. The following assumptions formalize the treatment assignment protocol:

Assumption A-1. D ~ M(R, X) :supp(R) × supp(X)→𝒟 R ⫫ X, where supp(D) = 𝒟, and supp denotes support

Let V_i represent the unobserved variables that affect outcomes for participant i. The vector of unobserved variables is V = (V_i;i ∈ ℐ). The assumption that unobserved variables are independent of the randomization device R is critical for guaranteeing that randomization produces independence between unobserved variables and treatment assignments, and can be stated as follows:

Assumption A-2. R ⫫ V.

Remark 4.1. The random variables R used to generate the randomization and the unobserved variables V are assumed to be independent. However, if initial randomization is compromised by reassignment based on X, the assignment mechanism depends on X. Thus, substantial correlation between final treatment assignments D and unobserved variables V can exist through the common dependence between X and V.

As noted in Section 2, some participants whose mothers were employed had their initial treatment status reassigned in an effort to lower program costs. One way to interpret the protocol as implemented is that the selection of reassigned participants occurred at random given working status. In this case, the assignment mechanism is based on observed variables and can be represented by M as defined in Assumption A-1. In particular, conditioning on maternal working status (and other variables used to assign persons to treatment) provides a valid representation of the treatment assignment mechanism and avoids selection bias. This is the working hypothesis of our paper.

Given that many of the outcomes we study are measured some 30 years after random assignment, and a variety of post-randomization period shocks generate these outcomes, the correlation between V and the outcomes may be weak. For example, there is evidence that earnings are generated in part by a random walk with drift (see, e.g., Meghir and Pistaferri (2004)). If this is so, the correlation between the errors in the earnings equation and the errors in the assignment to treatment equation may be weak. By the proximity theorem (Fisher (1966)), the bias arising from V correlated with outcomes may be negligible.¹⁹

Each element i in the outcome vector Y takes value Y_i,0 or Y_i,1. The vectors of counterfactual outcomes are defined by Y_d = (Y_i,d; i ∈ ℐ); d ∈ {0, 1}, i ∈ ℐ. Without loss of generality, Assumption A-3 postulates that outcomes Y_i,d, where d ∈ {0, 1}, i ∈ ℐ, are generated by a function f:

Assumption A-3. Y_i,d ≡ f(d, X_i, V_i); d ∈ {0, 1}, ∀i ∈ ℐ.²⁰

Assumptions A-1, A-2, and A-3 formally characterize the Perry randomization protocol.

The benefits of randomization

The major benefit of randomization comes from avoiding the problem of selection bias. This benefit is a direct consequence of Assumptions A-1, A-2, and A-3, and can be stated as a lemma:

Lemma L-1. Under Assumptions A-1, A-2, and A-3, (Y₁,Y₀) ⫫ D|X.

Proof. Conditional on X, the argument that determines Y_i,d for d ∈ {0, 1} is V, which is independent of R by Assumption A-2. Thus, R is independent of (Y₀, Y₁). Therefore, any function of R and X is also independent of (Y₀, Y₁) conditional on X. In particular, Assumption A-1 states that conditional on X, treatment assignments depend only on R, so (Y₀, Y₁) ⫫ D|X.

Remark 4.2. Regardless of the particular type of compromise to the initial randomization protocol, Lemma L-1 is valid whenever the randomization protocol is based on observed variables X, but not on V. Assumption A-2 is a consequence of randomization. Under it, randomization provides a solution to the problem of biased selection.²¹

Remark 4.3. Lemma L-1 justifies matching as a method to correct for irregularities in the randomization protocol.

The method of matching is often criticized because the appropriate conditioning set that guarantees conditional independence is generally not known, and there is no algorithm for choosing the conditioning variables without invoking additional assumptions (e.g., exogeneity).²² For the Perry experiment, the conditioning variables X that determine the assignment to treatment are documented, even though the exact treatment assignment rule is unknown (see Weikart, Bond, andMcNeil (1978)).

When samples are small and the dimensionality of covariates is large, it becomes impractical to match on all covariates. This is the “curse of dimensionality” in matching (Westat (1981)). To overcome this problem, Rosenbaum and Rubin (1983) propose propensity score matching, in which matches are made based on a propensity score, that is, the probability of being treated conditional on observed covariates. This is a one-dimensional object that reduces the dimensionality of the matching problem at the cost of having to estimate the propensity score, which creates problems of its own.²³ Zhao (2004) shows that when sample sizes are small, as they are in the Perry data, propensity score matching performs poorly when compared with other matching estimators. Instead of matching on the propensity score, we directly condition on the matching variables using a partially linear model. A fully nonparametric approach to modeling the conditioning set is impractical in the Perry sample.

4.3 Testing the null hypothesis of no treatment effect

Our aim is to test the null hypothesis of no treatment effect. This hypothesis is equivalent to the statement that the control and treated outcome vectors share the same distribution:

Hypothesis H-1. $Y_1\stackrel{d}{=}{Y}_0|X,\text{where}\stackrel{d}{=}$ denotes equality in distribution

The hypothesis of no treatment effect can be restated in an equivalent form. Under Lemma L-1, Hypothesis H-1 is equivalent to the following statement:

Hypothesis H-1′. Y ⫫ D|X.

The equivalence is demonstrated by the following argument. Let A_J denote a set in the support of a random variable J. Then

• Pr((D,Y) ∈ (A_D, A_Y )|X)

  • = E(1[D ∈ A_D] ⊙ 1[Y ∈ A_Y ]|X)

  • (where ⊙ denotes a Hadamard product²⁴)

  • = E(1[Y ∈A_Y ]|D ∈A_D, X) Pr(D ∈A_D|X)

  • = E(1[(Y₁ ⊙D + Y₀ ⊙(1 − D)) ∈ A_Y]|D ∈ A_D, X) Pr(D ∈ A_D|X)

  • = E(1[Y₀ ∈A_Y]|D ∈A_D, X) Pr(D ∈ A_D|X) by Hypothesis H-1

  • = E(1[Y₀ ∈ A_Y]|X) Pr(D ∈ A_D|X) by Lemma L-1

  • = Pr(Y ∈ A_Y|X)Pr(D ∈ A_D|X).

We refer to Hypotheses H-1 and H-1′ interchangeably throughout this paper. If the randomization protocol is fully known, then the randomization method implies a known distribution for the treatment assignments. In this case, we can proceed in the following manner:

Step 1. From knowledge of the treatment assignment rules, one can generate the distribution of D|X.

Step 2. Select a statistic T(Y, D,X) with the property that larger values of the statistic provide evidence against the null hypothesis, Hypothesis H-1 (e.g., t-statistics, χ², etc.).

Step 3. Create confidence intervals for the random variable T(Y, D, X)|X at significance level α based on the known distribution of D|X.

Step 4. Reject the null hypothesis if the value of T(Y, D,X) calculated from the data does not belong to the confidence interval.

Implementing these procedures requires solving certain problems. To produce the distribution of D|X requires precise knowledge of the ingredients of the assignment rules, which are only partially known. Alternatively, the analyst could use the asymptotic distribution of the chosen test statistic. However, given the size of the Perry sample, it seems unlikely that the distribution of T(Y, D,X) is accurately characterized by large-sample distribution theory. We address these problems by using permutation-based inference that addresses the problem of small sample size in a way that allows us to simultaneously account for compromised randomization when Assumptions A-1–A-3 and Hypothesis H-1 are valid. Our inference is based on an exchangeability property that remains valid under compromised randomization.

4.4 Exchangeability and the permutation-based tests

The main result of this subsection is that, under the null hypothesis, the joint distribution of outcome and treatment assignments is invariant for certain classes of permutations. We rely on this property to construct a permutation test that remains valid under compromised randomization. Permutation-based inference is often termed data-dependent because the computed p-values are conditional on the observed data. These tests are also distribution-free because they do not rely on assumptions about the parametric distribution from which the data are sampled. Because permutation tests give accurate p-values even when the sampling distribution is skewed, they are often used when sample sizes are small and sample statistics are unlikely to be normal. Hayes (1996) shows the advantage of permutation tests over the classical approaches for the analysis of small samples and nonnormal data.

Permutation-based tests make inferences about Hypothesis H-1 by exploring the invariance of the joint distribution of (Y, D) under permutations that swap the elements of the vector of treatment indicators D. We use g to index a permutation function π, where the permutation of elements of D according to π_g is represented by gD. Notationally, gD is defined as

$$gD=({\tilde{D}}_i;i\in ℐ|{\tilde{D}}_i=D_{{\pi }_g(i)}),$$

where π_g is a permutation function (i.e., π_g : ℐ → ℐ is a bijection).

Lemma L-2. Let the permutation function π_g : ℐ → ℐ within each stratum of X, such that X_i = X_πg(i) ∀i ∈ ℐ. Then, under Assumption A-1, $gD\stackrel{d}{=}D$.

Proof. gD ~ M(R, gX) by construction, but gX = X by definition, so gD ~ M(R, X).

Remark 4.4. An important feature of the exchangeability property used in Lemma L-2 is that it relies on limited information on the randomization protocol. It is valid under compromised randomization and there is no need for a full specification of the distribution D or the assignment mechanism M.

Let 𝒢_X be the set of all permutations that permute elements only within each stratum of X.²⁵ Formally,

$${𝒢}_X=\left\{g;{\pi }_g:ℐ\to ℐ\text{ is a bijection and }{X}_i=X_{{\pi }_g(i)},\forall i\in ℐ\right\}.$$

A corollary of Lemma L-2 is

$$\begin{array}{cc}D\stackrel{d}{=}gD& \forall g\in {𝒢}_X\end{array}.$$ (1)

We now state and prove the following theorem.

Theorem 4.1. Let treatment assignment be characterized by Assumptions A-1–A-3. Under Hypothesis H-1, the joint distribution of outcomes Y and treatment assignments D is invariant under permutations g ∈ 𝒢_X of treatment assignments within strata formed by values of covariates X, that is $(Y,D)\stackrel{d}{=}(Y,gD){\forall }_g\in {𝒢}_X$.

Proof. By Lemma L-2, $D\stackrel{d}{=}gD{\forall }_g\in {𝒢}_X$. But Y ⫫ D|X by Hypothesis H-1. Thus $(Y,D)\stackrel{d}{=}(Y,gD)\forall g\in 𝒢X$.

Theorem 4.1 is called the Randomization Hypothesis.²⁶ We use it to test whether Y ⫫ D|X. Intuitively, Theorem 4.1 states that if the randomization protocol is such that (Y, D) is invariant over the strata of X, then the absence of a treatment effect implies that the joint distribution of (Y, D) is invariant with respect to permutations of D that are restricted within strata of X.²⁷ Theorem 4.1 is a useful tool for inference about treatment effects. For example, suppose that, conditional on X (which we keep implicit), we have a test statistic T(Y, D) with the property that larger values of the statistic provide evidence against Hypothesis H-1 and an associated critical value c, such that whenever T(Y, D) >c, we reject the null hypothesis. The goal of our test is to control for a Type-I error at significance level α, that is,

• Pr(reject Hypothesis H-1|Hypothesis H-1 is true)

  • = Pr(T(Y, D) > c|Hypothesis H-1 is true) ≤ α.

A critical value can be computed by using the fact that as g varies in 𝒢_X under the null hypothesis of no treatment effect, conditional on the sample, T(Y, gD) is uniformly distributed.²⁸ Thus, under the null, a critical value can be computed by taking the α quantile of the set {T(Y, gD) : g ∈ 𝒢_X}. In practice, permutation tests compare a test statistic computed on the original (unpermuted) data with a distribution of test statistics computed on resamplings of that data. The measure of evidence against the randomization hypothesis, the p-value, is computed as the fraction of resampled data which yields a test statistic greater than that yielded by the original data. In the case of the Perry study, these resampled data sets consist of the original data with treatment and control labels permuted across observations. As discussed below in Section 4.5, we use permutations that account for the compromised randomization, and our test statistic is the coefficient on treatment status estimated using a regression procedure due to Freedman and Lane (1983), which controls for covariate imbalances and is designed for application to permutation inference.

We use this procedure and report one-sided mid-p-values, which are averages between the one-sided p-values defined using strict and nonstrict inequalities. As a concrete example of this procedure, suppose that we use a permutation test with J + 1 permutations g_j, where the first J are drawn at random from the permutation group 𝒢_X and g_J+1 is the identity permutation (corresponding to using the original sample).

Our source statistic Δ is a function of an outcome Y and permuted treatment labels _gjD. For each permutation, we compute a set of source statistics Δ^j = Δ(Y, _gjD). From these, we compute the rank statistic T^j associated with each source statistic Δ^j:²⁹

$$T^i\equiv \frac{1}{j+1}{\displaystyle \sum _{l=1}^{J+1}\mathbf{1}[{\Delta }^j\ge {\Delta }^l].}$$ (2)

.

Without loss of generality, we assume that higher values of the source statistics are evidence against the null hypothesis. Working with ranks of the source statistic effectively standarizes the scale of the statistic and is an alternative to studentization (i.e., standardizing by the standard error). This procedure is called prepivoting in the literature.³⁰ The mid-p-value is computed as the average of the fraction of permutation test statistics strictly greater than the unpermuted test statistic and the fraction greater than or equal to the unpermuted test statistic:

$$p\equiv \frac{1}{2(J+1)}\left({\displaystyle \sum _{j=1}^{J+1}\mathbf{1}[T^j\ge T^{j+1}]+}{\displaystyle \sum _{j=1}^{J+1}\mathbf{1}[T^j>T^{J+1}]}\right){.}^{31}$$ (3)

Web Appendix C.5. shows how to use mid-p-values to control for Type-I error.

4.5 Accounting for compromised randomization

This paper solves the problem of compromised randomization under the assumption of conditional exchangeability of assignments given X. A by-product of this approach is that we correct for imbalance in covariates between treatments and controls.

Conditional inference is implemented using a permutation-based test that relies on restricted classes of permutations, denoted by 𝒢_X. We partition the sample into subsets, where each subset consists of participants with common background measures. Such subsets are termed orbits or blocks. Under the null hypothesis of no treatment effect, treatment and control outcomes have the same distributions within an orbit.³² Equivalently, treatment assignments D are exchangeable (therefore permutable) with respect to the outcome Y for participants who share common preprogram values X. Thus, the valid permutations g ∈ 𝒢_X swap labels within conditioning orbits.

We modify standard permutation methods to account for the explicit Perry randomization protocol. Features of the randomization protocol, such as identical treatment assignments for siblings, generate a distribution of treatment assignments that cannot be described (or replicated) by simple random assignment.³³

Conditional inference in small samples

Invoking conditional exchangeability decreases the number of valid permutations within X strata. The small Perry sample size prohibits very fine partitions of the available conditioning variables. In general, nonparametric conditioning in small samples introduces the serious practical problem of small or even empty permutation orbits. To circumvent this problem and obtain restricted permutation orbits of reasonable size, we assume a linear relationship between some of the baseline measures in X and the outcomes Y. We partition the data into orbits on the basis of variables that are not assumed to have a linear relationship with outcome measures. Removing the effects of some conditioning variables, we are left with larger subsets within which permutation-based inference is feasible.

More precisely, we divide the vector X into two parts: those variables X^[L], which are assumed to have a linear relationship with Y, and variables X^[N], whose relationship with Y is allowed to be nonparametric, X = [X^[L],X^[N]].³⁴ Linearity enters into our framework by replacing Assumption A-3 with the following assumption:

Assumption A-4.$Y_{i,d}\equiv {\delta }_d{X}_i^{[L]}+f(d,X_i^{[N]},V_i);d\in \{0,1\},i\in ℐ$.

Under Hypothesis H-1, δ₁ = δ₀ = δ and Ỹ ≡ Y − δX^[L] = f(X^[N], V). Using Assumption A-4, we can rework the arguments of Section 4.4 to prove that, under the null, Ỹ ⫫ D|X^[N]. Under Hypothesis A-4 and the knowledge of δ, our randomization hypothesis becomes $(\tilde{Y},D)\stackrel{d}{=}(\tilde{Y},gD)$ such that g ∈ 𝒢_X[N], where 𝒢_X[N] is the set of permutations that swap the participants who share the same values of covariates X^[N]. We purge the influence of X^[L] on Y by subtracting δX^[L] and can construct valid permutation tests of the null hypothesis of no treatment effect by conditioning on X^[N]. Conditioning nonparametrically on X^[N], a smaller set of variables than X, we are able to create restricted permutation orbits that contain substantially larger numbers of observations than when we condition more finely on all of the X. In an extreme case, one could assume that all conditioning variables enter linearly, eliminate their effect on the outcome, and conduct permutations using the resulting residuals without any need to form orbits based on X.

If δ were known, we could control for the effect of X^[L] by permuting Ỹ = Y − δX^[L] within the groups of participants that share the same preprogram variables X^[N]. However, δ is rarely known. We address this problem by using a regression procedure due to Freedman and Lane (1983). Under the null hypothesis, D is not an argument in the function determining Y. Our permutation approach addresses the problem raised by estimating δ by permuting the residuals from a regression of Y on X^[L] in orbits that share the same values of X^[N], leaving D fixed. The method regresses Y on X^[L], then permutes the residuals from this regression according to 𝒢_X[N]. D is adjusted to remove the influence of X^[L]. The method then regresses the permuted residuals on adjusted D.

More precisely, define B_g as a permutation matrix associated with the permutation g ∈ 𝒢_X[N].³⁵ The Freedman and Lane regression coefficient for permutation g is

$${\Delta }_k^g\equiv {\left(D\prime Q_{X}D\right)}^{-1}D\prime Q_{X}B{\prime }_g{Q}_X{Y}^k,g\in {𝒢}_{X^{[N]}},$$ (4)

where k is the outcome index, the matrix Q_X is defined as Q_X ≡ (I−P_X), I is the identity matrix, and

$$P_X\equiv X^{[L]}{({(X^{[L]})}^{\prime }{X}^{[L]})}^{-1}{\left(X^{[L]}\right)}^{\prime }.$$

P_X is a linear projection in the space generated by the columns of X^[L], and Q_X is the projection into the orthogonal space generated by X^[L]. We use this regression coefficient as the input source statistic (Δ^j) to form the rank statistic (2) and to compute p-values via (3).

Expression (4) corrects for the effect of X^[L] on both D and Y. (For notational simplicity, we henceforth suppress the k superscript.) The term Q_XY estimates Ỹ. If δ were known, Ỹ could be computed exactly. The term D′Q_X corrects for the imbalance of X^[L] across treatment and control groups. Without loss of generality, we can arrange the rows of (Y, D,X) so that participants that share the same values of covariates X^[N] are adjacent. Writing the data in this fashion, B_g is a block-diagonal matrix, whose elements are themselves permutation matrices that swap elements within each stratum defined by values of X^[N]. For notational clarity, suppose that there are S of these strata indexed by s ∈ S ≡ {1, …, S}. Let the participant index set ℐ be partitioned according to these strata into S disjoint set {ℐ^s; s ∈ S} so that each participant in ℐ^s has the same value of pre-program variables X^[N]. Permutations are applied within each stratum s associated with a value of X^[N]. The permutations within each stratum are conducted independently of the permutations for other strata. All within-strata permutations are generated by B_g to form equation (4). That equation aggregates data across the strata to form ${\Delta }_k^g$. The same permutation structure is applied to all outcomes k in order to construct valid joint tests of multiple hypotheses. ${\Delta }_k^g$ plays the role of Δ^j in (2) to create our test statistic.

In a series of Monte Carlo studies, Anderson and Legendre (1999) show that the Freedman–Lane procedure generally gives the best results in terms of Type-I error and power among a number of similar permutation-based approximation methods. In another paper, Anderson and Robinson (2001) compare an exact permutation method (where δ is known) with a variety of permutation-based methods. They find that in samples of the size of Perry, the Freedman–Lane procedure generates test statistics that are distributed most like those generated by the exact method, and are in close agreement with the p-values from the true distribution when regression coefficients are known. Thus, for the Freedman–Lane approach, estimation error appears to create negligible problems for inference.

Interpreting our test statistic

To recapitulate, permutations are conducted within each stratum defined by X^[N] for the S strata indexed by s ∈ S ≡ {1, …, S}. Let D(s) be the treatment assignment vector for the subset ℐ^s defined by D(s) ≡ (D_i;i ∈ ℐ^s). Let Ỹ (s) ≡ (Ỹ_i;i ∈ ℐ^s) be the adjusted outcome vector for the subset ℐ^s. Finally, let ${𝒢}_{X^{[N]}}^S$ be the collection of all permutations that act on the |ℐ^s| elements of the set ℐ^s of stratum s.

Note that one consequence of the conditional exchangeability property $(\tilde{Y},D)\stackrel{d}{=}(\tilde{Y},gD)$ for g ∈ 𝒢_X[N] is that the distribution of a statistic within each stratum, T(s) : (supp(Ỹ (s)) × supp(D(s)))→ℝ, is the same under permutations g ∈ ${𝒢}_{X^{[N]}}^S$ of the treatment assignment D(s). Formally, within each stratum s ∈ S,

$$\begin{array}{cc}T\left(\tilde{Y}(s),D(s)\right)\stackrel{d}{=}T\left(\tilde{Y}(s),gD(s)\right)& \forall g\in {𝒢}_{X^{[N]}.}^S\end{array}$$ (5)

The distribution of any statistic T(s) = T(Ỹ (s), D(s)) (conditional on the sample) is uniform across all the values T^g(s) = T(Ỹ (s), gD(s)), where g varies in ${𝒢}_{X^{[N]}}^S$.³⁶

The Freedman–Lane statistic aggregates tests across the strata. To understand how it does this, consider an approach that combines the independent statistics across strata to form an aggregate statistic,

$$T={\displaystyle \sum _{s=1}^{S}T(s)w(s),}$$ (6)

where the weight w(s) could be, for example, (1/σ(s)) where σ(s) is the standard error of T(s). Tests of the null hypothesis could be based on T.

To relate this statistic to the one based on equation (4), consider the special case where there are no X^[L] variables besides the constant term so there is no need to estimate δ. Define D_i(s) as the value of D for person i in stratum s, i = 1,…, |ℐ^s|. Likewise, Ỹ_i(s) is the value of Ỹ for person i in stratum s. Define

$$T(s)=\frac{{\displaystyle \sum _{i\in {ℐ}^s}{\tilde{Y}}_i(s)D_i(s)}}{{\displaystyle \sum _{i\in {ℐ}^s}{D}_i(s)}}-\frac{{\displaystyle \sum _{i\in {ℐ}^s}{\tilde{Y}}_i(s)(1-D_i(s))}}{{\displaystyle \sum _{i\in {ℐ}^s}(1-D_i(s))}}.$$

We can define corresponding statistics for the permuted data.

In this special case where, in addition, the variance of Ỹ (s) is the same within each stratum (σ(s) = σ) and w(s) = |ℐ^s|/σ|ℐ| (i.e., w(s) is the proportion of sample observations in stratum s), test statistic (6) generates the same inference as the Freedman–Lane regression coefficient (4) used as the source statistic for our testing procedure.

In the more general case analyzed in this paper, the Freedman–Lane procedure (4) adjusts the Y and D to remove the influence of X^[L]. Test statistic (6) would be invalid, even if we use Ỹ instead of Y because it does not control for the effect of X^[L] on D.³⁷ The Freedman–Lane procedure adjusts for the effect of theX^[L], which may differ across strata.³⁸

4.6 Multiple-hypothesis testing: The stepdown algorithm

Thus far, we have considered testing a single null hypothesis. Yet there are more than 715 outcomes measured in the Perry data. We now consider the null hypothesis of no treatment effect for a set of K outcomes jointly. The complement of the joint null hypothesis is the hypothesis that there exists at least one hypothesis out of K that we reject.

Formally, let P be the distribution of the observed data, (Y, D)|X ~ P. We test the |𝒦| set of single null hypotheses indexed by 𝒦 = {1, …, K} and defined by the rule

$$P\in {𝒫}_k\iff Y^k⫫D|X.$$

The hypothesis we test is defined as follows:

Hypothesis H-2. H_𝒦 : P ∈ ∩_k∈𝒦 𝒫_k

The alternative hypothesis is the complement of Hypothesis H-2. Let the unknown subset of true null hypotheses be denoted by 𝒦_P ⊂ 𝒦, such that k ∈ 𝒦_P ⇔ P ∈ 𝒫_k. Likewise we define H_𝒦P :P ∈ ∩_k∈𝒦P 1D4AB;_k. Our goal is to test the family of null Hypotheses H-2 in a way that controls the family-wise error rate (FWER) at level α. FWER is the probability of rejecting any true null hypothesis contained in H_𝒦P out of the set of hypotheses H_𝒦. FWER at level α is

$$\mathrm{Pr}(\text{reject}{H}_k:k\in {𝒦}_P|H_{{𝒦}_P}\text{ is true })\le \alpha .$$ (7)

A multiple-hypothesis testing method is said to have strong control for FWER when equation (7) holds for any configuration of the set of true null hypotheses 𝒦_P.

To generate inference using evidence from the Perry study in a robust and defensible way, we use a stepdown algorithm for multiple-hypothesis testing. The procedure begins with the null hypothesis associated with the most statistically significant statistic and then “steps down” to the null hypotheses associated with less significant statistics. The validity of this procedure follows from the analysis of Romano and Wolf (2005), who provide general results on the use of stepdown multiple-hypothesis testing procedures.

The stepdown algorithm

Stepdown begins by considering a set of 𝒦 null hypotheses, where 𝒦 ≡ {1, …, K}. Each hypothesis postulates no treatment effect of a specific outcome, that is, H_k : Y^k ⫫ D|X; k ∈ 𝒦. The set 𝒦 of null hypotheses is associated with a block of outcomes. We adopt the mid-p-value p_k as the test statistic associated with each hypothesis H_k. Smaller values of the test statistic provide evidence against each null hypothesis. The first step of the stepdown procedure is a joint test of all null hypotheses in 𝒦. To this end, the method uses the maximum of the set of statistics associated with hypotheses H_k, k ∈ 𝒦.

The next step of the stepdown procedure compares the computed test statistic with the α-quantile of its distribution and determines whether the joint hypothesis is rejected or not. If we fail to reject the joint null hypothesis, then the algorithm stops. If we reject the null hypothesis, then we iterate and consider the joint null hypothesis that excludes the most individually statistically significant outcome—the one that is most likely to contribute to rejection of the joint null. The method steps down and is applied to a set of K−1 null hypotheses that excludes the set of hypotheses previously rejected. In each successive step, the most individually significant hypothesis —the one most likely to contribute to the significance of the joint null hypothesis— is dropped from the joint null hypothesis, and the joint test is performed on the reduced set of hypotheses. The process iterates until only one hypothesis remains.³⁹

Summarizing, we first construct single-hypothesis p-values for each outcome in each block. We then jointly test the null hypothesis of no treatment effect for all K outcomes. After testing for this joint hypothesis, a stepdown algorithm is performed for a smaller set of K − 1 hypotheses, which excludes the most significant hypothesis among the K outcomes. The process continues for K steps. The stepdown method provides K adjusted p-values that correct each single-hypothesis p-value for the effect of multiple-hypothesis testing.

Benefits of the stepdown procedure

Similar to traditional multiple-hypothesis testing procedures, such as the Bonferroni or Holm procedures (see, e.g., Lehmann and Romano (2005), for a discussion of these procedures), the stepdown algorithm of Romano and Wolf (2005) exhibits strong FWER control, in contrast with the classical tests like the F or χ².⁴⁰ The procedure generates as many p-values as there are hypotheses. Thus it provides a way to determine which hypotheses are rejected. In contrast with traditional multiple-hypothesis testing procedures, the stepdown procedure is less conservative. The gain in power comes from accounting for statistical dependencies among the test statistics associated with each individual hypothesis. Lehmann and Romano (2005) and Romano and Wolf (2005) discuss the stepdown procedure in depth. Web Appendix D summarizes the literature on multiple hypothesis testing and provides a detailed description of the stepdown procedure.

4.7 The selection of the set of joint hypotheses

There is some arbitrariness in defining the blocks of hypotheses that are jointly tested in a multiple-hypothesis testing procedure. The Perry study collects information on a variety of diverse outcomes. Associated with each outcome is a single null hypothesis. A potential weakness of the multiple-hypothesis testing approach is that certain blocks of outcomes may lack interpretability. For example, one could test all hypotheses in the Perry program in a single block.⁴¹ However, it is not clear if the hypothesis “did the experiment affect any outcome, no matter how minor” is interesting. To avoid arbitrariness in selecting blocks of hypotheses, we group hypotheses into economically and substantively meaningful categories by age of participants. Income by age, education by age, health by age, test scores by age, and behavioral indices by age are treated as separate blocks. Each block is of independent interest and would be selected by economists on a priori grounds, drawing on information from previous studies on the aspect of participant behavior represented by that block. We test outcomes by age and detect pronounced life cycle effects by gender.⁴²

5. Empirical results

We now apply our machinery to analyze the Perry data. We find large gender differences in treatment effects for different outcomes at different ages (Heckman (2005), Schweinhart et al. (2005)). We find statistically significant treatment effects for both males and females on many outcomes. These effects persist after controlling for compromised randomization and multiple-hypothesis testing.

Tables 3–6 summarize the estimated effects of the Perry program on outcomes grouped by type and age of measurement.⁴³ Tables 3 and 4 report results for females, while Tables 5 and 6 are for males. The third column of each table shows the control group means for the indicated outcomes. The next three columns are the treatment effect sizes. The unconditional effect (“uncond.”) is the difference in means between the treatment group and the control group. The conditional (full) effect is the coefficient on the treatment assignment variable in linear regressions. Specifically, we regress outcomes on a treatment assignment indicator and four other covariates: maternal employment, paternal presence, socioeconomic status (SES) index, and Stanford–Binet IQ, all measured at the age of study entry. The conditional (partial) effect is the estimated treatment effect from a procedure using nonparametric conditioning on a variable indicating whether SES is above or below the sample median and linear conditioning for the other three covariates. This specification is used to generate the stepdown p-values reported in this paper. The next four columns are p-values, based on different procedures explained below, for testing the null hypothesis of no treatment effect for the indicated outcome. The second-to-last column, “Gender Difference-in-Difference,” tests the null hypothesis of no difference in mean treatment effects between males and females. The final column gives the available observations for the indicated outcome. Small p-values associated with rejections of the null are bolded.

Table 3.

Main outcomes: Females, part 1.^a

		Effect				p-Values
Outcome	Age	Ctl. Mean	Uncond.b	Cond. (Full)c	Cond. (Part.)d	Naïvee	Full Lin.f	Partial Lin.g	Part. Lin. (adj.)h	Gender D-in-Di	Available Observations
Education
Mentally Impaired?	≤19	0.36	−0.28	−0.29	−0.31	0.008	0.009	0.005	0.017	0.337	46
Learning Disabled?	≤19	0.14	−0.14	−0.15	−0.16	0.009	0.016	0.009	0.025	0.029	46
Yrs. of Special Services	≤14	0.46	−0.26	−0.29	−0.34	0.036	0.013	0.013	0.025	0.153	51
Yrs. in Disciplinary Program	≤19	0.36	−0.24	−0.19	−0.27	0.089	0.127	0.074	0.074	0.945	46
High School Graduation	19	0.23	0.61	0.49	0.56	0.000	0.000	0.000	0.000	0.003	51
Grade Point Average	19	1.53	0.89	0.88	0.95	0.000	0.001	0.000	0.001	0.009	30
Highest Grade Completed	19	10.75	1.01	0.94	1.19	0.007	0.008	0.002	0.006	0.052	49
# Years Held Back	≤19	0.41	−0.20	−0.14	−0.21	0.067	0.135	0.097	0.178	0.106	46
Vocational Training Certificate	≤40	0.08	0.16	0.13	0.16	0.070	0.106	0.107	0.107	0.500	51
Health
No Health Problems	19	0.83	0.05	0.12	0.07	0.265	0.107	0.137	0.576	0.308	49
Alive	40	0.92	0.04	0.04	0.06	0.273	0.249	0.197	0.675	0.909	51
No Treat. for Illness, Past 5 Yrs.	27	0.59	0.05	0.14	0.10	0.369	0.188	0.241	0.690	0.806	47
No Non-Routine Care, Past Yr.	27	0.00	0.04	0.02	0.03	0.484	0.439	0.488	0.896	0.549	44
No Sick Days in Bed, Past Yr.	27	0.45	−0.05	−0.04	0.06	0.623	0.597	0.529	0.781	0.412	47
No Doctors for Illness, Past Yr.	19	0.54	−0.02	−0.01	−0.05	0.559	0.539	0.549	0.549	0.609	49
No Tobacco Use	27	0.41	0.11	0.08	0.08	0.208	0.348	0.298	0.598	0.965	47
Infrequent Alcohol Use	27	0.67	0.17	0.07	0.12	0.103	0.336	0.374	0.587	0.924	45
Routine Annual Health Exam	27	0.86	−0.06	−0.09	−0.05	0.684	0.751	0.727	0.727	0.867	47
Family
Has Any Children	≤19	0.52	−0.12	−0.05	−0.07	0.218	0.419	0.328	0.601	—	48
# Out-of-Wedlock Births	≤40	2.52	−0.29	0.51	0.05	0.652	0.257	0.402	0.402	—	42
Crime
# Non-Juv. Arrests	≤27	1.88	−1.60	−2.22	−2.14	0.016	0.003	0.003	0.005	0.571	51
Any Non-Juv. Arrests	≤27	0.35	−0.15	−0.18	−0.14	0.148	0.122	0.125	0.125	0.440	51
# Total Arrests	≤40	4.85	−2.65	−2.88	−2.77	0.028	0.037	0.041	0.088	0.566	51
# Total Charges	≤40	4.92	2.68	2.81	2.81	0.030	0.037	0.042	0.088	0.637	51
# Non-Juv. Arrests	≤40	4.42	−2.26	−2.62	−2.45	0.044	0.046	0.051	0.102	0.458	51
# Misd. Arrests	≤40	4.00	−1.88	−2.19	−2.02	0.078	0.078	0.085	0.160	0.549	51
Total Crime Costj	≤40	293.50	−271.33	−381.03	−381.03	0.013	0.108	0.090	0.090	0.858	51
Any Arrests	≤40	0.65	−0.09	−0.11	−0.13	0.181	0.280	0.239	0.310	0.824	51
Any Charges	≤40	0.65	0.09	0.13	0.13	0.181	0.280	0.239	0.310	0.799	51
Any Non-Juv. Arrests	≤40	0.54	−0.02	−0.02	−0.02	0.351	0.541	0.520	0.520	0.463	51
Any Misd. Arrests	≤40	0.54	−0.02	−0.02	−0.02	0.351	0.541	0.520	0.520	0.519	51

^aMonetary values adjusted to thousands of year-2006 dollars using annual national CPI. p-values below 0.1 are in bold.

^bUnconditional difference in means between the treatment and control groups.

^cConditional treatment effect with linear covariates Stanford–Binet IQ, Socioeconomic Status index (SES), maternal employment, father’s presence at study entry—this is also the effect for the Freedman–Lane procedure under a full linearity assumption, whose respective p-value is computed in column “Full Lin.”

^dConditional treatment effect as in the previous column except that SES is replaced with an indicator for SES above/below the median, so that the corresponding p-value is computed in the column “Partial Lin.” This specification generates p-values used in the stepdown procedure.

^eOne-sided p-values for the hypothesis of no treatment effect based on conditional permutation inference, without orbit restrictions or linear covariates—estimated effect size in the “Uncond.” column.

^fOne-sided p-values for the hypothesis of no treatment effect based on the Freedman–Lane procedure, without restricting permutation orbits and assuming linearity in all covariates (maternal employment, paternal presence, Socioeconomic Status index (SES), and Stanford–Binet IQ)—estimated effect size in the “conditional effect” column.

^gOne-sided p-values for the hypothesis of no treatment effect based on the Freedman–Lane procedure, using the linear covariates maternal employment, paternal presence, and Stanford–Binet IQ, and restricting permutation orbits within strata formed by Socioeconomic Status index (SES) being above or below the sample median and permuting siblings as a block.

^hp-values from the previous column, adjusted for multiple inference using the stepdown procedure.

ⁱTwo-sided p-value for the null hypothesis of no gender difference in mean treatment effects, tested using mean differences between treatments and controls using the conditioning and orbit restriction setup described in footnote f.

^jTotal crime costs include victimization, police, justice, and incarceration costs, where victimizations are estimated from arrest records for each type of crime using data from urban areas of the Midwest, police and court costs are based on historical Michigan unit costs, and the victimization cost of fatal crime takes into account the statistical value of life (see Heckman et al. (2010a) for details).

Table 6.

Main outcomes: Males, part 2.^a

		Effect				p-Values
Outcome	Age	Ctl. Mean	Uncond.b	Cond. (Full)c	Cond. (Part.)d	Naïvee	Full Lin.f	Partial Lin.g	Part. Lin. (adj.)h	Gender D-in-Di	Available Observations
Employment
Current Employment	19	0.41	0.14	0.13	0.16	0.101	0.144	0.103	0.196	0.373	72
Jobless Months in Past 2 Yrs.	19	3.82	1.47	1.31	1.50	0.784	0.763	0.781	0.841	0.102	70
No Job in Past Year	19	0.13	0.11	0.09	0.10	0.924	0.827	0.857	0.857	0.009	72
Jobless Months in Past 2 Yrs.	27	8.79	−3.66	−4.09	−4.50	0.059	0.057	0.033	0.065	0.908	69
No Job in Past Year	27	0.31	−0.07	−0.07	−0.09	0.260	0.295	0.192	0.294	0.157	72
Current Employment	27	0.56	0.04	0.09	0.10	0.367	0.251	0.219	0.219	0.220	69
Current Employment	40	0.50	0.20	0.29	0.29	0.059	0.011	0.011	0.024	0.395	66
Jobless Months in Past 2 Yrs.	40	10.75	−3.52	−4.59	−5.17	0.082	0.040	0.018	0.026	0.573	66
No Job in Past Year	40	0.46	−0.10	−0.15	−0.17	0.249	0.123	0.068	0.068	0.464	72
Earningsj
Monthly Earn., Current Job	19	2.74	−0.16	0.09	0.13	0.591	0.408	0.442	—	0.677	30
Monthly Earn., Current Job	27	1.43	0.88	0.99	1.01	0.017	0.014	0.011	0.018	0.752	68
Yearly Earn., Current Job	27	21.51	3.50	3.67	4.38	0.227	0.248	0.186	0.186	0.873	66
Yearly Earn., Current Job	40	24.23	7.17	4.62	7.02	0.147	0.270	0.150	0.203	0.755	66
Monthly Earn., Current Job	40	2.11	0.50	0.44	0.55	0.224	0.277	0.195	0.195	0.708	66
Earnings & Employmentj
Current Employment	19	0.41	0.14	0.13	0.16	0.101	0.144	0.103	0.279	0.373	72
Monthly Earn., Current Job	19	2.74	−0.16	0.09	0.13	0.591	0.408	0.442	0.736	0.677	30
Jobless Months in Past 2 Yrs.	19	3.82	1.47	1.31	1.50	0.784	0.763	0.781	0.841	0.102	70
No Job in Past Year	19	0.13	0.11	0.09	0.10	0.924	0.827	0.857	0.857	0.009	72
Monthly Earn., Current Job	27	1.43	0.88	0.99	1.01	0.017	0.014	0.011	0.037	0.752	68
Jobless Months in Past 2 Yrs.	27	8.79	−3.66	−4.09	−4.50	0.059	0.057	0.033	0.084	0.908	69
Yearly Earn., Current Job	27	21.51	3.50	3.67	4 38	0.227	0.248	0.186	0.360	0.873	66
No Job in Past Year	27	0.31	−0.07	−0.07	−0.09	0.260	0.295	0.192	0.294	0.157	72
Current Employment	27	0.56	0.04	0.09	0.10	0.367	0.251	0.219	0.219	0.220	69
Current Employment	40	0.50	0.20	0.29	0.29	0.059	0.011	0.011	0.035	0.395	66
Jobless Months in Past 2 Yrs.	40	10.75	−3.52	−4.59	−5.17	0.082	0.040	0.018	0.045	0.573	66
No Job in Past Year	40	0.46	−0.10	−0.15	−0.17	0.249	0.123	0.068	0.137	0.464	72
Yearly Earn., Current Job	40	24.23	7.17	4.62	7.02	0.147	0.270	0.150	0.203	0.755	66
Monthly Earn., Current Job	40	2.11	0.50	0.44	0.55	0.224	0.277	0.195	0.195	0.708	66
Economic
Car Ownership	27	0.59	0.15	0.18	0.19	0.089	0.072	0.059	0.152	0.887	70
Savings Account	27	0.46	−0.01	0.03	0.04	0.555	0.425	0.397	0.610	0.128	70
Checking Account	27	0.23	−0.04	−0.02	−0.02	0.591	0.610	0.575	0.575	0.777	70
Savings Account	40	0.36	0.37	0.36	0.38	0.002	0.002	0.001	0.003	0.071	66
Car Ownership	40	0.50	0.30	0.32	0.35	0.004	0.003	0.002	0.004	0.157	66
Credit Card	40	0.36	0.11	0.08	0.10	0.180	0.279	0.206	0.327	0.737	66
Checking Account	40	0.39	0.01	−0.01	0.01	0.463	0.558	0.491	0.491	0.675	66
Never on Welfare	16–40	0.82	−0.15	−0.17	−0.19	0.101	0.086	0.028	0.104	0.970	72
Never on Welfare (Self Rep.)	26–40	0.38	−0.18	−0.18	−0.20	0.058	0.075	0.051	0.147	0.118	64
>30 Mos. on Welfare	18–27	0.08	−0.01	−0.02	−0.01	0.571	0.482	0.430	0.619	0.087	66
# Months on Welfare	18–27	6.84	0.59	−0.14	0.37	0.563	0.566	0.517	0.646	0.122	66
Ever on Welfare	18–27	0.26	0.06	0.02	0.03	0.697	0.635	0.590	0.590	0.074	66

^aMonetary values adjusted to thousands of year-2006 dollars using annual national CPI. p-values below 0.1 are in bold.

^bUnconditional difference in means between the treatment and control groups.

^cConditional treatment effect with linear covariates Stanford–Binet IQ, Socioeconomic Status index (SES), maternal employment, father’s presence at study entry—this is also the effect for the Freedman–Lane procedure under a full linearity assumption, whose respective p-value is computed in column “Full Lin.”

^dConditional treatment effect as in the previous column except that SES is replaced with an indicator for SES above/below the median, so that the corresponding p-value is computed in the column “Partial Lin.” This specification generates p-values used in the stepdown procedure.

^eOne-sided p-values for the hypothesis of no treatment effect based on conditional permutation inference, without orbit restrictions or linear covariates—estimated effect size in the “Uncond.” column.

^fOne-sided p-values for the hypothesis of no treatment effect based on the Freedman–Lane procedure, without restricting permutation orbits and assuming linearity in all covariates (maternal employment, paternal presence, Socioeconomic Status index (SES), and Stanford–Binet IQ)—estimated effect size in the “conditional effect” column.

^gOne-sided p-values for the hypothesis of no treatment effect based on the Freedman–Lane procedure, using the linear covariates maternal employment, paternal presence, and Stanford–Binet IQ, and restricting permutation orbits within strata formed by Socioeconomic Status index (SES) being above or below the sample median and permuting siblings as a block.

^hp-values from the previous column, adjusted for multiple inference using the stepdown procedure.

ⁱTwo-sided p-value for the null hypothesis of no gender difference in mean treatment effects, tested using mean differences between treatments and controls using the conditioning and orbit restriction setup described in footnote f.

^jAge-19 measures are conditional on at least some earnings during the period specified—observations with zero earnings are omitted in computing means and regressions.

Table 4.

Main outcomes: Females, part 2.^a

		Effect				p-Values
Outcome	Age	Ctl. Mean	Uncond.b	Cond. (Full)c	Cond. (Part.)d	Naïvee	Full Lin.f	Partial Lin.g	Part. Lin. (adj.)h	Gender D-in-Di	Available Observations
Employment
No Job in Past Year	19	0.58	−0.34	−0.37	−0.38	0.006	0.007	0.003	0.007	0.009	51
Jobless Months in Past 2 Yrs.	19	10.42	−5.20	−5.47	−6.82	0.054	0.099	0.020	0.036	0.102	42
Current Employment	19	0.15	0.29	0.23	0.27	0.023	0.045	0.032	0.032	0.373	51
No Job in Past Year	27	0.54	−0.29	−0.25	−0.30	0.017	0.058	0.037	0.071	0.157	48
Current Employment	27	0.55	0.25	0.18	0.28	0.036	0.096	0.042	0.063	0.220	47
Jobless Months in Past 2 Yrs.	27	10.45	−4.21	−2.14	−4.23	0.077	0.285	0.165	0.165	0.908	47
No Job in Past Year	40	0.41	−0.25	−0.22	−0.24	0.032	0.092	0.056	0.111	0.464	47
Jobless Months in Past 2 Yrs.	40	5.05	−1.05	1.05	−0.60	0.343	0.654	0.528	0.627	0.573	46
Current Employment	40	0.82	0.02	−0.08	−0.01	0.419	0.727	0.615	0.615	0.395	46
Earningsj
Monthly Earn., Current Job	19	2.08	−0.61	−0.47	−0.51	0.750	0.701	0.725	–	0.677	15
Monthly Earn., Current Job	27	1.13	0.69	0.48	0.64	0.050	0.144	0.109	0.139	0.752	47
Yearly Earn., Current Job	27	15.45	4.60	2.18	4.00	0.169	0.339	0.277	0.277	0.873	47
Yearly Earn., Current Job	40	19.85	4.35	4.46	5.27	0.251	0.272	0.224	0.274	0.755	46
Monthly Earn., Current Job	40	1.85	0.21	0.27	0.38	0.328	0.316	0.261	0.261	0.708	46
Earnings & Employmentj
No Job in Past Year	19	0.58	−0.34	−0.37	−0.38	0.006	0.007	0.003	0.010	0.009	51
Jobless Months in Past 2 Yrs.	19	10.42	−5.20	−5.47	−6.82	0.054	0.099	0.020	0.056	0.102	42
Current Employment	19	0.15	0.29	0.23	0.27	0.023	0.045	0.032	0.064	0.373	51
Monthly Earn., Current Job	19	2.08	−0.61	−0.47	−0.51	0.750	0.701	0.725	0.725	0.677	15
No Job in Past Year	27	0.54	−0.29	−0.25	−0.30	0.017	0.058	0.037	0.094	0.157	48
Current Employment	27	0.55	0.25	0.18	0.28	0.036	0.096	0.042	0.094	0.220	47
Monthly Earn., Current Job	27	1.13	0.69	0.48	0.64	0.050	0.144	0.109	0.188	0.752	47
Jobless Months in Past 2 Yrs.	27	10.45	−4.21	−2.14	−4.23	0.077	0.285	0.165	0.241	0.908	47
Yearly Earn., Current Job	27	15.45	4.60	2.18	4.00	0.169	0.339	0.277	0.277	0.873	47
No Job in Past Year	40	0.41	−0.25	−0.22	−0.24	0.032	0.092	0.056	0.156	0.464	47
Yearly Earn., Current Job	40	19.85	4.35	4.46	5.27	0.251	0.272	0.224	0.423	0.755	46
Monthly Earn., Current Job	40	1.85	0.21	0.27	0.38	0.328	0.316	0.261	0.440	0.708	46
Jobless Months in Past 2 Yrs.	40	5.05	−1.05	1.05	−0.60	0.343	0.654	0.528	0.627	0.573	46
Current Employment	40	0.82	0.02	−0.08	−0.01	0.419	0.727	0.615	0.615	0.395	46
Economic
Savings Account	27	0.45	0.27	0.23	0.26	0.036	0.087	0.051	0.132	0.128	47
Car Ownership	27	0.59	0.13	0.12	0.18	0.164	0.221	0.147	0.250	0.887	47
Checking Account	27	0.27	0.01	−0.03	0.00	0.472	0.586	0.472	0.472	0.777	47
Credit Card	40	0.50	0.04	0.06	0.11	0.425	0.355	0.233	0.483	0.737	46
Checking Account	40	0.50	0.08	0.04	0.12	0.321	0.413	0.237	0.450	0.675	46
Car Ownership	40	0.77	0.06	0.03	0.11	0.280	0.409	0.257	0.394	0.157	46
Savings Account	40	0.73	0.06	−0.08	0.05	0.309	0.722	0.516	0.516	0.071	46
Ever on Welfare	18–27	0.82	−0.34	−0.21	−0.27	0.009	0.084	0.049	0.154	0.074	47
>30 Mos. on Welfare	18–27	0.55	−0.27	−0.18	−0.25	0.036	0.152	0.072	0.187	0.087	47
# Months on Welfare	18–27	51.23	−21.51	−11.39	−21.58	0.060	0.241	0.120	0.265	0.122	47
Never on Welfare	16–40	0.92	−0.16	−0.13	−0.12	0.110	0.129	0.132	0.221	0.970	51
Never on Welfare (Self Rep.)	26–40	0.41	0.09	0.14	0.06	0.759	0.787	0.664	0.664	0.118	46

^aMonetary values adjusted to thousands of year-2006 dollars using annual national CPI. p-values below 0.1 are in bold.

^bUnconditional difference in means between the treatment and control groups.

^cConditional treatment effect with linear covariates Stanford–Binet IQ, Socioeconomic Status index (SES), maternal employment, father’s presence at study entry—this is also the effect for the Freedman–Lane procedure under a full linearity assumption, whose respective p-value is computed in column “Full Lin.”

^dConditional treatment effect as in the previous column except that SES is replaced with an indicator for SES above/below the median, so that the corresponding p-value is computed in the column “Partial Lin.” This specification generates p-values used in the stepdown procedure.

^eOne-sided p-values for the hypothesis of no treatment effect based on conditional permutation inference, without orbit restrictions or linear covariates—estimated effect size in the “Uncond.” column.

^fOne-sided p-values for the hypothesis of no treatment effect based on the Freedman–Lane procedure, without restricting permutation orbits and assuming linearity in all covariates (maternal employment, paternal presence, Socioeconomic Status index (SES), and Stanford–Binet IQ)—estimated effect size in the “conditional effect” column.

^gOne-sided p-values for the hypothesis of no treatment effect based on the Freedman–Lane procedure, using the linear covariates maternal employment, paternal presence, and Stanford–Binet IQ, and restricting permutation orbits within strata formed by Socioeconomic Status index (SES) being above or below the sample median and permuting siblings as a block.

^hp-values from the previous column, adjusted for multiple inference using the stepdown procedure.

ⁱTwo-sided p-value for the null hypothesis of no gender difference in mean treatment effects, tested using mean differences between treatments and controls using the conditioning and orbit restriction setup described in footnote f.

^jAge-19 measures are conditional on at least some earnings during the period specified—observations with zero earnings are omitted in computing means and regressions.

Table 5.

Main outcomes: Males, part 1.^a

		Effect				p-Values
Outcome	Age	Ctl. Mean	Uncond.b	Cond. (Full)c	Cond. (Part.)d	Naïvee	Full Lin.f	Partial Lin.g	Part. Lin. (adj.)h	Gender D-in-Di	Available Observations
Education
Mentally Impaired?	≤19	0.33	−0.13	−0.19	−0.17	0.106	0.072	0.057	0.190	0.337	66
Yrs. in Disciplinary Program	≤19	0.42	−0.12	−0.26	−0.24	0.313	0.153	0.134	0.334	0.945	66
Yrs. of Special Services	≤14	0.46	−0.04	−0.10	−0.09	0.458	0.256	0.205	0.349	0.153	72
Learning Disabled?	≤19	0.08	0.08	0.08	0.07	0.840	0.841	0.766	0.766	0.029	66
Highest Grade Completed	19	11.28	0.08	−0.01	0.15	0.429	0.383	0.312	0.718	0.052	72
Grade Point Average	19	1.79	0.02	−0.01	0.07	0.464	0.517	0.333	0.716	0.009	47
Vocational Training Certificate	≤40	0.33	0.06	0.06	0.03	0.231	0.304	0.406	0.729	0.500	72
High School Graduation	19	0.51	−0.03	0.00	0.02	0.633	0.510	0.416	0.583	0.003	72
# Years Held Back	≤19	0.39	0.08	0.12	0.09	0.740	0.852	0.745	0.745	0.106	66
Health
Alive	40	0.92	0.05	0.05	0.06	0.160	0.174	0.146	0.604	0.909	72
No Sick Days in Bed, Past Yr.	27	0.38	0.10	0.14	0.12	0.208	0.135	0.162	0.582	0.412	70
No Treat. for Illness, Past 5 Yrs.	27	0.64	0.00	0.01	0.03	0.465	0.417	0.375	0.826	0.806	70
No Doctors for Illness, Past Yr.	19	0.56	0.07	0.02	0.02	0.210	0.435	0.453	0.835	0.609	72
No Non-Routine Care, Past Yr.	27	0.17	−0.03	−0.02	−0.01	0.600	0.548	0.548	0.823	0.549	63
No Health Problems	19	0.95	−0.07	−0.08	−0.08	0.849	0.843	0.862	0.862	0.308	72
Infrequent Alcohol Use	27	0.58	0.18	0.21	0.20	0.072	0.024	0.052	0.139	0.924	66
No Tobacco Use	27	0.46	0.12	0.10	0.09	0.143	0.220	0.260	0.436	0.965	70
Routine Annual Health Exam	27	0.74	−0.04	0.01	0.01	0.622	0.397	0.451	0.451	0.867	68
Crime
# Non-Juv. Arrests	≤27	5.36	−2.33	−2.64	−2.71	0.029	0.028	0.017	0.024	0.571	72
# Fel. Arrests	≤27	2.33	−1.12	−1.07	−1.15	0.046	0.081	0.043	0.101	—	72
Any Non-Juv. Arrests	≤27	0.72	−0.02	−0.05	−0.05	0.501	0.422	0.291	0.418	0.440	72
Any Fel. Arrests	≤27	0.49	0.00	−0.01	−0.01	0.494	0.575	0.442	0.442	—	72
Any Non-Juv. Arrests	≤40	0.92	−0.14	−0.12	−0.12	0.090	0.124	0.078	0.192	0.463	72
Any Fel. Arrests	≤40	0.44	−0.16	−0.15	−0.16	0.047	0.133	0.083	0.191	—	72
Any Arrests	≤40	0.95	−0.13	−0.11	−0.09	0.072	0.142	0.123	0.181	0.824	72
Any Misd. Arrests	≤40	0.87	−0.11	−0.08	−0.07	0.166	0.281	0.191	0.191	0.519	72
# Misd. Arrests	≤40	8.46	−3.13	−3.42	−3.64	0.037	0.043	0.021	0.039	0.549	72
# Non-Juv. Arrests	≤40	11.72	−4.26	−4.45	−4.85	0.039	0.053	0.025	0.041	0.458	72
# Total Arrests	≤40	12.41	−4.20	−4.44	−4.88	0.056	0.073	0.036	0.053	0.566	72
# Fel. Arrests	≤40	3.26	−1.14	−1.03	−1.20	0.112	0.173	0.092	0.092	—	72
# Non-Victimless Chargesj	≤40	3.08	1.59	1.65	1.65	0.029	0.048	0.027	0.061	0.175	72
# Total Charges	≤40	13.38	4.38	5.08	5.08	0.063	0.081	0.041	0.075	0.637	72
Total Crime Costk	≤40	775.90	−351.22	−515.10	−515.10	0.153	0.108	0.070	0.070	0.858	72
Any Non-Victimless Chargesj	≤40	0.62	0.16	0.15	0.15	0.105	0.179	0.112	0.259	0.957	72
Ever Incarcerated	≤40	0.23	−0.08	−0.11	−0.12	0.260	0.159	0.114	0.202	0.563	72
Any Charges	≤40	0.95	0.13	0.09	0.09	0.072	0.142	0.125	0.125	0.799	72

^aMonetary values adjusted to thousands of year-2006 dollars using annual national CPI. p-values below 0.1 are in bold.

^bUnconditional difference in means between the treatment and control groups.

^cConditional treatment effect with linear covariates Stanford–Binet IQ, Socioeconomic Status index (SES), maternal employment, father’s presence at study entry—this is also the effect for the Freedman–Lane procedure under a full linearity assumption, whose respective p-value is computed in column “Full Lin.”

^dConditional treatment effect as in the previous column except that SES is replaced with an indicator for SES above/below the median, so that the corresponding p-value is computed in the column “Partial Lin.” This specification generates p-values used in the stepdown procedure.

^eOne-sided p-values for the hypothesis of no treatment effect based on conditional permutation inference, without orbit restrictions or linear covariates—estimated effect size in the “Uncond.” column.

^fOne-sided p-values for the hypothesis of no treatment effect based on the Freedman–Lane procedure, without restricting permutation orbits and assuming linearity in all covariates (maternal employment, paternal presence, Socioeconomic Status index (SES), and Stanford–Binet IQ)—estimated effect size in the “conditional effect” column.

^gOne-sided p-values for the hypothesis of no treatment effect based on the Freedman–Lane procedure, using the linear covariates maternal employment, paternal presence, and Stanford–Binet IQ, and restricting permutation orbits within strata formed by Socioeconomic Status index (SES) being above or below the sample median and permuting siblings as a block.

^hp-values from the previous column, adjusted for multiple inference using the stepdown procedure.

ⁱTwo-sided p-value for the null hypothesis of no gender difference in mean treatment effects, tested using mean differences between treatments and controls using the conditioning and orbit restriction setup described in footnote f.

^jNon-victimless crimes are those associated with victimization costs: murder, rape, robbery, assault, burglary, larceny, and motor vehicle theft (see Heckman et al. (2010a) for details)

^kTotal crime costs include victimization, police, justice, and incarceration costs, where victimizations are estimated from arrest records for each type of crime using data from urban areas of the Midwest, police and court costs are based on historical Michigan unit costs, and the victimization cost of fatal crime takes into account the statistical value of life (see Heckman et al. (2010a) for details).

Outcomes in each block are placed in ascending order of the partially linear Freedman–Lane p-value, which is described below. This is the order in which the outcomes would be discarded from the joint null hypothesis in the stepdown multiple-hypothesis testing algorithm.⁴⁴ The ordering of outcomes differs in the tables for males and females. Additionally, some outcomes are reported for only one gender when insufficient observations were available for reliable testing of the hypothesis for the other gender.

Single p-values

Tables 3–6 show four varieties of p-values for testing the null hypothesis of no treatment effect. The first such value, labeled “Naïve,” is based on a simple permutation test of the hypothesis of no difference in means between treatment and control groups. This test uses no conditioning, imposes no restrictions on the permutation group, and does not account for imbalances or the compromised Perry randomization. These naive p-values are very close to their asymptotic versions. For evidence on this point, see Web Appendix E.

The next three p-values are based on variants of a procedure due to Freedman and Lane (1983) for combining regression with permutation testing for admissible permutation groups. The first Freedman–Lane p-value, labeled “Full Linearity,” tests the significance of the treatment effect by adjusting outcomes using linear regression with four covariates: maternal employment, paternal presence, SES, and Stanford–Binet IQ, all measured at study entry.⁴⁵ The second Freedman–Lane p-value, labeled “Partial Linearity,” allows for a nonparametric relationship between the SES index and outcomes while continuing to assume a linear relationship for the other three covariates. This nonparametric conditioning on SES is achieved by restricting the orbits of the permutations used in the test. Exchangeability of treatment assignments between observations is assumed only on subsamples with similar values of the SES index (specifically, whether subjects fall above or below the sample median). In addition, the permutation distribution for the partially linear p-values permute siblings as a block. Admissible permutations do not assign different siblings to different treatment and control statuses. These two modifications account for the compromised randomization of the Perry study.⁴⁶ The third p-value for the Freedman–Lane procedure incorporates an adjustment for multiple-hypothesis testing using the stepdown algorithm described below.

Stepdown p-values and multiple-hypothesis testing

We divide outcomes into blocks for multiple-hypothesis testing by type of outcome, similarities on the type of measure, and age if there is an obvious age pattern.⁴⁷ In Tables 3–6, these blocks are delineated by horizontal lines. Within each block, the “Partially Linear (Adjusted)” p-value is the set of p-values obtained from the partially linear model adjusted for multiple-hypothesis testing using the stepdown algorithm. The adjusted p-value in each row corresponds to a joint hypothesis test of the indicated outcome and the outcomes within each block.

The first row of each block constitutes a joint test of the null hypothesis of no treatment effect for any of the outcomes in that block. Each successive row eliminates one outcome from the joint null hypothesis. This stepwise ordering is the reason why we report outcomes placed in ascending order of their p-values. The stepdown-adjusted p-values are based on these values, and the most individually significant remaining outcome is removed from the joint null hypothesis at each successive step.

Statistics

We use the mid-p-value statistics based on the Freedman–Lane coefficient ${\Delta }_k^g$ for treatment status D. All p-values are computed using 30, 000 draws under the relevant permutation procedure. All inference is based on one-sided p-values under the assumption that treatment is not harmful. An exception is the test for differences in treatment effects by gender, which are based on two-sided p-values.

Main results

Tables 3–6 show many statistically significant treatment effects and gender differences that survive multiple-hypothesis testing. In summary, females show strong effects for educational outcomes, early employment, and other early economic outcomes, as well as reduced numbers of arrests. Males show strong effects on a number of outcomes, demonstrating a substantially reduced number of arrests and lower probability of imprisonment, as well as strong effects on earnings at age 27, employment at age 40, and other economic outcomes recorded at age 40.

A principal contribution of this paper is to simultaneously tackle the statistical challenges posed by the problems of small sample size, imbalance in the covariates, and compromised randomization. In doing so, we find substantial differences in inference between the testing procedures that use naive p-values versus the Freedman–Lane p-values which correct for the compromised nature of the randomization protocol. The rejection rate when correcting for these problems is often higher compared with what is obtained from procedures that do not make such corrections, sharpening the evidence for treatment effects from the Perry program. This pattern is largely found in the p-values for males. This is evidenced by increasing statistical significance of treatment effects moving from “Naïve” to “Full Linearity” and from “Full Linearity” to “Partial Linearity.” In several cases, outcomes that are statistically insignificant at a 10% level using naive p-values are shown to be statistically significant using p-values derived from the partially linear Freedman–Lane model. For example, consider the p-values for “Current Employment” at age 40 for males or “Nonjuvenile Arrests” at age 27 for females.

Schooling

Within the group of hypotheses for education, the only statistically significant treatment effect for males is the effect associated with being classified as mentally impaired through age 19 (Table 5). We fail to reject the overall joint null hypotheses for both school achievement and for lifetime educational outcomes. However, as Table 3 shows, there are strong treatment effects for females on high school GPA, graduation, highest grade completed, mental impairment, learning disabilities, and so on. The hypothesis of no difference between sexes in schooling outcomes is rejected for the outcomes of highest grade completed, GPA, high school graduation, and the presence of a learning disability. The unimpressive education results for males, however, do not necessarily mean that the pattern would be reproduced if the program were replicated today. We discuss this point in Section 6.⁴⁸ We discuss the effects of the intervention on cognitive test scores in Web Appendix G. Heckman, Malofeeva, Pinto, and Savelyev (2010b) discuss the impact of the Perry program on noncognitive skills. They decompose treatments effects into effects due to cognitive and noncognitive enhancements of the program.

Employment and earnings

Results for employment and earnings are displayed in Table 4 for females and Table 6 for males. The treatment effects in these outcomes exhibit gender differences and a distinctive age pattern. For females, we observe statistically significant employment effects in the overall joint null hypotheses at ages 19 and 27. Only one outcome does not survive stepdown adjustment: “Jobless Months in Past 2 Years” at age 27. At age 40, however, there are no statistically significant earnings effects for females considered as individual outcomes or in sets of joint null hypotheses by age. For males, we observe no significant employment effects at age 19. We reject the overall joint null hypotheses of no difference in employment outcomes at ages 27 and 40. We also reject the null hypotheses of no treatment effect on age-40 employment outcomes individually. When male earnings outcomes alone are considered, we reject only the overall joint null hypothesis at age 27. However, when earnings are considered together with employment, we reject both the overall age-27 and age-40 joint null hypotheses.

Economic activity

Tests for other economic outcomes, shown in Tables 4 and 6, reinforce the conclusions drawn from the analysis of employment outcomes above. Both treated males and females are generally more likely to have savings accounts and own cars at the same ages that they are more likely to be employed. The effects on welfare dependence are strong for males when considered through age 40, but weak when considered only through age 27; the converse is true for females.

Criminal activity

Tables 3 and 5 show strong treatment effects on criminal activities for both genders. Males are arrested far more frequently than females and, on average, male crimes tend to be more serious. There are no statistically significant gender differences in treatment effects for comparable crime outcomes. By age 27, control females were arrested 1.88 times on average during adulthood, including 0.27 felony arrests, while the corresponding figures for control males are 5.36 and 2.33.⁴⁹ In addition, treated males are significantly less likely to be in prison at age 40 than their control counterparts.⁵⁰ Figure 4 shows cumulative distribution functions for charges cited at all arrests through age 40 for the male subsample. Figure 4(a) includes all types of charges, while Figure 4(b) includes only charges with nonzero victim costs. The latter category of charges is relevant because the costs of criminal victimization resulting from crimes committed by the Perry subjects play a key role in determining the economic return to the Perry Preschool Program. This is reflected in the statistical significance of estimated differences in total crime costs between treated and untreated groups at the 10% level based on the Freedman–Lane procedure using the partially linear model for both males and females. Total crime costs include victimization, police, justice, and incarceration costs. Victimizations are estimated from arrest records for each type of crime using data from urban areas of the Midwest. Police and court costs are based on historical Michigan unit costs, and the victimization cost of fatal crime takes into account the statistical value of life.⁵¹ We reject the overall joint null hypotheses for the number of arrests for both males and females at age 27 and 40.

Figure 4.

CDF of lifetime charges: Males. (a) Includes all charges cited at arrests through age 40. (b) Includes all charges with nonzero victim costs cited at arrests through age 40.

Sensitivity analysis

Our calculations, which are based on the Freedman–Lane procedure under the assumption of partial linearity, rely on linear parametric approximations and on a particular choice of SES quantiles to define permutation orbits. Other choices are possible. Any or all of the four covariates that we use in the Freedman–Lane procedure under full linearity could have been used as conditioning variables to define restricted permutation orbits under a partial linearity assumption. We choose the SES index for nonparametric conditioning, since family background is known to be a powerful determinant of adult outcomes (see Cunha et al. (2006)). Specifically, we use a dummy variable for whether the SES index is above or below the sample median.

It is informative to conduct a sensitivity analysis on the effects of the choice of conditioning strata, which correspond to the covariates whose relationship with the outcome is assumed to be nonlinear rather than linear. To test the sensitivity of our results to the choice of stratum, we run a series of partially linear Freedman–Lane procedures with varying assumptions regarding the set of which covariates enter linearly.

The four preprogram covariates in question can be used either as Freedman–Lane regressors, which assume a linear relationship with outcomes, or as conditioning variables that limit the orbits of permutations to their selected quantiles, which allows for a nonlinear relationship. In Web Appendix F, we perform two types of sensitivity analyses. The first shows that the results reported in Tables 3–6 are robust to variations in the choice of SES index quantiles used to generate the strata on which permutations are restricted: median, tercile, or quartile. The second shows that our results are robust to the choice of which covariates enter the outcome model linearly.

Additional evidence on the effectiveness of the Perry Program

In related work (Heckman et al. (2010a)), we calculate rates of return to determine the private and public returns to the Perry Preschool Program. We avoid the multiple hypothesis-testing problem by focusing on a single economically significant summary of the program. We use the conditioning approach adopted in this paper to control for compromised randomization. We find statistically significant rates of return for both males and females in the range of 6–10% per annum. This supports the evidence of substantial treatment effects presented in the current paper.

Understanding treatment effects

While this paper tests for the existence of treatment effects due to the Perry Preschool Program, other recent work examines channels through which these beneficial effects are produced. Heckman et al. (2010a) estimate a model of latent cognitive and noncognitive traits. In the early years during and after the program, the IQ scores of treatment group participants surged, but by almost age 8, the treatment effect on IQ becomes nonexistent for males and relatively small for females. Their research shows that the effects of the Perry program arise primarily from boosts in noncognitive traits.

6. The representativeness of the Perry study

We next examine the representativeness of the Perry sample and characterize the target population within the overall African-American population. We construct a comparison group using the 1979 National Longitudinal Survey of Youth (NLSY79), a widely used, nationally representative longitudinal data set. The NLSY79 has panel data on wages, schooling, and employment for a cohort of young adults who were 14–22 at their first interview in 1979. This cohort has been followed ever since. For our purposes, an important feature is that the NLSY79 contains information on cognitive test scores as well as on noncognitive measures. It also contains rich information on family background. This survey is a particularly good choice for such a comparison as the birth years of its subjects (1957–1964) include those of the Perry sample (1957–1962). The NLSY79 also oversamples African Americans.

The matching procedure

We use a matching procedure to create NLSY79 comparison groups for Perry control groups by simulating the application of the Perry eligibility criteria to the full NLSY79 sample. Specifically, we use the Perry eligibility criteria to construct samples in the NLSY79. Thus, the comparison group corresponds to the subset of NLSY79 participants who would likely be eligible for the Perry program if it were a nationwide intervention.

We do not have identical information on the NLSY79 respondents and the Perry entry cohorts, so we approximate a Perry-eligible NLSY79 comparison sample. In the absence of IQ scores in the NLSY79, we use Armed Forces Qualification Test (AFQT) scores as a proxy for IQ. We also construct a pseudo-SES index for each NLSY79 respondent using the available information.⁵²

We use two different subsets of the NLSY79 sample to draw inferences about the representativeness of the Perry sample. For an initial comparison group, we use the full African-American subsample in NLSY79. We then apply the approximate Perry eligibility criteria to create a second comparison group based on a restricted subsample of the NLSY79 data.

The U. S. population in 1960 was 180 million people, of which 10.6% (19 million) were African-American.⁵³ According to the NLSY79, the black cohort born in 1957–1964 is composed of 2.2 million males and 2.3 million females. We estimate that 17% of the male cohort and 15% of the female cohort would be eligible for the Perry program if it were applied nationwide. This translates into a population estimate of 712, 000 persons out of the 4.5 million black cohort, who resemble the Perry population in terms of our measures of disadvantage.⁵⁴ For further information on the comparison groups and their construction, see Web Appendix H and Tables H.1 and H.2 for details.

How representative is the Perry sample of the overall African-American population of the United States?

Compared to the unrestricted African-AmericanNLSY79 subsample, Perry program participants are more disadvantaged in their family backgrounds. This is not surprising, given that the Perry program targeted disadvantaged children. Further, Perry participants experience less favorable outcomes later in life, including lower high school graduation rates, employment rates, and earnings. However, if we impose restrictions on the NLSY79 subsample that mimic the sample selection criteria of the Perry program, we obtain a roughly comparable group. Figure 5 demonstrates this comparability for parental highest grade completed at the time children are enrolled in the program. Web Appendix Figures H.1–H.5 report similar plots for other outcomes, including mother’s age at birth, earnings at age 27, and earnings at 40.⁵⁵ Tables H.1 and H.2 present additional details. The Perry sample is representative of disadvantaged African-American populations.

Figure 5.

Perry versus NLSY79: Mean parental highest grade completed. Unrestricted NLSY79 is the full African-American subsample. Restricted NLSY79 is the African-American subsample limited to those satisfying the approximate Perry eligibility criteria: at least one elder sibling, Socioeconomic Status (SES) index at most 11, and 1979 AFQT score less than the African-American median. The reported “t” test is for the difference in means between the two populations.

In Web Appendix I, we consider another aspect of the representativeness of the Perry experiment. Perry participants were caught up in the boom and bust of the Michigan auto industry and its effects on related industries. In the 1970’s, as Perry participants entered the workforce, the male-friendly manufacturing sector was booming. Employees did not need high school diplomas to get good entry-level jobs in manufacturing, and men were much more likely to be employed in the manufacturing sector than women. The industry began to decline as Perry participants entered their late 20’s.

This pattern may explain the gender patterns for treatment effects found in the Perry experiment. Neither treatments nor controls needed high school diplomas to get good jobs. As the manufacturing sector collapsed, neither group fared well. However, as noted in Web Appendix I, male treatment group members were some what more likely to adjust to economic adversity by migrating than were male controls, which may account for their greater economic success at age 40. The history of the Michigan economy helps to explain the age pattern of observed treatment effects for males, thereby diminishing the external validity of the study.

7. Relationship of this study to previous research

Schweinhart et al. (2005) analyze the Perry data through age 40 using large-sample statistical tests. They show substantial effects of the program for both males and females. They do not account for the compromised randomization of the experiment or the multiplicity of hypotheses tested. Heckman (2005) discusses the problems of the small-sample size, the need to use small sample-inference to analyze the Perry data, and the appropriate way to combine inference across hypotheses.

Anderson (2008) addresses the problem of multiple-hypothesis testing in the Perry data. He reanalyzes the Perry data (and data on other early childhood programs) using a stepdown multiple-hypothesis testing procedure due to Westfall and Young (1993). That procedure requires “subset pivotality,” that is, that the multivariate distribution of any subvector of p-values is unaffected by the truth or falsity of hypotheses corresponding to p-values not included in the subvector. This is a strong condition.⁵⁶ Our method for testing multiple hypotheses is based on the stepdown procedure of Romano and Wolf (2005), which uses an assumption about monotonicity of the test statistics. Romano and Wolf (2005) show that their monotonicity assumption is weaker than the subset pivotality assumption.

Anderson applies permutation inference to avoid relying on asymptotically justified test statistics. We confirm his finding that even in the small Perry sample, asymptotic statistics are valid, so concerns about the use of large-sample inference to analyze the Perry samples are misplaced. However, in constructing his tests, Anderson assumes that a simple randomization was conducted in the Perry experiment. He does not address the problem of compromised randomization; neither does he correct for covariate imbalances between treatments and controls.

Anderson reports no statistically significant effects of the Perry program for males. We find that the Perry program improved the status of both genders on a variety of measures. One explanation for the difference between Anderson’s conclusions and ours about the effectiveness of the program for males is that we adjust for covariate imbalances and compromised randomization while Anderson does not. As displayed in Tables 5 and 6, these adjustments sharpen the inference for males and lead to more rejections of the null hypothesis.

Another explanation for the contrast between our conclusions is differences in the blocks of variables used as the basis for the stepdown multiple-hypothesis testing procedures. To reduce the dimensionality of the testing problem, Anderson creates linear indices of outcomes at three stages of the life cycle. The outcomes used to create each index are quite diverse and group a variety of very different outcomes (e.g., crime, employment, education). It is difficult to interpret his indices. Moreover, the components of his indices change with age. We conduct inference for interpretable blocks of hypotheses defined at different stages of the life cycle that are based on comparable outcomes (crime as one block, employment as another block, etc.).

8. Summary and conclusions

Most social experiments are compromised by practical difficulties in implementing the intended randomization protocol. They also have a variety of outcome measures. This paper develops and applies a methodology for analyzing experiments as implemented and for generating valid tests of multiple hypotheses.

We apply our methods to analyze data from the Perry Preschool experiment. Evidence from the HighScope Perry Preschool Program is widely cited to support early childhood interventions. The consequences of imperfect randomization for inference are neglected by previous analysts of these data. This paper shows how to account for compromised randomization to produce valid test statistics.

Proper analysis of the Perry experiment also requires application of methods for small-sample inference and accounting for the large numbers of outcomes of the study. It is important to avoid the danger of artificially lowering p-values by selecting statistically significant outcomes that are “cherry picked” from a larger set of unreported hypothesis tests that do not reject the null.

We propose and implement a combination of methods to simultaneously address these problems. We account for compromises in the randomization protocol by conditioning on background variables to control for the violations of the initial randomization protocol and imbalanced background variables. We use small-sample permutation methods and estimate family-wise error rates that account for the multiplicity of experimental outcomes. The methods developed and applied here have applications to social experiments with small samples when there is imbalance in covariates between treatments and controls, reassignment after randomization, and multiple hypotheses.

The pattern of treatment response by gender varies with age. Males exhibit statistically significant treatment effects for criminal activity, later life income, and employment (ages 27 and 40), whereas female treatment effects are strongest for education and early employment (ages 19 and 27). There is, however, a strong effect of the program on female crime at age 40. The general pattern is one of strong early results for females, with males catching up later in life.

Our analysis of the representativeness of this program shows that Perry study families are disadvantaged compared to the general African-American population. However, application of the Perry eligibility rules to the NLSY79 yields a substantial population of comparable individuals. Based on the NLSY79 data, we estimate that the program targeted about 16% of the African-American population born during 1957–1964, which includes the birth years of the Perry participants.

We present some suggestive evidence that the limited effect of the Perry program on the education of males was due to the peculiarities of the Michigan economy. High school degrees were not required to work in well-paying manufacturing jobs. Perry treatment males appear to have adjusted to the decline in manufacturing that occurred in Michigan better than the controls. This accounts for the statistically significant treatment effects in employment and earnings found formales at age 40.

Few social experiments perfectly implement planned treatment assignment protocols. A proper analysis of such experiments requires recognizing the sampling plan as implemented. Our analysis shows that properly accounting for experiments as implemented can produce sharper results than analyses that proceed as if an ideal experiment was implemented.⁵⁷