Abstract
Manipulation and encapsulation of cells in microdroplets has found many applications in various fields such as clinical diagnostics, pharmaceutical research, and regenerative medicine. The control over the number of cells in individual droplets in such applications is important especially for microfluidic applications. There is a growing need for modeling approaches that enables control over cells within individual droplets. In this study, we developed statistical models based on negative binomial regression to determine the dependence of number of cells per droplet on three main factors: the cell concentration in the ejection fluid, droplet size, and cell size. These models were based on experimental data obtained by using a microdroplet generator, where the presented statistical models estimated the number of cells encapsulated in droplets. We also propose a stochastic model for the total volume of cells per droplet. The statistical and stochastic models introduced in this study are adaptable to various cell types and cell encapsulation technologies such as microfluidic and acoustic methods that require reliable control over number of cells per droplet provided that setting or interaction of the variables is similar to ours.
Keywords: Cell encapsulating droplets, microdroplets, modeling, negative binomial regression, Poisson regression, stochastic processes
1. INTRODUCTION
Microscale droplets (microdroplets) have widespread applications in various areas, such as inkjet printing1, colloidal research2, biology3, 4, and medicine5. Recently, cell encapsulation in microdroplets has found new fields of applications including microfluidics6, 7, cryobiology3, 8–11, clinical diagnostics12, cell patterning3, 13–16, tissue engineering13, 17, high throughput drug studies for cancer15, stem cells18, 19, and pharmaceutical research20. These applications require control over the number of cells encapsulated within individual droplets. For example, individual cells can be encapsulated in microscale droplets as single cell bioreactors13 to rapidly detect concentrations of secreted molecules. However, a stochastic model for predicting the number of cells in microdroplets with the current encapsulation methods has not been developed.
There has been a growing interest in cell encapsulation in nano- and micro-scale droplets for biological and genetic analysis21–25, in which the control over the number of cells in a droplet and cell-to-cell distances are essential26. On the other hand, in bottom-up tissue engineering approach, cell-encapsulating hydrogels are used as building blocks, where the number of cells per building block determines the overall cell density in the resulting constructs14, 27, 28. Cell density and cell-to-cell distance are critical, which affect the structural and functional properties of the engineered tissues29. These applications all require encapsulation of few cells in a small volume of fluids or microdroplets with highly controllable density for consistent and repeatable results.
There are currently several cell encapsulation techniques at microscale, such as pneumatic valve-based bioprinting14, 30, acoustic technologies3, 13, inkjet bioprinting31, 32, laser bioprinting33 and microfluidic based cell manipulation34–37, and encapsulation methods38–40. All these techniques aim to manipulate cells in microscale volumes, and control cell density and cell-to-cell distance. However, the variability in the number of cells per droplet due to stochastic nature of cell loading is a major barrier for effective use of these techniques.
Previously, the number of cells per droplet was reported and the dependence on the cell concentration in the suspension and droplet size were experimentally reported13. The data was fit to a Poisson distribution to estimate the probability of number of cells per droplet using a simplified model that is neither statistical nor stochastic. That is, we did not determine the statistical relationship between the variables explicitly. In this work, we perform this important aspect of cell encapsulation. We also include cell radius as a predictor in one of our three models. We developed statistical models to determine the relationship between the number of cells per droplet (denoted NCPD, henceforth), and the following factors: (i) the cell concentration in the ejection fluid, (ii) droplet size, and (iii) cell size in terms of radius. The models can also be used to predict and control NCPD. Furthermore, we develop stochastic models for total volume of cells per droplet based on the above statistical models, hence the three factors considered. This is attempted for the first time in literature in this article. We considered the ranges of these factors as follows: the cell concentration in the ejection fluid (1, 2, 4, 8, and 16 million cells per milliliter (mil/ml)), cell radius (1–28 µm) and droplet radius (300–700 µm). We developed a statistical model of NCPD by negative binomial regression as a function of these factors using generalized linear modeling techniques appropriate for count data (i.e., data that provides the numbers or counts of particles or units in a bounded region or time) and stochastic modeling of the number and volume of the cells as a form of negative binomial process. The novelty here is the statistical modeling of number of cells per droplet (as the response variable), based on the other variables (size of droplets and cell concentration) as predictor variables. The developed models can be used for reliable predictions and to improve the control over cell encapsulation in droplets, offering theoretical and experimental insights into the involved mechanisms.
2. MATERIALS AND METHODS
2.1. Cell-encapsulation in microdroplets
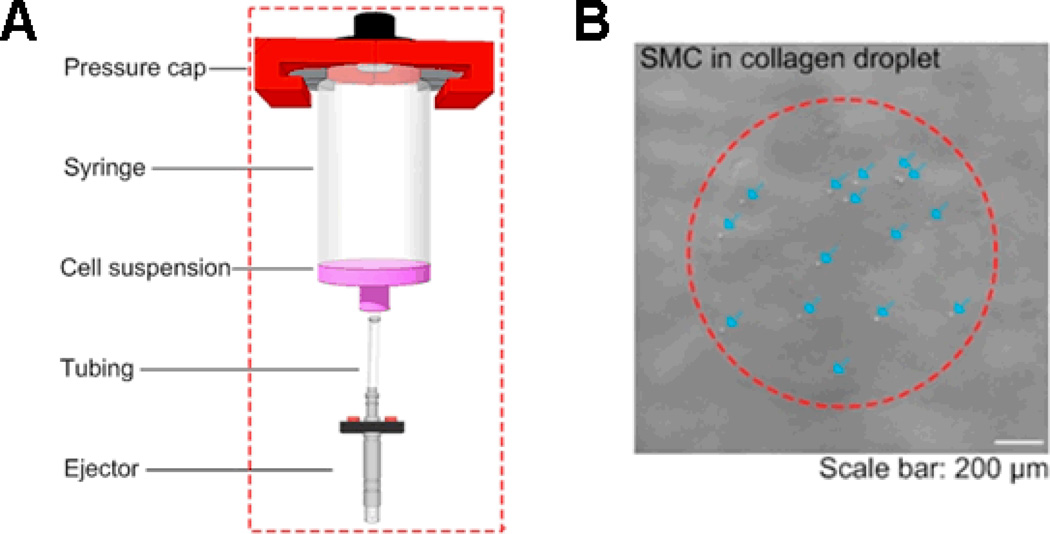
In this study, we used a droplet ejector to generate cell encapsulation microdroplet, which is commercially available (solenoid microvalve ejector, model G100–150300, from TechElan, Mountainside, NJ). We have used this ejector to eject droplets encapsulating various cell types (e.g., smooth muscle cells (SMCs), embryonic stem cells, cancer cells) with high cell viability14, 15, 17, 19, 30, Figure 1. The cell encapsulation systems involve in general formation of a breaking droplet that encapsulates cells within the contents. In this system, NCPD was controlled by changing the droplet radius or the cell concentration in the ejection fluid (i.e., cell suspension in a syringe before ejection). In this study, we used data based on smooth muscle cell (SMC) printing. We used primary bladder SMCs, which were from Sprague Dawley rat. Most cell types are generally spherical when suspended in solution. We perform ejection when the cells are in suspension. Cell suspension was mixed by manual pipetting before printing and the printing process took less than 1 minute, which prevented long-term effects of cell settling in the reservoir. During printing, a droplet was taken from the ejection fluid from the bottom of the syringe via tubing that connected syringe to the ejector (Fig. 1). We used the same culture medium for all cell types. Moreover, in this study, we used the same dispensing force, which was 5 psi. Images were taken under a bright-field microscope (Nikon TE2000). The number of cells was counted manually from the obtained 4× images. Cell radius was measured as the radius of a cell in a droplet, assuming a spherical geometry. Since a droplet radius in a three-dimensional (3D) spherical shape before landing on the substrate surface was challenging to measure, we used the two-dimensional (2D) radius of the droplets on the surface (i.e., droplet spread radius), which is correlated to the 3D droplet radius. For cell concentration in the ejection fluid, we used 1, 2, 4, 8, and 16 mil/ml. We collected cell droplet data from 178 droplets at five cell concentrations (see Table 1). There are several other factors affecting NCPD, which were fixed in our experiments. These factors are: (i) pressure in ejection reservoir (5 psi), (ii) cell type (rat SMCs), (iii) fluid viscosity (0.2% collagen) and (iv) droplet ejection rate (10 droplets per second). We provided the list of variables and abbreviations used in the article in Table 2, and the ranges of the variables in Table 3.
Figure 1.
A) Cell encapsulation system and microdroplet generation system. B) A typical printed cell-encapsulating collagen droplet. Arrows in the image represent the SMC cells encapsulated in droplet.
Table 1.
Number of droplets for each cell concentration
| Cell concentration (mil/ml) | 1 | 2 | 4 | 8 | 16 |
| Number of droplets | 23 | 55 | 30 | 30 | 37 |
Table 2.
Notation (variable names and abbreviations) and its description for statistical modeling of number of cells per droplet.
| Notation | Description |
|---|---|
| NCPD | Number of cells per droplet |
| XDR | Droplet radius (µm) |
| XCR | Cell radius (µm) |
| XCC | Cell concentration (million cells per milliliter) |
| XRR | Radius ratio |
| GLM | Generalized linear models |
| VT | Total volume of the cells in a droplet (µm3) |
| Vi | Volume of the cell i in a droplet (µm3) |
| α | Level of significance for hypothesis testing |
| λ | Poisson rate parameter |
| μ and σ2 | Mean and variance |
| n | Number of observations |
| Q1, Q3 | First and third quartile values |
Table 3.
Variables used in this study, their values and ranges.
| Variable | Values and ranges |
|---|---|
| Cell concentration | 1, 2, 4, 8, and 16 million cells per ml |
| Cell radius | 1–28 µm |
| Droplet radius | 300–700 µm |
2.2. Stochastic and statistical modeling of number of cells per droplet
We hypothesized that the number of cells per droplet (NCPD) highly depends on the droplet radius, cell radius, and cell concentration in the cell suspension. To test this hypothesis, we developed mathematical models to understand the stochastic processes for NCPD and the total cell volume (per droplet). We also assessed empirically these models by fitting to the experimental data. For count data, usually the relationship between the mean and the variance is determined as Var(Yi) = τμi, where Yi is the count variable with mean μi and τ is the dispersion parameter. Depending on the values of τ, two sets of models are used. If τ equals one (i.e., not significantly different than one), a Poisson regression model (a generalized linear model (GLM) model) with logarithm function as the canonical link function and Poisson distributed errors41 was fit to the data. When τ is significantly different than one, other GLMs such as the negative binomial model are more appropriate42. Our data are consistent with the underlying assumptions for a GLM model.
In the models, we used NCPD as the response (or dependent) variable and the other variables (see Table 3) as the predictor (or independent) variables in the GLM procedures. We applied a model selection procedure to obtain a concise and descriptive model (with least number of variables possible, but has high explanatory power). We started with a model containing all the variables (called “full model”) with some non-linear terms that were added to reflect significant relationship between NCPD and the predictor variables. The full model is then reduced using a stepwise backward elimination procedure together with Akaike Information Criteria (AIC)43, i.e., some insignificant variables were removed until each of the remaining variables has a significant effect on the NCPD at α = 0.05 level.
The underlying assumptions, model selection procedure, and some of the discussion on the model diagnostics for each model we consider are deferred to the SI file for brevity in presentation; additionally, they are also peripheral for the main message and results of the article.
3. RESULTS AND DISCUSSIONS
3.1. Modeling NCPD as a function of cell concentration and droplet radius (Model D-C2)
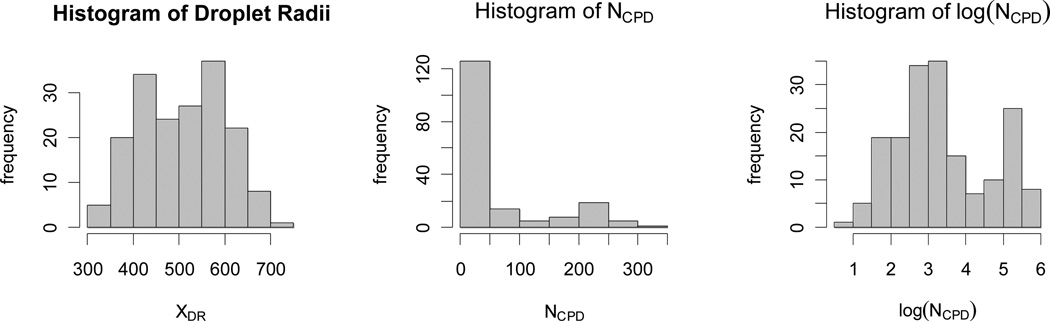
The summary statistics (such as mean, median and first quartile) of the variables of droplet radius, cell concentration, and NCPD are summarized in Table 4 and the corresponding histograms are plotted in Figure 2. The histograms indicate a mild leftward skew for droplet radii and severe rightward skew for NCPD whose mean, 63.63, is much larger than its median, 21), while the rightward skew is reduced for log(NCPD). In particular, the standard deviations for NCPD, droplet radius, cell concentration, and cell radius are 81.87, 91.99, 5.52, and 2.27 (Table 4). So among the variables, the variation of cell radius is much smaller compared to those of NCPD, cell concentration and droplet radius in our setup. Here one might be misled by the comparing the ranges (maximum minus minimum) of these variables which is not a robust measure of spread. Hence, we first model NCPD as a function of only cell concentration (XCC) and droplet radius (XDR) without considering the influence of cell radius (XCR). Our experimental data (Table 4) shows that the variance of NCPD is significantly larger than its mean: Var(NCPD) = 6734.12 and Mean(NCPD) = 63.82 with p < .0001 based on Dean’s PB test for overdispersion44). This indicates that negative binomial regression is more appropriate for our data compared to the more common Poisson regression.
Table 4.
Summary statistics of the variables (droplet radius, cell concentration, NCPD for models that ignores the cell radius (top three rows) and the cell radius (bottom row). The abbreviations are as in Table 2.
| n | mean | SD | min | Q1 | median | Q3 | max | |
|---|---|---|---|---|---|---|---|---|
| NCPD | 178 | 63.63 | 81.87 | 2.00 | 13.00 | 21.00 | 83.750 | 301.00 |
| XDR | 178 | 508.70 | 91.99 | 318.52 | 428.10 | 516.7 | 583.30 | 709.3 |
| XCC | 178 | 6.23 | 5.52 | 1.00 | 2.00 | 4.00 | 8.00 | 16.00 |
| XCR | 10247 | 6.28 | 2.27 | 0.0 | 4.97 | 5.61 | 7.00 | 28.75 |
Figure 2.
Histograms of droplet radii (left), NCPD values (middle) and logarithm of NCPD values (right).
We start with the negative binomial GLM which models logarithm of NCPD as a function of droplet radius and cell concentration and obtain the following model:
| (1) |
Since the model is log linear, we can translate these coefficients into multiplicative effects in the predicted NCPD as
| (2) |
Observe that the expected value of NCPD increases as droplet radius or cell concentration increases. For example, the expected log(NCPD) increase is 0.1890 for a one-unit increase in cell concentration (i.e., if cell concentration increases by 1 mil/ml). That is, a one-unit increase in cell concentration causes the expected NCPD to increase by a factor of exp(0.1890) = 1.2081, holding XDR constant. Notice also that the effect of the cell concentration and droplet radius are both strong in estimating NCPD, but droplet radius is much stronger.
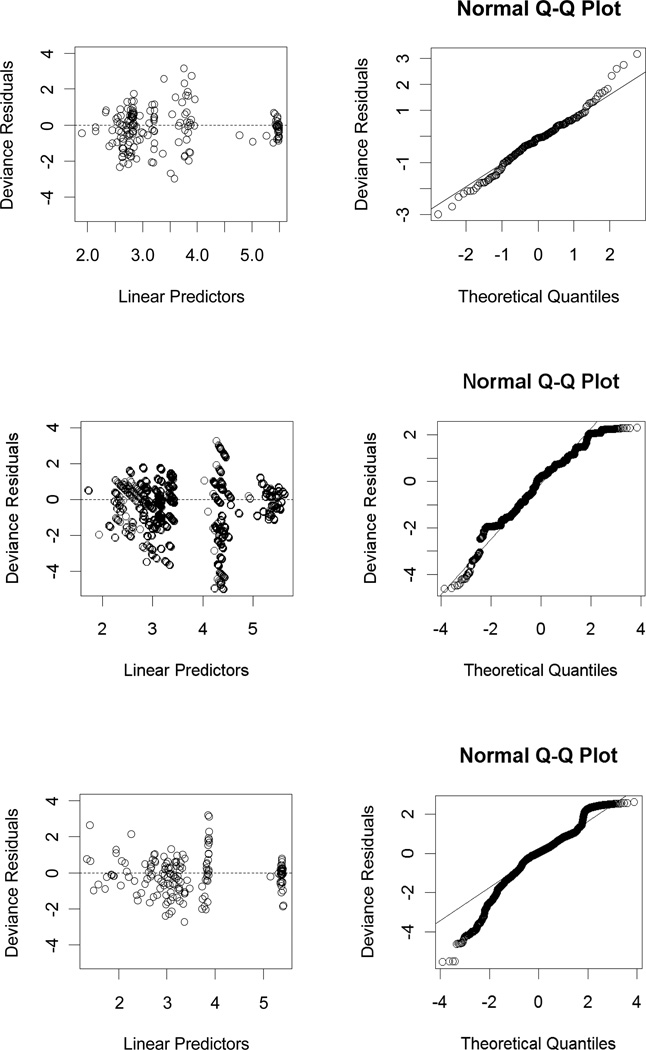
Based on the diagnostic plots in Figure 3, we observe that model assumptions are satisfied for Model D-C2. Hence, when the cell radius is fixed or its variation is negligible compared to the variation in the other variables (i.e., when the variance of cell radius is much smaller compared to the variances of other variables), Model D-C2 can be used to estimate the NCPD values for a given droplet radius and a cell concentration (within the variable ranges given in Table 3). For example, with droplet radius being 500 µm and cell concentration being 5 mil/ml, we estimate the expected NCPD to be
The notation of the models is summarized in Table 5.
Figure 3.
Diagnostic plots for Model D-C2 (top row), Model D-C3 (middle row) and Model R2-C2 (bottom row). The deviance residuals versus predicted values (left) and the normal QQ-plot for deviance residuals versus theoretical quantiles where the straight line passes through the first and third quartiles (right).
Table 5.
Abbreviations used in the Notation of the Models which are indicated by the bold face and capitalization in the description column. (*The MS Excel and R code of the three statistical models (i.e., D-C2, C-D3, and R2-C2) can be provided to interested readers upon request from Umut Atakan Gurkan <uag@mit.edu> or <uagurkan@gmail.com> and Elvan Ceyhan <elceyhan@ku.edu.tr>, respectively.)
| Models* | Description |
|---|---|
| Model D-C2 | Modeling NCPD as a function of Droplet radius and Cell Concentration |
| Model D-C3 | Modeling NCPD as a function of Droplet radius, Cell Concentration, and Cell radius |
| Model R2-C2 | Modeling NCPD as a function of the ratio of droplet Radius to cell Radius and Cell Concentration |
3.2. Modeling NCPD as a function of cell concentration, droplet radius, and cell radius (Model D-C3)
Unlike Model D-C2 (Table 5), at this stage of analysis, we consider the cell radius (XCR) as a potentially important factor in explaining or modeling the NCPD by incorporating cell radius into the modeling procedure. That is, the response variable of interest (NCPD) is modeled as a function of independent (predictor) variables, i.e., cell concentration (XCC), droplet radius (XDR), and cell radius (XCR). We treat each cell related data as a single data point, so for the cells in each droplet, NCPD values are replicated, as well as XCC and XDR values. Hence, we have 9539 sets of XDR, XCR, NCPD and XCC values from 148 droplets at five cell concentrations. Our experimental data showed that the variance of NCPD is significantly larger than its mean: Var(NCPD) = 8211.90 and Mean(NCPD) = 168.74 with p < .0001 based on Dean’s PB test for overdispersion. This indicated that negative binomial regression is more appropriate.
We implement the negative binomial GLM that models logarithm of NCPD as a function of droplet radius, cell radius, and cell concentration together with non-linear terms. By our model selection procedure, the model is reduced to one that only contains XDR and XCC as predictors. That is, in the presence of droplet radius and cell concentration, cell radius has no significant contribution to modeling NCPD. However, this does not necessarily mean that XCR has no impact in the modeling of NCPD. In particular, if cell radius is used as the only predictor variable in modeling the response variable NCPD, then it is significant. We construct models at each cell concentration value treating cell concentration as a qualitative factor (i.e., Model D-C3). This is justifiable, because in practice, usually an experimenter takes XCC to be any one of the 5 values specified. When many replications are taken at few levels of a numerical variable, it is a common practice to also treat this numerical variable as a categorical variable which sometimes provides a better fit of the model to the data at hand. With such modeling, we observe that the cell radius is significant at some cell concentration levels (1 and 8 mil/ml), but not at other levels (2, 4, 16 mil/ml). For example, for XCC = 1 mil/ml, we have
| (3) |
When these coefficients are translated into multiplicative effects in the predicted NCPD count, we get
| (4) |
See Table 6 for the explicit forms of Model D-C3 for each cell concentration. Notice that the dependence of NCPD on XCR and XDR is different at each XCC. Observe that NCPD increases with increasing droplet radius, while NCPD tends to decrease with increasing cell radius. For example, at XCC = 1 mil/ml, for a one-unit increase in cell radius from, say 5 to 6 µm (i.e., if cell radius value increases 1 µm at 5 µm), the expected log(NCPD) decrease is 0.0522 or expected NCPD decrease is by a factor of exp(−0.0522) = 0.9491, when XDR is held constant. Furthermore, the droplet radius has stronger influence on NCPD compared to cell radius.
Table 6.
Model D-C3: The negative binomial model for NCPD at each cell concentration value.
| Cell concentration (mil /ml) | The model | |
|---|---|---|
| XCC = 1 | ||
| XCC = 2 | ||
| XCC = 4 | ||
| XCC = 8 | ||
| XCC = 16 |
Based on the diagnostic plots presented in Figure 3, we observe that model assumptions are valid in this case. Hence, when the cell radius is considered, Model D-C3 is a good alternative to estimate the NCPD values for a given droplet radius and cell radius, at cell concentration tested in this study (1, 2, 4, 8, and 16 mil/ml). That is, if one wants to use any one of these particular cell concentration values in a cell encapsulation experiment, Model D-C3 can be employed. For example, for droplet radius being 500 µm, cell concentration being 1 mil/ml and cell radius being 15 µm, we estimate the expected NCPD to be
On the other hand, Model D-C2 is also applicable for any cell concentration value within 1–16 mil/ml. However, for concentration values other than 1, 2, 4, 8, and 16 mil/ml, one can also estimate NCPD values with linear interpolation. For example, at XDR = 500 µm and XCR = 15 µm, Model D-C3 estimates NCPD value to be 45 for XCC = 4 mil/ml and 110 for XCC = 8 mil/ml. Then at the same XDR = 500 µm and XCR = 15 µm values, for XCC = 5 mil/ml, by linear interpolation, we obtain .
3.3. Modeling NCPD as a function of cell concentration and the ratio of droplet radius to cell radius (Model R2-C2)
We model NCPD as a function of XCC and ratio of droplet radius to cell radius for each cell, called radius ratio and denoted XRR. Negative binomial regression is more appropriate here, since Var(NCPD) = 6846.88 is significantly larger than the mean: Mean(NCPD) = 65.89, p < .0001 based on Dean’s PB test for overdispersion. We have used cell droplet data on 171 droplets and 10226 cells at some concentrations. Radius values were not available for 1079 of the cells, hence removed from the analysis.
We implemented the negative binomial GLM with XRR and XCC as predictors and obtain the following reduced model
| (5) |
The coefficients of the log linear model can be translated into multiplicative effects in the predicted count as
| (6) |
Notice that NCPD tends to increase as XCC or XRR increases. That is, when cell concentration increases, it is more likely to have more cells per droplet. Similarly, when ratio of droplet radius to cell radius increases, the droplet volume tends to be much larger than cell volumes, so it is more likely to encapsulate more cells in such droplets. For example, the expected log(NCPD) increase is 0.0019 for a one-unit increase in radius ratio (i.e., if radius ratio increases by 1). That is, a one-unit increase in radius ratio causes the expected NCPD to increase by a factor of exp(0.0019) = 1.0019, holding XCC constant. When the cell radius is fixed or its variation is negligible compared to the variation in the other variables (i.e., when the variance of cell radius is much smaller compared to the variances of other variables), Model R2-C2 can be used to estimate the NCPD values for a given radius ratio and a cell concentration within the variable ranges of the variables. The ranges for the droplet radii and cell radii in Table 3 yields the range for XRR to be 10.71–700. For example, with radius ratio being 700 µm / 15 µm = 46.67 and cell concentration being 1 mil/ml, we estimate the expected NCPD to be
Furthermore, the model diagnostic plots in Figure 3 suggest that although the model assumptions seem to be not severely violated, the quantile-quantile (QQ)-plot suggests more severe non-normality compared to other models. Besides, the plot of the deviances indicates a worse fit compared to other models (see Figure 3).
3.4. Comparison and discussion of the models for NCPD
The models D-C2, D-C3, and R2-C2 have AIC values 106103.6, 101160.9, and 104479.1, respectively. Hence D-C3 with the smallest AIC value provides the best fit to the available data. Further, comparing the above three models, we find that the inclusion of cell radius and treating cell concentration as a categorical variable in Model D-C3 provides a significant improvement over Model D-C2 (likelihood ratio χ2 = 4974.7, df = 16, p < 0.0001). However, the effect of cell radius is not as strong as the other variables in the modeling of NCPD. In particular, for a thirty-fold increase in cell radius, which is roughly the ratio of the largest cell radius to the smallest cell radius in our data, the NCPD decreases by a factor of 0.9722 at cell concentration XCC = 1 mil/ml and increases by a factor of 1.0065 at cell concentration XCC = 8 mil/ml. Therefore, we can conclude that the influence of cell radius is statistically significant in modeling NCPD, but its practical significance is only moderate. Hence, for practical purposes, Model D-C2 is better along the lines of principle of parsimony, i.e., simple yet explanatory for estimating NCPD.
Comparing Model R2-C2 with Model D-C2, we observe that using the radius ratio instead of droplet radius does not significantly improve the model performance in the sense that the fit of Model R2-C2 is not better than that of Model D-C2. In fact, Model D-C2 is better in explaining the variation in NCPD compared to Model R2-C2 (the likelihood ratio χ2 = 1624.5, df = 0, p < 0.0001).
On the other hand, comparing Model R2-C2 to Model D-C3, we see that Model D-C3 is significantly better in explaining the variation in NCPD compared to Model R2-C2 (the likelihood ratio χ2 = 3350.2, df=16, p < 0.0001). That is, the raw radius values for droplets and cells are better for explaining the variation in NCPD compared to the radius ratios. Therefore, if the cell radius is fixed or its variation is negligible, Model D-C2 can be applied; otherwise Model D-C3 should be applied. These models explain the encapsulation process that determines the number of cells per droplet. Further, we can perform predictions to control the conditions that will yield designed cell encapsulation performance (i.e., NCPD with high probability).
Furthermore, if the cell concentration and droplet radius are fixed, the dependence of NCPD on cell radius can be determined more precisely. The cell radii can be measured by imaging cells in suspension. It takes time for the cells to attach to a surface and spread after ejection. We are ejecting the cells in suspension form; hence their spread sizes on the surface do not come into play. Some cells may seem larger in cultures since they spread, however, their sizes range within the tens of microns when they are suspended and become into spherical form. The cell concentration can be precisely controlled, and the cell radius is dependent on the cell type. The droplet radius is measured after the droplet lands on the substrate. However, this does not mean that we cannot control the droplet radius. We actually control the droplet size by controlling the valve-opening duration as now described in the methods. The longer the microvalve stays open the larger the droplet that is ejected. Hence, to make use of the presented models in this work in estimation or prediction, we also determine the conditions of the experimental settings to achieve specific droplet radius values of the image on the substrate. Therefore, for a given cell type, we can determine the required cell concentrations and droplet radius to achieve a predetermined number of cells per droplet with high probability. Additionally, for given cell concentration and droplet radius values, we can estimate the expected number of cells per droplet with high probability.
See also Table 7 for estimated values of NCPD for XDR = 500 µm, and XCR = 15 µm for each of 1, 2, 4, 8, and 16 mil/ml XCC values. For small XCC values (i.e., for XCC =1 and 2 mil/ml), the models agree in prediction of NCPD values. However, for larger XCC values, Model D-C3 is more reliable at these concentration values. For higher concentration values Models D-C2 and R2-C2 seem to be over-averaging, and hence underestimating the NCPD values. For concentration values other than 1, 2, 4, 8, and 16 mil/ml, one can perform a linear interpolation based on Model D-C3 as described at the end of Section 3.2.
Table 7.
Estimated NCPD values based on the models D-C2, D-C3, and R2-C2 for XDR = 500µm and XCR = 15µm.
| Cell concentration (million cells /ml) | 1 | 2 | 4 | 8 | 16 |
|---|---|---|---|---|---|
| D-C2 | 13 | 16 | 23 | 48 | 210 |
| D-C3 | 11 | 16 | 45 | 110 | 222 |
| R2-C2 | 13 | 16 | 22 | 47 | 283 |
4. Stochastic modeling of number and volume of cells per droplet
4.1. NCPD modeled as a negative binomial process
In Sections 3.1–3.3, we have presented that the volume of the droplet, i.e., droplet radius and cell concentration are the main factors to determine the NCPD values. For a 3D region R with a certain volume in the ejection fluid, the number of cells in R denoted N(R), can be modeled as a negative binomial process with the following probability distribution function (pdf):
| (7) |
where λ is the rate parameter with its unit chosen to be mil/ml (so λ = Xcc) and V(R) is the volume of the region R in ml and . Since the ejection fluid is assumed to be homogenized and droplets are taken from the fluid so that a droplet represents a region with volume V(D). In particular, the number of cells per droplet, NCPD, has the distribution as in Eq. (7) with V(R) being replaced by V(D).
4.2. Total volume of cells per droplet modeled as a compound spatial inhomogeneous negative binomial process
In the cell encapsulation procedure, the cell radius may vary in a range even for a given cell type. Furthermore, NCPD is also related with the cell radius (or volumes). Therefore, a more complex model that incorporates the randomness in the cell radius in addition to the negative binomial property of the number of cells is the compound homogeneous negative binomial process. Given a droplet, let VT(D) be the total volume of the cells at a droplet and Vi is the volume of cell i in the droplet for i = 1, 2, …,N(D) where N(D) = NCPD in the droplet. Then
| (8) |
where N(D) is the homogeneous negative binomial process described in the Section 3.5.1. In particular, using Eq. (8), we get
| (9) |
| (10) |
| (11) |
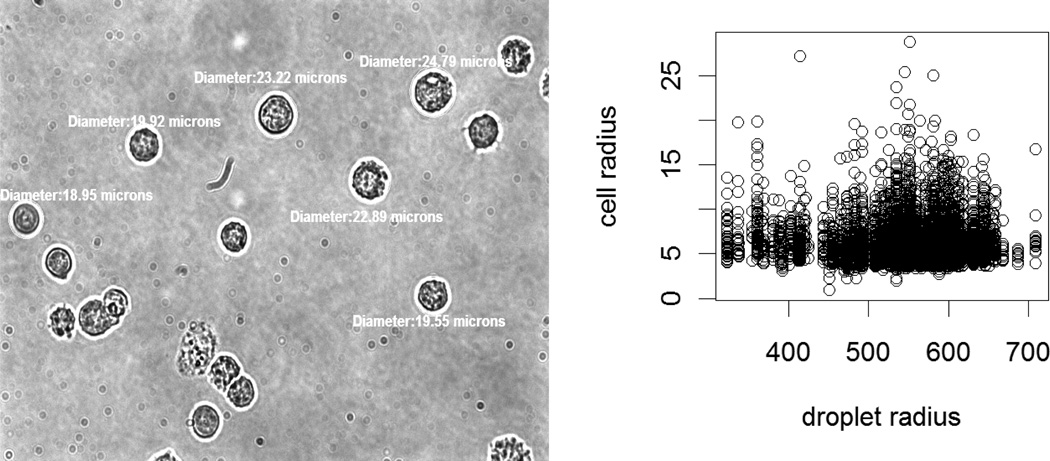
In the model in Eq. (10), N(D) directly depends on cell radius, so it is a dependent type compound negative binomial process. In model Eq. (9), N(D) only depends on droplet radius and cell concentration. There is a very positive relationship with a very small slope between cell radius and droplet radius (see Figure 4 (right)). So, the model in Eq. (9) can be assumed to be a compound negative binomial process.
Figure 4.
A sample figure for cell pictures taken to measure the cell diameters (left). A scatter plot of cell radius versus droplet radius values (right).
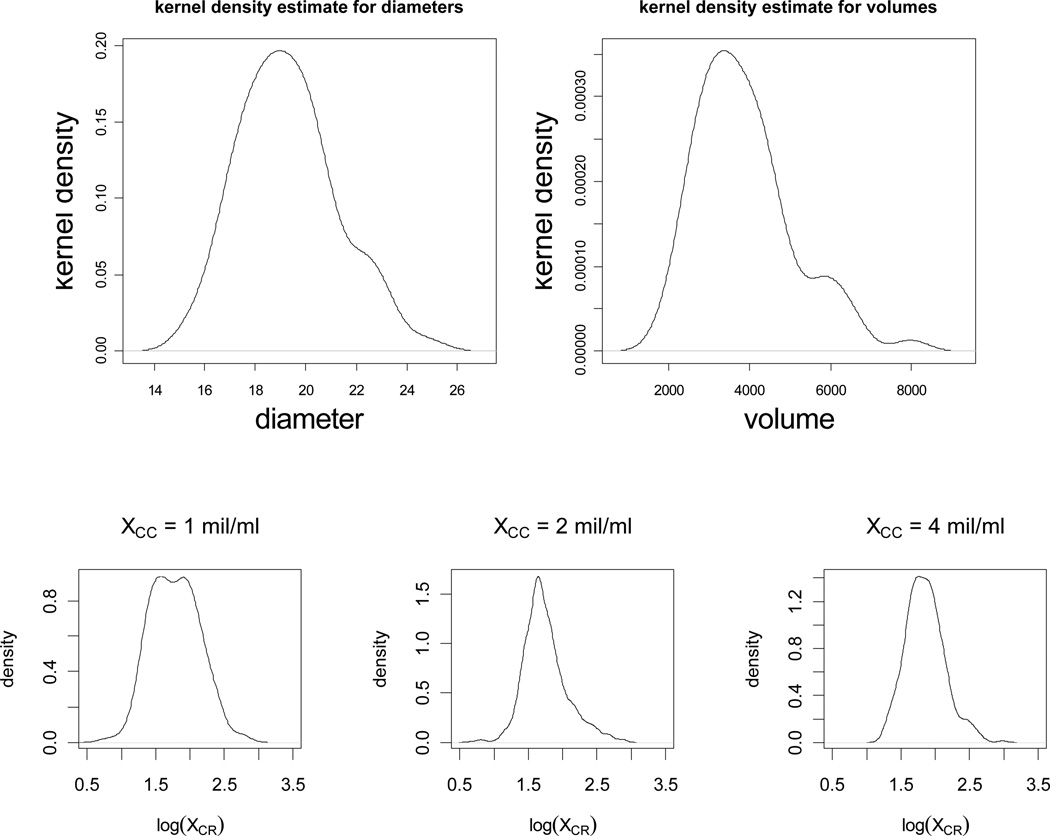
What remains is the distribution of the volume, Vi, of the cells that can be determined by measuring the cell diameters and assuming a spherical cell geometry, i.e., . Hence, it suffices to determine the distribution of the cell radii, XCR. We present the kernel density estimates of the cell radii for the cell concentration values (only 1, 2, and 4 mil/ml are presented) in Figure 5. The figures for the other concentrations are similar, hence not presented. These figures support the claim that cell radii are log-normal with different parameters at each cell concentration. The distribution of the logarithm of cell radius in our data can be modeled as a mixture of normal distributions. Therefore, the cell radii (pooled together in the aggregate data) as a mixture of log-normal distributions has the pdf where, n = 5, i stands for cell concentration 2i−1 mil/ml for i = 1,2, …,5, ai is the proportion of cells from concentration i, and fYi(x) being the pdf of cell radii at concentration i. That is, log(Yi) ~ N(μi,σi) (i.e., log(Yi) is distributed as normal distribution with mean μi and standard deviation σi). In particular, we presented the distribution parameters for each concentration in Table 8.
Figure 5.
Kernel density estimates for the cell diameters (top left) and volumes (top right). Kernel density estimates of the log of the cell radii for cell concentrations 1 mil/ml, 2 mil/ml, and 4 mil/ml, respectively (bottom row).
Table 8.
Mean and standard deviation values for the mixed log-normal distribution in Section 4.2.
| Cell concentration (million cells /ml) | 1 | 2 | 4 | 8 | 16 |
|---|---|---|---|---|---|
| μi | 6.29 | 6.07 | 6.65 | 5.95 | 5.83 |
| σi | 2.38 | 2.22 | 2.05 | 1.69 | 1.93 |
5. CONCLUSIONS
Our statistical models in Section 3 estimate the relationship between number and volume of cells per droplet (NCPD) and other variables including cell concentration (XCC), droplet radius (XDR), and cell radius (XCR) using negative binomial regression. Considering the nature of the relationships and the structure of statistical models, we conclude that the influential factors that affect NCPD are the cell concentration, droplet radius, and cell radius, with the former two having more influence. Further, if cell concentration is fixed, more subtle relationships are observed between NCPD values versus droplet and cell radiuses (see Model D-C3). On the other hand, our stochastic models in Section 4 incorporate the statistical models in Section 3 to describe the total volume of cells per droplet as a compound spatial inhomogeneous negative binomial process.
In conclusion, we have developed three statistical models, namely, Models D-C2, D-C3, and R2-C2. The models are more appropriate under different conditions (cell concentration, droplet radius, and cell radius) so that we can optimize NCPD, i.e., estimate the optimal conditions to encapsulate a desired number of cells within a nanoliter droplet volume. For example, if one wants to estimate NCPD at the specific cell concentration values in Table 3, Model D-C3 is the most appropriate choice, while if one wants to estimate for any cell concentration value within a vicinity of 1–3 mil/ml (i.e., around small cell concentration values relative to the ones considered), Model D-C2 could be employed. Considering Models D-C2, D-C3, and R2-C2 (Table 5) based on our experimental data, we conclude that each of the three variables (e.g., cell concentration, droplet radius, and cell radius) can be optimized for a specific goal when the other two are given. For example, for given droplet and cell radiuses, the cell concentration can be optimized to achieve a specific NCPD value. Thus, one can design the conditions to accurately obtain the desired NCPD, based on the models introduced here; or in a given setup, one can expect the number of cells per droplet reliably. In particular, at the specific cell concentration values in Table 3, one might employ Model D-C3 for estimation or prediction purposes. On the other hand, for smaller cell concentration values (i.e., between 1–3 mil/ml), one might employ Model D-C2 as well. For larger cell concentration values (i.e., 3–16 mil/ml), we recommend the linear interpolation based on Model D-C3 (see end of Section 3.2). Model R2-C2 is fit mostly for comparative purposes, and found to perform less efficiently than the other two models in the sense that the goodness of fit for the other models are better than Model R2-C2.
The models introduced in this paper are applicable to different cell types, other encapsulation medium and cell encapsulation technologies, which require a reliable control over number of cells per microdroplet. The models are usable when the experimental setup is replicated in the current form. Additionally, the models developed in this study and steps taken to validate the experimental and modeling results are applicable broadly to other cell encapsulation systems, since similar parameters such as cell concentration and droplet size analyzed here apply. For example, if the setup, e.g., dispenser does not seriously confound the relationship between number of cells per droplet and the other variables, then the models are applicable in that setting as well. Otherwise, the models are only instructive in forming models of dispenser families that affect the droplet formation or number of cells per droplet substantially different than our setup. Also, we expect viscosity to affect the overall system when ejecting different solutions. Since the droplet is generated under constant pressure, the viscosity will affect the droplet size with all the other conditions the same. However, we do not expect effect of viscosity on the number of cells per droplet if the droplet sizes are the same. The statistical and stochastic models introduced in this study are adaptable to various cell types and cell encapsulation technologies such as microfluidic and acoustic methods that require reliable control over number of cells per droplet provided that setting or interaction of the variables is similar to ours. Here, by adaptability we mean that certain parameters are common to all cell encapsulation systems, e.g., cell concentration and droplet size. A few restrictions of the model are provided in Section S1 of the SI file as the underlying assumptions for our models. Hence, the models developed in this study can be used to provide reliable predictions and to improve the control over cell encapsulation in droplets for a wide range of applications in biomedicine and biomedical research.
Supplementary Material
Acknowledgements
This work was performed at the Demirci Bio-Acoustic MEMS in Medicine (BAMM) Labs at the HST-BWH Center for Bioengineering, Harvard Medical School. This work was supported by the W.H. Coulter Foundation Young Investigator Award, the Center for Integration of Medicine and Innovative Technology under U.S. Army Medical Research Acquisition Activity Cooperative Agreements DAMD17-02-2-0006, W81XWH-07-2-0011, W81XWH-09-2-0001, NIH R21-AI087107, and NIH R21-HL095960. Also, this research is made possible by a research grant that was awarded and administered by the U.S. Army Medical Research & Materiel Command (USAMRMC) and the Telemedicine & Advanced Technology Research Center (TATRC), at Fort Detrick, MD. The information contained herein does not necessarily reflect the position or policy of the Government, and no official endorsement should be inferred.
References
- 1.Jeong HJ, Hwang WR, Kim C, Kim SJ. Journal of Materials Processing Technology. 2010;210:297–305. [Google Scholar]
- 2.Deegan RD, Bakajin O, Dupont TF, Huber G, Nagel SR, Witten TA. Nature. 1997;389:827–829. doi: 10.1103/physreve.62.756. [DOI] [PubMed] [Google Scholar]
- 3.Demirci U, Montesano G. Lab Chip. 2007;7:1428–1433. doi: 10.1039/b705809h. [DOI] [PubMed] [Google Scholar]
- 4.Leunissen ME, van Blaaderen A, Hollingsworth AD, Sullivan MT, Chaikin PM. Proceedings of the National Academy of Sciences of the United States of America. 2007;104:2585–2590. doi: 10.1073/pnas.0610589104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Reis AV, Guilherme MR, Mattoso LHC, Rubira AF, Tambourgi EB, Muniz EC. Pharmaceutical Research. 2009;26:438–444. doi: 10.1007/s11095-008-9732-y. [DOI] [PubMed] [Google Scholar]
- 6.Koster S, Angile FE, Duan H, Agresti JJ, Wintner A, Schmitz C, Rowat AC, Merten CA, Pisignano D, Griffiths AD, Weitz DA. Lab Chip. 2008;8:1110–1115. doi: 10.1039/b802941e. [DOI] [PubMed] [Google Scholar]
- 7.Di Carlo D, Irimia D, Tompkins RG, Toner M. Proc Natl Acad Sci U S A. 2007;104:18892–18897. doi: 10.1073/pnas.0704958104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Xu F, Moon S, Zhang X, Shao L, Song YS, Demirci U. Philos Transact A Math Phys Eng Sci. 2010;368:561–583. doi: 10.1098/rsta.2009.0248. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Song YS, Adler D, Xu F, Kayaalp E, Nureddin A, Anchan RM, Maas RL, Demirci U. Proc Natl Acad Sci U S A. 2010;107:4596–4600. doi: 10.1073/pnas.0914059107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Sakai A, Engelmann F. Cryoletters. 2007;28:151–172. [PubMed] [Google Scholar]
- 11.Samot J, Moon S, Shao L, Zhang X, Xu F, Song Y, Keles HO, Matloff L, Markel J, Demirci U. PLoS One. 2011;6:e17530. doi: 10.1371/journal.pone.0017530. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Teh SY, Lin R, Hung LH, Lee AP. Lab Chip. 2008;8:198–220. doi: 10.1039/b715524g. [DOI] [PubMed] [Google Scholar]
- 13.Demirci U, Montesano G. Lab Chip. 2007;7:1139–1145. doi: 10.1039/b704965j. [DOI] [PubMed] [Google Scholar]
- 14.Xu F, Moon S, Emre AE, Turali ES, Song YS, Hacking A, Nagatomi, Demirci U. Biofabrication. 2010 doi: 10.1088/1758-5082/2/1/014105. [DOI] [PubMed] [Google Scholar]
- 15.Xu F, Celli J, Rizvi I, Moon S, Hasan T, Demirci U. Biotechnology Journal. 2011;6:204–212. doi: 10.1002/biot.201000340. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Tumarkin E, Tzadu L, Csaszar E, Seo M, Zhang H, Lee A, Peerani R, Purpura K, Zandstra PW, Kumacheva E. Integrative Biology. 2011;3:653–662. doi: 10.1039/c1ib00002k. [DOI] [PubMed] [Google Scholar]
- 17.Xu F, Sridharan B, Wang SQ, Durmus NG, Gurkan UA, Demirci U. PLoS ONE. 2011 doi: 10.1371/journal.pone.0019344. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Moon S, Kim YG, Dong L, Lombardi M, Haeggstrom E, Jensen RV, Hsiao LL, Demirci U. PLoS One. 2011;6:e17455. doi: 10.1371/journal.pone.0017455. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Xu F, Sridharan B, Wang SQ, Gurkan AU, Syverud B, Demirci U. Biomicrofluidics. 2011 doi: 10.1063/1.3580752. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Kohanski MA, Dwyer DJ, Wierzbowski J, Cottarel G, Collins JJ. Cell. 2008;135:679–690. doi: 10.1016/j.cell.2008.09.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Kumaresan P, Yang CJ, Cronier SA, Blazej RG, Mathies RA. Anal. Chem. 2008;80:3522–3529. doi: 10.1021/ac800327d. [DOI] [PubMed] [Google Scholar]
- 22.Roach KL, King KR, Uygun K, Hand SC, Kohane IS, Yarmush ML, Toner M. Cryobiology. 2009;58:315–321. doi: 10.1016/j.cryobiol.2009.03.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Dittrich PS, Manz A. Nat Rev Drug Discov. 2006;5:210–218. doi: 10.1038/nrd1985. [DOI] [PubMed] [Google Scholar]
- 24.Baret JC, Beck Y, Billas-Massobrio I, Moras D, Griffiths AD. Chem. Biol. 2010;17:528–536. doi: 10.1016/j.chembiol.2010.04.010. [DOI] [PubMed] [Google Scholar]
- 25.Clausell-Tormos J, Lieber D, Baret JC, El-Harrak A, Miller OJ, Frenz L, Blouwolff J, Humphry KJ, Koster S, Duan H, Holtze C, Weitz DA, Griffiths AD, Merten CA. Chem. Biol. 2008;15:427–437. doi: 10.1016/j.chembiol.2008.04.004. [DOI] [PubMed] [Google Scholar]
- 26.Kenny HA, Krausz T, Yamada SD, Lengyel E. Int J Cancer. 2007;121:1463–1472. doi: 10.1002/ijc.22874. [DOI] [PubMed] [Google Scholar]
- 27.Roth EA, Xu T, Das M, Gregory C, Hickman JJ, Boland T. Biomaterials. 2004;25:3707–3715. doi: 10.1016/j.biomaterials.2003.10.052. [DOI] [PubMed] [Google Scholar]
- 28.Xu F, Wu CM, Keles HO, Rengarajan V, Demirci U. 2011 submitted. [Google Scholar]
- 29.Geckil H, Xu F, Zhang X, Moon S, Demirci U. Nanomedicine (Lond) 2010;5:469–484. doi: 10.2217/nnm.10.12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Moon S, Hasan SK, Song YS, Xu F, Keles HO, Manzur F, Mikkilineni S, Hong JW, Nagatomi J, Haeggstrom E, Khademhosseini A, Demirci U. Tissue Eng Part C Methods. 2010;16:157–166. doi: 10.1089/ten.TEC.2009.0179. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Ringeisen BR, Othon CM, Barron JA, Young D, Spargo BJ. Biotechnol J. 2006;1:930–948. doi: 10.1002/biot.200600058. [DOI] [PubMed] [Google Scholar]
- 32.Boland T, Xu T, Damon B, Cui X. Biotechnol J. 2006;1:910–917. doi: 10.1002/biot.200600081. [DOI] [PubMed] [Google Scholar]
- 33.Pirlo RK, Dean DMD, Knapp DR, Gao BZ. Biotechnol. J. 2006;1:1007–1013. doi: 10.1002/biot.200600127. [DOI] [PubMed] [Google Scholar]
- 34.Moon S, Keles HO, Ozcan A, Khademhosseini A, Haeggstrom E, Kuritzkes D, Demirci U. Biosens Bioelectron. 2009;24:3208–3214. doi: 10.1016/j.bios.2009.03.037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Song YS, Lin RL, Montesano G, Durmus NG, Lee G, Yoo SS, Kayaalp E, Haeggstrom E, Khademhosseini A, Demirci U. Anal Bioanal Chem. 2009;395:185–193. doi: 10.1007/s00216-009-2935-1. [DOI] [PubMed] [Google Scholar]
- 36.Song YS, Moon S, Hulli L, Hasan SK, Kayaalp E, Demirci U. Lab Chip. 2009;9:1874–1881. doi: 10.1039/b823062e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Kim YG, Moon S, Kuritzkes DR, Demirci U. Biosens Bioelectron. 2009;25:253–258. doi: 10.1016/j.bios.2009.06.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Chabert M, Viovy JL. Proc. Natl. Acad. Sci. U. S. A. 2008;105:3191–3196. doi: 10.1073/pnas.0708321105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Choi CH, Jung JH, Rhee YW, Kim DP, Shim SE, Lee CS. Biomedical Microdevices. 2007;9:855–862. doi: 10.1007/s10544-007-9098-7. [DOI] [PubMed] [Google Scholar]
- 40.Kumachev A, Greener J, Tumarkin E, Eiser E, Zandstra PW, Kumacheva E. Biomaterials. 2011;32:1477–1483. doi: 10.1016/j.biomaterials.2010.10.033. [DOI] [PubMed] [Google Scholar]
- 41.Cameron AC, Trivedi PK. Regression analysis of count data. Cambridge ; New York: Cambridge University Press; 1998. [Google Scholar]
- 42.McCullagh P, Nelder J. Generalized Linear Models. London: Chapman and Hall; 1989. [Google Scholar]
- 43.Burnham KP, Anderson D. Model Selection and Multi-Model Inference. New York: Springer; 2003. [Google Scholar]
- 44.Dean CB. J. Amer. Statist. Assoc. 1992;87:451–457. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.