Abstract
Nav1.5 sodium channels, encoded by SCN5A, have been identified in human gastrointestinal interstitial cells of Cajal (ICC) and smooth muscle cells (SMC). A recent study found a novel, rare missense R76C mutation of the sodium channel interacting protein telethonin in a patient with primary intestinal pseudo-obstruction. The presence of a mutation in a patient with a motility disorder, however, does not automatically imply a cause-effect relationship between the two. Patch clamp experiments on HEK-293 cells previously established that the R76C mutation altered Nav1.5 channel function. Here the process through which these data were quantified to create stationary Markov state models of wild-type and R76C channel function is described. The resulting channel descriptions were included in whole cell ICC and SMC computational models and simulations were performed to assess the cellular effects of the R76C mutation. The simulated ICC slow wave was decreased in duration and the resting membrane potential in the SMC was depolarized. Thus, the R76C mutation was sufficient to alter ICC and SMC cell electrophysiology. However, the cause-effect relationship between R76C and intestinal pseudo-obstruction remains an open question.
Keywords: Ion channel, Markov, SCN5A, computer model, motility disorder
1. Introduction
SCN5A encodes the pore-forming alpha subunit of the tetrodotoxin resistant voltage sensitive sodium channel Nav1.5. SCN5A mRNA and Nav1.5 have been identified in interstitial cells of Cajal (ICC) [1] and circular smooth muscle cells (SMC) of the human gastrointestinal (GI) tract [2,3]. Gastrointestinal Nav1.5 is perfectly homologous with its cardiac counterpart [3,4]. In the heart, many types of SCN5A mutations are known to cause disorders such as LQT3 syndrome [5] and some of these have been the subject of computational investigations (e.g. Bankston et al [6] and Clancy and Rudy [7, 8]). In the GI tract, Locke et al established a strong correlation between gastrointestinal symptoms (such as abdominal pain) and SCN5A mutations [9]. The same study also showed the absence of a link between the most common potassium channelopathy (encoded by KCNH2 and also expressed in the gastrointestinal tract) and gastrointestinal complaints suggesting the correlation was specific for SCN5A. More recent data suggest that SCN5A mutations are found in patients with irritable bowel syndrome and could therefore potentially cause gastrointestinal pathology [10].
Recently, patients with intestinal pseudo obstruction were screened for mutations in the exons of SCN5A and the channel’s interacting proteins. Mazzone et al reported a rare, novel missense R76C mutation of a sodium channel interacting protein telethonin (encoded by the TCAP gene) in a primary intestinal pseudo obstruction patient [11]. The same study demonstrated for the first time that telethonin is an interacting protein of the Nav1.5 sodium channel. Whole cell patch clamp experiments showed that this mutation (R76C) altered sodium channel kinetics in a heterologous expression system. However, the presence of genetic mutation in a patient with a diagnosed condition does not automatically imply that the mutation is responsible for the disease. This encompasses the motivation for this work; could this previously unknown R76C mutation contribute to intestinal pseudo-obstruction? The approach adopted here was to employ a computational approach to first model the effects of the R76C mutation on the Nav1.5 channel and then to study its impact on models of gastrointestinal cell electrophysiology.
2. Methods
Three groups of experimental data from Mazzone et al, labeled according to what was transfected into the expression system (HEK-293 cells), i.e., SCN5A (the SCN5A gene only), TCAP (the SCN5A gene with TCAP) and R76C (the SCN5A gene with R76C TCAP), were used to develop three computational models of human Nav1.5 electrophysiology [11].
2.1. Model topology
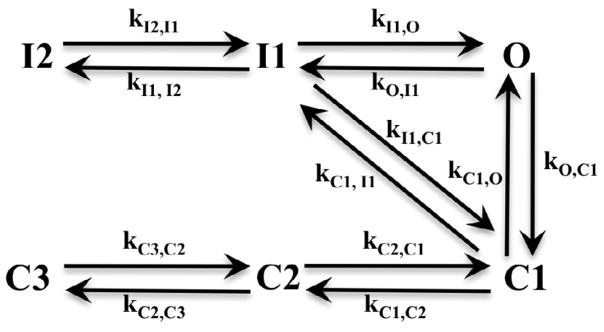
A Markov formalism was used to create the sodium channel models with a topology as shown in Fig. 1. This topology follows an existing cardiac sodium channel model and was selected due to identical protein structure homology between the cardiac and intestinal sodium channels [1, 7]. The model describes the sodium channel in terms of six states: three closed states (C1, C2, C3), two inactivated states (I1, I2) and one open state (O). A transition rate, ki,j, which depends on the free energy barrier that must be overcome for transition from state i to state j, can be described from reaction rate theory [12] and can assume a number of mathematical forms. For example, k = Aexp(B + CVm) was proposed by Stevens [13], the nonlinear form of by Destexhe and Huguenard [14] or its improved form k = Aexp(B(Vm − VC)2) + Dexp(E(Vm − VF)2) + ··· by Ozer [15]. In these expressions, ki,j depends on the transmembrane potential,Vm, and the parameters are unknowns whose values can be fitted to experimental data.
FIGURE 1.
Topology of the Markov sodium channel model including six states: three closed (C1, C2, C3), two inactivated (I1, I2) and one open (O). The transition rates, k, between states are voltage dependent and fitted to experimental data.
After experimenting with a number of different forms for the rate equations, the three parameter form k = Aexp(B + CVm) was selected as it was the simplest form that could adequately describe the data. The topology in Figure 1 depicts a total of 12 possible state transitions and the resulting sodium channel model therefore includes 12 of these transition rate equations for a total of 36 parameters to be determined. The system of first order differential equations that arises from Fig. 1 is listed below:
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
2.2. Derivation of open probability
Whole cell patch clamp data from the three groups (SCN5A, TCAP and R76C) from Mazzone et al were used to parameterize the sodium channel models [11]. These experiments provided the sodium current as a function of time, INa(t) for each cell and each clamping voltage. From the perspective of the models, a current will only flow if a channel is in the open state, thus, the recorded current must be reconciled with the channel open probability over time, PO(t). The whole cell sodium current is given by
| (7) |
where represents the maximum sodium conductance and ENa is the Nernst potential for sodium ions. INa(t) can be normalized using a single value of a recorded peak sodium current, , which occurs at clamping voltage and open probability such that is at a peak value:
| (8) |
Rearranging gives an expression that allows one to obtain PO(t) from the patch clamp data:
| (9) |
This approach has the advantage that the whole cell maximum sodium conductance need not be determined as it cancels out. is the clamping voltage that produced the peak current corrected for series resistance. Initially one might assume that should be 1.0, but physically this is not practical. implies that all of the sodium channels in the cell are open simultaneously which is highly unlikely in a channel that exhibits inactivation. Here, the single value of was estimated from the experimental data together using the analytic solution provided by Hodgkin-Huxley for their sodium channel model [16]:
| (10) |
In Eqn. 10, m∞ and τm are the steady state value and time constant for the activation gate, m, while h0 and τh are the initial value and time constant for the inactivation gate, h. tpeak is the time at which occurs. Note that Eqn. 10 is essentially the same equation form as Eqn. 7 when , therefore the open probability equation can be obtained from
| (11) |
Thus, given the time tpeak at which occurs, can be obtained. Here, the freely available program Stimfit (www.stimfit.org [17]) was used to determine the activation and inactivation constants required by Eqn. 11. The resulting was inserted into Eqn. 9 which was then used to generate PO(t) from the experimental INa(t) data.
2.3. Estimation of parameter values
Data from seven cells was available for each of the three different transfection groups. Each cell provided INa(t) at 24 clamping voltages (−80mV to 35mV at intervals of 5mV). After baseline corrections, the methodology described in previous section was applied across each set of seven cells to obtain PO(t) for each clamping voltage. A simple averaging procedure was performed that yielded three sets of 24 traces of from which the unknown parameter values were determined.
To estimate the parameter values, the model described in Fig. 1 was implemented in MATLAB and was subjected to the same voltage clamp protocol that was used in the patch clamp experiments [11]. The MATLAB function ode15s was chosen to integrate the system of ordinary differential equations during the fitting process [18]. Similarly, MATLAB’s fminsearch, which is based on the Simplex method [19], was selected to perform the parameter fitting. All of the clamping voltages were fitted simultaneously. The objective function for the minimization procedure, Fmin, was the sum of squared difference between the predicted open probability, and experimental data derived open probability, across all 24 traces.
| (12) |
To quantify the quality of the fit from the parameter estimation, Eqn. 13 was used to calculate the percentage error between the predicted open probability, and the experimental open probability, across all data points.
| (13) |
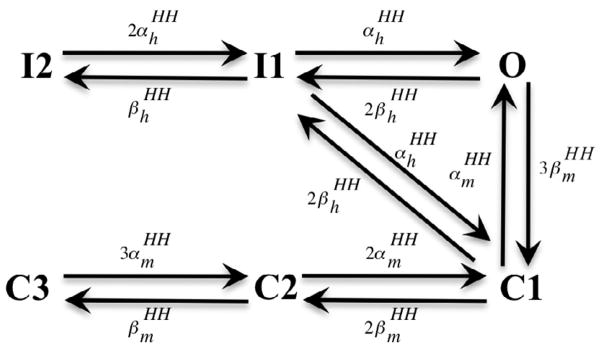
A good initial guess greatly facilitated the convergence of the parameter estimation. A method to obtain the initial guess was developed based on a multi-state version of the traditional Hodgkin-Huxley gating formalism [20]. With this approach, each transition rate in the Markov model was specified as an integer multiple of the rates in a two-state gating format. The two-state rate constants can be either fitted to the patch clamp data or taken from an existing sodium channel model. Fig. 2 illustrates the result of this adaptation for the six state model from Fig. 1. As an example, consider the transition I2 → I1 where kI 2,I1 is equivalent to ( is the opening rate of the Hodgkin-Huxley inactivation gate). Using the voltage dependent equation of of the Hodgkin-Huxley sodium channel model described, in e.g. ten Tusscher et al [21], the value of kI 2,I1 can be calculated for each of the 24 clamping voltages and then kI 2,I1 = Aexp(B + CVm) can be fitted to the results to obtain initial estimates of the unknowns, A, B and C. This process was repeated to obtain good initial estimates for the remaining state transitions.
FIGURE 2.
A multi-state Hodgkin-Huxley model, equivalent to the Markov sodium channel model in Fig. 1, was used to obtain a good initial guess for the fitting procedure. The rate value of each transition is assigned as an integer multiple of the rate value of an activation or inactivation gate in a Hodgkin-Huxley sodium channel model.
2.4. Estimation of maximum sodium channel conductance
Although expression systems such as HEK-293 cells are useful in examining channel kinetics, they do not provide direct information on whole cell maximum sodium conductance (or ion channel density) in native cell populations. Furthermore, since the maximum sodium conductance in a human GI ICC or SMC is not explicitly available in the existing literature, their physiological values were estimated using the SCN5A model in conjunction with published experimental data from human jejunal ICC and SMC [1,2]. The maximum sodium conductance, , was selected for each cell type such that the predicted maximum sodium current, from the ICC and SMC models matched the corresponding native cell experimental data. From Strege et al [1], the mean maximal peak sodium current of −177.5 pA gives an estimated of 31.09 nS in the ICC and from Holm et al [2], a mean maximal peak sodium current of −142 pA gives an estimated of 23.09 nS in the SMC.
3. Results
3.1. Markov sodium channel models
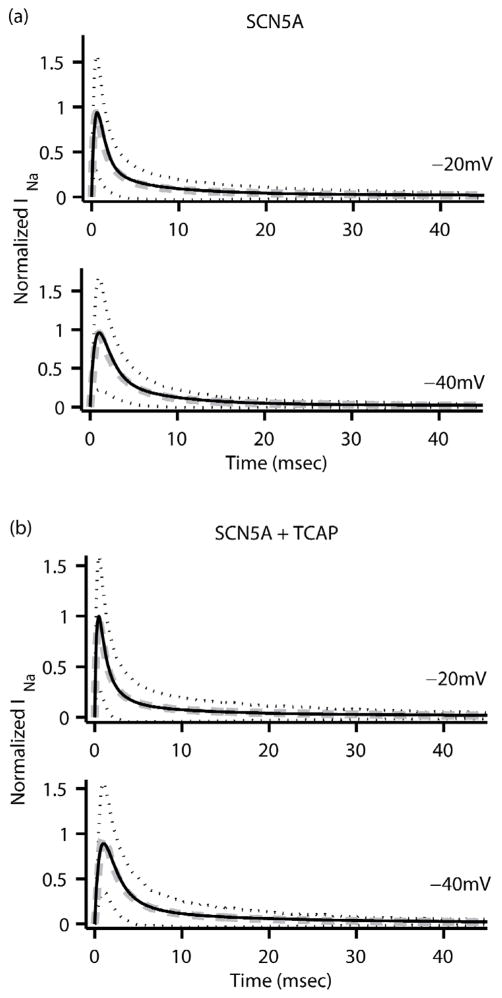
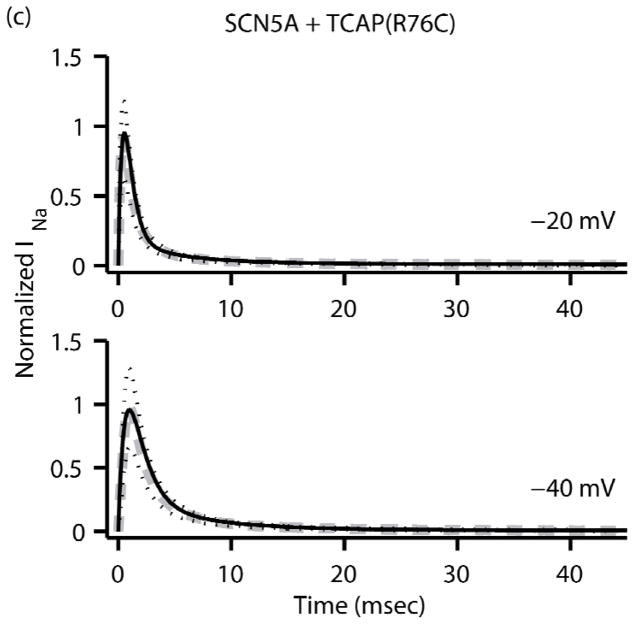
The fitting procedure was applied to the experimental data from each of the transfection groups resulting in three sodium channel (Nav1.5) models. The optimized rate equation parameters for the SCN5A, TCAP, and R76C models are listed in the appendix. Fig. 3 plots the normalized sodium current versus time for each of the three models along with the corresponding experimental data and shows that the two are in good agreement. The fitting errors for the SCN5A, TCAP and R76C models were calculated from Eqn. 13 to be 0.0713%, 0.0886% and 0.1063% respectively.
FIGURE 3.
Normalized INa (black solid line) as a function of time from the three Markov sodium channel models (a) SCN5A, (b) TCAP and (c) R76C at clamping voltages of −20mV (top) and −40 mV (bottom). The corresponding average experimental data (dashed grey line) is also plotted along with black dotted lines representing ± one standard deviation for the experimental data.
3.2. Nav1.5 behaviour in the human jejunal cells
The sodium channel models were created primarily using patch clamp data from HEK-293 cells. To get an indication of the value of the models in describing native wild-type channel behaviour, each of the three models were compared against sodium currents from the human jejunal ICC [1] and SMC [2]. Fig. 4a shows that the SCN5A model is in the closest agreement to the human ICC data, followed next by the TCAP model. Fig. 4b shows the same trend when the models were compared with human SMC data. Quantified differences between the human jejunal experimental data and the model data also indicated SCN5A model has the best agreement to the experimental data (the differences for the ICC are 0.143% for the SCN5A model, 0.166% for the TCAP model and 0.202% for the R76C model; the differences for the SMC are 0.110% for the SCN5A model, 0.128% for the TCAP model and 0.156% for the R76C model). Hence, the sodium channel model without exogenous telethonin augmentation (SCN5A) best reproduces the wild-type channel behaviour in human ICC and SMC. Although the three models agree well with the experimental data from the HEK-293 transfection studies, the sodium current differences were noted with the native cells, where the deviation is more pronounced with the SMC data. One explanation could be the influence of currents from unblocked channels in the cells under patch clamp measurements.
FIGURE 4.
Comparison of normalized peak sodium currents as a function of the clamping voltage. In (a) the three sodium channel models are compared to data from native human jejunal ICC while (b) compares the models against data from native human jejunal SMC. In both cases, the SCN5A model data are in closest agreement to the experimental data.
3.3. Cellular consequences of the R76C mutation
In the absence of human jejunal whole cell computational models, the ICC and SMC models of Corrias et al were chosen as a suitable platform to test the cellular consequences of the R76C mutation [22, 23]. These models are biophysically based and have been rigorously tested under both normal and altered conditions to ensure their robustness. The interested reader is also referred to the murine ICC models by Faville et al [24] and Youm et al [25] as possible cell model alternatives. These gastric models of single cell electrophysiology contain a description of the sodium channel but this was constructed based on limited experimental data. In each cell type the existing channel description was replaced by the Markov models developed here with the appropriate cell type’s whole-cell maximum conductance.
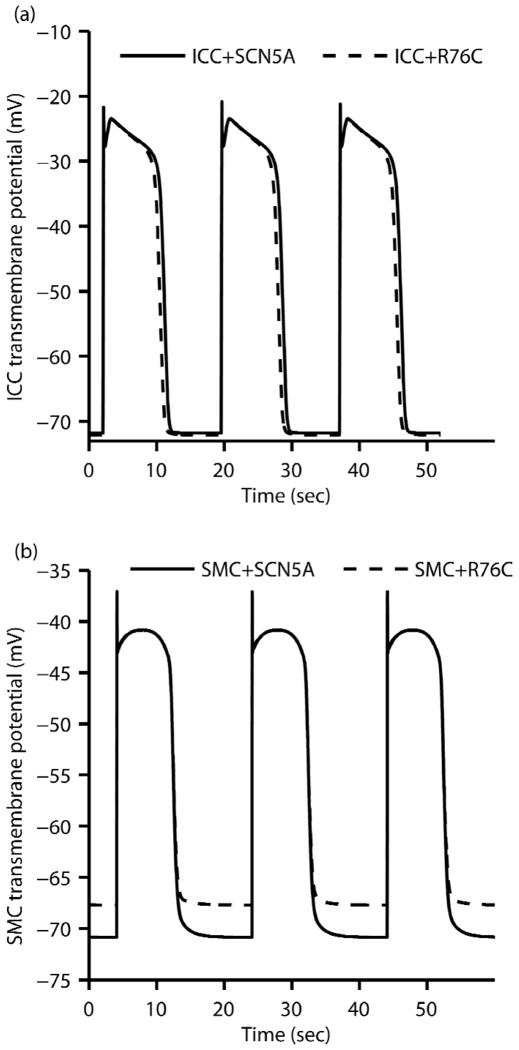
HEK-293 cells express native TCAP, hence the SCN5A model describes sodium channel behaviour in the presence of endogenous TCAP. Patch clamp simulation results showed that the SCN5A model presented similar gross kinetics to the TCAP model, confirming similar observations made in Mazzone et al’s experimental study (i.e. the steady-state values, time to peak values in Fig. 4 and the fast and slow inactivation tau values in Fig. 5 from Mazzone et al’s paper) [11]. This suggests similar kinetics between the SCN5A and TCAP models. Given that the SCN5A model matches better with human jejunal data than TCAP (Fig. 4), therefore the SCN5A and R76C models were used in each cell type to perform simulations of 300 seconds of electrical activity and to compare the results. Fig. 5a shows that the duration of the plateau phase of the ICC slow wave was slightly shortened by about 600 msec in the presence of the R76C mutation with negligble change in frequency. Fig. 5b shows that the resting membrane potential in the SMC depolarized by about 3.1 mV in the presence of R76C mutation. These differences, as well as similarities in ICC and SMC slow wave characteristics were quantified and are presented in Table 1. These results indicate that although the sodium channels are not the initiator of slow waves, as they are in other cells, the presence of the R76C mutation is sufficient to cause notable changes in cellular electrophysiology.
FIGURE 5.
(a) The ICC transmembrane potential with the SCN5A and R76C sodium channel models. The R76C mutation shortened the plateau phase by about 600ms. (b) The SMC transmembrane potential with the SCN5A and R76C sodium channel models. The R76C mutation depolarized the resting membrane potential by about 3.1mV.
Table 1.
ICC and SMC slow wave characteristics, see also Fig. 5.
| Slow wave metrics | ICC | SMC | ||
|---|---|---|---|---|
| SCN5A | R76C | SCN5A | R76C | |
| Maximum upstroke velocity (mVsec−1) | 377.44 | 377.44 | 761.14 | 761.14 |
| Peak potential (mV) | −21.59 | −21.59 | −39.82 | −39.91 |
| Resting membrane potential (mV) | −70.00 | −70.23 | −70.45 | −67.39 |
| Peak potential amplitude (mV) | 48.41 | 48.64 | 30.63 | 27.48 |
| Plateau phase duration (sec) | 8.85 | 8.27 | 8.59 | 8.59 |
| Slow wave period (sec) | 17.69 | 17.69 | 20.61 | 20.61 |
4. Discussion
In the construction of the sodium channel models, the Markov formalism was selected over the classical Hodgkin-Huxley formalism for its better representation of experimental sodium channel behaviour, despite a relative increase in computational cost [26]. While the Hodgkin-Huxley approach could fit channel activation, it was unable to adequately describe the time course of channel inactivation.
The sodium channel kinetics were assumed to be identical in both the ICC and SMC, given that identical alpha subunits exist in both cell types. Furthermore, it was inferred from native channel data that the ICC and SMC sodium channels behave in a similar manner [1–3]. Therefore, any of the three channel models could be integrated into either the ICC model or SMC model. However, it should be pointed out that telethonin expression in ICC is unknown. In the event that ICC is proven not to express telethonin, it is a simple matter of only including the Markov sodium channel models for study in the SMC model and not the ICC model.
Sodium channel activation and inactivation kinetics with and without the R76C mutation were analyzed by simulating the patch clamp protocol described by Mazzone et al [11]. The results were in agreement with those noted experimentally. The window current near the resting membrane potential was enlarged, the time to reach the peak current was slightly decreased and the fast τ of inactivation also decreased. These macroscopic observations were further examined in terms of the state transitions in the Markov models over the physiological range of membrane potentials (here, −70mV to −20 mV). For the transition between any pair of connected states, the steady-state was described by ki,j/(ki,j + kj,i) and the characteristic time constant by 1/(ki,j + kj,i) which are both, in general, dependent on the membrane voltage. It was found that near the resting membrane potential, mutation caused a substantial decrease in steady state values of C2 and C1 with a relatively minor increase in steady state values of O. These changes translate to a net shift in the opening direction whereby more channels reside in the open state which may explain the enlargement of window current. Upon depolarisation, more channels were able to open from a C1→ O transition alone in the R76C model. In the SCN5A model, more transitions from C1 and C2 were required to get the same proportion of channels in an open state. This could possibly explain the observed reduction in the time until the peak current. The time constant values for the forward transition to the open state were also decreased by the mutation at depolarized potentials. Finally, the time constant for the O → I1 transition was decreased in the presence of the mutation, this being the fast τ of inactivation, but the steady state inactivation kinetics (O → I1 & I1 → I2) were largely unchanged.
From the whole cell simulations, changes in the transmembrane potential profile of the ICC and SMC were observed upon the inclusion of the R76C mutation. The duration of the plateau phase in the ICC decreased slightly which was likely a consequence of a decrease in sodium current amplitude when compared to the wild-type channel. From Mazzone et al [11] and the Markov models findings, the R76C mutation resulted in smaller fast τ of inactivation values (in the order of milliseconds) over the physiological voltage range. Under the assumption that whole cell sodium channel conductance remains unchanged in the presence of the R76C mutation, and given the specific cellular conditions of the cell model, the smaller τ values caused the sodium current to decay more rapidly which resulted in an overall decrease in sodium current amplitude during the plateau phase region, thus shortening the plateau phase of the ICC slow wave. An expanded window current near the resting membrane potential, as observed in Mazzone et al, suggested that the resting membrane potential may increase with the increased inward current [11]. Indeed this agrees with the model predictions in the SMC where the resting membrane potential was noticeably depolarized. In the self-exciting single ICC model, the frequency of the slow waves was unchanged in the presence of the R76C mutation and this implies that the alteration of the sodium current was not sufficient to significantly change intracellular calcium handling and hence elicit a frequency change. The single SMC model received a prescribed stimulus input of fixed frequency and therefore unable to experience a change in its slow wave frequency.
Although the same sodium channel formulations were included in both the ICC and SMC models, significant differences were observed when comparing the effects of the mutation on resting membrane potential. The expansion of the window current near the resting membrane potential indicates an expected increase in the inward sodium current and hence a depolarization. However, the extent of this depolarization depends on the magnitude of the whole cell sodium channel conductance relative to the conductance values of the other channel types. Here the proportion of the whole cell conductance contributed by the sodium channels in the ICC at the resting membrane potential was substantially smaller than in the SMC, hence, upon the inclusion of the mutated channel the effects on the SMC resting membrane potential were substantially larger than that observed in the ICC.
In addition, the observed effects of the Markov sodium channel models in the simulated single cell membrane potential of ICC and SMC are contingent on the assumption that the whole cell sodium conductance remains unchanged in the presence of telethonin and/or its mutation. Future studies that unveil any effects on whole cell sodium conductance such as through alteration of SCN5A expression level and single sodium channel conductance would aid in the interpretation of the current findings.
Studies have shown the presence of Nav1.5 sodium channel in human intestinal ICC and SMC but to date no studies were found showing the presence or absence of Nav1.5 in the stomach. Furthermore, the R76C mutation of the Nav1.5 sodium channel was associated with intestinal pseudo-obstruction, a motility disorder of the intestines. Therefore it would be pertinent to confirm these results in human jejunal cell models when they become available, given that the whole-cell studies were performed in gastric cell models. In the intestine, the cells are tightly coupled and the consequences of the R76C mutation could also be examined at higher spatial scales to assess the effects on slow wave coordination and propagation velocity as an indicator of motility. Motility itself is a mechanical event initiated primarily via SMC intracellular calcium [27]. The electrical slow waves, as regulated by ICC and SMC, play a key role in coordinating smooth muscle contraction by regulating SMC intracellular calcium through mechanisms such as the voltage dependent L-type calcium channel [28]. Interestingly, when sodium ions in human jejunal circular smooth muscle cells were replaced with N-methyl-D-glucamine, the L-type calcium current was reduced [3]. Any change in slow wave activity could potentially be translated to a mechanical consequence through L-type calcium or other channels in the SMC. A mutation such as the R76C mutation that alters ICC and SMC electrophysiology could implicate SMC intracellular calcium regulation to disrupt smooth muscle contraction and cause motility disorder. An increase in intracellular calcium in the SMC model due to the R76C mutation was tracked from the simulation study where the area-under-curve for each slow wave increased by 0.149microMsec. The link between Nav1.5 channel genotype and motility phenotype could be better examined by first creating a continuum model of a piece of GI tissue (e.g. using an extended bidomain framework [29]) that integrates the electrical cell models of ICC and SMC containing the mutation descriptions. This would be a tissue model which incorporates ICC and SMC inter-cellular communication and tissue properties. The continuum model of GI electrics is then coupled to mechanical descriptions of smooth muscle contraction. Such an electromechanical model, extensible to the whole GI organ spatial scale, can predict effects of a channel and its mutations on electrics, contractions, and tissue deformability that will shed more light on the degree of contribution that the sodium channel and its mutations may have in motility and its disorders such as intestinal pseudo-obstruction [30].
The same voltage sensitive Nav1.5 sodium channels have been shown to be mechano-sensitive [31]. The presence of syntrophin and the actin cytoskeleton contribute to mechano-sensitivity in human jejunal circular smooth muscle [31 – 33]. Mechanical perturbations of human intestinal smooth muscle strips altered the frequency of electrical activity while patch clamp studies revealed increased in sodium current entry [1]. Recently, it was shown that mechano-activation can adjust the voltage sensitivity of Nav1.5 channels [34]. The motility process involves both extensions and contractions of the musculature and therefore, the mechano-sensitivity of the Nav1.5 channel may play a role in determining channel function.
4.1. Conclusion
Quantitative descriptions of gastrointestinal Nav1.5 sodium channel activity have been created. These descriptions consist of three sodium channel models, SCN5A, TCAP and R76C, which represent sodium channel behaviour without exogenous telethonin, with exogenous wild-type telethonin augmentation and with exogenous R76C telethonin augmentation respectively. Patch clamp study in HEK-293 cells revealed that the R76C mutation altered channel kinetics but further experimental studies using animal models or cultured cells have yet to be performed. This computational study has shown that the R76C mutation was sufficient to alter gastrointestinal ICC and SMC electrical activity at the cellular level. This suggests that the R76C mutation may play a role in the pathogenesis of GI motility disorders such as idiopathic primary intestinal pseudo-obstruction.
Markov models of wild-type and R76C mutant gastrointestinal sodium channel function have been created.
The resulting channel descriptions were included in whole cell ICC and SMC computational models.
Simulations of the ICC and SMC models were performed to assess the cellular effects of the R76C mutation.
The simulated ICC slow wave was decreased in duration and the resting membrane potential in the SMC was elevated.
These results indicate a possible role for this mutation in intestinal pseudo-obstruction.
Acknowledgments
Funding support from the Ministry of Education Academic Research Fund (grant T13-0902-P02) and the National Institutes of Health R01 Grants (DK52766 and DK57061) are gratefully acknowledged
7. Appendix
Parameter values of the transition rate equations for the Markov sodium channel models SCN5A, TCAP and R76C.
| General rate equation | A exp(B + CVm) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Model | SCN5A | TCAP | R76C | ||||||
| State transition | A (ms−1) | B | C (mV−1) | A (ms−1) | B | C (mV−1) | A (ms−1) | B | C (mV−1) |
| O→I1 | 1.3866 | 0.29313 | 0.010479 | 1.7237 | 0.40895 | 0.014457 | 1.7059 | 0.25972 | 0.010794 |
| I1→I2 | 0.035142 | 0.041374 | − 0.033438 | 0.12996 | 0.015000 | 0.0022014 | 0.093675 | 0.090650 | − 0.010767 |
| C3→C2 | 0.0079350 | −0.065834 | − 0.013845 | 0.0073060 | 0.11342 | 0.0086929 | 0.011545 | −0.28925 | − 0.00039366 |
| C2→C1 | 1.0124 | −0.22610 | 0.055314 | 0.86391 | 0.21571 | 0.055603 | 1.0577 | −0.38600 | 0.075900 |
| C1→O | 1.9749 | 0.014107 | 0.036386 | 1.8308 | −0.017678 | 0.038614 | 2.4818 | 0.010733 | 0.042291 |
| I2→I1 | 0.0021216 | 1.0872 | 0.0059559 | 0.00072900 | 1.9057 | 0.064341 | 0.0021109 | 1.2968 | 0.0017296 |
| C2→C3 | 0.72906 | −0.14341 | 0.029007 | 0.50717 | −0.13837 | 0.018489 | 0.68451 | −0.17156 | 0.028433 |
| C1→C2 | 2.6185 | 0.40492 | 0.063545 | 2.5038 | 0.48045 | 0.061622 | 2.8189 | 0.39519 | 0.072258 |
| O→C1 | 2.8053 | −11.322 | − 0.21378 | 2.3318 | −9.9069 | −0.18715 | 1.5057 | −12.211 | − 0.22722 |
| I1→C1 | 2.2638 | −2.2920 | 0.023417 | 4.3500 | −3.4824 | −0.0012705 | 1.4574 | −2.7369 | 0.0066217 |
| C1→I1 | 0.0015610 | −33.000 | 0.0029343 | 0.0014871 | −3.5997 | 0.0024190 | 0.0017829 | −32.331 | − 0.0031479 |
| I1→O | 0.28576 | −10.139 | 0.25936 | 0.081899 | −10.429 | 0.33356 | 0.41627 | −10.725 | 0.26954 |
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Contributor Information
Poh Yong Cheng, Email: yc@nus.edu.sg.
Arthur Beyder, Email: beyder.arthur@mayo.edu.
Peter R. Strege, Email: strege.peter@mayo.edu.
Gianrico Farrugia, Email: farrugia.gianrico@mayo.edu.
Martin L. Buist, Email: biebml@nus.edu.sg.
References
- 1.Strege PR, Ou Y, Sha L, Rich A, Gibbons SJ, Szurszewski JH, Sarr MG, Farrugia G. Sodium current in human intestinal interstitial cells of Cajal. Am J Physiol Gastrointest Liver Physiol. 2003;285 (6):G1111–21. doi: 10.1152/ajpgi.00152.2003. [DOI] [PubMed] [Google Scholar]
- 2.Holm AN, Rich A, Miller SM, Strege P, Ou Y, Gibbons S, Sarr MG, Szurszewski JH, Rae JL, Farrugia G. Sodium current in human jejunal circular smooth muscle cells. Gastroenterology. 2002;122 (1):178–87. doi: 10.1053/gast.2002.30346. [DOI] [PubMed] [Google Scholar]
- 3.Ou Y, Gibbons SJ, Miller SM, Strege PR, Rich A, Distad MA, Ackerman MJ, Rae JL, Szurszewski JH, Farrugia G. SCN5A is expressed in human jejunal circular smooth muscle cells. Neurogastroenterol Motil. 2002;14 (5):477–86. doi: 10.1046/j.1365-2982.2002.00348.x. [DOI] [PubMed] [Google Scholar]
- 4.Gellens ME, George AL, Jr, Chen LQ, Chahine M, Horn R, Barchi RL, Kallen RG. Primary structure and functional expression of the human cardiac tetrodotoxin-insensitive voltage-dependent sodium channel. Proc Natl Acad Sci U S A. 1992;89 (2):554–8. doi: 10.1073/pnas.89.2.554. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Ackerman MJ. Cardiac channelopathies: it’s in the genes. Nat Med. 2004;10 (5):463–4. doi: 10.1038/nm0504-463. [DOI] [PubMed] [Google Scholar]
- 6.Bankston JR, Sampson KJ, Kateriya S, Glaaser IW, Malito DL, Chung WK, Kass RS. A novel LQT-3 mutation disrupts an inactivation gate complex with distinct rate-dependent phenotypic consequences. Channels (Austin) 2007 Jul-Aug;1(4):273–80. doi: 10.4161/chan.4956. [DOI] [PubMed] [Google Scholar]
- 7.Clancy CE, Rudy Y. Linking a genetic defect to its cellular phenotype in a cardiac arrhythmia. Nature. 1999;400 (6744):566–9. doi: 10.1038/23034. [DOI] [PubMed] [Google Scholar]
- 8.Clancy CE, Rudy Y. Na+ channel mutation that causes both Brugada and long-QT syndrome phenotypes: a simulation study of mechanism. Circulation. 2002;105(10):1208–13. doi: 10.1161/hc1002.105183. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Locke GR, Ackerman MJ, Zinsmeister AR, Thapa P, Farrugia G. Gastrointestinal symptoms in families of patients with an SCN5A-encoded cardiac channelopathy: evidence of an intestinal channelopathy. Am J Gastroenterol. 2006;101 (6):1299–304. doi: 10.1111/j.1572-0241.2006.00507.x. [DOI] [PubMed] [Google Scholar]
- 10.Saito YA, Strege PR, Tester DJ, Locke GR, III, Talley NJ, Bernard CE, Rae JL, Makielski JC, Ackerman MJ, Farrugia G. 2008. Sodium channel mutation in the irritable bowel syndrome: Evidence for an ion channelopathy. Am J Physiol Gastrointest Liver Physiol. 2009;296(2):G211–8. doi: 10.1152/ajpgi.90571.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Mazzone A, Strege PR, Tester DJ, Bernard CE, Faulkner G, De Giorgio R, Makielski JC, Stanghellini V, Gibbons SJ, Ackerman MJ, Farrugia G. A mutation in telethonin alters Nav1.5 function. J Biol Chem. 2008;283 (24):16537–44. doi: 10.1074/jbc.M801744200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Eyring H, Lin SH, Lin SM. Basic chemical kinetics. New York: Wiley; 1980. [Google Scholar]
- 13.Stevens CF. Interactions between intrinsic membrane protein and electric field. An approach to studying nerve excitability. Biophys J. 1978;22 (2):295–306. doi: 10.1016/S0006-3495(78)85490-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Destexhe A, Huguenard JR. Nonlinear thermodynamic models of voltage-dependent currents. J Comput Neurosci. 2000;9(3):259–70. doi: 10.1023/a:1026535704537. [DOI] [PubMed] [Google Scholar]
- 15.Ozer M. A comparative analysis of linear, nonlinear and improved nonlinear thermodynamic models of voltage-dependent ion channel kinetics. Phys Stat Mech Appl. 2007;379 (2):579–86. [Google Scholar]
- 16.Hodgkin AL, Huxley AF. A quantitative description of membrane current and its application to conduction and excitation in nerve. J Physiol. 1952;117 (4):500–44. doi: 10.1113/jphysiol.1952.sp004764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Schmidt-Hieber C, Jonas P. Stimfit. 2011 May 2; < http://www.stimfit.org/Home.html>.
- 18.Shampine LF, Reichelt MW. The MATLAB ODE suite. Siam J Sci Comput. 1997;18 (1):1–22. [Google Scholar]
- 19.Lagarias JC, Reeds JA, Wright MH, Wright PE. Convergence properties of the Nelder-Mead simplex method in low dimensions. Siam J Optimiz. 1998;9 (1):112–47. [Google Scholar]
- 20.Balser JR, Bennett PB, Roden DM. Time-dependent outward current in guinea pig ventricular myocytes. Gating kinetics of the delayed rectifier. J Gen Physiol. 1990;96 (4):835–63. doi: 10.1085/jgp.96.4.835. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.ten Tusscher KHWJ, Noble D, Noble PJ, Panfilov AV. A model for human ventricular tissue. American journal of physiology. Am J Physiol Heart Circ Physiol. 2004;286 (4):H1573–89. doi: 10.1152/ajpheart.00794.2003. [DOI] [PubMed] [Google Scholar]
- 22.Corrias A, Buist ML. Quantitative cellular description of gastric slow wave activity. Am J Physiol Gastrointest Liver Physiol. 2008;294 (4):G989–95. doi: 10.1152/ajpgi.00528.2007. [DOI] [PubMed] [Google Scholar]
- 23.Corrias A, Buist ML. A quantitative model of gastric smooth muscle cellular activation. Ann Biomed Eng. 2007;35 (9):1595–607. doi: 10.1007/s10439-007-9324-8. [DOI] [PubMed] [Google Scholar]
- 24.Faville RA, Pullan AJ, Sanders KM, Koh SD, Lloyd CM, Smith NP. Biophysically based mathematical modeling of interstitial cells of Cajal slow wave activity generated from a discrete unitary potential basis. Biophys J. 2009;96(12):4834–52. doi: 10.1016/j.bpj.2009.03.058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Youm JB, Kim N, Han J, Kim E, Joo H, Leem CH, Goto G, Noma A, Earm YE. A mathematical model of pacemaker activity recorded from mouse small intestine. Philos Transact A Math Phys Eng Sci. 2006;364(1842):1135–54. doi: 10.1098/rsta.2006.1759. [DOI] [PubMed] [Google Scholar]
- 26.Fink M, Noble D. Markov models for ion channels: versatility versus identifiability and speed. Philos Transact A Math Phys Eng Sci. 2009;367 (1896):2161–79. doi: 10.1098/rsta.2008.0301. [DOI] [PubMed] [Google Scholar]
- 27.Ozaki H, Stevens RJ, Blondfield DP, Publicover NG, Sanders KM. Simultaneous measurement of membrane potential, cytosolic Ca2+, and tension in intact smooth muscles. Am J Physiol. 1991;260(5 Pt 1):C917–25. doi: 10.1152/ajpcell.1991.260.5.C917. [DOI] [PubMed] [Google Scholar]
- 28.Farrugia G. Ionic conductances in gastrointestinal smooth muscles and interstitial cells of Cajal. Annu Rev Physiol. 1999;61:45–84. doi: 10.1146/annurev.physiol.61.1.45. [DOI] [PubMed] [Google Scholar]
- 29.Buist ML, Poh YC. An extended bidomain framework incorporating multiple cell types. Biophys J. 2010;99(1):13–8. doi: 10.1016/j.bpj.2010.03.054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Farrugia G. Interstitial cells of Cajal in health and disease. Neurogastroenterol Motil. 2008;20 (Suppl 1):54–63. doi: 10.1111/j.1365-2982.2008.01109.x. [DOI] [PubMed] [Google Scholar]
- 31.Morris CE, Juranka PF. Nav channel mechanosensitivity: activation and inactivation accelerate reversibly with stretch. Biophys J. 2007;93 (3):822–33. doi: 10.1529/biophysj.106.101246. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Ou Y, Strege P, Miller SM, Makielski J, Ackerman M, Gibbons SJ, Farrugia G. Syntrophin gamma 2 regulates SCN5A gating by a PDZ domain-mediated interaction. J Biol Chem. 2003;278 (3):1915–23. doi: 10.1074/jbc.M209938200. [DOI] [PubMed] [Google Scholar]
- 33.Strege PR, Holm AN, Rich A, Miller SM, Ou Y, Sarr MG, Farrugia G. Cytoskeletal modulation of sodium current in human jejunal circular smooth muscle cells. Am J Physiol Cell Physiol. 2003;284 (1):C60–6. doi: 10.1152/ajpcell.00532.2001. [DOI] [PubMed] [Google Scholar]
- 34.Beyder A, Rae JL, Bernard CE, Strege PR, Sachs F, Farrugia G. Mechanosensitivity of Nav1.5, a voltage-sensitive sodium channel. J Physiol. 2010;588(Pt 24):4969–85. doi: 10.1113/jphysiol.2010.199034. [DOI] [PMC free article] [PubMed] [Google Scholar]