Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2012 Dec 18;2:989. doi: 10.1038/srep00989

Carbon-Nanotube Optoacoustic Lens for Focused Ultrasound Generation and High-Precision Targeted Therapy

Hyoung Won Baac 1,4, Jong G Ok 2, Adam Maxwell 3, Kyu-Tae Lee 1, Yu-Chih Chen 1, A John Hart 2, Zhen Xu 3, Euisik Yoon 1, L Jay Guo 1,2,a
PMCID: PMC3524551  PMID: 23251775

Abstract

We demonstrate a new optical approach to generate high-frequency (>15 MHz) and high-amplitude focused ultrasound, which can be used for non-invasive ultrasound therapy. A nano-composite film of carbon nanotubes (CNTs) and elastomeric polymer is formed on concave lenses, and used as an efficient optoacoustic source due to the high optical absorption of the CNTs and rapid heat transfer to the polymer upon excitation by pulsed laser irradiation. The CNT-coated lenses can generate unprecedented optoacoustic pressures of >50 MPa in peak positive on a tight focal spot of 75 μm in lateral and 400 μm in axial widths. This pressure amplitude is remarkably high in this frequency regime, producing pronounced shock effects and non-thermal pulsed cavitation at the focal zone. We demonstrate that the optoacoustic lens can be used for micro-scale ultrasonic fragmentation of solid materials and a single-cell surgery in terms of removing the cells from substrates and neighboring cells.

High-amplitude focused ultrasound can provide localized perturbation in liquids and tissues by inducing shock, acoustic cavitation, and heat deposition within focal volumes1,2,3,4. Such mechanical and thermal disturbances have been widely used to deliver targeted impacts to cells and tissues for biomedical therapy: for example, trans-membrane drug delivery (e.g. trans-dermal and blood-brain barrier opening)5,6,7, neural activity modulation in brain8,9, and thrombolysis10, often relying on acoustic cavitation or externally injected micro-bubbles. Remarkable progress have been made in clinical kidney-stone fragmentation11,12 as well as ablation-based tumor therapy under high-intensity focused ultrasound (HIFU)13,14,15. Moreover, cavitation-based ultrasound therapy such as histotripsy has shown some success as a new invasive mechanical ablation tool16.

Although the above beneficial effects have been confirmed over a broad range of biomedical applications, their focal dimensions are insufficiently large: typically >2 mm in a lateral plane and often >10 mm in an axial plane. This is because the focused ultrasound has been generated using low-frequency piezoelectric transducers (a few MHz)14. Moreover, the low-frequency pressure waves necessitate large lens sizes on the order of several centimeters which are not proper for intra-operative applications. High-frequency ultrasound (tens of MHz) would provide obvious advantages on spatial and temporal confinement, opening numerous opportunities for high-accuracy cell therapy as well as ablation-treatment over single tissue layers and micro-vasculatures. It should be also noted that tumors are very often grown adjacent to a vital blood vessel that should be kept intact, and can be hardly addressed by the bulky focal spots in a selective manner. Therefore, high-precision ablation is essential for use in surgery.

However, it is challenging to achieve therapeutic pressure amplitudes in the high-frequency regime (>10 MHz): for example, stronger tensile pressure (P) is required at higher frequency (f) to induce the acoustic cavitation (i.e. P ∝ f1/2 approximately17) which can create significant impacts upon adjacent media through liquid micro-jets and shock waves due to bubble collapse. Furthermore, such high pressure must be achieved at the focal spot in spite of severe acoustic attenuation for the high-frequency components (2.2 × 10−3 dB/(cm × MHz2) in water). The acoustic cavitation can be facilitated by heat deposition through repetitive pulses, but thermal heating should be avoided in many cases of cell therapy applications (e.g. gene therapy) because cellular metabolism is easily transformed by a slight temperature change. A single pulsed cavitation without heat deposition would be useful in these applications.

Alternatively, the high-frequency ultrasound has been generated using pulsed laser irradiation on light-absorbing materials which in turn causes thermo-elastic volume expansion. This method of optoacoustic generation could easily reach several tens of MHz, and even GHz18,19,20 in the acoustic frequency: however, poor energy conversion efficiency has been a major drawback, resulting in weak pressure amplitudes. The advantage of high frequency is further compromised by the frequency-dependent attenuation over long-range propagation. Due to these limitations, optoacoustic pressure as a high-frequency source has not been shown to be feasible for deep-tissue imaging as well as therapeutic purposes requiring high pressure amplitude of tens of MPa.

We demonstrate laser-generated focused ultrasound (LGFU) as a new modality which can produce high-frequency (>15 MHz) and unprecedented optoacoustic pressure of >50 MPa from a single-element lens of only 6 mm in diameter. The focused ultrasound is generated by using a uniquely designed optoacoustic transmitter, made of carbon-nanotube (CNT)-polymer composites, which is formed on a concave surface that directly enables acoustic focusing. Such high-amplitude ultrasound, going into a therapeutic regime, is obtained due to an efficient energy conversion process by the CNT-composites and a high focal gain in the optoacoustic lens platform. The acoustic performance of the LGFU is temporally and spatially characterized at the focal spot, which is as small as 75 μm in lateral and 400 μm in axial directions. Remarkably, it is shown that the LGFU produces powerful shock waves and single-pulsed cavitation, both of which can be used as strong sources of mechanical disruption. These enable micro-scale lithotripsy and high-precision targeted cell therapy. We demonstrate that the spatial dimension of the mechanical disruption can be controlled from 6~15 μm up to 300~400 μm within the focal zone.

Results

Nano-composite optoacoustic transmitters

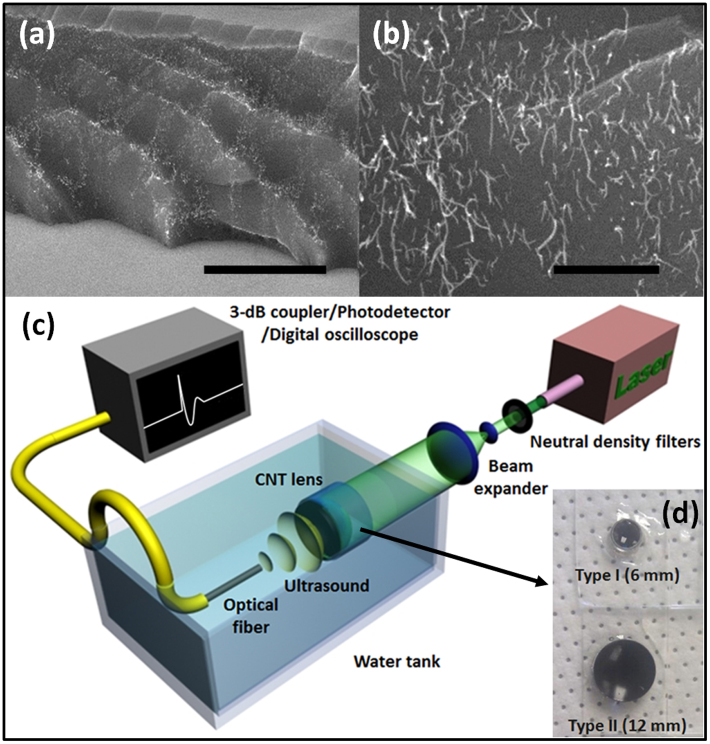
The optoacoustic source was devised to have high optical absorption, efficient heat transduction, and high thermal expansion. For the high optical absorption, we used multi-walled CNTs which were grown on fused silica substrates by chemical vapor deposition (CVD). The CNT length and areal density were controlled to have an optical extinction of 60~70% on the substrate. Then, we further increased the optical extinction up to >85% by depositing a gold (Au) layer of 20 nm onto the CNT films. Finally, an elastomeric polymer, poly-dimethylsiloxane (PDMS), was spin-coated onto the Au/CNT layer. Fig. 1(a) and 1(b) show cross-sectional views of the Au-coated CNT-PDMS composite layer fabricated on the concave lens.

Figure 1. Optoacoustic lenses and measurement setup.

Figure 1

Open in a new tab

The cross-sectional views of the gold-coated CNT-PDMS composite layer are shown in (a) (scale bar = 10 μm) and (b) (scale bar = 1 μm), taken by the scanning electron microscopy.The type II lens shown in (d) was used for the SEM characterization of (a) and (b). The layer thickness is ~16 μm. The PDMS is completely infiltrated among the CNT network as shown in (b); (c) An experimental setup for the LGFU characterization. The 6-ns pulsed laser beam is expanded (×5) and then irradiated onto the transparent side of the CNT lens (detailed explanation in the method section). The LGFU was optically detected by scanning the single-mode fiber-optic hydrophone. The optical output was 3-dB coupled and transmitted to the photodetector with an electronic bandwidth of 75 MHz; (d) Two CNT lenses used in this work. The CNTs were grown on the concave side of the plano-concave fused silica lenses.

The nano-scale dimensions and thermal properties of the CNTs were essential to realize the efficient optoacoustic transmitter. Rapid heat diffusion to a surrounding medium is one of the key characteristics of the nano-particles. For a given heat diffusion time determined by the characteristic dimension of the nano-structure, we can estimate a fraction of the thermal energy η within the absorbers after the laser21,

graphic file with name srep00989-m1.jpg

where τHD and τL are the heat diffusion time and the laser pulse duration (Fig. 1(c)). Considering the CNT as a cylinder with diameter d, the diffusion time is obtained as τHD = d2/16χ where χ is the thermal diffusivity of the surrounding medium. This results in τHD< 0.4 ns for the Au-coated CNT strand (~25 nm in diameter) surrounded by the PDMS (χ = 1.06 × 10−7 m2/s). This is much faster than the temporal width of the laser pulse (6 ns), suggesting that the negligible energy remains within the CNT (η = 0.06) after the optical pulse excitation. This means that, as soon as the CNTs are heated by the light absorption, they give out most of the thermal energy to the surrounding elastomeric polymer which can cause instantaneous thermal expansion with high amplitudes. The PDMS has a high thermal coefficient of volume expansion, 0.92 × 10−3 K−1, which is 4.5 fold higher than water (0.21 × 10−3 K−1), and >20 fold higher than typical metals (e.g. gold ~0.04 × 10−3 K−1). Our approach to simultaneously achieve rapid and large volume expansion using the CNT nano-composite is clear distinction from the use of micro-scale optical absorbers commonly used as optoacoustic imaging contrast agents. Comparatively, for a micro-scale cylinder of 1 μm in diameter, most of the generated heat is confined (η = 0.99) after the same pulse duration of 6 ns. Therefore, the volume deformation is dominated by the optical absorbers themselves.

Optoacoustic lenses with high focal gains

For acoustic focusing, the CNT-PDMS composite transmitters were produced on a concave surface. We used fused silica optical lenses as the concave substrate. Then, we took the unique advantage of the CNTs which can be directly grown on arbitrary shaped surfaces22. Because the growth of CNT films is conformal to the surface, we could use spherical lenses with deep curvatures (i.e. low f-number) to allow high focal gains.

We used two lenses for experimental demonstration. The first lens has 5.5-mm radius of curvature and 6-mm diameter (named as type I), and the second has 11.46-mm curvature and 12-mm diameter (type II). The focal gain G of spherical lens can be represented as a ratio of the pressure at the focus to the pressure on the spherical surface where the source layer is located23:

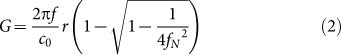graphic file with name srep00989-m2.jpg

Here, f, co, r, and fN are the acoustic frequency, the ambient sound speed, the radius of curvature, and the f-number which is defined as the ratio of the radius of curvature to the lens diameter. As both lenses have low f-numbers, 0.92 (type I) and 0.96 (type II), their focal gains are significantly greater than the typical HIFU transducers with fN > 2. According to the equation (2), the gain G at fN = 0.92 can be 5–11 fold higher than those at fN = 2–3. To account for the acoustic attenuation in water, we can obtain effective focal gains Geff by multiplying G with a frequency-dependent attenuation coefficient which is 2.2 × 10−3 dB/(cm × MHz2). Therefore, for the two chosen lenses, we estimate Geff (type I) ≈ 54 and Geff (type II) ≈ 100 at 15-MHz frequency.

Characterization of LGFU

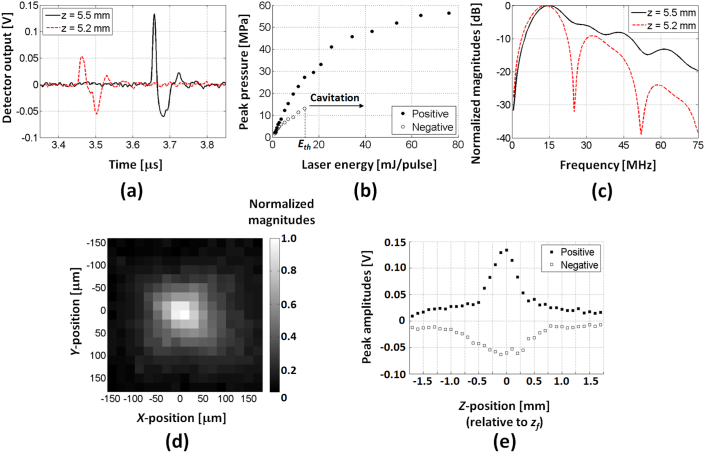
Using the type I optoacoustic lens, we observed strong shock waves at the lens focus, as measured using a single-mode fiber-optic hydrophone (Fig. 1(c)). Experimental waveforms of the LGFU are shown in Fig. 2(a). In principle, optoacoustic pressure waveforms should be close to the time-derivative of the original laser pulse (i.e. Gaussian) due to linear wave propagation in a far-field regime24. However, the measured waveform was highly asymmetric near the focal point (we assume radius-of-curvature of lens ≈ focal length, i.e. zf = 5.5 mm). The asymmetric distortion is caused by nonlinear propagation of the finite-amplitude pulse which leads to the development of pronounced shock front in the positive phase and longer trailing in the negative phase. This is similar to that observed in typical shockwave lithotripsy. We confirmed that the distortion only develops within the focal zone as a symmetric waveform is clearly observed in the pre-focal zone at z = zf − 0.3 = 5.2 mm. The peak positive pressure of the focal waveform of Fig. 2(a) corresponds to ~22 MPa and the negative is ~10 MPa, both of which were determined after excluding the bandwidth effect of the fiber (the detail of hydrophone sensitivity is described in the experimental section). These were obtained for the laser energy of ~12 mJ/pulse on the lens surface (laser fluence = 42.4 mJ/cm2/pulse). Note that the maximum-available laser energy, which does not cause transmitter damage, is 7-fold higher. For the focal waveform shown in Fig. 2(a), we estimated the optoacoustic conversion efficiency25 that is expressed as

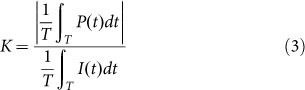graphic file with name srep00989-m3.jpg

where P(t), I(t), and T are the pressure, the optical intensity, and the temporal period ( = 50 ms). For the time-averaged optical intensity of 0.85 W/cm2, we obtain K = 1.4×10−3 Pa/(W/m2). This efficiency is two orders of magnitude higher than those of Cr films (~10−5).

Figure 2. Temporal and spatial characterization of the LGFU.

Figure 2

Open in a new tab

(a) Time-domain waveforms around the lens focus (z = 5.5 mm) and slightly in front of the focal point (z = 5.2 mm); (b) Measured pressure amplitudes versus laser energy at focal point (z = 5.5 mm); (c) Frequency spectra for the waveforms shown in (a).Note that the sensitivity of fiber hydrophone is ~6 mV/MPa (details in the experimental section). The negative amplitudes in (b) could be correctly determined only under a sub-threshold regime of acoustic cavitation. The laser energy for the cavitation threshold is denoted as Eth; (d) Spatial profile of the LGFU on the lateral plane at z = 5.5 mm. The peak amplitudes were normalized, and the image was obtained from the positive peaks; (e) Axial profile along the z-direction. Here, the z-position was relatively defined from z = zf = 5.5 mm, i.e. z < 0 means the fiber hydrophone position between the lens surface and the focus, and z > 0 beyond the focus. Step resolutions are 20 μm in (d) and 100 μm in (e). The laser energy of ~12 mJ/pulse on the lens surface was used for (a), (c), (d), and (e) (laser fluence = 42.4 mJ/cm2/pulse).

Next, we investigated the pressure amplitudes by increasing the excitation laser energy. We measured the focal waveforms from the type I lens, and then determined the peak positive and peak negative pressure. As shown in Fig. 2(b), the positive peak values were saturated to ~57 MPa over the high laser energy level. The saturation is attributed to the measurement reaching the bandwidth limit of the hydrophone. As a result, the highest frequency components of the shock wave cannot be accurately detected. For the negative amplitudes, the peak values could not be accurately determined at the high laser energy level. This is due to involvement of acoustic cavitation on the fiber surface which distorts the negative waveforms. In Fig. 2(b), the measurable negative peak values reach ~13.3 MPa at the laser energy of 14 mJ/pulse which is defined as the threshold laser energy Eth to induce the cavitation. However, by extrapolation, we estimate that >25 MPa can be reached in the negative phase.

Fig. 2(c) shows the corresponding frequency spectra of the LGFU. These experimental spectra include frequency bandwidth effects of the detector. Due to the finite diameter of the optical fiber (125 μm), its sensitivity has a primary peak around 12 MHz and higher-order peaks at 36 and 60 MHz26. These are confirmed for the frequency spectrum of the symmetric waveform at the pre-focal zone (z = 5.2 mm). In contrast, the spectrum at the focal zone (z = 5.5 mm) shows significant enhancement over the high-frequency amplitudes (>15 MHz), which manifests in the time domain as the distorted waveform with steep shock front. This also moved the experimental center frequency fC to ~15 MHz. Due to the strong nonlinear distortion, the higher-order spectral peaks were also observed around 2fC, 3fC, and 4fC.

The high-frequency characteristics of the optoacoustic focusing were further manifested spatially as a tightly focused spot. In Fig. 2(d) and 2(e), we show the focal profiles of the type I lens within the lateral plane and along the axial direction, respectively. We achieved tight focal widths of 75 μm in the lateral and 400 μm in the axial directions which were determined by 6-dB positive amplitudes. For the type II lens with two-fold longer focal length but the similar f-number, the lateral and axial widths broadened slightly to 100 μm and 650 μm because of acoustic attenuation of the high-frequency components over the long propagation distance.

LGFU-induced acoustic cavitation

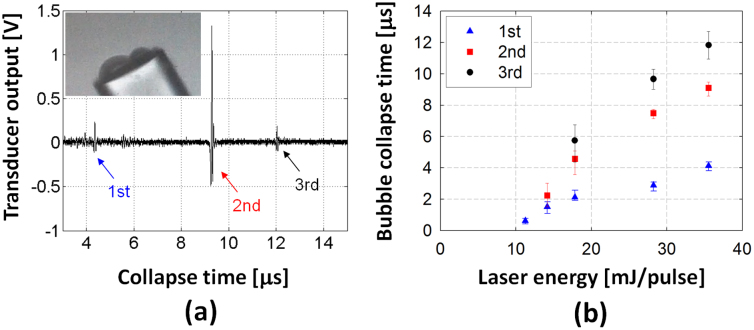
In the experiment performed for Fig. 2(b), the measurable maximum negative pressure was ~13.3 MPa before the cavitation inception. This corresponds to the cavitation threshold on the fiber surface. We visualized the micro-bubbles formed on the fiber surface using a high-speed camera recording as shown in the inset of Fig. 3(a) (a setup shown in Fig. S1). The diameter of the optical fiber is 125 μm. Under a single LGFU pulse, we were able to observe a few bubbles depending on the incident pressure amplitude. In the video, the bubbles existed transiently over a few μs to tens of μs.

Figure 3. Measurement of the collapse time of cavitation bubbles generated by a single LGFU pulse.

Figure 3

Open in a new tab

(a) Individual collapse events are detected in the time-domain. Each arrow (1st, 2nd, and 3rd) indicates the pressure signal emitted from each collapse. The inset shows the cavitation bubbles formed on the fiber surface (fiber diameter = 125 μm). Note that the image was separately taken by the high-speed camera (not exactly the same moment with the signal trace here). (b) The bubble collapse times are plotted as a function of the laser energy. No cavitation signal was observed for lower than 10 mJ/pulse which is the cavitation threshold for the type II lens.

We then characterized the bubble lifetime quantitatively. An example of bubble collapse signal is shown in Fig. 3(a). We used an additional detector (1.5-inch focal length and 15-MHz center frequency; a setup shown in Fig. S2) to measure the collapse signal which was aligned to have the same focus as the optoacoustic lens (type II). The transducer first receives direct acoustic reflection of the LGFU from the tip of the fiber hydrophone. After temporal delay, it is followed by short transient signals as shown in Fig. 3(a) which are emitted from the bubble collapse. Here, we define the temporal delay as the lifetime of the micro-bubbles. The lifetime was <15 μs at the laser energy <40 mJ/pulse. At the cavitation threshold (Eth = 10~11 mJ/pulse), we could only observe a single-bubble collapse. The detection rate of the bubble collapse was <50% for each laser pulse. Just above the cavitation threshold, the rate was increased to almost 100% (i.e. a single bubble forms per a single laser pulse). This is marked as a triangle at 11 mJ/pulse in Fig. 3(b). Then, the number of bubbles increased with the laser energy. The threshold for two bubbles was ~14 mJ/pulse, and for three bubbles ~18 mJ/pulse. Thus, by tuning the laser energy, we can controllably and predictably generate single bubbles.

We confirmed the size of the micro-bubbles formed on the fiber surface using the high-speed camera. However, it was not possible to simultaneously install the separate detector for measuring collapse time. For laser energy of >20 mJ/pulse, the bubble diameter was typically 20~50 μm, as shown in the inset of Fig. 3(a). These bubbles have a collapse time of >10 μs in Fig. 3(b). However, for the micro-bubbles with a shorter range of collapse time (~a few μs), the dimension could not be clearly determined as the camera does not have a sufficient amount of illumination to capture the high-speed image in our configuration.

Micro-scale fragmentation of solid materials

Strong impacts from the shock waves and the acoustic cavitation have been used for fragmentation of kidney stones12,27 and soft tissues10. We demonstrate the use of LGFU as a non-contact mechanical tool for micro-scale fragmentation of an artificial kidney-stone28 and a polymer film (poly[(methylmethacrylate)-co-(Disperse Red 1 acrylate)], Sigma Aldrich; i.e. PMMA-copolymer). First, the model stone was exposed to the focal zone of the type II lens under the laser irradiation of >40 mJ/pulse. Fig. 4(a) shows the treatment results. The single indentation near the top edge of the artificial stone was created by delivering >1000 pulses (or >50 sec). Under this saturated exposure condition, the destroyed spot was 300~400 μm in size. For comparison, we also produced line patterns by short exposure to the LGFU. Here, we translated the stone laterally at ~0.4 mm/sec while fixing the ultrasonic focal spot. This gave <30 pulses delivered at any position (or 1.5 sec dwell time) along the lines of the stone surface. The destroyed line width was ~150 μm. This dimension is an order of magnitude smaller than typically achieved by low-frequency transducers.

Figure 4. Micro-scale fragmentation of the solid materials by the LGFU.

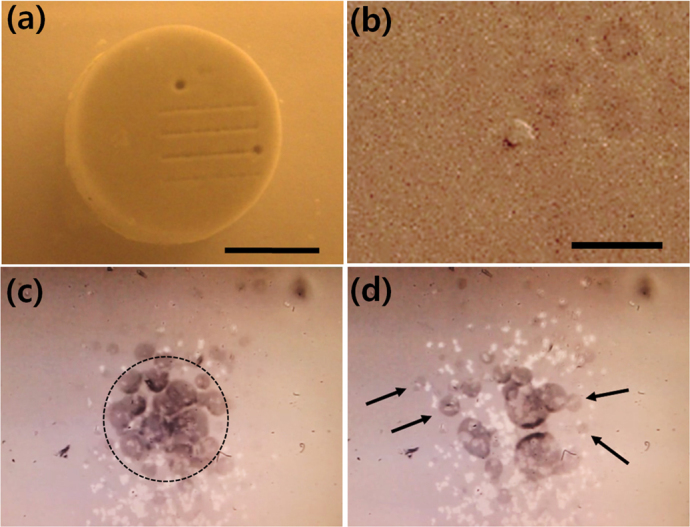
Figure 4

Open in a new tab

(a) The model kidney stone (scale bar = 4 mm) was treated by the LGFU.>1000 pulses were delivered on the single spot on the top (300~400 μm in diameter), and <30 pulses to each position of the line patterns (~150 μm in width); (b) A single micro-hole on the polymer film (dented at the center) was produced by a single LGFU pulse (scale bar = 20 μm). A polymer micro-piece was torn off from the substrate; (c) and (d) High-speed microscopic images of fragmentation process on the polymer-coated glass substrate. The transient bubbles were visualized by the high-speed camera. The focal spot of the LGFU is marked by the dotted circle in (c) (125 μm in diameter). The LGFU spot in (c) moves from the bottom to the top direction, leaving many bright dots which correspond to the polymer-removed regions. The same position on the polymer film is shown in (c) and (d) in the identical scale, but (d) is taken after the continued LGFU exposure of ~1.5 second. The black arrows in (d) indicate the preferential bubble formation along the micro-cracks.

We note that the width of the damage zone can be controlled by changing the laser energy and thereby manipulating the high-pressure area at the focal spot. The damage zone is determined by where the pressure amplitude is higher than a specific threshold level, i.e. depending on the hardness and acoustic impedance of the solid. In this experiment, the widths of the single indentation and the lines were larger than the FWHM of the type II lens (100 μm). This is because the focal pressure was sufficiently high, so that even the surrounding area (wider than the FWHM spot) was subject to pressure exceeding the threshold for the ultrasonic damage. By reducing the LGFU amplitude, we also confirmed that the disrupted dimension can be much smaller than the FWHM. As shown in Fig. 4(b), we could produce a micro-hole on the PMMA film. Here, we used the polymer film coated on the glass substrate for microscopic visualization. The micro-hole was produced by a single LGFU pulse as a micro-scale polymer piece was torn off from the substrate by the highly focused ultrasound. A typical dimension of the micro-hole was 6~15 μm for laser energy of 10~15 mJ/pulse. This is defined as the minimum size of a feature that can be machined using the current LGFU system.

Next, we investigated cavitational contribution in the fragmentation process by using a high-speed recording system on an inverted microscope (supplementary video clip). Fig. 4(c) shows the focal spot image including a cloud of micro-bubbles formed on the polymer film. The LGFU amplitude was ~40 MPa in the peak positive and higher than the cavitation threshold in the negative (laser energy: 20~25 mJ/pulse). As the LGFU-treated spot is scanned from the bottom to the top direction in Fig. 4(c), it leaves many bright dots due to the torn-off polymer micro-pieces. Fig. 4(d) is taken in the same spot but ~1.5 second after the image of Fig. 4(c). The prolonged exposure produced more micro-cracks than in Fig. 4(c). Because the damaged regions including such micro-cracks facilitate the cavitation process (indicated by the black arrows), the fragmentation was expedited by the collapse of the collateral micro-bubbles in contact with the polymer.

Targeted cell removal in high precision

The high-precision micro-machining capability of LGFU was further exploited in a demonstration of single-cell surgery by removing individual cells from substrates and from neighboring cells (supplementary video clip). Fig. 5(a) shows human ovarian cancer cells (2 days after inoculation) before the ultrasound exposure. The cells were cultured on a PMMA-copolymer film that was used as an adhesion layer on the glass substrate. Fig. 5(b) shows the result of LGFU exposure for the laser energy E ≈ 1.2Eth (12~13 mJ/pulse). The LGFU could selectively remove the single cell within the white dotted region. Continuously, the LGFU spot was slightly moved to the adjacent region (black dotted) where the cell-cell junction was formed beforehand. As shown in Fig. 5(c), the single cellular junction was ruptured exactly as intended using the LGFU. Several to tens of LGFU pulses were used to detach the cells, depending on the individual cell shape on the substrate and the formation of cellular network with the surrounding cells. Here, we were able to locally control damage to the cells with <25 μm which is smaller than the FWHM of the focal spot. However, under the higher pressure regime with laser irradiation of >40 mJ/pulse, a cluster of cells (>100 μm in diameter) could be removed.

Figure 5. Targeted cell removal by the LGFU (scale bar = 20 μm).

Figure 5

Open in a new tab

The images were captured from a video clip (supplementary): (a) Cultured ovarian cancer cells (SKOV3) before ultrasound exposure. The white arrow indicates the single cell to be detached by the LGFU; (b) After the LGFU exposure, the single cell was selectively removed (indicated by the white arrow). As a next target, the cell-cell junction is indicated by the black arrow; (c) As the LGFU spot was moved to the black-dotted region, the cellular interconnection was severed.

Discussion

We demonstrated that the focused nano-composite optoacoustic transmitters that can generate sufficient pressure amplitudes to induce shock waves and cavitation at tight focal spots. However, the experimental values reported here are certainly not the ultimate limits of the LGFU approach as these limits depend on lens designs, pulsed lasers for optical excitation, and nano-composite properties. One of the key advantages in the LGFU is the compact dimension of the transmitters. As we have achieved the pressure amplitudes of >50 MPa from the lens with 6-mm diameter, we expect that a few tens of MPa is still available from smaller lenses (<3 mm) which accommodate intra-vascular and intra-operative applications. The output pressure can be further enhanced by improving the composite properties and using lenses with lower f-numbers. This offers potential for use of LGFU transmitters for non-contact mechanical surgery in endoscopic platforms.

As ultrasonic transmitters, nano-scale optical absorbers including CNTs20, planar gold nano-structures19,29, and synthesized gold nano-composites30 have been introduced due to their efficient energy conversion under pulsed laser irradiation and along with their excellent high-frequency performances. Especially, CNT-PDMS composite films have exhibited several-fold higher optoacoustic efficiency than those of typical gold-nanostructures20 over a broad range of frequency up to 120 MHz. Moreover, as the current LGFU requires relatively high laser energy on the order of tens of mJ/pulse, a thermal damage threshold of the source material is an important factor which determines the maximum-available laser energy. We experimentally confirmed that the CNT-PDMS composite film has a damage threshold of 280–300 mJ/cm2 for a 6-ns laser pulse. This is 7–8 fold higher than those of PDMS-coated gold-nanostructures and thin metal films measured in the same configuration.

The LGFU performance, in terms of pressure amplitude, intensity, frequency spectrum, and focal spot sizes, can be controlled externally by the excitation lasers. Here, we used 6-ns in the laser pulse width, 20 Hz in the repetition rate, and tens of mJ in laser energy. For high-pressure amplitudes, narrow pulse widths will be preferred because the far-field optoacoustic pressure is proportional to the time-derivative of the original laser pulse. The narrower temporal pulse also increases the operation frequency resulting in a tighter focus. In our configuration, the spatial-peak pulse-average (SPPA) acoustic intensity of the LGFU waveform shown in Fig. 2(a) was ~4000 W/cm2 for laser energy of 12 mJ/pulse. However, the acoustic intensity decreases to ~8 mW/cm2 as we apply a temporal average (i.e. spatial-peak temporal-average; SPTA). This is due to the low repetition rate of the current laser pulses. For higher-intensity applications, lasers with higher-repetition rates are commercially available with the similar pulse energy (tens of mJ) and temporal width (5~8 ns). For example, a pulse repetition of 2 kHz would result in >2 W/cm2 in the SPTA with laser irradiation of >30 mJ/pulse. This would accumulate significant heat at focal volumes. We note that the heating is an essential mechanism for thermal ablation-based therapy, but this is unfavorable in some other applications such as drug delivery and thrombolysis31,32. Especially in cell environments, a temperature change of only a few °C can cause transformation of the cellular metabolism.

We demonstrated the single-cell removal from the substrates and the surrounding cell networks, as an example of high-precision treatment which cannot be addressed by low-frequency, high-amplitude ultrasound. Leveraging the single-cell precision, we expect that our technique can be extended into delicate tissue structures and fine vasculatures as a means of a non-contact and non-thermal surgery. The LGFU-induced shock can directly break cell adhesion with the surrounding contacts. Moreover, as the micro-bubbles quickly grow and collapse at the targeted spot, these produce localized liquid jet-stream and secondary shock waves. These become strong disruption sources to the cell in contact or from a distance of tens of μm. We also note that the polymer film was used as a cell supporting layer. Therefore, it is also possible to destroy the polymer film underneath the cells which forms physical contacts. As the polymer is fallen off, the cells lose their sites to the substrates. Without the polymer supporting layer, the threshold pressure for the cell detachment will depend on specific adhesion strength of the cells to substrates as well as the substrate conditions to induce the cavitation in terms of acoustic impedance and surface topography.

In conclusion, we presented a new approach to optoacoustically generate high-frequency and high-amplitude focused ultrasound. Unprecedented magnitude of optoacoustic pressure was achieved due to efficient optoacoustic energy conversion enabled by nano-composites of Au-coated CNTs and PDMS, the high-frequency nature of laser pulses, and the high focal gain from the low f-number lenses. The type I lens with 6-mm diameter was shown to generate a peak positive pressure amplitude of >50 MPa within a tight focal width of 75 μm in lateral and 400 μm in axial directions. The cavitation bubbles were tens of μm in dimensions and typical lifetime was shorter than 20 μs. We demonstrated applications of LGFU for non-contact targeted disruption in high precision: micro-scale fragmentation of solid materials and single-cell surgery. The dimensions of the disrupted area could be controlled from 6 μm up to 400 μm depending on the laser intensity and the incident LGFU amplitude. We demonstrated selective removal of a single cell from a cell-culture substrate and from neighboring cells with positional accuracy of <25 μm. The LGFU has great flexibility in terms of transmitter designs and excitation laser choices to control ultrasonic frequencies, amplitudes, and intensities. As a result, we expect that the LGFU will become a versatile modality as a high-accuracy tool for ultrasonic therapy of cells, blood vessels, and tissue layers.

Methods

Material preparation

For growth of CNTs, we prepared fused silica substrates coated by catalyst layers of Fe (~1 nm) and Al2O3 (~3 nm) deposited by using a sputtering system. The fused silica substrates were plano-concave optical lenses (purchased from Edmund Optics, Barrington, NJ) with 5.5-mm radius-of-curvature and 6-mm diameter (type I lens), and 11.46 mm and 12 mm (type II lens), respectively. Multi-walled CNTs were grown in a mixture of C2H4/H2/He in an atmospheric pressure tube furnace at 775°C. This process led to a tangled CNT layer that conformed to the curved surface of the lens. The as-grown CNTs, which have an optical extinction of 60~70%, were then coated by a gold layer of 20 nm. This further enhanced the optical extinction higher than 85% without increasing the overall source thickness significantly. Then, PDMS was spin-coated over the CNT-grown surface at 2000 r.p.m. for 2 minutes, and then cured at 100°C for 1 hour. We previously confirmed that the PDMS infiltrates the CNT network, forming a well-organized nano-composite film20.

Experimental configurations for temporal and spatial characterizations

Figure 1 shows the experimental schematic used for generation and characterization of the focused ultrasound. A 6-ns pulsed laser (Surelite I-20, Continuum, Santa Clara, CA) was used with a repetition rate of 20 Hz. The laser beam initially has 5 mm in diameter. The laser beam was first attenuated by the neutral density filters and then expanded (×5). The collimated beam was illuminated to the transparent (planar) side of the lens. The focused acoustic waves were detected by scanning the single-mode fiber-optic hydrophone (6-μm core and 125-μm cladding in diameters) at the focal zone. Both the lens and the optical fiber were mounted on 3-dimensional motion stages for accurate alignment. The optical output was 3-dB coupled and transmitted to the photodetector. The photodetector has a broad electronic bandwidth over 75 MHz. The hydrophone operation is similar with that reported elsewhere33, but our fiber hydrophone has a significantly smaller active sensing diameter (6-μm) which is suitable for measurement of the highly localized, high-frequency pressure field. Because of the finite aperture of the fiber, diffractive effects typically play a role in the frequency response, and a deconvolution of the waveform is required for such a probe. However, given that the lateral dimension of the LGFU focal spot is smaller than the fiber diameter, the diffractive effects are minimized. Then, the interaction of the incoming waves with the probe can be considered a pure reflection from an acoustically rigid surface for focal measurements. Based on this argument, the probe sensitivity was considered constant (i.e. doubled) over the bandwidth over >15 MHz. By substitution comparison with a calibrated reference hydrophone, we obtained a sensitivity of 4.5 mV/MPa at 3.5 MHz frequency. As this value is the result of ~1.5 fold enhancement due to the low-frequency diffraction effect26, we determined 6 mV/MPa as a final sensitivity of the current fiber-optic hydrophone. Both dc and ac signals were monitored by using a digital oscilloscope (WaveSurfer 432, LeCroy, Chestnut Ridge, NY). The waveforms in Fig. 3(a) are the result of averaging 20 signal traces in time-domain. For the passive detection measurement of the acoustic cavitation, we used a separate piezoelectric transducer with a center frequency of 15 MHz (Model V319, Panametrics, Waltham, MA). The transducer output was directly recorded by using the digital oscilloscope.

High-speed camera monitoring and microscope setup

In order to capture the transient growth of cavitation, we used a high-speed camera (V210, Vision Research, Wayne, NJ, USA). It was integrated into an inverted optical microscope. The experimental schematic and description are provided in the supplementary material. For the polymer fragmentation experiment, the ultrasonic focus and the microscope view were fixed while we moved the polymer film on the microscope stage. For the cell experiment, the cultured cell substrates were moved to a petri-dish including the culture media on the microscope stage aligned with the LGFU. The bright-field and the fluorescence images of the cells were obtained in real time under the LGFU exposure.

Cell culture

SKOV3 human ovarian cancer cells were provided from Dr. Buckanovich's laboratory (University of Michigan, Ann Arbor, MI). They were initially seeded on glass slides spin-coated with PMMA (950K PMMA A4 (4% solid contents) (Microchem, Newton, MA). Then, they were cultured in a Roswell Park Memorial Institute (RPMI) medium with 10% fetal bovine serum and 1% penicillin/streptomycin in a humidified incubator (5% CO2, 37°C). Trypsin/Ethylenediaminetetraacetic acid (EDTA) was used to re-suspend the cells in solution. These cells were diluted to 106 cells/mL and finally plated on the glass substrates spin-coated with the PMMA-based copolymer at 2000 r.p.m. for 30 seconds (from the solution of 4% by weight in tetrahydrofuran). Before the cell inoculation, the copolymer film was dried for 6 hours at 100°C to remove the solvent.

Author Contributions

H.W.B. proposed the concept of the LGFU, designed and fabricated the devices, performed the experiments, and wrote the manuscript. J.G.O. contributed to the CNT growth and the lens fabrication. A.M. produced the fiber-optic hydrophone, contributed to the acoustic characterization of the LGFU, and edited the manuscript. K.-T.L. contributed to the characterization of the LGFU. Y.-C.C. cultured the cells and contributed to the single-cell detachment experiment. A.J.H. gave valuable comments on the CNT properties, and edited the manuscript. The CNT growth was performed in his laboratory. E.Y. gave valuable comments on the cell detachment experiment, and the cell culture was carried out in his laboratory. Z.X. gave valuable comments on the characterization of the LGFU and the acoustic cavitation, and edited the manuscript. Finally, L.J.G. supervised the overall work, contributed to the analysis of the experimental results, and edited the manuscript.

Supplementary Material

Supplementary Information

High-speed video recording of micro-scale fragmentation

Download video file (4.3MB, mov)
Supplementary Information

Targeted removal of single cell

Download video file (4MB, mov)
Supplementary Information

Setups for high-speed camera recording in a microscopic stage and cavitation measurement

srep00989-s3.doc (409KB, doc)

Acknowledgments

The authors would like to acknowledge the support from the National Science grant DMR 1120187, the National Institute of Health, and the University of Michigan. The authors also wish to acknowledge Simone Park for using the high-speed camera. H.W.B. acknowledges the support from the National Institute for International Education through Korean Ministry of Education, Science and Technology.

References

  1. Hamilton M. F. & Blackstock D. T. Nonlinear Acoustics, Acoustical Society of America, Melville (2008). [Google Scholar]
  2. Coussios C. C. & Roy R. A. Applications of Acoustics and Cavitation to Noninvasive Therapy and Drug Delivery. Annu. Rev. Fluid Mech. 40, 395–420 (2008). [Google Scholar]
  3. Herbert E., Balibar S. & Caupin F. Cavitation pressure in water. Phys. Rev. E 74, 041603 (2006). [DOI] [PubMed] [Google Scholar]
  4. Filonenko E. A. & Khokhlova V. A. Effect of acoustic nonlinearity on heating of biological tissue by high-intensity focused ultrasound. Acoust. Phys. 47, 468–475 (2001). [Google Scholar]
  5. Mitragotri S. Healing sound: the use of ultrasound in drug delivery and other therapeutic applications. Nat. Rev. Drug Discov. 4, 255–260 (2005). [DOI] [PubMed] [Google Scholar]
  6. Choi J. J. et al. Noninvasive and localized blood-brain barrier disruption using focused ultrasound can be achieved at short pulse lengths and low pulse repetition frequencies. J. Cerebral Blood Flow Metabol. 31, 725–737 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Krasovitskia B., Frenkelb V., Shohama S. & Kimmela E. Intramembrane cavitation as a unifying mechanism for ultrasound-induced bioeffects. Proc. Natl Acad. Sci. USA 108, 3258–3263 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Tufail Y., Yoshihiro A., Pati S., Li M. M. & Tyler W. J. Ultrasonic neuromodulation by brain stimulation with transcranial ultrasound. Nat. Protocols 6, 1453–1470 (2011). [DOI] [PubMed] [Google Scholar]
  9. Yoo S.-S. et al. Focused ultrasound modulates region-specific brain activity. Neuroimage 56, 1267–1275 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Goldenstedt C., Birer A., Cathignol D. & Lafon C. Blood clot disruption in vitro using shockwaves delivered by an extracorporeal generator after pre-exposure to lytic agent. Ultrasound Med. Biol. 35, 985–990 (2009). [DOI] [PubMed] [Google Scholar]
  11. Lingeman J. E., McAteer J. A., Gnessin E. & Eva A. P. Shock wave lithotripsy: advances in technology and technique. Nat. Rev. Urology 6, 660–670 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Rassweiler J. J. et al. Shock Wave Technology and Application: An Update. Eur. Urol. 59, 784–796 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Kennedy J. E. High-intensity focused ultrasound in the treatment of solid tumours. Nat. Rev. Cancer 5, 321–327 (2005). [DOI] [PubMed] [Google Scholar]
  14. Zhou Y.-F. High intensity focused ultrasound in clinical tumor ablation. World J. Clin. Oncol. 2, 8–27 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Dubinsky T. J., Cuevas C., Dighe M. K., Kolokythas O. & Hwang J. H. High-intensity focused ultrasound: current potential and oncologic applications. Am. J. Roentgenol. 190, 191–199 (2008). [DOI] [PubMed] [Google Scholar]
  16. Xu Z. et al. Controlled ultrasound tissue erosion. IEEE Trans. Ultrason., Ferroelectr., Freq. Contr. 51, 726–736 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Apfel R. E. & Holland C. K. Gauging the likelihood of cavitation from short-pulse, low-duty cycle diagnostic ultrasound. Ultrasound in Med. & Biol. 17(2), 179–185 (1991). [DOI] [PubMed] [Google Scholar]
  18. Buma T., Spisar M. & O'Donnell M. High-frequency ultrasound array element using thermoelastic expansion in an elastomeric film. Appl. Phys. Lett. 79, 548–550 (2001). [Google Scholar]
  19. Hou Y., Kim J. S., Ashkenazi S., O'Donnell M. & Guo L. J. Optical generation of high frequency ultrasound using two-dimensional gold nanostructure. Appl. Phys. Lett. 89, 093901 (2006). [Google Scholar]
  20. Baac H. W. et al. Carbon nanotube composite optoacoustic transmitters for strong and high frequency ultrasound generation. Appl. Phys. Lett. 97, 234104 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. McKenzie A. L. Physics of thermal processes in laser-tissue interaction. Phys. Med. Biol. 35(9), 1175–1209 (1990). [DOI] [PubMed] [Google Scholar]
  22. Hart A. J. & Slocum A. H. Rapid growth and flow-mediated nucleation of millimeter-scale aligned carbon nanotube structures from a thin-film catalyst. J. Phys. Chem. B 110, 8250–8257 (2006). [DOI] [PubMed] [Google Scholar]
  23. Cobbold R. S. C. Foundations of Biomedical Ultrasound, Oxford University Press, New York (2007). [Google Scholar]
  24. Diebold G. J., Sun T. & Khan M. I. Photoacoustic monopole radiation in one, two, and three dimensions. Phys. Rev. Lett. 67, 3384–3387 (1991). [DOI] [PubMed] [Google Scholar]
  25. Pelivanov I. M., Kopylova D. S., Podymova N. B. & Karabutov A. A. Optoacoustic technique for thickness measurement of submicron metal coatings. Laser Phys. 19(6), 1350–1360 (2009). [Google Scholar]
  26. Krücker J. F. et al. Rigid piston approximation for computing the transfer function and angular response of a fiber-optic hydrophone. J. Acoust. Soc. Am. 107, 1994–2003 (2000). [DOI] [PubMed] [Google Scholar]
  27. Bailey M. R. et al. Cavitation in shock wave lithotripsy. Fifth International Symposium on Cavitation, Cav03-OS-2–1–006, Osaka, Japan (2003). [Google Scholar]
  28. Pishchalnikov Y. A. et al. Cavitation bubble cluster activity in the breakage of kidney stones by lithotripter shockwaves. J. Endourol. 17, 435–446 (2003). [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. O'Donnell M. et al. Optoacoustic generation of high frequency sound for 3-D ultrasonic imaging in medicine. Eur. Phys. J. Special Topics 153, 53–58 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Wu N. et al. High-efficiency optical ultrasound generation using one-pot synthesized polydimethylsiloxane-gold nanoparticle nanocomposite. J. Opt. Soc. Am. B 29(8), 2016–2020 (2012). [Google Scholar]
  31. Frenkel V. & Li K. C. P. Potential role of pulsed-high intensity focused ultrasound in gene therapy. Future Oncol. 2, 111–119 (2006). [DOI] [PubMed] [Google Scholar]
  32. Sakharov D. V., Hekkenberg R. T. & Rijken D. C. Acceleration of fibrinolysis by high-frequency ultrasound: the contribution of acoustic streaming and temperature rise. Thromb. Res. 100, 333–340 (2000). [DOI] [PubMed] [Google Scholar]
  33. Parsons J. E., Cain C. A. & Fowlkes J. B. Cost-effective assembly of a basic fiber-optic hydrophone for measurement of high-amplitude therapeutic ultrasound fields. J. Acoust. Soc. Am. 119, 1432–1440 (2006). [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

High-speed video recording of micro-scale fragmentation

Download video file (4.3MB, mov)
Supplementary Information

Targeted removal of single cell

Download video file (4MB, mov)
Supplementary Information

Setups for high-speed camera recording in a microscopic stage and cavitation measurement

srep00989-s3.doc (409KB, doc)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES