Multivariate Gene Selection and Testing in Studying the Exposure Effects on a Gene Set

Abstract

Studying the association between a gene set (e.g., pathway) and exposures using multivariate regression methods is of increasing importance in genomic studies. Such an analysis is often more powerful and interpretable than individual gene analysis. Since many genes in a gene set are likely not affected by exposures, one is often interested in identifying a subset of genes in the gene set that are affected by exposures. This allows for better understanding of the underlying biological mechanism and for pursuing further biological investigation of these genes. The selected subset of “signal” genes also provides an attractive vehicle for a more powerful test for the association between the gene set and exposures. We propose two computationally simple Canonical Correlation Analysis (CCA) based variable selection methods: Sparse Outcome Selection (SOS) CCA and step CCA, to jointly select a subset of genes in a gene set that are associated with exposures. Several model selection criteria, such as BIC and the new Correlation Information Criterion (CIC), are proposed and compared. We also develop a global test procedure for testing the exposure effects on the whole gene set, accounting for gene selection. Through simulation studies, we show that the proposed methods improve upon an existing method when the genes are correlated and are more computationally efficient. We apply the proposed methods to the analysis of the Normative Aging DNA methylation Study to examine the effects of airborne particular matter exposures on DNA methylations in a genetic pathway.

1 Introduction

Gene set and pathway analysis has attracted increasing interest in the last few years. Examples include Gene Set Enrichment Analysis [19] and extensions [4]. Analysis of a biologically meaningful set of genes that operate together in a recognizable process is both more powerful and interpretable than individual gene analysis. Since many genes in a gene set are likely not affected by exposures, one is often interested in identifying a subset of genes in the gene set that are affected by exposures. This allows for understanding the underlying biological mechanism and pursuing in-depth biological investigation of these genes. The selected subset of “signal” genes also allows for a more powerful test for the association between the gene set and exposures.

This paper is motivated by studying the effects of exposures to multiple airborne particulate matters on DNA methylation patterns in the Normative Aging Study (NAS) cohort [1], [2]. The primary goals of this study are: (1) to select a subset of genes in a pathway, e.g, the asthma pathway, that are associated with particulate matter exposures, e.g., black carbon and sulfate, while adjusting for covariates, e.g., age; (2) to test whether the DNA methylation pattern in the genetic pathway is associated with particulate matter exposures while controlling for confounders.

Two types of gene set analysis have been developed in the literature. One type of analysis focuses on studying the effects of the genes in a gene set on a single outcome [6,12,13]. Another type of analysis focuses on using the genes in a gene set as outcomes and studying the effects of categorical exposure groups on the gene set [5, 20]. [10] proposed the GlobalANCOVA to test for the effects of groups on a gene set while adjusting for confounders. This approach is based on individual gene analysis, and the individual regression results are then aggregated into a residual sum of squares measure. None of these papers considers gene selection. In this paper, we are interested in using the genes in a gene set as outcomes and identifying a subset of genes in the gene set that are associated with discrete or continuous exposures while adjusting for covariates. We are also interested in developing a powerful global test for testing the effects of exposures on the whole gene set while adjusting for covariates and accounting for variable selection.

There has been limited work on jointly selecting multivariate genes that are associated with multiple exposures. For gene expression analysis, common approaches are based on individual gene analysis and then control for multiple comparisons, e.g., using false discovery rate [3]. Examples include [7, 22]. Analyses based on individual-gene approaches have a few drawbacks. First, in the presence of weak signals, individual testing procedures can yield low power to detect exposure effects after correcting for multiple comparisons. Second, genes that are correlated with the exposure jointly with other genes but are marginally uncorrelated with the exposure will not be detected in individual gene analysis. Third, these methods do not test for the exposure effects on the whole pathway, and do not select a subset of genes that are jointly affected by exposures. [25] proposed sparse linear discriminant analysis for testing a binary exposure effect on gene expressions in a genetic pathway and for performing gene selection. However, this approach is not applicable to multiple continuous exposures and does not adjust for confounders.

The study of exposure effects on gene expression/DNA methylation pattern in a genetic pathway requires the use of statistical tools that account for both multivariate outcomes and multiple exposures. Canonical Correlation Analysis (CCA) is a well established supervised method for associating two sets of variables by maximizing the correlation of a linear combination of outcome variables and a linear combination of exposure variables. However, this method does not perform variable selection. Hence, when there exist a subset of outcome variables in a gene set that are unrelated to the exposures, which is often the case in many gene sets, traditional CCA that includes all the genes suffers from loss of power to detect the association between the exposures and the multi-outcome pathway.

Several authors recently developed CCA based shrinkage methods that incorporate variable selection ([16], [23] and [21]). These methods simultaneously select variables and estimate model parameters. However, they ignore the correlation among the outcome variables in the gene set and the correlation among exposure variables. As shown in the simulation studies, when such correlations are present, as commonly the case in practice, such approaches result in biased results. In addition, implementation of these methods involves maximizing a constrained objective function and is hence often computationally intensive. [23] also proposed a global test for the association between two sets of variables using the estimated shrunk canonical correlation. As we show in the paper, this approach often lacks good power, parallel to the classical fact that using R² as a test statistic in linear regression for association is subject to poor power in practice.

In this paper, we develop two simple and computationally efficient sparse outcome selection CCA-based methods, which select outcomes by maximizing the correlation between a linear combination of the selected multiple outcomes in a gene set and a linear combination of exposure variables. We here only consider selection of outcomes and do not consider selection of exposure variables, as in our application, the number of exposure variables is small while the number of genetic outcomes in a pathway is often large. Our approaches account for the between-outcome correlation in the gene set while performing variable selection. The two proposed methods differ in how they select outcomes, although they both use the traditional CCA to estimate the effects once outcomes are selected. Both methods require estimation of a tuning parameter that controls for the number of selected genes and the goodness of fit. We examine three model selection criteria for choosing the number of selected genes: predicted correlation, Bayesian Information Criterion [15], and Correlation Information Criterion (CIC) that we develop in this paper. We conduct extensive simulation studies to compare our methods with an existing method for different correlation structures and show our methods outperform the existing method in a good number of settings.

In addition, building upon these two outcome selection CCA methods, we propose a permutation-based testing procedure that uses the Wilks’ Lambda statistic [17] to test for the effects of the exposures on the overall gene expression/methylation pattern in a gene set while accounting for variable selection. We show via simulations that this testing procedure is more powerful than that without variable selection and the existing estimated canonical correlation based test. We apply the proposed methods to analyze the Normative Aging DNA methylation study to investigate the effects of exposure to airborne particulate matters on gene methylations in the asthma pathway.

The rest of the paper is organized as follows. In Section 2, we describe the two sparse outcome selection methods for studying the effects of exposures on multiple outcomes in a genetic pathway, and a global testing procedure of the exposure effects on a gene set. In Section 3, we present a simulation study to compare the performance of the proposed methods with an existing method. We also present a simulation study of the power of the proposed testing procedure. Section 4 applies the proposed methods to the Normative Aging data to study the effects of black carbon and sulfate particles on DNA methylations in the asthma pathway, followed by discussions in Section 5.

2 Methods

Suppose we have n observations, with each observation having m outcome variables y, e.g., DNA methylations in a genetic pathway, and p exposure variables x, e.g., black carbon and sulfate. Later we discuss how to adjust for covariates, e.g., age. Our interest lies in studying the association between methylation patterns in a pathway and exposures accounting for the fact that many genes in the pathway are not affected by exposures. We discuss two methods to model the pathway effect using a composite methylation score that is a linear combination of the individual gene methylation scores. That is, the pathway effect is characterized using b^Ty, where b_m×1 is a vector of loadings. The exposure effect is also modeled linearly using a^Tx with a_p×1 a loading vector. The proposed methods attempt to find the best loading vectors a and b to maximize the correlation between a^Tx and b^Ty while allowing for selecting a subset of y. In other words, if a gene j is not associated with exposures in the presence of other genes, its loading a_j is set to be 0.

CCA [9] is a method that relates two sets of variables by solving the following optimization problem

$$\underset{\mathit{a},\mathit{b}}{\text{max}}\mathit{\text{cor}}({\mathit{a}}^T\mathit{x},{\mathit{b}}^T\mathit{y}),\mathrm{s}.\mathrm{t}.{\mathit{a}}^T{\mathit{S}}_{XX}\mathit{a}={\mathit{b}}^T{\mathit{S}}_{YY}\mathit{b}=1,$$ (1)

where S_XX, S_YY are the estimated covariance matrices of x and y. In other words, it estimates the loading vectors a and b so that the correlation between the linear combinations a^Tx and b^Ty is maximized. The resulting correlation ρ̂ = cor(â^Tx, b̂^Ty) is the estimated canonical correlation. CCA can be used to estimate additional loading vectors associated with subsequent canonical correlations in the same manner, by constraining them to be uncorrelated with the previous loadings a and b. We here are mainly interested in the loading vectors associated with the largest canonical correlation.

Our goal is to estimate the vector of outcome loadings b allowing for sparsity, in accordance with the expectation that most gene-specific methylations in a pathway are not affected by the exposures. Denote by ℳ = {y_j|b_j ≠ 0} the set of variables having nonzero loadings. We are interested in estimating this signal set. The CCA estimators of a and b are generally not sparse, i.e., the estimated loadings for all genes in the pathway are non-zero. In other words, CCA does not perform variable selection. We are interested in incorporating variable selection in CCA. Note that for a fixed sample size, the estimated canonical correlation becomes larger as the number of variables increases even if the added genes are not associated with exposures. Thus, using the canonical correlation as a criterion for variable selection may lead to selection of genes that are not affected by the exposures, i.e. overfitting. We propose the following outcome selection CCA and model selection criteria to overcome these problems.

2.1 Sparse Outcome Selection CCA

The Sparse Outcome Selection (SOS) CCA starts with a screening step, in which a set of genes that are individually most correlated with the exposure variables is retained and the remaining genes having low correlation with exposures are discarded. The threshold for variable selection is determined using a model selection criterion. At the second step, CCA is applied to the selected genes and the exposure variables to calculate an optimal linear combination of exposures and an optimal linear combination of the selected outcome variables that maximizes their correlation. Specifically, SOS-CCA is a two step procedure:

1. Screening: regress each individual gene methylation score on the exposures as

   $$y_{ij}={\mathit{x}}_i^T{\mathit{\beta }}_j+{\epsilon }_{ij}\text{ for }j=1,\dots ,m,$$ (2)

   where y_ij denotes the methylation score of the jth gene for the ith individual. We compute the individual P-values P₁, … , P_m of the F-tests for testing the individual hypotheses H_0j : β_j = 0 for each gene j (j = 1, … m). Given a threshold λ, the genes are then selected if their corresponding P-values are smaller than λ. The screening step results in a set of selected outcomes ℳ_λ for a given threshold λ as Y_λ = (y_λ,(1), …, y_λ,(mλ))^T, which contains the methylation scores of the m_λ selected genes.

2. Estimation: Given (x, Y_λ), calculate the selected outcome loading vector b_λ and the exposure loading vector a_λ by solving the CCA optimization problem (1) for the matrices x and Y _λ. For an outcome y_j that is not selected by the screening step, set b_j = 0.

As shown in our simulation studies, this simple SOS-CCA approach is advantageous over other methods when the outcomes are both marginally associated with the exposures, and are also associated with each other.

2.2 Step - Forward CCA

The step-forward CCA (step-CCA) is a supervised procedure that sequentially selects outcome variables by adding a new outcome to an existing set of outcomes to maximize the canonical correlation between the new outcome set and the exposures. The procedure terminates once a model selection criterion achieves an optimal value. Once a final subset of response variables is selected, the loading vectors are estimated using CCA on the exposures and the selected outcomes, as SOS-CCA does. To summarize, step-CCA proceeds as follows:

1. Greedy (Sequential) selection:

   1. At the first step, for each gene methylation score j (j = 1, … , m), we calculate the canonical correlation of (y_j, X), where y_j is the vector of gene methylation scores for the j-th gene, and X is the exposure matrix. For each gene y_j (j = 1, … m), we obtain an estimated canonical correlation ρ̂_1j, j = 1, … , m. In this step, the canonical correlation is equivalent to the R measure from the linear regression of y_j on exposures. Denote the first selected gene by y₍₁₎, where $(1)=\underset{j}{\text{argmax}}{\widehat{\rho }}_{1j}$.
   2. At the (k + 1) step, suppose that k genes have already been selected. Denote the matrix of the selected gene methylation scores by Y_(k) = {y₍₁₎, … , y_(k)}^T. For each j ∉ {(1), … , (k)}, denote the jth new set {y_j ∪ Y_(k)}. We compute the estimated canonical correlation of (y_j ∪ Y_(k), x), ρ̂_k+1,j. The (k+1)-th selected gene is y_(k+1), where $(k+1)=\underset{j}{\text{argmax}}{\widehat{\rho }}_{k+1,j}$.

   We stop selecting genes when a pre-specified model selection criterion is optimized.

2. Estimation: Let ℳ_(K) be the set of outcome variables selected at the final step and let Y_(K) be the corresponding response matrix. The genes that were not selected are assigned with zero loadings. Then maximize the CCA objective function (1) with the selected genes Y_(K) and X to obtain the loading vectors b_(K) and a_(K).

The key properties of SOS-CCA are that outcomes are marginally selected and loadings are then estimated using CCA. In contrast, step-CCA selects each outcome sequentially while accounting for the previously selected outcomes, and then estimates the loadings using CCA. Step-CCA hence has an advantage when some genes are associated with exposures conditional on other genes, i.e, in the presence of non-marginal gene effects. At the same time, it is more prone to stochastic error, as is well known for stepwise methods.

2.3 Model Selection Criteria

The two proposed sparse outcome selection methods require selecting a subset of genes according to some model selection criterion. For instance, SOS-CCA generates a subset of genes ℳ_λ according to the cutoff value λ based on the P-values of individual genes. The optimal marginal p-value cutoff λ hence needs to be estimated. Step-CCA sequentially selects genes that increase the canonical correlation of a set of outcomes ℳ_(k) and exposures. However, as mentioned earlier, for finite samples, the canonical correlation increases with every addition of a variable even if that variable is independent of exposures. A stopping rule for assessing the need of adding variables is thus required.

Denote a set of selected genes by ℳ̃, and Ỹ the corresponding selected outcome matrix, and suppose it contains m̃ genes. We considered the following selection criteria for each set of selected outcome variables ℳ̃:

• Predicted correlation: Suppose a sparse outcome selection method provides the estimated loading vectors â and b̂ for (X, Ỹ). The predicted correlation is

  $$\widehat{\mathit{\text{cor}}}({\widehat{\mathit{a}}}^T{\mathit{X}}_{\mathit{\text{new}}},{\widehat{\mathit{b}}}^T{\mathit{Y}}_{\mathit{\text{new}}}),$$ (3)

  where (X_new, Y_new) is a validation data set of new observations. The best set of the outcomes is the one that maximizes this score.
• Bayesian Information Criterion (BIC): The Bayesian information criterion for correlation estimation ([15]) is

  $$n\mathit{\text{log}}(1-{\widehat{\rho }}^2)+(\tilde{m}+p)\mathit{\text{log}}(n),$$ (4)

  where n is the number of observations and ρ̂ is the estimated canonical correlation cor(â^T x, b̂^T ỹ). The best set of outcomes minimizes this score.
• Correlation Information Criterion (CIC): We propose the CIC criterion as

  $${\widehat{\rho }}^2-\mathit{\text{log}}\left\{1+\frac{(e-1)(\tilde{m}+p)}{n}\right\}.$$ (5)

  The best set of outcomes is the one that maximizes this score. This is motivated by the following.

  For fixed n, as the dimensions p and m̃ of X and Ỹ increase, their canonical correlation ρ increases as well, even if X and Ỹ are independent [11, 18]. We here try to remove this artifact by defining the model selection criterion as maximizing ρ̂² − f{ρ̂²(Σ_XY = 0)}}, where ρ̂ is the estimated canonical correlation, and ρ̂( Σ_XY = 0) is the estimated canonical correlation under independence between the outcomes and the exposures (i.e. the background artifact caused by the fact that the estimated canonical correlation increases as the number of variables increases), and f(·) is some monotone function. In other words, the penalty term of CIC tries to approximate some monotone function of the positive truly-null correlation ρ̂(Σ_XY = 0) found in finite samples. This approximation works better when the number of exposures is small, as in our setting, but as the number of exposure variables increases, the quality of the approximation becomes worse.

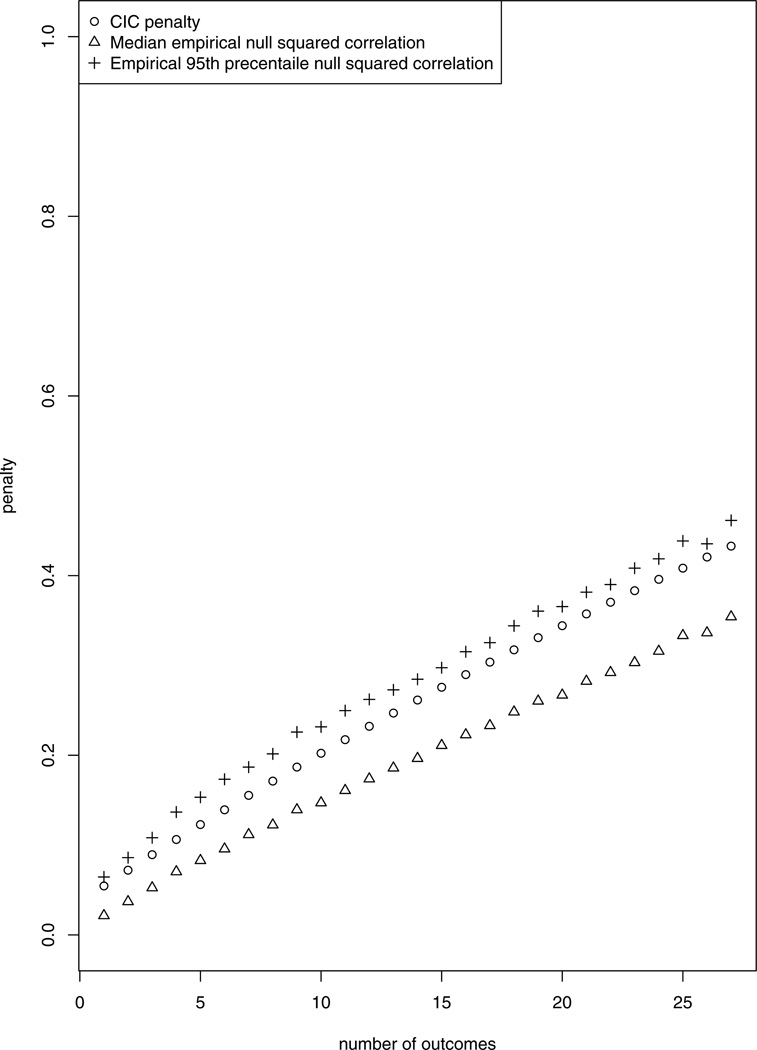
  To empirically demonstrate how well the approximation is, mimicking the asthma pathway, Figure 1 shows the median and the 95th percentile of the empirical distribution of the estimated squared canonical correlation between two normally distributed exposure variables and up to 27 normally distributed outcomes when the outcomes and the exposures are independent, based on 1000 simulations. One can see that the CIC penalty term closely approximates the empirical 95th percentile of the estimated squared canonical correlation under independence between X and Y.

For SOS-CCA, the thresholded P-value serves as the tuning parameter; while for step-CCA, the number of outcomes serves as the tuning parameters. Note that the predicted correlation criterion (3) uses half the data for model fitting and the other half for model selection, while BIC (4) and the CIC (5) use all of the data for both model fitting and model selection. Another alternative model selection criterion is cross validation using predicted correlation as an objective function. It is computationally time consuming. We do not consider it in this paper.

Fig. 1.

The CIC penalty (circles) and the median (triangles) and 95th percentile (crosses) of the empirical distribution of the square of the estimated canonical correlation from 1000 simulations conducted under independence between normally distributed outcomes and exposures. The number of samples is 92, the number of exposure variables is 2 and the number of outcomes is between 1 to 27, mimicking the asthma pathway.

2.4 Testing for the association between the exposure and the pathway

Besides selecting genes in a pathway to maximize the overall pathway-level correlation with exposures, in our application, we are also interested in testing the null hypothesis of no overall association between DNA methylations in a pathway and exposures accounting for gene selection. We here propose a permutation test based on the Wilks’ Λ test statistic.

Let S be the estimated covariance matrix for all variables, i.e. S = cov([X, Y]). Let S_XX and S_YY be the estimated covariance matrices of X and Y accordingly, such that:

$$\mathit{S}=\left(\begin{array}{cc}{\mathit{S}}_{XX}& {\mathit{S}}_{XY}\\ {\mathit{S}}_{YX}& {\mathit{S}}_{YY}\end{array}\right)$$

Let |X| be the determinant of a squared matrix X. The Wilks’ Λ test statistic is given by:

$$\Lambda =\frac{|\mathit{S}|}{|{\mathit{S}}_{YY}||{\mathit{S}}_{XX}|}$$ (6)

This statistic tests the null hypothesis of no association between X and Y. Its distribution, after an appropriate one-to-one transformation, can be approximated by a χ² distribution with pm degrees of freedom [17]. Note that the χ² approximation was derived under a normally distributed data assumption, and it may not work as well for, say, skewed distributions.

In order to test for the association between the exposures X and the genetic outcomes Y in a pathway accounting for gene selection, we first take the selected set of genes Ỹ estimated by any of the sparse outcome selection methods, and calculate the Wilks’ Λ statistic using the resulting subset of genetic outcomes and exposures. Denote this statistic by Λ_X,Ỹ and its observed value by Λ_X,Ỹ,obs. Since the distribution of the statistic depends upon the dimension of the matrices, we calculate a standardized statistic using the tail-probability of Λ_X,Ỹ,obs, calculated using the χ² approximation. We denote the standardized statistic by T_{X, Ỹ} = Prob(Λ_X,Ỹ ≥ Λ_X,Ỹ,obs). To account for variable selection in performing the test, we then permute the rows of the X matrix B times. For each permutation b = 1, … , B, we apply a proposed sparse outcome selection method on the permuted exposure matrix X_b and Y. Note that Y is the original, not the reduced/selected, outcome matrix. We calculate the resulting statistic T_b. Finally, the P-value for the test of the null hypothesis of no association between X and Y is given by $P-\text{value}=\frac{1}{B}{\Sigma }_{b=1}^Bℐ(T_b\le T_{X,\tilde{Y}})$.

[23] proposed calculating the P-value for the global effect based on permutation as well, but using the canonical correlation as the test statistic. Simulation results presented in Section 3 show that this permutation strategy is considerably less powerful than the approach based on Wilks’ Λ. This parallels the classical results in multiple linear regression, where testing for the effects of X on y is based on a F-test instead of R², as there is limited power using R² because correlation is more sensitive to noises.

The results discussed above assume there are no covariates. In many applications, one needs to study the exposure effects on outcomes while adjusting for confounders. We discuss here how to extend the results to handle this situation. Denote a set of additional covariates as X_c and the set of exposure variables of interest as X_e. To test for the association between X_e and Y while controlling for X_c, we propose partialling out X_c from both the outcomes and the exposures before performing the proposed sparse outcome selection methods.

Specifically, we regress each of the outcome variables y_j on X_c and calculate the residuals and denote them as ε_Y|Xc. Similarly, we regress each of the exposure variables x_e on X_c and calculate the residuals and denote them as ε_Xe|Xc. Then use ε_Y|Xc and ε_Xe|Xc as Y and X and proceed with the outcome selection methods.

3 Simulation studies

3.1 Small m simulations

We first consider the case when the number of outcomes m is small. We simulated X and Y matrices from a multivariate normal distribution by specifying the covariance matrix of the joint distribution of x and y. This allows us to gain insight into the performances of the proposed methods when different plausible scenarios of associations in the data are present. All the variables were sampled with mean 0 and variance 1. We assumed p = 2 exposure variables x’s and m = 13 outcomes variables y’s. Among the 13 outcomes, 3 were simulated to be associated with x’s at different degrees. Hence three y’s and 2 X’s were simulated using multivariate normal distributions with covariances given below. The rest 10 outcomes were simulated as independent standard normal random variables as noise outcomes. This simulation setting has a relatively small number of outcomes, and is designed mainly to demonstrate the properties of the sparse outcome selection methods.

Specifically, data sets were generated from three different covariance matrices with 2 exposures and 3 outcomes, and then 3 outcome variables were augmented by additional 10 nuisance outcome variables. From each covariance matrix, we sampled 100 observations and applied the two methods, SOS-CCA and Step-CCA. We generated 200 simulated data sets for each scenario. We also compared the performance of these methods to the sparse CCA method proposed by [24]. We denote this last method as PMA-CCA. The PMA-CCA optimizes the CCA objective function (1) by assuming that the outcomes are independent, i.e. Σ_YY = I_m×m, and the exposures are independent, i.e., Σ_XX = I_p×p, where Σ_XX and Σ_YY are the covariance matrices of the x and y variables, respectively, and I is an identity matrix with given dimensions. To perform variable selection, PMA-CCA imposes the constraint ||b||₁ ≤ c, where ||·||₁ represents the ℒ₁ norm and c is a user-defined constant. This constrained maximization is implemented through the use of an iterative algorithm that penalizes the singular value decomposition of a matrix. Note that c can be viewed as a tuning parameter and can be selected using any of our proposed model selection criteria. Although the PMA-CCA is a flexible method that can perform variable selection of both x and y by penalizing both a and b, motivated by our DNA methylation data example, we applied it by only penalizing b, in order to parallel our proposed step-CCA and SOS-CCA methods, i.e., we do not perform variable selection of x’s. We used the three model selection criteria discussed in Section 2.3 for comparing the methods.

The three covariance matrices used for the simulations were:

$$\begin{array}{ccc}\begin{array}{ccccc}{X}_1& X_2& Y_1& Y_2& Y_3\end{array}& \begin{array}{ccccc}{X}_1& X_2& Y_1& Y_2& Y_3\end{array}& \begin{array}{ccccc}{X}_1& X_2& Y_1& Y_2& Y_3\end{array}\\ \left(\begin{array}{ccccc}1& 0& 0.4& 0.4& 0.4\\ 0& 1& 0.4& 0.4& 0.4\\ 0.4& 0.4& 1& 0.3& 0.3\\ 0.4& 0.4& 0.3& 1& 0.3\\ 0.4& 0.4& 0.3& 0.3& 1\end{array}\right)& \left(\begin{array}{ccccc}1& 0& 0.4& 0.4& 0\\ 0& 1& 0.4& 0.4& 0\\ 0.4& 0.4& 1& 0.6& 0.6\\ 0.4& 0.4& 0.6& 1& 0.6\\ 0& 0& 0.6& 0.6& 1\end{array}\right)& \left(\begin{array}{ccccc}1& 0.3& 0.4& 0& 0\\ 0.3& 1& 0& 0.4& 0\\ 0.4& 0& 1& 0.6& 0\\ 0& 0.4& 0.6& 1& 0\\ 0& 0& 0& 0& 1\end{array}\right)\\ \text{covariance }1& \text{covariance }2& \text{covariance }3\end{array}$$

The performance of each method is evaluated by the proportion of the simulations in which the “true model” was selected, where the “true model” is the set of y variables that have theoretically non-zero loadings in the loading vector b in the model used for simulating the data. In other words, the true model corresponds to the asymptotic limits of the loadings when the sample size goes to infinity. It can hence be identified by maximizing the expected CCA objective function in (1) with S_XX and S_YY in the constraints replaced by the true covariance matrices. We also compare the numbers of variables that are selected as false positives and false negatives, which are the numbers of nonzero (zero) estimated loadings that are in fact zeroes (non-zeroes) respectively.

Table 1 shows the simulation results for the three covariance structures based on 200 simulations: the proportion of the true models, the numbers of variables that were chosen as false positives (FP) and false negatives (FN) using each of the three methods: SOS-CCA, step-CCA and PMA-CCA and each of the proposed model selection criteria: predicted correlation, BIC and CIC).

Table 1.

Simulation results comparing different sparse outcome selection methods using different model selection criteria for the three correlation settings when m is small (m = 13). For each of the three correlation matrices, the proportion of times out of 200 simulations in which the true model was selected (T), the mean number of variables that were false positives (FP) and false negatives (FN) are reported. The population CCA loadings of the outcome variables for the three correlation structures are b₁ = (0.58, 0.58, 0.58, 0, …, 0)^T, b₂ = (0.54, 0.54, −0.65, 0, …, 0)^T, b₃ = c(0.71, −0.71, 0, …, 0)^T respectively.

		cov1			cov2			cov3
Select	method	T	FP	FN	T	FP	FN	T	FP	FN
	Step-CCA	0.68	0.36	0.00	0.63	0.46	0.00	0.70	0.36	0.00
BIC	SOS-CCA	0.88	0.11	0.01	0.06	0.15	1.09	0.83	0.16	0.04
	PMA-CCA	0.93	0.06	0.02	0.01	0.06	1.15	0.04	0.63	0.79
	Step-CCA	0.65	0.43	0.00	0.83	0.18	0.00	0.62	0.48	0.00
CIC	SOS-CCA	0.88	0.12	0.00	0.07	0.34	0.94	0.79	0.23	0.02
	PMA-CCA	0.94	0.07	0.00	0.00	0.53	0.94	0.04	1.61	0.70
	Step-CCA	0.53	1.00	0.14	0.74	0.80	0.00	0.70	0.79	0.00
correlation	SOS-CCA	0.56	1.21	0.04	0.04	6.00	0.02	0.34	2.10	0.00
	PMA-CCA	0.38	1.96	0.00	0.01	2.57	0.81	0.02	2.92	0.62

In the first scenario (covariance 1), the true canonical correlation model has non-zero loadings for Y₁, Y₂ and Y₃. Because these three variables are equally marginally correlated with the exposure x, all methods are expected to perform similarly well in this scenario. The simulation results show that all the three methods indeed performed well. When the tuning parameter was selected using CIC and BIC, the marginal methods PMA-CCA and SOS-CCA performed better than step-CCA and almost always selected the true models. Step-CCA usually overfitted. When predicted correlation is used as the selection criterion, all the methods performed worse and overfitted significantly, with PMA-CCA having the worse performance. CIC and BIC had similar performance and they are significantly better than using predicted correlation.

In the second scenario (covariance 2), Y₃ is marginally uncorrelated with the x’s, but jointly with Y₁ and Y₂, Y₃ is correlated with the x variables. That is, Y₃ contributes to the canonical correlation between x and y through its correlation with Y₁ and Y₂. Hence, the true canonical correlation model contains non-zero loadings for Y₁, Y₂ and Y₃. Here, step-CCA is expected to detect all three variables. The other methods, SOS-CCA and PMA-CCA are expected to detect only Y₁ and Y₂ in theory, since they are all based on marginal variable selection, and Y₃ is marginally uncorrelated with the exposure variables. The simulation results support the theoretical results. In this scenario, step-CCA using CIC yielded the best results than using BIC. Prediction correlation based selection remained to have the worse performance.

In scenario 3 (covariance 3) the true model contains solely Y₁ and Y₂. The correlation between Y₁ and Y₂ is high and the marginal correlation of Y₂ with x is equal to that between Y₁ and x. Further, X₁ is correlated with X₂. The third outcome Y₃ is a pure noise variable and is not associated with the rest of the variables. In this case, both step-CCA and SOS-CCA performed well and detected both Y₁ and Y₂ whereas PMA-CCA usually detected only one of Y₁, Y₂. This is because PMA-CCA assumes the Y ’s are independent, but here Y₁ and Y₂ are strongly correlated. In fact, under the Σ_YY = ℐ_3×3 assumption assumed by PMA-CCA, the theoretical CCA results will yield a non-zero loading for only one of Y₁, Y₂. Step-CCA selected more false positives than SOS-CCA and a yielded smaller proportion of true model selection. The results using CIC and BIC are similar and better than those using prediction correlation.

These results show that step-CCA is robust for different specifications of outcome effects. The marginal variable selection method (SOS-CCA) and the working independence variable selection method (PMA-CCA), which ignore within-outcome and within-exposure correlations, fail to detect the underlying joint response pattern if their assumptions are violated. On the other hand, step-CCA is not as stable as SOS-CCA and PMA-CCA in the presence of nuisance variables and correlation among Y ’s. It is more likely to overfit. When outcomes and exposures are marginally correlated, the marginal methods such as SOS-CCA are more stable, i.e., they select less nuisance variables than step-CCA. PMA-CCA is unable to detect associations between a Y with x′s that are due to correlation among the Y ’s. BIC and CIC overall have a similar performance. Using prediction correlation as a model selection criterion is more likely to cause overfitting.

3.2 Large m simulations

To assess the performance of the proposed sparse association methods in the presence of a large number of outcomes, we simulated data with the sample size n = 100, p = 2 exposure variables and m = 102 outcomes. The simulations extend the small m simulations. In the small m simulation, we considered 3 outcome variables with various correlation structures among the outcomes and between the exposures and the outcomes. In each of the large m simulations, we divided outcomes in m/3 sets of 3 outcomes per set. Each set has the same correlation structure to that in the small m scenario. Only a single set of three outcomes is correlated to the exposures, in a similar manner to that in the small m scenario. In other words, we increased the number of “nuisance” outcomes, but created some correlations between these nuisance outcomes, as they could potentially affect the performance of different methods. The number of simulations were 200. The results are presented in Table 2.

Table 2.

Simulation results of the sparse association methods in combination with the model selection criteria for m = 102 assuming three different correlation structures for the exposure and outcome variables. For each of the three correlation matrices, the proportion of times out of 200 simulations in which the true model was selected (T), the mean number of variables that were false positives (FP) and false negatives (FN) are reported. The population CCA loadings of the outcome variables for the three correlation structures are b₁ = (0.58, 0.58, 0.58, 0, …, 0)^T, b₂ = (0.54, 0.54, −0.65, 0, …, 0)^T, b₃ = c(0.71, −0.71, 0, …, 0)^T respectively.

		cov1			cov2			cov3
Select	method	T	FP	FN	T	FP	FN	T	FP	FN
	Step-CCA	0.02	5.49	0.02	0.04	4.45	0.00	0.02	5.17	0.01
BIC	SOS-CCA	0.80	0.22	0.01	0.00	0.34	1.17	0.61	0.38	0.16
	PMA-CCA	0.92	0.11	0.02	0.00	0.16	1.19	0.00	1.11	1.14
	Step-CCA	0.02	4.22	0.02	0.29	1.25	0.00	0.02	4.80	0.00
CIC	SOS-CCA	0.76	0.28	0.00	0.00	0.70	1.06	0.56	0.55	0.12
	PMA-CCA	0.86	0.22	0.02	0.00	0.78	1.06	0.00	4.12	1.04
	Step-CCA	0.32	1.04	0.60	0.77	0.70	0.06	0.61	2.29	0.22
correlation	SOS-CCA	0.46	1.92	0.11	0.00	7.20	0.78	0.14	8.73	0.09
	PMA-CCA	0.30	7.66	0.05	0.00	10.16	0.98	0.01	21.50	0.80

The results show that having many nuisance variables in the model increased false positive selection, especially using step-CCA when implemented with either BIC or CIC. Interestingly, the step-CCA results when implemented with predicated correlation, did not change much. Using BIC and CIC, step-CCA tended to overfit more than SOS-CCA and PMA-CCA. CIC selected a slightly less number of false positives compared to the other methods. For scenario 1, where the assumptions required by SOS-CCA and PMA-CCA are approximately satisfied, both SOS-CCA and PMA outperformed step-CCA. For scenarios 2, where the assumptions for both SOS-CCA and PMA-CCA are not satisfied, step-CCA had a higher chance to select the true model, although still tending to overfit more than SOS-CCA and PMA-CCA. Both SOS-CCA and PMA-CCA had a higher number of false negatives. For scenario 3, which satisfies the assumption for SOS-CCA but not for PMA-CCA, SOS-CCA had the best performance, while PMA-CCA has more false negatives than step-CCA. Compared to the small m case, the numbers of false positives are higher for all the methods in the large m case. Using predicted correlation as the selection criterion, all methods performed worse. CIC has an overall slightly better performance than BIC.

3.3 Simulations for the power of the testing procedure

To study the power of different methods as a function of the canonical correlation, we set up simulations in the following manner. We used two exposure variables, x^T = [X₁,X₂] and 10 genes y^T = [Y₁, … , Y₁₀]. We generated x and y from a multivariate normal distribution such that X₁ was correlated with Y₁ and the rest of the outcomes were nuisance variables. We varied the correlation between X₁ and Y₁ in [0, 0.1, … , 0.6] and generated 400 data sets with sample size n = 50 for each case. We calculated P-values for the test of no association between x and y based on 300 permutations using SOS-CCA, step-CCA and PMA-CCA. We rejected the null hypothesis of no association when P-value ≤ 0.05.

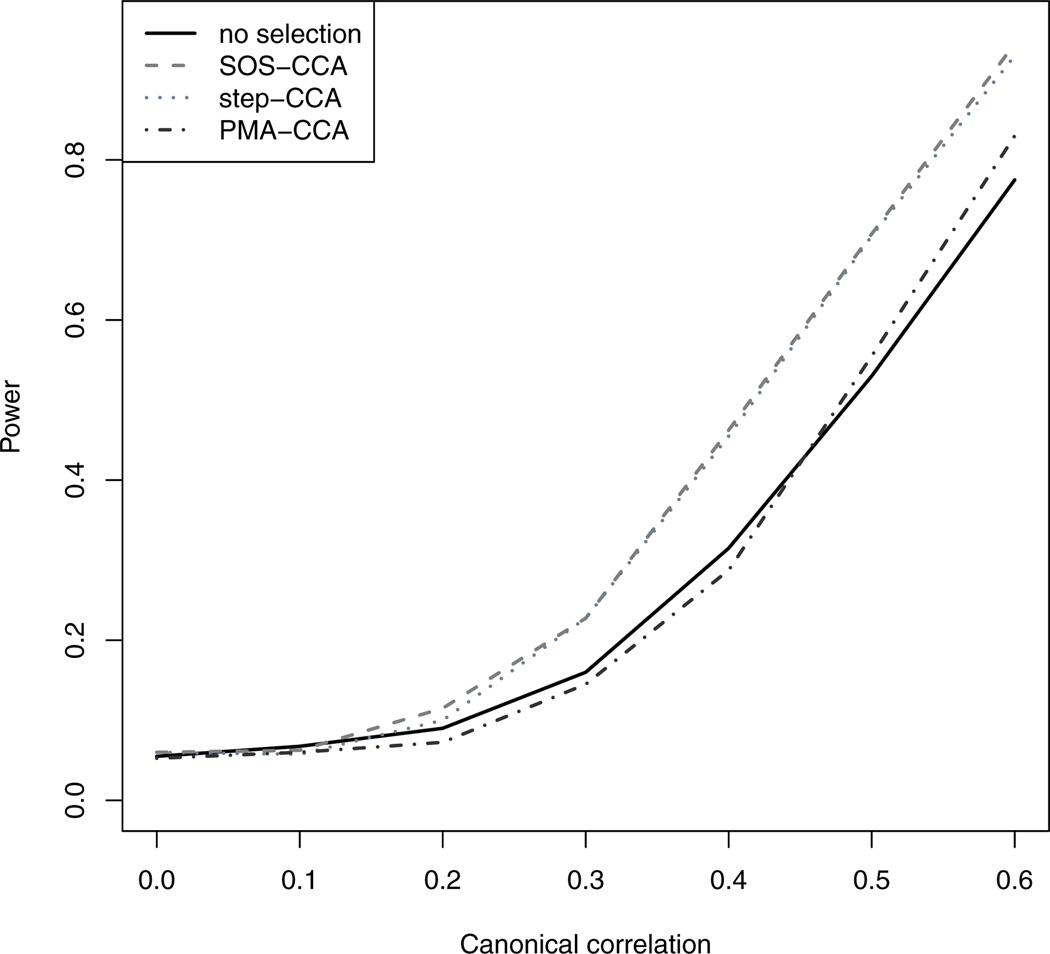
The size of the test, defined as the power calculated under the null, matched the nominal level. Figure 2 shows the power curves of the tests as a function of the true canonical correlation, for the three methods using the CIC model selection criterion, and the regular test without variable selection. The results show that the Wilks’ Λ-based permutation test used in conjunction with variable selection is more powerful than the same procedure used without variable selection, and the Wilks’ Λ-based Step-CCA, and SOS-CCA tests are more powerful than the canonical correlation based PMA-CCA test. Note that when implementing PMA-CCA with the Wilk’s Λ-based test, the performance of PMA-CCA is similar to those using the sparse outcome selection methods.

Fig. 2.

Simulation results of size and power as a function of between-outcome correlation. The type I error was set at the 0.05 level. Four tests were compared. For SOS-CCA and Step-CCA, we considered the proposed Wilks’ Λ based tests. For PMA-CCA, we considered the canonical correlation based test of [23]. We also included the regular test without gene selection. For all of the methods, CIC was used as the model selection criteria.

To assess the sensitivity of the testing procedure with respect to the normality assumption, we performed additional simulations by generating the data using the log-normal distribution. Our results show that the permutation based tests still have the correct sizes but a lower power compared to when the data are normally distributed (Results not shown due to limited space).

4 Data analysis: methylation in the asthma pathway

We applied the proposed methods to the DNA methylation data of the Normative Aging Study (NAS) described earlier. The number of study participants having measures of DNA methylation was 141, but due to missing sulfate measures, only 92 observations were retained. We restricted our analysis to the asthma pathway, which consists of 31 genes, of which 27 are available in the methylation data set. We used gene specific methylation scores calculated by mapping the probes to the genes and calculating the area under curve using the kernel smoothing method for each gene [14]. The methylation scores are not normally distributed, and the proposed variable selection methods and the permutation-based testing procedure do not require normality.

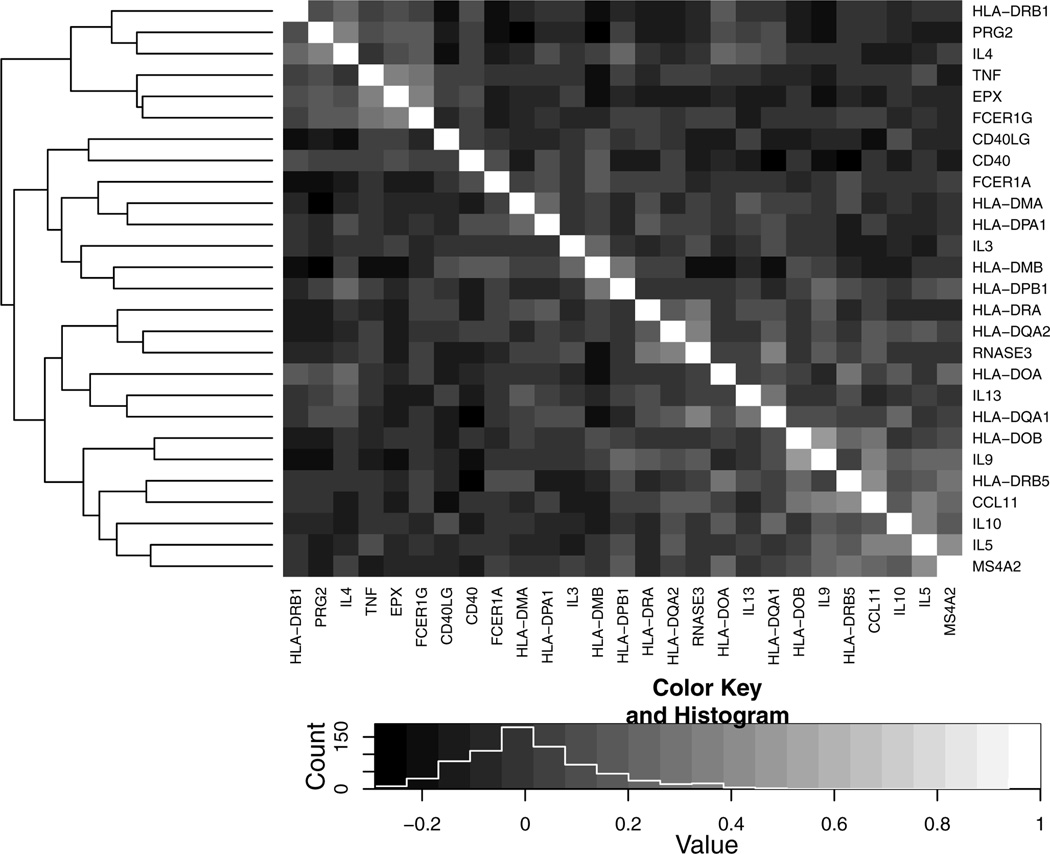
We assessed the association between gene methylation levels in the asthma pathway and air pollution, controlling for age. We first partialled out the covariate age, then standardized all the covariates to have mean 0 and variance 1, and finally applied step-CCA, SOS-CCA and PMA-CCA to the methylation scores for the 27 genes in the asthma pathway and the exposure variables: measured Black Carbon (bc) and Sulfate (sulfate), calculated by averaging over the daily measures in the month prior to a participant’s clinic visit. The pairwise correlations of the genes in the pathway were generally low, with most of them less than 0.2 and some close to 0.5, suggesting that the marginal method SOS-CCA is likely to perform better than step-CCA, and can be slightly better than PMA-CCA. Figure 3 presents a clustered heatmap of the correlations between the genes in the pathway.

Fig. 3.

Correlations between the genes in the asthma pathway.

Table 3 gives a list of genes with non-zero loadings estimated by each of the three methods using the CIC, and the resulting canonical correlation loadings using the selected variables. Table 3 also provides the P-value for the hypothesis of no overall association between methylation in the asthma pathway and air pollution exposures. Because no computationally efficient model selection criterion was proposed in [23], our implementation of PMA-CCA used the same model selection criterion CIC that we proposed in this paper. The P-values for testing for association of the pathway with the exposures using the proposed methods as well as that of the PMA-CCA were calculated using the testing procedure that used the Wilks’ Λ as the test statistic. This is because as shown in our simulations, this method is more powerful than the testing procedure based on canonical correlation.

Table 3.

Results of the sparse association methods applied to studying the air particulate matter effects on gene methylations in the asthma pathway in the Normative Aging Study. The estimated loadings of the genes and the exposures are provided, as well as the estimated canonical correlations and the P-values. The P-values were calculated using the proposed permutation and Wilks’ Λ statistic test procedure. All the methods used CIC as the model selection criteria. The last two columns report the P-values of the F-test and the correlation coefficient (R) of individual gene regression on the two exposures.

Gene	SOS-CCA	step-CCA	PMA	ind P-value	ind cor
HLA-DMA	– –	0.31	– –	0.30	0.16
HLA-DPA1	– –	−0.32	– –	0.38	0.15
HLA-DPB1	– –	−0.24	– –	0.64	0.10
HLA-DRA	– –	0.32	– –	0.07	0.24
HLA-DRB5	– –	– –	0.55	*0.01	0.30
FCER1G	−0.47	−0.30	−0.44	*0.01	0.30
IL5	0.50	0.45	0.60	**0.001	0.38
RNASE3	– –	−0.30	– –	0.24	0.18
CCL11	0.58	0.58	0.38	*0.02	0.36
Sulfate	1.01	1.06	0.90	–	–
Black Carbon	−0.04	−0.22	0.42	–	–
Estimated Correlation	0.48	0.61	0.48	–	–
P-value	0.03	0.02	0.01	–	–

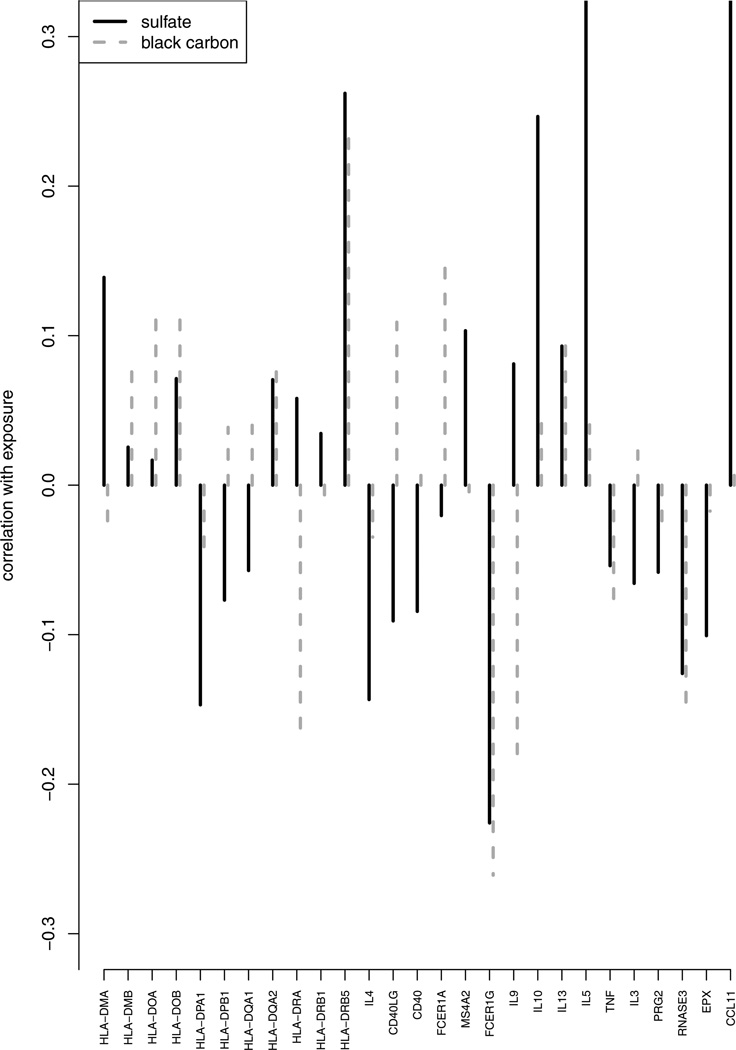
As shown in Table 3, SOS-CCA, step-CCA, and PMA-CCA selected three, eight and four genes respectively. All three methods selected IL5 and CCL11. Step-CCA gave the highest canonical correlation (0.61), while PMA-CCA gave the smallest P-value for the overall association between methylation in the asthma pathway and air pollution exposures (P-value = 0.01). The higher canonical correlation attained by step-CCA may be due to the larger selected model. SOS-CCA and PMA-CCA gave similar canonical correlations (0.48), with SOS-CCA selecting less variables. These results show a significant association between DNA methylation in the asthma pathway and air pollution exposures. Examination of the loadings of bc and sulfate show that sulfate, which represents pollution from power plants, is more strongly associated with methylation than black carbon, which measures pollution from traffic. Figure 4 demonstrates this difference graphically by plotting gene-specific correlations between methylation and the two exposure variables. One can see that the correlations of individual gene methylations and sulfate are generally larger than those of bc, supporting the results from the sparse outcome correlation analysis.

Fig. 4.

Marginal Correlations between the genes in the asthma pathway and the exposure covariates black carbon and sulfate.

To help better understand the pathway analysis results using the sparse outcome selection methods, we here also present individual gene analysis results, i.e. the results of regressing each gene of the pathway on the exposure variables bc and sulfate after partialling out (adjusting for) age. Since the pathway analysis aims at the overall association between the pathway and the two exposures, we limit our discussions of individual regression results to the significance of the joint exposure effects on each gene, not the significance of individual exposure effects, by calculating the P-value of the 2-df F-statistic for the overall exposure effect.

The individual gene analysis results are given in the last two columns of Table 3. The results show that HLA-DRB5, FCER1G, IL5 and CCL11 are marginally significantly associated with the air pollution exposures at the 0.05 level. These four genes were all selected by at least one of the methods, as illustrated in Table 3. PMA-CCA selected all of these genes, but SOS-CCA, step-CCA and PMA-CCA selected three of them. Individual gene analysis also shows some evidence of the marginal associations of HLA-DRA, IL9, IL10 with the exposures (P-values = 0.07, 0.06 and 0.06 respectively). Of these genes, HLA-DRA was selected by step-CCA. Step-CCA selected a few additional genes which have weaker marginal correlation with exposures.

The sparse association methods were applied to the data using the BIC criterion as well. In the analysis using BIC, SOS-CCA and PMA-SSA both selected only the two genes IL5 and CCL11, while step-CCA selected HLA-DMA in addition to these genes. These results are suboptimal, as we expect that most of the outcomes that are marginally correlated with exposure should be selected.

5 Discussions

We propose in this paper two sparse outcome selection methods for studying the association between multiple genes in a pathway and exposures. The performances of SOS-CCA and step-CCA depend on the structure of the underlying covariance among the outcomes. Step-CCA is robust and detects the underlying model in most settings, especially when some outcomes are marginally weakly correlated or uncorrelated with exposures but are correlated with other outcomes. In these settings, SOS-CCA and the existing shrinkage method (PMA-CCA) that assumes independence among outcomes fail and tend to underfit. When some outcomes are marginally correlated with exposures and correlation among outcomes are weak, SOS-CCA and PMA-CCA work better, as step-CCA generally tends to overfit. When some outcomes are marginally correlated with exposures and nuisance outcomes are weakly correlated with the signal outcomes, SOS-CCA works better than PMA-CCA. In general, step-CCA has a higher number of false positives and a smaller number of false negatives. A good balance may be struck by using SOS-CCA and PMA-CCA when the correlation between the outcomes is small, and step-CCA when part of the correlations between the outcomes are moderate/strong or when one concerns about underfitting. Future research is needed to study the theoretical properties of these methods.

The proposed methods are appropriate to use when the sample size is smaller than the number of outcomes. This is because SOS-CCA initializes with individual outcome screening and the step-CCA is a sequential method. Therefore, as long as the true signals are expected to be sparse, these methods can be applied. Further, these methods are computationally more efficient and stable than the existing shrinkage method when the number of outcomes is larger than the sample size. When outcomes are highly correlated, e.g., correlation among the outcomes is 0.9, we found that the proposed methods often select one of the highly correlated variables. To overcome this problem, one could consider ridge CCA.

The choice of the tuning parameter is important. We propose CIC as a model selection criterion for choosing the tuning parameter, and compare its performance with BIC and predicted correlation. Both BIC and CIC are functions of canonical correlation that penalize larger models. The CIC criterion performs well in simulations and is usually comparable to BIC. When the number of nuisance parameters is very large and larger than the sample size, we have found that BIC tends to overfit (results not shown). This is because the estimated canonical correlation becomes very close to 1 and the loss function in BIC dominates the penalty term. Hence in this case larger models are preferred by BIC.

The third model selection criterion using predicted correlation has inferior performance compared to BIC and CIC and often gives overfitted models. We provided empirical justifications for CIC. Future research is needed to provide more rigorous justifications for CIC, and to study the theoretical properties of these model selection criteria.

Analysis of sparse association of multiple genetic outcomes with exposures becomes more and more important in genomic studies. We focus on continuous DNA methylation of genes in a pathway. It is a future research interest to extend the proposed methods to discrete outcomes and mixed outcomes.