Revised AMBER parameters for bioorganic phosphates

Abstract

We report AMBER force field parameters for biological simulations involving phosphorylation of serine, threonine or tyrosine. The initial parameters used RESP fitting for the atomic partial charges and standard values for all other parameters such as Lennard-Jones coefficients. These were refined with the aid of a thermodynamic cycle consisting of experimentally determined pKa values, solvation energies from molecular dynamics free energy simulations, and gas phase basicities from QM calculations. A polarization energy term was included to account for the charge density change between the gas-phase and solution, and solvation free energies were determined using thermodynamic integration. Parameter adjustment is required to obtain consistent thermodynamic results with better balanced electrostatic interactions between water and the phosphate oxygens. To achieve this we modified the phosphate oxygen radii. A thermodynamically consistent parameter set can be derived for monoanions and requires an increase of the van der Waals phosphate oxygen radii of approximately 0.09 Å. Larger, residue-specific radii appear to be needed for dianions. The revised parameters developed here should be of particular interest for environments where simulations of multiple protonation states may be of interest.

1 Introduction

Protein phosphorylation is of utmost importance in cell signaling.^1–6 The study of phosphorylated proteins can shed light on many important questions regarding control and regulation in cell signaling. The phosphate anions ${\mathrm{HPO}}_4^{2-}$ and ${\mathrm{H}}_2{\mathrm{PO}}_4^{-}$ are the most abundant forms in solution at physiological pH⁷ and are therefore the most dominant forms involved in biological processes. Molecular dynamics simulations of systems with phosphate ions or phosphorylated compounds can give detailed insights into a plethora of biologically relevant questions: for example how protein phosphorylation changes the protein function and structure, how it alters the protein's binding behavior, and ultimately how these changes affect the function of the protein in the cell.

Computer simulations of phosphorylated proteins require accurate parameters for the phosphoric acid esters. One begins by defining a molecular topology and force field atom types. Force constants for bonds, angles and dihedrals are then assigned. Furthermore, obtaining the proper electrostatic interactions in the molecular mechanics model requires computation of atomic point charges. Several techniques to obtain these atomic charges exist. In CHARMM,^8,9 for example, Mulliken charges are assigned to the optimized structure followed by placing water molecules in the vicinity of the polar groups and refining the charge to accurately reproduce the interaction energy. In AMBER¹⁰ one starts with an electrostatic potential (ESP) arising from electronic structure calculations, and then uses a charge-fitting procedure (RESP¹¹) to calculate values of atomic partial charges that best reproduce the electrostatic potential at a grid of points surrounding the molecule.

For AMBER there already exist parameters for phosphorylated amino acids.¹² The atomic charges were obtained using the RESP methodology and the parameters have been successfully used in simulations of phosphorylated proteins that were carried out to elucidate the binding, unbinding, dynamics, and structural changes of the proteins.^13–15 This parameter set uses Lennard-Jones radii that are unchanged from values originally chosen for the phosphodiesters founds in nucleic acids. It is therefore desireable to check additional thermodynamic properties, particularly in terms of interaction of charged phosphate groups with water. Pearson¹⁶ developed a scheme for computing free energies of hydration by constructing a thermodynamic cycle (see 2) for which the gas phase basicities and pKa's of the system of interest are known. In this paper we use such cycles to refine the parameters giving rise to the solvation energies of phosphoric acid esters (labeled A for acid in the diagram). Experimental or high-level quantum chemistry estimates are available for many of the legs of the thermodynamic cycle; we report here parameters adjusted in such a way that the computed solvation free energies correctly complete the thermodynamic cycle, giving updated parameters for both the anionic and di-anionic forms of several phosphorylated amino acids.

2 Methods

The current study focuses on obtaining parameters of phosphates and phosphate derivatives (test molecules are shown in 1). Methyl and p-tolyl phosphate served as surrogates for the biologically important phosphoserine and phosphotyrosine residues, respectively. The diesters serve as model compounds for the phosphate groups in DNA and RNA. The parameters for all-atom simulations of the phosphoric acid esters were determined and refined using a thermodynamic cycle (2), sometimes called a “Pearson cycle”.¹⁶ Eight energy terms contribute : (1) the gas phase basicities; (2) the energy that arises (if needed) from changing units from standard concentration to the units of liquid state measurements; (3) and (4) are the polarization energies arising from changing the charge distribution (in the gas phase) to values used in the force field, which are aimed at being appropriate to the condensed phase^17–19 ; (5) and (6) are the solvation free energies that can be obtained from fixed charge free-energy simulations (we use thermodynamic integration here); (7) is the standard proton free energy of hydration; and (8) is the free energy calculated from the experimental pK_a value. Details of how the various terms were estimated are given next.

1. The gas phase basicities of the model compounds were computed using the Gaussian03 software package.²⁰ For each structure of the model compounds studied the optimal gas phase geometry was obtained using density functional theory (DFT) approximating the exchange-correlation energy functional with the hybrid functional (B3LYP) at an aug-cc-pVTZ basis set level. This pre-optimized structure was used as input geometry to compute gas phase basicities. Molecular energies were computed using Gaussian-3 (G3) theory.²¹ The general equation of basicity is given by $\Delta G_{Basicity}=\Delta G\left(G3\right)+G^{H+}-RT\Delta \ln \frac{m}{n}$, namely the sum of the free energy difference for the acid and base, the proton free energy and a multiplicity term that stems from the indistinguishable microscopic protonation states possible when placing r protons at s possible sites of each test compound. Each number (n,m) can be computed from the binomial coefficient, i.e. $n=\frac{s!}{(r-s)!r!}$. The symbol “Δ” denotes the difference between the acid and its conjugate base. The proton free energy in the gas-phase is given by the sum of ideal enthalpy ($\frac{5}{2}RT$) including the pV term and the proton entropy S=26.02 kcal/mol K at 298 K, obtained from the Sackur-Tetrode equation,²² leading to a proton free energy G^H+ = –6.28 kcal/mol.²³

2. Gas-phase polarization energies (3) and (4) were obtained using Gaussian03 and a polarizable continuum solvent model, using B3LYP, the aug-cc-pVTZ basis set and an external dielectric of 78.4, representing aqueous solution. Standard additional parameters of ε_∞ = 1.78 for the fast-response dielectric constant of water and R_solv = 1.385 Å for the probe radius have been used. The total energy of a compound was computed with the PCM term, additionally the energy was calculated without PCM but using the fixed orbital coefficients of the previous calculation. Comparing the second energy to the result of a pure vacuum calculation provides an estimate of the polarization energy a compound builds up when its charge density adapts to an aqueous environment. This procedure employs equation 2 of Ref.¹⁸ instead of the tensorial approach described there, so polarization energies were calculated here as

   $$E_{Pol.}=E^{SCF}\left[{\rho }_{PCM}\right]-E^{SCF}\left[{\rho }_{gas}\right]$$ (1)

   where ρ_PCM is the electron density obtained from a calculation including the PCM solvation model and ρ_gas is the gas phase electron density. E^SCF is the total energy of the compound calculated for a given density but without using the PCM model. Since the second term in Eq. 1 is always more negative than the first (since ρ_gas is the minimum energy density), a polarization energy is a positive energy contribution. We believe this approach to be a more robust calculation than the procedure of Swope, Horn and Rice¹⁸ for the case of these small highly symmetrical compounds, since multipoles higher than quadrupoles may be required for a good description of their electrostatic properties. We note that the RESP charges used in our study are not guaranteed to match the charge distribution from PCM calculations which may degrade the quality of the polarization energy estimates. However, only differences of polarization energies enter the thermodynamic cycle calculations and these differences are small compared to the solvation energies of ions under consideration here. For all of the systems in 3 and 4, with the exception of of the dianion of the phosphotyrosine model, the differences in polarization energies are less than 4.5 kcal/mol. Note that the polarization term for the p-tolyl phosphate is significantly higher than for the other compounds. This can be understood in terms of the high resonance stability an aromatic ring substituent provides to a phosphate anion, indicating that the charge distribution is easiest to shift and therefore polarization plays a larger role for this one compound. Using different estimates for this term, or even ignoring it entirely, would not lead to significant changes in the resulting target values. Still, the optimized Lennard-Jones parameters would change somewhat, since they are strongly affected by small changes in energy. We have repeated the analysis presented in 4, 3 and 4 below without a polarization correction in the target values and obtained radii changes that were consistently higher, by about 0.07 Å. Clearly, a representation of polarization effects is necessary for accurate results here.

3. Solvation free energies (5) and (6) were obtained from all-atom simulations using the AM-BER10 molecular modeling suite¹⁰ using thermodynamic integration,²⁴ as follows. For MD simulations, charges for each molecule were taken from RESP fitting calculations.¹² We term the parameter set with these charges and all other parameters (like van-der-Waals radii) taken from the AMBER ff99 set the ”standard parameter“ set. The test molecules were solvated in an octahedal box of approximately 750 TIP3P water molecules so that 12.0 Å distance or more lay between every solute atom and the simulation box boundary. The systems were heated to a temperature of 300 K over 5 ps and equilibrated for 1 ns. Bond lengths including hydrogen atoms were constrained using the SHAKE algorithm.²⁵ The electrostatic potential was evaluated using the Particle mesh Ewald (PME) method.^26,27 The cutoff between short- and long-range interactions was taken to be 9.0 Å. The length of the time step was 2 fs. Free energies were evaluated using thermodynamic integration with linear (trapezoidal) interpolation of the free energy curve between 9 λ-values (0.1, 0.2, ..., 0.9), with a total simulation length of 3 ns per window, collecting data from the last 2 ns only. The total free energy for each compound was computed from three consecutive TI transformation steps, first a removal of all partial charges in solution, then removal of solute-solvent vdW interactions followed by reintroducing all partial charges in vacuum. Such a breakdown of TI calculations into individual substeps is common and helps overcome simulation instabilities. Error estimation for the resulting TI solvation free energies was conducted as in previous work,²⁸ by computing the ∂V/∂λ-autocorrelation time τ to estimate the standard error of the mean from the standard deviation σ_∂V/∂λ for each simulation window as σ_SEM = σ_∂V/∂λ/√t_sim/2τ and combining individual λ-window results via Gaussian error propagation.

4. Values in the range of –249.5 to –264.0 kcal/mol based on various theoretical and experimental data have been suggested for the hydration free energy of the proton, (7).^29–31 Basically, relative solvation free energies of cations (and of anions) can be determined from experimental measurements, but the absolute scale of cation values relative to anions requires some extra-thermodynamic assumptions. The situation is further complicated by the fact that in real systems, the reversible work required to move an ion from solution to the gas phase includes a contribution from the “phase potential” associated with the vacuum liquid interface.³¹ The thermodynamic integration calculations used here correspond to an “intrinsic” or “absolute” transfer, which is independent of any phase potential. The cycle in 2 can be consistent with this if an “intrinsic” value is chosen for energy (7). Here, we use the result from polarizable force field ion simulations of Grossfield et al.,³⁰ –252.5 kcal/mol. This result is within 0.5 kcal/mol of the consensus value determined by Tissandier et al. , –252 kcal/mol (based on an estimated phase potential contribution), and is close to the value of -250 kcal/mol used for the current AMBER parameterization for alkali halide anions.³² Lamoureux and Roux³¹ have carried out polarizable ion simulations similar in spirit to those of Grossfield et al., arriving at a value of –247 kcal/mol. With this reference, cations are less favorably solvated, by about 5 kcal/mol, than with our choice, and anions such as phosphates would have solvation free energies that are more negative by the same amount. This change would have an effect on the optimized radii that can be estimated from 4 below. Our choice of –252.5 kcal/mol for energy (7) has the advantage of being consistent with the way other parts of the AMBER force fields have been developed.

With this thermodynamic cycle, we generated a refined parameter set by changing the phosphate oxygen van der Waals radii. Other refinement schemes are possible as well, such as charge redistribution within the phosphate group and changes to the hydrogen and phosphorus van der Waals parameters. Several such approaches were studied in preliminary work but did not yield closed thermodynamic cycles for chemically reasonable parameter values (data not shown). We introduce three new AMBER atom types for our test molecules, for the different types of oxygen atoms in phosphate groups, ’OP’ for a deprotonated phosphate oxygen, ’OQ’ for a protonated phosphate oxygen (a P-OH group) and ’OR’ for a bridging oxygen (e.g. a P-O-Me group). The types correspond to the ’O2’, ’OH’ and ’OS’ types in the AMBER forcefield. The different oxygen radii are summarized in 1.

3 Results and Discussion

The gas phase basicities (2) were estimated from Gaussian03 G3 calculations. Such calculations are usually fairly accurate for phosphoric acid esters.²³ For example, the computed gas phase basicity of phosphate (transition of H₃PO₄ to $H_{2}P{O}_4^{-}$) lay within 0.3 kcal/mol of the reported experimental value of 321.0 kcal/mol.³³ For the other model compounds, experimental gas phase basicities were not available, but we assume that G3 calculations produce useful results for these basicities as well. For the test molecules, the basicities for the neutral to singly charged transition were about 320 kcal/mol and for the singly to doubly negatively charged transition about 450 kcal/mol. p-Tolyl phosphate is an exception with a somewhat lower basicity of about 430 kcal/mol for the transition to the doubly negatively charged form.

3 and 4 summarize the free energies of the Pearson cycle and give the target solvation free energies that a refined parameter set should yield from the AMBER free energy simulations. A plot of the ion solvation energies as a function of oxygen radii is shown in 4.

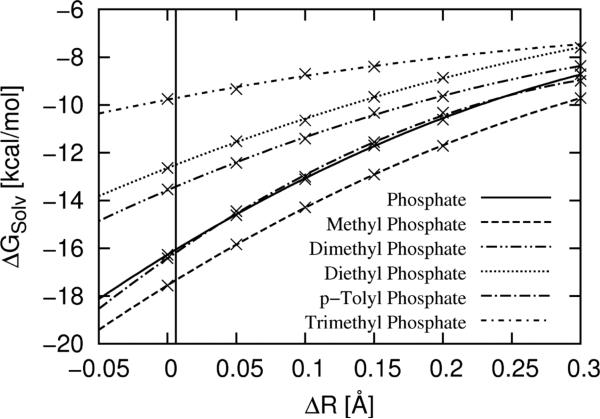
3 includes the solvation free energies for the neutral compounds, also computed from thermodynamic integration calculations. These numbers are also dependent on the chosen oxygen radii set, but unlike the results for the charged compounds, they can be calibrated with respect to experimental results. For this purpose, we used trimethyl phosphate, a molecule very similar to our test phosphates, but with a neutral form that is stable in aqueous solution. Trimethyl phosphate is the only compound presented here with a reliable, directly determined experimental solvation free energy: –8.7 kcal/mol.³⁷ Our polarizable continuum model suggests that the gas-phase polarization energy is 1.0 kcal/mol, suggesting a target value for the transfer of trimethyl-phosphate (with its solvated charge distribution) from gas to water to be –9.7 kcal/mol. We use the thermodynamic integration procedure outlined above to compute the solvation free energy of trimethyl phosphate and our test compounds for different radii sets (3). A second order polynomial was fit to the data points and the oxygen radius increase for which the simulation result matches the experimental target value of –9.7 kcal/mol was found to be 0.006 Å. This radius increase for the neutral compounds was used for all five test molecules to obtain the entries for row (5) in 3.

For neutral to single negatively charged transitions the standard parameters (with no change in oxygen radius) consistently oversolvated the anionic monoesters by 2-5 kcal/mol and phosphate itself by more than 15 kal/mol. The required oxygen radius change to reach the target values are as follows: methyl phosphate needed a 0.07 Å radius increase for –90.0 kcal/mol, p-tolyl phosphate 0.05 Å for –83.8 kcal/mol, dimethyl phosphate and diethyl phosphate required radii increases of 0.12 and 0.10 Å to reach target values of –87.2 and –84.7 kcal/mol respectively. For phosphoric acid itself, a large radius increase of 0.29 Å was necessary. In general, to close the cycle of the transition of neutral to single negatively charged phosphate esters, a rather uniform radius increase of approximately 0.09 Å was needed to make AMBER give free energies that are fairly consistent with thermodynamic data.

Interestingly, both for dimethyl phosphate and diethyl phosphate a substantial radius increase is suggested to close the thermodynamic cycle. These test molecules were included as equivalents to the phosphodiesters forming the backbone of nucleic acids biomolecules. The current AMBER forcefields contain phosphate parameters mainly to describe DNA and RNA, nevertheless our results show these to be somewhat oversolvated by more than 3 kcal/mol using standard parameters. Tests on nucleic acid systems with these expanded radii are planned.

A less uniform picture emerges from the data in 4 for the transition of negatively charged to doubly negatively charged molecules. The standard parameters suprisingly did work well for ptolyl phosphate (which required a small radius decrease of 0.03 Å). In comparison, the methyl phosphate dianion required a radius increase of 0.18 Å. For phosphoric acid itself, the dianion, like the anion before, was found to be strongly oversolvated and would need an oxygen radius increase of 0.33 Å to close the cycle.

Thermodynamic integration simulations were performed to compute the solvation free energy (see 5) of the test compounds with increasing phosphate oxygen radius. The question arises whether it is necessary to determine individual parameters for every phosphate derivative or if a universal parameter set can be given. The required radius increase of 0.006 Å for the neutral compounds is of little relevance in practice, since it is not only small, but the fully protonated compounds do not occur in significant amounts under physiological conditions. Anions and dianions are the most commonly simulated compounds, and we found above that a uniform oxygen radius increase of 0.09 Å is suitable for all monoanions except phosphate. For dianions, no uniform set can be given and we suggest using the individually fitted radii increases for each compound. For phosphoric acid, the very large radius increase suggested indicates that this is a molecule for which a molecular mechanics description is difficult in general (see below for a more detailed look at this compound). While this is not problematic for either nucleic acids or phosphorylated proteins, both of which contain only phosphate esters, many commonly used buffer solutions contain phosphoric acid and building accurate molecular mechanics models for these would be difficult.

We find that radii for nearly all anions studied needed to be increased. This overall result is in good agreement to the expectation that anions will have inflated outer electron shells. In the context of a fixed charge MD force field with isotropic van-der-Waals parameters, the best option to model inflated electron shells is to make the atoms appear larger in simulations.

3.1 Experimental and calculated solvation free energies for phosphoric acid

The scope of the current work is to consider a universal parameter set for phosphoric acid and phophoric acid esters. To ensure confidence in these parameters, they must be consistent with experimental data. Phosphoric acid exists in four different charge states and has experimentally available solvation free energies of varying accuracy for all states (see 6). The thermodynamic integration calculations of the solvation free energy without polarization correction for the neutral form of phosphoric acid (H₃PO₄) yielded a solvation free energy of –16.1 kcal/mol using adjusted radii. Suprisingly, this is smaller than the progression of values from trimethyl- to dimethyl- to methyl phosphate suggests (ΔG_Solv of –9.7, –13.4 and –17.3 kcal/mol). Instead, a value of –21.4 kcal/mol can be extrapolated from these numbers. Using this estimate for the neutral solvation energy above does not change the results significantly, though. Large radius increases of 0.18 and 0.28 Å would still be required for the anion and dianion to close the Pearson cycle.

QM calculations also suggest that the solvation free energy for neutral phosphate (5) in 3 is too low. Gaussian03 QM calculations using a aug-cc-pVTZ basis set and PCM solvation gave a solvation free energy of –22.3 kcal/mol for H₃PO₄. This QM result includes the charge polarization due to solvent, so to compare it to the TI result, the later also needs to include the polarization term. Phosphate values (3)+(5) from 3 give only –8.26 kcal/mol, suprisingly close to zero for such a polar molecule. If we use the QM value of –22.3 kcal/mol instead of the sum of (3) and (5) in 3, then a radius increase of only 0.03 Å for the anion and 0.19 Å for the dianion is found, a much more reasonable range. Since a fully protonated phosphoric acid molecule is not stable in water at neutral pH, no accurate solvation free energy can be assigned to it, but the approximate value of –26 kcal/mol given in Ref³⁹ is much closer to the QM than the MD result, leaving our results questionable for the case of unsubstituted phosphate. It appears that the H₃PO₄ molecule is much more difficult to treat in MD simulations than its esters.

For the charged forms of phosphoric acid, ($H_{2}P{O}_4^{-}$, $HP{O}_4^{2-}$, and $P{O}_4^{3-}$), solvation free energies from experiments exist and can be compared to simulation or QM data. Note that unlike the values in 5 the TI numbers in this paragraph include the polarization correction term (4), to be comparable to the QM and experimental numbers. For dihydrogenphosphate ($H_{2}P{O}_4^{-}$) the simulation target value gave the solvation energy to be computed from simulations as -75.3 kcal/mol, which lies in the range of the experimentally reported numbers of –68 kcal/mol⁴⁰ to –111 kcal/mol.⁴¹ Unfortunately this range of 45 kcal/mol is rather large and it therefore does not ensure accuracy of our reported number. For the doubly deprotonated phosphoric acid, the target solvation free energy of –263.7 kcal/mol using standard parameters is still within 10% of the experimental value of –299 kcal/mol.³⁹ This may be attributed to chance, since the expected errors on the experimental values are quite large. Even for fully deprotonated phosphate ($P{O}_4^{3-}$), the TI result using standard parameters is not far from experimental numbers^39,41 and much closer than the QM result, although molecular mechanics models would not be expected to yield reliable data on such highly charged compounds.

In summary, even though our parameter fitting scheme does provide radius adjustments for phosphate anions and dianions which ensure that the target values are matched, the uncertainties in the experimental values and the suprising discrepancy between the QM and TI calculation values for the solvation energy of neutral H₃PO₄ mean that the target values themselves may be inaccurate. The strong dependency of the fitted radii on changes in the target energy values explains why significantly larger radius changes are suggested for phosphates than for phosphate esters. While parameters for phosphoric acid and its anions can be given, for this molecule we may have reached the limit of our fitting scheme to obtain correct solvation free energies merely by changing one force field parameter.

4 Conclusions

Phosphorylation is of great importance in biology and a detailed understanding requires detailed microscopic data. All-atom simulations can provide insight into many questions on a molecular level. Here we investigated parameters derived from standard techniques for a variety of phosphoric acid esters. Existing parameters lead to oversolvation due to too strong electrostatic interactions of the negatively charged phosphate group oxygens. We find that for neutral molecules the standard parameters are suitable (requiring increased oxygen radii of only 0.006 Å) but for the biologically relevant negative charge states a larger increase of 0.09 Å is suggested. Doubly negative compounds require individually adapted oxygen radii.

We derived a parameter set for phosphate esters that is in agreement with experimental data and yields thermodynamically consistent results for the Pearson cycles. The derivation of all-atom parameters of charged molecules poses a considerable challenge, as highly charged molecules are more strongly solvated and polarized than neutral forms of the same molecule. Therefore, achieving reasonable results with only a single changed parameter for many of the test molecules was an unexpectedly fortunate finding. Beyond that and if very accurate thermodynamic data is desired, a case-by-case fitting procedure must be used.

The current study gives a recipe of determining parameters for charged groups by manipulating the van-der-Waals radii to shield the electrostatic interactions with water. Atoms of a polarized anionic molecule appear to require larger oxygen van-der-Waals radii than the neutral forms of the same molecule, and should therefore be parameterized as physically larger in an all-atom force field. In our study the increased van-der-Waals radius prevented water to get too close to the oxygen atoms reducing problems from overly strong electrostatic interactions and over-solvation.

Summarily, we have determined a parameter set for phosphates using as our variable the size of the phosphate oxygens. This parameter set reproduces the experimentally available solvation free energies and is thermodynamically consistent as tested using the thermodynamic Pearson cycle. Our derivation scheme is straightforward to adapt to other charged compounds.

Figure 1.

Chemical structures of the neutral forms of the phosphoric acid ester test molecules used in the current study.

Figure 2.

Pearson cycle used for the refinement of parameters for the test molecules. Here the numbers refer to energies of the Pearson cycle. Red text indicates the corresponding molecular process. The energies are given as: (1) the gas phase basicity, (2) the energy that arises from changing units to the units of liquid state measurements, (3) and (4) are the polarization energies, (5) and (6) are the solvation free energies, (7) is the proton hydration free energy, and (8) is the free energy due to the experimental pKa.

Figure 3.

Shown are the solvation free energies (computed with thermodynamic integration and the FF99SB force field of AMBER) for the neutral test molecules as a function of radius increase of the phosphate oxygen atoms. This plot also includes trimethyl phosphate as the one related neutral compound that is stable in water. The vertical black line indicates the oxygen radius increase at which the solvation free energy of trimethyl phosphate reaches the experimental target value. From this, a very small radius increase of 0.006 Å was determined.

Figure 4.

Solvation free energies (computed with thermodynamic integration and the FF99SB force field of AMBER) for the charged test molecules as a function of radius increase of the phosphate oxygen atoms. The target value for the test molecules are indicated by arrows. All plotted lines represent second order polynomial fits to the data point. Left: The solvation free energies for the singly charged test molecules. Right: Solvation free energies from simulations for the doubly negatively charged molecules, using the target values from 3 for the singly deprotonated compounds.

Table 1.

Phosphate oxygen radii used in the molecular dynamics simulations. A deprotonated phosphate oxygen is labelled ‘OP’, a protonated oxygen ‘OQ’ and a bridging one ‘OR’. The Lennard Jones well depth ε_LJ is given in kcal/mol, the radii are given in Angstrom (Å). The original radii r_orig. were taken from the AMBER FF99SB forcefield and r_opt gives modified radii for the mono-anions that match experimental data. No consistent radii set for dianions could be determined, see text for the optimized radii suggested for each individual species of dianion.

radius	ε LJ	rorig.	ropt
r(OP)	0.2100	1.6612	1.7493
r(OQ)	0.2100	1.7210	1.8091
r(OR)	0.1700	1.6837	1.7718

Table 2.

Molecular basicities, in kcal/mol, starting from G3 free energy estimates. See the text for a discussion of the various terms.

Molecule Phosphate	ΔG(G3)	m	n	$RT\ln \frac{m}{n}$	GH +	Δ GBasicity
$H_{2}P{O}_4^{-}-HP{O}_4^{2-}$	457.5	4	4	0.0	-6.28	451.2
$H_{3}P{O}_4-H_{2}P{O}_4^{-}$	327.9	6	4	0.24	-6.28	321.3
Methyl phosphate
$C{H}_{4}P{O}_4^{-}\text{-}C{H}_{3}P{O}_4^{2-}$	453.1	3	1	0.65	-6.28	447.5
$C{H}_{5}P{O}_4\text{-}C{H}_{4}P{O}_4^{-}$	329.6	3	3	0.0	-6.28	323.3
Dimethyl phosphate
$C_2{H}_{7}P{O}_4\text{-}{C}_2{H}_{6}P{O}_4^{-}$	332.3	2	1	0.41	-6.28	326.5
Diethyl phosphate
$C_4{H}_{11}P{O}_4\text{-}{C}_4{H}_{10}P{O}_4^{-}$	329.4	2	1	0.41	-6.28	323.5
p-Tolyl phosphate
$C_7{H}_{8}P{O}_4^{-}\text{-}{C}_7{H}_{7}P{O}_4^{2-}$	435.7	3	3	0.0	-6.28	429.4
$C_7{H}_{9}P{O}_4\text{-}{C}_7{H}_{8}P{O}_4^{-}$	324.4	1	3	-0.65	-6.28	317.47

Table 3.

Free energies (see 2) for the neutral/anion cycle (eg. $H_{3}P{O}_4\to H_{2}P{O}_4^{-}$), in kcal/mol. Shown are (1) the gas phase basicities computed from G3 calculation, (3) and (4) are the polarization contribution for the neutral species and the anion, (5) is the solvation free energy of the neutral compound obtained from thermodynamic integration using optimized radii (see text for details), (6=3+5+8-1-4-7) is the computed target value of the solvation free energy to make the Pearson sum equals to zero, (7) the proton hydration energy, and (8) the energy from the experimentally determined pKa's.

Energy	Phosphate	Methyl Phosphate	p-Tolyl Phosphate	Dimethyl Phosphate	Diethyl Phosphate
1	321.3	323.3	317.5	326.5	323.5
3	7.8	4.2	5.1	3.4	3.5
5	-16.1	-17.3	-16.2	-13.4	-12.5
7Ref. 30	-252.5	-252.5	-252.5	-252.5	-252.5
8	2.734	2.035	1.936	1.834	1.934
4	8.7	8.1	9.6	4.9	6.6
6	-83.1	-90.0	-83.8	-87.2	-84.7

Table 4.

Free energies for the anion/dianion Pearson cycle (eg. $H_{2}P{O}_4^{-}\to HP{O}_4^{2-}$). All energy units are given in kcal/mol. See 2 and the caption to 3 for a description of the various terms in the free energy cycle.

Energy	Phosphate	Methyl Phosphate	p-Tolyl Phosphate
1	451.2	447.5	429.4
3	8.7	8.1	9.6
5	-82.9	-90.0	-83.8
7	-252.5	-252.5	-252.5
8	9.334	8.634	8.038
4	8.6	11.0	21.8
6	-272.4	-279.3	-264.8

Table 5.

The effect of shielding the electrostatic interactions with an increasing van-der-Waals radius of the phosphate oxygens. Shown are the solvation free energies (energies 5 and 6 in 2) obtained from TI calculations with variable oxygen radius. For methyl and p-tolyl phosphate charges from Ref.¹² were used and RESP charges for the remaining compounds. The error estimation was conducted for the standard parameter set as described in Ref.²⁸

Molecule Phosphate	rOriginal	+0.05Å	+0.1Å	+0.15Å	+0.2Å	+0.3Å	Error Est.
$H_{2}P{O}_4^{-}$	-99.3	-95.7	-92.6	-89.8	-87.1	-82.6	0.30
$HP{O}_4^{2-}$	-307.8	-301.6	-295.8	-290.1	-285.0	-275.0	0.32
Methyl phosphate
$C{H}_{4}P{O}_4^{-}$	-94.1	-91.3	-88.7	-86.2	-82.1	-80.3	0.27
$C{H}_{3}P{O}_4^{2-}$	-297.5	-292.0	-287.1	-282.1	-277.2	-268.5	0.41
Dimethyl phosphate
$C_2{H}_{6}P{O}_4^{-}$	-92.8	-90.5	-88.1	-86.1	-82.3	-80.9	0.34
Diethyl phosphate
$C_4{H}_{10}P{O}_4^{-}$	-89.1	-86.8	-84.9	-83.0	-81.0	-77.8	0.36
p-Tolyl phosphate
$C_7{H}_{8}P{O}_4^{-}$	-86.6	-83.6	-80.9	-79.3	-77.4	-73.7	0.32
$C_7{H}_{7}P{O}_4^{2-}$	-262.38	-257.8	-253.7	-249.7	-246.0	-239.0	0.41

Table 6.

Comparison of Solvation free energies (in kcal/mol) from experiment, quantum mechanical calculations, and MD simulations reported here. All values are in kcal/mol. For the quantum mechanical calculations, Gaussian03 values using B3LYP, a aug-cc-pVTZ basis set and PCM solvation model are reported. The TI results differ from the target values in 3 and 4 because they include the polarization correction term to be comparable to experiment and QM results.

Phosphate	Experiment	QM	TI
$P{O}_4^{3-}$	-660.941/-63739	-495.3	-632.3
$HP{O}_4^{2-}$	-29939	-232.9	-263.7
$H_{2}P{O}_4^{-}$	-111.141/-6840/-7639	-71.5	-75.3
H 3 PO 4	-2639	-22.3	-8.3