A machine learning approach to predicting protein-ligand binding affinity with applications to molecular docking

Abstract

Motivation

Accurately predicting the binding affinities of large sets of diverse protein-ligand complexes is an extremely challenging task. The scoring functions that attempt such computational prediction are essential for analysing the outputs of Molecular Docking, which is in turn an important technique for drug discovery, chemical biology and structural biology. Each scoring function assumes a predetermined theory-inspired functional form for the relationship between the variables that characterise the complex, which also include parameters fitted to experimental or simulation data, and its predicted binding affinity. The inherent problem of this rigid approach is that it leads to poor predictivity for those complexes that do not conform to the modelling assumptions. Moreover, resampling strategies, such as cross-validation or bootstrapping, are still not systematically used to guard against the overfitting of calibration data in parameter estimation for scoring functions.

Results

We propose a novel scoring function (RF-Score) that circumvents the need for problematic modelling assumptions via non-parametric machine learning. In particular, Random Forest was used to implicitly capture binding effects that are hard to model explicitly. RF-Score is compared with the state of the art on the demanding PDBbind benchmark. Results show that RF-Score is a very competitive scoring function. Importantly, RF-Score’s performance was shown to improve dramatically with training set size and hence the future availability of more high quality structural and interaction data is expected to lead to improved versions of RF-Score.

1 INTRODUCTION

Molecular Docking is a computational technique that aims to predict whether and how a particular small molecule will stably bind to a target protein. It is an important component of many drug discovery projects when the structure of the protein is available. Although it is primarily used as a virtual screening tool, and subsequently for lead optimisation purposes, there are also applications in target identification (Cases and Mestres, 2009). Beyond drug discovery, these bioactive molecules can be used as chemical probes to study the biochemical role of a particular target (Xu et al., 2009). Furthermore, this technique can also be applied to a range of structural bioinformatics problems, such as protein function prediction (Favia et al., 2008). Molecular Docking has two stages: docking molecules into the target’s binding site (pose identification), and predicting how strongly the docked conformation binds to the target (scoring). Whereas there are many relatively robust and accurate algorithms for pose identification, the imperfections of current scoring functions continue to be a major limiting factor for the reliability of Docking (Kitchen et al., 2004; Leach et al., 2006; Moitessier et al., 2008). Indeed, accurately predicting the binding affinities of large sets of diverse protein-ligand complexes remains one of the most important and difficult un-solved problems in computational biomolecular science.

Scoring functions are typically classified into three groups: force field, empirical and knowledge-based. Force-field scoring functions parameterise the potential energy of a complex as a sum of energy terms arising from bonded and non-bonded interactions (Huang et al., 2006). The functional form of each of these terms is characteristic of the particular force field, which in turn contains a number of parameters that are estimated from experimental data and detailed computer-intensive simulations. These force fields were designed to model intermolecular potential energies, and thus do not account for entropy (Kitchen et al., 2004). Knowledge-based scoring functions use the three dimensional co-ordinates of a large set of protein-ligand complexes as a knowledge base. In this way, a putative protein-ligand complex can be assessed on the basis of how similar its features are to those in the knowledge base. The features used are often the distributions of atom-atom dis-tances between protein and ligand in the complex. Features commonly observed in the knowledge base score favourably, whereas less frequently observed features score unfavourably. When these contributions are summed over all pairs of atoms in the complex, the resulting score is converted into a pseudo-energy function, typically through a reverse Boltzmann procedure, in order to provide an estimate of the binding affinity (e.g. Mitchell et al., 1999a,b; Muegge and Martin, 1999; Gohlke et al., 2000). Some knowledge-based scoring functions now include parameters that are fitted to experimental binding affinities (e.g. Velec et al., 2005). Lastly, empirical scoring functions calculate the free energy of binding as a sum of contributing terms, which are individually identified with physico-chemically distinct contributions to the binding free energy such as: hydrogen bonding, hydrophobic interactions, van der Waals interactions and the ligand’s conformational entropy, among others. Each of these terms is multiplied by a coefficient and the resulting set of parameters estimated from binding affinity data. In addition to scoring functions, there are other computational techniques, such as those based on Molecular Dynamics simulations, that provide a more accurate prediction of binding affinity. However, these expensive calculations remain impractical for the evaluation of large numbers of protein-ligand complexes and are currently typically limited to family-specific simulations (Huang et al., 2006; Guvench and MacKerell Jr, 2009).

Scoring functions do not fully account for a number of physical processes that are important for molecular recognition, which in turn limits their ability to select and rank-order small molecules by computed binding affinities. It is generally believed (Guvench and MacKerell Jr, 2009) that the two major sources of error in scoring functions are their limited description of protein flexibility and the non-explicit treatment of solvent. In addition to these simplifications, there is an important issue that has received little attention so far. Each scoring function assumes a predetermined theory-inspired functional form for the relationship between the variables that characterise the complex, which also include a set of parameters that are fitted to experimental or simulation data, and its predicted binding affinity. The inherent problem of this rigid approach is that it leads to poor predictivity in those complexes that do not conform to the modelling assumptions. For instance, the van der Waals potential energy of non-bonded interactions in a complex is often modelled by a Lennard-Jones 12-6 function with parameters calibrated with experimental data. However, there could be many cases for which this particular functional form is not sufficiently accurate. Clearly, there is no strong theoretical reason to support the use of the r⁻¹² repulsive term. Furthermore, while the r⁻⁶ attractive term can be shown to arise as a result of dispersion interactions between two isolated atoms, this does not include the significant higher order contributions to the dispersion energy, as well as the many-body effects that are present in protein-ligand interactions (Leach, 2001). Moreover, resampling strategies, such as cross-validation or bootstrapping, are still not systematically used to guard against the overfitting of calibration data in parameter estimation for scoring functions (Irwin, 2008).

As an alternative to modelling assumptions in scoring functions, non-parametric machine learning can be used to implicitly capture binding effects that are hard to model explicitly. By not imposing any particular functional form for the scoring function, any possible kind of interaction can be directly inferred from experimental data. The first study of this kind that we are aware of (Deng et al., 2004) was based on the distance-dependent interaction frequencies between a set of pre-defined atom types observed in two separate modestly sized datasets. Kernel Partial Least Squares was trained on these data, and finally validated against several small external test sets (6 or 10 compounds). This study was a valuable proof-of-concept that machine learning can produce useful scoring functions. More recently (Amini et al., 2007), Support Vector Regression (SVR) was applied to produce family-specific scoring functions for five different protein-ligand systems using data sets ranging from 26 to 72 complexes. Excellent correlation coefficients on the cross-validation data partitions were obtained. Importantly for the interpretability of data, Inductive Logic Programming was used in combination with SVR to derive a set of quantitative rules that can be used for hypothesis generation in drug lead optimisation. In contrast to machine learning based scoring functions, there has been much more research on machine learning approaches to Quantitative Structure-Activity Relationships (QSAR). However, QSAR bioactivity predictions are exclusively based on ligand molecule properties. Hence, unlike scoring functions, QSAR performance is inherently limited by the fact that the information from the protein structure is not also exploited.

Here we present the first application of Random Forests (Breiman, 2001) to predicting protein-ligand binding affinity. Random Forest (RF) is a machine learning technique based on an ensemble of decision trees generated from bootstrap samples of training data, with predictions calculated by consensus over all trees. RF does not assume any a priori relationship between the descriptors that characterise the complex and binding data, and thus should be sufficiently flexible to account for the wide variety of binding mechanisms observed across diverse protein-ligand complexes. RF is particularly suited for this task, as it has been shown (Svetnik et al., 2003) to perform very well in nonlinear regression. In addition, RF can be also used to estimate variable importance as a way to identify those protein-ligand contacts that contribute the most to the binding affinity prediction across known complexes. Lastly, the availability of substantially more data suggests that machine learning should now be an even more fruitful approach, leading to scoring functions with greater generality and prediction accuracy.

The rest of the paper is arranged as follows. Section 2 describes the benchmark used to validate scoring functions. Section 3 presents the scoring functions and experimental setup used in this study, with particular attention to RF. In Section 4, we will construct and study a RF-based scoring function (RF-Score). Lastly, in Section 5, we will present our conclusions as well as outline the future prospects of this promising class of scoring functions.

2 MATERIALS

2.1 Validation using the PDBbind benchmark

A number of studies (e.g. Wang et al., 2003; Ferrara et al., 2004; Wang et al., 2004; Cheng et al., 2009) have validated scoring functions based on their ability to predict the binding affinities of diverse protein-ligand complexes. Indeed, since current algorithms are generally able to find poses that are close to the co-crystallised ligand, it makes sense to focus on the much harder scoring task so that the intrinsic properties of scoring functions are studied in isolation. Otherwise, confounding factors present in alternative enrichment validations such as the adopted docking algorithm, the particular target considered, or the composition of the ligand and decoy sets could even lead to contradictory conclusions (Cheng et al., 2009). Consequently, this approach permits a reliable assessment of the proposed function for re-scoring purposes.

The PDBbind benchmark (Cheng et al., 2009) is an excellent choice for validating generic scoring functions. It is based on the 2007 version of the PDBbind database (Wang et al., 2005), which contains a particularly diverse collection of protein-ligand complexes, as it was assembled through a systematic mining of the entire Protein Data Bank (PDB; Berman et al., 2000). The first step was to identify all the crystal structures formed exclusively by protein and ligand molecules. This excluded protein-protein and protein-nucleic acid complexes, but not oligopeptide ligands as they do not normally form stable secondary structures by themselves and therefore may be considered as common organic molecules. Secondly, Wang et al. collected binding affinity data for these complexes from the literature. Emphasis was placed on reliability, as the PDBbind curators manually reviewed all binding affinities from the corresponding primary journal reference in the PDB.

In order to generate a refined set suitable for validating scoring functions, the following conditions were additionally imposed by the curators. First, only complete and binary complex structures with a resolution of 2.5Å or better were considered. Second, complexes were required to be non-covalently bound and without serious steric clashes. Third, only high quality binding data were included. In particular, only complexes with known dissociation constants (K_d) or inhibition constants (K_i) were considered, leaving those complexes with assay-dependent IC₅₀ measurements out of the refined set. Also, because not all molecular modelling software can handle ligands with uncommon elements, only complexes with ligand molecules containing just the common heavy atoms (C, N, O, F, P, S, Cl, Br, I) were considered. In the 2007 PDBbind release, this process led to a refined set of 1300 protein-ligand complexes with their corresponding binding affinities.

Still, the refined set contains a higher proportion of complexes belonging to protein families that are overrepresented in the PDB. This is detrimental to the goal of identifying those generic scoring functions that will perform best over all known protein families. In order to minimise this bias, a core set was generated by clustering the refined set according to BLAST sequence similarity (a total of 65 clusters were obtained using a 90% similarity cutoff). For each cluster, the three complexes with the highest, median and lowest binding affinity were selected, so that the resulting set had a broad and fairly uniform binding affinity coverage. By construction, this core set is a large, diverse, unbiased, reliable and high quality set of protein-ligand complexes suitable for validating scoring functions. The PDBbind benchmark essentially consists of testing the predictions of scoring functions on the 2007 core set, which comprises 195 diverse complexes with measured binding affinities spanning more than 12 orders of magnitude.

3 METHODS

3.1 Intermolecular interaction features

Machine learning-based regression techniques can be used to learn the nonlinear relationship between the structure of the protein-ligand complex and its binding affinity. This requires the characterisation of each structure as a set of features that are relevant for binding affinity. In this work, each feature will comprise the number of occurrences of a particular protein-ligand atom type pair interacting within a certain distance range. Our main criterion for the selection of atom types was to generate features that are as dense as possible, while considering all the heavy atoms that are commonly observed in PDB complexes. As the number of protein-ligand contacts is constant for a particular complex, the more atom types are considered the more sparse the resulting features will be. Therefore, a minimal set of atom types was selected by considering atomic number only. Furthermore, a smaller set of intermolecular features has the additional advantage of leading to computationally faster scoring functions. However, this simple representation has the drawback of averaging over occurrences of the same element in different covalently bonded environments. More easily chemically interpretable features would arise from the additional consideration of the atom’s hybridisation state and bonded neighbours. This is out of the scope of the present work, but it will be studied in detail in the future.

Here we consider nine common elemental atom types for both the protein P and the ligand L:

$${\left\{P\left(j\right)\right\}}_{j=1}^9=\{C,N,O,F,P,S,Cl,Br,I\}{\left\{L\left(i\right)\right\}}_{i=1}^9=\{C,N,O,F,P,S,Cl,Br,I\}$$

The occurrence count for a particular j-i atom type pair is evaluated as:

$$x_{z\left(P\left(j\right)\right),Z\left(L\left(i\right)\right)}\equiv {\sum }_{k=1}^{K_j}{\sum }_{l=1}^{L_i}ϴ(d_{cutoff}-d_{kl})$$

where d_kl is the Euclidean distance between k^th protein atom of type j and the l^th ligand atom of type i calculated from the PDBbind structure; K_j is the total number of protein atoms of type j and L_i is the total number of ligand atoms of type i in the considered complex; Z is a function that returns the atomic number of an element and it is used to rename the feature with a mnemonic denomination; Θ is the Heaviside step function that counts contacts within a d_cutoff=12Å neighbourhood of the given ligand atom. For example, x_7,8 is the number of occurrences of protein nitrogen interacting with a ligand oxygen within a 12Å neighbourhood. This cutoff distance was suggested in PMF (Muegge and Martin, 1999) as sufficiently large to implicitly capture solvation effects, although no claim about the optimality of this choice is made. This representation leads to a total of 81 features, of which 45 are necessarily zero across PDBbind complexes due to the lack of proteinogenic amino acids with F, P, Cl, Br and I atoms. Therefore, each complex will be characterised by a vector with 36 features:

$$\overrightarrow{x}=(x_{6,6},x_{6,7},x_{6,8},x_{6,9},x_{6,15},x_{6,16},x_{6,17},x_{6,35},x_{6,53},x_{7,6},\dots ,x_{8,53},x_{16,6},\dots ,x_{16,53})\in {\aleph }^{36}$$

On the other hand, the binding affinities uniformly spanned many orders of magnitude and are hence log-transformed. We merge K_d and K_i measurements in a single binding constant K, as this increments the amount of data that can be used to train the machine learning algorithm and preliminary tests showed no significant performance gain from making such a distinction (data not shown). By applying this process to a group of N complexes, the following pre-processed data set would be obtained:

$$D={\left\{\left(y^{\left(n\right)},{\overrightarrow{x}}^{\left(n\right)}\right)\right\}}_{n=1}^{N}y\equiv -{\log }_{10}K$$

3.2 Random Forests for regression

Random Forest (RF) is an ensemble of many different decision trees randomly generated from the same training data. RF trains its constituent trees using the CART algorithm (Breiman et al., 1984). As the learning ability of an ensemble of trees improves with the diversity of the trees (Breiman, 2001), RF promotes diverse trees by introducing the following modifications in tree training. First, instead of using the same data, RF grows each tree without pruning from a bootstrap sample of the training data (i.e. a new set of N complexes is randomly selected with replacement from the N training complexes, so that each tree grows to learn a closely related but slightly different version of the training data). Second, instead of using all features, RF selects the best split at each node of the tree from a typically small number (m_try) of randomly chosen features. This subset changes at each node, but the same value of m_try is used for every node of each of the P trees in the ensemble. RF performance does not vary significantly with P beyond a certain threshold (e.g. Svetnik et al., 2003) and thus we subscribe to the common practice of using P=500 as a sufficiently large number of trees. By contrast, m_try has some influence on performance and thus constitutes the only tuning parameter of the RF algorithm. In regression problems, the RF prediction is made by averaging the individual predictions T_p of all the trees in the forest. Thus, in our case, the binding affinity of a given complex ${\overrightarrow{x}}^{\left(n\right)}$ is predicted by RF as:

$$RF({\overrightarrow{x}}^{\left(n\right)};m_{try})\equiv \frac{1}{P}{\sum }_{p=1}^P{T}_p({\overrightarrow{x}}^{\left(n\right)};m_{try})T_p:{\aleph }^{36}\to {\Re }^{+}\forall p$$

The performance of each tree on predicting Out-Of-Bag (OOB) data, that is complexes not selected in the bootstrap sample and thus not used to grow that tree, gives an internal validation of RF. OOB is a fast resampling strategy carried out in parallel to RF training that yields estimates of prediction accuracy that are very similar to those derived from more computationally expensive k-fold cross-validations (Svetnik et al., 2003). The Mean Square Error (MSE) expressed in terms of the OOB samples is:

$$MS{E}^{OOB}\left(m_{try}\right)=\frac{1}{{\sum }_{p=1}^P\mid I_p^{OOB}\mid }{\sum }_{p=1}^P\sum _{n\in I_p^{OOB}}{(y^{\left(n\right)}-T_p({\overrightarrow{x}}^{\left(n\right)};m_{try}))}^2$$

where I_p^OOB comprises the indices of those complexes that were not used for training the p^th regression tree and |I_p^OOB| is the cardinal of such set. Possible m_try values cover all the feature subset sizes up to the number of features ({2, …,36} in our case), which gives rise to a family of 35 RF models. It is expected that the m_try value with best internal validation on OOB data, i.e. data not used for training, will also provide the best generalisation to independent test data sets. Thus, the selected RF predictor is:

$$RF({\overrightarrow{x}}^{\left(n\right)};m_{try}=m_{best})m_{best}\equiv \underset{m_{try}\in \{2,\dots ,36\}}{\text{arg min}}\left(MS{E}^{OOB}\left(m_{try}\right)\right)$$

RF has also a built-in tool to measure the importance of individual features across the training set based on the process of “noising up” (replacing the value of a given feature with random noise) and measuring the resultant decrease in prediction performance (equivalently, increase in MSE^OOB). The higher the increase in error, the more important that particular feature will be for binding affinity prediction.

In summary, RF has a number of strengths relevant to this nonlinear regression problem, in particular it can handle large numbers of features even when some are uninformative, provides a fast and reliable internal validation estimate, can measure the importance of each feature across data instances, and is generally not strongly affected by overfitting.

3.3 Scoring functions for comparative assessment

A comparative assessment of 16 well established scoring functions, implemented in mainstream commercial software or released by academic research groups, was very recently carried out (Cheng et al., 2009). In our study, we will be using these scoring functions to assess the performance of RF-Score relative to the state of the art. Five scoring functions in the Discovery Studio software version 2.0 (Accelrys, 2001): LigScore (Krammer et al., 2005), PLP (Gehlhaar et al., 1995), PMF (Muegge and Martin,1999; Muegge, 2000; Muegge, 2001; Muegge, 2006), Jain (Jain, 1996) and LUDI (Böhm, 1994; Böhm, 1998). Five scoring functions (D-Score, PMF-Score, G-Score, ChemScore, and F-Score) in the SYBYL software version 7.2 (Tripos, 2006). GlideScore (Friesner et al., 2004; Friesner et al., 2006) in the Schrödinger software version 8.0 (Schrödinger, 2005). Three scoring functions in the GOLD software version 3.2 (Jones et al.,1995; Jones et al.,1997): GoldScore, ChemScore (Eldridge, 1997; Baxter, 1998) and ASP (Mooij and Verdonk, 2005). In addition, two stand-alone scoring functions released by academic groups, that is, DrugScore (Gohlke et al., 2000; Velec et al., 2005) and X-Score version 1.2 (Wang et al., 2002). Several of these scoring functions have different versions or multiple options, including LigScore (LigScore1 and LigScore2); PLP (PLP1 and PLP2), and LUDI (LUDI1, LUDI2, and LUDI3) in Discovery Studio; GlideScore (GlideScore-SP and GlideScore-XP) in the Schrödinger software; DrugScore (Drug-Score^PDB and DrugScore^CSD); and X-Score (HPScore, HMScore, and HSScore). However, for the sake of practicality, only the version/option of each scoring function that performed best on the PDBbind benchmark was considered in (Cheng et al., 2009). We will also restrict our scope here to the best version/option of each scoring function, as listed in Table 1.

Table 1.

Scoring functions tested in the PDBbind benchmark.

Software	Scoring Function	Type
Academic (stand-alone)	DrugScoreCSD	Knowledge-based
	X-Score::HMScore v1.2	Empirical
Discovery Studio v2.0	DS::PLP1	Empirical
	DS::LUDI3	Empirical
	DS::LigScore2	Empirical
	DS::PMF	Knowledge-based
	DS::Jain	Empirical
SYBYL v7.2	SYBYL::ChemScore	Empirical
	SYBYL::G-Score	Force field
	SYBYL::D-Score	Force field
	SYBYL::PMF-Score	Knowledge-based
	SYBYL::F-Score	Empirical
Schrödinger v8.0	GlideScore-XP	Empirical
GOLD v3.2	GOLD::GoldScore	Force field
	GOLD::ChemScore	Empirical
	GOLD::ASP	Knowledge-based

4 RESULTS AND DISCUSSION

4.1 Building RF-Score

The process of training RF to provide a new scoring function (RF-Score) starts by separating the 195 complexes of the core set from the remaining 1105 complexes in the refined set. The former constitutes the test set of the PDBbind benchmark, while the latter is used here as training data. Consequently, the training and test sets do not have complexes in common. Next, each of these sets is pre-processed, as explained in Section 3.1 and implemented in the C code provided in the Supplementary Information. Thereafter, the protocol detailed in Section 3.2 is followed using the training data set only (this is implemented in the R code provided in the Supplementary Information). As a result, it was found that the RF model with the best generalisation to internal validation data corresponded to m_best=5, which obtained an error of RMSE^OOB=1.51 (square root of the MSE^OOB). RF-Score is therefore defined as:

$$f_{RE-Score}\left(\overrightarrow{x}\right)\equiv RF(\overrightarrow{x};m_{try}=5)$$

RF-Score reproduces the training data with very high accuracy. Figure 1 shows the correlation between measured and predicted binding affinities. This is quantified through Pearson’s correlation coefficient (R), which is defined as the ratio of the covariance of both variables over the product of their standard deviations. In this training set, R=0.952, which indicates a very high linear dependence between these variables over the training data. Another commonly reported performance measure is the Root Mean Square Error (RMSE):

$$RMSE\equiv \sqrt{\frac{1}{N}\sum _{n=1}^N{(y^{\left(n\right)}-f\left({\overrightarrow{x}}^{\left(n\right)}\right))}^2}=\sqrt{\frac{N-1}{N}}SD$$

Figure 1.

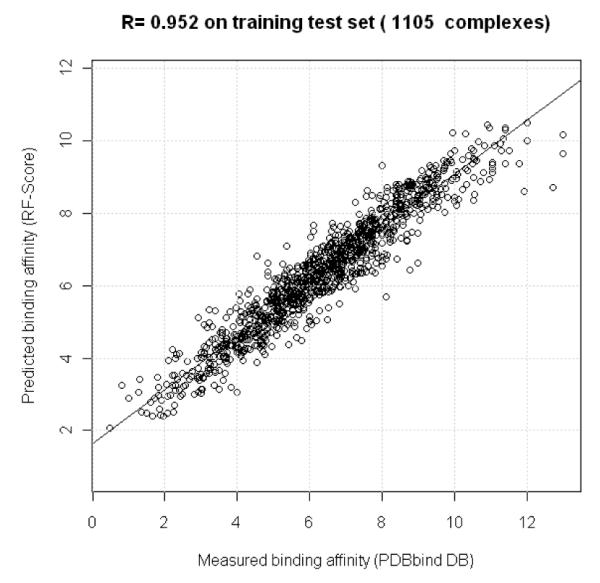
RF-Score reproduces its training data with very high accuracy (Pearson correlation coefficient R=0.952 and RMSE=0.74).

Indeed, RMSE is practically the same as the Standard Deviation (SD) used elsewhere (e.g. Wang et al, 2002), specially for large sets such as this (with N=1105, both RMSE and SD are 0.74 log K units on the training set). The performance on the OOB samples (R^OOB=0.699 and RMSE^OOB=1.51) is a more realistic and useful estimation of RF-Score’s predictive accuracy, since merely fitting the training set does not constitute prediction. Figure 2 shows the increase in error observed when individually noising up each of the 36 intermolecular features. As explained in Section 3.2, this is an estimate of the importance of the given feature for binding affinity prediction across the training data. Among the most important features (%incMSE>20), we find the occurrence counts of hydrophobic interactions (x_6,6), of polar-nonpolar contacts (x_8,6, x_7,6, x_6,8, x_16,6), and also of those intermolecular features correlated with hydrogen bonds (x_7,8, x_8,8, x_8,7, x_7,7).

Figure 2.

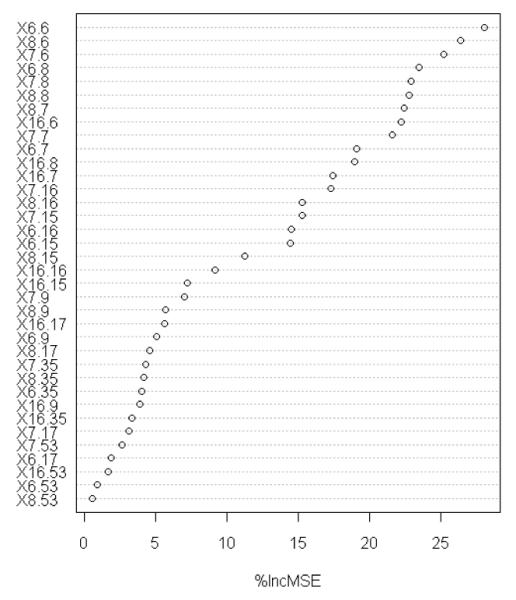
Estimation of feature importance based on internal validation data. Overall, it shows the importance of each type of protein-ligand contact across training complexes, which are by construction representative of the entire PDB.

4.2 RF-Score on the PDBbind benchmark

RF-Score is next tested on an independent external test set. This constitutes a real-world application of the developed scoring function, where the goal is to predict the binding affinity of a diverse set of protein-ligand complexes not used for training/calibration, feature/descriptor selection or model selection. RF-Score predicts binding affinity for test complexes with high accuracy (R=0.778, RMSE=1.58 log K units; see Figure 3). The OOB estimates are close to the performance obtained on the test set, which further supports the usefulness of this validation approach.

Figure 3.

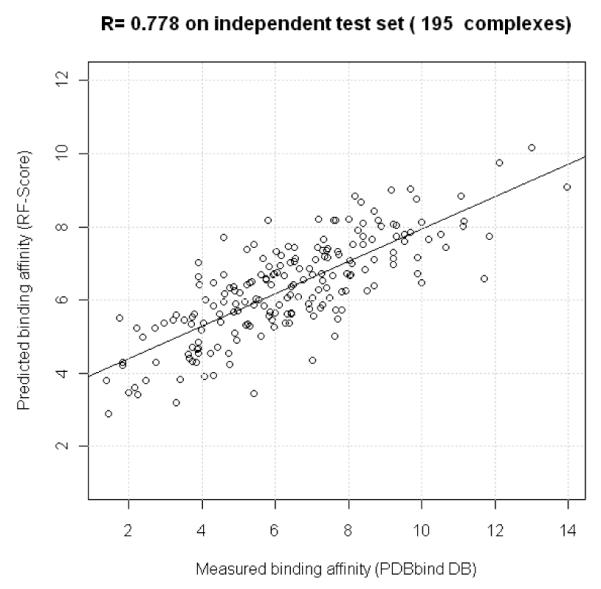
RF-Score predicts the test data with high accuracy (Pearson correlation coefficient R=0.778 and RMSE=1.58).

There is also the question of how much of the predictive ability of RF-Score is due to learning the true relationship between the atomic-level description of structures and their binding affinities. To investigate this, we destroyed any such relationship in the training set by performing a random permutation of y-data (binding affinities), while leaving the intermolecular features untouched. Thereafter, the training process in Section 3.2 was carried out again with this modified data and the resulting RF-Score function used to predict the test set. Over ten independent trials, performance on the test set was on average R=−0.018 with standard deviation S_R=0.095 (average RMSE=2.42 with S_RMSE=0.04). These results demonstrate the negligible contribution of chance correlation to RF-Score’s prediction ability. Such y-scrambling validation is very useful in the validation of QSAR studies (e.g. Rucker et al., 2007), where an optimal set of features is selected over a very large pool of not always relevant molecular (ligand) descriptors and thus the likelihood of chance correlation is much higher.

Importantly for the resulting prediction’s accuracy and generality, we were able to train and validate RF-Score with an unusually large and diverse set of high quality data. This was possible because RF is sufficiently flexible to effectively assimilate large volumes of training data. We have trained and validated RF-Score with randomly chosen differently sized subsets of the training data (see Table 2). Results show that RF-Score’s performance on the test set improves dramatically with increasing training set size (N_train). This strongly suggests that ongoing efforts to compile and curate additional experimental data will be of great importance to improve generic scoring functions further. Also, as expected, the RMSE^OOB generalisation estimate becomes more accurate, i.e. closer to RMSE on the test set, as the training set, and thus the validation set, grows. This is reflected in the ΔRMSE values.

Table 2.

Dependence of RF-Score on size of training set (N_train)

Ntrain	R	Rs	RMSE	mbest	RMSEOOB	ΔRMSE
1105	0.778	0.765	1.58	5	1.51	0.07
900	0.750	0.740	1.63	9	1.51	0.12
700	0.734	0.735	1.69	4	1.52	0.17
500	0.685	0.684	1.77	6	1.44	0.33
300	0.609	0.628	1.90	10	1.46	0.44
100	0.562	0.572	2.01	7	1.56	0.45

R, R_s and RMSE are evaluated over the test set. R_s is the Spearman correlation coefficient, which measures here the ability of a scoring function to predict the correct ranking of complexes according to binding affinity. ΔRMSE≡RMSE-RMSE^OOB

4.3 Comparing with the state of the art

A wide selection of scoring functions has very recently been tested against the PDBbind benchmark (Cheng et al., 2009). These scoring functions are listed in Section 3.3, with references to their original papers. Table 3 presents the performance of these 16 scoring functions along with that obtained in the previous section by RF-Score. Results show that RF-Score obtains the best performance among the tested scoring functions on this benchmark.

Table 3.

Performance of scoring functions on the PDBbind benchmark.

scoring function	R	Rs	SD
RF-Score	0.778	0.765	1.58
X-Score::HMScore	0.644	0.705	1.83
DrugScoreCSD	0.569	0.627	1.96
SYBYL::ChemScore	0.555	0.585	1.98
DS::PLP1	0.545	0.588	2.00
GOLD::ASP	0.534	0.577	2.02
SYBYL::G-Score	0.492	0.536	2.08
DS::LUDI3	0.487	0.478	2.09
DS::LigScore2	0.464	0.507	2.12
GlideScore-XP	0.457	0.435	2.14
DS::PMF	0.445	0.448	2.14
GOLD::ChemScore	0.441	0.452	2.15
SYBYL::D-Score	0.392	0.447	2.19
DS::Jain	0.316	0.346	2.24
GOLD::GoldScore	0.295	0.322	2.29
SYBYL::PMF-Score	0.268	0.273	2.29
SYBYL::F-Score	0.216	0.243	2.35

Pearson’s correlation coefficient (R), Spearman’s correlation coefficient (R_s) and standard deviation of the difference between predicted and measured binding affinity (SD). Scoring functions are ordered in decreasing R, as in (Cheng et al.,2009).

The performance results for the other 16 scoring functions shown in Table 3 were extracted from Cheng et al. (2009). This procedure has a number of advantages. First, it ensured that all scoring functions are objectively compared on the same test set under the same conditions. Like Cheng et al., we consider that a fair comparison of scoring functions requires a common benchmark. Second, by using an existing benchmark, the danger of constructing a benchmark complementary to our own scoring function is avoided. The latter would lead to unrealistically high performance and thus to poor generalisation to other test datasets. Third, the results reported in Table 3 correspond to the version/option of each scoring function that performed best on the PDBbind benchmark. Most importantly, thanks to the team maintaining the PDBbind database, future scoring functions can be unambiguously incorporated into this comparative assessment. Moreover, the free availability of RF-Score codes permits the reproduction of our results and facilitates application of RF-Score to other sets of protein-ligand complexes. Lastly, it could be argued that RF-Score’s performance is somehow artificially enhanced by its training set being related to the test set by the non-redundant sampling explained in Section 2.1. The rationale would be that the other scoring functions could have used training sets chosen without any reference to the test set. Actually, unlike RF-Score, top scoring functions such as X-Score::HMScore, DrugScore^CSD, SYBYL::ChemScore and DS::PLP1 have a number of training complexes in common with the test set (Cheng et al., 2009). In order to investigate whether these overlaps could provide scoring functions with an advantage, the second best performing function in Table 3, X-Score::HMScore, was recalibrated using exactly the same 1105 training complexes as RF-Score in Section 4.1 (i.e. ensuring that training and test sets have no complexes in common). This gave rise to a version we labelled X-Score::HMScore v1.3, which obtained practically the same performance as v1.2 in Table 3 (R=0.649 versus R=0.644). This suggests that training-test links as strong as having data instances in common have little impact on performance on this benchmark. In addition, since RF-Score and our retrained X-Score::HMScore v1.3 used exactly the same training/calibration set and were tested on exactly the same test set, all the performance gain (R=0.778 versus R=0.649) is guaranteed to come from the scoring function characteristics, ruling out any influence of using different training sets on performance.

5 CONCLUSIONS

We have presented a new scoring function called RF-Score. RF-Score was constructed in an entirely data-driven manner by circumventing the need for problematic modelling assumptions via non-parametric machine learning. RF-Score has been shown to be particularly effective as a re-scoring function and can be used for virtual screening and lead optimization purposes. It is very encouraging that this initial version has already obtained a high correlation with measured binding affinities in such a diverse test set.

In the future, we plan to study the use of distance-dependent features, which could result in further performance improvements given that the strength of intermolecular interactions naturally depends on atomic separation. Also, less coarse atom types will be investigated by considering the atom’s hybridisation state and bonding environment. This will enhance the interpretability of features in terms of the intermolecular interactions. Admittedly, a lack of interpretability is currently a drawback of this approach. However, it is important to realise that, although the terms comprising model-based scoring functions provide a description of protein-ligand binding, such a description is only as good as the accuracy of the scoring function. Lastly, machine learning based scoring functions constitute an effective way to assimilate the fast growing volume of high quality structural and interaction data in the public domain and are expected to lead to more accurate and general predictions of binding affinity.