Integrating Sequence Variation and Protein Structure to Identify Sites under Selection

Abstract

We present a novel method to identify sites under selection in protein-coding genes. Our method combines the traditional Goldman–Yang model of coding-sequence evolution with the information obtained from the 3D structure of the evolving protein, specifically the relative solvent accessibility (RSA) of individual residues. We develop a random-effects likelihood sites model in which rate classes are RSA dependent. The RSA dependence is modeled with linear functions. We demonstrate that our RSA-dependent model provides a significantly better fit to molecular sequence data than does a traditional, RSA-independent model. We further show that our model provides a natural, RSA-dependent neutral baseline for the evolutionary rate ratio ω = dN/dS Sites that deviate from this neutral baseline likely experience selection pressure for function. We apply our method to the influenza proteins hemagglutinin and neuraminidase. For hemagglutinin, our method recovers positively selected sites near the sialic acid-binding site and negatively selected sites that may be important for trimerization. For neuraminidase, our method recovers the oseltamivir resistance site and otherwise suggests that few sites deviate from the neutral baseline. Our method is broadly applicable to any protein sequences for which structural data are available or can be obtained via homology modeling or threading.

Introduction

Many approaches to detect sites under selection aim to identify sites with evolutionary rate ratio significantly larger than one (Nielsen and Yang 1998; Suzuki and Gojobori 1999). Maximum-likelihood models are fit to sequence alignments and values for each site are estimated using either random-effects (REL) or fixed-effects (FEL) likelihood models (Nielsen and Yang 1998; Yang et al. 2000; Kosakovsky Pond and Frost 2005; Kosakovsky Pond et al. 2010). Most REL models prespecify a number of rate classes and fit the values for each class as well as the fraction of sites belonging to each class (Nielsen and Yang 1998; Yang et al. 2000; Kosakovsky Pond and Frost 2005). Rates for individual sites are recovered via an empirical Bayes approach. Some works have also attempted to determine the optimal number of rate classes, either via a goodness-of-fit criterion (Kosakovsky Pond et al. 2010) or by employing a Dirichlet process, which fits the number of rate classes as well as their properties (Huelsenbeck et al. 2006; Rodrigue et al. 2010). In contrast, FEL models directly fit an individual value to each site (Kosakovsky Pond and Frost 2005), thus allowing for as many different rates as there are sites in the sequence alignment.

One inherent limitation of all these approaches is that they cannot provide a baseline expectation for the value of a given site. For example, a site with would not be identified as being under positive selection, yet might be unusually high—and possibly indicative of selection for function—if the baseline expectation for this site in this protein was Likewise, sites with particularly low —indicative of negative selection and likely functional importance—cannot be identified at all without a baseline expectation.

Here, we develop maximum-likelihood models that can provide a baseline expectation for and can identify sites that deviate from this baseline. Our method is based on the observation that the evolutionary conservation of a site is correlated with the site’s relative solvent accessibility (RSA, a measure of solvent exposure of the focal amino acid in the folded, three-dimensional protein structure) (Goldman et al. 1998; Mirny and Shakhnovich 1999; Bustamante et al. 2000; Bloom et al. 2006; Franzosa and Xia 2009; Ramsey et al. 2011; Tóth-Petróczy and Tawfik 2011; Scherrer et al. 2012). In our models, is described by linear functions of RSA. We use a model-fit criterion to identify the optimal number of linear functions required to describe all sites in a protein, and for each site, we identify to which linear function it most likely belongs.

We apply our method to two viral proteins, influenza hemagglutinin and neuraminidase. We find that models in which is RSA dependent always provide a better fit than conventional, RSA-independent models. Further, we find that the number of different linear functions needed to describe these viral proteins is small, on the order of 6–10. In general, most sites in a protein fall into an RSA-dependent range of values that we consider the baseline expectation. Sites outside the baseline are candidates for functional selecton. In the case of hemagglutinin, these off-baseline sites are enriched in sites near the sialic acid-binding region. In the case of neuraminidase, few sites fall clearly outside the baseline region, with the exception of the well-known oseltamivir resistance site 274. Our method is easily implemented and broadly applicable to a wide range of scenarios, as long as a crystal structure is available for the protein of interest.

Materials and Methods

Sequence Preparation

Sequences were downloaded for hemagglutinin 3 (H3) and neuraminidase 1 (N1) from the influenza Research Database (Squires et al. 2012). We selected human influenza A sequences, including strains isolated from all geographic regions and years. The full set of H3 and N1 included more than 10,000 nucleotide sequences from each protein. This set was then pared to remove all duplicated sequences. After processing, 2,078 sequences remained for hemagglutinin and 3,322 sequences remained for neuraminidase. Next, a protein structure was downloaded from the protein data bank (PDB) corresponding to each of the two proteins (PDB ID: 1rd8 for hemagglutinin; PDB ID: 1nn2 for neuraminidase). All nucleotide sequences were translated and aligned to the amino acid sequence from the corresponding PDB file, using the MUSCLE sequence alignment tool with default settings (Edgar 2004). After alignment, gaps that were introduced relative to the sequence in the PDB file were removed, and the amino acids were reverted to their nucleotide codons. To make the subsequent evolutionary rate fitting more computationally tractable, we randomly selected 500 of the original pared sequences to be included for further analysis.

For both alignments of 500 sequences, we generated a phylogenetic tree with RAxML (Stamatakis 2006). We used the GTRCAT substitution approximation available in RAxML; this approximation was chosen to make computing a phylogenetic tree computationally tractable with the large number of sequences used here. Similarly, the multithreading option was used in the RAxMLHPC version to speed up the computation. The following command was used to generate the phylogenetic tree:

RSA Determination and Binning

Hemagglutinin and neuraminidase are both functional multimers in solution. We used the crystal symmetry of their X-ray structures to determine the most likely multimeric form for each protein. The DSSP version 1.0 (Kabsch and Sander 1983) program was used to calculate the solvent accessibility (SA) per site on both the monomeric and physiologically relevant multimeric forms, and the absolute accessibility was normalized as described previously (Bloom et al. 2006). The sequence data were then subdivided into eight evenly spaced bins according to the RSA of their sites in the protein structure, as described by Scherrer et al. (2012).

Evolutionary Rate Determination

We implemented a variant of the Goldman–Yang codon evolution model (GY94, Goldman and Yang 1994) in the phylogenetic modeling language HyPhy (Kosakovsky Pond et al. 2005). The model we used is an extension of the model proposed by Scherrer et al. (2012). Briefly, we used the standard GY94 matrix but made the evolutionary-rate ratio the branch length t, and the transition to transversion ratio linear functions in RSA. We express their RSA dependence as:

(1)

(2)

(3)

Further, and are random effects, drawn from discrete distributions with a finite set of categories. Specifically, the distribution of is described by pairs of values such that where Similarly, the distribution of is described by pairs of values where The parameter determines the number of slopes in our model, and the parameter determines the number of intercepts. All other parameters () are fixed effects.

The infinitesimal matrix generator Q for the GY94 model has the usual form (for )

(4)

where is the frequency of codon j, the indices i and j run over all 61 sense codons, and and are RSA dependent, as stated earlier. The transition matrix for finite evolutionary time t becomes

(5)

Here, the branch length t is also a linear function of RSA. Since t can be considered equivalent to the synonymous substitution rate, our model does not assume a single fixed synonymous substitution rate at every site, as is the case in the conventional GY94 model. Scherrer et al. (2012) had previously found that models with RSA-dependent t and fit yeast data better than models with constant t and We confirmed this observation here for influenza proteins.

Optimum Model Determination

We chose to implement a random-effects model (Yang et al. 2000) with independent slopes and intercepts. Optimization of fit parameters was performed by maximum-likelihood estimation in HyPhy. All parameters except the codon frequencies were determined by maximum likelihood. Estimated codon frequencies were calculated from the entire sequence alignment using the F3x4 model.

To identify the overall best-fitting model, we used the Akaike information criterion (AIC) (Akaike 1974; Burnham and Anderson 2004). We fit between zero and five slopes and between one and five intercepts in all pairwise combinations. We defined the best-fitting model as the one with the minimum AIC value.

Structural Mapping

To assign sites to rate classes, we calculated posterior probabilities using the empirical Bayes approach (Nielsen and Yang 1998). For further analysis, we considered sites to either evolve at the rate given by the class with the highest posterior probability or at an average rate calculated over all classes and weighted by the posterior probabilities.

For each of the proteins tested, sites were selected that showed a high and a low RSA or, conversely, a low and a high RSA. Sites of interest were mapped back to the original protein structure using the molecular visualization tool PYMOL (Schrödinger LLC 2010). For comparison, other predicted or verified sites were mined from the literature. In cases where the numbering convention used for the published sites was unclear, we three-dimensionally aligned the protein structure in the literature with our reference structure, using the PYMOL plugin CEALIGN. After three-dimensional alignment, corresponding sites could be mapped regardless of the numbering convention used for each protein.

Results

General Approach

We introduced an RSA dependence to the evolutionary rate the transition/transversion ratio and the branch length t. RSA was incorporated by making and t linear functions of RSA. For example, with RSA dependence becomes as described previously (Scherrer et al. 2012). In the context of REL models, the intercept the slope or both can be either random or fixed effects. Note that Scherrer et al. (2012) used fixed effects for both and Here, we systematically evaluated all possible combinations of fixed and random effects. We fit models with multiple intercepts and a single slope ( is a random effect and is a fixed effect), with a single intercept and multiple slopes ( is a fixed effect and is a random effect), and with both multiple intercepts and multiple slopes (both and are random effects). For comparison, we also fit a model with one intercept and one slope (both and are fixed effects). We treated and t as fixed effects in all models. We represented the traditional, RSA-independent approach by a random-effects model with multiple intercepts for and no slope for t, or In each case, we identified the optimal number of rate classes by AIC.

Conventionally, one would use an RSA-independent model to identify sites with Including an RSA dependence allows us to identify a subset of sites with that likely experience functional selection (e.g., sites that experience a combination of purifying and diversifying selection, such that the resulting value falls below one but is still elevated relative to typical sites at this RSA). The RSA dependence also allows us to identify sites under particularly strong negative selection. Figure 1 shows a schematic representation of a typical result from our model. A canonical trapezoidal shape emerges, where we expect a vast majority of sites to be found. This shape is determined by the structure of the protein, and its exact location and size will vary among structures. We consider any site outside of this region to be important and likely under selection (positive or negative) for function. As sites with would be found by traditional analysis, additional sites found by our method are sites with low RSA and comparatively high and sites with high RSA and very low

Fig. 1.

Regions of interest in –RSA plot. Most sites in proteins fall into a trapezoidal region we consider the neutral baseline. Sites with are generally considered to be under positive diversifying selection. In addition to such sites, our method can also identify sites with an but either larger or smaller than expected given their RSA. These sites fall into the triangular regions below that are either above or below the neutral baseline. Sites in these regions experience either an accelerated or a reduced rate of evolution relative to the baseline and are likely to be functionally important.

Unexpectedly conserved sites are particularly difficult to find by traditional analysis. Sites with low are abundant, because most sites experience some negative selection pressure solely due to the requirement that the protein folds properly and remains stable. With no baseline expectation for at each site, it is unclear which of the sites with low are particularly important, for example, because they are critical for function. As the majority of conserved sites have low RSA values, conserved sites with high RSA stand out as unusual. By incorporating RSA into models of protein evolution, we can identify sites under purifying selective pressure that would normally be missed. Similarly, with our method, sites that have a high RSA and correspondingly high (possibly exceeding one by a small amount) can be included in the null hypothesis (the neutral baseline in fig. 1); such sites might otherwise be considered to be undergoing positive selection.

Application to Influenza Hemagglutinin and Neuraminidase

We applied our method to the influenza proteins H3 and N1. We fit a total of 30 different models to each protein; in these models, the number of intercept classes varied between one and five, and the number of slope classes varied between zero and five. The models were directly compared by subtracting the AIC of each model from the global minimum AIC (corresponding to the best-fitting model). For hemagglutinin, the model containing three slopes and three intercepts provided the global minimum AIC (fig. 2). For neuraminidase, the global minimum was found in the model with two slopes and three intercepts (supplementary fig. S1, Supplementary Material online). Furthermore, all models with at least one slope (i.e., incorporating RSA) gave a substantially better fit than those not incorporating RSA. Likelihood values and numbers of fitted parameters for all models are given in supplementary tables S1 (for hemagglutinin) and S2 (for neuraminidase), Supplementary Material online.

Fig. 2.

Model fit as a function of the number of slopes and intercepts in the model for the influenza hemagglutinin trimer. The shading reflects the difference in AIC between the best model (three slopes and three intercepts in this case) and all other models.

Hemagglutinin forms a homotrimer on the surface of quiescent influenza virus, and neuraminidase is only enzymatically active as a homomultimer (tetramer) within infected cells. Therefore, for both proteins, it is not clear whether RSA measurements should be performed on the monomeric or multimeric forms. It seems likely that both the monomeric and multimeric forms will have some influence on sequence evolution. For example, the monomeric form of a protein should evolve to prevent unfavorable homomultimerization. In contrast, the multimer must evolve to form a stable quaternary structure. Both the monomeric and multimeric forms will evolve to prevent aggregation, but they may do so on different surfaces. Further complicating matters, even for proteins that function only as multimers, we generally have no information about the fraction of time they spend as multimers. If, in solution, the proteins spend very little time multimerized, evolution due to biophysical constraints will act more often on the monomeric forms. We calculated RSA values on both the monomeric and multimeric forms for both hemagglutinin and neuraminidase. For both proteins, the multimeric form provided a better fit than the monomeric form for every combination of slopes and intercepts (not shown). Therefore, we considered only the multimeric forms of these proteins for further analysis.

After fitting the models, we assigned individual evolutionary rates to each site. We employed the empirical Bayes approach to calculate posterior probabilities for each site to belong to each rate class. We then considered two alternatives of how to convert rate classes into site-specific rates. First, we assigned sites to their most probable slope and intercept and then calculated evolutionary rates given each site’s RSA. Second, we calculated an average rate by weighting each rate class with the probability that a site falls into that class. To calculate the weighted average we write

(6)

where is the slope in category i, is the intercept in category j, and is the posterior probability of slope i and intercept j at the site of interest.

Figure 3 shows the results for hemagglutin obtained under the first approach. We selected four representative cases. The top left graph represents the traditional, RSA-independent case. The top right and bottom left graphs represent the mixed models with a single slope and multiple intercepts and with multiple slopes and a single intercept, respectively. The bottom right represents the overall best-fitting model, with Supplementary figure S2, Supplementary Material online, shows the same four cases with rates calculated under the averaging scheme. In comparison to figure 3, averaging reduces some of the very high values. Note also that values are less sensitive to the exact model specification. For the four models shown in supplementary figure S2, Supplementary Material online, the values for the best model correlate with the values for the other three models with Spearman and respectively (in order top left, top right, and bottom left). All correlations are highly significant.

Fig. 3.

Assignments of sites to rate classes, for the influenza hemagglutinin trimer. Each graph shows each site’s dN/dS plotted against the site’s RSA. Sites are assumed to evolve at a dN/dS determined by the rate class they are most likely to fall into. Top left: The best model with multiple intercepts and no slope (no RSA dependence). Top right: The best model with multiple intercepts and one slope. Bottom left: The best model with multiple slopes and a single intercept. Bottom right: The overall best model with three intercepts and three slopes. AIC values are calculated relative to the overall best model. Figure S2 shows the same results but averaged over rate classes.

By fitting an RSA-dependent model to hemagglutinin data, we could identify sites with high that may not experience accelerated evolution. The RSA-independent model (supplementary fig. S2, Supplementary Material online, top left) showed that there are a number of sites with By incorporating RSA, we were able to filter out those sites with high that had correspondingly high RSA. For hemagglutinin, the best-fitting model suggested that at least one site with elevated evolutionary rate should be considered part of the neutral baseline (fig. 4). We also found a set of exposed sites that were highly conserved. In total, for hemagglutinin we found 33 sites that we predicted to experience accelerated evolution (above the upper dashed line in fig. 4) and nine sites that we predicted to be exceptionally conserved (below the lower dashed line in fig. 4). These sites are listed in supplementary table S3, Supplementary Material online.

Fig. 4.

Average versus RSA for hemagglutinin, obtained from the optimal model (three slopes and three intercepts). Dashed lines indicate the trapezoidally shaped neutral baseline (as ascertained by eye). Sites highlighted in red are within 8 Å of the sialic acid-binding region. Sites above the upper dashed line are significantly enriched in sites near the sialic acid-binding region (Fisher’s exact test, OR = 6.6, ).

Hemagglutinin is an important target for protective immunity and has therefore been the topic of many previous analyses. It is well known that many sites in human-influenza hemagglutinin experience adaptive evolution, in particular in domain 1 of the protein, which contains the sialic acid-binding site (Bhatt et al. 2011). Here, we asked whether sites in the sialic acid-binding region were enriched in sites experiencing accelerated evolution. The sialic acid-binding site is expected to be under positive selection, as it is a major target for host range shifts and antibody binding (Whittle et al. 2011). We identified all sites within 8 Å of sialic acid in the hemagglutinin structure and analyzed where they fell in the –RSA plot. We found 39 such sites. (Note that we neither expect all of these sites to have high nor do we expect all sites with high to be near the sialic acid-binding region.) Of these 39 sites, ten fell above the dashed line in figure 4 and 29 below. This represents a significant positive enrichment of such sites at high (Fisher’s exact test, odds ratio = 6.6, ).

We visualized all sites evolving at either accelerated or reduced by mapping them onto the hemagglutinin structure (fig. 5). We found that the majority of the sites with accelerated fell near the top of the hemagglutinin structure, but others occurred in small clusters throughout the structure (fig. 5A). The clustering of these remaining sites suggests that their evolutionary rate is driven by selection pressure mediated by antibody binding. The sites with unusually low given their RSA, fell into three categories. Three sites (69, 121, and 141) were relatively close to the sialic acid-binding region (figs. 5B and C), even though not within the 8 Å we used as cutoff to identify sites near the sialic acid-binding region. (Their distances to the sialic acid-binding region were 17, 18, and 12 Å, respectively). These sites may provide a crucial structural support for proper functioning of the hemagglutinin protein. Three more (163, 236, and 238) seemed to be involved in the trimer interface (figs. 5B and C). The remaining sites were located throughout the protein, and their possible function was not readily apparent (fig. 5A).

Fig. 5.

Sites of interest identified for hemagglutinin. Sites that fall above the upper dashed line in fig. 4 are colored orange. Sites that fall below the lower dashed line in fig. 4 are colored light blue. The polypeptide backbone is colored green. Sialic acid is represented by the space-filling model near the top of the molecule. (A) View of the entire hemagglutinin monomer. (B) View of the sialic acid-binding region. Sites that are highlighted as “SA binding?” are unusually conserved and close to (though not within 8 Å of) the sialic acid. Sites that are highlighted as “trimer interface” are unusually conserved and seem to be important for trimerization. (C) View of the trimer-interface region. Labeling of sites is as in part (B).

We next considered neuraminidase. Overall, neuraminidase showed substantially lower values than does hemagglutinin. Although hemagglutinin had many sites with neuraminidase had just a few. The model with multiple intercepts and no slopes placed five sites at (supplementary figs. S3 and S4, Supplementary Material online, top left). No individual site seemed to stand out particularly under the RSA-independent approach. In contrast, under our best model for neuraminidase, with two slopes and three intercepts, one site stood out as having low RSA and particularly high (supplementary figs. S3 and S4, Supplementary Material online, bottom right). This site is position 274; a common oseltamivir resistance mutation occurs at this site (most commonly H274Y). For neuraminidase, we did not find any highly exposed sites that were particularly conserved. In total, for neuraminidase, we found nine sites that we predicted to experience accelerated evolution (supplementary table S3, Supplementary Material online).

Comparison of Identified Sites with Prior Work

The sites under selection we found here were broadly in agreement with previously identified sites. In a seminal article, Bush et al. (1999) used positively selected sites in H3 to predict influenza evolution. Of the 18 sites they found, 11 sites fell above our null expectation (supplementary fig. S5, Supplementary Material online, left). More recently, Kryazhimskiy et al. (2008) identified 24 sites under directional selection in hemagglutinin; we identified 11 of those 24 sites (supplementary fig. S5, Supplementary Material online, right). Both studies also identified a few sites that had a very low in our analysis. Some of the differences between our and their results are likely due to differences in the sequences analyzed.

Neuraminidase is the protein responsible for enzymatic cleavage of sialic acid following viral entry. In comparison to hemagglutinin, neuraminidase is a less commonly studied protein due, in part, to its intracellular function. As neuraminidase is never exposed to the periplasm, it is not likely to be a major target of protective immune responses. Therefore, we do not expect many of the sites in neuraminidase to evolve rapidly. Indeed, most of its sites show very high conservation; as mentioned previously, neuraminidase contains very few sites with (supplementary figs. S3 and S4, Supplementary Material online).

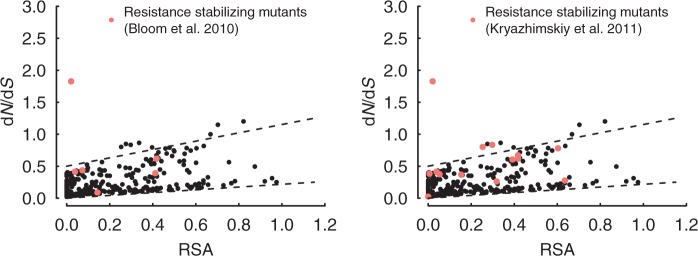
Of those sites found previously by Bloom et al. (2010), we found only the oseltamivir resistance site (site 274 in the PDB structure 1NN2, site 275 in Kryazhimskiy et al. 2011) to be under positive selection (fig. 6, left). Those Bloom sites conferring epistatic stability to the resistance mutation were generally elevated relative to a regression line, but they did not fall significantly above the baseline expectation.

Fig. 6.

Comparison of our results with previous work on neuraminidase. Left: Sites found by Bloom et al. (2010) to be involved in the evolution of oseltamivir resistance are highlighted in red. Right: Site 274 and sites found by Kryazhimskiy et al. (2011) to have 274 as trailing site are highlighted in red.

We also compared our results with the recent work by Kryazhimskiy et al. (2011) (fig. 6, right). They identified sites in neuraminidase that enabled subsequent substitutions at other sites. We specifically considered sites that they identified as leading to substitutions at the oseltamivir resistance site. Among these sites were half of the sites identified by Bloom et al. (2010), so these two studies gave highly congruent results. We found two sites from Kryazhimskiy et al. (2011) significantly above the baseline expectation. Our sites congruent with Kryazhimskiy et al. (2011) are 220 and 430 (in PDB structure 2HU0), both near the sialic acid–cleaving active site. The remaining sites from Kryazhimskiy et al. (2011) were also generally elevated but did not rise above the baseline expectation.

Discussion

We have described a new method for identifying important sites in protein-coding sequences. Furthermore, we have shown that this new method fits molecular sequence data better than a conventional REL approach. To generate improved models, we used the correlation between RSA and evolutionary rate (Franzosa and Xia 2009) to define a new, more accurate evolutionary null expectation. We applied our method to two influenza proteins, H3 and N1; we classified sites with greater than expected given their RSA as positively selected, and sites with lower than expected as negatively selected. Sites found by our method are in agreement with experimentally validated sites and with results from other computational studies. Our method goes beyond previous approaches by finding sites that would previously have been missed (reducing Type II errors) and by including some sites in the null that would normally have been rejected (reducing Type I errors).

Several approaches to fitting evolutionary rate have been developed and improved in the last two decades (Goldman and Yang 1994; Muse and Gaut 1994; Nielsen and Yang 1998; Suzuki and Gojobori 1999; Yang et al. 2000; Kosakovsky Pond and Muse 2005; Kosakovsky Pond and Frost 2005; Yang 2006; Rodrigue et al. 2010; Kosakovsky Pond et al. 2010). One approach, FEL-based fitting (Kosakovsky Pond and Frost 2005), involves estimating an independent value at each site; although an FEL approach limits Type I errors, it can lead to model overparameterization as there is no obvious way to penalize overparameterized models. Another approach, counting methods (Kosakovsky Pond and Frost 2005), is conceptually simpler but estimates independent and t parameters at each site. Although may vary substantially among sites, and t are not likely to do so; therefore, estimating them per site leads to overfitting. Moreover, as sites are treated independently, both FEL and counting methods require a large number of sequences per gene to gain power (Kosakovsky Pond and Frost 2005). Traditional REL-based rate estimation relies on a predefined distribution for and a prespecified number of rate classes (Kosakovsky Pond and Frost 2005). As a result, all sites are aggregated to increase power when a large number of sequences are not available; however, with a very small number of sequences, REL methods tend to lead to increased Type I errors (Kosakovsky Pond and Frost 2005). In addition, estimating the number of rate classes becomes a potential complicating factor for REL methods. Although a model with k classes is nested into a model with k + 1 classes, one cannot simply carry out a likelihood ratio test to determine which model provides the better fit, because the nesting is not identifiable (Azaïs et al. 2009).

Here, we chose to identify the optimal number of classes by testing all plausible candidate REL models and ranking them according to their AIC. We found that the total number of classes needed was relatively small: two to three slopes and three intercepts were sufficient to describe relatively large alignments of hemagglutinin and neuraminidase. In general, the number of classes for optimal fit will likely vary among proteins. Alternative methods of identifying the optimal number of rate classes include adding classes until a goodness-of-fit criterion fails (Kosakovsky Pond et al. 2010) or using a Dirichlet process to fit number of classes as a parameter in the model (Huelsenbeck et al. 2006; Rodrigue et al. 2010). Either of these approaches could be employed with our RSA-dependent model of codon evolution.

When using a random-effects model, one has to decide how to assign values to individual sites. We considered two alternative approaches. To each site we assigned either the value corresponding to the most probable rate class for the site or an average value calculated as a weighted average over all classes. We think that both approaches are valuable. The first approach produces simpler graphs, as it highlights the linear RSA dependency employed in the model. Using this approach, we can easily tell which sites fall into common rate classes (i.e., are part of the neutral baseline) and which sites have unusual given their RSA. A downside of this approach is that sites which have comparable posterior probabilities for two or more classes will appear to belong exclusively to a single class. This downside is alleviated by the second approach, which will place those sites at intermediate, averaged values. A second advantage of the averaging approach is that average values are relatively insensitive to the model specification (exact number of slopes and intercepts).

We analyzed a Goldman–Yang model (Goldman and Yang 1994) in which both the evolutionary-rate ratio and time t were RSA dependent, but only was implemented as a random effect that could vary independently among sites. An alternative model would be a structure-aware Muse–Gaut model (Muse and Gaut 1994). The Muse–Gaut model uses parameters and instead of and t, with and In models that incorporate site variability but no structural information, the Muse–Gaut model is generally preferred over the Goldman–Yang model (Kosakovsky Pond and Muse 2005; Delport et al. 2009; Kosakovsky Pond et al. 2010), because the Muse–Gaut model naturally allows for variation in both synonymous and nonsynonymous evolutionary rates (by treating both and as random effects). In contrast, when RSA is taken into account but other site variation is ignored, the Goldman–Yang model performs better than the Muse–Gaut model, indicating that varies linearly with RSA and does not (Scherrer et al. 2012). Whether the Muse–Gaut or the Goldman–Yang formulation should be preferred in the most general case, incorporating both structural information and synonymous and nonsynonymous rate variation remains an open question for future research.

We have shown that accounting for biophysical constraints in models of sequence evolution can reduce the frequency of Type I errors, by excluding sites with at high RSA. For hemagglutinin, we were able to exclude at least one site with high evolutionary rate that had proportionately high RSA values. Our model also likely reduces Type II errors, by identifying sites with as experiencing accelerated evolution. Several of the sites identified by Bush et al. (1999) or Kryazhimskiy et al. (2008) (supplementary fig. S5, Supplementary Material online), or of the sites near the sialic acid-binding region (fig. 4), fell into this category. One drawback of our method is that defining which sites fall into the null expectation and which fall outside it ultimately lies with the human researcher carrying out the analysis. Since our method is fundamentally prospective, geared toward identifying sites of potential interest in further experimental analysis, we do not consider this drawback as particularly severe. It is also important to keep in mind that sites with above the baseline but below one could either be subject to a mixture of positive and negative selection pressures or they could simply be subject to very little selection pressure at all, despite of their location in the protein. Finally, we saw some discrepancies between the sites we identified and sites found in previous works (supplementary fig. S5, Supplementary Material online). We have no reason to believe that the inclusion of RSA into our model caused these discrepancies, since they also arose in our RSA-independent model. Most likely, these discrepancies were caused by differences in the alignments analyzed.

Several previous articles have proposed models of coding-sequence evolution that incorporate structural information. The simplest approach is to partition coding sequences according to a structural property (e.g., partition all sites into buried and exposed sites) and fit a fixed-effects model whose model parameters may vary by partition (Yang and Swanson 2002; Bao et al. 2007; Conant and Stadler 2009; Scherrer et al. 2012). These partitioned models tend to fit sequence data better than do nonpartitioned models. They are good at identifying differences among partitions, but they cannot identify individual sites that show unusual rates given their partition. More sophisticated models contain selection terms incorporating SA or energetic interactions among residues in a structure (Robinson et al. 2003; Rodrigue et al. 2005, 2006, 2009; Choi et al. 2007). These models also tend to fit sequence data better than comparable models without structural information. However, it is not clear whether they can be used in a straightforward manner to identify individual sites under selection. The advantage of our method is that it is straightforward to implement, it requires only moderate amounts of processing time, and it produces results that are easily interpretable. A limitation of all these methods, including ours, with respect to viral evolution is that they assume site independence when sites in most viral proteins are actually tightly linked. This limitation may cause overinflated variability in evolutionary rates or even biased estimates. The exact consequences of this limitation have received little attention and remain poorly understood, however.

One complicating factor in our approach comes from the proper measurement and interpretation of physiologically relevant protein structures. We tested both the monomeric and multimeric forms of each protein and found that the multimeric forms produced a better model fit in both cases. It is unclear whether the multimeric RSA would always be preferred. Goodness of fit may be related to the most common state of free, solvated protein. RSA values may also be incorrect because crystal structures reflect a single protein conformation but solvated proteins fluctuate among neighboring conformations. In future work, one could attempt to improve the accuracy of RSA calculations by estimating these fluctuations using molecular dynamics simulations.

Even though we introduced RSA dependence into the rate parameters of our model (, t, and ), we held the equilibrium codon frequencies constant throughout all sites in the protein. Holding codon frequencies constant is a convenient approximation that is usually employed when calculating evolutionary rates. However, in the structural context, it would be desirable to make codon frequencies depend on the structure as well. Amino-acid frequencies vary with RSA, the most hydrophobic amino acids being the most common at low RSA values and the most hydrophilic ones being the most common at high RSA values (Porto et al. 2004; Ramsey et al. 2011). Consequently, codon frequencies must similarly vary with RSA. We suspect that some of this variation was absorbed into and t in our model. Nevertheless, a more realistic model would be desirable. At present, however, we are not sure how to formulate such a model. We could make the linear functions of RSA as well, but this modeling choice would add a large number of parameters and possibly lead to an overparametrized model.

In summary, our work has shown that accounting for RSA in evolutionary-rate models improves model fit. In addition, we were able to find the best-fitting model by exhaustively testing different numbers of slopes and intercepts. We could confirm extensive selection pressure near the sialic acid-binding site in the influenza protein hemagglutinin. Further, we could show that the oseltamivir-resistance site 274 in influenza neuraminidase stands out among the sites in this protein as experiencing particularly strong positive selection. Finally, our analysis of hemagglutin and neuraminidase offers new, potentially important sites for experimental investigation.

Supplementary Material

Supplementary tables S1–S3 and figures S1–S5 are available at Molecular Biology and Evolution online (http://www.mbe.oxfordjournals.org/).