Skip to main content
PMC home page
Human Genomics logoLink to Human Genomics
. 2005 Jun 1;2(2):81–89. doi: 10.1186/1479-7364-2-2-81

Large-scale SNP analysis reveals clustered and continuous patterns of human genetic variation

Mark D Shriver 1,✉, Rui Mei 2, Esteban J Parra 3, Vibhor Sonpar 1, Indrani Halder 1, Sarah A Tishkoff 4, Theodore G Schurr 5, Sergev I Zhadanov 5,6, Ludmila P Osipova 6, Tom D Brutsaert 7, Jonathan Friedlaender 8, Lynn B Jorde 9, W Scott Watkins 9, Michael J Bamshad 9,10, Gerardo Gutierrez 1, Halina Loi 2, Hajime Matsuzaki 2, Rick A Kittles 11, George Argyropoulos 12, Jose R Fernandez 13, Joshua M Akey 14, Keith W Jones 2
PMCID: PMC3525270  PMID: 16004724

Abstract

Understanding the distribution of human genetic variation is an important foundation for research into the genetics of common diseases. Some of the alleles that modify common disease risk are themselves likely to be common and, thus, amenable to identification using gene-association methods. A problem with this approach is that the large sample sizes required for sufficient statistical power to detect alleles with moderate effect make gene-association studies susceptible to false-positive findings as the result of population stratification [1,2]. Such type I errors can be eliminated by using either family-based association tests or methods that sufficiently adjust for population stratification [3-5]. These methods require the availability of genetic markers that can detect and, thus, control for sources of genetic stratification among populations. In an effort to investigate population stratification and identify appropriate marker panels, we have analysed 11,555 single nucleotide polymorphisms in 203 individuals from 12 diverse human populations. Individuals in each population cluster to the exclusion of individuals from other populations using two clustering methods. Higher-order branching and clustering of the populations are consistent with the geographic origins of populations and with previously published genetic analyses. These data provide a valuable resource for the definition of marker panels to detect and control for population stratification in population-based gene identification studies. Using three US resident populations (European-American, African-American and Puerto Rican), we demonstrate how such studies can proceed, quantifying proportional ancestry levels and detecting significant admixture structure in each of these populations.

Keywords: population genetics, population genomics, human evolution, migration, admixture, population stratification

Introduction

Substantial progress has been made using genetic markers to elucidate the evolutionary histories of populations, yet this work has primarily been accomplished using large numbers of individuals and small numbers of genetic markers [6,7]. More recently, studies screening large numbers of markers have demonstrated their effectiveness at clarifying more subtle patterns of population stratification [8,9]. Such studies can facilitate the exploration of the genetic structure that may exist among and within populations and also provide a valuable source of ancestry informative markers (AIMs) to quantify and adjust for this structure in gene-identification studies.

Results

Here, we analysed 11,555 single nucleotide polymorphism (SNP) markers in 12 population samples using a new microarray-genotyping platform called Whole Genome Sampling Amplification (WGSA; Affymetrix, Santa Clara, CA). Populations were selected to represent a broad spectrum of world variation (Table 1). Four populations stand out as having similarly elevated heterozygosity (Burunge, Spanish, Indian and Altaian). Four groups (Nahua, Quechua, Nasioi and Mbuti) have lower levels of variability, while the two East Asian populations and the Mende are intermediate. These results are largely consistent with expectations for populations known to have experienced restrictions in population size (eg Mbuti, Nasioi, Nahua and Quechua), reducing levels of genetic variability relative to other populations;[9,10] however, ascertainment bias in terms of the population (s) in which markers were first discovered precludes making strong statements about differences in variability using SNP data [11]. In addition, ascertainment bias -- such as that resulting from both a limited representation of populations and small numbers of individuals in discovey panels-- can lead to deviations in linkage disequilibrium estimates,[12] artefactually elevated FST levels (see Ronald and Akey in this issue of Human Genomics) and higher derived allele frequencies in non-African than in African populations [13]. Despite the general importance of considering ascertainment bias on a number of population genetic parameter estimates, there is no evidence or theory that predicts problems from ascertainment bias on estimates of measures of individual relatedness or deviations from Hardy - Weinberg equilibrium (HWE). Randomly mating populations are expected to show genotype frequencies that are consistent with HWE expectations. The results of tests for HWE are presented as the proportion of loci that have deviations from equilibrium expectations (Table 1). Some populations show slightly higher or lower proportions of significant results. The most notable deviation is seen when all the populations are combined, at which point over half (56 per cent) of the SNPs show significant HWE deviations. These deviations highlight the importance of taking population structure into account in gene-association studies. Extensive admixture structure is created by combining these samples, leading to HWE deviations and, presumably, allelic associations among unlinked markers at loci showing large frequency differences across populations [3].

Table 1.

Populations and summary statistics for autosomal single nucleotide polymorphism (SNP) loci

Population Location Sample size Heterozygositya Monomorphic SNP loci % HWE deviationsb
Mbuti Ituri forest 20 0.280 0.126 0.050
Mende Sierra Leone 22 0.323 0.074 0.058
Burunge Tanzania 20 0.341 0.049 0.062
Spanish Valencia 20 0.346 0.057 0.063
Indian India 22 0.356 0.042 0.050
 Upper caste India 11 0.357 0.070 0.047
 Lower caste India 11 0.352 0.077 0.040
Nasioi Melanesia 19 0.280 0.181 0.031
Altaian Siberia 20 0.350 0.048 0.046
East Asian USA 20 0.327 0.096 0.045
Chinese USA 10 0.327 0.135 0.023
Japanese USA 10 0.324 0.146 0.022
Nahua Mexico 20 0.295 0.156 0.069
Quechua Peru 20 0.297 0.127 0.062
Total sample 203 0.377 0.000 0.536
Open in a new tab

a Average unbiased heterozygosity.

b Proportion of deviations from Hardy-Weinberg equilibrium (HWE) using α = 0.05 with standard χ2 test.

The proportion of the total genetic variation due to differences among populations was estimated using FST. Figure 1 shows a histogram of the FST distribution, with the autosomal SNPs plotted separately from the X-linked SNPs. The average level of FST for autosomal SNPs (0.148) is within the range of previously published FST estimates (5 - 15 per cent), confirming the well-known fact that most variability in human populations is observed within populations [4-6,14,15]. The average FST observed for the X-chromosomal SNPs (0.224) is substantially higher than that for the autosomal SNPs (p < 0:0001), which is consistent with both the smaller effective population size and the higher levels of natural selection for X-chromosome genes [16-18]. It is also notable that these distributions are not described well by averages, since they are highly skewed and have long tails, highlighting the fact that unlinked loci can have different evolutionary histories [19].

Figure 1.

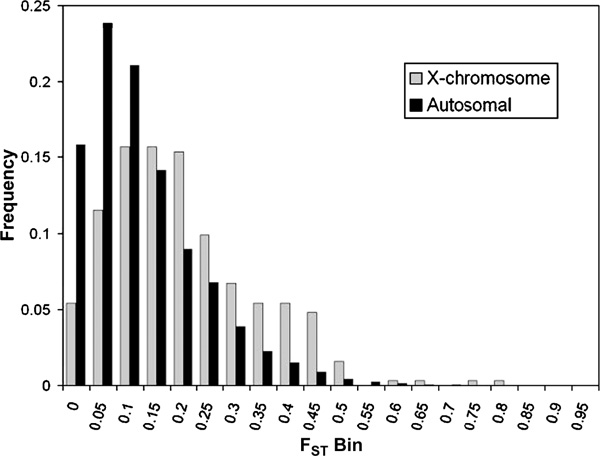
Figure 1

Open in a new tab

Distribution of locus-specific FST for autosomal (n = 11,078, grey bars) and X-linked (n = 313, black bars) single nucleotide polymorphism loci.

For calculating heterozygosity and FST, population divisions were assumed to be known and individuals were grouped using ethnic and geographical information. Given the large number of markers in our dataset, population genetic analyses can be performed at the level of the individual, making no presumption of group membership [18,20]. Two methods were used to investigate clustering among individuals: neighbour-joining trees [21] and principal coordinates (PCs) analysis, using the allele-sharing distance (ASD)[22] for all pairwise combinations of individuals. Figure 2 shows a neighbour-joining tree of individuals, constructed with the ASD measure matrix, using 11,078 autosomal SNPs. The root of the tree, based on the combined ape out-group, is located between the Mende and Mbuti. This supports an African origin for modern humans. The next group to diverge from the main trunk is the East African Burunge. Most populations have population-specific branches of substantial length, the largest being the Melanesians and the indigenous Americans. In addition to the Burunge, the South Asian Indians and the Altaians have relatively short population-specific branches, consistent with gene flow between these groups and other populations. The largest internal branch separates the three African from the non-African populations, and the next group to diverge is the Spanish, followed by the South Asian Indians. No clear separation of the upper and lower caste populations is seen here (but see Figure 3).

Figure 2.

Figure 2

Open in a new tab

Neighbour-joining tree of the 203 individuals included in this study, using an allele-sharing distance matrix. The genotype of the ancestral state (ROOT) is taken from those markers showing one common homozygous genotype for two chimpanzees and two gorillas. Individual population affiliations are indicated by the following abbreviations: MBti (Mbuti), Brng (Burunge), Sp (Spanish), Indl (Indian lower caste), Indu (Indian upper caste), Bgvl (Nasioi), Qech (Quechua), Nah (Nahua), Alt (Altaian), Ch (Chinese), Jp (Japanese).

Figure 3.

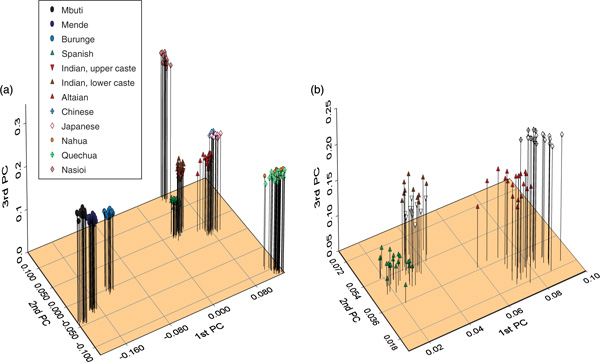
Figure 3

Open in a new tab

Principal components (PCs) plot of the 203 individuals based on the allele-sharing distance matrix. Individuals are the basis of analysis and have been labelled with symbols as indicated in the figure legend. The first three of four significant PCs (using the broken-stick method) axis are shown on this plot. (a) Space showing all individuals. (b) Enlarging the segment of the plot with the European and Asian populations.

Although trees provide a useful means of illustrating relationships among populations or individuals, they are limited by the assumption of bifurcating topologies. PC analysis is an alternative analytical method, which lacks this assumption. Figure 3a shows the first three PC axes for all populations. As with the tree, individuals from one population cluster tightly, to the exclusion of individuals from other populations. The first PC axis shows a separation of the African and non-African populations, with the Burunge being closer to the non-Africans than either of the other two African populations. The second PC axis shows the indigenous Americans and Melanesians to be on opposite sides of the axis. On the tree, the two indigenous American populations are separated into monophyletic clusters, while the PC analysis shows overlapping clusters. When focusing on the Eurasian populations (Figure 3b), there is a clinal relationship across all three PC axes for these populations, which is consistent with their geographic positions from Spanish in the lower left to Japanese in the upper right. Notable are the near separation of the Indian sample into lower and upper caste, with the upper caste individuals positioned closer to the Spanish [23,24]. Additionally, the Altaians are intermediate between the East Asians and the Europeans, a finding that is consistent with Y-chromosomal studies showing Central Asian origins for components of the European gene pool [25].

Another way of exploring the PC analysis results is to examine the pairwise plots of the PC components. As the first four components were significant using the broken stick test, not all can be plotted in three-dimensional space. The six possible pairwise plots are presented in Figures 4a-f.

Figure 4.

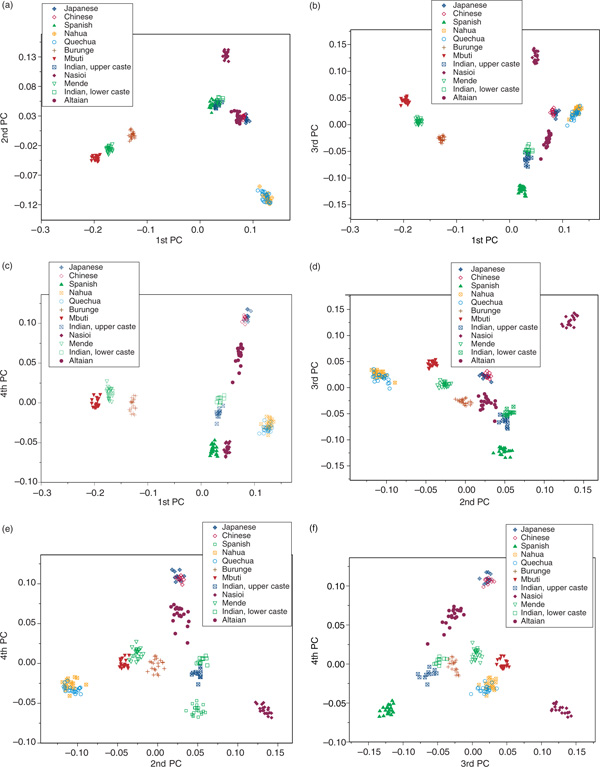
Figure 4

Open in a new tab

Bivariate plots for the six possible combinations of the four significant principal coordinates. Symbols used to indicate populations are consistent across figures (a) to (f) (see individual keys) and the components presented are indicated on the X and Y axes: (a) 1st and 2nd, (b) 1st and 3rd, (c) 1st and 4th, (d) 2nd and 3rd, (e) 2nd and 4th and (f) 3rd and 4th.

In addition to these 12 geographically well-defined population samples, we have analysed three cosmopolitan samples collected in the USA (African-Americans, European-Americans and Puerto Ricans). These populations are known to have been subject to both within-continent and among-continent admixture in the recent past. We estimated the individual biogeographical ancestry levels for each person in these three samples. These maximum likelihood estimates of proportional ancestry (Figure 5) show a greater tendency for the European-American subjects to cluster together, by comparison with the other two population samples. The African-Americans and Puerto Ricans both show relatively high levels of variability in individual ancestry levels, with most of the non-African ancestry in the African-Americans being from Europe. The Puerto Ricans show some individuals with more indigenous American ancestry, as well as substantial West African ancestry.

Figure 5.

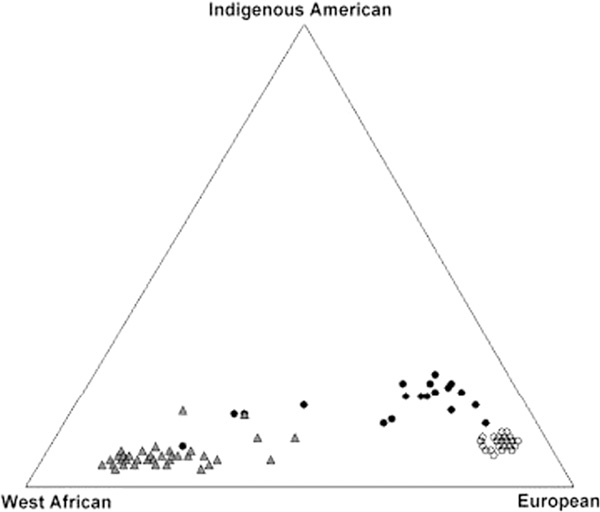
Figure 5

Open in a new tab

Triangle plot of three populations, illustrating maximum likelihood estimates of individual ancestry. Puerto Ricans (n = 20) are shown as filled circles, African-Americans (n = 42) as grey triangles and European-Americans (n = 41) as open circles. Parental populations in this analysis are the average of the Nahua and Quechua as the indigenous American; Mende as the West African; and Spanish as the European.

Another test for the presence of admixture structure is based on correlations in individual ancestry indices calculated from independent (unlinked) panels of markers [26]. We tested for significant correlations using two types of individual indices, PCs (Table 2) and biogeographical ancestry (Table 3), calculated separately from the even and odd chromosomal SNPs. To do this, we divided the SNPs into two groups; all of the SNPs on even chromosomes in one group and all of the SNPs on odd chromosomes in the other group. Unless there is structure which is related to the axes of ancestry measured by these indices within a population, no significant relationship between the two estimates is expected [25]. The correlation results on the PC components show that only three (upper caste Indian, Altaian and Nasioi) of the 12 world populations show evidence of population structure. The combined Indian sample (upper caste and lower caste together) also shows significant correlations, while the combined East Asian (Japanese and Chinese) population does not. Alternatively, all three cosmopolitan samples tested (African-American, European-American and Puerto Rican) show significant correlations between the even and odd chromosome PC analyses. Significant correlations are also seen for the estimates of biogeographical ancestry in these three populations (Table 3). It is notable that, not only are there high correlations in the African-American and Puerto Rican samples, but also in the European-American sample, indicating the presence of admixture structure in a population generally assumed to be homogeneous [27].

Table 2.

Correlation coefficients for comparisons between principal components (PC) estimates from the even and odd chromosome marker sets

Population First PC Second PC Third PC Fourth PC
African-American 0.796 (<0.0001) 0.495 (0.001) 0.125 (NS) 0.219 (NS)
European-American 0.498 (0.001) 0.021 (NS) 0.134 (NS) 0.078 (NS)
Puerto Rican 0.624 (0.003) 0.761 (<0.0001) 0.417 (NS) 0.412 (NS)
Mbuti 0.098 (NS) 0.004 (NS) 0.014 (NS) 0.41 (NS)
Mende 0.170 (NS) 0.236 (NS) 0.353 (NS) 0.302 (NS)
Burunge 0.197 (NS) 0.114 (NS) 0.051 (NS) 0.265 (NS)
Spanish 0.203 (NS) 0.065 (NS) 0.014 (NS) 0.157 (NS)
Indian, all 0.183 (NS) 0.659 (0.001) 0.612 (0.002) 0.483 (NS)
Indian, lower caste 0.145 (NS) 0.565 (NS) 0.236 (NS) 0.491 (NS)
Indian, upper caste 0.500 (NS) 0.736 (0.01) 0.342 (NS) 0.191 (NS)
Altaian 0.136 (NS) 0.784 (<0.0001) 0.108 (NS) 0.448 (NS)
East Asian 0.158 (NS) 0.403 (NS) 0.047 (NS) 0.043 (NS)
Chinese 0.515 (NS) 0.127 (NS) 0.188 (NS) 0.376 (NS)
Japanese 0.503 (NS) 0.539 (NS) 0.049 (NS) 0.24 (NS)
Quechua 0.160 (NS) 0.380 (NS) 0.384 (NS) 0.399 (NS)
Nahua 0.047 (NS) 0.215 (NS) 0.097 (NS) 0.165 (NS)
Nasioi 0.015 (NS) 0.283 (NS) 0.742 (<0.0001) 0.775 (<0.0001)
Open in a new tab

Shown is Spearman's correlation coefficient and p value in parentheses. Significant corrections among even and odd chromosomal estimates are shown in bold.

Table 3.

Correlation coefficients for comparisons between biogeographical ancestry estimates from the even and odd chromosome marker sets

Population (n)/ancestral C component West African European Indigenous American
African American (n = 42) 0.951 (p < 0.0001) 0.904 (p < 0.0001) 0.635 (p < 0.0001)
European American (n = 41) 0.766 (p < 0.0001) 0.750 (p < 0.0001) 0.395 (p = 0.0011)
Puerto Rican (n = 20) 0.881 (p < 0.0001) 0.924 (p < 0.0001) 0.810 (p < 0.0001)
Open in a new tab

Shown is Spearman's correlation coefficient and p value in parentheses.

Discussion

The large number of markers used in these analyses has provided an opportunity to assess genetic variation at the level of the individual in a number of populations from around the world. These multilocus genotype data on a large panel of SNPs provide a new level of resolution in the distribution of variation within and among populations. Individuals cluster into groups comprising other individuals from their own or closely-related populations when diverse groups from around the world are analysed [28,29]. By contrast, when samples from the more cosmopolitan US resident populations are analysed, clustering patterns are less discrete. Substantial levels of variation in ancestry are observed within the African-American and Puerto Rican samples, while smaller, but significant, admixture structure is evident in the European-American sample. Whether the admixture structure in the European-American sample is the result of intraor intercontinental gene flow is an important outstanding question. Thus, although discrete clustering of individuals may be useful in describing some of the variation in diverse, well-defined population samples, continuous measures -- such as biogeographical ancestry or PC indices -- are required to describe the same axes of population structure in populations that have experienced recent admixture.

Methods

SNP genotyping

WGSA technology was used to genotype individuals in this study using the GeneMapping 10 K Array Xba 131 (Affymetrix Inc., Santa Clara, CA). Details of this method have been published elsewhere;[29,30] in brief, fractions of the genome are obtained by restriction enzyme (Xba I) digestion of genomic DNA, ligated with adaptors and subsequently amplified with a universal primer that is directed to the linker. The amplified target (a smear of polymerase chain reaction products of 400 to 800 base pairs [bps] in length) is fragmented, labelled with terminal transferase and biotin-ddATP and hybridised overnight to synthetic microarrays [31,32]. Genotypes are called by interpreting signals from allele-specific probes using a model-based algorithm. The accuracy of this method is in excess of 99.5 per cent. SNPs were chosen from The SNP Consortium (TSC) database on the basis of their predicted location on 400 -800 bp fragments generated by in silico digestion of human genome sequences with various restriction enzymes. Predicted SNPs were then assayed against a panel of 108 individuals from diverse populations. If two individuals were observed with each of the three genotypes, and the clustering patterns were acceptable, the SNP was considered to be confirmed and retained as part of the panel.

Samples

The population samples used in this study were collected under Internal Review Board approvals from the various institutions involved. The Mbuti population samples were collected in the Ituri Forest, the Mende samples from Sierra Leone. The Cushitic-speaking Burunge samples were collected in Tanzania but are thought to be of Ethiopian descent. The Spanish samples were collected in Valencia in Eastern Spain. The Nasioi were collected in Bougainville, Melanesia. The Altaian samples were collected in Siberia, Russia. The upper and lower caste groups were both sampled from Vishakapatnam, Andhra Pradesh, India. The Chinese (NA17011-NA17020) and Japanese (NA17051-NA17060) samples are from US residents, curated at the Coriell Institute. Quechua were sampled in Lima (n = 9) or Cerro de Pasco, Peru, at 4,338 meters (n = 11). In the former case, the subjects were highland natives, as both parents and grandparents were born on the Altiplano. Quechua subjects were selected to represent a subgroup of subjects with the lowest possible European admixture from a larger total sample of n = 71. Similarly, the Nahua, who were sampled in the city of Tlapa, Guerrero, Mexico, were also selected as a subset of individuals showing low European ancestry, as measured with an independent set of markers. African-Americans (subset of 42 from NA17100-17199) and European-Americans (subset of 42 from NA17200-NA17285) are represented by samples curated at the Coriell Institute. For these analyses, one individual initially classified as 'Caucasian' (Coriell Institute Cat# NA17205) was excluded from the European-American sample, as he/she clusters with South Asians, which, in combination with the lack of monophyletic clustering of South Asians and Spanish in this study, highlights the inappropriateness of the category 'Caucasian' in biomedical research. The Puerto Ricans are women born in Puerto Rico and living in New York City at the time of data collection.

Statistical analyses

FST was calculated using Weir and Cockerham's unbiased estimator [33]. Pairwise individual genetic distances were estimated using the ASD [22]. The tree of individuals, based on the ASD distance, was constructed using the neighbour-joining method,[21] using the Molecular Evolutionary Genetics Analysis software package (MEGA version 2.1) [34]. The PC analysis was carried out using NTSYS software (Rohlf, F. J. [1992], NTSYS-pc version 1.70). The statistical significance of PC axes was determined using the broken stick model, resulting in four significant axes. These axes together explain 23.6 per cent of the total variation (12.6 per cent by the first axis, 5.5 per cent by the second, 3.5 per cent by the third and 1.9 per cent by the fourth). All pairwise PC axis plots for these four axes are presented in the online supplementary information. The STRUCTURE 2.0 [8] computer program was used to infer the presence of genetic structure in the sample. The analysis was performed both with and without the admixture model for K = 2 to K = 6, the model previously having been determined to show the highest posterior probabilities for these data. A total of 25,000 simulation iterations were run for the burn-in period; 75,000 additional iterations were run to get parameter estimates. Biogeographical ancestry estimates were calculated for the 42 African-American subjects, the 41 European-American subjects and the 20 Puerto Rican women, using the maximum likelihood algorithm previously described,[26] whereby the allele frequencies for the three parental populations were taken to be indigenous American (Nahua and Quechua averaged together), West African (Mende) and European (Spanish). For testing the correlation between subsets of markers, autosomal SNPs were divided by chromosome into those on odd and even chromosomes, respectively. Spearman's correlation coefficient was then calculated for four significant PCs and the three ancestral components between using the odd and even estimates of these statistics. As has been demonstrated, estimates -- even for highly admixed populations -- will be uncorrelated unless there is substantial non-random mating in the population that is related to ancestry [35].

Acknowledgements

We would like to thank Kateryna Makova, Ken Weiss, Anne Buchanan and S. Malia Fullerton for helpful comments and discussions on this paper. We would also like to acknowledge the trust and generosity of the people and populations who contributed the DNA samples on which this study is based. Additionally, for the collection of the Spanish population sample, we acknowledge Jose Americo Montoro from the blood transfusion centre in Valencia (Servei Valencia de Salut). This work was supported in part by grants: NIH/NHGRI (HG02154) to MDS; NJH/NIA (P30AG/NR15294-01) to JRF; NSF (SBR-9514733 and SBR-9818215) to LBJ;

References

  1. Risch N, Burchard E, Ziv E, Tang H. Categorization of humans in biomedical research: Genes, race and disease. Genome Biol. 2002;3:1–12. doi: 10.1186/gb-2002-3-7-comment2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Kittles RA, Chen W, Panguluri RK. et al. CYP3A4-V and prostate cancer in African Americans: Causal or confounding association because of population stratification? Hum Genet. 2002;110:553–560. doi: 10.1007/s00439-002-0731-5. [DOI] [PubMed] [Google Scholar]
  3. Hoggart CJ, Parra EJ, Shriver MD. et al. Control of confounding of genetic associations in stratified populations. Am J Hum Genet. 2003;72:1492–1504. doi: 10.1086/375613. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Devlin B, Roeder K. Genomic control for association studies. Biometrics. 1999;55:997–1004. doi: 10.1111/j.0006-341X.1999.00997.x. [DOI] [PubMed] [Google Scholar]
  5. Pritchard JK, Stephens M, Rosenberg NA, Donnelly P. Association mapping in structured populations. Am J Hum Genet. 2000;67:170–181. doi: 10.1086/302959. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Cavalli-Sforza LL, Menozzi P, Piazza A. The History and Geography of Human Genes, Princeton University Press, Princeton, NJ; 1994. [Google Scholar]
  7. Ke Y, Su B, Song X. et al. African origin of modern humans in East Asia: A tale of 12,000 Y chromosomes. Science. 2001;292:1151–1153. doi: 10.1126/science.1060011. [DOI] [PubMed] [Google Scholar]
  8. Rosenberg NA, Pritchard JK, Weber JL. et al. Genetic structure of human populations. Science. 2002;298:2381–2385. doi: 10.1126/science.1078311. [DOI] [PubMed] [Google Scholar]
  9. Bamshad MJ, Wooding S, Watkins WS. et al. Human population genetic structure and inference of group membership. Am J Hum Genet. 2003;72:578–589. doi: 10.1086/368061. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Watkins WS, Rogers AR, Ostler CT. et al. Genetic variation among world populations: Inferences from 100 Alu insertion polymorphisms. Genome Res. 2003;13:1167–1618. doi: 10.1101/gr.894603. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Rodgers AR, Jorde LB. Ascertainment bias in estimates of average heterozygosity. Am J Hum Genet. 1996;58:1033–1041. [PMC free article] [PubMed] [Google Scholar]
  12. Nielsen R, Signorovitch J. Correcting for ascertainment biases when analyzing SNP data: Applications to the estimation of linkage disequilibrium. Theor Popul Biol. 2003;63:245–255. doi: 10.1016/S0040-5809(03)00005-4. [DOI] [PubMed] [Google Scholar]
  13. Mountain JL, Cavalli-Sforza LL. Inference of human evolution through cladistic analysis of nuclear DNA restriction polymorphisms. Proc Natl Acad Sci USA. 1994;91:6515–6519. doi: 10.1073/pnas.91.14.6515. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Bowcock AM, Ruiz-Linares A, Tomfohrde J. et al. High resolution of human evolutionary trees with polymorphic microsatellites. Nature. 1994;368:455–457. doi: 10.1038/368455a0. [DOI] [PubMed] [Google Scholar]
  15. Lewontin R. The apportionment of human diversity. Evol Biol. 1972;6:381–398. [Google Scholar]
  16. Charlesworth B, Coyne JA, Barton NH. The relative rates of evolution of sex chromosomes and autosomes. Am Nat. 1987;130:113–149. doi: 10.1086/284701. [DOI] [Google Scholar]
  17. Payseur BA, Nachman MW. Natural selection at linked sites in humans. Gene. 2002;300:31–42. doi: 10.1016/S0378-1119(02)00849-1. [DOI] [PubMed] [Google Scholar]
  18. Shriver MD, Kennedy GC, Parra EJ. et al. The genomic distribution of human population substructure in four populations using 8525 SNPs. Hum Genomics. 2004;1:274–286. doi: 10.1186/1479-7364-1-4-274. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Cavalli-Sforza LL. Population structure and human evolution. Proc R Soc Lond B Biol Sci. 1966;164:362–379. doi: 10.1098/rspb.1966.0038. [DOI] [PubMed] [Google Scholar]
  20. Mountain J, Cavalli-Sforza LL. Multilocus genotypes, a tree of individuals and human evolutionary history. Am J Hum Genet. 1997;61:705–718. doi: 10.1086/515510. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Saitou N, Nei M. The neighbor-joining method: A new method for reconstructing phylogenetic trees. Mol Biol Evol. 1987;4:406–425. doi: 10.1093/oxfordjournals.molbev.a040454. [DOI] [PubMed] [Google Scholar]
  22. Chakraborty R, Jin L. In: A unified approach to study hypervariable polymorphisms: Statistical considerations of determining relatedness and population distances. Pena SDJ, Jefferys AJ, Epplen J, Chakraborty R, editor. Vol. 67. DNA Fingerprinting: Current State of the Science, EXS; 1993. pp. 153–175 Birkhauser, Basel, Switzerland,. [DOI] [PubMed] [Google Scholar]
  23. Basu A, Mukherjee N, Roy S. et al. Ethnic India: A genomic view, with special reference to peopling and structure. Genome Res. 2003;13:2277–2290. doi: 10.1101/gr.1413403. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Bamshad M, Kivisild T, Watkins WS. et al. Genetic evidence on the origins of Indian caste populations. Genome Res. 2001;11:994–1004. doi: 10.1101/gr.GR-1733RR. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Semino O, Passarino G, Oefner PJ. et al. The genetic legacy of Paleolithic Homo sapiens sapiens in extant Europeans: A Y chromosome perspective. Science. 2000;290:1155–1159. doi: 10.1126/science.290.5494.1155. [DOI] [PubMed] [Google Scholar]
  26. Shriver MD, Parra EJ, Dios S. et al. Skin pigmentation, biogeographical ancestry, and admixture mapping. Hum Genet. 2003;112:387–399. doi: 10.1007/s00439-002-0896-y. [DOI] [PubMed] [Google Scholar]
  27. Wacholder S, Rothman N, Caporaso N. Counterpoint: Bias from population stratification is not a major threat to the validity of conclusions from epidemiological studies of common polymorphisms and cancer. Cancer Epidemiol Biomarkers Prev. 2002;11:513–520. [PubMed] [Google Scholar]
  28. Mountain J, Cavalli-Sforza LL. Inference of human evolution through cladistic analysis of nuclear DNA restriction polymorphisms. Proc Natl Acad Sci USA. 1994;91:6515–6519. doi: 10.1073/pnas.91.14.6515. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Wilson JF, Weale ME, Smith AC. et al. Population genetic structure of variable drug response. Nat Genet. 2001;29:265–269. doi: 10.1038/ng761. [DOI] [PubMed] [Google Scholar]
  30. Kennedy GC, Matsuzaki H, Dong S. et al. Large-scale genotyping of complex DNA. Nat Biotechnol. 2003;21:1233–1237. doi: 10.1038/nbt869. [DOI] [PubMed] [Google Scholar]
  31. Matsuzaki H, Loi H, Dong S. et al. Parallel genotyping of over 10,000 SNPs using a one-primer assay on a high-density oligonucleotide array. Genome Res. 2004;14:414–425. doi: 10.1101/gr.2014904. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Chee M, Yang R, Hubbell E. et al. Accessing genetic information with high-density DNA arrays. Science. 1996;274:610–614. doi: 10.1126/science.274.5287.610. [DOI] [PubMed] [Google Scholar]
  33. Weir BS, Cockerham CC. Estimating F-statistics for the analysis of population substructure. Evolution. 1984;38:1358–1370. doi: 10.2307/2408641. [DOI] [PubMed] [Google Scholar]
  34. Kumar S, Tamura K, Jakobsen IB, Nei M. MEGA2: Molecular Evolutionary Genetics Analysis software. Bioinformatics. 2001;17:1244–1245. doi: 10.1093/bioinformatics/17.12.1244. [DOI] [PubMed] [Google Scholar]
  35. Parra EJ, Kittles RA, Shriver MD. Implications of correlations between skin color and genetic ancestry for biomedical research. Nat Genet. 2004;36:S54–S60. doi: 10.1038/ng1440. [DOI] [PubMed] [Google Scholar]

Articles from Human Genomics are provided here courtesy of BMC

RESOURCES