Competing event risk stratification may improve the design and efficiency of clinical trials: Secondary analysis of SWOG 8794

Abstract

Background

Composite endpoints can be problematic in the presence of competing risks when a treatment does not affect events comprising the endpoint equally.

Methods

We conducted secondary analysis of SWOG 8794 trial of adjuvant radiation therapy (RT) for high-risk post-operative prostate cancer. The primary outcome was metastasis-free survival (MFS), defined as time to first occurrence of metastasis or death from any cause (competing mortality (CM)). We developed separate risk scores for time to metastasis and CM using competing risks regression. We estimated treatment effects using Cox models adjusted for risk scores and identified an enriched subgroup of 75 patients at high risk of metastasis and low risk of CM.

Results

The mean CM risk score was significantly lower in the RT arm vs. control arm (p=0.001). The effect of RT on MFS (HR 0.70; 95% CI, 0.53–0.92; p=0.010) was attenuated when controlling for metastasis and CM risk (HR 0.76; 95% CI, 0.58–1.00; p=0.049), and the effect of RT on overall survival (HR 0.73; 95% CI, 0.55–0.96; p=0.02) was no longer significant when controlling for metastasis and CM risk (HR 0.80; 95% CI, 0.60–1.06; p=0.12). Compared to the whole sample, the enriched subgroup had the same 10-year incidence of MFS (40%; 95% CI, 22–57%), but a higher incidence of metastasis (30% (95% CI, 15–47%) vs. 20% (95% CI, 15–26%)). A randomized trial in the subgroup would have achieved 80% power with 56% less patients (313 vs. 709, respectively).

Conclusion

Stratification on competing event risk may improve the efficiency of clinical trials.

Introduction

Event-free survival (EFS) endpoints are widely implemented in clinical research. These endpoints are generally defined as composite endpoints that comprise one or more disease-specific events (e.g. disease recurrence or death due to disease) and death from any cause.^1,2 Provided that the events comprising the endpoint are of comparable clinical importance, and the treatment affects each event similarly, composite endpoints are useful for determining the benefit of the therapy being tested.

However, when treatments have differing effects on the primary events of interest, the use of composite endpoints, particularly event-free survival endpoints, can lead to problems in the design and interpretation of clinical trials.^3,4 Such is often the case with oncology trials, because cancer therapies typically are not expected to reduce both cancer-specific and non-cancer events. In settings where the probability of non-cancer mortality is high (e.g. prostate cancer), the impact of varying risk for non-cancer mortality on both study efficiency and treatment effect interpretation becomes accentuated. Increasing risk for non-cancer mortality degrades the statistical power of studies of cancer therapies, and attenuates estimates of composite treatment effects.^5–7

Given the expense of conducting clinical trials, maximizing their efficiency is becoming an increasingly important question. We conducted a secondary analysis of the SWOG 8794 randomized trial of adjuvant radiation therapy versus observation for high-risk prostate cancer patients following radical prostatectomy, in order to investigate the impact of variations in competing mortality risk on clinical trial efficiency and interpretation.^8,9 We also sought to determine the importance of stratification according to competing mortality risk for future clinical trial designs.

Materials and Methods

Trial design and participants

Inclusion and exclusion criteria for SWOG 8794 have been previously reported.^8,9 Patients were randomized within 16 weeks of surgery to immediate pelvic radiation therapy 60–64 Gy in 30–32 fractions (n=214) or observation (n=211). The primary endpoint was metastasis-free survival, defined as the time from randomization to the first evidence of metastatic disease or death from any cause. Reporting of first recurrence was required, and patients were also followed for metastasis or death after local recurrence. Prostate-specific antigen (PSA) testing was not initially mandated but became part of the protocol early in the study. However some early subjects did not have post-prostatectomy PSA values (47 of 425). The trial was powered to detect an alternative hazard ratio of 0.667 for MFS with one-sided type I error of 0.05, power of 0.80, and median MFS of 12 years.⁸

Statistical analysis

The primary events of interest for this analysis were time from randomization to first evidence of metastatic disease (i.e. time to metastasis), and time to death from any cause in the absence of metastatic disease (i.e. competing mortality). Metastasis-free survival time was defined as time to metastasis or death from any cause. Subjects without an event were censored at the date of their last follow-up. The cumulative probabilities of events of interest were calculated using non-parametric cumulative incidence functions.^10,11 For estimating effects of covariates we used both the Cox proportional hazards model¹² the Fine-Gray semi-parametric model for subdistribution hazards.¹³ For the competing risk analysis we regard first events contributing to the event-free survival endpoint (metastasis or death in the absence of metastasis) as mutually exclusive, such that the occurrence of one event type precludes the observation of the complementary (competing) event.

The primary effect of interest was the treatment assignment (i.e., radiation therapy). Covariates included in the competing risk model were age (continuous), black race (vs. non-black), log body mass index (BMI) (continuous), Charlson Comorbidity Index (CCI) score ≥ 1, Eastern Cooperative Oncology Group (ECOG) performance status ≥ 1, Gleason score ≥ 8, post-prostatectomy PSA ≥ 0.2, and presence of seminal vesicle invasion. All covariate data was obtained prospectively, except for CCI, which was obtained retrospectively from clinical trial flow sheets. Flow sheets were reviewed by two authors (BSR, SG) who were blinded to the group assignment and outcome. Comorbidity was scored according to the CCI¹⁴ with the exception that the presence of prostate cancer was not scored.

To stratify patients according to both competing mortality and metastasis risk, stepwise Fine-Gray competing risks regression was used and variables with p<0.10 were retained in the model. Treatment was not used in the development of risk scores, since we planned to use risk scores to adjust the treatment effect. The significance cutoff for variables was chosen because of the relatively smaller cohort in SWOG 8794 compared to previous population based studies. Cutoffs for metastasis and competing mortality risk scores were chosen to group patients into high, medium, and low risk competing mortality cohorts and high and low risk metastasis cohorts. The effect of radiotherapy was estimated using both the Cox proportional hazards model applied to the cause-specific hazard,¹⁵ and Fine-Gray competing risks regression. Effects were also estimated while adjusting for metastasis and competing mortality risk scores. Interactions between competing mortality and metastasis risk scores were tested in the Cox proportional hazards model. Note that, Cox models on the cause-specific hazard tend to isolate the putative effect of treatment on the cause-specific outcome, without the concurrent influence of it and other covariates on the competing outcomes.¹⁶

We used the Welch two sample t-test for normally distributed data and Pearson’s Chi-squared test or the Wilcoxon rank sum test with continuity correction for non-normally distributed data. Normality was tested with the Shapiro-Wilk test. Power and sample size estimates for the competing risk setting were obtained using Pintilie’s method.¹⁷ For the analysis of power and sample size, we assumed exponential event distribution, 6-year accrual, 6-year follow-up, equal sized arms, evaluation at 10 years, one-sided type I error (α) of 0.10, and type II error (β) of 0.20. Cumulative cause-specific hazards were used to calculate the hazard rates for composite endpoints in the power calculations. Statistical analysis was conducted in R version 2.9.2.

Results

Demographic data by treatment assignment, including information on BMI, comorbidity, and performance status not previously reported, is given in Supplementary Table 1. The distributions of race, BMI, performance status, comorbidity, PSA, Gleason score, and extent of disease were similar in the two arms. However, the mean age was significantly higher in the observation arm (65.2 vs 63.5, p=0.0062).

Table 1.

Parameter estimates for competing mortality and metastasis risk models

	Coefficient	Hazard Ratio	Hazard Ratio 95% Confidence interval	P Value
Competing Mortality
Age	0.0591	1.06	1.03–1.09	<.001
Charlson comorbidity index ≥ 1	0.643	1.90	1.28–2.82	.001
Performance status ≥ 1	0.356	1.43	0.99–2.05	.06
Metastasis
Prostate specific antigen ≥ 0.2	0.692	2.00	1.25–3.20	.004
Seminal vesicle invasion	1.085	2.96	1.85–4.73	<.001
Gleason score ≥ 8	0.522	1.69	0.92–3.07	.09

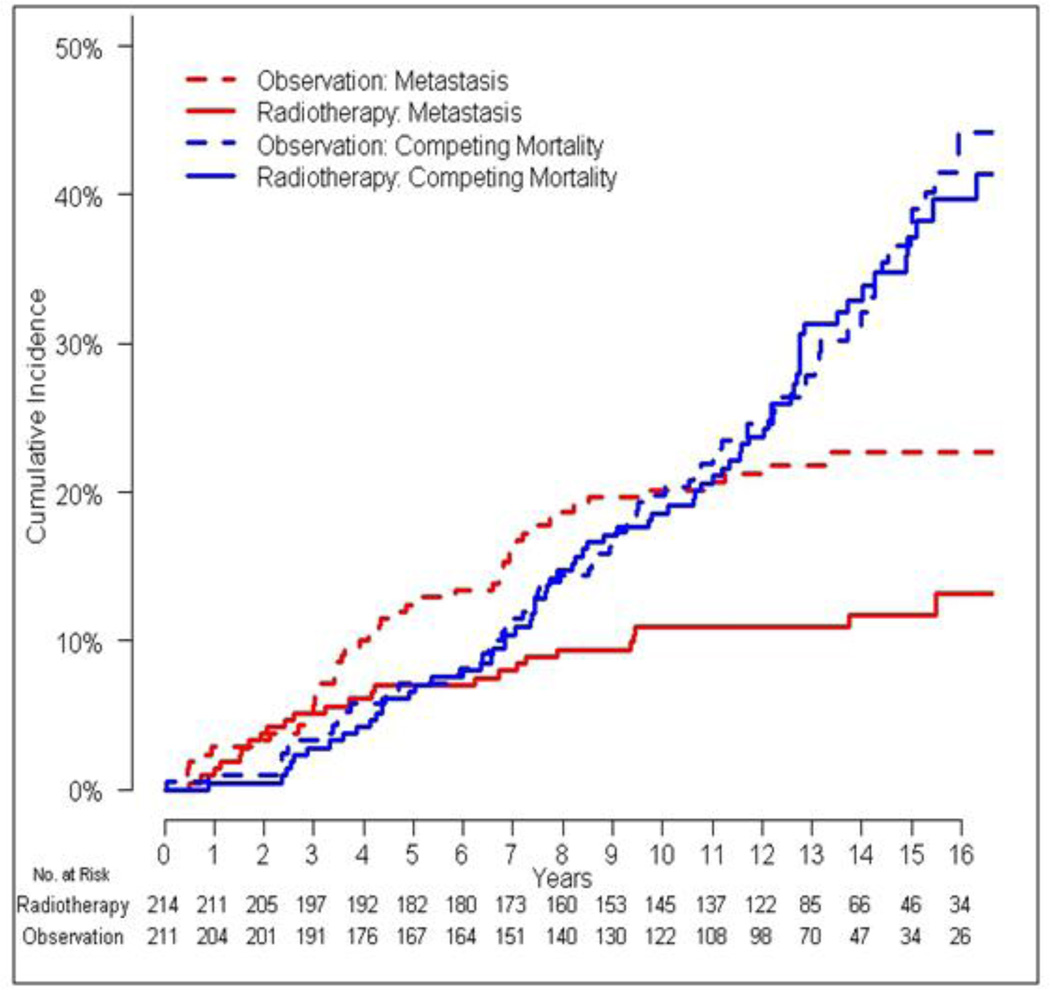
The total number of primary events in the observation arm was 119 (46 metastasis events, 73 competing mortality events), compared to 96 in the radiation therapy arm (25 metastasis events, 71 competing mortality events). Time to metastasis was significantly reduced in patients who received radiation (HR 0.50, 95% CI 0.31–0.81, p=0.0051), whereas time to competing mortality was not (HR 0.82, 95% CI 0.59–1.14, p=0.24) (Figure 1). Metastasis-free survival (HR 0.70, 95% CI 0.53–0.92, p=0.0095) and overall survival (HR 0.73, 95% CI 0.55–0.96, p=0.022) were significantly improved in the radiation arm. For patients who died in the absence of prostate cancer metastasis, cause of death information was available for 24% (35/144 patients). Causes of death included cardiovascular (11), lung cancer (7), pneumonia (2), end-stage liver disease (2), hepatocellular carcinoma (2), gastric cancer (2), lymphoma (1), esophageal carcinoma (1), glioblastoma multiforme (1), acute myeloid leukemia (1), renal cell carcinoma (1), colorectal carcinoma (1), neuroendocrine carcinoma (1), motor vehicle accident (1), and smoke inhalation (1).

Figure 1.

Cumulative incidences of metastasis and competing mortality according to treatment assignment.

Competing mortality and metastasis risk models

Increased age, CCI, and performance status score were associated with a significantly increased hazard for competing mortality, whereas increased PSA and Gleason score and presence of seminal vesicle invasion were associated with a significantly increased hazard for metastasis (Table 1). The distribution of CCI was as follows: 0: n=349, 1: n=54, 2: n=15, 3: n=6, 4: n=1. The distribution of PS was: 0: n=321, 1: n=91, 2: n=7, missing: n=6. The risk score for competing mortality (R_CM) was calculated as:

$${\mathrm{R}}_{\text{CM}}={0.0591}^{*}(\text{Age}-64.3)+{0.643}^{*}(\text{CCI}\ge 1)+{0.356}^{*}(\text{PS}\ge 1)$$ (1)

where age is in years (age was mean-centered in the regression), and CCI ≥ 1 and PS ≥ 1 indicate the presence (value =1) or absence (value =0) of the indicated condition. Competing mortality risk scores ranged from -1.23 to 1.78 with a median score of 0.22 and standard deviation of 0.54. To divide patients into tertiles of low, medium, and high competing mortality risk, cutoffs were chosen at 0.04 and 0.50.

The risk score for metastasis (R_M) was calculated as:

$${\mathrm{R}}_{\mathrm{M}}={0.692}^{*}(\text{PSA}\ge 0.2)+{1.085}^{*}(\text{SVI})+{0.522}^{*}(\text{GS}\ge 8)$$ (2)

where PSA ≥ 0.2, SVI, and GS≥8 indicate the presence (value=1) or absence (value =0) of the indicated condition. 188 patients had a metastasis risk score of 0 and the remaining 237 patients had metastasis risk scores ranging from 0.52 to 2.30. Metastasis risk was dichotomized into high R_M>0 and low stratifications R_M=0. The Spearman rank correlation between R_M and R_CM was 0.046, p=0.35. There was no significant difference in mean R_M according to treatment (0.63 (radiation) versus 0.62 (observation), p=0.82). There was a significant difference in competing mortality risk score, however, favoring the radiation arm (0.12 (radiation) versus 0.28 (observation), p=0.001). Both the metastasis and competing mortality risk scores were not normally distributed (p<0.001 for both tests). When adjusting for competing mortality risk, the effect of radiation on time to metastasis was unchanged, whereas the effect on both metastasis-free survival and overall survival was attenuated (Table 2). There was no significant effect of radiation on competing mortality in either the unadjusted or adjusted time-to-event models. We did not find evidence of a significant interaction between competing mortality and metastasis risk scores and treatment assignment.

Table 2.

Unadjusted and adjusted effects of radiation therapy

	Unadjusted				Adjusted for Metastasis and Competing Mortality Risk*
	HR† (95%CI)	p	SDHR‡ (95%CI)	p	HR† (95%CI)	p	SDHR‡ (95%CI)	p
Metastasis	0.50	.005	0.51	.007	0.49	.005	0.49	005
	(0.31– 0.81)		(0.31– 0.83)		(0.30– 0.81)		(0.30– 0.81)
Competing	0.82	.24	0.94	.73	0.94	.71	1.10	.56
Mortality	(0.59– 1.14)		(0.68– 1.30)		(0.67– 1.31)		(0.79– 1.53)
Metastasis-	0.70	.01	0.70	.009	0.76	.049	0.76	.05
Free Survival	(0.53– 0.92)		(0.53– 0.92)		(0.58– 1.00)		(0.58– 1.00)
Overall Survival	0.73	.02	0.73	.02	0.80	.12	0.80	.12
	(0.55– 0.96)		(0.55– 0.96)		(0.60– 1.06)		(0.60– 1.06)

HR = hazard ratio; SDHR = subdistribution hazard ratio; CI = confidence interval.

^*Only metastasis and competing mortality risk scores were used to estimate adjusted effects.

^†Calculated using Cox proportional hazards regression.

^‡Calculated using Fine-Gray regression.

Effect of event composition on power

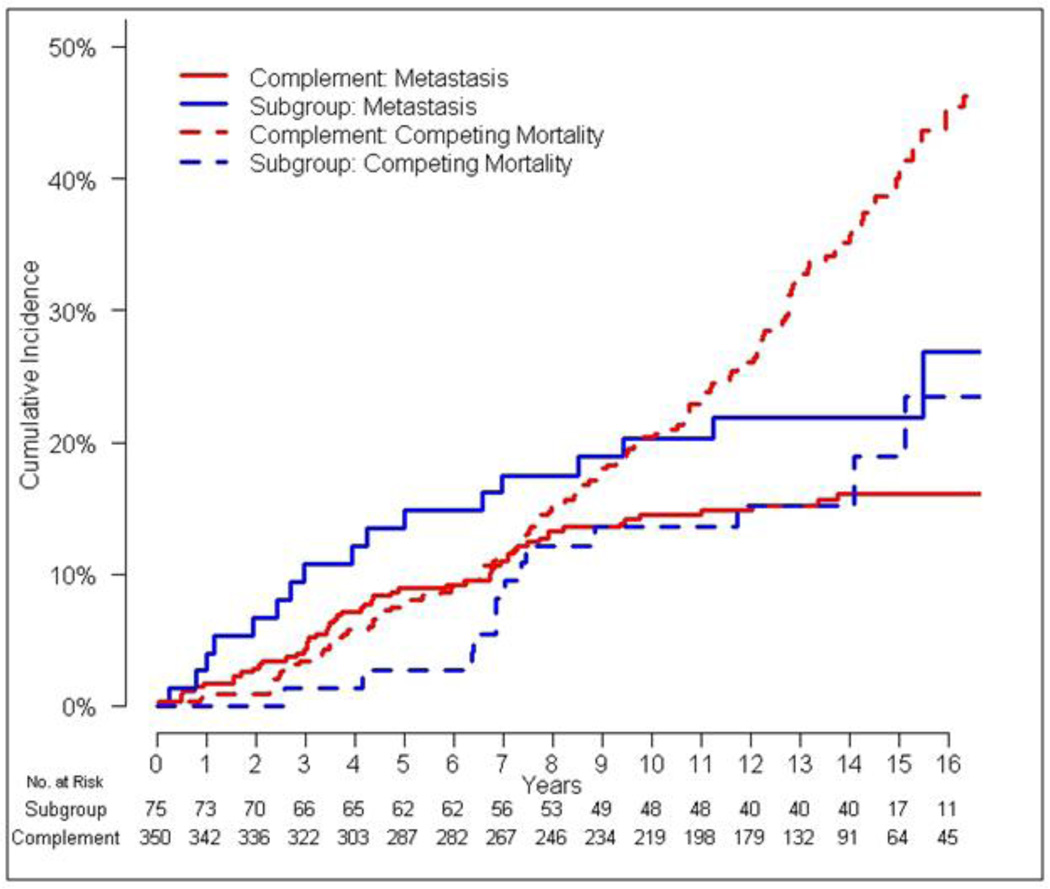
Using cutoffs of R_M > 0 and R_CM < 0.04, we defined an enriched subgroup of patients with high risk of metastasis and low risk of competing mortality. This set of cutoffs was chosen because 188 patients had metastasis risk score of 0 which limited stratification of metastasis risk as compared to competing mortality risk, in which the lowest tertile of patients was chosen. This resulted in a subgroup of 75 subjects, which was compared to its complement of 350 subjects (i.e., the subgroup with low risk of metastasis or high risk of competing mortality). Interestingly, the cumulative incidence of metastasis or death from any cause was identical in both subgroups (Table 3). However, the enriched subgroup had a higher 10 year baseline incidence of metastasis (30%; 95% CI 15–47% vs. 19%; 95% CI, 13–25%) and lower competing mortality (10%; 95% CI 3–24% vs. 21%; 95% CI, 16–28%) (Figure 2). The higher proportion of metastasis events (i.e., the events principally affected by radiation) in the composite endpoint resulted in a lower hazard ratio for metastasis-free survival in the subgroup compared to its complement (0.60 vs 0.74, respectively). The estimated sample size to achieve 80% power for a clinical trial restricted to the enriched population was 313 patients, compared with 709 patients in the original population. Aside from factors used in the risk model, we did not observe significant differences in demographic characteristics of the subgroup compared to the complement (Table 4).

Table 3.

Event composition, power, and sample size estimates for the enriched subgroup and its complement

	Enriched Subgroup (n=75)		Complement (n=350)		Whole Sample (n=425)
	10 year Cumulative Incidence (95% CI)	Sample size for 80% power	10 year Cumulative Incidence (95% CI)	Sample size for 80% power	10 year Cumulative Incidence (95% CI)	Sample size for 80% power
Metastasis	30% (15–47%)	231	19% (13–25%)	378	20% (15–26%)	349
Competing Mortality	10% (3–24%)	-	21% (16–28%)	-	20% (15–26 %)	-
Metastasis or Death	40% (22–57%)	313	40% (33–47%)	835	40% 33–47%)	709

CI = confidence interval.

Figure 2.

Cumulative incidences of metastasis and competing mortality in the enriched subgroup versus everyone else (complement).

Table 4.

Patient and tumor characteristics for the enriched subgroup and its complement

	Enriched Subgroup (n=75)	Complement (n=350)	P Value
Mean age, years	57.8	65.7	<.001
Ethnicity, n (%)			.29
White	50 (66.7)	245 (70.0)
Black	13 (17.3)	70 (20.0)
Asian	0	3 (0.9)
Missing	12 (16)	32 (9.1)
Mean body mass	28.0	27.6	.49
index
Performance status, n (%)			.002
0	69 (92.0)	252 (72.0)
1	4 (5.3)	87 (24.9)
2	1 (1.3)	6(1.7)
Missing	1 (1.3)	5(1.4)
Charlson comorbidity index, n (%)			<.001
0	74 (98.7)	275 (78.6)
1	1 (1.3)	53 (15.1)
2	0	15 (4.3)
3	0	6 (1.7)
4	0	1 (0.3)
Seminal Vesicle			<.001
Invasion, n (%)
Present	50 (66.7)	89 (25.4)
Absent	25 (33.3)	261 (74.6)
Gleason score, n (%)			<.001
≤6	28 (37.3)	192 (54.9)
7	23 (30.7)	85 (24.3)
8–10	19 (25.3)	31 (8.9)
Missing	5 (6.7)	42 (12.0)
Prostate specific antigen,n (%)			<.001
<0.2ng/ml	22 (29.3)	157(44.9)
≥0.2ng/ml	47 (62.7)	152 (43.4)
Missing	6 (8.0)	41 (11.7)

Discussion

Despite randomization, we found there was an imbalance in risk factors for competing mortality in SWOG 8794, favoring the radiation arm. Adjusting for this imbalance dampened the estimated effects of adjuvant radiation therapy on metastasis-free and overall survival, and the effect of RT on overall survival was no longer statistically significant. Our results highlight the need to collect data on predictors for competing mortality in future clinical trials in prostate cancer and other malignancies. Most trials routinely stratify for cancer specific risk factors. However, in this trial we found that greater than half of all primary events were competing mortality events. Stratifying subjects according to competing mortality risk would help ensure balanced allocation of key risk factors, such as age and comorbidity. Additionally, reporting both the composition of primary events and the cause-specific treatment effects is necessary for a thorough interpretation of clinical trial results.

In this study, we identified an enriched subgroup of patients at high risk for the primary cause-specific event of interest (metastasis) relative to the competing event (mortality in the absence of metastasis). The higher relative proportion of primary metastasis events in this subgroup accentuated the effect of treatment on the primary endpoint, despite an identical probability of metastasis-free survival in the non-enriched subgroup. The criteria developed in our analysis would have selected for younger patients with higher-risk prostate cancer, better performance status, and fewer comorbidities. Importantly, race was not a selection criterion, and we did not observe interactions between treatment effects and cause-specific event risk. The efficiency of a clinical trial conducted in an enriched subpopulation could be significantly augmented, potentially leading to cost savings. While restricting a study through selection would decrease its accrual rate, enrichment increases power and decreases sample size, which leaves uncertain impact on overall accrual length. The implications of selection criteria variation on the dynamics and cost of clinical trials require further study.

Strengths of this study included long follow-up, a high probability of both disease-specific and competing events, and detailed information regarding demographic and tumor characteristics, which allowed for the development of an effective stratification model. Unlike population-based studies of competing mortality,¹⁸ randomization allowed us to obtain unbiased estimates of the treatment effect on competing events within subpopulations. The comorbidity data was limited because there was no requirement to collect comorbidity data in this trial and because of retrospective collection via clinical trial flow sheets, which could under-estimate the true prevalence of comorbidity. However, we do not have reason to suspect that the data were biased with respect to treatment assignment, and we expect that inaccuracies would only have served to mitigate observed effects of comorbidity on competing mortality. External validation would lend additional support to our findings. We also lacked data regarding other possible risk factors for competing mortality, such as socioeconomic status and marital status, and some subjects had missing PSA data, which might have facilitated increased event stratification. Misclassification in ascribing cause of death could theoretically affect our findings, however, we suspect the impact of such errors was small, considering the absence of significant effects of treatment or other disease-specific factors on competing mortality.

Composite endpoints are associated with multiple problems in oncology, particularly in competing risks settings. First, power and composite effect sizes are frequently reduced, increasing potential for bias toward the null hypothesis or waste. Second, both type I or type II error can arise owing to imbalances in risk factors for competing events across groups being compared. Third, inferences can be problematic because all or part of the effect of a treatment on a composite endpoint may be attributable to its effect on one or more competing events. Despite these shortcomings, composite endpoints have several important merits. First, competing events are unlikely to be random or occur independently of other events. Second, cause of death assignment may be unknown, unreliable, or biased. Third, treatments may adversely affect competing events. For these reasons, regulatory bodies have generally favored composite endpoints, which overcome these complexities and capture the net impact of treatment “at the end of the day.” Such advantages do not, however, obviate the need to establish the specificity and mechanism of treatment effects in randomized trials.

In summary, we found that variation in competing mortality risk had a large effect on the composition of EFS events and on interpretation of treatment effect, power, and sample size. Combined endpoint decomposition was necessary for a complete interpretation of the treatment effect. These results indicate that stratification according to competing event risk would improve the design and efficiency of clinical trials, particularly in populations with a high incidence of competing risks.