Conformational Free-Energy Landscapes for a Peptide in Saline Environments

Abstract

The conformations that proteins adopt in solution are a function of both their primary structure and surrounding aqueous environment. Recent experimental and computational work on small peptides, e.g., polyK, polyE, and polyR, have highlighted an interesting and unusual behavior in the presence of aqueous ions such as ClO₄⁻, Na⁺, and K⁺. Notwithstanding the aforementioned studies, as of this writing, the nature of the driving force induced by the presence of ions and its role on the conformational stability of peptides remains only partially understood. Molecular-dynamics simulations have been performed on the heptapeptide AEAAAEA in NaCl and KCl solutions at concentrations of 0.5, 1.0, and 2.0 M. Metadynamics in conjunction with a three-dimensional model reaction coordinate was used to sample the conformational space of the peptide. All simulations were run for 2 μs. Free-energy landscapes were computed over the model reaction coordinate for the peptide in each saline assay as well as in the absence of ions. Circular dichroism spectra were also calculated from each trajectory. In the presence of Na⁺ and K⁺ ions, no increase in helicity is observed with respect to the conformation in pure water.

Introduction

The population of the different conformations accessible to a protein in solution is, to a large extent, determined by its primary structure (1). The resulting conformational equilibrium is also influenced by the surrounding aqueous environment (2), specifically its ionic components (3). The effect of ions on the protein conformation was first noted by Franz Hofmeister in 1888 (4) and has been investigated extensively in recent years, with studies focusing on the impact of the structure of water (5) and charged side chains on the conformational equilibria of proteins.

Since Hofmeister’s initial work, ionic effects on proteins have been described by changes in the structure of water that are a function of electrolyte identity and concentration. Small kosmotropic ions such as lithium and fluoride have been said to create order in the structure of water, whereas large chaotropic ions such as guanidinium or iodide, disrupt it (6). The proposed model has been lately questioned based on results accrued in a number of experimental studies. Bakker and co-workers (7–9) have studied the orientational correlation times of water molecules in various saline environments, which revealed that many biologically relevant ions have no influence on the dynamics of bulk water and only tend to reorient water molecules in the first coordination shell, hence casting doubts on the traditional view of electrolyte influence on the structure of water. Similar questions were raised in the light of additional studies (10–12), which have each concluded that there is no relationship between ion effect on protein stability and the structure of water.

As contributions from the structure of water have largely been dismissed in the past years, other molecular forces have been proposed to alter the stability of peptides in saline solutions. The proposed forces include electrostatic screening in charged side-chain interactions, the effect of ion-induced peptide backbone polarization, and ion side-chain binding. The latter effect remains only partially understood and has proven to be more intricate than anticipated in recent work, where it was observed that salts had much different effects on peptides than on small molecular ions (13). With the development of improved parameters for monovalent and polyvalent ions (14,15), computational studies of proteins in saline solutions are becoming increasingly relevant to the biophysical community.

In their computational investigation, Fedorov et al. (16) examined the effects of sodium and potassium ions on the conformational stability of poly-glutamic acid (PGA) and concluded that sodium shifts the conformational equilibrium of PGA, so that the α-helix could be stabilized due to electrostatic screening of side-chain interactions. It was further inferred that sodium screened charged side-chain interactions to a larger extent than potassium, as sodium has a higher affinity for carboxylate groups found at the surface of proteins, such as those in PGA (17–21). Despite the fact that electrostatic screening appears to be the dominating molecular force, as reflected by the work of Fedorov, studies on various peptide sequences have yielded a different picture.

In particular, the recent joint study of Asciutto et al. (22) has unveiled the effects of sodium perchlorate on a small, poly-alanine peptide, indicating that the salt stabilized the α-helical conformation of the peptide by altering the hydration of the peptide backbone. Perchlorate ions were further shown to have a higher affinity for the backbone than water does, essentially dehydrating the backbone. Such dehydration stabilizes the α-helix by promoting intrapeptide hydrogen bonding, as opposed to hydrogen bonding between the peptide and water molecules. We believe that such hydration effects are the driving force that underlies the influence of the ionic environment on the conformation of proteins. This work aims at providing further insight into the molecular forces responsible for salt effects on the conformation of proteins.

Here, we describe molecular-dynamics (MD) simulations performed on a small, alanine-rich peptide containing two glutamic acid residues, in various NaCl and KCl solutions, with the peptide effectively acting as a model for PGA and the poly-alanine peptide described above. The intrapeptide electrostatic interactions are greatly simplified from the work done by Fedorov et al. (16), allowing us to study the manner by which ions affect a single pair of interacting glutamic-acid side chains. The alanine-rich sequence promotes the formation of stable α-helices (22), where changes in the stability of the helix in different saline solutions can be used to evaluate ionic effects on this conformer. Peptides rich in alanine have also been investigated extensively in the literature (23–27).

Hénin et al. (28) have recently modeled complex reaction coordinates by employing a combination of collective variables and computed a multidimensional conformational free-energy landscape of a small peptide. The technique that they have established can be used to probe the relative stability of many different conformations of the peptide. In this work, an implementation of the metadynamics algorithm developed by Laio and Parrinello (29) was utilized alongside a multidimensional model-reaction coordinate to sample the conformational space of the peptide over timescales amenable to MD simulations. We examined the relative stability of different conformations of our model peptide in a variety of saline assays, as well as the potential stabilization mechanisms based on the computed free-energy landscapes.

Methods

The peptide sequence considered in this study is AEAAAEA, where A stands for alanine and E, glutamic acid. One set of simulations included the terminally blocked peptide featuring an acetylated N-terminus and an n-methyl group on the C-terminus (Ace-AEAAAEA-Nme), whereas another set included its zwitterionic structure. In all simulations, the glutamic-acid residues were deprotonated. The saline solutions consisted of one peptide (17 mg/mL) immersed in water boxes at 0.5, 1.0, and 2.0 M concentrations of either NaCl or KCl, with two additional cations being added in each condensed phase system to ensure electric neutrality. Each peptide was also simulated in pure water with only the two counter cations.

Metadynamics simulations were performed utilizing the collective variables module available in the NAMD 2.8 package (30). A three-dimensional model reaction coordinate (MRC), analogous to that described by Hénin et al. (28), was employed to sample, in a more effective fashion, the conformational space of the peptide by lifting the degeneracy of the free energy. The collective variables were chosen to be the distance root-mean-squared deviation of the backbone atoms of the peptide with respect to an ideal PPII conformer, α-helix, and turn of the peptide, respectively, for the three dimensions forming the MRC. The turn conformation was extracted from the trajectory of a short, classical MD simulation of the peptide. The Φ- and Ψ-backbone torsional angles from the turn conformation are listed in Table 1. Each dimension of the MRC was discretized and explored over a range of 0–7 Å, with a bin size of 0.1 Å. Gaussian biasing potentials with a height of 0.01 kcal/mol were added every 100 steps.

Table 1.

Φ- and Ψ-backbone torsional angles of the turn conformer used as one of the three reference conformations

Residue	Φ/°	Ψ/°
A3	−62	−47
A4	−119	−34
A5	−95	108

The CHARMM27 force field with CMAP corrections was employed to describe intra- and intermolecular interactions (31). The TIP3P water model was employed in all simulations (32). The initial cell dimensions for all systems were 45 × 37 × 36 Å³. Periodic boundary conditions were enforced. For all simulations, short-range van der Waals and electrostatic interactions were truncated smoothly at a cutoff distance of 12 Å with a switching function applied over distances > 10 Å. Long-range electrostatic forces were determined using the particle-mesh Ewald method (33). Short-range and long-range interactions were calculated using time steps of 2.0 and 4.0 fs, respectively (34). Bonds involving hydrogen atoms were constrained to their equilibrium length using the RATTLE and SETTLE algorithms (35,36). Simulations were carried out in the NPT ensemble over 2 μs for each equilibrated system, with a fixed pressure and temperature of 1 atm and 298 K, respectively, using the Langevin piston algorithm (37) and damped Langevin dynamics.

Results and Discussion

The three-dimensional free-energy landscapes determined from the capped peptide simulations are displayed in Fig. 1 and were generated using VMD 1.9 (38). In each plot, five colored spheres are shown, indicating the position of five conformations of interest on the MRC that we have defined. The conformations of interest, which are highlighted in Fig. 2, include the α-helix, π-helix, 3₁₀ helix, 2.5₁ helix, and PPII conformer. These conformations have been observed experimentally in the Asher laboratory at the University of Pittsburgh (S. Asher, University of Pittsburgh, personal communication, 2010) for PGA, polyK, and polyR peptides. The global free-energy minimum in each landscape of the capped peptides is located in the α-helix basin. This observation is in accordance with experimental work on alanine-rich peptides, which have been shown to form unusually strong helices (26). As shown in Fig. 1, some differences in the relative free-energy values for the various conformations accessible to the peptide can be noticed when comparing the free-energy landscape from the pure water simulation to those constructed for each saline solution. The free-energy basin around the extended random coil (conformation A) emerging in KCl is not as well delineated in NaCl or in pure water.

Figure 1.

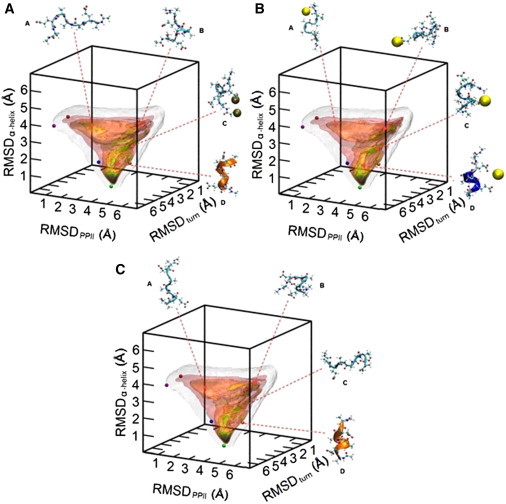
Free-energy surfaces for Ace-AEAAAEA-Nme in 1.0 M KCl (A), 1.0 M NaCl (B), and water (C) over our defined MRC. The five colored spheres in each plot show the location of five relevant conformations for small peptides: PPII (purple), 2.5₁ helix (red), 3₁₀ helix (blue), α-helix (green), and π-helix (orange). Colored isosurfaces represent specific free energy values (pink, <7 kcal/mol; red-orange, <6 kcal/mol; yellow, <5 kcal/mol; green, <4 kcal/mol; blue, <3 kcal/mol; violet, <2 kcal/mol; and black, <1 kcal/mol). Isosurfaces (white) show the portion of conformational space sampled during a given simulation. Selected conformers observed in respective trajectories are shown around each plot, while their locations on the MRC are also indicated. Ions that were observed to be interacting with a conformer are represented as large, colored spheres: sodium (yellow) and potassium (bronze).

Figure 2.

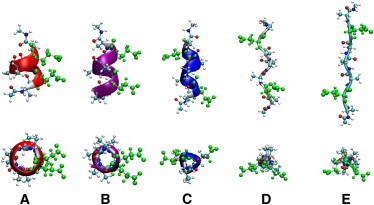
Five conformations of interest for the polypeptide, AEAAAEA. The conformers are the π-helix (A), α-helix (B), 3₁₀ helix (C), PPII (D), and 2.5₁ helix (E). Each conformer is displayed from the side (top row) and looking down on the N-terminus of the peptide (bottom row). The color of each backbone matches the corresponding colored spheres in Figs. 1 and 3. (Green ball-and-stick representation) Glutamic-acid side chains.

More noticeable is the stabilization of the π-helix in both NaCl and KCl as compared to pure water. The appearance of the green isosurface near the orange sphere in Fig. 1, A and B, as compared to the yellow isosurface in Fig. 1 C, is indicative of a deeper free-energy well and suggests a more stable structure at the 1.0 M concentration. However, this salt-induced stabilization of the π-helix is not observed at other concentrations, as can be seen in Fig. S1 in the Supporting Material. Stabilization effects on the semiformed helix (conformation D) also appear to be salt-specific, according to Fig. 1. The free-energy basin to which this conformer belongs is very similar in pure water and KCl, whereas in NaCl, there is a shift in the location of the local minima over the MRC. A similar effect is observed at additional concentrations, as can be seen in Fig. S1.

Certain stabilization effects appear to be salt-specific, whereas others are concentration-dependent. The basin of the partially folded conformer (conformation B) contains green isosurfaces in the landscapes characterizing the 0.5 M salt solutions, which are absent in both pure water and solutions of higher ionic strength. The changes in this basin denote that each salt only notably stabilizes conformation B at low ionic strength. As displayed in Fig. 1, several of the configurations of the peptide belonging this basin are oriented in such a way that the negatively charged glutamic-acid side chains are far apart, stemming from electrostatic repulsion. At higher ionic strengths, screening diminishes the enthalpically favored repulsion, which is the source of the destabilization of the latter free-energy basin with increasing ionic strength. The stabilization of this conformation at low salt concentrations may arise from cation side-chain binding, stemming from the affinity of sodium and potassium ions to side-chain carboxylate groups on proteins (17–21).

As mentioned earlier, the basin containing the helical conformation (conformation D) shows changes in its topology specific to the aqueous environment, where it appears similar in pure water and KCl but different in NaCl, and there does not appear to be any influence of the ionic strength. The conformations belonging to this basin consist of compact structures, suggesting that electrostatic screening may not be as relevant in the stabilization of compact conformations, although salt-specific enthalpic effects govern their stabilization.

Table S1 in the Supporting Material summarizes the relative populations of the dominant types of conformations observed in the free-energy landscapes displayed in Fig. 1. The conformations were divided into three basic types based on the value of the backbone Ψ-angles throughout the trajectory, which included helical (Ψ < 0°), extended (Ψ > 180°), and other (0° < Ψ < 180°). The populations for each of these simulations reflect the characteristics of the landscapes in Fig. 1, with the helical state being the most populated in each case and the population differences between water and saline solutions being minute.

Free-energy landscapes for the zwitterionic peptide are displayed in Fig. 3. The deepest free-energy well for each system contains the loosely-formed helix (conformation C) and does not appear to change significantly from one saline assay to another. One of the only noticeable differences between the landscapes is found in the basin containing the conformer resembling a 3₁₀-helix (conformation D), as well as in the transition state between conformations C and D. The basin around conformation D is stabilized in NaCl and destabilized in KCl, in comparison with pure water. In addition, the height of the barrier between conformers C and D appears to decrease significantly in NaCl when compared to the same barrier measured from the pure-water landscape, while the corresponding barrier in KCl shows an increase in height.

Figure 3.

Free-energy landscapes for the zwitterionic AEAAAEA peptide in 1.0 M KCl (A), 1.0 M NaCl (B), and water (C) over our defined MRC. The five colored spheres in each plot show the location of five relevant conformations for small peptides: PPII (purple), 2.5₁ helix (red), 3₁₀ helix (blue), α-helix (green), and π-helix (orange). Colored isosurfaces represent specific free energy values (pink, <7 kcal/mol; red-orange, <6 kcal/mol; yellow, <5 kcal/mol; green, <4 kcal/mol; blue, <3 kcal/mol; violet, <2 kcal/mol; and black, <1 kcal/mol). Isosurfaces (white) show the portion of conformational space sampled during a given simulation. Selected conformers observed in respective trajectories are shown around each plot, while their locations on the MRC are also indicated. Ions that were observed to be interacting with a conformer are represented as large, colored spheres (sodium, yellow; potassium, bronze; and chloride, cyan).

As can be seen in Fig. S2, the salt-specific stabilizing effects on the basin are observed at all concentrations. On the other hand, at a concentration of 2.0 M, not only are the heights of the analogous barriers between conformers C and D significantly lowered, but the basin containing conformer A appears to increase in well depth in each saline solution. This observation is a likely consequence of the high ionic strength of the solution, thus, causing electrostatic screening of intrapeptide Coulombic interactions and leading to larger entropic contributions on conformational stability. The lack of large free-energy basins and the presence of larger barriers at lower ionic strengths indicate that enthalpic contributions are more significant in solutions of lower ionic strength, where less electrostatic screening occurs.

The most interesting trend evident in Fig. 3 involves the α-helix basin, which is highlighted by a green isosurface near the green sphere in the free-energy landscape characterizing each system. In each NaCl solution, a blue isosurface is also present in this basin, suggesting that NaCl has a greater stabilizing effect on this basin than KCl. At lower concentrations, the corresponding basins in pure water and KCl appear similar, albeit KCl also seems to have increased the stabilization of this basin at 2.0 M. Such effects may arise from electrostatic screening, in the spirit of the phenomena described with the blocked peptide. Yet, it would appear that salt-specific effects also play a role in the stabilization of the α-helix. At each concentration, its basin has a noticeably larger well depth in NaCl than in KCl, which may arise from interactions of sodium ions and the peptide backbone. Both sodium and potassium ions have an appreciable affinity for the carbonyl groups of the backbone; however, sodium ions have been shown to be a stronger binder (17,21), which is likely responsible for salt-specific stabilization effects.

Sodium ions also interact in a stronger fashion with carbonyl groups than would water molecules, hence disrupting the water-carbonyl hydrogen bonds that stabilize less compact conformations. This leads to the promotion of intrapeptide hydrogen bonding characteristic of an α-helix and other compact conformations. Despite the disparity observed between the NaCl and KCl basins, the general trend of greater α-helical stabilization with increasing ionic strength coincides well with the conclusions made by Crevenna et al. (39) in recent experimental and computational work on small peptides containing multiple alanine and glutamic-acid residues, where it was observed that higher concentrations of each NaCl and KCl stabilized the helical structure of this peptide, with NaCl typically inducing marginally increased helicity.

One interesting point to consider when comparing results from simulations of blocked and zwitterionic peptides is the difference in nonspecific electrostatics within the systems. The presence of charged moieties on or near the peptide termini have been shown to have significant effects on the stability of the peptide conformations (40,41). Comparison of the free-energy landscapes corresponding to each type of peptide reveals many similar characteristics regarding the topology of the surfaces, yet many of the well-depths and barrier heights are noticeably different. For each homolog, local minima are present at similar positions on the MRC in all surrounding environments, as displayed in Figs. 1 and 3. Such minima correspond to conformations including the α-helix, the turn, and the dominant conformations discussed above. Despite the shared local minima between the landscapes, there are obvious shifts in the relative stabilities of the corresponding conformations. The global minimum on our MRC shifts from the α-helix for the blocked peptide to a loosely-formed helix (conformation C in Fig. 3) for the zwitterionic peptide.

It is also obvious that in Fig. 3, the darker isosurfaces, which correspond to conformations of lower free energy, are more widely spread throughout the conformational space than in Fig. 1. Because an identical coloring scheme was used for the isosurfaces in each figure, this observation suggests that the free-energy differences between many of the conformations of the zwitterionic peptide are smaller than those of the blocked peptide. Such an effect may arise from the introduction of the helix-dipole induced by the charged termini of the zwitterionic peptide, which tends to induce shifts in the relative populations of stable conformations for a given peptide.

The computational work performed on a 21-residue PGA in NaCl and KCl by Fedorov et al. (16) revealed salt-specific stabilization effects on PGA. The most stable conformation of PGA in pure water was an extended PPII conformer, which was also found to be more stable in a KCl solution. Yet, the α-helix was found to be the most stable conformation of PGA in NaCl. This salt-specific phenomenon was ascribed to sodium ions exhibiting a higher affinity for glutamic-acid side chains than potassium ions, causing more electrostatic screening of the repulsion between the negatively charged side chains of the peptide in NaCl solution, which in turn allowed intrapeptide hydrogen bonds to form and the α-helical conformation to emerge.

Electrostatic screening may have been the dominant molecular force behind salt-induced effects on conformational stability of a peptide with a plethora of electrostatic interactions. Other forces, however, may be more important in peptides with different sequences. Here, electrostatic screening plays a smaller role on account of the significantly lower number of electrostatic interactions possible within a given peptide molecule, meaning that additional forces are driving the shifts in conformational stability, as indicated in the free-energy landscapes. Due to the wide range of available primary structures for different peptides, salt-induced peptide stabilization is proving to be a very complex phenomenon and much work ought to be completed before one can draw definitive conclusions on a specific molecular interaction that constitutes the driving force underlying shifts in peptide conformational equilibria.

Visual inspection of the three-dimensional free-energy surfaces in Fig. 1 reveals a potential pathway of low free energy in the landscape over which the peptide may undergo conformational transitions. The pathway is displayed as a red line in Fig. 4 A and is located along a narrow section of green isosurfaces in the landscapes in Fig. 1. The green isosurface forms a curved tube, which delineates a pathway of low free energy between the α-helix basin and a basin characterizing a random coil. When the peptide undergoes conformational transitions, it is most likely to do so by navigating between low-energy configurations, suggesting that the green isosurface represents a reasonable candidate of the space through which the peptide isomerizes. The pathway was employed to define a model unidimensional reaction coordinate (ξ), which follows the red line in Fig. 4 A and connects the α-helix basin (ξ = 0) to the random coil basin (ξ = 1), over which a one-dimensional potential of mean force (PMF) can be constructed. Such PMFs are created using information from the computed free-energy landscapes displayed in Fig. 1 and can lend insight into changes in the potential transition pathway within different saline environments. Fig. 4 B shows the PMFs determined from the pure water, 1.0 M KCl, and 1.0 M NaCl simulations.

Figure 4.

(A) Free-energy landscape of Ace-AEAAAEA-Nme illustrating the path used as the model unidimensional reaction coordinate (ξ) to construct the one-dimensional free-energy profiles shown in Fig. 5. (Thick, red line) Path is indicated on the plot, where the initial and final states of ξ are defined as the α-helix (ξ = 0) and a random coil (ξ = 1), respectively. (B) Potential of mean force plots obtained from the computed three-dimensional landscapes for Ace-AEAAAEA-Nme in pure water (black), 1.0 M KCl (blue), and 1.0 M NaCl (red). The reaction coordinate (ξ) is described visually here, as going from the α-helix to a random coil.

The three profiles are remarkably similar barring only a few characteristic differences—those for the pure water and 1.0 M KCl simulations are the most similar, and that for the 1.0 M NaCl simulation having some unique features. The NaCl PMF has lower free-energy values over the ranges ξ = 0–0.3 and ξ = 0.6–0.8 compared to the pure water and KCl PMFs. The barriers for the NaCl PMF are larger over the range ξ = 0.3–0.6. The local minima in the regions were ξ ≈ 0.3 and 0.8 for the NaCl PMFs are long-lived intermediates from the unfolding of the α-helix. This conclusion is consistent with that of von Hansen et al. (21), who have demonstrated that the unfolding of a small, α-helical peptide composed of alanine, glutamic-acid, and lysine residues was an order-of-magnitude slower in the presence of sodium salts as compared to potassium salts. Their rationale for this observation is that the stabilization of compact, partially unfolded intermediates of the peptide arises from the tight binding of sodium to the peptide carbonyl and side-chain carboxyl groups. Such stabilization is responsible for the deeper free-energy wells present in the NaCl PMF in Fig. 4 B, as the peptide consists of compact structures over the entire reaction pathway.

Circular-dichroism (CD) spectra have been calculated for the different trajectories using the method described by Sreerama and Woody (42). The average spectra are shown in Fig. 5 and can be employed to estimate qualitatively the populations of the various conformations accessible to the peptide based on the location and intensity of the bands within a given spectrum. Here, we utilize the spectra to confirm conclusions drawn from the three-dimensional free-energy landscapes. As seen in Fig. 5, the spectra corresponding inferred from the different trajectories have notably similar characteristics. The spectra characterizing the blocked peptide contain several bands indicative of specific conformations. Two negative bands are present at 208 and 222 nm, and a positive band at 192 nm, highlighting the presence of the α-helix. This coincides with our qualitative observations from the free-energy landscapes, with the α-helix basin consistently corresponding to the deepest well. The depth of the negative bands almost systematically increases in the spectra computed from simulations of saline systems when compared to that of pure water, demonstrating a more thorough sampling of the α-helix and a higher population of α-helices. Spectra from the zwitterionic peptide simulations show much weaker negative bands at 208 and 222 nm, but a significantly sharper positive band near 195 nm. The disappearance of the negative bands is congruent with the decrease in the well-depth of the α-helix basin characteristic of the zwitterionic peptide. The spectra are also qualitatively similar to those observed experimentally for similar alanine-based peptides (25).

Figure 5.

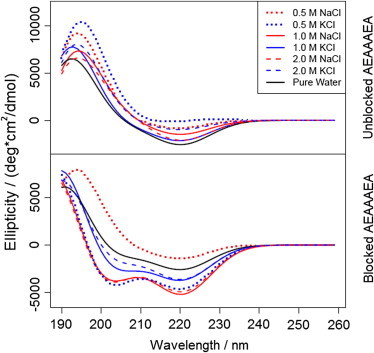
Computed circular-dichroism spectra of zwitterionic AEAAAEA (top panel) and Ace-AEAAAEA-Nme (bottom panel) in various aqueous systems.

Further inspection of the negative band at 222 nm reveals an interesting salt-dependent trend in the α-helicity of each type of peptide. For the blocked peptide, this band is less deep for the pure water system than for each of the saline systems, excluding the 0.5 M NaCl environment. Conversely, this band is the sharpest for the pure water system out of the entire collection of zwitterionic peptide simulations. These trends indicate that the zwitterionic α-helix may be destabilized by salts in the presence of a helix-dipole, whereas the blocked α-helix is largely stabilized by salts when the helix-dipole is absent. This further suggests that ionic screening of the charged side chains may not be as large of a factor in the presence of a helix-dipole, as one would expect the addition of ions to screen the repulsion between two negatively charged side chains. It is also possible that the charged termini alter the inherent stability of the α-helix, as has been observed in prior work on alanine-rich peptides (41), which could alter the screening effects induced by ions; however, additional work must be done to confirm this.

Conclusions

We have studied the effects of NaCl and KCl on the conformational stability of a peptide of sequence AEAAAEA by probing its conformational space using a three-dimensional MRC coupled with the metadynamics preferential-sampling algorithm (29). The α-helix was found to be the most stable conformer in each saline assay for the peptide with blocked termini, arising from the formation of additional intrapeptide hydrogen bonds offered by the capping moieties. Local minima were observed in the α-helix basin in all free-energy landscapes of this peptide, with wells of increasing depth in the presence of NaCl. Our observations from these landscapes are in line with features observed on CD spectra computed from each trajectory. The PMFs were generated over a model unidimensional reaction coordinate, ξ, using select free-energy landscapes. They confirmed the existence of long-lived intermediates in the unfolding of small peptides containing charged side chains in the presence of sodium salts, consistent with the conclusions of von Hansen et al. (21).

Stabilization effects have been shown to be dependent upon either salt concentration or identity. More compact conformations have been stabilized in environments with high ionic strength, suggesting that screening reduces the favorable repulsion between the glutamic-acid side chains and induces the stabilization of compact conformations. However, the stability of compact conformations is influenced by the identity of the salt present in solution and strayed from the concentration-dependent trend. These findings notably differ from those of Fedorov et al. (16) on the stabilization effects of NaCl and KCl on PGA, where each salt had opposite effects on the conformational stability of PGA. This discrepancy can be ascribed to the large number of deprotonated glutamic-acid residues in PGA, increasing the influence of electrostatic screening and cation side-chain binding on the repulsion between its side chains. Our work has shown that a simple explanation of the screening effects on this phenomenon is not sufficient, as compact conformations do not show changes in stabilization with increasing ionic strength. The conformational stability of peptides in saline environments thus emerges as a function of the peptide sequence in addition to both the identity and concentration of the ions.

The techniques employed here have proven instrumental in sampling a large number of the conformations accessible to a peptide on a predefined MRC. The principal challenge in using the metadynamics algorithm (29) is selecting the optimal heights and widths for the Gaussian potentials incorporated into the artificial energy term. Convergence of our free-energy calculations was difficult to attain despite simulation times exceeding 2 μs in length, which is indicative of suboptimal choices for the characteristics of the Gaussian potentials. This issue is discussed in detail in the Supporting Material. Refined assessments of the potential heights and widths would allow enhanced sampling of the conformational space of a peptide on timescales somewhat more amenable to MD simulations. Nonetheless, this work highlights the strength of the metadynamics algorithm coupled with a carefully chosen multidimensional MRC for examining the conformational stability of peptides in any environment.