Self-organization of domain structures by DNA-loop-extruding enzymes

Abstract

The long chromosomal DNAs of cells are organized into loop domains much larger in size than individual DNA-binding enzymes, presenting the question of how formation of such structures is controlled. We present a model for generation of defined chromosomal loops, based on molecular machines consisting of two coupled and oppositely directed motile elements which extrude loops from the double helix along which they translocate, while excluding one another sterically. If these machines do not dissociate from DNA (infinite processivity), a disordered, exponential steady-state distribution of small loops is obtained. However, if dissociation and rebinding of the machines occurs at a finite rate (finite processivity), the steady state qualitatively changes to a highly ordered ‘stacked’ configuration with suppressed fluctuations, organizing a single large, stable loop domain anchored by several machines. The size of the resulting domain can be simply regulated by boundary elements, which halt the progress of the extrusion machines. Possible realizations of these types of molecular machines are discussed, with a major focus on structural maintenance of chromosome complexes and also with discussion of type I restriction enzymes. This mechanism could explain the geometrically uniform folding of eukaryote mitotic chromosomes, through extrusion of pre-programmed loops and concomitant chromosome compaction.

INTRODUCTION

Eukaryote chromosomal DNAs of up to a few centimeters in length are compacted to fit inside few-micron-diameter nuclei. Similarly, the millimeter-length chromosomal DNAs of bacterial cells are compacted into micron-size nucleoids. It has been proposed that chromosomes might simply occupy maximum-entropy conformations, in the manner of confined random-coil polymers (1,2). However, sequence position analyses reveal DNA to be spatially ordered. Chromosomes of Escherichia coli (3–5) and Caulobacter crescentus (6) have loci precisely positioned inside the cell, with fluctuations too small to be consistent with random-polymer statistics (7). In eukaryote cells, interphase chromosomes in differentiated cells occupy distinct territories (8). Furthermore, analyses of DNA juxtapositions inside eukaryote nuclei reveal that loci up to tens of megabases apart along chromosomes are positioned near one another in the nucleus (9,10), with statistical properties inconsistent with random-polymer organization (10).

Detailed characterizations of specific cases of in cis gene regulation also indicate that chromosomes have a well-defined ‘loop domain’ organization, with specific but distant sequences along the same chromosome positioned to be near one another (11). It is thought that ‘chromatin-bridging’ proteins (12) somehow stabilize these loop structures, but the processes by which sequence-defined chromatin loops are established and maintained are unknown.

Strong correlations of juxtaposed DNA sequences are especially clear during eukaryote mitosis, when chromosomes are compactly folded, following their replication. Chromosomes are ‘condensed’ by folding along their length into linear paired-chromatid noodle-like structures, with a well-defined thickness and strikingly uniform structural and mechanical properties (13). As mitotic chromosomes are folded, sequences that are a few megabases apart somehow ‘know’ to associate, while more distant sequences know to stay apart, implying a highly regulated lengthwise condensation distinct from usual polymer condensation (14,15). Similar considerations apply to the loop domain organization of meiotic prophase chromosomes, solidifying the conclusion that strong long-range correlations in DNA sequence position are maintained in living cells.

The default mechanism for chromosome looping is random-polymer motion leading to loop formation. However, while random motions can quickly form small loops comparable in size to a polymer’s persistence length (a few kilobases at most for chromatin) (16), reproducible formation of specific large loops by random collision is inefficient, especially when self-avoidance effects are taken into account. For the case of mitotic/meitoic chromosome condensation, a random-collision model of contact formation cannot lead to linearly condensed chromosomes since the underlying DNA sequence distance between juxtapositions cannot be sensed: the result will be conventional polymer collapse of chromosomes into spherical globules with no tendency toward linear organization (17). Formation of chromatin bridges through random collision would inevitably lead to the gluing together of chromatids into spherical chromatin masses, as has been demonstrated using synthetic AT-hook proteins (18). Random formation of polymer loops is not by itself likely to be the main mechanism underlying the spatial self-organization of chromosomes.

It is thought that structural maintenance of chromosome (SMC) complexes are in general involved in mediating distant-site interactions in chromatin (19), with condensin SMCs playing a key role in mitotic chromosome folding (20), and with cohesin SMCs playing an important role in sister chromatid cohesion and in defining interphase chromatin loops (21). While the mechanistic details of how SMCs associate with and organize DNA in vivo remain poorly understood, a few aspects of their function are established experimentally. Immuno-inactivation of condensin complexes in Xenopus egg extracts (an in vitro system capable of assembling mitotic chromosomes) (22), or siRNA depletion of even one subunit of condensin complexes (23,24) in tissue culture cells, causes defective mitotic chromosome condensation. Cells where one condensin subunit can be inducibly knocked out also show chromosome condensation defects (25). In biophysical experiments, purified condensin is known to efficiently and systematically condense DNA molecules without the need of other cofactors (26).

Condensins are thought to be capable of interacting with distinct stretches of chromatin, by a mechanism possibly involving encirclement of two DNA segments (27). Few details are known concerning how condensins act to facilitate mitotic chromosome compaction (28). However, in single-DNA experiments, condensins have been observed to dramatically compact naked DNA in an adenosine triphosphate (ATP)-dependent and processive manner, through 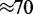nm steps comparable in size to the condensin SMCs themselves (26). The fact that the single-DNA reactions proceeded to complete condensation of DNA through steps of relatively uniform size argues against a mechanism based on random loop capture by DNA-bridging protein interactions or multivalent positive ions, and which would be expected to generate steps with a broad distribution of sizes and of larger mean 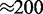nm (29).

The same experiments (26) showed that in the absence of ATP, condensins are able to bind DNA, but without any compaction effect. This indicates that the initial condensin–DNA association does not involve loop capture, but instead involves binding of condensin to DNA in a non-loop-trapping mode. In those experiments, after subsequent washing away of solution-phase protein and addition of ATP, condensins were observed to reorganize ‘along’ single DNAs, driving step-wise condensation (26). This result suggests that binding and step-wise condensation are decoupled processes, the latter strictly dependent on hydrolyzable ATP.

The idea that condensins act as condensation machines, rather than simple chromatin crosslinkers, is supported by the single-molecule experiments (26), and also by consideration of what would happen to chromosomes if condensins did act by a simple binding mechanism. Without some sort of loop-binding regulation, purely DNA-bridging factors will lead to indiscriminate binding of chromatin to itself, in the manner of ‘poor solvent’ condensation of flexible polymers (30). The result will be establishment of a surface tension between chromatin and cytoplasm, causing minimization of interfacial area so as to form spherical aggregates, strong sticking of different chromosomes to one another (17) and interchromosome/chromatid entanglement.

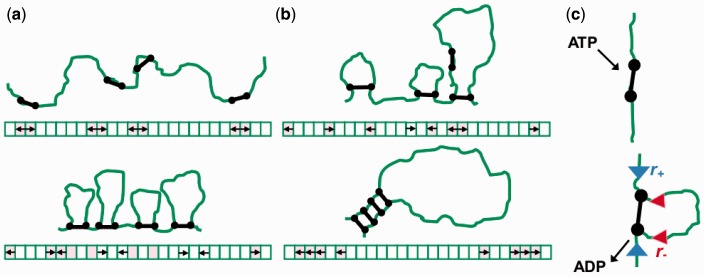
Here, we describe an active mechanism able to form specific and large loop domains of precise size, based on hypothetical DNA-loop-extruding enzyme machines with general properties consistent with those of condensins. We consider a DNA lattice of some finite length, on which M enzymes are bound; each enzyme is assumed to have two binding domains which can bind and therefore bridge two DNA sites (Figure 1). The size of the lattice sites is comparable to the persistence length of DNA (or chromatin), and also to the size of the machines, 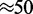nm. When a machine binds to the DNA lattice, it associates with adjacent lattice sites, i.e. DNA sites separated by a distance comparable to the size of the enzyme. We suppose that ATP hydrolysis causes each binding domain (motile element) to move along the DNA, away from its partner; the protein link between the two motile elements leads the motility to drive extrusion of a DNA loop. The only interaction between the pairs considered in our model is their steric repulsion. Beyond this the only other ingredient is whether or not dissociation of the machines from DNA is permitted. In the absence of dissociation, a relatively disordered series of variable-size loops results (Figure 1a). However, when dissociation and re-association of the machines occur, they self-organize into a robustly ordered ‘stack’, anchoring a sturdy loop domain (Figure 1b).

Figure 1.

Schematic drawing of machine positions on the lattice as time progresses; lattice model equivalent is sketched below each panel. Black dumbbell shapes (and arrows in the lattice sketch) depict enzymes and green lines show DNA. Panel (a) depicts the starting point and the progression of infinitely processive machines, while Panel (b) shows machines with lower processivity (disassociation rate is still relatively small, see text). Panel (c) depicts a single step, with ATP binding, hydrolysis and release associated with extrusion of a small amount of DNA.

At the outset, we emphasize that the application of this model to condensin self-organization in chromosomes is speculative. We also note that other enzymes that extrude DNA loops are known and have been characterized, most notably type I restriction enzymes (31), and our model may prove useful for describing their self-organization.

MATERIALS AND METHODS

We consider a DNA segment of contour length 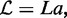divided into lattice sites of size 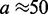nm, with a total number of sites 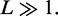At time t = 0, M motile element pairs are dispersed randomly, each pair initially occupying adjacent sites of this lattice. The DNA-binding motile elements (referred to below as ‘motors’) then move along the DNA with rates independent of position; steps that move a motor away from its partner (‘forward’ steps that extrude a DNA loop) occur at a rate 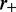and steps that move a motor back toward its partner (‘reverse steps’ that retract the loop) occur at a rate 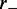(Figure 1). We suppose the motion to be directed by energy gained from ATP hydrolysis, with 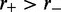(when there is 1D diffusion of each motor; when the motors are driven together which is not of interest here). The motor pairs are assumed to have left/right symmetry, i.e. the left and right motors move with the same rates.

We also suppose the motors to sterically occlude one another: only one motor can occupy each position on the lattice, making them unable to pass through one another. The endpoints of the lattice (sites 1 and L) are ‘domain boundaries’: the motors are unable to move past them.

The final ingredient of the model is the dissociation of a motor pair from the DNA; this is taken into account by a slow-dissociation rate 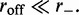In the non-dissociating case, 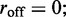when 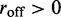and a dissociation event occurs, we then replace the motor pair on a randomly chosen pair of adjacent, empty lattice sites.

We have performed numerical simulations of this model using Gillespie’s ‘event-driven’ algorithm for simulating stochastic processes (32). This method is most simply applied to processes where there are a sequence of transitions between a set of discrete states, such as the rate model described above. At each step of the simulation, the approach considers which of the possible transitions that are possible at that moment actually is the next transition to occur. At an initial time t, one makes a list of all possible transitions that might occur, and their rates (for our model, 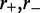and 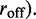Suppose there are K possible ‘candidate’ transitions with rates 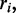i running from 1 to K. Two properties of the next transition event must be determined: the time interval 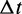between the initial time t to the event, and which of the K transitions will actually be the next event.

The rate at which the next event occurs (regardless of type) is just the sum of the K rates, 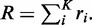The time increment 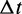to the event is distributed over the range 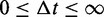exponentially, with probability distribution 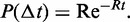The actual realization of 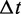is drawn from this continuous distribution. Which of the K transitions actually occurs is determined from their probability distribution 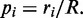This second, discrete, distribution is be used to select which of the K candidates actually is next.

Once 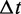and i are determined, the state of the system is changed, and time is increased to 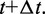The algorithm is then repeated to propagate the system forward from event to event, for as many transition steps as one requires (or for as long a total time as is required). The result is a series of transition events, distributed in time according to the rates that define the model. There is no time discretization; events can occur separated by arbitrarily small 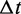s, as in reality (this method is sometimes described as ‘continuous-time’ simulation for this reason). Event-driven simulation is efficient for models with a finite set of possible transitions at each moment in time (e.g. the model studied here), since all computation is focused on determining the sequence and times at which events occur.

To obtain steady-state properties, individual simulations were run for times of from 10⁴ to 10⁵ times 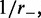roughly 1000 times longer than the time required to reach the steady state. Large numbers of independent simulations (typically 10⁴–10⁵) were run to obtain accurate steady-state averages with small statistical errors; in some cases, the error bars are smaller than the plot lines and are not plotted (errors are described numerically in those cases). All error bars shown indicate standard errors. In some cases, exact or approximate analytical results for statistical properties of the steady state can be computed to compare with the simulations.

RESULTS

Results for non-dissociating machines

In the case with no dissociation (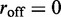), the ordering of the enzymes along the molecule is preserved over time, and the total number of forward and reverse steps taken by the two motors of any one machine are given by the total distance between them. This makes it possible to describe the steady state as governed by an effective potential energy E proportional to the inter-motor distance. One contribution to E acts between the two coupled motors of each machine, 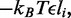where 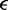is a constant dependent on the rates 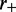and 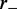(see below), 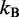is the Boltzmann constant, T is the absolute temperature and 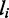is the distance (in lattice units) between the motors of the ith pair (the size of the loop anchored by machine i). 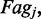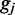If an external force F pulls on the endpoints of the lattice, there is an extra term added to the effective energy where is the length of the gap between the motor pairs. Here, 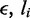and 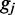are all dimensionless. DNA torsional stress could be added to the model, e.g. as a bias on the initial loop formation/binding rate, but we leave this out of the model at present, in part due to the high concentrations of topoisomerase in vivo that will tend to relax torsional stress, and in part due to observations of a null effect of torsional stress in single-DNA-condensin experiments (26).

The total effective energy is the sum of the terms for the loops and gaps,

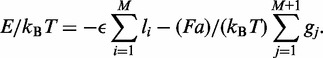(1)

The hard-core repulsion constrains 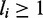and 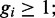furthermore, we have the total length constraint 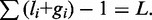The value of 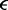is determined by the ratio of forward and reverse stepping rates to be 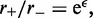which just reflects the conversion of forward and reverse reaction rates into an effective energy biasing forward over reverse steps. If the external force 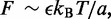it should be kept in mind that the rates 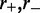might be themselves significantly force dependent.

We can then use an effective Boltzmann partition function 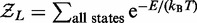to calculate statistical properties of the steady state. This partition function describes a thermal equilibrium which coincides with the steady state for the active system defined through rates 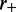and 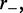even though the model as stated describes an active system where energy is not conserved (the motors are hydrolyzing ATP). As we show in the appendix, the partition function is solvable exactly, as

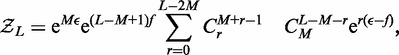(2)

where 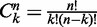is the binomial coefficient and 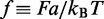is the force in units of 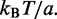The summed variable r is the total length found in loops (between motors). The probability distribution function for length l in a loop follows by a similar computation (see the appendix) as

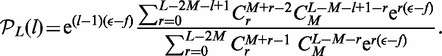(3)

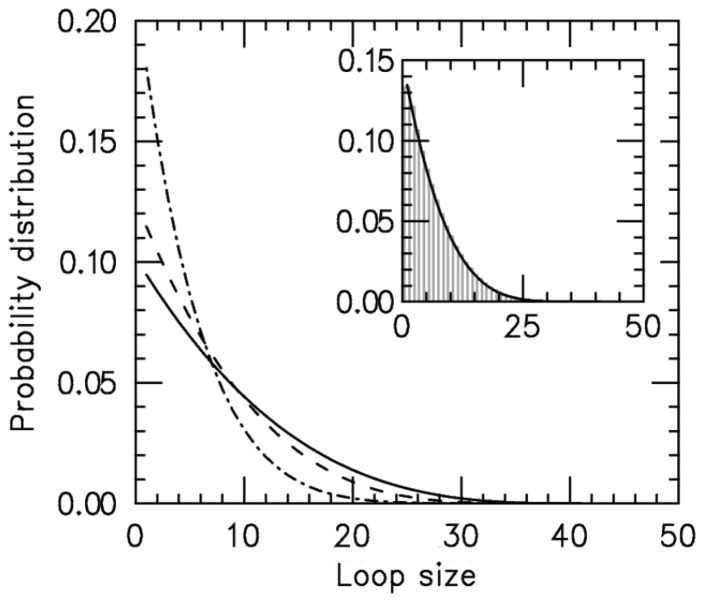
Results for the loop-size distribution are shown in Figure 2; for each value of 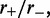an exponential-like distribution is obtained, corresponding to random fluctuations of loop size in the effective potential.

Figure 2.

Loop-size distribution for M = 5 pairs of non-disassociating loop-extruding machines on a lattice of size L = 50. The probability distribution broadens as the bias (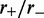) increases. Main figure shows results for 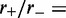1.05 (dot-dashed line), 1.5 (dashed line) and 4.0 (solid line). Inset: comparison of steady-state loop-size distributions for exact statistical theory (solid black line) and kinetic simulation 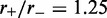(gray bars); difference between them is negligibly small. The simulation was run 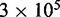times, each for a time of 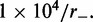Standard errors for the histogram bars have a maximum value of 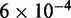and are invisible on this plot.

The effective Boltzmann steady-state loop-size distribution matches the simulation’s steady state

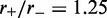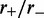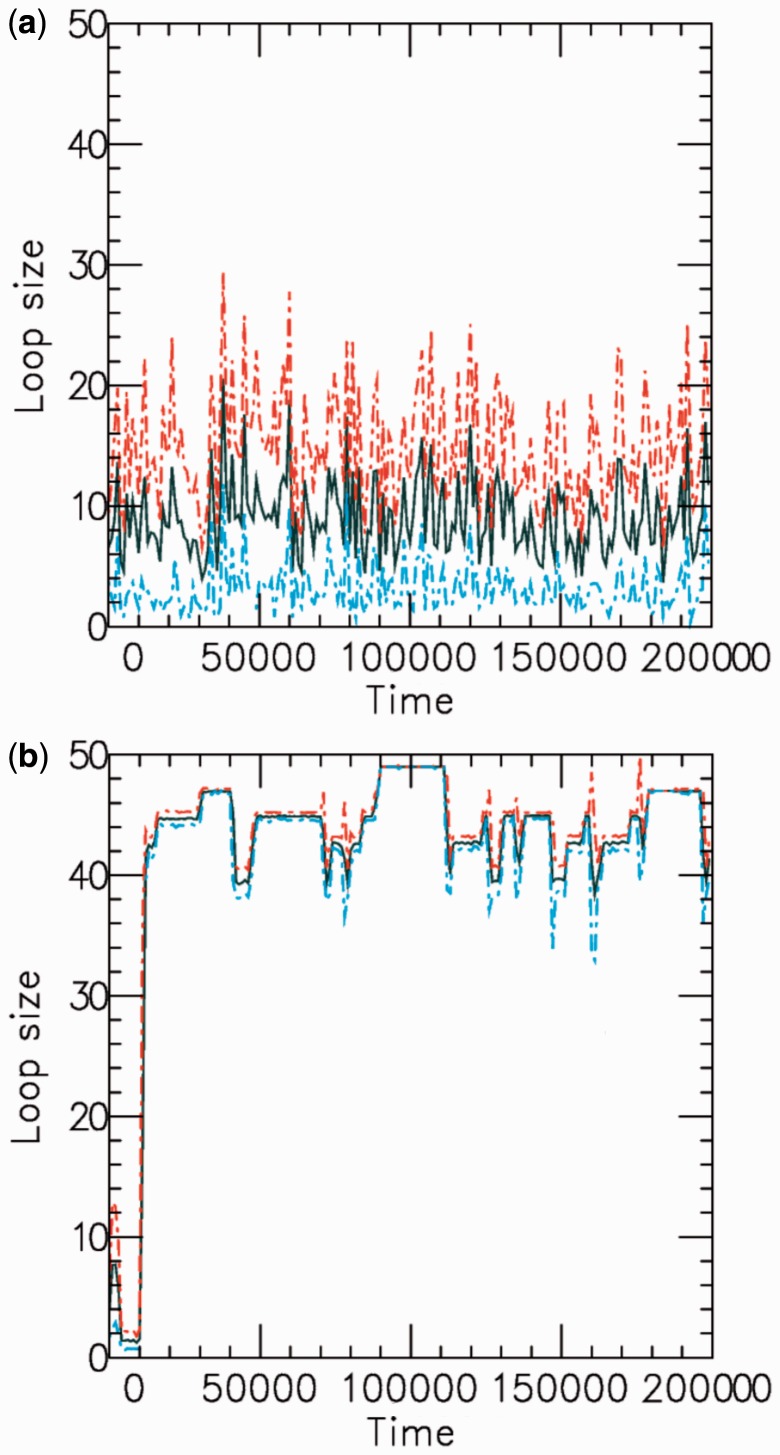
To verify that the effective potential computation is a correct description of the steady state, we compared the above results with simulation results and found them to be equal. One case (L = 50, ) is shown in the inset of Figure 2; similarly precise agreement was found for other values of and L for steady-state properties, validating the effective inter-motor potential. As the motor bias is increased, the simulations reach the steady state more slowly, but for biases up to 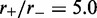we have found precise agreement of the effective Boltzmann result with the simulated steady state. Figure 3a shows typical dynamics of mean loop size for M = 5, L = 50 and 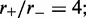the mean loop size 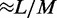and show strong fluctuations as a function of time.

Figure 3.

Example time series of loop size for 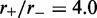for a (a) non-disassociating and a (b) dissociating case (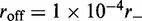), for M = 5 machines on a substrate of length L = 50. The dark solid line shows the average of the sizes of the M loops, and the red and blue dashed lines indicate the width (one standard deviation) of the distribution of loop sizes subtended by the machines as a function of time. As in all cases mentioned in this article, time is in units of .

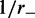The loop distribution peaks at small sizes and flattens as bias increases

Figure 2 shows that the loop-size distribution is similar for various values of motor bias (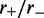); in each case, an exponential-like decaying distribution peaked at zero loop size is obtained, with the distribution broadening as 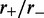is increased. In conclusion, the model with 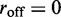generates a broad distribution of relatively small loops, because the initially adjacently bound motors cannot move past one another and generate essentially independent loop-size fluctuation against the inter-motor effective potential. We note that even though the peak is at the lowest allowable value for all biases, the average loop size depends on the bias.

Results for machines that dissociate and rebind

We again consider M machines on a lattice of L sites, but now we suppose that the machines can disassociate at a rate 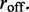As mentioned above, dissociated enzymes are considered to immediately rebind at an unoccupied pair of lattice sites chosen at random (the total number of bound machines is thus constant in time). We focus on the case where the disassociation rate 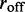is much smaller than 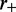and 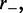which is the regime where the machines are able to interact (collide) with one another between dissociation events. Since the machines bind so as to occupy adjacent lattice sites, there is no possibility of binding where two motor pairs cross one another. This is a simple consequence of the steric hindrance of the motor pairs and the relative inflexibility of the underlying DNA or chromatin at the scale of the lattice size 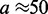nm.

Dark solid curves in Figure 3 show the average loop size as a function of time for both non-disassociating and dissociating cases, for 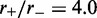and L = 50. The dashed colored curves indicate the distribution of loop size. Without dissociation (Figure 3a), the loop sizes fluctuate strongly, reflecting the stochastic dynamics of individual machines. Adding dissociation rebinding leads to loop sizes being driven toward their maximum possible value, with strong suppression of loop-size fluctuations.

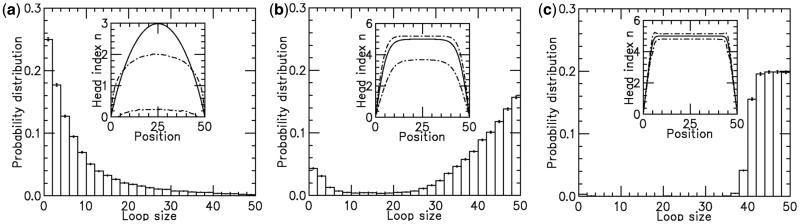
Increased bias leads to ‘stacked’ machines, large loops and suppressed fluctuations

With dissociation, as the motor bias 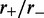was increased, fluctuations in the loop size trapped by each motor decreased, indicating the onset of ‘stiffening’ of the steady state (Figures 3b and 4). Furthermore, as the bias was increased, we observed a gradual increase in the probability of large loop sizes, eventually leading to a peak of the loop-size distribution at values close to the lattice length L (Figures 4 and 3b). Thus, dissociation allowed self-organization of the machines so as to ‘stack’ up in the manner shown in Figure 1b. To understand this phenomenon, note that since 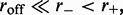when a machine dissociates and then rebinds, most of the DNA lattice is already captured by loops, and so it is likely that rebinding occurs ‘inside some loop’. But then this enzyme will proceed to move along the loop it is inside, until it catches up with the other enzymes ‘anchoring’ that loop (Figure 1b). Repetition of this process results in the ‘stacking’ of enzymes on top of one another at the loop base; the multiple enzymes anchoring the large loop make it robust against dissociation of individual enzymes. Gradually, the entire lattice becomes a single organized loop domain, with a series of motor pairs at the base of the loop, each subtending 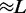lattice sites.

Figure 4.

Results for model with dissociation, for L = 50, M = 5 and 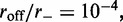for different motor biases 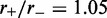(a), 1.50 (b) and 4.00 (c). Panels (a–c) show loop-size distributions for the simulation steady state: as bias is increased, a peak grows at 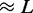as motor pairs begin to trap the entire domain. Each panel was computed using 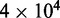simulations each of total time 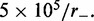The maximum size of the standard error bars for the histograms are 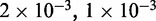and 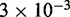for panels (a)–(c), respectively. The insets show the motor position (labeled ‘head index’) index 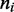along the lattice: dashed lines show the average ( 1 SD for the simulations (standard error bars for the insets are invisible on this plot); solid curves show average obtained from approximate effective Boltzmann description of the steady state. As bias is increased, fluctuations are suppressed and the motors become ‘stacked’.

Effective Boltzmann model for the steady state of enzymes with dissociation is a ‘restricted solid-on-solid’ model and can be solved using transfer matrix method

We sought an effective Boltzmann description of the steady state including dissociation. To do this, we need to keep track of the ‘nesting’ of loops corresponding to the ‘stacked’ motor pairs. We define a ‘motor position index’ 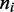for each lattice site, defined as follows:

(4)

The motors are now described by the positions of up and down ‘steps’ in the 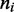variable along the lattice. The number of up and down steps must each be constrained to be M; note that also 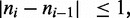and 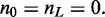Apart from these constraints, all configurations of the 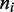s are permitted.

The effective energy must keep track of the distance the motor pairs should have moved from their initial adjacent positions to obtain the configuration 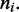This is done using

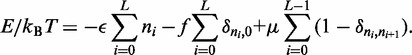(5)

The first term in the right-hand side (RHS) of Equation (5) is the product of the bias factor 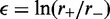and the total looped length, with the 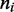doing the necessary multiple counting of regions enclosed by more than one motor pair. The second term couples the external force f to the unlooped region of the lattice with 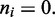The last term uses a chemical potential 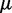to fix the average number of machines on the lattice at M. Equation (5) is a ‘restricted solid-on-solid’ model used to describe interface fluctuations, some properties of which can be solved exactly (33). However, the average 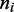profile requires a numerical solution of this problem; we use a transfer matrix method (34) to obtain this.

Equation (5) cannot describe the 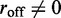steady state exactly, since when an enzyme dissociates, ‘memory’ is lost of the number of forward and reverse steps taken by that motor, eliminating the possibility of an exact potential-energy-based description. However, in the slow-dissociation case of interest, we do not expect this to be a severe problem since the motor pairs will reach a steady state between dissociation events. We expect the Boltzmann distribution for Equation (5) to describe the statistics of the 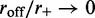limit quantitatively, and small values of 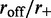at least qualitatively (note that 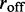does not appear in the Boltzmann model as 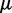is used to control ).

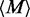Agreement of effective Boltzmann and simulation results improve as motor bias increases

The insets in Figure 4a–c show the results for motor position index (labeled ‘head index’ in insets) 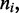for the average of the effective Boltzmann theory (solid line), and for simulations with 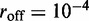(dashed lines indicate 1 SD around the average), for increasing motor bias (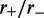) values. Here, 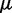has been adjusted in the Boltzmann theory to obtain 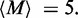For small motor bias, effective Boltzmann and simulation results are in discord (as expected), but as motor bias is increased, progressively better agreement occurs. For the largest simulated bias value, the 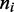profile obtained from the Boltzmann theory is closely bracketed by the small range of fluctuation obtained in the simulation. The profile indicates that essentially all the motors are at the ends of the lattice, with 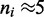in the entire interior region of the lattice. This indicates formation of a robust loop structure as sketched in Figure 1b.

Increasing domain size increases robustness of loop domain ordering

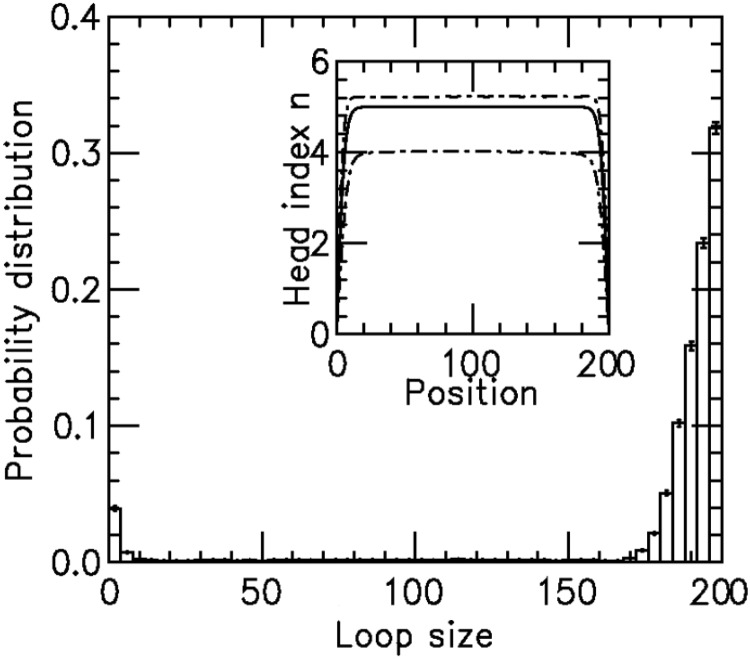
To examine how the robustness of the loop-domain ordering in the model was affected by loop size, we performed simulations with L = 200 and M = 5; this kept the motor numbers the same as in Figure 4, but increased the lattice size by 4-fold (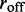 remained the same). Figure 5 shows the results for motor bias 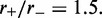Comparing with the inset in Figure 4b, it is clear that the increased size has resulted in a suppression of fluctuations and a pileup of motors at the domain endpoints. The agreement between the effective Boltzmann and simulation results is much closer than in the 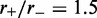case for the smaller (L = 50) lattice.

Figure 5.

Loop-size distribution and motor position index profile for larger lattice (L = 200) with bias 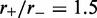, and M = 5 motor pairs. The simulation was run 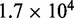times, each for a time of 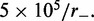The maximum size of the standard error bars is 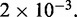For the 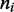profile (inset, labeled ‘head index’), the solid line is the effective Boltzmann theory, dashed lines show average ± 1 SD of the simulation 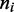distribution; standard errors of the simulation results are negligibly small. Dissociation rate is .

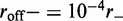DISCUSSION

We have shown that two-DNA-site-binding and in cis-translocating machines are capable of robust self-organization of large loop domains along a long DNA molecule. Loop formation through this mechanism is efficient even for low motor biases thanks to the synchronization of multiple motors, which occurs due to their mutual steric hindrance. The main requirement for the machines is that they be sufficiently processive so they can traverse the length of the loop domain before their dissociation. Below, we discuss the regulation of formation of multiple loop domains along a single long DNA, with the application of mitotic chromosome condensation in mind. We then discuss the speculative proposal that this model might be applicable to condensin activity during mitotic chromosome condensation; however, we note that this type of loop-domain self-organization could occur for any DNA-loop-extruding enzyme, e.g. type I restriction enzymes (31).

Formation of multiple loop domains on a long DNA and mitotic chromosome structure

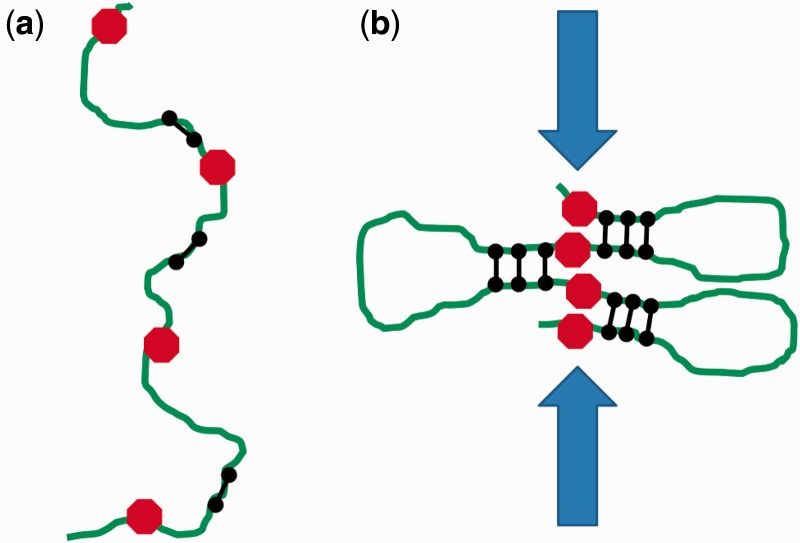
Here, we have considered formation of a single loop domain. The boundaries of our 1D lattice model act as boundary elements for the loop self-organization process. One may ask how the formation of many loop domains along a whole chromosome might be regulated. A straightforward scheme to do this could be based on periodic sequence-defined boundary markers (e.g. proteins bound to specific locations) that would provide a stop signal to the loop-forming machines (by promoting either halting or dissociation). The outcome would be formation of a series of loop domains anchored by discrete clusters of condensing machines, with domain sizes programmed by domain boundaries (Figure 6) (13).

Figure 6.

Condensation of multiple loop domains. (a) Initially condensins (black dumbbell shapes) bind along a long stretch of chromatin (green), between condensation boundary elements (red octagons). (b) As condensation proceeds, condensins organize into a ‘stacked’ configuration at the bases of chromatin loops defined by the boundary elements. The resultant crowding of chromatin at the bases of the loops generates inter-chromatid tension that will drive topo II to remove inter-chromatid entanglements.

In application to eukaryote mitotic chromosome folding, this scheme could produce metaphase chromatids with the tightly regulated shape seen in vivo, given periodic location of domain boundary markers. This cis-condensation mechanism would drive topological separation of entangled chromatids through the buildup of inter-chromatid tension which would direct topo II to remove entanglements as condensation proceeds (13,17).

For very long DNAs, one might ask about the effect of poorly regulated binding events that inadvertently cause ‘crosslinks’ between different chromatids or ‘pseudoknots’ along one chromatid. Such non-local binding events will be suppressed by the fact that the local concentration of polymer segments ‘seen’ at a given polymer locus is dominated by nearby segments along the same polymer. Therefore, pseudoknots and inter-chromatid crosslinks can be expected to be relatively rare, appearing as ‘defects’ among arrays of gradually loop-translocating machines. Dissociation of a machine participating in a pseudoknot or crosslink will release it. Contrast this with dissociation of one machine in a loop cluster; we have shown that this does not disturb the loop organization. The effect of pseudoknot/crosslink defects could be tested in our model by adding a background of randomly oriented single-motor walkers, which when sufficiently dilute should be outcompeted by the collective effect of self-organization of the loop-forming machines.

The length scale relevant to our model (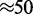 nm) is much longer than the screening length for electrostatic interactions under physiological conditions (<2 nm for 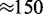mM univalent salt), and we expect our results to be insensitive to small changes in ionic or other ‘solvent quality’ conditions that may occur through mitosis. We emphasize that the amount of simple adhesion of chromatin to itself must be low during mitotic chromosome condensation, to avoid derailing the processes of formation of linear chromosomes and resolution of sister chromatids and chromosomes (13,17). The essential point of this article is that the ‘loop-extrusion’ mechanism discussed in this article can accomplish a high degree of chromosome compaction, while maintaining non-adhering conditions for chromatin fibers, and thus allowing packing of the fibers together to facilitate chromatid and chromosome separation.

Are mitotic chromosomes organized by condensin through loop extrusion?

A number of pieces of evidence suggest that the ‘loop-extrusion’ mechanism may be relevant to eukaryote mitotic chromosome condensation through mitotic condensin activity. Recently, it has been discovered that condensins interact with DNA through a ‘topological embrace’ mechanism whereby condensins are linked to DNA through their tripartite ring-like structure (27). This topological interaction could constrain condensins to interact with DNA in cis, could facilitate their sliding along a chromatin loop in the manner sketched in Figure 6 and could enforce the steric hindrance necessary for the loop-organization process discussed above.

In our model, condensation (and chromatid resolution) depends on processive translocation (or effective translocation, e.g. treadmilling, see below) of loop-extruding machines from starting points where the two motor elements of a machine are bound along a single stretch of chromatin, near to one another and in opposite orientations. Evidence exists that condensin–DNA interactions favor binding along a stretch of chromatin, from single-DNA experiments where in the absence of ATP condensins bind along DNA without any loop-formation-type condensation signal (26), suggestive of a strong preference for condensin initially occupying a single position along DNA.

The motion of individual condensin complexes on chromatin or DNA has not been directly observed. Indeed, the molecular details of how condensin binds DNA are not fully understood (28). It is known that the condensin complex has a well-defined overall shape in solution, with its ATP-hydrolyzing heads held in relative spatial position by the kleisin subunit. Therefore, it appears likely that initial binding of condensin to DNA is constrained by the geometry of the complex. Further evidence for this comes from the apparent binding of condensin to DNA in the absence of ATP observed by Strick et al. (26) without observation of any random loop capture. In those same experiments, addition of ATP to condensin pre-bound to DNA resulted in systematic step-wide condensation, suggesting distinct and well-defined DNA-binding and DNA-condensing modes of condensin–DNA interaction. Furthermore, experiments that observe an ATP-dependent (35) and phosphorylation-regulated (36) DNA supercoiling activity of condensin indicate that condensin is able to impose 3D constraints on the bound DNA, so as to generate positive writhe (37). Therefore, initial binding is likely to lead to a well-defined relative alignment of condensin along DNA/chromatin that will bias successive ATP-dependent unbinding/rebinding and possible translocation steps.

The observation of 70 nm condensation steps by Strick et al. (26) that depend on hydrolizable ATP and which are decoupled from initial condensin–DNA binding suggests a highly constrained release-rebinding behavior: if any DNA orientation could be rebound during enzyme release rebinding, one would expect to see a much broader distribution of condensation steps with a larger mean step size; theoretically, a broad distribution centered at roughly 200 nm is expected for the 0.4 pN forces used in the Strick et al. (26) experiment (see (16) for theory and (29) for experimental validation using non-specific DNA–loop-binding proteins). The Strick et al. experiments showing a defined step size indicate a rather tightly controlled condensin unbinding/rebinding cycle. Furthermore, the progressive condensation dominated by condensation steps (with de-condensation steps of the same size) observed in the experiments of the same group indicates a directed reaction.

Use of our loop-extrusion-condensation model to control global mitotic chromosome architecture requires sequence-correlated condensin–DNA interactions, perhaps through other components of chromatin. Condensin is known to be ‘loaded’ onto yeast chromosomes at specific locations (38), but it is not yet known if this is true in higher eukaryotes. A piece of evidence in favor of sequence-defined chromosome condensation in mammalian cells is the observation that insertions of non-eukaryote DNA into chromosomes lead to chromosomes which ‘thin’ at those locations when put under stress (39), indicating that the foreign DNA induces chromosome condensation defects. While it is unknown how DNA sequence controls mitotic chromosome condensation, one possibility is that cohesin SMCs, which act to hold sister chromatids together until late in mitosis, act as the boundaries. The gradual loss of cohesins known to occur during mitosis would be required to facilitate condensation and separation of sister chromatids.

It is also conceivable that other DNA-binding proteins which trigger condensin unbinding, or which inhibit condensin activity, could define condensation domain boundaries. Notably, the protein MCPH1 has recently been observed to control condensin activity; its suppression leads to ‘dumpy’, over-condensed chromosomes (40). It is also feasible that a wide variety of interactions of condensins with chromatin proteins regulate mitotic chromosome condensation activity, including interactions with core histones (41). Finally, it is also possible that condensins might associate with replicated sister chromatids during DNA replication, with the advance of condensin condensation within replication bubbles controlled by enzymes associated with the replication forks.

Another piece of evidence in favor of application of our model to mitotic condensin activity is observation of condensin-rich regions in the axial ‘core’ regions of mitotic chromatids (23). This can be simply understood in the context of our model as a consequence of relocation of condensin units to the bases of chromatin loops. A prediction of our model is that the condensin-rich chromatid cores actually consist of a series of isolated condensin clusters (Figure 6). This prediction is consistent with experiments indicating that cutting DNA alone is sufficient to entirely dissolve eukaryote metaphase chromosomes (13,42,43).

Alternatives to translocation by individual condensins

While translocation might literally apply in the sense that individual condensins may move along DNA (their ATPase domains are homologous to those of ABC transporters (20)), it is alternately possible that individual condensins do not actually translocate on DNA. However, the model of this article could also describe condensin driven mitotic chromosome condensation even in the absence of translocation of individual condensins. Movement of condensin clusters along DNA could result from simple binding and release dynamics at adjacent positions (e.g. through ‘treadmilling’) without actual translocation of individual condensin units.

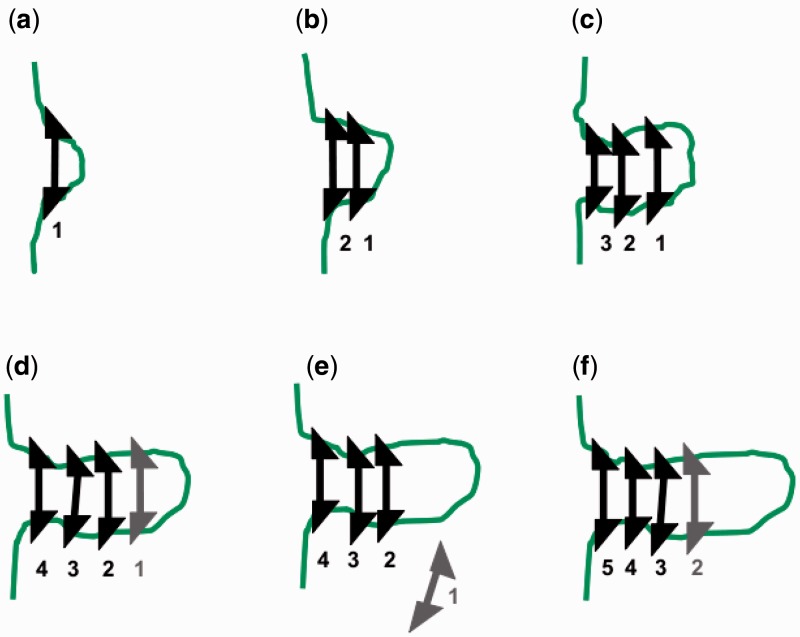
Figure 7 sketches this process, where the triangular binding sites indicate the role of the asymmetric shape of condensins in regulating an asymmetric ‘elongation’ process (this asymmetry was present for the translocating machines discussed above in the directed motion of the motor elements). The combination of structural asymmetry and ATP hydrolysis could drive ‘directional polymerization’ of condensins on chromatin so as to move condensin clusters along DNA by a treadmilling process reminiscent of cytoskeletal filament polymerization (44).

Figure 7.

Treadmilling as an alternative to individual machine translocation. Binding of machines with ATP bound (black machines) leads to multiple-machine cluster [(a–d)]; ATP hydrolysis [gray machine in (d)] followed by machine release (e) leads to effective translocation of a machine cluster and formation of a loop domain, following a mechanism similar to treadmilling of monomers of cytoskeletal filaments. Numbers indicate binding order of machines in a cluster.

Other motors, notably the chromokinesin KIF4A that controls chromosome condensation and the chromatid-axial distribution of condensins in metaphase chromosomes (45) might also contribute to condensin relocation. Another mechanism for the generation of translocation energy might be simply the polymer free energy of a chromatin loop subject to constraint by condensins, which will be minimized by locating the complexes at the base of a large chromatin loop. To detect condensin motion and clustering (as predicted by our model), ChIP-seq analysis during progressive stages of prophase and metaphase might be useful. Combining ChIP-seq data with chromosome-conformation-capture analysis could correlate condensin binding with distant-site-looping.

In bacteria, SMC complexes also play a major role in chromosome condensation and segregation. The E. coli SMC complex MukBEF forms clusters near OriC and appears to mediate chromosome condensation and OriC segregation after replication (46). The clustering and chromosome segregation functions of bacterial SMCs may be due to the same mechanism as in the eukaryote case, and we speculate that the translocation-stacking mechanism discussed in this article is operative in bacteria. For both bacterial and eukaryote condensins, it may be possible to directly observe the mechanism of DNA compaction, e.g. through single-molecule fluorescence imaging methods.

FUNDING

The National Science Foundation (NSF) [DMR-0715099, DMR-1206868 and MCB-1022117]; National Institutes of Health (NIH) [1U54CA143869-01 (NU-PS-OC)]. Funding for open access charge: NIH.

Conflict of interest statement. None declared.

APPENDIX

With non-disassociating enzymes, each lattice site is either in ‘one’ loop or in no loop (gap). Therefore, for M enzymes, the total length of the lattice is the sum of the lattice length caught in each loop and gap.

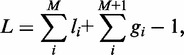(A1)

where the smallest loop and gap sizes are l = 1 and g = 1; Note that for M pairs of motors, there are M loops and M + 1 gaps (counting the gaps at the ends as well as the ones in between machines).

The effective energy is given by Equation (1), i.e.

(A2)

where 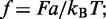F is the applied force and a is the length of each lattice site.

To calculate the probability distribution functions, we need to calculate the partition function Z. In order to do so, we relax the length constraint, adding a tension term 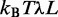coupled to the total length to the energy to control the average length.

The partition function Z then becomes

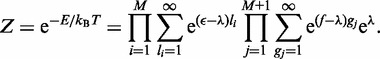(A3)

The sum is calculated using the geometric series 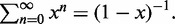The partition function Z, then follows as

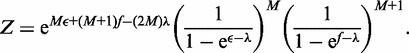(A4)

We rewrite the RHS of the above equation by factoring out powers of 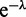and finding the coefficients of each term. These coefficients (for a given L of the ‘grand canonical’ (fluctuating-L) partition function Z are themselves the partition function for the fixed length (canonical) system .

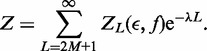(A5)

By expanding Z in powers of 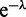(Equation (A4) can be expanded in powers of 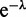using Newton’s generalized binomial theorem (47), and then terms with a net fixed power of 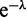can be selected) the fixed-L partition function is obtained:

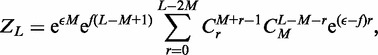(A6)

where r is the looped length. Note that in the non-disassociating case, the maximum length of any loop occurs when the other loops are of size 1, making the maximum allowable loop size equal to L – 2 M.

To find the probability of any loop being of size l, we recalculate the fluctuating-L partition function but now with the constraint that one loop is of size l:

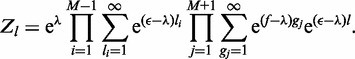(A7)

This constrained partition function then can be calculated using the same steps as above:

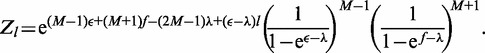(A8)

Expanding 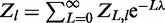gives

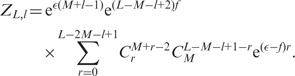(A9)

The probability distribution follows as

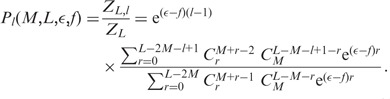(A10)