Small γ-Ray Doses Prevent Rather than Increase Lung Tumors in Mice

Abstract

We show evidence for low doses of γ rays preventing spontaneous hyperplastic foci and adenomas in the lungs of mice, presumably via activating natural anticancer defenses. The evidence partly relates to a new study we conducted whereby a small number of female A/J mice received 6 biweekly dose fractions (100 mGy per fraction) of γ rays to the total body which prevented the occurrence of spontaneous hyperplastic foci in the lung. We also analyzed data from a much earlier Oak Ridge National Laboratory study involving more than 10,000 female RFMf/Un mice whereby single γ-ray doses from 100 to 1,000 mGy prevented spontaneous lung adenomas. We point out the possibility that the decrease in lung cancer mortality observed in The National Lung Screening Trial Research Team study involving lung tumor screening using low-dose computed tomography (CT) may relate at least in part to low-dose X-rays activating the body’s natural anticancer defenses (i.e., radiation hormesis). This possibility was apparently not recognized by the indicated research team.

INTRODUCTION

Humans worldwide have been and are currently exposed to low-level ionizing radiation in excess of the natural background level, which varies with geographical location. This includes radiation exposures during radiological emergencies such as is ongoing in Japan related to the Fukushima incident triggered by the March 2011 earthquake and tsunami. It also includes exposures related to applications of diagnostic medical devices (e.g., CT scans) and procedures (e.g., nuclear medicine) (NCRP 2009). A key concern of many is the perceived low-level-radiation exposure related elevated risk of cancer (McCollough et al. 2009). The perceived risk is linked to the linear-no-threshold (LNT) hypothesis, which implies that any amount of radiation, no matter how small, will cause cancer in one or more members of a very large irradiated population (Muller 1954; Kathren 1996; Brenner and Hall 2007; Puskin 2009). With the LNT-based, risk-assessment paradigm, each member of the irradiated population (e.g., down-wind communities from the Fukushima nuclear power facility) is led by experts to believe that they could with low probability be a victim who develops cancer as a result of their exposure to low-level radiation (Ten Hoeve and Jacobson 2012).

In the recent article by Ten Hoeve and Jacobson (2012) they attempted to quantify worldwide health effects (hypothetical cancers) of the Fukushima Daiichi nuclear accident. The researchers used an atmospheric transport model to attempt to quantify the worldwide movement of long-lived radionuclides (Cs-134, Cs-137, and I-131) released by the Fukushima nuclear plant. The transport outside of Japan involved very small amounts of added radiation. The researchers then incorporated the calculated deposition of the transported radionuclides into a grid-model of target populations and arrived at the collective dose (very small average individual dose multiplied times the very large population size). Radiation health effects were supposedly accounted for using the LNT model which can be implemented on the bases of the collective dose. Using this approach, the authors calculated up to 1100 hypothetical cancer-related mortalities and up to 1800 hypothetical cancer-related morbidities worldwide. However, it is no longer acceptable to use collective dose for the purpose of low-dose-radiation risk assessment for large populations (NCRP 1995). In addition, the LNT model is an invalidated empirical model that unfortunately remains the basis for policy in radiation protection (Cohen 2008; Jaworowski 1999, 2008).

Historically, the LNT-based, risk-assessment paradigm has predominated, but now due in part to increasing evidence for beneficial effects rather than harm from low-level radiation exposure, a radiation benefit paradigm (Scott 2011) has emerged and is rapidly evolving. With the novel radiation benefit paradigm, there is a hierarchy of presumably epigenetically-regulated, protective adaptive-response mechanisms that comprise a system of radiation activated nature protection (ANP). Components of the ANP system include DNA damage repair, apoptosis of damaged and aberrant cells (e.g., neoplastically transformed cells), anticancer immunity (including enhanced and more efficient tumor cell killing), and suppression of cancer-promoting inflammation caused by other agents (e.g., cigarette smoke carcinogens) (Kondo 1998; Trosko 1998; Wolff 1998; Rothkamm and Löbrich 2003; Sakai et al. 2003; Sakai 2006; Bauer 2007; Liu 2007; Cohen 2008; Jaworowski 2008; Scott 2008a,b; Scott et al. 2008, 2009; Tubiana 2008; Averbeck 2009; Tubiana et al. 2009; Nowosielska et al. 2012; Rödel et al. 2012; Sanders 2012).

Components of the radiation ANP system can be differentially activated by doses of radiation above the natural background level and the activation is thought to involve epigenetic reprogramming (epireprogramming) of the genome (Scott et al. 2009). The epigenetic activation of protective adaptive-response genes has been called epiactivation (Scott et al. 2009). Radiation doses much higher than encountered in nature promote epigenetically silencing (episilencing [Scott et al. 2009]) of adaptive-response genes and can significantly suppress the immune system (Liu 2007), facilitating development of cancer and other diseases. Low-dose-radiation activation and high-dose-radiation suppression of protection constitutes a hormetic response (i.e., radiation hormesis).

The indicated system of ANP appears to be more efficiently activated by low linear-energy-transfer (LET) radiation than high-LET radiation and this may relate to a link between the microscopic dose (e.g., to the cell nucleus) distribution in space and in time and the intensity of the protective intercellular signaling associated with ANP (Feinendegen et al. 2007a,b). It could also relate to life having originated in the oceans where defense against low-LET radiation was likely needed early on rather than defense against high-LET radiation because of the short range of a particles in water (Karam and Leslie 1999).

For combined exposure to low- and high-LET radiation as occurs for radon in the environment and home and for mixed neutron and γ-ray fields, harm from the high-LET component of the radiation dose appears to be prevented by low-LET-radiation ANP (Rithidech and Scott 2008; Sanders and Scott 2008; Scott et al. 2009; Sanders 2010). Further, low-LET radiation ANP in animal models has delayed the occurrence of spontaneous cancer (Mitchel et al. 2003), prevented chemical-carcinogen-induced cancer (Sakai et al. 2003; Bruce et al. 2012), prevented cancer metastasis (Hashimoto et al. 1999; Nowosielska et al. 2006), and extended the lifespan of diseased animals (Sakai 2006; Lacoste-Collin et al. 2007). Indeed, for low doses and dose rates of low-LET or low- plus high-LET radiation (e.g., for residential radon), ANP rather than harm appears to be more the rule than the exception (Sanders 2010; Scott 2011). The benefit of radiation ANP for children is less clear (Scott et al. 2008) although there is evidence for chronic low-rate exposure to γ rays being protective (Chen et al. 2007) but not for computed-tomography-(CT)-related X-rays (Pearce et al. 2012). However, there appears to be no unirradiated group in the CT study of Pearce et al. (2012), so that radiation ANP for children cannot be ruled out.

Research results presented in this paper provide additional data supporting the low-dose-radiation benefit paradigm. We show data from a study we conducted that demonstrates that repeated low doses of γ rays (fractionated exposure) can prevent spontaneous hyperplastic foci in the lung of mice. This is consistent with lung tumor data of other as is discussed in this paper.

METHODS

Animals

Female, 10 week-old, A/J mice were purchased from Jackson Laboratories (Bar Harbor, ME). At 42 weeks after the start of fractionated radiation exposure of 18 mice with 8 control unexposed mice, the mice were humanely euthanized by i.p. injection of a lethal dose of Euthasol.

Irradiation

The eighteen γ-ray exposure group mice received 6 biweekly fractions of whole-body irradiation (WBI) (dose fraction size 100 mGy) using a Gammacell 1000 irradiator (¹³⁷Cs source) (Best Theratronics, Ontario, CA). The 100 mGy dose fractions were delivered at 1.78 mGy sec⁻¹. Mice were exposed individually in polypropylene tubes set inside a stainless steel sample canister. The dose received was evaluated based on nanoDot dosimeters (Optically Stimulated Luminescence Technology, 1 cm², Landauer, Inc., Glenwood, IL) attached to the outside of the tubes containing the mice. Dose measurements obtained outside the exposure tube were essentially the same as were obtained when nanoDots were inserted into the chests of mouse carcasses, thus we relied on measurements obtained outside the exposure tubes. Control mice were not sham exposed or placed in tubes. Sham exposure (no radiation) was not possible inside our Gammacell 1000 unit (Cs-137 source) because of ever-present leakage radiation.

Histology

Hyperplastic foci cases were used as a measure of increased lung cancer risk since the foci can progress to adenoma and then to carcinoma (Bruce et al. 2012). To facilitate detecting the foci, lungs were inflated with neutral buffered formalin at a constant hydrostatic pressure of 25 cm for 6 hours and fixed further by immersion in formalin for > 48 hours. Left lung lobes were systematically trimmed in a dorsoventral-transverse direction at 3–4 mm intervals with the first slice randomly positioned within the cranial 4 mm of tissue to yield 3–5 slices per lobe. A single slice along the axial airway of each of the right lung lobes was also made. Trimmed tissue was histoprocessed routinely, and 5 μm-thick paraffin sections were mounted and stained with hematoxylin and eosin for light-microscopic identification and enumeration of hyperplastic foci and other lesions. The distribution of hyperplastic foci cases among the 26 mice used in this study is presented in Table 1.

TABLE 1.

Hyperplastic foci among control and irradiated female A/J mice

Group	Hyperplastic foci per animal	Group	Hyperplastic foci per animal
Control	1	Irradiated	0
Control	1	Irradiated	1
Control	1	Irradiated	0
Control	0	Irradiated	0
Control	0	Irradiated	0
Control	1	Irradiated	0
Control	0	Irradiated	1
Control	1	Irradiated	0
Irradiated	1	Irradiated	0
Irradiated	0	Irradiated	0
Irradiated	0	Irradiated	0
Irradiated	1	Irradiated	0
Irradiated	1	Irradiated	1

Data Analysis and Modeling

The hyperplastic foci data in Table 1 were evaluated in the context of a modified version of our hormetic relative risk (HRR) model (Scott 2011). Because animals had at most a single hyperplastic foci in the lung, the foci case data were modeled as a Bernoulli random variable (foci present, response = 1; foci absent, response = 0) with different case probabilities for the controls and irradiated groups. For controls, the individual-specific probability (prob) of being a foci case is given by P. Had the animals received a single radiation dose, the individual-specific probability of being a foci case would be given by the following equation:

$$\mathit{prob}=\left(1-\mathit{profac}•B\left(x\right)\right)•P,$$ (1)

where profac is the individual-specific probability of the foci being prevented by γ-ray ANP (all protective mechanisms assumed activated). The benefit function B(x) for radiation dose x is the probability of ANP. For the 6 fractions radiation exposure scenario used, B(x) is assumed to be 1 (ANP for each individual).

To accommodate the 6-fraction exposure scheme, profac is replaced by profac_n, with n indicating the number of dose fractions used. Thus, for the irradiated group, the probability of being a foci case is given by the following equation:

$$\mathit{prob}=\left(1-{\mathit{profac}}_{\text{n}}\right)•P,$$ (2)

with n taking on the value of 6 for six dose factions. In the analysis of the data generated with the fractionated exposure, we have assumed each dose fraction to be independent. This allows for evaluating profac_n for n taking on other values, e.g., n = 1, 2, 3, …. The related mathematical relationships are provided in the Appendix.

Bayesian inference implemented via Markov chain Monte Carlo (MCMC) (Lunn et al. 2000) was used to obtain posterior distributions for P, profac₆, and the product (1 – profac₆)•P. With the HRR model the population average for profac_n is PROFAC_n (the on-average proportion of the population that do not develop the outcome of interest when ANP occurs with probability 1). Thus, the population average, PROFAC₆ for 6 fractions, was evaluated (estimated) as the posterior distribution mean for profac₆. During the generation of the posterior distribution for profac₆, posterior distributions were also generated for profac₁, profac₂, profac₄, profac₈, and profac₁₆, assuming independent actions of the different fractions (see the Appendix for more details). This allowed for estimating population averages PROFAC₁, PROFAC₂, PROFAC₄, PROFAC₈, and PROFAC₁₆ in addition to PROFAC₆.

The prior distribution used for P was uniform from 0 to 1. The prior distribution used for profac₆ was uniform from 0 to 1. A single MCMC chain was used. Convergence was assumed when ratio MCMC error/posterior distribution standard deviation < 0.05 for a given random variable (Spiegelhalter et al. 2003). 25,000 iterations were used with 5,000 burn-in (data points discarded). The choices of the total iterations and burn-in were based on autocorrelation results obtained after the fist 5,000 iterations. The autocorrelation results indicated that convergence of the chain could be assumed after the first 5,000 iterations (a conservative choice). This was confirmed by checking to ensure that the ratio MCMC error/posterior distribution standard deviation < 0.05 for each random variable considered. A total of 20,000 data points per stochastic node (i.e., stochastic parameter or function) of interest were retained for the analysis carried out.

RESULTS

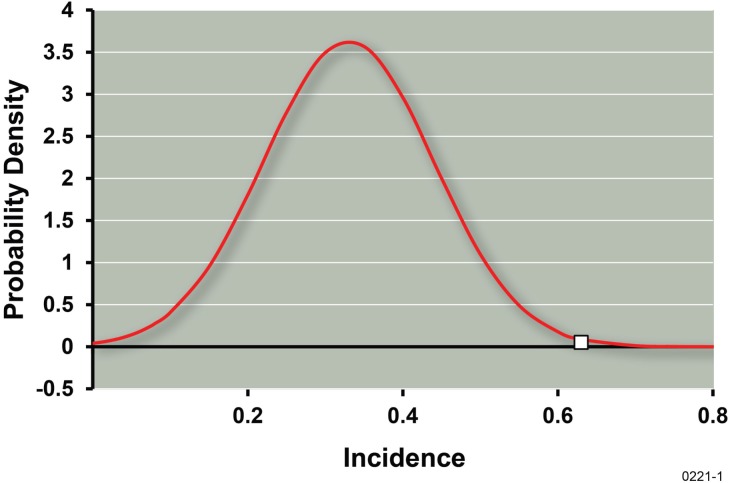
No spontaneous adenomas or carcinomas were found in controls and none were found in irradiated mice. Regarding the data in Table 1, five out of 8 control mice each had a single hyperplastic focus (incidence = 0.63 ± 0.17). Six out of the 18 irradiated mice each had a single hyperplastic focus (incidence = 0.33 ± 0.11). The standard errors reported are based on assuming the number of foci cases per exposure group to have a binomial distribution. Based on the central limit theorem, the average incidence of foci cases after repeated γ-ray exposure would be expected to have an approximate normal distribution. Figure 1 shows a normal distribution with mean of 0.33 (observed incidence for irradiated group) and standard error of 0.11, with a point on the horizontal axis at the value of 0.63 (control incidence). The indicated results points to a significant protective effect of the fractionated γ-ray exposure (p < 0.005 implicated).

FIGURE 1.

Normal distribution with mean 0.33 and standard error 0.11. Single data point along the horizontal axis at 0.63 represents the control incidence of hyperplastic foci.

The data in Table 1 have also been analyzed in the context of our HRR model using the approach indicted in the Methods section and Appendix of this paper. The posterior distribution means and percentiles (5%, 10%, 50%, 90%, 95%) for stochastic nodes P, profac₁, profac₂, profac₄, profac₆, profac₈, profac₁₆, and the product (1– profac₆)*P are presented in Table 2. The posterior distribution means for profac_n are estimates of PROFAC_n as already indicated. The posterior distributions were not Gaussian. None of the posterior distributions had a mode located at zero protection (2.5% percentile values were all > 0). A mode at zero protection would be expected in the absence of a γ-ray protective effect.

TABLE 2.

MCMC results for stochastic nodes^a

Stochastic node	Mean	St. dev.	MCMC error	5%	10%	50%	90%	95%
P	0.588	0.137	1.32E-03	0.365	0.409	0.587	0.771	0.816
profac1	0.09	0.052	5.08E-04	0.013	0.024	0.086	0.161	0.183
profac2	0.17	0.094	9.18E-04	0.026	0.047	0.164	0.296	0.333
profac4	0.302	0.153	1.52 E-03	0.05	0.092	0.302	0.504	0.555
profac6	0.406	0.19	1.91 E-03	0.075	0.135	0.417	0.65	0.703
profac8	0.489	0.213	2.16 E-03	0.098	0.178	0.513	0.754	0.802
profac16	0.693	0.238	2.46E-03	0.187	0.321	0.762	0.939	0.961
(1-profac6)•P	0.335	0.097	6.35 E-04	0.184	0.214	0.331	0.464	0.502

^aStochastic parameter (e.g., profac₆) or function [e.g., function = (1–profac₆)•P].

DISCUSSION

Results in Table 2 are based on uniform prior distributions for P and profac₆. To assess the reliability of the results, evaluations were also carried out using beta prior distributions for P and profac₆ with the two parameters of the distribution set at 2 and 4. With this choice, the probability density has the structure y(1–y)³, where y (with 0 < y < 1) is replaced by P or profac₆ as appropriate. Posterior distribution means obtained with the beta priors were systematically lower but differed by < 30 % from those obtained with uniform priors indicating that the results presented in Table 2 can be considered reasonably reliable.

Our finding of a protective effect of low-dose γ rays against spontaneous foci in the lung is consistent with data of Ullrich and Storer (1979) showing the prevention of spontaneous lung adenomas in female RFMf/Un mice by single doses of γ rays. A subset (lowest four dose groups and controls) of the data of Ullrich and Storer (1979) for the age-adjusted lung adenoma incidence are presented in Table 3 and involved more than 10,000 mice. The lung tumor relative risk was systematically reduced by doses of 100, 250, 500, and 1000 mGy. We have calculated the corresponding values for PROFAC₁, with all values being significantly > 0 (p < 0.05; based on PROFAC₁ – 2 standard errors being > 0). This relates to the central limit theorem indicating that average values tend to have an approximate normal distribution. Even though the γ-ray doses ranged from 100 to 1000 mGy, PROFAC₁ was independent of the dose level (R² = 0.00043; p > 0.5), indicating that all of the doses were in the central part of the hormetic zone (Zone of Maximal Protection where ANP is expected for all animals so that B(x) = 1 [Scott 2011]).

TABLE 3.

Age-adjusted lung adenoma incidence data of Ullrich and Storer (1979) for female RFMf/Un mice exposed to single γ-ray doses

Dose, mGy	Number of mice	Incidence	Incidence standard error	PROFAC1	PROFAC1 standard errora
0	4014	0.302	0.015
100	2827	0.239	0.017	0.209	0.069
250	965	0.202	0.027	0.331	0.095
500	1143	0.22	0.025	0.272	0.09
1000	1100	0.225	0.027	0.255	0.097

^aCalculated via error propagation. Also equals the standard error for relative risk (RR) since for data evaluated RR = 1 – PROFAC₁ (a characteristic of the hormetic relative risk model for the Zone of Maximal Protection [Scott et al. 2009; Scott 2011]).

The average and standard error for the measured 4 values of PROFAC₁ are 0.27 ± 0.03, a significant protective effect (more than 1 out of each 4 spontaneous adenomas cases prevented).

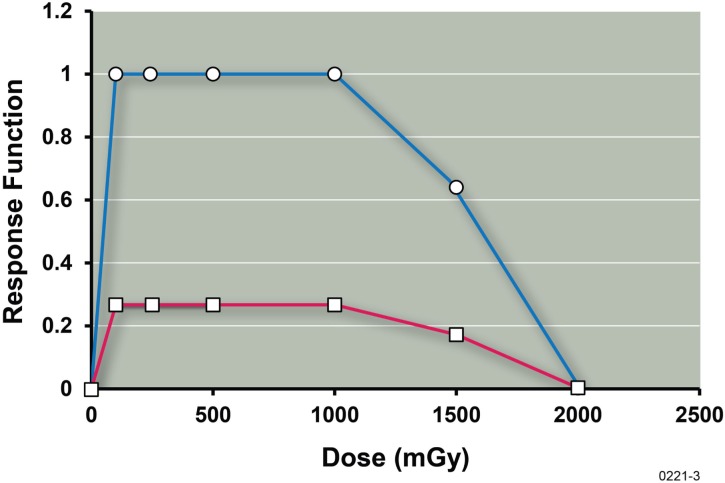
Figure 2 shows a plot of the values (estimates) of B(x) for lung tumor prevention derived from the data of Ullrich and Storer (1979) with x representing the radiation dose in mGy. Also shown is a plot of the lung cancer prevention function (given by the product B(x)•PROFAC₁). Data for the 1500 and 2000 mGy groups have been included. Full benefit (i.e., B(x) = 1) was assumed for doses of 100 to 1000 mGy, based on results of our correlation analysis already presented indicating that the dose range considered was likely within the Zone of Maximal Protection. The average of the separate values of PROFAC₁ presented Table 3 (i.e., 0.27) was used to calculate the other data points for B(x) at doses of 1500 and 2000 and also the results for the prevention function. B(x) was evaluated based on the following equation:

$$B\left(x\right)=\left(1-RR\left(x\right)\right)/\mathit{average}\left\{{\mathit{PROFAC}}_1\right\}.$$ (3)

FIGURE 2.

Benefit function B(x) estimate (upper curve) for low-dose-γ-ray stimulation of the body’s natural defenses against spontaneous lung tumors (adenomas) in female RFMf/Un mice based on data from Ullrich and Storer (1979) involving thousands of mice and the hormetic relative risk model (Scott 2011). Also shown is the related prevention function (lower curve, B(x)•PROFAC₁) for lung cancer prevention. Points were simply joined by straight lines.

The notation average{} indicates that an average value for the enclosed quantity is used. RR(x) is the lung tumor relative risk at dose x of radiation. The points in Figure 2 were simply joined by straight lines. The results indicate that the threshold dose (value for which the prevention function becomes zero) for causing excess (greater than spontaneous frequency) adenoma cases is around 2,000 mGy (2 Gy). Thus, the threshold for lung adenoma induction by γ rays appears to be quite large for the mouse strain studied.

There are two possibilities related to the observed protective effects of low-dose γ rays against spontaneous hyperplastic foci and adenomas in the lung: (1) the lesion of interest (hyperplastic foci or lung adenoma) was already present in the lung at the time the radiation exposure occurred and was subsequently eliminated as a result of radiation ANP (e.g., anticancer immunity); (2) the lesion of interest was not present at the time of irradiation and the lesion was prevented from occurring at a later time via radiation ANP.

Irrespective of the correct explanation for the radiation protective effect, our findings have important implications related to the new guidelines that focus on only screening aged heavy smokers for lung cancer via use of low-dose computed tomography (CT) rather than more widespread screening. New lung cancer screening guidelines from medical groups recommend use of low-dose CT scans but only for persons 55 to 74 years of age and only for heavy smokers. The guides are based in part on The National Lung Screening Trial Research Team (2011) publication that compared lung cancer mortality for persons screened with low-dose CT as compared to radiography (the latter which delivers a lower X-ray dose than from CT but results in more difficulty in detecting tumors). The study involved 53,454 persons at high risk of lung cancer and was carried out at 33 U.S. medical centers. The study demonstrated a significant benefit of low-dose CT screening over screening with radiography so far as reducing lung cancer mortality. The reduction was credited to more reliable early diagnosis of lung tumors with low-dose CT because of better imaging. No consideration was given to the possibility that the higher dose X-rays from CT scanning may have more efficiently stimulated the body’s natural anticancer defenses (i.e., radiation hormesis) and this may have helped to reduce lung cancer mortality.

There are now new data from our research group showing that repeated low doses of γ rays can prevent cigarette-smoke-carcinogen-induced lung adenomas in mice. Bruce et al. (2012) show that 6 repeated biweekly 100-mGy γ-ray doses prevent cigarette smoke carcinogen benzo[a]pyrene (B[a]P) induced lung adenomas (but not carcinomas) in female A/J mice followed for 46 weeks after B[a]P injection. The 6 γ-ray dose fractions were given biweekly starting 1 month after B[a]P injection. Based on the indicated results, it is expected that repeated low doses of X-rays would also prevent some cigarette-smoke-carcinogen-induced adenomas in the lung. If so, then the rationale for limiting the lung cancer screening via low-dose CT to heavy smokers 55 to 74 years of age needs to be reconsidered, especially for younger heavy smokers. The scans could provide a previously unrecognized benefit, the reduction of lung cancer incidence and mortality via radiation ANP.

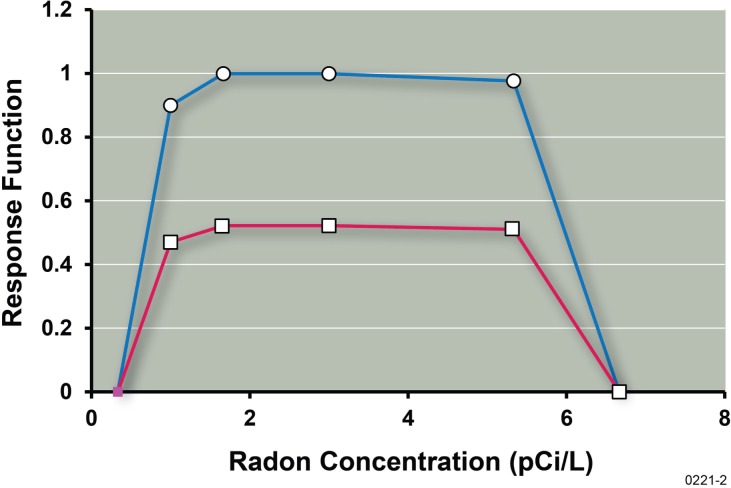
The protective effects of low-dose γ rays we demonstrated are consistent with the observation that low-rate exposure to a small γ-ray dose can prevent lung tumor induction in rats by highly ionizing α particles (Scott et al. 2008; Sanders 2010) and the observation that residential radon (which involves both low-LET γ rays and high-LET a particles) appears to prevent lung cancers caused by other agents (Thompson et al. 2008; Scott 2011). In addition, the benefit function, B(x), for lung cancer prevention by residential radon (and progeny) exposure has a similar shape as in Figure 2 when plotted against the average radon level in the home. The radon benefit function B(x) and the related lung cancer prevention function (given by the product B(x)•PROFAC) based on the data of Thompson et al. (2008) is presented in Figure 3. The central estimate of the chronic exposure PROFAC of 0.52 (Scott 2011) was used in evaluating the prevention function. Note that at and near the Environmental Protection Agency’s action level of 4 pCi L⁻¹ for residential radon, everyone appears to benefit from radon ANP (i.e., B(x) = 1 for Zone of Maximal Protection). Equally important, for heavy smokers that would normally develop lung cancer, 52% would be expected to have their cancers prevented as a result of their chronic residential radon exposure.

FIGURE 3.

Radon (residential) benefit function B(x) estimate (upper curve) for radon ANP against lung cancer caused by smoking and by other agents based on data of Thompson et al. (2008) as analyzed by Scott (2011) in the context of the hormetic relative risk model. The benefit is presumed to relate to the low-LET radiation component of the radiation dose. Also shown is the related prevention function (lower curve, B(x)•PROFAC) for lung cancer prevention. Points were simply joined by straight lines.

CONCLUSIONS

Low dose γ-rays prevent lung tumors in mice. The protection (an adaptive response) is presumed to be due to radiation ANP which is thought to be epigenetically regulated (Scott et al. 2009). Based on our research findings, the recently-introduced, new guidelines for screening heavy smokers for lung tumors using low-dose CT that is restricted to persons 55–74 years of age should be re-evaluated, especially for younger, long-term, heavy smokers. The younger heavy smoker could benefit from CT ANP against lung tumors which may also be the case for persons 55–74 years of age. In addition, further protection from smoking-related lung cancer would be expected by residing long-term in homes with average radon concentrations at or near (below or above) the EPA’s action level of 4 pCi L⁻¹ of air.

APPENDIX. Analytical Solution for profac_n

An analytical solution was developed for profac_n assuming that each dose fraction acts independently. Thus, profac₁ can be evaluated as a function of a known value for profac₆ as follows:

$$1-{\mathit{profac}}_6={\left(1-{\mathit{profac}}_1\right)}^6.$$ (A1)

Thus,

$${\mathit{profac}}_1=1-{\left(1-{\mathit{profac}}_6\right)}^{1/6}.$$ (A2)

Since Equation A1 also would apply when 6 is replaced by n for any number of independent fractions, it follows that profac_n for n = 2, 3, …, can be evaluated as a function of profac₁ using the following equation:

$${\mathit{profac}}_n=1-{\left(1-{\mathit{profac}}_1\right)}^n.$$ (A3)

Equations A2 and A3 were used in our Bayesian analysis via Markov chain Monte Carlo of the hyperplastic foci data presented in Table 1. As the Bayesian analysis posterior distribution was generated for profac₆ based on the data in hand, posterior distributions (projected distributions) were also obtained for profac₁, profac₂, profac₄, profac₈, and profac₁₆. For each value of profac₆ comprising the posterior distribution, corresponding values for profac₁ (Equation A2) and profac_n (Equation A3, for n = 2, 4, 8, and 16) were generated.