Abstract
Using complex roots of unity and the Fast Fourier Transform, we design a new thermodynamics-based algorithm, FFTbor, that computes the Boltzmann probability that secondary structures differ by 
base pairs from an arbitrary initial structure of a given RNA sequence. The algorithm, which runs in quartic time 
and quadratic space 
, is used to determine the correlation between kinetic folding speed and the ruggedness of the energy landscape, and to predict the location of riboswitch expression platform candidates. A web server is available at http://bioinformatics.bc.edu/clotelab/FFTbor/.
Introduction
In [1], we developed a dynamic programming algorithm, RNAbor, pronounced RNA neighbor, which simultaneously computes for each integer 
, the Boltzmann probability 
of the subensemble of structures whose base pair distance to a given initial, or reference, structure 
is 
. (Here, 
denotes the partition function, defined as the sum of all Boltzmann factors 
, over all secondary structures 
of a given RNA sequence, and 
denotes the universal gas constant and 
absolute temperature. Similarly 
denotes the sum of all Boltzmann factors of all structures 
, whose base pair distance to the initial structure 
is exactly 
.) RNAbor stores the value of the (partial) partition functions 
for all 
and 
, each of which requires quadratic time to compute. Thus it follows that RNAbor runs in time 
and space 
, which severely limits its applicability to genomic annotation. This restriction is somewhat mitigated by the fact that in [2], we showed how to use sampling [3] to efficiently approximate RNAbor in cubic time 
and quadratic space 
, provided that the starting structure 
is the minimum free energy (MFE) structure. We expect that a more efficient version of RNAbor could be used in applications in genomics and synthetic biology, to detect potential conformational switches – RNA sequences containing two or more (distinct) metastable structures.
In this paper, we describe a radically different algorithm, FFTbor, prounounced FFT neighbor, that uses polynomial interpolation to compute the coefficients 
of the polynomial
 |
(1) |
where 
is defined by 
. Due to severe numerical instability issues in both the Lagrange interpolation formula and in Gaussian elimination, we employ the Fast Fourier Transform (FFT) to compute the inverse Discrete Fourier Transform (DFT) on values 
, where 
and 
is the principal 
th complex root of unity and 
is defined in (1). This gives rise to an improved version of RNAbor, denoted FFTbor, which runs in time 
and space 
. Once two metastable structures 
are identified, we can subsequently evaluate the feasibility of transition between structures 
and 
, by computing the barrier energy using algorithms, such as that described in Dotu et al. [4] or Flamm et al. [5].
Background
Let 
denote an RNA sequence, i.e. a sequence of letters in the alphabet of nucleotides 
. A secondary structure 
is a set of base pairs 
, where 
and 
represents the minimum number of unpaired nucleotides in a hairpin loop (due to steric constraints, 
is usually taken to be 
), such that if 
and 
both belong to 
, then 
(a nucleotide is involved in at most one base pair) and 
(no pseudoknots are allowed).
The secondary structure 
is compatible with 
if for every base pair 
in 
, the pair 
is contained in the set 
of six Watson-Crick and wobble base pairs. Often we write that 
is a secondary structure on
, or equivalently, a secondary structure of
, in place of stating that 
is compatible with 
. Throughout this paper, by structure, we always mean a secondary structure which is compatible with an arbitrary, but fixed RNA sequence 
.
Given two secondary structures 
on s , we define the base pair distance 
between 
and 
to be the number of base pairs that they have that are not in common, i.e.
 |
(2) |
Structures 
are said to be 
- neighbors if 
.
For 
, let 
denote the restriction of 
to interval 
of 
, i.e. the set of base pairs 
. The notion of 
-neighbor can also be applied to restrictions of secondary structures; i.e. a secondary structure 
is a 
-neighbor of 
if
 |
In the following, we often omit the sequence 
and initial secondary structure 
in our notation, since these are arbitrary, but fixed. In particular, we write 
– see following paragraph for definitions.
Given an RNA sequence 
and compatible secondary structure 
, let 
denote the sum of the Boltzmann factors 
of all 
-neighbors 
of 
; i.e.
 |
where 
denotes the Turner (nearest neighbor) energy [6], [7] of 
, 
kcal/mol denotes the universal gas constant and 
denotes absolute temperature. Since the maximum base pair distance between a given initial structure 
and any other structure 
on RNA sequence 
must satisfy
 |
(3) |
it follows that the full partition function
 |
(4) |
Moreover, since 
, we need to compute at most the values 
– this observation will later prove useful. The Boltzmann probability 
that a secondary structure 
has base pair distance 
from the initial structure 
can be defined from the partition function by
 |
By graphing the probabilities 
as a function of 
, we expect to see one or more peaks at base pair distance 
when there is a meta-stable (low energy) structure 
at base pair distance 
from 
. See Figure 1 for an illustration.
Figure 1. FFTbor output for the RNA attenuator for the phenylalanyl-tRNA synthetase (pheST) operon in E. coli K-12 substr.
DH10B, located adjacent to the phenylalanyl-tRNA synthetase operon leader, with GenBank accession code CP000948.1/1887748-1887820 (complement). The 
-axis represents base pair distance to the minimum free energy structure 
; 
-axis represents Boltzmann probability 
that a structure has base pair distance 
to 
. (Left) Probability 
that base pair distance to MFE structure is 
. (Center) Cumulative probability 
that base pair distance to MFE structure is at most 
. (Right) Finite difference (Derivative) 
of probability that base pair distance to MFE structure is 
.
Recursions for structural neighbors
For the rest of the paper, we consider both 
as well as the secondary structure 
on 
to be fixed. We now recall the recursions from Freyhult et al. [8] to determine the partition function 
with respect to the Nussinov-Jacobson energy 
model [9], defined by 
times the number of base pairs; i.e. 
. Although we describe here the recursions for the Nussinov-Jacobson model, for the sake of simplicity of exposition, both RNAbor [8] as well as our current software FFTbor, concern the Turner energy model, consisting of free energy parameters for stacked bases, hairpins, bulges, internal loops and multiloops. The full recursions for FFTbor are described for the the Turner energy model in the appendix.
The base case for 
is given by
 |
(5) |
since the only 
-neighbor to a structure 
is the structure 
itself, and
 |
(6) |
since the empty structure is the only possible structure for a sequence shorter than 
nucleotides, and so there are no 
-neighbors for 
. The recursion used to compute 
for 
and 
is
 |
(7) |
where 
if positions 
can pair in sequence 
, and otherwise 
. Additionally, 
if 
is base-paired in 
and 
otherwise, and 
. This holds since in a secondary structure 
on 
that is a 
-neighbor of 
, either nucleotide 
is unpaired in 
or it is paired to a nucleotide 
such that 
. In this latter case it is enough to study the smaller sequence segments 
and 
noting that, except for 
, base pairs outside of these regions are not allowed, since there are no pseudoknots. In addition, for 
to hold, it is necessary for 
to hold, where 
and 
, since 
is the number of base pairs that differ between 
and a structure 
, due to the introduction of the base pair 
.
Methods
Given RNA sequence 
and compatible initial structure 
, we define the polynomial
 |
(8) |
where coefficients 
. Moreover, because of (3) and the fact that the minimum number of unpaired bases in a hairpin loop 
is 
, we know that 
, so that 
is a polynomial of degree strictly less than 
. If we evaluate the polynomial 
for 
distinct values
 |
(9) |
then the Lagrange polynomial interpolation formula guarantees that 
, where the polynomials 
have degree at most 
and are given by the Lagrange formula
 |
(10) |
Since the polynomials 
can be explicitly computed, it follows that we can compute the coefficients 
of polynomial 
. As we describe below, the evaluation of 
for a fixed value of 
can be done in time 
and space 
. It follows that the coefficients 
can be computed after 
evaluations of 
, where the space for each evaluation of 
is re-used; hence these evaluations can be performed in time 
and space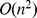 
. Finally, Lagrange interpolation is clearly computable in time 
. Although this approach is theoretically sound, there are severe numerical stability issues related to the interpolation method [10], the choice of values 
in the interpolation, and floating point arithmetic (round-off error) related to the astronomically large values of the partition functions 
, for 
. After many unsuccessful approaches including scaling (see File S1), we obtained excellent results by interpolating the polynomial 
, defined in equation (1), rather than the polynomial 
, defined in equation (9), and performing interpolation with the Fast Fourier Transform (FFT) [11] where 
are chosen to be 
th complex roots of unity, 
. One advantage of the FFT is that interpolation can be performed in 
time, rather than the cubic time required by using the Lagrange formula (10) or by Gaussian elimination. Fewer numerical operations implies increased numerical stability in our application. Details now follow.
Recursions to compute the polynomial 
Given an initial secondary structure 
of a given RNA sequence 
, our goal is to compute
 |
(11) |
where 
can be any structure compatible with 
. As previously mentioned, the recurrence relation for RNAbor with respect to the Nussinov energy model 
is
 |
(12) |
where 
if 
and 
can base-pair and otherwise 
, and 
if 
is base paired in 
and 
otherwise, and 
. The following theorem shows that an analogous recursion can be used to compute the polynomial
defined by
 |
(13) |
where
 |
Here, in the summation, 
runs over structures on 
, which are 
-neighbors of the restriction 
of initial structure 
to interval 
, and 
denotes the Nussinov-Jacobson energy of 
.
Theorem 1: Let 
be a given RNA sequence. For any integers 
, let
 |
where
 |
Then for 
, 
and for 
we have the recurrence relation
 |
(14) |
where 
if 
is base-paired in 
and 
otherwise, and 
.
Proof: First, some notation is necessary. Recall that if 
is an arbitrary polynomial [resp. analytic] function, then 
denotes the coefficient of 
[resp. the kth Taylor coefficient in the Taylor expansion of 
] – for instance, in equation (1), 
, and in equation (9), 
.
By definition, it is clear that 
if 
, where we recall that 
is the minimum number of unpaired bases in a hairpin loop. For 
, we have
 |
By induction, the proof of the theorem now follows. 
Notice that if one were to compute all terms of the polynomial 
by explicitly performing polynomial multiplications, then the computation would require 
time and 
space. Instead of explicitly performing polynomial expansion in variable
, we instantiate 
to a fixed complex number 
, and apply the following recursion for this instantiation:
 |
(15) |
In this fashion, we can compute 
in 
time and 
space. For 
distinct complex values 
, we can compute and save only the values 
, each time re-using the 
space for the next computation of 
. It follows that the computation resources used to determine the (column) vector
 |
(16) |
where 
is thus quartic time 
and quadratic space 
.
Polynomial interpolation using the FFT
Let 
be the principal 
th complex root of unity. Recall that the Vandermonde matrix 
is defined to be the 
matrix, whose 
entry is 
; i.e.
 |
The Fast Fourier Transform (FFT) is defined to be the 
algorithm to compute the Discrete Fourier Transform (DFT), defined as the matrix product 
:
 |
On page 837 of [11], it is shown that the 
entry of 
is 
and that
 |
(17) |
for 
.
Since we defined 
in (16) by 
, where 
and 
, it follows that the coefficients 
in the polynomial 
defined in (8) can be computed, at least in principle, by using the FFT. It turns out, however, that the values of 
are so astronomically large, that the ensuing numerical instability makes even this approach infeasible for values of 
that exceed 
(data not shown). Nevertheless, our approach can be modified as follows. Define 
by 
, where 
, and 
is the partition function defined in (4). Using the FFT to compute the inverse DFT, it follows from (17) that we can compute the probabilities 
that are coefficients of the polynomial 
defined in equation (1). For genomics applications, we are only interested in the 
most significant digits of each 
, as described in the pseudocode below.
Algorithm for FFTbor
This pseudocode computes the 
most significant digits of probabilities 
.
Input: RNA sequence 
, and initial secondary structure 
of 
, and integer 
.
Output: Probabilities 
to 
significant digits for 
.
generate roots of unity
for 
, where 
and 
note that the partition function
for
to 
compute
using recursion (15)
//normalize 
compute
where 
by using FFT in (17)for
to 
//truncate to
most significant digits
Speed-up in our implementation of FFTbor
In this subsection, we show that we need only evaluate the polynomial 
, as defined in equation (8), for 
of the complex 
th roots of unity. It is first necessary to recall the definition of complex conjugate. Recall that the complex conjugate of 
is denoted by 
; i.e. if 
where 
are real numbers and 
, then 
.
Lemma 1: If 
is the complex polynomial defined in equation (8), then for any complex 
th root of unity 
, it is the case that 
. In other words, if 
is a complex 
th root of unity of the form 
, where 
and 
, and if 
where 
, then it is the case that
 |
Proof: Letting 
, if 
, then 
is the principal 
th complex root of unity, and 
together constitute the complete collection of all 
th complex roots of unity – i.e. the 
unique solutions of of the equation 
over the field 
of complex numbers. Clearly, for any 
, 
. Moreover, if 
where 
, then we have 
. It follows that for any 
th root of unity of the form 
, where 
, the number 
is also an 
th root of unity.
Recall that 
, where 
are real numbers representing the partition function 
over all secondary structures of a given RNA sequence 
, whose base pair distance from initial structure 
is 
. Thus, in order to prove the lemma, it suffices to show that for all values 
, if 
is a complex 
th root of unity, where 
and 
, and if 
where 
, then
. Indeed, we have the following.
 |
 |
 |
 |
It follows that each term of the form 
, for 
, is the complex conjugate of 
, and thus 
is the complex conjugate of 
. Since 
is a sum of terms of the form 
, it follows that 
is the complex conjugate of 
. This completes the proof of the lemma. 
Lemma 1 immediately entails that we need only evaluate 
on 
many of the complex 
th roots of unity – namely, those of the form 
, where 
. The remaining values of 
are obtained by taking conplex conjugates of the first 
values. This, along with a precomputation of powers of the complex 
th roots of unity, leads to an enormous performance speed-up in our implementation of FFTbor.
Results
Applications of FFTbor
In this section, we consider two applications of FFTbor: (i) correlation between kinetic folding speed and the ruggedness of the energy landscape near the minimum free energy structure, (ii) computational detection of riboswitch expression platform candidates.
Kinetic folding speed and energy landscape ruggedness
The output of FFTbor, as shown in Figure 2, is a probability distribution, where the 
-axis represents the base pair distance from an arbitrary, but fixed secondary structure 
, and the 
-axis represents the Boltzmann probability 
that a secondary structure has base pair distance 
from 
. Arguably, this probability distribution is an accurate one-dimensional projection of the rugged, high dimensional energy landscape near structure 
, of the sort artistically rendered in the well-known energy landscape depicted in Figure 1 of [12]. In the sequel, we may call the FFTbor probability distribution a structural neighbor profile, or simply structural profile
. A hypothesis behind theoretical work in biomolecular folding theory in [13] is that kinetic folding slows down as the energy landscape becomes more rugged. This is borne out in our computational experiments for RNA using FFTbor, as reported in Figure 2.
Figure 2. Output from FFTbor on two randomly selected thiamine pyrophosphate riboswitch (TPP) aptamers, taken from the Rfam database.
[23]
. The 
-axis represents base pair distance from the minimum free energy structure for each given sequence; the 
-axis represents Boltzmann probabilities 
, where 
denotes the sum of Boltzmann factors or all secondary structures, whose base pair distance from the MFE structure is exactly 
. (Left) The 97 nt sequence BX842649.1/277414-277318 appears to have a rugged energy landscape near its minimum free energy structure, with distinct low energy structures that may compete with the MFE structure during the folding process. (Right) The 99 nt sequence, AACY022101973.1/389-487 appears to have a smooth energy landscape near its MFE structure, with no distinct low energy structures to might compete with the MFE structure. Based on the FFTbor output or structural profile near MFE structure 
, one might expect folding time for the first sequence to increase due to competition from metastable structures, while one might expect the second sequence to have rapid folding time. Computational Monte Carlo folding experiments bear out this fact. Kinfold [15] simulations clearly show that the second sequence folds at least four times more quickly than the first sequence. See text for details. Subfigure A Subfigure B Subfigure C Subfigure D.
We randomly chose two TPP riboswitch aptamers from the seed alignment for Rfam family RF00059. The first sequence has EMBL accession code BX842649.1/277414-277318 and is comprised of the 97 nt sequence ACCUGACGCU AGGGGUGUUG GUGAAUUCAC CGACUGAGAA UAACCCUUUG AACCUGAUAG AGAUAAUGCU CGCGCAGGGA AGCAAGAAUA GAAAGAU, while the second sequence has EMBL accession code AACY022101973.1/389-487 and is comprised of the 99 nt sequence UAUAAGUCCA AGGGGUGCCA AUUGGCUGAG AUGGUUUUAA CCAAUCCCUU UGAACCUGAU CCGGUUAAUA CCGGCGUAGG AAUGGAUUUU CUCUACAGC. Rfam consensus and minimum free energy structures for both sequences are depicted in Figure 3. Despite the fact that there is no sequence homology according to pairwise BLAST [14], this figure clearly demonstrates that consensus and minimum free energy structures closely resemble each other, and that the structures of both TPP riboswitch aptamers are quite similar, with the exception of the leftmost hairpin loop [resp. multiloop]. The MFE structures differ from the consensus structures principally by the addition of base pairs not determined by covariation in the Rfam alignment. Indeed, if we let 
denote the Rfam consensus structure resp. MFE structure for the 97 nt sequence with EMBL accession code BX842649.1/277414-277318, then 
has 
base pairs, and 
has 
base pairs. If we let 
denote the Rfam consensus structure resp. MFE structure for the 99 nt sequence with EMBL accession code AACY022101973.1/389-487, then 
has 
base pair, and 
has 
base pairs.
Figure 3. Rfam consensus structures (Rfam) and minimum free energy (MFE) secondary structures for two thiamine pyrophosphate (TPP) riboswitch aptamers, chosen at random from RF00059 Rfam family seed alignment [23].
Using pairwise BLAST [14], there is no sequence similarity, although the secondary structures are very similar, as shown in this figure. (A) Rfam consensus structure for BX842649.1/277414-277318. (B) MFE structure for BX842649.1/277414-277318. (C) Rfam consensus structure for AACY022101973.1/389-487. (D) Rfam consensus structure for AACY022101973.1/389-487.
We ran FFTbor on each of the TPP riboswitch aptamer sequences, with the MFE structure of each sequence taken as the initial structure 
for that sequence. For the first sequence, BX842649.1/277414-277318, the FFTbor output suggests that there are low energy structures at a distance from the MFE structure, which might compete with the MFE structure and hence slow the kinetics of folding. In contrast, for the second sequence, AACY022101973.1/389-487, the FFTbor output suggests that there are no such competing low energy structures, hence the second sequence should fold more quickly than the first.
To test the hypothesis that folding is slower for rugged energy landscapes, we ran the kinetic folding software, Kinfold [15], on each of the two TPP riboswitch aptamer sequences, BX842649.1/277414-277318 and AACY022101973.1/389-487, to determine the mean first passage time (MFPT) to fold into the MFE structure, when starting from the empty structure. In this computational experiment, we took MFPT to be the average number of Monte Carlo steps taken by Kinfold, each step consisting of the addition or removal of a single base pair (or shift – see [15]), to fold the empty structure into the MFE structure, where the average was taken over 
runs, with an absolute maximum number of Monte Carlo steps taken to be 
. The first sequence, BX842649.1/277414-277318, converged within 
steps only for 20 out of 30 runs. Assigning the maximum step count of 
for the 10 runs that did not converge, we found a mean first passage time of 
steps for this sequence. The second sequence, AACY022101973.1/389-487, converged within 
steps in 29 out of 30 runs, and we found a mean first passage time of 
steps for this sequence. From computational experiments of this type, it is suggestive that FFTbor may prove useful in synthetic biology, where one would like to design rapidly folding RNA molecules that fold into a designated target structure. (See [16], [17], [18], [19] for more on synthetic biology.) In particular, one could use RNAinverse [20], RNA-SSD [21], INFO-RNA [22], or our recent constraint programming exact solution of RNA inverse folding, RNAiFold (to appear in Journal of Bioinformatics and Computational Biology, see http://bioinformatics.bc.edu/clotelab/RNAiFold/), to output a list of sequences, whose minimum free energy structure is a designated target structure. Subsequently, using FFTbor, one could prioritize sequences in terms of FFTbor structural profile, on the grounds that sequences with a profile similar to the right panel of Figure 2 are likely to fold more rapidly than those whose profile resembles the left panel of Figure 2.
In order to more systematically determine the relation between kinetic folding speed and the ruggedness of an energy landscape near the MFE structure, we need to numerically quantify ruggedness. To this end, in the following we define the notion of expected base pair distance to a designated structure. Let 
be an arbitrary secondary structure of the RNA sequence 
. The expected base pair distance to 
is defined by
 |
(18) |
where 
denotes the set of secondary structures for 
, 
is the Boltzmann probability of 
, and 
denotes base pair distance between 
and 
. If we run FFTbor on an input sequence 
and secondary structure 
, then clearly 
, where 
, obtained from the program output. If 
is the empty structure, then FFTbor output is simply the probability distribution of the number of base pairs per secondary structure, taken over the Boltzmann ensemble of all structures.
For the benchmarking assay, we took all 61 selenocysteine insertion sequence (SECIS) sequences from the seed alignment of Rfam family RF00031 [23]. Average length was 
nt. For each sequence, we ran both FFTbor and a Monte Carlo folding algorithm, developed by E. Freyhult and P. Clote (unpublished). Using the Monte Carlo algorithm, we determined the mean first passage time (MFPT), defined as the average taken over 50 runs, of the number of Monte Carlo steps taken to fold the empty structure into the MFE structure, where an absolute upper bound of 5 million steps was allowed in the simulation. After unsuccessful attempts due to ruggedness of the energy landscape near the MFE structure, by using the Hartigan-Hartigan dip test of unimodality [24], expected base pair distance from MFE structure, total variation distance between FFTbor output and the exponential distribution estimated by the method of moments [25], etc., we ran FFTbor when starting from the empty structure (rather than the MFE structure) as initial structure. As mentioned above, in this case, FFTbor output is simply the probability distribution for the number of base pairs per structure, taken over the ensemble of all secondary structure for the input RNA sequence. Surprisingly, we found that there is a significant correlation of 
with one-tailed 
-value of 
between the standard deviation of the FFTbor output (when starting from the empty structure) and logarithm base 
of the mean first passage time. Table 1 and Figure 4 explain this phenomenon in detail.
Table 1. Pearson correlation between various aspects of selenocysteine insertion sequences from the seed alignment of Rfam family RF00031 [23].
|
|
|
len | MFE | logMFPT | |
|
1 | |||||
|
−0.43722448 | 1 | ||||
|
−0.691411183 | 0.943650913 | 1 | |||
| len | 0.707683898 | −0.158951202 | −0.364591789 | 1 | ||
| MFE | −0.569474125 | 0.739515083 | 0.759622716 | −0.368485646 | 1 | |
| logMFPT | −0.036291124 | 0.48436192 | 0.376230235 | 0.405865529 | 0.399015556 | 1 |
For each of the 61 RNA sequences, we ran FFTbor, starting from empty initial structure 
, and we ran a Monte Carlo folding algorithm, developed by E. Freyhult and P. Clote (unpublished). Using the Monte Carlo algorithm, we determined the mean first passage time (MFPT), defined as the average taken over 50 runs, of the number of Monte Carlo steps taken to fold the empty structure into the MFE structure, where an absolute upper bound of 5 million steps was allowed in the simulation. From the output of FFTbor, we computed (1) the mean number (
) of base pairs per structure, taken over the ensemble of all secondary structures for the given sequence, (2) the standard deviation (
) of the number of base pairs per structure, (3) the coefficient of variation 
, (4) the RNA sequence length, and (5) the minimum free energy (MFE). Additionally, we computed the logarithm base 10 of mean first passage time (log10MFPT), taken over 50 Monte Carlo runs per sequence (log base 10 of the standard deviation of number of Monte Carlo steps per run was approximately 9% of log10MFPT on average). The table shows the correlation between each of these aspects. Some correlations are obvious – for example, (i) the standard deviation 
is highly correlated with the coefficient of variation 
; (ii) the mean 
is negatively correlated with the coefficient of variation 
; (iii) the mean 
is negatively correlated with the minimum free energy (MFE) – if most low energy structures in the ensemble have many base pairs, then it is likely that the minimum free energy is very low (i.e. since MFE is negative, the absolute value of MFE increases); (iv) sequence length is negatively correlated with MFE – as sequence length increases, the minimum free energy (MFE) decreases. However, it may appear surprising that (v) the mean 
number of base pairs per structure is independent of MFPT (correlation 
), although (vi) MFE is correlated with MFPT (correlation 
) – i.e. from (iii), lower MFE is correlated with a larger average 
number of base pairs per structure, from (vi) higher MFE is correlated with longer folding time, but from (v) the average 
number of base pairs per structure is independent of folding time. The most important insight from this table is that (vii) standard deviation 
is correlated with mean first passage time – the correlation is statistically significant, with one-tailed 
-value of 
.
Figure 4. This figure represents the graphical output of FFTbor, when the empty structure is chosen as initial structure .
. The 
-axis represents the number of base pairs per structure, taken over the ensemble of all secondary structures for the given RNA sequence; the 
-axis represents Boltzmann probability 
, where 
is the partition function for all secondary structures having exactly 
base pairs. (Left) For the selenocysteine (SECIS) element AB030643.1/4176-4241 from Rfam family RF00031, the standard deviation 
of the number of base pairs, taken over the ensemble of all secondary structures, is 
, while the logarithm base 10 of the mean first passage time (logMFPT) is 
. (Center) For the selenocysteine (SECIS) element AL645723.11/192421-192359 from Rfam family RF00031, the standard deviation 
of the number of base pairs, taken over the ensemble of all secondary structures, is 
, while logMFPT is 
. Among the 61 sequences in the seed alignment of RF00031, AB030643.1/4176-4241 was the fastest folder, while AL645723.11/192421-192359 was the slowest folder. (Right) Superimposition of output of FFTbor for two TPP riboswitch aptamers: the 97 nt sequence BX842649.1/277414-277318 and the 99 nt sequence AACY022101973.1/389-487, both obtained when taking the empty structure for the initial structure 
. The mean 
for the FFTbor structural profile near the empty structure is 
[resp. 
], the standard deviation 
for the FFTbor structural profile is 
[resp. 
], and the Kinfold MFPT is 
[resp. 
] for the TPP riboswitch aptamer AB030643.1/4176-4241 [resp. AL645723.11/192421-192359]. The right panel of this figure should be compared with Figure 2. These anecdotal results bear up the correlation between standard deviation 
and logMFPT described in Table 1.
In the right panel of Figure 4, we applied FFTbor to each of the two randomly chosen TPP riboswitch aptamers BX842649.1/277414-277318 and AACY022101973.1/389-487, starting from the empty reference structure 
. The mean for the FFTbor structural profile near the empty structure is 
[resp. 
], the standard deviation 
for the FFTbor structural profile is 
[resp. 
], and the Kinfold MFPT is 
[resp. 
] for the TPP riboswitch aptamer AB030643.1/4176-4241 [resp. AL645723.11/192421-192359]. This anecdotal evidence supports the hypothesis that small standard deviation in FFTbor distribution is correlated with fast folding.
Additionally, in following a suggestion of one of the anonymous referees, we randomized the TPP riboswitches BX842649.1/277414-277318 and AACY022101973.1/389-487 by using our implementation of the Altschul-Erikson dinucleotide shuffle algorithm [26], and then applied FFTbor to these sequences, starting from the empty structure. The mean 
and standard deviation 
for the FFTbor distribution for randomized BX842649 are respectively 
and 
, while those for randomized AACY022101973 are 
and 
. Running Kinfold, with a maximum of 500,000 steps with 30 replicates (as explained in the text), we found that for randomized BX842649, all 30 runs converged yielding a mean first passage time (MFPT) of 13022.58 with standard deviation of 15221.78. In contrast for randomized AACY022101973, only 15 out of 30 runs converged within 500,000 steps, and discounting these nonconvergent data, we obtain an average mean first passage time (MFPT) of 94446.93 with standard deviation of 157107.43. This additional test provides more anecdotal evidence supporting our hypothesis that small standard deviation 
in FFTbor probability density is correlated with fast folding, as measured by MFPT.
Riboswitch expression platform prediction
A bacterial riboswitch is a portion of the 
untranslated region (UTR) of messenger RNA, that performs gene regulation by undergoing a conformational change upon binding with a ligand, such as guanine, thiamine pyrophosphate, lysine, etc. [27]. This conformational change may either turn on or off the corresponding gene by either transcriptional or translational regulation of the messenger RNA [28], depending on the particular riboswitch. The common feature shared by all riboswitches is that a gene is regulated by conformational change upon ligand binding. Bacterial riboswitches are often found upstream of operons, regulating groups of genes, as in purine de novo synthesis and salvage [29].
A riboswitch consists of two equally important parts: an upstream aptamer, capable of highly discriminative binding to a particular ligand, and a downstream expression platform, capable of undergoing a radical conformational change upon binding of a ligand with the discriminating aptamer. Since aptamers have been under strong evolutionary pressure to bind with high affinity (e.g. 
nM for guanine [30]), there is strong sequence conservation found in the aptameric region of orthologous riboswitches. In contrast, while secondary structure is conserved in the terminator loop of the expression platform in purine riboswitches, there is relatively low sequence conservation (data not shown). While a number of methods exist to computationally predict riboswitch aptamers [31], [32], [33], [34], [35] (and especially INFERNAL [36], which latter is used to predict riboswitch aptamers in Rfam), it is an important biological problem to determine the expression platform, since the structure of the expression platform can suggest whether there is transcriptional regulation via a terminator loop or translational regulation via the sequestration of the Shine-Dalgarno sequence [28]. Determination of the precise location and structure of the expression platform is difficult due to low conserved sequence identity (in-house computations, data not shown). Although this problem remains open, we report here how FFTbor may provide help to biologists in the selection and prioritization of riboswitch candidates.
Figure 5 depicts the gene OFF structure of the xpt G-box purine riboswitch in B. subtilis, as determined by inline-probing – this structure was taken from Figure 1 of [27]. Note that this structure is only partial, since there are regions with no base pairs depicted, despite the fact that additional base pairs could be added. By using blastn, it is found that this 161 nt purine riboswitch can be found on the complement strand of GenBank accession number CP002906.1/c2165302-2165142 in complete genome of B. subtilis subsp. subtilis RO-NN-1. Figure 6 depicts the result of three computational experiments with FFTbor. The left panel displays the expected base pair distance to the following secondary structure
 |
(19) |
as a function of window offset, where window size equals the size of this target structure. This structure was obtained by removing all leading and trailing unpaired positions from the structure depicted in Figure 5, except for the leftmost [resp. rightmost] unpaired position adjacent to the leftmost [resp. rightmost] base-paired position. The reason for removal of the leading and trailing unpaired positions was that the structure of [27], depicted in Figure 5, is clearly only partial, as earlier mentioned. The center panel displays the expected base pair distance to the following secondary structure
 |
(20) |
as a function of window offset, where window size equals the size of this target aptamer structure. Similarly, the right panel displays the expected base pair distance to the following secondary structure
 |
(21) |
as a function of window offset, where window size equals the size of this target expression platform structure. Figure 6 determines the precise location of the xpt riboswitch, both aptamer and expression platform.
Figure 5. Gene OFF secondary structure of the xpt G-box purine riboswitch in B. subtilis; structure taken from that in Figure 1A of [27].
Figure 6. Graph of the expected distance from target secondary structure, as a function of window offset position in the .
untranslated region (UTR) of the xpt gene of
B. subtilis
; i.e. GenBank accession code CP002906.1/c2165402-2165042
B. subtilis
subsp. subtilis RO-NN-1. In a moving window application, FFTbor computed the Boltzmann probability 
that secondary structures of the current window contents have base pair distance 
from the target (or initial) structure 
. In each case, the size of the window was set to equal the length of 
. (Left) Target structure 
comprises the entire secondary of the xpt riboswitch, as depicted in Figure 5, with the exception that the leading and trailing unpaired positions were removed, as explained in the text – see displayed dot bracket structure in (19). (Center) Target structure 
comprises only the aptamer secondary structure, as displayed in dot bracket structure in (20). (Right) Target structure 
comprises only the expression platform secondary structure, as displayed in dot bracket structure in (21). The number of points displayed on the 
-axis differs in each case, since the window size differs, as explained above. The very well-defined minimum in each panel corresponds to the exact location of the entire riboswitch (left panel), aptamer (center panel) and expression platform (right panel). Note that the base line value for the expected base pair distance in the left panel (entire riboswitch) is approximately 
, while that for both the center panel (aptamer) and right panel (expression platform) is approximately 
.
If the biologically functional target structure is unknown, one can instead attempt a similar moving window computation, where the target structure is taken to be the minimum free energy structure of the current window contents. In this case, one may hope to determine a bimodal distribution, as displayed in Figure 7. Given an input RNA sequence, or genomic region, the web server http://bioinformatics.bc.edu/clotelab/FFTbor creates a movie as follows, described here for the xpt riboswitch previously discussed. We extended the 161 nt xpt G-box purine riboswitch described in Figure 5, with GenBank accession number CP002906.1/c2165302-2165142, to a sequence of length 200 nt, by appending flanking downstream genomic nucleotides. Running FFTbor on all prefixes of the resulting sequence of lengths 
, we produced a movie, displayed on the webserver http://bioinformatics.bc.edu/clotelab/FFTbor. Figure 5 displays the output of FFTbor on the 166 nt prefix, clearly showing a bimodal distribution. Attempting to automate the identification of non-unimodal FFTbor output, we have applied the Hartigan-Hartigan dip-test [24], implemented in R; however, the dip-test appears to be too sensitive, in that a probability distribution is reported to be non-unimodal, even when visual inspection indicates that it appears overwhelmingly to be unimodal (data not shown). It is for this reason that the web server http://bioinformatics.bc.edu/clotelab/FFTbor produces a movie of prefixes, where the user can start/stop the movie, move forward/backward, or download all raw data output by FFTbor.
Figure 7. The 161 nt xpt G-box purine riboswitch described in.
Figure 1A
of
[27]
, found on the complement strand of GenBank accession number CP002906.1/c2165302-2165142 in complete genome of
B. subtilis subsp. subtilis RO-NN-1
. We extended this 161 nt sequence to a sequence of length 200 nt, by appending flanking downstream genomic nucleotides. The web site http://bioinformatics.bc.edu/clotelab/FFTbor displays a movie of all prefixes of the resulting 200 nt sequence, where prefix lengths range from 
.
Benchmarking results
Total variation distance for density of states
Recall that the total variation distance between two probability distributions 
and 
, defined on the same sample space 
, is defined by
 |
The density of states for an RNA sequence 
with respect to an initial structure 
of 
is defined to be the probability distribution 
where 
. In all our tests, for RNA of length up to 400 nt, we found the total variation distance between 
, as computed to 6 decimal places by RNAbor and by FFTbor, to be 
. It follows that FFTbor can reliably be used in place of RNAbor to determine Boltzmann probabilities 
.
Run time comparison of RNAbor and FFTbor
As visible from the defining recursions, the algorithmic time complexity of RNAbor is 
and space complexity is 
, where 
is the length of input RNA sequence. In contrast, the time complexity of FFTbor is 
and space complexity is 
. Figure 8 displays run time curves for both RNAbor and FFTbor, when the initial structure 
is taken to be either the empty structure or the minimum free energy (MFE) structure.
Figure 8. Run times in seconds for RNAbor and FFTbor, on random RNA of length .
in step size of 20 nt. Each algorithm was run with the empty initial structure
, see rows RNAbor (empty), FFTbor (empty), and with the minimum free energy structure as the initial structure
, see rows RNAbor (MFE) and FFTbor (MFE). Note that for both RNAbor and FFTbor, the run time increases when 
is the MFE structure, rather than the empty structure. Notice the radical improvement in the run time of FFTbor over that of RNAbor.
Here, we compare the run time of RNAbor [1] and the (unparallelized version of) FFTbor, using a Dell Power Edge 1950, 2× Intel Xeon E5430 Quad core with 2.80 GHz and 16 GB RAM. For 
, in step size of 20 nt, we generated 
random RNA sequences of length 
with equal probability for each nucleotide A,C,G,U (i.e. a 
th order Markov chain). For values of 
, 
random sequences of length 
were generated, while for values of 
, only 
sequences of length 
were generated. RNA sequences larger than 300 nt were not tested, due to 
memory constraints required by RNAbor. For each RNA sequence, RNAbor and FFTbor were both run, each starting with empty initial structure 
, and also with initial sequence 
taken to be the MFE structure. Each data point in the table comprises the average run time for three independent evaluations.
OpenMP parallelization of FFTbor
OpenMP is a simple and flexible multi-platform shared-memory parallel programming environment, that supports parallelizations of C/C++ code – see http://openmp.org/. Using OpenMP primitives, we created multiple threads to evaluate the polynomial 
on different complex 
th roots of unity. The table in the left panel of Figure 9 and Table 2 together present benchmarks, executed on a 24-core AMD Opteron 6172 with 2.10 GHz and 64 GB RAM, for the speedup of FFTbor as a function of the number of cores. The table in Figure 9 describes average run time in seconds (
one standard deviation) for running FFTbor on random RNA of length 200,250,300,400,450,500 with either 1 or 2 cores. Table 2 presents similar data for running FFTbor on 2,3,6,4,12,15,20 cores. Although FFTbor clearly has quartic 
run time as a function of RNA sequence length, least-squares fit of run times from Table 2 instead shows a quadratic run time for RNA sequences of length up to 
nt. There appears to be a power law dependence of FFTbor speedup, as a function of number of cores. For instance, for random RNA of length 200 nt, least-squares fit of the data from the table yields a run time of 
with 
value of 
. A power law behavior is demonstrated, with similarly high 
values, for each fixed sequence length in Table 2, with different coefficients of variable 
but with approximately the same exponent of 
(data not shown, but easily computable from data in Table 2).
Figure 9. (Left) Table showing parallel run times in seconds for FFTbor, using OpenMP .
http://openmp.org/
. Column headers 1,2 indicate the number of cores used in the computational experiment. For each sequence length 
, five random RNAs were generated using equal probability for each nucleotide A,C,G,U. Run time in seconds, plus or minus one standard deviation, are given for a 24-core AMD Opteron 6172 with 2.10 GHz and 64 GB RAM, with only 1 (resp. 2) cores used. (Right) Graph showing parallel run time of FFTbor on an AMD Opteron 6172 with 2.10 GHz and 64 GB RAM, using respectively 1,2,3,4,6,9,12,15,20 cores.
Table 2. Table showing parallel run times of FFTbor, using OpenMP http://openmp.org/. Column headers 2,3, etc. indicate the number of cores used in the computational experiment.
| Len | 2 | 3 | 4 | 6 | 9 | 12 | 15 | 20 |
| 200 | 61.8 8.0 |
41.6 6.0 |
31.6 4.2 |
21.1 2.9 |
15.0 2.3 |
11.3 1.1 |
9.6 1.3 |
7.6 1.5 |
| 250 | 166.1 13.7 |
111.5 8.7 |
84.1 7.1 |
56.9 4.0 |
38.8 3.8 |
30.3 2.6 |
24.6 1.6 |
18.9 2.7 |
| 300 | 365.2 30.1 |
246.4 20.5 |
184.5 14.9 |
125.1 9.6 |
85.5 6.6 |
64.9 6.5 |
53.6 5.9 |
42.1 5.2 |
| 350 | 698.4 46.9 |
470.1 32.6 |
352.0 23.0 |
242.6 15.8 |
163.3 12.4 |
125.1 6.7 |
104.2 8.9 |
76.2 3.9 |
| 400 | 1,129.5 104.3 |
757.5 68.9 |
571.6 53.9 |
391.2 36.4 |
265.1 24.2 |
207.2 18.4 |
165.6 14.5 |
125.9 14.9 |
| 450 | 1,980.9 126.5 |
1,326.3 85.1 |
1,000.0 59.0 |
688.9 44.8 |
469.2 29.1 |
355.1 25.4 |
289.8 21.2 |
223.1 18.2 |
| 500 | 3,389.8 788.4 |
2,067.9 99.2 |
1,555.0 72.2 |
1,074.3 53.7 |
728.1 40.9 |
548.3 24.0 |
451.5 25.7 |
338.1 22.7 |
For each sequence length 
, five random RNAs were generated using equal probability for each nucleotide A,C,G,U. Run time in seconds, plus or minus one standard deviation, are given for a 24-core AMD Opteron 6172 with 2.10 GHz and 64 GB RAM. Least-squares fit of the data indicates a quadratic dependency of run time on sequence length (despite the obvious 
theoretical run time), and a power law dependence of approximately 
on the number of cores 
.
Conclusion and Discussion
In this paper, we have used a dynamic programming computation to evaluate the polynomial
 |
(22) |
on the complex 
th roots of unity 
, where the coefficients 
are equal to the sum of Boltzmann factors over all secondary structures of a given RNA sequence, whose base pair distance to a given initial structure 
is 
. Recall the definition of polynomial
 |
(23) |
obtained from 
, whose coefficients are Boltzmann probabilities 
that a secondary structure has base pair distance 
to 
. By using the fast Fourier transform to compute the inverse discrete transform, we can approximate to 
decimal places the coefficients 
of 
, and thus the 
most significant positions of 
. Interpolation is performed for 
, rather than 
, due to issues concerning numerical instability. The computational advantage of FFTbor over its predecessor RNAbor [1] is that the new algorithm runs in quartic time 
and quadratic space 
, in contrast to the 
run time and 
space required by RNAbor. We have additionally provided a parallelization of FFTbor using OpenMP primitives. Additionally, we have described applications of FFTbor to determine the correlation between kinetic folding speed and the ruggedness of the energy landscape, and to predict the location of riboswitch expression platform candidates.
It is important to point out that the algorithm and software RNAbor is more general than that of FFTbor – in particular, RNAbor not only computes the partition function values 
, for all 
, but as well as computes the structures 
, defined to be the minimum free energy structure over all 
-neighbors of initial structure 
. In contrast, FFTbor only computes the 
most significant digits of the probabilities 
, for 
, where by multiplication of 
by the partition function 
, one obtains an approximation of the partition function values 
. There is no possibility that FFTbor can compute the structures 
, nor can at present we see how to use FFTbor to sample structures from the Boltzmann ensemble of structures having base pair distance 
from 
.
In [37], [38], we introduced the a related parametric RNA structure algorithm, RNAmutants, which computes the partition function 
and minimum free energy structure 
over all secondary structures of all 
-point mutants of a given RNA sequence 
. In [39], RNAmutants was extended to sample low energy structures over 
-point mutants within a certain range of GC-content. Some of the ideas in [39] foreshadowed the results of this paper, and in the future, we intent to apply interpolation and the FFT to similarly provide a more efficient version of RNAmutants. Nevertheless, this future, more efficient version will be incapable of efficiently sampling low energy structures over 
-point mutants, analogous to the current differences between RNAbor and FFTbor.
Supporting Information
Supplementary information.
(PDF)
Acknowledgments
FFTbor depends heavily on the use of the Fast Fourier Transform implementation FFTW of Frigo and Johnson [40] at http://www.fftw.org/.
Funding Statement
Source of funding provided by National Science Foundation grants DMS-1016618 and DMS-0817971 to PC, www.nsf.gov. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1. Freyhult E, Moulton V, Clote P (2007) Boltzmann probability of RNA structural neighbors and riboswitch detection. Bioinformatics 23: 2054–2062. [DOI] [PubMed] [Google Scholar]
- 2. Clote P, Lou F, Lorenz W (2012) Maximum expected accuracy structural neighbors of an RNA secondary structure. BMC Bioinformatics 13: S6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Ding Y, Lawrence CE (2003) A statistical sampling algorithm for RNA secondary structure prediction. Nucleic Acids Res 31: 7280–7301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Dotu I, Lorenz WA, VAN Hentenryck P, Clote P (2010) Computing folding pathways between RNA secondary structures. Nucleic Acids Res 38: 1711–1722. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Flamm C, Hofacker IL, Maurer-Stroh S, Stadler PF, Zehl M (2001) Design of multistable RNA molecules. RNA 7: 254–265. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Matthews D, Sabina J, Zuker M, Turner D (1999) Expanded sequence dependence of thermodynamic parameters improves prediction of RNA secondary structure. J Mol Biol 288: 911–940. [DOI] [PubMed] [Google Scholar]
- 7. Xia T, J SantaLucia J, Burkard M, Kierzek R, Schroeder S, et al. (1999) Thermodynamic parameters for an expanded nearest-neighbor model for formation of RNA duplexes with Watson-Crick base pairs. Biochemistry 37: 14719–35. [DOI] [PubMed] [Google Scholar]
- 8. Freyhult E, Moulton V, Gardner P (2005) Predicting RNA structure using mutual information. Appl Bioinformatics 4: 53–59. [DOI] [PubMed] [Google Scholar]
- 9. Nussinov R, Jacobson AB (1980) Fast algorithm for predicting the secondary structure of single stranded RNA. Proceedings of the National Academy of Sciences, USA 77: 6309–6313. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Higham N (2004) The numerical stability of barycentric Lagrange interpolation. IMA J Numer Anal 24: 547–556. [Google Scholar]
- 11.Cormen T, Leiserson C, Rivest R (1990) Algorithms. McGraw-Hill. 1028 pages.
- 12. Wolynes PG (2005) Energy landscapes and solved protein-folding problems. Philos Transact A Math Phys Eng Sci 363: 453–464. [DOI] [PubMed] [Google Scholar]
- 13. Bryngelson JD, Onuchic JN, Socci ND, Wolynes PG (1995) Funnels, pathways, and the energy landscape of protein folding: a synthesis. Proteins 21: 167–195. [DOI] [PubMed] [Google Scholar]
- 14. Altschul SF, Gish W, Miller W, Myers EW, Lipman DJ (1990) Basic local alignment search tool. J Mol Biol 215: 403–410. [DOI] [PubMed] [Google Scholar]
- 15. Flamm C, Fontana W, Hofacker I, Schuster P (2000) RNA folding at elementary step resolution. RNA 6: 325–338. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Shetty RP, Endy D, Knight TF (2008) Engineering BioBrick vectors from BioBrick parts. J Biol Eng 2: 5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Knight TF (2005) Engineering novel life. Mol Syst Biol 1: 2005–2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Waldminghaus T, Kortmann J, Gesing S, Narberhaus F (2008) Generation of synthetic RNA-based thermosensors. Biol Chem 389: 1319–1326. [DOI] [PubMed] [Google Scholar]
- 19. Zadeh JN, Wolfe BR, Pierce NA (2011) Nucleic acid sequence design via efficient ensemble defect optimization. J Comput Chem 32: 439–452. [DOI] [PubMed] [Google Scholar]
- 20. Hofacker I (2003) Vienna RNA secondary structure server. Nucleic Acids Res 31: 3429–3431. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Andronescu M, Fejes A, Hutter F, Hoos H, Condon A (2004) A new algorithm for rna secondary structure design. J Mol Biol 336: 607–624. [DOI] [PubMed] [Google Scholar]
- 22. Busch A, Backofen R (2006) Info-rna, a fast approach to inverse rna folding. Bioinformatics 22: 1823–1831. [DOI] [PubMed] [Google Scholar]
- 23. Gardner PP, Daub J, Tate J, Moore BL, Osuch IH, et al. (2011) Rfam: Wikipedia, clans and the “decimal” release. Nucleic Acids Res 39: D141–D145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Hartigan J, Hartigan P (1985) The dip test of unimodality. Ann Statist 13: 70–84. [Google Scholar]
- 25.Zar J (1999) Biostatistical Analysis. Prentice-Hall, Inc.
- 26. Altschul S, Erikson B (1985) Significance of nucleotide sequence alignments: A method for random sequence permutation that preserves dinucleotide and codon usage. Mol Biol Evol 2 ((6)) 526–538. [DOI] [PubMed] [Google Scholar]
- 27. Serganov A, Yuan Y, Pikovskaya O, Polonskaia A, Malinina L, et al. (2004) Structural basis for discriminative regulation of gene expression by adenine- and guanine-sensing mRNAs. Chem Biol 11 ((12)) 1729–1741. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Tucker BJ, Breaker RR (2005) Riboswitches as versatile gene control elements. Curr Opin Struct Biol 15: 342–348. [DOI] [PubMed] [Google Scholar]
- 29. Mandal M, Boese B, Barrick J, Winkler W, Breaker R (2003) Riboswitches control fundamental biochemical pathways in Bacillus subtilis and other bacteria. Cell 113 ((5)) 577–586. [DOI] [PubMed] [Google Scholar]
- 30. Mandal M, Breaker RR (2004) Adenine riboswitches and gene activation by disruption of a transcription terminator. Nat Struct Mol Biol 11: 29–35. [DOI] [PubMed] [Google Scholar]
- 31. Bengert P, Dandekar T (2004) Riboswitch finder–a tool for identification of riboswitch RNAs. Nucl Acids Res 32: W154–159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Chang TH, Huang HD, Wu LC, Yeh CT, Liu BJ, et al. (2009) Computational identification of riboswitches based on RNA conserved functional sequences and conformations. RNA 15: 1426–1430. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Abreu-Goodger C, Merino E (2005) RibEx: a web server for locating riboswitches and other conserved bacterial regulatory elements. Nucleic acids research 33. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Singh P, Bandyopadhyay P, Bhattacharya S, Krishnamachari A, Sengupta S (2009) Riboswitch Detection Using Profile Hidden Markov Models. BMC Bioinformatics 10: 325+. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Bergig O, Barash D, Nudler E, Kedem K (2004) STR2: a structure to string approach for locating G-box riboswitch shapes in pre-selected genes. In Silico Biol 4: 593–604. [PubMed] [Google Scholar]
- 36. Nawrocki EP, Kolbe DL, Eddy SR (2009) Infernal 1.0: inference of RNA alignments. Bioinformatics [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Clote P, Waldispühl J, Behzadi B, Steyaert JM (2005) Exploring the energy landscape of k-point mutagens of rna. Bioinformatics 21: 4140–4147. [DOI] [PubMed] [Google Scholar]
- 38. Waldispuhl J, Devadas S, Berger B, Clote P (2008) Efficient algorithms for probing the RNA mutation landscape. PLoS Comput Biol 4: e1000124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39. Waldispühl J, Ponty Y (2011) An unbiased adaptive sampling algorithm for the exploration of RNA mutational landscapes under evolutionary pressure. Journal of Computational Biology 18: 1465–79. [DOI] [PubMed] [Google Scholar]
- 40. Frigo M, Johnson SG (2005) The design and implementation of FFTW3. Proceedings of the IEEE 93: 216–231. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary information.
(PDF)