A practical approach to parameter estimation applied to model predicting heart rate regulation

Abstract

Mathematical models have long been used for prediction of dynamics in biological systems. Recently, several efforts have been made to render these models patient specific. One way to do so is to employ techniques to estimate parameters that enable model based prediction of observed quantities. Knowledge of variation in parameters within and between groups of subjects have potential to provide insight into biological function. Often it is not possible to estimate all parameters in a given model, in particular if the model is complex and the data is sparse. However, it may be possible to estimate a subset of model parameters reducing the complexity of the problem. In this study, we compare three methods that allow identification of parameter subsets that can be estimated given a model and a set of data. These methods will be used to estimate patient specific parameters in a model predicting baroreceptor feedback regulation of heart rate during head-up tilt. The three methods include: structured analysis of the correlation matrix, analysis via singular value decomposition followed by QR factorization, and identification of the subspace closest to the one spanned by eigenvectors of the model Hessian. Results showed that all three methods facilitate identification of a parameter subset. The ”best” subset was obtained using the structured correlation method, though this method was also the most computationally intensive. Subsets obtained using the other two methods were easier to compute, but analysis revealed that the final subsets contained correlated parameters. In conclusion, to avoid lengthy computations, these three methods may be combined for efficient identification of parameter subsets.

1 Introduction

Mathematical models have long been used to better understand cardiovascular dynamics, but have not until recently been used in conjunction with analysis of patient specific data. Some efforts have been made to develop patient specific models for prediction of blood flow and pressure in networks of arteries [37,51,52,62,69]. Most of these models use patient specific geometry to predict blood flow and pressure in arterial vessels or networks, e.g., in preparation for or when studying the impact of a given surgery. For example, a model could use blood flow values obtained from magnetic resonance measurements combined with a 3D fluid dynamics model to predict the distribution of flow and wall-shear stress in a given artery before and after inserting a stent. While this type of model provide excellent predictions in specified domains, it cannot easily be expanded to analyze dynamics associated with the full system. An example of a systems level model is one that predicts the impact of blood pressure changes in response to a stress challenge such as head-up tilt. Models designed for this purpose typically utilize compartmental formulations, and thus ordinary differential equations. While compartment models have been around for a long time (e.g., Guyton’s elaborate model of the overall physiological control system developed in 1972 [26]), only few attempts have been made to integrate models with clinical studies. One problem is that system models often strive to incorporate as many physiological principals as possible enabling excellent prediction of the system dynamics, but at the expense of complex models that describe population rather than patient specific dynamics. One way to render models patient specific, is to use them to describe the essential mechanisms governing the dynamics, and combine these with parameter estimation allowing prediction of a set of parameters and associated initial conditions. This approach is based on the assumption that for all subjects studied the system dynamics can be modeled by the same biological mechanisms, but that the system may be tuned differently for each subject reflecting the different strength of the individual mechanisms constituting the system.

Knowledge of how parameters change within and between groups of subjects has potential to be used to improve diagnosis and treatment strategies. For example, in [47] we showed that in aging and hypertension the afferent baroreflex gain is reduced, the sympathetic delay is increased, and the parasympathetic dampening of the sympathetic response is increased. Moreover, we showed that modulation of these parameters allowed us to ”treat” the model in place of the patient, making the healthy elderly young, and the hypertensive elderly healthy. These parameters reflect quantities that are desirable to assess, while they cannot easily be measured directly.

Estimation of model parameters involves solution of the inverse problem: given a model and data predict the model parameters [3]. This problem is difficult to solve, and typically, no unique analytical or numerical solution can be found [71]. Therefore, most studies addressing parameter estimation techniques use examples involving a ”correct” model, good initial parameter values, and a comprehensive set of data, see e.g., [12]. However, in practice, only some parameters can be estimated given a model and available observations. Finding the set of parameters that can be estimated reliably given a model and observations involves parameter identification [45]. Following suggestions by Liang [40] we propose to utilize sensitivity and correlation analysis methods for this purpose.

More specifically, we test three parameter identification methods using a nonlinear differential equations model developed to predict regulation of heart rate during head-up tilt. This model was chosen, since it contains complex nonlinear dynamics, a large number of parameters, and sparse data. Data for this model is considered sparse since only one output quantity is measured (heart rate), though it is sampled at a high resolution in time. The model is complex since it contains nonlinear dynamics as well as several time scales including fast inter-beat dynamics and slow dynamics associated with changes observed during head-up tilt. The model is developed from first principles describing the underlying mechanisms, with model parameters representing physiological quantities including gain and timing associated with the firing of afferent neurons, and time scales related to the change in neurotransmitters acetylcholine and noradrenaline.

The article is organized as follows. In section 2 we introduce and discuss three parameter estimation methods. Section 3 derives the example model, discusses how simulated data are generated, and show results of applying the three parameter identification methods to the proposed model. Finally, in section 4 we discuss our findings.

2 Parameter identification and estimation

Parameters are identifiable if it is possible to predict their values given a model and a complete set of data [3,45]. However, for most systems data are not available for all states, and even given data for all states, the model may not be structural identifiable [45]. For many systems only a subset of model outputs can be measured, and therefore, only a subset of parameters may be identifiable. Parameters identified from partial data are sometimes denoted conditionally identifiable [45,56, 71].

The history of parameter identifiability and estimation is voluminous. Some of the first discussions of identifiability and estimability can be found in early work by Koopmans and Reiersol [39] and Fisher [21] who introduced these concepts in statistics and econometrics. Subsequently development took place in the field of system theory in engineering in particular for applications described by linear state space models [2,43]. Along with these developments theories and refined concepts took form. Berman and Schoenfeld [7] were among the first to address the actual identifiability problem although they did not use this term. The term ’structural identifiability’ appeared for the first time in 1970, in a paper by Bellman and Astrom [6] on compartmental systems. This manuscript spun off a stream of papers on identifiability in the 1970s and 1980s; see for example [1,11,13,25,32]. These methods are still discussed extensively today (see e.g., [58,61,64,68] and the recent review by Miao et al. [45] that summarizes seminal contributions for parameter identification).

Structural identifiability provides a priori information about the model parameters. It is a necessary but not sufficient condition for successful parameter estimation from real data, which are typically incomplete (only limited number of states can be measured, though they may be measured with a high resolution) and noisy. Furthermore, the fact that the model may not be ”correct” further complicates the concept [61,64]. Thus, recently a number of practical identifiability methods have been proposed as summarized in the review by Miao et al. [45], and methods for analysis of sensitivities and confidence intervals have been discussed in the chapter by Banks et al. [3], though more work still needs to be done to obtain efficient and reliable methods. Along with parameter identification comes reliable methods for estimation of model parameters. A large number of techniques exist including Monte Carlo methods [28,29,68], various forms of principal component methods [55], local [33,35,53,56,63] and global [33,44,59,61] methods, as well as Kalman filtering methods [4,8,31].

In this study, we devise three techniques for practical identification of parameter subsets and apply them to a mathematical model predicting heart rate regulation during head-up tilt. [46,48, 49]. The heart rate model can be described by a system of nonlinear delay differential equations that cannot be solved in closed form. Therefore, we use numerical techniques to solve the differential equations and the associated parameter identification and estimation problems. The model uses measured blood pressure data as an input predicting heart rate as an output. In agreement with Ljung [42] we use the concept ”subset selection” to denote the process involving identification of a parameter subset that can be estimated given the model and a data set, and the concept ”parameter estimation” to denote the optimization involved with computation of parameter values that minimize the least squares error between computed and measured outputs. The latter is done using both simulated and real values of heart rate.

All parameter identification methods discussed here are derived for models that can be described by a nonlinear system of differential equations of the form

$$\frac{\mathit{\text{dx}}}{\mathit{\text{dt}}}=f(t,x;\theta ),$$ (1)

where f : R^1+n+q → Rⁿ, t ∈ R denotes time, x ∈ Rⁿ denotes the state vector, and θ ∈ R^q the parameter vector. Associated with the states we assume an output vector y ∈ R^m corresponding to the available data. We assume that this output can be computed algebraically as a function of the time t, the states x, and the model parameters θ, i.e.,

$$y=g(t,x;\theta ),$$ (2)

where g : R^1+n+q →R^m. Associated with each component of the model output y we assume existence of a set of data Y sampled at time t_i, where the sampling rate may vary between output components. To solve the inverse problem we assume that the data and associated model outputs can be evaluated at times where the data are sampled. These are given by

$$Y={(Y_1(t_{11}),Y_1(t_{12}),\dots ,Y_1(t_{1k_1}),\dots ,Y_m(t_{m1}),Y_m(t_{m2}),\dots ,Y_m(t_{{\mathit{\text{mk}}}_m}))}^T,$$ (3)

$$y={(y_1(t_{11}),y_1(t_{12}),\dots ,y_1(t_{1k_1}),\dots ,y_m(t_{m1}),y_m(t_{m2}),\dots ,y_m(t_{{\mathit{\text{mk}}}_m}))}^T,$$ (4)

where Y_ℓ and y_ℓ to denote the ℓ’th component of the vectors Y and y, respectively, ℓ = 1,…,K, and K denoting the total number of observations.

Given the model (1) and its associated output (2), for all ℓ, we assume that the ℓ’th component of the data satisfies the statistical model

$$Y_{\ell }=y_{\ell }+{\epsilon }_{\ell },\ell =1,\dots ,K,$$ (5)

where ε_ℓ denotes the measurement error associated with y_ℓ. We assume that the errors can be represented by independent identically distributed random variables with zero mean and finite variance [3,66]. Given this assumption, parameters may be estimated via solution of the inverse problem obtained by predicting the maximum likelihood estimate, which is equivalent to minimizing the least squares error between computed and measured values of the model output. The least squares error J, which also approximates the model variance σ², is given by

$$J={\sigma }^2=R^{T}R=\frac{1}{K-q}{\displaystyle \sum _{\ell =1}^K}|y_{\ell }-Y_{\ell }{|}^2,$$ (6)

where R = (r₁, r₂,…, r_K)^T, q is the number of parameters, and r_ℓ denotes the model residual for the ℓ’th observation. The latter is defined by

$$r_{\ell }=\frac{y_{\ell }-Y_{\ell }}{\sqrt{K-q}}.$$ (7)

2.1 Sensitivity analysis

Classically [18,22], the sensitivity of the model output y to the model parameters θ can be predicted from the so called sensitivity matrix

$$S=\frac{\partial y}{\partial \theta }=\left[\begin{array}{ccc}\hfill \partial y_1/\partial {\theta }_1(t_{11})\hfill & \hfill \cdots \hfill & \hfill \partial y_1/\partial {\theta }_q(t_{11})\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill \\ \hfill \partial y_1/\partial {\theta }_1(t_{1k_1})\hfill & \hfill \cdots \hfill & \hfill \partial y_1/\partial {\theta }_q(t_{1k_1})\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill \\ \hfill \partial y_m/\partial {\theta }_1(t_{m1})\hfill & \hfill \cdots \hfill & \hfill \partial y_1/\partial {\theta }_q(t_{m1})\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill \\ \hfill \partial y_m/\partial {\theta }_1(t_{{\mathit{\text{mk}}}_m})\hfill & \hfill \cdots \hfill & \hfill \partial y_1/\partial {\theta }_q(t_{{\mathit{\text{mk}}}_m})\hfill \end{array}\right]$$ (8)

Sensitivities can be computed analytically [65], using automatic differentiation [16], or using finite differences [53]. For simple problems, the first two approaches are preferable, since they are more accurate, but for complex problems, it is often necessary to use finite differences to compute the sensitivities.

For a given parameter and a given model output, sensitivities S_i, i = 1,…,q (represented by columns in the matrix (8)) reflect how sensitive the model output is to a given value of the parameter at the instances of measurements. Since model parameters and model outputs may have different units, it may be advantageous to compute relative sensitivities defined as

$$\mathrm{S̃}=\frac{\partial y}{\partial \theta }\frac{\theta }{y}.$$ (9)

Furthermore, it may be difficult to compare parameter sensitivities directly from the various instances of measurements. Consequently, we predict ranked sensitivities (S̅_i, i = 1,…,q) by imposing a norm across all points (along each column of S or S̃). To do so, we use the operator two-norm, i.e., we define

$${\mathrm{S̅}}_i={\Vert S_i\Vert }_2,i=1,\dots ,q.$$ (10)

It should be noted that ranked sensitivities can also be computed from the relative sensitivities S̃.

The resulting ranked sensitivities can be sorted from the most to the least sensitive, and parameters may be separated into two groups with ρ sensitive and q − ρ insensitive parameters. Insensitive parameters cannot be estimated, consequently, the subset of identifiable parameters should be found among the sensitive parameters.

To our knowledge, no theoretically based technique exists to separate parameters between those that are sensitive and those that are not. In a recent paper [63], the authors used relative sensitivity analysis combined with analysis of measurement uncertainties to identify sensitive parameters. For this study the parameters naturally got separated in two distinct groups (sensitive and insensitive parameters). However, for the heart rate model, studied here, the ranked sensitivities approximately follow a straight line if depicted on a log-scale without any clear demarcation (see Fig. 4).

Fig. 4.

Normalized ranked sensitivities computed for the log scaled parameters. Note that sensitivities decrease almost linearly and that all sensitivities are larger than the computational bound of 10⁻³.

Thus we analyzed the computational accuracy to separate ”sensitive” from ”insensitive” parameters: If the differential equations are solved numerically with an absolute error 𝒪(10^−χ) and sensitivities are computed using finite differences, then the error of the sensitivities are 𝒪(10^−χ/2) [54]. Parameters with sensitivities smaller than this bound should be included in the set of insensitive parameters. The insensitive parameters should not be included in further analysis, since these, can as discussed by Gutenkunst et al. give rise to ”sloppy” models [29,30].

When using the sensitivity analysis proposed here with a nonlinear model, one should be aware that the analysis is local, i.e., that results depend on the actual values of the parameters. Thus the better the initial estimates of the parameters, the more accurate the analysis. If the method is used for parameters with a high uncertainty, it may be beneficial to repeat the analysis for more samples, e.g., using a global sensitivity method as proposed in [38]. In addition, sensitivity analysis could be repeated using optimized parameter values. It should be kept in mind, that we use this analysis to identify insensitive parameters, thus it may in particular be of importance to investigate if insensitive parameters remain insensitive if the parameters are sampled at different values.

2.2 Subset selection

In addition to being insensitive parameters may be correlated, see [14,32,45,63] and references therein. As discussed by Miao et al. [45], two classes of methods can be used to reveal parameter correlations: Structural identification, which is used directly on the model (without data) to analyze if the model parameters can be identified given the system of equations, i.e., given information about all states defined by the model; and practical identification, which aims at predicting a subset of parameters that can be identified given the model and available data. Structural identifiability is a necessary condition for practical identifiability, though typically, as we do here, the model is assumed to be structural identifiable. Thus the aim is to devise practical identifiability methods. The importance of practical identifiability, stems from the fact that for many ”real” models, only some data is available. Thus even if the model is structurally identifiable, it may only be possible to estimate a small subset of model parameters, and it may be of biological importance to determine what parameters can be included in this subset.

In this study, we identify and estimate a subset of uncorrelated parameters in given a model that predicts heart rate regulation during head-up tilt. This model uses measured blood pressure data as an input to predict heart rate dynamics. The model is formulated using a system of 5 differential equations (described later) related using a number of model parameters. So the objective is to predict how many model parameters that can be estimated given the model output (heart rate).

We compare three methods that can easily be applied to practical problems: The first method is based on structured analysis of correlations computed from the covariance matrix (this method is similar to the one described in section 4.2 in the review by Miao et al. [45]); the second method (discussed in [53]) uses singular value decomposition of the sensitivity matrix S followed by QR factorization; and the third method is based on minimizing distances between parameter subspaces and subspaces spanned by eigenvectors for the model Hessian (this method is a variant of the orthogonal method described in section 5.3 in [45]). Below we describe each of these methods in detail.

2.2.1 Structured correlation analysis

The structured correlation subset selection method is adapted from methods described by Daun et al. [14], Jacquez [32], and Miao et al. [45]. As a point of departure, this method uses the model Hessian [64] (a positive definite symmetric matrix sometimes denoted the Fisher information matrix [12]), which for problems with constant variance σ² can be defined as ℋ = σ⁻²S^T S.

The basic structure to be analyzed is the correlation matrix c, which can be computed from the model covariance matrix C = ℋ⁻¹ as

$$c_{i,j}=\frac{C_{i,j}}{\sqrt{C_{i,i}{C}_{j,j}}}.$$ (11)

Note, the matrix C only exists if det(ℋ) ≠ 0.

Analysis of the correlation matrix c reveals parameter sets that are pairwise correlated. In general, a parameter pair (i, j) is correlated, iff |c_i,j| > γ for γ → 1. However, no theoretical predictions exist to define an actual value for γ. In the analysis conducted here we have investigated results for γ ∈ [0.85,0.95].

In addition to providing information about pairwise correlations, the covariance matrix C can be used for computation of the standard error [12], defined by

$$s_k=\sqrt{C_{k,k}},k=1,\dots ,q$$

and the confidence interval, which at the 100(1 − α)% level, can be computed as

$${\Theta }_{\text{conf},k}=[{\theta }_k-t_{1-\alpha /2}{s}_k;{\theta }_k+t_{1-\alpha /2}{s}_k],k=1,\dots ,q,$$

where α ∈ [0, 1] and t_1−α/2 ∈ R₊. Given a small α value (e.g., α = 0.05 for 95% confidence intervals), the critical value t_1−α/2 is computed from the student’s t-distribution t_{K−q, α} with K − q degrees of freedom. The value of t_1−α/2 is determined by the probability P{T ≥ t_1−α/2} = α/2, where T ~ t_K−q. For problems where K is large (K ≫ 40), the degree of freedom may be approximated by ∞, and the critical value t_1−α/2 ≈ 1.96. A confidence interval can be constructed for each possible realization of data of size K that could have been collected, 100(1 − α)% of these intervals would contain the true parameter value θ_k. Thus, confidence intervals provide further information on the extent of uncertainty involved in estimating θ using the given estimator and sample size K. However, it should be noted that the confidence intervals are statistically optimistic due to the use of a linear approximation of the non-linear model in the neighborhood of the best parameter estimates [15,61]. Similarly, the standard error can be used to test if model parameters are significantly different from zero. This can be done by testing if

$$\left|\frac{{\theta }_i}{s_k}\right|>t_{K-q,\alpha },i=1,\dots ,q.$$

A number of subsets can be generated from analysis of the correlation matrix. In this study we used a structured approach to identify correlated parameters. Results from this analysis is a tree that maps parameter correlations. At the root of the tree correlations found among the original set of parameters are listed, at each subsequent generation one (correlated) parameter is eliminated from the original set of parameters. This parameter will be considered a constant that is kept fixed at its a priori value. The specific structure of the tree depends on the problem, the set of parameters, and the value γ used for identifying if a given set of parameters are correlated.

Branching continues until there are no more correlated parameters in the parameter set. We have chosen to sort correlated parameters from the least to the most sensitive, consequently the left-most vertex in the tree contains the maximal sensitive uncorrelated parameters (i.e., the least sensitive of the correlated parameters have been eliminated), while the right-most vertex has eliminated the most sensitive parameters. An example of such a tree is illustrated in Fig. 5 for the heart rate model analyzed here. The process of generating the tree is outlined in the following algorithm:

Fig. 5.

Subsets computed using the structured correlation method. Parameters noted in the tree are those appearing in pairwise correlations. Brackets below the tree show the actual parameters in each subset.

Structured covariance analysis

1. Compute c using (11) and identify all correlated parameters, e.g., identify parameter pairs for which |c_i,j| > γ.

2. Calculate S̅_k, k = 1,…,q using (10) and sort parameters according to their sensitivity. List all parameters ordered from the least to the most sensitive at the next available level and position in the tree. The first set of correlated parameters is placed at the root of the tree.

3. Remove the least sensitive correlated parameter from θ and recompute c_i,j with the reduced parameter set (this set can easily be created by deleting the corresponding column of S, see (8)). The parameter removed from θ should be kept fixed at its a priori value.

4. Continue from 1 until |c_i,j| < γ for all i, j.

5. When no more correlations are present, record the subset, go back one level in the tree, if there are more parameters to analyze, choose the next parameter and continue from 1 along this sub-branch.

With this method a correlation tree is formed. Rather than showing a general tree we refer to the tree shown in Fig. 5, generated using the heart rate model discussed in section 3.

2.2.2 Singular value decomposition followed by QR factorization

Subset selection via singular value decomposition followed by QR factorization (SVD-QR) follows ideas put forward by Golub and van Loan [24,23], and have been used in various applications, see Velez-Reyes [67], Burth et al. [10], and Pope et al. [53,54]. The last three studies used the method in models predicting blood pressure and flow. Ideas used here are also related to the eigenvalue method described in section 5.4 of the paper by Miao et al. [45].

The SVD-QR method is based on analysis of singular values obtained by decomposing the sensitivity matrix S. S can be decomposed as S =UΣV^T, whereU and V are the left and right singular vectors, while Σ is a matrix of singular values. The singular values (extracted from Σ) are used to identify the number of parameters ρthat can be included in the subset. This is done by computing a numerical rank of the singular value matrix Σ. Subsequently, QR decomposition with column pivoting after the maximal element is used to determine which ρ parameters that can be identified. Similar to the sensitivity analysis, the numerical rank ρ can be found by analyzing computational accuracy of the singular values. The SVD-QR subset selection method can be summarized in the following algorithm:

Subset selection using SVD-QR

1. Given a set of parameters θ, compute the sensitivity matrix S using (8) and use singular value decomposition to rewrite as S = UΣV^T, where Σ is a diagonal matrix containing the singular values of S in decreasing order, andU and V are orthogonal matrices with left and right singular vectors.

2. Determine ρ, the rank of the sensitivity matrix S.

3. Partition the matrix V of eigenvectors on the form V = [V_ρV_q−ρ].

4. Determine a permutation matrix P by constructing a QR decomposition with column pivoting after the maximal element for $V_{\rho }^T$, see [23]. That is, determine P such that $V_{\rho }^{T}P=\mathit{\text{QR}}$, where Q is an orthogonal matrix and the first ρ columns of R form an upper triangular matrix with diagonal elements in decreasing order.

5. Use P to re-order the parameter vector θ according to θ̂ = P^Tθ.

6. Make the partition θ̂ = [θ̂ρ θ̂_q−ρ]. The subset of identifiable parameters θ̂_ρ, the first ρ elements of θ̂.

2.2.3 Subspace selection

The subspace selection method is based on an analysis similar to the SVD-QR method. However, instead of using singular values to identify the number of identifiable parameters, this method is based on predicting eigenvalues of the model Hessian ℋ = S^T S, which can be decomposed as ℋ = WΛW^T, where Λ is a diagonal q × q matrix with the eigenvalues in the diagonal and the columns of W contain the associated eigenvectors. Similar to the SVD-QR method we partition the sorted eigenvalues (from lowest to highest) and associated eigenvectors into two groups: eigenvalues {λ₁,…,λ_ρ} and {λ_ρ+1,…,λ_q}, and the corresponding eigenvectors {w₁,…,w_ρ} and {w_ρ+1,…,w_q}. These two groups are associated with parameters that can be identified (the first group) and those that cannot. We denote the subspace spanned by the first ρ eigenvectors 𝒲_a = span{w₁,…,w_ρ}. The corresponding matrix, W_a = [w₁,…,w_ρ], comprises the identifiable subspace and its dimension ρ gives the number of identifiable parameters. Hence, W_a denotes the orthogonal projection matrix onto the subspace 𝒲_a.

The subspace, taken from the set of all subspaces of dimension ρ spanned by the canonical basis that is closest to 𝒲_a, comprises the subset of identifiable parameters. To predict this, we compute the subspaces spanned by ρ canonical basis vectors, ℰ = {span{e_i1,…, e_iρ} : 1 ≤ i₁ < … < i_ρ ≤ q}. The number of subspaces in ℰ can be found as $|ℰ|=\left(\begin{array}{c}\hfill q\hfill \\ \hfill \rho \hfill \end{array}\right)$.

Next, we define a metric on the set of all subspaces with dimension ρ. Let X and Y be arbitrary subspaces of R^q such that dim(X) = dim(Y) = ρ and let P_X and P_Y be the orthogonal projection onto X and Y, respectively. The distance between X and Y is defined as dist(X,Y) = ‖P_X − P_Y‖₂, where the norm is the operator two-norm on the space of linear operators, see [23]. Note, the distance dist defines a metric on the set of subspaces with the same dimension. If X = image(W_X) for some orthogonal projection matrix W_X and Y = image(W_Y) for some orthogonal projection matrix W_Y then $\mathit{\text{dist}}(X,Y)={\Vert W_X^T{W}_Y^{\perp }\Vert }_2={\Vert W_Y^T{W}_X^{\perp }\Vert }_2,\text{ where }{W}_X^{\perp }$ is an orthogonal projection matrix onto X⊥ and $W_Y^{\perp }$ is an orthogonal projection matrix onto Y⊥.

The subset of identifiable parameters is then the subspace spanned by the canonical basis vectors which is closest to 𝒲_a. This subspace can be found by minimizing dist(𝒲_a,E_(i)ρ), where E_(i)ρ ∈ ℰ. Here the subscript (i)_ρ represent an ordered ρ-dimensional multi-index (i)_ρ = (i₁,…, i_ρ) with 1 ≤ i₁ < … < i_ρ ≤ q. The minimization may be done through inspection of $|ℰ|=\left(\begin{array}{c}\hfill q\hfill \\ \hfill \rho \hfill \end{array}\right)$ possibilities.

In summary, the subspace selection algorithm can be written as:

Subspace selection

1. Given a set of parameters θ, compute the sensitivity matrix S using (8) and the model Hessian ℋ = S^T S. Then, eigenvalue decomposition is used to write ℋ =WΛW^T.

2. Determine ρ, the numerical rank of the eigenvalue matrix Λ.

3. Partition the matrix of eigenvectors inW = [W_ρW_q−ρ].

4. Calculate the 𝒲_a = span{W₁,…,W_ρ}.

5. Collect all subspaces spanned by the canonical basis vectors E_(i)ρ = span{e₁,…, e_ρ} of dimension ρ.

6. Predict the distances $\mathit{\text{dist}}={\Vert (W_a^T)E_{(i)\rho }\Vert }_2$.

7. Find the smallest distance d = min(dist) over all E_(i)ρ and find parameters associated with the eigenvectors spanning the subspace minimizing dist.

2.2.4 Concluding remarks

When estimating a subset of model parameters a question arise what to do with the remaining parameters not included in the subset. We have chosen to keep both insensitive parameters (not impacting the model outcome) and correlated parameters fixed at their a priori values. While this approach may not impact the predicted system dynamics, keeping these parameters fixed reduces the order of the model and bias values obtained for the remaining estimated parameters [9,57]. Estimating more parameters will decrease the bias, but if too many parameters are estimated the variance will increase, and as discussed in the studies by Thompson et al. [63] and Wu et al. [70], the goal is to balance the bias and the variance allowing estimation with a small prediction error.

Two steps were taken to minimize the bias: one involves investigation of the a priori knowledge for a given parameter. If two parameters are correlated, and an initial value can be estimated with high fidelity (from data) for one of these, then it may be reasonable to keep this parameter at its a priory value while estimating the more uncertain parameter. If two sensitive parameters are correlated, that are both uncertain, the bias can be reduced by fixing the parameter that is less sensitive. Alternatively, these two parameters could be estimated using a Monte-Carlo based approach.

Moreover, it is essential to develop a strategy for analysis of parameters over multiple datasets. The objective could either be to estimate the best set of parameters that minimize the least squares error over all data, or to estimate a parameter subset for each dataset. If the objective is to use statistical analysis to understand how parameters change within or between datasets, it is essential that the same parameters are estimated for all datasets. As discussed in the study by Pope et al. [53], a common subset can be obtained by including parameters appearing with the highest frequency.

Finally, the methods may be combined, to do so we propose to first use either the SVD-QR or the subspace method to estimate a subset of parameters. If the subset contains correlated parameters then the least sensitive among them may be kept fixed at its a priori value, i.e., the original parameter set will be reduced. Subsequently, the SVD-QR or subspace methods should be repeated on the reduced parameter set. These steps should be continued iteratively until no more correlations can be detected.

2.3 Parameter estimation

All three methods described above, lead to identification of a subset of parameters that can be estimated given the model and available data. We used a trust-region variant of the gradient-based Gauss-Newton optimization method to estimate parameters that minimize the least squares error J defined in (6). Gauss-Newton is an iterative method [33] that at each iteration uses a solution based on a local linear approximation to compute the next iterate. When a subset of uncorrelated parameters is identified. Convergence can be predicted theoretically [35], even if the initial parameter estimates are far from the solution, and for parameters near the solution, theory predicts that fast convergence. In general, this method provides more accurate estimates if parameters are of the same order of magnitude. One way to ensure this is to scale parameters, e.g., using logarithmic scaling. Thus, instead of estimating θ one could estimate θ̃ = log(θ). This approach is used for the example discussed below. Finally, it should be noted, that if gradients cannot be computed from the model one could use the Nelder-Mead simplex method, implicit filtering, or genetic algorithms to estimate the model parameters. Discussion of advantages/disadvantages of these methods can be found in books by Kelley [33,34].

3 Example: Heart rate regulation

Heart rate is one of the most important quantities controlled by the body to maintain homeostasis. The control of heart rate is mainly achieved by the autonomic nervous system involving a number of subsystems that operate on several time and length scales. One of the major contributors to autonomic regulation of heart rate is the baroreflex system, which operates on a fairly fast time-scale (seconds). Baroreflex control consists of three parts: an affecter part, a control center, and an effector part, see Fig. 1. The afferent baroreceptor neurons respond to changes in stretch of the arterial wall modulated through changes in arterial pressure. The afferent neurons terminate in the nucleus solitary tract (NTS) within the medulla. Sympathetic and parasympathetic outflows are generated in NTS, parasympathetic outflow travel along the vagal nerve, whereas sympathetic outflow travel via a vast network of interconnected neurons. The main neurotransmitters involved with modulating heart rate are acetylcholine, which is released by the vagal nerves and noradrenaline released from the postganglionic sympathetic nerves.

Fig. 1.

Afferent baroreceptor nerves in the carotid sinus and the aorta are stimulated in response to changes in stretch of the arterial wall, and consequently by changes in arterial pressure. Afferent signals are integrated in the NTS, where sympathetic and parasympathetic efferent signals are generated. These travel to the heart (among other organs), where heart rate is either stimulating or inhibited.

Clinically, baroreflex regulation of heart rate is assessed by imposing postural challenges such as head-up tilt or sit-to-stand. In this study we adapt a model (outlined in Fig. 2) developed in previous studies [47,48,50] to study heart rate dynamics during head-up tilt. The objective is to use the three methods discussed above to identify and estimate a subset of model parameters given our model, input blood pressure data, and a set of simulated outflow data. Simulated data are used to ensure that the parameter estimation method converge with a least squares error that is close to zero.

Fig. 2.

Model components. Mean blood pressure, age and resting heart rate is used as an input to the model. The model consists of 5 components: a module predicting averaged arterial blood pressure, a module predicting the baroreflex firing rate, modules predicting sympathetic and parasympathetic outflow, and a heart rate module. Dependencies between modules are marked by arrows.

For this study we assume that changes in arterial wall stretch is proportional to the change in the filtered blood pressure (p̅) computed as

$$\mathrm{p̅}=\alpha {\displaystyle {\int }_{-\mathrm{\infty }}^t}p(s)e^{-\alpha (t-s)}\mathit{\text{ds}}\iff \frac{d\mathrm{p̅}}{\mathit{\text{dt}}}=\alpha (-\mathrm{p̅}+p),$$ (12)

where p is obtained from pressure data. Using the averaged blood pressure we predict the afferent firing rate n as

$$n={\displaystyle \sum _i}{n}_i+N,i=1,2,$$

where N denotes a baseline firing rate and n_i denote the firing rates related to fiber of type i, which is computed as

$$\frac{{\mathit{\text{dn}}}_i}{\mathit{\text{dt}}}={\kappa }_i\frac{d\mathrm{p̅}}{\mathit{\text{dt}}}\frac{n(M-n)}{{(M/2)}^2}-\frac{n_i}{{\tau }_i},i=1,2.$$ (13)

Here M denotes the maximum firing rate, κ_i the gain, dp̅/dt denotes the time derivative of the average pressure and τ_i, i = 1,2 are time scales [49,50].

The afferent firing rate n is integrated in the NTS, where sympathetic f_sym and parasympathetic f_par outflows are generated. To account for complexity of the sympathetic pathway, we predict the sympathetic outflow as a function of n(t − τ_d), where τ_d is a constant time delay. The delay along the parasympathetic pathway is negligible, and consequently the parasympathetic outflow is modeled directly as a function of n. The resulting equations predicting sympathetic and parasympathetic outflow are given by [49,50]

$$f_{\mathit{\text{par}}}=\frac{n}{M},f_{\mathit{\text{sym}}}=\frac{1-n(t-{\tau }_d)/M}{1+\beta f_{\mathit{\text{par}}}}.$$

The next step involves prediction of the concentration of neurotransmitters acetylcholine C_ach and noradrenaline C_nor, which can be obtained from

$$\frac{{\mathit{\text{dC}}}_{\mathit{\text{nor}}}}{\mathit{\text{dt}}}=\frac{f_{\mathit{\text{sym}}}-C_{\mathit{\text{nor}}}}{{\tau }_{\mathit{\text{nor}}}},$$ (14)

$$\frac{{\mathit{\text{dC}}}_{\mathit{\text{ach}}}}{\mathit{\text{dt}}}=\frac{f_{\mathit{\text{par}}}-C_{\mathit{\text{ach}}}}{{\tau }_{\mathit{\text{ach}}}},$$ (15)

where τ_nor and τ_ach are time scales, [49,50]. Finally, we computed heart rate as

$$h=h_0(1+m_{\mathit{\text{nor}}}{C}_{\mathit{\text{nor}}}-m_{\mathit{\text{ach}}}{C}_{\mathit{\text{ach}}}),$$ (16)

where h₀ denotes the intrinsic heart rate and m_nor and m_ach are factors attenuating/accentuating impact of neurotransmitters on the heart rate.

In terms of the general theory outlined in section 2, n = 5 corresponding to the five model states x = (p̅,n₁,n₂,C_ach,C_nor), m = 1 corresponds to the computed output (heart rate) y = h, and y = (y₁(t₁), y₁(t₂),…, y₁(t_K))^T. The model has 14 parameters (q = 14) given by

$$\theta ={(\alpha ,N,M,{\kappa }_1,{\kappa }_2,{\tau }_1,{\tau }_2,{\tau }_{\mathit{\text{ach}}},{\tau }_{\mathit{\text{nor}}},\beta ,h_0,m_{\mathit{\text{nor}}},m_{\mathit{\text{ach}}},{\tau }_d)}^T.$$ (17)

It should be noted that this model is idealized through a system of delay differential equations, whereas the method presented earlier is formulated for a system of ordinary differential equations. This system of equations has been solved with Radar5 a fortran library developed by Guglielmi and Hairer [27], using parameters and initial conditions described below.

Initial conditions The initial condition for the mean pressure p̅(0) defined in (12) is set to the mean pressure during rest obtained from data. For the firing rates defined by (13), we assume that n₁(0) and n₂(0) are zero initially, i.e., the total firing rate n(0)= N, we also assume that this firing rate is obtained τ_d time-steps back, i.e., we assume n_i(t) = 0, for i = 1,2 and −τ_d ≤ t ≤ 0. Consequently,

$$f_{\mathit{\text{par}}}(0)=N/M\text{ and }{f}_{\mathit{\text{sym}}}(t)=\frac{1-N/M}{1+\beta N/M},-{\tau }_d\le t\le 0.$$

On average, the concentrations of noradrenaline C_nor and C_ach defined in (14–15) are not changing initially implying that C_ach(0) = f_par(0) and C_nor(0) = f_sym(0). Finally, we assume that the firing rate at rest h(0) used to predict the heart rate h defined in (16) can be obtained from data.

Model parameters Model parameters given in Table 1 are obtained partly from literature and partly using patient specific calculations. We assume that the maximum heart rate (beats/min), h_M = 217 − 0.85 · age, is obtained when n = M, i.e., for f_par = 1 and f_sym = 0. Hence,

$$h_M=h_0(1-m_{\mathit{\text{ach}}})\iff m_{\mathit{\text{ach}}}=\frac{h_M-h_0}{h_0}.$$

Table 1.

Nominal and estimated model parameters. The top row shows all 14 parameters listed along with their unit, parameters marked n.d. are non-dimensional. The second row shows initial parameter values, the third row shows parameters (marked in bold) estimated using simulated data, while the bottom row shows parameter estimations obtained using real data. Parameters estimated include: θ = {N, κ₁, τ₁, τ₂, τ_ach, τ_nor, h₀, m_nor, m_ach}.

α	N	M	κ1	κ2	τ1	τ2	τach	τnor	β	h0	mnor	mach	τd
Hz	Hz	Hz	mmHg−1	mmHg−1	sec	sec	sec	sec	n.d.	beats/sec	n.d.	n.d.	sec
1.5	75	120	1.5	1.5	0.5	250	0.5	0.5	6	1.67	0.96	0.7 0	7
1.5	74.9	120	1.504	1.5	0.511	248	0.509	0.507	6	1.67	0.959	0.699	7
1.5	115	120	0.945	1.5	0.896	229	0.634	0.558	6	2.17	0.963	0.555	7

Similarly the minimum heart rate h_m is obtained when N = 0, i.e., f_par = 0 and f_sym = 1. Consequently,

$$h_m=h_0(1+m_{\mathit{\text{nor}}})\iff m_{\mathit{\text{nor}}}=\frac{h_m-h_0}{h_0}.$$

The parameter N is obtained such that at rest, the heart rate h defined in (16) equals that found at t = 0. Using the above definitions for m_nor and m_ach we get

$$h\equiv h(0)=h_0(1+m_{\mathit{\text{nor}}}\frac{1-N/M}{1+\beta N/M}-m_{\mathit{\text{ach}}}\frac{N}{M}),$$

$$N=M\frac{-b+\sqrt{b^2-4\mathit{\text{ac}}}}{2a},\text{ where}$$

$$a=\beta m_{\mathit{\text{ach}}},$$

$$b=\frac{\beta (h-h_0)}{h_0}+m_{\mathit{\text{nor}}}+m_{\mathit{\text{ach}}},$$

$$c=\frac{h-h_0}{h_0}-m_{\mathit{\text{nor}}}.$$

3.1 Experimental and simulated data

To compare the three subset selection methods we used simultaneous measurements of heart rate and blood pressure data obtained by Dr. Mehlsen, Frederiksberg Hospital, Denmark. Data are sampled at 100 Hz during head-up tilt in a healthy young subject. Heart rate values are derived from a standard 3-lead ECG, while blood pressure measurements are obtained with a Finapres devise.

Blood pressure is measured in a finger at the level of the carotid arteries. During supine position, baroreceptors are at the level of the heart. Thus, the blood pressure measured in the finger can be used directly as a stimulus for the baroreceptors. As the subject is tilted carotid sinus baroreceptors are lifted above the heart, while aortic baroreceptors remain at the level of the heart. This differentiation generates a hydrostatic pressure differential exposing carotid baroreceptors to a larger drop in blood pressure than the aortic baroreceptors, much discussion on the relative role of these receptors can be found in the literature. In humans it is believed that the carotid baroreceptors play a more prominent role in short term blood pressure regulation, see e.g., [19,20]. Fig. 3 shows carotid blood pressure and heart rate during head-up tilt, gravity imposes a drop in pressure at the level of the baroreceptors during head-up tilt. Heart rate increases in response to the drop in the observed blood pressure.

Fig. 3.

The figure shows blood pressure (blue), heart rate data (red), and simulated heart rate (cyan) as a function of time.

The model analyzed in this study does not integrate all mechanisms involved in heart rate regulation. In particular, our model does not incorporate stimulation from the muscle sympathetic system, the vestibular system, or from the mental system, neither do we include respiratory contributions to parasympathetic response, this part of the response gives rise to fast oscillations observed in the blood pressure data input to the model. These were included in previous studies [47–49] via introduction of an impulse input stimulating parasympathetic withdrawal. Another important factor, not modeled, is the hormonal regulation, which operates over longer time scales (min-hours).

The aim in this study is to develop methods that allow identification of a subset of parameters given a model and data. Due to the model deficiencies we first estimated model parameters using simulated data before employing the real data. Both simulated and measured heart rate data are shown in Fig. 3. We used the simulated data to compare the ability to estimate model parameters from each subset. Once, a ”best” subset was obtained we estimated parameters minimizing the least squares error between the model and the measured heart rate data.

3.2 Sensitivity analysis

In our simulations we computed the k × 14 sensitivity matrix S = ∂h/∂θ̃ calculated using (8), where h denotes the heart rate computed using (16), and θ̃ = log(θ) is the log-scaled parameters. For each cardiac cycle k, k = 1…479, S is evaluated at time t_k denoting the time when the heart beats.

The differential equations are solved numerically with an absolute and relative tolerance of tol = 10⁻⁸, thus the tolerance for the sensitivity matrix S is 𝒪(10⁻⁴) [33]. For each parameter θ̃_i, ranked sensitivities were computed using the operator two-norm S̅_i = ‖S_i‖₂, i = 1,…,q defined in (10). The ranked sensitivities were normalized with respect to the largest sensitivity. For the heart rate model studied here, all sensitivities are larger than the predicted error bound, i.e., S̅_i ≤ 10⁻³ for all i = 1,…,q.

3.3 Biological considerations

Sensitivity analysis is a tool used to asses if model parameters are identifiable given a model and a set of data. For this study all model parameters are sensitive, at least when measured against the error-bound. In addition, biological arguments may eliminate estimation of certain parameters. The heart rate model discussed here contain three parameters of this type:

• –The parameter α used to smooth the pressure data. A large value of α provides almost no smoothing, while a small α will smooth the pressure data. But using α ≪ 1 introduces a phase shift in p̅. To achieve some smoothing, but only a small phase shift we kept this parameter constant.
• –The maximum firing rate M. This parameter serves as a scale for the afferent firing rate; n always appears normalized in the equations as n/M. Thus, this parameter could be eliminated by rescaling the system equations. In this study, we work with the original equations, but keep this parameter constant.
• –The delay parameter τ_d. Calculating the heart rate sensitivity with respect to this parameter is difficult since it involves analysis of both the instantaneous and delayed states resulting in an infinite dimensional problem [4]. So, to use the theory for ordinary differential equations developed here we keep this parameter constant.

Keeping these three parameters fixed at their a priori values leaves an 11-dimensional parameter vector given by

$$\theta ={(N,{\kappa }_1,{\kappa }_2,{\tau }_1,{\tau }_2,{\tau }_{\mathit{\text{ach}}},{\tau }_{\mathit{\text{nor}}},\beta ,h_0,m_{\mathit{\text{nor}}},m_{\mathit{\text{ach}}})}^T.$$ (18)

3.4 Subset selection

We applied the three subset selection methods outlined in sections 2.2.1, 2.2.2, and 2.2.3 to the heart rate model. The reduced parameter set listed in (18) has 11 parameters (q = 11). While this is a reduction compared to the original 14 parameters it is still not feasible to estimate all 11 parameters. Results given in Table 2 shows that even though estimation of all 11 parameters gives a small least squares error, both the average and maximum error is large, i.e., it is not possible to retrieve accurate values for all 11 parameters.

Table 2.

Subsets obtained with the three methods. The first column lists parameters in the subset, the second shows the subset number. The 3’rd and 4’th columns list the value of the final gradient from the Levenberg-Marquart optimization method and the least squares error calculated using (6). The 5’th column lists the subspace distance, the 6’th column lists the mean and maximum error in percent and column 7 lists the parameter associated with the largest error. Column 8 lists correlated parameters in the subsets (NA denotes Not Applicable), and the final column shows the rank of the given subsets within each method. These are found by sorting the least squares errors from smallest to largest.

subset	subset #	grad ×10−5	l.s.e.	dist	error	parm	corr	rank
Correlation analysis
N κ1 τ1 τ2 τach τnor h0 mnor mach	1	8.98	3.31·10−8	1.15	1.36/3.39	mnor	NA	1
N κ1 τ1 τ2 τach τnor β h0 mach	2	2.46	6.63·10−8	1.20	1.64/4.65	τnor	NA	2
N κ1 κ2 τ1 τ2 τach τnor h0 mnor	3	5.37	1.07·10−7	1.18	3.69/14.63	mnor	NA	3
N κ1 κ2 τ1 τ2 τach τnor β h0	4	5.91	1.43·10−7	1.23	2.45/6.68	τnor	NA	6
N κ1 τ1 τ2 τach τnor mnor mach	5	9.49	1.26·10−7	1.42	3.38/9.12	mnor	NA	4
N κ1 τ1 τ2 τach τnor β mach	6	1.39	1.29·10−7	1.49	2.16/5.96	τnor	NA	5
κ1 κ2 τ1 τ2 τach τnor mach	7	8.77	1.13·10−6	1.69	4.02/8.27	τnor	NA	14
N κ1 κ2 τ1 τ2 τach τnor	8	7.64	1.67·10−7	1.64	2.17/8.15	τnor	NA	7
N κ1 κ2 τ1 τach τnor mnor	9	5.10	6.32·10−7	1.58	5.85/11.9	mnor	NA	10
N κ1 κ2 τ1 τach τnor β	10	8.25	7.68·10−7	1.64	3.77/9.93	τnor	NA	12
κ1 κ2 τ1 τach τnor mach	11	5.45	7.83·10−7	1.74	4.17/9.56	τnor	NA	15
κ1 κ2 τ1 τ2 τach τnor	12	4.46	2.89·10−7	1.91	1.74/7.15	τnor	NA	8
κ1 κ2 τ1 τach τnor mnor	13	6.15	8.41·10−7	1.81	7.61/19.3	mnor	NA	13
N κ1 κ2 τ1,τach τnor	14	5.14	7.61·10−7	1.69	3.80/9.63	τnor	NA	11
κ1 κ2 τ1 τach τnor β	15	4.14	4.96·10−7	1.87	5.39/9.73	τnor	NA	9
SVD-QR
N κ1 κ2 τ1 τ2 τach τnor β h0 mnor mach	S11	7.88	2.30·10−7	0	7.63/17.3	κ2	(κ2, β,mnor,mach)	1
N κ1 κ2 τ1 τach τnor h0 mnor mach	S9	8.76	8.89·10−7	0.927	5.63/16.9	mnor	(κ2,N,mach,h0)	3
N κ1 τ1 β h0 mnor mach	S7	6.80	6.73·10−7	1.31	3.44/9.3	mnor	(mnor,h0)	2
Subspace analysis
N κ1 κ2 τ1 τach τnor h0 mnor mach	S9	8.76	8.89·10−7	0.927	5.63/16.9	mnor	(κ2,N,mach,h0)	2
N κ1 κ2 τ1 h0 mnor mach	S7	2.37	5.46·10−8	1.25	3.49/12.9	mnor	(κ2,N,mach)	1

Quantities important for subset selection are the sensitivity matrix, which for the reduced problem is a matrix of dimension 479 × 11 (the data we use include 479 cardiac cycles, i.e., K = 479), and the model Hessian approximated by ℋ = S^T S, ℋ, a positive definite symmetric matrix of dimension 11 × 11. Subsets obtained with each of the three method are printed in column 1 of Table 2. In addition, the table lists the gradient, the least squares error, the subspace distance, the average and maximal error in percent, the parameter that had the largest error, possibly correlations, and the rank within each method.

It should be noted that the largest error either always was in either m_nor and τ_nor. As shown in Fig. 4, τ_nor is the least sensitive parameter, thus it is expected that this parameter is the hardest to predict. The fact that m_nor is difficult to predict may be related to relative sensitivities (9). According to this ranking (results not shown) m_nor is the 2nd least sensitive parameter.

3.4.1 Structured correlation subsets

The subsets obtained using the structured correlation method are shown in Fig. 5. Starting at the root of the tree, analysis of all 11 parameters reveal that parameters {κ₂, β ,m_nor,m_ach,h₀} appear in correlations. The correlations are all pairwise: κ₂ is correlated with m_ach; h₀ and m_nor are correlated with β; and m_ach is correlated with h₀. At each sub-branch the correlation matrix was recomputed eliminating (keeping it fixed at its a priori value) the least sensitive correlated parameter. For the first step, the least sensitive parameter κ₂ was eliminated from the correlation matrix. After removing this parameter, the correlation matrix was recomputed. The new correlation matrix revealed that the parameters β and m_nor are correlated. Subsequently, eliminating either of these parameters gave rise to a reduced matrix without pairwise correlations. The final subsets labeled by ”[1]” and ”[2]” are listed below the tree and in Table 2.

During the structured correlation analysis, some pairwise correlations will appear more than once. For each set of this type, the edge associated with the leftmost occurrence of the subset(s) have been marked with a given color. Subsequent occurrences of the same subset(s) are marked with ovals of the same color. Results shown here were computed using γ = 0.9, i.e., parameters were marked as correlated if |c_{i, j}| > 0.9. We investigated results for other values of γ as well. For γ = 0.95 the root would contain only one correlated parameter pair (κ₂,m_ach), the sub-branches stemming from these leaves would remain the same. For γ= 0.85, the root of the tree would remain the same, but some of the sub-branches would be longer. For either value of γ, the ”best” subset (subset 1) is included in the tree.

3.4.2 SVD-QR subsets

The SVD-QR method requires prediction of ρ, the number of elements to be included in the subset. We predicted ρ from analysis of computational accuracy. The model is solved using an absolute and relative error tolerance of order 𝒪(10⁻⁸). Since sensitivities are computed using finite differences, the sensitivity matrix is accurate to order 𝒪(10⁻⁴). Consequently, the smallest singular value (shown in Fig. 6) accepted is 10⁻³. The latter condition is equivalent to choosing columns of S that form a matrix with a condition number no greater than 10³. For our system, this bound allows inclusion of all 11 parameters in the subset. As shown in Table 2, estimating all 11 parameters gives rise to large errors and several parameters are correlated. While the model can predict the simulated data with this bound, the least squares error is small, the values of the parameters cannot be predicted well. Thus, we investigated the impact of increasing this bound to 5 ·10⁻³ and to 10⁻². The first bound allowed inclusion of 9 parameters, the latter 7. Table 2 shows results of estimating all 11, 9, and 7 parameters picked by the SVD-QR method. Estimating fewer parameters (9 and 7 vs. 11) only has a small impact on the least squares error (it is still of order 10⁻⁷), yet both subsets have smaller errors but some parameters still appear as correlated.

Fig. 6.

Singular values associated with the sensitivity matrix.

3.4.3 Subspace selection subsets

Similar to the SVD-QR subset selection method the subspace selection method requires selection of the number of parameters to be identified. This first step of the analysis is the same as the one used by the SVD-QR method, except that eigenvalues and not singular values are used for predicting ρ. Since analysis of eigenvalues is equivalent to analysis of the singular values we used the same number of parameters as in the SVD-QR method. Consequently, we calculated subspace distances using ρ = 7,9 and 11 parameters. The complete parameter set included 11 parameters, thus the subspace distance for this parameter set is 0. Results including all 11 parameter values is listed under the SVD-QR method. Parameter sets with ρ = 7 and ρ = 9 parameters are listed in Table 2. The total number of subspaces examined were computed as $\left(\begin{array}{c}\hfill 11\hfill \\ \hfill \rho \hfill \end{array}\right)$, where ρ denotes the number of parameters in the subspace. For ρ = 9 the total number of subspaces is 55, while for ρ = 7 the number of subspaces is 330. The subspace distances computed with ρ = 9 parameters are shown in Fig. 7. Note, there are gaps between the subspaces. Similar to results obtained with the SVD-QR method minimum distance subspaces all contain correlated parameters, also note that the subset with ρ = 9 parameters (the one with the smallest subspace distance) is the same subset we obtained with the SVD-QR method.

Fig. 7.

Subspace distance for subsets including 9 parameters. Note the gaps in the distances.

3.4.4 Combining methods

Since subsets obtained with the SVD-QR and subspace selection methods contain correlated parameters, we investigated if combining either of these methods with structured correlation analysis would lead to an optimal subset. The combined approach was applied to subsets with ρ = 9. As a point of departure we ordered correlated parameters (κ₂,N,m_ach,h₀) from the least to the most sensitive. We kept the least sensitive parameter κ₂ fixed at its a priori value and eliminated it from the original parameter vector. Then, we reapplied the SVD-QR or the subspace selection method on the 10-dimensional parameter vector

$$\theta ={(N,{\kappa }_1,{\tau }_1,{\tau }_2,{\tau }_{\mathit{\text{ach}}},{\tau }_{\mathit{\text{nor}}},\beta ,h_0,m_{\mathit{\text{nor}}},m_{\mathit{\text{ach}}})}^T.$$

The resulting subset was the same as the one found using the structured correlation analysis (subset 1).

3.5 Optimization of parameters

For the heart rate example discussed in this study, we used the Levenberg-Marquart method to estimate model parameters. During the optimization, parameters not in the subset were kept fixed at their a priori values listed in Table 1. For each subset, comparison of the model prediction was done using the simulated data. For these simulations, the optimization algorithm converges since the residual approaches zero at optimal parameter values. Initial values for the parameters to be estimated were obtained by scaling the initial parameter values randomly by a factor 0.9. For a more complete investigation, in particular, for problems that do not rely on simulated data, one should choose a number of initial parameter sets from random distributions and then run simulations with each method for each parameter set.

For each set of optimized model parameters we calculated the value of the gradient, the least squares error, the subspace distance, and the mean and maximum percent deviation of the optimized parameters from the true parameters, listed the parameter that was predicted with the largest error. These results are reported in Table 2.

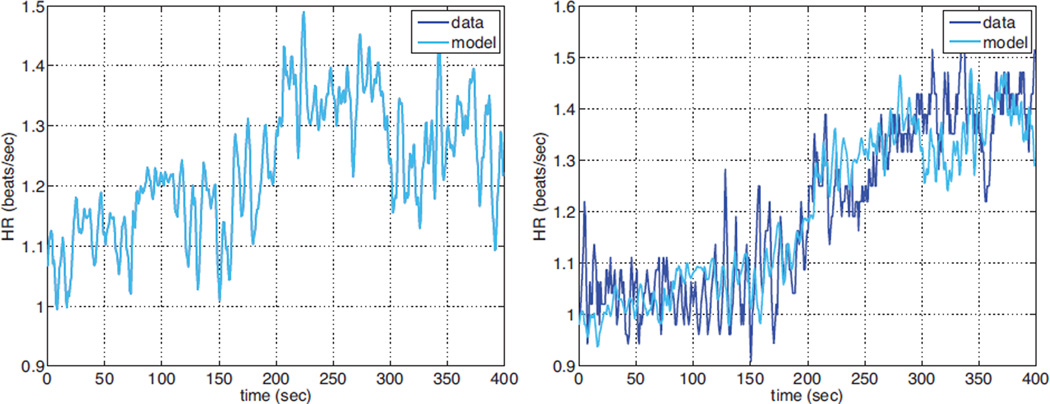
Finally Fig. 8 shows heart rate prediction using the ”best” parameter subset (subset 1). Results are shown both against the simulated and the real data. Initial and optimized parameter values are given in Table 1.

Fig. 8.

Left panel shows simulated data and model result (an almost perfect match) and the right panel shows model results compared to the real data, both results are obtained with subset 1 identified using the structured correlation method.

4 Discussion

This study has used three methods for identifying subsets of parameters that can be predicted given a model, a set of parameters, and a set of experimental data. The methods are denoted ’the structured correlation method’, ’the SVD-QR method’, and ’the subspace selection method’. We compared the three methods and showed that the ”best” subset, i.e., the subset with the smallest least squares error is found using the structured correlation method. This subset is placed the furthest to the left in the tree. We also compared optimization results among all three methods. Results showed that subsets found using the structured correlation analysis method gave more robust optimization results, the predicted parameters had a smaller error. We base this on results where optimizations were done using 10 random variations of the initial parameter values. We believe that these subsets provide more reliable parameter estimates since they contain no correlated parameters. It should be noted that the ”best” subset found with the correlation analysis method does not necessarily give rise to a minimum distance as defined by the subspace method. Furthermore, the ”best” subset, remains even if the parameter γ is varied from 0.85 to 0.95. Results obtained using either subspace analysis or the SVD-QR method did not differ significantly. An advantage of these methods is that they are computationally faster than the structured correlation method. The biggest computational effort is the parameter estimation, and for these methods it is only done once for the subset in question, whereas for the structured correlation analysis an optimization is performed for each potential subset. However, the subsets found using the SVD-QR and the sub-space selection methods contained correlated parameters. The latter gave rise to larger errors in the predicted parameter estimates.

As a consequence, we investigated the impact of combining methods. This was done by keeping the least sensitive correlated parameter (κ₂), appearing in the 9-parameter subset, fixed at its a priori value and then re-applying the SVD-QR or the subspace selection method on the 10 remaining parameters. This combination of methods resulted in subset ”1”, the ”best” subset found using the structured correlation method.

While it is evident that sensitivity analysis is important, it is less clear how to distinguish sensitive from insensitive parameters. In this study, we included all parameters in the set of sensitive parameters. Though similar to the subset selection, enforcing a less strict bound on ρ, may be advantageous, i.e., parameters predicted may have a smaller error. For example, increasing the bound from 10⁻³ to 10⁻² corresponds to marking τ_nor as insensitive. Note, this was the parameter that contained the largest error.

One potential problem with the structured correlation method is that it is computational intensive. For each subset, the method requires an optimization step for each potential subset. Consequently, for bigger models it may be better to use one of the other two methods e.g. combined with correlation analysis as discussed above. Another disadvantage is that no theoretical results exist to predict the level at which two parameters are correlated. In this study we denoted parameters where |c| > γ for γ → 1 as correlated. In this study results were shown for γ = 0.9, this is a somewhat arbitrary choice. Though it should be noted, that the ”best” subset would remain the same for γ∈ [0.85,0.95]. Moreover, this method only reveals pairwise correlations. Another option would be to develop a method based on partial correlations, which may have potential to offer more insight into the system, for more details see [45] and references therein.

While the SVD-QR method and the subspace selection method are fast and easy to implement (only one optimization is required), they also have some potential problems. Both methods require computation of a numerical rank ρ, which for most problems only can be estimated but not predicted theoretically. In the analysis presented here we computed the rank based on the numerical accuracy, though this bound was too low, since our computations resulted in a subset including all model parameters. A further disadvantage of the SVD-QR method is that from a parameter estimation point of view, no theoretical results support column pivoting after the maximal elements as is commonly done by most QR factorization algorithms. The latter disadvantage does not exist with the subspace selection method, in which the parameter combinations are directly found from the eigenvector associated with the smallest subspace distance. One way to remedy the problems discussed above, is to combine the methods as discussed earlier.

Finally, in addition to identify a subset, parameters should be estimated. In this study parameters were estimated, both using simulated and real data. Simulated data were used to identify a subset of parameters that can be estimated given the model output, then these parameters were estimated using the real heart rate data. When computations are done with real data, the true parameter values are not known. Consequently, the initial set of parameter values, used for the identifiability analysis, provides one estimate. But, since the models are nonlinear, results may not reveal that the chosen subset of parameters only are identifiable within a given parameter space. If this parameter space is too small, for practical method it may be necessary to use a global analysis for better results. Again, the problem with this approach is that for practical applications the computations may be excessive, and therefore difficult to cary out in practice.

In summary, we conclude that it is essential to identify a subset of parameters that can be estimated reliably given a model and a set of data, and that simulated data can be used to predict what method is the most appropriate for finding the ideal subsets. Results with the example analyzed in this study, showed that structured correlation or a combination of SVD-QR or subspace selection with correlation analysis allows prediction of a parameter subset that can be estimated given data. These subset selection methods, should be preceded or combined with a sensitivity analysis, which has potential to provide further insight into the parameter dynamics. We recommend that both the sensitivity and identifiability analysis is repeated for a number of initial parameter values, in particular for highly nonlinear models. Finally, this analysis should be combined with knowledge about the model, which often is essential for a priori reduction of the parameter set.