Electrostatic Rate Enhancement and Transient Complex of Protein-Protein Association

Abstract

The association of two proteins is bounded by the rate at which they, via diffusion, find each other while in appropriate relative orientations. Orientational constraints restrict this rate to ~10⁵ – 10⁶ M⁻¹s⁻¹. Proteins with higher association rates generally have complementary electrostatic surfaces; proteins with lower association rates generally are slowed down by conformational changes upon complex formation. Previous studies (Zhou, Biophys. J. 1997;73:2441–2445) have shown that electrostatic enhancement of the diffusion-limited association rate can be accurately modeled by k_D = k_D0 exp(−<U_el>*/ k_BT), where k_D and k_D0 are the rates in the presence and absence of electrostatic interactions, respectively, <U_el>* is the average electrostatic interaction energy in a “transient-complex” ensemble, and k_BT is thermal energy. The transient-complex ensemble separates the bound state from the unbound state. Predictions of the transient-complex theory on four protein complexes were found to agree well with experiment when the electrostatic interaction energy was calculated with the linearized Poisson-Boltzmann (PB) equation (Alsallaq and Zhou, Structure 2007, 15:215–224). Here we show that the agreement is further improved when the nonlinear PB equation is used. These predictions are obtained with the dielectric boundary defined as the protein van der Waals surface. When the dielectric boundary is instead specified as the molecular surface, electrostatic interactions in the transient complex become repulsive and are thus predicted to retard association. Together these results demonstrate that the transient-complex theory is predictive of electrostatic rate enhancement and can help parameterize PB calculations.

INTRODUCTION

The association of two proteins is bounded by the rate at which they find each other through diffusion. To form a stereospecific complex, the two molecules must have appropriate relative orientations when they come together. The orientational constraints severely restrict the diffusion-limited rate, which is estimated at 10⁵ – 10⁶ M⁻¹s⁻¹ according to several theoretical models.^1–3 In particular, antibody-protein association rates are typically observed in this range.^4–6 However, in a wide array of biological processes, rapid association between proteins is crucial; in these cases rates much higher than 10⁶ M⁻¹s⁻¹ have been observed. These include binding of cytotoxic nucleases with inhibitors (for self protection of the host cell),^7,8 binding of toxins to a potassium channel⁹ and acetylcholinesterase¹⁰ (for inhibition of neural transmission in the prey), and binding between many partners along the signaling pathway leading to the stimulation of actin polymerization.^11,12 In these cases the binding surfaces across the interface are usually found to have opposite electrostatic potentials (see Fig. 1), implicating electrostatic rate enhancement. Building on earlier work,^2,13–17 we have now fully developed a theory for predicting diffusion-limited association rates under the influence of electrostatic interactions.¹⁸ The theory has been found to be very promising when tested on four protein complexes and 23 mutants over wide ranges of ionic strength.¹⁹ Here we further apply this theory to examine electrostatic contributions to association rates.

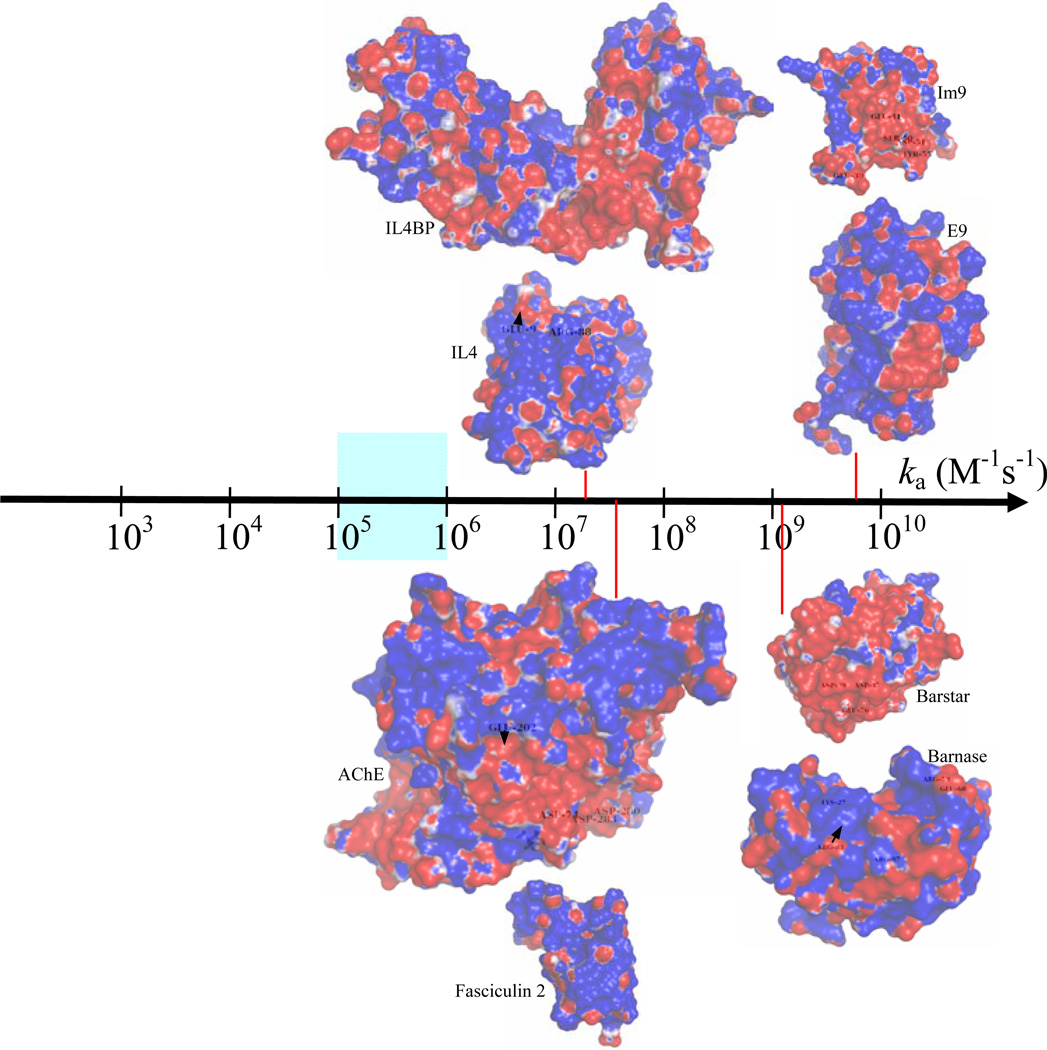
Fig. 1.

The wide spectrum of protein-protein association rates. The value 10⁵ M⁻¹s⁻¹ serves as the demarcation point separating the diffusion-limited regime from the conformational change-limited regime. In the diffusion-limited regime, rates in the narrow range of 10⁵ – 10⁶ M⁻¹s⁻¹ are observed for association between proteins, such as antibody and antigen, which do not involve significant electrostatic contributions. Proteins that associate with higher rates typically have complementary electrostatic surfaces, as illustrated by the four protein complexes studied here. The association rates indicated for the E9:Im9, Bn:Bs, AChE:Fas, and IL4:IL4BP complexes are experimental results measured at ionic strengths of 25, 13, 50 and, 150 mM, respectively.^7,8,10,43 Electrostatic potential surfaces are generated by the APBS program⁶⁸ and displayed by PyMOL (http://www.pymol.org).

The first theoretical result for the association rate was obtained by Smoluchowski,²⁰ who found that the diffusion-limited rate for two uniformly reacting spheres to form a complex is k_D0 = 4πDR, where D is the relative translational diffusion constant and R is the contact distance between the two sphere centers. Debye recognized that the association rate between oppositely charged molecules can be increased by electrostatic interactions; for two uniformly reacting spheres with a centrosymmetric interaction potential U(r), he found the diffusion-limited rate to be $k_{\mathrm{D}}=4\pi D/{\displaystyle {\int }_R^{\mathrm{\infty }}}{e}^{U(r)/k_{\mathrm{B}}T}{r}^2\mathit{\text{dr}}$, where r is the inter-sphere distance and k_BT is thermal energy.²¹ Throughout this paper we will use k_D0 to denote the diffusion-limited rate in the absence of an interaction potential (also referred to as the basal rate), and use k_D to denote the counterpart in the presence of an interaction potential.

The stereospecific association of two proteins involves significant orientational constraints, thus the formulas of Smoluchowski and Debye are of little use. Solc and Stockmayer tackled the problem of orientational constraints through a quasi-chemical approximation.²² For two spheres each with a reactive patch, they found the diffusion-limited rate to be

$$k_{\mathrm{D}0}=\frac{4\pi {\mathit{\text{DRF}}}_1{F}_2}{{\mathrm{\Lambda }}_1{\mathrm{\Lambda }}_2+{[{(1-{\mathrm{\Lambda }}_1)}^{-1}{(1-{\mathrm{\Lambda }}_2)}^{-1}+{(1-{\mathrm{\Lambda }}_1)}^{-1}{({\mathrm{\Lambda }}_2-F_2)}^{-1}+{(1-{\mathrm{\Lambda }}_2)}^{-1}{({\mathrm{\Lambda }}_1-F_1)}^{-1}]}^{-1}}$$ (1)

where F₁ and F₂ are the surface fractions covered by the reactive patches. An approximate expression, obtained by Berg,²³ for Λ_i (i = 1 or 2), in the case of a patch spanning polar angles between 0 and δ_i, is given by

$${\mathrm{\Lambda }}_i/F_i=\frac{{\xi }_i+\text{cot}({\delta }_i/2)}{{\xi }_i+\text{sin}({\delta }_i/2)\text{cos}({\delta }_i/2)}$$ (2)

where ξ_i = [(1 + D_iR²/D)/2]^1/2 and D_i is the rotational diffusion constant. For small patches one finds

$$k_{\mathrm{D}0}/4\pi \mathit{\text{DR}}=F_1{\xi }_2\text{ tan}({\delta }_2/2)+F_2{\xi }_1\text{ tan}({\delta }_1/2)$$ (3)

For medium-sized proteins, R, D, and D_i are of the orders of 40 Å, 20 Ųns⁻¹, and 0.02 ns⁻¹, respectively. The basal rate for forming a complex with three or more steteospecific contacts, obtained by Brownian dynamics simulations,¹ is 10⁵ – 10⁶ M⁻¹s⁻¹, which is four orders of magnitude lower than the unrealistic Smoluchowski result. Such a rate is predicted by Equation 3 for reactive patches with δ₁ ~ δ₂ ~ 5°. Results similar to Equation 1 for the basal rate have been obtained by a number of different methods.^13,24–26 Within the model of two spheres with reactive patches, the influence of an interaction potential on the association rate has also been studied and expressions for k_D in the presence of a centrosymmetric potential were obtained.^2,13

Brownian dynamics simulations make it possible to calculate the association rate for protein shapes and interaction potentials beyond the scope of analytical theories.^1,13,27–35 In one Brownian dynamics simulation study,¹³ it was discovered that the rate enhanced by electrostatic interactions to a good approximation is given by

$$k_{\mathrm{D}}=k_{\mathrm{D}0}\text{ exp}(-{<U_{\text{el}}>}^{*}/k_{\mathrm{B}}T)$$ (4)

where <U_el>* is the average electrostatic interaction energy of the proteins in the reactive region. Analysis on the expressions of k_D for the model of two spheres with reactive patches in the presence of an interaction potential showed that the validity of Equation 4 depends on two conditions.^2,13 First, the reaction region is small, meaning that the complex formed is stereospecific. Second, the interaction potential is long-ranged. A proof of Equation 4 as a good approximation under the two conditions was also found.¹⁴ The necessity for the condition of small reaction region can be demonstrated on the model of two uniformly reacting spheres. A blind use of Equation 4 to this model would predict k_D = 4πDRexp[−U(R)]/k_BT], which significantly overestimates the effect of the interaction potential as found in the exact result of Debye.

Fortuitously (and fortunately) the two conditions for the accuracy of Equation 4 are satisfied for the stereospecific association of proteins under the influence of electrostatic interactions. The accuracy of Equation 4 has been demonstrated on protein-ligand binding rates by direct comparison with results for k_D obtained by Brownian dynamics simulations.^15,36,37 Equation 4 allows the diffusion-limited rate to be calculated without expensive Brownian dynamics simulations in the presence of electrostatic interactions. The computational cost of calculating forces and torques in such simulations has necessitated simplified treatment of electrostatic interactions.^27–30

The overall association process between two proteins, A and B, can be viewed as consisting of two steps:

$$\mathrm{A}+\mathrm{B}\underset{k_{-\mathrm{D}}}{\overset{k_{\mathrm{D}}}{\rightleftarrows }}\mathrm{A}*\mathrm{B}\stackrel{k_{\mathrm{c}}}{\to }\text{AB}$$ (5)

The first is to reach a reactive region (with rate k_D) through translational and rotational diffusion; the transient complex thus formed, A*B, can also dissociate (with rate k_−D). The second is to reach the final bound state (with rate k_c) through conformational rearrangements. Assuming that the transient complex is in steady state, the overall association rate is

$$k_{\mathrm{a}}=\frac{k_{\mathrm{D}}{k}_{\mathrm{c}}}{k_{-\mathrm{D}}+k_{\mathrm{c}}}$$ (6)

The ensemble of configurations making up the transient complex serves as the dividing surface between the bound and unbound states. Something like this ensemble has been implied by a loosely defined term called “encounter complex.”²⁸ As demonstrated on a model system,³⁸ the overall association rate k_a calculated according to Equation 6 should be insensitive to the precise location of the dividing surface. However, practical considerations lead to an unequivocal compromise for the specification of the transient complex.^17,18 In general, overall translational and rotational diffusion and long-range electrostatic interactions dominate outside the dividing surface, whereas conformational rearrangements and short-range interactions become dominant inside the dividing surface. For the diffusion-limited rate k_D to be a good estimate for the overall association rate k_a, the dividing surface should be as close to the bound state as possible. On the other hand, placing the dividing surface inside the potential well of the bound state would require modeling conformational rearrangements along with overall translational and rotational diffusion. The compromise is then to put the dividing surface right at the outer boundary of the bound-state potential well.¹⁸

Note that the ensemble of configurations on the dividing surface, formerly referred to as the transition state for association,^16–19 is now referred to as the transient complex. The change in nomenclature is intended to avoid misidentification of Equation 4 as a naive application of the Eyring-type transition-state theory developed for barrier crossing.³⁹ Equation 4 is fundamentally different from Eyring’s transition-state theory. First of all, the former is applied to a diffusion-limited process ― reaching the transient complex does not require energy activation, whereas the latter is applied to an activation-limited process. Second, k_D only involves the process up to the formation of the transient complex; what happens afterward has no bearing. Effectively the transient-complex ensemble serves as an absorbing boundary. In contrast, the speed of decomposition of the activated complex is an integral part of the formulation of Eyring’s transition-state theory. Third, the prefactor k_D0 is the rate in the absence of interactions; favorable interactions, corresponding to a negative <U_el>*, in the transient complex serves to enhance the association rate, opposite to the role played by an activation barrier in Eyring’s theory. Fourth, unlike Eyring’s theory, Equation 4 does not require a reaction coordinate. In fact, as we will describe later, the specification of the transient-complex ensemble requires at least six degrees of freedom ― three for relative translation and three for relative rotation. In short, there is no connection between Equation 4 and Eyring’s transition-state theory.

Equation 4 together with the specification of the transient-complex ensemble will now be referred to as the transient-complex theory for protein association. This theory was tested on a large set of experimental data for association rates, with promising results.¹⁹ In this paper we use the theory and the experimental data to investigate details of calculating electrostatic contributions to association rates. We find that calculations with the nonlinear Poisson-Boltzmann equation instead of the linearized version lead to an improvement, albeit modest, in agreement between theory and experiment. In addition, changing the boundary between the protein and solvent dielectrics from the van der Waals surface to the molecular surface turns electrostatic rate enhancement into retardation.

THEORETICAL METHODS

Protein Complexes Studied

The same four protein complexes studied in an earlier paper¹⁹ are studied here. They are formed between colicin E9 and immunity protein Im9, between barnase (Bn) and barstar (Bs), between acetylcholinesterase (AChE) and fasciculin 2 (Fas), and between interlukin-4 (IL4) and IL4-binding protein (IL4BP). The Protein Data Bank (PDB) codes for the X-ray structures of the native complexes and the number of atoms and net charge of each subunit are listed in Table I. We will use the abbreviated names of two proteins, separated by a colon, in the form of E9:Im9, to denote a complex.

TABLE I.

Overall Properties of Four Protein Complexes

Complex	PDBa	# of atomsb	Net chargesb	# of inter- face atoms	Nc in native complexc	Nc*
E9:Im9	1emvB; A	2124; 1308	+7; −9	203	42 (18)	24
Bn:Bs	1brsC; F	1727; 1433	+2; −6	210	38 (21)	14
AChE:Fas	1mahA; F	8340; 906	−9; +4	271	52 (23)	23
IL4:IL4BP	1iarA; B	2111; 2959	+7; −5	181	35 (14)	16

^aX-ray structures were determined by Kuhlmann et al.,⁶⁴ Buckle et al.,⁶⁵ Bourne et al.,⁶⁶ and Hage et al.,⁶⁷ respectively. After the PDB entry name, the chains (separated by a semicolon) used for the two subunits in each complex are also listed.

^bData for the two subunits in each complex are given separately.

^cThe number of native contacts among all contacts are given inside parentheses.

Our study also covers 23 mutants of the four protein complexes, for which experimental data on association rates are available.^8,10,40–44 There are five single mutants on the E9:Im9 complex, each replacing an Im9 residue by alanine. These are: E9:E30A; E9:E41A; E9:S50A; E9:D51A; and E9:Y55A. Note that, throughout the paper, substitutions, such as E30A, before and after a colon refer to mutations on the first and second protein, respectively, of a complex. Twelve of the mutants are on the Bn:Bs complexes: K27A:Bs; R59A:Bs; E60A:Bs; R83Q:Bs; R87A:Bs; Bn:D35A; Bn:D39A; Bn:E76A; K27A:D39A; R59A:D35A; R83Q:D39A; and R87A:D39A. There are four AChE:Fas mutants (Fas:D74N; Fas:E202Q; Fas:D280V; and Fas:D283Q) and two IL4:IL4BP mutants (E9Q:IL4BP and R88A:IL4BP). All mutations, except for E202Q:Fas, are in or around the interfaces of the complexes. Two mutations, E60A:Bs and E9Q:IL4BP, increase the net charges on the mutated proteins; the E9:Y55A reduce the polarity of the mutated side chain; all the other mutations decrease the net charges on the mutated proteins.

As described previously,^45,46 hydrogens are added to all heavy atoms in the X-ray structure of each protein complex and energy-minimized in the InsightII program (Accelrys, San Diego). Each mutation is modeled by replacing the side chain and energy-minimizing its conformation with the rest of the protein complex fixed.

Energy Landscape for Protein Association

As noted in the Introduction, the transient complex on the pathway to stereospecific association consists of the ensemble of configurations located at the outer boundary of the bound-state potential well. The identification of these configurations, as outlined previously,^18,19 is based on mapping the energy landscape over the bound state and the surrounding region. To that end, configurations in the bound state and the transition region to the unbound state are uniformly sampled. The two subunits in a protein complex are treated as rigid; therefore there are only six relevant degrees of freedom: three for relative translation and three for relative rotation (Fig. 2A). Each subunit is frozen in its conformation found in the native complex, leading to a smoothed energy landscape. For easy reference, the larger and smaller subunits will be designated A and B, respectively.

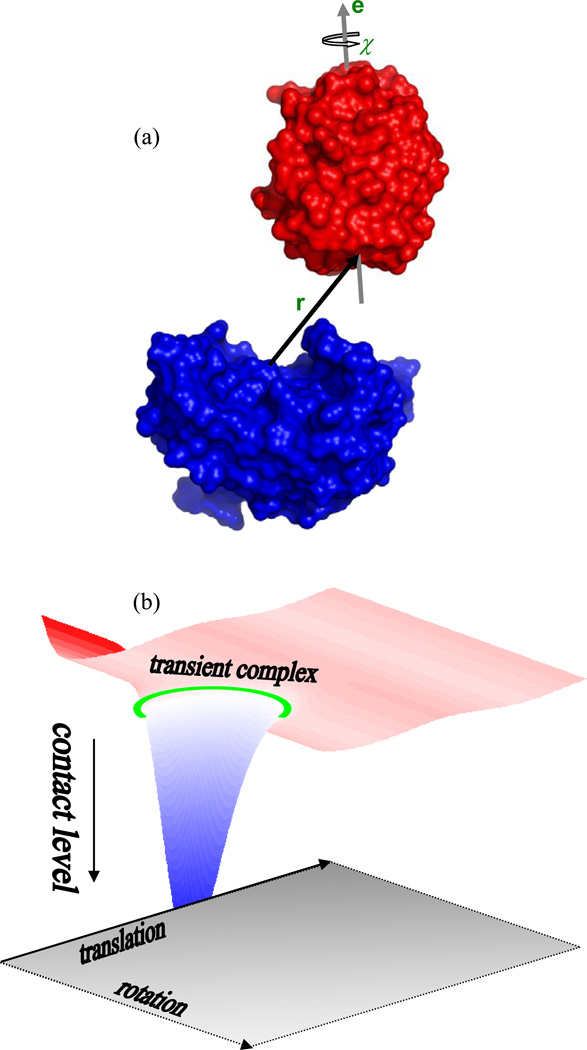
Fig. 2.

(a) Definition of six translational and rotational coordinates for two associating proteins. One protein, shown in blue, is fixed in space; the other, shown in red, can freely translate and rotate. The three translational degrees of freedom are represented by the displacement vector r between the centers of the binding surfaces on the two proteins. Of the three rotational degrees of freedom, two are a unit vector e attached to the moving protein and the remaining one is the rotational angle χ around the unit vector. The unit vector is perpendicular to a plane defined by the binding surface. (b) Illustration of the energy landscape for protein-protein association. The bound state is located in a deep “well” with high levels of contact. The transient-complex ensemble, indicated by a green ring, marks the termination of sharp decrease in contact level and the onset of sharp increase in translational and rotation freedom.

The six relative translational and rotational coordinates are defined as follows. On the X-ray structure of the native complex, interface atoms, taken as heavy atoms having interfacial contacts less than 5 Å, are collected (the number of interface atoms in each of the four protein complexes studied is listed in Table I). The geometric center of the interface atoms is body-fixed on the two subunits, to become the centers of the respective binding surfaces. The normal to the least-squares plane of the interface atoms, pointing from subunit A to subunit B, is also body-fixed on the two subunits to define two unit vectors. Subunit A is then fixed in the laboratory frame, and subunit B is translated and rotated. The vector, r, from the center of the binding surface on subunit A to the counterpart on subunit B defines the relative translational coordinates. The unit vector, e, attached to subunit B and the rotation angle, χ, around the unit vector together define the three relative rotational coordinates.

The displacement vector r is represented in spherical coordinates (r, θ, ϕ), with the laboratory z axis along the unit vector attached to subunit A. Subunit B has a body-fixed frame, with z axis along the unit vector e. The rotation of subunit B is represented by the three Euler angles (ξ, ζ, χ) of the body-fixed frame relative to the laboratory frame. Note that ξ and ζ are the polar and azimuthal angles, respectively, of the unit vector e in the laboratory frame. The native complex corresponds to r = 0, ξ = 0, and χ = 0. To sample the bound state and the transition region to the unbound state, the six translational and rotational coordinates are randomly generated, with only one restriction: r ≤ r₀. The value of r₀ is set to 6 Å.

The energy landscape over the bound state and the transition region to the unbound state is mapped by detecting steric clashes, which are to be avoided, and by calculating the number of contacts, which favor the bound state, in the randomly generated configurations. Clash is defined through clash distances assigned to three types of atoms: hydrogen, polar (nitrogen and oxygen), and nonpolar (carbon and others). The clash distance within one type or between two types of atoms is set to the minimum distance of such pairs in the X-ray structure of the native complex. Typical values are: 2.5–2.7 Å between polar atoms, 3.2–3.5 Å between nonpolar atoms, 2.8–3.1 Å between polar and nonpolar pairs, 1.6–2.1 Å between hydrogens, 1.6–1.7 Å between polar and hydrogen atoms, and ~2.5 Å between nonpolar and hydrogen atoms. Exhaustive clash detection involves testing all atoms on subunit A against all atoms on subunit B. To speed up this process, atoms are trimmed from the two full lists as much as possible before testing for clash. First, the minimum and maximum z coordinates of each subunit are found; these, expanded from both below and above by the maximum clash distance, define the range of z coordinates for the subunit. The overlap region of the z ranges of the two subunits is then obtained. If the overlap is empty, the two subunits cannot clash. Otherwise atoms on the two subunits, with z coordinates within the overlap region, are retained for further test. This procedure is repeated for x and y coordinates, each time starting from the previous trimmed lists of atoms. The two final trimmed lists of atoms are tested exhaustively for clash.

For configurations that pass the clash test, contacts, either native or nonnative, are counted. Contacts are assumed to occur between interaction-locus atoms, which are selected from the interface atoms. The purpose of the selection is two-fold: to increase the chance that retained native contacts are distinct from each other; and to decrease the chance of nonnative contacts so there is a proper balance between native and nonnative contacts. The selection for interaction-locus atoms proceeds as follows. All cross-interface pairs are sorted in ascending order of interatomic distances in the native complex; each pair is evaluated against preceding pairs for possible elimination. Specifically, a pair is eliminated if it is within 3.5 Å of a preceding pair on either side of the interface in the native complex. The final remaining list constitutes the native pairs of interaction-locus atoms. The number of native pairs of interaction-locus atoms in each of the four protein complexes studied is listed in Table I.

Now the identification of native and nonnative contacts in clash-free configurations can be described. For that purpose, the interatomic distance of each native pair is equally divided between the two interaction-locus atoms across the interface to define their contact radii. For a native pair of interaction-locus atoms, the upper limit in distance for forming a contact is the native contact distance (equal to the sum of their contact radii) plus 3.5 Å. For a nonnative pair of interaction-locus atoms to form a contact, their distance has to be within the upper limit set at the sum of their contact radii plus 2.5 Å. The total number of contacts, both native and nonnative, is recorded for each configuration. This will be denoted as N_c. The value of N_c for each of the four protein complexes studied, in its X-ray structure, is also listed in Table I.

The energy landscape over the bound state and the transition region to the unbound state, as represented by the contact level N_c as a function of the six translational and rotational coordinates, has general features illustrated in Fig. 2B.¹⁸ The bound state is represented by a deep well, in which translation and rotation are restricted. Outside the deep well, at most a few contacts are made, but translational and rotational freedom is gained. The outer boundary of the bound state marks the end point of a sharp decrease in contact level and the start point of a sharp increase in translational and rotational freedom.

Specification of the Transient Complex

The energy landscape for stereospecific association, featuring a sharp transition from contact domination in the bound state to translational/rotational-freedom domination in the unbound state, allows for an unequivocal specification of the transient complex. We identify the transient complex with the contact level, N_c*, at which the transition occurs. In particular, when N_c > N_c*, the sampled χ values are restricted to a small range around zero. As N_c further decreases, the range of sampled χ values sharply increases. Therefore σ_χ(N_c), the standard deviation of χ sampled at a given contact level, experiences a sharp increase at N_c* (Fig. 3). The sharp increase in σ_χ coincides with the maximum in the difference, Ξ, between σ_χ and its average at all lower contact levels. We thus obtain N_c* as the contact level at which the function

$$\mathrm{\Xi }(N_{\mathrm{c}})={<{\sigma }_{\chi }(N_{\mathrm{c}}\text{'})>}_{N_{\mathrm{c}}\text{'}<N_{\mathrm{c}}}-{\sigma }_{\chi }(N_{\mathrm{c}})$$ (7)

is maximal (Fig. 3). In all, 436058, 1033047, 74620, and 231683 collision-free configurations are accumulated for the E9:Im9, Bn:Bs, AChE:Fas, and IL4:IL4BP complexes, respectively. The transient-complex contact levels identified from these configurations are listed in Table I.

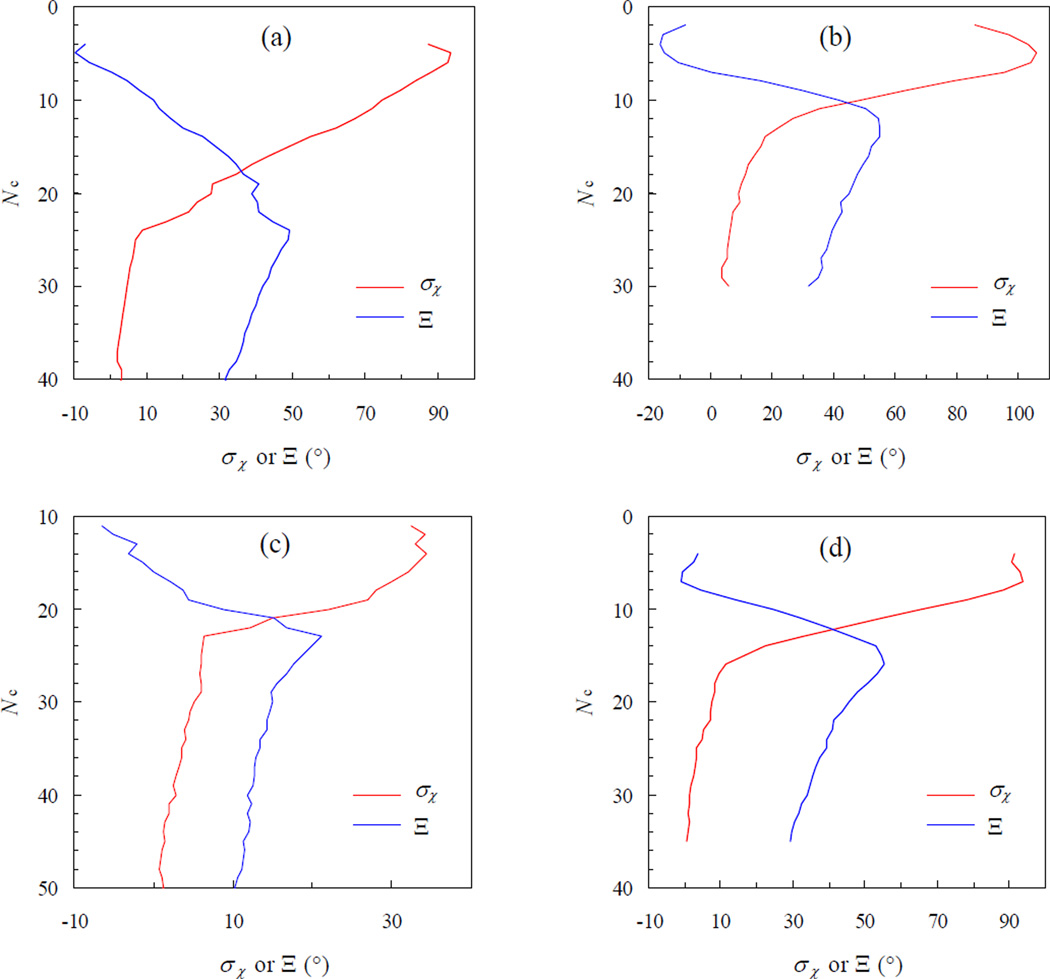
Fig. 3.

Transition of the standard deviation of χ, σ_χ, from the bound state (with high contact levels) to the unbound state (with low contact levels). The start of the sharp increase in σ_χ marks the transient complex, with the corresponding contact level N_c* uniquely determined by the maximum of Ξ. Panels (a) – (d) are for the E9:Im9, Bn:Bs, AChE:Fas, and IL4:IL4BP complexes, respectively.

Configurational Volume of the Bound State

The bound state is now explicitly defined by the condition N_c > N_c*. The configurational volume of the bound-state region is given by

$${𝒱}_{\mathrm{b}}={(8{\pi }^2)}^{-1}{\displaystyle \underset{N_{\mathrm{c}}>N_{\mathrm{c}}*}{\int }}I(r,\theta ,\varphi ,\xi ,\zeta ,\chi )r^2\mathit{\text{drd}}\text{cos}\theta d\varphi d\text{ cos}\xi d\zeta$$ (8)

where I is 1 if the configuration (r, θ, ϕ, ξ, ζ, χ) is clash-free and 0 otherwise. In our configurational sampling, r is randomly picked from 0 to r₀, cosθ and cosξ are randomly picked from −1 to 1, and ϕ, ζ, and χ are randomly picked from 0 to 2π. Equation 8 can be expressed as

$${𝒱}_{\mathrm{b}}=4\pi f_{\mathrm{c}}{f}_{\mathrm{b}}{r}_0<r^2{>}_{\mathrm{b}}$$ (9)

where f_c is the fraction of configurations that are clash-free among all the randomly generated configurations, f_b is the fraction of configurations that satisfy N_c > N_c* among all clash-free configurations, and <r²>_b is the average of r² among all bound-state configurations. In particular, as described later, 𝒱_b will play a prominent role in the calculation of the basal association rate k_D0.

Calculation of the Electrostatic Interaction Free Energy

For each of the four protein complexes studied, the transient-complex ensemble is represented by 100 configurations with the contact level N_c*. The electrostatic interaction energy in each configuration is calculated as

$$U_{\text{el}}=U_{\text{el}}(\text{AB})-U_{\text{el}}(\mathrm{A})-U_{\text{el}}(\mathrm{B})$$ (10)

The three terms on the right-hand side represent the electrostatic energies of the protein complex and the two subunits each by itself, respectively. The same 100 configurations of a wild-type complex are used for all its mutants. To that end, the two subunits in the native complex of each mutant are superimposed to their counterparts in each of the 100 transient-complex configurations. The average electrostatic interaction energy, <U_el>*, of the transient complex is calculated over the 100 configurations.

Electrostatic energies are calculated by solving the Poisson-Boltzmann (PB) equation using the UHBD program.⁴⁷ Four types of calculations are carried out. Either the nonlinear or linearized PB equation is solved, with the dielectric boundary specified to be either the van der Waals (vdW) surface or the molecular surface (MS). The latter is defined as the surface of the solute region excluded to a 1.4-Å solvent probe, and also known as the solvent-exclusion surface. The nonlinear PB equation is selected by adding the “full” option in the input script for the UHBD program; the MS specification is selected by adding the “nmap 1.5, nsph 500” option. Other details of the UHBD calculations are described in previous studies of salt and mutation effects on the binding stability of the four protein complexes.^45,46

Protein charges are taken from the Amber force field,⁴⁸ and atomic radii are adapted from OPLS⁴⁹ and Bondi radii,⁵⁰ with values of 1.9, 1.2, 1.625, 1.48, and 1.775 Å for C, H, N, O, and S, respectively. The temperature is 298 K; the solute and solvent dielectric constants are 4 and 78.5, respectively. Ionic strengths correspond to salt concentrations in the experimental studies.^{7,8,10,40–44}

Determination of Basal Rate by Brownian Dynamics Simulations

The basal rate k_D0 in Equation 4 refers to the diffusion-limited rate for reaching the transient complex in the absence of electrostatic interactions between the two subunits. This can be obtained by simulating the translational and rotational motion of the proteins. For this purpose we follow an algorithm developed previously.^13,51

To start a Brownian dynamics simulation, subunit A is fixed in the laboratory frame, and subunit B is randomly placed in the bound state, which is specified by the condition N_c > N_c*. While inside the bound state, subunit B is assigned a uniform rate γ for reacting with subunit A to form the native complex. A trajectory consists of repetitions of three steps. (1) A move of force-free Brownian translation and rotation is attempted. (2) Steric clash with subunit A is tested on the trial move. If the trial move is clash-free, it is accepted; otherwise the old configuration is accepted. (3) Whether reaction with subunit A has occurred during this move is tested. If yes, the trajectory is terminated. All trajectories are otherwise propagated to a preset cutoff time t_cut. For each trajectory, the lifetime of the trajectory is recorded for later use. First let us further explain the three steps.

For generating the Brownian translation and rotation of subunit B, we follow the extension of the Ermak-McCammon algorithm⁵² by Fernandes and de la Torre.⁵³ For simplicity, we set the center of diffusion to the center of geometry, and assume isotropic translational and rotational diffusion. The translational and rotational diffusion constants are denoted as D and D_r, respectively. The principal axes of rotation are aligned with the axes of the body-fixed frame in subunit B. The center of diffusion, R, is propagated according to

$$\mathbf{R}(t_1)=\mathbf{R}(t_0)+{\mathbf{ℳ}}^{\mathrm{b}\to 1}(t_0)·\mathrm{\Delta }\mathbf{s}$$ (11)

where t₁ = t₀ + Δt, ℳ^b→l is the rotation matrix for transforming a body-fixed vector into the laboratory frame, and Δs is a displacement vector with components sampled from a Gaussian distribution, which has a standard deviation of (2DΔt)^1/2. If Δs is set to the displacement vector, in the body-fixed frame, from the center of diffusion to the center of the binding surface, Equation 11 then gives the coordinates of the center of the binding surface (i.e., r) in the laboratory frame. The rotation matrix ℳ^b→l is propagated by rotations around the three principal axes,

$${\mathbf{ℳ}}^{\mathrm{b}\to 1}(t_1)={\mathbf{ℳ}}^{\mathrm{b}\to 1}(t_0)·{\mathbf{ℬ}}_x(\mathrm{\Delta }{\phi }_x)·{\mathbf{ℬ}}_y(\mathrm{\Delta }{\phi }_y)·{\mathbf{ℬ}}_z(\mathrm{\Delta }{\phi }_z)$$ (12)

where ℬ_x,y,z are the usual transformation matrices for rotations around the principal axes. The rotational angles Δϕ_x,y,z are sampled from a Gaussian distribution with a standard deviation of (2D_rΔt)^1/2. The relative translational diffusion constant, D, is the sum of diffusion constants of the two subunits. Diffusion constants are estimated from the molecular weights of the subunits.⁵⁴ The resulting translational diffusion constants are 23, 24, 19, and 21 Ųns⁻¹, respectively, for E9:Im9, Bn:Bs, AChE:Fas, and IL4:IL4BP. The rotational diffusion constants of the moving subunits in these complexes, Im9, Bs, Fas, and IL4BP, are 0.029, 0.028, 0.035, and 0.015, respectively. Variable timesteps are used. When r < r₀, Δt is set to a constant value ~ 5 × 10⁻⁵ ns; when r > r₀ Å, Δt is increased by 10⁻²(r − r₀)²/2D. The value of r₀ is 6 Å.

Test for steric clash is done in the same way as described earlier for mapping the energy landscape. A minor exception is that when subunit B is too far away, clash is not possible and thus not tested. Also in keeping with configurational sampling done for mapping the energy landscape, subunit A is fixed in the laboratory frame. This is done to speed up the test for steric clash, which is the most expensive part of the simulation. The neglect of rotational diffusion for subunit A leads to a very small underestimate of diffusion-limited association rate.

Whether reaction occurs during a move is determined by comparing the probability for reaction with a random number uniformly distributed between 0 and 1. This reaction probability is exp(−γΔt) if subunit B is inside the bound-state region both before and after the move, is exp(−γΔt/2) if subunit B moves into or moves out of the bound-state region by the move, and is 0 if subunit B stays in the unbound region. Reaction occurs when the random number is smaller than the reaction probability.

The bound-state configurations, i.e., those with N_c > N_c*, obtained in the sampling for mapping the energy landscape are used as initial configurations for the Brownian dynamics simulations. For the E9:Im9, Bn:Bs, AChE:Fas, and IL4:IL4BP complexes, 24174, 45046, 14711, and 5130 trajectories, respectively, are generated. From the lifetimes of the trajectories, the survival fraction, S(t), at times up to t_cut is calculated. This survival fraction is equal to the time-dependent association rate, k_a(t), scaled by its initial value, k_a(0) = 𝒱_bγ.⁵⁵ We thus have

$$k_{\mathrm{a}}(t)={𝒱}_{\mathrm{b}}\gamma S(t)$$ (13)

The steady-state value, k_a(∞), is the desired association rate. This value is obtained by extrapolation through the asymptotic behavior of k_a(t),⁵¹

$$k_{\mathrm{a}}(t)=k_{\mathrm{a}}(\mathrm{\infty })[1+k_{\mathrm{a}}(\mathrm{\infty }){(\pi \mathit{\text{Dt}})}^{-1/2}/4\pi D+\cdots ]$$ (14)

Specifically, k_a(∞) is obtained as the intercept of a fit of the long-time portion of k_a(t) as a linear function of (πDt)^−1/2. The linearity is ensured when t_cut is sufficiently large. The value of t_cut used is ~10⁴ ns. The association rate thus obtained depends on the reactivity γ. The actual value of γ, 25–50 ns⁻¹, is selected to make S(t) approach 0.5 at t = t_cut, such that the uncertainty on S(t_cut) is minimized. The diffusion-limited association rate k_D0 is the limit of k_a(∞) at γ = ∞. This is obtained from the formula⁵¹

$$\frac{1}{k_{\mathrm{a}}(\mathrm{\infty })}=\frac{1}{k(0)}+\frac{1}{k_{\mathrm{D}0}}$$ (15)

In comparing association rates predicted by Equation 4 against experimental data, we treat the basal rate k_D0 as an adjustable parameter. Specifically, for each protein complex, the value of k_D0 is obtained by fitting experimental data for the salt dependence of the association rate of the wild-type proteins. This fitted value is then used without further adjustment for all the mutants. Whether any discrepancy between the fitted value and the result from the Brownian dynamics simulations is acceptable is addressed below.

RESULTS

Placement of the Transient Complex

An essential part of our theory for predicting electrostatic enhancement of protein association rates is the specification of the transient complex. In general terms, the transient complex separates the bound state, with numerous short-range interactions but restricted translational and rotational freedom, and the unbound state, with at most a small number of interactions but expanded configurational freedom. As reasoned in the Introduction, we specifically place the transient complex at the outer boundary of the bound state. As Fig. 3 shows, the outer boundary of the bound state corresponds to the onset of a sharp increase in the sampling range of the rotational angle χ, as measured by the standard deviation σ_χ. The contact level, N_c*, defining the transient complex is uniquely identified by the maximum in the function Ξ given in Equation 7. The transient-complex contact levels are 24, 14, 23, and 16, respectively, for the E9:Im9, Bn:Bs, AChE:Fas, and IL4:IL4BP complexes. These are to be compared with the corresponding contact levels of 42, 38, 52, and 35 in the native complexes.

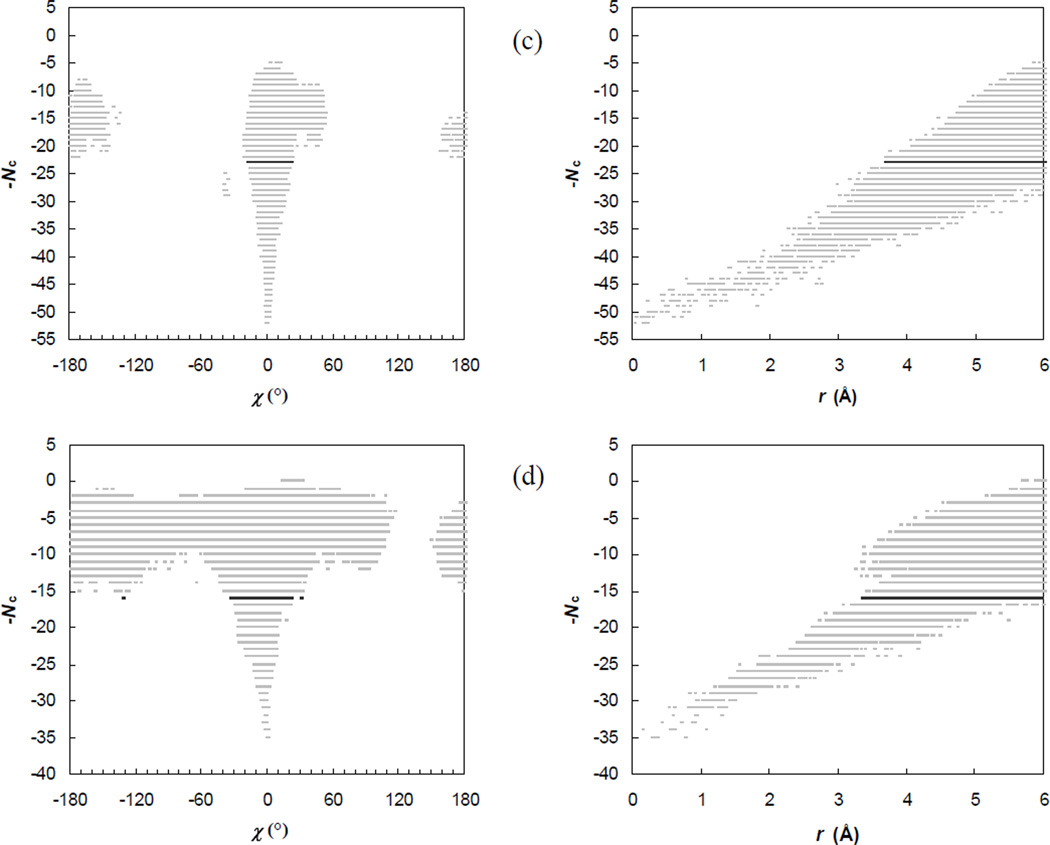
The full energy landscape over the bound state, the transient complex, and beyond can be presented by a 7-diemsnional scatter plot, consisting of points that pair configurations with corresponding contact levels. Glimpses into this energy landscape are provided by projections of the 7-dimensional scatter plot into the N_c-χ and N_c-r planes, as shown in Fig. 4. These projected scatter plots clearly show the sharp transition from contact domination in the bound state to translational/rotational-freedom domination in the unbound state. (The transition in the N_c-r plots could be better shown had we extended the upper limit in r from 6 Å during the random sampling of configurations, as was presented previously for the Bn-Bs complex with a upper limit of r at 10 Å.¹⁸ The choice of the 6-Å upper limit is made to ensure adequate sampling of the bound state and the transient complex.) In the N_c-χ and N_c-r plots shown in Fig. 4, the transient-complex contact level, N_c*, is also highlighted. As expected, this contact level is precisely where the transition occurs. For the other four coordinates, θ, ϕ, ξ, ζ, there are no apparent transitions in the ranges of sampled values (data not shown).

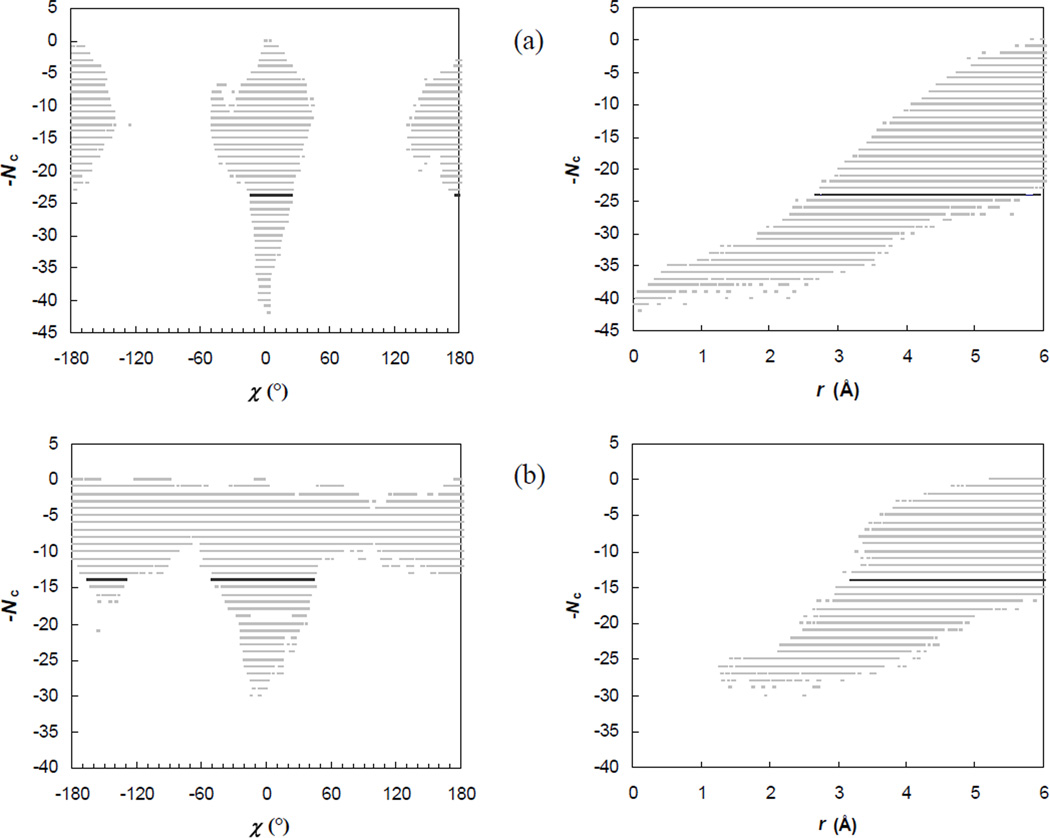
Fig. 4.

Scatter plots of the contact level N_c versus the rotation angle χ or the relative separation r. For clarity, the full range of χ, from −180° to 180° is divided into 500 bins and, at each contact level, at most one sampled χ value is saved for displaying. The sampled configurations are selected in an analogous manner for displaying in the N_c-r scatter plot, with the sampled range of r, from 0 to 6 Å, divided into 500 pins. The N_c-χ and N_c-r pairs of plots labeled (a) – (d) are for the E9:Im9, Bn:Bs, AChE:Fas, and IL4:IL4BP complexes, respectively.

In the N_c-χ and N_c-r plots, absences of configurations that have high contact levels but large rotations or large separations and configurations that have small separations but high contact levels are reflections of the deep potential well of the bound state (as illustrated in Fig. 2b). However, there are also voids around χ = ±90°, regardless of contact level, for the E9:Im9 and AChE:Fas complexes, and at χ around +90° for the IL4:IL4BP complex. The voids arise from the shape complementarity of the binding surfaces across the interface of a protein complex. Rotating one subunit by 90° with respect to the other subunit may lead to steric clash, which eliminates that configuration in the N_c-χ plot. There is an apparent asymmetry between χ = +90° and χ = −90° in the IL4:IL4BP complex. Interestingly, in all the four protein complexes, rotation angles around 180° can be sampled with moderately high contact levels, indicating that a 180° flip can be tolerated more than a 90° rotation. This is in line with the well-known difficulty of outscoring the correct configuration against a 180°-flipped alternative in protein-protein docking.

Among the transient-complex configurations of the E9:Im9, Bn:Bs, and AChE:Fas complexes, positive and negative values of χ are sampled nearly equally, leading to averages of χ close to zero. In the IL4:IL4BP complex, however, there is a bias toward negative χ, consistent with the above-mentioned asymmetry between χ = +90° and χ = −90°; the average χ value in the transient complex is −9°. The standard deviations of transient-complex χ are 9°, 18°, 6°, and 11°, respectively, for the four protein complexes (see Fig. 3). The variation among the four complexes, with Bn:Bs showing the largest spread in χ, appears to be dictated by the overall curvatures and smoothness of the binding surfaces. The relative separation r averages 3.9, 4.9, 5.1, and 4.4 Å, respectively, among the transient-complex configurations of the four protein complexes, with standard deviations all around 0.5 Å.

Basal Rate from Brownian Dynamics Simulations

The basal rate k_D0 is calculated from the initial value k_a(0) = 𝒱_bγ and the long-time limit, k_a(∞), of the time-dependent association rate k_a(t), according to Equation 15. To obtain the bound-state configurational volume 𝒱_b, the clash-free fraction f_c, the bound fraction f_b, and <r²>_b are needed (see Equation 9). The values of f_c are 5.4 × 10⁻⁵, 1.0 × 10⁻⁴, 9.0 × 10⁻⁶, and 8.6 × 10⁻⁵, respectively, for the E9:Im9, Bn:Bs, AChE:Fas, and IL4:IL4BP complexes. The corresponding values of f_b are 0.059, 0.055, 0.198, and 0.032, and the corresponding values of <r²>_b are 19.5, 10.5, 20.3, and 13.4 Ų. The resulting values of 𝒱_b are 2.4× 10⁻³, 8.7 × 10⁻³, 2.7 × 10⁻³, and 2.8 × 10⁻³ ų for the four protein complexes.

With γ = 26, 26, 50, and 26 ns⁻¹ for the four complexes, k_a(0) has values of 0.06, 0.23, 0.14, and 0.07 ųns⁻¹, and the corresponding values of k_a(∞) from the Brownian dynamics simulations are 0.03, 0.13, 0.04, and 0.04 ųns⁻¹. The basal rates are thus 3.4 × 10⁴, 1.9 × 10⁵, 3.6 × 10⁴, and 4.1 × 10⁴M⁻¹s⁻¹ for the E9:Im9, Bn:Bs, AChE:Fas, and IL4:IL4BP complexes. The higher k_D0 value of the Bn:Bs complex appears to be a result of the wider span of its transient complex in configurational space, as indicated by the fact that Bn:Bs has the largest transient-complex σ_χ and the largest 𝒱_b among the four protein complexes.

As will be seen shortly, the basal rates obtained from the Brownian dynamics simulations underestimate the values required to fit experimental data for the salt dependences of the association rates of the protein complexes, by up to an order of magnitude. As noted previously,¹⁹ the underestimate is not unexpected, since in the Brownian dynamics simulations the proteins are treated as rigid. Local induced fit would allow the two proteins to reach configurations that are forbidden in the rigid treatment, thus enlarging the span of the transientcomplex configurations and possibly leading to the desired higher basal rate. An additional explanation for the discrepancy on the basal rates will be presented under Discussion.

Salt Dependences of Association Rates for Wild-Type Complexes

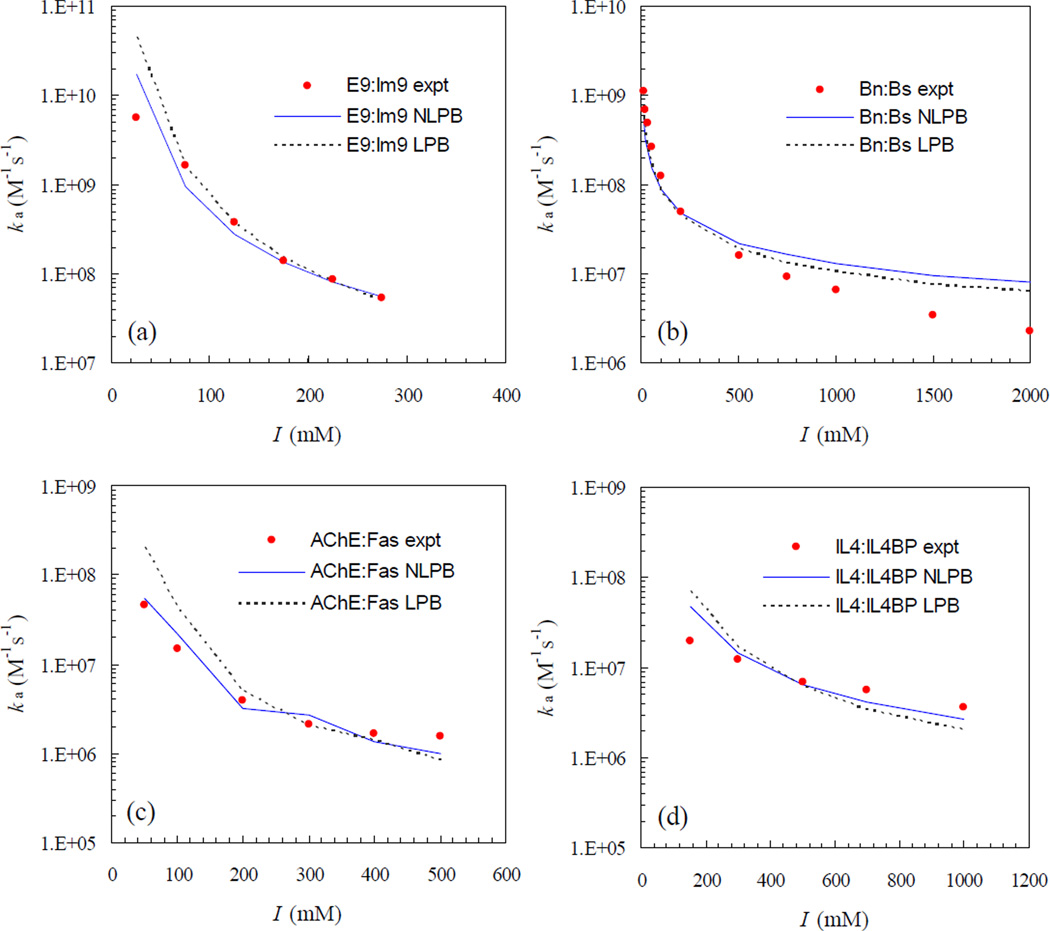
In our previous study,¹⁹ we have already found that the transient-complex theory predicts well the salt and mutation effects on the association rates of the four protein complexes when the average electrostatic interaction energy, <U_el>*, is calculated by the linearized PB equation with the dielectric boundary specified as the van der Waals (vdW) surface. In Fig. 5, we show that the agreement between theory and experiment for the salt dependences of the association rates is further improved when <U_el>* is calculated by the nonlinear PB equation, again with the dielectric boundary specified as the vdW surface. The overestimations at low ionic strengths for the E9:Im9, AChE:Fas, and IL4:IL4BP complexes by the linearized PB results are now reduced by the nonlinear PB results. For the Bn:Bs complex, the difference between linearized and nonlinear PB results is small.

Fig. 5.

Salt dependences of the association rates of the four protein complexes. Experimental results are shown in circles; predictions by the nonlinear (NLPB) and linearized (LPB) Poisson-Boltzmann equations are shown in solid and dotted curves, respectively.

As reported previously,¹⁹ in the comparison between experimental data and the linearized PB results for the salt dependences of the association rates, the basal rate k_D0 is treated as a fitting parameter. The fitted values are 5 × 10⁵, 1.4 × 10⁶, 5 × 10⁴, and 5 × 10⁴ M⁻¹s⁻¹, respectively, for E9:Im9, Bn:Bs, AChE:Fas, and IL4-IL4BP complexes. With <U_el>* calculated by the nonlinear PB equation, small upward adjustments in the basal rate are required, leading to values at 9 × 10⁵, 2 × 10⁶, 9 × 10⁴, and 10⁵ M⁻¹s⁻¹ for the four complexes. It is important to note that these values fall in the range of 10⁵ – 10⁶ M⁻¹s⁻¹ expected of the basal rate.^1–3 While these k_D0 values are consistently higher than those obtained from Brownian dynamics simulations (as already noted and rationalized), it is interesting that among both sets the Bn:Bs complex has the highest k_D0 values.

Mutation Effects on Association Rates

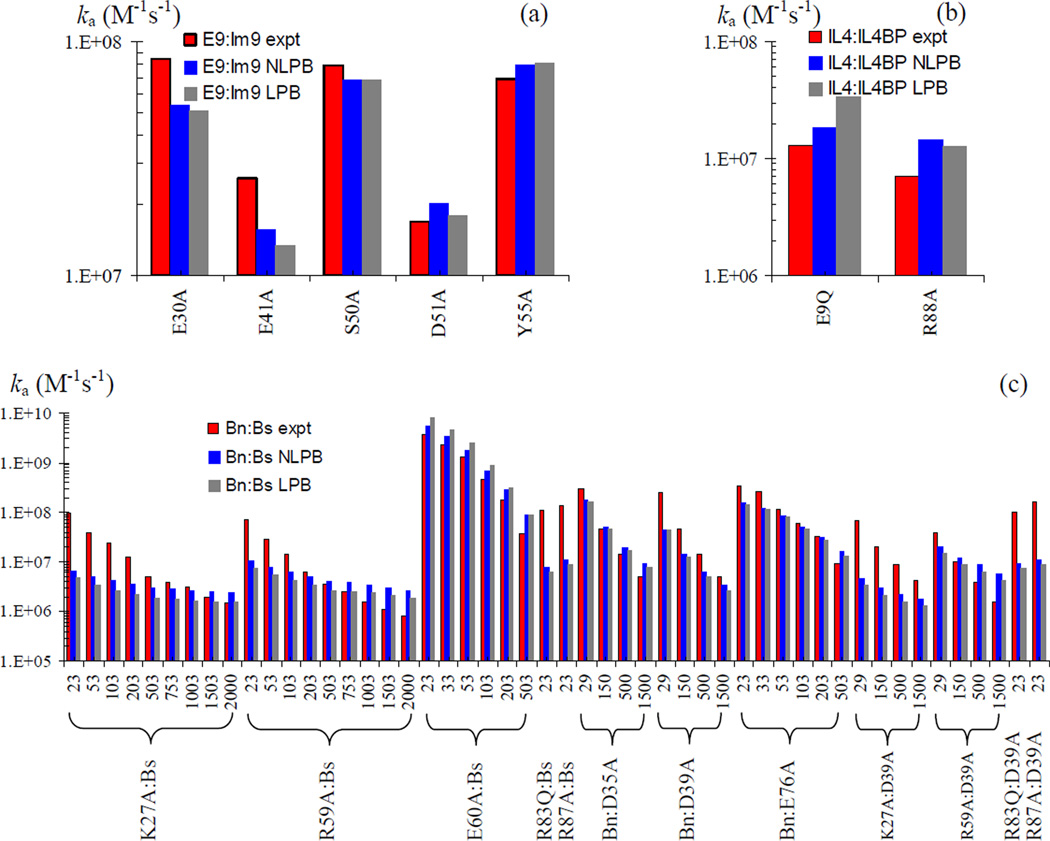
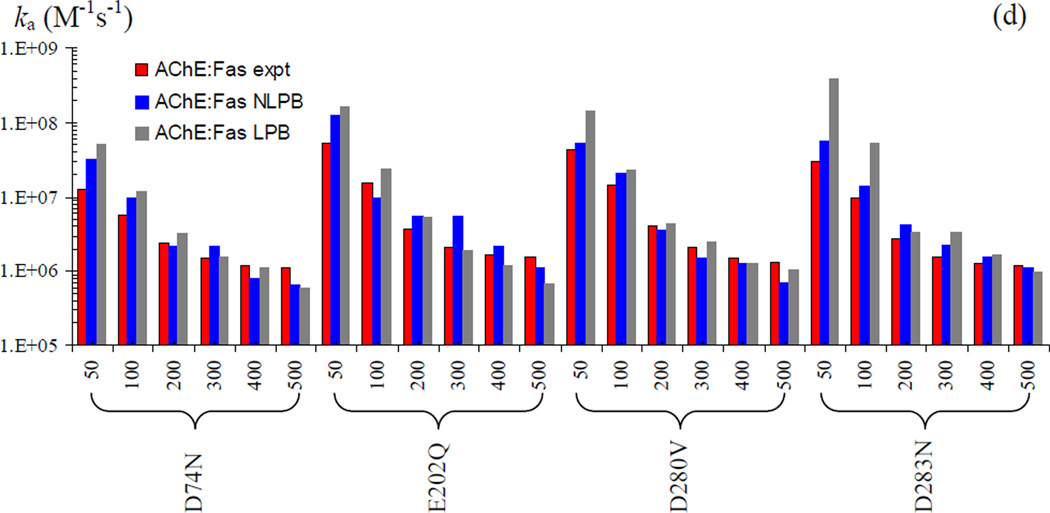
In Fig. 6, we show that the improvement in agreement between theory and experiment upon calculating <U_el>* by the nonlinear PB equation also extends to the 23 mutants of the four protein complexes. The fitted values of k_D0 reported above are used on the mutants without further adjustment. For most of these mutants, studied over various ionic strengths, the nonlinear PB results move from the linear PB results modestly toward the corresponding experimental results. This can be seen, e.g., on the E9Q mutant of the IL4:IL4BP complex, the E60A mutant of the Bn:Bs complex, and the D283N mutant of the AChE:Fas complex.

Fig. 6.

Mutation effects on the association rates of the four protein complexes. Experimental and predicted (NLPB and LPB) rates are shown as red, blue, and black bars, respectively. (a) Rates for five Im9 mutations in the E9:Im9 complex at I = 225 mM. (b) Rates for two IL4 mutations in the IL4:IL4BP complex at I = 150 mM. (c) Rates for 12 mutations on the Bn:Bs complex at the various ionic strengths (in mM) indicated. (d) Rates for four AChE mutations in the AChE:Fas complex at the various ionic strengths (in mM) indicated.

Electrostatic Rate Retardation Predicted by PB-MS Calculations

In previous studies on electrostatic contributions to the binding energies of proteins, it was found that, when PB calculations with the vdW surface give negative values for the electrostatic interaction energies of oppositely charged subunits, the electrostatic interaction energies can become positive when the molecular surface (MS) is used.^45,46,56,57 Here we find the same sign reversal on the transient-complex electrostatic interaction energies of all the four protein complexes. When the dielectric boundary is changed from the vdW surface to MS, the sign of <U_el>* changes from negative to positive, leading to electrostatic rate retardation instead of enhancement. For example, for the Bn:Bs complex, when the ionic strength is varied from 13 mM to 2000 mM, <U_el>* calculated by the nonlinear PB equation with the vdW surface varies from −3.30 to −0.82 kcal/mol. Correspondingly, <U_el>* calculated by the nonlinear PB equation with MS varies from 2.50 to 5.13 kcal/mol. For the latter results to be consistent with the experimental data for the association rate would require a basal rate in the order of 10¹⁰ – 10¹¹ M⁻¹s⁻¹, which clearly seems unphysical.

DISCUSSION

We have demonstrated the predictive power of the transient-complex theory for association rates on four protein complexes and a large number of their mutants. We found that use of the nonlinear Poisson-Boltzmann equation instead of the less rigorous, linearized version in calculating electrostatic interaction energies leads to improved agreement with experiment. We also found that specifying the dielectric boundary as the molecular surface in the electrostatic calculations leads to rate retardation instead of enhancement, an apparently unphysical result.

Overview on the Spectrum of Protein-Protein Association Rates

As illustrated in Fig. 1, protein-protein association rates span many orders of magnitude. Rates toward the high end are limited by diffusion; rates toward the low end are limited by conformational changes that accompany complex formation. The demarcation point between these two regimes lies probably around 10⁵ M⁻¹s⁻¹. In the diffusion-limited regime, association rates for proteins that do not involve significant electrostatic contributions, such as antibodies and protein antigens, fall within the narrow range of 10⁵ – 10⁶ M⁻¹s⁻¹. Higher association rates implicate electrostatic enhancement, resulting from complementary electrostatic surfaces.

A value in the range of 10⁹ – 10¹⁰ M⁻¹s⁻¹ calculated from the Smoluchowski result 4πDR has sometimes been used as a benchmark for determining whether protein-protein association is diffusion-limited. As we have emphasized, the Smoluchowski model is inappropriate for stereospecific association. With more realistic models such as spheres with stereospecific contacts, one arrives at a basal rate for diffusion-limited association in the range of 10⁵ – 10⁶ M⁻¹s⁻¹. This range should be used as the basis for whether to propose diffusion control for the association of a particular pair of proteins.

In general, rates beyond the 10⁵ – 10⁶ M⁻¹s⁻¹ range implicate electrostatic enhancement. A hallmark of electrostatically enhanced diffusion-limited association is manifested by disparate ionic-strength effects on the association rate k_a and the dissociation rate k_d.¹⁷ Specifically, k_a decreases significantly with increasing ionic strength, but k_d is affected by ionic strength only marginally. A sample of 10 complexes, including the four studied here, that exhibit such a telltale sign for electrostatically enhanced diffusion-limited association are listed in a recent paper.⁵⁸ The disparate ionic-strength effects on k_a and k_d provided strong experimental support for the present transient-complex theory, because these effects are precisely what the theory predicts.¹⁷ Since the transient complex lies at the outer boundary of the bound state and is very closer to the latter, ionic strength will affect the electrostatic interaction energies of the transient complex and the bound state to similar extents. Hence ionic strength will affect k_a almost as strongly as the association constant K_a. The dissociate rate k_d, given by k_a/K_a, will therefore only be weakly affected by ionic strength. In the present paper, we have gone beyond qualitative explanation and shown that ionic-strength effects on k_a can be quantitatively predicted by the transient-complex theory.

Absence of Energy Barrier for Diffusion-Limited Protein-Protein Association

Of the host of theoretical models for diffusion-limited association discussed in this paper, none requires an energy barrier. In the Smoluchowski model, the contact surface r = R is absorbing; beyond it the energy landscape is flat. The Debye model introduces an energy function such as the Coulomb type, −Q/r, that for practical purposes most likely will give rise to a funnel-like landscape. The models for stereospecific association involve a dividing surface that is reflecting everywhere except for a small absorbing patch. Outside the dividing surface, the energy landscape is either flat, as in the case of force-free diffusion (leading to the basal rate k_D0), or funnel-like when electrostatic rate enhancement is involved. Any local minimum in the energy surface has no particular significance in determining the diffusion-limited association rate, k_D. Inside the dividing surface, i.e., within the bound state, there may well be energy barriers, but these have no bearing on k_D.

When a flat or funnel-like multi-dimensional energy surface is reduced to a potential of mean force in a single “reaction coordinate,” an entropy barrier may arise.^59,60 In treating diffusion-limited stereospecific association, involving six translational and rotational degrees of freedom, it does not seem to make much sense to identify a single reaction coordinate. Reduction to two coordinates, i.e., r and χ, appears to have some merit, since these are the only coordinates that exhibit sharp transitions in the ranges of sampled values on going from the bound state to the unbound state. In our previous study, we found that the potential of mean force in r and χ is still funnel-like, without a barrier.¹⁸ It may be tempting to regard the orientational constraints of a stereospecific association model, leading to a four order of magnitude reduction in basal rate relative to the Smoluchowski model, as an entropy barrier. However, that does not provide any additional insight into the diffusional process leading to the bound state, nor does it lead to a quantitative formulation of the association rate. Our transientcomplex theory, in the form of Equation 4, accomplishes that.

Modulation of Protein Association Rate by Electrostatic Interactions

The transient-complex electrostatic interaction energy, <U_el>*, has values as negative as −5.8 kcal/mol among the four protein complexes studied. That, according to Equation 4, corresponds to a rate enhancement of 10⁴-fold. It should be noted that such a dramatic rate enhancement is only possible for stereospecific association. In the Debye model, for example, for a Coulomb potential −Q/r, with the contact value (i.e., −Q/R) at −5.8 kcal/mol, gives merely a 10-fold rate enhancement.

The remarkable ability of electrostatic interactions in modulating protein association rates is demonstrated by the 10³-fold difference between two Rho GTPases, Cdc42 and TC10, in the rates of associating with the Wiskott-Aldrich syndrome protein.¹¹ Cdc42 and TC10 share 70% sequence identity. The large difference in association rates between related proteins suggests that association rate, in addition to binding affinity, can provide a mechanism for specificity. Other possible biological roles of association rates have also been proposed.¹⁹

The ability of electrostatic interactions to contribute up to 10⁴-fold rate enhancement is directly related to their long-range nature, which, it should be recalled, is one of the two conditions for the validity of Equation 4. As shown by calculations on model systems, short-range interactions have much less effects on the association rate.⁶¹ In a previous study we found that short-range interactions are present in the transient complex.¹⁸ More specifically, the transient complex is surrounded by a broad shallow basin, arising from one or a few loosely formed native interactions. Such interactions may contribute to a small enhancement in the association rate. If this effect from the short-range interactions is taken into consideration, the basal rate required to fit with experimental data will be reduced, bringing it into closer agreement with the value of k_D0 obtained from Brownian dynamics simulations.

Calculation of Electrostatic Rate Enhancement

Our assessment of the electrostatic contributions to association rates obtained from four types of Poisson-Boltzmann calculations against experimental data demonstrates that details of treating electrostatic interactions are important. This is especially true when the two proteins are close. In studies of electrostatic rate enhancement by Brownian dynamics simulations, the prohibitive cost of calculating forces and torques from a rigorous implementation of the Poisson-Boltzmann equation on the fly led to approximate treatments, such as those using test charges or effective charges.^27–30 The errors of such treatments can be significant when two proteins are in close proximity, leading to uncertainty about predicted electrostatic rate enhancement. Our transient-complex theory appears to provide the only viable option for rigorous treatment of electrostatic interactions in studying protein association.

As noted already, the calculated electrostatic interaction energy is sensitive to the precise specification of the dielectric boundary.^{45,46,56,57,62,63} Past efforts in discriminating between two choices, van der Waals and molecular surfaces, have relied on experimental data for mutational effects on folding stability or binding affinity. In this paper we make use of experimental data on association rates, which offer two important advantages. First, as presented by earlier arguments, rate enhancement is dominated by long-ranged electrostatic interactions; thus experimental data on association rates are not appreciably “contaminated” by short-range nonelectrostatic effects. In the past, comparison of calculated electrostatic contributions to experimental data on binding affinity, which may contain nonelectrostatic contributions, always raised concerns, which bring out the second advantage of using experimental data on association rates. That is, in the past, in order to cancel nonelectrostatic contributions in experimental data on binding affinity, comparisons have been restricted to relative effects of mutations. The problem is that the relative effects of mutations obtained by vdW and MS calculations are often very similar. Here we test calculated results against experimental data for absolute rates instead of relative rates. Our results show that vdW calculations lead to electrostatic rate enhancement, but MS calculations lead to rate retardation. We suggest that the latter is unphysical.