Abstract
Accurate gene tree reconstruction is a fundamental problem in phylogenetics, with many important applications. However, sequence data alone often lack enough information to confidently support one gene tree topology over many competing alternatives. Here, we present a novel framework for combining sequence data and species tree information, and we describe an implementation of this framework in TreeFix, a new phylogenetic program for improving gene tree reconstructions. Given a gene tree (preferably computed using a maximum-likelihood phylogenetic program), TreeFix finds a “statistically equivalent” gene tree that minimizes a species tree-based cost function. We have applied TreeFix to 2 clades of 12 Drosophila and 16 fungal genomes, as well as to simulated phylogenies and show that it dramatically improves reconstructions compared with current state-of-the-art programs. Given its accuracy, speed, and simplicity, TreeFix should be applicable to a wide range of analyses and have many important implications for future investigations of gene evolution. The source code and a sample data set are available at http://compbio.mit.edu/treefix.
Keywords: Gene tree error correction, phylogenetics, reconciliation
Gene trees and species trees play a fundamental part in many phylogenetic analyses. Although species trees represent evolutionary histories at the species level, gene trees depict the evolutionary histories of families of genes. By reconstructing gene trees and reconciling (i.e., comparing) them to a species tree, one can infer the history of gene duplications, losses, and other important evolutionary events that have occurred within a gene family (Page 1994; Vilella et al. 2009). In addition, gene trees can be used to infer orthologs and paralogs, allowing functions to be mapped across different species (Eisen 1998), or gene trees can be reconstructed on the genome-wide scale to gain insight into how gene families expand and contract (Hahn et al. 2007) or to understand the evolutionary impact of genome-wide events (Jiao et al. 2011).
Although gene trees have many powerful applications, all of these analyses depend strongly on the accuracy of the reconstruction (Hahn 2007; Rasmussen and Kellis 2011). However, unlike species tree reconstruction, which can benefit from the use of well-behaved gene families as well as multigene phylogeny construction methods (Delsuc et al. 2005; Burleigh et al. 2011), gene tree reconstruction is complicated by the fact that many genes lack enough information to confidently support a single gene tree topology. Thus, “sequence-only” algorithms that reconstruct gene trees using only the sequence data [e.g., PAUP* (Swofford 2002), BioNJ (Gascuel 1997), PhyML (Guindon and Gascuel 2003), RAxML (Stamatakis 2006), MrBayes (Ronquist and Huelsenbeck 2003)] often produce incorrect and poorly supported gene trees. However, recent studies have found that incorporating species tree information can drastically improve gene tree accuracy (Vilella et al. 2009; Rasmussen and Kellis 2011). This has led to the formulation of “species tree aware” methods, which often combine sequence likelihood with a topology prior based on a known species tree, with the most principled methods adopting a Bayesian approach [e.g., PrIME-GSR (Arvestad et al. 2004), SPIMAP (Rasmussen and Kellis 2011)], though simpler models [e.g., TreeBest (Vilella et al. 2009), SPIDIR (Rasmussen and Kellis 2007)] also exist. However, these models often require additional parameters, such as estimates of divergence times and duplication–loss rates, and they tend to be very computationally intensive.
In parallel, several “hybrid” methods have been developed for resolving gene tree and species tree incongruence to produce “error-corrected” gene trees. These are often based on a reconciliation framework and attempt to minimize a species tree aware cost function based on the inferred evolutionary events. For example, both NOTUNG (Durand et al. 2006) and tt (Górecki and Eulenstein 2011) consider local rearrangements around an initial gene tree to find an error-corrected gene tree that has minimum duplication–loss cost after reconciliation. Although these algorithms only require a known species tree topology and are therefore much simpler than model-based species tree aware approaches, they suffer from 2 important drawbacks: (1) they limit their search space and can therefore miss the correct tree topology if it is distant from the initial tree and (2) because they ignore whether the corrected gene tree is supported by the sequence data, they cannot guarantee that the corrected gene tree does not overfit to the species tree.
To address these shortcomings, we present a novel hybrid method TreeFix. Like other hybrid methods, TreeFix rearranges an input gene tree to minimize the number of inferred duplications and losses. However, TreeFix is novel in that it also uses the sequence data (i.e., nucleotide or peptide alignment) to guarantee that the final corrected gene tree is “statistically equivalent” in likelihood to the initial input tree (i.e., the difference in likelihood between the 2 trees is not significant). In essence, TreeFix recognizes that although phylogenetic programs often return a single optimal gene tree (or possibly a consensus tree across multiple bootstraps), multiple gene trees are often statistically equivalent, as measured by likelihood ratio tests, such as the Kishino–Hasegawa (KH) test (Kishino and Hasegawa 1989), the Shimodaira–Hasegawa (SH) test (Shimodaira and Hasegawa 1999), or many others (Shimodaira and Hasegawa 2001). Furthermore, one of these statistically equivalent gene trees will often more accurately reflect the true gene tree topology. By incorporating this statistical test with a reconciliation cost, such as the duplication–loss cost, we can therefore improve phylogenetic accuracy. In addition, because of this guarantee, TreeFix is free to use an expanded search algorithm that can explore more distant parts of the tree space. We find that together, these techniques lead to a simple yet powerful method that requires few modeling assumptions or parameters and produces highly accurate gene trees ideal for inferring the evolutionary history of gene families.
We have applied TreeFix to both real and simulated data sets and compared its performance with that of several other gene tree reconstruction methods. We find that TreeFix shows drastic improvement over existing sequence-only and hybrid approaches, with performance comparable to the most sophisticated species tree aware Bayesian approaches.
Methods
Gene Tree Landscape
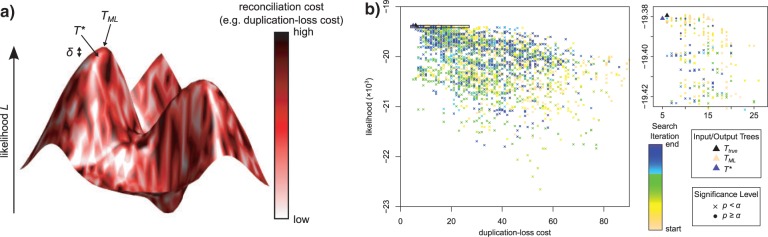
To understand the basic idea behind TreeFix, consider the likelihood landscape of the gene tree space (Fig. 1a). Ideally, TreeFix is given as input the maximum-likelihood (ML) tree (models with non-unique ML trees should not be used). This tree corresponds to the highest peak in the landscape, but often this peak is located in a plateau of high likelihood topologies. Methods such as NOTUNG and tt make local rearrangements to explore this surrounding plateau for the topology that minimizes some user-defined cost function (e.g., the number of inferred duplications and losses), where this cost function is used as a heuristic for improving gene tree accuracy. However, these local moves may result in a topology outside the plateau that has significantly worse likelihood than the ML topology. Furthermore, the likelihood landscape may also contain multiple peaks and valleys, necessitating a larger search to explore distant plateaus. TreeFix essentially searches among topologies within the landscape that lie above a certain threshold, using reconciliation cost as a heuristic to determine an optimal tree among these topologies. In this way, TreeFix is able to move beyond local rearrangements to find a minimum cost gene tree without overfitting to the species tree.
Figure 1.
Gene tree landscape. a) Each point within the landscape corresponds to a gene tree Tx, whose optimality can be measured through its likelihood Lx (height) and its reconciliation cost cx (color). The ML tree TML is located at the peak of this landscape but may have a high cost. Rearranging TML to a nearby tree Tx can result in a negligible decrease in likelihood (δx = LML − Lx < δthr) while simultaneously reducing the tree cost (cx < cML), thus producing a more congruent gene tree that is statistically equivalent to the ML tree. TreeFix utilizes this basic idea by balancing the 2 optimality criteria to return an optimal tree T* for which δ* is negligible and c* is minimal. b) The landscape for a simulated gene family shows a wide range of likelihood and cost values. In this instance, TreeFix searched over 3560 gene trees of the 8.2 × 1021 possible unrooted topologies (number of genes = 21). Although most trees have statistically worse likelihoods compared with the ML tree (×), a subset of high likelihood trees are statistically equivalent (circles). As the search progresses, the search space generally moves toward the top-left, corresponding to topologies with high likelihood and low duplication–loss cost (enlarged at right, accepted trees per iteration shown as squares). In this case, TreeFix has rearranged TML (beige triangle) to produce a new optimal tree T* (purple triangle) with equivalent likelihood and lower cost. Note that T* is incorrect because the true tree Ttrue (black triangle) has a slightly higher duplication–loss cost. (Likelihoods were computed with ϵ = 2.)
Note that TreeFix inherently assumes that regions of high sequence likelihood and low reconciliation cost overlap, an assumption held up in practice (Fig. 1b). When this is not the case, TreeFix errs on the side of sequence support (rather than species tree support) and returns a gene tree with high sequence likelihood and high reconciliation cost.
Major Components
Our goal is to find, among all gene tree topologies that are statistically equivalent to the ML tree, one that minimizes a user-defined reconciliation cost. Thus, at its core, TreeFix consists of 3 basic components: (i) a test of statistical equivalence to filter out gene tree topologies that are suboptimal, (ii) a gene tree and species tree reconciliation method to compute the reconciliation cost, and (iii) a tree search to explore the space of alternative gene tree topologies. We elaborate on each of these below.
Statistical comparison of sequence support for multiple topologies
Many statistical tests have been developed for computing the equivalence of 2 or more tree topologies chosen a priori (Kishino and Hasegawa 1989; Shimodaira and Hasegawa 1999; Goldman et al. 2000; Shimodaira and Hasegawa 2001). In essence, these tests compute a test statistic that captures the observed likelihood difference between trees, then rely on hypothesis testing in which the null hypothesis is that the trees are equally supported by the sequence data, and the alternative hypothesis is that the trees are not equally supported. Because sequence evolution is a stochastic process, these tests determine a p-value that represents the probability of obtaining a test statistic at least as extreme as the one that was actually observed, assuming that the null hypothesis is true. Given a significance level α that represents the probability of false rejection (i.e., we believe the trees are not equally supported when they actually are), we then reject the null hypothesis and say the trees are not equally supported if p < α, or we fail to reject the null hypothesis and say that the trees are equally supported if p ≥ α. Note that if α = 0, all trees are equally supported, effectively removing the statistical test and causing TreeFix to return the minimum cost gene tree regardless of sequence support, whereas if α = 1, no trees are equally supported, effectively causing TreeFix to return only the tree with highest sequence support, for example, the ML tree.
Although users may implement their own statistical module, by default, TreeFix uses the SH test provided by the RAxML package. For further information on likelihood tests, including a discussion of statistical power, how to correct for multiple comparisons, and an error rate analysis, see Supplementary Sections S1 and S2 (available at http://datadryad.org, doi:10.5061/dryad.44cb5).
Gene tree and species tree reconciliation
To calculate a species tree aware cost, we make use of the reconciliation framework, in which any incongruence between the gene tree and species tree topologies is explained by postulating evolutionary events, such as gene duplication, gene loss, horizontal gene transfer, or incomplete lineage sorting (Maddison 1997). Although users may implement their own cost module, by default, TreeFix uses maximum parsimony reconciliation (Page 1994; Zmasek and Eddy 2001) with the duplication–loss cost function (Goodman et al. 1979), which seeks the reconciliation with the fewest total number of inferred duplications and losses. In addition to being the standard model used in many species tree aware and hybrid approaches, for example, in SPIMAP, TreeBest, NOTUNG, and tt, we found the reconciliation cost to be highly correlated with gene tree topological accuracy (Supplementary Section S3), lending support to our approach of using this metric to incorporate information from the species tree into the gene tree reconstruction.
Tree search
Because it is impractical to search through the space of all possible gene tree topologies, we use a heuristic hill climbing search strategy. The idea is to start with the given input gene tree and find a better tree in its neighborhood (defined using some tree edit operation). This constitutes one local search step. This better tree then becomes the starting point for the next local search step, and so on, for either a predefined number of local search steps or until a local optima is reached. Local search forms the basis of almost all known parsimony and likelihood-based phylogeny construction programs, for example, in PAUP*, RAxML, PhyML, and others and has been used for gene tree error correction as well.
In our implementation, we use nearest neighbor interchange (NNI) and subtree prune and regraft (SPR) (Felsenstein 2003, Ch. 4) to define the neighborhood in each local search step. In addition, we use the reconciliation cost to prescreen topology proposals. In particular, on each iteration, we perform a random NNI or SPR operation on the current optimal gene tree and compute its cost. This proposal is always accepted if it has a lower cost and is accepted with some predefined probability if it has a higher cost, and we repeat this local search until we have nq proposals, after which only those proposals with a cost lower than the optimal are retained. We then sort the proposals by their costs, set the first proposal with statistically equivalent likelihood as the new optimal, and repeat this entire process for ni iterations. Notably, this search strategy allows us to “jump” over valleys of low tree cost or low likelihood and explore distant parts of the gene tree landscape.
Algorithm
TreeFix takes as input a gene tree Tin (often the ML tree), a multiple alignment A, a species tree Ts, a test statistic stat and significance level α ∈ [0, 1] for likelihood equivalence. Additionally, it takes 3 search parameters: ni, nq ≥ 1 that control the number of tree proposals and f ∈ [0, 1] that specifies the fraction of proposals to reroot.
For an arbitrary gene tree Tx, TreeFix evaluates 2 functions in order to determine how the tree fits within the likelihood landscape: (1) cx = c(Tx; Ts) ≥ 0, that is, the cost of the gene tree based on the species tree and (2) px, δx = LHstat(Tx; A, Tin), that is, the statistical significance and change in likelihood Lin − Lx of the gene tree (against the input gene tree) based on the test statistic, multiple alignment, and input tree.
TreeFix outputs the optimal rooted gene tree T*, that is, the gene tree with minimum cost and statistically equivalent likelihood, if such a tree is found. If multiple trees have minimum cost and are statistically equivalent, the one with minimum change in likelihood is returned. The main algorithm is as follows (Supplementary Fig. S1):
Compute cin, and initialize T* = Tin, c* = cin, and δ* = Lin − L* = 0.
Make nq proposals {Tx}, computing cx for all Tx in {Tx} and rerooting f of them to have minimum cost.
Sort {Tx} in order of increasing cost, and retain only those for which cx ≤ c*. Call this [Tx].
For each Tx in [Tx], compute px and δx. If px ≥ α and either (a) cx < c* or (b) cx = c* and δx < δ*, set T* = Tx, c* = cx, and δ* = δx, and go to step 5. Else consider the next proposal.
Repeat steps 2–4 for ni iterations, or until c* = 0.
Although users can input any tree, in practice, we recommend that users input a ML tree, for example, from RAxML or PhyML, and use the same likelihood model as the input tree when computing the test statistic.
Note that TreeFix does nothing if the input gene tree contains ≤2 genes, is unrooted and contains ≤3 genes, or has a reconciliation cost of 0. Furthermore, if the gene family contains one gene per species, TreeFix first checks the likelihood and reconciliation cost of the gene tree topology that is congruent to the species tree topology.
To measure the uncertainty of different topologies and events, we also implemented a bootstrapping procedure. To bootstrap the entire pipeline would require resampling the alignments, reconstructing the ML trees using these alignments, then passing both the resampled alignments and associated ML trees to TreeFix for error correction. However, such a procedure would be computationally expensive and infeasible for large data sets. Furthermore, we envision TreeFix as a tool to be used in conjunction with existing ML programs, most of which store only the bootstrap trees and not the bootstrap alignments. Therefore, we have implemented an approximation in which we bootstrap only the TreeFix stage of the pipeline. If bootstrapping is enabled, then TreeFix resamples the alignment and error corrects the input gene tree for each resampled alignment. Note that we reuse the original ML tree topology (reconstructed from the full data) across these bootstraps; that is, we do not explore the uncertainty in the topology of Tin. However, the likelihood test does optimize the branch lengths and recalculates the likelihood of Tin on each resampled alignment. Therefore, as long as the ML tree topology reconstructed from the full alignment can be considered as a good proxy for the ML tree topology that would have been reconstructed from the bootstrapped alignments, this approximation should have little effect on the statistical significance of alternative topologies and the resulting TreeFix corrected gene trees.
Results
We evaluated TreeFix using 2 clades of species, the 12 Drosophila and 16 fungi (Supplementary Fig. S2), and using the same data sets used to evaluate SPIMAP (Rasmussen and Kellis 2011). This included 1000 simulated gene families (generated under the SPIMAP model) across each clade, as well as 5351 real gene families across the 16 fungal genomes.
For comparison, we also evaluated several phylogenetic programs, including the “sequence-only” probabilistic program RAxML, the “species tree aware” programs SPIMAP and TreeBest, and the “hybrid” programs NOTUNG and tt [pipeline and algorithm parameters provided in Supplementary Section S4; results using sequence-only methods BioNJ, PHYML, and MrBayes, and species tree aware method PrIME-GSR can be found in Rasmussen and Kellis (2011)].
Reconstruction Accuracy
Simulated data set
In the simulated data set, the correct phylogeny is unambiguously known, allowing us to analyze several different aspects of the phylogenetic programs.
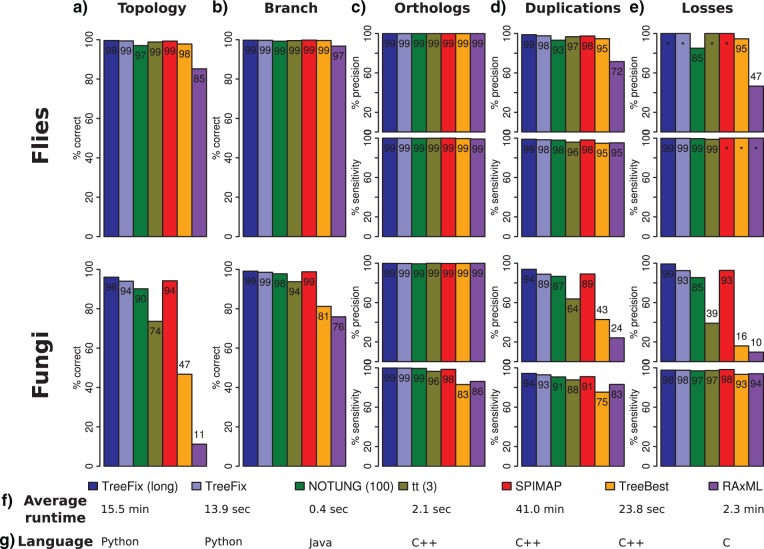
To measure accuracy, we evaluated several different metrics including topological accuracy, branch accuracy, and sensitivity and precision of duplication, loss, and ortholog inference (Fig. 2). Although we ran TreeFix on both the fly and fungi clades, we focus our discussion here on the results of the larger fungi clade, as the phylogenetic programs performed similarly across many of the metrics using the smaller fly clade.
Figure 2.
Phylogenetic accuracy and runtime using several phylogenetic methods on simulated fly and fungal data sets. a) Both hybrid and species tree aware methods have high reconstruction accuracy for correctly inferring the full gene tree topology for the fly data set. TreeFix has the highest reconstruction accuracy for the larger fungal data set. b) The percent of accurately reconstructed branches is similar across all methods for the fly data set, but the hybrid methods and SPIMAP show significant improvement over TreeBest and RAxML for the fungal data set. c) Despite topological and branch inaccuracies, pairwise ortholog detection is robust across all methods in both precision and sensitivity. d,e) TreeFix (long) and SPIMAP infer duplications and losses with a high degree of sensitivity and precision, with both these methods offering a slight improvement over TreeFix and NOTUNG (100). Again, the hybrid methods and SPIMAP greatly outperform TreeBest and RAxML, particularly in terms of precision for the fungal data set. f) TreeFix achieves performance comparable to SPIMAP at a fraction of the runtime (average runtimes provided for the fungal data set). Note that TreeBest and RAxML were run with 100 bootstraps, whereas all other methods were run without bootstrapping. g) TreeFix runtime can likely be improved if the program were ported to a more efficient programming language. For more metrics, see Supplementary Table S1.
We found that TreeFix significantly improves on the input RAxML trees, improving topological accuracy by 82.8–84.8%, branch accuracy by 22.7–23.2%, and duplication and loss precision by 64.6–69.6% and 82.9–89.6%. (The other metrics are less sensitive to gene tree errors, showing between 0.3% reduction and 13.6% improvement.) Additionally, TreeFix performance is comparable to that of the most sophisticated reconstruction method analyzed (SPIMAP), and both of these dramatically outperform all other methods.
The low performance of RAxML is, of course, expected as it uses only sequence data. Among the species tree aware and hybrid methods, TreeBest performs by far the worst, which we believe can be attributed to its relatively simple penalized likelihood approach. (Results presented here used default parameters for TreeBest. Analysis using a variety of parameter settings for TreeBest did not show an appreciable change in accuracy.)
Using quick search parameters, TreeFix performs slightly better than NOTUNG (3.9% improvement in topological accuracy, 2.3% and 7.2% in duplication/loss precision) and significantly better than tt (20.4%, 25.1%, 53.5% improvement). Furthermore, we found that 1.8% of the NOTUNG trees and 1.1% of tt trees fail the SH test (compared with the input RAxML trees at α = 0.05), suggesting that the decreased performance of these hybrid methods is at least partially a result of overfitting to the species tree.
In light of this, we analyzed TreeFix to determine the effect of overfitting on gene tree error. We ran TreeFix with α = 0, effectively removing the likelihood test and finding the minimum duplication–loss tree. We found that 7.4% of the resulting trees fail the SH test (at α = 0.05), and that topological accuracy decreases by 5.2% to (a level of) 88.8%, and duplication precision decreases by 9.0% to (a level of) 79.8%. This suggests that, as expected, ignoring sequence information is detrimental to gene tree accuracy and further supports our strategy of balancing a tree search strategy with a likelihood test. Further analysis showed that TreeFix performance remains relatively stable for 10−3 ≤ α ≤ 0.2 (Supplementary Fig. S5). Within this range, the Robinson–Foulds (RF) distances (Robinson and Foulds 1981) against the TreeFix trees at α = 0.05 are also highly similar (average RF < 0.009), suggesting there exists a good compromise between sequence and species tree information.
Impressively, TreeFix performance is comparable to, and, using expanded search parameters, even exceeds, that of SPIMAP (4.8% and 6.6% improvement in duplication/loss precision, <3.3% difference in all other metrics). This is despite the SPIMAP model being used to generate the simulated trees, and SPIMAP incorporating a number of additional parameters, including species divergence times, duplication and loss rates, and lineage-specific gene rates, in its model, whereas TreeFix uses only the species tree topology. It is possible that given a longer search time, SPIMAP would perform the best, though it is also worthwhile to note that SPIMAP already has an average runtime 2.3× that of RAxML+TreeFix (long) and 16.4× that of RAxML+TreeFix (with default search parameters).
Our goal with TreeFix was to develop a method that is feasible enough to include in a phylogenomic pipeline containing thousands of trees and a variety of family sizes. Thus, we also evaluated its reconstruction speed and scalability with gene family size. We found that TreeFix reconstructs gene trees with accuracy comparable to species tree aware Bayesian methods at a fraction of the runtime (Fig. 2f). Furthermore, TreeFix consistently outperforms other methods across a range of gene family sizes, and its runtime increases at the same rate as RAxML runtime (Supplementary Section S6, and Supplementary Fig. S6), meaning that TreeFix can easily be inserted into existing phylogenetic pipelines without a noticeable increase in runtime complexity.
Real data set
We have also assessed the performance of TreeFix on a real data set. Most TreeFix trees were well supported: the minimum and mean bootstraps averaged over all trees were 51.8% and 85.8%, respectively. (This is similar to RAxML support at 54.0% and 86.8%.) As the ground truth is not known for real data, we used several informative metrics to assess the quality of reconstructed gene trees (Table 1).
Table 1.
Evaluation of several phylogenetic programs on real fungal dataset
| Programa | % Orthsb | # Orthsc | # Dupsc | # Lossesc | DCSd | % GCe | % Fail SHf | RFg | Runtimeh |
|---|---|---|---|---|---|---|---|---|---|
| TreeFix (long) | 96.4 | 574,946 | 6,062 | 10,981 | 0.649 | 97.3 | * | 0.306 | 21.35 min |
| TreeFix | 95.2 | 569,664 | 6,505 | 12,532 | 0.609 | 94.6 | * | 0.302 | 45.68 s |
| NOTUNG (100) | 96.1 | 582,581 | 6,161 | 10,835 | 0.659 | 89.2 | 19.2 | 0.285 | 0.41 s |
| NOTUNG (90) | 89.1 | 556,685 | 9,906 | 23,917 | 0.395 | 94.6 | 7.5 | 0.211 | 0.38 s |
| NOTUNG (50) | 70.1 | 487,875 | 18,322 | 54,101 | 0.191 | 89.2 | 0.8 | 0.051 | 0.40 s |
| tt (3) | 82.8 | 522,834 | 9,780 | 26,621 | 0.354 | 89.2 | 16.3 | 0.224 | 3.29 s |
| tt (2) | 76.5 | 503,323 | 12,552 | 35,898 | 0.272 | 89.2 | 10.7 | 0.171 | 0.18 s |
| tt (1) | 70.0 | 482,439 | 16,310 | 48,036 | 0.206 | 89.2 | 5.1 | 0.100 | 0.05 s |
| SPIMAP | 96.5 | 557,981 | 5,407 | 10,384 | 0.650 | 83.8 | – | – | 21.89 min |
| TreeBest | 79.5 | 480,680 | 11,240 | 34,287 | 0.266 | 81.1 | – | – | 25.72 s |
| RAxML | 63.8 | 462,039 | 21,083 | 64,037 | 0.159 | 89.2 | – | – | 4.32 min |
aSee Supplementary Section S4 for program details.
bPercentage of 183,374 syntenic orthologs recovered.
cNumber of pairwise orthologs, duplications, and losses inferred across all gene trees.
dAverage duplication consistency score.
ePercentage of 37 recent gene converted paralogs recovered.
fFor the hybrid methods, percentage of trees that fail the SH test compared with the input RAxML trees at α = 0.05. By design, TreeFix always returns a statistically equivalent tree (* = 0).
gFor the hybrid methods, average RF distance compared with the input RAxML trees.
hAverage runtime for reconstructing each gene tree. Note that TreeBest and RAxML were run with 100 bootstraps.
For the first metric, we assessed each program's ability to infer syntenic orthologs, defined as pairwise orthologs that are highly likely to be orthologs given their surrounding conserved gene order. We found that TreeFix recovers syntenic orthologs with 95.2–97.6% sensitivity, comparable to SPIMAP at 96.5% and NOTUNG at 96.1% and a significant improvement over RAxML, which performed the worst, at 63.8%. However, note that these high sensitivities are also accompanied by predictions of as many as 24.4% more orthologs compared with other methods, suggesting that the improvement in sensitivity could be tied to a loss in specificity.
The second metric evaluates the total number of inferred duplications and losses across the clade. We, of course, expect the hybrid methods to infer much fewer duplications and losses compared with RAxML, as their objective is to minimize the duplication–loss cost by rearranging the input RAxML gene tree. Here, SPIMAP infers the fewest number of events, though again, TreeFix, SPIMAP, and NOTUNG found far fewer events than the other methods, inferring at least 33.5% fewer duplications and 47.6% fewer losses.
For the third metric, we used the duplication consistency score (Vilella et al. 2009) to evaluate the plausibility of the inferred duplications by each method. For each duplication node, this score computes the percentage of species overlap in the 2 child subtrees, under the assumption that a low species overlap is indicative of a false duplication (followed by many compensating losses). We found that TreeFix, SPIMAP, and NOTUNG show similar duplication consistency distributions (Supplementary Fig. S3) and again outperform the other methods, with SPIMAP detecting the fewest fully inconsistent duplications (score = 0) and NOTUNG detecting the most fully consistent duplications (score = 1).
The fourth metric assesses each program's ability to recover more recent duplications due to gene conversion events, which effectively tests the ability of species tree aware and hybrid methods to properly weigh conflicting species information and sequence information. Here, we found that TreeFix performs the best, recovering 94.6% of recent gene converted paralogs compared with the next best methods at 89.2%. This suggests that our approach of balancing species and sequence information using a likelihood ratio test may be superior to Bayesian (SPIMAP) or penalized likelihood (TreeBest) approaches, as well as approaches that ignore sequence information (NOTUNG, tt) or species information (RAxML) in the final tree. (One parameterization of NOTUNG was also able to recover 94.6% of these paralogs but only at the expense of far lower scores across the other metrics.) Interestingly, while neither the species tree aware nor the hybrid methods model gene conversion, the hybrid methods (>89.2%) outperform the species tree aware methods (81.1–83.8%) and are able to attain performance at least as well as the sequence-only method (89.2%), suggesting that the underlying assumptions of these hybrid methods do not tend to cause species information to override sequence information at the expense of recovering gene conversion events.
Note that, according to our metrics, TreeFix shows performance comparable to that of SPIMAP and NOTUNG. The high performance of SPIMAP is unsurprising because it uses a sophisticated Bayesian approach. In addition, SPIMAP requires extensive preparation and training, and due to excessive runtimes, cannot easily be applied to larger data sets. In fact, we believe this demonstrates the advantages of TreeFix, as it is able to achieve these high levels of accuracy while requiring far fewer modeling assumptions and no additional training or parameter estimation.
We also believe that TreeFix has advantages over NOTUNG in several ways. For example, as we previously showed (Fig. 2), our first metric of ortholog sensitivity may not reflect topological inaccuracies, and NOTUNG was only able to achieve these high levels of performance by considering all branches with bootstrap support <100% of the maximum bootstrap as weak. Furthermore, both NOTUNG and tt operate under the implicit assumption that by only using minor rearrangements, the final output tree is still supported by the sequence data. This assumption may not hold, however; if we compare output trees against input trees, we found that RF distance and p-value have little correlation (Supplementary Fig. S4). Although NOTUNG can attain high performance using our metrics, almost 19.2% of the resulting trees are no longer supported by the sequence data (e.g., they fail the SH test at α = 0.05). In comparison, TreeFix can attain higher RF scores, reaching parts of the tree space unreachable by the other hybrid methods, while also returning a tree supported by the sequence data.
Effect of Using Alternative Species Tree Topologies
In practice, the true species tree is not known with certainty. Therefore, we also evaluated how robust TreeFix is to incorrect species tree topologies. For the 16 fungi data set, we assumed the correct species tree topology matched that of Butler et al. (2009), which used additional evidence from genomic rearrangements, synteny, and nucleotide, purine + pyrimidine, and peptide alignments. Here, we re-evaluated the simulated fungi data sets using four alternative species tree topologies (Supplementary Fig. S7a). These topologies were chosen by evaluating a real data set of 739 one-to-one syntenic orthologs. A concatenated nucleotide alignment of these 739 families supported topology T4, which differs from our assumed species tree topology T in 3 branches (the single branch differences make up topologies T1 − T3). However, the differences in sequence support between the alternative topologies and the assumed true topology were also found to be negligible (SH-test, p ≈ 1 in all cases).
For the simulated data set, topological accuracy decreases dramatically (by 62.5–92.3%) when an incorrect species tree is used (Supplementary Fig. S7), as expected. Surprisingly, however, using this metric, TreeFix using a species tree topology with a single branch error outperformed RAxML using the correct topology (recall that while RAxML is a sequence-only method, the resulting tree is still reconciled against the correct species tree). This suggests that incorrect species tree topologies still provide a lot of correct information, and furthermore, this additional information is sufficient to overcome gene tree errors caused by uncertainty in the sequence data. Using more robust metrics, we found that branch accuracy and duplication precision are reduced, though to a lesser effect (by 10.0–22.6% and 5.0–24.6%), and that ortholog inference is robust to species tree topology errors (>98.6% accuracy), as is duplication sensitivity (>92.2% accuracy, <0.7% difference). Again, using branch accuracy as our metric, TreeFix using species tree topologies with a single error outperformed TreeBest and RAxML using the correct topology. Even using a species tree topology with 3 branch errors, TreeFix performed as well as RAxML using the correct topology. This improvement is even more pronounced for duplication accuracy: TreeFix using an incorrect topology is able to outperform all other evaluated phylogenetic methods except SPIMAP using the correct topology. However, species tree topology errors do seem to cause errors in loss inference (17.1–60.7% decrease in sensitivity, 32.3–82.3% decrease in precision), an unsurprising result, as many of the inferred losses have likely migrated to other parts of the gene tree.
For the real data set, we found that using alternative species tree topologies, TreeFix shows similar improvement over RAxML as with the assumed correct species tree topology (e.g., higher recovery of syntenic orthologs, lower number of inferred duplications and losses, higher duplication consistency, higher recovery of gene conversion events; Supplementary Tables S3 and S4). Furthermore, we found high agreement between ortholog calls (>97.3%), with less agreement in duplication and loss inference (55.6–69.2%, 29.7–71.1%).
Using the real data set, we also analyzed support for our alternative species tree topologies using RAxML and TreeFix gene trees. Indeed, one of the main applications of gene tree error correction is to determine the species tree topology most supported by the corrected gene trees (Górecki and Eulenstein 2011), that is, the species tree topology with the fewest event counts. One advantage of this approach is that it allows us to make use of all gene families rather than only one-to-one gene families, as is the case when testing sequence support using concatenated alignments. Rather than looking only at event counts, however, we tested whether the differences in event counts between multiple species tree topologies are significant. That is, we found event count distributions using bootstrapped gene trees with the assumed correct species tree topology, then determined the p-value of the event counts with the alternative species tree topologies. If p < α, the gene trees support one species tree topology over the other, whereas if p ≥ α, there is not enough evidence to support a single species tree topology. As with the concatenated alignment, we found that all alternative topologies are equally supported (RAxML – T1: p = 0.27, T2: p = 0.28, T3: p = 0.26, T4: p = 0.14; TreeFix – T1: p = 0.61, T2: p = 0.64, T3: p = 0.64, T4: p = 0.51; one-sided test). Interestingly, TreeFix returns higher p-values than RAxML. Thus, if we used a different significance level, for example, an α for which pRAxML < α < pTreeFix, we might conclude that an alternative species tree topology is not supported by the RAxML gene trees but is supported by the TreeFix trees. Because TreeFix returns gene trees that are statistically equivalent to the RAxML trees, this suggests that when using sequence-only methods, the evidence supporting one species tree topology over another can be partly attributed to insufficient sequence information. Therefore, care should be taken when using gene tree parsimony methods that reconstruct species trees based on sequence-only gene trees.
In summary, we found that TreeFix is more accurate than RAxML even when the species tree topology contains possible errors. In practice, if the species tree topology is uncertain, one conservative approach is to run TreeFix with multiple topologies and take the intersection of their inferred orthologs and events. Alternatively, if the multiple topologies are believed to be equally likely, then one could combine gene tree bootstraps into a single pool and from that pool, perform tree consensus to get branch bootstrap values.
Effect of Species Tree Divergence and Size
We are also interested in how TreeFix performs for a variety of species trees; in particular, how might features of the species tree, such as speciation rate and tree size (number of extant taxa), affect performance? To address this, we simulated species trees using TreeSample (Hartmann et al. 2010) with a constant-rate birth–death model and a variety of settings for the speciation rate (0.05–1 events/species/myr) and tree size (5–100 extant species). In all cases, TreeFix shows dramatic improvement over most other programs (Supplementary Fig. S8). (SPIMAP was not run on these gene trees due to model differences, and NOTUNG performed better than TreeFix in some cases, for reasons discussed below.)
As the speciation rate increases, in effect causing shorter branches in the species tree, we found that the topology and branch accuracy of TreeFix and NOTUNG remain relatively constant whereas the duplication and loss precision decrease. In contrast, all other methods show a decrease in performance across all metrics, which is understandable, as shorter branches result in more similar gene sequences, making it harder for typical phylogenetic methods to accurately reconstruct gene trees. Also note that for high speciation rates, NOTUNG is able to outperform TreeFix if we lower the threshold for uncertain branches. We believe this is because fast speciation rates with a constant tree size result in shorter species tree depths and fewer total gene duplications and losses (under our simulation model), thus producing gene trees that are highly congruent to the species trees. Therefore, ignoring sequence data and reconstructing the gene trees most congruent to the species tree, as in NOTUNG, results in high accuracy.
Furthermore, we found that TreeFix (with long search settings) shows consistent or only minor degradations in performance as the tree size increases, suggesting that high accuracy is achievable by balancing sequence and species tree information and increasing the tree search space. In contrast, the performances of RAxML, NOTUNG, tt, and, to some degree, TreeBest and TreeFix (with quick search settings) decrease dramatically with increasing tree size. This can be attributed to larger species trees resulting in more duplication and loss events per gene tree and thus more incongruence between gene trees and species trees. Note that for large tree sizes, NOTUNG is again able to outperform TreeFix if many rearrangements are allowed. With such a parameter setting, NOTUNG performance, as measured by duplication and loss precision, increases with increasing tree size. We believe this is a result of large species trees generating large gene trees so that many branches in the gene tree reconstruction are uncertain. This allows NOTUNG more freedom in its reconstruction compared with small gene trees, and this larger search space translates to increased accuracy. Finally, note that TreeFix is scalable to many species, and again scales at the same rate as RAxML, whereas one major limitation of Bayesian approaches is their inability to handle large species trees.
As sequencing costs continue to decline, both the net speciation rate and size of species trees will only increase. Given its improved accuracy over other methods and its scalability compared with more complex approaches, we believe that TreeFix should be useful for future phylogenetic analyses.
Discussion
In this article, we have presented a new framework for combining sequence and species tree information in a principled manner. In addition, we have described a novel phylogenetic algorithm TreeFix that uses this framework to dramatically improve gene tree reconstructions, with performance comparable to the most sophisticated gene tree reconstruction algorithms achievable at a fraction of the runtime.
A major feature of TreeFix is its simplicity. There are few assumptions or parameters, and the algorithm's behavior is easy to understand and control. The output gene tree from TreeFix is guaranteed to be statistically equivalent to the input tree, which is a condition that is directly interpretable and can be easily controlled through the test statistic and significance level. In contrast, other hybrid methods are not as careful in balancing the trade-off between species tree congruence and sequence data likelihood, likely resulting in their lower performance in our evaluations. Methods that do balance these 2 types of information in a more principled way (e.g., SPIMAP and PrIME-GSR) require more modeling assumptions and parameters, which may be difficult to make or obtain in many situations. Thus, we feel that TreeFix offers a useful and powerful approach that will likely be applicable to many phylogenetic data sets.
Additionally, TreeFix's modeling assumptions are fully contained within the sequence likelihood and reconciliation model. We have used some of the most basic phylogenetic assumptions in our analysis (GTR-Γ model of evolution and a duplication–loss reconciliation cost). Therefore, unlike species tree aware methods that tend to make many assumptions on gene tree evolution, TreeFix is applicable to a variety of data sets and compatible with a wide range of downstream algorithms, including those that account for more complicated evolutionary events. Used in conjunction, TreeFix would correct for gene tree errors due to uncertainty, and other algorithms would correct for errors due to events such as horizontal gene transfer and deep coalescence.
TreeFix is also highly modular. It has no dependency on the method used to compute the input gene tree, and it is very straightforward to substitute other likelihood tests and cost functions. For example, while our current implementation uses RAxML-computed likelihoods and the SH test, users who prefer other likelihood models or test statistics only need to implement a small Python plugin module. We have also implemented a similar modular approach to the cost heuristic, thereby allowing users to incorporate other reconciliation models, such as those that account for horizontal gene transfer (Conow et al. 2010; David and Alm 2011; Doyon et al. 2011), deep coalescence (Maddison 1997; Degnan and Rosenberg 2009), or non-binary reconciliations (Chen et al. 2000), or other sources of information, such as synteny or local region properties. This leaves the complexity of the likelihood and reconciliation models to the user and allows TreeFix to serve as a useful framework for measuring the effects of different statistical tests or cost heuristics on gene tree accuracy.
Along these lines, note that while many statistical tests compare the likelihoods of multiple trees, and we have formulated the gene tree landscape using likelihood values, the framework discussed here could easily be extended to other probabilistic measures, in particular to penalized likelihoods, as in TreeBest, or to a posteriori probabilities, as in Bayesian reconstruction methods. Of course, some of these probabilities rely on topology priors and therefore, our statistical comparisons would no longer be based solely on sequence support. In our approach, we have chosen to differentiate sequence support and species tree support, using likelihood-based statistical tests for the former and a reconciliation cost for the latter.
As with any phylogenetic method, users must decide whether the models for sequence evolution and gene tree-species tree reconciliation used in TreeFix are appropriate for a given data set. The duplication-loss reconciliation cost was chosen as the default in TreeFix as it is broadly applicable, especially in eukaryotes (Goodman et al. 1979; Page 1994; Page 2000; Wapinski et al. 2007; Vilella et al. 2009; Burleigh et al. 2011; Ness et al. 2011) and is the model used by many species tree aware and hybrid methods (Arvestad et al. 2004; Durand et al. 2006; Rasmussen and Kellis 2007; Vilella et al. 2009; Górecki and Eulenstein 2011; Rasmussen and Kellis 2011). Still, if the species under analysis are closely related, it may be appropriate to use more advanced models that combine the duplication, loss, and deep coalescence processes (Rasmussen and Kellis 2012). Similarly, when working with prokaryotic species, models that incorporate horizontal gene transfer may yield better performance (David and Alm 2011; Doyon et al. 2011; Tofigh et al. 2011). As we have mentioned, users have multiple options for correcting possible model mismatches. Because a TreeFix tree is statistically equivalent to the ML tree and equally supported by the sequence data, users can simply run TreeFix as an intermediate step between initial ML gene tree reconstruction and other methods that account for these evolutionary events. Alternatively, users may incorporate the evolutionary model directly into TreeFix by implementing their own reconciliation cost function.
Aside from improved gene tree reconstruction, because TreeFix guarantees that the final error-corrected gene tree is equivalent to the input tree in terms of sequence likelihood, it can also be used to measure the robustness of existing trees in a manner similar to bootstrapping. Furthermore, TreeFix can be used to validate biological conclusions based on phylogenetic analysis. For example, studies that compare duplication and loss counts or posit genome-wide events based on event distributions across the species trees can run TreeFix on their existing gene trees to determine whether their conclusions hold for the TreeFix-corrected gene trees. Those conclusions that are no longer supported should then be further analyzed using other methods. Similarly, TreeFix can be used to test multiple species tree topologies. If multiple topologies are equally supported, then gene trees may be insufficient to resolve the underlying species phylogeny, and other metrics, such as synteny, should be used.
Although we have shown that TreeFix likely would not dramatically increase runtime complexity if applied to RAxML trees, it does currently perform significantly slower than other hybrid methods. This is most likely because we have implemented TreeFix using Python compared with the efficient programming languages (NOTUNG: Java, tt: C++) used by the other programs. Furthermore, while we have not implemented many optimizations thus far, many of the techniques used by NOTUNG and tt to reuse computation between tree proposals could also be applied to TreeFix, or the species tree topology or likelihood landscape could be used to more efficiently guide the tree search. Recent advances using GPU computation (Suchard and Rambaut 2009) may also be leveraged. Thus, future speed improvements are likely possible.
In conclusion, we believe that the concepts presented here offer a simple yet powerful alternative to existing hybrid and Bayesian models of gene tree reconstruction, and we feel that TreeFix will be a valuable addition to the phylogenetists' toolkit, as it can be easily integrated into existing phylogenomic pipelines to significantly improve gene tree reconstructions.
Supplementary Material
Supplementary material, including data files and/or online-only appendices, can be found at http://datadryad.org and in the Dryad data repository (doi:10.5061/dryad.44cb5).
Funding
This work was supported by a Kambourides Fellowship [to Y.W.] and National Science Foundation CAREER award [0644282 to M.K.].
Acknowledgements
We thank the MIT CompBio group for helpful comments, feedback, and discussions. We are also grateful to Lacey Knowles, Laura Kubatko, Ruriko Yoshida, and two anonymous reviewers for their constructive comments on the article.
References
- Arvestad L., Berglund A.-C., Lagergren J., Sennblad B. Proceedings of the Eighth Annual International Conference on Research in Computational Molecular Biology RECOMB '04 ACM. New York (NY): ACM; 2004. Gene tree reconstruction and orthology analysis based on an integrated model for duplications and sequence evolution; pp. 326–335. [Google Scholar]
- Burleigh J.G., Bansal M.S., Eulenstein O., Hartmann S., Wehe A., Vision T.J. Genome-scale phylogenetics: Inferring the plant tree of life from 18,896 gene trees. Syst. Biol. 2011;60:117–125. doi: 10.1093/sysbio/syq072. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Butler G., Rasmussen M.D., Lin M.F., Santos M.A.S., Sakthikumar S., Munro C.A., Rheinbay E., Grabherr M., Forche A., Reedy J.L., Agrafioti I., Arnaud M.B., Bates S., Brown A.J.P., Brunke S., Costanzo M.C., Fitzpatrick D.A., de Groot P.W.J., Harris D., Hoyer L.L., Hube B., Klis F.M., Kodira C., Lennard N., Logue M.E., Martin R., Neiman A.M., Nikolaou E., Quail M.A., Quinn J., Santos M.C., Schmitzberger F.F., Sherlock G., Shah P., Silverstein K.A.T., Skrzypek M.S., Soll D., Staggs R., Stansfield I., Stumpf M.P.H., Sudbery P.E., Srikantha T., Zeng Q., Berman J., Berriman M., Heitman J., Gow N.A.R., Lorenz M.C., Birren B.W., Kellis M., Cuomo C.A. Evolution of pathogenicity and sexual reproduction in eight Candida genomes. Nature. 2009;459:657–662. doi: 10.1038/nature08064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen K., Durand D., Farach-Colton M. NOTUNG: A program for dating gene duplications and optimizing gene family trees. J. Comput. Biol. 2000;7:429–447. doi: 10.1089/106652700750050871. [DOI] [PubMed] [Google Scholar]
- Conow C., Fielder D., Ovadia Y., Libeskind-Hadas R. Jane: A new tool for the cophylogeny reconstruction problem. Algorithms Mol. Biol. 2010;5:16. doi: 10.1186/1748-7188-5-16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- David L.A., Alm E.J. Rapid evolutionary innovation during an Archaean genetic expansion. Nature. 2011;469:93–96. doi: 10.1038/nature09649. [DOI] [PubMed] [Google Scholar]
- Degnan J.H., Rosenberg N.A. Gene tree discordance, phylogenetic inference and the multispecies coalescent. Trends Ecol. Evol. 2009;24:332–340. doi: 10.1016/j.tree.2009.01.009. [DOI] [PubMed] [Google Scholar]
- Delsuc F., Brinkmann H., Philippe H. Phylogenomics and the reconstruction of the tree of life. Nat. Rev. Genet. 2005;6:361–375. doi: 10.1038/nrg1603. [DOI] [PubMed] [Google Scholar]
- Doyon J.-P., Scornavacca C., Gorbunov K.Y., Szöllősi G.J., Ranwez V., Berry V. An efficient algorithm for gene/species trees parsimonious reconciliation with losses, duplications and transfers. In: Tannier E, editor. Comparative genomics. Vol. 6398. Berlin/Heidelberg: Springer; 2011. pp. 93–108. Lecture Notes in Computer Science. [Google Scholar]
- Durand D., Hallórsson B.V., Vernot B. A hybrid micro–macroevolutionary approach to gene tree reconstruction. J. Comput. Biol. 2006;13:320–335. doi: 10.1089/cmb.2006.13.320. [DOI] [PubMed] [Google Scholar]
- Eisen J.A. Phylogenomics: Improving functional predictions for uncharacterized genes by evolutionary analysis. Genome Res. 1998;8:163–167. doi: 10.1101/gr.8.3.163. [DOI] [PubMed] [Google Scholar]
- Felsenstein J. Inferring phylogenies. 2nd. Sunderland (MA): Sinauer Associates; 2003. [Google Scholar]
- Gascuel O. BIONJ: An improved version of the NJ algorithm based on a simple model of sequence data. Mol. Biol. Evol. 1997;14:685–695. doi: 10.1093/oxfordjournals.molbev.a025808. [DOI] [PubMed] [Google Scholar]
- Goldman N., Anderson J.P., Rodrigo A.G. Likelihood-based tests of topologies in phylogenetics. Syst. Biol. 2000;49:652–670. doi: 10.1080/106351500750049752. [DOI] [PubMed] [Google Scholar]
- Goodman M., Czelusniak J., Moore G.W., Romero-Herrera A., Matsuda G. Fitting the gene lineage into its species lineage, a parsimony strategy illustrated by cladograms constructed from globin sequences. Syst. Zool. 1979;28:132–163. [Google Scholar]
- Górecki P., Eulenstein O. In: A linear time algorithm for error-corrected reconciliation of unrooted gene trees. Chen J., Wang J., Zelikovsky A., editors. Vol. 6674. Berlin / Heidelberg: Springer; 2011. Pages 148–159–159 in Lecture Notes in Computer Science. [Google Scholar]
- Guindon S., Gascuel O. A simple, fast, and accurate algorithm to estimate large phylogenies by maximum likelihood. Syst. Biol. 2003;52:696–704. doi: 10.1080/10635150390235520. [DOI] [PubMed] [Google Scholar]
- Hahn M. Bias in phylogenetic tree reconciliation methods: Implications for vertebrate genome evolution. Genome Biol. 2007;8:R141. doi: 10.1186/gb-2007-8-7-r141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hahn M.W., Han M.V., Han S.-G. Gene family evolution across 12 Drosophila genomes. PLoS Genet. 2007;3:e197. doi: 10.1371/journal.pgen.0030197. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hartmann K., Wong D., Stadler T. Sampling trees from evolutionary models. Syst. Biol. 2010;59:465–476. doi: 10.1093/sysbio/syq026. [DOI] [PubMed] [Google Scholar]
- Jiao Y., Wickett N.J., Ayyampalayam S., Chanderbali A.S., Landherr L., Ralph P.E., Tomsho L.P., Hu Y., Liang H., Soltis P.S., Soltis D.E., Clifton S.W., Schlarbaum S.E., Schuster S.C., Ma H., Leebens-Mack J., dePamphilis C.W. Ancestral polyploidy in seed plants and angiosperms. Nature. 2011;473:97–100. doi: 10.1038/nature09916. [DOI] [PubMed] [Google Scholar]
- Kishino H., Hasegawa M. Evaluation of the maximum likelihood estimate of the evolutionary tree topologies from DNA sequence data, and the branching order in hominoidea. J. Mol. Evol. 1989;29:170–179. doi: 10.1007/BF02100115. [DOI] [PubMed] [Google Scholar]
- Maddison W.P. Gene trees in species trees. Syst. Biol. 1997;46:523–536. [Google Scholar]
- Ness R.W., Graham S.W., Barrett S.C. Reconciling gene and genome duplication events: Using multiple nuclear gene families to infer the phylogeny of the aquatic plant family pontederiaceae. Mol. Biol. Evol. 2011;28:3009–3018. doi: 10.1093/molbev/msr119. [DOI] [PubMed] [Google Scholar]
- Page R.D. Maps between trees and cladistic analysis of historical associations among genes,organisms, and areas. Syst. Biol. 1994;43:58–77. [Google Scholar]
- Page R.D. Extracting species trees from complex gene trees: Reconciled trees and vertebrate phylogeny. Mol. Phylogenet. Evol. 2000;14:89–106. doi: 10.1006/mpev.1999.0676. [DOI] [PubMed] [Google Scholar]
- Rasmussen M.D., Kellis M. Accurate gene-tree reconstruction by learning gene- and species-specific substitution rates across multiple complete genomes. Genome Res. 2007;17:1932–1942. doi: 10.1101/gr.7105007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rasmussen M.D., Kellis M. A Bayesian approach for fast and accurate gene tree reconstruction. Mol. Biol. Evol. 2011;28:273–290. doi: 10.1093/molbev/msq189. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rasmussen M.D., Kellis M. Unified modeling of gene duplication, loss, and coalescence using a locus tree. Genome Res. 2012;22:755–765. doi: 10.1101/gr.123901.111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robinson D., Foulds L. Comparison of phylogenetic trees. Math. Biosci. 1981;53:131–147. [Google Scholar]
- Ronquist F., Huelsenbeck J.P. MrBayes 3: Bayesian phylogenetic inference under mixed models. Bioinformatics. 2003;19:1572–1574. doi: 10.1093/bioinformatics/btg180. [DOI] [PubMed] [Google Scholar]
- Shimodaira H., Hasegawa M. Multiple comparisons of log-likelihoods with applications to phylogenetic inference. Mol. Biol. Evol. 1999;16:1114–1116. [Google Scholar]
- Shimodaira H., Hasegawa M. CONSEL: For assessing the confidence of phylogenetic tree selection. Bioinformatics. 2001;17:1246–1247. doi: 10.1093/bioinformatics/17.12.1246. [DOI] [PubMed] [Google Scholar]
- Stamatakis A. RAxML-VI-HPC: Maximum likelihood-based phylogenetic analyses with thousands of taxa and mixed models. Bioinformatics. 2006;22:2688–2690. doi: 10.1093/bioinformatics/btl446. [DOI] [PubMed] [Google Scholar]
- Suchard M.A., Rambaut A. Many-core algorithms for statistical phylogenetics. Bioinformatics. 2009;25:1370–1376. doi: 10.1093/bioinformatics/btp244. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Swofford D.L. PAUP*. Phylogenetic analysis using parsimony (*and other methods). 4th. Sinauer Associates; 2002. [Google Scholar]
- Tofigh A., Hallett M., Lagergren J. Simultaneous identification of duplications and lateral gene transfers. IEEE/ACM Trans. Comput. Biol. Bioinformatics. 2011;8:517–535. doi: 10.1109/TCBB.2010.14. [DOI] [PubMed] [Google Scholar]
- Vilella A.J., Severin J., Ureta-Vidal A., Heng L., Durbin R., Birney E. EnsemblCompara GeneTrees: Complete, duplication-aware phylogenetic trees in vertebrates. Genome Res. 2009;19:327–335. doi: 10.1101/gr.073585.107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wapinski I., Pfeffer A., Friedman N., Regev A. Natural history and evolutionary principles of gene duplication in fungi. Nature. 2007;449:54–61. doi: 10.1038/nature06107. [DOI] [PubMed] [Google Scholar]
- Zmasek C.M., Eddy S.R. A simple algorithm to infer gene duplication and speciation events on a gene tree. Bioinformatics. 2001;17:821–828. doi: 10.1093/bioinformatics/17.9.821. [DOI] [PubMed] [Google Scholar]