Pruning Rogue Taxa Improves Phylogenetic Accuracy: An Efficient Algorithm and Webservice

Abstract

The presence of rogue taxa (rogues) in a set of trees can frequently have a negative impact on the results of a bootstrap analysis (e.g., the overall support in consensus trees). We introduce an efficient graph-based algorithm for rogue taxon identification as well as an interactive webservice implementing this algorithm. Compared with our previous method, the new algorithm is up to 4 orders of magnitude faster, while returning qualitatively identical results. Because of this significant improvement in scalability, the new algorithm can now identify substantially more complex and compute-intensive rogue taxon constellations. On a large and diverse collection of real-world data sets, we show that our method yields better supported reduced/pruned consensus trees than any competing rogue taxon identification method. Using the parallel version of our open-source code, we successfully identified rogue taxa in a set of 100 trees with 116 334 taxa each. For simulated data sets, we show that when removing/pruning rogue taxa with our method from a tree set, we consistently obtain bootstrap consensus trees as well as maximum-likelihood trees that are topologically closer to the respective true trees.

An important task in phylogenetic analysis is to assess to which degree inferred phylogenetic relationships are supported by the underlying data. Irrespective of the phylogenetic inference method used, support values are generally extracted from a set of trees. Bayesian sampling (e.g., Ronquist and Huelsenbeck 2003) produces a set of trees that is used for calculating Bayesian support values. For inferences under maximum likelihood (e.g., Stamatakis 2006) or parsimony (e.g., Swofford 2003), the nonparametric bootstrap is typically applied (Felsenstein 1985): the original alignment is resampled and a so-called bootstrap tree is inferred for each alignment replicate under the given optimality criterion. Subsequently, the resulting collection of bootstrap trees is either used for computing a consensus tree or for drawing branch support values onto the best-known tree.

The resolution in a consensus tree and the branch support on the best-known tree can be substantially deteriorated by rogues (the term rogue/rogue taxa was introduced by Wilkinson 1996), which assume varying and often contradictory positions in the tree set. The rogue phenomenon is usually attributed to ambiguous or insufficient phylogenetic signal (Sanderson and Shaffer 2002).

The degree of resolution in a consensus tree is also determined by the chosen consensus threshold. A consensus tree only contains those branches (also referred to as bipartitions or splits) that occur more often in all bootstrap trees than specified by the threshold. Common thresholds are the strict consensus (SC) threshold (only bipartitions contained in all trees) or majority-rule consensus (MRC) threshold (bipartitions that are present in more than half of the trees).

Determining the “correct” position of a rogue in a phylogenetic tree is tedious (Shafer and Hall 2010) and therefore rogues, once identified, are mostly simply excluded (pruned) in current studies. Stability measures based on triplet frequencies (Thorley and Wilkinson 1999) or node distances (Maddison and Maddison 2008) are often applied (Dunn et al. 2008; Sperling et al. 2009; Thomson and Shaffer 2010a,b) to identify rogues. Recently, Pattengale et al. introduced a fast method to approximate the expected increase of resolution in the consensus tree when rogues are pruned. We refer to this algorithm as bipartition merging algorithm (BMA). Our exact, but significantly slower, single-taxon algorithm (STA) explicitly calculates the exact support improvement induced by pruning only one taxon at a time (Aberer and Stamatakis 2011). We have already demonstrated that the STA and BMA consistently identify rogues with a more harmful effect on consensus tree support than rogues identified by triple frequency or node distance methods.

Our novel algorithm overcomes the drawbacks of both the STA and the BMA approach: for each set of putative rogue taxa, we can now exactly calculate the support value change induced by pruning the taxa. In contrast to the STA, our scalable algorithm can resolve complex rogue taxon constellations, where multiple taxa need to be pruned simultaneously to improve support values. Excessive runtime requirements limited the size of trees that could be analyzed with the STA in reasonable times to approximately 100 taxa. In addition, for the BMA, memory consumption represented a significant limitation with respect to the tree sizes (~ 2500 taxa) that can be handled on desktop systems. For appropriate parameter settings, our algorithm is several orders of magnitude faster than the STA and substantially more memory-efficient than the BMA (i.e., requiring between 56.2% and 83.5% less memory for data sets with > 1000 taxa considered in this study). Therefore, it can be applied to bootstrap tree sets of extremely large trees exceeding 100 000 taxa.

We also make available a freely accessible webservice for rogue taxon analysis that implements our new algorithm as well as alternative algorithms. It also offers advanced workbench features that allow systematists to assess and visually compare results of rogue taxon inferences using various methods and parameter settings, before taking a final decision on which taxa to prune.

Algorithm

We outline the fundamental ideas of our algorithm (referred to as RogueNaRok) omitting technical details. A more formal problem and algorithm description is provided in Supplementary Material Online, Appendix A).

Rogue taxon identification can be formulated as optimization problem. The task is to identify a set of taxa that, if pruned from the underlying bootstrap trees, yields a reduced consensus tree containing additional bipartitions or increased support values. Compared with the BMA, we use a more fine-grain optimality criterion, the relative bipartition information criterion (RBIC). It is defined as the sum of all support values divided by the maximum possible support in a fully bifurcating tree with the initial (i.e., before pruning any rogues) set of taxa.

If (rogue) taxa are pruned from bootstrap trees, the support values in the resulting reduced consensus tree change, because previously distinct bipartitions become identical (i.e., they merge). As a consequence, such merged bipartitions are then contained in all trees that contained any of the previously distinct bipartitions. If the support of the resulting merged bipartition exceeds the consensus threshold (e.g., 50% for MRC), the consensus tree will contain an additional bipartition. The support of existing consensus bipartitions can also increase by such mergers.

For each bipartition pair, we can determine the minimal set of taxa that induces a merger (referred to as dropset). This is computationally challenging and previous experiments (Aberer and Stamatakis 2011) indicate that, for the optimization problem at hand, small dropsets are sufficient (because, e.g., large dropsets are likely to induce a merger between consensus bipartitions, thus decreasing consensus tree resolution). Because of this, we parameterize our algorithm with l, dropsets larger than l are not considered. Through adequate sorting and indexing, dropsets up to a size of l taxa can be computed efficiently.

We store the information about bipartition merging behavior in a data structure called merger graph. In such a graph 2 bipartitions share an edge, if there exists a dropset no larger than l. Edges are labeled with the smallest dropset that induces the merger. In the next step, the algorithm iterates over all dropsets encountered in the previous labeling phase and determines all mergers that are induced by the dropset. Finally, we evaluate for each dropset how our optimality criterion, the RBIC, changes. The dropset yielding the highest RBIC increase is then permanently removed from the taxon set and our algorithm starts over again. Because permanently pruning a dropset only induces changes in a small part of the merger graph, we can simply keep most edges from the first iteration in subsequent iterations and only update the graph as required. Thus, significant runtime improvements can be obtained for all but the first iteration. The algorithm stops, if the RBIC cannot be further improved by pruning more taxa.

Software and Webservice

The RogueNaRok algorithm is available as open-source code at https://github.com/aberer/RogueNaRok. Apart from the RogueNaRok algorithm, it also implements the maximum agreement subtree, the triple frequency (i.e., quartet frequency for unrooted trees), and node distance methods as well as a tool for pruning taxa from a set of input trees.

The corresponding webservice for interactive deployment of RogueNaRok and related methods is available at http://exelixis-lab.org/roguenarok.html. After uploading a set of bootstrap trees, the user can explore how various parameters (e.g., the maximum dropset size) influence rogue taxon identification. If a best-known ML tree has also been uploaded, RogueNaRok can be used to detect rogue taxa that affect support values on the best-known tree. In analogy to the BMA, the user may wish to increase the resolution in a consensus, that is, no rogue taxa will be removed that marginally increase support values, but only those taxa will be pruned that give rise to additional resolution in the consensus tree. Beside using frequency thresholds for consensus trees (SC, MRC, or user-defined), RogueNaRok can also carry out a computationally expensive rogue search that strives to optimize the overall support in a greedily refined MRC tree (see Bryant 2003). Moreover, users can also mark a specific set of taxa as “unprunable” when they need to be contained in the tree or for exploring how rogue identification is affected by such a constraint.

The results of all searches with the RogueNaRok algorithm and alternative stability measures are summarized in a single table. Based on this information, users can manually prune taxa from the input data set, visualize, and subsequently retrieve the pruned result tree. For visualization, we employ the Archaeopteryx tree viewer (Zmasek and Eddy 2001). The tree viewer is configured to also display all previous visualizations and to highlight taxa that are in the current pruning selection. Thus, it is easy for users to determine the topological position of rogue taxa before pruning.

Benchmark

We executed the RogueNaRok algorithm (RNR), the STA, and the BMA on collections of bootstrap trees from 26 real-world multiple sequence alignments. All tree sets contain 1000 trees. The number of taxa ranges between 24 and 7764. Runtime measurements were performed on unloaded 48-core AMD Magny-Cours nodes and averaged over 4 runs. Missing data points represent runs with excessive execution times that were interrupted.

Runtimes

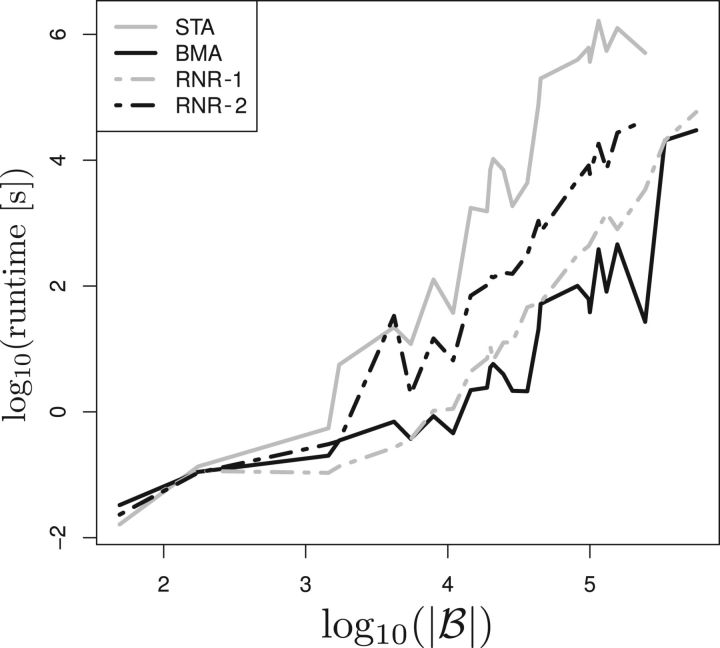
Figure 1 depicts the sequential execution times for the 3 algorithms. We executed the RNR algorithm for maximum dropset sizes of l:= 1 and l:= 2 (denoted as RNR-1 and RNR-2). For all, except the smallest data sets, RNR-1 is significantly faster than STA while yielding qualitatively identical results. Overall, we observe an average runtime improvement between 2 and 3 orders of magnitude. In the case with 2308 taxa and 1000 trees containing 45 022 distinct bipartitions, the RNR-1 algorithm is over 3640 times faster than STA. As indicated in the algorithm description, the largest fraction of the speed improvement in RogueNaRok can be attributed to successive merger graph updates (instead of full recomputations) between iterations. For instance, in the first iteration of the data set with 2000 taxa, RNR-1 spends 137 s in Step 1 to compute the edges (and thereby the minimal dropsets) of the merger graph. In subsequent iterations, updating the merger graph takes between 0.05 and 10 s (mean: 1.2 s).

Figure 1.

Runtimes for the STA, BMA, and RNR algorithm with maximum dropset size l:= 1 and l:= 2. x-axis refers to the initial number of bipartitions |ℬ| for a bootstrap tree collection. Runtimes for MRC as consensus threshold (SC similar).

When choosing a larger value for l, the identification of edges induced by subdropsets for the quadratically growing number of possible dropsets starts dominating runtimes. Nevertheless, RNR-2 is—in most cases—still significantly faster than STA (Fig. 1), while at the same time more complex rogue taxon constellations are identified. Although RNR-2 is considerably slower than the BMA, RNR-1 achieves runtimes that are comparable to the BMA. However, the RNR algorithm can typically identify at least 10 times more potential rogues than the BMA. In terms of runtime per identified rogue, RNR-1 is faster than the BMA in all but 2 cases.

Finally, we deployed the parallel version of RogueNaRok to identify rogue taxa on a set of 100 trees with 116 334 taxa containing a total of 1 002 254 bipartitions using the MRC threshold. On 48 cores, the search took approximately 61 h. By pruning 6864 rogue taxa, the RBIC of the MRC tree could be improved from 72.6% to 75.9%.

Qualitative Improvement

Here, we evaluate how various input parameters of the RNR algorithm affect and improve the support in SC and MRC trees and compare this improvement to consensus trees that are produced after pruning rogues as suggested by the BMA. In general, comparisons to the BMA are difficult, because the BMA optimality criterion penalizes dropsets as a function of the number of taxa that are pruned. We thus adapted BMA (referred to as BMA-mod) to assess how a less conservative criterion for approximating support gain improves resolution. To achieve this, we changed the BMA scoring scheme for dropsets such that it prunes dropsets with the highest per-taxon resolution improvement. Because the inherent approximation errors of the BMA-mod increase rapidly with the number of iterations, we also computed the exact overall support in the consensus tree after each BMA iteration (substantially increasing runtimes). In our analysis, we only consider the intermediate result of BMA which yields the highest overall support with respect to the exact evaluation based on the consensus trees for each iteration. A qualitative comparison of RNR with STA is not required, because RNR and STA can be modified such that RNR-1 and STA yield exactly identical results.

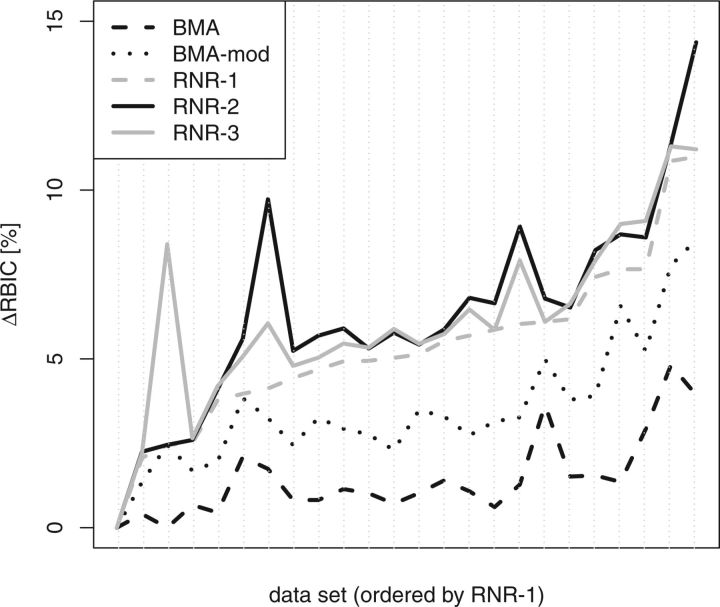
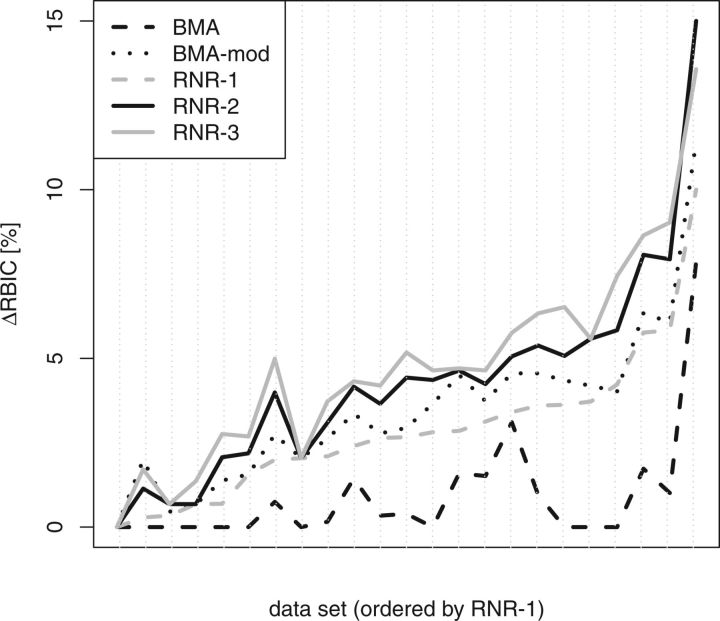
Figures 2 and 3 depict the RBIC improvements obtained by the BMA, BMA-mod, and the RNR algorithm (with l:= 1, l:= 2, and l:= 3). Overall, BMA-mod recovers substantially more support than the default BMA. For MRC trees, RNR-1 performs consistently and substantially better than the BMA and BMA-mod. Although RNR-1 still performs better than BMA for SC trees (Fig. 3), we have to chose l > 1 to outperform BMA-mod. This is in agreement with our previous observations (Aberer and Stamatakis 2011), that is, BMA is more accurate when a SC threshold is used. On the other hand, when using a MRC threshold, RNR may yield less optimal results for l:= 3 compared with l:= 2. Here, RNR-3 performs worse, because 2 dropsets of size 2 pruned in subsequent iterations may yield a higher overall per-taxon RBIC improvement than a single larger dropset of size 3. If the larger dropset is optimal for an iteration, it will be pruned by RNR-3 (unlike RNR-2 which does not evaluate this dropset). Thereby, the possibility of achieving the same effect as pruning the 2 dropsets of size 2 can be lost. RNR-4 is capable of finding the optimal solution in such a scenario; however, the general problem of local optima remains (e.g., RNR-4 may prune a dropset of size 4 instead of 2 dropsets of size 3). Finally, the inferior performance of RNR-3 suggests that for the MRC threshold, dropsets of size 3 (or larger) are rarely necessary or they do not noticeably increase the RBIC of a consensus tree.

Figure 2.

Support improvement (in %) for optimization with a MRC threshold. RNR-l depicts RNR runs with l ∈ [1,3], BMA-mod is a less conservative modification of the BMA.

Figure 3.

Support improvement (in %) for optimization with a SC threshold. RNR-l depicts RNR runs with l ∈ [1,3], BMA-mod is a less conservative modification of the BMA.

Phylogenetic Accuracy

In the previous section, we have shown that pruning rogue taxa as determined by RogueNaRok increases support in the resulting consensus tree to a larger degree than any alternative method. Here, we assess if the support recovered by pruning rogue taxa is biologically meaningful.

For this purpose, we simulated 400 data sets (for details see Supplementary Material Online, Appendix B) for which the “true” tree is known. Thereby we can determine how pruning rogue taxa as identified by RogueNaRok affects the topological congruence between consensus trees as well as best-known trees and the corresponding “true” trees.

When rogue taxa are identified based on support values that are drawn onto a best-known tree, we observe that pruning these rogues yields trees that are topologically closer to the true tree. For each simulated data set, we also identified rogue taxa that affect the support values in the corresponding consensus trees. We detected a linear relationship between the increase of support in the consensus after pruning rogues and the increase of agreement with the true tree. Moreover, under both scenarios (best tree and consensus tree), pruning a taxon set of equal size (as the calculated dropset) at random had a negative effect on the congruence with the true tree.

Thus, the increased support on the best-known tree and the consensus tree obtained through informed rogue pruning is not just a random effect of taxon pruning and thereby reduced tree search space. Instead, our simulations indicate that pruned trees based on an informed rogue taxon removal are topologically closer to the true tree.

Supplementary Material

Supplementary material, including data files and online-only appendices, can be found in the Dryad data repository at http://datadryad.org, doi:10.5061/dryad.sv515.

Funding

This work was supported by the Heidelberg Institutional for Theoretical Studies gGmbH.