Global radiation damage: temperature dependence, time dependence and how to outrun it

The temperature and time dependence of global radiation damage are discussed in the context of outrunning damage at or near room temperature using synchrotron X-ray sources.

Abstract

A series of studies that provide a consistent and illuminating picture of global radiation damage to protein crystals, especially at temperatures above ∼200 K, are described. The radiation sensitivity shows a transition near 200 K, above which it appears to be limited by solvent-coupled diffusive processes. Consistent with this interpretation, a component of global damage proceeds on timescales of several minutes at 180 K, decreasing to seconds near room temperature. As a result, data collection times of order 1 s allow up to half of global damage to be outrun at 260 K. Much larger damage reductions near room temperature should be feasible using larger dose rates delivered using microfocused beams, enabling a significant expansion of structural studies of proteins under more nearly native conditions.

1. Introduction  

X-ray radiation damage is a major factor limiting the amount and quality of structural information that can be obtained from protein and virus crystals (Blake & Phillips, 1962 ▶; Hendrikson, 1976 ▶; Garman, 2003 ▶, 2010 ▶; Nave & Garman, 2005 ▶; Owen et al., 2006 ▶; Holton, 2009 ▶; Holton & Frankel, 2010 ▶). Prior to the 1990s, nearly all structural data sets were collected at temperatures near 300 K. Radiation damage was addressed by using very large crystals and/or by collecting and merging data from multiple crystals. As X-ray sources became more intense and improved X-ray optics and detectors increased diffraction signal-to-noise, much faster data collection and use of much smaller crystals became possible. The effects of global radiation damage then became increasingly limiting. Following practice in electron microscopy, it was eventually shown that crystals cooled to T ≃ 100 K could tolerate much larger X-ray doses without excessive damage, that the cooling itself need not excessively disorder the crystals, and that reduced thermal motions at 100 K often improved diffraction resolution. Development of hardware for easy sample storage, shipping and T = 100 K data collection then led to rapid adoption of cryocrystallographic methods (Rodgers, 1994 ▶; Garman & Schneider, 1997 ▶; Garman, 2003 ▶). Today at least 95% of structures are determined at T = 100 K (Garman, 2010 ▶), and many younger crystallographers have never collected a room-temperature data set.

While cryocrystallography has helped drive the revolution in structural biology, it can impose significant costs. Cooling can cause large (factor of 10 to 100) increases in crystal mosaicity, which in turn can lead to diffraction peak overlap devastating to work on important targets including large macromolecular complexes and viruses. Cooling often introduces significant nonisomorphism, which makes merging of, for example, MAD data sets from multiple small crystals difficult or impossible. Cooling generally does not affect the overall protein fold. However, substantial and relatively obvious structural differences between room and T = 100 K structures are often observed (Deacon et al., 1997 ▶; Karplus et al., 1997 ▶; Sandalova et al., 1999 ▶; Scheidig et al., 1999 ▶). A recent study (Fraser et al., 2009 ▶) using new analysis tools (van den Bedem et al., 2009 ▶; Lang et al., 2010 ▶) showed that catalytically important minor conformations deduced from room-temperature crystallography and NMR can be eliminated on cooling to T = 100 K. Subsequent analysis of data from 30 proteins (Fraser et al., 2011 ▶) indicated that cooling changes or ‘remodels’ the distribution of side-chain conformations for 35% of residues. Cryoprotectants can alter a protein’s hydration structure (Charron et al., 2002 ▶), and may have subtle but important effects such as those examined by Fraser et al., although this has not been systematically explored.

Protein dynamics plays a critical role in catalysis (Rasmussen et al., 1992 ▶; Tilton et al., 1992 ▶), and the relation between structure, dynamics and function is a major focus of structural biology and especially of NMR studies (Benkovic & Hammes-Schiffer, 2006 ▶; Hammes-Schiffer & Benkovic, 2006 ▶; Henzler-Wildman et al., 2007 ▶; Nashine et al., 2010 ▶). At T = 100 K, frozen solvent and protein scaffolding by vitrified solvent inhibit large collective motions, and prevent measurement of the protein’s dynamic response to many biologically relevant perturbations (Moffat, 1989 ▶, 2001 ▶; Schotte et al., 2003 ▶, 2004 ▶; Ihee et al., 2005 ▶; Henzler-Wildman & Kern, 2007 ▶; Bourgeois & Weik, 2009 ▶). Room-temperature crystallographic data can provide highly complementary information to NMR and assist in, for example, identification of allosteric networks (Fraser et al., 2009 ▶).

Crystallographers thus need robust techniques for data collection at or near room temperature, and these must include methods for managing radiation damage in the present era of third- and fourth-generation synchrotron sources. Here we summarize a range of recent studies that enhance our understanding of radiation damage. Our discussion culminates in the exciting possibility that a large fraction of global damage to unfrozen crystals can be outrun by rapid data collection using synchrotron source [not just free-electron laser (FEL) source] intensities.

2. Radiation damage processes and timescales  

The processes that lead to global radiation damage to protein crystals, schematically illustrated in Fig. 1 ▶, take place on an enormous range of timescales. X-ray–electron and electron–electron interactions (Fig. 1a ▶) occur in femtoseconds, and lead to the generation of hundreds of electrons with energies in the 10–100 eV range (Nave & Hill, 2005 ▶; Finfrock et al., 2010 ▶; Sanishvili et al., 2011 ▶) (Fig. 1b ▶). These interact with water and protein, breaking bonds and creating radicals (Dertinger & Jung, 1970 ▶; Coggle, 1983 ▶) (Fig. 1c ▶). These primary damage processes are at most weakly temperature dependent. At sufficiently high temperature, atomic and molecular radicals can diffuse and react with the protein, breaking additional bonds (Fig. 1d ▶); near room temperature, most radical reactions should be complete within a few microseconds (Pryor, 1986 ▶). X-ray- and radical-induced bond breaking increases average atomic separations, creating internal stress that drives lattice expansion. Local bond breaking and other chemical damage trigger local conformational relaxation of, for example, side chains, flexible loops and other more weakly constrained regions (Fig. 1e ▶). The larger of these local structural relaxations likely take place on the microsecond to millisecond timescale of conformation changes observed in undamaged protein (Henzler-Wildman & Kern, 2007 ▶; Bourgeois & Weik, 2009 ▶). As radiochemistry and local relaxation cause ever larger changes to individual protein molecules, the molecules will displace and rotate (Fig. 1f ▶), the local lattice may deform and reorient (Fig. 1g ▶), and the build-up of stress may eventually cause plastic failure and cracking of the crystal (Fig. 1h ▶). These larger motions will proceed on timescales of microseconds to hours or even days. In part because they involve substantial motions of solvent as the protein molecules move from their ideal lattice positions, these timescales will increase as the temperature is decreased toward the glass transition.

Figure 1.

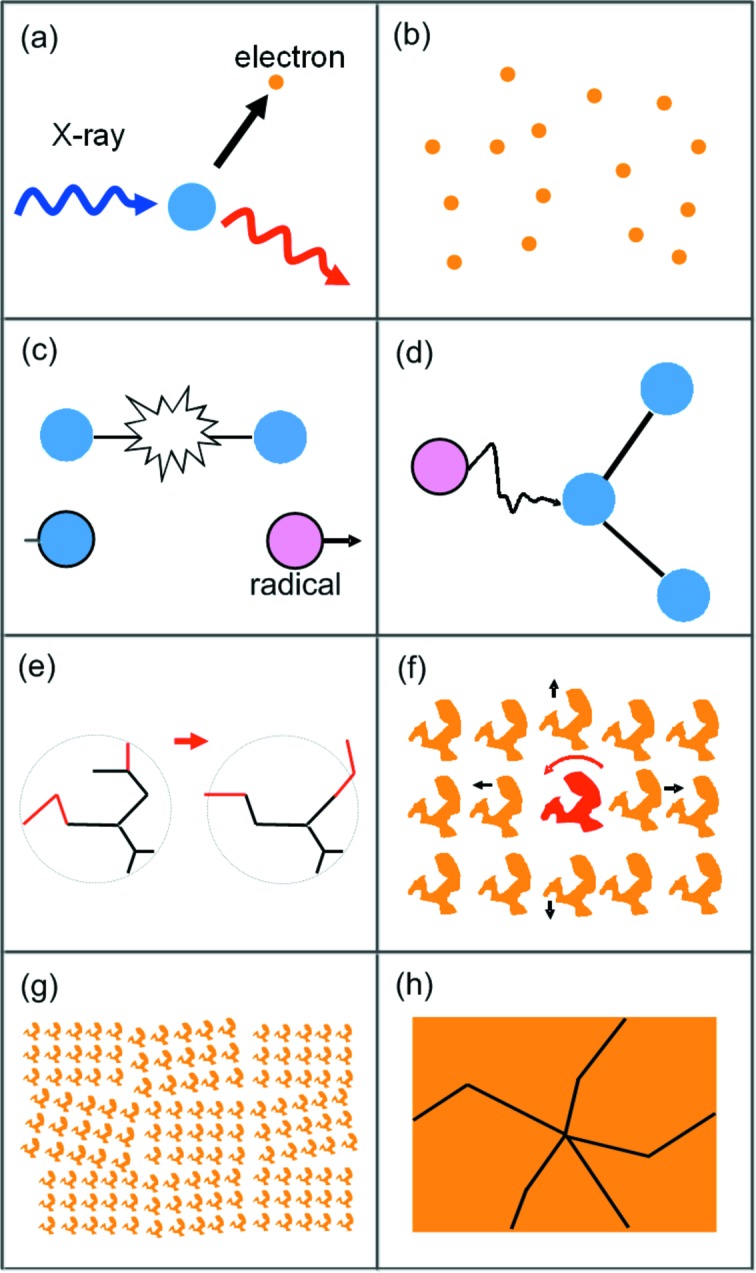
Illustration of some processes involved in the radiation damage cascade. (a) X-ray-induced ejection of a primary photoelectron. (b) Generation of several hundred relatively low-energy (∼100 eV) electrons. (c) Bond breaking leading to internal stress and radical formation. (d) Radical attack of the protein. (e) Conformation changes of side chains and flexible loops in response to chemical damage. (f) Displacement and reorientation of individual damaged molecules. (g) Deformation and reorientation of local lattice domains. (h) Plastic failure and crystal cracking.

Much of the literature on radiation damage to proteins has focused on radiochemistry, but a survey of the broader radiation damage literature [especially for inorganic materials (Billington, 1962 ▶; Dupuy, 1975 ▶)] indicates the importance of structural relaxations of molecules and the crystal lattice following chemical damage. Recent crystallographic analyses of the distribution of damage by residue within the unit cell (Juers & Weik, 2011 ▶; Warkentin et al., 2012b ▶) suggest that, while solvent-exposed residues are more sensitive than buried residues at higher temperature, half of the damage is manifested uniformly over the entire structure (Warkentin et al., 2012b ▶) (i.e. it affects surface and buried residues equally), suggesting the importance of lattice scale rather than bond-scale disorder.

3. Temperature dependence of global damage  

At T = 100 K, studies to date suggest that all protein crystals are comparably radiation sensitive, as quantified by how an appropriate metric such as relative B factor or integrated intensity varies with dose (energy deposited by ionizing particles per kg) (Sliz et al., 2003 ▶; Kmetko et al., 2006 ▶; Leiros et al., 2006 ▶; Owen et al., 2006 ▶; Holton, 2009 ▶), with a maximum tolerable dose in structure determination of roughly 30 MGy (Henderson, 1990 ▶; Owen et al., 2006 ▶; Holton & Frankel, 2010 ▶). At T = 300 K, protein crystals are much more radiation sensitive, and substantial protein-to-protein variations are observed. Measured ratios of 300 K to 100 K radiation sensitivities are typically 30–50, although some large cell and large solvent content crystals can have much larger ratios (Blake & Phillips, 1962 ▶; Teng & Moffat, 2000 ▶, 2002 ▶; Kmetko et al., 2006 ▶, 2011 ▶; Southworth-Davies et al., 2007 ▶; Barker et al., 2009 ▶; Warkentin & Thorne, 2010b ▶). This reduction has long been attributed to the freeze-out of long-range diffusion of both solvent and protein atoms, leaving only harmonic motions at T = 100 K.

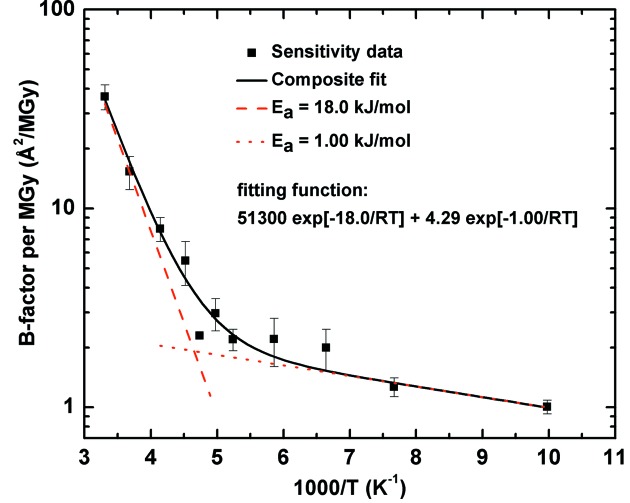
To better understand the origin of the large difference between 300 and 100 K sensitivities, we determined the temperature dependence of the global radiation sensitivity of thaumatin crystals for temperatures from 100 K to 300 K, as shown in Fig. 2 ▶ (Warkentin & Thorne, 2010a ▶). These measurements were enabled by methods that allow high-quality ice-free diffraction to be obtained from protein crystals at all temperatures. The global sensitivity was determined by repeatedly measuring diffraction data from a small angular wedge, to maximize dose uniformity within the X-ray illuminated volume. Each repetition increased the total dose received by the illuminated volume. The radiation sensitivity was obtained by scaling all the wedges together and then determining the B-factor increase per unit dose.

Figure 2.

Global radiation sensitivity of thaumatin crystals versus temperature (Warkentin & Thorne, 2010a ▶). The data are fit by a model with two Arrhenius functions, with an activation energy of 18 kJ mol⁻¹ dominating above the kink near T = 200 K.

As shown in Fig. 2 ▶, on cooling from 300 K to 100 K, at least 90% of the decrease in radiation sensitivity, and roughly 80% of the decrease in thermal B factors (Tilton et al., 1992 ▶; Kurinov & Harrison, 1995 ▶; Teeter et al., 2001 ▶; Warkentin & Thorne, 2009 ▶), occurs between 300 K and 200 K. Consequently, much of the benefit of cooling to 100 K can be achieved by cooling to much higher temperatures where the solvent remains fluid.

As might have been anticipated from temperature-dependent studies of other properties of protein crystals and their internal solvent (Rasmussen et al., 1992 ▶; Tilton et al., 1992 ▶; Chong et al., 2001 ▶; Weik et al., 2001a ▶, 2001b ▶, 2005 ▶; Warkentin & Thorne, 2009 ▶), the radiation sensitivity shows a clear transition in behaviour near T ≃ 200 K. Above 200 K, the sensitivity’s strong temperature dependence could be approximated by an Arrhenius law with an activation energy of 18 kJ mol⁻¹. Below 200 K, the sensitivity is only weakly temperature dependent with an activation energy of only ∼1 kJ mol⁻¹.

Protein and solvent dynamics in crystallo and in solution show a similar ‘dynamical transition’ near T = 200 K, believed to reflect a glass transition arising from coupling between protein and solvent (Ringe & Petsko, 2003 ▶). Solvent coupling thus provides a natural explanation for the transition in radiation sensitivity. Moreover, the sensitivity’s 18 kJ mol⁻¹ activation energy above 200 K is comparable to that observed for translational diffusion of protein hydration water in molecular dynamics simulations, in neutron scattering and in NMR (Lagi et al., 2008 ▶), to activation energies for the rates of many radical reactions in aqueous solutions (Buxton et al., 1988 ▶), and to activation energies for protein conformational motions and unfolding (Socci et al., 1996 ▶; Wolynes et al., 1996 ▶; Schuler et al., 2002 ▶; Muñoz et al., 2006 ▶).

Below 200 K, translational diffusion of atomic and larger species is frozen out and scaffolding by the frozen solvent network prevents larger conformational motions. The activation energy of ∼1 kJ mol⁻¹ is comparable to those describing the radiation sensitivity of many solvent-free organic crystals, not just below 200 K but over the entire temperature range between 100 K and 300 K (Warkentin & Thorne, 2010a ▶).

Based on this discussion, we concluded that, as the temperature is reduced toward the glass transition, diffusive motions of both solvent and protein slow, and this is responsible for a large part of the reduction in radiation damage. Below 200 K, these diffusive motions are largely frozen out, and a different set of processes dominates radiation damage (Meents et al., 2010 ▶; Warkentin & Thorne, 2010a ▶).

4. Time dependence of global damage: dark progression  

Even though the majority of damage processes may occur very quickly at all temperatures, there are reasons to expect that those processes responsible for the atomic motions that dominate the decay of X-ray diffraction patterns at temperatures above 200 K may be relatively slow, and that their timescales grow and thus become more experimentally accessible on cooling below room temperature.

To test the hypothesis that some global radiation damage processes proceed on readily accessible timescales (seconds to hours) at temperatures near the solvent glass transition, we collected a series of wedges of diffraction data from the same region of each crystal, as described above. However, at some point in the series, data collection and thus X-ray irradiation were interrupted, the crystal was left ‘in the dark’ for a fixed time, and then data collection and irradiation were resumed, as illustrated in the inset to Fig. 3 ▶. If the plot of change in B factor versus dose showed an upward jump, called ‘dark progression’, following this interruption, then some damage must have occurred while the X-ray beam was off. By varying the ‘dark’ time and measuring the amount of progression, the rate at which damage continued following irradiation could be estimated.

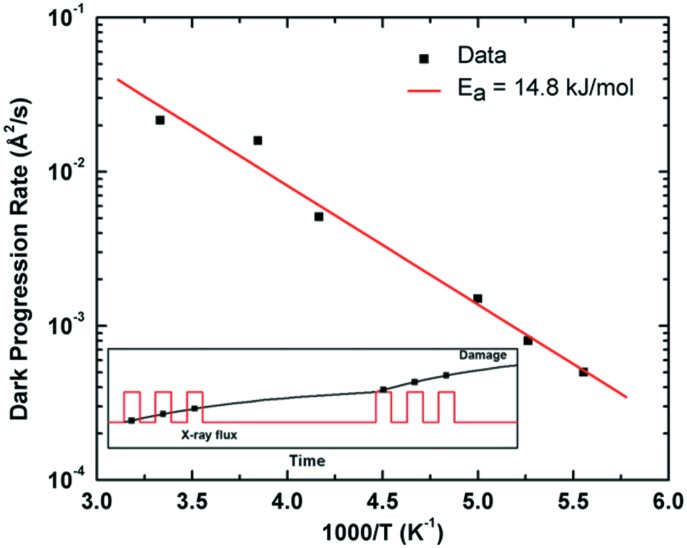
Figure 3.

Rate of ‘dark progression’ (see text) as a function of temperature in thaumatin crystals (from Warkentin et al., 2011 ▶, with additional data at T = 260 K and 300 K). The line is a fit to a thermally activated model with an activation energy of 14.8 kJ mol⁻¹. Agreement between this energy and that for the high-temperature regime in Fig. 1 ▶ suggests that the underlying processes are similar. The inset schematically illustrates how the interrupted dose curves used to measure dark progression were measured (see text). From Warkentin et al. (2011 ▶), with additional data at 260 K and 300 K.

These dark progression measurements were performed using thaumatin crystals at temperatures between 25 and 300 K (Warkentin et al., 2011 ▶). At most temperatures, no dark progression was observed on the several-minute timescale probed in the experiments, indicating that all damage processes were either much faster or much slower than that timescale. Between 180 and 240 K, however, significant dark progression was observed, and was quantified as the rate of B-factor increase per unit time (B s⁻¹). Subsequent experiments using a faster detector allowed measurement of dark progression rates at 260 K and 300 K. Fig. 3 ▶ shows the measured rates versus temperature. These data can be fit by an Arrhenius law with an activation energy of 15 kJ mol⁻¹, similar to that for global radiation damage above 200 K in Fig. 2 ▶, suggesting that at least some of the processes responsible for dark progression also contribute to the overall temperature dependence of global damage.

Note that the Arrhenius behaviour in Fig. 3 ▶ extends down to 180 K, below the transition in Fig. 1 ▶, and where the observed dark-progressing component of damage is a very small fraction of total damage. This provides further evidence that there are in fact two distinct sets of damage processes. One set dominates at high temperatures, has large activation energies, and occurs on relatively slow timescales. The other set dominates at low temperatures, has small activation energies, and is effectively instantaneous.

5. Outrunning radiation damage  

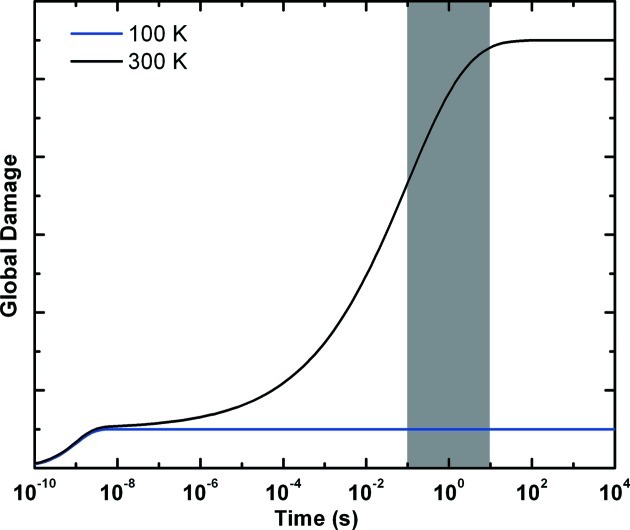
The preceding discussion suggests that the time evolution of radiation damage in response to a brief intense X-ray dose is as schematically shown in Fig. 4 ▶. If diffraction data can be collected before the damage plateaus, then measured damage will be reduced and the amount of diffraction data that can be collected before damage becomes unacceptable will be increased. In our dark progression experiments at T = 240 K, up to ∼27% of the ‘long time’ damage was outrun by collecting data in a few minutes, using dose rates of ∼8 kGy s⁻¹. How much more damage could be outrun with larger dose rates and faster data collection?

Figure 4.

Schematic illustration of the time evolution of damage as manifested in X-ray diffraction at T = 100 K and 300 K. Some processes occur very quickly, but have only small effects on atomic positions and diffraction. Other processes take place over a range of timescales, but eventually have large effects on diffraction. The shaded area represents the range of timescales relevant to data collection with a detector framing at 10 Hz: one frame takes 100 ms, while a 100-frame data set takes 10 s. At 100 K the slower diffusive damage processes no longer contribute, and the much smaller long-time damage is determined by the remaining fast processes.

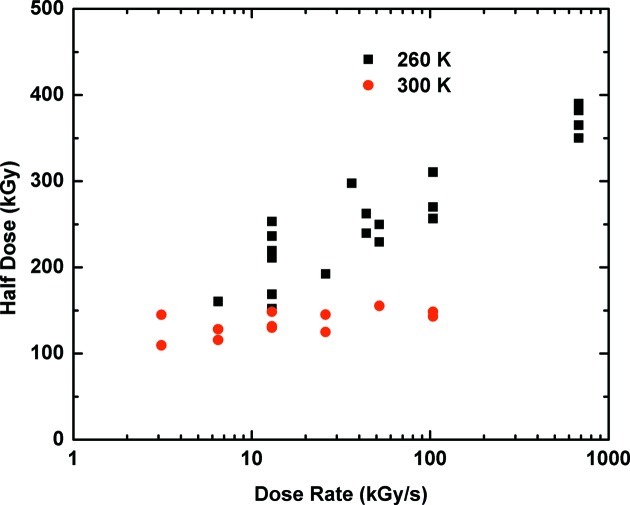
In March 2011 we conducted experiments at APS beamline 17-ID using flux densities up to 1.7 × 10¹⁵ photons s⁻¹ mm⁻² and a PILATUS 6M detector with a frame rate of 12.5 Hz (Warkentin et al., 2012a ▶). Measurements of scaling B factor versus dose at dose rates up to 680 kGy s⁻¹ at T = 260 K and up to 100 kGy s⁻¹ at T = 300 K (due to limited beam time) were collected from a total of 17 thaumatin crystals, either using multiple consecutive wedge data sets as discussed above or, at the highest dose rates, single still frames. Fig. 5 ▶ shows the measured half-dose as a function of dose rate, with each point derived from a complete B factor versus dose curve on a single crystal. At 260 K the half-dose approximately doubles as the dose rate increases from 6.5 kGy s⁻¹ to 680 kGy s⁻¹, corresponding to data collection times to the half-dose of 25 s and 0.5 s. This implies that approximately half of global damage is outrun by collecting data in ∼0.5 s at 260 K.

Figure 5.

The lifetime (as expressed by the half dose) of thaumatin crystals as a function of dose rate (Warkentin et al., 2012a ▶). At T = 260 K there is a factor-of-two increase in lifetime as the dose rate is increased to 680 kGy s⁻¹. This indicates that half of global damage is being outrun. At 300 K, the data do not extend to high enough dose rates to reliably establish a half-dose increase. Such an increase has been observed in recent 300 K measurements at dose rates up to 1 MGy s⁻¹ (Owen et al., 2012a ▶).

At T = 300 K, the half dose shows a small upward trend, but the data do not extend to high enough dose rates to establish whether this trend is real. Recently, Owen et al. (2012a ▶) found T = 300 K increases in half-dose of 30–80% when data were collected at dose rates approaching 1 MGy s⁻¹ from three crystal systems: a soluble protein (immunoglobulin γ Fc receptor IIIa), a virus (bovine enterovirus serotype 2) and a membrane protein (human A_2A adenosine G-protein coupled receptor). The observed half doses are consistent with our finding for thaumatin at 260 K.

Note that these ‘dose-rate effects’ are fundamentally a consequence of the timescales required for damage to manifest, as indicated by our dark progression measurements. Assuming this to be strictly true, then the fraction of the long-time damage that can be outrun by collecting data in a much shorter time should be independent of the dose rate. Large dose rates are needed only to produce measurable damage on short timescales. This distinguishes the behaviour observed here from a ‘true’ dose rate effect, for which the long-time damage should depend on dose rate.

6. Implications and future directions  

In light of the success of FEL experiments (Chapman et al., 2011 ▶), that radiation damage can be outrun is no surprise. The surprise is that significant damage can be outrun not only in femtoseconds at FELs but in seconds using synchrotron sources.

The long timescales for diffraction spot fading near room temperature can be compared with measured radical lifetimes of nanoseconds to microseconds (Pryor, 1986 ▶); a tiny fraction of radicals can persist for much longer times, but their presence and decay has no impact on diffraction (Weik et al., 2002 ▶; Owen et al., 2006 ▶, 2012b ▶; Southworth-Davies & Garman, 2007 ▶; Macedo et al., 2009 ▶; McGeehan et al., 2009 ▶; De la Mora et al., 2011 ▶). These long spot fading timescales strongly indicate that structural relaxation processes downstream of radical production and reaction dominate the manifestation of radiation damage in diffraction at these temperatures. The dominance of structural rather than chemical processes is also consistent with large protein-to-protein variations observed in room-temperature radiation sensitivities.

Results to date indicate that near room temperature at least half of global radiation damage can be outrun or, alternatively, at least twice as much data can be collected from a given crystal, by collecting data in ∼1 s. How much more damage might be outrun, and how much more data per crystal might be collected, with larger dose rates and faster detectors?

Current third-generation synchrotron source beamlines can, with microfocusing optics, yield monochromatic flux densities approaching 10¹⁷ photons s⁻¹ mm⁻², corresponding to dose rates of at least 25 MGy s⁻¹. As dose rates increase, heating of the illuminated volume will in general increase, and eventually have unacceptable consequences. X-ray beam heating of a spherical uniformly illuminated crystal (Kriminski et al., 2003 ▶; Mhaisekar et al., 2005 ▶) and a cylindrical crystal illuminated along its axis by a beam smaller than its diameter (Warkentin et al., 2012a ▶; also see supplementary material1) have been analysed. The latter analysis shows that the portion of the crystal beyond the irradiated region (as well as any surrounding solvent) acts like a ‘fin’, increasing the surface area from which heat transfer to the surrounding gas can occur and decreasing the amount of heating for a given dose rate. The steady-state temperature rise for uniform crystal illumination increases with flux density. But for a fixed maximum allowable temperature rise (occurring at the center of the illuminated area), the maximum allowable flux density can be increased by reducing the beam size while keeping the total flux fixed. With dose rates of 25 MGy s⁻¹, sample heating of 10 K or less should be feasible. Consequently, the optimal data collection strategy for outrunning damage is to use the smallest most intense beam allowed by heating limits, to collect data up to roughly the half-dose, and then to repeat at other points in the crystal (e.g. using helical scanning) until a complete data set is obtained (or until the entire crystal has been irradiated).

Detector speeds provide another constraint on the maximum feasible flux densities, dose rates and radiation sensitivity reductions. At a dose rate of 25 MGy s⁻¹, a thaumatin crystal at 300 K will receive its low-dose rate half-dose in ∼5 ms; the irradiation time to the effective half dose at this dose rate may be an order of magnitude larger. Collecting diffraction data in this time should pose no challenge for current rotation stages with rotation speeds of 17 µs per degree and soon-to-be available detectors with 10 kHz frame rates. When flux densities are increased by microfocusing, total fluxes and detector count rates will remain relatively constant. But when fluxes are increased (e.g. using wider-bandpass monochromators or higher synchrotron beam currents), photon-counting detector count rates may eventually become too large for dead-time corrections. In the recent Owen et al. (2012a ▶) study with dose rates of 1 MGy s⁻¹ in a 20 µm × 20 µm beam, the maximum count rate observed for any reflection was only ∼10% of the maximum recommended for their PILATUS 6M detector. Fluxes and data collection rates could thus be increased by a factor of ten.

With large dose rates and short data collection times, it may be possible to outrun much of the ‘excess’ damage associated with diffusive processes (given by the difference between the high and low temperature fits in Fig. 2 ▶) at and near room temperature. Increases in half-doses of an order of magnitude or more may be feasible, leaving protein crystals only several times more radiation sensitive at room temperature than at 100 K. These increases in half-dose will lead to corresponding decreases in the number of crystals required to solve a structure. Consequently, the development of high-speed ultra-high-dose-rate data collection should enable a large expansion in structural studies on protein crystals with unfrozen solvent and under more nearly native conditions, and more detailed investigations of the connections between structure, dynamics and function.