Improved data visualization techniques for analyzing macromolecule structural changes

Abstract

The empirical phase diagram (EPD) is a colored representation of overall structural integrity and conformational stability of macromolecules in response to various environmental perturbations. Numerous proteins and macromolecular complexes have been analyzed by EPDs to summarize results from large data sets from multiple biophysical techniques. The current EPD method suffers from a number of deficiencies including lack of a meaningful relationship between color and actual molecular features, difficulties in identifying contributions from individual techniques, and a limited ability to be interpreted by color-blind individuals. In this work, three improved data visualization approaches are proposed as techniques complementary to the EPD. The secondary, tertiary, and quaternary structural changes of multiple proteins as a function of environmental stress were first measured using circular dichroism, intrinsic fluorescence spectroscopy, and static light scattering, respectively. Data sets were then visualized as (1) RGB colors using three-index EPDs, (2) equiangular polygons using radar charts, and (3) human facial features using Chernoff face diagrams. Data as a function of temperature and pH for bovine serum albumin, aldolase, and chymotrypsin as well as candidate protein vaccine antigens including a serine threonine kinase protein (SP1732) and surface antigen A (SP1650) from S. pneumoniae and hemagglutinin from an H1N1 influenza virus are used to illustrate the advantages and disadvantages of each type of data visualization technique.

Introduction

At the heart of the study of protein biochemistry lies understanding the interrelationships between the structure and function of these complex macromolecules. Structural aspects are best considered in the light of protein three-dimensional structures as determined by X-ray crystallography and nuclear magnetic resonance. In many cases, however, such structures are unavailable or suffer from experimental limitations such as their origin in the crystalline state or the requirement for high concentrations and/or isotope labeling. Thus, physical methods of lower structural resolution such as circular dichroism (CD), fluorescence, light scattering, Fourier transform infrared spectroscopy (FTIR), and differential scanning calorimetry (DSC) are often used, especially in combination with environmental perturbations such as temperature, pH, and solute additives (e.g. chaotropes) to evaluate macromolecule higher-order structure and stability in solution.

As an intermediate approach, results from multiple lower resolution methods can be combined to produce a more information-rich characterization of protein structure. One such method is known as the empirical phase diagram (EPD). This approach consists of a colored map of macromolecule behavior in which the structure of a macromolecule (or its complexes), as a function of various solution and environmental conditions, is represented by vectors corresponding to individual measurements such as CD, FTIR spectra, intrinsic fluorescence, dye binding, DSC, and light scattering. Using singular value decomposition (SVD), the three largest contributions to a vector are obtained and reduced to color based on an RGB scheme.^1,2 Although the actual colors are somewhat arbitrary, changes in color are useful, because they represent structural changes. In addition, differences between EPDs can be directly compared (e.g., between mutants of the same protein) by processing all the data together.³ By making measurements as a function of variables such as temperature, pH, concentration, ionic strength, and mechanical stress, the colored EPD diagram represents an information rich type of “stress/response” diagram that has been useful in a wide variety of applications including stabilization and formulation of protein therapeutics and a variety of macromolecular vaccines.^1–10

The current EPD method suffers from a number of deficiencies that primarily reflect the use of color to represent the state of the protein's structural integrity. This includes the lack of meaningful relationship between color itself and actual molecular features (in EPDs, structural changes are represented by color transitions^1,2,9) as well as limitations resulting from color deficiencies in vision and blindness, which are possessed by a substantial portion of the human population. Red-green color vision defects are found in about 8% of males and 0.5% of females among people of Northern European origin, 5% among Chinese and Japanese populations, and 4% or less among individuals of African origin.¹¹ Here, we describe three alternative data visualization approaches to the current EPD methodology, which not only overcome these difficulties, but may also provide additional information leading to the enhancement of the EPD macromolecular structure characterization tool.

In the first approach, we take advantage of the direct relationships between far UV CD spectra and protein secondary structure, intrinsic fluorescence spectra and protein tertiary structure changes, and light scattering measurements and quaternary structure (or aggregation state) to assign direct protein structural meaning to colors. In the second and third methods, we eliminate the use of the color altogether through the employment of radar (or star) charts¹² and Chernoff faces.^13–15 These techniques are popular iconic displays of multivariate data in which attribute values are mapped to the features of the icons.¹⁶ For radar plots, values from the multiple physical measurements are related to the spikes of equiangular polygons. For the Chernoff face approach, these same data sets are represented by the position and size of facial features in a model face. The resulting patterns exhibit characteristics of the data, which can be recognized by preattentive perception.¹⁶ These data visualization methods have been used in many other fields including information visualization,^16,17 computer science,^18,19 biology,²⁰ education,²¹ and health care.^22,23 In this work, we explore the utility of three different representations with six different proteins using temperature and solution pH as independent stress variables and discuss the advantages and disadvantages of each data visualization approach.

Results

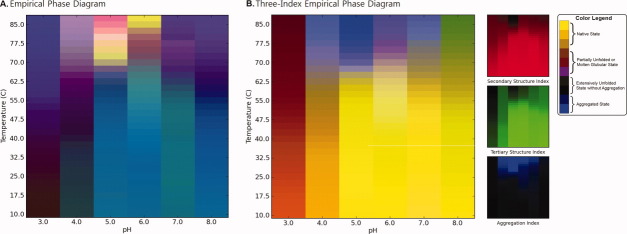
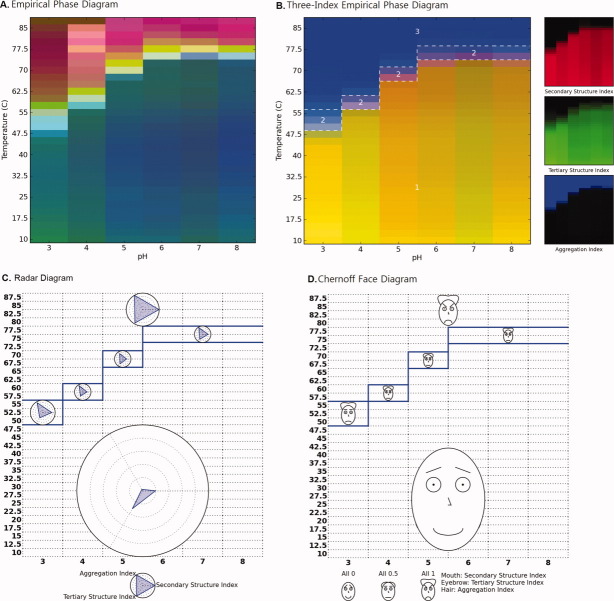
Figure 2 compares two EPD data visualization approaches derived from the physical data of Figure 1 (effect of temperature and pH on BSA as measured by CD, fluorescence, and light scattering; see Methods section). Figure 2(A) shows an EPD constructed using the previously published data¹⁰ by the current EPD method. The newly developed three-index EPD displayed in Figure 2(B), which is constructed using three structural indices calculated from the same experimental data as described in the Methods section. The two EPDs show very similar transitions in color patterns, which indicate the structural changes of BSA in response to pH and temperature. In both cases, a region of pH and temperature with similar color represents related structural states defined by the specific experimental data. For example, the region from pH 5 to 8 below 60°C colored blue in Figure 2(A) and yellow in Figure 2(B) represents the native state of BSA. The native structure is altered due to lower pH or higher temperature as depicted by the purple phase in Figure 2(A) or brown phase in Figure 2(B). The aggregation of the protein is seen as the yellow/red region in Figure 2(A) or the blue region in Figure 2(B) from pH 4 to 6 above 70°C. A structural interpretation of the original EPD could not be achieved without direct reference to the underlying experimental data. In contrast, the three-index EPD depicts the type of structural change the protein undergoes by simple reference to color. For example, yellow or shades of yellow always reflect the native state of the protein, with no aggregation or change in the secondary and tertiary structure of the protein. The blue color represents an aggregated state. Brown and green colors define a structurally altered state with minimal or no aggregation. In short, the three-index EPD, when properly constructed, adds meaning to the colors in the EPD. The individual RGB components are also provided on the right side of Figure 2(B) for a better understanding of the three-index EPD. Because each RGB component represents its associated structural indices, the additional color plots on the right hand side in Figure 2(B) visually clarify the source of the transitions seen in the three-index EPD, in this case, in terms of data from each analytical instrument (CD, fluorescence, and static light scattering, respectively).

Figure 2.

EPDs of the conformational stability of BSA as a function of pH and temperature. (A) Original EPD created using biophysical data in Figure 1(A–C). (B) Three-index EPD created using structural indices as shown in Figure 1(D–F).

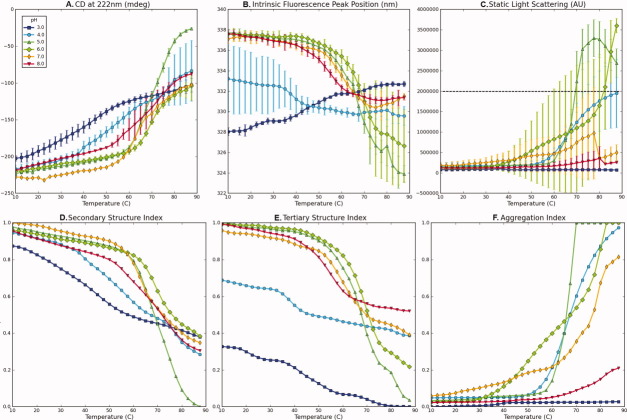
Figure 1.

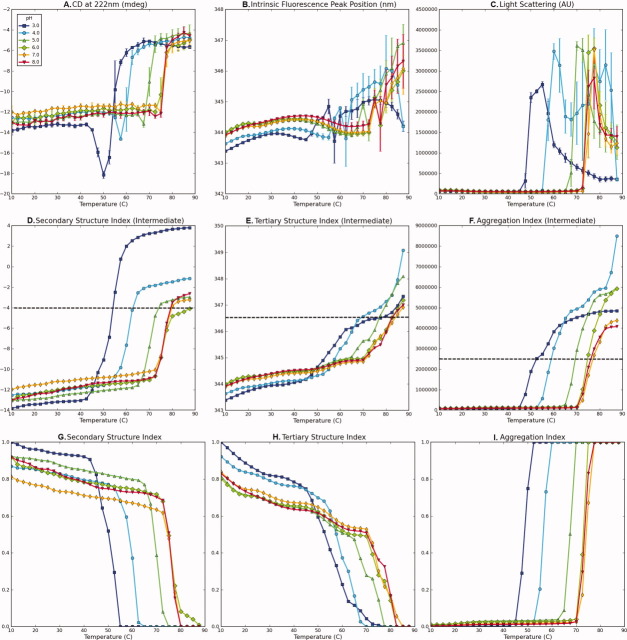
Experimental data for bovine serum albumin (BSA) measured as a function of temperature at indicated pH values (A–C) and their corresponding structural indices (D–F). (A) CD signal at 222 nm, (B) intrinsic fluorescence peak position, (C) static light scattering at 295 nm, (D) secondary structure index calculated from (A), (E) tertiary structure index calculated from (B), and (F) aggregation index calculated from (C). A dashed line in (C) represents a cut-off value. Data in Figure 1(A–C) were published previously.¹⁰

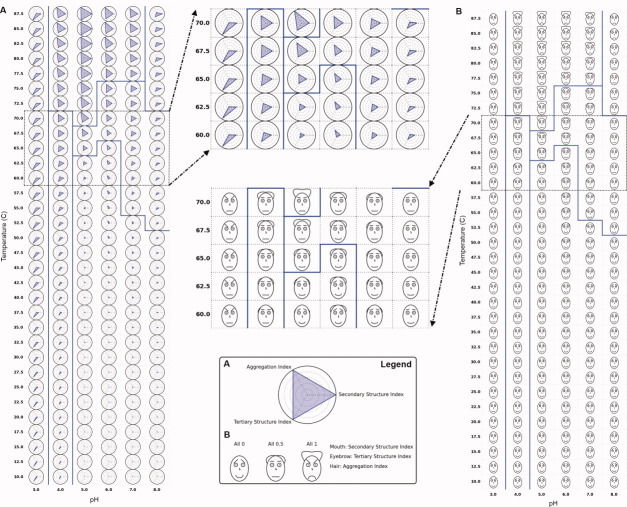
The radar and Chernoff face diagrams of the same BSA stability data set (Fig. 1; see Methods section) are shown in Figure 3. In both cases, the secondary and tertiary structure indices are inverted to represent the native state either as a dot or a smiling face. These settings are used to more easily perceive small deviations from the native state. It is seen that all three of the data visualization approaches shown in Figures 2 and 3 display the same structural transitions of BSA as a function of pH and temperature in terms of changes in either colors, shape of polygons, and facial features.

Figure 3.

(A) Radar chart and (B) Chernoff face diagram of the conformational stability of BSA as a function of pH and temperature using data from the three structural indices from Figure 1(D–F). Secondary and tertiary structure indices are inverted for both cases to represent the native state as (A) a dot and (B) a smiling face. Solid blue lines indicate an example of clustering results (see text).

The solid blue lines in Figure 3 illustrate an example of clustering results. Clustering was performed using a k-means clustering algorithm with k = 6 and manually corrected afterward based on interpretation of raw data. After several trials of different values of k, the k number was selected in which its result most closely matches our interpretation of raw data. One of the clustering results is displayed for all three diagrams in Figures 3 and 4. In addition, Figure 4(B,C) shows clustered radar and Chernoff face diagrams in which each cluster is represented by a single radar chart and Chernoff face. This single iconic plot is generated by an average value of the data inside a cluster and exhibits the characteristic of the cluster.

Figure 4.

(A) Three-index EPD, (B) clustered radar chart, and (C) clustered Chernoff face diagram for the conformational stability of BSA (using data from three structural indices from Figure 1(D,E). Each cluster is represented as a radar chart or Chernoff face diagram, which averages the structural indices of all images that belong to the cluster. Six structural phases were observed empirically: (1) native state, (2) molten globular state, (3) aggregated, and (4–6) structurally altered states due to low pH and/or high temperature without aggregation.

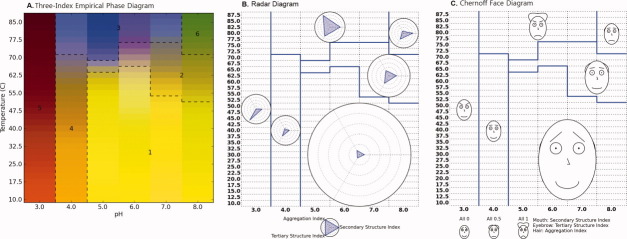
The original EPD and three different data visualization diagrams for the protein antigen SP1732 are shown in Figure 5(A–D). The data from SP1732 provides a good example of a protein that clearly displays a molten globular state (see data in Fig. 6 in Methods section). The EPD constructed using previously published data for SP1732²⁴ is shown in Figure 5(A). SP1732 was found to be most stable at temperature below 45°C at low pH and below 70°C at pH 6–8. Aggregation of SP1732 is observed in the pink region in the EPD. A molten globule state is also seen in the interface between these two “apparent” phases. It should be noted that “apparent” phases do not refer to equilibrium thermodynamic phases (i.e. no reversibility is implied), but rather simple, empirical representations of the physical behavior of the macromolecule.^1–3 As shown in Figure 5(B), a small pink-colored region between the native and unfolded state is also observed in the three-index EPD. The calculated structural indices used for the construction of the three-index EPD for the protein antigen SP1732 are shown in Figure 6(G–I; see Methods section). A decrease in the CD signal is seen at pH 3 at about 40°C. This transition increases in temperature with increasing pH. At pH 6–8, this transition is observed only at about 75°C. Similar trends are observed with intrinsic fluorescence and static light-scattering data.

Figure 5.

(A) EPD, (B) three-index EPD, (C) radar chart, and (D) Chernoff face diagram for the protein antigen SP1732 as a function of temperature and pH. Figure 7(A) is created using biophysical data in Figure 2(A–C), while Figure 7(B–D) is created using structural indices shown in Figure 2(G–I). Three structural regions are observed: (1) native state, (2) molten globular state, and (3) aggregated state.

Figure 6.

Experimental data for SP1732 measured as a function of temperature at indicated pH values (A–C), their intermediate structural indices (D–F), and the final structural indices (G–I). (A) CD signal at 222 nm, (B) intrinsic fluorescence peak position, (C) static light scattering at 295 nm, (D) intermediate secondary structure index calculated from (A), (E) intermediate tertiary structure index calculated from (B), (F) intermediate aggregation index calculated from (C), (G) secondary structure index, (H) tertiary structure index, and (I) aggregation index. Dashed lines in (D–F) represent cut-off values. Data in Figures 2(A–C) were published previously.²⁴

As discussed earlier, one of the limitations of the EPD is that the investigator needs to study the original data independently to better understand the origin of the colored regions. The three-index EPD remedies this shortcoming by manifesting the native state of the protein antigen SP1732 as a rich yellow color as seen in Region 1 in Figure 5(B). Aggregation along with unfolding of the protein appears blue in Region 3. Molten globule states usually present as a red or a pink-colored phase as seen in Region 2. These indices are also mapped onto the radar and Chernoff face diagrams in Figure 5(C,D), respectively. In the radar diagram, the native state of the protein antigen SP1732 is represented as blue triangles occupying minimal area. Transitions are seen as the blue triangle increasing its area at the corresponding angle. This is seen in Region 3 of Figure 5(C) at high temperatures at all pH values, where we see an equilateral triangle that extends to the circumference of the circle, indicating a total loss of structure and aggregation. Molten globule behavior appears as states with increases in aggregation and loss of tertiary structure as seen in Region 2 of Figure 5(C). In the Chernoff diagram, the indices for SP1732 are mapped to the mouth, eyebrow, and hair of the Chernoff face. The native state appears as a “happy and bald” face in Region 1 of Figure 5(D), with the mouth, eyebrows, and the hair representing the secondary, tertiary, and quaternary (aggregation) structure indices, respectively (see Methods section). The molten globule state shows the presence of aggregates in the form of hair and intermediate secondary and tertiary structures in the form of “poker faces” and horizontal mouth and eyebrows [Fig. 5(D)].

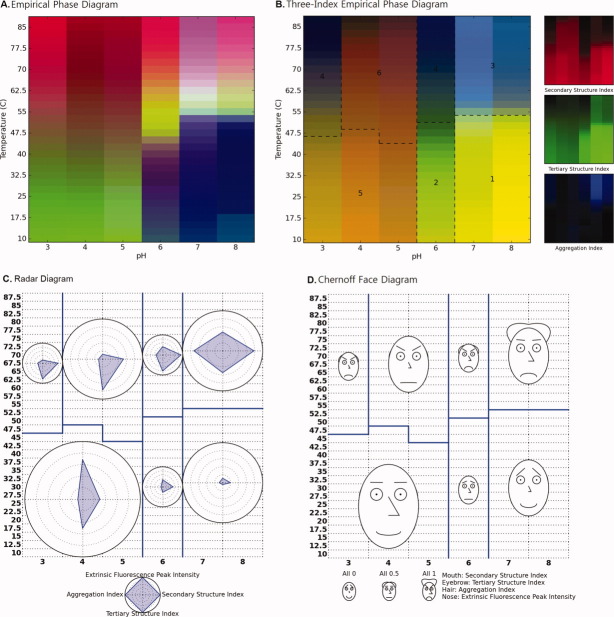
The original EPD and the three different data visualization diagrams for protein antigen HAC1 are shown in Figure 7. The previously published data²⁵ and newly constructed structural indices are included as Supporting Information Figure S1. As shown in the EPD in Figure 7(A), the native state of the HAC1 protein is seen at pH values of 7 and 8 at temperatures lower than 50°C. The protein is conformationally altered at pH 6 at temperatures below 40°C as reflected in the purple phase in Figure 7(A). As the pH drops to 5 and below, the structure again changes and is represented by the green phase. Increasing temperature in all apparent phases is accompanied by unfolding or aggregation of the protein. As shown in Figure 7(B), the pH-dependent conformational changes for HAC1 are more pronounced in the three-index EPD, in which Regions 1 and 2 are more clearly differentiated. In addition, Region 1, which was identified as the native state, is again represented by a yellow color. The conformationally altered protein at pH 6 is shown by the appearance of green hinting at possible changes in the protein's secondary structure. The brown color seen at pH 5 and below indicates the presence of native secondary structure, but low levels of tertiary structure [Fig. 7(B)].

Figure 7.

(A) EPD, (B) three-index EPD, (C) radar chart, and (D) Chernoff face diagram for the protein antigen HAC1 as a function of temperature and pH. Figure 8(A) is created using biophysical data in Supporting Information Figure S1(A–D), while Figure 8(B–D) is created using structural indices shown in Supporting Information Figure S1(E–H). Six structural phases are observed: (1) native state, (3) aggregated state, and (2, 4–6) structurally altered state due to low pH and/or high temperature without aggregation.

One potential limitation of the three-index EPD is an inability to include data from more than three experiments. For example, no major change in color was observed at pH 4 and 5 with changes in temperature [Fig. 7(B)]. The changes observed in the EPD arise from the ANS data [Fig. 7(A) and Supporting Information Fig. S1]. The three-index EPD presumably does not show the changes because of the absence of the ANS data. This limitation can be offset by the construction of radar and Chernoff face diagrams. In these diagrams, the ANS data are mapped on the fourth arm in the radar diagram [Fig. 7(C)] or onto the size of the nose in the face diagrams [Fig. 7(D)]. The native state of the protein antigen HAC1 is again shown by a quadrilateral of minimum area in the radar diagram. In the Chernoff face diagram, this native state is shown with a happy face, a bald scalp, and a small nose. As the protein conformation changes, the quadrilateral and the face change in accordance with the changes observed in the data [e.g., angle changes in the radar diagram in Fig. 7(C) and the presence of hair at high temperatures at pH 7 and 8 in Fig. 7(D) reflecting aggregation of the protein].

Data obtained for several other proteins including aldolase,¹⁰ chymotrypsin,¹⁰ and SP1650²⁴ were also used in the construction of the original EPDs as well as the new data visualization methods (three-index EPDs, the radar diagrams, and the Chernoff face diagrams). The previously obtained data and the newly constructed structural indices for aldolase, chymotrypsin, and SP1650 are shown in Supporting Information Figures S2, S4, and S6, respectively. The various data visualization diagrams constructed for each of these proteins are shown in Supporting Information Figures S3, S5, and S7. Each of these versions of the four diagrams (for aldolase, chymotrypsin, and SP1650) demonstrates the same trends discussed earlier (for BSA, SP1732, and HAC1).

Discussion

Three new data visualization methods are presented in this work in the context of evaluating six different proteins in terms of conformational stability as a function of pH and temperature. The three-index EPD approach describes three aspects of macromolecular structure with a predefined color scheme. Given a range of environmental perturbations, the amount of tertiary and secondary structure and state of aggregation were measured by intrinsic fluorescence peak position, CD spectroscopy, and static light scattering, respectively. After the measurement, these data were interpreted and converted to structural indices representing the relative amount of structural change, which were then mapped to specific colors. As seen in several examples in this study, the color yellow represents the native state of a macromolecule and the color blue an aggregated state. A darker color, close to black, represents a maximally altered conformational state without any notable aggregation. These colors are considered the major indicators, while other colors (e.g., such as brown and green) represent partially altered states depending on the differentially reduced color levels of tertiary and secondary structure. For example, the colors red or pink are interpreted as indicators of molten globular states for the protein antigen SP1732 as seen in Figure 5(B).

The assignment of color to the degree of structural change in the three-index EPD is achieved by displaying only three experimental data sets as measures of secondary, tertiary, and quaternary structures. Currently, more than three types of experimental data can be summarized in the other approaches including the original EPD, the radar charts, and the Chernoff face diagram. In Figure 7, the difference among visualization techniques when using four different data visualization methods to evaluate the same biophysical data sets is clearly shown for the protein antigen HAC1. In this case, extrinsic ANS fluorescence spectroscopy data (see Supporting Information Fig. S1) were not included in the three-index EPD, because it provides a measure of the amount of dye binding to either the apolar surface(s) of a macromolecule or a positively charged binding site, neither of which can be simply related to macromolecular structure. The ANS data does, however, clearly highlight the structural transition regions from pH 6 to 8 around 55°C and distinguishes the region at pH 4–5 above 50°C in the EPD from the same regions in the three-index EPD. A method to calculate structural indices from more experimental data is thus still needed and is under investigation.

The introduction of the structural index not only enhances the visualization and interpretability of the experimental data, but it also performs an initial analysis of the data. The curated index provides a sigmoidal melting curve that preserves the initial positions and slope changes of the original data. The alignment of changing directions and proper cut-offs permits the comparison of signals within the area of interest in a more straightforward manner. One additional analysis would be the subtraction of a tertiary structure index from a secondary structure index to observe a peak indicating the existence of molten globular states (data not shown). This peak is also seen as the color pink (or red) in the three-index EPDs. Another benefit of the structural indices is for use in computational methods, which includes clustering analyses. Clustering analyses may provide inaccurate partitioning, however, if the same value has different meaning. For instance, a decrease in the light scattering at higher temperature is often observed after it reaches a peak intensity value [e.g., see Fig. 6(C) for data with the protein SP1732]. The same level of light-scattering data before and after the peak intensity may not have the same interpretation, but the clustering algorithms would identify the two regions as the same state. Thus, instead of using raw data, the use of an index for computational methods can maximize the accuracy of the results.

The two other data visualization approaches presented in this work, the radar chart and the Chernoff face diagram, have similar properties to one another. A specific shape or image of an icon (i.e., an equiangular polygon or a human face) is designed to reflect the characteristics of the underlying data and distinguished differences as a function of solution variables. Each type and magnitude of selected experimental data is explicitly expressed in these diagrams. This result is in contrast to original EPDs that cannot identify the origin of the experimental technique and structural features that cause color changes. We currently consider these diagrams alternatives to color-based EPDs, because they have the significant advantage that they can accommodate more different kinds of data. It is, however, difficult to read an exact value or to detect subtle changes in values with these two approaches, especially for Chernoff face diagrams. Both the diagrams require more space to represent the same number of environmental stresses than EPDs; therefore, an individual shape or a face becomes too small to be easily recognized if the entire diagram is presented. Alternatively, the clustered versions of diagrams may become a useful tool to symbolize selected characteristics of macromolecules.

The utility of EPDs to summarize the effect of environmental stresses on protein conformational stability has recently been enhanced by the availability of multimodal spectrophotometers with multiple sample holders that can simultaneously or sequentially measure CD, fluorescence, and UV absorption spectra as well as light scattering and turbidity as a function of temperature in an automated mode with a single sample.^10,26 Thus, the multiple data visualization diagrams of the type described in this work can be obtained rapidly, within a single day is possible, with a minimal amount of protein and effort.

Materials and Methods

Materials

To demonstrate various visualization techniques, previously published data (e.g., intrinsic Trp and extrinsic ANS fluorescence spectroscopy, CD, and static light scattering) were used in this work including bovine serum albumin (BSA),¹⁰ aldolase,¹⁰ and chymotrypsin¹⁰ as well as serine threonine kinase protein (SP1732)²⁴ and pneumococcal surface antigen A (SP1650)²⁴ from S. pneumonia and hemagglutinin from the H1N1 influenza virus (HAC1).²⁵ The EPDs were constructed using these previously published data and then compared to the three newly proposed data visualization techniques introduced in this work: the three-index EPD, radar diagram, and Chernoff face diagram. All six of the protein macromolecules were dialyzed into a 20 mM citrate phosphate buffer (pH 3–8) at a total ionic strength of 0.15 using appropriate amounts of NaCl. A detailed description of the experimental methods used to generate the structural data used in this work are described elsewhere.^10,24,25

Construction of EPDs

The experimental data for each of the six proteins were previously obtained from multiple techniques (e.g., CD, fluorescence, and light scattering) as a function of pH and temperature.^10,24,25 The combinations of those conditions are aligned to form an m × n input matrix, in which m is the number of experimental techniques and n is the number of condition combinations (e.g., number of pH values × number of temperature measurements). SVD of the input matrix is used to produce a factorization of unitary orthonormal bases matrices and a diagonal matrix composed of singular values. The three largest singular values determine the major contributing factors in the form of orthonormal basis vectors. These factors are then mapped to a RGB color scheme and are visualized as an EPD. Thus, regions of the plot with similar color indicate similar physical states of the macromolecule. A detailed explanation of the calculations involved in construction of EPDs can be found elsewhere.^1–3

Calculation of structural indices

We define a structural index as the degree of corresponding structural change within a given range of environmental stress conditions. Secondary, tertiary, and quaternary (aggregation) structure indices are used here to represent the state of a macromolecule. The structural index is allowed to vary from a value of zero to one while indicating the lowest to highest amount of the corresponding structure. As an example, native tertiary structure can be represented by a value of 1 while significantly conformationally altered tertiary structure by 0. Similarly, the aggregation index (AI) is defined to have a range from 0 to 1 where the number 0 implies no aggregation, whereas a value of 1 indicates the maximum level of protein aggregation observed during an experimental study.

Each index is calculated in accordance with the experimental data that reflect corresponding conformational or association changes in a given protein. There is no limitation to the choice of experimental variables, as long as the experiment is a measure of the amount of structure. Taking BSA as an example, intrinsic fluorescence peak position shifts were used as an indicator of tertiary structural change. Far UV CD spectroscopy at a specific wavelength (e.g. 222 nm) was selected to monitor changes in secondary structure. Static light scattering experiments were used to detect the amount of aggregation. If a certain experimental technique is not applicable to a specific macromolecule (e.g., fluorescence in a protein lacking Trp), alternative biophysical methods can be substituted (e.g., near UV absorption or CD for tertiary structural change, and FTIR for secondary structure). To calculate a structural index, an initial interpretation of the original experimental data is necessary. If the experimental data shows a monotonic change over the experimental variables, simple normalization (and optional inversion) would be sufficient to calculate the index from zero to one.

To illustrate the basic procedure for preparing structural indices, the CD signal at 222 nm for BSA from pH 3 to 8 as a function of temperature [Fig. 1(A)] decreased with distinct transitions seen as the temperature increased, indicating a loss of protein secondary structure. The data defines the range of possible changes for BSA's secondary structure over the given pH and temperature range as examined by CD. As seen in Figure 1(D), the secondary structure index (SI) of BSA was calculated by normalizing the inverted CD signals at a given pH and temperature with an increase in negative signal, indicating a loss of structure.

The intrinsic fluorescence peak position shift in proteins is sensitive to the microenvironmental changes around tryptophan resides and was therefore selected to prepare a structural index for tertiary structure. Changes in the hydration state of indole side chains can produce either red or blue shifts corresponding to increases or decreases in surface exposures, respectively. This change can therefore be interpreted in terms of tertiary structural changes of the macromolecule. For example, the peak position of the intrinsic fluorescence spectra for BSA at pH 3–8 from 10 to 90°C is presented in Figure 1(B). Unlike the previous CD data, the peak position shift at pH 3 occurs in a different direction than the shift at other pH values. Therefore, obtaining an index by normalization of the peak position shift data at all pH values could lead to the misinterpretation of the tertiary structural index at pH 3, because it suggests that the tertiary structure is returning to a more native state as temperature increases. In this case, a comparison of the amount of deviation on each side of the native state value becomes more important than that of the direction. In such cases, we therefore invert the shift value to make it comparable to the behavior at other pH values. The same procedures are then applied to obtain the tertiary structure index (TI) as shown in Figure 1(E). The AI [Fig. 1(F)] was determined from light-scattering data [Fig. 1(C)] as discussed below.

It is common to obtain experimental data that does not manifest the slower, continuous changes observed with BSA. For example, the CD signal at 222 nm for the protein antigen SP1732, as measured from pH 3 to 8 and 10–90°C, shows a sharp negative change that decreases in magnitude and converges as illustrated in Figure 6(A). The sharp negative response may be induced by intermolecular interactions. The CD signal then disappears as the secondary structure of SP1732 becomes increasingly disrupted and aggregation sets in. Normalization of the inverted CD signal may not provide an accurate SI, because higher values of the index at a negative peak do not necessarily indicate the secondary structure content in the native state. Thus, in this case, it is necessary to calculate the amount of the signal's deviation from its initial value. One method is to integrate the absolute value of the first derivative of the signal as described in Eq. (1). The constant C can be determined by the nature of the signal. The value of C should be either 1 or −1 for positive or negative correlation, respectively, between the signal and the amount of structure. In other words, a positive correlation (C = 1) is defined when higher signal indicates less structure.

(1)

where f is the experimental measurement, x₀ the initial value, and C: ±1, based on the nature of the signal.

Figure 6(D) shows the result of applying Eq. (1) to data in Figure 6(A) with C = 1. The CD signals are converted to increasing sigmoidal curves. The larger negative peak at pH 3, however, results in a much larger deviation from the initial value compared to other pH values. This result is inconsistent with the original CD signal in which the signals converge to indicate a particular level of unfolded structure at higher temperature. Normalization of individual pH values may adjust this inconsistency, but it will cause the difference in initial values to be lost. Rather, introducing an upper (or lower if C = −1)-bound cut-off might be a better option, because deviations beyond a certain level can be considered to be the same maximally unfolded (or structurally altered) state of the macromolecule. In addition, this approach conserves the initial values. The cut-off threshold value should be carefully chosen after the initial interpretation of the experimental data. Figure 6(G) shows the final SI after applying cut-off criteria to Figure 6(D), followed by inversion and normalization as presented in Eq. (2). Equation (2) simply represents a combined procedure for cut-off, normalization, and inversion of the result from Eq. (1).

(2)

where I_max is the maximum or upper cut-off value of I(x) and I_min the minimum or lower cut-off value of I(x)

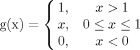The combination of Eqs. (1) and (2) was applied to calculate the TI and AI from intrinsic fluorescence peak position shift and static light-scattering data, respectively, as described in Figure 6(H,I). The cut-off value for the AI [Fig. 6(I)] should be selected with the following considerations. It is generally observed that the intensity of the static light scattering signal decreases at higher temperature after it reaches a peak. This decrease in scattering intensity is usually caused by precipitation and settling of the sample, not by aggregation itself. The corresponding AI, therefore, should reach and remain one after its peak value. Another consideration is the comparison among different environmental conditions (e.g. pH), when occasionally scattering signals are too excessive causing suppression of other signals. In this case, the choice of cut-off value will be subjective as to whether to use a lower cut-off value (to emphasize other relatively lower signals) or use a higher cut-off value (to highlight more intense aggregation conditions). Figure 6(C,F) demonstrates the use of a lower cut-off value to exhibit aggregation at pH 4 and 7. Otherwise, these data might be overlooked because of higher signals at pH 5 and 6.

In summary, Eqs. (1) and (2) are generalized equations to calculate structural indices from any sets of experimental data as illustrated in the two examples presented. Equation (1) converts any data set into a monotonically changing signal with its initial value and the amount of deviation from its initial values, preserved. Equation (2) is then applied to the results from the Eq. (1) for inversion, normalization, and cut-off. The constant C in Eqs. (1) and (2) determines the direction of the signal. The I_max and I_min parameters in Eq. (2) determine the range of the signal for normalization and cut-off. It should be noted that experimental noise in the measurements may affect the resulting structural index derived from Eq. (1), because small fluctuations in the first derivative will be accumulated and resulted in a gradual increase of the index. Thus, an appropriate smoothing algorithm such as the Savitzky–Golay smoothing filter²⁷ should be applied to the data to improve the signal to noise ratio, before application of Eq. (1).

Construction of three-index EPDs

The purpose of the three-index empirical phase diagram (EPD) is to present a colored diagram that not only displays the degree of change in a macromolecule's structure and association state in response to its environmental conditions, but the color itself can also be related to changes in specific elements of protein structure. The degree of change is commonly studied using three structural levels: secondary structural change, tertiary structural change, and aggregation. The change in each aspect is defined by the previously introduced structural indices: SI, TI, and AI.

The three-index EPD is constructed simply by mapping each structural index to an RGB color component. Because a color in an RGB scheme is expressed as a tuple of red, green, and blue components, we have assigned SI to red, TI to green, and AI to blue. Thus, a color produced by the summation of these three color components is mapped to a specific state of the target macromolecule. Table I lists the resultant colors and their interpretation in ideal cases. In the native state of a macromolecule, TI and SI would have a value of 1, and AI would be zero, because the amount of tertiary structure and second structure would be highest, and there will be no aggregation. This combination confers a yellow color to the native state, because a range of index value from zero to one is assigned to a color gradation from black to the full color of the index respectively. In some cases, a red color will be observed as the amount of tertiary structure decreases but the secondary structure content remains high. This may also indicate a molten globular state in which tertiary structure change occurs before secondary structure alteration. A brown color, however, will more frequently appear, because the amount of secondary structure will probably be reduced slightly compared to the native state, although it is still relatively higher than the fractional amount of tertiary structure. At the same time, some aggregation may be observed in the molten globular state, which forms a pink color. Once the macromolecule becomes fully unfolded, the amount of both tertiary and secondary structure becomes minimal, and therefore the red and green color components decrease to black. If there is no aggregation, the resulting color will be black. This conformationally altered state attains a blue color if the macromolecule extensively aggregates.

Table I.

The Relationship of Colors to Protein Structural Features in Three-Index Empirical Phase Diagrams

Color	Protein structure
Yellow (green + red)	Native state
Red, brown, or pink (red + blue)	Molten globular state
Blue	Aggregated state
Black	Extensively unfolded state without aggregation

As an optional feature, the individual RGB components can be provided alongside the three-index EPD. Because it is difficult to determine the amount of an RGB component with a given color, the explicit display of its RGB components could be helpful in understanding the interpretation of a color. The three-index EPD accompanied with its RGB component diagrams, therefore, enable facile identification of changes at each level of structure in the protein.

Construction of radar (star) diagrams

The radar diagram is a widely used graphical representation for multivariate data.^12,17–23 It has many similar forms and names such as star glyph, star chart, and spider chart. The major idea for this data visualization approach is to arrange multiple axes in evenly spaced angles from the same starting point to form a polar coordinate system. Multivariate data, represented as n-dimensional vectors, is plotted on the n-axes and connected to each other to form a (filled) polygon.

The radar diagram used in this work is composed of multiple radar charts arranged in two-dimensional Cartesian coordinates of environmental stress conditions. Each radar chart represents physical data measured at the given stress conditions. For simplicity, all polar axes in a radar plot are adjusted to a display value between zero and one in which zero is mapped to the axial starting point and one to the outer rim. Therefore, stability data should first be converted to the corresponding structural indices using Eqs. (1) and (2). In each environmental condition (e.g., solution pH and temperature), the values in the associated data indices are mapped to points in the polar coordinates of the radar chart. The points are then connected to each other. To enhance the display of the relative magnitude of these data, circular grids are placed every 0.2 interval between zero and one in a radar chart. Unlike the three-index EPD described earlier, the radar diagram can display any number of variables. Figure 8(A) shows an example of a radar chart with eight axes (e.g., using eight different experimental readouts). The radar diagram is known to be well suited to identify similarity and difference in patterns. The radar diagrams in this work are also able to aid in the recognition of a range of environmental conditions in which a macromolecule shows similar structural behavior. To better serve this purpose, two guidelines are proposed: (1) Some of the normalized data (i.e., structural indices) should be inverted, so that the native state of a macromolecule will be displayed as a dot (or smallest area). The magnitude of signal changes will thus represent the amount of deviation from a native state. (2) Experimental methods should be grouped on the radar chart according to which structural feature is being measured, that is, tertiary and secondary structure and aggregation.

Figure 8.

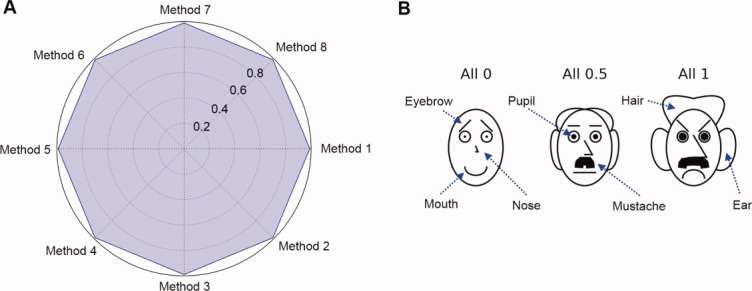
(A) Example of a radar chart with eight variables (experimental methods). All variables are set to a value of 1 with intervals of 0.2 (see text). (B) Chernoff face diagrams with seven variables. Each variable can vary from zero to one. Three faces are constructed with all variables set at 0, 0.5, and 1. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

With regard to the first point, one of the most critical pieces of information explored in a protein characterization study is the environmental conditions under which a macromolecule starts to be structurally altered. If the native state is described as a dot, small transitions from the native state become more easily detectable. More importantly, the nature of the experimental method that detects a transition becomes readily evident. Second, the order of presentation of experiments in the radar plot is an important factor in intuitive pattern recognition. If there are multiple experiments that measure similar properties, they should be grouped together instead of undergoing random placement. For example, three tertiary structure sensitive measurements (e.g., intrinsic fluorescence peak position shift, UV absorbance second derivative peak positions, and near UV CD) can be placed in the positions of Methods 1–3 in Figure 8(A), two secondary structure measurements (e.g., CD and FTIR) in the positions of Methods 4–5, and three aggregation measurements (e.g., static and dynamic light scattering and optical density) in the positions of Methods 6–8. Such a grouping of data should increase the visual interpretability by assigning the type of measurement to an appropriate angular placement in the radar diagram.

Construction of Chernoff face diagrams

H. Chernoff invented the Chernoff face diagram as a multivariate data visualization technique.^13–15 The key idea of this approach is to use the sensitive ability of human face recognition as an efficient tool to read and partition multivariate data represented as human faces. There is no restriction on how to map multivariate data to human facial features such as the shape, size, and location of eyebrows, eyes, nose, mouth, ear, hair, and face. Although the number of variables can be quite large, seven key facial features were implemented here for exploratory purposes as presented in Figure 8(B).

The Chernoff face diagram has the same format as the radar diagram except each plot at any coordinate is a Chernoff face instead of a radar chart. Because each facial feature is defined to have a parameter value ranging from zero to one, all physical data should be converted to the corresponding structural indices using Eqs. (1) and (2). In each stress condition (e.g., pH and temperature), the values in the associated data indices are mapped to display associated facial features. In general, three or four facial variables are adequate to represent macromolecular conformational stability data as shown later in this work. The native state of a macromolecule is assigned to a smiling face for better recognition [along with a short noise combined with no hair or ears; see Fig. 8(B)].

Clustering analysis of phases

One of the objectives of “stress/response” diagrams is to better understand macromolecular behaviors induced by environmental stresses. Macromolecular structural behavior observed by multiple experimental techniques is displayed in a two-dimensional environmental stress grid by color in the three-index EPD, an equiangular polygon in the radar diagram, and a human face in the Chernoff face diagram. All visualization techniques emphasize the detection of similarity and outliers, which is suited to identifying boundaries where macromolecular structure initiates alteration. In many cases, however, changes in color, the shape of polygons, and human facial characteristics may be too subtle for human visual perception to recognize a distinct boundary. Computational clustering algorithms can be helpful in determining such boundaries. A number of clustering algorithms have been developed for various types of problems.^28,29 The development and performance evaluation of a certain clustering algorithm and its parameters are out of the scope of this study. Rather, visualization of clustering results will be demonstrated for each of the three data visualization approaches.

The k-means clustering algorithm^28,29 was chosen for this study because of its popularity. The k-means clustering algorithm is a widely used method to calculate k central points (or centroids) in which all samples belong to each cluster whose mean is the calculated centroid. The number of clusters k must be postulated, and therefore, various values of k are tried and selected after evaluation. The result is not always optimal, because the algorithm tries to converge rapidly to a local optimum from random initial centroid locations. Therefore, the results can be manually correctable based on the interpretation of raw data. In addition, the same observation values under different environmental conditions are usually chosen as the same cluster by the algorithm, although actual interpretation may be different. In this case, clustering of indices rather than raw data might produce better results.

Once the clusters are obtained, they can be displayed on the three-index EPD, the radar diagram, and the Chernoff face diagram as line boundaries. For the radar and Chernoff face diagrams, a cluster can be represented as a single radar chart or a Chernoff face, which displays averaged values of all images in the cluster. This clustered version of a radar chart or Chernoff face diagram provides a more compact view in summarizing the characteristics of each cluster. We generally find the clustered radar, or Chernoff face diagrams provide the best summary of the data, as shown in the Results section.

Supplementary material

Additional Supporting Information may be found in the online version of this article.