An Ancestral Recombination Graph for Diploid Populations with Skewed Offspring Distribution

Abstract

A large offspring-number diploid biparental multilocus population model of Moran type is our object of study. At each time step, a pair of diploid individuals drawn uniformly at random contributes offspring to the population. The number of offspring can be large relative to the total population size. Similar “heavily skewed” reproduction mechanisms have been recently considered by various authors (cf. e.g., Eldon and Wakeley 2006, 2008) and reviewed by Hedgecock and Pudovkin (2011). Each diploid parental individual contributes exactly one chromosome to each diploid offspring, and hence ancestral lineages can coalesce only when in distinct individuals. A separation-of-timescales phenomenon is thus observed. A result of Möhle (1998) is extended to obtain convergence of the ancestral process to an ancestral recombination graph necessarily admitting simultaneous multiple mergers of ancestral lineages. The usual ancestral recombination graph is obtained as a special case of our model when the parents contribute only one offspring to the population each time. Due to diploidy and large offspring numbers, novel effects appear. For example, the marginal genealogy at each locus admits simultaneous multiple mergers in up to four groups, and different loci remain substantially correlated even as the recombination rate grows large. Thus, genealogies for loci far apart on the same chromosome remain correlated. Correlation in coalescence times for two loci is derived and shown to be a function of the coalescence parameters of our model. Extending the observations by Eldon and Wakeley (2008), predictions of linkage disequilibrium are shown to be functions of the reproduction parameters of our model, in addition to the recombination rate. Correlations in ratios of coalescence times between loci can be high, even when the recombination rate is high and sample size is large, in large offspring-number populations, as suggested by simulations, hinting at how to distinguish between different population models.

DIPLOIDY, in which each offspring receives two sets of chromosomes, one from each of two distinct diploid parents, is fairly common among natural populations. Mathematical models in population genetics tend to assume, however, that all individuals in a population are haploid, simplifying the mathematics. Mendel’s laws describe the mechanism of inheritance as composed of two main steps, equal segregation (first law) and independent assortment (second law). The first law proclaims gametes are haploid, i.e., carry only one of each pair of homologous chromosomes. Most models in population genetics are thus models of chromosomes or gene copies. Mendel’s second law proclaims independent assortment of alleles at different genes, or loci, into gametes. Linkage of alleles on chromosomes, resulting in nonrandom association of alleles at different loci into gametes, is of course an important exception to the second law.

Coalescent processes (Kingman 1982a,b; Hudson 1983b; Tajima 1983) describe the ancestral relations of chromosomes (or gene copies) drawn from a natural population. The coalescent was initially derived from a Cannings (1974) haploid exchangeable population model. Related ancestral processes take into account population structure (Notohara 1990; Herbots 1997), selection (Krone and Neuhauser 1997; Neuhauser and Krone 1997; Etheridge et al. 2010), and recombination between linked loci (Hudson 1983a; Griffiths 1991; Griffiths and Marjoram 1997). The coalescent has proved to be an important advance in theoretical population genetics and a valuable tool for inference of evolutionary histories of populations.

Ancestral recombination graphs (ARGs) (Hudson 1983a; Griffiths 1991; Griffiths and Marjoram 1997) trace ancestral lineages of gene copies at linked loci, in which linkage is broken up by recombination. An ARG is a branching–coalescing graph, in which recombination leads to branching of ancestral chromosomes and coalescence to segments rejoining. Coalescence events in an ARG may not lead to coalescence of gene copies at individual loci. An example ARG for two linked loci is given below, labeled as ARG(1), with notation borrowed from Durrett (2002). The labels a and b refer to the two alleles (types) at loci 1 and 2, respectively. A single chromosome with two linked alleles is denoted by (ab), while chromosomes carrying ancestral alleles at only one locus are denoted (a) and (b). When coalescence occurs at either locus, the number of alleles at the corresponding locus is reduced by one. The absorbing state, either (ab) or (a)(b), is reached when alleles at both loci have coalesced:

$$\begin{array}{c}\text{ARG}\left(1\right):\left(ab\right)\left(ab\right)\stackrel{r}{\to }\left(a\right)\left(b\right)\left(ab\right)\stackrel{c}{\to }\left(ab\right)\left(b\right)\\ \stackrel{r}{\to }\left(a\right)\left(b\right)\left(b\right)\stackrel{c}{\to }\left(a\right)\left(b\right)\\ \text{ARG}\left(2\right):\left(ab\right)\left(ab\right)\stackrel{r}{\to }\left(a\right)\left(b\right)\left(ab\right)\stackrel{r}{\to }\left(a\right)\left(b\right)\left(a\right)\left(b\right)\stackrel{c}{\to }\left(a\right)\left(b\right).\end{array}$$

In ARG(1), the first transition is a recombination, denoted by $\stackrel{r}{\to }$, followed by a coalescence $\left(\stackrel{c}{\to }\right)$, in which the two alleles at locus 1 coalesce. Graph ARG(1) serves to illustrate two important concepts we are concerned with, namely correlation in coalescence times between alleles at different loci and the restriction to binary mergers of ancestral lineages.

Correlation in coalescence times between types at different loci follows from linkage. Alleles at different loci can become associated due to a variety of factors, including changes in population size, natural selection, and population structure. Within-generation fecundity variance polymorphism induces correlation between a neutral locus and the locus associated with the fecundity variance (Taylor 2009). Sweepstake-style reproduction (Hedgecock et al. 1982; Avise et al. 1988; Palumbi and Wilson 1990; Beckenbach 1994; Hedgecock 1994; Árnason 2004; Hedgecock and Pudovkin 2011), in which few individuals produce most of the offspring, has also been shown to induce correlation in coalescence times between loci (Eldon and Wakeley 2008). Understanding genome-wide correlations in coalescence times becomes ever more important as multilocus genetic data become ubiquitous.

The ARG exemplified by ARG(1) is characterized by admitting only binary mergers of ancestral lineages; i.e., exactly two lineages coalesce in each coalescence event. The restriction to binary mergers follows from bounds on the underlying offspring distribution, in which the probability of large offspring numbers becomes negligible in a large population (Kingman 1982a,b). Sweepstake-style reproduction, in which few individuals contribute very many offspring to the population, has been suggested to explain the “shallow” gene genealogy observed for many marine organisms (Hedgecock et al. 1982; Avise et al. 1988; Palumbi and Wilson 1990; Beckenbach 1994; Hedgecock 1994; Árnason 2004; Hedgecock and Pudovkin 2011). Large offspring-number models are models of extremely high variance in individual reproductive output. Namely, individuals can have very many offspring or up to the order of the population size with nonnegligible probability (Sagitov 2003; Schweinsberg 2003; Eldon and Wakeley 2006; Sargsyan and Wakeley 2008; Birkner and Blath 2009). Such models do predict shallow gene genealogies and can be shown to give better fit to genetic data obtained from Atlantic cod (Árnason 2004) than the Kingman coalescent (Birkner and Blath 2008; Birkner et al. 2011; Eldon 2011; Steinrücken et al. 2012). Different large offspring-number models will no doubt be appropriate for different populations, and the identification of large offspring-number population models for each population is an open problem. For the sake of simplicity and mathematical tractability, the simple large offspring-number model considered by Eldon and Wakeley (2006) is adapted to our situation.

The coalescent processes derived from large offspring-number models belong to a large class of multiple-merger coalescent processes introduced by Donnelly and Kurtz (1999), Pitman (1999), and Sagitov (1999). Multiple-merger coalescent processes (Λ-coalescents), as the name implies, admit multiple mergers of ancestral lineages in each coalescence event, in which any number of active ancestral lineages can coalesce, and at most one such merger occurs each time. In simultaneous multiple-merger coalescent processes (Schweinsberg 2000a; Möhle and Sagitov 2001), any number of multiple mergers can occur each time; i.e., distinct groups of active ancestral lineages can coalesce each time. The ancestral recombination graph derived from our diploid large offspring-number model admits simultaneous multiple mergers of ancestral lineages, as exemplified in ARG(2). The last transition in ARG(2) is a simultaneous multiple merger, in which the two types at each locus coalesce to separate ancestral chromosomes.

To investigate correlations in coalescence times among loci due to skewed offspring distribution, we formally derive an ancestral recombination graph, or a coalescent process for many linked loci, from our diploid large offspring-number model. The key to the proof of convergence to an ancestral recombination graph from our diploid model lies in resolving the separation-of-timescales phenomenon we observe. Following Mendel’s laws, the two chromosomes of an offspring come from distinct diploid parents. Chromosomes can therefore coalesce only when in distinct individuals. The ancestral process consists of two phases, a dispersion phase occurring on a “fast” timescale and a coalescence and recombination phase occurring on a “slow” timescale. In the dispersion phase, chromosomes paired together in diploid individuals disperse into distinct individuals. Coalescence and recombination occur only on the slow timescale. Similar separation-of-timescales issues arise in models of populations structured into infinitely many subpopulations (demes) (Taylor and Véber 2009). When viewing the diploid individuals in our model as “demes,” our scenario departs from those describing structured populations by allowing only active ancestral lineages residing in separate demes to coalesce. A simple extension of a result of Möhle (1998) yields convergence in our case.

The limiting process we formally obtain is an ancestral recombination graph for many loci admitting simultaneous multiple mergers of ancestral chromosomes (lineages). In simultaneous multiple-merger coalescent processes, so-called Ξ-coalescents, different groups of active ancestral lineages can coalesce to different ancestors at the same time. Such coalescent processes were first studied as more abstract mathematical objects by Schweinsberg (2000a) and derived from general single-locus population models by several authors (Möhle and Sagitov 2001; Sagitov 2003; Sargsyan and Wakeley 2008; Birkner et al. 2009). A Ξ-coalescent with necessarily up to quadruple simultaneous multiple mergers arises at each marginal locus (i.e., considering each locus separately) in our model, since four parental chromosomes are involved in each reproduction event. This structure is intrinsically owed to our diploidy assumptions.

Formulas for the correlation in coalescence times between two alleles at two loci are obtained using our ARG. As predicted by J. E. Taylor (personal communication), these correlations will not necessarily be small even for loci separated by a high recombination rate. This is a novel effect not visible in classical models. The correlation structure will of course depend on the underlying coalescent parameters introduced by the large offspring-number model we adopt. An approximation of the expected value of the statistics r², commonly used to quantify linkage disequilibrium, is also investigated using our ARG. In addition, we employ our ARG to investigate correlations in ratios of coalescence times between loci for samples larger than two at each locus, using simulations.

A Diploid Population Model with Multilocus Recombination and Skewed Offspring Distribution

The forward population model

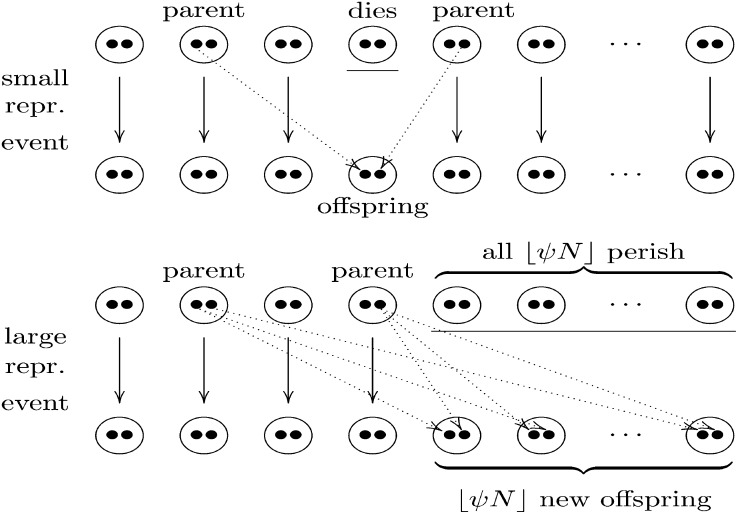
Consider a population consisting of N ∈ ℕ ≡ {1, 2, …} diploid individuals, meaning that each individual contains two chromosomes. Each chromosome is structured into L ∈ ℕ loci. We assume Moran-type dynamics: At each time step (“generation”), either a small or a large reproduction event occurs. In a small reproduction event, a single individual chosen uniformly at random from the population dies, and two other distinct individuals are chosen as parents. A diploid offspring is then formed by choosing one chromosome from each parent (see Figure 1). The parents always persist. A small reproduction event occurs with probability 1 − ɛ_N, in which ɛ_N ∈ (0, 1) depends on N. In a large reproduction event, a fraction ψ ∈ (0, 1) of the population perishes, meaning that ⌊ψN⌋ individuals die (⌊x⌋ for x ≥ 0 denotes the largest integer smaller than x). Two distinct individuals are then chosen uniformly from the remaining N − ⌊ψN⌋ individuals to act as parents of ⌊ψN⌋ offspring, and each offspring is formed independently by choosing one (potentially recombined) chromosome from each parent (see Figure 1). The population size always stays constant at N diploid individuals. Individuals that neither reproduce nor die simply persist.

Figure 1 .

Illustration of “small” and “large” reproduction events without recombination. The dotted arrows indicate the copying of parental chromosomes into offspring chromosomes. The solid arrows indicate individuals that persist.

Given the two parents, genetic types of the offspring individuals are then obtained as follows. Each parent generates a large number of potential offspring chromosomes, of which a fraction 1 − r_N are exact copies of the original parental chromosomes and a fraction r_N are recombinants. Each chromosome is structured into L loci. Recombination occurs only between loci and never within. If recombination between a pair of chromosomes in a parent occurs between loci ℓ and ℓ + 1 ∈ {1, … , L} (where we say that X ∈ {1, … , L − 1} is the crossover point), the two chromosomes exchange types at all loci from ℓ + 1 to L. Only one crossover point is allowed in each recombination event. Let $r_N^{\left(\ell \right)}$ denote the probability of recombination between loci ℓ and ℓ + 1 (i.e., the probability that the potential crossover point X equals ℓ). An offspring chromosome is a recombinant with probability $r_N=r_N^{\left(1\right)}+\dots +r_N^{\left(L-1\right)}$. Given that recombination happens, we thus have

$$\mathbb{P}\left\{X=\ell \right\}=\frac{r_N^{\left(\ell \right)}}{r_N^{\left(1\right)}+\cdots +r_N^{\left(L-1\right)}},1\le \ell \le L-1.$$

Each pair of recombined chromosomes is formed independently of all other pairs. From this large pool of chromosomes, each new offspring is randomly assigned (independently of all other offspring in the case of a large reproduction event), one potentially recombined chromosome generated by each parent. In addition, the reproduction mechanism in different generations is assumed to be independent.

Ancestral relationships—notation

Now we switch from the forward population model to its ancestral process, running backward in time. Our sample consists of n ∈ {1, … , 2N} chromosomes, each subdivided into L loci. Hence, we need to keep track of the ancestry of nL segments (types/alleles). This implies that the different segments could end up on up to nL distinct chromosomes in nL distinct ancestral individuals. The required notation is now introduced, and our discourse will therefore necessarily become a little bit technical. However, we believe that a precise description of the objects we are working with is essential. The key to understanding our notation is that we are working with enumerated chromosomes and ordered loci on chromosomes.

At present (that is, time step m = 0), assume that we consider an even number n of chromosomes carried by n/2 individuals. The chromosomes are enumerated from 1 to n, attaching consecutive numbers to chromosomes found in the same individual. Our ancestral process keeps track of the chromosomal ancestral information, that is, which locus is ancestral to which set of sampled chromosomes. That is, in each generation m ∈ ℕ₀ (backward in time), we record all chromosomes that are active in the sense that they carry at least one locus that is ancestral to the same locus of at least one chromosome in generation 0. Denote the number of active chromosomes in generation m ∈ ℕ₀ by β(m) ∈ ℕ. The number β(m) of active chromosomes can both increase, due to recombination, and decrease, due to coalescence, going back in time.

Now we explain our notation for the loci. For each chromosome j ∈ [n] := {1, … , n}, denote by ${\mathbb{L}}_{\ell }^{\left(j\right)}\left(m\right)$ locus ℓ ∈ [L] on chromosome j at time m. The subsets ${\mathbb{L}}_{\ell }^{\left(j\right)}\left(m\right)$ of [n] contain all the numbers of chromosomes at present (time-step 0) to which locus ℓ on active chromosome number j at time step m is ancestral. With this convention, and for each m ∈ ℕ and ℓ ∈ [L], the collection

$$\left\{{\mathbb{L}}_{\ell }^{\left(\mathrm{j}\right)}\right(m),j=1,\dots ,\beta (m\left)\right\}.$$

which describes the configuration of segments (i.e., which ones have coalesced and which ones have not) at locus ℓ at time m, is a partition of [n]; i.e.,

$${\mathbb{L}}_{\ell }^{\left(\mathrm{j}\right)}\left(m\right)\cap {\mathbb{L}}_{\ell }^{\left(\widehat{j}\right)}\left(m\right)=Ø\hspace{0.17em}\text{for}\hspace{0.17em}j\ne \widehat{j};$$

and

$${\displaystyle \underset{j=1}{\overset{\beta \left(m\right)}{\cup }}{\mathbb{L}}_{\ell }^{\left(j\right)}\left(m\right)=\left[n\right].}$$

Thus, with our notation we can correctly describe the configuration of segments among chromosomes at any given time. By C^(j)(m) we denote chromosome number j at time m. At time m = 0,

$$C^{\left(j\right)}\left(0\right):=\left\{{\mathbb{L}}_1^{\left(j\right)}\left(0\right),\dots ,{\mathbb{L}}_L^{\left(j\right)}\left(0\right)\right\}:=\{\left\{j\right\},\dots ,\left\{j\right\}\}.$$

For m > 0, consider the jth active chromosome at generation m, where j ∈ [β(m)]. The corresponding ancestral information at generation m is encoded via an ordered list of subsets of [n], setting

$$\begin{array}{c}{C}^{\left(j\right)}\left(m\right):=\left\{{\mathbb{L}}_1^{\left(j\right)}\left(m\right),\dots ,{\mathbb{L}}_L^{\left(j\right)}\left(m\right)\right\},\\ {\mathbb{L}}_{\ell }^{\left(j\right)}\left(m\right)\subset \left[n\right],\hspace{0.17em}\ell \in \left[L\right].\end{array}$$ (1)

Chromosomes are carried by diploid individuals. Keeping track of the grouping of active chromosomes into individuals is important, since by our diploid reproduction mechanism, chromosomal lineages can coalesce only when in distinct individuals (see Example B below). In analogy with our previous nomenclature for our ancestral process, an active individual will carry at least one (and at most two) active chromosome(s). Let b(m) denote the number of active individuals at generation m, where β(m)/2 ≤ b(m) ≤ β(m) for all m. The ordered list of active chromosomes and the number of active individuals (called a “configuration”) at time m ≥ 0 are denoted by

$${\xi }^{n,N}\left(m\right):=\left\{C^{\left(1\right)}\left(m\right),\dots ,C^{\left(\beta \left(m\right)\right)}\left(m\right);b\left(m\right)\right\}.$$ (2)

An individual number i at generation m is denoted by $\mathbb{I}$_i(m), for i ∈ [b(m)]. An active individual is single marked, if carrying one active chromosome, and is double marked, if carrying two active chromosomes. Specifying the arrangement of chromosomes in individuals completes our description of the (prelimiting) ancestral process. However, since all active individuals are single marked in the limiting process, our description of the arrangement of chromosomes in individuals is given in section A1.1 in the Appendix. That is, each configuration ξ^n,N(m) begins with the 2(β(m) − b(m)) ordered consecutive chromosomes of the β(m) − b(m) double-marked individuals, followed by the 2b(m) − β(m) chromosomes contained in single-marked individuals. With this convention, the set of single- and double-marked individuals and the grouping of chromosomes into individuals at generation m are uniquely determined by a configuration ${\xi }^{n,N}\left(m\right)$ of form (2). For notational convenience, the time index m is omitted if there is no ambiguity.

For a given sample size n, the set of all possible ancestral configurations ξ^n,N is denoted by ${\mathcal{A}}_n$. The subset ${\mathcal{A}}_n^{\mathrm{sm}}\subset {\mathcal{A}}_n$ of all configurations ξ^n,N = {C⁽¹⁾, …, C^(β); b} with b = β, i.e., configurations consisting only of single-marked individuals, will play an important role later on. Indeed, all configurations in the limiting model will be confined to the set ${\mathcal{A}}_n^{\mathrm{sm}}$, and the pairing of chromosomes in individuals will become irrelevant.

The mapping “complete dispersion” (cd),

$$\text{cd}:{\mathcal{A}}_n\to {\mathcal{A}}_n^{\text{sm}}$$

breaks up the pairing of chromosomes into diploid double-marked individuals. More precisely, we define

$$\text{cd}\left(\left\{C^{\left(1\right)},\dots ,C^{\left(\beta \right)};b\right\}\right):=\left\{C^{\left(1\right)},\dots ,C^{\left(\beta \right)};\beta \right\}.$$ (3)

Configurations in ${\mathcal{A}}_n^{\text{sm}}$ describe configurations in which all active individuals are single marked, i.e., carry only one active chromosome.

The effects of recombination and coalescence on the ancestral configurations in the case of two typical situations are now illustrated. Example A illustrates recombination, and Example B illustrates coalescence of two chromosomes.

Example A.

Suppose the most recent previous event in the history of a given configuration ξ^n,N(m) was a small reproduction event (at time m + 1), and suppose that the resulting offspring individual is currently part of our configuration at time m, but neither of its parents is, and that the offspring individual is single marked, i.e., carries one active chromosome. We obtain ξ^n,N(m + 1) as follows:

• If there is no recombination during the reproduction event, then the configuration in the previous generation remains unchanged; i.e., ξ^n,N(m + 1) = ξ^n,N(m).

• If there is recombination, say at a crossover point X ∈ {1, … , L − 1}, suppose the (single) offspring chromosome is

  $$C^{\left(j\right)}\left(m\right)=\left\{{\mathbb{L}}_1^{\left(j\right)}\left(m\right),\dots ,{\mathbb{L}}_L^{\left(j\right)}\left(m\right)\right\}.$$

Necessarily, the two parental chromosomes will be part of the configuration ξ^n,N(m + 1), residing in the same double-marked individual. More precisely, the two parental chromosomes, say $C^{\left(\stackrel{\sim }{j}\right)}\left(m+1\right)$ and $C^{\left(\stackrel{\sim }{j}+1\right)}\left(m+1\right)$, are determined by (for $\ell \in \left[L\right]$)

$${\mathbb{L}}_{\ell }^{\left(\stackrel{\sim }{j}\right)}\left(m+1\right)=\{\begin{array}{ll}{\mathbb{L}}_{\ell }^{\left(j\right)}\left(m\right):\hfill & 1\le \ell \le X,\hfill \\ \mathrm{Ø}:\hfill & X+1\le \ell \le L,\hfill \end{array}$$

and

$${\mathbb{L}}_{\ell }^{\left(\stackrel{\sim }{j}+1\right)}\left(m+1\right)=\{\begin{array}{ll}\mathrm{Ø}:\hfill & 1\le \ell \le X,\hfill \\ {\mathbb{L}}_{\ell }^{\left(j\right)}\left(m\right):\hfill & X+1\le \ell \le L,\hfill \end{array}$$

in which Ø denotes loci not carrying any ancestral segments. The offspring chromosome is of course not part of ξ^n,N(m + 1). This transition can be partially trivial (a “silent recombination” event), if the crossover point is not in an “active” area, i.e., if ${\mathbb{L}}_{\ell }^{\left(j\right)}=Ø$ for X + 1 ≤ ℓ ≤ L (or for all 1 ≤ ℓ ≤ X). By way of example, with L = 3, if chromosome C^(j) = {{j}, {j}, {j}} was a recombinant, and the crossover point occurred between loci 2 and 3, the two parental chromosomes are given by $C^{\left(\stackrel{\sim }{j}\right)}=\left\{\left\{j\right\},\left\{j\right\},\mathrm{Ø}\right\}$ and $C^{\left(\stackrel{\sim }{j}+1\right)}=\left\{\mathrm{Ø},\mathrm{Ø},\left\{j\right\}\right\}$.

Example B.

Suppose the most recent previous event in the history of a given configuration ξ^n,N(m) of chromosomes at generation m is a small reproduction event at time m + 1, leading to a coalescence of lineages. This is the case, e.g., if a single-marked offspring individual with active chromosome $C^{\widehat{j}}\left(m\right)$ is in our configuration ξ^n,N(m), as well as its single-marked parent [say with currently active chromosome C^j(m)], from which it actually obtained its active chromosome. Then, to obtain the configuration ξ^n,N(m + 1), the offspring chromosome $C^{\left(\widehat{j}\right)}\left(m\right)$ is deleted, and the resulting ancestral chromosome C^(j)(m + 1) is given by the family of the union of the sets ${\mathbb{L}}_{\ell }^{\left(j\right)}$ and ${\mathbb{L}}_{\ell }^{\left(\widehat{j}\right)}$,

$$C^{\left(j\right)}\left(m+1\right)=\left\{{\mathbb{L}}_1^{\left(j\right)}\left(m\right)\cup {\mathbb{L}}_1^{\left(\widehat{j}\right)}\left(m\right),\dots ,{\mathbb{L}}_L^{\left(j\right)}\left(m\right)\cup {\mathbb{L}}_L^{\left(\widehat{j}\right)}\left(m\right)\right\}.$$ (4)

All other chromosomes in ξ^n,N(m + 1) are copied from ξ^n,N(m). Again, taking L = 3, if chromosomes C^(j) = {{j}, {j}, {j}} and C^(k) = {{k}, {k}, {k}} coalesce, the resulting ancestral chromosome is given by C^(j) = {{j, k}, {j, k}, {j, k}}.

Scaling and classification of transitions

To obtain a nontrivial scaling limit for {ξ^n,N(m)} as N → ∞, the limit theorem of Möhle and Sagitov (2001) (cf. also the special case considered in Eldon and Wakeley 2006) suggests one should, for some constant c > 0, choose probability 1 − c/N² for the small reproduction events, choose c/N² for the large reproduction events, i.e., setting

$${\varepsilon }_N=\frac{c}{N^2},$$ (5)

and speed up time by N². For the recombination rate to be nontrivial in the limit (i.e., neither 0 nor infinitely large), we require that all recombination values $r_N^{(\cdot )}$ scale in units of N; i.e., for each crossover point ℓ ∈ [L]\{L},

$$r_N^{\left(\ell \right)}:=\frac{r^{\left(\ell \right)}}{N},0<r^{\left(\ell \right)}<\mathrm{\infty }.$$ (6)

Thus, even though our timescale is in units of N² time steps, recombination is scaled in units of N time steps. On the level of single lineages the probability of recombination is of the order O(N⁻²). Indeed, after a small reproduction event, the probability of drawing an offspring is 1/N. The probability that the offspring carries a recombined chromosome is of order O(1/N).

Given the cornucopia of possible transitions from ξ^n,N(m) to ξ^n,N(m + 1), it is important to identify those transitions that are expected to be visible in the limiting process.

All possible transitions fall into the following three regimes:

• Those transitions that happen at probability of order O(N⁻²) per generation, which will be visible in the limit (since time is scaled by N²): They are called effective transitions and will appear at a finite positive rate in the limit.

• Further, there are transitions that happen less frequently, typically with probability of order O(N⁻³) or smaller per generation, which will thus become negligible as N → ∞ and hence be invisible in the limit. These are called negligible transitions.

• Finally, there are transitions that happen much more frequently [with probability of order O(N⁻¹) or even O(1) per generation]. At first sight, one might think that their presence might lead to chaotic behavior in the limit. However, this is not the case. Instead, these transitions will happen “instantaneously” in the limit and result in a projection of the states of our process from ${\mathcal{A}}_n$ into the subspace ${\mathcal{A}}_n^{\mathrm{sm}}$, which will be the limiting state space. This is proved below. Such transitions are called projective or instantaneous transitions. The identity transition is a special case of a projective transformation.

In the Appendix (section A1), a full classification of all transitions into the above groups is provided.

Instantaneous and effective transitions

The most important transitions and their effect for the limiting process are now described in detail. Consider the following most recent events in the history of a set of lineages, i.e., events occurring at time m + 1, from the perspective of the ancestral process ξ^n,N(m) at time m:

• Event 1 (silent): A small reproduction event occurs, but the offspring is not active. This is the most likely event and is of the order O(1), but does not affect our ancestral configuration process ξ^n,N(m); i.e., ξ^n,N(m+1) = ξ^n,N(m). This event leads to an identity transition (a trivial instantaneous transition).

• Event 2 (dispersion): A small reproduction event occurs, the offspring is active in our sample but neither parent is, and recombination does not occur. This is a relatively frequent event that occurs with a probability of the order O(N⁻¹) per generation [since the probability that the offspring is in the sample is b(m)/N]. If the offspring carries only one active chromosome, we again see an identity transition; i.e., ξ^n,N(m + 1) = ξ^n,N(m). If the offspring carries two active chromosomes, i.e., is a double-marked individual, the two active chromosomes will disperse to two separate individuals, who will then become single-marked individuals. Formally, for $\xi =\left\{C^{\left(1\right)},\dots ,C^{\left(\beta \right)};b\right\}\in {\mathcal{A}}_n$ with at least one double-marked individual (b < β), define the map ${\text{disp}}_i(\cdot ):{\mathcal{A}}_n\to {\mathcal{A}}_n$ dispersing the chromosomes paired in individual i,

  $$\begin{array}{l}{\text{disp}}_i\left(\xi \right)=\{C^{\left(1\right)},\dots ,C^{\left(2i-2\right)},C^{\left(2i+1\right)},C^{\left(2i+2\right)},\\ \dots ,C^{\left(2\left(\beta -b\right)\right)},C^{\left(2i-1\right)},C^{\left(2i\right)},C^{\left(2\left(\beta -b\right)+1\right)},\\ \dots ,C^{\left(\beta \right)};b+1\}\end{array}$$ (7)

  if 1 ≤ i ≤ β − b and disp_i(ξ) := ξ otherwise. Recall that the ith double-marked individual has chromosomes labeled 2i − 1 and 2i. For ξ^n,N(m), if the ith double-marked individual is affected, we have the transition ξ^n,N(m + 1) = disp_i(ξ^n,N(m)).

The dispersion events will happen instantaneously as N → ∞ (recall we are speeding time up by N²) and thus will, in the limit, lead to an immediate complete dispersion of all chromosomes paired in double-marked individuals. If in the course of events, a new double-marked individual emerges due to pairing of active chromosomes in the same diploid individual, a dispersion of the chromosomes will occur immediately. Event 2 will hence result in a permanent instantaneous transition, mapping our current state $\xi \in {\mathcal{A}}_n$ into the subspace ${\mathcal{A}}_n^{\mathrm{sm}}$ by means of the map cd defined in (3). Our limiting process will thus live, with probability one for each given t > 0, in ${\mathcal{A}}_n^{\mathrm{sm}}$, even if we start with a configuration from ${\mathcal{A}}_n\backslash {\mathcal{A}}_n^{\mathrm{sm}}$ at time t = 0.

• Event 3 (recombination): A small reproduction event occurs, a single-marked offspring but neither parent is in our sample, and recombination affecting the active chromosome at a crossover point x. This event has probability of the order O(N⁻²) per generation and will thus be visible with finite positive rate in the limit. It is an effective transition, which can be described formally as follows. Define the recombination operation recomb acting on chromosome j and crossover point x for a configuration $\xi \in {\mathcal{A}}_n^{\mathrm{sm}}$ as

  $$\begin{array}{l}{\text{recomb}}_{j,x}\left(\xi \right):=\{C^{\left(1\right)},\dots ,C^{\left(j-1\right)},{\tilde{C}}^{\left(j,1\right)},\\ {\tilde{C}}^{\left(j,2\right)},C^{\left(j+1\right)},\dots ,C^{\left(\beta \right)};\beta +1\},\end{array}$$ (8)

  where

  $${\tilde{C}}^{\left(j,1\right)}=\left\{{\tilde{\mathbb{L}}}_1^{\left(j,1\right)},\dots ,{\tilde{\mathbb{L}}}_L^{\left(j,1\right)}\right\}$$

  with

  $${\tilde{L}}_{\ell }^{\left(j,1\right)}=\{\begin{array}{ll}{\mathbb{L}}_{\ell }^{\left(j\right)}\hfill & :1\le \ell \le x-1,\hfill \\ \mathrm{Ø}\hfill & :x\le \ell \le L,\hfill \end{array}$$

  and

  $${\tilde{C}}^{\left(j,2\right)}=\left\{{\tilde{\mathbb{L}}}_1^{\left(j,2\right)},\dots ,{\tilde{\mathbb{L}}}_L^{\left(j,2\right)}\right\}$$

  with

  $${\tilde{\mathbb{L}}}_{\ell }^{\left(j,2\right)}=\{\begin{array}{ll}\mathrm{Ø}:\hfill & 1\le \ell \le x-1,\hfill \\ {\mathbb{L}}_{\ell }^{\left(j\right)}:\hfill & x\le \ell \le L\hfill \end{array}$$

  (if one of ${\tilde{C}}^{\left(j,1\right)}$, ${\tilde{C}}^{\left(j,2\right)}$ = {Ø, … , Ø}, we define recomb_j,α(ξ) := ξ, giving rise to a silent recombination event).
• Event 4 (pairwise coalescence): A small reproduction event occurs, one single-marked parent and a single-marked offspring are in the sample, the active chromosome is inherited from the parent in the sample, and recombination does not occur. This event occurs with probability of order O(N⁻²) and will therefore be visible in the limit with finite positive rate and hence gives rise to an effective transition. It will lead to a binary coalescence of lineages and can formally be described as follows. The ancestral chromosome ${\tilde{C}}^{\left(j_1\right)}$ formed by the coalescence of chromosomes j₁ and j₂ is given by

  $${\tilde{C}}^{\left(j_1\right)}=\left\{{\mathbb{L}}_1^{\left(j_1\right)}\cup {\mathbb{L}}_1^{\left(j_2\right)},\dots ,{\mathbb{L}}_L^{\left(j_1\right)}\cup {\mathbb{L}}_L^{\left(j_2\right)}\right\}$$ (9)

  if 1 ≤ j₁ < j₂ ≤ β. Define the binary coalescence operation pairmerge acting on chromosomes j₁ and j₂ (1 ≤ j₁ < j₂) in a configuration $\xi \in {\mathcal{A}}_n^{\mathrm{sm}}$ as

  $$\begin{array}{l}{\text{pairmerge}}_{j_1,j_2}\left(\xi \right):=\{C^{\left(1\right)},\dots ,{\tilde{C}}^{\left(j_1\right)},\dots ,\\ C^{\left(j_2-1\right)},C^{\left(j_2+1\right)},\dots ,C^{\left(\beta \right)};\beta -1\}\end{array}$$ (10)

  if 1 ≤ j₁ < j₂ ≤ β (otherwise, we put ${\text{pairmerge}}_{j_1,j_2}\left(\xi \right):=\xi$).
• Event 5 (multiple-merger coalescence): A large reproduction event occurs, neither parent but (possibly several) single-marked offspring are in our sample, and recombination does not occur. This is again an event with probability of order O(N⁻²) per generation and therefore will be visible in the limit with finite positive rate and hence gives rise to an effective transition. The offspring chromosomes are assigned their parental chromosomes independently and uniformly at random, since due to an immediate complete dispersion via Event 2 each offspring individual will carry precisely one active chromosome. Now we formally define the multiple-coalescence operation groupmerge for $\xi \in {\mathcal{A}}_n^{\mathrm{sm}}$ and pairwise disjoint subsets J₁, J₂, J₃, J₄, ⊂ [β] in which either at least one |J_i| ≥ 3 or at least two of the |J_i| ≥ 2. This transition is, thus, really different from a pairmerge transition. Let J_j denote the set of offspring chromosomes derived from parental chromosome j. Then

  $$\begin{array}{l}{\text{groupmerge}}_{J_1,J_2,J_3,J_4}\left(\xi \right)\\ :=\{{\tilde{C}}^{\left(1\right)},{\tilde{C}}^{\left(2\right)},{\tilde{C}}^{\left(3\right)},\\ {\tilde{C}}^{\left(4\right)},C^{\left(j\right)},j\in [\beta ]\backslash \left(J_1\cup J_2\cup J_3\cup J_4\right);\tilde{\beta }\}\end{array}$$ (11)

  with ((x)⁺ := max(x, 0))

  $$\tilde{\beta }=\beta -{\displaystyle \sum _{j=1}^4{\left(\left|J_j\right|-1\right)}^{+}}$$

  and the four parental chromosomes, at least one of which is involved in a merger, are given by (1 ≤ i ≤ 4),

  $${\tilde{C}}^{\left(i\right)}=\left\{{\displaystyle \underset{j\in J_i}{\cup }{\mathbb{L}}_1^{\left(j\right)}},\dots ,{\displaystyle \underset{j\in J_i}{\cup }{\mathbb{L}}_L^{\left(j\right)}}\right\}.$$

  The chromosome(s) C^(j) appearing in ${\text{groupmerge}}_{J_1,J_2,J_3,J_4}\left(\xi \right)$ denote the chromosomes in ξ that are not involved in a merger.

• All other events: These will either not affect our ancestral process or have a probability of order smaller than N⁻² so that they will be absent in the limit after rescaling. A complete classification of these events is given in the Appendix (section A1).

The limiting dynamics and state space

The expected dynamics of the limiting continuous-time Markov chain {ξ(t), t ≥ 0}, taking values in ${\mathcal{A}}_n$, as N → ∞, is now briefly discussed:

• Complete dispersion (Event 2) of the sampled chromosomes is the first event to occur (between times t = 0 and t = 0⁺). By ℕ_i we denote individual number i (see section A1.1 in Appendix). At time t = 0 when $\xi \left(0\right)\in {\mathcal{A}}_n$ we assume all n sampled chromosomes are paired in double-marked individuals (n even):

  $$\begin{array}{l}\xi \left(0\right)=\{{\mathbb{I}}_i:{\mathbb{I}}_i=\left\{C_0^{\left(2i-1\right)},C_0^{\left(2i\right)}\right\},1\le i\le \frac{n}{2}\}\end{array}$$ (12)

  Immediately (at time 0⁺), the chromosomes disperse into single-marked individuals,

  $$\begin{array}{c}\xi \left(0^{+}\right)=\text{cd}\left(\xi \left(0\right)\right)\\ =\left\{{\mathbb{I}}_i:{\mathbb{I}}_i=\left\{C_0^{\left(i\right)},\mathrm{Ø}\right\},1\le i\le n\right\}\\ =\left\{C_{0^{+}}^{\left(1\right)},\dots ,C_{0^{+}}^{\left(n\right)};n\right\}\in {\mathcal{A}}_n^{\mathrm{sm}}.\end{array}$$ (13)
• Throughout the evolution of the process, whenever double-marked individuals appear (e.g., from a coalescence-of-lineages event), Event 2 will immediately change our configuration to the corresponding “all dispersed” configuration; i.e., for each t > 0,

  $$\xi \left(t^{+}\right)=\text{cd}\left(\xi \left(t\right)\right)\in {\mathcal{A}}_n^{\mathrm{sm}}.$$

  Such “flickering” states will not affect any quantities of interest of our genealogy, so we can assume that they will be removed from the limit by choosing the càdlàg modification of {ξ(t), t ≥ 0}, taking only values in ${\mathcal{A}}_n^{\mathrm{sm}}$ for all t > 0 (this modification does not affect the finite-dimensional distributions of {ξ(t), t ≥ 0}).
• Recombination (Event 3) appears in the limiting process at total rate r = r⁽¹⁾ +⋯+ r^(L−1), where a certain recombination involving a given crossover point ℓ appears with rate r^(ℓ) on any lineage. Indeed, from our scaling considerations, we have that the probability of not seeing a recombination at ℓ in a small resampling event for more than N²t scaled time units for a given single-marked individual satisfies $\left(r_N^{\left(\ell \right)}=r^{\left(\ell \right)}/N\right)$

  $${\left(1-\left(1-\frac{c}{N^2}\right)r_N^{\left(\ell \right)}\frac{1}{N}\right)}^{N^{2}t}\to e^{-r^{\left(\ell \right)}t},$$

  as N→∞ [recall (6); the probability for any given individual to be the child in a small reproduction event is 1/N]; hence the waiting time for this event to happen is exponential with rate r^(ℓ).

• Coalescences appear according to the effective transitions described by Events 4 and 5. From the point of view of a given pair of active chromosomes in different individuals, a single pairwise coalescence will occur at rate $1+c({\psi }^2/4)C_{\beta ;2;\beta -2}$ with C_β;2;β−2 from (15) (with r = 1, s = β − 2), where the 1 comes from a pairwise coalescence according to a small reproduction event and the $c({\psi }^2/4)C_{\beta ;2;\beta -2}$ from a large merger event (the rates can be easily derived from considerations similar to the recombination rate r above), recalling that both coalescing chromosomes have to “successfully flip a ψ-coin” to take part in the large coalescence event and then are uniformly distributed into four groups according to the choice of any of the four potential parental chromosomes.

Given that large coalescence events (involving at least three individuals or at least two simultaneous pairwise mergers) happen with overall rate $c({\psi }^2/4)$ times the corresponding coalescence rate of a Ξ-coalescent, obtained from the number of individuals taking part in the merger independently with probability ψ, the participating individuals are then distributed uniformly into four groups according to the chosen parental chromosome. The corresponding rate is given in the third line of (14) [cf. also (15)].

The limiting ancestral process

According to the above consideration, it is now plausible to consider the following limiting Markov chain as the ancestral limiting process. This fact is proved below, with most computations provided in the Appendix. The mth falling factorial is given by (a)_m := a(a − 1) … (a − m + 1), (a)₀ := 1. The operations pairmerge, recomb, and groupmerge for elements of ${\mathcal{A}}_n^{\mathrm{sm}}$ were defined above in the section on scaling. Now we define the generator of the continuous-time ancestral recombination graph derived from our model.

Definition 1.1 (limiting multilocus diploid ancestral recombination graph). The continuous-time Markov chain {ξ(t), t ≥ 0} with values in ${\mathcal{A}}_n^{\mathrm{sm}}$, initial condition ξ(0) := cd(ξ) for $\xi \in {\mathcal{A}}_n$ and transition matrix G, with entries for elements ${\xi }^{\prime },\xi \in {\mathcal{A}}_n^{\mathrm{sm}}$, ξ′ ≠ ξ, is given by (J := (J₁, …, J₄))

$$G\left(\xi ,{\xi }^{\prime }\right)=\{\begin{array}{ll}1+c\frac{{\psi }^2}{4}{C}_{\beta ;2;\beta -2}\hfill & \mathit{if}\hspace{0.17em}\hspace{0.17em}{\xi }^{\prime }={\text{pairmerge}}_{j_1,j_2}\left(\xi \right)\hfill \\ r^{\left(\ell \right)}\hfill & \mathit{if}\hspace{0.17em}\hspace{0.17em}{\xi }^{\prime }={\text{recomb}}_{j,\ell }\left(\xi \right)\hfill \\ c\frac{{\psi }^2}{4}{C}_{\beta ;\left|J\right|}\hfill & \mathit{if}\hspace{0.17em}\hspace{0.17em}{\xi }^{\prime }={\text{groupmerge}}_J\left(\xi \right)\hfill \\ 0\hfill & \mathit{for}\hspace{0.17em}\mathit{all}\hspace{0.17em}\mathit{other}\hspace{0.17em}\hspace{0.17em}{\xi }^{\prime }\ne \xi \hfill \end{array}$$ (14)

(where in the penultimate line we consider only cases where either at least one |J_i| ≥ 3 or at least two of the |J_i| ≥ 2), with

$$C_{\beta ;\left|J\right|}:=C_{\beta ;\left|J_1\right|,\left|J_2\right|,\left|J_3\right|,\left|J_4\right|;\beta -\left(\left|J_1\right|+\left|J_2\right|+\left|J_3\right|+\left|J_4\right|\right)}$$

and (s = b − k₁ −⋯− k_r ≥ 0, x ∧ y := min(x, y)),

$$\begin{array}{l}{C}_{b;k_1,\dots ,k_r;s}=\frac{4}{{\psi }^2}{\displaystyle \sum _{l=0}^{s\wedge \left(4-r\right)}\left(\begin{array}{c}s\\ l\end{array}\right)\frac{{\left(4\right)}_{r+l}}{4^{k_1+\dots +k_r+l}}}\cdot \\ {\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\left(1-\psi \right)}^{s-l}{\left(\psi \right)}^{k_1+\dots +k_r+l}\end{array}$$ (15)

For the diagonal elements, one has of course

$$G\left(\xi ,\xi \right)=-{\displaystyle \sum _{{\xi }^{\prime }\ne \xi ,{\xi }^{\prime }\in {\mathcal{A}}_n^{\mathrm{sm}}}G\left(\xi ,{\xi }^{\prime }\right)}.$$ (16)

The rates in (15) are the transition rates of the Ξ-coalescent (a simultaneous multiple-merger coalescent) with

$$\Xi ={\delta }_{\left(\psi /4,\psi /4,\psi /4,\psi /4,0,0,\dots \right)},$$

when r distinct groups of ancestral lineages merge. The number of lineages in each group is given by k₁, … , k_r, given β active ancestral lineages. The number s = β − (k₁ + … + k_r) ≥ 0 gives the number of lineages (ancestral chromosomes) unaffected by the merger (cf. Schweinsberg 2000a, Theorem 2). The particular form of Ξ given above follows from the fraction ψ of the population replaced by the offspring of the two parents in a large reproduction event and our assumption that each parent contributes exactly one chromosome to each offspring. We have the following convergence result:

Theorem 1.2. Let {ξ^n,N(m), m ≥ 0} be the ancestral process of a sample of n chromosomes in a population of size N and assume the scaling relations (5) and (6). Then, starting from ${\xi }^{n,N}\left(0\right)\in {\mathcal{A}}_n$, we have that

$$\left\{{\xi }^{n,N}\left(\lfloor N^{2}t\rfloor \right)\right\}\to \left\{\xi \left(t\right)\right\},\hspace{0.17em}\text{as}\hspace{0.17em}N\to \mathrm{\infty },$$

in the sense of the finite-dimensional distributions on the interval (0, ∞). The initial value of the limiting process is given by

$$\xi \left(0\right)=\text{cd}\left({\xi }^{n,N}\left(0\right)\right)\in {\mathcal{A}}_n^{\mathrm{sm}}.$$

A proof can be found in the Appendix. If c = 0, the classical ancestral recombination graph for a diploid population with recombination in the spirit of Griffiths and Marjoram (1997) results.

General Diploid Moran-Type Models: “Random” ψ

One of the aims of the present work is to understand the genome-wide correlations in gene genealogies induced by sweepstake-style reproduction. So far, we have discussed this for a very simple example of a sweepstake mechanism (analog to the one considered in Eldon and Wakeley 2006). More precisely, the fraction ψ ∈ (0, 1) of the population replaced by the offspring of a single pair of individuals in a large offspring-number event has hitherto been assumed to be (approximately) constant. Along the lines of the previous discussion, an ancestral recombination graph with a randomized offspring distribution can be derived (a comprehensive discussion of single-locus haploid Moran models in the domain of attraction of Λ-coalescents can be found in a recent article by Huillet and Möhle 2011). Even though ψ is now considered a random variable, the population size stays constant at N diploid individuals. Allowing ψ to be random may be biologically more realistic than taking ψ to be a constant. On the other hand, the problem of identifying suitable classes of probability distributions for ψ, reflecting the specific biology of given natural populations, is still open and an area of active research.

To explain the convergence arguments when ψ is random, let the random variable Ψ_N, taking values in [N − 2], denote the random number of diploid offspring contributed by the single reproducing pair of parents at each time step; a new realization of Ψ_N is drawn before each reproduction event. Again, we consider the effect of such a reproduction mechanism on coalescence events in a sample. The probability that two given chromosomes residing in two single-marked individuals in the sample coalesce in the previous time step given the value of Ψ_N is

$$\begin{array}{l}\mathbb{P}\left(\left\{\text{pair}\hspace{0.17em}\text{coalescence}\right\}|{\Psi }_N=k\right)\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}=\frac{1}{4}{\delta }_{\left\{k=1\right\}}\frac{4}{N\left(N-1\right)}+\frac{1}{4}{\delta }_{\left\{k>1\right\}}\left(\frac{4k}{N\left(N-1\right)}+\frac{k\left(k-1\right)}{N\left(N-1\right)}\right),\end{array}$$ (17)

where the first and second terms on the right-hand side describe the case where one parent and one offspring are drawn, the third term covers the case where two offspring are drawn, and the 1/4 accounts for the probability that the two chromosomes in question must descend from the same parental chromosome. Define

$$c_N:=4\mathbb{P}\left(\{\text{pair}\hspace{0.17em}\text{coalescence}\}\right)$$ (18)

$$={\displaystyle 4\sum _{k=1}^{N-2}\mathbb{P}\left(\left\{\text{pair}\hspace{0.17em}\text{coalescence}\right\}|{\Psi }_N=k\right)\mathbb{P}\left({\Psi }_N=k\right)}$$

$$=\mathbb{E}\left[\frac{{\Psi }_N\left({\Psi }_N+3\right)}{N\left(N-1\right)}\right]$$ (19)

(the factor 4 facilitates comparison with the haploid case). The sequence of laws ℒ(Ψ_N), N ∈ ℕ, is assumed to satisfy the following three conditions,

$$c_N\to 0\hspace{0.17em}\text{as}\hspace{0.17em}N\to \mathrm{\infty },$$ (20)

$$\begin{array}{l}\frac{c_N}{\mathbb{E}\left[{\Psi }_N/N\right]}=\frac{1/\mathbb{E}\left[{\Psi }_N/N\right]}{1/c_N}=\frac{\mathbb{E}\left[{\Psi }_N\left({\Psi }_N+3\right)\right]}{\left(N-1\right)\mathbb{E}\left[{\Psi }_N\right]}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\to 0\hspace{0.17em}\text{as}\hspace{0.17em}N\to \mathrm{\infty },\end{array}$$ (21)

and there exists a probability measure F on [0, 1] such that

$$\frac{1}{c_N}\mathbb{P}{\left({\Psi }_N>Nx\right)}_{\overrightarrow{N\to \mathrm{\infty }}}{\displaystyle {\int }_x^1\frac{1}{y^2}F\left(dy\right)}$$ (22)

for all continuity points x ∈ (0, 1] of F.

Condition (20) is necessary for any limit process of the genealogies to be a continuous-time Markov chain, condition (21) ensures that a separation-of-timescales phenomenon occurs, and (22) fixes the limit dynamics of the large merging events [it is analogous to Sagitov 1999, necessary condition (13) in the haploid case]. In the proof of convergence to a limit process we recall equivalent conditions to (22) (see Appendix, section A4). Condition (20) implies (see section A4 in the Appendix)

$$\mathbb{E}\left[\frac{{\Psi }_N}{N}\right]\to 0\hspace{0.17em}\text{as}\hspace{0.17em}N\to \mathrm{\infty };$$ (23)

i.e., the probability for a given individual to be an offspring in a given reproduction event becomes small. Hence, (23) and (21) together show that there will be two diverging timescales: The “short” timescale 1/$\mathbb{E}$[Ψ_N/N] on which chromosomes paired in double-marked individuals disperse into single-marked individuals and the “long” timescale 1/c_N over which we observe nontrivial ancestral coalescences.

To obtain a nontrivial genealogical limit process, we then speed up time by a factor of 4/c_N; i.e., 4/c_N reproduction events correspond to one coalescent time unit (see Theorem 1.3 below). This time rescaling is chosen for two chromosomes to coalesce at rate 1 in the limit. The required scaling relation for the recombination rates is now

$$r_{\text{N}}^{\left(\ell \right)}\sim \frac{c_N}{4\mathbb{E}\left[{\Psi }_N/N\right]}{r}^{\left(\ell \right)}\hspace{0.17em}\text{as}\hspace{0.17em}N\to \mathrm{\infty }$$ (24)

with r^(ℓ) ∈ [0, ∞) fixed for ℓ = 1, … , L − 1 [where f(N) ∼ g(N) means lim_N→∞f(N)/g(N) = 1]. An intuitive explanation for the requirement (24) is that since the probability for a given individual to be an offspring in a given reproduction event is $\mathbb{E}$[Ψ_N/N], after speeding up time by 4/c_N, on any lineage recombination events between loci ℓ and ℓ + 1 occur as a Poisson process with rate r^(ℓ).

A simple sufficient condition for (21) is the following: For any ɛ > 0,

$$N\mathbb{P}\left({\Psi }_N>\varepsilon N\right)\to 0\hspace{0.17em}\text{as}\hspace{0.17em}N\to \mathrm{\infty }.$$ (25)

Indeed, we have, by assuming N > ɛN,

$$\begin{array}{c}\mathbb{E}\left[{\Psi }_N^2\right]={\displaystyle \sum _{k=1}^{\lfloor \varepsilon N\rfloor }{k}^2\mathbb{P}\left({\Psi }_N=k\right)}+{\displaystyle \sum _{k=\lfloor \varepsilon N\rfloor +1}^N{k}^2\mathbb{P}\left({\Psi }_N=k\right)}\\ \le {\displaystyle \sum _{k=1}^{\lfloor \varepsilon N\rfloor }k\varepsilon N\mathbb{P}\left({\Psi }_N=k\right)}+{\displaystyle \sum _{k=\lfloor \varepsilon N\rfloor +1}^N{N}^2\mathbb{P}\left({\Psi }_N=k\right)}\\ \le \varepsilon N\mathbb{E}\left[{\Psi }_N\right]+N^2\mathbb{P}\left({\Psi }_N>\varepsilon N\right).\end{array}$$

Dividing by N$\mathbb{E}$[Ψ_N] gives

$$\frac{\mathbb{E}\left[{\Psi }_N^2\right]}{NE\left[{\Psi }_N\right]}\le \varepsilon +\frac{N\mathbb{P}\left({\Psi }_N>\varepsilon N\right)}{\mathbb{E}\left[{\Psi }_N\right]},$$

and, since $\mathbb{E}$[Ψ_N] > 1,

$$\underset{N\to \mathrm{\infty }}{\text{lim}\hspace{0.17em}\text{sup}}\frac{\mathbb{E}\left[{\Psi }_N^2\right]}{N\mathbb{E}\left[{\Psi }_N\right]}<\varepsilon +\underset{N\to \mathrm{\infty }}{\text{lim}\hspace{0.17em}\text{sup}}N\mathbb{P}\left({\Psi }_N>\varepsilon N\right)=\varepsilon .$$

Condition (21) is now obtained since we can choose ɛ to be as small as we like.

The limiting genealogical process will then be a continuous-time Markov chain on ${\mathcal{A}}_n^{\text{sm}}$ with generator matrix G whose off-diagonal elements are given by [for the values on the diagonal we again have (16)]

$$G\left(\xi ,{\xi }^{\prime }\right)=\{\begin{array}{ll}{C}_{\beta ;2}\hfill & \text{if}{\xi }^{\prime }={\text{pairmerge}}_{j_1,j_2}\left(\xi \right)\hfill \\ r^{\left(\ell \right)}\hfill & \text{if}{\xi }^{\prime }={\text{recomb}}_{j,\ell }\left(\xi \right)\hfill \\ C_{\beta ;\left|J\right|}\hfill & \text{if}{\xi }^{\prime }={\text{groupmerge}}_{J_1,J_2,J_3,J_4}\left(\xi \right)\hfill \\ 0\hfill & \text{for}\hspace{0.17em}\text{all}\hspace{0.17em}\text{other}{\xi }^{\prime }\ne \xi ,\hfill \end{array}$$ (26)

where

$$C_{\beta ;\left|J\right|}:=C_{\beta ;\left|J_1\right|,\left|J_2\right|,\left|J_3\right|,\left|J_4\right|;\beta -\left(\left|J_1\right|+\left|J_2\right|+\left|J_3\right|+\left|J_4\right|\right)},$$

k = (k₁, …, k_r), |k| = k₁ + … + k_r, and

$$\begin{array}{l}{C}_{b;k;s}=4{\displaystyle \sum _{l=0}^{s\wedge \left(4-r\right)}\left(\begin{array}{c}s\\ l\end{array}\right)\frac{{\left(4\right)}_{r+l}}{4^{\left|k\right|+l}}}\\ \cdot {\displaystyle {\int }_{\left[0,1\right]}{x}^{\left|k\right|+l}{\left(1-x\right)}^{s-l}\frac{1}{x^2}F\left(dx\right)}\\ =F\left(\left\{0\right\}\right){\delta }_{\left\{r=1,k_1=2\right\}}+4{\displaystyle \sum _{l=0}^{s\wedge \left(4-r\right)}\left(\begin{array}{c}s\\ l\end{array}\right)\frac{{\left(4\right)}_{r+l}}{4^{\left|k\right|+l}}}\\ \cdot {\displaystyle {\int }_{\left(0,1\right]}{x}^{\left|k\right|+l}{\left(1-x\right)}^{s-l}\frac{1}{x^2}F\left(dx\right)}\end{array}$$ (27)

with F from (22). As in the case of constant ψ, the third line in (26) gives the transition rates for a given merger into r (≤4) groups of sizes k₁, … , k_r when β active ancestral lineages are present, with s = β − |k| ≥ 0 lineages unaffected by a given merger of the Ξ-coalescent with

$$\Xi ={\displaystyle {\int }_{\left[0,1\right]}{\delta }_{\left(x/4,x/4,x/4,x/4,0,0,\dots \right)}F\left(dx\right)}$$

(cf. Schweinsberg 2000a, Theorem 2). By way of example, C_2;2;0 = 1. Now we can state the convergence of our ancestral recombination graph process with random ψ. The analog of Theorem 1.2 is the following:

Theorem 1.3. Let {ξ^n,N(m), m ≥ 0} be the ancestral process of a sample of n chromosomes in a population of size N with offspring laws ℒ(Ψ_N) that satisfy (20), (21), and (22), and assume the scaling relation (24) for the recombination rates. Then, starting from ξ^n,N(0) ∈ ${\mathcal{A}}_n$, we have that

$$\left\{{\xi }^{n,N}\left(\lfloor \frac{4t}{c_N}\rfloor \right)\right\}\to \left\{\xi \left(t\right)\right\},\hspace{0.17em}\mathit{as}\hspace{0.17em}N\to \mathrm{\infty },$$

in the sense of the finite-dimensional distributions on the interval (0, ∞). The process {ξ(t)} is the Markov chain with generator matrix (26) and initial value ξ(0) given by

$$\xi \left(0\right)=\text{cd}\left({\xi }^{n,N}\left(0\right)\right)\in {\mathcal{A}}_n^{\text{sm}}.$$

The proof is given in section A4 in the Appendix.

While c_N ≥ 1/N² by definition, in principle any decay behavior of c_N that is consistent with lim inf_N→∞N²c_N ≥ 1, and hence any there-from–derived scaling relation between coalescent timescale and model census population size, is possible via a suitable choice of the family ℒ(Ψ_N), N ∈ ℕ.

For an extreme example, let Ψ_N = ⌊N^γ⌋ for some γ ∈ (0, 1); then c_N ∼ N^−2(1−γ) and (22) is satisfied with F = δ₀.

The relation with the “fixed-ψ” model is as follows: For Theorem 1.2, we used the simple mixture distribution for Ψ_N,

$$\mathbb{P}\left({\Psi }_N=\lfloor \psi N\rfloor \right)=1-\mathbb{P}\left({\Psi }_N=1\right)=\frac{c}{N^2}$$ (28)

for Ψ_N, in which ψ ∈ (0, 1) and c > 0 are both constants. Our choice (28) of law for Ψ_N gives, using (17),

$$\begin{array}{l}{c}_N=\mathbb{E}\left[\frac{{\Psi }_N\left({\Psi }_N+3\right)}{N\left(N-1\right)}\right]\\ =\left(1-\frac{c}{N^2}\right)\frac{4}{N\left(N-1\right)}+\frac{c}{N^2}\frac{\psi N\left(\psi N+3\right)}{N\left(N-1\right)}\\ \sim \frac{1}{N^2}\left(4+c{\psi }^2\right).\end{array}$$

Define 1_(0,ψ)(x) = 1 if x ∈ (0, ψ) and 1_(0,ψ)(x) = 0 otherwise. Our choice (28) further gives

$$\begin{array}{c}\mathbb{P}\left({\Psi }_N>\lfloor Nx\rfloor \right)=1_{\left(0,\psi \right)}\left(x\right)\mathbb{P}\left({\Psi }_N>Nx\right)\\ =1_{\left(0,\psi \right)}\left(x\right)c{N}^{-2},\end{array}$$

and therefore

$$\begin{array}{l}\frac{1}{c_N}\mathbb{P}\left({\Psi }_N>\lfloor Nx\rfloor \right)\to 1_{\left(0,\psi \right)}\left(x\right)\frac{c}{4+c{\psi }^2}\\ ={\displaystyle {\int }_{\left(x,1\right]}{y}^{-2}F\left(dy\right)}\end{array}$$

with

$$F=\frac{4}{4+c{\psi }^2}{\delta }_0+\frac{c{\psi }^2}{4+c{\psi }^2}{\delta }_{\psi }.$$

Furthermore, $\mathbb{E}$[Ψ_N/N] = 1/N + O(1/N²); thus

$$\frac{c_N}{4\mathbb{E}\left[{\Psi }_N/N\right]}\sim \frac{1}{N}\frac{4+c{\psi }^2}{4}$$

and Theorem 1.2 follows from Theorem 1.3 [after rescaling time in the limit process {ξ(t)} by a factor of (4 + cψ²)/4].

The constant $C_{b;k}:=C_{b;k_1,\dots ,k_r;s}$ (27) depends on the probability measure F. The form of F will no doubt be different for different populations. We reiterate that resolving the mechanism of sweepstake-style reproduction will require detailed knowledge of the reproductive behavior and the ecology of the organism in question, along with comparison of model predictions to multilocus genetic data. A candidate for F may be the beta distribution with parameters ϑ > 0 and γ > 0, in which case the constant C_b;k in (26) takes the form (|k|:= k₁ + ⋯ + k_r)

$$\begin{array}{l}{C}_{b;k}=4{\displaystyle \sum _{\ell }\left(\begin{array}{c}s\\ \ell \end{array}\right){\left(4\right)}_{r+\ell }{\left(\frac{1}{4}\right)}^{\left|k\right|+\ell }}\\ \cdot \frac{B\left(\left|k\right|+\ell +\vartheta -2,s+\gamma -\ell \right)}{B\left(\vartheta ,\gamma \right)},\end{array}$$ (29)

B(⋅,⋅) being the Beta function.

Different Scaling Regimes

The mechanism of sweepstake-style reproduction may be different for different populations, and the frequency of large offspring-number events may also be different. The particular timescale of the large reproduction events (we chose ɛ_N = c/N²) results in a separation of timescales of the limit process. Resolving the separation-of-timescales problem results in the ARG with generator (14). Different scalings of ɛ_N result in different limit processes. By way of example, if N²ɛ_N → 0, large offspring-number events are negligible in a large population, and we obtain the ARG associated with the usual Wright–Fisher reproduction, which can be read off Equation 14 by taking c = 0. One other scaling regime may seem reasonable, namely taking large offspring-number events to be more frequent than in assumption (5), but not too frequent. In mathematical notation, N²ɛ_N → ∞ and Nɛ_N → 0. The ancestral process in this regime is again characterized by instantaneous separation of marked chromosomes into single-marked individuals, followed by coalescence and recombination occurring on the slow timescale. The probability of recombination is proportional to Nɛ_N since the slow timescale must be in units proportional to 1/ɛ_N. Hence, small reproduction events become negligible in the limit, and the generator of the limit process is given by

$$G\left(\xi ,{\xi }^{\prime }\right)=\{\begin{array}{ll}\frac{{\psi }^2}{4}{C}_{\beta ;2;\beta -2}\hfill & \text{if}{\xi }^{\prime }={\text{pairmerge}}_{j_1,j_2}\left(\xi \right)\hfill \\ r^{\left(\ell \right)}/r\hfill & \text{if}{\xi }^{\prime }={\text{recomb}}_{j,\alpha }\left(\xi \right)\hfill \\ \frac{{\psi }^2}{4}{C}_{\beta ;\left|J\right|}\hfill & \text{if}{\xi }^{\prime }={\text{groupmerge}}_J\left(\xi \right)\hfill \\ 0\hfill & \text{for all other}{\xi }^{\prime }\ne \xi \hfill \end{array}$$ (30)

in which C_⋅;⋅;⋅ is given by Equation 15. The requirement Nɛ_N → 0 is needed to prevent an unreasonably high rate of recombination.

Haploid Analogs

A haploid version of the above model, where only one parent contributes offspring at each time step, is a specific example of a Λ-coalescent, where

$$\Lambda \left(dx\right)={\delta }_0\left(dx\right)+c{\psi }^2{\delta }_{\psi }\left(dx\right),\hspace{0.17em}\psi \in \left(0,1\right),\hspace{0.17em}c\in \left[0,\mathrm{\infty }\right)$$

(see, e.g., Eldon and Wakeley 2006 and Birkner and Blath 2009). More precisely, as the population size N tends to infinity, assume probability 1 − c/N² for the small reproduction events and c/N² for the large reproduction events (i.e., choose ɛ_N = c/N²), and speed up generation time by N². Again, by randomizing ψ and/or switching to different scaling regimes, it is possible to obtain any given Λ-coalescent as limiting genealogy.

Two-Sex Extensions

Recent studies of the spawning behavior of Atlantic cod indicate that cod adopts a lekking behavior, in which males compete for females, and females exercise mate choice (Nordeide and Folstad 2000). Direct microsatellite DNA analysis indicates that although multiple paternity is sometimes detected, the reproductive success is highly skewed among the males; i.e., most of the successfully fertilized eggs can be attributed to a single male (Hutchings et al. 1999). Our model thus seems a good approximation to the actual reproduction mechanism of cod. Modifications to allow two distinct genders, and multiple paternity, are in principle straightforward.

More General Recombination Models

Our model can easily be enriched to allow also more general recombination events involving more than one crossover point at a time. Furthermore, by letting the number L of loci tend to infinity, a continuous model, where [0, 1] represents a whole chromosome (as in Griffiths and Marjoram 1997), can be accommodated into our framework.

Correlations in Coalescence Times

The marginal process

Every marginal process (marginal with respect to one fixed locus under consideration) of our ancestral recombination graph is a Ξ-coalescent (see Schweinsberg 2000a for notation and details) with

$$\Xi ={\delta }_0+c\frac{{\psi }^2}{4}{\delta }_{\left(\psi /4,\psi /4,\psi /4,\psi /4,0,0,\dots \right)}.$$

For r = 0, all marginals are identical (realization-wise), in particular times to the most recent common ancestor for different loci have correlation 1. However, in contrast to the classical setting, for r → ∞ one expects that the loci will not completely decorrelate, but instead keep positive correlations, as pointed out to us by J. E. Taylor (personal communication). In particular, one will not obtain the product distribution. This observation is a potential starting point for designing tests for the presence of large reproduction events, by comparing correlations for loci at large distance (hence with high recombination rate) under a Kingman- and a Ξ-coalescent–based ARG.

Correlation in coalescence times at two loci

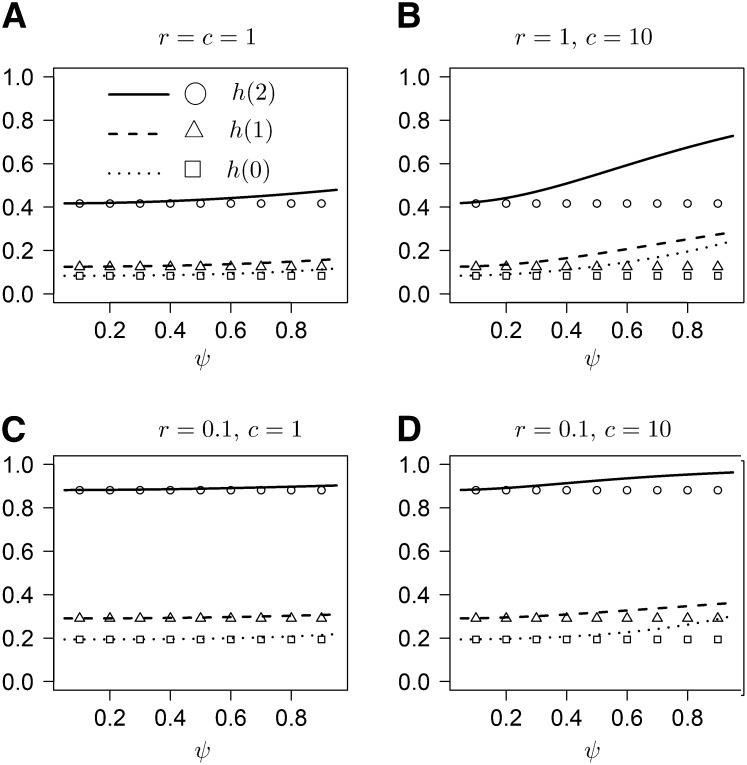
Correlations in coalescence times between two loci have been considered in the context of quantifying association between loci (McVean 2002). Eldon and Wakeley (2008) consider correlations in coalescence times for a haploid population model, admitting large offspring numbers, in which the ancestral process admits only asynchronous multiple mergers of ancestral lineages. To illustrate the effects of the reproduction parameters on the coalescence times, we also consider the probability that coalescence occurs at the same time at the two loci, as well as the expected time until coalescence.

The calculations to obtain the correlations for a sample of size two at two loci (following the approach and notation of Durrett 2002) are shown in the Appendix, section A5. As we are now considering the gene genealogy of unlabeled lineages, let us briefly state the sample space. Let a and b denote the types at loci a and b, respectively. The three sample states before coalescence at either locus has occurred can be denoted as (ab)(ab), (ab)(a)(b), and (a)(b)(b)(b). By (ab)(ab) we denote the state of two chromosomes, each carrying ancestral material at both loci. By (ab)(a)(b) we denote the state of one (ab) chromosome in addition to two chromosomes (a) and (b) carrying ancestral types at loci 1 and 2 only, respectively. The notation (a)(a)(b)(b) denotes the state of four chromosomes, each carrying ancestral types at only one locus. Let

$$h\left(i\right):=\mathbb{P}\left(\left\{T_a=T_b\right\}|i\right),i\in \left\{0,1,2\right\}$$

denote the probability that coalescence at the two loci occurs at the same time, given that the process starts in state i, in which i refers to the number of double-marked chromosomes (2, 1, or 0). As we are working with the limiting model, all marked individuals are effectively single marked. Under the usual (Kingman-coalescent–based) ARG, lim_r→∞h(i) = 0 as one would expect. Our model yields

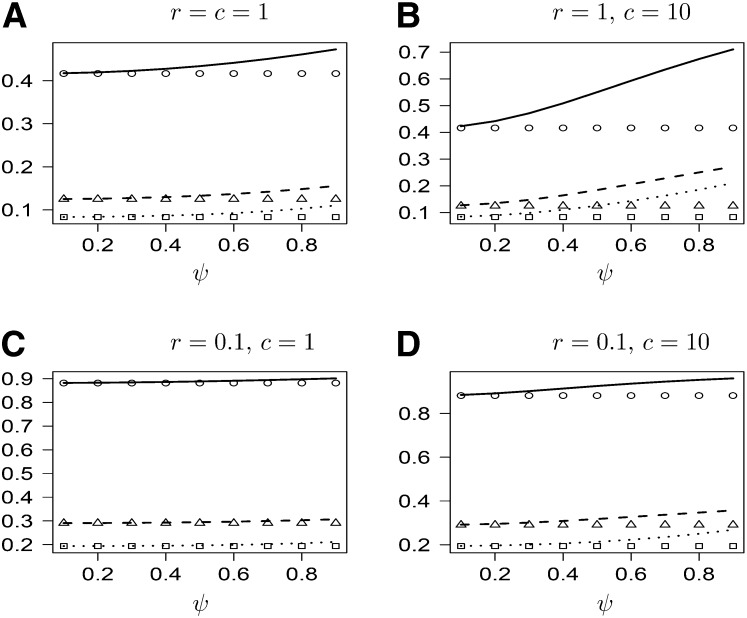
$$\underset{r\to \mathrm{\infty }}{\text{lim}}h\left(i\right)=\frac{c{\psi }^4}{32+8c{\psi }^2-c{\psi }^4},i\in \left\{0,1,2\right\},$$ (31)

indicating that even unlinked loci remain correlated due to sweepstake-style reproduction. Figure 2 shows graphs of h(i) as a function of ψ for different values of c and r. As expected, h(i) increases with ψ, at a rate that increases with c.

Figure 2 .

(A and B) The probabilities h(2), h(1), and h(0) as functions of ψ (lines) for different values of r and c. Values of h(⋅) obtained from the usual Moran model are shown for reference (symbols).

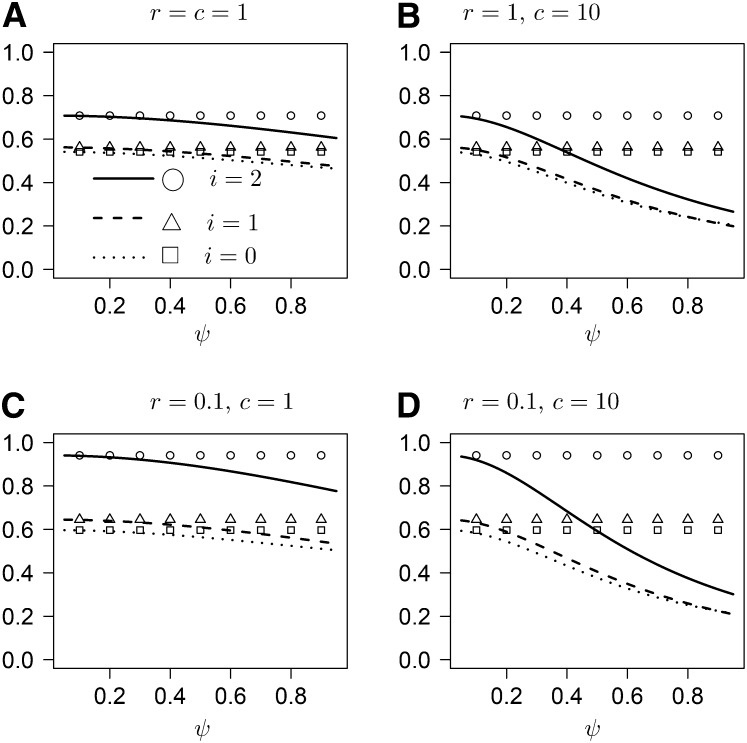
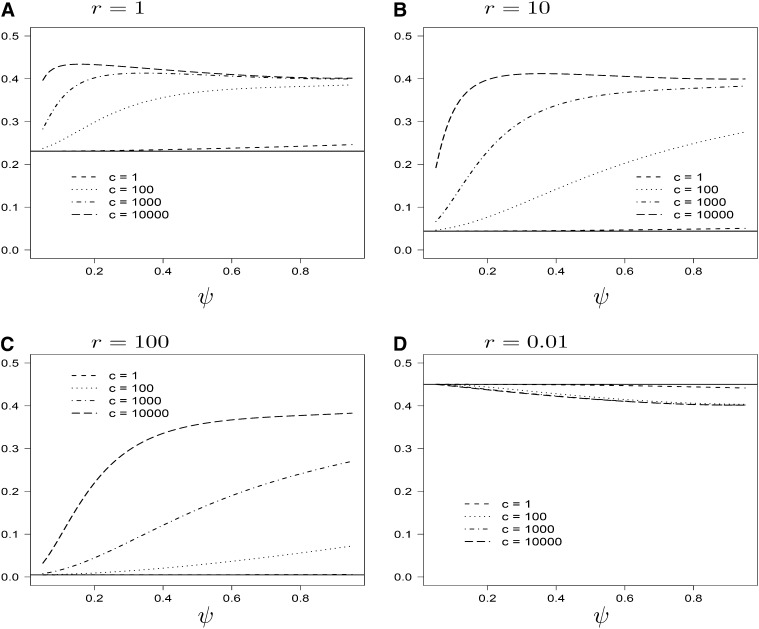
Under the usual ARG, the expected time $\mathbb{E}$_i[T_s] until coalescence at either locus, starting from state i is given by $\mathbb{E}$_i[T_s] = (1 + h(i))/2. The random variable T_s can be viewed as the minimum of the time until coalescence occurs at the two loci. As r → ∞, the times T₁ and T₂ until coalescence at the two loci, respectively, become independent and identically distributed exponentials (i.i.d.e.) with rate 1, whose minimum has expected value 1/2. Under our model, the mean of T_s is not the minimum of two i.i.d.e. with rate 1+cψ²/4, another reflection of the correlation in gene genealogies induced by sweepstake-style reproduction. Indeed, our model gives

$$\underset{r\to \mathrm{\infty }}{\text{lim}}{\mathbb{E}}_i\left[T_s\right]=\frac{1}{2}\left(\frac{1}{1+\chi c{\psi }^2/4}\right),i\in \left\{0,1,2\right\},$$

in which χ = 1 − ψ²/8.

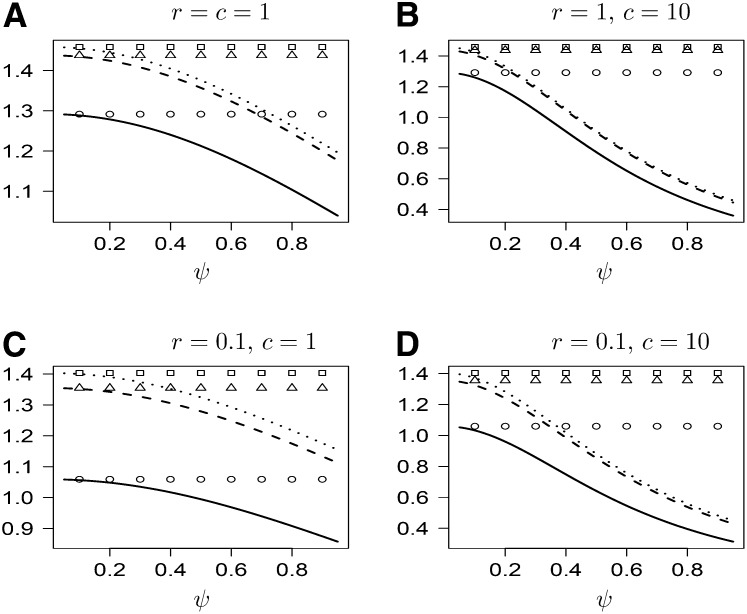
Under our model, $\mathbb{E}$_i[T_s] decreases with ψ, and the rate of decrease increases with c (Figure 3). The same pattern holds for the expected time $\mathbb{E}$_i[T_l] until coalescence has occurred at both loci (Figure 4). As r → ∞, $\mathbb{E}$_i[T_l] associated with the usual ARG approaches the expected value (3/2) of the maximum of two i.i.d.e. with rate 1. Under our model,

$$\begin{array}{l}\underset{r\to \mathrm{\infty }}{\text{lim}}{\mathbb{E}}_i\left[T_l\right]=\frac{3}{2}\frac{1}{1+c{\psi }^2/4}\frac{1}{1+c{\psi }^2/4-c{\psi }^4/32}\\ +\frac{c{\psi }^2\left(6-{\psi }^2\right)}{\left(c{\psi }^2+4\right)\left(4+c{\psi }^2-c{\psi }^4/8\right)}\end{array}$$

while the maximum of two i.i.d.e. with rate λ has expected value 3/(2λ).

Figure 3 .

The expected time ${\mathbb{E}}_i$[T_s] as a function of ψ for different values of c and r. Values of ${\mathbb{E}}_i$[T_s] associated with the case c = 0 are shown for reference (symbols).

Figure 4 .

The expected time ${\mathbb{E}}_i$[T_s] as a function of ψ for different values of c and r. For explanation of symbols, see Figure 3.

The correlation cor_i(T₁, T₂) between T₁ and T₂ when starting from one of the three possible sample states i ∈ {0, 1, 2} (see Appendix) increases with ψ and more so if c is large (Figure 5). One obtains the following limit relations between h(i) and cor_i(T₁, T₂) for i ∈ {0, 1, 2}:

$$\underset{r\to \mathrm{\infty }}{\text{lim}}{\text{cor}}_i\left(T_1,T_2\right)=\underset{r\to \mathrm{\infty }}{\text{lim}}h\left(i\right)\hspace{0.17em}(\text{see}\hspace{0.17em}\text{Equation}\hspace{0.17em}31);$$

$$\underset{r\to 0}{\text{lim}}{\text{cor}}_i\left(T_1,T_2\right)=\underset{r\to 0}{\text{lim}}h\left(i\right)\hspace{0.17em}(\text{see}\hspace{0.17em}\text{Equation}\hspace{0.17em}\text{A}35);$$

$$\underset{c\to \mathrm{\infty }}{\text{lim}}{\text{cor}}_i\left(T_1,T_2\right)=\underset{c\to \mathrm{\infty }}{\text{lim}}h\left(i\right)\hspace{0.17em}(\text{see}\hspace{0.17em}\text{Equation}\hspace{0.17em}\text{A}34).$$

Figure 5 .

Correlation of the time to coalescence at two loci as a function of ψ, for different values of c and r. For explanation of symbols, see Figure 3.

Quantifying the association between alleles at different loci can give insight into the evolutionary history of populations. Let f_a and f_b denote the frequencies of alleles a at locus 1 and b at locus 2, and let f_ab denote the frequency of chromosome ab in the total population. The statistic D_ab := f_ab − f_af_b measures the deviation from independence, since if the two loci were evolving independently, f_ab = f_af_b. A related quantity is the r² statistic, defined as

$$r^2:=\frac{D^2}{f_a\left(1-f_a\right)f_b\left(1-f_b\right)}$$

(Hill and Robertson 1968), assuming f_a, f_b ∉ {0, 1}. In applications, one wants to compare observed values of r² calculated from data to the expected value $\mathbb{E}$[r²], obtained under an appropriate population model. Calculating the expected value of r² is not straightforward, since r² is a ratio of correlated random variables. The expected value of r² is, instead, approximated by the ratio 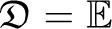[D²]/$\mathbb{E}$[f_a(1 − f_a)f_b(1 − f_b)] (Ohta and Kimura 1971).

A prediction of linkage disequilibrium in the population can be framed in terms of correlations in coalescence times between two loci for a sample of size two, assuming a small mutation rate (McVean 2002). The prediction rests on approximating the expected value $\mathbb{E}$[r²] of the squared correlation statistic r² (Hill and Robertson 1968) of association between alleles at two loci by the ratio of expected values (Ohta and Kimura 1971). Following, e.g., Durrett (2002) one can obtain expressions for correlations in coalescence times between two loci for a sample of size two (see Appendix). Under our model, one obtains the limit results

When ψ is small but c large, one obtains

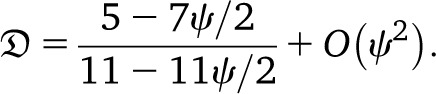Under the usual ARG, lim_r→0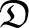 = 5/11. Thus, even in the presence of a high recombination rate, if large offspring-number events are frequent enough, one may see only evidence of low recombination rate in data. Further, the prediction 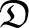can be substantially higher than Kingman-coalescent–based predictions if c is large and the recombination rate is not too small (Figure 6).

Figure 6 .

The estimate 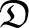of the expected value $\mathbb{E}$[r²] as a function of ψ for different values of c and r. The solid lines represent the value of associated with the usual Wright–Fisher model.

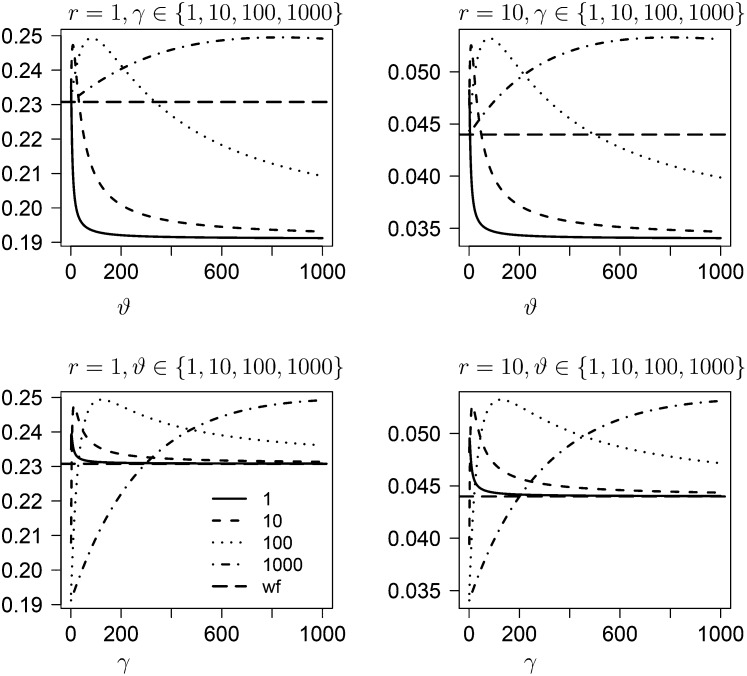
For particular examples of probability measures F from Equation 27 associated with the generator derived from our random offspring distribution model one can compute the quantities considered above in relation to fixed ψ. One such example distribution can be the Beta(ϑ, γ) distribution (see Figure 7 for ). One obtains for i ∈ {0, 1, 2},

$$\underset{r\to \mathrm{\infty }}{\text{lim}}h\left(i\right)=\frac{4\gamma \left(1+2\vartheta +\gamma \right)}{8\gamma \left(1+\gamma \right)+10\gamma \vartheta +7\vartheta \left(1+\vartheta \right)}.$$

Define $\tilde{h}\left(i\right):={\text{lim}}_{r\to \mathrm{\infty }}h\left(i\right)$. For i ∈ {0, 1, 2} one obtains

$$\begin{array}{l}\underset{r\to \mathrm{\infty }}{\text{lim}}{\mathbb{E}}_i\left[T_s\right]=4\tilde{h}\left(i\right)+\frac{4\gamma \left(1+2\vartheta +\gamma \right)}{8\gamma \left(1+\gamma \right)+10\gamma \vartheta +7\vartheta \left(1+\vartheta \right)},\\ \underset{r\to \mathrm{\infty }}{\text{lim}}{\mathbb{E}}_i\left[T_l\right]=\frac{3}{2}-\frac{1}{2}\tilde{h}\left(i\right)+\frac{3\gamma }{2\left(8\gamma \left(1+\gamma \right)+10\gamma \vartheta +7\vartheta \left(1+\vartheta \right)\right)}.\end{array}$$ (32)

The form of the relation shown in (32) between h(i) and $\mathbb{E}$_i[T_s] and $\mathbb{E}$_i[T_l] resembles the one obtained for the Kingman-coalescent–based ARG, with the addition of a “correction” term due to simultaneous multiple mergers.

Figure 7 .

The prediction of linkage disequilibrium obtained from the ARG associated with the Beta(ϑ, γ) distribution. The different lines represent different values of γ (top panels) or ϑ (bottom panels). The broken horizontal line represents the prediction obtained from the usual ARG.

Variance of pairwise differences

The expected variance of pairwise differences was employed by Wakeley (1997) to estimate the recombination rate in low offspring-number (Wright–Fisher) populations, under the usual ancestral recombination graph. Let the random variable K_ij denote the number of differences between sequences i and j, with K_ii = 0. The average number π of pairwise differences for n sequences is

$$\pi =\frac{2}{n\left(n-1\right)}{\displaystyle \sum _{i<j}{K}_{ij}}.$$

The (empirical) variance $S_{\pi }^2$ of pairwise differences is defined as

$$S_{\pi }^2=\frac{2}{n\left(n-1\right)}{\displaystyle \sum _{i<j}{\left(K_{ij}-\pi \right)}^2}.$$

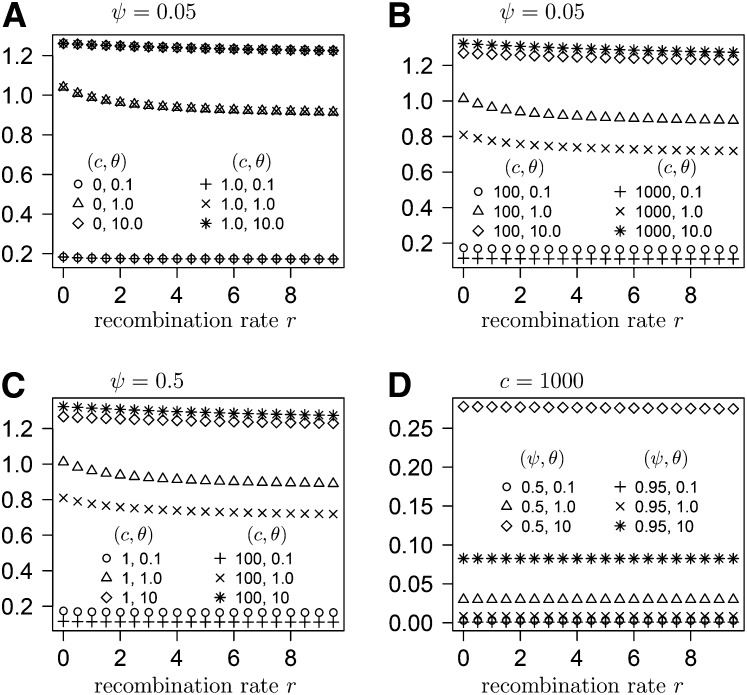
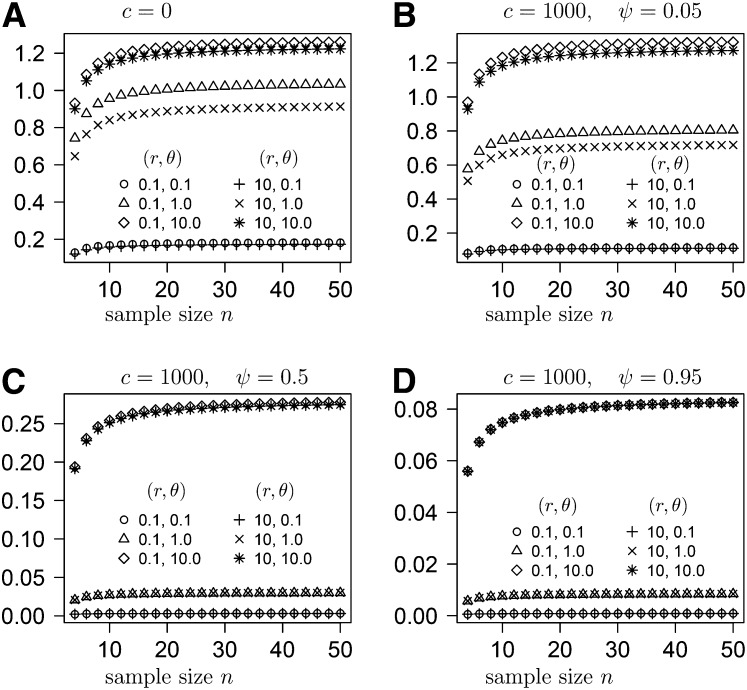
In the Appendix we derive the expected variance of pairwise differences $\mathbb{E}\left[S_{\pi }^2\right]$ under the ancestral recombination graph described by the generator G (Equation 14) derived from our large offspring-number model. Under our model, $\mathbb{E}\left[S_{\pi }^2\right]$ is a function of the parameters c and ψ, in addition to being a function of r and θ (Figure 8 and Figure 9). In Figure 8, $\mathbb{E}\left[S_{\pi }^2\right]$, when only two loci are considered, is graphed as a function of the recombination rate and in Figure 9 as a function of sample size. Figures 8 and 9 show that $\mathbb{E}\left[S_{\pi }^2\right]$ is primarily influenced by the mutation rate (θ), when the values of c and ψ are fairly modest. However, $\mathbb{E}\left[S_{\pi }^2\right]$ can be quite low when both c and ψ are large, even when θ is also large (Figure 9). When c and ψ are both large, two sequences are more likely to coalesce before a mutation separates them.

Figure 8 .

(A–D) The expected variance of pairwise differences for sample size 50 as a function of the recombination rate r for different values of the parameters c, ψ, and θ as shown.

Figure 9 .

(A–D) The expected variance of pairwise differences as a function of sample size for different values of the parameters c, ψ, r, and θ as shown.

The variance of pairwise differences alone will not suffice to yield estimates of r if both c and ψ are unknown. To jointly estimate the four parameters (c, ψ, r, θ) of our model one probably needs to employ computationally heavy likelihood and importance sampling methods in the spirit of Fearnhead and Donnelly (2001). However, given knowledge of c and ψ, one can, in principle, use the variance of pairwise differences to quickly obtain estimates of the recombination rate.

Correlations in ratios of coalescence times

The behavior of the correlations in ratios of coalescence times for sample sizes larger than two is investigated using Monte Carlo simulations.

Let L_i denote the total length of branches ancestral to i sequences at one locus, let L denote the total length of the genealogy at the same locus, and define R_i := L_i/L. Thus, R₁ is the total length of external branches to the total size of the genealogy. The idea behind estimating the expected value $\mathbb{E}$[R_i] is as follows. Assuming the infinitely many sites mutation model, let S_i denote the total number of mutations in i copies and S denote the total number of segregating sites, and define V_i := S_i/S. The key idea behind deriving the coalescent was to separate the (neutral) mutation process from the genealogical process. The same principle also applies to predicting patterns of genetic variation using the coalescent: First, one constructs the genealogy and then superimposes mutations on the genealogy. The shape of the genealogy is thus a deciding factor in the genetic patterns one predicts. The relative lengths R_i of the different types of branches should therefore predict the relative number V_i of mutations of each class. This idea is exploited by Eldon (2011) to estimate coalescence parameters in the large offspring-number models introduced by Schweinsberg (2003) and Eldon and Wakeley (2006). Namely, the claim is

$$\underset{n\to \mathrm{\infty }}{\text{lim}}\mathbb{E}\left[R_i\right]=\underset{n\to \mathrm{\infty }}{\text{lim}}\mathbb{E}\left[V_i\right]=f\left(\varpi ,i\right),$$ (33)

where n denotes the sample size, and ϖ denotes the coalescence (reproduction) parameters. Indeed, it follows from the results of Berestycki et al. (2007, 2008) that (1 < α < 2)

$$\underset{n\to \mathrm{\infty }}{\text{lim}}\mathbb{E}\left[R_i\right]=\underset{n\to \mathrm{\infty }}{\text{lim}}\mathbb{E}\left[V_i\right]=\frac{\Gamma \left(i+\alpha -2\right)\left(\alpha -1\right)\left(2-\alpha \right)}{\Gamma \left(\alpha \right)i!}$$

when associated with the Beta(2 − α, α) coalescent derived by Schweinsberg (2003) from a population model in which the offspring law is stable with index α. A key feature of expression (33) is the absence of mutation rate in the function f(ϖ, i); thus given a large number of DNA sequences (possibly in the thousands), one hopes to be able to obtain estimates of the coalescence parameters ϖ without having to jointly estimate the mutation rate. In our model, there are four parameters to estimate, namely mutation and recombination rates, along with the coalescence parameters c and ψ. Even though full-likelihood methods exist (Birkner and Blath 2008; Birkner et al. 2011), applying them to large data sets consisting of thousands of sequences may represent a challenge.

Estimates of $\mathbb{E}$[R_i] as functions of the sample size n and the coalescence parameters c and ψ are shown in Table 1. In nearly all cases the estimates of ${\stackrel{-}{R}}_i$ decreased as sample size increased; the exception was ${\stackrel{-}{R}}_1$ when (c, ψ) = (1000, 0.5) (Table 1). When both c and ψ are large enough, we observe a nonmonotonic behavior in ${\stackrel{-}{R}}_1$ as sample size increases (results not shown). The nonmonotonic behavior may be related to the property of the marginal haploid process (the point-mass part obtained as c → ∞) of a single locus of not coming down from infinity (Schweinsberg 2000b); i.e., when one starts with an infinite number of lineages (sample size), the number of lineages stays infinite. For such processes that do not come down from infinity, the ratio R₁ should go to one; i.e., the gene genealogy should become completely star-shaped (see, e.g., Eldon 2011). As both c and ψ increase, one expects the deviation from Kingman-coalescent–based predictions to increase. By way of example, for sample size 50 the vector ($\mathbb{E}$[R₁], … , $\mathbb{E}$[R₄)] is estimated to be ∼(0.24, 0.12, 0.08, 0.06) when associated with the Kingman coalescent (c = 0), while being ∼(0.58, 0.20, 0.09, 0.05) when (c, ψ) = (1000, 0.5). In all cases the estimate ${\widehat{R}}_i$ of the standard deviation of R_i decreases as sample size increases, indicating convergence.

Table 1 .

Estimates _i of the expected values E[R_i] of the ratios R_i := L_i/L for 1≤ i ≤ 4 at one marginal locus, along with estimates ${\widehat{R}}_i$ of the standard deviations of R_i

ψ	c	n	${\stackrel{-}{R}}_1$	${\stackrel{-}{R}}_2$	${\stackrel{-}{R}}_3$	${\stackrel{-}{R}}_4$	${\widehat{R}}_1$	${\widehat{R}}_2$	${\widehat{R}}_3$	${\widehat{R}}_4$
—	0	6	0.466	0.219	0.138	0.100	0.183	0.167	0.198	0.124
		10	0.378	0.180	0.117	0.085	0.156	0.132	0.120	0.110
		20	0.300	0.146	0.096	0.070	0.119	0.097	0.088	0.081
		50	0.235	0.116	0.077	0.057	0.080	0.063	0.058	0.055
0.005	1	6	0.466	0.219	0.138	0.100	0.183	0.167	0.198	0.124
		10	0.377	0.181	0.117	0.085	0.156	0.133	0.120	0.111
		20	0.299	0.146	0.095	0.071	0.118	0.097	0.088	0.082
		50	0.234	0.116	0.076	0.057	0.080	0.064	0.057	0.054
	1000	6	0.467	0.219	0.137	0.100	0.182	0.167	0.198	0.124
		10	0.377	0.181	0.117	0.085	0.156	0.133	0.120	0.110
		20	0.299	0.146	0.095	0.071	0.119	0.097	0.088	0.082
		50	0.235	0.116	0.077	0.057	0.080	0.064	0.058	0.054
0.5	1	6	0.468	0.217	0.138	0.099	0.184	0.166	0.199	0.124
		10	0.381	0.179	0.115	0.085	0.157	0.132	0.120	0.110
		20	0.304	0.145	0.095	0.070	0.120	0.097	0.088	0.081
		50	0.242	0.117	0.077	0.056	0.081	0.064	0.058	0.054
	1000	6	0.541	0.173	0.116	0.089	0.184	0.152	0.177	0.116
		10	0.566	0.117	0.078	0.058	0.159	0.101	0.090	0.082
		20	0.743	0.101	0.035	0.022	0.084	0.053	0.033	0.027
		50	0.576	0.195	0.089	0.046	0.058	0.051	0.037	0.026

Estimates are obtained from 10⁵ simulated gene genealogies.

The rationale behind comparing the statistics in Tables 2 and 3 is as follows. As sequencing technologies advance, and the genomic sequences of more organisms become available, a case in point being the recently published genomic sequence of Atlantic cod (Star et al. 2011), genomic scans of thousands of individuals will become more common. Given DNA sequence data for many loci, one could calculate correlations for counts and ratios of counts of mutations and compare them to predictions based on different ancestral recombination graphs. Similarly for the single-locus statistics (Table 1), the idea is that the correlations of the coalescence time statistics (L_i and R_i) should reflect correlations of mutation counts (S_i). In particular, under the usual ARG one expects (see Tables 2 and 3)

$$\underset{r\to \mathrm{\infty }}{\text{lim}}\text{cor}\left(L_i^{\left(1\right)},L_j^{\left(2\right)}\right)=\underset{r\to \mathrm{\infty }}{\text{lim}}\text{cor}\left(R_i^{\left(1\right)},R_j^{\left(2\right)}\right)=0,$$

where the superscript refers to locus numbers 1 and 2, respectively, while under an ARG admitting simultaneous multiple mergers one expects

$$\begin{array}{l}\underset{r\to \mathrm{\infty }}{\lim }\text{cor}\left(L_i^{\left(1\right)},L_j^{\left(2\right)}\right)=f\left(i,j,\varpi \right)\\ \underset{r\to \mathrm{\infty }}{\lim }\text{cor}\left(R_i^{\left(1\right)},R_j^{\left(2\right)}\right)=g\left(i,j,\varpi \right),\end{array}$$

where f and g are functions of the particular statistics indicated by i and j as well as the vector ϖ of coalescence (reproduction) parameters.

Table 2 .

Estimates of the correlation cor(X⁽¹⁾, Y⁽²⁾) between X⁽¹⁾ and Y⁽²⁾, where X⁽¹⁾ represents a statistic for locus 1 and Y⁽²⁾ that for locus 2, as follows: the time T until the most recent common ancestor at a locus; L, the total length of the gene genealogy at a locus; and R_i := L_i/L, in which L_i denotes the total length of branches ancestral to i sequences

c	ψ	r	cor(T(1), T(2))	cor(L(1), L(2))	$\text{cor}\left(L^{\left(1\right)},L_1^{\left(2\right)}\right)$	$\text{cor}\left(L^{\left(1\right)},L_2^{\left(2\right)}\right)$	$\text{cor}\left(L_3^{\left(1\right)},L_3^{\left(2\right)}\right)$	$\text{cor}\left(L_4^{\left(1\right)},L_4^{\left(2\right)}\right)$
0	—	1	0.311	0.418	0.586	0.501	0.434	0.378
		10	0.016	0.058	0.169	0.089	0.047	0.036
1	0.005	1	0.306	0.415	0.588	0.508	0.431	0.380
		10	0.015	0.055	0.171	0.090	0.049	0.034
1000	0.005	1	0.308	0.419	0.585	0.509	0.438	0.376
		10	0.013	0.051	0.168	0.093	0.052	0.030
1	0.5	1	0.328	0.447	0.601	0.516	0.449	0.389
1		10	0.024	0.085	0.193	0.107	0.064	0.036
1000		1	0.982	0.995	0.976	0.950	0.918	0.879
		10	0.924	0.947	0.763	0.623	0.503	0.396
c	ψ	r	$\text{cor}\left(L_1^{\left(1\right)},L_2^{\left(2\right)}\right)$	$\text{cor}\left(L_1^{\left(1\right)},L_3^{\left(2\right)}\right)$	$\text{cor}\left(L_1^{\left(1\right)},L_4^{\left(2\right)}\right)$	$\text{cor}\left(L_2^{\left(1\right)},L_3^{\left(2\right)}\right)$	$\text{cor}\left(L_2^{\left(1\right)},L_4^{\left(2\right)}\right)$	$\text{cor}\left(L_3^{\left(1\right)},L_4^{\left(2\right)}\right)$
0	—	1	−0.031	−0.031	−0.021	−0.005	−0.018	0.009
		10	0.005	−0.006	−0.001	0.012	0.005	0.013
1	0.005	1	−0.035	−0.025	−0.021	−0.001	−0.019	0.009
		10	0.000	−0.002	0.008	0.009	0.005	0.014
1000	0.005	1	−0.036	−0.029	−0.021	−0.006	−0.018	0.010
		10	−0.002	−0.003	0.003	0.014	0.004	0.005
1	0.5	1	−0.022	−0.014	−0.007	0.004	−0.004	0.023
		10	0.009	0.006	0.010	0.022	0.014	0.025
1000		1	0.326	0.314	0.305	0.238	0.218	0.176
		10	0.311	0.284	0.266	0.289	0.239	0.262

Estimates are based on 10⁵ simulated ancestral recombination graphs each for a sample of size 50.

Table 3 .

Estimates of the correlation cor(X⁽¹⁾, Y⁽²⁾) between X⁽¹⁾ and Y⁽²⁾, where X⁽¹⁾ represents a statistic for locus 1 and Y⁽²⁾ that for locus 2, as follows: the time T until most recent common ancestor at a locus; L, the total length of the gene genealogy at a locus; and R_i := L_i/L, in which L_i denotes the total length of branches ancestral to i sequences

c	Ψ	r	$\text{cor}\left(R_1^{\left(1\right)},R_2^{\left(2\right)}\right)$	$\text{cor}\left(R_2^{\left(1\right)},R_2^{\left(2\right)}\right)$	$\text{cor}\left(R_3^{\left(1\right)},R_3^{\left(2\right)}\right)$	$\text{cor}\left(R_4^{\left(1\right)},R_4^{\left(2\right)}\right)$
0	—	1	0.570	0.548	0.486	0.431
		10	0.116	0.089	0.052	0.042
1	0.005	1	0.566	0.552	0.487	0.435
		10	0.115	0.091	0.054	0.035
1000	0.005	1	0.570	0.551	0.491	0.434
		10	0.115	0.095	0.059	0.031
1	0.5	1	0.583	0.557	0.504	0.447
		10	0.135	0.102	0.063	0.038
1000	0.5	1	0.955	0.927	0.900	0.866
		10	0.679	0.469	0.384	0.304
c	ψ	r	$\text{cor}\left(R_1^{\left(1\right)},R_2^{\left(2\right)}\right)$	$\text{cor}\left(R_1^{\left(1\right)},R_3^{\left(2\right)}\right)$	$\text{cor}\left(R_1^{\left(1\right)},R_4^{\left(2\right)}\right)$	$\text{cor}\left(R_2^{\left(1\right)},R_3^{\left(2\right)}\right)$	$\text{cor}\left(R_2^{\left(1\right)},R_4^{\left(2\right)}\right)$	$\text{cor}\left(R_3^{\left(1\right)},R_4^{\left(2\right)}\right)$
0	—	1	−0.023	−0.040	−0.042	−0.026	−0.042	−0.014
		10	−0.022	−0.023	−0.020	0.003	−0.005	0.005
1	0.005	1	−0.024	−0.038	−0.042	−0.023	−0.046	−0.014
		10	−0.027	−0.018	−0.015	0.001	−0.007	0.011
1000	0.005	1	−0.028	−0.038	−0.038	−0.031	−0.043	−0.012
		10	−0.030	−0.024	−0.016	0.003	−0.008	−0.001
1	0.5	1	−0.023	−0.035	−0.035	−0.028	−0.034	−0.007
1	0.5	10	−0.029	−0.023	−0.015	0.004	0.000	0.016
1000		1	−0.622	−0.348	−0.112	−0.100	−0.038	−0.016
		10	−0.330	−0.255	−0.135	0.009	0.004	0.096

Estimates are based on 10⁵ simulated ancestral recombination graphs each for a sample of size 50.

In general, the results reported in Tables 2 and 3 indicate that high values of both ψ and c are required for high correlations when recombination rate is high, when associated with our model. In particular, the correlations between $R_i^{\left(1\right)}$ and $R_i^{\left(2\right)}$ (i.e., between corresponding R_i’s at different loci) can be quite high, even when recombination is high, when both c and ψ are large enough, another indicator of the genome-wide correlations induced by sweepstake-like reproduction.

A different question concerns the limit behavior as sample size n increases. Fix the recombination rate and consider the limits

$$\underset{n\to \mathrm{\infty }}{\text{lim}}\text{cor}\left(R_i^{\left(1\right)},R_j^{\left(2\right)}\right),\hspace{0.17em}\underset{n\to \mathrm{\infty }}{\text{lim}}\text{cor}\left(V_i^{\left(1\right)},V_j^{\left(2\right)}\right)$$ (34)

Under the usual ARG, one expects the limits in (34) to be only functions of the recombination rate (and i and j). If the ARG also admits simultaneous multiple mergers, one expects the limits in (34) also to be functions of ϖ. Considering unlinked loci, one would be interested in the limits

$$\underset{r\to \mathrm{\infty }}{\text{lim}}\underset{n\to \mathrm{\infty }}{\text{lim}}\text{cor}\left(R_i^{\left(1\right)},R_j^{\left(2\right)}\right),\underset{r\to \mathrm{\infty }}{\text{lim}}\underset{n\to \mathrm{\infty }}{\text{lim}}\text{cor}\left(V_i^{\left(1\right)},V_j^{\left(2\right)}\right).$$ (35)

Resolving the limits (35) for different ARGs promises not only to yield insights into genome-wide correlations, but also to provide tools for inference, e.g., to distinguish between different population models.

The C program written to perform the simulations was checked by comparing correlation in coalescence times for sample size two at two loci to analytical results. The program is available upon request.

Comparison with Eldon and Wakeley (2008)

Eldon and Wakeley (2008) consider correlations in coalescence times and the prediction of linkage disequilibrium, under a modified Wright–Fisher sweepstake-style reproduction model, and observe correlations in coalescence times between loci despite high recombination rate. Our work differs from theirs in important ways. To begin with, we treat diploidy in detail, in which each offspring receives its two chromosomes from two distinct diploid parents. This leads to a separation of timescales of the ancestral process. We formally derive an ancestral recombination graph that admits simultaneous multiple mergers of ancestral lineages, which naturally arise in diploid models. Eldon and Wakeley observed correlations in coalescence times when considering only sample size two at each locus in a model that contains diploid individuals only implicitly; it is not a priori obvious that the correlations would still hold for large sample sizes. We confirm this using our formally obtained ARG that allows us also to investigate correlations in coalescence times and in ratios of coalescence times, for sample sizes larger than two at each locus. In addition, one can apply our ARG to inference problems. Indeed, we show how the variance of pairwise differences can, in principle, be used to obtain estimates of the recombination rate. Finally, we obtain a large class of ARGs by randomizing the offspring distribution; thus one is not restricted to the simple case of fixed ψ.

Furthermore, since the estimate 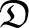of the expected value of r² can be expressed in terms of correlations in coalescence times, Eldon and Wakeley consider 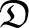under their modified Wright–Fisher model. However, 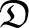is based on approximating an expected value of a ratio of correlated random variables by the ratio of expected values of the corresponding random variables and is also derived for a sample of size two at two loci. Thus, 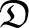may not be the ideal quantity to quantify association between loci for large sample sizes. A more natural way may be to investigate correlations in coalescence times for samples larger than two the way we do.

Discussion

Understanding the genome-wide effects of sweepstake-like reproduction on gene genealogies was our main aim. To this end, we derived ancestral recombination graphs for many loci arising from population models admitting large offspring numbers. High variance in individual reproductive success, or sweepstake-style reproduction, has been suggested to explain the low genetic diversity observed in many marine populations (Hedgecock et al. 1982; Avise et al. 1988; Palumbi and Wilson 1990; Beckenbach 1994; Hedgecock 1994; Árnason 2004). Hedgecock and Pudovkin (2011) review the sweepstake-style reproduction hypothesis and conclude that it provides the correct framework in which to investigate many natural marine populations.

Multiple-merger (Donnelly and Kurtz 1999; Pitman 1999; Sagitov 1999) and simultaneous (Schweinsberg 2000a; Möhle and Sagitov 2001) multiple-merger coalescent models arise from population models incorporating sweepstakes reproduction by admitting large offspring numbers (Sagitov 2003; Eldon and Wakeley 2006; Sargsyan and Wakeley 2008). While multiple-merger coalescent processes describing the ancestral relations of alleles at a single locus have received the most attention from mathematicians, ancestral processes for multiple linked loci have hitherto remained unexplored. We derive an ancestral recombination graph for many loci from a diploid biparental population model, in which one pair of diploid individuals (parents) contributes offspring to the population at each time step. Thus, each offspring necessarily receives its chromosomes from distinct individuals, as diploid individuals tend to do. Incorporating diploidy into our model the way we do leads to a separation-of-timescales problem. Our limiting object is essentially a “haploid” process, in which chromosomes either coalesce or recombine. By extending a result of Möhle (1998), we show that diploidy, a fundamental characteristic of many natural populations, can thus be treated as a “black box,” since the limiting object does not depend on the location of chromosomes in individuals.

By adopting a Moran-type model, in which only a single pair of individuals gives rise to offspring at each reproduction event, we chose mathematical tractability over more biologically realistic scenarios, in which, for example, many individuals contribute offspring at each time step. It should be straightforward to extend our model in many ways, for example by allowing a random number of parents or introducing population structure. Indeed, we do extend our model in one way, by taking a random offspring distribution. These extensions still leave open the question of distinguishing among different large offspring-number models. Our work on ancestral recombination graphs incorporating information from many loci is a step in this direction.

Sweepstake-style reproduction induces correlation in coalescence times even between loci separated by a high rate of recombination. The correlation follows from the multiple-merger property of our ancestral recombination graph, since many chromosomes coalesce at the same time in a multiple-merger event. The correlation remains a function of the coalescence parameters (c and ψ) of our population model. An immediate question is the effects on predictions of linkage disequilibrium (LD). The approximation 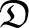by McVean (2002) predicts low LD when the recombination rate is high. However, when the rate of large reproduction events is high (c → ∞), 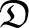remains a function of the coalescence parameters. The dependence of 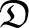on coalescence parameters has implications for the use of LD in inference for populations exhibiting sweepstake-style reproduction. Using simulations, Davies et al. (2007) found little effect of multiple mergers on the prediction r² of linkage disequilibrium, when comparing the exact Wright–Fisher model with recombination to the usual (continuous-time) ARG. However, by directly incorporating large offspring-number events the way we do, we can show that large offspring-number events do induce correlation in coalescence times and hence influence predictions of linkage disequilibrium.

The genome-wide correlation in coalescence times (Tables 2 and 3) induced by sweepstake-style reproduction offers hints about how to distinguish between large offspring number and ordinary Wright–Fisher reproduction. We are unaware of any published multilocus methods derived to distinguish among different population models. Full-likelihood methods may be preferable to the simple moment-based methods we consider. However, likelihood-based inference tends to be computationally intensive and more so for large samples. For large samples, one should be able to quickly obtain a good idea of the underlying processes by comparing correlations in ratios of mutation counts with predictions based on different population models.

In conclusion, ancestral recombination graphs admitting simultaneous multiple mergers of ancestral lineages are derived from a diploid population model of sweepstake-style reproduction, suggested to be common in many diverse marine populations. Our calculations show that sweepstake-style reproduction results in genome-wide correlation of gene genealogies, even for large sample sizes. Estimates of linkage disequilibrium and of recombination rates are confounded by the coalescence parameters of our population model. The genome-wide correlation in gene genealogies induced by sweepstake-style reproduction implies that examining correlations between loci should provide a means of distinguishing between ordinary Wright–Fisher and sweepstake-style reproduction.

Appendix

A1: Overview of Transitions and Their Probabilities in the Finite Population Model

A1.1: Basic setup and notation

We now classify all transitions and their probabilities of our population model relevant for the ancestral process under the scaling ɛN² = c/N², in which N denotes the population size. Fix a sample size n for this section. Usually we suppress the dependence on the sample size in the notation below. Recall the state space ${\mathcal{A}}_{\mathit{n}}$ of our ancestral process (respectively ${\mathcal{A}}_n^{\mathrm{sm}}$ for the “effective” limiting model).

Let Π_N be the transition matrix of the Markov chain {ξ^{n, N}(m)}_{m=0, 1,…} on ${\mathcal{A}}_{\mathit{n}}$ describing the ancestral states of an n sample in a population of size N. Our aim is to decompose Π_N into

$${\Pi }_N=A_N+\frac{1}{N^2}{B}_N+R_N,$$ (A1)

where the matrix A_N contains all transitions whose probability is O(1) or O(N⁻¹) per generation, so that they will happen “instantaneously” in the limit and are either identity transitions or projections from ${\mathcal{A}}_{\mathit{n}}$ to ${\mathcal{A}}_n^{\mathrm{sm}}$ by means of dispersing chromosomes paired in double-marked individuals. The matrix B_N contains all transition probabilities that are positive and finite after multiplication with N² and N → ∞, that is, our “effective transitions.” The remainder matrix R_N carries only transition probabilities that are of order O(N⁻³) or smaller that will thus vanish after scaling.

Once we have established this decomposition, we can apply Lemma 1.7 below in a suitable way to identify the limit given in Definition 1.1 and establish the convergence result, i.e., Theorem 1.2.

In Table A1, Table A2, and Table A3 we schematically deal with all possible transitions that can happen to a current sample over one time step.

Analogous to the notation and convention of Möhle and Sagitov (2003), we assume that in every configuration ξ^n,N(m) from (2), for the order of chromosomes in individuals $\mathbb{I}$_i for i ∈ [b(m)] we have

$$\begin{array}{l}{\mathbb{I}}_{\text{i}}\left(m\right)=\{C^{\left(2i-1\right)}\left(m\right),C^{\left(2i\right)}\left(m\right)\}\hspace{0.17em}\text{if}\hspace{0.17em}1\le i\le \beta \left(m\right)-b\left(m\right);\\ {\mathbb{I}}_{\text{i}}\left(m\right)=\left\{C^{\left(\beta \left(m\right)-b\left(m\right)+i\right)}\left(m\right),Ø\right\}\hspace{0.17em}\text{if}\hspace{0.17em}\beta \left(m\right)-b\left(m\right)+1\le i\le b\left(m\right).\end{array}$$ (A2)

Table A1 .

Transitions of type 2

	Parent with marked chromosome(s) (Ø means no parent in sample)
Offspring	Ø	$\mathbb{I}$′
$\mathbb{I}$″	{$\mathbb{I}$′, $\mathbb{I}$′}(A)	{$\mathbb{I}$′, $\mathbb{I}$′}, {$\mathbb{I}$″, $\mathbb{I}$′}
	O(N−1)a	O(N−2), (B)
$\mathbb{I}$′	{$\mathbb{I}$′}(A)	{$\mathbb{I}$′}, {$\mathbb{I}$″}, {$\mathbb{I}$′, $\mathbb{I}$′}, (B)
	O(N−1)b	O(N−2)c
	$\stackrel{\sim }{\mathbb{I}}\prime$	$\hat{\mathbb{I}}″$
$\mathbb{I}$″	O(N−2), (B)	O(N−2), (B)d
$\mathbb{I}$′	{$\mathbb{I}$″}, {$\mathbb{I}$′, $\mathbb{I}$′}, (B)	{$\mathbb{I}$′, $\mathbb{I}$″}, {$\mathbb{I}$′}, (B)
	O(N−2)	O(N−2)

^aOffspring double-marked, no parent in sample.

^bOffspring single marked, no parent in sample.

^cOffspring single marked, one single-marked parent in sample.

^dOffspring double-marked, one double-marked parent in sample.

Table A2 .

Transitions of type 4, neither parent in sample

Offspring	Parent: Ø
$\mathbb{I}$″	{$\mathbb{I}$″, $\mathbb{I}$′}, O(N−2), (B)
	{$\mathbb{I}$″, $\mathbb{I}$″}, O(N−3), (R)
$\mathbb{I}$′	$\mathbb{I}$″, O(N−2), (B)

Table A3 .

Transitions of type 5

Offspring	Parent: Ø
k1$\mathbb{I}$′, k2$\mathbb{I}$″	{$\mathbb{I}$″, $\mathbb{I}$″}, O(N−2), (B)
	{$\mathbb{I}$″, $\mathbb{I}$′}, O(N−2), (B)
	{$\mathbb{I}$′, $\mathbb{I}$′}, O(N−2), (B)
	$\mathbb{I}$″, O(N−2), (B)
	$\mathbb{I}$′, O(N−2), (B)

For ease of presentation, we denote by $\mathbb{I}$′ a single-marked individual carrying one active chromosome, by $\mathbb{I}$″ a double-marked individual carrying two active chromosomes, by $\stackrel{\sim }{\mathbb{I}}\prime$ a single-marked individual (parent) whose marked chromosome is not passed on in the sample during a given reproduction event, and by $\hat{\mathbb{I}}″$ a double-marked individual (parent) where one marked chromosome is passed on and the other is not during a given reproduction event.

The symbols (A), (B), and (R) in the tables denote whether the corresponding transitions belong to A_N (A), to B_N (B), or to the “remainder term” (R) in (A1) according to the decomposition mentioned above. After that, we compute all the important probabilities explicitly. The order of the probability of each transition is also noted in Tables A1–A3.

A1.2: Transition type 1: Small or large reproduction event, no offspring in the sample

If a reproduction event takes place, say at generation m, which does not affect our sample, this will not affect the state of our ancestral process at m + 1, and we have ξ^n,N(m) = ξ^n,N(m + 1). Hence, we see an identity transformation. We now compute the probability that our sample is not affected. Given the current state $\xi \in {\mathcal{A}}_n$ with b individuals and β chromosomes (hence β − b double-marked and 2b − β single-marked individuals), the probability that no child is in the sample is

$$\left(1-\varepsilon \right)\frac{N-b}{N}+{\varepsilon }_N\frac{\left(\begin{array}{c}N-b\\ \lfloor \psi N\rfloor \end{array}\right)}{\left(\begin{array}{c}N\\ \lfloor \psi N\rfloor \end{array}\right)}=1-O\left(N^{-1}\right).$$

A1.3: Transition type 2: Small reproduction event, offspring in the sample, at most one parent in the sample, no recombination

Here, we need to distinguish only whether the offspring is single or double marked and whether there is a parent in the sample. For example, it is immediate to see that the probability of a transition from a double-marked ($\mathbb{I}$″) offspring to two single-marked ({$\mathbb{I}$′,$\mathbb{I}$′}) individuals is of order O(N⁻¹) when no parent is in the sample and no recombination happens. Table A1 lists all corresponding events. By way of example, the state-labeled {$\mathbb{I}$′, $\mathbb{I}$′} denotes that two single-marked individuals, each carrying one active chromosome, are reached from the sample configuration. One such configuration is if the sample contains one offspring, but neither parent (Ø), and the offspring is carrying two active chromosomes ($\mathbb{I}$″).

A1.4: Transition type 3: Small reproduction event, offspring in the sample, both parents in the sample

If both parents and offspring are in the sample in a small event, this immediately gives a transition probability of order O(N⁻³) or smaller (depending on the presence of recombination) and hence will be irrelevant and be part of R_N. We omit a detailed table listing the different single- and double-marked individuals.

A1.5: Transition type 4: Small reproduction event, offspring and at most one parent in the sample, recombination occurs

Table A2 lists transitions due to recombination and when neither parent is in the sample. The probability of the presence of both an offspring and at least one parent in a sample, when recombination occurs, is of order O(N⁻³) and so will vanish in the limit.

A1.6: Transition type 5: Large reproduction event, offspring in the sample, no parent in the sample, no recombination

Table A3 lists all possible transitions when a large reproduction event occurs, no parent is in the sample, and recombination does not occur. The probabilities of the events listed in Table 1 in the main text are of order O(N⁻²) and so will appear as effective transitions in the limit.

A1.7: Transition type 6: Large reproduction event, offspring in the sample, recombination occurs, and/or at least one parent is in the sample

The probability that a large reproduction event takes place and at least one child and at least one parent are in the sample is O(N⁻³). In addition, the probability that a large reproduction event takes place, at least one child is in the sample, and also a recombination event happens in the sample is O(N⁻³). Hence all such events are negligible.

A2: The Convergence Result

A2.1: The limit of the projection matrix A_N

Some care is needed to make sure A_N converges in the right sense to the desired projection matrix. The only relevant transitions of order O(1) or O(N⁻¹) are transitions of types 1 and 2. The only one that is not an identity transition is the first dispersion event of Table A1. For $\xi \in {\mathcal{A}}_n$ with b < β (i.e., at least one marked individual is double marked), that is

$$\xi \mapsto {\text{disp}}_i\left(\xi \right).$$

This event will become part of A_N and has probability

$$A_N\left(\xi ,{\text{disp}}_i\left(\xi \right)\right)=\left(1-{\varepsilon }_N\right)\frac{1}{N}\frac{\left(\begin{array}{c}N-b-1\\ 2\end{array}\right)}{\left(\begin{array}{c}N\\ 2\end{array}\right)}{\left(1-r_N\right)}^2,1\le i\le \beta -b$$ (A3)

(this is the probability of the event a listed in Table A1; event b in Table A1 leads to an identity transition). Otherwise, we have

$$A_N\left(\xi ,\xi \right)=1-\left(1-{\varepsilon }_N\right)\frac{\beta -b}{N}\frac{\left(\begin{array}{c}N-b-1\\ 2\end{array}\right)}{\left(\begin{array}{c}N\\ 2\end{array}\right)}{\left(1-r_N\right)}^2.$$

Of course, A_N has to leave elements of the subspace ${\mathcal{A}}_n^{\text{sm}}$ invariant; hence we set, for ξ with b = β,

$$A_N\left(\xi ,{\xi }^{\prime }\right):=1_{\left\{\xi ={\xi }^{\prime }\right\}}.$$

Proposition 1.4. With the above settings, A_N is a stochastic matrix for each N and

$$\underset{C\to \mathrm{\infty }}{\text{lim}}\underset{N\to \mathrm{\infty }}{\text{lim}}\underset{r\ge CN}{\text{sup}}\Vert A_N^r-P\Vert =0$$ (A4)

for all C > 0 large enough, where P is the canonical projection from ${\mathcal{A}}_n$ to ${\mathcal{A}}_n^{\mathrm{sm}}$; i.e.,

$$P\left(\xi ,{\xi }^{\prime }\right)=1_{\left\{{\xi }^{\prime }=\text{cd}\left(\xi \right)\right\}}.$$

Proof of Proposition 1.4. The Markov chain with transition matrix A_N can change state only by dispersing the chromosomes paired in a double-marked individual. We see from (A3) that

$$A_N\left(\xi ,{\text{disp}}_i\left(\xi \right)\right)\ge \frac{K\left(n,r,c\right)}{N}$$

for some suitable constant K(n, r, c), uniformly in b and i ≤ β − b and N (for all N large enough). Hence, starting from ξ with β − b double-marked individuals, the number of A_N steps required until complete dispersion has occurred is dominated by the sum of β − b independent geometric random variables ${\gamma }_1^{\left(N\right)}+\dots +{\gamma }_{\beta -b}^{\left(N\right)}$, with success probability K(n, r, c)/N. By Markov’s inequality,

$$\underset{N\in \mathbb{N}}{\text{sup}}\mathbb{P}\{{\gamma }_1^{\left(N\right)}+\dots +{\gamma }_{\beta -b}^{\left(N\right)}\ge CN\}\le \frac{1}{CN}\mathbb{E}\left[{\gamma }_1^{\left(N\right)}+\dots +{\gamma }_{\beta -b}^{\left(N\right)}\right]=\frac{N\left(\beta -b\right)}{C\cdot N\cdot K\left(n,r,c\right)}\to 0\hspace{0.17em}\text{as}\hspace{0.17em}C\to \mathrm{\infty }.$$

The proof can now be completed with a coupling argument, noting that two Markov chains run according to A_N resp. P, started in $\xi \in {\mathcal{A}}_n$, both get stuck in cd(ξ), and this happens after at most CN steps with high probability (for C large).

A2.2: Proof of the convergence result

With the definition of A_N from the previous section, put

$$B_N^{*}:=N^2\left({\Pi }_N-A_N\right)$$ (A5)

and let P be the canonical projection from ${\mathcal{A}}_n$ to ${\mathcal{A}}_n^{\mathrm{sm}}$ defined in Proposition 1.4. The following lemma identifies G as the limit containing all the effective transitions of $B_N^{*}$ when projecting on the subspace ${\mathcal{A}}_n^{\mathrm{sm}}$:

Lemma 1.5. We have

$${\widehat{B}}_N:=P{B}_N^{*}P\to G\hspace{0.17em}\text{as}\hspace{0.17em}N\to \mathrm{\infty }$$ (A6)

with G from (14).

Remark 1.6. We do believe that in fact the sequence of (formally larger) matrices $B_N^{*}$ on ${\mathcal{A}}_n$ converges as well, but the statement about ${\widehat{B}}_N$ is sufficient for our purposes below [see (A13) in Lemma 1.7] and simpler to prove since it allows us to restrict to the “completely dispersed” configurations in ${\mathcal{A}}_n^{\mathrm{sm}}$.

Proof of Lemma 1.5. We inspect the types of events listed in Tables A1–A3 that are marked with (B). Events that are marked with (R) have probability of order at most O(N⁻³); hence their total contribution to any entry of ${\widehat{B}}_N$ is at most O(N⁻¹) (since we are following a finite sample, there are only finitely many possible one-step events altogether). It suffices to consider ${\widehat{B}}_N\left(\xi ,\text{cd}\left(\eta \right)\right)$ for $\xi =\left\{C^{\left(1\right)},\dots ,C^{\left(\beta \right)};\beta \right\}\in {\mathcal{A}}_n^{\mathrm{sm}},\eta \in {\mathcal{A}}_n$ (because P projects to ${\mathcal{A}}_n^{\mathrm{sm}}$).

Regarding ${\xi }^{\prime }={\text{pairmerge}}_{j_1,j_2}\left(\xi \right)$, this transition can happen in a small reproduction event (these events are listed at c in Table A1; note that events listed at d in Table A1 lead to a trivial transition once P is applied) or in a large reproduction event as in Table A3 if the grouping is suitable. Up to four parental chromosomes are involved in any reproduction event. Hence, a large reproduction event can lead to a given pair merger in the sample if up to five individuals in the sample are children. Thus

$$\begin{array}{c}{\widehat{B}}_N\left(\xi ,{\xi }^{\prime }\right)=N^2\left(1-{\varepsilon }_N\right)\left(1-r_N\right)2\times \frac{1}{N}\frac{1\cdot \left(N-b\right)}{\left(\begin{array}{c}N-1\\ 2\end{array}\right)}\frac{1}{2}\frac{1}{2}\\ +N^2{\varepsilon }_N{\displaystyle \sum _{c=2}^5{\left(1-r_N\right)}^c\left(\begin{array}{c}\beta -2\\ c-2\end{array}\right)\frac{\left(\begin{array}{c}N-\beta \\ \lfloor N\psi \rfloor -c\end{array}\right)}{\left(\begin{array}{c}N\\ \lfloor N\psi \rfloor \end{array}\right)}{\left(4\right)}_{c-1}{\left(\frac{1}{4}\right)}^c+O\left(N^{-1}\right)}.\end{array}$$ (A7)

For the first term on the right note that either j₁ or j₂ can be the child, and the two factors of $\frac{1}{2}$ come from the requirement that the chromosome in the child we are following is the one from the parent in the sample and is also the one we are following in the parent. For the second term on the right note that once we decide on c children in the sample [$\left((\beta -2)/(c-2)\right)$ choices because j₁ and j₂ are already chosen], there are (4)_c−1 ways to assign them to the four parental chromosomes. For comparison with (15) and the first line in (14) observe

$$\frac{\left(\begin{array}{c}N-\beta \\ \lfloor N\psi \rfloor -c\end{array}\right)}{\left(\begin{array}{c}N\\ \lfloor N\psi \rfloor \end{array}\right)}=\frac{\left(N-\beta \right)!\lfloor N\psi \rfloor !\left(N-\lfloor N\psi \rfloor \right)!}{\left(\lfloor N\psi \rfloor -c\right)!\left(N-\beta -\lfloor N\psi \rfloor +c\right)!N!}\sim \frac{{\left(N\psi \right)}^c{\left(N\left(1-\psi \right)\right)}^{\beta -c}}{N^{\beta }}={\psi }^c{\left(1-\psi \right)}^{\beta -c}.$$

Regarding ξ′ = recomb_j,ℓ(ξ) [assuming that α is such that C^(j) can be nontrivially cut into two by a recombination event between loci ℓ − 1 and ℓ], this transition can happen in a small reproduction event as listed at b in Table A1 or in another event that has probability O(N⁻³). Hence

$${\widehat{B}}_N\left(\xi ,{\xi }^{\prime }\right)=N^2\left(1-{\varepsilon }_N\right)\times \frac{1}{N}\frac{\left(\begin{array}{c}N-b\\ 2\end{array}\right)}{\left(\begin{array}{c}N-1\\ 2\end{array}\right)}\frac{r^{\left(\ell \right)}}{N}+O\left(N^{-1}\right)=r^{\left(\ell \right)}+O\left(N^{-1}\right).$$ (A8)

Regarding ${\xi }^{\prime }={\text{groupmerge}}_{J_1,J_2,J_3,J_4}\left(\xi \right)$, this can occur only through a large reproduction event as listed in section A1.6. Write k_i := |J_i|; we assume k₁ ≥ … ≥ k_a ≥ 2 for some a ∈ [4], k_a+1 = … = k₄ = 0 (if a = 1, k₁ ≥ 3), and s := β − (k₁ + ⋯ + k_a) is the number of singletons (nonparticipating chromosomes) in the merger. Note that by the structure of the diploid model, with a groups merging there can be up to k₁ + ⋯ + k_a + (4 − a)⁺ children in the sample [put differently, up to (4 − a)⁺ “nonmerging children”]. Then

$$\begin{array}{c}{\widehat{B}}_N\left(\xi ,{\xi }^{\prime }\right)=N^2{\varepsilon }_N{\displaystyle \sum _{c^{\prime }=0}^{{\left(4-a\right)}^{+}}\left(\begin{array}{c}\beta -k_1-\dots -k_a\\ c^{\prime }\end{array}\right){\left(1-r_N\right)}^{k_1+\dots +k_a+c^{\prime }}}\\ \times \frac{\left(\begin{array}{c}N-\beta \\ \lfloor N\psi \rfloor -\left(k_1+\dots +k_a+c^{\prime }\right)\end{array}\right)}{\left(\begin{array}{c}N\\ \lfloor N\psi \rfloor \end{array}\right)}{\left(4\right)}_{a+c^{\prime }}{\left(\frac{1}{4}\right)}^{k_1+\dots +k_a+c^{\prime }}+O\left(N^{-1}\right).\end{array}$$

It remains to check that the diagonal terms behave correctly, i.e., that as N → ∞,

$${\widehat{B}}_N\left(\xi ,\xi \right)\to G\left(\xi ,\xi \right)=-{\displaystyle \sum _{{\xi }^{\prime }\ne \xi ,{\xi }^{\prime }\in {\mathcal{A}}_n^{\text{sm}}}G\left(\xi ,{\xi }^{\prime }\right)}.$$ (A9)

Because Π_N and A_N are both stochastic matrices (as is P), we have

$${\widehat{B}}_N\left(\xi ,\xi \right)=-{\displaystyle \sum _{{\xi }^{\prime }\ne \xi ,{\xi }^{\prime }\in {\mathcal{A}}_n^{\text{sm}}}{\widehat{B}}_N\left(\xi ,{\xi }^{\prime }\right)}$$ (A10)

for each N. By inspection and the discussion above, all terms in Π_N with decay rate 1/N are accounted for in A_N, and all nondiagonal terms in Π_N − A_N with decay rate 1/N² appear after multiplication with N² in ${\widehat{B}}_N$ with their correct limits, namely the corresponding terms in G, while terms with a faster decay rate disappear in the limit. Hence (A10) implies (A9).

A3: Markov Chains with Two Timescales—A Variation on a Lemma of Möhle

Conceptually, our convergence result rests on a separation-of-timescales phenomenon. It can be established with the help of a variant of a well-know result; see Lemma 1 from Möhle (1998).

Let E be a finite set. We equip matrices A = (A(x, y))_x,y∈E on E with the matrix norm $\Vert A\Vert :={\text{max}}_{x\in E}{\displaystyle {\sum }_{y\in E}\left|A\left(x,y\right)\right|}$. Note that then ‖AB‖ ≤ ‖A‖‖B‖ and ‖A‖ = 1 if A is a stochastic matrix.

Lemma 1.7. Assume that for N ∈ ℕ, A_N is a stochastic matrix on E such that

$$\underset{C\to \mathrm{\infty }}{\text{lim}}\underset{N\to \mathrm{\infty }}{\text{lim}}\underset{r\ge CN}{\text{sup}}\Vert A_N^r-P\Vert =0$$ (A11)

for some matrix P. Then we have for any 0 < c, K, t <∞

$$\underset{N\to \mathrm{\infty }}{\text{lim}}\underset{\Vert B\Vert \le K}{\text{sup}}\Vert {\left(A_N+c{N}^{-2}B\right)}^{\left[t{N}^2\right]}-{\left(P+c{N}^{-2}B\right)}^{\left[t{N}^2\right]}\Vert =0.$$ (A12)

Furthermore, if (B_N)_N∈ℕ is a sequence of matrices on E such that

$$G:=\underset{N\to \mathrm{\infty }}{\text{lim}}P{B}_{N}P\hspace{0.17em}\mathit{exists},$$ (A13)

then

$$\underset{N\to \mathrm{\infty }}{\text{lim}}{\left(A_N+c{N}^{-2}{B}_N\right)}^{\left[t{N}^2\right]}=P{e}^{ctG}\hspace{0.17em}\mathit{for}\hspace{0.17em}\mathit{all}\hspace{0.17em}\mathit{t}>0.$$ (A14)

Remark 1.8. Instead of timescales N and N² one can allow more generally any a_N, b_N → ∞ with b_N/a_N → ∞, with only notational modifications in the proof.

Proof of Lemma 1.7. We begin with (A12). Without loss of generality assume K = 1; otherwise replace B by B/K and c by cK. Fix c, t > 0 and a matrix B with ‖B‖ ≤ 1, and abbreviate m := ⌊tN²⌋. Let ɛ > 0 and choose C₀ < ∞ and N₀ ∈ ℕ such that

$$\Vert A_N^r-P\Vert \le \varepsilon \text{for}N\ge N_0,r\ge C_{0}N$$ (A15)

[as guaranteed by (A11)]. Note that

$$\begin{array}{l}\Vert {\left(A_N+c{N}^{-2}B\right)}^m-{\left(P+c{N}^{-2}B\right)}^m\Vert \\ \le \Vert A_N^m-P\Vert +\stackrel{m}{{\displaystyle \sum }_{k=1}}{\left(\frac{c}{N^2}\right)}^k{\displaystyle \sum }_{\begin{array}{c}{m}_1,\dots ,m_{k+1}\in {\mathbb{N}}_0\\ m_1+\dots +m_{k+1}=m-k\end{array}}\Vert A_N^{m_1}\stackrel{k+1}{{\displaystyle \prod }_{j=2}}\left(B{A}_N^{m_j}\right)-P^{m_1}\stackrel{k+1}{{\displaystyle \prod }_{j=2}}\left(B{P}^{m_j}\right)\Vert .\end{array}$$

Mimicking the proof in Möhle (1998), we split the second summand into (the ellipses refer to the term inside the large-norm brackets on the right of the last line of the previous formula)

$$S_1:={\displaystyle \sum _{k=1}^m{\left(\frac{c}{N^2}\right)}^k}{\displaystyle \sum }_{\begin{array}{c}{m}_1,\dots ,m_{k+1}\ge C_{0}N\\ m_1+\dots +m_{k+1}=m-k\end{array}}\dots \hspace{0.17em}\text{and}\hspace{0.17em}{S}_2:={\displaystyle \sum _{k=1}^m{\left(\frac{c}{N^2}\right)}^k}{\displaystyle \sum }_{\begin{array}{c}{m}_1,\dots ,m_{k+1}\in {\mathbb{N}}_0\\ m_1+\dots +m_{k+1}=m-k\\ \exists j:m_j<C_{0}N\end{array}}\dots$$

As in Möhle (1998, p. 509) we have S₁ ≤ 2e^t(t + 1)ɛ for all N large enough, and our estimate for S₂ is a small variation of the corresponding estimate in Möhle (1998). Each of the matrix norms appearing in the big sum in S₂ is at most 2, and hence (with x ∧ y := min(x, y))

$$\begin{array}{l}{S}_2\le 2{\displaystyle \sum _{k=1}^m{\left(\frac{c}{N^2}\right)}^k\#\left\{\left(m_1,\dots ,m_{k+1}\right)\in {\mathbb{N}}_0^k:\begin{array}{c}{m}_1+\dots +m_{k+1}=m-k,\\ \exists j:m_j<C_{0}N\end{array}\right\}}\\ \le 2{\displaystyle \sum _{k=1}^m{\left(\frac{c}{N^2}\right)}^k\left(k+1\right)}{\displaystyle \sum _{m_1=0}^{C_{0}N\wedge \left(m-k\right)}\left(\begin{array}{c}m-m_1-1\\ k-1\end{array}\right)}\\ \le 2{\displaystyle \sum _{k=1}^m{\left(\frac{c}{N^2}\right)}^k\left(k+1\right)C_{0}N\left(\begin{array}{c}m-1\\ k-1\end{array}\right)=2C_{0}N\frac{c}{N^2}{\displaystyle \sum _{k=0}^{m-1}{\left(\frac{c}{N^2}\right)}^k\left(k+2\right)\left(\begin{array}{c}m-1\\ k\end{array}\right)}}\\ \le C^{\prime }\frac{1}{N}.\end{array}$$

[We use in the last estimate that for |x| < 1, n ∈ ℕ, ${\displaystyle {\sum }_{n=0}^{\mathrm{\infty }}\left(\begin{array}{c}n\\ k\end{array}\right)x^k={\left(1+x\right)}^n}$, and ${\displaystyle {\sum }_{n=0}^{\mathrm{\infty }}k\left(\begin{array}{c}n\\ k\end{array}\right)x^k=nx{\left(1+x\right)}^{n-1}}$.]

The derivation of (A14) from (A12) is literally the same as in Möhle (1998, pp. 509–511) (read c_N = c/N² there).

A4: The Convergence Result with General Random Ψ_N

In this section we briefly indicate how the proof of Theorem 1.2 can be modified to yield Theorem 1.3. In each reproduction event, a random number Ψ_N of individuals die and are replaced by the same number of offspring, and we recall assumptions (20), (22) and (24). By short timescale we refer to the scaling a_N given by

$$a_N=\frac{N}{\mathbb{E}\left[{\Psi }_N\right]}$$

and by long timescale the scaling b_N given by

$$b_N=\frac{1}{c_N}=\frac{N\left(N-1\right)}{\mathbb{E}\left[{\Psi }_N\left({\Psi }_N+3\right)\right]}.$$

Assumption (20) yields b_N → ∞ as N → ∞, and b_N/a_N → ∞ by assumption (21). To check (23), i.e., that indeed a_N → ∞, observe that Ψ_N/N is a positive random variable, bounded by 1. Condition (20) is equivalent to $\mathbb{E}$[(Ψ_N/N)²] →ℕ0, which implies Ψ_N/N → 0 in probability and $\mathbb{E}$[Ψ_N/N] → 0 and hence (23).

For use below, we recall implications of (22) provided that (20) holds (cf. Sagitov 1999):

$$\text{For}\hspace{0.17em}\text{all}j\ge 3:\frac{1}{c_N}\mathbb{E}\left[{\left(\frac{{\Psi }_N}{N}\right)}^j\right]\to {\displaystyle {\int }_{\left[0,1\right]}{x}^{j-2}F\left(dx\right)}.$$ (A16)

Indeed, integration by parts yields

$$\begin{array}{l}\frac{1}{c_N}\mathbb{E}\left[{\left(\frac{{\Psi }_N}{N}\right)}^j\right]=\frac{1}{c_N}{\displaystyle {\int }_{\left(0,1\right]}j{x}^{j-1}\mathbb{P}\left(\frac{{\Psi }_N}{N}>x\right)dx}\underset{N\to \mathrm{\infty }}{\to }{\displaystyle {\int }_{\left(0,1\right]}j{x}^{j-1}}{\displaystyle {\int }_{\left(x,1\right]}{y}^{-2}F\left(dy\right)dx}={\displaystyle {\int }_{\left(0,1\right]}\left({\displaystyle {\int }_{\left(0,1\right]}{1}_{\left\{x\le y\right\}}j{x}^{j-1}dx}\right)y^{-2}F\left(dy\right)}={\displaystyle {\int }_{\left(0,1\right]}{y}^{j-2}F\left(dy\right)}.\end{array}$$ (A17)

Furthermore for the case j = 2 one obtains

$$\underset{N\to \mathrm{\infty }}{\text{lim}\hspace{0.17em}\text{sup}}\frac{1}{c_N}\mathbb{E}\left[{\left(\frac{{\Psi }_N}{N}\right)}^2\right]=\underset{N\to \mathrm{\infty }}{\text{lim}\hspace{0.17em}\text{sup}}\frac{E\left[{\Psi }_N^2\right]}{E\left[{\Psi }_N\left({\Psi }_N+3\right)\right]}\le 1<\mathrm{\infty }.$$ (A18)

Let ${\tilde{\Psi }}_N$ have the following reweighted distribution (relative to Ψ_N):

$$\mathbb{P}\left({\tilde{\Psi }}_N=k\right)=\frac{k\left(k+3\right)}{E\left[{\Psi }_N\left({\Psi }_N+3\right)\right]}\mathbb{P}\left({\Psi }_N=k\right),k=1,\dots ,N-2$$ (A19)

and then

$$\frac{{\tilde{\Psi }}_N}{N}\stackrel{d}{\to }F\hspace{0.17em}\text{as}\hspace{0.17em}N\to \mathrm{\infty }.$$ (A20)

Indeed, for any ℓ ∈ ℕ

$$\begin{array}{l}\mathbb{E}\left[{\left(\frac{{\tilde{\Psi }}_N}{N}\right)}^{\ell }\right]=\frac{N\left(N-1\right)}{\mathbb{E}\left[{\Psi }_N\left({\Psi }_N+3\right)\right]}\mathbb{E}\left[{\left(\frac{{\Psi }_N}{N}\right)}^{\ell +1}\frac{{\Psi }_N+3}{N-1}\right]\\ =\frac{1}{c_N}\mathbb{E}\left[{\left(\frac{{\Psi }_N}{N}\right)}^{\ell +2}\right]\frac{N}{N-1}+\frac{3}{\left(N-1\right)}\frac{1}{c_N}\mathbb{E}\left[{\left(\frac{{\Psi }_N}{N}\right)}^{\ell +1}\right]\underset{N\to \mathrm{\infty }}{\to }\underset{\left(0,1\right]}{{\displaystyle \int }}{y}^{\ell }F\left(dy\right)\end{array}$$ (A21)

by (A17) and (A18), so (A20) follows because the moments characterize a probability law on [0, 1]. One can check (along the lines of Sagitov 1999) that under assumption (20), both (A17) and (A18) are in fact equivalent to (22).

The proof of Theorem 1.3 is now a relatively straightforward adaptation of the proof of Theorem 1.2 discussed in sections A1 and A2 above. Scaling by N is throughout replaced by scaling with a_N = N/$\mathbb{E}$[Ψ_N] and scaling by N² becomes scaling with b_N = N(N − 1)/$\mathbb{E}$[Ψ_N (Ψ_N+ 3)]:

1. When currently following b ≥ 1 individuals, the probability that none of them is an offspring in the previous reproduction event (and hence the sample configuration remains unchanged) is

   $$\mathbb{E}\left[\frac{\left(\begin{array}{c}N-b\\ {\Psi }_N\end{array}\right)}{\left(\begin{array}{c}N\\ {\Psi }_N\end{array}\right)}\right]=\mathbb{E}\left[{\displaystyle \prod _{j=0}^{{\Psi }_N-1}\frac{N-b-j}{N-j}}\right]=\mathbb{E}\left[{\displaystyle \prod _{j=0}^{{\Psi }_N-1}\left(1-\frac{b}{N-j}\right)}\right]=1-O\left(b\frac{\mathbb{E}\left[{\Psi }_N\right]}{N}\right)=1-O\left(a_N^{-1}\right).$$

   This is analogous to transitions discussed in section A1.2 and happens “all the time” (leading to the projecting transitions part in the limit).
2. When currently following b ≥ 1 individuals, say the kth of which is double marked, the probability that the ith individual is the only offspring in the sample, and that the sample also does not contain a parent, is [we write (x)k = x(x − 1)…(x −k + 1) for the ith falling factorial]

   $$\mathbb{E}\left[\frac{{\Psi }_N{\left(N-{\Psi }_N-2\right)}_{b-1}}{{\left(N\right)}_b}\right]\sim \mathbb{E}\left[\frac{{\Psi }_N}{N}{\left(1-\frac{{\Psi }_N}{N}\right)}^{b-1}\right]=a_N^{-1}\left(1+o\left(1\right)\right).$$

   The projection matrix A_N now becomes

   $$A_N\left(\xi ,{\text{disp}}_i\left(\xi \right)\right)=\mathbb{E}\left[\frac{{\Psi }_N{\left(N-{\Psi }_N-2\right)}_{b-1}}{{\left(N\right)}_b}\right]{\left(1-r\right)}^2,1\le i\le \beta -b$$ (A22)

   and $A_N\left(\xi ,\xi \right)=1-\left(\beta -b\right)\mathbb{E}\left[{\Psi }_N{\left(N-{\Psi }_N-2\right)}_{b-1}/{\left(N\right)}_b\right]{\left(1-r\right)}^2$; the analogue of Proposition 1.4 is then

   $$\underset{C\to \mathrm{\infty }}{\text{lim}}\underset{N\to \mathrm{\infty }}{\text{lim}}\underset{r\ge C{a}_N}{\text{sup}}\left|A_N^r-P\right|=0.$$ (A23)
3. From now on we can work on the “projected” space ${\mathcal{A}}_n^{\mathbf{sm}}$. The distinction between small and large reproduction events is irrelevant in the general case. Hence, it is more suitable to distinguish whether a parent and an offspring are in the sample or whether several offspring (but no parent) are in the sample. In analogy with (A5) and (A6), we split Π_N into fast and slow parts and define

   $$B_N^{*}:=b_N\left({\Pi }_N-A_N\right),{\widehat{B}}_N:=P{B}_N^{*}P.$$ (A24)

   It then remains to check that

   $${\widehat{B}}_N\to G\hspace{0.17em}\text{with}\hspace{0.17em}G\hspace{0.17em}\text{defined}\hspace{0.17em}\text{in}\hspace{0.17em}\left(26\right),$$ (A25)

   whence Theorem 1.3 follows from Lemma 1.7 together with Remark 1.8.

   We now verify (A25):

4. Recombination events give the correct limit; see the discussion below (24).

5. “Large” is the probability that exactly k ≥ 2 individuals among b (excluding the parents) is, using (A19),

   $$\mathbb{E}\left[\frac{{\left({\Psi }_N\right)}_k{\left(N-{\Psi }_N-2\right)}_{b-k}}{{\left(N\right)}_b}\right]=\mathbb{E}\left[{\Psi }_N\left({\Psi }_N+3\right)\right]\mathbb{E}\left[\frac{{\left({\tilde{\Psi }}_N\right)}_k{\left(N-2-{\tilde{\Psi }}_N\right)}_{b-k}}{{\tilde{\Psi }}_N\left({\tilde{\Psi }}_N+3\right){\left(N\right)}_b}\right];$$ (A26)

   thus 1/c_N times this probability is

   $$\begin{array}{l}N\left(N-1\right)\mathbb{E}\left[\frac{{\left({\tilde{\Psi }}_N\right)}_k{\left(N-2-{\tilde{\Psi }}_N\right)}_{b-k}}{{\tilde{\Psi }}_N\left({\tilde{\Psi }}_N+3\right){\left(N\right)}_b}\right]=\frac{1}{{\left(N-2\right)}_{b-2}}\mathbb{E}\left[{\left({\tilde{\Psi }}_N-2\right)}_{k-2}{\left(N-2-{\tilde{\Psi }}_N\right)}_{b-k}\right]+O\left(\frac{1}{N}\right)\\ \underset{N\to \mathrm{\infty }}{\to }{\displaystyle {\int }_{\left(0,1\right]}{y}^{k-2}{\left(1-y\right)}^{b-k}F\left(dy\right)}\end{array}$$ (A27)

   by (A20). Furthermore, the probability that at least two offspring and at least one parent are in the sample is at most

   $$b\left(\begin{array}{c}b-1\\ 2\end{array}\right)\mathbb{E}\left[\frac{2{\left({\Psi }_N\right)}_2}{{\left(N\right)}_3}\right]=O\left(c_N/N\right);$$ (A28)

   hence such events become negligible in the limit.

6. “Small” is a merger of a single pair, which can result either from one offspring and one parent in the sample or from two offspring but no parent in the sample: Here, the weight of F({0}) plays a role.

The probability that exactly two given single-marked individuals in a sample of size b are offspring (and none are parents) is

$$\mathbb{E}\left[\frac{{\left({\Psi }_N\right)}_2{\left(N-2-{\Psi }_N\right)}_{b-2}}{{\left(N\right)}_b}\right];$$ (A29)

and the probability that among a pair of two given single-marked individuals, one is a parent, the other is an offspring, and no other element of the sample is affected by the reproduction event is

$$\mathbb{E}\left[\frac{2{\left(2\right)}_1{\left({\Psi }_N\right)}_1{\left(N-{\Psi }_N-2\right)}_{b-2}}{{\left(N\right)}_b}\right];$$ (A30)

thus, 1/c_N times the probability that exactly one given pair (of single-marked individuals) is involved in a reproduction event is

$$\begin{array}{l}\frac{1}{c_N}\mathbb{E}\left[\frac{{\Psi }_N\left({\Psi }_N+3\right){\left(N-{\Psi }_N-2\right)}_{b-2}}{{\left(N\right)}_b}\right]\\ =\mathbb{E}\left[\frac{{\left(N-2-{\tilde{\Psi }}_N\right)}_{b-2}}{{\left(N-2\right)}_{b-2}}\right]\\ \underset{N\to \mathrm{\infty }}{\to }{\displaystyle {\int }_{\left[0,1\right]}{\left(1-y\right)}^{b-2}F}\left(dy\right)=F\left(\left\{0\right\}\right)+{\displaystyle {\int }_{\left(0,1\right]}{\left(1-y\right)}^{b-2}F\left(dy\right)}\end{array}$$ (A31)

by (A20).

1. (Combinatorial connections between participation in reproduction events and merging of ancestral chromosomes) The rest of the argument to replace (15) by (27) is purely combinatorial; it is concerned only with possible groupings of the k single-marked offspring into up to four groups depending on which of the four parental chromosomes they descend from.

In both cases considered in (6) the probability that the chromosomes actually coalesce is $\frac{1}{4}$ because they must descend from the same chromosome in the same parent or from the particular chromosome in the particular parent we are following, respectively.

A5: Correlation in Coalescence Times

In this section we outline the calculations to obtain the correlation in coalescence times T₁ and T₂ of types at two loci (1 and 2). As our sample consists of two unlabeled chromosomes typed at two loci, we sometimes find it convenient to denote an unlabeled chromosome carrying ancestral segments at both loci with the symbol ⊢⊣ and chromosomes carrying ancestral segments at only one locus with the symbols ⊢ and ⊣. Loci at which types have coalesced are denoted by •− or •⊣. The states S of the unlabeled process for a sample of size two at two loci are also numbered as

• S In symbols

• 2(⊢⊣)(⊢⊣)

• 1(⊢⊣)(⊢)(⊣)

• 0(⊢)(⊢)(⊣)(⊣)

• −1 (⊣)(⊣)

• −2 (⊢))(⊢)

in which states {0, 1, 2} denote the three possible sample states, before coalescence at either loci has occurred. States {−1, −2} will be needed when deriving the variance of pairwise differences.

Let h(i): = ℙ({T₁ = T₂} | i) denote the probability of the event T₁ = T₂, when B is in state i. Excluding large offspring numbers, one readily obtains (h(i) = 0 for i ≠ {0, 1, 2, })

$$\begin{array}{l}h\left(2\right)=\frac{r+9}{2r^2+13r+9}\\ h\left(1\right)=\frac{3}{2r^2+13r+9}\\ h\left(0\right)=\frac{2}{2r^2+13r+9}.\end{array}$$ (A32)

For each i ∈ {0, 1, 2}, the expression for h(i) is the same as the one for the correlation between T₁ and T₂ when in state i, excluding large offspring numbers. The expected value w(i) = $\mathbb{E}$[T_s] of the time T_s until a coalescence event at either locus starting from state i ∈ {0, 1, 2} is, again excluding large offspring numbers,

$$\begin{array}{l}w\left(2\right)=\frac{r+9}{2\left(2r^2+13r+9\right)}+\frac{1}{2}=\frac{1}{2}\left(1+h\left(2\right)\right)\\ w\left(1\right)=\frac{3}{2\left(2r^2+13r+9\right)}+\frac{1}{2}=\frac{1}{2}\left(1+h\left(1\right)\right),\\ w\left(0\right)=\frac{1}{2r^2+13r+9}+\frac{1}{2}=\frac{1}{2}\left(1+h\left(0\right)\right),\end{array}$$

obtained by solving the recursions.

$$\begin{array}{l}w\left(2\right)=\frac{1+2rw\left(1\right)}{1+2r}\\ w\left(2\right)=\frac{1+2rw\left(1\right)}{1+2r}\\ w\left(1\right)=\frac{1+w\left(2\right)+rw\left(0\right)}{r+3}\\ w\left(0\right)=\frac{1+4w\left(1\right)}{6}.\end{array}$$

Let v(i):=${\mathbb{E}}_i\left[T_s^2\right]$ denote the expected value of $T_s^2$ when starting from state i ∈ {0, 1, 2}. One can follow Durrett (2002) to obtain the recursions

$$v\left(i\right)=\frac{2}{q_i^2}+\frac{2}{q_i}{\displaystyle \sum _{k\ne i}\frac{q_{ik}}{q_i}w\left(k\right)}+{\displaystyle \sum _{k\ne i}\frac{q_{ik}}{q_i}v\left(k\right)}$$ (A33)

in which $q_i={\displaystyle {\sum }_{k\ne i}{q}_{ik}}$ is the sum of the transition rates out of state i. To obtain (A33) let J denote the exponential waiting time until the first transition and X_J be the state of the process immediately after the first transition. The random variables J and X_J are independent. One can write

$$\begin{array}{l}\mathbb{E}\left[T_s^2|J,X_J\right]=\mathbb{E}\left[\left(T_s-J+J\right)\left(T_s-J+J\right)|J,X_J\right]\\ =\mathbb{E}\left[{\left(T_s-J\right)}^2+2J\left(T_s-J\right)+J^2|J,X_J\right]\\ =\mathbb{E}\left[{\left(T_s-J\right)}^2|J,X_J\right]+2J\mathbb{E}\left[T_s-J|X_J\right]+\mathbb{E}\left[J^2\right].\end{array}$$

Taking expectations gives (A33).

The variance $\mathbb{V}$_i[T_s] of T_s when starting in state i is given by

$$\begin{array}{l}{\mathbb{V}}_2\left[T_s\right]=\frac{r^3+31r^2/2+153r/2+81}{\left(2r+1\right)\left(r+6\right)\left(2r^2+13r+9\right)}+\frac{1}{2}-\frac{1}{4}{\left(1+h\left(2\right)\right)}^2\\ {\mathbb{V}}_1\left[T_s\right]=\frac{r+9}{\left(r+6\right)\left(2r^2+13r+9\right)}+\frac{1}{2}-\frac{1}{4}{\left(1+h\left(1\right)\right)}^2\\ {\mathbb{V}}_0\left[T_s\right]=\frac{r+8}{\left(r+6\right)\left(2r^2+13r+9\right)}+\frac{1}{2}-\frac{1}{4}{\left(1+h\left(0\right)\right)}^2.\end{array}$$

Hence, lim_r→∞ $\mathbb{V}$_i[T_s] = 1/4 for i ∈ {2, 1, 0}, and

$$\begin{array}{l}\underset{r\to 0}{\text{lim}}{\mathbb{V}}_2\left[T_s\right]=1\\ \underset{r\to 0}{\text{lim}}{\mathbb{V}}_1\left[T_s\right]=\frac{2}{9}\\ \underset{r\to 0}{\text{lim}}{\mathbb{V}}_0\left[T_s\right]=\frac{89}{324}.\end{array}$$

Denote by T_l the time until coalescence has occurred at both loci. The marginal coalescence times are exponential with rate 1, when excluding large offspring numbers. Solving the recursions

$$\begin{array}{l}{\mathbb{E}}_2\left[T_l\right]=\frac{1+2r{\mathbb{E}}_1\left[T_l\right]}{1+2r}\\ {\mathbb{E}}_1\left[T_l\right]=\frac{1+{\mathbb{E}}_2\left[T_l\right]+r{\mathbb{E}}_0\left[T_l\right]+2}{r+3}\\ {\mathbb{E}}_0\left[T_l\right]=\frac{1+4{\mathbb{E}}_1\left[T_l\right]+2}{6}\end{array}$$

yields

$$\begin{array}{l}\mathbb{E}\left[T_l^{\left(2\right)}\right]=\frac{3}{2}-\frac{r+9}{2\left(2r^2+13r+9\right)}=\frac{1}{2}\left(3-h\left(2\right)\right)\\ \mathbb{E}\left[T_l^{\left(1\right)}\right]=\frac{3}{2}-\frac{3}{2\left(2r^2+13r+9\right)}=\frac{1}{2}\left(3-h\left(1\right)\right)\\ \mathbb{E}\left[T_l^{\left(0\right)}\right]=\frac{3}{2}-\frac{1}{2r^2+13r+9}=\frac{1}{2}\left(3-h\left(0\right)\right).\end{array}$$

Applying the recursions (A33) yields the variances $\mathbb{V}$_i[T_l],

$$\begin{array}{l}{\mathbb{V}}_2\left[T_l\right]=\frac{2r^3+111r^2/4+171r/2-81/4}{{\left(2r^2+13r+9\right)}^2}+\frac{5}{4}\\ {\mathbb{V}}_1\left[T_l\right]=\frac{4r^2+17r-45/4}{{\left(2r^2+13r+9\right)}^2}+\frac{5}{4}\\ {\mathbb{V}}_0\left[T_l\right]=\frac{2r^2+7r-10}{{\left(2r^2+13r+9\right)}^2}+\frac{5}{4}\end{array}$$

with lim_r→∞ $\mathbb{V}$_i[T_l] = 5/4 for i ∈ {0, 1, 2}, and

$$\begin{array}{l}\underset{r\to 0}{\text{lim}}{\mathbb{V}}_2\left[T_l\right]=1,\\ \underset{r\to 0}{\text{lim}}{\mathbb{V}}_1\left[T_l\right]=\frac{10}{9},\\ \underset{r\to 0}{\text{lim}}{\mathbb{V}}_0\left[T_l\right]=\frac{365}{324}.\end{array}$$

Now we admit large offspring numbers, taking ɛ_N = c/N² and r_N = r/N. Ignoring the labeling of the chromosomes, the limit process has three effective sample states, depending on the number of double-marked chromosomes (⊢⊣). Denote the three sample states by

$$\begin{array}{c}(⊢⊣)\\ (⊢⊣)\end{array},$$

$$(⊢⊣)\begin{array}{c}(⊢)\\ (⊣)\end{array},$$

and

$$\begin{array}{c}(⊢)\\ (⊢)\end{array}\begin{array}{c}(⊣)\\ (⊣)\end{array},$$

in which ⊢ and ⊣ denote single-marked chromosomes. The states of the limit process are composed of single-marked individuals only and are therefore the same as those of the haploid Wright–Fisher process. By •− denote a chromosome carrying a common ancestor at one locus, and (•−•) denotes the absorbing states. The transition rates are summarized in the following table:

$$\begin{array}{ccccccc}& \begin{array}{c}(⊢⊣)\\ (⊢⊣)\end{array}& (⊢⊣)\begin{array}{c}(⊢)\\ (⊣)\end{array}& \begin{array}{c}(⊢)\\ (⊢)\end{array}\begin{array}{c}(⊣)\\ (⊣)\end{array}& \left(•-\right)\begin{array}{c}(⊣)\\ (⊣)\end{array}& \left(•-\right)(⊣)& (•-•)\\ \begin{array}{c}(⊢⊣)\\ (⊢⊣)\end{array}& & 2r& & & & 1+c\frac{{\psi }^2}{4}\\ (⊢⊣)\begin{array}{c}(⊢⊣)\\ (⊣)\end{array}& 1+c\frac{{\psi }^2}{4}\left(1-\frac{\psi }{4}\right)& & r& & 2+c\frac{{\psi }^2}{2}\left(1-\frac{\psi }{4}\right)& c\frac{{\psi }^3}{16}\\ \begin{array}{c}(⊢)\\ (⊢)\end{array}\begin{array}{c}(⊣)\\ (⊣)\end{array}& c\frac{3{\psi }^4}{32}& 4+c\left({\psi }^2-\frac{{\psi }^3}{2}-\frac{{\psi }^4}{8}\right)& & 2+c\left(\frac{{\psi }^2}{2}-\frac{{\psi }^3}{4}-\frac{{\psi }^4}{16}\right)& c\frac{{\psi }^3}{4}\left(1-\frac{\psi }{4}\right)& c\frac{{\psi }^4}{16}\\ \left(•-\right)\begin{array}{c}(⊣)\\ (⊣)\end{array}& & & & & 2+c\frac{{\psi }^2}{2}\left(1-\frac{\psi }{4}\right)& 1+c\frac{{\psi }^2}{4}\\ \left(•⊣\right)(⊣)& & & & r& & 1+c\frac{{\psi }^2}{4}.\end{array}$$

By way of example, the rate of the transition from 1 to 2 by coalescence of the chromosomes ⊢ and ⊣ is 1 + cC_3;2;1, the transition rate from 0 to 1 is 4(1 + cC_4;2;2), and the transition rate from 0 to the absorbing state [(•−• or (•−)(−•)] is c(C_4;4;0 + C_4;2;2;0).

As before, let h(i) denote the probability the two loci coalesce at the same time. One obtains limit results

$$\begin{array}{l}\underset{r\to \mathrm{\infty }}{\text{lim}}h\left(i\right)=\frac{c{\psi }^4}{32+8c{\psi }^2-c{\psi }^4},i\in \left\{0,1,2\right\}\\ \underset{c\to \mathrm{\infty }}{\text{lim}}h\left(2\right)=1\\ \underset{c\to \mathrm{\infty }}{\text{lim}}h\left(1\right)=\frac{2}{6-\psi }\\ \underset{c\to \mathrm{\infty }}{\text{lim}}h\left(0\right)=\frac{56{\psi }^2/3-272\psi +544}{\left(\psi -6\right)\left(3{\psi }^2+16\psi -48\right)}-\frac{5}{3}.\end{array}$$

The first equation in (A34) tells us that the loci remain correlated due to multiple mergers even when they are far apart on a chromosome. When the recombination rate r is quite small, one obtains

$$\begin{array}{l}\underset{r\to 0}{\text{lim}}h\left(2\right)=1\\ \underset{r\to 0}{\text{lim}}h\left(1\right)=\frac{2\left(c{\psi }^2+4\right)}{-c{\psi }^3+6c{\psi }^2+24}\\ \underset{r\to 0}{\text{lim}}h\left(0\right)=\frac{1}{3}\left(\frac{8c{\psi }^2+32}{-c{\psi }^3+6c{\psi }^2+24}+\frac{-80c{\psi }^3+208c{\psi }^2+832}{-3c{\psi }^4-16c{\psi }^3+48c{\psi }^2+192}-5\right).\end{array}$$

Let $\mathbb{E}$_i[T_s], as before, denote the time until coalescence at either locus, starting from state i. Admitting large offspring numbers, one obtains

$$\begin{array}{l}\underset{r\to \mathrm{\infty }}{\text{lim}}{\mathbb{E}}_i\left[T_s\right]=\frac{16}{32+8c{\psi }^2-c{\psi }^4},i\in \left\{0,1,2\right\},\\ \underset{c\to \mathrm{\infty }}{\text{lim}}{\mathbb{E}}_i\left[T_s\right]=0,i\in \left\{0,1,2\right\},\\ \underset{r\to 0}{\text{lim}}{\mathbb{E}}_2\left[T_s\right]=\frac{4}{c{\psi }^2+4}\\ \underset{r\to 0}{\text{lim}}{\mathbb{E}}_1\left[T_s\right]=\frac{c\left(16{\psi }^2-2{\psi }^3\right)+64}{-c^2{\psi }^5+6c^2{\psi }^4-4c{\psi }^3+48c{\psi }^2+96}\\ \underset{r\to 0}{\text{lim}}{\mathbb{E}}_0\left[T_s\right]=\frac{16}{3\left(c\left(6{\psi }^2-{\psi }^3\right)+24\right)}-\frac{4\left(\psi -8\right)}{\left(3\psi +16\right)\left(c{\psi }^2+4\right)}-\frac{32\left(39\psi -32\right)}{3\left(c\left(3{\psi }^4+16{\psi }^3-48{\psi }^2\right)-192\right)\left(3\psi +16\right)}.\end{array}$$

Let $\mathbb{E}$_i[T_l], as before, denote the expected value of the time T_l until coalescence has occurred at both loci, when starting from state i. Admitting large offspring numbers, one obtains the limits

$$\begin{array}{l}\underset{r\to \mathrm{\infty }}{\text{lim}}{\mathbb{E}}_i\left[T_l\right]=\frac{c\left(48{\psi }^2-8{\psi }^4\right)+192}{\left(c{\psi }^2+4\right)\left(-c{\psi }^4+8c{\psi }^2+32\right)},i\in \left\{0,1,2\right\},\\ \underset{c\to \mathrm{\infty }}{\text{lim}}{\mathbb{E}}_i\left[T_l\right]=0,i\in \left\{0,1,2\right\},\\ \underset{r\to 0}{\text{lim}}{\mathbb{E}}_2\left[T_l\right]=\frac{4}{c{\psi }^2+4}\\ \underset{r\to 0}{\text{lim}}{\mathbb{E}}_1\left[T_l\right]=\frac{c\left(32{\psi }^2-6{\psi }^3\right)+128}{-c^2{\psi }^5+6c^2{\psi }^4-4c{\psi }^3+48c{\psi }^2+96}\\ \underset{r\to 0}{\text{lim}}{\mathbb{E}}_0\left[T_l\right]=\frac{\left(28{\psi }^7-56{\psi }^6-800{\psi }^5+1600{\psi }^4\right)c^2+\left(-608{\psi }^4-3200{\psi }^3+12,800{\psi }^2\right)c+25,600}{a}\end{array}$$

in which

$$\begin{array}{c}a=3c^3{\psi }^9-2c^3{\psi }^8-144c^3{\psi }^7+288c^3{\psi }^6+12c^2{\psi }^7-80c^2{\psi }^6-1152c^2{\psi }^5\\ +3456c^2{\psi }^4-288c{\psi }^4-2304c{\psi }^3+13,824c{\psi }^2+18,432.\end{array}$$

Considering the variance 񡖉_i[T_s] of the time T_s when starting from state i ∈ {0, 1, 2}, and admitting large offspring numbers, one obtains

$$\begin{array}{l}\underset{r\to \mathrm{\infty }}{\text{lim}}{\mathbb{V}}_i\left[T_s\right]=\frac{256}{{\left(c\left(8{\psi }^2-{\psi }^4\right)+32\right)}^2},i\in \left\{0,1,2\right\},\\ \underset{c\to \mathrm{\infty }}{\text{lim}}{\mathbb{V}}_2\left[T_s\right]=0,i\in \left\{0,1,2\right\},\\ \underset{r\to 0}{\text{lim}}{\mathbb{V}}_2\left[T_s\right]=\frac{16}{{\left(c{\psi }^2+4\right)}^2}\\ \underset{r\to 0}{\text{lim}}{\mathbb{V}}_1\left[T_s\right]=\frac{\left(12{\psi }^6-128{\psi }^5+384{\psi }^4\right)c^2+\left(3072{\psi }^2-512{\psi }^3\right)c+6144}{{\left(c{\psi }^2+4\right)}^2{\left(-c{\psi }^3+6c{\psi }^2+24\right)}^2}.\end{array}$$

Correlations in coalescence times have been employed to quantify LD (McVean 2002), in which LD is quantified as the square of the correlation coefficient of types at two loci (Hill and Robertson 1968). A description of how one can quantify linkage disequilibrium as the square of the correlation coefficient of types at two loci can be found in Hartl and Clark (1989). Assuming a very small mutation rate, McVean (2002) related to covariances in coalescence times. Writing Cov_i(T₁, T₂) as the covariance of T₁ and T₂ when starting from state i ∈ {0, 1, 2}, McVean (2002) obtained

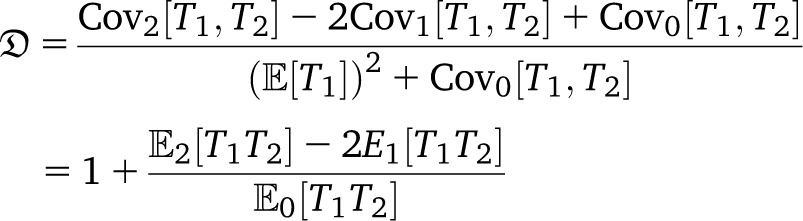in which T₁ and T₂ denote the times until coalescence at the two loci, respectively, and the covariances are conditional on the sample configurations, as indicated. Following, e.g., Durrett (2002) one can obtain the covariances under any population model. Under our population model, 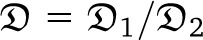, in which

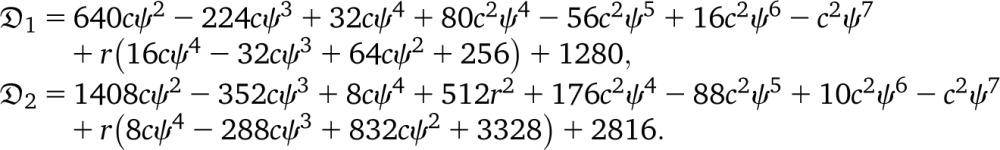One obtains the limit results

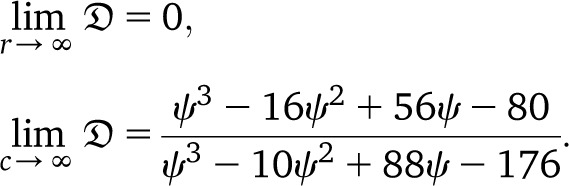A6: Correlations in Coalescence Times for Random ψ

In this section we consider the simple example of the probability measure F, evoked in relation to a random offspring distribution, taking the beta distribution with parameters ϑ and γ. The following transition rates for a sample of size two at two loci are obtained:

$$\begin{array}{ccccccc}& \begin{array}{c}\left(\mathrm{⊢⊣}\right)\\ \left(\mathrm{⊢⊣}\right)\end{array}& \left(\mathrm{⊢⊣}\right)\begin{array}{c}\left(\mathrm{⊢}\right)\\ \left(\mathrm{⊣}\right)\end{array}& \begin{array}{c}\left(\mathrm{⊢}\right)\\ \left(\mathrm{⊢}\right)\end{array}\begin{array}{c}\left(\mathrm{⊣}\right)\\ \left(\mathrm{⊣}\right)\end{array}& \left(•-\right)\begin{array}{c}\left(\mathrm{⊣}\right)\\ \left(\mathrm{⊣}\right)\end{array}& \left(•-\right)\left(\mathrm{⊣}\right)& \left(•-•\right)\\ \begin{array}{c}\left(\mathrm{⊢⊣}\right)\\ \left(\mathrm{⊢⊣}\right)\end{array}& & 2r& & & & 1\\ \left(\mathrm{⊢⊣}\right)\begin{array}{c}\left(\mathrm{⊢}\right)\\ \left(\mathrm{⊣}\right)\end{array}& \frac{\gamma +3\vartheta /4}{\vartheta +\gamma }& & r& & 2\frac{\gamma +3\vartheta /4}{\vartheta +\gamma }& \frac{\vartheta }{4\left(\vartheta +\gamma \right)}\\ \begin{array}{c}\left(\mathrm{⊢}\right)\\ \left(\mathrm{⊢}\right)\end{array}\begin{array}{c}\left(\mathrm{⊣}\right)\\ \left(\mathrm{⊣}\right)\end{array}& \frac{3}{8}\frac{\left(1+\vartheta \right)\vartheta }{\left(1+\vartheta +\gamma \right)\left(\vartheta +\gamma \right)}& \frac{4\left(1+\gamma \right)\gamma +3\vartheta \gamma +(3/2)\left(1+\vartheta \right)\vartheta }{\left(1+\vartheta +\gamma \right)\left(\vartheta +\gamma \right)}& & \frac{2\left(1+\gamma \right)\gamma +(3/2)\vartheta \gamma +(3/4)\left(1+\vartheta \right)\vartheta }{\left(1+\vartheta +\gamma \right)\left(\vartheta +\gamma \right)}& \frac{\vartheta \gamma +(3/4)\left(1+\vartheta \right)\vartheta }{\left(1+\vartheta +\gamma \right)\left(\vartheta +\gamma \right)}& \frac{\left(\vartheta +1\right)\vartheta }{4\left(\vartheta +\gamma +1\right)\left(\vartheta +\gamma \right)}\\ \left(•-\right)\begin{array}{c}\left(\mathrm{⊣}\right)\\ \left(\mathrm{⊣}\right)\end{array}& & & & & 2\frac{\gamma +3\vartheta /4}{\vartheta +\gamma }& 1\\ \left(•\mathrm{⊣}\right)\left(\mathrm{⊣}\right)& & & & r& & 1.\end{array}$$

As before, the transition rates given above can be employed to derive correlations in coalescence times. Here we consider only the probability h(i). One obtains lim_ϑ→0h(i) = lim_γ→∞h(i) and the limit results are those obtained from the usual ARG (A32).

A7: Variance of Pairwise Differences

The variance of pairwise differences between DNA sequences has been employed to estimate recombination rates in low offspring number populations (Wakeley, 1997). Let the random variable K_ij denote the number of differences between sequences i and j, with K_ii = 0. The average number π of pairwise differences for n sequences is

$$\pi =\frac{2}{n\left(n-1\right)}{\displaystyle \sum _{i<j}{K}_{ij}}.$$

Under the infinitely many sites mutation model, $\mathbb{E}$[π] = θ$\mathbb{E}$[T], in which T is the time until coalescence of two sequences. Under our model, $\mathbb{E}$[T] = 1/(1 + cψ²/4). Define the variance $S_{\pi }^2$ of pairwise differences as

$$S_{\pi }^2=\frac{2}{n\left(n-1\right)}{\displaystyle \sum _{i<j}{\left(K_{ij}-\pi \right)}^2}.$$

To obtain an estimate of the recombination rate, one needs to compute the expected value $\mathbb{E}\left[S_{\pi }^2\right]$,

$$\mathbb{E}\left[S_{\pi }^2\right]=\frac{2}{n\left(n-1\right)}{\displaystyle \sum _{i<j}\mathbb{E}\left[{\left(K_{ij}-\pi \right)}^2\right]=\mathbb{E}\left[{\left(K_{12}-\pi \right)}^2\right]}.$$

Thus, it suffices to consider $\mathbb{E}$[(K₁₂ − π)²]. Expanding, one obtains

$$\mathbb{E}\left[{\left(K_{12}-\pi \right)}^2\right]=\mathbb{E}\left[{\left(\frac{2}{n\left(n-1\right)}{\displaystyle \sum _{i<j}\left(K_{12}-K_{ij}\right)}\right)}^2\right]=\frac{4}{n^2{\left(n-1\right)}^2}{\displaystyle \sum _{i<j}{\displaystyle \sum _{\widehat{i}<\widehat{j}}\mathbb{E}\left[\left(K_{12}-K_{ij}\right)\left(K_{12}-K_{\widehat{i}\widehat{j}}\right)\right]}}.$$

Define the event $A_{ij}^{\left(\ell \right)}$ by

$$A_{ij}^{\left(\ell \right)}:=\left\{\text{sequences}i\text{and}j\text{differ at locus}\ell \right\}.$$

Assuming each sequence consists of L loci, and $1_{A_{ij}^{(\cdot )}}$ are indicator functions,

$$K_{12}-K_{ij}={\displaystyle \sum _{\ell =1}^L\left(1_{A_{12}^{\left(\ell \right)}}-1_{A_{ij}^{\left(\ell \right)}}\right)}$$

yielding, in case i = i¹ = 1, and $j=\widehat{j}=3$,

$$\begin{array}{c}\mathbb{E}\left[{\left(K_{12}-K_{13}\right)}^2\right]={\displaystyle \sum _{\ell =1}^L{\displaystyle \sum _{\widehat{\ell }=1}^L\mathbb{E}\left[\left(1_{A_{12}^{\left(\ell \right)}}-1_{A_{13}^{\left(\ell \right)}}\right)\left(1_{A_{12}^{\left(\widehat{\ell }\right)}}-1_{A_{13}^{\left(\widehat{\ell }\right)}}\right)\right]}}\\ =2{\displaystyle \sum _{\ell =1}^L{\displaystyle \sum _{\widehat{\ell }=1}^L\mathbb{P}\left(A_{12}^{\left(\ell \right)}\cap A_{12}^{\left(\widehat{\ell }\right)}\right)-\mathbb{P}\left(A_{12}^{\left(\ell \right)}\cap A_{13}^{\left(\widehat{\ell }\right)}\right)}}.\end{array}$$

In general,

$$\begin{array}{l}\mathbb{E}\left[\left(K_{12}-K_{ij}\right)\left(K_{12}-K_{\widehat{i}\widehat{j}}\right)\right]={\displaystyle \sum _{\ell =1}^L{\displaystyle \sum _{\widehat{\ell }=1}^L\mathbb{E}\left[\left(1_{A_{12}^{\left(\ell \right)}}-1_{A_{ij}^{\left(\ell \right)}}\right)\left(1_{A_{12}^{\left(\widehat{\ell }\right)}}-1_{A_{\widehat{i}\widehat{j}}^{\left(\widehat{\ell }\right)}}\right)\right]}}\\ ={\displaystyle \sum _{\ell =1}^L{\displaystyle \sum _{\widehat{\ell }=1}^L\mathbb{P}\left(A_{12}^{\left(\ell \right)}\cap A_{12}^{\left(\widehat{\ell }\right)}\right)-\mathbb{P}\left(A_{12}^{\left(\ell \right)}\cap A_{\widehat{i}\widehat{j}}^{\left(\widehat{\ell }\right)}\right)-\mathbb{P}\left(A_{12}^{\left(\widehat{\ell }\right)}\cap A_{ij}^{\left(\ell \right)}\right)+\mathbb{P}\left(A_{ij}^{\left(\ell \right)}\cap A_{\widehat{i}\widehat{j}}^{\left(\widehat{\ell }\right)}\right)}}.\end{array}$$ (A36)

Now consider the probability $\mathbb{P}\left(A_{12}^{\left(\ell \right)}\cap A_{12}^{\left(\widehat{\ell }\right)}\right)$ of the event that sequences 1 and 2 differ at both loci ℓ and $\widehat{\ell }$. Admitting mutation introduces two new states, namely the states

$$\begin{array}{c}\left(\mathrm{⊢}\right)\\ \left(\mathrm{⊢}\right)\end{array}$$

and

$$\begin{array}{c}\left(\mathrm{⊣}\right)\\ \left(\mathrm{⊣}\right)\end{array}.$$

Define

Thus, $\mathbb{P}\left(A_{12}^{\left(\ell \right)}\cap A_{12}^{\left(\widehat{\ell }\right)}\right)=g\left(2\right)$, $\mathbb{P}\left(A_{12}^{\left(\ell \right)}\cap A_{13}^{\left(\widehat{\ell }\right)}\right)=g\left(1\right)$, and $\mathbb{P}\left(A_{12}^{\left(\ell \right)}\cap A_{34}^{\left(\widehat{\ell }\right)}\right)=g\left(0\right)$, for $\ell \ne \widehat{\ell }$. Now,

$$\begin{array}{l}g\left(2\right)=\frac{{\theta }_{1}g\left(-1\right)+{\theta }_{2}g\left(-2\right)+2rg\left(1\right)}{{\theta }_1+{\theta }_2+1+c\frac{{\psi }^2}{4}+2r}\\ g\left(-1\right)=\frac{{\theta }_2}{{\theta }_2+1+c\frac{{\psi }^2}{4}}\\ g\left(-2\right)=\frac{{\theta }_1}{{\theta }_1+1+c\frac{{\psi }^2}{4}}\\ g\left(1\right)=\frac{{\theta }_{1}g\left(-1\right)+{\theta }_{2}g\left(-2\right)+rg\left(0\right)+\left(1+c{\psi }^2/4\right)g\left(2\right)}{{\theta }_1+{\theta }_2+r+3+3c({\psi }^2/4)\left(1-\psi /4\right)+c({\psi }^3/16)}\\ g\left(0\right)=\frac{{\theta }_{1}g\left(-1\right)+{\theta }_{2}g\left(-2\right)+c(3{\psi }^4/32)g\left(2\right)+\left(c\left({\psi }^2-{\psi }^3/2-{\psi }^4/8\right)+4\right)g\left(1\right)}{c(3{\psi }^4/32)+c\left({\psi }^2-{\psi }^3/2-{\psi }^4/8\right)+c\left({\psi }^2/2-{\psi }^3/4-{\psi }^4/16\right)+6+c({\psi }^3/4)\left(1-\psi /4\right)+c({\psi }^4/16)+{\theta }_1+{\theta }_2}.\end{array}$$

In view of expression (A36), one obtains

$$\begin{array}{l}\mathbb{P}\left(A_{12}^{\left(\ell \right)}\cap A_{12}^{\left(\ell \right)}\right)=\mathbb{P}\left(A_{12}^{\left(\ell \right)}\right)=\frac{{\theta }_{\ell }}{{\theta }_{\ell }+1+c{\psi }^2/4},\\ \mathbb{P}\left(A_{12}^{\left(\ell \right)}\cap A_{13}^{\left(\ell \right)}\right)=\frac{{\theta }_{\ell }}{3{\theta }_{\ell }/2+{\lambda }_3}+\frac{{\lambda }_2}{3{\theta }_{\ell }/2+{\lambda }_3}\frac{{\theta }_{\ell }}{{\theta }_{\ell }+{\lambda }_2},\\ \mathbb{P}\left(A_{12}^{\left(\ell \right)}\cap A_{34}^{\left(\ell \right)}\right)=\frac{2{\theta }_{\ell }}{2{\theta }_{\ell }+{\lambda }_4}\frac{{\theta }_{\ell }}{2{\theta }_{\ell }+{\lambda }_4}+\frac{{\lambda }_{4;2}}{2{\theta }_{\ell }+{\lambda }_4}\left(\frac{{\theta }_{\ell }/2}{3{\theta }_{\ell }/2+{\lambda }_3}+{\left(\frac{{\theta }_{\ell }/2}{3{\theta }_{\ell }/2+{\lambda }_3}\right)}^2\right).\end{array}$$ (A37)

The event $A_{12}^{\left(\ell \right)}\cap A_{34}^{\left(\ell \right)}$ (Equation A37) occurs if the first two events in the history of the four sequences are mutations on appropriate ancestral lineages or if lineages labeled 2 and 3 coalesce, followed by appropriately placed mutations.