Abstract
We couple a species range limit hypothesis with the output of an ensemble of general circulation models to project the poleward range limit of gray snapper. Using laboratory-derived thermal limits and statistical downscaling from IPCC AR4 general circulation models, we project that gray snapper will shift northwards; the magnitude of this shift is dependent on the magnitude of climate change. We also evaluate the uncertainty in our projection and find that statistical uncertainty associated with the experimentally-derived thermal limits is the largest contributor (∼ 65%) to overall quantified uncertainty. This finding argues for more experimental work aimed at understanding and parameterizing the effects of climate change and variability on marine species.
Introduction
Temperature is a dominant factor shaping the distribution of marine species [1] [2]–[3]. This overarching effect results from the influence of temperature on a number of biological processes [4] [5]–[6]. Using the terminology of Fry [7], temperature is a lethal factor, a controlling factor and a directive factor. All animals have thermal limits above and below which death is rapid. Within these limits, temperature controls a number of rate processes including gene expression, enzyme kinetics, metabolism, activity, consumption, and growth. As a directive factor, fishes respond behaviorally, metabolically, and ecologically to changes in temperature; the best examples comes from seasonal migrations, which are distributional responses related to changes in temperature [8]. Fry’s [7] factors are analogous to the concept of the ecological niche [9], defined as a multidimensional space within which a species can persist; environmental and biological conditions define the dimensions [10]. Temperature is a dominant environmental factor determining the size and distribution of the niche of many fish species [11].
The relation between temperature, a host of biological processes, and species distributions leads to the expectation that species distribution will change in response to changing temperatures [12]–[13]. Seasonal migrations by fishes are common in temperate ecosystems [14] and variation in the timing of seasonal migrations has been linked to interannual variability in the seasonal cycle of temperature [15]. Inter-annual differences in fish species distributions are also common and in many cases have been linked to interannual temperature variability [16]–[17]. Further, an increasing number of studies document directional shifts in fish distributions and increases in abundance, and link these biological changes to climate variability and change [18]–[25].
In addition to observing changes in fish distribution and abundance in the recent past, studies are developing projections of changes in fish distribution and abundance under climate change [26]. Earlier studies were based primarily on atmospheric general circulation models, an understanding of atmosphere-ocean links, and documented environmental influences on fish population; these three pieces were combined conceptually to consider the effect of climate change on various fisheries [27] [28]–[29]. More recent studies used IPCC-class general circulation models, including coupled atmospheric-ocean dynamics, combined with biological models to project changes in abundance and distribution of fishes [30]–[34]. In all instances, with either conceptual links or coupled models, climate change is predicted to change the distribution of marine fishes; the magnitude of distributional changes depends on the magnitude of climate change.
One approach to projecting changes in species range is the niche-based model. This approach develops a statistical relationship between current distribution and environmental conditions. General circulation models, which project future environmental conditions, are then used to project future species distribution [35]–[36]. As a specific example, Cheung et al. [37] [30] developed niche-based models for more than 1700 species of fish and projected changes in distribution. The model of Cheung et al. [37] [30] also included dispersal and recently has been revised to include biogeochemical processes [38]. There are other specific approaches to niche based modeling [34], but the common theme is to statistically relate current species distribution to current environmental conditions and use this statistical relationship in climate projections.
Here we develop a different type of niche model, one based on a specific hypothesis that is supported by laboratory experiments and field observations. Our study species is gray snapper (Lutjanis griseus), which is a common coastal marine species found along the southeast coast of the United States. We hypothesize that the northern range is determined by overwinter mortality of juveniles in nearshore and estuarine nursery habitats [39]. We empirically link this hypothesis to the projections of general circulation models and predict changes in the northern limit of gray snapper along the east coast of the United States. We argue that the projections are directly relevant to the numerous other species with estuarine juvenile stages along the east coast of North America. Further, we believe that the general approach is applicable globally to coastal species whose ranges are limited by overwinter mortality. Finally, we identify the main factors contributing to uncertainty in our projections and outline future research necessary to reduce this uncertainty.
Materials and Methods
Background on Species
Gray snapper (Lutjanus griseus) is a reef associated, tropical species that occurs in the central Western Atlantic, extending from Florida, through the Gulf of Mexico and along the northern and central coast of Brazil [40]. Young-of-the-year gray snapper have been reported as far north as Massachusetts [14], but adults are rarely reported north of Florida [41]. Gray snapper make diel, seasonal and ontogenetic movements between habitats [42]–[44], as well as onshore-offshore movements related to spawning [43]. However, there is no evidence of large-scale, seasonal north-south movements that would allow juveniles from north of Cape Hatteras to move south and join adult populations off of Florida. Thus, it is likely that juveniles in northern estuarine habitats are expatriates and perish as water temperatures cool in the fall and early winter [45].
Here, we use chronic and acute thermal tolerance metrics for juvenile gray snapper reported by Wuenschel et al. [39]. They quantified the chronic threshold as the cumulative degree days below 17°C survived by juveniles in the laboratory under ambient decreasing fall temperatures. The value of 17°C is the physiological threshold for growth under ad libitum ration [46]. They quantified the acute thermal threshold as the lethal minimum temperature for juveniles exposed to a constant rate of temperature decline (3°C day−1).
Overview of Modeling Approach
Our goal was to project the future northern limit of gray snapper based on the hypothesis that northern range is limited by thermal tolerance of juveniles during winter [39]. We also aimed to quantify uncertainty in our projections using different climate change scenarios, an ensemble of general circulation models, and including statistical uncertainty in the empirical relationships used to link species distribution to temperature. We develop an empirical link between air temperature and thermal tolerance metrics and then estimate the latitude where thermal tolerance will be exceeded in the future under different climate scenarios. Specifically, six steps were taken to develop the projections of species northern range and to quantify uncertainty and these are explained in detail below. The notation used for variables and equations through these six steps are summarized in Table 1.
Table 1. Summary of the notation used for variables and equations.
| Symbol | Variable | Description |
| i | Climate model | 14 climate models (see Table 2) |
| e | Estuary | 12 estuaries (see Figure 1) |
| y | Year | |
| k | Climate scenario | 3 scenarios: commitment, B1, and A1B scenarios |
| t | Time periods | 3 time periods: 1980–2000, 2040–2060, and 2080–2100 |
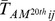
|
Mean minimum monthly winter air temperature for estuary j and climate model i estimate from the 20th century model runs | |
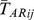
|
Mean minimum monthly winter air temperature for estuary j and climate model j from the NCEP/NCAR reanalysis | |
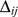
|
Mean bias correction for each climate model and estuary | |
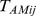
|
Modeled mean minimum monthly winter air temperature for estuary j estimated by climate model i in the future | |
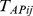
|
Projected (modeled – bias correction) minimum monthly winter air temperature for estuary j estimated by climate model i in the future | |
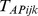
|
Projected minimum monthly mean air temperature from model i and for estuary j and climate scenario k | |
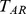
|
Minimum mean monthly winter air temperature from the NCEP/NCAR reanalysis combining data across estuaries and years | NCEP/NCAR grid cells matched to estuary locations. Only used continental grid cells in the comparison of NCEP/NCAR and estuarine temperatures |
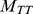
|
Thermal tolerance metrics for gray snapper including degree days <17°C and minimum daily winter temperature combining data across estuariesand years | data from daily temperature measurements in 12 estuaries over approximately 13 years [39] |
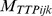
|
Projected thermal tolerance metrics for estuary j, model i, and climate scenario k | |
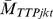
|
Ensemble average projection of thermal tolerance metrics for estuary j, climate scenario k and time period t | Ensemble average developed by averaging the projections of all 14 climate models for the given estuary, climate scenario, and time period |
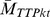
|
Ensemble average projection of thermal tolerance metrics for climate scenario k and time period t; data from each estuary is used to develop a predictive relationship for latitude (Lat) | |
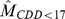
|
Estimated thermal tolerance for gray snapper relative to the cumulative degree days <17°C metric | [39] |
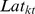
|
Latitude of a given thermal tolerance value for climate scenario k and time period t | |
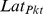
|
Projected latitude of northern range limit for climate scenario k and time period t | |
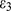
|
Unexplained error associated with the statistical relationship between 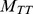 and and 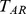 (eq. 3) (eq. 3) |
|
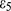
|
Unexplained error associated with the statistical relationship between and 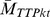 and and 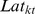 (eq. 5) (eq. 5) |
Step 1 General Circulation Models and Mean Bias Correction
The Fourth Assessment Report (AR4) of the Intergovernmental Panel on Climate Change (IPCC) [46] included simulations from 23 different GCMs run with standardized CO2 emission scenarios. Here we use 14 of these models (Table 2) and three emission scenarios: the commitment scenario, in which atmospheric CO2 is fixed at 350 ppm through the 21st century; the B1 scenario, in which CO2 increases to 550 ppm by the end of the 21st century; and the A1B scenario, in which CO2 increases to 720 ppm by the end of the 21st century. The 14 GCMs were chosen because the results are publically available for the three climate scenarios (commit, B1, and A1B) and for a retrospective analysis of the 20th century (seen Table 2). Also, the models and scenarios included simulations through 2100. Some of the models have more than one run for one or more of the climate scenarios; only one run was included for each model and scenario to ensure that the models were treated similarly.
Table 2. List of general circulation models (GCMs) used in this study and their associated modeling centers.
| Modeling Center | GCM |
| Bjerknes Centre for Climate Research, Norway | BCM2.0 |
| Canadian Centre for Climate Modeling and Analysis, Canada | CGCM3(T47 resolution) |
| Centre National de Recherches Meteorologiques, France | CM3 |
| Australia's Commonwealth Scientific and Industrial Research Organization, Australia | Mk3.0 |
| Meteorological Institute, University of Bonn, GermanyMeteorological Research Institute of KMA, KoreaModel and Data Group at MPI-M, Germany | ECHO-G |
| Institute of Atmospheric Physics, China | FGOALS-g1.0 |
| Geophysical Fluid Dynamics Laboratory, USA | CM2.1 |
| Goddard Institute for Space Studies, USA | E-R |
| Institute for Numerical Mathematics, Russia | CM3.0 |
| Institut Pierre Simon Laplace, France | CM4 |
| National Institute for Environmental Studies, Japan | MIROC3.2 medres |
| Meteorological Research Institute, Japan | CGCM2.3.2 |
| National Centre for Atmospheric Research, USA | CCSM3 |
| UK Met. Office, United Kingdom | HadCM3 |
Three CO2 emission scenarios from 14 GCMs were used. Data were obtained from the Model and Data Group (M&D) at the Max-Planck-Institute for Meteorology (http://www.mad.zmaw.de/IPCC_DDC/html/SRES_AR4/index.html).
A given climate model may have systematic errors that result in an overall bias [26]. To correct for this bias, we compared air temperatures from the models’ 20th century runs to observed air temperatures during the overlapping time period. For air temperature observations, we used the National Centers for Environmental Prediction (NCEP) and the National Center for Atmospheric Research (NCAR) reanalysis (http://www.esrl.noaa.gov/psd/data/gridded/data.ncep.reanalysis.derived.surface.html) [47]. This product combines observations and an atmospheric model to produce an even grid of atmospheric variables, in our case monthly mean surface air temperature with a spatial resolution of 2.5° latitude by 2.5° longitude.
Our goal was to forecast thermal tolerance criteria at 12 estuaries along the east coast of the United States (see below). For each estuary (j), the closest NCEP/NCAR grid cells were identified and these were then matched to the closest grid cell in each climate model (i). Minimum mean monthly winter air temperatures (December through March) were calculated for each year in the 20th century model runs and in the NCEP reanalysis. Means from overlapping years (1948–2000, 1948–2001, or 1948–2005 depending on the climate model) were then calculated for the yearly mean minimum monthly winter temperature for the 20th century model runs (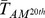 ) and for the NCEP/NCAR reanalysis (
) and for the NCEP/NCAR reanalysis (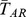 ) minimum over the overlapping years. The difference between these two means was defined as the mean bias correction (Δij) for the specific climate model (i) and estuary (j).
) minimum over the overlapping years. The difference between these two means was defined as the mean bias correction (Δij) for the specific climate model (i) and estuary (j).
| (1) |
This value (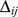 ) was used to adjust the air temperatures from the climate models (
) was used to adjust the air temperatures from the climate models (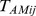 ) to correct for systematic model bias and to estimate the projected air temperature (
) to correct for systematic model bias and to estimate the projected air temperature (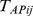 ) in each model (i) for each estuary (j).
) in each model (i) for each estuary (j).
| (2) |
Understanding the cause of systematic model bias is an active area of research [48] [49–26]. A key assumption when applying a simple bias correction is that the bias is independent of the projected change [50]. We evaluated this assumption by calculating the correlation between bias and projected change for each model (i), climate scenario (k), and estuary (j). There were no significant correlations between bias and air temperature projections. There were negative trends between bias and latitude, but these trends were significant for only one of the fourteen climate models. These analyses indicate that the bias corrections are appropriate as a first order approach to remove systemic model bias from the long-term projections.
Step 2 Relationship between Winter Water and Air Temperatures
The next step was to develop a statistical model to predict estuarine thermal tolerance thresholds from minimum monthly mean winter air temperature. The thermal tolerance metrics were cumulative degree days below 17°C and minimum daily winter temperature; these are the thermal tolerance criteria developed by Wuenschel et al. [39]. The winter air temperature metric was minimum mean monthly winter temperature. This metric links estuarine-specific water temperature to large-scale temperature forcing over the scale of the eastern United States [51]–[54] [39] and matches the mechanistic hypothesis of gray snapper range limit [39] with the output of climate models. We used air temperatures from climate models because there is a close association between air temperature and water temperature in shallow estuarine systems [51] [53]–[55]. Further, the scale of the AR4-class climate models is typically 1–2° latitude in the ocean and 2–3° latitude in the atmosphere [26], which is too course to resolve most of the estuarine systems along the east coast of the U.S. To develop the statistical relationship between thermal tolerance metrics and air temperatures, we require daily records of estuarine water temperature (to estimate the thermal tolerance metrics) and annual records of minimum monthly mean winter air temperature.
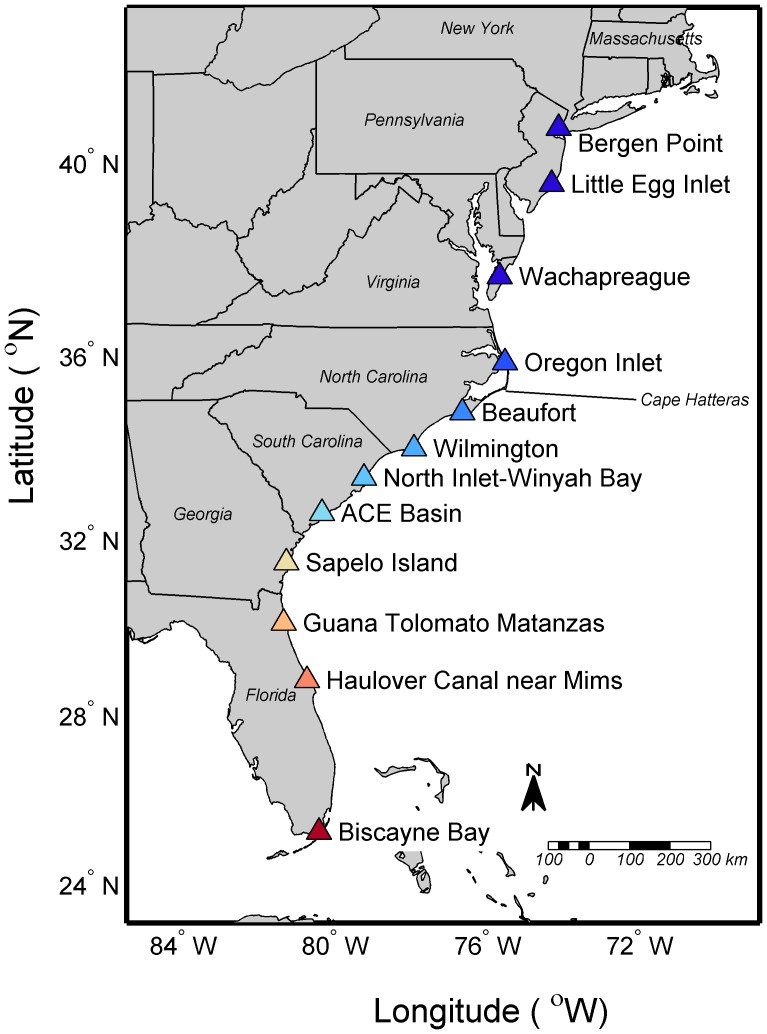
Daily estuarine water temperatures were obtained from 12 sites along the east coast of the United States from Florida to New Jersey (Figure 1). There are numerous records of coastal and estuarine water temperatures along the east coast of the United States [56], [57]. We choose locations based on several criteria: geographic coverage, estuarine location (as opposed to coastal), ongoing data collection, and more than 10 years of data collection. The chosen locations are operated by several organizations and overall have an average of 13 years of daily water temperature observations. Two metrics were calculated from the daily temperature records for each estuary: cumulative degree days below 17°C and minimum daily winter temperature.
Figure 1. Map showing estuarine locations from which observed temperature records were used and for which projections were made for winter estuarine water temperatures.
Color-coding for sites is based on latitude (red more southern, blue more northern). Full list of sites is provided in [39] http://dx.doi.org/10.1016/j.jembe.2012.08.012.
Minimum monthly mean winter air temperatures were derived from the NCEP/NCAR reanalysis (see above). For each estuary, the closest continental NCEP/NCAR grid cell was identified. Winter air temperatures over the ocean were warmer than over land and thus we only used grid cells over land to have a consistent comparison between air and estuarine temperatures. In addition, some of the estuaries were proximate to one NCEP/NCAR grid cell, whereas other estuaries were in between grid cells. In this latter case, air temperature values from the two proximate grid cells were averaged for comparison to the estuarine thermal tolerance metrics. After matching the NCEP grid to the location of the estuaries, minimum mean monthly winter temperature (December through March) was extracted from the NCEP/NCAR reanalysis for each of the 12 estuaries.
Annual thermal tolerance metrics (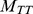 ) were compared to annual minimum mean monthly winter air temperatures from the NCEP/NCAR reanalysis (
) were compared to annual minimum mean monthly winter air temperatures from the NCEP/NCAR reanalysis (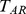 ) combining data across all estuaries (j) and years with data (y) with the goal of developing a predictive equation that could be used to project estuarine thermal tolerance metrics from air temperatures and ultimately from climate models. Numerous empirical formulations were evaluated including least squares regression and generalized linear models with Gaussian and Gamma distributions. We determined that the best model was a second order polynomial least squares regression with a square-root transformation of the thermal tolerance metrics:
) combining data across all estuaries (j) and years with data (y) with the goal of developing a predictive equation that could be used to project estuarine thermal tolerance metrics from air temperatures and ultimately from climate models. Numerous empirical formulations were evaluated including least squares regression and generalized linear models with Gaussian and Gamma distributions. We determined that the best model was a second order polynomial least squares regression with a square-root transformation of the thermal tolerance metrics:
| (3) |
where a3, b3, and c3 are parameters estimated with linear least squares regression and 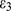 is the unexplained error associated with the regression (eq. 3). The square root transformation addresses the issue that the cumulative degree thermal tolerance metric could not go below zero and the second order polynomial addresses additional nonlinear aspects of the relationship between air temperatures and estuarine water temperatures across estuarine locations.
is the unexplained error associated with the regression (eq. 3). The square root transformation addresses the issue that the cumulative degree thermal tolerance metric could not go below zero and the second order polynomial addresses additional nonlinear aspects of the relationship between air temperatures and estuarine water temperatures across estuarine locations.
Step 3 Thermal Tolerance Metric Projections
The predictive equation developed above (eq. 3) was then used in combination with the mean bias correction (eq. 2) to project the two thermal tolerance metrics 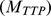 from the projected minimum mean monthly air temperature
from the projected minimum mean monthly air temperature 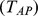 for each climate model (i), estuary (j), and climate scenario (k):
for each climate model (i), estuary (j), and climate scenario (k):
| (4) |
Thermal tolerance metrics were forecast from 2010 to 2100 for 12 estuaries along the U.S. east coast.
Step 4 Relationship between Projected Winter Water Temperature and Latitude
Once estuarine thermal tolerance metrics were projected with the climate models, a statistical relationship was derived between the projected metrics and latitude (Lat). First, the projected thermal tolerance metrics (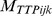 ) were averaged over three time periods (t): 1980–2000, 2040–2060, and 2080–2100. This averaging is necessary because climate models do not produce annual predictions. Due to climate variability, a given year in the model is not expected to match that in nature. Averaging over 20 years reduces the climate variability signal and allows the climate change signal to be examined [26]. The 1980–2000 period was chosen because these years were included in all the 20th century model runs. Second, for each estuary (j), climate scenario (k), and time period (t), the projected thermal tolerance metrics were averaged over the 14 climate models (i), which resulted in ensemble average projected thermal tolerance metrics (
) were averaged over three time periods (t): 1980–2000, 2040–2060, and 2080–2100. This averaging is necessary because climate models do not produce annual predictions. Due to climate variability, a given year in the model is not expected to match that in nature. Averaging over 20 years reduces the climate variability signal and allows the climate change signal to be examined [26]. The 1980–2000 period was chosen because these years were included in all the 20th century model runs. Second, for each estuary (j), climate scenario (k), and time period (t), the projected thermal tolerance metrics were averaged over the 14 climate models (i), which resulted in ensemble average projected thermal tolerance metrics (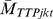 ) for each estuary, scenario, and time period.
) for each estuary, scenario, and time period.
We then developed the statistical relationship between latitude (Lat) and the ensemble averaged thermal tolerance metrics (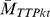 ) using the data from the different estuaries. Again, numerous empirical formulations were evaluated including least squares regression and generalized linear models with Gaussian and Gamma distributions. We determined that the best model was a first order polynomial least squares regression with a square-root transformation:
) using the data from the different estuaries. Again, numerous empirical formulations were evaluated including least squares regression and generalized linear models with Gaussian and Gamma distributions. We determined that the best model was a first order polynomial least squares regression with a square-root transformation:
| (5) |
where a5 and b5 are parameters estimated with linear least squares regression and 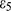 is the unexplained error associated with the regression (eq. 5).
is the unexplained error associated with the regression (eq. 5).
The statistical models represented by equation 5 are generalizations of the projected changes in the latitudinal gradient of thermal tolerances. Changes in latitude with climate change can then be calculated for any specific thermal tolerance value for either metric.
Step 5 Projections of Northern Range Limits
Cumulative degree days below 17°C (CDD <17) was the thermal criteria most closely linked to northern range limit in gray snapper [39] and thus this metric was used to project changes in range of gray snapper. The specific thermal tolerance of gray snapper (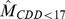 = 210.7±122 [95% confidence interval] days below 17°C) was substituted into regression equation (5) and used to estimate latitude at the thermal criteria for the three climate scenarios (commit, B1, and A1B) and the three time periods (1980–2000, 2040–2060, and 2080–2100).
= 210.7±122 [95% confidence interval] days below 17°C) was substituted into regression equation (5) and used to estimate latitude at the thermal criteria for the three climate scenarios (commit, B1, and A1B) and the three time periods (1980–2000, 2040–2060, and 2080–2100).
| (6) |
Rates of change were then calculated (km yr−1) from the current period to compare with other studies.
Step 6 Assessing Uncertainty
Planque et al. [58] reviewed the incorporation of uncertainty into projections of species shifts as a response to climate change. They identified seven types of uncertainty: observational process, conceptual model formulation, numerical model formulation, parameter estimates, model evaluation, spatial and temporal scales, and adaptability of living systems. Within this construct, we focus our analysis of uncertainly on the climate model formulations and parameter estimate uncertainty. We treat the other sources of uncertainty in the discussion. Overall, we assess which aspects of our approach created the most uncertainty as a way to guide future research and to develop more precise projections.
To consider the effect of climate model formulation, emission scenario, statistical downscaling, and parameter estimate uncertainty, we performed the above 5 steps for each climate model, scenario, and time period recalculating equations 3, 5, and 6 and incorporating the error terms ε3 and ε 5 and the uncertainty in the thermal tolerance estimates (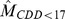 ). For each model (n = 14), scenario (n = 3), and time period (n = 3), 100 iterations of equations 3, 5, and 6 were performed adding the error terms from a normal probability distribution with a μ = 0 and σ = (model mean squared error)½ (for ε3 and ε5) or σ = thermal estimate standard error (for error on
). For each model (n = 14), scenario (n = 3), and time period (n = 3), 100 iterations of equations 3, 5, and 6 were performed adding the error terms from a normal probability distribution with a μ = 0 and σ = (model mean squared error)½ (for ε3 and ε5) or σ = thermal estimate standard error (for error on 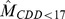 ). This resulted in 12,600 estimates of the latitude of northern range. These results were analyzed using a general linear model with model, scenario, and time period as categorical variables and the error values as continuous variables. The goal was to determine which factor was responsible for the greatest amount of variability (e.g., uncertainty) in the estimate of northern range. The sums of squares were used to assign a proportion of variance to each factor and these proportions were ranked.
). This resulted in 12,600 estimates of the latitude of northern range. These results were analyzed using a general linear model with model, scenario, and time period as categorical variables and the error values as continuous variables. The goal was to determine which factor was responsible for the greatest amount of variability (e.g., uncertainty) in the estimate of northern range. The sums of squares were used to assign a proportion of variance to each factor and these proportions were ranked.
Results
Relationship between Winter Water and Air Temperature
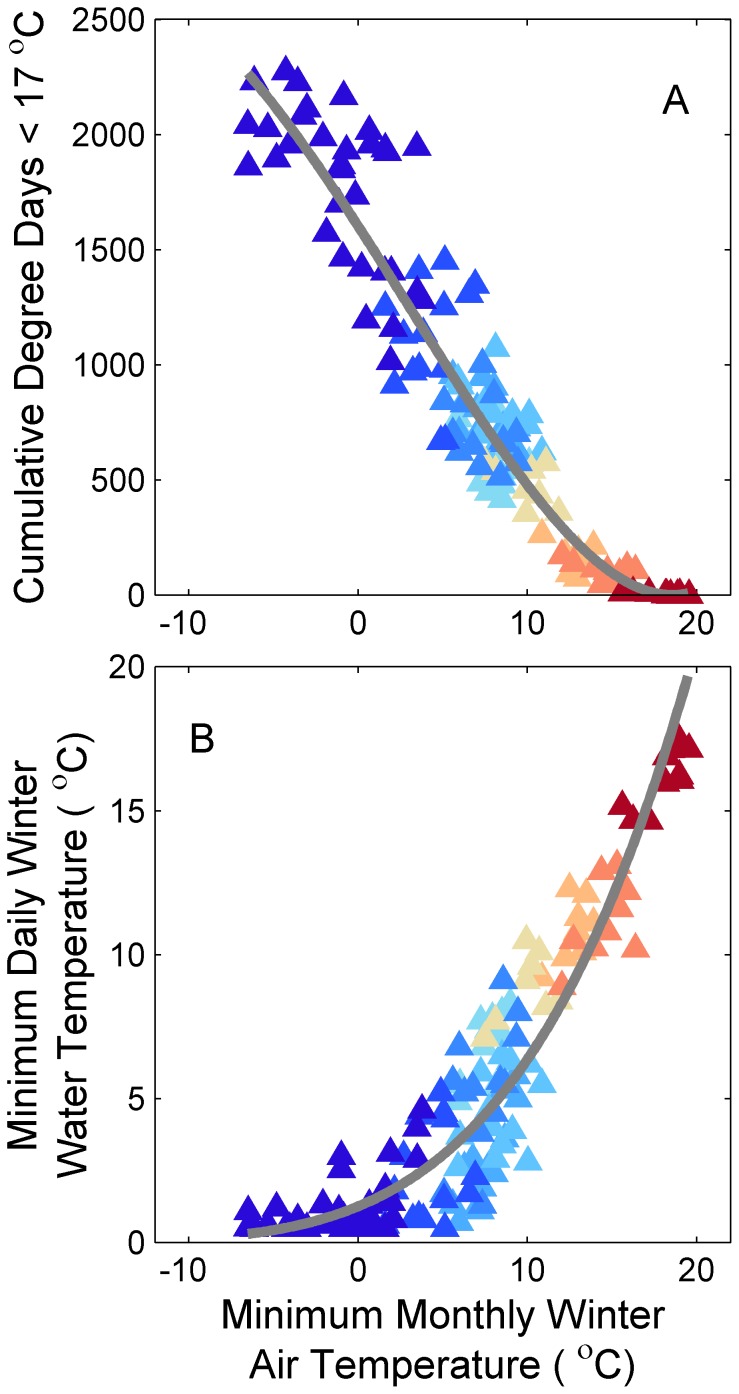
Over the scale of the east coast of the United States, thermal tolerance metrics could be predicted from air temperatures (Figure 2). Most of the variability in cumulative degree days <17°C could be predicted by minimum mean monthly air temperature (r2 = 0.92; Figure 2A). Similarly, most of the variability in minimum daily winter temperature could be predicted by minimum mean monthly air temperature (r2 = 0.83; Figure 2B). The resulting predictive equations were then used to estimate thermal tolerance metrics from monthly winter air temperatures derived from the climate models (eq. 4).
Figure 2. Relations between winter water temperature and air temperature in 12 estuaries along the east coast of the United States.
Points represent winter temperatures in a given year in a given estuary. Estuarine water temperatures are expressed as (A) cumulative degree days <17°C and (B) minimum daily winter temperature (Dec-Mar). Air temperature is expressed as minimum monthly mean winter temperature. Gray line represents the least squares regression fit based on eq. 3. Color of the symbol represents the latitude of the source estuary for the water temperature data (see Figure 1).
Winter Water Temperature Projections
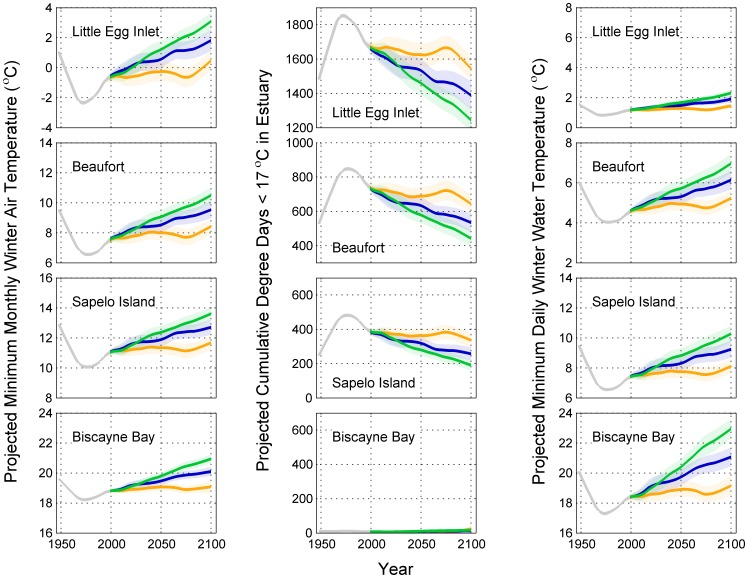
Climate model projections indicated increasing minimum mean monthly winter air temperatures over the course of the 21st century (Figure 3, column 1). The magnitude of warming increased with latitude and depended on the climate scenario, with greater atmospheric CO2 resulting in greater warming.
Figure 3. Projections of winter temperature metrics at four estuaries along the east coast of the United States (metrics: minimum mean monthly winter air temperature, cumulative degree days <17°C, and minimum daily estuarine water temperature).
Gray line represents observations, orange line represents projections under the commit scenario (350 ppm CO2 by 2100), blue line represents projections under the B1 scenario (550 ppm CO2 by 2100), and the green line represents projections under the A1B scenario (720 ppm CO2 by 2100). A 40 year LOWESS filter (tension = 0.25) of the mean annual projections from 14 general circulation models is displayed (see Table 1). Shading represents standard error around mean. Observed and projected thermal tolerance metrics were blended over the period 2001 to 2010; the blended value in 2005 is 0.5 * observed +0.5 * projected.
Cumulative degree days <17°C were projected to decrease through the 21st century in all estuaries (Figure 3, column 2). The magnitude of decrease increased with latitude and depended on climate scenario, with a greater decrease occurring at higher atmospheric CO2 concentrations.
Minimum estuarine daily temperatures were projected to increase through the 21st century in all estuaries (Figure 3, column 3). The magnitude of change decreased with increasing latitude owing to the non-linear relationship with air temperature (see Figure 2). Further, the magnitude of change increased with increasing atmospheric CO2.
Relationship between Projected Winter Water Temperature and Latitude
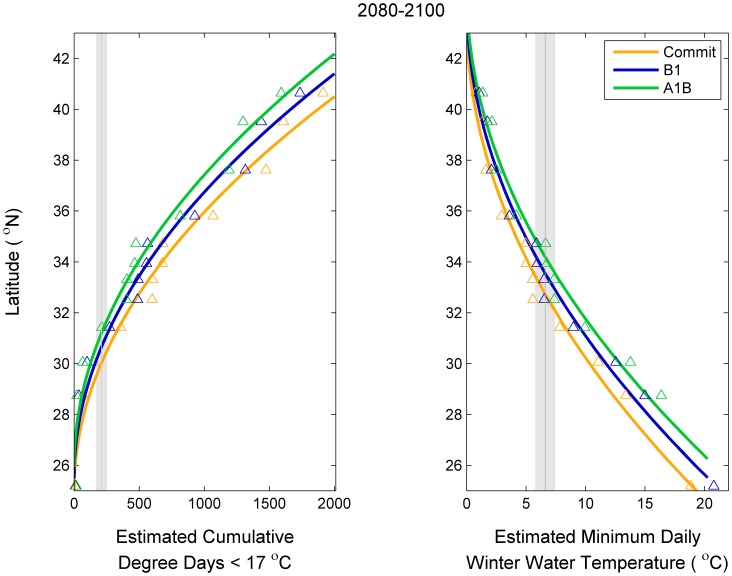
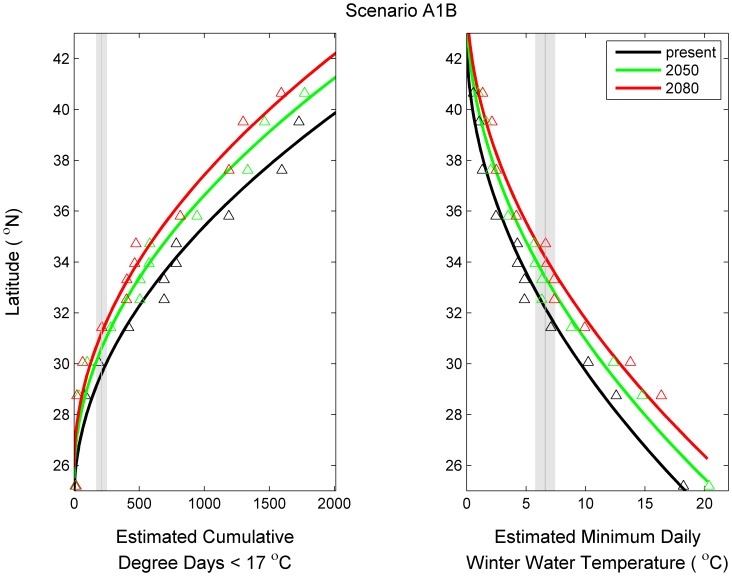
Not surprisingly, latitude was well estimated using the two winter water temperature metrics: cumulative degree days <17°C and minimum daily winter temperatures (Figure 4 and 5). The linear models using the square root of thermal tolerance metrics as independent variables (eq. 5) explained on average 97 and 98% across the climate scenarios (commit, B1, and A1B) and time periods (1980–2000, 2040–2060, and 2080–2100). The latitude of a given value of cumulative degree days <17°C increased as the amount of CO2 in the atmosphere increased (Figure 4A) and increased into the future (Figure 5A). The same pattern was observed for daily minimum winter temperature. The relation between thermal temperature metrics and latitude may not be continuous; there may be breaks associated with biogeographic breaks (e.g., Cape Canaveral and Cape Hatteras). However, more complex models did not statistically improve the fit and thus, the relatively simple empirical relationship (eq. 5) was used here.
Figure 4. Estimated latitude of thermal tolerance metrics in 2080–2100 under three climate change emission scenarios.
The gray line and shading represent the thermal tolerance metric and 95% confidence intervals for gray snapper juveniles as determined from an experimental study [39].
Figure 5. Estimated latitude of thermal tolerance metrics under the A1B emission scenario at three time periods.
The gray line and shading represent the thermal tolerance metric and 95% confidence intervals for gray snapper juveniles as determined from an experimental study [39].
Projections of Northern Range Limits
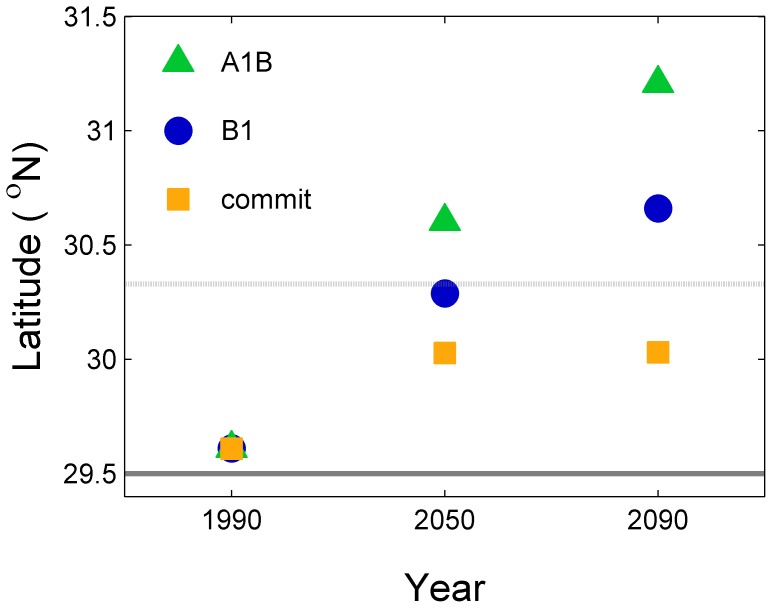
Gray snapper range was projected to move northward through time and with increased CO2 emissions (Figure 6). The greatest projected northern range was for the period 2080–2100 and the A1B scenario. Under the commit scenario, there is an initial northward movement (0.8 km yr−1), but then this movement ceases. Estimated rate of northward shifts were 1.0–1.3 km yr−1 under the B1 scenario and 1.7–1.8 km yr−1 under the A1B scenario.
Figure 6. Estimated northern range limit of gray snapper during three time periods and under three emission scenarios.
The heavy and light gray lines represent the estimate of current northern range limit and standard error as determined from field observations [39].
Assessing Uncertainty
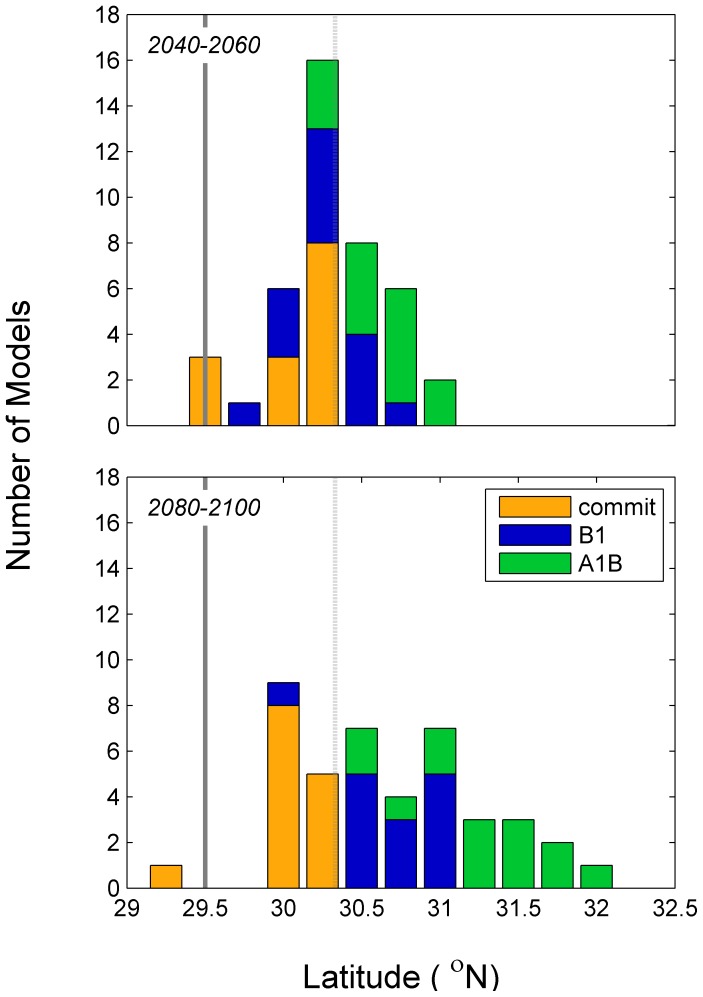
Most of the variance in the estimate of northern latitude resulted from uncertainty in the thermal tolerance estimate (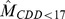 ) (Table 3; i.e., the variance in CDD <17°C thermal tolerance metric). Uncertainty resulting from the relationship between thermal tolerance and latitude (εe5) also contributed a large amount of variance. A relatively small amount of uncertainty was attributed to the climate models themselves; under scenarios B1 and A1B, all individual models projected a poleward range extension (Figure 7). If each scenario and time period is analyzed separately, the average variance attributable to climate models is <0.1%. Thus, a majority of uncertainly is related to the biological parameterization of thermal tolerance (
) (Table 3; i.e., the variance in CDD <17°C thermal tolerance metric). Uncertainty resulting from the relationship between thermal tolerance and latitude (εe5) also contributed a large amount of variance. A relatively small amount of uncertainty was attributed to the climate models themselves; under scenarios B1 and A1B, all individual models projected a poleward range extension (Figure 7). If each scenario and time period is analyzed separately, the average variance attributable to climate models is <0.1%. Thus, a majority of uncertainly is related to the biological parameterization of thermal tolerance (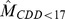 ) and the estimate of the spatial distribution of the thermal tolerance metrics (eq. 5). There is relatively little uncertainty related to differences among the 14 climate models. Further, there is relatively little uncertainty associated with the method of statistical downscaling (eq. 3).
) and the estimate of the spatial distribution of the thermal tolerance metrics (eq. 5). There is relatively little uncertainty related to differences among the 14 climate models. Further, there is relatively little uncertainty associated with the method of statistical downscaling (eq. 3).
Table 3. Percent variance in estimate of gray snapper northern range attributable to different factors.
| Parameter | Percent Variance |
| Thermal Tolerance Estimate | 65.3 |
| Mapping to Latitude | 20.8 |
| Unexplained Error | 6.0 |
| Time Period | 5.6 |
| Scenario | 1.8 |
| Model | 0.5 |
| Statistical Downscaling | 0.0 |
Value calculated by dividing sums of squares from a general linear model by the total error.
Figure 7. Estimated northern range limit of gray snapper during two time periods and under three emission scenarios.
Results for each of the 14 GCMs are provided to present the range of projections that compose the ensemble. The heavy and light gray lines represent the estimate of current northern range limit and standard error as determined from field observations [39].
Discussion
Projected Poleward Movement
The modeling conducted here projects that adult gray snapper distribution will move northwards over this century. The rate of movement is dependent on CO2 emissions, with greater northward shifts projected with increasing CO2 emissions. Under the ensemble average and A1B emission scenario, gray snapper are estimated to be distributed half way up the coast of Georgia by 2100 (31.2° N); the most extreme climate model projections estimates that gray snapper will be found up to the Georgia-South Carolina border by the end of the century (31.9° N) (Figure 7).
The rates of poleward movement estimated in our study are broadly consistent with observed and projected changes from other studies. Nye et al. [22] estimated an annual change of 1.5 km yr−1 in the center of biomass of fishes on the northeast U.S. continental shelf. These rates of change are lower than the 19 km yr−1 observed for marine species in general [59] and lower than the 4.5–5.9 km yr−1 projected for marine fishes globally from 2000–2050 [30]. These differences may result from many factors. 1) Our estimates are species specific whereas the estimates cited above are global averages over more than a 1000 fish species and more than 50 marine taxa respectively [30] [59]. 2) Our estimates are regionally specific (east coast of the United States) whereas the estimates cited above are again global in nature [37] [59]. Regional differences in the effect of climate change on marine fishes have been found [37]. Our results also demonstrate regional differences; the decrease in cumulative degree days <17°C is greater further towards the pole (Figure 4 and 5) suggesting greater range extensions for species that are more tolerant of colder winters. 3) The link between air temperature and estuarine temperature may mediate the effect of climate change on coastal fishes. Similar projections for land animals indicate a 0.6 km y−1 rate of change [13]. Thus, changes in the ocean may be greater than changes over land [30]; changes in estuarine and coastal systems may be intermediate between the land and ocean. There are other possible explanations, some of which are discussed in more detail below. The overarching conclusion of these studies and other observations are consistent across species and systems; marine species are shifting poleward and will continue to shift poleward in the future. The extent of the poleward shift is dependent in large part on the future of CO2 emissions.
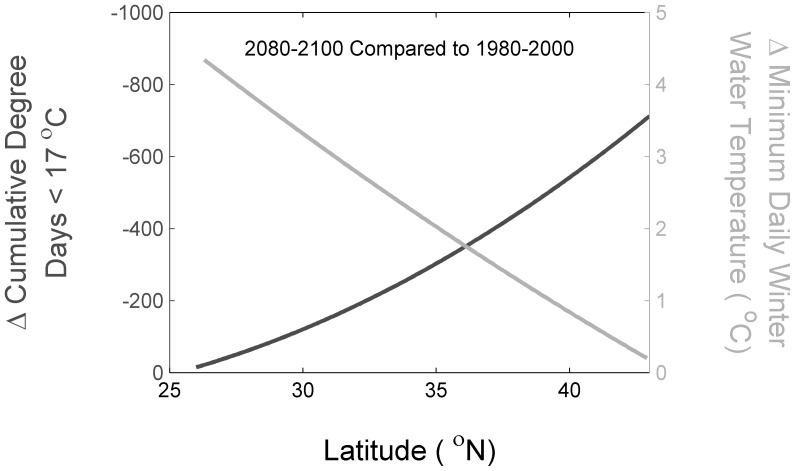
Our results suggest a differential rate of winter estuarine warming over the U.S. east coast. Many of the climate models used in our ensemble project increased warming with increased latitude. This is consistent with historic ocean observations, with a greater rate of warming in the northeast U.S. shelf compared to the southeast U.S. shelf [56]. This result is also consistent with the idea of differential warming between the northeast and southeast United States [60]. These results suggest that for species at the northern edge of their range, the more cold-tolerant the species is, the more habitat that will open along the east coast of the U.S. This ‘opening of thermal habitat,’ however, is simply dependent on degree days and does not consider other aspects of habitat. The rate of change in cumulative degree days <17°C is higher at higher latitudes whereas the rate of change of minimum daily temperature is higher at lower latitudes (Figure 8). The implication is at a given latitude, the importance of chronic versus acute thermal tolerances could switch at some point in the future. Thus, there is the potential for a switch in the dominant factor affecting the northern range in gray snapper; currently cumulative degree days appear to be limiting, but at some point in the future minimum daily temperature may become more important. These results emphasize the need to better understand both the physiology and ecology of thermal tolerance as well as the physics of temperature extremes [61]. Higher latitude areas are projected to warm faster, particularly in the northern hemisphere [62], but whether our results are applicable to other temperate marine systems remains unclear.
Figure 8. Change in projected cumulative degree days <17°C (dark line) and change in minimum daily temperature (gray line) by latitude under the A1B scenario comparing 1980–2000 and 2080–2100.
One novel aspect of this study is the formal assessment of uncertainty in the climate projection of northern range of gray snapper. The full range of factors contributing to uncertainty identified by Planque et al. [58] was not examined, but a number of important factors were considered. Limitations of the observation methodology (observational uncertainty) were not included. A number of observations were used to develop the projections presented here and uncertainty in these observations was not included in the projection model: for example, estuarine temperatures, diver-based adult censuses, and cold-tolerance experiments with juveniles. We are making the implicit assumption that measurement error makes only a small contribution to the overall uncertainty in our projections.
Uncertainty in the conceptual model also was not examined, but a formal hypothesis was presented that can be tested in the future. We hypothesize that northern range of gray snapper is determined by overwinter survival of young-of-the-year related to thermal tolerance. We did not identify a specific mechanism of overwinter mortality (e.g., predation vs. starvation vs. physiology). Our conceptual model is more specific than general niche-based models, in that we identified a specific ontogenetic stage and season in which distribution is determined and we developed specific parameters measuring the physiological boundary of wintertime niche for juvenile gray snapper. It would be interesting in the future to compare projections among a number of niche-based models including the more general models [30] and our more specific model to begin to understand conceptual model uncertainty. It would also be useful be develop this approach using bioenergetic models that would capture the physiological tradeoffs of metabolism, growth, and activity [63].
Uncertainty in the numerical model formulation was evaluated through the use of 14 general circulation models (GCM’s). Each general circulation model simulates the ocean-atmosphere-land system. Overall these models are similar, but differ in numerous details and this ensemble-based approach is becoming the norm in climate projections of living marine resources [26]. We used a bias correction, which is a simple approach. We did not evaluate uncertainty in the model specific bias term but our use of an ensemble of models includes the uncertainty in the bias correction between models. Additionally, other downscaling approaches could be used; we did not evaluate the uncertainty introduced by our choice of using a simple bias correction relative to other techniques. Future studies could examine the magnitude of uncertainty related to these issues. In our evaluation, very little of the overall uncertainty was attributed to the specific GCM and all GCM’s projected an increase in the poleward extent of gray snapper (Figure 7). Thus, we conclude that numerical model formulation contributes only a minimal amount of uncertainty in our specific case. This result is qualitatively similar to Hare et al. [32] in which 14 GCM’s all projected a similar response of Atlantic croaker to climate change.
The dominant source of uncertainty that we were able to evaluate was parameter uncertainty. We included three CO2 emission scenarios, each of which contributes a suite of parameters to the GCM’s. We also included uncertainty in our mapping of temperature on latitude and in the thermal limit of gray snapper. Parameter uncertainty is relatively straightforward to include in climate projections since it is often obtained from the statistical error of a parameter estimate [58]. Parameter uncertainty in the estimate of thermal tolerance was the dominant source of uncertainty (Table 3), indicating the need to improve parameter estimates for inclusion in coupled biology-climate models.
Uncertainty in the performance of projection models can result in the uncertain identification of the “best” predictive model [58]. Validation of independent datasets is likely the best form of model evaluation. In the case of gray snapper, our ability to evaluate model performance is limited. The model correctly projects the current northern limit of gray snapper but there is no historical time series of species distribution with which to compare. Further, there is little trend in temperatures along the southeast U.S. [60], so past changes in distribution along the southeast U.S. shelf might be minimal. In the Gulf of Mexico, gray snapper have spread northward as overwintering conditions have become more favorable [23], thus supporting our choice of a model based on overwinter mortality. These comparisons are qualitative and the best evaluation of our model will be revisiting the projections in the future and comparing with observations.
The scale of data, models, and projections also can generate uncertainty [58]. As an example, scaling mismatch between the grain size of environmental variables and distributional data (i.e., species data) can amplify the uncertainties inherent in each of the datasets. We did not include scale uncertainty in our projections, but our parameterization of mapping thermal conditions to latitude was a major source of uncertainty (Table 3). Higher spatial resolution of the observation and models could reduce this uncertainty. We used a simple averaging approach to match temperatures from the 2–3° climate model grid to each specific estuary. Given the large-scale coherence in temperature along the U.S. east coast [54]–[56], this simple routine is likely adequate. However, there is no doubt that higher resolution climate models would reduce the spatial uncertainty of our model. In addition, increasing the spatial resolution of temperature observations could improve the model. This increase in spatial resolution could be achieved by both observations for more estuarine areas along the coast and from mapping temperatures within each specific estuary. There are likely areas of thermal refuge that vary from estuary to estuary [64] [65]–[66]. Quantifying the amount of thermal habitat in each estuary could be used to derive an estimate of total area of overwintering habitat available, which could be relevant to range and population abundance.
The final source of uncertainty identified by Planque et al. [58] is the adaptability of living systems. We assume the thermal tolerance of gray snapper will remain constant into the future, yet adaptation may generate unexpected resilience to climate change [67]. The selective pressures on marine fish can be mitigated by the ability to move [68]–[69], potentially limiting the selective pressures for adaptation. For gray snapper specifically, larvae are dispersed along the entire U.S. east coast. Genetic differences exist between gray snapper from the Gulf of Mexico and the eastern coast of Florida [70]; this pattern is seen in many other fishes as well [71]–[72]. In gray snapper from the Gulf of Mexico, there is evidence for isolation-by-distance [70], so despite the potential for broad larval dispersal, there is the possibility for local genetic differences to arise. Such genetic separation has yet to be evaluated on the southeast coast of the United States. Further, the broader issue of adaptation in thermal tolerance of marine fish needs to be investigated in detail [73].
Our analyses allowed assessment of the relative magnitude of uncertainty generated by different aspects of the forecasting approach. These results suggest that most of the uncertainty can be assigned to the parameter uncertainty related to the thermal tolerance threshold. This emphasizes the need for experimental studies to support the development of ecological climate forecasts. This need has been pointed out by others in much broader context [74] [75]–[76], but it remains important to emphasize that experimental studies are critical to developing and improving the predictions of the effect of climate change on living marine resources.
Conclusions
Our results indicate that gray snapper along the southeast coast of the United States will spread northward in the coming decades. Larvae are already dispersed well north of the adult range and the northward spread of adults will occur as a result of warming during the winter. This projection is based on the hypothesis that northern range of gray snapper is determined by distribution of overwinter mortality of young-of-the-year [39]. This hypothesis and the resulting projection do not include ecological interactions such as predation and structural habitat requirements. Inclusion of additional factors in a range model will serve to restrict projected range. By analogy the realized niche (determined by ecological interactions) is a subset of the fundamental niche (determined by environmental tolerances) and the forecasts here represent a maximum range extension, not limited by other environmental or ecological processes. These other processes will also be changed by climate, therefore additional complexity incorporating ecological interactions will be needed to develop more complete models of species distributions. In addition, it is important to more fully capture uncertainty in projections, which will serve to communicate the certainty in a projection (e.g., gray snapper will spread northward) and also can be used to identify key areas of research (e.g., improved estimates of thermal tolerance). The major source of uncertainty identified here is the parameter estimate of thermal tolerance, not the climate model, climate scenario, or statistical downscaling approach. This identifies the biological parameterization of coupled climate-biology models as the highest priority in future research to understand the effect of climate change on the distribution and abundance of marine species.
Acknowledgments
NCEP Reanalysis Derived data provided by the NOAA/OAR/ESRL PSD, Boulder, Colorado, USA, from their Web site at http://www.esrl.noaa.gov/psd/. Beth Phelan, Matthew Poach, and anonymous reviewers commented on and improved earlier drafts. Acknowledgment of the above individuals does not imply their endorsement of this work; the authors have sole responsibility for the content of this contribution. The views expressed herein are those of the authors and do not necessarily reflect the views of NOAA or any of its subagencies.
Funding Statement
The authors have no support or funding to report.
References
- 1. Hutchins LW (1947) The bases for temperature zonation in geographical distribution. Ecological Monographs 17: 325–335. [Google Scholar]
- 2. Hubbs CL (1948) Changes in the fish fauna of western North America correlated with changes in ocean temperature. Journal of Marine Research 7: 459–482. [Google Scholar]
- 3. Tittensor DP, Mora C, Jetz W, Lotze HK, Ricard D, et al. (2010) Global patterns and predictors of marine biodiversity across taxa. Nature 466: 1098–1101. [DOI] [PubMed] [Google Scholar]
- 4.Brett JR (1979) Environmental factors and growth. In: Hoar WS, Randal DJ, Brent JR, editors. Fish physiology. New York, New York: Academic Press. 599. [Google Scholar]
- 5. Pörtner HO, Berdal B, Blust R, Brix O, Colosimo A, et al. (2001) Climate induced temperature effects on growth performance fecundity and recruitment in marine fish developing a hypothesis for causes and effect relationships in Atalntic cod (Gadus morhua) and common eelpot (Zoarces viviparus. Continental Shelf Research 21: 1975–1997. [Google Scholar]
- 6. Pörtner HO (2002) Climate variations and the physiological basis of temperature dependent biogeography: systemic to molecular hierarchy of thermal tolerance in animals. Comparative Biochemistry and Physiology-Part A: Molecular & Integrative Physiology 132: 739–761. [DOI] [PubMed] [Google Scholar]
- 7.Fry FEJ (1971) The effect of environmental factors on the physiology of fish. In: Hoar WS, Randall DJ, editors. Fish physiology. New York, New York: Academic Press. 1–98. [Google Scholar]
- 8. Sette OE (1950) Biology of the Atlantic mackerel (Scomber scombrus) of North America: Part II - Migrations and habits. Fishery Bulletin 51: 251–358. [Google Scholar]
- 9. Hutchinson GE (1957) Concluding remarks. Cold Spring Harbor Symposium on Quantatative Biology 22: 415–427. [Google Scholar]
- 10. Kerr SR, Werner EE (1980) Niche theory in fisheries rcology. Transactions of the American Fisheries Society 109: 254–260. [Google Scholar]
- 11.Magnuson JJ, DeStasio BT, editors (1997) Thermal niche of fishes and global warming. Cambridge Cambridge University Press. 377–408 p. [Google Scholar]
- 12. Walther GR, Post E, Convey P, Menzel A, Parmesan C, et al. (2002) Ecological responses to recent climate change. Nature 416: 389–395. [DOI] [PubMed] [Google Scholar]
- 13. Parmesan C, Yohe G (2003) A globally coherent fingerprint of climate change impacts across natural systems. Nature 421: 37–42. [DOI] [PubMed] [Google Scholar]
- 14.Able KW, Fahay MP (2010) Ecology of Estuarine Fishes: Temperatre Waters of the Western North Atlantic. Baltimore, Maryland: John Hopkins University Press. 566 p. [Google Scholar]
- 15. Sims DW, Wearmouth VJ, Genner MJ, Southward AJ, Hawkins SJ (2004) Low-temperature-driven early spawning migration of a temperate marine fish. Journal of Animal Ecology 73: 333–341. [Google Scholar]
- 16. Shannon LV, Crawford RJM, Brundrit GB, Underhill LG (1988) Responses of fish populations in the Benguela ecosystem to environmental change. Journal du Conseil: ICES Journal of Marine Science 45: 5–12. [Google Scholar]
- 17. Murawski SA (1993) Climate change and marine fish distributions: forecasting from historical analogy. Transactions of the American Fisheries Society 122: 647–658. [Google Scholar]
- 18. Parker RO, Dixon RL (1998) Changes in a North Carolina reef fish community after 15 years of intense fishing - global warmig implications. Transactions of the American Fisheries Society 127: 908–920. [Google Scholar]
- 19. Brander KM, Blom G, Borges MF, Erzini K, Henderson G, et al. (2003) Changes in fish distribution in the eastern North Atlantic: are we seeing a coherent response to changing temperature? ICES Journal of Marine Science 291: 261–270. [Google Scholar]
- 20. Perry AL, Low PJ, Ellis JR, Reynolds JD (2005) Climate change and distribution shifts in marine fishes. Science 308: 1912–1915. [DOI] [PubMed] [Google Scholar]
- 21. Mueter FJ, Litzow MA (2008) Warming climate alters the demersal biogeography of a marginal ice sea. Ecological Applications 18: 309–320. [DOI] [PubMed] [Google Scholar]
- 22. Nye JA, Link JS, Hare JA, Overholtz WJ (2009) Changing spatial distribution of fish stocks in relation to climate and population size on the Northeast United States continental shelf. Marine Ecology Progress Series 393: 111–139. [Google Scholar]
- 23. Tolan JM, Fisher M (2009) Biological response to changes in climate patterns: population increases of gray snapper(Lutjanus griseus) in Texas bays and estuaries. Fishery Bulletin 107: 36–44. [Google Scholar]
- 24. Figueira WF, Booth DJ (2010) Increasing ocean temperatures allow tropical fishes to survive overwinter in temperate waters. Global Change Biology 16: 506–516. [Google Scholar]
- 25. Fodrie F, Heck KL, Powers SP, Graham WM, Robinson KL (2010) Climate related, decadal scale assemblage changes of seagrass associated fishes in the northern Gulf of Mexico. Global Change Biology 16: 48–59. [Google Scholar]
- 26. Stock CA, Alexander MA, Bond NA, Brander KM, Cheung WWL, et al. (2011) On the use of IPCC-class models to assess the impact of climate on Living Marine Resources. Progress In Oceanography 88: 1–27. [Google Scholar]
- 27. Wright DG, Hendry RM, Loder JW, Dobson FW (1986) Oceanic changes associated with global increases in atmospheric carbon dioxide: a preliminary report for the Atlantic coast of Canada. Canadian Technical Report of Fisheries and Aqautic Sciences 1426: 78. [Google Scholar]
- 28. Frank KT, Perry RI, Drinkwater KF (1990) Predicted response of Northwest Atlantic invertebrate and fish stocks to CO2-induced climate change. Transactions of the American Fisheries Society 119: 353–365. [Google Scholar]
- 29. Drinkwater KF (2005) The response of Atlantic cod (Gadus morhua) to future climate change. ICES Journal of Marine Science 62: 1327–1337. [Google Scholar]
- 30. Cheung WL, Lam VW, Sarmiento JL, Kearney K, Watson R, et al. (2009) Projecting global marine biodiversity impacts under climate change scenarios. Fish and Fisheries 10: 235–251. [Google Scholar]
- 31. Hollowed AB, Bond NA, Wilderbuer TK, Stockhausen WT, A'Mar ZT, et al. (2009) A framework for modelling fish and shellfish responses to future climate change. ICES Journal of Marine Science 66: 1584–1594. [Google Scholar]
- 32. Hare JA, Alexander M, Fogarty MJ, Williams E, Scott J (2010) Forecasting the dynamics of a coastal fishery species using a coupled climate-population model. Ecological Applications 20: 452–464. [DOI] [PubMed] [Google Scholar]
- 33. Lehodey P, Senina I, Sibert J, Bopp L, Calmettes B, et al. (2010) Preliminary forecasts of Pacific bigeye tuna population trends under the A2 IPCC scenario. Progress In Oceanography 86: 302–315. [Google Scholar]
- 34. Lenoir S, Beaugrand G, Lecuyer É (2011) Modelled spatial distribution of marine fish and projected modifications in the North Atlantic Ocean. Global Change Biology 17: 115–129. [Google Scholar]
- 35. Guisan A, Zimmermann NE (2000) Predictive habitat distribution models in ecology. Ecological modelling 135: 147–186. [Google Scholar]
- 36. Guisan A, Thuiller W (2005) Predicting species distribution: offering more than simple habitat models. Ecology Letters 8: 993–1009. [DOI] [PubMed] [Google Scholar]
- 37.Cheung WL, Lam VW, Pauly D (2008) Modelling present and climate-shifted distribution of marine fishes and invertebrates. Vancaouver: Univeristy of British Columbia. [Google Scholar]
- 38. Cheung WWL, Dunne J, Sarmiento JL, Pauly D (2011) Integrating ecophysiology and plankton dynamics into projected maximum fisheries catch potential under climate change in the Northeast Atlantic. ICES Journal of Marine Science: Journal du Conseil 68: 1008–1018. [Google Scholar]
- 39. Wuenschel MJ, Hare JA, Kimball ME, Able KW (2012) Evaluating juvenile thermal tolerance as a constraint on adult range of gray snapper (Lutjanus griseus): a combined laboratory, field and modeling approach. Journal of Experimental Marine Biology and Ecology 436–437: 19–27. [Google Scholar]
- 40.Robins CR, Ray C, Douglass J (1999) A field guide to Atlantic Coast fishes: North America. Boston, Massachusetts: Houghton Mifflin Harcourt. [Google Scholar]
- 41. Starck WA, Schroeder RE (1971) Investigations on the gray snapper, Lutjanus griseus. Studies in Tropical Oceanography 10: 1–224. [Google Scholar]
- 42. Faunce CH, Serafy JE (2007) Nearshore habitat use by gray snapper (Lutjanus griseus) and bluestriped grunt (Haemulon sciurus): environmental gradients and ontogenetic shifts. Bulletin of Marine Science 80: 473–495. [Google Scholar]
- 43. Luo J, Serafy JE, Sponaugle S, Teare PB, Kieckbusch D (2009) Movement of gray snapper Lutjanus griseus among subtropical seagrass, mangrove, and coral reef habitats. Marine Ecology Progress Series 380: 255–269. [Google Scholar]
- 44. Jones DL, Walter JF, Brooks EN, Serafy JE (2010) Connectivity through ontogeny: fish population linkages among mangrove and coral reef habitats. Marine Ecology Progress Series 401: 245–258. [Google Scholar]
- 45. McBride RS, McKown KA (2000) Consequences of dispersal of subtropically spawned crevalle jacks, Caranx hippos, to temperate estuaries. Fishery Bulletin 98: 528–538. [Google Scholar]
- 46.IPCC (2007) Climate Change 2007: The Physical Science Basis. Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change; Solomon S, Qin D, Manning M, Chen Z, Marquis M et al., editors. Cambridge, United Kingdom and New York, NY, USA: Cambridge University Press, 996 p. [Google Scholar]
- 47. Kalnay EC, Kanamitsu M, Kistler R, Collins W, Deaven D, et al. (1996) The NCEP/NCAR 40-year reanalysis project. Bulletin of the American Meteorological Society 77: 437–471. [Google Scholar]
- 48. DelSole T, Shukla J (2010) Model fidelity versus skill in seasonal forecasting. Journal of Climate 23: 4794–4806. [Google Scholar]
- 49. Jamison N, Kravtsov S (2010) Decadal variations of North Atlantic sea surface temperature in observations and CMIP3 simulations. Journal of Climate 23: 4619–4636. [Google Scholar]
- 50. McAfee SA, Russell JL, Goodman PJ (2011) Evaluating IPCC AR4 cool-season precipitation simulations and projections for impacts assessment over North America. Climate Dynamics 37: 2271–2287. [Google Scholar]
- 51. Roelofs EW, Bumpus DF (1953) The hydrography of Pamlico Sound. Bulletin of Marine Science of the Gulf and Caribbean 3: 181–205. [Google Scholar]
- 52. Taylor CC, Bigelow HB, Graham HW (1957) Climatic trends and the distribution of marine animals in New England. Fishery Bulletin 57: 293–345. [Google Scholar]
- 53. Hettler WF, Chester AJ (1982) The relationship of winter temperature and spring landings of pink shrimp, Penaeus duorarum, in North Carolina. Fishery Bulletin 80: 761–768. [Google Scholar]
- 54. Joyce TM (2002) One hundred plus years of wintertime climate variability in the eastern United States. Journal of Climate 15: 1076–1086. [Google Scholar]
- 55. Hare JA, Able KW (2007) Mechanistic links between climate and fisheries along the east coast of the United States: explaining population outbursts of Atlantic croaker (Micropogonias undulatus). Fisheries Oceanography 16: 31–45. [Google Scholar]
- 56. Shearman RK, Lentz SJ (2010) Long-term sea surface temperature variability along the U.S. East Coast. Journal of Physical Oceanography 40: 1004–1017. [Google Scholar]
- 57. Maul GA, Davis AM, Simmons JW (2001) Seawater temperature trends at USA tide gauge sites. Geophysical Research Letters 28: 3935–3937. [Google Scholar]
- 58. Planque B, Bellier E, Loots C (2011) Uncertainties in projecting spatial distributions of marine populations. ICES Journal of Marine Science 68: 1045–1050. [Google Scholar]
- 59. Sorte CJB, Williams SL, Carlton JT (2010) Marine range shifts and species introductions: comparative spread rates and community impacts. Global Ecology and Biogeography 19: 303–316. [Google Scholar]
- 60. Knutson TR, Delworth TL, Dixon KW, Held IM, Lu J, et al. (2006) Assessment of Twentieth-Century regional surface temperature trends using the GFDL CM2 coupled models. Journal of Climate 10: 1624–1651. [Google Scholar]
- 61. Madeira D, Narciso L, Cabral HN, Vinagre C (2012) Thermal tolerance and potential impacts of climate change on coastal and estuarine organisms. Journal of Sea Research 70: 32–41. [Google Scholar]
- 62. Furrer R, Knutti R, Sain SR, Nychka DW, Meehl GA (2007) Spatial patterns of probabilistic temperature change projections from a multivariate Bayesian analysis. Geophys Res Lett 34: L06711. [Google Scholar]
- 63. Teal LR, van Hal R, van Kooten T, Ruardij P, Rijnsdorp AD (2012) Bio-energetics underpins the spatial response of North Sea plaice (Pleuronectes platessa L.) and sole (Solea solea L.) to climate change. Global Change Biology 18: 3291–3305. [Google Scholar]
- 64. Torgersen CE, Price DM, Li HW, McIntosh BA (1999) Multiscale thermal refugia and stream habitat association of chinook salmon in northeastern Oregon. Ecological Applications 9: 301–319. [Google Scholar]
- 65. Hurst TP, Conover DO (2002) Effects of temperature and salinity on survival of young-of-the-year Hudson River striped bass (Monrone saxatilis) implications for optmal overwintering habitats. Canadian Journal of Fisheries and Aquatic Science 59: 787–795. [Google Scholar]
- 66. Manderson JP, Phelan BA, Meise CJ, Stehlik LL, Bejda AJ, et al. (2002) Spatial dynamics of habitat suitability for the growth of newly settled winter flounder Pseudopleuronectes americanus in an estuarine nursery. Marine Ecology Progress Series 228: 227–239. [Google Scholar]
- 67. Hof C, Levinsky I, AraÚJo MB, Rahbek C (2011) Rethinking species' ability to cope with rapid climate change. Global Change Biology 17: 2987–2990. [Google Scholar]
- 68. Hurst TP (2007) Causes and consequences of winter mortality in fishes. Journal of Fish Biology 71: 315–345. [Google Scholar]
- 69. Berg MP, Kiers ET, Driessen G, Van Der Heijden M, Kooi BW, et al. (2010) Adapt or disperse: understanding species persistence in a changing world. Global Change Biology 16: 587–598. [Google Scholar]
- 70. Gold JR, Saillant E, Ebelt ND, Lem S (2009) Conservation genetics of gray snapper (Lutjanus griseus) in US waters of the northern Gulf of Mexico and western Atlantic Ocean. Copeia 2009: 277–286. [Google Scholar]
- 71. Avise JC (1992) Molecular population structure and the biogeographic history of a regional fauna: a case history with lessons for conservation biology. Oikos 63: 62–76. [Google Scholar]
- 72. Gold JR, Richardson LR (1998) Mitochondrial DNA diversification and population structure in fishes from the Gulf of Mexico and Western Atlantic. Journal of Heredity 89: 404–414. [Google Scholar]
- 73. Somero GN (2010) The physiology of climate change: how potentials for acclimatization and genetic adaptation will determine 'winners' and 'losers'. Journal of Experimental Biology 213: 912–920. [DOI] [PubMed] [Google Scholar]
- 74. Helmuth B, Mieszkowska N, Moore P, Hawkins SJ (2006) Living on the edge of two changing worlds: Forecasting the responses of rocky intertidal ecosystems to climate change. Annual Review of Ecology, Evolution, and Systematics 37: 373–404. [Google Scholar]
- 75. Helmuth B (2009) From cells to coastlines: how can we use physiology to forecast the impacts of climate change? Journal of Experimental Biology 212: 753–760. [DOI] [PubMed] [Google Scholar]
- 76. Pörtner HO (2010) Oxygen- and capacity-limitation of thermal tolerance: a matrix for integrating climate-related stressor effects in marine ecosystems. Journal of Experimental Biology 213: 881–893. [DOI] [PubMed] [Google Scholar]