On Bayesian Methods of Exploring Qualitative Interactions for Targeted Treatment

Abstract

Providing personalized treatments designed to maximize benefits and minimizing harms is of tremendous current medical interest. One problem in this area is the evaluation of the interaction between the treatment and other predictor variables. Treatment effects in subgroups having the same direction but different magnitudes are called quantitative interactions, while those having opposite directions in subgroups are called qualitative interactions (QIs). Identifying QIs is challenging since they are rare and usually unknown among many potential biomarkers. Meanwhile, subgroup analysis reduces the power of hypothesis testing and multiple subgroup analyses inflate the type I error rate. We propose a new Bayesian approach to search for QI in a multiple regression setting with adaptive decision rules. We consider various regression models for the outcome. This method is illustrated in two examples of Phase III clinical trials. The algorithm is straightforward and easy to implement using existing software packages. A sample code was provided in the appendix.

1. Introduction

Recent rapid development of biological drugs has moved cancer treatment into a new era. Because they are more effective and less toxic than traditional chemotherapy, the biological drugs have received increasing attention and are being used as single agents or in conjunction with chemotherapy as an approved treatment in many malignancies. Although mechanisms of how these biological drugs elicit their actions are relatively well studied in pre-clinical models, determine the groups of patients which will derive maximal clinical benefit from them is harder to determine. It is likely that drugs that will be effective for one subgroup may be potentially harmful to another. We present two motivating examples, both from oncology. A large phase III study [1] comparing epidermal growth factor receptor (EGFR) inhibitor, gefitinib, with carboplatin plus paclitaxel as a first-line treatment for patients with pulmonary adenocarcinoma showed that progression-free survival (PFS) was significantly longer among patients receiving gefitinib than among those receiving carboplatin-paclitaxel only if patients were positive for EGFR mutation (hazard ratio for progression, 0.48; 95% CI, 0.36 to 0.64; P< 0.001). However, for patients lacking a EGFR mutation, PFS was significantly shorter in the gefitinib arm as compared to the carboplatin-paclitaxel arm (hazard ratio, 2.85; 95% CI, 2.05 to 3.98; P< 0.001). Another example is the CO.17 study [2] examining the effect of monoclonal anti-EGFR antibody, cetuximab, compared with supportive care alone among patients with advanced colorectal cancer. Cetuximab as compared with best supportive care alone was associated with significantly improved overall survival (OS) (hazard ratio for death, 0.55; 95% CI, 0.41 to 0.74; P< 0.001) and PFS (hazard ratio for progression or death, 0.40; 95% CI, 0.30 to 0.54; P< 0.001) in patients with the wild-type K-ras gene. The response rate to cetuximab was almost exclusively detected in patients with the wild-type K-ras (12.8% vs. 1.2%). However, patients with mutated K-ras tumors had no OS or PFS benefit from cetuximab.

The phenomenon in the first example can be described as a qualitative interaction (QI) between treatment and a predictive factor. This happens when the treatment effects have opposite directions in different subgroups defined by the predictor. The term QI was first introduced by [3]. When the treatment effects in subgroups have the same direction but different magnitudes (as in the second example above), it is called a quantitative interaction. There may be no harm when a quantitative interaction exists, as both patient groups benefit. However, when a true QI is ignored, an experimental treatment that is effective in one subgroup could be rejected for not reaching statistical significance in the overall group. On the other hand, a treatment that reaches statistical significance in the overall group due to its effectiveness in a majority group could be ineffective or harmful to a subgroup. These latter patients would bear unnecessary toxicity and cost from the treatment. It is of great importance to identify rare but significant QI, and hence, deliver personalized treatment, aiming to maximize the probability of reaching the desired outcome.

Identifying QIs is challenging, since they are rare and usually unknown among many potential biomarkers. It is well-known that subgroup analysis reduces the power of hypothesis testing, and that multiple subgroup analyses inflate the type I error rate. In addition, when there are other interactions in the model, QI cannot be considered independently. Many algorithms searching for interaction effects do not distinguish between QI and quantitative interactions. The importance of identifying QI was discussed in detail and a likelihood ratio test was developed by [4]. Previous work on the study of interactions was discussed and a Bayesian method for subset specific treatment effects was developed by [5]. Recently, [6] developed supervised learning algorithms for this problem. [7] developed an approach using Bayes Factor to test for QI restricted to one factor/variable within multiple subgroups. All these methods dealt with a fixed number of subgroups without any subgroup selection. Hence, in general, they yield low power of detecting QI. In the hypothesis-generating/exploratory setting, the number of potential covariates is often large. Appropriate statistical methods for identifying QI with variable selection are lacking. We propose a Bayesian approach to search for QI in a multiple regression setting. The algorithm is straightforward and easy to implement.

The remainder of this paper is organized as follows. Section 2 describes the hierarchical model structure and decision rules with different outcome variables. An adaptive decision rule is developed for a large number of candidate predictors as well. Section 3 demonstrates the properties of our proposed method through simulated studies. Section 4 illustrates the implementation of our method in two Phase III trials and a concluding discussion is given in Section 5.

2. Method

We frame our proposed method using a hierarchical regression model. Estimation of parameters will be the focus rather than prediction. Furthermore, due to the small sample sizes in subgroups formed by more than one predictor, only treatment-covariate interactions will be considered in this paper. When sample size is sufficiently large, exploring covariate-covariate interactions or treatment-covariate-covariate interactions is a straightforward extension of the methodology proposed here. We start with introducing the method in the linear regression setting, followed by logistic regression, and by the Cox proportional hazards model. We consider the problem of modeling binary covariates first. Then we extend the method to accommodate categorical covariates with more than two levels and continuous covariates. We extend our method further to include an adaptive variable screening phase if the number of covariates is large.

2.1. Linear Multiple Regression Model with Latent Variables

Let y be an N × 1 vector of continuous outcomes, where N is the total sample size. Let α₀ be the intercept, α₁ the coefficient of the two treatment options denoted by an N × 1 vector of indicator variable z with 0 for control and 1 for experimental agent. Let x_j be an N × 1 vector of the indicator variable for the jth covariate, j = 1,…, p. For simplicity, x_j+p is the interaction term corresponding to the main effect term x_j. For a simple linear regression with normally distributed errors ∈ ~ N(0, σ²), we have

$$y={\alpha }_0+{\alpha }_{1}z+\sum _{j=1}^p{\beta }_j{x}_j+\sum _{j=p+1}^{2p}{\beta }_j{x}_{j}z+∊.$$ (1)

We assume that the intercept and the treatment effects will be always in the model, and the variable selection only occurs on the covariates and the treatment-covariate interactions. Diffuse normal priors and inverse gamma prior are specified for α₀, α₁, and α, respectively. A mixture normal prior, first used by [8], can be specified for each coefficient β_j,

$${\beta }_j\mid {\gamma }_j~(1-{\gamma }_j)N(0,{\tau }^2)+{\gamma }_{j}N(0,c^2{\tau }^2).$$ (2)

The binary latent variables γ_j = 1 indicates a true predictor. The tuning parameters c and Γ are set to distinguish the distribution of the coefficient of a true predictor from that of a false predictor. The Γ² should be small enough so that β_j is close to zero when γ_j = 0. The tuning parameter c determines the magnitude of the difference between the two mixture normal distributions (Equation 2) representing the signal and noise. In our previous experiences [9–11], we followed the recommendation of choosing these two tuning parameters that is given in [8]. Choosing c between 10 and 100 worked well when implementing MCMC and simulation results were not sensitive to the choice in this range. Using the latent variable γ, model selection and identifying a QI is a by-product of the Markov chain Monte Carlo (MCMC) algorithm.

Since interaction terms represent deviations from an additive effect, we adopt the convention that a model containing interactions should also contain the corresponding main effects [12]. Hence, we modify the before mentioned hierarchical structure by adding a restricted prior for γ that corresponds to main effects,

$$\mathit{Pr}({\gamma }_j=1\mid {\pi }_j)=\{\begin{array}{cc}{\pi }_j\hfill & \text{for interaction}j=p+1,\dots ,2p\hfill \\ {\pi }_j^{(1-{\gamma }_{p+j})}\hfill & \text{for main effect}j=1,\dots ,p\hfill \end{array}\phantom{\}},$$ (3)

where π_j could be a constant or follow a distribution, such as π_j ~ Beta(a, b). To favor parsimonious models or when n < p, the parameters (a, b) in the Beta prior can be set to force a small π_j. Table 1 illustrates different prior distributions of the model space under assumptions of π_j, indicating that the prior weight of each model can be flexibly specified.

Table 1.

Prior distributions of model space with one covariate (p = 1) under different assumptions of π_main and π_int

model		joint prior prob of each model
main	int	πmain = 0.5	πmain = 0.2	πmain = 0.5
		πint = 0.5	πint = 0.2	πint = 0.33
0	0	.25	.64	.33
1	0	.25	.16	.33
0	1	0	0	0
1	1	.5	.2	.33

π_main is equivalent to π₁ in Equation (3), since p = 1.

π_int is equivalent to π₂ in Equation (3), since p = 1.

Other prior assumptions could be used for γ. For example, no restriction of any kind or to restrict the selection of higher order terms based on the existence of the lower order terms. However, the prior structure for γ specified here yields higher power to detect interactions, see [10] for more thorough comparisons. The joint posterior distribution of γ₁,…, γ_j reflects the probability of each model approximating the true unknown model. Hence, the “best” model or a set of “good” models can be selected accordingly using iterations from MCMC.

The simplified treatment effect δ_j in each subgroup of the jth covariate based on equation (1) is

$$\{\begin{array}{cc}{\delta }_j\mid x_j=0\hfill & ={\alpha }_1\hfill \\ {\delta }_j\mid x_j=1\hfill & ={\alpha }_1+{\beta }_{p+j}\hfill \end{array}\phantom{\}}j=1,\dots ,p.$$

The QI are the terms that satisfy the condition α₁ × (α₁ + β_p+j) < 0 and γ_p+j = 1. In other words, the significance of the interaction is decided by γ_p+j = 1 and the direction of the interaction is decided by α₁ and α_p+j. Using the output from the MCMC algorithm, the posterior distribution Pr{α₁ × (α₁ + β_p=j) < 0|M_l, Data} can be easily obtained at the iterations where the joint distribution of γ₁,…,γ_j,…,γ_2p corresponds to the selected model M_l.

If the selected model M_l has more than one interaction term, we test interaction terms for QI using Bayesian loss to control the false discoveries due to multiple testings. We use two-dimensional complementary Bayesian losses $\overline{\mathrm{FDR}}$ and $\overline{\mathrm{FNR}}$. Let ${\overline{\mathit{QI}}}_j$ denote the marginal posterior probability of the j^th covariate having a QI with treatment, ${\overline{\mathit{QI}}}_j$ = Pr{α₁ × (α₁ + β_p+j) < 0|M_l, Data}. Since a decision d_j is a function of M_l and data, $\overline{\mathrm{FDR}}$ and $\overline{\mathrm{FNR}}$ can be denoted as follows.

$$\overline{\mathrm{FDR}}=\{\begin{array}{cc}\frac{\Sigma d_j(1-{\overline{\mathit{QI}}}_j)}{D}\hfill & \text{if}D>0\hfill \\ 0\hfill & \text{if}D=0\hfill \end{array}\phantom{\}},$$

and

$$\overline{\mathrm{FNR}}=\{\begin{array}{cc}\frac{\Sigma (1-d_j){\overline{\mathit{QI}}}_j}{m-D}\hfill & \text{if}D<m\hfill \\ 0\hfill & \text{if}D=m\hfill \end{array}\phantom{\}},$$

where D = Σd_j, and m the total number of interactions in consideration. To control the $\overline{\mathrm{FDR}}$ at certain level α_QI while minimizing the $\overline{\mathrm{FNR}}$, one can find a set of thresholds t_QI such that a decision $d_j\equiv I({\overline{\mathit{QI}}}_j>t_{\mathit{QI}}),j=1,\dots ,m$, results in $\overline{\mathrm{FDR}}\le {\alpha }_{\mathit{QI}}$. Since $\overline{\mathrm{FNR}}$ is minimized by min{t_QI}, the optimal threshold is $t_{\mathit{QI}}^{\ast }\equiv \min \{t_{\mathit{QI}}:\overline{\mathrm{FDR}}\le {\alpha }_{\mathit{QI}}\}$. The proof follows directly from Muller et al. [13].

2.2. Logistic Multiple Regression Model

Now we consider the situation of a binary response. Assume a logistic link for binomially distributed outcome data y with probability θ ≡ Pr(y = 1|x₁,…, x_p). The regression model takes the form

$$\mathrm{logit}\left(\theta \right)=\ln \left(\frac{\theta }{1-\theta }\right)={\alpha }_0+{\alpha }_{1}z+\sum _{j=1}^p{\beta }_j{x}_j+\sum _{j=p+1}^{2p}{\beta }_j{x}_{j}z,$$

which yields the following treatment effects in the form of odds ratios (ORs):

$$\{\begin{array}{cc}{\mathrm{OR}}_j\mid x_{j=0}\hfill & =\exp \left\{{\alpha }_1\right\}\hfill \\ {\mathrm{OR}}_j\mid x_{j=1}\hfill & =\exp \{{\alpha }_1+{\beta }_{p+j}\}\hfill \end{array}\phantom{\}}j=1,\dots ,p.$$

The posterior distribution ${\overline{\mathit{QI}}}_j$ = Pr{α₁ × (α + β_p+j) < 0|M_l, Data} can then be used for inferring QI in the Logistic regression setting as well.

2.3. Cox Proportional Hazard Model

For the Cox model, we used the counting process notation introduced by [14] since it can be easily extended to frailty models, time-dependent covariates, and multiple events. [15] discussed estimation of the baseline hazard and regression parameters using MCMC methods. The implementation of this counting process formulation can be found in the survival analysis of the BUGS manual. For subjects i = 1,…, n, we observe N_i(t) which counts the number of failures occurred up to time t, and Y_i(t) which takes the value 1 if subject i is observed at time t and 0 otherwise. Let dN_i(t) denote the counting process increment of N_i over the small time interval [t, t + dt), which is assumed to follow a Poisson distribution dN_i(t) ~ Poisson(I_i(t)dt), where the intensity process I_i(t) is

$$I_i\left(t\right)=Y_i\left(t\right){\lambda }_0\left(t\right)\exp \left({\alpha }_1{x}_i+\sum _{j=1}^p{\beta }_j{x}_{\mathit{ij}}+\sum _{j=p+1}^{2p}{\beta }_j{x}_{\mathit{ij}}{z}_i\right).$$

We can write the dλ₀(t)dt as dΛ₀(t) and assume the conjugate independent increments prior suggested by [16] as dΛ₀(t) ~ Gamma($c_{0}d{\Lambda }_0^{\ast }\left(t\right),c_0$). Small values of c₀ correspond to weak prior beliefs, where $d{\Lambda }_0^{\ast }\left(t\right)$ can be thought of as a prior distribution for the unknown hazard function. In the simulation and application sections below, we set $d{\Lambda }_0^{\ast }\left(t\right)=0.1\ast (t_{h+1}-t_{\left(h\right)})$ where t_(h), h = 1,...,T, are ordered unique event times.

The treatment effects in the form of hazard ratios (HRs) are as follows

$$\{\begin{array}{cc}{\mathrm{HR}}_j{\mid }_{x_j=0}\hfill & =\exp \left\{{\alpha }_1\right\}\hfill \\ {\mathrm{HR}}_j{\mid }_{x_j=1}\hfill & =\exp \{{\alpha }_1+{\beta }_{p+j}\}\hfill \end{array}\phantom{\}}j=1,\dots ,p.$$

The posterior distributions of ${\overline{\mathit{QI}}}_j$ = Pr{α₁ × (α + β_p+j) < 0|M_l, Data} are again used for detecting QI.

2.4. Multi-level Covariates

When covariates with more than two qualitative levels are considered for sub-group analysis, multiple dummy variables are used as regressors in the model. In our model selection procedure, we incorporating restrictions on grouped regressors based on the idea of the “all included, or all excluded ” grouping principle by [17]. Instead of the one-to-one mapping of β_j and γ_j in formula (2), a many-to-one mapping of ${\beta }_j^1,\dots ,{\beta }_j^g$ for g dummy variables of the (g + 1)-level covariate j to a single γ_j is assigned as follows:

$${\beta }_j^1,\dots ,{\beta }_j^g\mid {\gamma }_j\stackrel{\mathrm{iid}}{~}(1-{\gamma }_j)N(0,{\tau }^2)+{\gamma }_{j}N(0,c^2{\tau }^2).$$

The hierarchical restriction between an interaction term and its main effects is used in conjunction with this grouping principle. Let ${\delta }_j^1,\dots ,{\delta }_j^g$ denote the treatment effects in the subgroups of jth covariate, then a QI can be detected by estimating the quantity ${\overline{\mathit{QI}}}_j=1-\mathrm{Pr}[{\delta }_j^1>0,\dots ,{\delta }_j^g<0\mid M_l,\text{Data}]-\mathrm{Pr}[{\delta }_j^1>0,\dots ,{\delta }_j^g>0\mid M_l,\text{Data}]$.

2.5. Continuous Covariates

When continuous covariates are considered in the modeling for clinical decision, two common approaches are used. The first is to convert the continuous variables to categorical covariates. The threshold is based on prior clinical knowledge or empirical evidence (e.g., using the median or tertiles of a continuous variable). This is a straightforward unsupervised threshold, where the decision of threshold is independent of the observed treatment outcomes in the current study. This approach subsumes a strong assumption of same treatment effect within each subgroup within levels defined by the discrete variable.

The second approach is to fit the continuous covariates as is or with higher order polynomials, so that the relationship between the covariate and outcome will be fully described. Thus, for a continuous covariate the subgroup analysis, the focus of this paper, is a problem of finding thresholds, such that the preferred treatment changes when the measurement of that continuous covariate is above or below that threshold. Figure 1 illustrates four scenarios in a simple linear regression that only the last scenario the QI effect exists. Scenarios (a) through (c) all favor one treatment than the other through the observed range of the continuous predictor, even though (b) and (c) indicate treatment-covariate interactions. In scenario (d), the preferred treatment would be 0 when the predictor value is less than the threshold (the intersection) but 1 otherwise.

Figure 1.

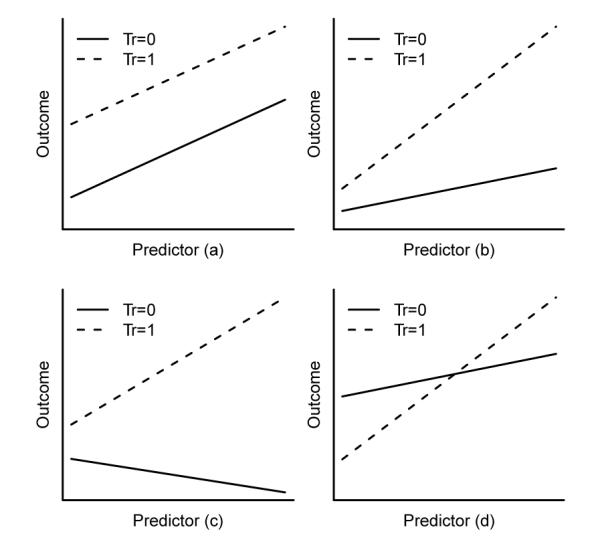
Four scenarios of interactions between treatment group and continuous predictor: (a) no interaction; (b) quantitative interaction with same directions; (c) quantitative interaction with opposite directions; (d) qualitative interaction.

Theoretically, there is always an intersection for the two fitted lines if the two slopes are not identical. Similar to the problem of extrapolation, only the intersection that lies within the observable range of the continuous covariate would be of interest and considered as a tentative threshold in practice. This type of threshold is supervised in that the threshold depends on the treatment outcomes. The supervised threshold would increase the chance of finding a QI effect compared to the unsupervised threshold. Nonetheless, the resulting threshold should be verified using an independent external data to avoid the problem of overfitting.

Here we denote by g(θ) the common parametric component of the linear, logistic, and Cox regression models, where$g\left(\theta \right)={\alpha }_{1}z+{\Sigma }_{j=1}^p{\beta }_j{x}_j+{\Sigma }_{j=p+1}^{2p}{\beta }_j{x}_{j}z$. We have

$$\{\begin{array}{cc}g\left(\theta {\mid }_{z=0}\right)\hfill & ={\beta }_j{x}_j+{\Sigma }_{j^{\prime }\ne j}{\beta }_{j^{\prime }}{x}_{j^{\prime }}\hfill \\ g\left(\theta {\mid }_{z=1}\right)\hfill & ={\alpha }_1+{\beta }_j{x}_j+{\beta }_{p+j}{x}_j+{\Sigma }_{j^{\prime }\ne j}{\beta }_{j^{\prime }}{x}_{j^{\prime }}+{\Sigma }_{j^{\prime }\ne j}{\beta }_{p+j^{\prime }}{x}_{j^{\prime }}\hfill \end{array}\phantom{\}}j=1,\dots ,p.$$

The intersection of two regression lines with respect to x_j is at x_j = $\frac{-{\alpha }_1-{\Sigma }_{j^{\prime }\ne j}{\beta }_{p+j^{\prime }}{x}_{j^{\prime }}}{{\beta }_{p+j}}$. The term ${\Sigma }_{j^{\prime }\ne j}{\beta }_{p+j^{\prime }}{x}_{j^{\prime }}$ reflects the contribution from other covariates whose interactions with treatment are selected as well. Holding $x_{j^{\prime },j^{\prime }\ne j}$, at its mean if it is continuous or at zero if it is categorical, we test for the QI effect of x_j using posterior probability ${\overline{\mathit{QI}}}_j=\mathrm{Pr}\{c_1<\frac{-{\alpha }_1-{\Sigma }_{j^{\prime }\ne j}{\beta }_{p+j^{\prime }}{x}_{j^{\prime }}}{{\beta }_{p+j}}$ < c₂|M_l, Data}, where c₁ and c₂ could be approximated by the minimum and maximum of the observed x_j, respectively. This is equivalent to $\mathrm{Pr}\left\{\right({\alpha }_1+{\Sigma }_{j^{\prime }\ne j}{\beta }_{p+j^{\prime }}{x}_{j^{\prime }}+c_1{\beta }_{p+j}\left)\right({\alpha }_1+{\Sigma }_{j^{\prime }\ne j}{\beta }_{p+j^{\prime }}{x}_{j^{\prime }}+c_2{\beta }_{p+j})<0\mid M_l,\text{Data}\}$. The model with categorical covariates is a special case when c₁ = 0 and c₂ = 1.

All of these parameters can be estimated from posterior distributions using standard MCMC output. At each MCMC iteration where the selected model occurs, we estimate the intersection. Hence, a distribution of the intersection could be obtained. Bayesian credible interval of the intersection between the observed range of that continuous covariate could be obtained as well. A tentative threshold could be decided based on the posterior distribution of the intersection, e.g. the median. The percentage of the patient population that will benefit from utilizing this threshold could be presented graphically as well; see Section 4.2 for an example. Given the practical importance of this problem, we anticipate that this method will serve as a springboard for future work.

2.6. Variable Screening with large p

When the number of candidate predictors increases, the above described Bayesian model selection (BMS) method tends to fail, as does any other modeling approach, due to the lack of information. Two features of BMS are vulnerable: first, the probabilities of main effects being included in the model are inflated more with increased p based on the hierarchical prior structure in equation (3). Second, the highest joint posterior distribution of γ₁,…,γ_2p is driven by the prior when n is not sufficiently larger than p. When less information is available, the effect of the prior becomes stronger. The Beta hyperprior in the hierarchical model can be viewed as a penalty or shrinkage effect. The use of a larger penalty as in the second to the last panel of Table 1 will reduce the power to identify QI. If we set the Beta hyperprior to favor larger models (see the first panel of Table 1), the coefficient of interest, a key component in identifying QI, will be estimated with less efficiency. Hence, the power will be reduced in this case as well.

We believe that a model with an interaction term should also include its main effect and we do not wish to lose the power to detect rare QI by requiring a large shrinkage effect. The solution to improve the performance of BMS lies in variable screening. It is common sense to screen the candidate variables before fitting a “best” model. The rule of thumb that at least 10 events per predictor [18] can be used here to decide if variable screening is necessary.

We propose adaptive BMS (ABMS) by adding an adaptive decision rule to screen the variables if necessary. We begin with the model selection phase given all the candidate variables. If under the decision rule there is no model selected, the variable screening phase will be triggered to reduce the model space. Then the process of selecting a model will be reiterated. The algorithm will oscillate between variable screening and model selection phases until there is a “best” model or models selected, or there are no remaining candidate variables, or the variable screening phase does not result in a reduced number of candidates.

At the model selection phase for m candidate models (M₁,…, M_m), we have m corresponding decisions d = (d₁,…, d_m) with value 1 for selected or 0 otherwise. Let vector ν with elements ν_l = Pr(M_l|Data), l = 1,…, m, denote the posterior probabilities of models estimated by the proportion of occurrences of model M_l in the MCMC process. Let ${\overline{\nu }}_1=\frac{{\Sigma }_{l=1}^m{d}_l{\nu }_1}{{\Sigma }_{l=1}^m{d}_l}$ and ${\overline{\nu }}_2=\frac{{\Sigma }_{l=1}^m(1-d_l){\nu }_1}{{\Sigma }_{l=1}^m(1-d_l)}$ donted the mean ν_l the set of selected models S₁ and the set of non-selected models S₂, respectively. The decision of selecting a model is based on two posterior expected losses simultaneously: the first, L₁(d,ν), assesses how-well the selected set S₁ of models “separates” from the non-selected set S₂ using a squared Euclidean distance:

$$\begin{array}{cc}\hfill L_1(d,\nu )& =\sum _{k=1}^2\sum _{{\nu }_1\in S_k}{\Vert {\nu }_1-{\stackrel{‒}{\nu }}_k\Vert }^2\hfill \\ \hfill & =\sum _{l=1}^m{d}_l{({\nu }_1-{\stackrel{‒}{\nu }}_1)}^2+\sum _{l=1}^m(1-d_l){({\nu }_1-{\stackrel{‒}{\nu }}_2)}^2;\hfill \end{array}$$ (4)

the second,

$$L_2(d,\nu )={\lambda }_2\overline{\mathit{FD}}+(1-{\lambda }_2)\overline{\mathit{FN}},$$

is the posterior false discovery $\overline{\mathit{FD}}$ and the false non-discovery $\overline{\mathit{FN}}$ of the decision with modification constant λ₂, where $\overline{\mathit{FD}}={\Sigma }_{l=1}^m{d}_l(1-{\nu }_l)\text{and}\overline{\mathit{FN}}={\Sigma }_{l=1}^m(1-d_l){\nu }_l$.

Let λ₁ denote the modification constant, we consider the following optimal rule under the posterior expected loss L(d,ν),

$$\underset{d}{\text{argmin}}L(d,\nu )=\underset{d}{\text{argmin}}\left(L_1\right(d,\nu )+{\lambda }_1{L}_2(d\nu \left)\right).$$

Theorem 1

Under the loss function L(d,ν), the optimal decision takes the form d_l = I(ν_l > ν_(m–D)), where D* is the optimal number of discoveries.

Proof

Let D = Σd_l (to simplify the notation, in what follows we omit the subscript l = 1 and superscript m), we find from directly deriving from (4) that

$$\begin{array}{cc}\hfill L_1(d,\nu )& =\Sigma d_l{\nu }_1^2-2{\stackrel{‒}{\nu }}_1+\Sigma d_l{\nu }_l+D{\stackrel{‒}{\nu }}_1^2+\Sigma (1-d_l){\nu }_1^2-2{\stackrel{‒}{\nu }}_2\Sigma (1-d_l){\nu }_l+(m-D){\stackrel{‒}{\nu }}_2^2\hfill \\ \hfill & =\Sigma {\nu }_1^2-D{\stackrel{‒}{\nu }}_1^2-(m-D){\stackrel{‒}{\nu }}_2^2\hfill \\ \hfill & =\Sigma {\nu }_l^2-\frac{{\left(\Sigma d_l{\nu }_l\right)}^2}{D+∊}-\frac{{\left(\Sigma \right(1-d_l\left){\nu }_l\right)}^2}{m-D+∊}\hfill \\ \hfill & =\Sigma {\nu }_l^2-\frac{(m-D){\left(\Sigma d_l{\nu }_l\right)}^2+D({\left(\Sigma {\nu }_l\right)}^2-2\Sigma {\nu }_l\Sigma d_l{\nu }_l+{\left(\Sigma d_l{\nu }_l\right)}^2)}{D(m-D)+∊}\hfill \\ \hfill & =\Sigma {\nu }_l^2-\frac{{\left(\Sigma {\nu }_l\right)}^2}{m-D+∊}-\frac{\Sigma d_l{\nu }_l(m\Sigma d_l{\nu }_l-2D\Sigma {\nu }_l)}{D(m-D)+∊}\hfill \end{array}$$ (5)

$$L_2(d,\nu )={\lambda }_{2}D+(1-{\lambda }_2)\Sigma {\nu }_l-\Sigma d_l{\nu }_l,$$ (6)

where the additional term ∈ avoids a zero denominator. Subject to a fixed total number of discoveries D, only the last terms in (5) and (6) involve the decision d_l. For any given D, L₁ and L₂ are minimized by setting d_l=1 for the D largest ν_l, such that d_l ≡ I(ν_l > ν(_m–D)), where ν_{(m – D)} is the (m – D)th order statistics of ν₁,…, ν_m. Given D, the local minimums are

$$\begin{array}{cc}\hfill & \min \left(L_1\right(d,\nu \mid D\left)\right)=\Sigma {\nu }_l^2-\frac{{\left(\Sigma {\nu }_l\right)}^2}{m-D+∊}-\frac{\sum _{l=m-D+1}^m{\nu }_l\left(m\sum _{l=m-D+1}^m{\nu }_l-2D\Sigma {\nu }_l\right)}{D(m-D)+∊}\hfill \\ \hfill & \min \left(L_2\right(d,\nu \mid D\left)\right)={\lambda }_{2}D+(1-{\lambda }_2)\Sigma {\nu }_l-\sum _{l=m-D+1}^m{\nu }_l\hfill \end{array}$$

Thus, we conclude that the global optimum must be the same form. The optimum D* is found by minimizing

$$\begin{array}{cc}\hfill L(d,& \nu \mid D)=\hfill \\ \hfill \Sigma {\nu }_l^2& -\frac{{\left(\Sigma {\nu }_l\right)}^2}{m-D+∊}+{\lambda }_1{\lambda }_{2}D+{\lambda }_1(1-{\lambda }_2)\Sigma {\nu }_l\hfill \\ \hfill -& \frac{\sum _{l=m-D+1}^m{\nu }_l\left(m\sum _{l=m-D+1}^m{\nu }_l-2D\Sigma {\nu }_l+{\lambda }_{1}D(m-D)\right)}{D(m-D)+∊}\hfill \end{array}$$

with respect to D.

Remark 1

L₁ is equivalent to the k-mean clustering approach [19] in one dimension with a squared Euclidean distance metric. The models based on this part of the loss function will be partitioned into 2 groups, S₁ and S₂. L₁ is considered providing a soft threshold to partition the models, where the decision is solely driven by the data.

Remark 2

The addition of L₂ penalizes the partition through the loss from false discovery and false non-discovery with a modification constant λ₂. L₂ is considered providing a hard threshold to select the models. The decision is invariant to the data. From (6), we have

$$L_2(d,\nu )=\Sigma d_l({\lambda }_2-{\nu }_l)+(1-{\lambda }_2)\Sigma {\nu }_l.$$

Thus the minimum is achieved when d_l = I(ν_l > λ₂). Note that the distribution of ν_l changes when the total number of models m changes. Hence, it is difficult to use L₂ alone for decision making.

Remark 3

In some cases, if ν_l ≡ ν, the expected loss L₁ ≡ 0 is invariant to any decision d_l. To see that, we have from the definition in (4),

$$L_1{\mid }_{{\nu }_1\equiv \nu }=\Sigma d_l{(\nu -\nu )}^2+\Sigma (1-d_l){(\nu -\nu )}^2=0.$$

Thus, the decision will be solely based on L₂ Hence, we recommend to set λ₂ = 0.5, which is linked to traditional hypothesis testing problems [20].

The variable screening phase has two sequential steps due to the restricted hierarchical structure in (3). At the first step, we apply the adaptive decision rule to the interaction terms. Selected interaction terms and their main effects will be kept for the next model selection phase. At the second step, the adaptive decision rule will be applied to the remaining main effects. The selected additional main effects will be kept for the next model selection phase as well. The formulation of the decision rule for the variable screening phase is the same as that of the model selection phase. Let a vector ν with elements ν_l = Pr(γ_l|Data),l = 1,…, p, denote the posterior marginal probability of a regressor being in the true model, where ν_l is estimated by the proportion of occurrences of the l^th regressor in the MCMC iterations produced in the model selection phase. If the variable screening phase yields a reduced number of p, the model selection phase is reiterated in a new MCMC process.

Remark 4

The modification constant λ₁ reflects the relative weighting between L₁ and L₂. Note that L₁ and L₂ are on different scales. In our experience, the scale of L₂ has been more than 100 times greater than L₁. The process of variable screening is to reduce the dimension of the model space. When the loss function is used for screening variables, more weight is recommended for L₁ (e.g. λ₁ ∈ [0, 0.01)). When the loss function is used for selecting models, more weight is recommended for L₂ (e.g. ₁ ∈ (0.01, 1]).

3. Simulation Studies

Our interest lies in evaluating the frequentist power to detect the QI under various conditions, such as outcome types, sample size, number of covariates, and treatment effect. We set the number of covariates p = 5 and 25 with a sample size of 200, and assume that all of the p covariates are independent and from a Bin(n, 0.5) distribution. The treatment group z was generated from Bin(n, 0.5) to represent 1:1 randomized clinical trials. Three types of outcomes were simulated: linear, binary, and survival outcomes. Several true models were considered for different outcomes. The first true model was η₁ = −.7z + 0.5x₁ + 1.4x₁z. This is equivalent to a treatment Odds Ratio (OR) or Hazard Ratio (HR) of 0.5 when x₁ = 0 and 2 when x₁ = 1. The second true model, with an additional interaction term, was η₂ = −.7z + 0.5x₁ + 0.5x₂ + 1.4x₁z – x₂z. The third true model, with smaller treatment effect, was η₃ = –.5z + 0.5x₁ + 0.5x₂ + x₁z – x₂z. This is equivalent to a treatment OR or HR of 0.6 when x₁ = 0 and 1.64 when x₁ = 1. For linear outcomes, ∈ ~ N(0, 1) was used. We used a logit link and an exponential link for the binary and survival outcomes, respectively. The uniform distribution on [0, c] was used to generate non-informative censoring, where c chosen to generate 30% censoring . We generated 500 replications for each setting. For the binary outcomes, the frequency of y = 1 was about 56% from model 1, 2, and 3.

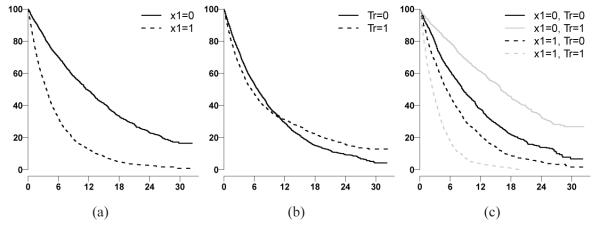
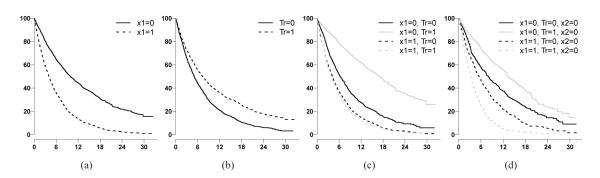
The KM curves for one simulated survival dataset under model 1 and 3 were plotted (Figure 2 and 3). x1 is a prognostic factor (Figure 2(a) and Figure 3(a)). As demonstrated, if the QI effect of x1 is ignored, the treatment effect will not be detected (Figure 2(b)). In addition, the QI effect is not detectable if the other interaction is ignored (Figure 3(c)). The QI effect could be detected only if other interactions (QI or quantitative interaction), such as x₂ in model 3 , were jointly considered (Figure 3(d)).

Figure 2.

KM curves by subgroups under simulated model 1. Horizontal axis is months from randomization. Vertical axis is probability of survival. Fig(2(a)) grouped by x₁ status; Fig(2(b)) grouped by treatment arms; Fig(2(c)) grouped by x₁ and treatment arms.

Figure 3.

KM curves by subgroups under simulated model 3. Horizontal axis is months from randomization. Vertical axis is probability of survival. Fig(3(a)) grouped by x₁ status; Fig(3(b)) grouped by treatment arms; Fig(3(c)) grouped by x₁ and treatment arms; Fig(3(d)) grouped by x₁ and treatment arms when x₂ = 0.

For all of the simulated data sets, we applied the method with c = 10, Γ = .15, and Beta(2,2). The length of the two parallel MCMC chains was set to be 10, 000, from which the first 1, 000 iterations were discarded. The data generation for the simulations was conducted in R. Through the R package R2WinBUGS, the model estimation was conducted in BUGS [21], a popular Bayesian software package for performing Bayesian inference using Gibbs sampling [22, 23]. The “best” model in this method of BMS was selected based on the highest joint posterior distribution of γ. The λ₁ equal to 1 for selecting models and 0.01 for selecting variables were used in the ABMS method with the expected loss L(d, ν). The α_QI = 0.5 was used as the threshold for $\overline{\mathrm{FDR}}$.

The power was calculated as the proportion of occurrences among all the simulations in which the true QI effect was detected. The FDR was calculated as the average over 500 simulations of proportions of falsely detected QIs among all detected QI. The results were presented in Table 2.

Table 2.

Estimated Power and FDR of testing QI under true models (n=200)

Outcomes		BMS						ABMS
		p = 5			p = 25			p = 5			p = 25
		η 1	η 2	η 3	η 1	η 2	η 3	η 1	η 2	η 3	η 1	η 2	η 3
Linear	Power (%)	99.2	96	86.8	89.8	83.8	58.2	99.4	94.2	81.2	98.2	92.4	78.6
	FDR (%)	5.5	9.3	5.3	14.1	12.8	16.1	8.3	8.8	5	10.6	9.2	6.3
	m Tests	1	1.7	1.8	8.2	7.7	8.5	1	1.5	1.6	1.1	1.5	1.7
Binary*	Power (%)	77	64.8	50	33.8	32.4	13.8	76.4	58.4	38.2	58.6	46.6	27.6
	FDR (%)	13.3	12.3	17.8	20.8	16.1	19.6	7	8.2	13.6	10.4	8.7	14.6
	m Tests	1.4	1.8	1.6	12.6	12	12.2	1	1.1	1	0.8	0.9	0.7
Survival§	Power (%)	98	93.2	74.2	78.4	72.6	41	98.2	88	62.6	97.8	85.8	61.8
	FDR (%)	1.3	4.1	7.5	12	11.2	16.1	0.8	4.3	9	2.9	5.8	12.4
	m Tests	1	1.6	1.6	9.5	8.9	9.6	1	1.5	1.4	1.1	1.6	1.5
Survival§§	Power (%)	82.6	71.2	47.8	35.2	31.4	13.6	80.8	64.2	36.4	69.4	59.2	33
	FDR (%)	5.5	7.1	11.7	13.1	9.7	12.9	3	8.1	15.2	11.8	13.6	20.2
	m Tests	1.1	1.5	1.4	11.9	11.5	11.8	1	1.2	0.9	1.1	1.2	1

m_Tests: number of multiple tests for QI average over the 500 simulations

^*minor frequency of binary outcome is 44% average over the 500 simulations

^§average number of events are 70% and 30%, respectively.

^§§average number of events are 70% and 30%, respectively.

Our simulation study suggests the feasibility of detecting the QI using the BMS or the ABMS approach for a relatively large number of predictors. Our simulated data have one or two true interaction terms for η₁ or η₂ and η₃, respectively. The m_Tests ideally should be close to one or two for η₁ or η₂ and η₃ accordingly. A deviation towards smaller value indicates the selected model missed true interaction terms. Conversely, a deviation towards larger values indicates that false interaction terms were included in the selected model for the QI test. When p = 25, the much smaller m_Tests from ABMS method indicates the advantage of using the adaptive variable screen phase. The BMS method does not involve a variable screening phase. It tends to have poor power if the number of covariates is large relative to the sample size. However, the ABMS method could falsely remove important predictors during the variable screening phase. Apparently, when the number of main effects is relatively small (p = 5) to the sample size, the BMS method is better than ABMS. To obtain reasonably stable estimates of the regression coefficients, the rule of thumb is to have a minimum of 10 subjects in the smaller category in logistic regression or 10 events in the Cox model per predictor variable [18, 24]. A relaxed version could be used in guiding the choice of BMS or ABMS. If the number of main effects is larger than 1/10th of the effective sample size, the ABMS method is recommended.

4. Applications

4.1. Colorectal Cancer Phase III Trial

We illustrate the method using the data from a previously reported randomized Phase III trial [11, 25]. The primary objective of the study was to compare the effect of combinations of chemotherapy agents in patients with advanced colorectal cancer. At the time of planning the trial, two chemotherapy drugs had been approved by the Food and Drug Administration (FDA) for treatment of advanced colon cancer: 5-fluorouracil (5-FU) and irinotecan (CPT-11), while Oxaliplatin (OXAL), a cis-platinum analogue with activity in colorectal cancer, was an investigational agent in the U.S. and Canada. Two experimental combinations of regimens,5-FU+OXAL and OXAL+CPT-11, were compared to the standard regimen, 5-FU+CPT-11, in the trial. We refer to these regimens as Arm F, Arm G and the control as Arm A, respectively. A total of 1705 patients were included in the study, of which 513 (115 patients in arm A, 292 patients in arm F, and 106 patients in arm G) were genotyped for 23 biomarkers. These biomarkers were selected based on previous reports indicating that they were related to bioactivity of the chemotherapies by direct or indirect mechanisms. Descriptive summaries of the covariates were reported in Table 1 in [11].

For the purpose of illustration, we focus on the treatment comparison between Arm F and the standard treatment Arm A, and prespecified primary endpoint progression free survival. We applied the ABMS method with c = 10, Γ = .15, and Beta(2, 2). The λ₁ equal to 1 for selecting models and 0.01 for selecting variables were used with the expected loss L(d,ν). The length of the two parallel MCMC chains was set to be 20,000, from which the first 1,000 iterations were discarded. The posterior mean of ${\overline{\mathit{QI}}}_j$ = Pr{α₁ × (α₁ + β_p+j) < 0|M_l, Data} was used as for testing for QI. Results from the simulation studies (Table 2) suggest that with a total of about 140 events in 1:1 randomization and 25 potential predictors, the powers to detect a true QI from models η₁ and η₂ are 0.978 and 0.858, respectively. Hence, in this application data set with 296 events and 2:1 randomization, we expect that the power is not less than 80%.

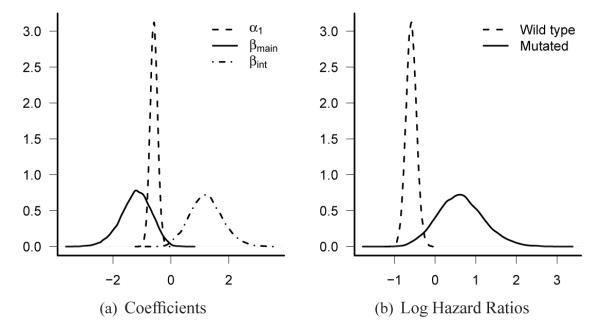
Our ABMS method resulted in making inference of QI with two iterations of the model selection phase. At the second iteration, a model with posterior probability of 0.64 was selected. The selected model only contains one QI with posterior probability of 0.87. The coefficients and the log HR of treatment effect under the selected model are plotted in Figure4. The KM curves by subgroups defined by the status of selected marker (dpyd_6) and treatment groups are plotted in Figure 5. A different λ₁ value was used for sensitivity analysis, and the results are almost the same (results not shown). The marker dpyd_6 was a prognostic marker since the wild-type carriers had poor prognosis. It was also a predictive marker with a qualitative interaction effect. The posterior distribution (Figure 4(b)) of the HR in the dpyd_6 mutated group suggests that the treatment was superior overall (arm F) may not benefit this subgroup. Clearly this result is hypothesis generating only and would require confirmation in independent trials. However, since a majority of the patients had wild-type dpyd_6, giving experimental treatment to all the patients ignoring the status of dpyd_6 will not affect the conclusion that experimental treatment is more effective than the standard treatment.

Figure 4.

Posterior distributions of coefficients (Fig 4(a)) and log HR of treatment effect in wild type group with 272 events (dashed line) and in mutated group with 24 events (solid line) (Fig 4(b)) in the colorectal cancer study.

Figure 5.

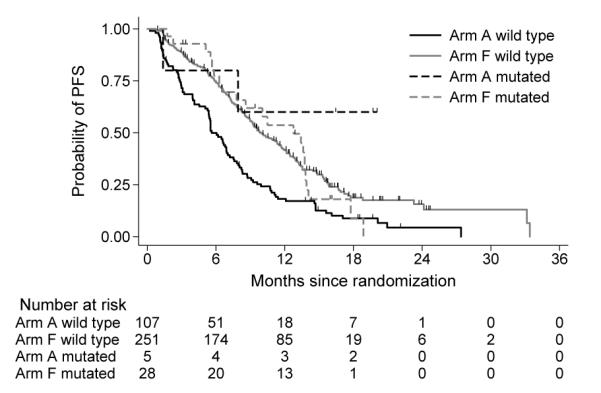
KM curves by subgroups based on marker status and treatment arms for colonrectal cancer study.

We underline the importance of simulated power and FDR to guide the choice of different approaches (BMS or ABMS), as well as the sensitivity analysis of tuning parameters. The results of the example in this section may appear not persuasive regarding the merits of the proposed method. Nevertheless, these are likely the typical results in searching for rare QI effects in cancer clinical trials in practices.

4.2. Non-Small Cell Lung Cancer (NSCLC) Phase III Trial

DNA excision repair protein ERCC1 activity may serve as a marker in resistance to platinum chemotherapy drugs in patients with gastric, ovarian, colorectal, NSCLC, and bladder cancers. In NSCLC, patients whose tumors were surgically removed and received no further therapy have a better survival if ERCC1 high than if ERCC1 low. Thus, high ERCC1 is a favorable prognostic marker. However, NSCLC patients with high levels of ERCC1 do not benefit from adjuvant platinum chemotherapy, whereas ERCC1 low patients receive substantial benefit. High ERCC1 is thus a negative predictive marker for adjuvant platinum chemotherapy [26, 27]. Most of reported studies evaluated the ERCC1 at the RNA level, except for [26], in which the ERCC1 was measured by standard immunohistochemical (IHC) method. The median value of semiquantitative H scores was a priori chosen as the cutoff point for ERCC1 positivity tumors in [26]. Tissue microarray (TMA) is an efficient way to evaluate the protein activity in the exploratory phases. A fluorescent-based IHC method combined with automated quantitative analysis (AQUA)[28] allows rapid automated analysis of protein activities. AQUA identifies the separation of tumor from stromal elements and the sub-cellular localization of signals. The resulted quantitative scores lead to the question of identifying cutoff point for high or low protein activity.

We illustrate our QI searching method with a randomized Phase III NSCLC [29], where the biomarker activity was measured as a continuous covariate. The trial was conducted in patients with previously untreated stage IIIB/IV NSCLC, a performance of status of 2, and measurable disease by RECIST. Blanced randomization to control arm treated with gemcitabine and experimental arm gemcitabine and carboplatin. A total of 170 patients were randomized between March 2004 and December 2006. The trial was terminated due to low patient accrual.

Of the 65 patients with available protein expression of ERCC1 and RRM1, 5 had stage IIIB tumors and all randomized to experimental arm. Since stage is a well known prognostic factor, we focus our inference on the 60 stage IV patients whose ERCC1 and RRM1 activity were available. There were no significant differences between the groups of patients with and without biomarker data (Table 1 from [29]).

The covariates considered were age, gender, log2(RRM1), log2(ERCC1), and histology (adenocarcinoma, squamous, and other). Except for gender, which is binary, and histology, which is categorical with three levels, the remaining covariates were continuous. Each continuous covariate was scaled by dividing its range to make the estimated coefficients comparable to those of categorical covariates. The ABMS method was used because of relatively small effective samples size (49 OS events) to the number of covariates. The same choices of tuning parameters and decision rules were used here as in Section 4.1.

At the second iteration, a model with Arm, log2(ERCC1), and histology as main effects and log2(ERCC1)*Arm as an interaction were selected. The posterior distribution of intersection and the histogram of observed log2(ERCC1) are plotted in Figure 6. The Bayesian credible interval of intersection between the minimum and maximum observed log2(ERCC1) was 84.3%. Using the median of the posterior distribution of intersection, a tentative cutoff of 15 on original scale of ERCC1 was used to separate the patients into ERCC1 high and low subgroups. The KM curves by subgroups are plotted in Figure 7.

Figure 6.

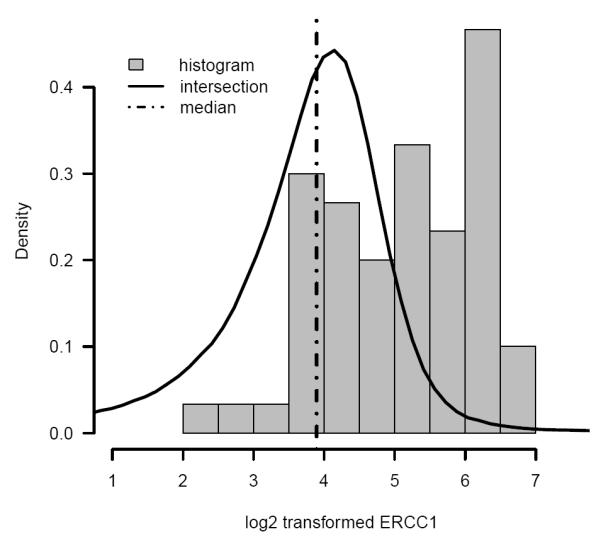
Posterior distribution of intersection (solid line), median of posterior distribution of intersection (dash dotted line), and histogram of log2 transformed observed ERCC1 protein activity in the NSCLC study.

Figure 7.

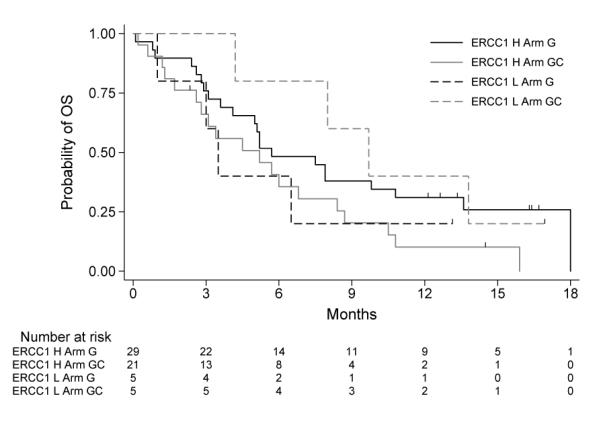
KM curves by subgroups based on tentative marker High and Low groups and treatment arms for NSCLC study.

In this data, the histology was identified as a prognostic factor and ERCC1 a predictive factor. Although only 10 out of 60 (17%) stage IV patients were classified as ERCC1 low using the ABMS method (Figure 6, left side of dot-dashed line classified as ERCC1 Low), the result was consistent to the literature.

5. Discussion

In this work, we proposed BMS and ABMS methods using Bayesian regression model for subgroup analysis. We have addressed issues of qualitative interactions in cancer treatment. The endpoints considered were linear, categorical and censored continuous variables, which are very common in most phase III clinical trial settings. Our methods increased the power of detecting QI, which becomes more important in defining targeted group for treating complex diseases in heterogeneous population.

In addition to the power to detect a QI, another critical issue in subgroup analysis is the family wise type I error rate (FWER), which is inflated due to multiple testing of covariates. With our proposed methods, we reduce the FWER by reducing the number of interactions to be tested for QI. We first select a best model based on the joint posterior distribution of possible models. This process does not involve multiple testing. If the best model contains interaction terms, we then test for QI based on marginal poster distribution ${\overline{\mathit{QI}}}_j$ for each selected term. This process involves multiple testing if the number of interaction terms selected in the final model is larger than one. A Bayesian FDR rule was used to control the proportion of falsely identified QI.

The estimated FDR from our simulations is small and well controlled at α_QI = 0.5 across three different true models (Table 2). The cutoff α_QI = 0.5 can be interpreted as among the identified QI terms, half of them are genuine QI terms. Since the QI is rare and our method reduces number of multiple tests greatly, especially the ABMS method, setting α_QI at 0.5 is not unreasonable. Simulation results in Table 2 suggest that the resulted FDR was affected by, but not limited to, decision rules, effective sample size, number of covariates, and effect sizes. Because little is known about the truth of complex real data, before analyzing the real data the distribution of FDR should be studied using simulations with various settings. We hope that the proposed study stimulates further research on the use of FDR-controlling procedures in this setting.

Appendix. Sample WinBUGS code for selection of QI for survival outcomes

model { ############# Set up data for(i in 1:N) { for(j in 1:T) { # risk set = 1 if obs.t >= t Y[i,j] <- step(obs.t[i] - t[j] + eps) # counting process jump = 1 if obs.t in [ t[j], t[j+1] ) # i.e. if t[j] <= obs.t < t[j+1] dN[i, j] <- Y[i, j] * step(t[j + 1] - obs.t[i] - eps) * fail[i] } } ### create interaction terms for(j in 1:p_int){ for (i in 1:N) {X_int[i,j]<-X[i,j]_*Treat[i]} } ############# model for(j in 1:T) { for(i in 1:N) { dN[i, j] ~ dpois(Idt[i, j]) # Likelihood Idt[i, j] <- Y[i, j] * exp(eta[i]) * dL0[j] # Intensity } dL0[j] ~ dgamma(mu[j], c) mu[j] <- dL0.star[j] * c # prior mean hazard } c <- 0.001 r <- 0.1 for (i in 1:N) { eta[i]<-alpha1_*Treat[i]+inprod(X[i,],Beta[])+inprod(X_int[i,],Beta_int[])} for (j in 1:T) { dL0.star[j] <- r * (t[j + 1] - t[j]) } ############# for alpha alpha1~dnorm(0,0.04) ############# for Beta p is the number of covariates # assume all the elements in Beta are apriori independent for( i in 1:p_int) { Sig_int[i]<-(1-Gamma_int[i])_*cont+Gamma_int[i]_*cons_*cont Sig_int_inv[i]<-1/pow(Sig_int[i],2) Beta_int[i]~dnorm(0,Sig_int_inv[i]) Gamma_int[i]~dbern(pi_int[i]) # bernoulli-beta pi_int[i]~dbeta(a,b) } ### main effects are constrained by interactions for( i in 1:p) { Sig[i]<-(1-Gamma[i])*cont+Gamma[i]*cons*cont Sig_inv[i]<-1/pow(Sig[i],2) Beta[i]~dnorm(0,Sig_inv[i]) PI[i]<-pow(pi[i],step(-Gamma_int[i])) Gamma[i]~dbern(PI[i]) # bernoulli-beta pi[i]~dbeta(a,b) } }