Hydrodynamic turbulence as a problem in nonequilibrium statistical mechanics

Abstract

The problem of hydrodynamic turbulence is reformulated as a heat flow problem along a chain of mechanical systems describing units of fluid of smaller and smaller spatial extent. These units are macroscopic but have a few degrees of freedom, and they can be studied by the methods of (microscopic) nonequilibrium statistical mechanics. The fluctuations predicted by statistical mechanics correspond to the intermittency observed in turbulent flows. Specifically, we obtain the formula 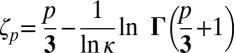for the exponents of the structure functions (). The meaning of the adjustable parameter κ is that when an eddy of size r has decayed to eddies of size 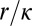, their energies have a thermal distribution. The above formula, with 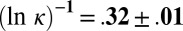is in good agreement with experimental data. This lends support to our physical picture of turbulence, a picture that can thus also be used in related problems.

Hydrodynamic turbulence is known to be a chaotic phenomenon (1–4). This means that the time evolution of a turbulent fluid system belongs to a much studied class of deterministic dynamics with sensitive dependence on initial conditions (5–8). The statistical properties of turbulence are described by an ergodic invariant state ρ for 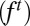, and because chaotic dynamical systems have (uncountably) many ergodic states, a choice has to be made. A physically reasonable choice is that of so-called Sinai-Ruelle-Bowen (SRB) states (refs. 9–11 and references therein).

It is fair to say that the chaotic nature of turbulence has been largely ignored by the turbulence community and that the choice of an ergodic state to describe the statistical properties of turbulence has been made by ad hoc assumptions (closure assumptions, Gaussianity, multifractal structure). Indeed, the study of SRB or “physical” states for Navier–Stokes dynamics appears impossibly difficult at first. Nevertheless, we propose here an approach of this sort: We bypass the mathematical problems of SRB states by using our understanding of the physics of a specific dynamical system, namely, that corresponding to heat conduction, as seen from the point of view of nonequilibrium statistical mechanics. Our approach will thus use basic physical ideas and approximations rather than ad hoc assumptions. In this manner, we shall obtain a surprisingly coherent view of the fluctuations in turbulence (intermittency).

We shall concern ourselves with incompressible fluids in three dimensions, described by the Navier–Stokes equation, but without paying too much attention to the specific form of the dissipative term. The fluid, with velocity field v, will be enclosed in a cube 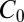of side 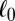, which, for simplicity, we may consider to have periodic boundary conditions. We choose an integer 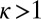and divide 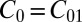into cubes 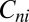of side 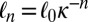, with , where n is a positive integer. Let 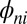be the homothety mapping 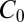to 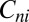. 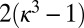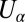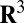One can choose real vector fields on with 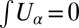, , 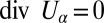and such that if the velocity field v satisfies 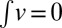, , 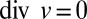there is a unique representation

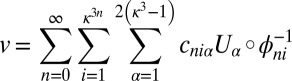with 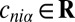. This means that v has a wavelet decomposition into components (roughly) localized in the cubes .

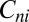We think now of the standard physical situation in which energy is put into the fluid at a large spatial wavelength (i.e., small n) and dissipated at a small spatial wavelength (i.e., large n). Intermediate values of n correspond to the inertial range, where the time evolution should, in some sense, be Hamiltonian. Specifically, Arnold (12) has shown how an inviscid flow could be interpreted as geodesic flow on the group of volume-preserving diffeomorphisms. The corresponding Hamiltonian is the kinetic energy of the velocity field.

We may thus think of the time evolution for (the finitely many) coefficients 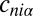as Hamiltonian, with external forces acting at low n and high n. This is related to the physical concept of eddies as dynamical structures localized in space. However, instead of a cascade of eddies of smaller and smaller size, we think of a system of coupled Hamiltonian systems, which we can label 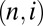. If we assume that the different systems 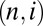are weakly coupled, we can reinterpret the global dynamics as a heat flow from small n, where energy is input, to large n, where it is dissipated (i.e., rapidly carried away to structures of the molecular size of the fluid). Note that the multifractal description of eddy cascades (13–16) ignores interactions between 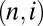and 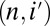, except when these eddies are created from a common 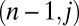. This corresponds to saying that the lateral interaction between the systems 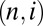and 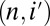is weak, but this assumption does not appear to be essential in our approach.

There is no hope for an exact study of the dynamics of the coupled systems 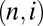, but we can get a first approximation from the Kolmogorov scaling theory of homogeneous turbulence (17). Because this theory gives unique answers, the problem of selecting an SRB state does not occur here. According to the Kolmogorov theory (17), the fluid velocity corresponding to 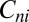is 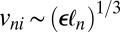, where ɛ is the mean dissipation per unit volume, and the kinetic energy corresponding to 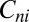is

(we have put the fluid density equal to 1); the corresponding temperature is

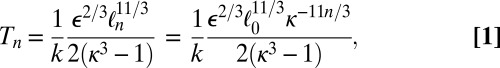where k is Boltzmann’s constant. In view of the value of k, we see that 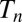is huge for small n, such that the flow of heat from high temperature to low temperature agrees with the energy cascade from small to large in the fluid. Notice that the heat resistance 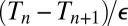is very large, which agrees with a weak coupling between the systems for different values of n.

We see the situation as follows: A heat flow interpretation of the energy cascade in homogeneous turbulence is possible, using scaling laws, but ignores fluctuations (intermittency). To understand fluctuations, we have to study the fluctuations of the energy flow in the Hamiltonian system of the coupled 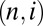. This is a problem of nonequilibrium statistical mechanics, which is a problem that is known to be difficult (18–20). In general, one would need the systems 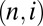to be chaotic in some sense (this is physically reasonable for 3D hydrodynamics), but the Anosov assumptions of Dolgopyat and Liverani (19) and Ruelle (20) are unreasonably strong. In the present situation, a rigorous analysis appears quite out of reach at this time. An approximate study is possible, however, and will give more specific results than earlier multifractal approaches (13–16), and there will be a physical justification rather than ad hoc assumptions.

Although we have no detailed understanding of heat flow from the point of view of rigorous statistical mechanics at this time, we expect that Fourier’s law should hold under normal conditions. This is no great help, however, because Kolmogorov’s theory yields the precise temperature distribution (Eq. 1). With regard to the “microscopic” fluctuations, they are a difficult problem in nonequilibrium (21, 22), being different in nature from the well-understood equilibrium fluctuations. Here, we shall use the assumption that the systems 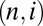have weak mutual coupling to justify a Boltzmannian energy distribution for each Hamiltonian system .

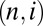Because of the large temperature gradient, the flow of energy is overwhelmingly from the system 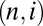to the systems 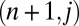. To study this energy flow, we use the conservation of energy and scaling as in the multifractal approaches (14) to write

Note that 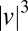is proportional to the kinetic energy 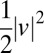with a weight 1/time spent in a certain spatial frequency range. We then interpret Eq. 2 to mean that, given the energy 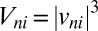in 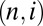, the velocity 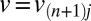is fluctuating with a Boltzmannian distribution

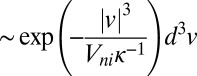Therefore, the energy 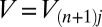has the normalized distribution

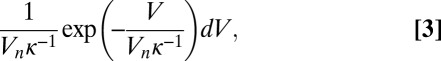where we write 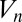from now on instead of 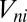, for example. We view Eq. 3 as an approximate but physically motivated relation, the validity of which will be discussed below. Note that if we replace 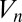by 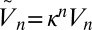, we have that 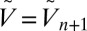is distributed according to

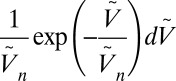We now discuss the structure functions, that is, the moments

for positive integer p and the exponents 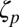such that

We have here

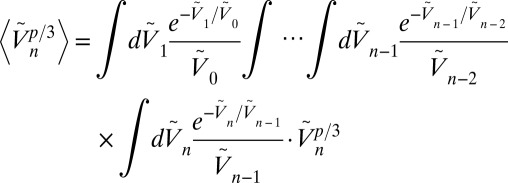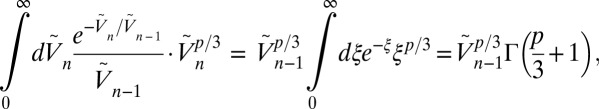such that, by induction, we find

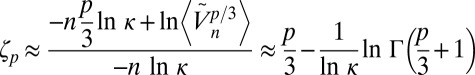In conclusion, we have the (approximate) prediction

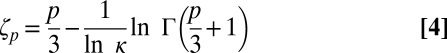Note that Eq. 4 gives .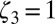

Using either the heat propagation or the eddy cascade picture, we see that κ should be chosen such that the initial 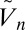distribution concentrated on one value for 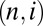thermalizes to values of 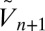for the systems 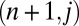distributed according to

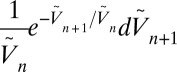This requires that κ be sufficiently large. However, if the value of κ is too large, several different temperatures will be present among the systems 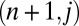connected with 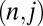and the 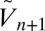distribution will not be Boltzmannian. The picture we have in mind is a situation in 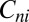that depends on the spatial wavelength. At a wavelength on the order of the size of support 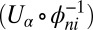, a single value of the kinetic energy is present. The distribution broadens as the wavelength diminishes and becomes a thermal distribution when it is divided by κ; at smaller wavelengths, there are several patches with different temperatures. Of course, a rigorous justification of this picture is well beyond the power of current mathematical methods. We can only claim this: κ should be such that when an eddy of size r has decayed to eddies of size 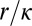, their energies have a thermal distribution, after which the process can start again. In the dissipative range, the distribution of 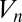should be cut off at large 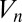. Numerically, one finds that in the experimental range 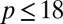, Eq. 4 fits the small set of experimental data (23) well with 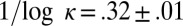(i.e., κ between 20 and 25). [The fit of the data in the study by Vincent and Meneguzzi (24) obtained by numerical simulation is less good.] Note that the Boltzmannian distribution we used can only be approximate in view of the way it has been obtained. In fact, Eq. 4 must break down after about 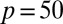because it gives decreasing 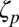in contradiction to a Hölder inequality prediction. Also, Eq. 2 may be valid as an average and acceptable in a mean field sense (25) but would not hold for the very large velocity increments described by the moments 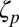for large p.

From a physical point of view, one can try the following interpretation: The change of behavior as one passes from a large wavelength to a small wavelength corresponds to what is observed at the onset of turbulence. We use here the physical fact that transport is much faster in the turbulent regime than in the laminar regime. Therefore, when sufficiently small scales are reached and we are in the turbulent regime, thermalization takes place. We may compute the length ratio 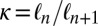in terms of the Reynolds number 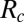for the onset of turbulence. If ɛ is the energy dissipation per unit volume and ν is the kinematic viscosity, the Kolmogorov length is 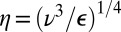, such that 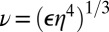. The velocity corresponding to the length λ is given in the turbulent regime by 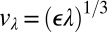. Therefore, if the onset of turbulence corresponds to λ, we have

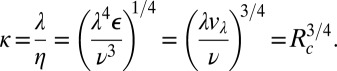The critical Reynolds number 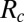is not defined with precision, but the value 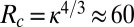is not unreasonable. Clearly, the calculation we have made is quite rough, but the exponent 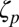should not be very sensitive to details, particularly because κ occurs only as its logarithm in Eq. 4. Notice also that the estimate 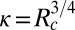is proposed instead of a fundamental calculation, which is beyond current possibilities. Altogether, the agreement of Eq. 4 with the experiment, with a plausible value of κ, supports the physical picture of turbulence that we have presented. This picture can thus also be used in related problems.