Kinetic characterization of the critical step in HIV-1 protease maturation

Abstract

HIV maturation requires multiple cleavage of long polyprotein chains into functional proteins that include the viral protease itself. Initial cleavage by the protease dimer occurs from within these precursors, and yet only a single protease monomer is embedded in each polyprotein chain. Self-activation has been proposed to start from a partially dimerized protease formed from monomers of different chains binding its own N termini by self-association to the active site, but a complete structural understanding of this critical step in HIV maturation is missing. Here, we captured the critical self-association of immature HIV-1 protease to its extended amino-terminal recognition motif using large-scale molecular dynamics simulations, thus confirming the postulated intramolecular mechanism in atomic detail. We show that self-association to a catalytically viable state requires structural cooperativity of the flexible β-hairpin “flap” regions of the enzyme and that the major transition pathway is first via self-association in the semiopen/open enzyme states, followed by enzyme conformational transition into a catalytically viable closed state. Furthermore, partial N-terminal threading can play a role in self-association, whereas wide opening of the flaps in concert with self-association is not observed. We estimate the association rate constant (k_on) to be on the order of ∼1 × 10⁴ s⁻¹, suggesting that N-terminal self-association is not the rate-limiting step in the process. The shown mechanism also provides an interesting example of molecular conformational transitions along the association pathway.

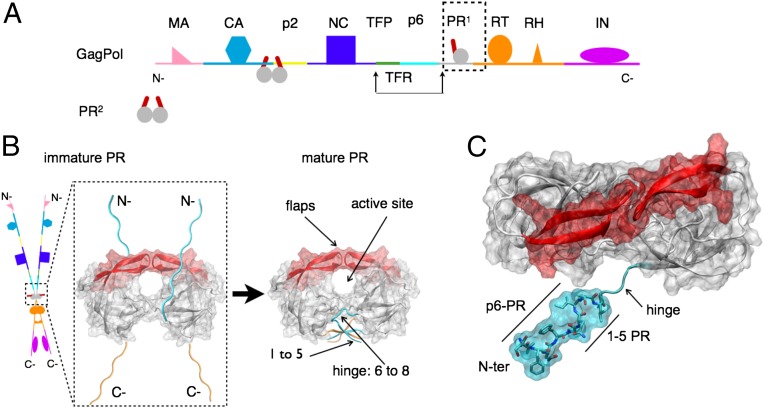
HIV, along with all retroviruses, achieves infectious maturation of nascent virus particles through cleavage of polyprotein precursors by the viral protease. In particular, the GagPol chains contain several covalently linked proteins including the protease itself (Fig. 1A). Thus, maturation of the virus is initiated by autocatalysis of viral protease initially embedded in GagPol precursors. HIV-1 protease is functional only in dimeric form (1, 2) because activity of monomeric protease precursor is three orders of magnitude less than the mature dimer (3), and yet only a single monomer is embedded within each precursor. Two individual monomers in different GagPol chains must, therefore, come together to form an embedded dimeric protease, which ultimately cleaves itself into a mature form (Fig. 1B).

Fig. 1.

(A) Schematic representation of a GagPol polyprotein precursor of HIV. GagPol is composed of a linear heteropolymer chain. Only a single monomer of protease (PR) is present on each GagPol chain. Mature protease cleaves GagPol at recognized cleavage sites between proteins. (B) Schematic representation of transient dimerization of two GagPol chains to form an embedded protease dimer. This precursor autocatalyzes its own liberation into the mature form of the dimeric protease that consists of natively folded N-terminal (cyan) and C-terminal (orange) chains in an interdigitated four-stranded β-sheet. A pair of β-hairpin structures termed the “flaps” (red) mediate active site access. (C) Structural representation of N-terminal (N-ter) construct (cyan) of immature HIV-1 protease, with 5-aa (VFSNF) extension corresponding to the p6-PR cleavage site. An unstructured hinge region connects the tertiary structure to the N-ter region.

Experiments indicate initial cleavage by a precursor protease still embedded in the GagPol chain occurs through an intramolecular, concentration-independent mechanism with the precursor protease cleaving its own terminus (4) and critically modulated by the N-terminal region (5–8). Mutations that block N-terminal cleavage result in severe loss of efficiency in catalytic activity. Cleavage at the protease (PR), reverse transcriptase (RT) junction at the C-terminal end of the protease by the precursor protease occurs via an intermolecular, concentration-dependent mechanism (9); mutations that block C-terminal cleavage, do not significantly affect either in vitro enzymatic activity and protease dimerization (9) or in vivo GagPol cleavage and virus maturation, suggesting that the precursor protease is well formed once the N terminus is cleaved. Therefore, experimentally, the only absolute prerequisite for mature-like catalytic activity and completion of viral precursor processing is autoprocessing at the N terminus of protease.

Structurally, this process of intramolecular cleavage requires that HIV-1 protease self-associate the precleaved N terminus to its own active site. Access to this site is modulated by a pair of flexible β-hairpin flaps (Fig. 1C) that must first open to allow entry and then close (10–15) to make substrate cleavage viable through a structurally conserved recognition pattern (16–19). Recent advances in paramagnetic relaxation enhancement (PRE) (20) reveal transient N-terminal contacts within the active site, but a complete structural characterization of this transient process in full atomic detail remains an outstanding challenge and is the aim of this work.

All-atom molecular dynamics simulation is a powerful computational tool to investigate such transient events (21) at the atomic level. Here, we present a computational study of the process of N-terminal self-association of HIV-1 protease. Using high-throughput ensembles of unbiased all-atom explicit solvent molecular dynamics simulations using ACEMD (22) on a distributed computing network (23), we investigate at full-atomic resolution the complete self-association process of the cleavage recognition site (VSFNF-PQIT) at the N terminus of HIV-1 protease (Fig. 1C), representing immature protease in GagPol precursor.

Although the above treatment provides evidence of the intramolecular cleavage mechanism, it is further interesting to understand more quantitatively the role of molecular conformational transitions along the self-association pathway. The existence of conformational ensembles in free enzyme is well established (24, 25). We have shown previously that several conformations in HIV-1 protease preexist in apo form (15).

Our investigation is partitioned as follows. Firstly, we perform 417 × 400 ns simulations (run set E1) of an immature protease in an initially N-terminal disassociated state with flaps in a semiopen conformation. These demonstrate that N-terminal active site entry is possible. However, further flap rearrangements are necessary to complete self-association to a catalytically viable closed-conformation within the structural envelope of existing peptidic ligand complexes (16–19). We, therefore, also perform 416 × 400 ns simulations (run set E2) of an immature protease starting from an initially self-associated N terminus and with flaps in a semiopen conformation, exploring the transition into a closed conformation.

Results and Discussion

Observation of N-Terminal Self-Association and Closed-Flap Catalytic Viability.

No atomic resolution structure exists of an N-terminal self-associated HIV-1 protease, nor of the p6-PR octapeptide complex, which shares sequence identity to the N-terminal region. Therefore, we derived a putative N-terminal self-associated HIV-1 protease with closed-flap conformation (R1) from an existing crystal structure of MA-CA cleavage region peptide-bound HIV-1 protease, which shares partial sequence and structural overlap to the p6-PR cleavage region (SI Materials and Methods). The structure was subsequently relaxed in a molecular dynamics simulation for 1 μs. We tested the validity of this N-terminal self-association construct R1 by comparing against two control sets of molecular simulations: (i) MA-CA–bound (control C1) and (ii) p6-PR–bound (control C2) HIV-1 protease complexes (SI Materials and Methods and Figs. S1 and S2). Analysis showed that the cleavage peptide region of the construct maintains a stable conformation with cleavable geometry. Based on these analyses, the final structure of the R1 simulation was selected as a reference structure to compare unbiased self-association simulations of systems E1 and E2 (SI Materials and Methods).

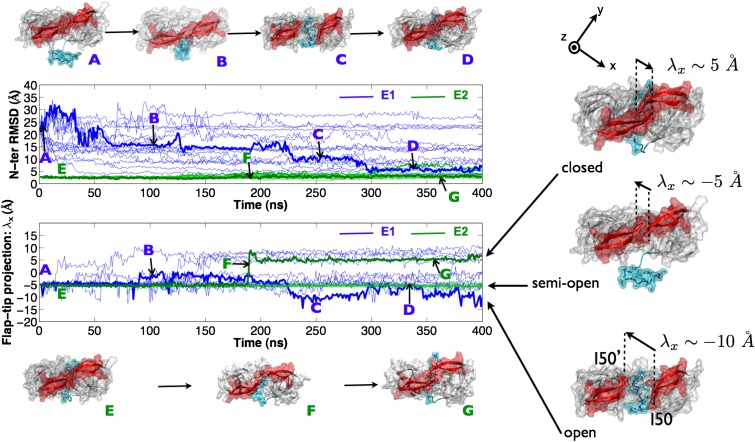
The time evolution of a sample of trajectories for each of the two run sets is shown in Fig. 2 and highlights, in particular, a single trajectory from each set (E1, E2) with corresponding structural representations at various time points. The root-mean-square deviation (rmsd) of the N-terminal region with respect to the reference closed-flap N-terminal self-associated structure (R1) was measured along the time course for each run set. The flap conformation was measured using a 1D metric λ_x, which sharply separates open (λ_x ≈ −10 Å), semiopen (λ_x ≈ −5 Å), and closed (λ_x ≈ 5 Å) flap conformations (Fig. 2).

Fig. 2.

N-terminal rmsd and flap-tip λ_x values for several of the 400 trajectories from each of the E1 (blue) and E2 (green) run sets. Representative trajectories showing capture of N-terminal self-association from unbound state (A through D) and enzyme-conformational flap-closure from an N-ter self-associated state (E through G) are in bold. Open, semiopen, and closed flap conformations can be sharply distinguished by a 1D metric based on the I50-I50′ flap-tip separation vector projected on the frame-aligned x axis (λ_x).

For run set E1, from 417 simulations each run for 400 ns from a HIV-1 protease with an initially disassociated N terminus [Fig. 2 (A)] and with flaps in a semiopen conformation, we captured 18 events (4.5%) of self-association to the active site within 5-Å rmsd to the reference structure R1 and two events (0.5%) within 3-Å rmsd. However, the latter were not accompanied by a flap transition to the closed state. The majority of trajectories did not exhibit N-terminal entry, although a significant number of all trajectories (38%) formed an encounter complex (15 Å > rmsd > 10 Å) in which the N-terminal region was associated to the side of the active site but did not enter [Fig. 2 (B)]. N-terminal entry was observed via a mixture of modes, making use of an open-flap conformation [Fig. 2 (C) and Movie S1], as well as lateral threading to a self-associated state [Fig. 2 (D) and Movie S2]. The N terminus was also observed to adopt a hairpin conformation that initiated self-association, followed by flap opening. In vivo, lateral threading is not possible because the N-terminal region continues into the much longer upstream GagPol chain and is an artifact of the system construct. By contrast, a combined hairpin and flap-opening mechanism is physiologically permissible. For run set E2, from 416 simulations each for 400 ns starting from an initially tightly (rmsd < 3 Å) self-associated [Fig. 2 (E)] N-terminal region with a semiopen-flap conformation, around 70% of the trajectories stayed within 3-Å rmsd. Eight trajectories (2%) exhibited greater flexibility, sampling regions of rmsd > 5 Å.

For E1, only 10 trajectories (2.5%) remained exclusively within the semiopen conformation (−6 Å > λ_x > −1 Å); indeed, reversible flap transitions between semiopen and open (λ_x < −8 Å) occurred in 306 trajectories (73%); this is expected given the <10-ns timescale measured previously for the transition (10). Transitions between semiopen and closed (λ_x ≈ 5 Å) were also observed in 158 trajectories (38%). For E2, 392 trajectories (94%) remained within the semiopen conformation, 22 (5.3%) made transitions to an open conformation and only two made (0.5%) a sharp transition [Fig. 2 (F)] into a catalytically viable closed conformation [Fig. 2 (G) and Movie S3]. The fact that both self-association from a disassociated state and conformational reversal from semiopen associated state to a catalytically viable closed-flap state occur provides compelling evidence that autocatalytic maturation of HIV-1 protease occurs via an intramolecular mechanism.

Analysis of Conformational Transitions.

In this study, the entire ensemble of trajectories covers all steps of the complete association and dissociation pathway, thus permitting to assemble a kinetic model of the entire process using appropriate statistical methods. Recently, Markov (state) models (MSMs), also termed kinetic networks (or transition networks), have received a surge of interest (26–29) and have been used successfully to calculate several slow processes from ensemble molecular dynamics data (30–32) (SI Text). Here, we chose to build an MSM based on the two informative order parameters λ_x and N-ter rmsd. The 2D parameter space was discretized into 1,400 states based on a 1.0-Ų bin size. Each data point from the aggregate of ∼335-μs simulation trajectories was assigned to a corresponding state. A transition matrix T(τ) was then constructed using a reversible estimator from a count matrix of transitions between these states at a lag time of τ = 50 ns (Fig. S3) and validated using a Chapman–Kolmogorov test (Fig. S4) as described previously (28).

Energetics and conformations.

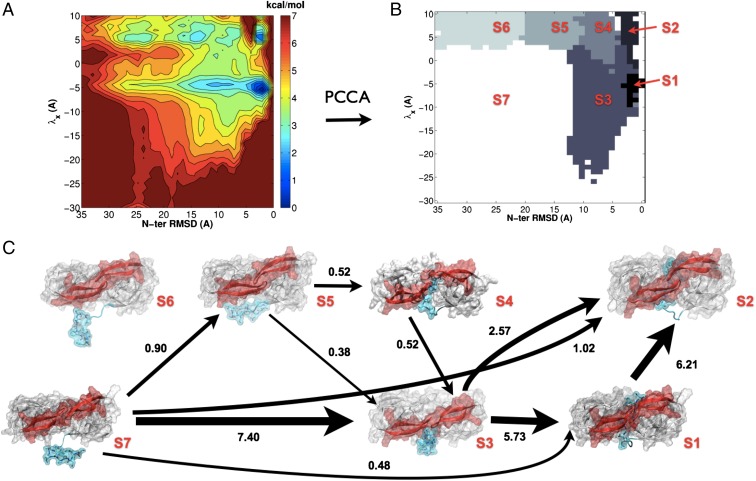
Fig. 3A shows the potential of mean force (PMF) on the two selected order parameters. The PMF energy is generated as F(x, y) = −logπ_i(x, y)/kT, where π_i is the stationary probability of state x, y estimated from the MSM transition matrix. Seven metastable energy wells are identifiable from the energetic map. Kinetic clustering to seven metastable states using Perron cluster cluster analysis (PCCA⁺) results in state partitioning consistent with the energetic wells described by the PMF, and the corresponding states, S1 to S7, are labeled (Fig. 3B). Conformations A through G, described before, correspond to locations within this discretization space. Conformations A, B, E, and G lie within the energy wells of metastable states S7, S3, S2, and S1, respectively, conformations C and D are grouped together in S3, whereas conformation F is a transition state between S2 and S1.

Fig. 3.

(A) PMF from a MSM in the discretized λ_x N-terminal rmsd projection. (B) Kinetic clustering of the discretized λ_x N-terminal rmsd space into seven distinct metastable states, S1 through S7, using the PCCA method (44). (C) Network of the 90 most relevant transition pathways from the disassociated semiopen state S7 to the self-associated catalytically viable state S2. The thickness of the arrows indicates the flux of folding trajectories between each pair of states. For each state, S1 to S7, a representative structure is shown. The numbers next to the arrows give the normalized net flux (in ×10³ s⁻¹).

The free energy of the most popular state was arbitrarily set to zero, and all other states were compared relative to it. Structurally, states S7 (1.3 kcal/mol) and S6 (1.7 kcal/mol) correspond to N-ter–disassociated semiopen/open and closed conformations, respectively. States S5 (1.3 kcal/mol) and S4 (1.7 kcal/mol) to closed-flap intermediate complexes, whereas S3 (0.6 kcal/mol) corresponds to a semiopen/open flap intermediate complex. Finally, states S2 (1.3 kcal/mol) and S1 (0 kcal/mol) correspond to the closed and semiopen N-ter–associated conformations. Our analysis shows that S1 is the energetically favored state, whereas S2 is by comparison an excited state with ΔG = 1.3 kcal/mol. The free energy of all states is within a range of 2 kcal/mol of each other. The equilibrium favored flap conformation in the disassociated state is semiopen/open (S7). We validated the convergence of the PMF calculation by applying a bootstrapping method that allowed determination of the error in the calculation (SI Text). The mean PMF was almost identical to that calculated from the entire dataset, and the SD was less than 0.4 kcal/mol for all relevant microstates within any given macrostate (Fig. S5), except for S2, which reached an error of 0.8 kcal/mol. The highest regions of error (1.6 kcal/mol) corresponded to poorly sampled regions at the extremities of the conformational landscape (Fig S6).

Kinetics and mechanism.

The kinetics of interconversion between the disassociated state S7 and the catalytically viable state S2 was determined by computing the total net flux between the states [(1.07 ± 0.44) × 10⁴ s⁻¹], from which the self-association constant could be calculated (30) to be k_on = (1.12 ± 0.56) × 10⁴ s⁻¹. Furthermore, the total flux was decomposed into pathways along pairs of states from which the flux for all pathways along sets of states between S7 to S2 could be identified and sorted (Table S1). The flux network from the 90% most relevant transition pathways is shown in Fig. 3C. The remaining 10% of the flux is in minor pathways between the states shown in Fig. 3C and is omitted for clarity of visualization. Most of the flux passes through state S3 (8.3 × 10³ s⁻¹); the state, therefore, acts as a major transition hub for the process. State S6, on the other hand, is a “dead-end” state, with insignificant flux passing through it.

The most probable transition pathway is S7→S3→S1→S2 and accounts for 53.6 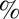of the total flux, with a flux of (5.73 ± 2.78) × 10³ s⁻¹. This pathway corresponds to the process of prior self-association in the semiopen/open conformation, followed by an induced-fit mechanism of flap closure into a catalytically viable state. The other most relevant pathways are in order: S7→S3→S2 (15.5% of total flux), S7→S2 (9.6% of total flux), S7→S1→S2 (4.5% of total flux), S7→S5→S4→S3→S2 (4.2% of total flux), and S7→S5→S3→S2 (3.6% of total flux).

The pathways corresponding to self-association via prior selection of a closed-flap conformation by a self-associating N terminus, that is, those that do not pass through S3 or S1 (S7→S6→S5→S4→S2, S7→S6→S4→S2, S7→S5→S4→S2, S7→S6→S2, S7→S5→S2, and S7→S4→S2) are far weaker (lying within the 10% residual flux not displayed), and combined, carry 7.6% of the total flux. The statistical error in the flux calculations was estimated by computing the SD of the fluxes obtained from 10 subsets of 400 trajectories taken from the entire dataset (Materials and Methods). The fluxes between each pair of states and from all 10 subsets are listed in full in Tables S2 and S3.

Interestingly, a seven-state model does not kinetically separate semiopen and open conformations in either the disassociated (S7) or intermediate states (S3). This agrees well with previous calculations and experimental measurements of the relaxation rate of fast-flap conformational opening, which exhibits a small kinetic barrier (k_flap ≈ 0.1 ns⁻¹) (10, 15, 33, 34). Even though self-association via both flap opening and lateral threading was observed, it is difficult to attribute any event solely to either one or the other mechanism. In our data, self-association events occur via a mixture of the two modes on a nanosecond timescale. The intermediate state, therefore, permits both threading and partial flap opening concurrently and is reflected in the results of the kinetic clustering procedure that assign state S3 to both conformations. Although, in vivo, the flaps must open for GagPol to reach the linear peptide formation required for cleavage, our study shows that a threading mechanism may also partially contribute to traversal across the active site. This is further supported by the previous observation of lateral substrate binding (35). In vivo, threading could be achieved by a hairpin peptide formation, followed by flap opening and reclosing in conjunction with unfolding of the hairpin. The fact that there is a small flux from S4 to S2 suggests that a minor contribution to the hairpin-threading mechanism may also come from a partially closed flap form.

A wide-open flap conformation in the free enzyme has been characterized previously (14, 15). Here, a wide-open conformation corresponds to λ_x < −20 Å. Only a few trajectories transiently exhibited wide-opening, consistent with the experimentally observed 100-μs relaxation timescale (33) and with previous simulations of the mature protease (15). This also places a lower limit of ∼100 μs on the wide-opening relaxation time for an immature protease. Interestingly, we did not observe any wide-opening events in conjunction with N-terminal self-association, as reflected in the PMF (Fig. 3A), demonstrating that flap opening not wide opening is sufficient for N-terminal self-association and suggesting that the kinetic behavior of the flaps is connected to the state of the N terminus. Many events of flap wide opening do, however, show simultaneous association of the N terminus to the dimer interface, resembling the exterior strand of the mature dimer interface. Therefore, wide opening might predominantly occur in mature-like protease dimers; however, to determine accurate kinetics for it in either the mature or immature protease would require at least an order of magnitude greater sampling.

Of the 18 trajectories that exhibited self-association, most occur via a mixture of lateral threading, N-terminal hairpin formation, and flap opening. Therefore, we recalculate the association constant while excluding those trajectories for which the initial entry event was lateral threading. This does not qualitatively change the results; the same energetic minima appear in the PMF, and a seven-state kinetic model yields a similar separation of states (Fig. S4). The calculated association rate constant is k_on = 1.18 × 10⁴ s⁻¹, which is similar to the former result. Therefore, because flap-opening kinetics are fast, the kinetics of self-association are not rate-limited by the requirement that the flaps open in vivo.

The self-associated open state is also kinetically indistinguishable from the semiopen, S1. The tapering of the PMF in the low N-ter rmsd region shows that from the intermediate state, increased N-ter self-association sharply reduces the probability of maintaining an open state. This is consistent with a picture in which any instance of an open self-associated state converges rapidly to a semiopen state and is supported by nanosecond-timescale observations of flap closure after manual placement of ligands into a flap-open protease active site (36, 37).

Conclusions

We have investigated the proposed intramolecular mechanism by which immature HIV-1 protease autocatalyzes its own release from nascent GagPol polyprotein precursors, using all-atom explicit solvent molecular dynamics simulations of an immature dimeric HIV-1 protease construct. The observed overlap between forward and reverse processes, together with the completion of closed-form self-association, is compatible with N-terminal intramolecular autocatalysis and proceeds via flexible rearrangement of the N terminus, structurally coordinated opening of the flaps to allow entry, followed by closure of the flaps to form a catalytically viable complex. Furthermore, partial N-terminal threading plays a role in self-association, whereas wide opening of the flaps in concert with self-association is not observed. From these data, we construct an MSM process that permits a quantitative kinetic analysis. The most probable transition pathway from a disassociated to a catalytically viable state is first via self-association in the semiopen/open state of the protease, followed by a flap-conformational change into closed form.

The on rate (k_on) of self-association to a closed state is estimated from our simulations to be of the order of ∼1 × 10⁴ s⁻¹, whereas the rate constant of intramolecular autocatalytic cleavage, k_first, is several orders of magnitude smaller (k_first ≈ 7 × 10⁻⁴ s⁻¹) (5). Therefore, not only is N-ter self-association from a dimeric precursor possible, but it is also comparatively fast, not being the rate-limiting step in the overall autocatalytic process.

This indicates that either initial dimerization or postcleavage formation of the native fold is rate-limiting. However, because cleavage of the N terminus results in mature-like activity, formation of the postcleaved native fold is likely not to play a limiting role either. Structurally, this can be explained because the N-terminal junction serves as a tether that restricts the diffusion and, thus, function of the protease, but once cleaved, the protease is free to move around and process other substrates more easily. Thus, by elimination, the limiting step in the autocatalytic process is likely to be the initial dimerization of the GagPol chains to form an immature dimer capable of N-terminal cleavage, as seen also by Tang et al. (20).

The necessary function of the N terminus in autocatalysis makes targeting the preliberated structure a potentially resistance-proof strategy for a class of antiretroviral allosteric inhibitors of the immature protease.

Materials and Methods

System Preparation.

Five different HIV-1 protease systems were constructed for this study. These were the E1, E2, R1, C1, and C2 constructs (Table 1). E1 was constructed to investigate initial N-ter self-association, and E2 was constructed to investigate subsequent flap closure to a catalytically viable state. R1 served as a reference closed-flap self-associated state, whereas C1 and C2 were MA-CA and p6-PR ligand–bound octapeptide control complexes against which R1 was validated. The exact protocol for preparation depended on the specific requirements of each system and are described in SI Materials and Methods. Corresponding crystal structures were taken from the Protein Data Bank (38). The standard AMBER force field (ff03) with standard ions (39) was used to describe all parameters. Each system was solvated using TIP3P water (40) and electrically neutralized (ionic concentration, 0.15 M NaCl) with long-range Coulomb interactions handled using the particle mesh Ewald summation method (PME) (41, 42). See SI Materials and Methods for the simulation settings and protocols. Experimental accuracy of the molecular simulation protocol for the HIV-1 protease has been validated previously using NMR S² order parameters (15). All production simulations were carried out using ACEMD (22). Production-ensemble simulations were deployed for systems E1, E2, C1, and C2 on the GPUGRID compute infrastructure (23). A set of 417 × 400 ns and 416 × 400 ns was used for the analysis of E1 and E2 sets, respectively. Similarly, a subset of 100 × 100 ns each was used for the analysis of the C1 and C2 control sets.

Table 1.

HIV-1 protease maturation system constructs

System	Definition	Flaps	Protease	Bound ligand	Production runs, ns
E1	Disassociated N-ter	Semiopen	PR+:PR	no	417 × 400
E2	Self-associated N-ter	Semiopen	PR+:PR	no	416 × 400
R1	Self-associated N-ter	Closed	PR+:PR	no	1 × 1,000
C1	MA-CA bound complex	Closed	PR:PR	SQNY-PIVQ	100 × 100
C2	p6-PR bound complex	Closed	PR:PR	SFNF-PQIT	100 × 100

PR⁺ is PR with VSFNF N-terminal extension.

Analysis.

N-terminal self-association proximity was measured using rmsd of the C_α atoms of residues −4 to +4 of the N terminus relative to the closed-bound reference structure (R1). Visual inspection confirms N-terminal active-site entry corresponds to an rmsd of within 5 Å to R1 and is, thus, used to define self-association. Catalytic viability of the N-terminal region requires closer self-association, to within 3-Å rmsd (SI Materials and Methods), as well as a conformational change in the flap region from the equilibrium semiopen to the closed conformation. We devised a 1D metric based on the I50-I50′ flap-tip separation vector that can distinguish these conformations sharply. The λ_x metric is the projection of this vector on the frame-aligned x axis. The x axis was chosen to be the vector between the center of mass (COM) of the backbone atoms of residues 23, 24, and 85 of the second and first monomers, respectively, each frame. These residues are within the β-sheeted region that supports each side of the active site and exhibit very small root-mean-square fluctuations (rmsfs) compared with other residues (15). The use of frame-aligned vector projection allows for opposite flap-handedness between semiopen and closed conformations to be represented by opposite signs (Fig. 2).

To describe the dynamics of the molecular system, we analyzed the sequence of transitions between discretized states by a MSM. The MSM construction was performed using a combination of the ACEMD toolkit (ACEMDTK) (http://multiscalelab.org/acemd/protocols) and the EMMA package (43). See SI Materials and Methods for details of the MSM construction. The aggregate of ∼335 μs of simulation data from ensemble sets E1 and E2 was used to construct a discretized MSM using a 2D projection in the λ_x N-ter rmsd space from which a PMF was calculated (Fig. 3).

Other reaction coordinates were also considered but the chosen 2D projection can clearly decompose flaps dynamics with N-terminal binding. N-terminal binding could be defined in terms of rmsd because there is a well-defined bound structure for comparison, but flap conformations are not sharply separated using rmsd in a single dimension. For example, relative to a closed conformation, several conformations yield similar (within 2 Å) rmsds to each other and, thus, degenerate states in the MSM. The λ_x metric exploits the symmetry of the protease and distinguishes the conformations of interest, and yet only uses a single dimension that is independent of any reference structure.

The discretized model was further clustered into a smaller set of coarse-grained metastable states using the PCCA method (44). Kinetic fluxes between these states was computed using the methodology presented previously (30). The error in the PMF and the fluxes was calculated by applying a bootstrapping method (Fig. S5). The flux was calculated for each subset based on the metastable state definitions obtained in the PCCA⁺ clustering from the entire dataset (Tables S1 and S2).