Abstract
This paper describes the implementation and performance of a nonlinear time-domain model of the cochlea for transient stimulation and human otoacoustic emission generation. The nonlinearity simulates compressive growth of measured basilar-membrane impulse responses. The model accounts for reflection and distortion-source otoacoustic emissions (OAEs) and simulates spontaneous OAEs through manipulation of the middle-ear reflectance. The model was calibrated using human psychoacoustical and otoacoustic tuning parameters. It can be used to investigate time-dependent properties of cochlear mechanics and the generator mechanisms of otoacoustic emissions. Furthermore, the model provides a suitable preprocessor for human auditory perception models where realistic cochlear excitation patterns are desired.
INTRODUCTION
Time-domain models of the cochlea can simulate cochlear traveling waves and have successfully been used to investigate the mechanisms underlying otoacoustic emission (OAE) generation (van Hengel, 1996; Talmadge et al., 1998; Elliott et al., 2007; Choi et al., 2008; Moleti et al., 2009; Epp et al., 2010; Liu and Neely, 2010; Verhulst et al., 2011b). All these models represent the cochlea as a cascade of coupled two-port networks, but differ in how they represent compression in local basilar-membrane (BM) motion. For applications and research purposes, it is useful to have direct control over the tuning (Q) properties of the BM and the variation of Q with intensity. The representation of the active process related to outer-hair-cell processing, whether based on micromechanical properties of the cells (Elliott et al., 2007; Moleti et al., 2009; Choi et al., 2008; Liu and Neely, 2010) or, functionally, as an intensity dependent gain reduction in the BM admittance (van Hengel, 1996; Epp et al., 2010), has a large effect on the frequency and level-dependence of Q. Unfortunately, in most models it is difficult to evaluate or manipulate BM tuning properties as they result from a specifically designed set of cochlear parameters.
The model proposed here provides an alternative to the described models by giving the user direct control over the poles of the BM admittance, and thus over the tuning and gain properties of the model along the cochlear partition. A functional, rather than a micromechanical, approach for the nonlinearity design is followed with the purpose of realistically representing level-dependent BM impulse response (IR) behavior (Recio and Rhode, 2000; Shera, 2001). The model simulates both forward and reverse traveling waves (OAEs), which provides a double advantage. Recorded human OAEs can be used to constrain the parameters in the model, and secondly, changes in OAEs can be predicted (and afterwards recorded) when varying cochlear parameters to known stimuli. The model was calibrated using data from human click-evoked (CE) and stimulus-frequency (SF) OAE recordings, and can simulate distortion-product (DP) and spontaneous (S)OAEs.
THE MODEL
Cochlear mechanics
The cochlea was modeled as an uncoiled fluid-filled tube containing an array of oscillators that are coupled through the incompressible fluids in the scalae. It was assumed that the pressure was uniformly distributed in the directions perpendicular to the BM by assuming that the wavelength of the traveling wave is large compared to the height of the scalae at all locations along the BM (i.e., long-wave approximation; de Boer, 1991). The cochlear series impedance Z(s) and shunt admittance Y(s) were described in Zweig (1991) for s = jω/ωc, and were solved here for a cochlea of N = 1000 sections.1 The center frequency for each section was determined by the Greenwood (1961) map and the cochlea was tapered so that the input impedance of the cochlea was resistive by making the BM stiffness proportional to the scalae area (Zweig, 1991; Shera and Zweig, 1991). The parameters describing the cochlear model are given in Table TABLE I..
TABLE I.
Parameters used in the transmission-line model of the cochlea.
| Parameter | Value | Units | Ref. | Physical meaning |
|---|---|---|---|---|
| x | 35 e − 3 | m | a | BM length |
| b | 1e − 3 | m | a | BM width |
| h | 1e − 3 | m | a | Scala height |
| N | 1000 | — | No of cochlear sections | |
| dx | x/N | m | a | Width of section n |
| Ast | 3e − 6 | m2 | a | Area of the stapes |
| ρ | 1e3 | kg m−3 | a | Density cochlear fluid |
| fcl | 20682 | Hz | b | High frequency limit |
| fch | 140.6 | Hz | b | Low frequency limit |
| A | 61.765 | — | b | |
| l | — | |||
| Nw | 1.5 | — | No. of wavelengths | |
| ωc0 | 2π (fch) | s−1 | b | Characteristic angular frequency at base |
| ωcn | 2π (fch10−An − fcl) | s−1 | b | Characteristic angular frequency at section n |
| K0 | kg m−3 s−2 | c | Stiffness constant | |
| Ms0 | kg m−5 | c | Acoustical mass at base | |
| Mp0 | kg m−3 | c | Acoustical mass at base | |
| Msn | kg m−5 | c | Acoustical mass at section n | |
| Mpn | kg m−3 | c | Acoustical mass at section n | |
| MME | 1 | kg m−4 | Acoustical mass middle ear (dummy) | |
| RME | kg m−4 s−1 | Middle ear resistance |
Based on the values chosen by van Netten and Duifhuis (1983), Duifhuis et al. (1986), and van Hengel (1996) for the human cochlea.
The parameters describing the place-frequency distribution of the cochlea were chosen to agree with the experimental data of Greenwood (1961).
A proportionality between Cp and Ms was maintained to account for tapering in the cochlea, leading to the parameters indicated by footnote c. Zweig (1991); Shera and Zweig (1991).
The helicotrema boundary (i.e., n = N) at the apex was modeled as a short circuit and the middle-ear boundary (i.e., n = 0) was modeled as an impedance matching network, leading to a resistance RME at the middle-ear boundary. When the value of RME is chosen to equal the cochlear input impedance [i.e., near the base of the cochlea where is small], standing waves between the middle-ear boundary and the traveling-wave peak are not generated. Changing RME to a value that does not match Zin adds reflectivity to the middle-ear boundary. This allows for reflection of reverse travelling waves back into the cochlea as forward traveling waves, and can lead to the generation of multiple internal reflections (Zweig and Shera, 1995) and spontaneous otoacoustic emissions (Shera and Guinan, 2003). Middle-ear transmission was modeled by applying the forward and reverse middle-ear gain functions (Puria, 2003) to the stimulus and reverse traveling wave, respectively.
An instantaneous nonlinearity was included in the model to account for the compressive nonlinearity observed in measured BM impulse responses (IRs) (Recio and Rhode, 2000). These data are characterized by a near-invariance of the IR fine-structure when increasing stimulus intensity (Recio and Rhode, 2000; Shera, 2001). Shera (2001) developed a model in the frequency domain that describes the level-dependent BM IR behavior through a careful placement of the poles of the BM admittance Y(s). Near the peak of the traveling-wave, Y(s) is dominated by two closely spaced poles near s = j (that can be represented by a coinciding double pole; Zweig, 1990), of which the pole location α* relative to the imaginary axis of the complex s-plane determines the stability of the model. The value of α* is related to δ, ρ, and ψ in Eq. 1 through the equations derived in footnote 8 of Shera (2001). For an active (but stable) model solution where δ is negative, the double pole is placed close to the positive imaginary axis of the complex s-plane on the negative side of the real axis (Zweig, 1991; Shera, 2001). For passive model solutions where δ is positive, the double pole is situated further away from the positive imaginary s-axis (Shera, 2001), i.e., takes a more negative real value. When the double-pole trajectory between the active and passive model solutions in the s-plane is kept horizontal, the IR fine-structure remains invariant while the BM IR shows increased compression (Shera, 2001). As α* increases from a smaller value (more active) to a larger value (less active) following the horizontal trajectory, the BM IR becomes shorter and the auditory filters become wider (see Fig. 1). This nonlinearity concept that moves the location of the double pole of Y(s) depending on the local BM motion, and thus indirectly on the intensity of the input, was adapted and implemented in the present model. A pole-trajectory was designed for all locations along the BM for stimulus levels between 30 and 97 dB sound pressure level (SPL) with a compression slope of 0.4 dB/dB.2 The model includes an algorithm that adaptively determines the pole locations in Y(s) at each time step depending on the local BM velocity, vBM, in the previous time step.
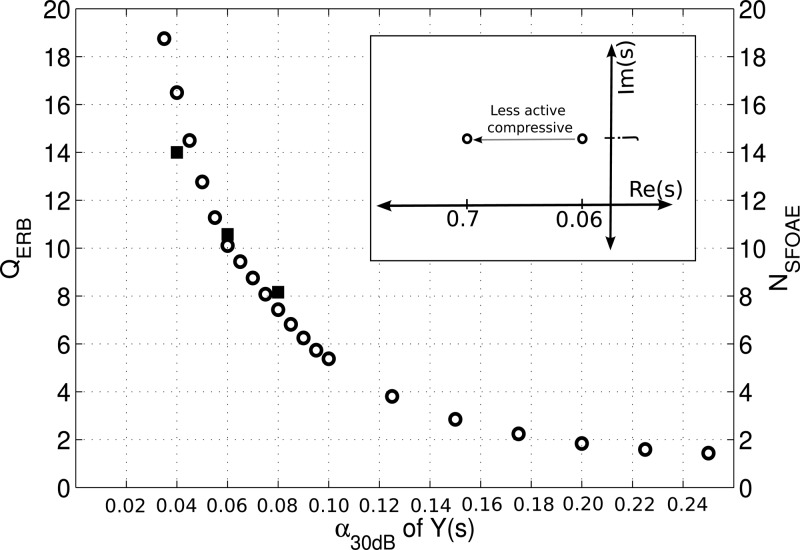
Figure 1.
Relationship between α*30 from Eq. 4 describing the compressive nonlinearity and QERB and NSFOAE. α*30 was varied while the stimulus was a 40-dB-peSPL click. QERB = fc/BWrect where the bandwidth of the filter BWrect was determined from a rectangular filter with the same power as the area under the spectrum of the BM IR at 1 kHz. was determined from the negative slope of the unwrapped CEOAE phase-vs-frequency plot evaluated at f = 1 kHz for CEOAEs simulated to a 40-dB-peSPL click. As CEOAEs and SFOAEs are equivalent for low level stimuli (Kalluri and Shera, 2007), NCEOAE evaluated at 1 kHz reflects NSFOAE at 1 kHz.
Otoacoustic emissions
The simulation of otoacoustic emissions has two prerequisites: the traveling-wave equation needs to be calculated over time, and secondly, reverse traveling waves, manifest at the eardrum as OAEs, need to be generated. The transmission-line matrix determined by Eqs. 2, 3 was calculated using Gaussian elimination (Gentle, 1998) and was solved over time using the fourth order Runge–Kutta method (Diependaal et al., 1987). One of the most extensive and thoroughly tested models of otoacoustic emission generation infers that the forward traveling wave is reflected by pre-existing random BM impedance irregularities (Zweig and Shera, 1995; Shera and Guinan, 1999; Shera et al., 2008). These irregularities are believed to be inherent to a healthy cochlea and may reflect small cell-to-cell differences in outer-hair cell amplification and alignment, that can be thought of as place-fixed BM impedance irregularities. Through the mechanism of coherent reflection, the BM irregularities give rise to backwards-traveling waves that can be recorded in the ear canal as reflection-source emissions (Shera and Guinan, 1999). An additional source of emission generation comes from the compressive nonlinearity in the cochlea that gives rise to waveform distortion and leads to distortion-source emissions (Shera and Guinan, 1999).
Because the presented model contains a compressive nonlinearity, distortion-source emissions are implicit, and reflection-source emissions are accounted for by introducing BM irregularities in Y(s). Two parameters were allowed to vary randomly along the cochlear partition: First, the double pole location applied below the nonlinearity threshold at 30 dB, α*30, was varied with maximum excursions of 5% around its initial value. Second, the vBM threshold for the compressive nonlinearity was allowed to vary by 1 dB around its center value of 30 dB. Adding small variations of these two parameters across the cochlear partition mimics small cell-to-cell differences in outer-hair cell amplification and nonlinearity threshold and determines the strength of the reflection-source emissions. A random vector of α*30 and vBM30 values was generated using a random number generator with a specific starting seed for every model subject. Consequently, every model subject had a fixed set of random BM irregularities which, in analogy to frozen noise, led to frozen models where all parameters but the irregularity vector were identical. In the model, the irregularities can either be turned on (reflection-source and distortion-source OAEs simulated) or off (only distortion-source emission generated), and the nonlinearity can be turned off (only reflection-source emissions generated), making the model suitable for studies investigating otoacoustic emission generator mechanisms.
Calibration
The model was calibrated by considering the simulated emission amplitude and group delay. The amplitude of the simulated OAE depends on α*30 [the pole location that determines δ in Y(s)], the size of the BM irregularities (variation in % of α*30 and in dB of vBM30), and the number of sections N in the model. With each doubling of the number of cochlear sections N, the mean stimulus-frequency (SF) OAE magnitude across 40 frozen models decreases by 3 dB. Furthermore, a 6-dB increase in SFOAE magnitude occurs when doubling the magnitude of the irregularities added. Since there is little physiological evidence relating the number of cochlear sections to the number of rows of outer-hair cells, or constraining the size of cochlear irregularities, these parameters were adjusted to simulate realistic SFOAE level-curves. Since Kalluri and Shera (2007) demonstrated that CEOAE and SFOAE level-curves show a near-equivalence for low-level stimuli, it was assumed that fitting the model parameters to SFOAE level-curve data yields realistic CEOAE levels. For the simulations shown in Figs. 12, N was 1000, Δα*30 5%, and ΔvBM30 1 dB.
Figure 2.
(A) Overlaid yBM BM IRs simulated for the 1-kHz cochlear CF location for clicks with intensities between 0 and 90 dB peSPL. The IRs were normalized by the pressure at the stapes of the cochlea such that compression is observed as a reduction of the IR amplitude. (B) I/O functions calculated as stimulus level in dB SPL versus rms level of yBM evaluated at CF (1-kHz location) and at one octave above and below CF. The stimulus was a 1-kHz pure tone with intensities between 10 and 100 dB SPL. (C) Cochlear excitation patterns calculated as the rms level of yBM per cochlear section n for stimulation with a pure tone of 1 kHz with stimulus intensities between 10 and 90 dB SPL. (D) CEOAE level curve calculated as the level of the click in dB peSPL versus the rms level of the CEOAE (i.e., waveform starting 5 ms after click onset) for 10 frozen models. Level curves are shown for a smooth model where the BM irregularities were turned off, and for a rough model where the irregularities were turned on. The rough model was either nonlinear or linear. The level difference between the smooth and rough (non)linear level curve reflects OAE gain. (E) SFOAE level curve calculated as the level of the pure tone versus the level of the SFOAE for ten different subjects. The SFOAE levels were obtained from the spectral level difference at the pure tone frequency between a recording where the BM irregularities were first turned on, and then turned off. (F) Group delay in ms, calculated as the negative slope of the unwrapped phase of the CEOAE, shown as an average over 40 frozen models for four different stimulus levels.
The location of the poles α* in the complex s-plane has an influence on the gain and tuning (QERB) of the auditory filters in the model. QERB measures the tuning of a rectangular filter with the same power as the area under the spectrum of the BM IR at 1 kHz [i.e., QERB = fc/BWrect where BWrect is the equivalent rectangular bandwidth; Moore and Glasberg (1983)]. Its value is not only controlled by the damping parameter in Y(s), but is also influenced by the coupling of the different cochlear sections through the cochlear fluids. QERB can be established from the tuning of an auditory filter evaluated at a section n of the cochlea, and inferred from the group delay of otoacoustic emissions, , recorded in the ear canal (Shera and Guinan, 2003; Shera et al., 2010). Figure 1 shows the relation between α*30 and QERB and the delay (in cycles) for a specific frequency in the OAE, evaluated at f = 1 kHz for stimulation with a 40-dB-peSPL click. All model parameters, except for α*30, were kept constant. As α*30 increases linearly from 0.035 to 0.25, QERB decreases from 19 to 1.75, demonstrating a power-law relation between α*30 and QERB. NSFOAE (black squares) shows a similar decreasing trend for poles of 0.04, 0.06, and 0.08 with a QERB/NSFOAE ratio close to 1, in agreement with ratios found in Shera et al. (2010) at 1 kHz. The model described here employs the concept of scaling symmetry so that QERB remains constant along the cochlear partition. The value of α*30 can be varied as a parameter so that the influence of auditory filter tuning on BM mechanics and OAE properties can be investigated. The default value of α*30 was 0.06, corresponding to a model QERB of 10 and a NSFOAE of 10.7. This value was found to match well with the psychoacoustically obtained QERB value of 9.26 and 11 for humans in Glasberg and Moore (1990) and Oxenham and Shera (2003), respectively. Furthermore, Shera and Guinan (2003) found an NSFOAE value of 10 at 1 kHz for humans. All model performance plots in Fig. 2 were obtained for a model with α*30 = 0.06 and a compression slope of 0.4 dB/dB.
MODEL PERFORMANCE
The main characteristics of the model are presented in Fig. 2. Panel (A) shows normalized BM impulse responses from the 1-kHz cochlear characteristic frequency (CF) location for different excitation levels (in peSPL). The simulated BM IRs show increased compression and a shift of the envelope maxima towards shorter latencies as stimulus intensity increases. At the same time, the BM IR fine-structure is near invariant with stimulus level. These results are in qualitative agreement with recorded BM IRs (Recio and Rhode, 2000) and demonstrate that the model nonlinearity was implemented appropriately.
Panel (B) of Fig. 2 shows BM I/O functions (i.e., stimulus level vs rms level of the BM displacement yBM) for pure-tone stimulation. The I/O functions were obtained at CF (1 kHz) as well as at cochlear locations corresponding to one octave above and below CF. At CF, the I/O function shows a compression slope of 0.4 dB/dB for stimulation levels between 30 and 97 dB SPL, and linear behavior beyond these boundaries. One octave above and below CF, the I/O functions are nearly linear.
Panel (C) shows cochlear excitation patterns, calculated as the rms level of yBM as a function of cochlear location for a stimulus consisting of a 1-kHz pure tone with different intensities. The excitation patterns become broader and their maxima move basally as stimulus level increases. These simulations are in good agreement with empirical longitudinal BM-velocity patterns recorded in chinchilla and gerbil (Rhode and Recio, 2000; Ren, 2002). Both studies reported a basal shift of the pattern maxima, together with a broadening of the patterns for increasing intensities. Rhode and Recio (2000) linked the basal shift of the BM patterns to the shift of the local transfer-function maxima to lower frequencies for increased stimulus intensity. This feature is also present in the model.
Panels (D)–(F) in Fig. 2 show characteristics of the simulated otoacoustic emissions. Panel (D) shows CEOAE level curves obtained as the rms level of the emission for 10 frozen models (different traces) vs click level in dB peSPL. The emissions were extracted from the waveform energy starting 5 ms after the click onset, and the BM irregularities were either turned on (rough) or off (smooth). CEOAE level curves were obtained for rough linear and nonlinear model implementations. The difference between the smooth and rough level curves reflects OAE emission gain (∼20 dB).
Panel (E) contains SFOAE level curves for the same frozen models as in panel (D). SFOAE levels were derived from the difference in spectral level at the stimulus frequency obtained from two simulations. In the first simulation, the BM irregularities were turned on (SFOAE response in the emission), and in the second simulation, the BM irregularities were turned off (no SFOAE). Unlike the CEOAE level curves in panel (D), the SFOAE level curves show irregular growth patterns. Notches in SFOAE growth curves have been observed experimentally by Schairer et al. (2006), and these may be explained by the shift of the SFOAE fine-structure patterns with level curves (Kalluri and Shera, 2007). When probing a frequency close to a dip of the fine structure, irregularities in the level curves are expected as the fine-structure dip shifts with intensity. This effect is expected to be less prominent when probing a frequency close to the peak of the fine-structure since they are more robust to changes in stimulus level. The location of the 1-kHz pure tone in relation to the SFOAE fine-structure was random for the frozen models presented in panel (E), leading to irregular SFOAE growth curves.
Mean group delays, representing the negative slope of the unwrapped phase spectrum of CEOAEs for 40 frozen models, were calculated for clicks between 50 and 80 dB peSPL and are shown in panel (F). The mean group delay at 1 kHz for stimulus levels of 50 dB peSPL was 9.5 ms. The group delay decreases with increasing frequency to 5.5 and 2 ms at 2 and 4 kHz, respectively. These values are within the range of the experimental group delays found by Pigasse (2008) for tone-burst OAEs at 66 dB peSPL (i.e., 9.5, 7, and 4 ms at 1, 2, and 4 kHz), and Shera et al. (2002) for low level SFOAEs (i.e., 11, 7, and 4.5 ms at 1, 2, and 4 kHz). The simulated group delays decrease more rapidly with frequency than the experimental data, which may result from simplified model assumption that QERB is constant along the BM (Shera et al., 2010).
DISCUSSION AND PERSPECTIVES
This study describes the implementation of a nonlinear, time-domain transmission-line model of the cochlea. This approach is computationally expensive, currently allowing the probing of 20 cochlear sections at once with stimulus durations up to 100 ms. Future development can improve this calculation performance, but the simulations are worth the wait as the cascaded model approach preserves the timing across the cochlear partition much better than parallel auditory filterbanks. This benefit is mainly due to the simulation of forward and reverse traveling waves rather than the simulation of a series of uncoupled BM IRs. Whereas parallel filterbanks generally require adjustments to account for BM coupling characteristics (e.g., delay of the filters, frequency glides, two-tone suppression), these characteristics are implicit in a cascaded transmission-line model.
The model was calibrated for transient stimuli using measured BM IRs and data from reflection-source emissions such as stimulus-frequency and click-evoked OAEs. Even though the model also simulates distortion-product (DP) OAEs, the model parameters were not calibrated in terms of DPOAE amplitudes. However, such a calibration can be performed with data from existing DPOAE emission recordings. Because the reflection and distortion-source emission components can be analyzed independently, the relative contribution of these two components can be adjusted to reflect characteristic DPOAE fine-structure properties. Since the model can also simulate spontaneous otoacoustic emissions through manipulation of the middle-ear resistance RME, the model is well suited to study the generator mechanisms of human otoacoustic emissions.
The model described here is scaling symmetric so that QERB is constant along the cochlear partition. Consequently, the implemented nonlinearity works equally well at all cochlear sections. The downside of this approach is that variation in QERB and the breaking of scaling symmetry, in humans often observed for frequencies below 1 kHz (Shera et al., 2010), is not accounted for. The model can easily be adapted to allow section dependent QERB variations, though this was not incorporated in the current version. This feature may be especially interesting for studying the consequences of different gradations of outer-hair-cell-related hearing loss. Regardless of the QERB variation across frequency, QERB can be set as a cochlear parameter, thereby allowing the user full control over the BM tuning properties. The model thus provides an alternative to the existing parallel auditory filterbank models as preprocessors for human auditory perception models where realistic excitation patterns are desired. The model and instructions on how to run it are available at http://bit.ly/L3zuw3. Over time, the model will be fully integrated in the Auditory Model Toolbox (Søndergaard et al., 2011).
ACKNOWLEDGMENTS
The authors would like to thank Diek Duifhuis and Peter Van Hengel for providing the original source code of the fortran models presented in van Netten and Duifhuis (1983), Duifhuis et al. (1985), van Hengel (1996), and Duifhuis (2012). The code of these models is available at http://extras.springer.com/2012/978-1-4419-6117-4. Bastian Epp is acknowledged for help in compiling the different fortran files into an executable, and Peter L. Soendergaard is thanked for help in adjusting the model to read in.wav files and for future integration of the model into the Auditory Model Toolbox. Work supported by DTU, the Oticon Foundation, and Grant No. R01 DC003687 from the NIDCD, National Institutes of Health.
Footnotes
| (1) |
| (2) |
| (3) |
where RME is a matching resistor.
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |
| (9) |
References
- Choi, Y., Lee, S., Parham, K., Neely, S. T., and Kim, D. O. (2008). “Stimulus-frequency otoacoustic emission: Measurements in humans and simulations with an active cochlear model,” J. Acoust. Soc. Am. 123(5), 2651–2669. 10.1121/1.2902184 [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Boer, E. (1991). “Auditory physics. Physical principles in hearing theory. III,” Phys. Rep. 203, 127–229. 10.1016/0370-1573(91)90068-W [DOI] [Google Scholar]
- Diependaal, R. J., Duifhuis, H., Hoogstraten, H. W., and Viergever, M. A. (1987). “Numerical methods for solving 1-dimensional cochlear models in the time domain,” J. Acoust. Soc. Am. 82(5), 1655–1666. 10.1121/1.395157 [DOI] [PubMed] [Google Scholar]
- Duifhuis, H. (2012). Introduction to a Time Domain Analysis of the Nonlinear Cochlea (Springer-Verlag, New York). [Google Scholar]
- Duifhuis, H., Hoogstraten, H. W., Netten, S. M.van, Diependaal, R. J., and Bialek, W. (1985). “Modelling the cochlear partition with coupled Van der Pol oscillators,” in Peripheral Auditory Mechanisms, edited by Allen J. B., Hall J. L., Hubbard A. E., Neely S. T., and Tubis A. (Springer-Verlag, New York), pp. 290–297. [Google Scholar]
- Elliott, S. J., Ku, E. M., and Lineton, B. (2007). “A state space model for cochlear mechanics,” J. Acoust. Soc. Am. 87, 2592–2605. [DOI] [PubMed] [Google Scholar]
- Epp, B., Verhey, J. L., and Mauermann, M. (2010). “Modeling cochlear dynamics: Interrelation between cochlea mechanics and psychoacoustics,” J. Acoust. Soc. Am., 128(4), 1870–1883. 10.1121/1.3479755 [DOI] [PubMed] [Google Scholar]
- Gentle, J. E. (1998). “Gaussian Elimination 3.1,” in Numerical Linear Algebra for Applications in Statistics (Springer-Verlag, Berlin: ), pp. 87–91. [Google Scholar]
- Glasberg, B. R., and Moore, B. C. J. (1990). “Derivation of auditory filter shapes from notched-noise data,” Hear Res. 47, 103–138. 10.1016/0378-5955(90)90170-T [DOI] [PubMed] [Google Scholar]
- Greenwood, D. D. (1961). “Critical bandwidth and the frequency coordinates of the basilar membrane,” J. Acoust. Soc. Am. 33, 1344–1356. 10.1121/1.1908437 [DOI] [Google Scholar]
- Kalluri, R., and Shera, C. A. (2007). “Near equivalence of human click-evoked and stimulus-frequency otoacoustic emissions,” J. Acoust. Soc. Am. 121(4), 2097–2110. 10.1121/1.2435981 [DOI] [PubMed] [Google Scholar]
- Kemp, D. T., and Chum, R. A. (1980). “Properties of the generator of stimulated otoacoustic emissions,” Hear. Res. 2, 213–232. 10.1016/0378-5955(80)90059-3 [DOI] [PubMed] [Google Scholar]
- Liu, Y., and Neely, S. T. (2010). “Distortion product emissions from a cochlear model with nonlinear mechanoelectrical transduction in outer hair cells,” J. Acoust. Soc. Am. 127(4), 2420–2432. 10.1121/1.3337233 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moleti, A., Paternoster, N., Bertaccini, D., Sisto, R., and Sanjust, F. (2009). “Otoacoustic emissions in time-domain solutions of nonlinear non-local cochlear models,” J. Acoust. Soc. Am. 126(5), 2425–2436. 10.1121/1.3224762 [DOI] [PubMed] [Google Scholar]
- Moore, B. C. J., and Glasberg, B. R. (1983). “Suggested formulae for calculating auditory-filter bandwidths and excitation patterns,” J. Acoust. Soc. Am. 74, 750–753. 10.1121/1.389861 [DOI] [PubMed] [Google Scholar]
- Oxenham, A. J., and Shera, C. A. (2003). “Estimates of human cochlear tuning at low levels using forward and simultaneous masking,” J. Assoc. Res. Otolaryngol. 4, 541–554. 10.1007/s10162-002-3058-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pigasse, G. (2008). “Deriving cochlear delays in humans using otoacoustic emissions and auditory evoked potentials,” Ph.D. thesis, Technical University of Denmark. [Google Scholar]
- Prieve, B. A., and Falter, S. R. (1995). “COAEs and SSOAEs in adults with increased age,” Ear Hear. 16(5), 521–528. 10.1097/00003446-199510000-00009 [DOI] [PubMed] [Google Scholar]
- Probst, R., Coats, A. C., Martin, G. K., and Lonsbury-Martin, B. L. (1986). “Spontaneous, click-, and toneburst-evoked otoacoustic emissions from normal ears,” Hear. Res. 21, 261–275. 10.1016/0378-5955(86)90224-8 [DOI] [PubMed] [Google Scholar]
- Puria, S. (2003). “Measurements of human middle ear forward and reverse acoustics: Im- plications for otoacoustic emissions,” J. Acoust. Soc. Am. 113(5), 2773–2789. 10.1121/1.1564018 [DOI] [PubMed] [Google Scholar]
- Recio, A., and Rhode, W. S. (2000). “Basilar membrane responses to broadband stimuli,” J. Acoust. Soc. Am. 108(5), 2281–2298. 10.1121/1.1318898 [DOI] [PubMed] [Google Scholar]
- Ren, T. (2002). “Longitudinal pattern of basilar membrane vibration in the sensitive cochlea,” Proc. Natl. Acad. Sci. 99(26), 17101–17106. 10.1073/pnas.262663699 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rhode, W. S., and Recio, A. (2000). “Study of mechanical motions in the basal region of the chinchilla cochlea,” J. Acoust. Soc. Am. 107(6), 3317–3331. 10.1121/1.429404 [DOI] [PubMed] [Google Scholar]
- Schairer, K. S., Ellison, J. C., Fitzpatrick, D., and Keefe, D. H. (2006). “Use of stimulus-frequency otoacoustic emission latency and level to investigate cochlear mechanics in human ears,” J. Acoust. Soc. Am. 120(2), 901–914. 10.1121/1.2214147 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shera, C. A. (2001). “Intensity-invariance of fine time structure in basilar-membrane click responses: Implications for cochlear mechanics,” J. Acoust. Soc. Am. 110(1), 332–348. 10.1121/1.1378349 [DOI] [PubMed] [Google Scholar]
- Shera, C. A., and Guinan, J. J. (1999). “Evoked otoacoustic emissions arise by two fundamentally different mechanisms: A taxonomy for mammalian OAEs,” J. Acoust. Soc. Am. 105, 782–798. 10.1121/1.426948 [DOI] [PubMed] [Google Scholar]
- Shera, C. A., and Guinan, J. J. (2003). “Stimulus-frequency-emission group delay: A test of coherent reflection filtering and a window on cochlear tuning,” J. Acoust. Soc. Am. 113(5), 2762–2772. 10.1121/1.1557211 [DOI] [PubMed] [Google Scholar]
- Shera, C. A., Guinan, J. J., Jr., and Oxenham, A. J. (2002). “Revised estimates of human cochlear tuning from otoacoustic and behavioural measurements,” Proc. Natl. Acad. Sci. USA 99, 3318–3323. 10.1073/pnas.032675099 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shera, C. A., Guinan, J. J., and Oxenham, A. J. (2010). “Otoacoustic estimation of cochlear tuning: Validation in the chinchilla,” J. Assoc. Res. Otolaryngol. 11, 343–365. 10.1007/s10162-010-0217-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shera, C. A., Tubis, A., and Talmadge, C. A. (2008). “Testing coherent reflection in chinchilla: Auditory-nerve responses predict stimulus-frequency emissions,” J. Acoust. Soc. Am. 124(1), 381–395. 10.1121/1.2917805 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shera, C. A., and Zweig, G. (1991). “A symmetry suppresses the cochlear catastrophe,” J. Acoust. Soc. Am. 89(3), 1276–1289. 10.1121/1.400650 [DOI] [PubMed] [Google Scholar]
- Søndergaard, P. L., Culling, J. F., Dau, T., Le Goff, N., Jepsen, M. L., Majdak, P., and Wierstorf, H. (2011). “Towards a binaural modelling toolbox,” in Proceedings of Forum Acousticum 2011.
- Talmadge, C. L., Tubis, A., Long, G. K., and Piskorski, P., (1998). “Modeling otoacoustic emission and hearing threshold fine structures,” J. Acoust. Soc. Am. 104(3), 1517–1543. 10.1121/1.424364 [DOI] [PubMed] [Google Scholar]
- van Hengel, P. W. J. (1996). “Emissions from cochlear modelling,” Ph.D. thesis, Rijksuniversiteit Groningen, Groningen. [Google Scholar]
- van Netten, S. M., and Duifhuis, H. (1983). “Modelling an active, nonlinear cochlea,” in Mechanics of Hearing, edited by de Boer E. and Viergever M. A. (Martinus Nijhoff Publishers, Den Haag and Delft University Press, Delft: ), pp. 143–151. [Google Scholar]
- Verhulst, S., Harte, J. M., and Dau, T. (2011a). “Temporal suppression of the click-evoked otoacoustic emission level-curve,” J. Acoust. Soc. Am. 129(3), 1452–1463. 10.1121/1.3531930 [DOI] [PubMed] [Google Scholar]
- Verhulst, S., Shera, C. A., Harte, J. M., and Dau, T. (2011b). “Can a static nonlinearity account for the dynamics of otoacoustic emission suppression?,” in What Fire is in Mine Ears: Progress in Auditory Biomechanics, Proceedings of the 11th International Mechanics of Hearing Workshop, edited by Shera C. A. and Olson E. (AIP, Melville, NY), pp. 257–263. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zweig, G. (1990). “The impedance of the organ of Corti,” in Mechanics and Biophysics of Hearing, Lecture Notes in Biomathematics, edited by Dallos P., Geisler C. D., Matthews J. W., Ruggero M. A., and Steele C. R., Vol. 87, pp. 362–369.
- Zweig, G. (1991). “Finding the impedance of the organ of Corti,” J. Acoust. Soc. Am. 89(3), 1229–1254. 10.1121/1.400653 [DOI] [PubMed] [Google Scholar]
- Zweig, G., and Shera, C. A. (1995). “The origin of periodicity in the spectrum of evoked otoacoustic emissions,” J. Acoust. Soc. Am. 98(4), 2018–2047. 10.1121/1.413320 [DOI] [PubMed] [Google Scholar]