Single-step holographic fabrication of large-area periodically corrugated metal films

Abstract

We have developed a simple, high-throughput, and cost-effective method to fabricate one-dimensional and two-dimensional periodically corrugated silver films over centimeter scale areas. This fabrication uses a single-step holographic patterning technique with laser intensities as low as 88.8 mW/cm² to deposit silver nanoparticles directly from solution to create gratings with periodicities of 570 nm. A dip in the transmission spectrum for these samples is observed due to certain visible wavelengths coupling to surface plasmon polaritons (SPPs) and the peak wavelength of this dip has a linear relationship with the surrounding material's refractive index (RI) with a sensitivity of 553.4 nm/RIU. The figure of merit (the ratio of refractive index sensitivity to the full width at half maximum (FWHM)) is typically in the range of 12–23. Our technique enables single-step fabrication of uniform, sub-wavelength periodic metal structures over a large area with low cost. Such sub-wavelength periodic metal structures are promising candidates as disposable sensors in applications such as affordable environmental monitoring systems and point-of-care diagnostics.

INTRODUCTION

Surface plasmon polaritons (SPPs) are the coherent oscillations of unbound electrons at a metal-dielectric interface excited by incident light.¹ The excitation wavelength of SPPs greatly depends on the refractive index (RI) of surrounding materials.^{2, 3, 4} Therefore, SPPs have been widely used for label-free and real-time biological and chemical sensing applications.^{3, 5, 6, 7, 8, 9} Integration of SPPs and microfluidic chip system enables the miniaturized biosensing platform for low cost and rapid analysis.^{10, 11, 12, 13, 14} Recently, fabrication of portable, fast, and disposable sensors based on SPPs has become an active area of research in order to fulfil the end users' requirement.^{15, 16, 17, 18}

SPPs cannot be directly excited by illumination on a flat metal surface because the momentum of light in free space is not sufficient to match the momentum of the SPPs. A traditional solution is the Kretschmann configuration (i.e., the prism-coupling technique).⁵ Even though sensors based on this technique showed great sensitivity up to 1.38 × 10⁴ nm/RIU (refractive index unit),⁵ they are not applicable for disposable and multi-analyte sensing because of the requirement of expensive optical prisms and tedious optical alignment.

An alternative technique is to use sub-wavelength, periodically structured metal films to excite SPPs through direct illumination.^{19, 20, 21, 22, 23} By measuring the normal incidence transmission or reflection, the excitation wavelength can be determined from the peak wavelength of the spectra, and only simple optical setup is required for this method. Miniaturized sensors have been developed based on this technique. The high surface area and strong local confinement of surface plasmon fields on the structured metal films can enhance the interaction with the analyte layer,^{24, 25} resulting in high sensitivity and low detection limit. For most applications, the analytes are in an aqueous solution which has a strong absorption at 970 nm and 1160 nm.¹⁸ Therefore, to avoid these absorption wavelengths, the periodicities of such structures are typically designed so that the resonance wavelength of SPPs is in the visible region. Sensors using periodic metal structures have shown sensitivity in the range of ∼70 to ∼800 nm/RIU,⁷ which are much lower than sensors using the Kretschmann configuration. To further improve the sensitivity and accuracy of this type of sensor, one key step is to fabricate uniform sub-wavelength structures over the whole detection area.¹⁸ In addition, in order to achieve multi-analyte sensing through multichannel sensors, uniform structures over a large area are required.

To date, it remains a challenge to fabricate uniform, sub-wavelength periodic metal structures over a large area with low cost. Electron-beam lithography (EBL)²⁶ and focused ion beam (FIB) milling¹ can fabricate most desired patterns with high yield and outstanding resolution, but they are limited by their low processing speeds, high capital cost, and difficulty in accessing the facilities. Nanosphere lithography (NSL) was reported as a more practical method, but it suffers from the low sensitivity (∼150 nm/RIU) because it is difficult to fabricate defect-free patterns over large areas.²⁷

Nanoimprint lithography (NIL) is a low-cost process with high resolution and throughput which has produced sensitive sensors (800 nm/RIU) based on metal nanostructures.⁷ Massively parallel nanofabrication using NIL is ideal for low-cost sensor fabrication. However, in the NIL approach, EBL or FIB is still needed for fabrication molds with sub-wavelength structures,²⁸ and multiple steps are required to transfer the pattern to the metal surface.²⁹ Direct nano-imprinting of metal has been reported recently.^{30, 31, 32} However, it requires either high-temperature and high-pressure control,³¹ or multi-step preparations including spin-coating of polymer and metal deposition by sputtering or thermal deposition.³² Therefore, capital cost is still high for sensor fabrication by the NIL method.

Holographic lithography transfers a multi-beam interference pattern into a photosensitive material which enables large-scale fabrication at low cost with high uniformity.³³ It has been implemented to fabricate two-dimensional (2D)^{34, 35, 36, 64} and three-dimensional (3D) micro/nanostructures.^{37, 38, 39, 40, 41} Direct patterning of metals by lasers has mainly focused on the generation of surface structures based on high-power-laser-induced ablation, melting, evaporation, phase transformations, or thermal decomposition of metal ions.^{42, 43, 44, 45, 46} These methods require expensive femtosecond lasers,⁴² nanosecond lasers,^{43, 44} or CW lasers with high power density (e.g., 8 × 10⁶ W/cm²);^{45, 46} furthermore, they rely on laser irradiation and melting-induced mass transfer, making it difficult to generate patterns with sub-micron resolution.

Here, we demonstrate a single-step, high-throughput method to fabricate one-dimensional (1D) and 2D, sub-wavelength periodic silver structures over centimeter scale areas by direct deposition of silver from solutions using holographic patterning at room temperature. This setup uses only a low-power (157 mW) green laser and a simple prism. Each sample uses only a standard glass slide, 1 ml of ammonia, 0.02 g of silver oxide, and 0.5 g of glucose. The fabricated silver structure shows a periodicity of 570 nm. The periodic structure enables the excitation of SPPs. The 1D periodically corrugated silver film showed a high sensitivity of 553.4 nm/RIU to changes in the surrounding RI. The figure of merit (FoM) was calculated by dividing the sensitivity by the full width at half maximum (FWHM) of the transmission dip. The FoM of the 1D periodically corrugated silver film is in the range of 12–23. The sensitivity of our system is comparable to other disposable SPP sensors; however, it does not require the high capital cost of nanofabrication equipment such as EBL or FIB, a cost inherent in most existing techniques. With its simplicity, low cost, and competitive sensitivity, our method is promising for disposable sensing applications.

EXPERIMENTAL

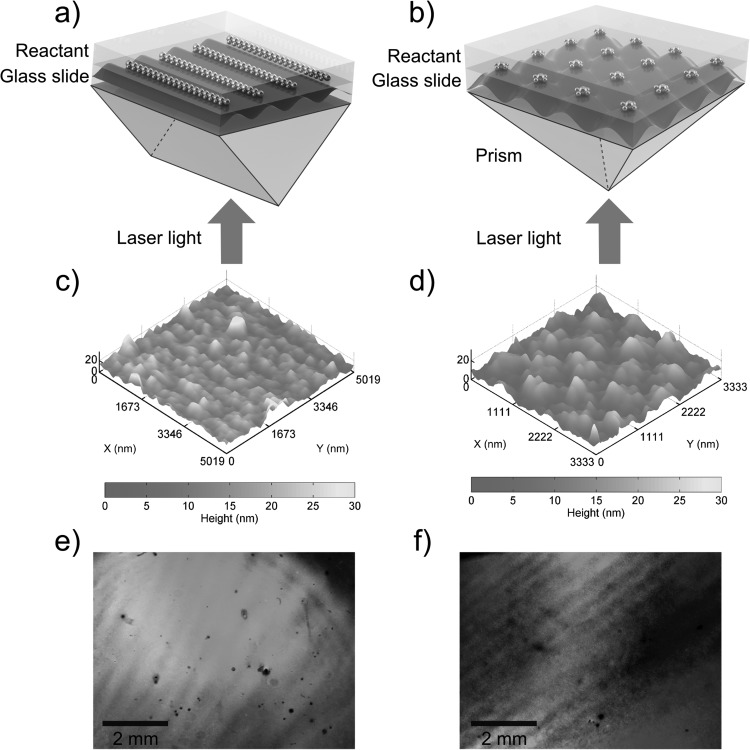
The experimental setups are shown in Figs. 1a, 1b, respectively. The patterning experiment was carried out in a dark ambient environment at room temperature. Standard glass slides were cleaned with acetone, methanol, isopropyl alcohol (IPA), and deionized (DI) water in ultrasonic baths for 15 min each. Then, a reusable polydimethylsiloxane (PDMS) well, with the dimensions of approximately 30 mm× 10 mm × 5 mm, was placed on top of a glass slide. Next, the glass slide was placed on the top of a prism. A collimated laser beam with a wavelength of 514 nm and a power of 157 mW impinged upon the bottom of the prism, and was divided into two beams by the right-angle prism [Fig. 1a] and four beams by the square pyramid prism (tilting angle of the facet, θ_t = 45°) [Fig. 1b]. The beam size was 1.5 cm in diameter, so the intensity of the laser beam was 88.8 mW/cm². In both cases, the prisms are made of BK7 glass with a RI of 1.517, and the separated light beams interfere at an angle of 34.43°. The periodicity can be calculated according to the equation: a = λ/(2 sinθ), where a is the periodicity of the interference light pattern, λ is the wavelength of the incident laser beams, and θ is the half angle formed by the two laser beams. Using this equation, the periodicities in both the 1D and 2D cases should be 572 nm.

Figure 1.

Schematics of the experiment setup for fabrication of (a) 1D and (b) 2D periodically corrugated silver films. The incident laser beam from the bottom of the prism was split at the prism surface to form interference patterns on the reservoir containing Ag(NH₃)₂⁺ and glucose mixture. A visualization of the interference patterns is shown in the glass slides. Silver was generated faster at positions where the light intensity was high, resulting in a silver film with surface profile that mimics the interference pattern. (c) and (d) are the AFM images showing the surface profile of the 1D and 2D periodically corrugated silver film, respectively. Both (e) 1D and (f) 2D periodically corrugated silver films showed diffraction colors under illumination with white light.

The solution containing silver-ammonia complex ions, Ag(NH₃)₂⁺, was made by adding 5 ml ammonia (Ricca Chemical Co.) drop-by-drop into 0.1 g silver oxide (Alfa Aesar). The reaction at this step is described as Ag₂O + 4 NH₃ + H₂O → 2 Ag(NH₃)₂⁺ + 2 OH⁻. After centrifugation, 1 ml of the purified solution was mixed with 1 ml 50% (w/v) glucose solution (BDH Chemicals) by vortex mixing, then immediately injected into the PDMS well and exposed to the interference laser pattern. The exposure time was optimized to be 20 min according to the diffraction efficiency (refer to Fig. S1⁶⁵). This silver deposition method is known as the Tollens' reaction: Ag(NH₃)₂⁺(aq) + RCHO(aq) → Ag(s) + RCOOH(aq). Finally, the glass slide was removed from the prism, detached from the PDMS well, rinsed with DI water, and dried with nitrogen. The PDMS well can be reused during the next sample fabrication.

The fabricated silver films were examined by measuring the transmission spectra. The dependence of the transmission spectra on incident angle was studied by rotating the sample slides while fixing the position of the light source and detection fiber. The RI sensitivity of the 1D grating was evaluated by recording the transmission spectra at a normal incident angle while fluids with various RIs, such as air (n = 1), DI water (n = 1.333), and several CaCl₂ solutions at different concentrations (n = 1.3343–1.437), were subsequently sandwiched in between the sample slide and a glass slide.

RESULTS AND DISCUSSION

The surface profiles for both 1D and 2D periodic corrugated silver films were characterized by atomic force microscopy (AFM) and the results are given in Figs. 1c, 1d. Both periodicities measured by AFM (570 nm) agree well with the theoretical calculation (572 nm). The surface roughness is caused by the grain size of the silver particles during deposition. The 1D and 2D gratings have a total size of 10 mm × 8 mm and 10 mm × 10 mm, respectively.

The formation of the gratings was also indicated by the “rainbow” colors on both samples under general room lighting, as shown in Figs. 1e, 1f. The “rainbow” colors are caused by light diffracted into different directions on gratings surface. To show the diffraction color more clearly, we used an UV–VIS light source from an optical fiber. As shown in Fig. S2⁶⁵, the 1D grating sample shows different colors as the incident angle changes.

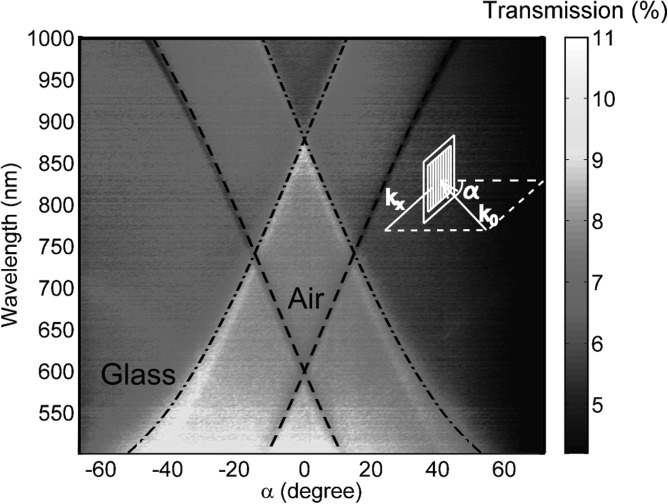
Analysis of the transmission as a function of the incident angle, α, verifies that the transmission loss is consistent with SPP theory.⁴⁷ As α varies, the minimum and maximum transmission wavelengths of the 1D silver grating change (as shown by the abrupt color changes in Fig. 2). The surface roughness is caused by the grain size of silver particles and these periodic corrugated silver films can be considered as arrays of nanoparticle cluster. As in our case, the interparticle distance is small and near-field coupling is dominant, the SPP wavelength will not shift with the particle size.⁴⁸ Therefore, for SPP wavelength calculations, we can model the 1D silver grating without any surface roughness. A calculation based on surface plasmon theory⁴⁷ shows that the surface plasmons excited at the silver/air interface cause minimums in the transmission, while the surface plasmons at the silver/glass interface enhance the transmission. Surface plasmons are excited when their momentum matches the momentum of the incident photon and the grating, as follows:¹

$$k_{\mathit{sp}}=k_x\pm m{G}_x,$$ (1)

where $k_x=(2\pi /\lambda )\times \sin \hspace{0.17em}\alpha$ is the component of the incident light's wave vector in the plane of the grating, as shown in the inset of Fig. 2, λ is the free-space wavelength of the incident light, $G_x=2\pi /a$ is the grating momentum wave vector, and m is an integer.¹ The wave vector of surface plasmons, $k_{\mathit{sp}}$, can be expressed as⁴⁹

$$k_{\mathit{sp}}=2\pi /\lambda \times \sqrt{{\epsilon }_m{\epsilon }_d/({\epsilon }_m+{\epsilon }_d)},$$ (2)

where ${\epsilon }_m$ and ${\epsilon }_d$ are the dielectric constants of silver and adjacent dielectric (${\epsilon }_{\mathit{air}}=1$ or ${\epsilon }_{\mathit{glass}}=2.3$ in this case).

Figure 2.

Experimental transmission intensity of the 1D periodically corrugated silver film as a function of wavelength and incident angle α, with theoretical calculations for the surface plasmons at silver/air interface (dashed line) and silver/glass interface (dashed dotted line). The inset shows the geometry of the experiment.

At a certain incident angle, the free-space wavelength which excites surface plasmons can be theoretically calculated at silver/air (${\epsilon }_d={\epsilon }_{\mathit{air}}$) and silver/glass (${\epsilon }_d={\epsilon }_{\mathit{glass}}$) interfaces using Eq. 1. The dashed line in Fig. 2 is the theoretical calculation of the surface plasmons on a silver/air interface, which fits well with the minimum transmission from the experimental results. The dashed-dotted line is the calculation of the surface plasmons on silver/glass interface and it fits well with the maximum transmission.

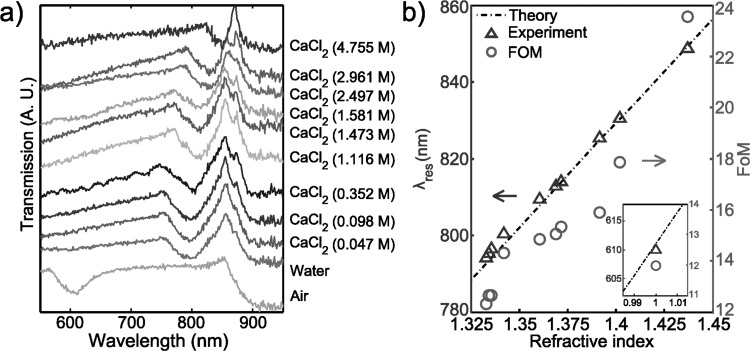
At normal incidence, as the RI of surrounding media increased, the transmission minimum (λ_res) red-shifted, while the transmission maximum (λ_res,glass) remained unchanged, as shown in Fig. 3a. This is expected because the fluid in contact with the grating is altered while the glass remains at the same position. The experimental results were fitted by a linear function using a least-squares regression, λ_res = 553.4 n + 56.43. The slope, 553.4 nm/RIU, can be taken as the sensitivity factor. This value is comparable to sensors fabricated by FIB milling (400 nm/RIU)⁵⁰ and much better than the substrates prepared by NSL (150 nm/RIU).²⁷

Figure 3.

(a) At normal incidence, the transmission spectra of the 1D periodically corrugate silver film immersed into air, DI water, and several solutions of CaCl₂ at different concentrations. The spectra have been arbitrarily displaced along the ordinate for clarity and corresponding materials information areindicated by the side of each curve. (b) Dependence of the resonance wavelength of surface plasmons at the interface of silver and surrounding materials and the FoM calculated from (a). The inset shows the data point when the surrounding material is air.

The linear relationship between λ_res and n can be predicted using SPP theory as expressed in Eqs. 1, 2, with the assumption that ε = n² for the fluid in contact with the grating. This relationship is shown as the dashed line in Fig. 3b and the theoretical sensitivity (slope) was 573 nm/RIU. As discussed, λ_res,glass remains constant. The calculated wavelength of λ_res,glass using ε_glass = 2.3 is 887 nm, and the experimental value ranges from 860 to 870 nm. The differences between the theoretical prediction and the experimental results could be caused by uncertainty in the experimental incident light angle and/or tarnishing of silver due to the presence of atmospheric sulphur.⁵¹ As the RI of materials becomes close to that of the glass slide, λ_res approaches λ_res,glass, making the dip narrower, as shown in Fig. 3a. Therefore, the FoM increases with the increase of RI, as shown in Fig. 3b.

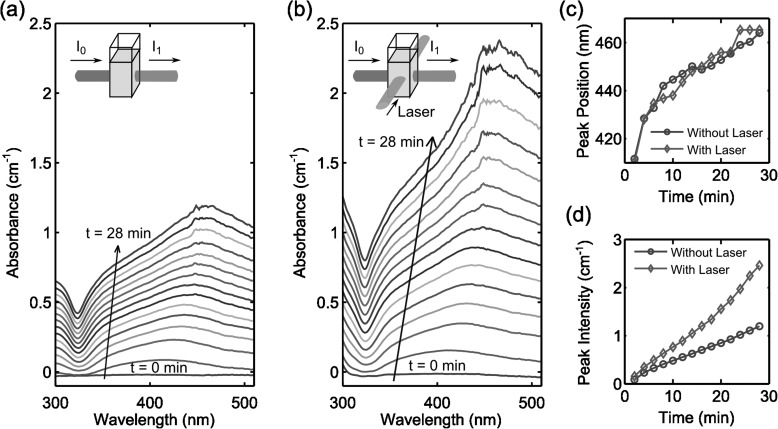
The grating formation should mainly be attributed to the photo-enhanced chemical reaction.^{52, 53, 54} To confirm this hypothesis, a control experiment was carried out. In the control experiment, we measured the absorbance spectra of the reaction between Ag(NH₃)₂⁺ and glucose in real-time without and with laser exposure, as shown in Figs. 4a, 4b. A peak in the absorbance spectra and continuous red-shift of that peak indicates the nucleation and growth of silver nanoparticles, respectively, owing to the localized surface plasmon resonances (LSPR) of the nanoparticles.^{27, 55} Figs. 4c, 4d show the peak position and intensity as a function of time without and with laser exposure. In Fig. 4c, there is no significant difference in the peak positions with or without laser exposure, indicating that the laser irradiation does not affect the nanoparticles shape or size during the growing process. However, the absorbance peak value of the sample under laser exposure grows much faster than without laser exposure [Fig. 4d]. Therefore, we can conclude that when the Ag(NH₃)₂⁺ and glucose mixture was subjected to holographic exposure, the rate of silver nanoparticle formation was much faster in the regions of high light intensity, thus a grating was formed in accordance with the interference pattern of the light.

Figure 4.

The absorbance of the mixture of Ag(NH₃)₂⁺ and glucose solution (a) without and (b) with 514 nm laser exposure. The insets show the schematic of the experimental setup. (c) The peak position and (d) the peak intensity of the absorbance of the mixture as a function of time without and with laser exposure. The data of (c) and (d) are extracted from (a) and (b).

Studies that examine photo-induced silver deposition in liquid phase are generally based on two main mechanisms: photoreduction^{56, 57} and thermally induced decomposition.^{45, 52, 56} Usually, pure photoreduction of silver occurs only under UV irradiation,⁵² while thermally induced decomposition takes place in the presence of significantly elevated temperatures (>80 °C).⁴⁵ In our case, however, the incident photons at 514 nm do not have sufficient energy to break the chemical bonds in Ag(NH₃)₂⁺, and the low laser intensity (88.8 mW/cm²) cannot produce discernible increases in the bulk fluid temperature. Therefore, we explain the enhancement in silver production in a different way. In our experiment, small silver nanoparticles are first nucleated based on the Tollens' reaction. Afterwards, the rise in local temperature due to the light-to-heat conversion related to LSPR^{58, 59, 60, 61, 62} could be inducing decomposition of Ag(NH₃)₂⁺,⁵⁴ increasing the reaction rate in the immediate vicinity of the silver particles.⁶³ As a result, with laser exposure, LSPRs can significantly enhance the photochemical reaction, leading to a nearly exponential increase in nanoparticle nucleation.^{52, 53}

SUMMARY

In summary, we have developed a simple and cost-effective method to holographically fabricate 1D and 2D periodic corrugated silver films over large areas. The fabrication consists of a single-step process and only requires laser power density as low as 88.8 mW/cm². The gratings have a high sensitivity (553.4 nm/RIU) to their surroundings refractive index, which makes them promising for disposable chemical/biological sensing applications.