Abstract
Harmonics are considered unresolved when they interact with neighboring harmonics and cannot be heard out separately. Several studies have suggested that the pitch derived from unresolved harmonics is coded via temporal fine-structure cues emerging from their peripheral interactions. Such conclusions rely on the assumption that the components of complex tones with harmonic ranks down to at least 9 were indeed unresolved. The present study tested this assumption via three different measures: (1) the effects of relative component phase on pitch matches, (2) the effects of dichotic presentation on pitch matches, and (3) listeners' ability to hear out the individual components. No effects of relative component phase or dichotic presentation on pitch matches were found in the tested conditions. Large individual differences were found in listeners' ability to hear out individual components. Overall, the results are consistent with the coding of individual harmonic frequencies, based on the tonotopic activity pattern or phase locking to individual harmonics, rather than with temporal coding of single-channel interactions. However, they are also consistent with more general temporal theories of pitch involving the across-channel summation of information from resolved and/or unresolved harmonics. Simulations of auditory-nerve responses to the stimuli suggest potential benefits to a spatiotemporal mechanism.
INTRODUCTION
Many natural sounds in our environment are complex harmonic sounds that can be decomposed into a series of frequency components that are multiples of a common fundamental frequency (F0). Such sounds usually evoke a pitch sensation corresponding to F0, even when the physical energy at F0 is removed from the signal (Seebeck, 1841). In fact, the pitch stays unchanged when additional components are removed or masked, as long as the harmonic relationship between the remaining harmonics is not altered (e.g., Schouten, 1940; Mathes and Miller, 1947; Davis et al., 1951; Licklider, 1954; Thurlow and Small, 1955); see Plack and Oxenham (2005) for a review.
The question of how pitch is coded in the auditory system and, in particular, whether the representation is based primarily on place information or temporal features, remains a focus of research. The frequency analysis that takes place along the basilar membrane and the tonotopic organization of the auditory pathways (Merzenich et al., 1975) allow a fine internal representation of the spectral content of sounds. In addition, the synchronous firing of auditory-nerve fibers to specific phases of the basilar-membrane vibration (Rose et al., 1967) enables an accurate internal representation of the temporal features of incoming sounds. This possibility for both high spectral and temporal resolution in the human auditory system, together with the fact that spectral and temporal information usually covary, has made it difficult to elucidate the specific type(s) of information used for pitch extraction.
The limitations imposed by the varying frequency-selective power of the cochlea as a function of frequency provide an important tool in the attempt to isolate place and temporal pitch cues. On a linear scale, the auditory filters broaden as frequency increases (Fletcher, 1940; Glasberg and Moore, 1990; Shera et al., 2002). This means that low-numbered harmonics (lower than about the 6th) are generally considered resolved by the cochlea, giving rise to peaks of excitation on the tonotopic axis, whereas higher harmonics (above about the 12th) are generally considered unresolved, interacting with neighboring components within the same filter, such that their individual frequencies cannot be retrieved from the tonotopic pattern of excitation after cochlear filtering. Resolved harmonics could be coded by this tonotopic information (e.g., Wightman, 1973), by their temporal fine structure (TFS) (e.g., Meddis and Hewitt, 1991), or both (e.g., Shamma and Klein, 2000). Because unresolved harmonics can evoke a low pitch when presented alone (Ritsma, 1962), as can amplitude-modulated broadband noise (Burns and Viemeister, 1976), and because this pitch is salient enough for melody recognition (Moore and Rosen, 1979; Burns and Viemeister, 1981), it is believed that temporal mechanisms are responsible for this low pitch, based on the periodicity in the temporal envelope of the filtered waveform (Plack and Oxenham, 2005).
There is less agreement about the resolvability of harmonics between about the 6th and 12th, and the nature of their coding. Shifting the frequencies of all the components within a harmonic complex by the same amount on a linear frequency scale (de Boer, 1956a; Schouten et al., 1962) results in a waveform with the same periodic temporal envelope but with TFS that differs in successive envelope periods and with a spectrum that is no longer harmonic. Moore and Moore (2003) found that when a complex contained only components centered around the 16th harmonic, the pitch did not change when the harmonics were shifted, suggesting that the pitch was based on the temporal envelope. However, when the complex contained harmonics centered around the 5th or 11th harmonic, the pitch changed when the component frequencies were shifted, suggesting that listeners had access either to TFS or to a place representation of the individual components. In a follow-up study, Moore et al. (2006a) found situations in which three-component harmonic complexes produced low (good) F0 discrimination, suggesting access to TFS (as opposed to just the temporal envelope), but showed a dependence of thresholds on the phase relations of the components, suggesting that the harmonics were unresolved. This led them to conclude that it was the TFS near peaks in the temporal envelope of the waveform that was used to extract pitch (de Boer, 1956b; Ritsma and Engel, 1964). On the other hand, Oxenham et al. (2009) found that when the conditions of Moore et al. were reproduced with sufficient noise to mask potentially resolved distortion products, no conditions were found in which good F0 discrimination was accompanied by phase dependence, in line with expectations based on resolved harmonics being necessary for good F0 discrimination.
The limitations imposed by phase-locking in the auditory nerve have previously provided an important constraint on temporal theories of pitch. Specifically, because phase-locking is believed to be degraded above about 2–3 kHz (e.g., Köppl, 1997), it has often been assumed that listeners do not have access to TFS above about 4 kHz (e.g., Sęk and Moore, 1995; Oxenham et al., 2004). However, the limit of phase-locking in the human auditory nerve remains unknown, and recent studies have claimed sensitivity to TFS at much higher frequencies (Moore and Sęk, 2009; Santurette and Dau, 2011), which may be because the limit in the human auditory nerve is different from that in the typical animal models (such as cat or guinea pig), or because some residual phase-locking remains even at very low values of synchrony (Heinz et al., 2001a; Recio-Spinoso et al., 2005).
Santurette and Dau (2011) recently addressed these issues using a pitch-matching task with inharmonic transposed tones (van de Par and Kohlrausch, 1997; Oxenham et al., 2004), to which the F0 of a broadband pulse train was matched. The pitch matches clustered around frequencies corresponding to the reciprocal of the time interval between TFS peaks close to adjacent envelope maxima in the stimulus waveform, rather than to the envelope repetition rate. Because listeners were not able to “hear out” individual harmonics, Santurette and Dau (2011) concluded that the harmonics were unresolved. Despite the consistency of such results with the TFS hypothesis, it is important to keep in mind that, had the components been resolved, a place model of pitch perception could have correctly predicted the ambiguous pitch of the transposed tones, e.g., by using a histogram built from subharmonics of known partial frequencies (Schroeder, 1968; Terhardt, 1974). Also, the inability of listeners to “hear out” the individual components may have been due to their high absolute frequency of 4 kHz and higher: Moore and Ohgushi (1993) found that high-frequency components were more difficult to hear out than lower-frequency components, despite roughly equivalent spectral resolution based on auditory-filter bandwidths. This was confirmed by Moore et al. (2006b), who found a decreasing ability to hear out partials above 3.5 kHz. Finally, it remains unclear whether the noise used by Santurette and Dau (2011) was sufficient to fully mask lower-frequency (and better resolved) distortion products that may have influenced the results.
The aim of the present study was to clarify the possibility of a place code for the low pitch of high-frequency complex tones, such as those used in the aforementioned studies. More specifically, the effects of relative component phases (experiment 1) and dichotic presentation (experiment 2) were studied, and a more direct test of resolvability, involving hearing out individual partials, was performed (experiment 3). Finally, the potential neural pitch representations of the stimuli used in experiment 1 were studied, involving place, time, and place-time codes. This was achieved by generating spatiotemporal activity patterns from a physiologically realistic model of the auditory periphery, and using the place information, the temporal information, or both types of information contained in such patterns, for pitch estimation.
METHODS
Listeners
Eleven normal-hearing listeners (ages: 18–32 years) participated in the study, and subgroups of these eleven were included in each experiment. All experiments were approved by the Science-Ethics Committee for the Capital Region of Denmark (reference H-KA-04149-g) and by the Institutional Review Board at the University of Minnesota. All listeners had hearing thresholds better than 20 dB hearing level (HL) at all audiometric frequencies in both ears. In experiments 1 and 3, the listeners were tested monaurally in their best ear, defined as the ear with the lowest average hearing threshold between 2 and 8 kHz. In experiment 2, they were tested binaurally. All listeners had some form of musical training and played an instrument as a hobby. In describing the results, each listener is assigned a unique number, which is kept the same throughout. Listener 6 was the first author. All other listeners provided informed written consent prior to testing and were paid an hourly rate for their participation.
Experimental set-up
All stimuli were generated in matlab and presented with a 96-kHz sampling rate, either via an RME DIGI96/8 soundcard (32-bit resolution) and Sennheiser HDA200 headphones (listeners 1 to 6 and 10) or a LynxStudio L22 soundcard (24-bit resolution) and Sennheiser HD580 headphones (listeners 7 to 9 and 11), in double-walled sound-attenuating listening booths. 256-tap finite-impulse-response (FIR) equalization filters were applied to all stimuli, in order to flatten the frequency response of the different headphones.
EXPERIMENT 1: INFLUENCE OF RELATIVE COMPONENT PHASES ON PITCH MATCHES
This experiment investigated the influence of relative component phase on the low pitch of high-frequency complex tones with intermediate component ranks. A pitch-matching experiment similar to that of Santurette and Dau (2011) was carried out, in which the reference stimuli were five-component complex tones added either in sine phase (SIN configuration) or alternating sine and cosine phase (ALT configuration), as illustrated in Fig. 1. Shackleton and Carlyon (1994) showed that the pitch of complex tones in the ALT configuration differed from that of complexes in the SIN configuration when the lowest harmonic had an approximate rank of 16, but not when this rank was lowered to about 6, for F0 = 250 Hz. According to their definition of resolvability, the present stimuli would lie around the upper limit of the transition region between resolved and unresolved components, suggesting that phase effects may occur. The finding of phase effects would therefore support the assumption that the components in the complexes tested by Santurette and Dau (2011) were indeed unresolved. In order to clarify the influence of the use of masking noise to mask combination tones (CTs), pitch matches were also compared for conditions where the background-noise level was sufficient to mask all CTs vs conditions in which no background noise was present in spectral regions containing the most prominent cubic difference tones. Six listeners (1, 2, 3, 6, 7, 9) participated in the experiment.
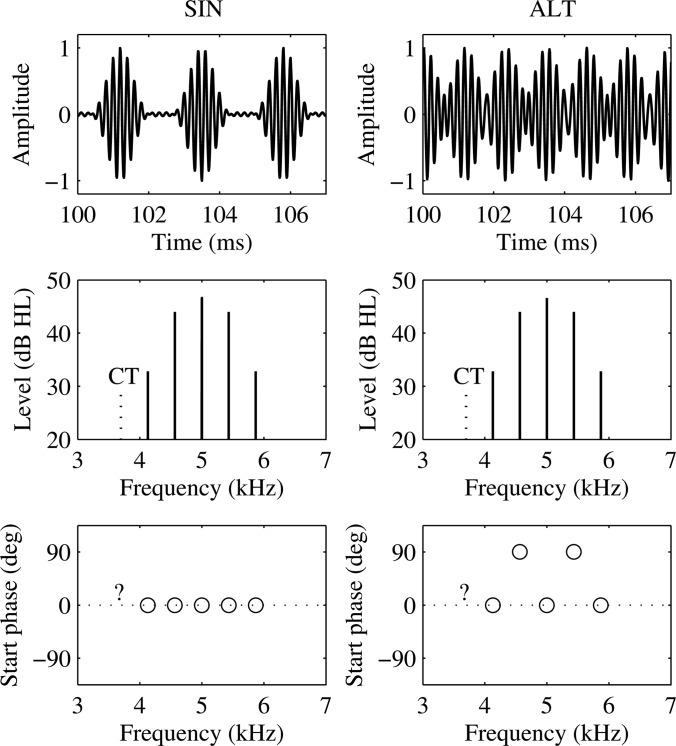
Figure 1.
Temporal waveform (upper panel), component levels (middle panel), and component starting phases (lower panel) for two complex tones with center frequency fc = 5 kHz and component spacing fenv = fc/N, with N = 11.5. Components were either added in sine phase (SIN configuration, left column) or in alternating phase (ALT configuration, right column). CT indicates the frequency of the most prominent CT, fCT = fc × (N − 3)/N = fc − 3fenv.
Reference stimuli
The inharmonic complex tones consisted of five primary tones and had a center frequency, fc, of 3, 5, or 7 kHz. The ratio, N, between fc and the envelope repetition rate (or component spacing) fenv was always equal to 11.5. In all conditions, the level of the center component was 46.6 dB HL,2 that of the components at fc ± fenv was 44.0 dB HL, and that of the components at fc ± 2fenv was 32.8 dB HL, leading to an overall stimulus level of 50.0 dB HL. Such levels were chosen for comparison purposes, as they were similar to the component levels of the transposed tones used in Santurette and Dau (2011). In the present study, however, the components were generated independently in order to control their relative phases. An example of the temporal waveform and frequency spectrum of the stimuli for the fc = 5 kHz conditions is given in Fig. 1. The components were added either in sine phase (SIN configuration: 0 starting phase for all components, left column in Fig. 1) or in alternating phase (ALT configuration: π/2 starting phase for components at fc ± fenv, 0 starting phase for other components, right column in Fig. 1).
Procedure
The listeners were asked to adjust the fundamental frequency, fp, of broadband pulse trains, which were generated by adding pure tones at harmonic frequencies of fp with identical starting phases, starting at the fifth harmonic, then bandpass filtered between 2 and 10 kHz using a 512-tap FIR filter designed after a fourth-order Butterworth response. The value of fp could be varied in steps of 4, 1, or 1/4 semitones, and the starting value for each presentation was randomly chosen from a uniform distribution of values between 0.8fenv and 1.2fenv. Listeners were able to play the 500-ms reference and matching stimuli as many times as they wished, with no lower or upper limit for fp, until they were satisfied with the match. All stimuli were gated with 30-ms onset and offset cosine ramps, and the overall level of the pulse trains was 55 dB HL. A background pink noise, bandpass-filtered from 100 to 12 000 Hz (512-tap FIR filter designed after a fourth-order Butterworth response), was played continuously throughout the matching procedure. In the “high noise” (HN) conditions, the spectrum level of the noise at 1 kHz was set to 13.5 dB HL for fc values of 3 and 5 kHz and to 17.0 dB HL for fc at 7 kHz, which was found sufficient to mask the most prominent cubic difference tone (indicated by “CT” in Fig. 1) in a preliminary experiment.1 In the “low noise” (LN) conditions, the upper cut-off frequency of the noise was lowered to 700 Hz, such that the most prominent difference tone at fenv remained masked, while other CTs were potentially audible. Each listener performed 10 runs of 60 matches each, with 10 matches per (fc, phase configuration) pair, presented in a random order. The CTs were masked in half of the runs and potentially audible in the other half, with alternating “high noise” and “low noise” runs. Matches from the last 8 runs were included in the final results for each listener, i.e., 40 matches per condition per subject. Before the experiment, it was ensured that the pitch-matching accuracy of novice listeners was similar to that of those already familiar with the task, by collecting pure-tone matches to reference broadband pulse-trains, as described in Santurette and Dau (2011).
Results and discussion
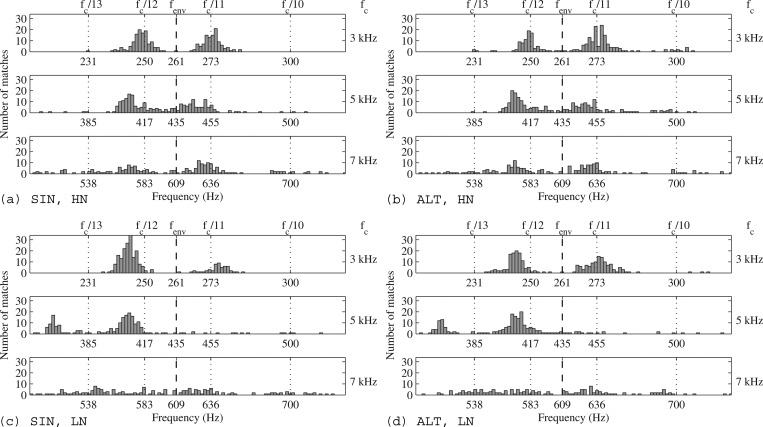
The distributions of matches for the whole listener group (240 matches per condition) are illustrated in Fig. 2, using histograms with a bin width of fenv/250. For each condition, Gaussian mixture models were fitted to the data using the same procedure as Santurette and Dau (2011), resulting in an estimation of the mean, variance, and mixing proportion of the distribution of matches at each pitch location.
Figure 2.
Pitch matching of the fundamental frequency of broadband pulse trains (horizontal axis) to five-component high-frequency complex tones with a center component at fc and an envelope repetition rate fenv = fc/11.5, for component phases in the SIN (left panels) and ALT (right panels) configurations, and for “high-noise” (HN, upper panels) and “low-noise” (LN, lower panels) conditions. The total distribution of pitch matches for all six listeners is shown, with 40 matches per condition per listener. The vertical dashed lines indicate fenv for each condition, while the dotted lines indicate subharmonics of fc.
Effects of component phase relations
As can be observed by comparing the left and right panels in Fig. 2, there was no major effect of phase relations on the distribution of pitch matches in any of the conditions. If the pitch had relied on the time intervals between the most prominent TFS peaks in the stimulus waveform, one would have expected the distribution means for the ALT configuration to have approximately twice the values of those for the SIN configuration (cf. Fig. 1). However, this was clearly not the case, neither in the pooled data, nor in the individual data. Only a few matches lay approximately one octave higher than fenv. Moreover, when present, such matches occurred for both the SIN and ALT configurations and represented only a small proportion of the data. In fact, an analysis of the individual data showed that these “octave” matches were almost all obtained in the same listener, and that they were totally absent in four of the listeners. This indicates that they were probably the result of octave confusions by two of the listeners, which may have arisen since there was no upper limit for the pulse-train F0 in the matching procedure. Moreover, one-sample left-tail t-tests performed on the pooled data over all fc values confirmed that the ALT-phase matches were significantly below 1.5fenv for both HN (p < 0.0001, 95% CI [−∞,1.15fenv]) and LN (p < 0.0001, 95% CI [−∞,1.30fenv]) conditions.
In order to statistically compare the obtained distributions of pitch matches, two-sample Kolmogorov-Smirnov tests were also performed on the individual data sets for each condition. Out of 36 comparisons (six fc values for each of the six listeners), 25 showed no significant difference between the SIN and ALT configurations (p > 0.05), while only 11 showed a significant difference (p < 0.05), even with no correction for multiple comparisons. Moreover, in all 11 data sets for which a significant difference was found, this was never the result of a difference in the means of the distributions of pitch matches. Instead, it was either due to a change in the proportions of matches between several ambiguous pitches (in which case a higher pitch was generally preferred in the ALT configuration) or to a lack of salient pitch.
In summary, the configuration of relative component phases had no consistent effect on the location of the perceived pitches of the complex tones considered here. Such results are consistent with those of Houtsma and Smurzynski (1990), who found that complex tones in Schroeder phase gave rise to poorer melody identification and F0 discrimination than sine phase complexes when the rank of the lowest harmonic was 13, but to similar performance when this rank was 10. Despite some uncertainty about CT audibility in their study, this may not have been a crucial factor, as the present results confirm the absence of phase effects for a lowest rank of 9.5, even when all CTs are properly masked (HN conditions). Had phase effects been present here, this would have indicated the use of temporal cues for pitch perception. However, the absence of such effects does not rule out the possibility of a temporal mechanism. The implications of the lack of phase effects on the temporal or spatial nature of pitch mechanisms are discussed further in Sec. 6.
Influence of the background noise
The results shown in the upper panels of Fig. 2 indicate that a salient low pitch could be perceived for all fc values when CTs were adequately masked (HN conditions), even for fc = 7 kHz where the noise level was substantially higher than in Santurette and Dau (2011). Nevertheless, a comparison of the upper and lower panels in Fig. 2 reveals an influence of the use of background noise on the perceived pitch. Several effects were found.
First, some distribution means were placed further away from subharmonics of fc for LN than for HN conditions. This was mainly observed for distributions around fc/12, for which a clear downward pitch shift between HN and LN conditions was observed for four listeners (1, 2, 7, 9) for fc values of 3 and 5 kHz, and for listener 6 at 3 kHz. Such pitch shifts are in line with those reported by Smoorenburg (1970), who explained these shifts by the fact that the center of gravity of the internal spectral representations is shifted downwards on a tonotopic axis by audible CTs. However, pitch shifts between HN and LN conditions were not always observed in the present study. For distributions around fc/11, there was generally no pitch shift. In addition, listeners 6 and 7 also showed distribution means lower than fc/12 in the HN condition for fc = 5 kHz, which is reflected in the group data (Fig. 2, upper left panel).
Second, the proportions of matches below fenv were always higher for LN than for HN conditions, for fc values of 3 and 5 kHz. This indicates that, in the presence of several ambiguous pitches, the listeners tended to choose a lower pitch when the background noise was absent. Such a trend was clearly visible in the individual results of listeners 1, 2, 6, and 7. As the presence of CTs considerably extends the aural spectrum toward lower regions, it is possible that a difference in timbre between the HN and LN conditions played a role in the observed change in pitch preference.
Third, for fc = 7 kHz, the pitch was less salient3 when the background noise was absent (LN) than when it was present (HN). Therefore, the potential audibility of CTs was not found to increase pitch salience for fc = 7 kHz. Instead, there was a beneficial effect of background noise on pitch salience. One possible explanation is the occurrence of mechanisms of spectral completion, which may enable listeners to infer the presence of additional lower stimulus components (Houtgast, 1976; Hall and Peters, 1981; McDermott and Oxenham, 2008; Oxenham et al., 2011).
In summary, a salient low pitch was still present in all tested spectral regions when CTs were adequately masked. Removal of the masking noise was found to introduce pitch shifts and to affect pitch preference among several ambiguous pitches. However, the fact that CTs may have been audible in the absence of noise did not appear to increase pitch salience.
Possibility of experimental bias
In experiment 1, the starting values for the F0 of the pulse train, fp, that the listeners were asked to adjust, were randomly chosen between 0.8fenv and 1.2fenv. As these starting values never lay around 2fenv, the listeners could have been biased against making pitch matches in this octave region. In order to test whether such bias occurred, and whether it could account for the observed lack of phase effects on the pitch matches, the experiment was repeated using four listeners, including two participants from the original experiment (2, 3) as well as two novice listeners (5, 10). The procedure was the same as in the first experimental session, except that the starting values of fp were randomly chosen between 0.8fenv and 2.2fenv and only HN conditions were used. Twenty matches per condition were obtained in each listener.
The pooled results of this rerun of experiment 1 over the four listeners are shown in Fig. 3. Despite the use of starting values of fp that could extend up to 2.2fenv, the majority of matches still lay in the “lower” octave (below 1.5fenv). On average, 18.1% of matches were found to lie in the “upper” octave (above 1.5fenv). In all listeners, all these octave matches were obtained for starting values of fp also in the upper octave. This indicates that the listeners were biased by the starting value of fp when searching for a pitch match. The extent of this bias differed across listeners, as reflected by the individual proportions of matches in the upper octave (4.2, 10.8, 25.0, and 32.5%). However, matches in the lower octave were on average still predominant (71.6%) for starting values in the upper octave.
Figure 3.
Results of the rerun of experiment 1 with an extended range of starting values for fp. Left panel: SIN configuration. Right panel: ALT configuration. The vertical dashed lines indicate fenv and 2fenv for each condition, while the dotted lines indicate subharmonics of fc and their octave values. The horizontal axis is cropped around 1.5fenv for readability, due to a very small number of outlying matches in this region.
Despite an influence of the starting value of fp, the effect was similar for the SIN and ALT phase configurations, as can be seen in Fig. 3 (compare left and right panels). The percentage of matches in the upper octave for the SIN stimuli was similar (slightly lower in three subjects, slightly higher in the fourth subject) to that for the ALT stimuli. Moreover, a one-sample left-tail t-test performed on the pooled data over all fc values confirmed that the ALT-phase matches were significantly below 1.5fenv (p < 0.0001, 95% CI [−∞,1.29fenv]). Two-sample Kolmogorov–Smirnov tests performed on the individual data sets also revealed a lack of statistical difference between the distribution of matches for the SIN and ALT phase configurations: Out of 12 comparisons, 11 showed no significant difference (p > 0.05).
Therefore, it is reasonable to conclude that the presence of experimental bias due to the choice of starting values of the F0 of the matching stimulus cannot account for the lack of phase effects observed in the results of experiment 1 and that, independent of this bias, the pitches of these SIN and ALT phase stimuli do not differ significantly.
EXPERIMENT 2: INFLUENCE OF DICHOTIC PRESENTATION ON PITCH MATCHES
This experiment used pitch matching to investigate the effect on the low pitch of presenting every other stimulus component to the opposite ear. Such a dichotic presentation mode was previously used by Houtsma and Goldstein (1972), who found that performance in musical interval recognition was essentially the same for monaural and dichotic presentation at low presentation levels, and argued that the small differences between the two presentation modes at higher levels were due to differences in CT audibility. Their finding indicated that the peripheral interaction of components was not necessary for complex pitch perception and that pitch mechanisms operated centrally, based on inputs of the same nature, whether these resulted from monaural or dichotic stimulation. Using a similar approach, Bernstein and Oxenham (2003) found that, for 12-component complex tones with F0s of 100 and 200 Hz, dichotic presentation of even harmonics to one ear and odd harmonics to the other ear elicited a pitch at F0 when harmonics below the 10th were present, whereas a pitch at 2F0 was heard if the lowest harmonic rank was 15 or higher. That pattern of results can be explained if it is assumed that information is integrated across the ears to elicit the true F0 when resolved harmonics are present, and if the envelope repetition rate (which is 2F0) determines the pitch when only unresolved harmonics are present. The present experiment investigated the effect of dichotic presentation on the pitch of the inharmonic complex tones of interest here, containing five components of intermediate ranks. The prediction was that, if these intermediate components behave as unresolved components and temporal cues based on their interactions are used, then presenting the components dichotically may lead to reduced pitch salience (due to wider peripheral component spacing) and a perceived pitch corresponding more closely to the envelope repetition rate in each ear (i.e., 2fenv). On the other hand, if the components are resolved and place cues are available, then the pitch and pitch salience should be roughly equal for monaural and dichotic presentation (e.g., Houtsma and Goldstein, 1972; Bernstein and Oxenham, 2003).
Method
Four listeners (6, 7, 8, 9) participated in this part of the study. The stimuli and procedure were the same as in experiment 1, except that components at fc − 2fenv, fc, and fc + 2fenv were presented to the left ear, while components at fc − fenv and fc + fenv were presented to the right ear.4 All components had a starting phase of 0. The same background noise as in the HN condition of experiment 1 was presented diotically, and the matching pulse trains were presented monaurally in each listener's best ear.
Results and discussion
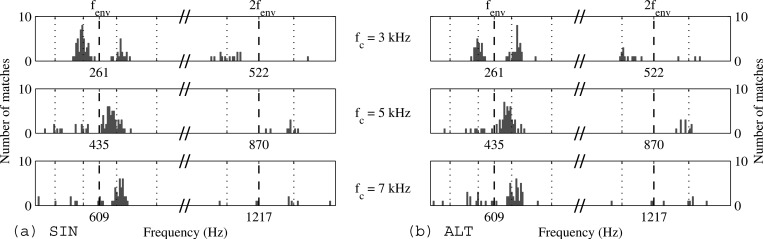
The distributions of matches for the whole listener group (160 matches per condition) are illustrated in Fig. 4.
Figure 4.
Pitch matching of the fundamental frequency of broadband pulse trains (horizontal axis) to five-component high-frequency complex tones with a center component at fc and an envelope repetition rate fenv = fc/11.5, for dichotic presentation and masked CTs. See the caption of Fig. 2 for more details.
As can be observed by comparing the distributions of matches in Fig. 4 to those in Fig. 2a, 2b, there was no clear or consistent effect of dichotic presentation on the locations of the different pitches, with similar distribution means for the dichotic and monaural conditions. Only 0.4% of all obtained matches were higher than 1.5fenv in the dichotic case, and in none of the listeners did the matches cluster around 2fenv, which would have been expected if the pitch had relied on independent temporal information from the left and right peripheral channels. A one-sample left-tail t-test performed on the pooled data over all fc values confirmed that the matches for the dichotic condition were significantly below 1.5fenv (p < 0.0001, 95% CI [−∞,1.11fenv]). Overall pitch salience was similar for the monaural and dichotic conditions. The three listeners who had also participated in experiment 1 (listeners 6, 7, and 9) all showed an overall increase of the proportion of matches above fenv in the dichotic condition, compared to the monaural conditions. Listener 9 reported he sometimes heard two different pitches in the left and right ears. However, this was not reflected in his matches, which always corresponded to a combined percept from the two ears. Because the starting values for the matching procedure were centered around fenv, it is possible that matches were biased towards fenv, rather than 2fenv. However, based on the control conditions from experiment 1, it seems unlikely that this would have led to a differential effect between the monaural and dichotic conditions.
The absence of a clear difference in the low pitch and in its salience for monaural vs dichotic presentation is consistent with the use of place cues that are combined across the two ears, and is not consistent with a temporal model that calculates the pitch from the TFS within single frequency channels. However, a temporal autocorrelation mechanism that integrates information across the ears may also be able to account for the present results (Bernstein and Oxenham, 2003). These aspects are discussed further in Sec. 6.
EXPERIMENT 3: ABILITY OF THE LISTENERS TO HEAR OUT INDIVIDUAL COMPONENTS
The lack of phase effects in experiment 1 suggested that the components of the complex tones may not have been completely unresolved. Similarly, no evidence for the use of timing information from component interactions was found in experiment 2. In the final experiment, component resolvability was evaluated more directly by testing whether the listeners were able to hear out the three lowest spectral components, using a method similar to that described by Bernstein and Oxenham (2003).5 The procedure was slightly modified compared to that used in the similar experiment of Santurette and Dau (2011). In particular, it was ensured here that each listener was trained with similar stimuli to those used in the measurement runs and could perform the task above chance level when the components were unambiguously resolved (N = 5.5). Six listeners (2, 4, 6, 7, 9, 11) participated in this experiment.
Method
The task of the listeners was to identify which of two tones was higher in frequency. A two-interval, two-alternative forced-choice procedure was used. In each trial, two 1-s intervals separated by a 375-ms silent gap were presented. The first interval contained three bursts of a 300-ms sinusoidal comparison tone with frequency fcomp, each including 20-ms onset and offset cosine ramps, separated by 50-ms silent gaps. The second interval contained a 1-s complex tone, in which the target component with frequency ftarg was gated on and off in the same way as the comparison tone in the first interval, but all the other tones in the complex were presented continuously for the entire 1-s duration. The complex tones had identical component amplitudes to those used in the previous three experiments, but all components were generated with random starting phase. The comparison and target tones were both presented at the same level as that of the corresponding component in the original complex tone. No background noise was present in this experiment. In each trial, fcomp was either lower or higher than ftarg, with equal probability, and the absolute frequency difference between fcomp and ftarg was chosen from a uniform distribution of values between 0.035ftarg and 0.05ftarg. In order to reduce the availability of absolute-frequency cues, the center frequency of the complex fc was roved between 0.935fc and 1.065fc, and all conditions were presented in random order within one run. Each run contained 30 trials for each of nine conditions (three target components for each of the three fc values), and the last 25 trials were included in the results. In each run, the N parameter was fixed, and the first five trials for each condition were not included in the final results. Each listener first performed one run for N = 5.5 and one for N = 8.5, in both of which feedback was provided. Two runs for N = 11.5 were then performed, in which feedback was not provided. All listeners performed training runs with N = 5.5 until their performance reached 90% correct in at least one condition.
Results and discussion
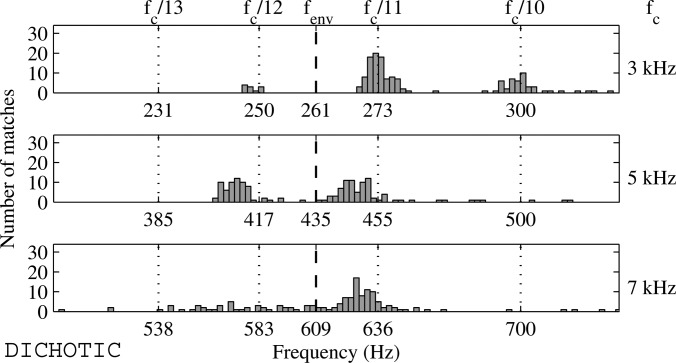
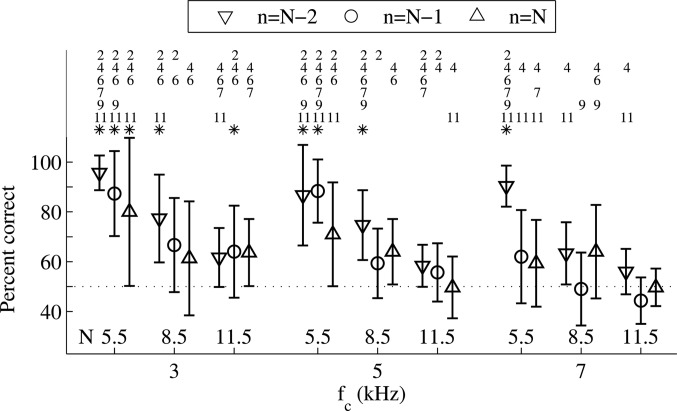
The average results and standard deviations over all listeners are plotted in Fig. 5 as a function of fc and the rank n = ftarg/fenv of the target component. For a given condition, a star indicates that the mean score was significantly above chance level (68% correct required for significance for N of 5.5 or 8.5, and 60% for N = 11.5, according to a one-sided binomial test without correction for multiple comparisons). Given the large across-listener variability, the conditions in which individual scores were significantly above chance level are also marked with listener numbers.
Figure 5.
Ability of six listeners (means and standard deviations) to hear out the three lowest components of five-component complex tones, as a function of the rank N and frequency fc of the center component. n = ftarg/fenv indicates the rank of the target component. Listener numbers indicate individual percent correct scores significantly above chance level (stars for mean scores).
Overall, performance worsened with increasing fc and increasing n. A within-listeners two-way ANOVA confirmed significant effects of both fc [F(2,135) = 11.14, p < 0.0001] and n [F(8,135) = 9.74, p = 0.0001], and there was no interaction between the two factors [F(16,135) = 0.78, p = 0.71]. For fc of 3 and 5 kHz, performance remained significantly above chance in a majority of listeners up to n = 6.5. For n ≥ 7.5, the average scores approached chance level. However, a few listeners still scored significantly above chance for some conditions where n ≥ 7.5, especially for low fc values. This contrasts with the results of Santurette and Dau (2011), whose listeners' performance did overall not rise significantly above chance level for any fc value in a similar experiment. However, given the across-listener standard deviations reported in both studies, the group data do actually not differ as a whole. The improvement in performance with decreasing fc observed here was nevertheless not reflected in the results of Santurette and Dau (2011). The fact that no background noise was used and that the listeners were provided with stimulus-specific and individualized training in the present study may explain these slightly higher scores for low fc values. Another explanation for the drop in performance with increasing fc is the fact that the range of relative differences between fcomp and ftarg was kept the same for all fc values in the present experiment. As frequency difference limens for pure tones are known to increase with absolute frequency (Wier, 1977), when expressed as the Weber fraction, the present task may have been more difficult toward high fc values.
As the group data do not allow a definitive conclusion for N = 11.5, it is of interest to compare the individual results to the pitch-matching data with identical stimuli. Listeners 2, 6, 7, and 9 had also participated in experiment 1. The pitch salience, as reflected by the standard deviations of the different clusters of pitch matches, was strongest in listeners 6 and 7, and weakest in listener 9. This is broadly consistent with the performance of these listeners in hearing out individual components, with listener 9 never scoring significantly above chance level for any component. The fact that listeners 6 and 7 could only hear out the lowest component for fc = 5 kHz, whereas both the lowest and center components were heard out for fc = 3 kHz, might also explain why these two listeners showed slight downward pitch shifts from fc/12 for fc = 5 kHz, but not for fc = 3 kHz, even when CTs were masked.
Such observations could suggest that both pitch and pitch salience are determined by which components of the stimuli are resolved, and how well. However, this possibility is weakened by the fact that both listeners 2 and 6 could clearly hear a salient pitch for fc = 7 kHz, despite an inability to hear out any of the stimulus components. This confirms the findings of Santurette and Dau (2011) that the ability to hear out individual partials is not necessary for a salient low pitch to be evoked. This outcome is in line with the fact that the low pitch sensation arises “automatically,” without an active effort of the listeners, whereas the listeners must focus their attention on the target component to perform the task of experiment 3, which is cognitively more demanding. Therefore, a definition of resolvability based on the ability of listeners to hear out individual partials does not satisfactorily account for the present pitch matches, should they rely on the presence of resolved components. This is particularly true for the high frequencies used here. As mentioned earlier, hearing out partials that are not pulsed on and off (Moore and Ohgushi, 1993; Moore et al., 2006b) also becomes more difficult at higher absolute frequencies, even in cases where peripheral resolvability is not thought to play a role. Thus, particularly at high frequencies, a task involving hearing out individual components may not provide a satisfactory measure of peripheral resolvability, even when the target component is pulsed.
IMPLICATIONS FOR PITCH MECHANISMS
The psychophysical results of experiments 1 and 2 remain inconclusive concerning the use of place vs timing information for pitch coding of intermediate harmonics. In order to further investigate whether the pitch-matching results could be accounted for by different pitch theories, spatiotemporal representations of the stimuli at the output of the cochlea were obtained from a peripheral auditory model in which the acuity of basilar-membrane frequency resolution and of place-dependent phase-locking to the TFS could be freely adjusted. Pitch predictions were then derived from these internal representations based on mechanisms using place information, within-channel temporal information, or operating directly on the two-dimensional spatiotemporal activity pattern.
Model simulations
Basilar-membrane model
A nonlinear transmission-line model of the human cochlea (Verhulst et al., 2012) was used, which provides basilar-membrane displacement and velocity waveforms as a function of cochlear place. The tuning of the model parameters is based on psychophysical and otoacoustic human data, and allows the computation of realistic tonotopic excitation patterns and the temporal output activity as a function of cochlear section, including human-based phase delays of the cochlear traveling wave. This made it possible to compute two-dimensional spatiotemporal activity patterns at the cochlea output.
These patterns were obtained by feeding 50-ms samples of the SIN- and ALT-phase complex tones used in experiment 1 to the model, with fc = 5 kHz, at a sampling rate of 400 kHz and an input stimulus level of 50 dB SPL.6 The basilar-membrane displacement waveforms were used as the temporal outputs in 380 frequency channels with characteristic frequencies (CFs) ranging from 1.56 to 10.47 kHz, selected from 1000 equally spaced channels based on the tonotopic-location vs CF map of Greenwood (1961). As the model allows for adjustments of auditory-filter tuning (QERB), simulations were obtained for two different estimates of human frequency selectivity: QERB ≈ 9.26, as estimated by Glasberg and Moore (1990), and QERB ≈ 11, as estimated by Oxenham and Shera (2003). This was achieved by setting the α*30 parameter in the model to 0.65 and 0.55, respectively (Verhulst et al., 2012).
Hair-cell transduction
In order to study the implications of degraded phase-locking to the TFS at high frequencies for the predictions obtained with different pitch theories, the spatiotemporal output of the basilar-membrane model was processed further using four different schemes.
-
(1)
Preserved phase-locking to the TFS (“TFS” scheme). Half-wave rectification (HWR) was applied to the temporal waveform in each channel without further processing, leaving TFS information unrealistically intact at all CFs.
-
(2)
Substantial residual phase-locking to the TFS (“LP2” scheme). HWR was applied to the temporal waveform in each channel followed by low-pass filtering, in order to simulate hair-cell transduction (e.g., Schroeder and Hall, 1974; Palmer and Russell, 1986; Jepsen et al., 2008). A 2nd-order Butterworth filter with a 4-kHz cut-off was used, leading to a substantial amount of residual TFS information at high frequencies, more than is usually assumed in peripheral auditory models (e.g., Zhang et al., 2001; Jepsen et al., 2008).
-
(3)
Poor residual phase-locking to the TFS (“LP7” scheme). Same as LP2, with a 4-kHz cut-off frequency, except that a 7th-order Butterworth filter was used, leaving only a poor amount of residual TFS information at higher frequencies, more similar to what has been typically assumed in auditory models (e.g., Zhang et al., 2001; Heinz et al., 2001b).
-
(4)
Absent phase-locking to the TFS (“ENV” scheme). The temporal envelope of the waveform in each channel was extracted using the Hilbert transformation, removing TFS information at all CFs, as if phase-locking was only to the temporal envelope.
Internal profiles and pitch predictions
Hypothetical internal profiles were derived from the output of the peripheral model for each of the four schemes described above. It was investigated whether these profiles could be used to qualitatively predict the pitch ambiguity and the lack of phase effects observed in experiment 1, depending on auditory-filter bandwidth and on the degree of phase-locking to the TFS.
Excitation-pattern (EP) profile
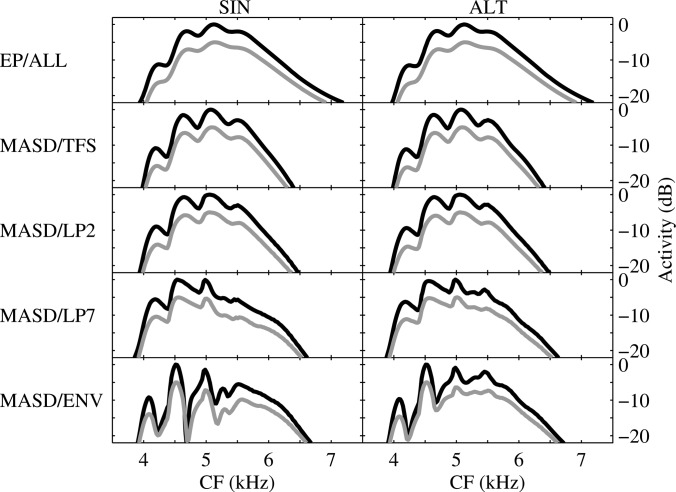
Tonotopic EPs were obtained using the root-mean-square (rms) value of the output waveform in each frequency channel. These patterns of overall activity as a function of CF are plotted in the top panels of Fig. 6 for the SIN and ALT stimuli, on a dB scale relative to the maximum activity value. The black line corresponds to the sharper auditory-filter tuning (QERB ≈ 11, Oxenham and Shera, 2003), the gray line to the broader tuning (QERB ≈ 9.26, Glasberg and Moore, 1990). The gray line is shifted 5 dB down on the ordinate axis to improve readability. As the EP profile is solely based on the amount of activity as a function of place, it is not influenced by the choice of phase-locking scheme. It is also very similar for the SIN and ALT stimuli, with the same peak locations for the two stimulus configurations, since they have identical amplitude spectra.
Figure 6.
Excitation-pattern (EP) and mean-average-spatial-derivative (MASD) tonotopic profiles for the SIN (left column) and ALT (right column) complex tones used in experiment 1, with fc = 5 kHz. Panels in the upper row show the EP profiles, identical for all phase-locking schemes. Panels in the four lower rows show the MASD profiles for each of the four phase-locking schemes described in Sec. 6A2. All profiles are plotted in dB relative to their maximum activity value. The black curves correspond to QERB ≈ 11, the gray curves to QERB ≈ 9.26. The gray curves are shifted by −5 dB on the ordinate axis for readability.
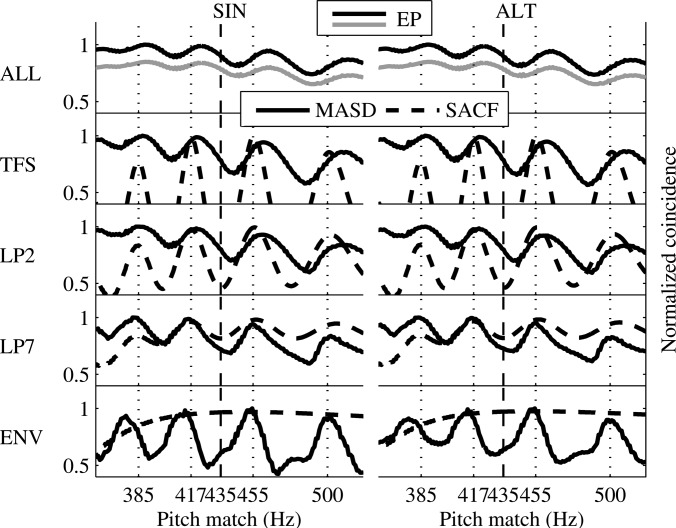
The EPs were used to obtain pitch predictions based on a pattern-matching mechanism (e.g., Wightman, 1973). For F0 values ranging from fc/14 to fc/9, in steps of 1 Hz, the coincidence of harmonics 6 to 16 of each F0 with the EP profile was determined. The coincidence value for a given F0 was obtained by summing the rms activity of all channels whose CFs were the closest to the frequency of each harmonic. The normalized coincidence values, relative to their maximum, are plotted in the upper row of Fig. 7 for the SIN and ALT stimuli, with the sharper tuning (black curve) and broader tuning (gray curve, shifted down by 0.15 units for readability).
Figure 7.
Pitch predictions obtained from the hypothetical internal profiles shown in Figs. 68 for the SIN (left column) and ALT (right column) complex tones used in experiment 2, with fc = 5 kHz. Panels in the upperrowshow the EP-profile predictions for QERB ≈ 11 (black curve) and QERB ≈ 9.26 (gray curve, shifted by −0.15 on the ordinate axis for readability). Panels in the four lower rows show the MASD-profile predictions (solid curve) and SACF-profile predictions (dashed curve) for each of the four phase-locking schemes described in Sec. 6A2, with QERB ≈ 11. The vertical dashed line indicates fenv, and the vertical dotted lines subharmonics of fc.
The occurrence of several coincidence peaks shows that the EP profile is able to predict the pitch ambiguity of the inharmonic stimuli. The EP profile also correctly predicts the same pitch locations for the SIN and ALT stimuli, and correctly predicts no overall differences in preference among several ambiguous pitches between the two conditions. As the EP profile is independent of the presence of phase-locking, it cannot account for the decrease in pitch salience with increasing fc if QERB remains constant or increases as a function of place. Although the two different QERB estimates used here did not lead to major differences in pitch predictions, the sharpness of the auditory filters at high frequencies remains a limiting factor for the amount of accurate place information provided by the EP profile. Moreover, a more realistic rate-place representation would be affected by the saturation of the firing rate of auditory-nerve fibers at the stimulus levels used here (e.g., Zhang et al., 2001), further limiting the usability of EP information for pitch retrieval (Cedolin and Delgutte, 2010).
Summary-autocorrelation-function (SACF) profile
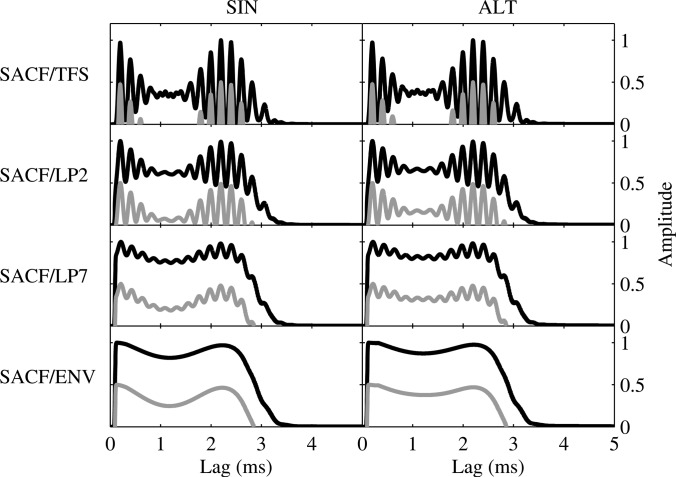
Autocorrelation was performed independently in each frequency channel, including a CF-dependent availability of lags, such that the range of available lags in each individual channel was limited between 0.5/CF and 15/CF, as suggested by Moore (2003). All temporal outputs were then summed across channels to obtain an SACF (Meddis and Hewitt, 1991). The normalized SACFs, relative to their maximum amplitude, are plotted in Fig. 8 for the SIN and ALT stimuli.
Figure 8.
Summary-autocorrelation-function (SACF) temporal profiles for the SIN (left column) and ALT (right column) complex tones used in experiment 2, with fc = 5 kHz and QERB ≈ 11 (black curves) or QERB ≈ 9.26 (gray curves, shifted by −0.5 on the ordinate axis for readability). The SACF profiles for each of the four phase-locking schemes described in Sec. 6A2 are shown in the different rows. In each panel, the SACF amplitude is normalized by its maximum value.
The normalized amplitude of the SACF as a function of the inverse of temporal lags was used to obtain the pitch predictions shown in the four lower rows of Fig. 7 (dashed curves). As auditory-filter tuning had only a negligible effect on the location and amplitude of SACF maxima (black vs gray curves in Fig. 8), only plots for the sharper tuning are presented in Fig. 7. It can be seen that maxima in the SACF occur near subharmonics of fc (vertical dotted lines) as long as some residual phase-locking to the TFS is present. For the TFS scheme, the SACF shows clear peaks, while these become less well defined as the amount of residual phase-locking to the TFS is progressively reduced (LP2 and LP7 schemes). As long as residual phase-locking is present, these SACF maxima are able to correctly predict the perceived pitch ambiguity (Fig. 7, three middle rows). However, if TFS information is completely removed (ENV scheme), the SACF shows a single broad maximum that cannot predict pitch ambiguity (Figs. 78, lower row). The SACF profile is thus highly dependent on the acuity of phase-locked TFS information. As with the EP profile, it also correctly predicts an overall absence of phase effects on the pitch locations for the present stimuli.
Mean-absolute-spatial-derivative (MASD) profile
The MASD profile relies on a spatiotemporal operation that emphasizes the phase-transition cues created by the cochlear traveling wave (Cedolin and Delgutte, 2010), by assuming a lateral-inhibition mechanism (Shamma, 1985). It is obtained by calculating the derivative of the activity pattern along the CF dimension, then integrating its absolute value over time. The result is a one-dimensional profile as a function of CF. The MASD profiles were obtained here using discrete derivation, by subtracting the temporal outputs of neighboring channels, followed by trapezoidal numerical integration. They are shown in the four lower rows of Fig. 6. Pitch predictions were derived in the same way as for the EP profile and are shown in the four lower rows of Fig. 7 (solid lines). As the pitch predictions for the two QERB values were very similar, coincidence curves are shown in Fig. 7 for the sharper tuning only.
In contrast to the EP profiles (Fig. 6, upper row), the MASD profiles show more defined contours, with maxima occurring at CFs corresponding roughly to the frequencies of the stimulus components with the largest amplitude. The simulated lateral-inhibition process thus enhances the internal spatial representation of the stimuli. Unlike the EP profile, the MASD profiles are affected by the degree of phase-locking to the TFS (Fig. 6, four lower rows). However, they still show clearly defined peaks when the amount of residual phase-locking is reduced (LP2 and LP7 schemes) as well as when envelope information only is present (ENV scheme). The MASD profile is thus able to correctly predict pitch ambiguity over varying degree of phase-locking to the TFS, as shown in the four lower rows of Fig. 7 (solid lines). Therefore, even in the absence of TFS information, the across-channel comparison of solely envelope information enables plausible pitch predictions. The peak locations in the MASD profiles are similar for the SIN and ALT stimuli, consistent with an absence of phase effects on the perceived pitch. However, the relative amplitude of the activity peaks differs for SIN and ALT phase, which might be used to account for any changes in pitch preference between several ambiguous pitches, as was observed for some of the individual subjects.
Overall, the MASD profile requires neither well-defined EP ripples nor phase-locking to the TFS to obtain accurate pitch predictions. Note, however, that the MASD model predictions are based on results obtained at a single sound level. The effects of level on the bandwidth, phase characteristics, and best frequency of the cochlear filters are likely to complicate the neural implementation and interpretation of a more general and physiologically realistic MASD mechanism. For instance, Carlyon et al. (2012) analyzed auditory-nerve data from guinea-pig recordings and found that level-dependencies rendered across-channel timing cues relatively unreliable as a method for determining the frequency of pure tones. Similar limitations are likely to apply to the current scheme.
Summary of simulation outcomes
All three types of hypothetical profile were able to predict the lack of phase effects on pitch locations and the pitch ambiguity observed in experiment 1, albeit under different premises. The EP profile allows correct pitch predictions provided that the auditory filters are sharp enough and the firing rates of the nerve fibers are not saturated. The SACF profile allows correct pitch predictions provided that there is sufficient residual phase-locking to the TFS. The MASD profile provides reasonable pitch predictions with or without phase-locking to the TFS, as well as in the absence of well-defined rate-place representations. Both place and time cues can thus in principle be used to predict the main trends in the psychophysical data. However, by combining both types of information, the MASD profile is the only one that makes it possible to account, within a single framework, for reduced pitch salience at high frequencies, as well as pitch retrieval above the putative phase-locking range. In regions where phase-locking to the TFS is weak or absent, the pitch of inharmonic complex tones could indeed be coded via the comparison of temporal envelope information across frequency channels. Note that the similarity in pitch perception for the dichotic and monotic conditions (experiment 2) could also be accounted for by combined EP, SACF, or MASD profiles across ears, simply derived from the sum of the left-ear and right-ear spatiotemporal activity patterns.
OVERALL SUMMARY AND CONCLUSIONS
The pitch matches obtained in experiment 1 to inharmonic complex tones with a center-component rank N = 11.5 indicated no effect of relative component phases (SIN or ALT) on the perceived pitch, in contrast to what is typically found for unresolved harmonics. Therefore, no evidence favoring the use of temporal cues for pitch extraction of intermediate harmonics was found here, even though such a result cannot rule out the use of temporal information.
In experiment 2, it was found that presenting neighboring stimulus components to opposite ears did not affect the low pitch, compared to monaural presentation of all components as in experiment 1. The results are not consistent with predictions based on peripheral interactions of components within a single channel, as posited by de Boer (1956b), Schouten et al. (1962), and Moore et al. (2006a). However, it may be possible to explain the results in terms of temporal mechanisms, if one allows for across-ear and across-channel integration of the temporal information.
Experiment 3 investigated the ability of the listeners to hear out the individual stimulus components. This ability decreased as a function of target-component rank and absolute frequency in a way that was consistent with the pitch salience observed in individual listeners in experiment 1. This suggests a link between the accuracy of the representation of individual partials at the cochlear output and the perceived pitch. However, the ability to hear out partials was not a necessary condition to perceive a salient pitch, indicating either that the low pitch does not exclusively rely on place cues, or that the task of hearing out harmonics does not provide an adequate measure of the availability of place cues for pitch extraction.
The observed mismatch between the two typical measures of resolvability, illustrated by a simultaneous absence of phase effects and an inability to hear out partials, raises the question of an adequate definition of resolvability. In the recent studies that have suggested a role of TFS information for high-frequency complex pitch, either by measuring the ability of listeners to discriminate harmonic and frequency-shifted complex tones (Moore et al., 2009b; Moore and Sęk, 2009) or by obtaining pitch matches to similar inharmonic stimuli (Santurette and Dau, 2011), the use of temporal pitch cues was assumed on the basis of unresolved partials, and the components were considered unresolved as long as the listeners could not hear them out from the complex. However, it might be that the partials were resolved enough to allow salient pitch perception based on place cues, without being sufficiently resolved for the listeners to hear them out. In summary, although these psychophysical findings do not rule out the use of TFS cues for the low pitch of high-frequency complex tones with “intermediate” component ranks, they do not provide evidence against the use of place cues either.
In an attempt to determine the extent to which the use of spatial and temporal information can account for the present results, pitch predictions were obtained using either place, timing, or both types of information. Three hypothetical internal pitch representations of the complex tones were derived using a peripheral auditory model: an EP profile, an SACF profile, and an MASD profile. Simple pitch-extraction algorithms were then used to obtain pitch predictions from these three profiles. All three profiles could in principle predict the pitch ambiguity of the complex tones, with pitches near subharmonics of fc, as well as the absence of a pitch dependence on the relative phase of the stimulus components. The MASD profile was less susceptible to the limitations imposed by the sharpness of auditory-filter tuning and the saturation of the firing rate of auditory-nerve fibers than the EP profile. It also provided correct pitch predictions in the absence of phase-locked TFS information, in contrast to the SACF profile. Therefore, spectrotemporal mechanisms combining temporal information across nerve fibers with different CFs can account for high-frequency complex pitch perception, even if TFS information is not conveyed via phase-locking and only envelope information is available, and even if accurate EP-based rate-place information is lacking. In principle, such mechanisms can thus overcome some major limitations affecting temporal mechanisms based on within-channel periodicity information in individual channels and purely spectral mechanisms based on tonotopic maxima in firing rate. However, physiological evidence for their existence remains scant, and it remains questionable whether such a mechanism can provide a sufficiently robust representation of pitch, given the level-dependencies found in physiological auditory-nerve recordings (Carlyon et al., 2012). The questions of the presence of harmonic templates, implied by the use of EP or MASD profiles, and of how tonotopic representations of the stimuli would map to such templates, also remain unsolved. Finally, quantifying the accuracy of rate-place information at high frequencies as well as the frequency dependence of phase-locking in humans will be important in determining which pitch coding scheme is the most plausible.
At this stage, it is not possible to exclude a role of either place or timing information. Overall, the results from the experiments and modeling do not support the claim that only temporal models can account for the results using harmonics in the range between 7 and 15, and suggest that either place, temporal, or place-time models that combine information across frequency (and across ears) are consistent with the available data.
ACKNOWLEDGMENTS
The authors would like to thank Christophe Micheyl for scientific discussions and for his help with analyzing the pitch-matching data, as well as Christopher J. Plack, Brian C. J. Moore, and one anonymous reviewer for insightful comments on earlier versions of this manuscript. This work was supported by the Danish Research Foundation and NIH Grant No. R01 DC 05216.
Portions of this work were presented at the 163rd meeting of the Acoustical Society of America, Hong Kong, May 2012 [J. Acoust. Soc. Am. 131, 3516–3517 (2012)].
Footnotes
A preliminary experiment, reported in Santurette (2011), revealed that the background-noise level used by Santurette and Dau (2011) was sufficient to mask CTs for fc ≤ 5 kHz, with some uncertainty about CT audibility for fc = 7 kHz, hence the present use of a higher spectrum level in the latter condition. Estimations of the level of the most prominent CT (indicated by “CT” in Fig. 1) showed that it may have been as high as that of the lowest stimulus component in some listeners for the SIN configuration, and lower for the ALT than for the SIN stimuli.
Levels referred to as dB HL correspond to SPL values adjusted using formula (12) in Moore and Glasberg (1987). Such a correction was applied so that the audibility of the complex tones was approximately the same in all tested spectral regions.
In order to evaluate pitch salience, discrimination thresholds for equal frequency shifts of all stimulus components were predicted from the pitch matches, using an approach based on estimation theory (Edgeworth, 1908) and described in Micheyl et al. (2010). The d′ values predicted by this procedure can be used as an estimate of pitch salience. The methods and d′ values corresponding to the present data are reported in Santurette (2011).
No randomization was used here, in contrast to Bernstein and Oxenham (2003) who randomized which ear received the odd harmonics in each run.
Note that this paradigm, in which the target component in pulsed on and off, leads to higher performance than in the absence of pulsing (Moore et al., 2009a). It remains unclear whether this difference is due to changes in peripheral representations or more central limitations (Moore et al., 2012). Thus, the pulsed-component method provides a more conservative estimate of whether components are unresolved, in the sense that it would be more likely to classify a component as being resolved than the method without pulsing.
The background noise was not included in these simulations. The average model output with added background noise did not lead to different peak locations in any of the three profiles. The two main effects of the noise were an increase in activity at low CFs in the EP and MASD profiles, and a loss of resolution in the SACF due to the random temporal fluctuations, especially if only few averages were used.
References
- Bernstein, J. G., and Oxenham, A. J. (2003). “ Pitch discrimination of diotic and dichotic tone complexes: Harmonic resolvability or harmonic number?,” J. Acoust. Soc. Am. 113, 3323–3334. 10.1121/1.1572146 [DOI] [PubMed] [Google Scholar]
- Burns, E. M., and Viemeister, N. F. (1976). “ Nonspectral pitch,” J. Acoust. Soc. Am. 60, 863–869. 10.1121/1.381166 [DOI] [Google Scholar]
- Burns, E. M., and Viemeister, N. F. (1981). “ Played-again SAM: Further observations on the pitch of amplitude-modulated noise,” J. Acoust. Soc. Am. 70, 1655–1660. 10.1121/1.387220 [DOI] [Google Scholar]
- Carlyon, R. P., Long, C. J., and Micheyl, C. (2012). “ Across-channel timing differences as a potential code for the frequency of pure tones,” J. Assoc. Res. Otolaryngol. 13, 159–171. 10.1007/s10162-011-0305-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cedolin, L., and Delgutte, B. (2010). “ Spatiotemporal representation of the pitch of harmonic complex tones in the auditory nerve,” J. Neurosci. 30, 12712–12724. 10.1523/JNEUROSCI.6365-09.2010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davis, H., Silverman, S. R., and McAuliffe, D. R. (1951). “ Some observations on pitch and frequency,” J. Acoust. Soc. Am. 23, 40–42. 10.1121/1.1906725 [DOI] [Google Scholar]
- de Boer, E. (1956a). “ Pitch of inharmonic signals,” Nature 178, 535–536. 10.1038/178535a0 [DOI] [PubMed] [Google Scholar]
- de Boer, E. (1956b). “ On the ‘residue’ in hearing,” Ph.D. thesis, University of Amsterdam, pp. 12–89. [Google Scholar]
- Edgeworth, F. Y. (1908). “ On the probable errors of frequency-constants,” J. R. Stat. Soc. 71, 499–512. 10.2307/2339293 [DOI] [Google Scholar]
- Fletcher, H. (1940). “ Auditory patterns,” Rev. Mod. Phys. 12, 47–66. 10.1103/RevModPhys.12.47 [DOI] [Google Scholar]
- Glasberg, B. R., and Moore, B. C. J. (1990). “ Derivation of auditory filter shapes from notched-noise data,” Hear. Res. 47, 103–138. 10.1016/0378-5955(90)90170-T [DOI] [PubMed] [Google Scholar]
- Greenwood, D. D. (1961). “ Critical bandwidth and the frequency coordinates of the basilar membrane,” J. Acoust. Soc. Am. 33, 1344–1356. 10.1121/1.1908437 [DOI] [Google Scholar]
- Hall, J. W., and Peters, R. W. (1981). “ Pitch for nonsimultaneous successive harmonics in quiet and noise,” J. Acoust. Soc. Am. 69, 509–513. 10.1121/1.385480 [DOI] [PubMed] [Google Scholar]
- Heinz, M. G., Colburn, H. S., and Carney, L. H. (2001a). “ Evaluating auditory performance limits: I. One-parameter discrimination using a computational model for the auditory nerve,” Neural Comput. 13, 2273–2316. 10.1162/089976601750541804 [DOI] [PubMed] [Google Scholar]
- Heinz, M. G., Zhang, X., Bruce, I. C., and Carney, L. H. (2001b). “ Auditory nerve model for predicting performance limits of normal and impaired listeners,” Acoust. Res. Lett. Online 2, 91–96. 10.1121/1.1387155 [DOI] [Google Scholar]
- Houtgast, T. (1976). “ Subharmonic pitches of a pure tone at low S/N ratio,” J. Acoust. Soc. Am. 60, 405–409. 10.1121/1.381096 [DOI] [PubMed] [Google Scholar]
- Houtsma, A. J. M., and Goldstein, J. L. (1972). “ The central origin of the pitch of pure tones: Evidence from musical interval recognition,” J. Acoust. Soc. Am. 51, 520–529. 10.1121/1.1912873 [DOI] [Google Scholar]
- Houtsma, A. J. M., and Smurzynski, J. (1990). “ Pitch identification and discrimination for complex tones with many harmonics,” J. Acoust. Soc. Am. 87, 304–310. 10.1121/1.399297 [DOI] [Google Scholar]
- Jepsen, M. L., Ewert, S. D., and Dau, T. (2008). “ A computational model of human auditory signal processing and perception,” J. Acoust. Soc. Am. 124, 422–438. 10.1121/1.2924135 [DOI] [PubMed] [Google Scholar]
- Köppl, C. (1997). “ Phase locking to high frequencies in the auditory nerve and cochlear nucleus magnocellularis of the Barn Owl, Tyto,” J. Neurosci. 17, 3312–3321. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Licklider, J. C. R. (1954). “ ‘Periodicity’ pitch and ‘place’ pitch,” J. Acoust. Soc. Am. 26, 945–945. 10.1121/1.1928005 [DOI] [Google Scholar]
- Mathes, R. C., and Miller, R. L. (1947). “ Phase effects in monaural perception,” J. Acoust. Soc. Am. 19, 780–797. 10.1121/1.1916623 [DOI] [Google Scholar]
- McDermott, J. H., and Oxenham, A. J. (2008). “ Spectral completion of partially masked sounds,” Proc. Natl. Acad. Sci. USA 105, 5939–5944. 10.1073/pnas.0711291105 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meddis, R., and Hewitt, M. J. (1991). “ Virtual pitch and phase sensitivity of a computer model of the auditory periphery. I: Pitch identification,” J. Acoust. Soc. Am. 89, 2866–2882. 10.1121/1.400725 [DOI] [Google Scholar]
- Merzenich, M. M., Knight, P. L., and Roth, G. L. (1975). “ Representation of cochlea within primary auditory cortex in the cat,” J. Neurophysiol. 38, 231–249. [DOI] [PubMed] [Google Scholar]
- Micheyl, C., Divis, K., Wrobleski, D. M., and Oxenham, A. J. (2010). “ Does fundamental-frequency discrimination measure virtual pitch discrimination?,” J. Acoust. Soc. Am. 128(4), 1930–1942. 10.1121/1.3478786 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moore, B. C. J. (2003). An Introduction to the Psychology of Hearing, 5th ed. (Academic Press, London: ), Chap. 6, p. 224. [Google Scholar]
- Moore, B. C. J., and Glasberg, B. R. (1987). “ Formulae describing frequency selectivity as a function of frequency and level, and their use in calculating excitation patterns,” Hear. Res. 28, 209–225. 10.1016/0378-5955(87)90050-5 [DOI] [PubMed] [Google Scholar]
- Moore, B. C. J., Glasberg, B. R., and Flanagan, H. J. (2006a). “ Frequency discrimination of complex tones; assessing the role of component resolvability and temporal fine structure,” J. Acoust. Soc. Am. 119, 480–490. 10.1121/1.2139070 [DOI] [PubMed] [Google Scholar]
- Moore, B. C. J., Glasberg, B. R., and Jepsen, M. L. (2009a). “ Effects of pulsing of the target tone on the audibility of partials in inharmonic complex tones,” J. Acoust. Soc. Am. 125, 3194–3204. 10.1121/1.3109997 [DOI] [PubMed] [Google Scholar]
- Moore, B. C. J., Glasberg, B. R., Low, K. E., Cope, T., and Cope, W. (2006b). “ Effects of level and frequency on the audibility of partials in inharmonic complex tones,” J. Acoust. Soc. Am. 120, 934–944. 10.1121/1.2216906 [DOI] [PubMed] [Google Scholar]
- Moore, B. C. J., Glasberg, B. R., and Oxenham, A. J. (2012). “ Effects of pulsing of a target tone on the ability to hear it out in different types of complex sounds,” J. Acoust. Soc. Am. 131, 2927–2937. 10.1121/1.3692243 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moore, B. C. J., Hopkins, K., and Cuthbertson, S. (2009b). “ Discrimination of complex tones with unresolved components using temporal fine structure information,” J. Acoust. Soc. Am. 125, 3214–3222. 10.1121/1.3106135 [DOI] [PubMed] [Google Scholar]
- Moore, G. A., and Moore, B. C. J. (2003). “ Perception of the low pitch of frequency-shifted complexes,” J. Acoust. Soc. Am. 113, 977–985. 10.1121/1.1536631 [DOI] [PubMed] [Google Scholar]
- Moore, B. C. J., and Ohgushi, K. (1993). “ Audibility of partials in inharmonic complex tones,” J. Acoust. Soc. Am. 93, 452–461. 10.1121/1.405625 [DOI] [PubMed] [Google Scholar]
- Moore, B. C. J., and Rosen, S. M. (1979). “ Tune recognition with reduced pitch and interval information,” Q. J. Exp. Psychol. 31, 229–240. 10.1080/14640747908400722 [DOI] [PubMed] [Google Scholar]
- Moore, B. C. J., and Sęk, A. (2009). “ Sensitivity of the human auditory system to temporal fine structure at high frequencies,” J. Acoust. Soc. Am. 125, 3186–3193. 10.1121/1.3106525 [DOI] [PubMed] [Google Scholar]
- Oxenham, A. J., Bernstein, J. G. W., and Penagos, H. (2004). “ Correct tonotopic representation is necessary for complex pitch perception,” Proc. Natl. Acad. Sci. USA 101, 1421–1425. 10.1073/pnas.0306958101 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oxenham, A. J., Micheyl, C., and Keebler, M. V. (2009). “ Can temporal fine structure represent the fundamental frequency of unresolved harmonics?,” J. Acoust. Soc. Am. 125, 2189–2199. 10.1121/1.3089220 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oxenham, A. J., Micheyl, C., Keebler, M. V., Loper, A., and Santurette, S. (2011). “ Pitch perception beyond the traditional existence region of pitch,” Proc. Natl. Acad. Sci. USA 108, 7629–7634. 10.1073/pnas.1015291108 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oxenham, A. J., and Shera, C. A. (2003). “ Estimates of human cochlear tuning at low levels using forward and simultaneous masking,” J. Assoc. Res. Otolaryngol. 4, 541–554. 10.1007/s10162-002-3058-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- Palmer, A. R., and Russell, I. J. (1986). “ Phase locking in the cochlear nerve of the guinea-pig and its relation to the receptor potential of inner haircells,” Hear. Res. 24, 1–15. 10.1016/0378-5955(86)90002-X [DOI] [PubMed] [Google Scholar]
- Plack, C. J., Oxenham, A. J. (2005). “ The psychophysics of pitch.” Pitch—Neural Coding and Perception, Springer Handbook of Auditory Research (Springer, New York: ), Chap. 2, pp. 7–55. [Google Scholar]
- Recio-Spinoso, A., Temchin, A. N., van Dijk, P., Fan, Y. H., and Ruggero, M. A. (2005). “ Wiener-kernel analysis of responses to noise of chinchilla auditory-nerve fibers,” J. Neurophysiol. 93, 3615–3634. 10.1152/jn.00882.2004 [DOI] [PubMed] [Google Scholar]
- Ritsma, R. J. (1962). “ Existence region of the tonal residue. I,” J. Acoust. Soc. Am. 34, 1224–1229. 10.1121/1.1918307 [DOI] [Google Scholar]
- Ritsma, R. J., and Engel, F. L. (1964). “ Pitch of frequency-modulated signals,” J. Acoust. Soc. Am. 36, 1637–1644. 10.1121/1.1919257 [DOI] [Google Scholar]
- Rose, J. E., Brugge, J. F., Anderson, D. J., and Hind, J. E. (1967). “ Phase-locked response to low-frequency tones in single auditory nerve fibers of squirrel monkey,” J. Neurophysiol. 30, 769–793. [DOI] [PubMed] [Google Scholar]
- Santurette, S. (2011). “ Neural coding and perception of pitch in the normal and impaired human auditory system,” Ph.D. dissertation, Technical University of Denmark, Kgs. Lyngby, Vol. 10, Chap. 6, pp. 159–197. [Google Scholar]
- Santurette, S., and Dau, T. (2011). “The role of temporal fine structure information for the low pitch of high-frequency complex tones,” J. Acoust. Soc. Am. 129, 282–292. 10.1121/1.3518718 [DOI] [PubMed] [Google Scholar]
- Schouten, J. F. (1940). “ The residue, a new component in subjective sound analysis,” Proc. Kon. Acad. Wetensch. 43, 356–365. [Google Scholar]
- Schouten, J. F., Ritsma, R. J., and Lopes Cardozo, B. (1962). “ Pitch of the residue,” J. Acoust. Soc. Am. 34, 1418–1424. 10.1121/1.1918360 [DOI] [Google Scholar]
- Schroeder, M. R. (1968). “ Period histogram and product spectrum: New methods for fundamental-frequency measurement,” J. Acoust. Soc. Am. 43, 829–834. 10.1121/1.1910902 [DOI] [PubMed] [Google Scholar]
- Schroeder, M. R., and Hall, J. L. (1974). “ Model for mechanical to neural transduction in the auditory receptor,” J. Acoust. Soc. Am. 55, 1055–1060. 10.1121/1.1914647 [DOI] [PubMed] [Google Scholar]
- Seebeck, A. (1841). “ Beobachtungen über einige Bedidungen der Entstehung von Tönen (Observations over some conditions of the emergence of tones),” Ann. Phys. Chem. 53, 417–436. [Google Scholar]
- Sęk, A., and Moore, B. C. J. (1995). “ Frequency discrimination as a function of frequency, measured in several ways,” J. Acoust. Soc. Am. 97, 2479–2486. 10.1121/1.411968 [DOI] [PubMed] [Google Scholar]
- Shackleton, T. M., and Carlyon, R. P. (1994). “ The role of resolved and unresolved harmonics in pitch perception and frequency modulation discrimination,” J. Acoust. Soc. Am. 95, 3529–3540. 10.1121/1.409970 [DOI] [PubMed] [Google Scholar]
- Shamma, S. A. (1985). “ Speech processing in the auditory system II: Lateral inhibition and the central processing of speech evoked activity in the auditory nerve,” J. Acoust. Soc. Am. 78, 1622–1632. 10.1121/1.392800 [DOI] [PubMed] [Google Scholar]
- Shamma, S., and Klein, D. (2000). “ The case of the missing pitch templates: How harmonic templates emerge in the early auditory system,” J. Acoust. Soc. Am. 107, 2631–2644. 10.1121/1.428649 [DOI] [PubMed] [Google Scholar]
- Shera, C. A., Guinan, J. J., and Oxenham, A. J. (2002). “ Revised estimates of human cochlear tuning from otoacoustic and behavioral measurements,” Proc. Natl. Acad. Sci. USA 99, 3318–3323. 10.1073/pnas.032675099 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smoorenburg, G. F. (1970). “ Pitch perception of two-frequency stimuli,” J. Acoust. Soc. Am. 48, 924–942. 10.1121/1.1912232 [DOI] [PubMed] [Google Scholar]
- Terhardt, E. (1974). “ Pitch, consonance and harmony,” J. Acoust. Soc. Am. 55, 1061–1069. 10.1121/1.1914648 [DOI] [PubMed] [Google Scholar]
- Thurlow, W. R., and Small, A. M., Jr. (1955). “ Pitch perception for certain periodic harmonic stimuli,” J. Acoust. Soc. Am. 27, 132–137. 10.1121/1.1907473 [DOI] [Google Scholar]
- van de Par, S., and Kohlrausch, A. (1997). “ A new approach to comparing binaural masking level differences at low and high frequencies,” J. Acoust. Soc. Am. 101, 1671–1680. 10.1121/1.418151 [DOI] [PubMed] [Google Scholar]
- Verhulst, S., Dau, T., and Shera, C. A. (2012). “ Nonlinear time-domain cochlear model for transient stimulation and human otoacoustic emission,” J. Acoust. Soc. Am. 132, 3842–3848. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wier, C. C., Jesteadt, W., and Green, D. M. (1977). “ Frequency discrimination as a function of frequency and sensation level,” J. Acoust. Soc. Am. 61, 178–184. 10.1121/1.381251 [DOI] [PubMed] [Google Scholar]
- Wightman, F. L. (1973). “ The pattern-transformation model of pitch,” J. Acoust. Soc. Am. 54, 407–416. 10.1121/1.1913592 [DOI] [PubMed] [Google Scholar]
- Zhang, X., Heinz, M. G., Bruce, I. C., and Carney, L. H. (2001). “ A phenomenological model for the responses of auditory-nerve fibers: I. Nonlinear tuning with compression and suppression,” J. Acoust. Soc. Am. 109, 648–670. 10.1121/1.1336503 [DOI] [PubMed] [Google Scholar]