A backscatter difference technique for ultrasonic bone assessment

Abstract

Ultrasonic backscatter techniques may offer a useful approach for detecting changes in cancellous bone caused by osteoporosis and other diseases. The goal of this study was to investigate the utility of a backscatter difference technique for ultrasonic bone assessment. Measurements were performed on 22 cube-shaped specimens of human cancellous bone using four broadband transducers with center frequencies 2.25, 5, 7.5, and 10 MHz. The backscatter difference spectrum D(f) was obtained by subtracting power spectra (in dB) from two different portions of the same backscatter signal. D(f) was found to be a monotonically increasing, quasi-linear function of frequency when averaged over multiple measurement sites on multiple specimens. The frequency slope of D(f) demonstrated weak to moderate correlations with specimen density (R = 0.21–0.80). The frequency averaged mean of D(f) demonstrated moderate to good correlations with density (R = 0.70–0.95). These results suggest that parameters based on the frequency averaged mean of the backscatter difference spectrum may be useful for bone assessment purposes.

INTRODUCTION

Ultrasonic backscatter techniques may offer a useful approach for detecting changes in cancellous bone caused by osteoporosis and other diseases. A variety of backscatter techniques are being evaluated for bone assessment purposes. Some studies have measured a parameter called broadband ultrasonic backscatter (BUB), which is the frequency averaged backscatter coefficient. BUB has been shown to be sensitive to the density, mechanical properties, and microstructure of cancellous bone (Chaffai et al., 2002; Hakulinen et al., 2004; Hakulinen et al., 2005; Hakulinen et al., 2006; Jenson et al., 2006; Padilla et al., 2008). BUB also may be sensitive to bone composition (Riekkinen et al., 2007a; Karjalainen et al., 2009).

Measurements of BUB require knowledge of the attenuation along the path of the ultrasonic wave. If the attenuation is not known, it is more convenient to measure parameters based on the apparent backscattered power. The term “apparent” means that the received backscatter signal is not compensated for the frequency-dependent effects of attenuation and diffraction. Apparent backscatter parameters, such as apparent integrated backscatter (AIB) and frequency slope of apparent backscatter (FSAB) have demonstrated moderate to good correlations with the density and mechanical properties of cancellous bone in vitro (Hoffmeister et al., 2006; Riekkinen et al., 2007b; Hoffmeister et al., 2008; Karjalainen et al., 2009; Hoffmeister, 2011). A recent in vivo study showed that AIB measurements at the hip could be used to discriminate human subjects with previous hip fractures from control subjects (Karjalainen et al., 2012).

Backscatter parameters such as BUB, AIB, and FSAB are determined from the power spectrum of a single gated portion of the backscatter signal. In contrast, the present study uses a technique that compares power spectra from two different gated portions of the signal. The power spectra (in dB) are subtracted to obtain a backscatter difference spectrum $D\left(f\right)$. Two parameters are determined from the difference spectrum. The mean of the backscatter difference spectrum (MBD) is obtained by frequency averaging $D\left(f\right)$ over the analysis bandwidth. The slope of the backscatter difference spectrum (SBD) is obtained by measuring the frequency slope of $D\left(f\right)$ over the same bandwidth.

Backscatter difference techniques have not been applied previously to bone. However, they have been used to study soft tissues. For example, backscatter difference techniques were used to estimate the ultrasonic attenuation of human liver in vivo (Kuc, 1980; Fink et al., 1983; Ophir et al., 1984; Ophir et al., 1985). The goal of the present study is to investigate the utility of backscatter difference techniques for ultrasonic bone assessment.

THEORETICAL BACKGROUND

Backscatter difference parameters

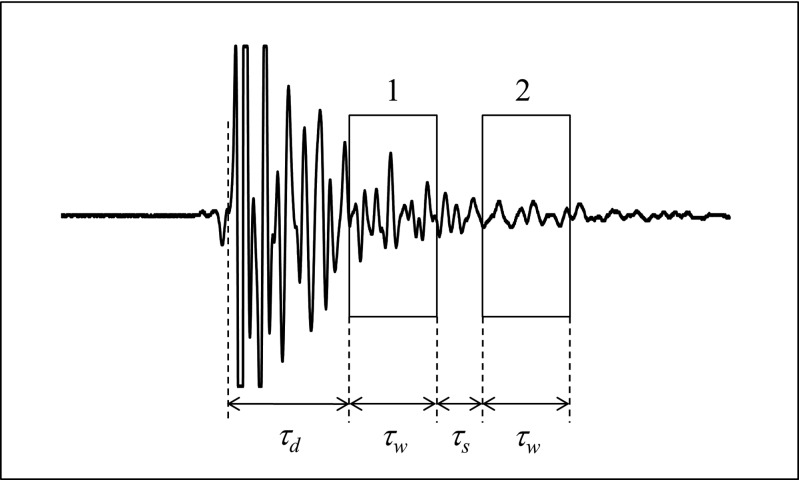
Figure 1 shows a backscatter signal that was acquired from a cube-shaped specimen of cancellous bone in a water bath. The backscatter difference spectrum $D\left(f\right)$ is determined by placing two analysis gates on the signal. The two gates have the same duration, or width, ${\tau }_w$. The first gate (gate 1) is delayed by an amount ${\tau }_d$ to avoid the specular echo (allowed to clip in Fig. 1) that is produced by the front surface of the specimen. The second gate (gate 2) is separated from the first by an amount ${\tau }_s$. Power spectra $P_1\left(f\right)$ and $P_2\left(f\right)$ from the first and second gated portions of the backscatter signal are converted to decibels and subtracted to obtain the difference spectrum,

$$D\left(f\right)=10{\log }_{10}{P}_1\left(f\right)-10{\log }_{10}{P}_2\left(f\right)=10\log \left(\frac{P_1\left(f\right)}{P_2\left(f\right)}\right).$$ (1)

Figure 1.

The backscatter difference technique analyzes two portions of a backscatter signal as indicated by the two rectangles superimposed on this backscatter signal from cancellous bone. The gated portions of the signal have the same durations (or width) ${\tau }_w$ and are separated by an amount ${\tau }_s$ as shown. The first gated portion of the signal is delayed by an amount ${\tau }_d$ to avoid the specular echo from the front surface of the specimen (allowed to clip).

The difference spectrum $D\left(f\right)$ can be related to physical mechanisms that affect the backscatter signal. The approach that follows was developed by Sigelmann and Reid (1973) and later adapted for tissue characterization studies by O'Donnell and Miller (1981). Different approaches have been suggested by other investigators (Madsen et al., 1984; Wear et al., 1989; Chen et al., 1997).

The power spectrum from either of the two gated portions of the backscatter signal is expressed as

$$P\left(f\right)=\frac{4P_0\left(f\right)E\left(f\right)V\left(f\right)\eta \left(f\right)T^2}{r^{2}A\left(f\right)},$$ (2)

where $P_0\left(f\right)$ is the power spectrum of the transmitted pulse, $E\left(f\right)$ is the two-way electromechanical power conversion efficiency of the measurement system, $V\left(f\right)$ is the gated scattering volume of the specimen, $\eta \left(f\right)$ is the backscatter coefficient of the specimen, T is the intensity transmission coefficient at the water-specimen interface, and r is the distance from the transducer to the center of the scattering volume. Single scattering is assumed. $A\left(f\right)$ is an attenuation term given by

$$A\left(f\right)=e^{4\alpha \left(f\right)x}\left[\frac{2\alpha \left(f\right)c{\tau }_w · e^{\alpha \left(f\right)c{\tau }_w}}{e^{\alpha \left(f\right)c{\tau }_w}-e^{-\alpha \left(f\right)c{\tau }_w}}\right].$$ (3)

It includes attenuation of the ultrasonic pulse up to the start of the analysis gate (through a thickness x of intervening specimen) and within the gated region. The term c is the speed of sound in the specimen and $\alpha \left(f\right)$ is the attenuation coefficient of the specimen.

The backscatter difference spectrum $D\left(f\right)$ in decibels is given by

$$D\left(f\right)=10\log \frac{P_1\left(f\right)}{P_2\left(f\right)}=10\log \frac{\frac{4P_0\left(f\right)E\left(f\right)V_1\left(f\right){\eta }_1\left(f\right)T^2}{{r_1}^2{A}_1\left(f\right)}}{\frac{4P_0\left(f\right)E\left(f\right)V_2\left(f\right){\eta }_2\left(f\right)T^2}{{r_2}^2{A}_2\left(f\right)}},$$ (4)

where the subscripts 1 and 2 indicate quantities associated with the first and second gated portions of the backscatter signal, respectively (see Fig. 1). As $P_0\left(f\right)$, $E\left(f\right)$, and T are the same for both gated portions of the signal, Eq. 4 can be simplified to yield

$$D\left(f\right)=10\log \frac{V_1\left(f\right){\eta }_1\left(f\right)/{r_1}^2{A}_1\left(f\right)}{V_2\left(f\right){\eta }_2\left(f\right)/{r_2}^2{A}_2\left(f\right)}.$$ (5)

Two parameters are determined from the backscatter difference spectrum. MBD is determined by frequency averaging $D\left(f\right)$ over the analysis bandwidth. SBD is determined by fitting a line to $D\left(f\right)$ over the analysis bandwidth.

Small d approximation

The distance d between the centers of the two gated portions of the backscatter signal is

$$d=c\left({\tau }_w+{\tau }_s\right)/2,$$ (6)

where c is the speed of sound in cancellous bone (assumed to be constant over the distance d), and ${\tau }_w$ is the same for both gates as shown in Fig. 1. The small d approximation assumes that the two gated portions of the signal are close enough that ${\eta }_1\left(f\right)\cong {\eta }_2\left(f\right)$ and ${\alpha }_1\left(f\right)\cong {\alpha }_2\left(f\right)$. Also, d is assumed to be small enough compared to the distance r between the transducer and the scattering volumes $V_1\left(f\right)$ and $V_2\left(f\right)$ that $r_1\cong r_2$ and $V_1\left(f\right)\cong V_2\left(f\right)$. Using these approximations in Eq. 5 gives

$$D\left(f\right)\cong 10\log \frac{A_2\left(f\right)}{A_1\left(f\right)}=10\log e^{4\alpha \left(f\right)\left(x_2-x_1\right)}=10\log e^{4\alpha \left(f\right)c\left({\tau }_w+{\tau }_s\right)},$$ (7)

which can be simplified further to yield

$$D\left(f\right)\cong \left(40\log e\right)c\left({\tau }_w+{\tau }_s\right)\alpha \left(f\right).$$ (8)

Equation 8 shows that $D\left(f\right)$ depends on only four quantities in the small d approximation: the speed of sound c, the gate width ${\tau }_w$, the gate separation ${\tau }_s$, and the attenuation coefficient $\alpha \left(f\right)$.

Normalized backscatter difference parameters

Different choices of ${\tau }_w$ and ${\tau }_s$ in Eq. 8 will give different results for $D\left(f\right)$ and thus different results for MBD and SBD. For this reason, it is useful to define a normalized difference spectrum that does not depend on these choices,

$$\mathrm{n}D\left(f\right)\equiv D\left(f\right)/\left({\tau }_w+{\tau }_s\right)\cong \left(40\log e\right)c\alpha \left(f\right).$$ (9)

In the small d approximation, the normalized difference spectrum $nD\left(f\right)$ depends only on the attenuation coefficient $\alpha \left(f\right)$ and the speed of sound c. This is an interesting result because the speed of sound and attenuating properties of bone are used widely for bone assessment purposes. The backscatter difference parameters MBD and SBD may be normalized in a similar manner:

$$\text{nMBD}\equiv \text{MBD}/\left({\tau }_w+{\tau }_s\right),$$ (10)

and

$$\text{nSBD}\equiv \text{SBD}/\left({\tau }_w+{\tau }_s\right).$$ (11)

EXPERIMENTAL METHODS

Specimen preparation

Twenty-two cube-shaped specimens of human cancellous bone were prepared from 14 fresh frozen femoral heads from 7 donors (4 males, 3 females, ages 45–91 years). The side lengths of the cubes were ∼15 mm. The faces of the cubes were aligned along the principal anatomic axes of the femoral head. A water jet was used to remove as much marrow as possible from the intertrabecular spaces.

Density measurements

The specimens were allowed to dry at room temperature, and their mass was measured periodically using an electronic scale to track their dehydration. Approximately 24 h were required for the mass to stabilize, indicating that the specimens were fully air dried. Digital calipers were used to measure the dimensions of the specimens. Apparent density was determined by dividing the mass of the cube by the volume. The term “apparent” is used in this context to indicate the dehydrated mass density of the specimen with the marrow removed.

Ultrasonic backscatter measurements

Ultrasonic measurements were performed in a water tank at room temperature with four different broadband transducers: 2.25 MHz planar, 5 MHz focused, 7.5 MHz focused, and 10 MHz focused. Transducer information from the manufacturer, including the center frequency, transducer diameter, −6 dB beam diameter, focal length, and model number is provided in Table TABLE I..

TABLE I.

Transducer information specified by manufacturer

Transducer center frequency (MHz)	Transducer diameter (mm)	−6 dB beam diameter at focus (mm)	Focal length (mm)	Model (Panametrics)
2.25	6.4	1.81	16.8 a	V323
5	12.7	1.23	50.8	V309
7.5	12.7	0.82	50.8	V320
10	12.7	0.62	50.8	V311

^aNear field distance for this planar transducer.

The specimens were degassed under vacuum for 10 min prior to ultrasonic measurement. The transducer was positioned one focal length away from the front surface of the specimen. The transducer was connected to a three axis mechanical scanner (Sonix) and ultrasonic pulses were generated with an ultrasonic pulser-receiver (Panametrics Model 5800). The received signals were digitized by an 8 bit analog to digital converter (Sonix STR*8100) operating at 100 MSa/s (2.25 MHz transducer) or 500 MSa/s (5, 7.5, and 10 MHz transducers).

The transducer was moved in a 20 × 20 mm scan with a step size equal to one-half of the beam diameter of the transducer. Backscatter signals were acquired from a square region of interest (ROI) centered on the specimen. Care was taken so that the edge of the ROI was at least one beam diameter away from the edge of the specimen. Details of the ROIs for each transducer are given in Table TABLE II.. All six sides of each specimen were scanned.

TABLE II.

Scan information

Transducer center frequency, fc (MHz)	ROI size	Scan step size (mm)	Analysis gate delay, τd (μs)	Analysis gate width, τw (μs)
2.25	8 × 8	0.91	4.78	4.44
5	16 × 16	0.62	2.80	2.00
7.5	26 × 26	0.41	2.18	1.33
10	36 × 36	0.31	1.12	1.00

Backscatter signal analysis

Two analysis gates were placed on each backscatter signal as shown in Fig. 1. The duration, or width, of each gate ${\tau }_w$ was chosen to be $10/f_c$ where $f_c$ is the center frequency of the transducer. A rectangular windowing function was used for all gates. The gate delay ${\tau }_d$ was chosen to be two times the duration of the echo from an optical glass flat. Values for ${\tau }_d$ and ${\tau }_w$ are given in Table TABLE II.. The second gate was separated from the first by an amount ${\tau }_s$. Analyses were performed for three different choices of gate separation: ${\tau }_s=0$, $5/f_c$, and $10/f_c$. Power spectra $P_1\left(f\right)$ and $P_2\left(f\right)$ for the first and second gated portions of the backscatter signal, respectively, were obtained by performing a fast Fourier transform. The spectra were converted to decibels and subtracted to obtain the backscatter difference spectrum $D\left(f\right)$. MBD was determined by frequency averaging $D\left(f\right)$ over the analysis bandwidth. SBD was determined by fitting a line to $D\left(f\right)$ over the analysis bandwidth and measuring the slope. The normalized quantities $nD\left(f\right)$, nMBD (normalized mean of the backscatter difference spectrum) and nSBD (normalized slope of the backscatter difference spectrum) were obtained by dividing $D\left(f\right)$, MBD, and SBD, respectively, by $\left({\tau }_w+{\tau }_s\right)$.

The analysis bandwidth was determined using the following procedure. Power spectra from the first gated portion of the backscatter signals $10\log P_1\left(f\right)$ were averaged over all measurements on all specimens to obtain a single average spectrum for each combination of transducer and gate separation. Power spectra from the second gated portion $10\log P_2\left(f\right)$ were averaged in a similar manner. The −6 dB bandwidth of each average spectrum was determined. The analysis bandwidth was chosen to be the intersection of these two bandwidths. Analysis bandwidths are reported in Table TABLE III. for each combination of transducer and gate separation.

TABLE III.

Analysis bandwidths for each choice of transducer and gate separation τ_s

Transducer center frequency fc (MHz)	Analysis bandwidth (MHz)
	τs = 0	τs = 5/fc	τs = 10/fc
2.25	0.4–1.8	0.4–1.4	0.4–1.4
5	1.0–4.4	1.0–3.9	1.0–3.4
7.5	1.5–7.3	1.5–6.8	1.5–5.9
10	2.0–6.8	2.0–6.8	2.0–5.9

RESULTS

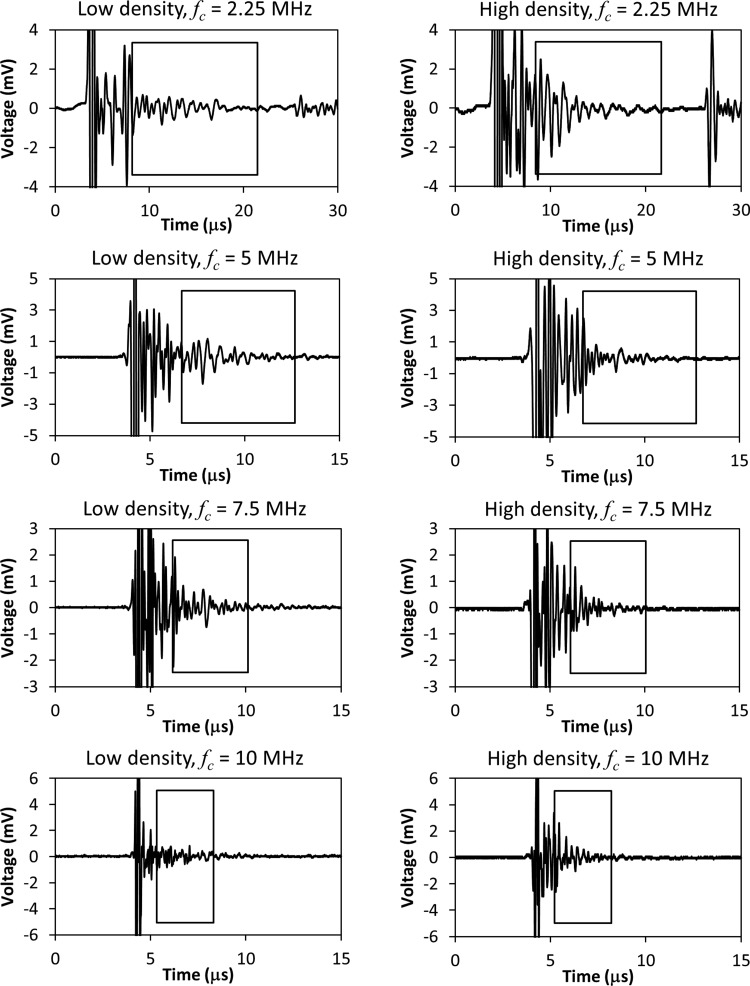
Figure 2 shows backscatter signals acquired from the lowest and highest density specimens used in the study. The signals were selected from the center of the anterior ROI. Signals from all four transducers (f_c = 2.25, 5, 7.5, and 10 MHz) are shown. The rectangle superimposed on each signal in Fig. 2 indicates the portion of the signal that was analyzed. The left edge of the rectangle indicates the start of the first analysis gate, and the right edge indicates the end of the second analysis gate for the maximum gate separation ${\tau }_s=10/f_c$.

Figure 2.

Examples of backscatter signals from the lowest density (left column) and highest density (right column) specimens of bone. The center frequency f_c of the transducer is indicated above each signal. The rectangle superimposed on each signal indicates the portion of the signal that was analyzed. The left edge of the rectangle indicates the start of the first analysis gate, and the right edge indicates the end of the second analysis gate for the maximum gate separation ${\tau }_s=10/f_c$.

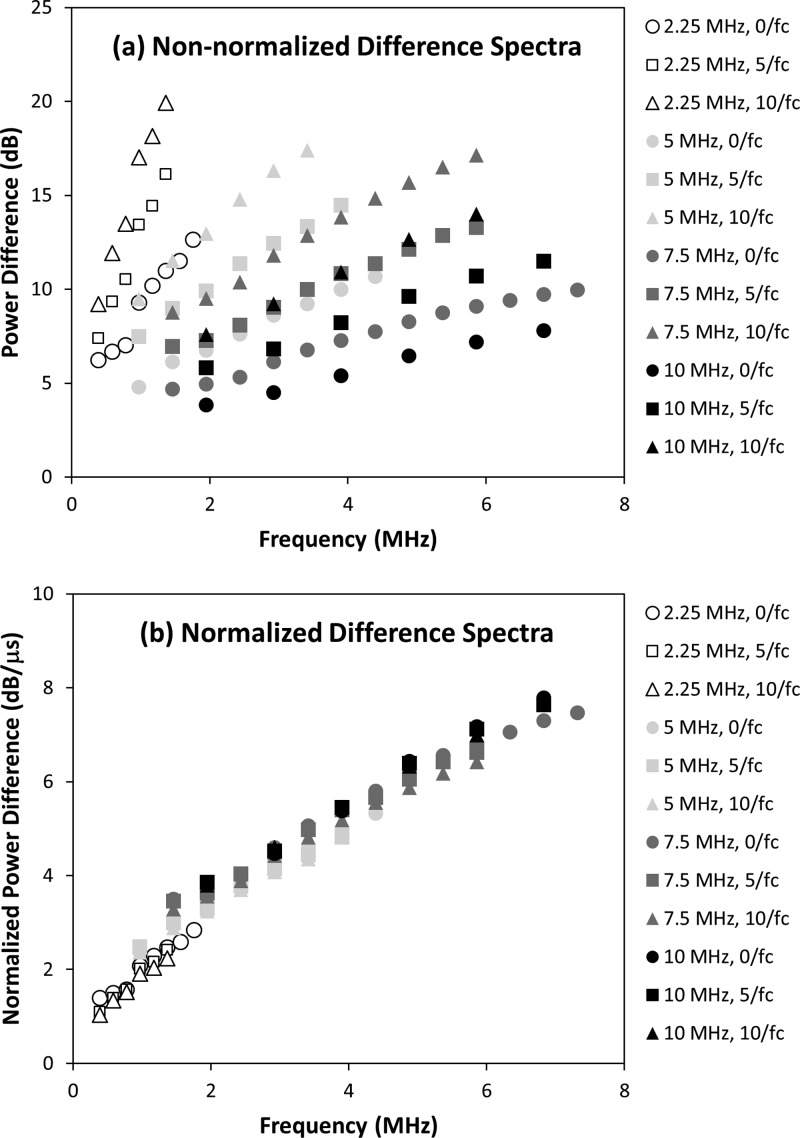
Figure 3a illustrates difference spectra that were obtained by averaging difference spectra from all measurement sites on all specimens of bone. A total of 12 difference spectra are shown corresponding to each choice of transducer (2.25, 5, 7.5, and 10 MHz) and gate separation (${\tau }_s=0$, $5/f_c$ and $10/f_c$). Figure 3b shows the same difference spectra after they are normalized using Eq. 9.

Figure 3.

Results for (a) the difference spectra $D\left(f\right)$ and (b) the normalized difference spectra $nD\left(f\right)$ for all transducers (2.25, 5, 7.5, and 10 MHz) and all three choices of gate separation (${\tau }_s=0$, $5/f_c$, and $10/f_c$). Individual data series were generated by averaging all measurements from all specimens for each choice of transducer and gate separation.

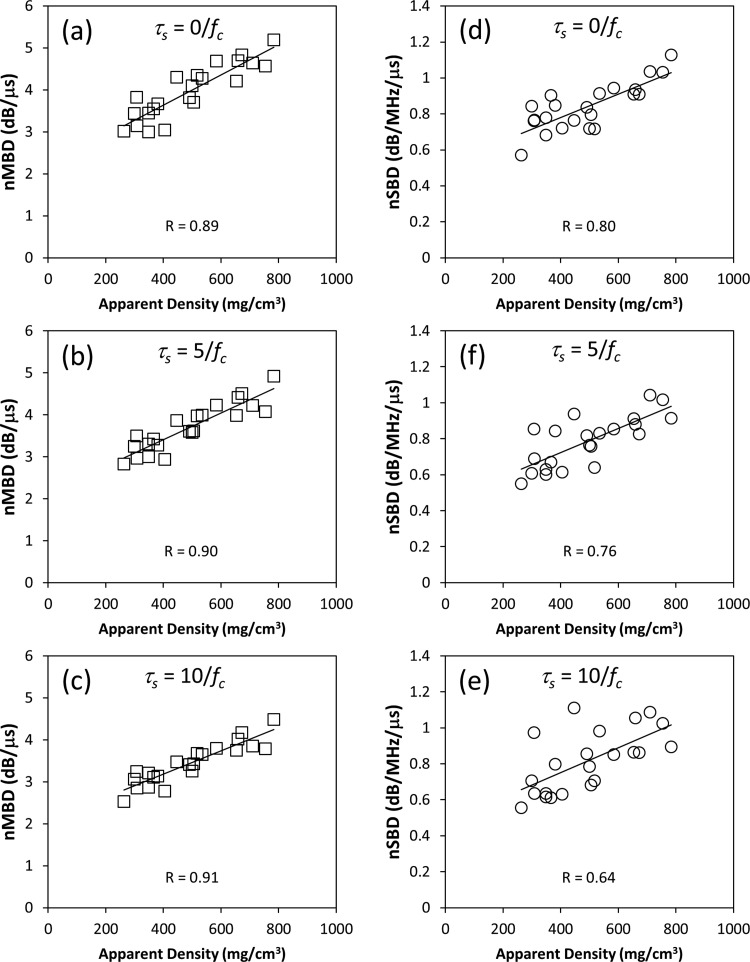
Figure 4 illustrates nMBD and nSBD plotted as a function of apparent density for the 5 MHz transducer. Individual data points on the graphs in Fig. 4 represent mean values of nMBD or nSBD for individual specimens obtained by averaging over all measurement sites on individual specimens. Linear regression analysis was used to determine the correlation coefficient R between the backscatter parameters and apparent density. Similar analyses were performed for the 2.25, 7.5, and 10 MHz transducers. The resulting correlation coefficients are reported in Tables 4, TABLE V.. Tables 4, TABLE V. also report means and standard deviations for nMBD and nSBD, respectively.

Figure 4.

Graphs like these examples were used to determine the correlation between the ultrasonic parameters considered in this study (nMBD and nSBD) and the apparent density of the specimens. Data in this example were acquired with the 5 MHz transducer.

TABLE IV.

Mean ± standard deviation of the normalized mean of the backscatter difference spectrum (nMBD) for each transducer and gate separation τ_s. ^a

Transducer center frequency fc (MHz)	nMBD (dB/μs)
	τs = 0	τs = 5/fc	τs = 10/fc.
2.25	2.1 ± 0.2 (0.79*)	1.8 ± 0.2 (0.77*)	1.7 ± 0.2 (0.70*)
5	4.0 ± 0.7 (0.89*)	3.7 ± 0.6 (0.90*)	3.4 ± 0.5 (0.91*)
7.5	5.7 ± 1.0 (0.94*)	5.4 ± 0.9 (0.92*)	4.9 ± 0.8 (0.90*)
10	5.8 ± 1.3 (0.95*)	5.8 ± 1.3 (0.95*)	5.4 ± 1.1 (0.95*)

^aLinear correlation coefficients with bone density are given in parentheses. *p < 0.001.

TABLE V.

Mean ± standard deviation of the normalized frequency slope of the backscatter difference spectrum (nSBD) for each transducer and gate separation τ_s. ^a

Transducer center frequency fc (MHz)	nSBD (dB/MHz/μs)
	τs = 0	τs = 5/fc	τs = 10/fc.
2.25	1.12 ± 0.25 (0.21)	1.36 ± 0.21 (0.33)	1.25 ± 0.17 (0.40)
5	0.84 ± 0.13 (0.80*)	0.78 ± 0.14 (0.76*)	0.82 ± 0.17 (0.64)
7.5	0.73 ± 0.10 (0.58)	0.72 ± 0.08 (0.67*)	0.75 ± 0.09 (0.73*)
10	0.85 ± 0.20 (0.77*)	0.81 ± 0.15 (0.72*)	0.83 ± 0.12 (0.73*)

^aLinear correlation coefficients with bone density are given in parentheses. *p < 0.001.

DISCUSSION

The backscatter difference spectrum

As seen in Fig. 3a, the difference spectrum is a monotonically increasing, quasi-linear function of frequency for any choice of transducer and gate separation. The slopes of the normalized difference spectra [see Fig. 3b] are approximately the same for the 5, 7.5, and 10 MHz transducers, but noticeably greater for the 2.25 MHz transducer. This is consistent with the values reported in Table TABLE V. that show nSBD to be greatest for the 2.25 MHz transducer. These results suggest that the frequency dependence of the difference spectrum is not constant over the full frequency range of the study (0.4–7.3 MHz).

Increases in the gate separation cause the difference spectra in Fig. 3a to shift upward (to greater power differences) for each transducer. This is expected because the power difference between the first and second gated portions of the backscatter signal (see Fig. 1) should increase as the gate separation τ_s is increased. The normalization procedure largely removes this effect [see Fig. 3b]. The normalization procedure also appears to remove most of the effects of gate duration which was different for different transducers. The ability of the normalization procedure to remove these effects suggests that the assumptions that lead to Eq. 8 are reasonable for the choices of gate separation and gate duration used in this study.

Anisotropy

To test if the results for nMBD and nSBD possess a directional dependence, spatially averaged values of nMBD and nSBD were determined for each of the six measurement directions (anterior, posterior, medial, lateral, proximal, and distal) for each specimen. Measurements along different directions were compared using a single factor ANOVA test with a 95% confidence interval. No significant difference was found among measurement directions for any choice of transducer and gate separation.

It is interesting that no anisotropy is observed for the backscatter difference parameters considered in this study. A previous study of specimens prepared from the femoral head also found little evidence of anisotropy in other backscatter parameters such as AIB and FSAB (Hoffmeister et al., 2008). These results suggest that cancellous bone tissue from the femoral head may not be highly anisotropic. However, it is possible that measurements based on apparent backscatter may not be very sensitive to the structural anisotropy of cancellous bone. A previous study involving cube-shaped specimens of cancellous bone prepared from the proximal end of bovine tibiae found no anisotropy in AIB using 1 and 5 MHz transducers (Hoffmeister et al., 2006).

Utility of nMBD and nSBD as bone assessment parameters

The utility of bone assessment parameters can be assessed, in part, by how well they correlate with bone density. The correlation coefficients reported in Tables 4, TABLE V. are comparable to values reported in recent studies for BUB, AIB, and FSAB (Hakulinen et al., 2004; Hakulinen et al., 2005; Jenson et al., 2006; Hoffmeister et al., 2008; Padilla et al., 2008; Hoffmeister, 2011). The correlation coefficients in Tables 4, TABLE V. were analyzed statistically using a Fisher R to z transformation and a two-tailed test with a 95% confidence interval. nMBD demonstrated a significantly stronger correlation with bone density than nSBD for most choices of transducer and gate separation. Parameters measured with the 2.25 MHz transducer generally correlated more weakly with density than parameters measured with the higher frequency transducers.

The results of this in vitro study suggest that higher frequency transducers $\left(f_c>2.25\hspace{0.17em}\text{MHz}\right)$ are good choices for backscatter difference measurements of bone. In vivo measurements at similar frequencies may be feasible. Karjalainen et al. (2012) recently used a 5 MHz transducer to perform ultrasonic backscatter measurements at the hip (trochanter and femoral neck) in elderly women. Based on their results, it seems possible to perform backscatter difference measurements at the same location using transducers with center frequencies around 5 MHz.

Data presented in this study are highly spatially averaged. Spatial averaging was accomplished by performing measurements along six different directions (three perpendicular axes), and at multiple sites for each direction. The benefits of spatially averaging backscatter measurements of bone have been discussed previously (Hoffmeister, 2011). Clinical applications of backscatter difference techniques likely will benefit from spatial averaging as well. Spatial averaging along three perpendicular axes will be difficult in vivo. However, there are other ways to accomplish spatial averaging such as interrogating multiple sites and/or multiple bones (both hips, for example).

A source of error that should be considered in all in vivo ultrasonic measurements of bone is the effect of intervening tissues. Ultrasonic waves must propagate through intervening layers of soft tissue (skin, fat, muscle, etc.) and also the outer bone cortex to reach interior regions of cancellous bone. These intervening tissues can produce substantial signal loss and phase cancellation errors. A technique called dual frequency ultrasound has been proposed as a way to address some of these challenges for backscatter measurements of bone (Karjalainen et al., 2008). The backscatter difference technique described in the present study may offer another way to reduce errors caused by intervening tissues. In the backscatter difference approach, the two gated portions of the backscatter signal (see Fig. 1) are affected by intervening tissues in similar ways. Many of the effects should cancel when the power spectra are divided in Eq. 1 to obtain the difference spectrum. As a specific example, consider an intervening layer of soft tissue with thickness $x_S$ and frequency dependent attenuation coefficient ${\alpha }_S\left(f\right)$. Equation 3 can be modified to account for the attenuating effects of the soft tissue in the following way:

$$A\left(f\right)=e^{4{\alpha }_S\left(f\right)x_S}{e}^{4\alpha \left(f\right)x}\left[\frac{2\alpha \left(f\right)c{\tau }_w\cdot e^{\alpha \left(f\right)c{\tau }_w}}{e^{\alpha \left(f\right)c{\tau }_w}-e^{-\alpha \left(f\right)c{\tau }_w}}\right].$$ (12)

When the difference spectrum is computed in Eq. 5, the term $e^{4{\alpha }_S\left(f\right)x_S}$ that represents attenuation by the soft tissue will cancel because it is the same for gates 1 and 2.

SUMMARY AND CONCLUSIONS

This study investigates the utility of a backscatter difference technique for ultrasonic bone assessment. The backscatter difference spectrum $D\left(f\right)$ is determined by subtracting two power spectra (in dB) from two different gated portions of a backscatter signal. When averaged over multiple measurement sites on multiple specimens of human cancellous bone, the backscatter difference spectrum is found to be a monotonically increasing function of frequency. The difference spectrum varies approximately linearly with frequency over the bandwidth of each transducer used in the study. The difference spectrum can be normalized to reduce effects that different choices of gate separation and gate duration have on the difference spectrum. nSBD, which is a normalized parameter related to the frequency slope of the difference spectrum, demonstrates weak to moderate correlations with bone density. nMBD, which is a normalized parameter related to the frequency averaged difference spectrum, demonstrates stronger correlations with density. These results suggest that nMBD may be a useful parameter for ultrasonic bone assessment.