Improving image-guided radiation therapy of lung cancer by reconstructing 4D-CT from a single free-breathing 3D-CT on the treatment day

Abstract

Purpose: One of the major challenges of lung cancer radiation therapy is how to reduce the margin of treatment field but also manage geometric uncertainty from respiratory motion. To this end, 4D-CT imaging has been widely used for treatment planning by providing a full range of respiratory motion for both tumor and normal structures. However, due to the considerable radiation dose and the limit of resource and time, typically only a free-breathing 3D-CT image is acquired on the treatment day for image-guided patient setup, which is often determined by the image fusion of the free-breathing treatment and planning day 3D-CT images. Since individual slices of two free breathing 3D-CTs are possibly acquired at different phases, two 3D-CTs often look different, which makes the image registration very challenging. This uncertainty of pretreatment patient setup requires a generous margin of radiation field in order to cover the tumor sufficiently during the treatment. In order to solve this problem, our main idea is to reconstruct the 4D-CT (with full range of tumor motion) from a single free-breathing 3D-CT acquired on the treatment day.

Methods: We first build a super-resolution 4D-CT model from a low-resolution 4D-CT on the planning day, with the temporal correspondences also established across respiratory phases. Next, we propose a 4D-to-3D image registration method to warp the 4D-CT model to the treatment day 3D-CT while also accommodating the new motion detected on the treatment day 3D-CT. In this way, we can more precisely localize the moving tumor on the treatment day. Specifically, since the free-breathing 3D-CT is actually the mixed-phase image where different slices are often acquired at different respiratory phases, we first determine the optimal phase for each local image patch in the free-breathing 3D-CT to obtain a sequence of partial 3D-CT images (with incomplete image data at each phase) for the treatment day. Then we reconstruct a new 4D-CT for the treatment day by registering the 4D-CT of the planning day (with complete information) to the sequence of partial 3D-CT images of the treatment day, under the guidance of the 4D-CT model built on the planning day.

Results: We first evaluated the accuracy of our 4D-CT model on a set of lung 4D-CT images with manually labeled landmarks, where the maximum error in respiratory motion estimation can be reduced from 6.08 mm by diffeomorphic Demons to 3.67 mm by our method. Next, we evaluated our proposed 4D-CT reconstruction algorithm on both simulated and real free-breathing images. The reconstructed 4D-CT using our algorithm shows clinically acceptable accuracy and could be used to guide a more accurate patient setup than the conventional method.

Conclusions: We have proposed a novel two-step method to reconstruct a new 4D-CT from a single free-breathing 3D-CT on the treatment day. Promising reconstruction results imply the possible application of this new algorithm in the image guided radiation therapy of lung cancer.

INTRODUCTION

Lung cancer is the leading lethal cancer type worldwide. For people who are diagnosed with nonsmall cell lung cancer, more than half of them will receive radiation therapy on the treatment.^{1, 2} Image guided radiation therapy (IGRT) is the state of the art technology to help better deliver radiation therapy to cancerous tissue, while minimize the dose to the nearby normal structures. IGRT of lung tumor is a highly challenging problem since the lung tumors move with the respiratory cycle, and it may change size, location, and shape during the course of daily treatment.^{3, 4} Recently, 4D-CT imaging, with respiration phase as the fourth dimension, has been developed and becomes more and more popular since it is able to capture full range of respiration motion of lung.^{5, 6} It has been shown that 4D-CT imaging helps reduce artifacts from patient motion and provides more accurate delineation of tumor and other critical structures.^{6, 7, 8}

For treating lung cancer with radiation therapy, generally a 4D-CT and a free-breathing 3D-CT are acquired on the planning day.⁹ With these images, physician can manually delineate the outlines of tumor, lung, heart, and other critical structures from the free-breathing 3D-CT, 4D-CT or sometimes maximum intensity projection of 4D-CT.^{10, 11} Automatic methods to determine the lung motion envelope by using deformable registration methods have also been developed in Refs. ^{5, 12, 13}. With the estimated motion information, an appropriate margin of planning target volume (PTV) can be estimated to assure that the moving tumor is always covered by the radiation field. Then, the intensity of radiation field can be optimized to have PTV sufficiently treated and the dose of nearby normal structures minimized. On the treatment day, a free-breathing 3D-CT image will be acquired for image-guided patient setup. Due to CT dose and the limit of technology and time in treatment room, 4D-CT scanning normally is not performed daily before the treatment of patient. Instead, a free-breathing 3D-CT is acquired and registered with the free-breathing 3D-CT acquired on the planning day. The image registration is often rigid, mostly focusing on the alignment of bony landmarks around tumor or even tumor itself if it is visible. The result of image registration will be finally used to shift the treatment plan, so that the original treatment fields designed in the planning day can target at the right anatomy of patient, for accurate delivery of radiation therapy.

Accurate patient setup is crucial for the quality of radiation therapy. Unfortunately, the setup of lung patient has been one of the most challenging tasks in radiation therapy due to respiratory motion. The commonly used imaging technology is 2D radiograph based or 3D free-breathing based method. 3D CT has been more and more adopted because soft tissue like tumor can be imaged much clearly than 2D films. However, it is not straightforward to register two free-breathing 3D-CT images. The difficulty mainly comes from the inconsistent image information included in the two free-breathing 3D-CT images, since their corresponding slices could be acquired from the completely different respiratory phases on the planning and treatment days. Also, since the free-breathing 3D-CT is actually a mixed-phase image that never exists in the reality, it could provide misleading information to the observers. For example, as demonstrated in Refs. ¹⁴ and ¹⁵, a moving spherical object could be acquired with different shapes under the free-breathing condition, depending on which phase the scanner starts to acquire the images. 4D-CT, which can capture the motions of tumor and anatomic structures, can be a very useful tool to help the patient setup. However, in reality, 4D-CT is often not used on the treatment days due to various reasons: (1) The scheduled short treatment time for each patient does not allow the extended time for 4D-CT acquisition and reconstruction; (2) Daily 4D-CT yields significant dose on patient; (3) 4D-CT is not available in most treatment rooms. Therefore, 4D-CT is not used for the routine patient setup, for helping accurate delivery of radiation treatment.

In this paper, we propose a novel method to reconstruct a new 4D-CT from a single free-breathing 3D-CT on the treatment day, with the guidance from the super-resolution 4D-CT model initially built from the planning day 4D-CT and later adapted to estimate new motions on the treatment day. Thus, the planning day 4D-CT can be fully utilized to guide patient setup on treatment day, and finally the calculated treatment dose can be more accurately delivered to the patient. Specifically, our method consists of two steps as detailed below.

In the first step of our method (planning day), we apply a novel spatiotemporal registration algorithm¹⁶ to simultaneously register all phase images of the 4D-CT acquired on the planning day, for building a super-resolution 4D-CT model. Specifically, all phase images are simultaneously deformed from their own domains toward the group-mean image sitting in a common space,³² with the temporal correspondences across phases being consistent with the respiration. Here, the group mean acts as the unbiased representative image and also a common space, to which all phase images in 4D-CT will be aligned. To enhance the poor superior-inferior resolution in 4D-CT, super-resolution technique is then utilized to integrate anatomical information from different phase images for building a super-resolution group-mean image, which encompasses more anatomical details than any individual phase image. Finally, the super-resolution 4D-CT model, which consists of (1) the temporal correspondences across respiratory phases and (2) the spatiotemporal-resolution-enhanced planning day 4D-CT, is built to guide the reconstruction of a new 4D-CT on the treatment day.

In the second step of our method (treatment day), a new 4D-CT on the treatment day will be reconstructed from a free-breathing 3D-CT image by a novel 4D-to-3D image registration method. The main challenge comes from the mixed-phase image information in the free-breathing 3D-CT image which might mislead the image registration with the planning day 4D-CT. To solve this problem, we present an iterative method which consists of two steps: (1) we determine an optimal phase for each image patch in the free-breathing (mixed-phase) 3D-CT of the treatment day and thus obtain a sequence of partial 3D-CT images on the treatment day, where each new 3D-CT image has only partial image information in certain slices; and (2) we reconstruct a new 4D-CT for the treatment day by warping the 4D-CT of the planning day to the sequence of partial 3D-CT images on the treatment day, with the guidance from the 4D-CT model built on the planning day.

Each of the two above-described steps has been evaluated in our experiments. Specifically, the super-resolution 4D-CT model built in the first step has been tested on a dataset with ten lung 4D-CT images,¹⁷ each having a set of manually identified landmarks in both selected phase images and across all phase images. The respiratory motion estimated by our algorithm achieves the best accuracy, compared to diffeomorphic Demons (Ref. ¹⁸) and SyN,¹⁹ which are the state-of-the-art deformable registration algorithms among 14 registration algorithms evaluated in Ref. 20. Our 4D-CT reconstruction algorithm for the treatment day has been evaluated on both simulated data and the real patient data. The result indicates its excellent performance in reconstructing 4D-CT from a single free-breathing 3D-CT.

METHODS

The goal of our method is to reconstruct a 4D-CT T = {T_s|s = 1, …, N} with N phases for the treatment day, based on a single free-breathing 3D-CT image I taken on the treatment day, and also to build a super-resolution 4D-CT model M from the planning day 4D-CT P = {P_s|s = 1, …, N} to guide the described 4D-CT reconstruction. Therefore, our whole method consists of two steps: (1) build a 4D-CT model M by registering all phase images of the planning day 4D-CT to the common space C; and (2) reconstruct the 4D-CT T for the treatment day by utilizing the 4D-CT model M built on the planning day.

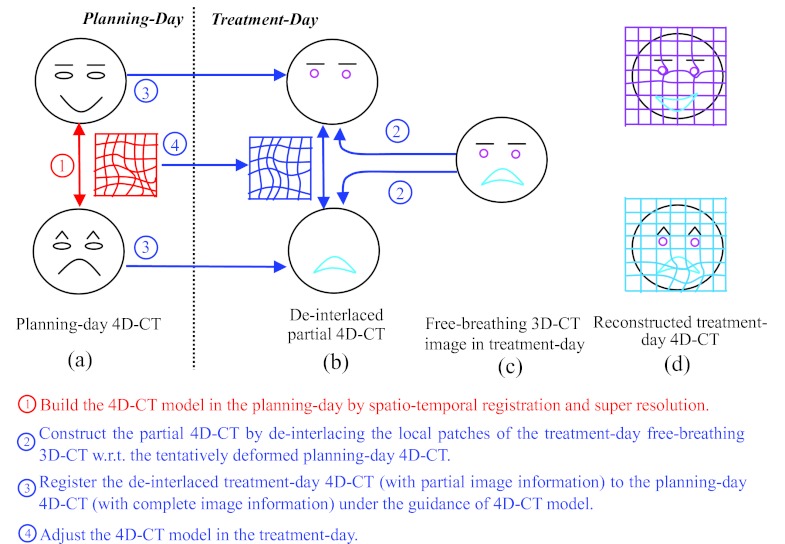
Figure 1 gives an overview of our method, and also explains the difficulty in registration of the free-breathing 3D-CT images. For simplicity and easy demonstration, we use face expression, instead of lung motion, as an example, as shown in Fig. 1a. Here, we assume only two phases, i.e., smiling and angry phases, in the whole cycle of face expression change. It can be observed that the shapes of mouth and eyebrows are the keys to distinguish the smiling and angry phases. Assume that a subject's face turns from smile to anger during the image acquisition, which can be used to simulate the effect of respiration in the lung imaging when patient breathes freely. Thus, the top half face (i.e., eyes and eyebrows) can be scanned with smiling expression, while the bottom half face (i.e., mouth) can be scanned with angry expression. As the result, a mixed-expression face is obtained in Fig. 1c. To simulate the possible shape changes during free-breathing acquisition (e.g., tumor shrinkage after treatment), we also simulate some local distortions around eyes (i.e., deformed from ellipse to circle) and mouth (i.e., deformed from close to open), as shown in pink and cyan in Fig. 1c, respectively.

Figure 1.

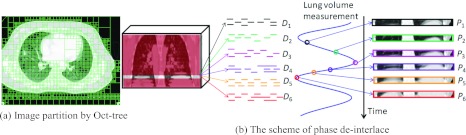
The overview of our proposed method for estimating the 4D-CT images in the treatment day (d) from a free-breathing image in the treatment day (c), by using the 4D-CT model built in the planning day (a). Our method first deinterlaces the free-breathing image into the respective phase images (b), and then reconstructs a new 4D-CT in the treatment day (d) by warping the planning day 4D-CT onto the deinterlaced images, with the guidance of the 4D-CT model built in the planning day.

Assume we can align either smiling or angry face to the mixed-expression face [half smiling and half angry face shown in Fig. 1c] with perfect registration algorithm, the registered phase images will be all half smiling and half angry expression faces which may never happen in the reality. The reason of this unreasonable 4D-CT reconstruction is that the reference image is already biased by the mixed-phase information.

To address this difficulty, we first build a 4D-CT model on the planning day by a robust spatiotemporal registration algorithm, which we will explain later in Sec. 2A. After that, the temporal transformations along all phases can be obtained, as displayed by the deformation grid in Fig. 1a. On the treatment day, we first determine the appropriate phase for each image patch of the free-breathing image by looking for the best matched patch in the corresponding phase image of the 4D-CT, as shown in Fig. 1b. Thus, the whole free-breathing image can be deinterlaced into several 3D-CT images, denoted as D = {D_s|s = 1, …, N}, where the image information in each D_s is not complete, i.e., mouth and eyes are missing in the smile and angry phases, respectively. Then, the spatial deformation fields $\mathit{H}=\left\{h_s\left(x\right)|x\in {\Omega }_{P_s\to D_s},s=1,...,N\right\}$ between the 4D-CT on the planning day and the image sequence {D_s} can be estimated in two ways: (1) For the existing image patches in D_s, their correspondences can be determined with P_s directly. (2) For other missing image patches in D_s, their correspondences can be compensated from other phase images according to the 4D-CT model built on the planning day. In the face example, the deinterlaced results and the final reconstructed results are shown in Figs. 1b, 1d, respectively. It can be seen that the final reconstruction results are reasonable (i.e., the smiling face is still the smiling face, and the angry face is still the angry face), and also the local distortions around the mouth and eyebrows are well preserved in each phase image.

In the following, we first present the construction of super-resolution 4D-CT model M on the planning day. Then, we detail an algorithm for reconstruction of a new 4D-CT T from a free-breathing image I on the treatment day. Before we introduce the whole method in Sec. 2A, important notations used in this paper are summarized in Table 1.

Table 1.

Summary of important notations.

Symbol	Description
I	Free-breathing 3D-CT image.
P	4D-CT on the planning day, P = {Ps|s = 1, …, N}.1
T	The reconstructed 4D-CT on the treatment day, T = {Ts|s = 1, …, N}.
F	The deformation field from group-mean image to each phase image Ps in constructing the 4D-CT model on the planning day.
D	The partial 4D-CT after phase deinterlace, D = {Ds|s = 1, …, N}.
H	The collection of deformation fields from each Ds to Ps, H = {hs|s = 1, …, N}.
Φ	The collection of temporal deformation fields between any planning day phase images.1
Ψ	The collection of temporal deformation fields between any treatment day phase images.
Xs	The set of Qs key points in particular partial phase image Ds, i.e., ${\mathit{X}}^s=\left\{x_i^s|i=1,...,Q_s\right\}$.

¹P and Φ represent the roughly aligned planning day 4D-CT and the planning day temporal deformation pathway by bone alignment in Sec. 2B.

Construction of super-resolution 4D-CT model on the planning day

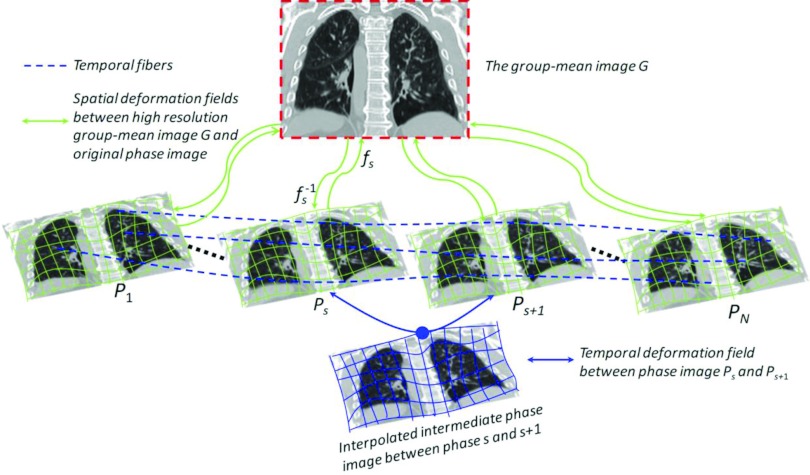
Given the 4D-CT image P on the planning day, we apply our developed spatiotemporal registration method¹⁶ to simultaneously register all phase images P_s to the group-mean image G in the common space by estimating the deformation fields $\mathit{F}=\left\{f_s\left(x\right)|x\in {\Omega }_{\mathcal{C}}\right\}$, where each f_s denotes the deformation field from group-mean image G to P_s. Specifically, key points with distinctive image features are hierarchically selected to represent the shape of group-mean image, which are used to guide the registration with respect to each phase image by robust feature matching. Since the inferior-superior resolution (usually at 2–3 mm) in 4D-CT is much lower than intraslice resolution (usually at 1 × 1 mm²), motion artifacts, such as blur, overlap, and gapping,^{8, 21} are obvious in 4D-CT, which challenges the image registration in establishing accurate correspondences. To alleviate this issue, super-resolution technique is utilized here to construct the super-resolution group-mean image (shown in the top of Fig. 2) by integrating the complementary information of all tentatively aligned phase images. Thus, the registration between the group-mean image and each phase image become relatively easy by taking advantage of the clear anatomy in the super-resolution group-mean image. Meanwhile, by mapping the group-mean image onto the domain of each phase image, every key point in the group-mean shape has several warped landmarks in different phase images, which can be assembled into a time sequence (with respect to respiratory phase) to form a virtual temporal fiber (displayed by dashed curves in Fig. 2). Therefore, the temporal coherence of 4D-CT registration can be maintained by applying kernel smoothing along all these temporal fibers. For more information, please refer to our previous paper.¹⁶

Figure 2.

The schematic illustration of our spatiotemporal registration on 4D-CT. The deformation fields {f_s} are estimated based on the correspondences between key points by robust feature matching with respect to their shape and appearance. Meanwhile, the temporal continuity is preserved by performing kernel regression along the temporal fiber bundles Φ (see the blue dashed curves).

To make each deformation field f_s smooth and invertible, we further model f_s by an exponential model with constant velocity field to bring forth the diffeomorphism^{18, 22, 23} which we will explain at Step 5 in Sec. 2B. Hereafter, we use $f_s^{-1}$ to denote the inverse of deformation field f_s. Thus, the temporal correspondence between any two phases can be obtained through the domain of group-mean image. For example, the deformation pathway φ_{s, s+1} (curve in Fig. 2) from phase s to the next phase s + 1 can be calculated as ${\phi }_{s,s+1}=f_s\circ f_{s+1}^{-1}$, where “○” denotes the operation of deformation composition (in this paper, we follow the definition of deformation composition in Ref. 23). In the following, we use Φ = {φ_{s, t}|s = 1, …, N, t = 1, …, N, s ≠ t} to denote all possible temporal deformation field between two phases s and t.

Generally, only a limited number of phase images are collected in the 4D-CT scan. For example, 4D-CT usually consists of ten phases for the complete respiration cycle or six phases from maximum inhale to maximum exhale stages. However, the temporal phase-to-phase transition might not be continuous in the original 4D-CT, especially for the fast-motion area, e.g., diaphragm. In order to remedy this motion judder, we propose to interpolate intermediate phase images between phase s and next phase s + 1 by following the temporal deformation pathway φ_{s, s+1} and deform the phase image P_s to the middle point of φ_{s, s+1}, as shown in the bottom of Fig. 2. After we perform the intermediate phase image interpolation within any possible neighboring phases, we can construct a temporal-resolution-enhanced 4D-CT on the planning day. To be simple, we still use P to denote the 4D-CT image sequence with N phases; however, the set of phase images has been augmented by including intermediate phase images. The advantage of phase interpolation not only lies in making the lung motion visually fluid but also brings forth more complete anatomical information of lung with respect to respiration, which is very important to clean up the mixed phases in the free-breathing 3D-CT during the reconstruction of treatment day 4D-CT. We will show this point in Sec. 2B.

Therefore, a super-resolution 4D-CT model M = {P, Φ} can be built on the planning day, which consists of temporal resolution enhanced planning day 4D-CT P and the set of temporal deformation pathways between any two phases Φ.

Reconstruction of 4D-CT on the treatment day

The goal here is to reconstruct the 4D-CT T from a single free-breathing image I acquired on the treatment day, based on the 4D-CT model M built on the planning day. The principle behind our 4D-CT reconstruction method is that the free-breathing 3D-CT does convey the information of respiratory motion, although it is mixed and incomplete. Thus, the key point here is how to utilize the limited motion information hidden in the free-breathing 3D-CT to reconstruct the 4D-CT on the treatment day. Although it is straightforward to obtain the treatment day 4D-CT by registering each phase image P_s to the free-breathing 3D-CT I, the registration is difficult due to the mixed phase information in the free-breathing 3D-CT.

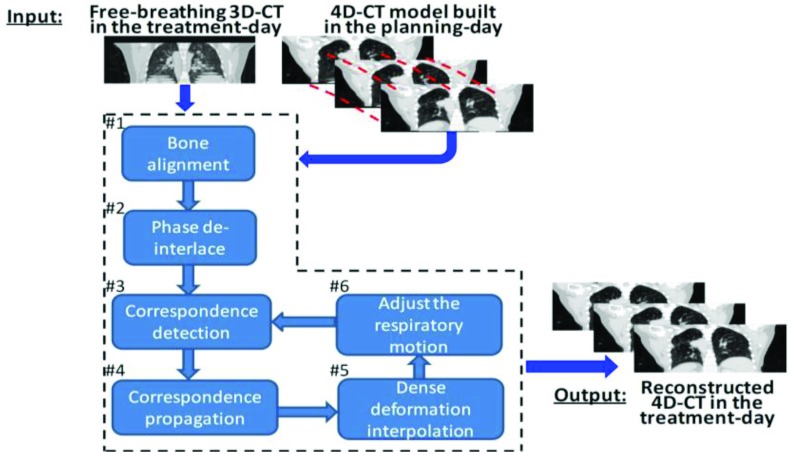
The overview of our 4D-CT reconstruction method is shown in Fig. 3, which consists of six steps. First, each planning day phase image P_s is roughly registered with free-breathing 3D-CT I by the alignment of bones since the bone will almost not move with lung. Following the estimated transformations of bones, the temporal deformation pathway Φ can be approximately transformed to the domain of free-breathing image I. To be simple, we still use P and Φ to denote the roughly aligned planning day 4D-CT and the temporal deformation pathway, respectively. After that, we partition the free-breathing 3D-CT I into image patches by Oct-tree technique²⁴ and then determine the appropriate phase for each image patch by measuring the patch similarity across respiratory phases. By assigning each image patch into the corresponding phase images, we can obtain a partial 4D-CT D with limited image content in each phase image. This procedure is called as “phase deinterlace” in this paper. Next, the problem of 4D-CT reconstruction turns to the deformable registration between the partial 4D-CT D and the complete 4D-CT P. Specifically, for each phase image D_s, a small number of key points will be detected to drive the estimation of entire deformation field h_s. For each key point $x_i^s$ in D_s, robust correspondence detection will be performed with respect to P_s. Note that the temporal corresponding locations of $x_i^s$ in all other phase images D_t (t ≠ s) can be designated by following the respiratory motion Ψ = {ψ_s,t|s = 1, …, N, t = 1, …, N, s ≠ t} on the treatment day, where each ψ_s,t expresses the temporal correspondence between any two phase images. Thus, the established spatial correspondence on $x_i^s$ can be propagated to other phases by requiring each corresponding location in other phase image D_t have the same spatial correspondence as $x_i^s$ but toward P_t. In this way, the image-content-missing area in D_t will have the correspondence toward P_t consequently. Thin-plate splines (TPS) will be then used to interpolate the dense deformation h_s from the sparsely established correspondences in each phase image domain, where we further model the deformation field in the space of diffeomorphism.¹⁸ Finally, the respiratory motion Ψ on the treatment day is adjusted according to the temporal deformation pathway Φ on the planning day and also the tentatively estimated deformation field H to guide the next correspondence propagation step. In the end of reconstruction, each treatment day phase image T_s can be obtained by deforming the roughly aligned planning day phase image P_s according to the deformation field h_s, i.e., T_s = h_s(P_s). In the following, we will explain these six steps one by one.

Figure 3.

The pipeline of reconstructing 4D-CT in the treatment day. First, the free-breathing 3D-CT is roughly aligned with planning day 4D-CT by bone alignment. Then, the mixed phase information in I will be deinterlaced into partial 4D-CT D according to the respiratory motion. Next, 4D-to-4D image registration is performed between the partial 4D-CT D and the complete 4D-CT P to reconstruct the treatment day 4D-CT T by iteratively establishing spatial correspondences on key points, propagating correspondences along the respiratory motion, interpolating the dense deformation field, and adjusting the treatment day respiratory motion.

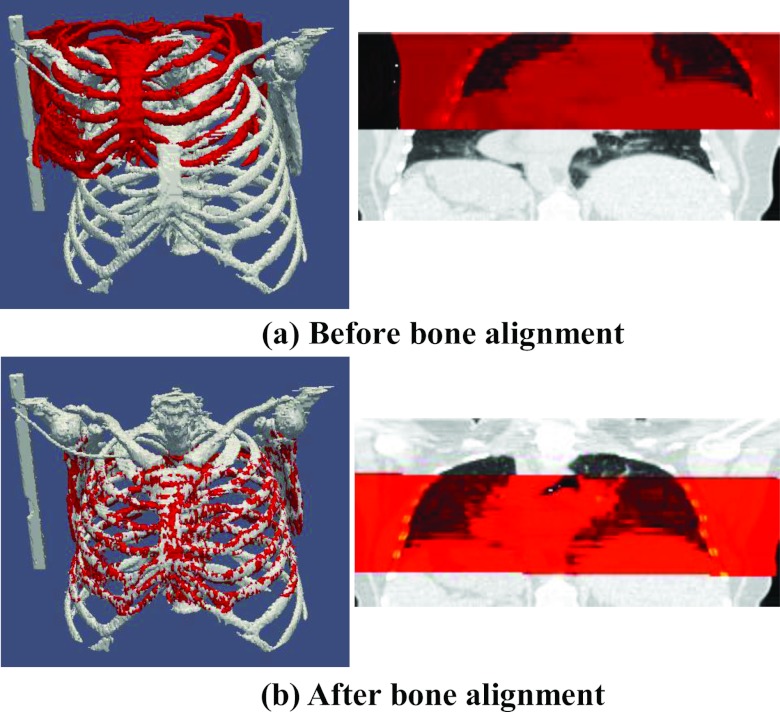
Step 1: Bone alignment

Bone is easy to extract in CT images by just keeping the image points with large intensity value. Then, we use FLIRT (the affine registration program in FSL software package developed by the Analysis Group, FMRIB, Oxford, UK) to estimate the 4 × 4 affine transformation matrix between free-breathing 3D-CT I and each phase image P_s of 4D-CT on the planning day. The results before and after bone alignment are shown in Figs. 4a, 4b, respectively, where the bone in I and particular P_s are displayed in red and gray, respectively. Since bone will not move a lot with lung during respiration, we can roughly transform each phase image P_s of the planning day 4D-CT to the domain of the free-breathing 3D-CT I by the bone alignment. Also, we apply the affine transformation matrix to each temporal deformation field in Φ to roughly transfer the planning day respiratory motion into the domain of the free-breathing 3D-CT.

Figure 4.

The result of bone alignment. (a) shows the fusion of bone in treatment-day free-breathing 3D-CT (with smaller rib cage) over the particular phase image (with longer rib cage) before bone alignment. (b) shows the same fusion result after bone alignment. It is clear that the bones in and are approximately registered.

Step 2: Phase deinterlace

Phase deinterlace is a very important step before image sequence registration since it cleans up the mixed phase information in the free-breathing 3D-CT I. The assumption here is that we regard lung as a moving 3D object when taking CT scans from patients. Therefore, each slice in I may contain image information from different respiratory phases. Moreover, the mixture image content could also be observed within the single slice. Fortunately, we can determine the appropriate phase for each image patch in I by looking for the similar patch across the roughly registered phase images P. Since only very few phases are sampled in the original 4D-CT during entire respiration cycle (∼5 s), it may be difficult for particular image patch in the free-breathing 3D-CT to find its matched patch in the existing phase images of the original 4D-CT. To alleviate this issue, as mentioned, we interpolated intermediate phase images when building the planning day 4D-CT model, in order to improve the temporal resolution and facilitate the deinterlace procedure. It is worth noting that only 2D patch is used here since the interslice thickness (>2 mm) is often larger than the intraslice resolution (<1 mm).

To clean up the misleading phase information in I, we first adaptively partition the entire image I into a number of 2D nonoverlapped image patches by Oct-tree technique.²⁴ Here, for each image patch, we use its intensity entropy as the complexity measurement to decide whether necessary to further divide it into smaller patches. The partition result on a free-breathing 3D-CT is shown in Fig. 5a. Next step is to construct the partial 4D-CT D by assigning each patch into the appropriate phase image D_s, as demonstrated in Fig. 5b. Specifically, we use θ_I(x, l) to denote the image patch in 3D-CT I with top-left position x and patch size l × l, which is determined by Oct-tree partition. Then, the appropriate phase s* for each image patch θ_I(x, l) is determined by

$$\begin{array}{c}\hfill s^{*}=arg\underset{s}{min}\delta \left(s\right),\delta \left(s\right)=\underset{y\in n_1\left(x\right)}{min}{\Vert {\theta }_I\left(x,l\right)-{\theta }_{P_s}\left(y,l\right)\Vert }^2,\end{array}$$ (1)

where ${\theta }_{P_s}\left(y,l\right)$ is the image patch in P_s with top-left position y. n₁(x) denotes a small search neighborhood (with radium 1 mm in this paper) for finding the best match with minimal intensity difference. Finally, we move image patch θ_I(x, l) to the phase image $D_{s^{*}}$ by letting ${\theta }_{D_{s^{*}}}\left(x,l\right)={\theta }_I\left(x,l\right)$. Thus, each image patch will be assigned to only one particular phase image D_s. Since there is no overlap between any two image patches, the combination of existing image information in all D_ss turns to be the free-breathing 3D-CT image I, i.e., ${\cup }_{s=1}^N{D}_s=I$. As shown in Fig. 5b, each D_s only contains limited image content after we disseminate each image patch θ_I(x, l) to the particular $D_{s^{*}}$. After obtaining D, we will repeat the following four steps to reconstruct the treatment day 4D-CT T by gradually estimating the dense transformation field h_s between each pair of roughly aligned P_s and D_s. Since the transformation field H is iteratively estimated during 4D-CT reconstruction, we use k to denote the kth iteration in the following text.

Figure 5.

The scheme of constructing partial 4D-CT D from a free-breathing 3D-CT I by phase deinterlace. First, the entire image I is portioned into a number of local 2D patches by Oct-tree technique. Then we disseminate each local patch θ_I(x, l) to the particular phase image $D_{s^{*}}$, which hold the best matched local patch with respect to θ_I(x, l).

Step 3: Correspondence detection by robust feature matching

The goal of this step is to establish the correspondence for any existing image patch ${\theta }_{D_s}(x,l)$ in the partial phase image D_s with respect to the roughly registered phase image P_s. Here, we follow the hierarchical registration framework in Ref. 16 to detect correspondence by robust feature matching.

For each image point in the partial phase image D_s and in the complete phase image P_s, we incorporate both local image appearance (i.e., image intensity) and edge information (i.e., gradients) in a 2D circular neighbor (with radius r, i.e., r = 3 in our experiments), into the attribute vector $\stackrel{\rightharpoonup }{a}$. Then, the normalized cross correlation is used to evaluate the similarity between point x in D_s and point y in P_s, which is denoted as $NCC\left({\stackrel{\rightharpoonup }{a}}_D^s\left(x\right),{\stackrel{\rightharpoonup }{a}}_P^s\left(y\right)\right)$. (Note that, in ${\stackrel{\rightharpoonup }{a}}_D^s$, we use D instead of D_s since s is already included as superscript.) In order to measure the difference between two points, we further define the feature discrepancy as $\eta \left({\stackrel{\rightharpoonup }{a}}_D^s\left(x\right),{\stackrel{\rightharpoonup }{a}}_P^s\left(y\right)\right)=\frac{1-NCC\left({\stackrel{\rightharpoonup }{a}}_D^s\left(x\right),{\stackrel{\rightharpoonup }{a}}_P^s\left(y\right)\right)}{2}$, which ranges from 0 to 1.

We use the importance sampling strategy²⁵ to hierarchically select key points in each D_s. Specifically, we smooth and normalize the gradient magnitude values over the whole image domain and use the obtained values as the importance (or probability) to select key points. For example, a set of key points ${\mathit{X}}^s=\left\{x_i^s|i=1,...,Q_s\right\}$ can be sampled via Monte Carlo simulation, with higher importance value indicating the higher likelihood of the underlying location being selected in the nonuniform sampling. Note that Q_s is the total number of key points in D_s, which is small in the beginning of reconstruction and then increases gradually until all image points are considered as key points in the end of reconstruction.

In (k + 1)th iteration, we will estimate the incremental deformation ${\varphi }_s^{k+1}$ for each partial phase image D_s. As we will explain in Step 5, the refined deformation field $h_s^{k+1}$ in the end of (k + 1)th iteration can be obtained by integrating the incremental deformation field ${\varphi }_s^{k+1}$ and the latest estimated transformation field $h_s^k$. Exhaustive search is performed to refine the correspondence of each $x_i^s$ with respect to the candidate point u in a search neighborhood $n_2\left(h_s^k\left(x_i^s\right)\right)$, according to two criteria: (1) the feature discrepancy should be as small as possible between ${\stackrel{\rightharpoonup }{a}}_D^s\left(x\right)(x\in {\Omega }_{D_s})$ and ${\stackrel{\rightharpoonup }{a}}_P^s\left(u\right)(u\in {\Omega }_{P_s})$; (2) the spatial distance between candidate point u and the tentatively estimated correspondence location ${\varphi }_s^{k+1}\left(x_i^s\right)$, i.e., $\Vert {\varphi }_s^{k+1}\left(x_i^s\right)-u{\Vert }^2$, should be as close as possible.

Since there are a lot of uncertainties in correspondence matching, encouraging multiple correspondences is proven effective to alleviate the ambiguity issue.^{26, 27, 28} Thus, for a particular key point $x_i^s$, a probability ${\pi }_{i,u}^s$ (called as spatial assignment) is assigned to each candidate point $u\in n_2\left(h_s^k\left(x_i^s\right)\right)$ during the correspondence matching. For the sake of robustness, the candidate points even with large matching discrepancy still might have the chance to contribute to the correspondence matching in the beginning of registration, in order to encourage multiple correspondences. As the registration progresses, only the candidates with the most similar attribute vectors will be considered until the exact one-to-one correspondence is considered in the end of registration for achieving the registration specificity. This dynamic procedure can be encoded with the entropy term on the probability, i.e., ${\pi }_{i,u}^s·\log {\pi }_{i,u}^s$. Here, high degree of entropy implies the fuzzy assignment while low degree means almost binary matching. We use a scalar value σ^k+1 to act as the temperature to enforce the dynamic change on correspondence assignment. Thus, the total energy function in estimating the incremental deformation field ${\varphi }_s^{k+1}$ is given as

$$\begin{array}{ccc}\hfill E\left({\varphi }_s^{k+1}\right)& =& \sum _{i=1}^{Q_s}\sum _{u\in n_2\left(h_s^k\left(x_i^s\right)\right)}\hfill \\ & & \times \{{\pi }_{i,u}^s·\left[\eta \left({\stackrel{\rightharpoonup }{a}}_D^s\left(x_i^s\right),{\stackrel{\rightharpoonup }{a}}_P^s\left(u\right)\right)+\Vert {\varphi }_s^{k+1}\left(x_i^s\right)-u{\Vert }^2\right]\hfill \\ & & +{\sigma }^{k+1}·\left[{\pi }_{i,u}^s·\log \left({\pi }_{i,u}^s\right)\right]\}+\beta ·B\left({\varphi }_s^{k+1}\right),\hfill \end{array}$$ (2)

where B(.) measures the bending energy²⁹ of incremental deformation field ${\varphi }_s^{k+1}$.

The spatial assignment ${\pi }_{i,u}^s$ can be calculated by letting $\partial E/\partial {\pi }_{i,u}^s=0$

$$\begin{array}{c}\hfill {\pi }_{i,u}^s=\exp \left\{-\frac{\eta \left({\stackrel{\rightharpoonup }{a}}_D^s\left(x_i^s\right),{\stackrel{\rightharpoonup }{a}}_P^s\left(u\right)\right)+{‖{\varphi }_s^{k+1}\left(x_i^s\right)-u‖}^2}{{\sigma }^{k+1}}\right\}.\end{array}$$ (3)

It is clear that the spatial assignment ${\pi }_{i,u}^s$ is penalized in the exponential way. Notice that the temperature σ^k+1 is the denominator of the exponential function in Eq. 3. Therefore, when σ^k+1 is very high in the beginning of registration, even though the discrepancy η might be large or the candidate location is far away, the candidate point still might have the contribution to the correspondence detection procedure. As registration progresses, the specificity of correspondence will be encouraged by gradually decreasing the temperature σ^k+1 to a small degree, until only the candidate point with the smallest discrepancy being selected as the correspondence in the end of registration.

After obtaining ${\pi }_{i,u}^s$ for each candidate u, the estimated incremental deformation on key point $x_i^s$ can be computed by optimizing energy function E in Eq. 2 with respect to ${\varphi }_s^{k+1}\left(x_i^s\right)$

$${\widehat{\varphi }}_s^{k+1}\left(x_i^s\right)=\sum _{u\in n_2\left(h_s^k\left(x_i^s\right)\right)}{\pi }_{i,u}^s·u/\sum _{u\in n_2\left(h_s^k\left(x_i^s\right)\right)}{\pi }_{i,u}^s.$$ (4)

The estimated incremental deformation field ${\widehat{\varphi }}_s^{k+1}$ is too sparse to derive the accurate deformation between D_s and P_s since there are no key points located at the image-content-missing areas after phase deinterlace. In order to compensate the deformations at the image-content-missing areas in D_s, we propose to propagate the spatial correspondence on $x_i^s$ to all other phases by following the tentatively estimated treatment day respiratory motion.

Step 4: Correspondence propagation along respiratory motion

Given the previous estimated treatment day respiratory motion Ψ^k, we are able to find the corresponding locations of each $x_i^s$ in all other phases. For example, the corresponding location of $x_i^s$ in phase t is ${\psi }_{s,t}^k\left(x_i^s\right)$, where ${\psi }_{s,t}^k$ is the temporal deformation field from phase s to phase t. Since these temporal corresponding locations have the same anatomical structure, it is reasonable to require they hold the same local deformations by

$${\widehat{\varphi }}_t^{k+1}\left({\psi }_{s,t}^k\left(x_i^s\right)\right)={\widehat{\varphi }}_s^{k+1}\left(x_i^s\right).$$ (5)

The advantage of correspondence propagation is obvious in registering the partial 4D-CT with the complete 4D-CT, so that the image-content-missing area can also have the motion immediately. Taking the angry and smiling phases in Fig. 1 as an example, there is no mouth in the smiling face and no eyes in the angry face. If we only register the deinterlaced smiling face and angry face to the smiling and angry faces on the planning day, the local distortions at mouth (from close to open) and eye (from ellipse to circle) are unable to capture. However, if we know the temporal correspondence between the angry and smiling faces on the treatment day, the local deformation estimated from the existing anatomical structures in a particular phase can be propagated to other phases to compensate the motion for the same anatomical structure in other phases. As a result, the mouth in the reconstructed smiling face is open although it is impossible to detect this local change between the planning day smiling face and the deinterlaced treatment day smiling face. Similar results can also be observed at the eyes and eyebrows of the reconstructed angry face in Fig. 1.

Step 5: Interpolate the dense deformation field

For each D_s, it not only has the spatial correspondences on key points by robust feature matching in Step 3, but also receives the compensated displacements at the image-content-missing areas from the key points in other phase images in Step 4. Then TPS (Ref. ²⁹) can be used to interpolate dense incremental deformation field ${\widehat{\varphi }}_s^{k+1}$ for the partial phase image D_s by considering the key points X^s and the points receiving displacements in Step 4 as control points.

In order to ensure the invertability of deformation field $h_s^{k+1}$ between each pair of D_s and P_s, we follow an efficient nonparametric diffeomorphic approach¹⁸ to adapt the optimization of $h_s^{k+1}$ to the space of diffeomorphic transformation. The basic idea here is to consider the incremental deformation fields ${\widehat{\varphi }}_s^{k+1}$ in the vector space of velocity fields and then map them to the space of diffeomorphism through the exponentials, i.e., $\exp \left({\widehat{\varphi }}_s^{k+1}\right)$. Specifically, the following steps will be applied to calculate the deformation field ${\widehat{h}}_s^{k+1}$ under the framework of diffeomorphism: (1) compute the exponential of incremental deformation field $\exp \left({\widehat{\varphi }}_s^{k+1}\right)$ by the scaling and squaring method;¹⁸ (2) compose the exponential with the previously estimated deformation field by ${\widehat{h}}_s^{k+1}=h_s^k\circ \exp \left({\widehat{\varphi }}_s^{k+1}\right)$; (3) the inverse deformation field can be computed by ${\left({\widehat{h}}_s^{k+1}\right)}^{-1}=\exp \left(-{\widehat{\varphi }}_s^{k+1}\right)\circ {\left(h_s^k\right)}^{-1}$.

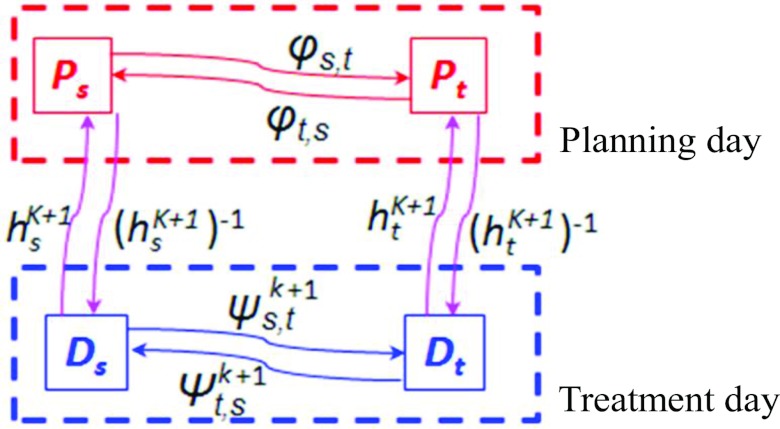
Step 6: Adjust the respiratory motion on the treatment day

Recall that we have built the 4D-CT model M on the planning day which includes the respiratory motion Φ (temporal correspondences between any two phases) on the planning day estimated from the planning day 4D-CT P by spatiotemporal registration. Obviously, the respiratory motion Φ on the planning day cannot be directly used on the treatment day, since the patient may breathe differently between planning and treatment days. Our solution to find the treatment day respiratory motion Ψ^k+1 in the (k + 1)th iteration is summarized in Fig. 6. It is apparent that the deformation fields between the roughly registered planning day phase images, the respiratory motion on the planning day, and the respiratory motion on the treatment day form a closed loop. Then, given the tentatively estimated deformation fields H^k+1 in the (k + 1)th iteration, the temporal correspondence from the arbitrary phase s to another phase t can be computed as

$${\psi }_{s,t}^{k+1}={\left(h_t^{k+1}\right)}^{-1}\circ {\phi }_{s,t}\circ h_s^{k+1}.$$ (6)

On the other hand, the temporal correspondence from phase t to s can be calculated by

$${\psi }_{t,s}^{k+1}={\left(h_s^{k+1}\right)}^{-1}\circ {\phi }_{t,s}\circ h_t^{k+1}.$$ (7)

After we have obtained Ψ^k+1, we will use it in Step 4 again to propagate the spatial correspondence established in one phase to the image-content-missing areas of all other phases.

Figure 6.

The scheme of adjusting the treatment day respiratory motion between any phases s and t.

Summary of our 4D-CT reconstruction algorithm

Our 4D-CT reconstruction method can be summarized as below:

Input: Planning day 4D-CT P and the treatment day free-breathing 3D-CT I.

• 0.  Set k = 1 and all deformation fields $h_s^k$ (from deinterlace phase image D_s to phase image P_s) to identity.

• 1.  Build the super-resolution 4D-CT model M = {P, Φ} by spatiotemporal registration method in Ref. 16.

• 2.  Extract the bone in I and each phase image P_s of the planning day 4D-CT.

• 3.  Register the bone in P_s with the bone in I by FLIRT (Ref. ³⁰) and obtain the roughly aligned planning day phase image.

• 4.  Integrate the affine transformation matrix to each temporal deformation field φ_{s, t} and obtain the roughly aligned planning day respiratory motion Φ which sits in the free-breathing 3D-CT image space.

• 5.  Use the mixed phase information in the free-breathing 3D-CT I to construct the deinterlaced 4D-CT D, with each phase image only having limited image content.

• 6.  Calculate the image attribute for each point of D_s and the roughly aligned P_s, and then select the key point X^s in each D_s.

• 7.  Establish the correspondence for each key point $x_i^s$ with respect to the roughly aligned phase image P_s.

  • 7.1.  Compute the spatial assignment for each candidate point in a search neighborhood of key point $x_i^s$ by Eq. 3;
  • 7.2.  Compute incremental correspondence of $x_i^s$ by Eq. 4.

• 8.  Propagate the correspondence on each $x_i^s$ from phase s to all other phases [Eq. 5] by following the respiratory motion Ψ^k on the treatment day.

• 9.  Compute the dense deformation field H^k.

  • 9.1.  Interpolate each dense incremental deformation field ${\varphi }_s^k$ by TPS by considering both the key points and the points receiving the displacements from other phases in Step 8 as control points;
  • 9.2.  Compute the exponential of ${\varphi }_s^k$ and update the deformation field $h_s^k$ by $h_s^k=h_s^k\circ \exp \left({\varphi }_s^k\right)$;
  • 9.3.  Compute the inverse deformation field by ${\left(h_s^k\right)}^{-1}=\exp (-{\varphi }_s^k)\circ {\left(h_s^k\right)}^{-1}$.

• 10.  Adjust the respiratory motion Ψ^k on the treatment day by Eqs. 6, 7.

• 11.  k ← k + 1.

• 12.  If not converged (e.g., k is less than the total number of iteration K), increase the number of key points Q_s and go to Step 6.

• 13.  Obtain the phase image on the treatment day by deforming each roughly aligned planning day phase image P_s according to the estimated deformation field $h_s^K$, i.e., $T_s=h_s^K\left(P_s\right)$. Then, T = {T_s|s = 1, …, N} is the finally reconstructed 4D-CT on the treatment day.

RESULTS AND DISCUSSION

To demonstrate the performance of our proposed method, we first evaluate the accuracy of respiratory motion in building 4D-CT model on DIR-lab data,¹⁷ with comparison to the state-of-the-art diffeomorphic Demons algorithm¹⁸ and SyN (Ref. ¹⁹) registration method. Then, we validate our algorithm in the reconstruction of 4D-CT for the treatment day from both the simulated and real free-breathing 3D-CT data.

Evaluation of 4D-CT model on the planning day

The respiratory motion Φ estimated on the planning day is very important to guide the reconstruction of 4D-CT on the treatment day. In this experiment, we demonstrate the accuracy of estimated respiratory motion in 4D-CT on DIR-lab dataset¹⁷ (the abbreviation of DIR stands for deformable image registration), which has ten cases with each having a 4D-CT of six phases. The intraslice resolution is around 1 × 1 mm², and the slice thickness is 2.5 mm. For each case, 300 corresponding landmarks in the maximum inhale (MI) and the maximum exhale (ME) phases are manually delineated by the expert. Also, correspondences of 75 landmarks are provided for each phase. Thus, the registration accuracy can be evaluated by the Euclidean distance between the expert-placed and computer-estimated landmark points. For comparison, we use diffeomorphic Demons (Ref. ¹⁸) and SyN (Ref. ¹⁹) as the comparison methods.

The registration results by diffeomorphic Demons,³³ SyN, and our method on 300 landmarks between MI and ME phases are shown in Table 2. Here, the MI phase image is selected as the reference image for diffeomorphic Demons and SyN. It can be observed that our method achieves the lowest mean registration errors. Table 3 shows the mean and standard deviation on 75 landmark points over all 6 phases by diffeomorphic Demons, SyN, and our method. Again, our method achieves the lowest registration errors. It is worth noting that the maximum registration errors among 300 landmarks are 6.08 mm by diffeomorphic Demons, 5.81 mm by SyN, and 3.67 mm by our method, respectively. These results demonstrate the accuracy of respiratory motion estimated by our method on the planning day, which will be used to guide the 4D-CT reconstruction on the treatment day.

Table 2.

The mean and standard deviation of registration errors (mm) on 300 landmark points between maximum inhale and exhale phases.

	300 landmark points between MI and ME
#	Initial	Diffeomorphic Demons	SyN	Our method
1	3.89 ± 2.78	2.14 ± 1.69	1.82 ± 1.43	0.64 ± 0.61
2	4.34 ± 3.90	2.10 ± 1.71	1.83 ± 1.06	0.56 ± 0.63
3	6.94 ± 4.05	2.58 ± 1.45	2.67 ± 1.25	0.70 ± 0.68
4	9.83 ± 4.85	4.81 ± 4.26	2.36 ± 1.35	0.91 ± 0.79
5	7.48 ± 5.50	1.99 ± 1.32	2.12 ± 1.37	1.10 ± 1.14
6	10.89 ± 6.97	7.94 ± 5.21	6.67 ± 5.25	3.28 ± 3.45
7	11.03 ± 7.42	6.79 ± 4.76	6.15 ± 3.34	1.68 ± 1.22
8	14.99 ± 9.01	6.30 ± 3.71	6.69 ± 3.15	1.70 ± 1.69
9	7.92 ± 3.98	4.47 ± 2.02	4.64 ± 2.14	1.72 ± 1.32
10	7.30 ± 6.35	3.67 ± 2.96	2.95 ± 2.05	1.48 ± 1.84

Table 3.

The mean and standard deviation of registration errors (mm) on 75 landmark points across all six phases.

	75 landmark points across all six phases
#	Initial	Diffeomorphic Demons	SyN	Our method
1	2.18 ± 2.54	1.31 ± 0.99	1.29 ± 1.05	0.51 ± 0.39
2	3.78 ± 3.69	1.58 ± 1.20	1.44 ± 0.89	0.47 ± 0.34
3	5.05 ± 3.81	1.45 ± 0.85	1.56 ± 0.65	0.55 ± 0.32
4	6.69 ± 4.72	2.63 ± 2.01	2.08 ± 1.12	0.69 ± 0.49
5	5.22 ± 4.61	1.28 ± 0.85	1.24 ± 0.87	0.82 ± 0.71
6	7.42 ± 6.56	4.49 ± 3.06	3.87 ± 2.42	1.72 ± 1.83
7	6.66 ± 6.46	3.59 ± 2.56	2.65 ± 1.54	0.97 ± 0.70
8	9.82 ± 8.31	3.75 ±2.32	3.67 ± 2.05	1.70 ± 1.69
9	5.03 ± 3.79	2.45 ± 1.30	2.52 ± 1.24	1.15 ± 0.78
10	5.42 ± 5.84	2.29 ± 1.78	1.85 ± 1.51	1.06 ± 1.22

Evaluation of 4D-CT reconstruction on the treatment day

Simulated dataset

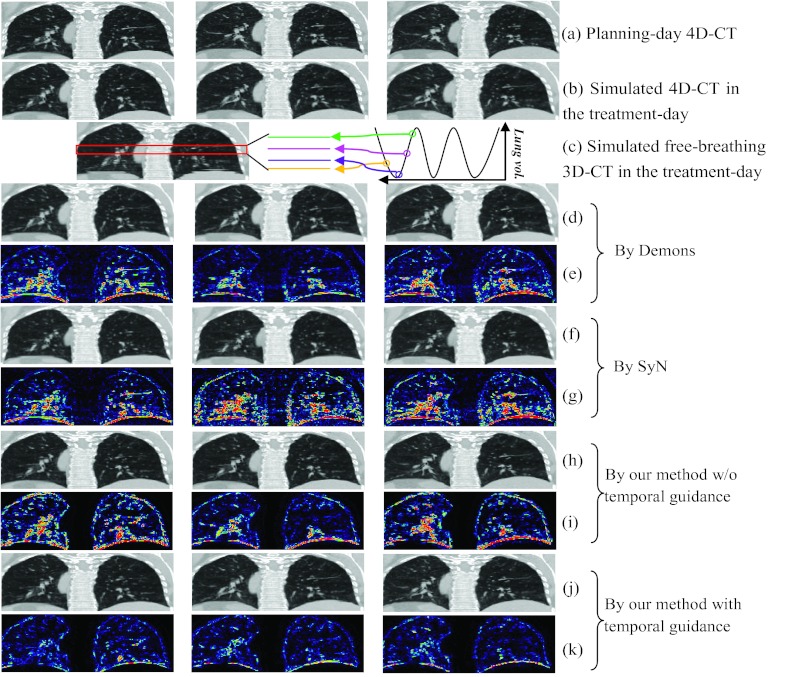
Given the planning day 4D-CT [shown in Fig. 7a, with the inhale, middle, and exhale phases displayed from left to right], we first simulate the treatment day 4D-CT [shown in Fig. 7b] with following three steps: (1) we take the phase image at maximum inhale stage as the reference image and register all other phase images to this reference image; (2) we simulate the local distortions on the reference image by randomizing the parameters of B-spline control points, and apply this simulated deformation field (by B-spline interpolation) upon the reference image, thus obtaining the deformed reference image in the treatment day; (3) for other phases, we concatenate the deformation fields in Steps (1) and (2) to deform other phase images of planning day 4D-CT to the treatment day space. In this way, we are able to obtain the simulated 4D-CT on the treatment day, which consists of the deformed phase images in Steps (2) and (3).

Figure 7.

The performance of 4D-CT reconstruction from a simulated free-breathing 3D-CT. A planning day 4D-CT is first obtained, with its maximum inhale, middle, and maximum exhale phases shown in (a). The simulated treatment day 4D-CT is displayed in (b), along with a simulated free-breathing 3D-CT of the treatment day shown in (c). The registration results between the planning day 4D-CT and the free-breathing 3D-CT by diffeomorphic Demons and SyN are shown in (d) and (f), with their difference images with respect to ground-truth (b) displayed in (e) and (g), respectively. The reconstruction results by our method without/with temporal guidance are displayed in (h) and (i), along with their corresponding difference images with respect to the ground-truth (b) shown in (i) and (k), respectively.

Next, we need to simulate the free-breathing 3D-CT based on the simulated treatment day 4D-CT in Fig. 7b. By mimicking the free-breathing scan procedure, we can assemble the free-breathing 3D-CT on the treatment day [Fig. 7c] by extracting the image slice from particular phase image of the simulated treatment day 4D-CT at the same couch table position, where the corresponding phase is determined by sequentially sampling along respiration [the demonstration of simulation in the box is shown in the right of Fig. 7c].

To validate the performance of our reconstruction method, we can now estimate the treatment day 4D-CT from this free-breathing 3D-CT [Fig. 7c] by (1) directly registering each phase image on the planning day 4D-CT with the free-breathing 3D-CT by diffeomorphic Demons, (2) directly registering each phase image on the planning day 4D-CT with the free-breathing 3D-CT by SyN, (3) reconstruction by our method without temporal guidance (Step 4: temporal correspondence propagation in Sec. 2B), and (4) reconstruction by our method with temporal guidance. The respective results are reported in Figs. 7d, 7f, 7h, 7j, respectively, and also their difference images with respect to the ground-truth treatment day 4D-CT images [Fig. 7b] are given in Figs. 7e, 7g, 7i, 7k, respectively. It can be seen from the difference images that our full method (with temporal guidance) achieves the best reconstruction result, which suggests the importance of temporal guidance from the 4D-CT model built on the planning day.

Real clinic data from lung cancer treatment

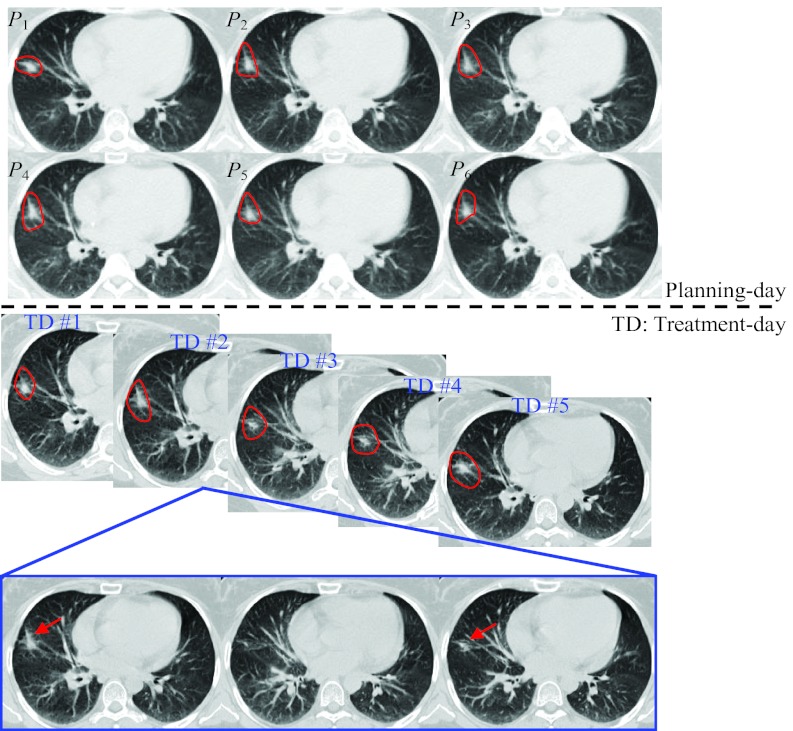
Ten lung cancer cases are evaluated in this experiment. Each case includes the 4D-CT on the planning day and the free-breathing 3D-CT in the followup treatment days. The CT images on the planning day and treatment days of a typical case are shown in Fig. 8. As shown in the top of Fig. 8, 4D-CT is able to provide the full range of lung motion by sorting the CT segments according to the respiration at each couch table position. Thus, it is useful for radiation oncologist to determine the range of tumor motion when designing the treatment plan. On the other hand, contouring the tumor on the free-breathing 3D-CT is much more difficult because of a lot of motion induced image artifacts. For example, we show three consecutive slices of the free-breathing 3D-CT taken in the second treatment day in the bottom of Fig. 8. It is apparent that the tumor appears at superior and inferior slices (indicated by arrows in Fig. 8) but disappears in the middle slice. Therefore, the radiation margins will have to be expanded in all directions, in order to cover the whole tumor in the radiation therapy. In the following, we will demonstrate the reconstruction of 4D-CT on the treatment day from the single free-breathing 3D-CT on the treatment day, which shows the inconsistency of tumor in the free-breathing 3D-CT.

Figure 8.

The CT images scanned in a typical subject during lung cancer radiation therapy. The 4D-CT (with 6 phase images P₁, …, P₆) scanned in the planning-day and the free-breathing 3D-CT images taken in the five treatment days are displayed in the top and middle panels of figure, respectively, with tumor also delineated by contours. Three consecutive slices of the second-treatment-day free-breathing 3D-CT are shown in the bottom for demonstrating the inconsistency for the tumor regions (indicated by arrows).

Evaluation of 4D-CT reconstruction on the planning day

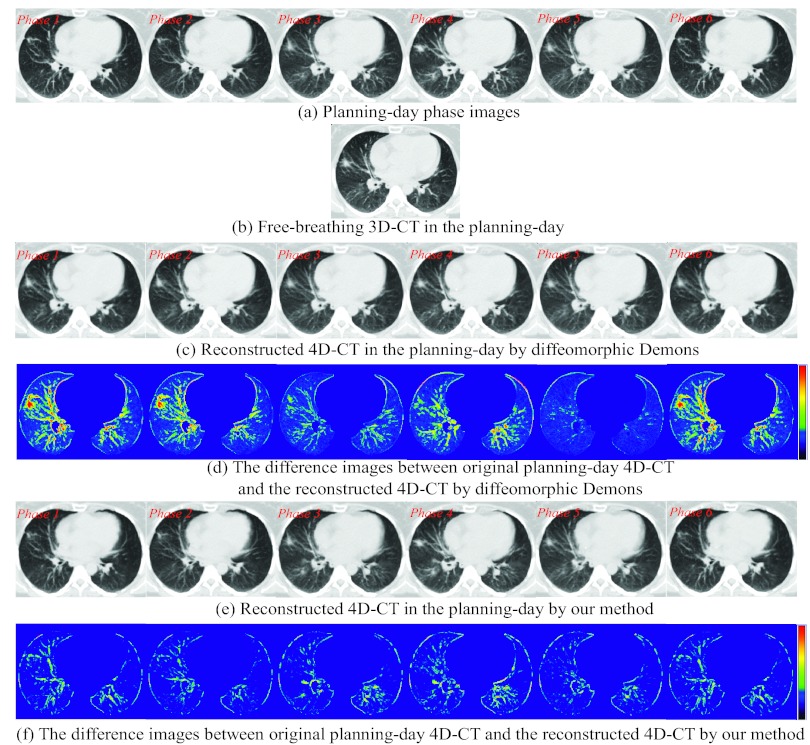
Since some patients have taken both 4D-CT and free-breathing 3D-CT on the planning day, we can evaluate the reconstruction performance of our proposed method by reconstructing 4D-CT from the free-breathing 3D-CT on the planning day. A 4D-CT and a free-breathing 3D-CT of the planning day are displayed in Figs. 9a, 9b, respectively. The reconstructed 4D-CT by simply registering each phase image P_s [Fig. 9a] with the free-breathing 3D-CT I [Fig. 9b] by diffeomorphic Demons (where bone alignment is also performed first to remove the global difference) is displayed in Fig. 9c. Obviously, all the phase images in the reconstructed 4D-CT are similar to the free-breathing 3D-CT. However, in this case, the information of respiratory motion is almost lost completely, i.e., the lung does not move from phase to phase. The reconstructed 4D-CT by our proposed method is shown in Fig. 9e. First of all, there are obvious respiratory motions across different phases. Second, since the anatomical structures do not change for the images acquired at the same planning time, each image patch in the particular phase image of the reconstructed 4D-CT should be very similar to the corresponding one in the planning day free-breathing 3D-CT. Thus, we evaluate the image difference between the planning day 4D-CT and the reconstructed 4D-CT at every respiratory phase. The difference images by diffeomorphic Demons and our method are shown in Figs. 9d, 9f, respectively. According to the color bar shown in the right, the reconstruction error by our method is much smaller than that by diffeomorphic Demons, indicating better performance of our reconstruction method.

Figure 9.

Evaluation of the reconstructed 4D-CT from a single free-breathing 3D-CT in the planning day. The 4D-CT P and free-breathing 3D-CT in the planning day are shown in (a) and (b), respectively. The reconstructed 4D-CT T by diffeomorphic Demons and our method are shown in (c) and (e), with their difference images with respect to the planning day 4D-CT phase images displayed in (d) and (f), respectively.

Reconstruction of 4D-CT from a single free-breathing 3D-CT on the treatment day

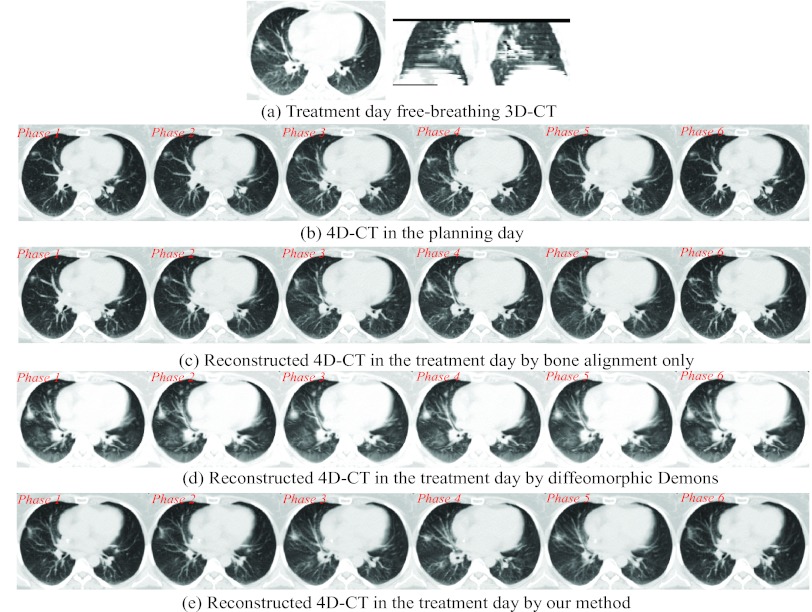
We have performed our reconstruction over ten patients, each one with the 4D-CT on the planning day and the free-breathing 3D-CT on the followup treatment days. In clinical treatment, the therapists usually set up the patient by aligning the bones manually or semiautomatically. In Fig. 10c, we show the reconstructed 4D-CT by applying bone alignment (as explained in Step 1 in Sec. 2B) between the free-breathing 3D-CT I [Fig. 10a] on the treatment day and each phase image of the planning day 4D-CT [Fig. 10b].

Figure 10.

Reconstructed 4D-CT from a single free-breathing 3D-CT in the treatment day. The free-breathing 3D-CT in the treatment day is shown in (a). The reconstructed 4D-CTs from (a) by bone alignment, diffeomorphic Demons, and our reconstruction method are displayed in (b), (c), and (d), respectively.

Although conventional deformable registration methods, e.g., diffeomorphic Demons, can be used to register each roughly aligned planning day phase image P_s (after bone alignment with respect to the free-breathing 3D-CT I), the reconstruction result is limited by the mixed phase information in the free-breathing 3D-CT. The reconstructed 4D-CT by performing diffeomorphic Demons in the conventional way is shown Fig. 10d. Since the free-breathing 3D-CT is always used as the template image during registration, the reconstructed phase images in Fig. 10d are biased by the misleading image content in the free-breathing 3D-CT I. That is, the reconstructed phase images are too similar to perceive the respiratory motion in 4D-CT, which is not physically reasonable in real 4D-CT. The reconstructed 4D-CT by our method is demonstrated in Fig. 10e. As we can observe, first, each phase image of reconstructed 4D-CT keeps the major anatomical structures as the planning day 4D-CT, which makes the reconstructed 4D-CT on the treatment day clinically reasonable. Second, the respiratory motion can be clearly observed in our reconstructed 4D-CT. We will evaluate the reconstruction accuracy of our method as follows.

The tumor on the treatment day free-breathing 3D-CT I is first manually delineated by radiologist. Similarly, we can obtain the tumor contours in all phase images of planning day 4D-CT P. Then, we deform these tumor masks to the treatment day by using either the conventional bone alignment or deformation fields H estimated by our reconstruction method. The tumor movement field can finally be calculated by combining the deformed tumor masks across all phases. In this way, we obtain the tumor movement field in the reconstructed 4D-CT on the treatment day by the bone alignment and our reconstruction method, as shown with larger surface in Figs. 11a, 11b, respectively.

Figure 11.

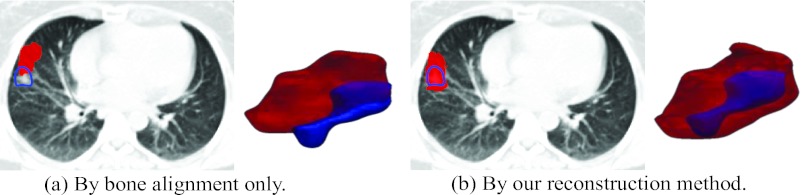
The overlap of tumor contour drawn on the free-breathing 3D-CT and the tumor movement field in the reconstructed treatment-day 4D-CT. The shape of tumor in the treatment-day free-breathing 3D-CT and the tumor movement field in the reconstructed treatment-day 4D-CT is displayed by small surface and large surface, respectively.

Since the tumor usually could move with lung freely, it is very difficult to align the tumor seen in the planning CT with the tumor seen in the free-breathing treatment day 3D-CT, if aligned only with bones. As shown in Fig. 11a, the estimated tumor movement field is unable to cover the entire tumor in the free-breathing 3D-CT on the treatment day due to the insufficient alignment. To address this issue, the treatment margin has to be expanded on the treatment-plan design stage in all directions.

On the contrary, by using our reconstruction method, the tumor extracted in the free-breathing 3D-CT is always within the estimated tumor movement field [Fig. 11b]. With better estimation of 4D lung/tumor motion, we will be able to deliver the radiation dose more accurately onto the tumor. Moreover, it can allow the reduction of the margin of radiation treatment field. This makes the dose escalation of tumor possible which often means better tumor control.^{3, 11} Meanwhile, the critical structures around the tumor can be better spared as the result of tighter field margin. Consequently, we can make the margin of radiation treatment filed smaller than the conventional patient setup methods, which implies the possible dose escalation of tumor and fewer side effects to the normal structures.

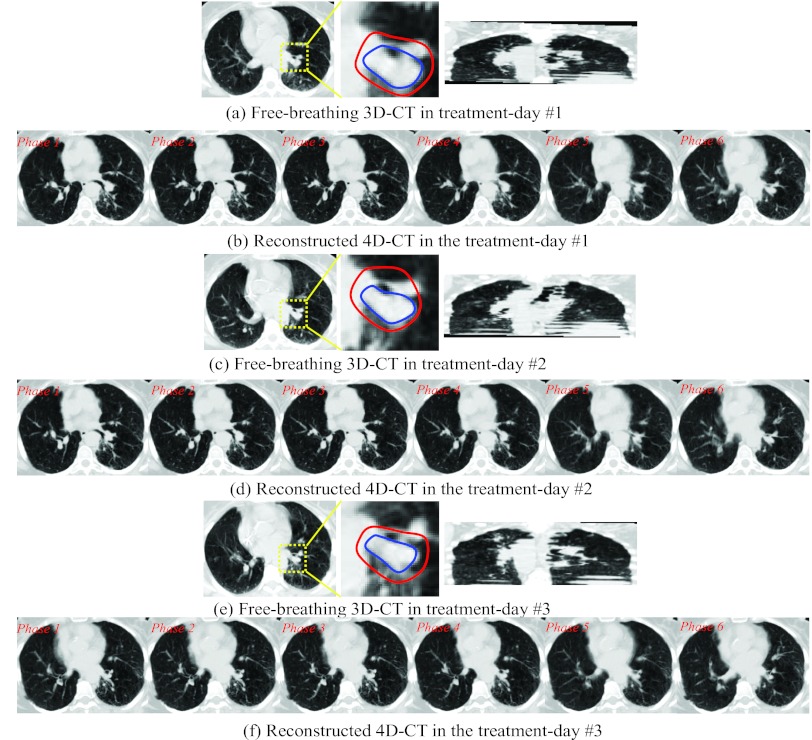
The reconstructed 4D-CT by our method on another patient in three treatment days are also shown in Fig. 12, with the free-breathing 3D-CT in three treatment days shown in (a), (c), and (e), respectively. The reconstructed 4D-CTs are displayed in (b), (d), and (f) for each treatment day. To further demonstrate the performance of our reconstruction method with respect to the tumor motion, we manually extract the contour of tumors on each treatment day free-breathing 3D-CT and each phase image of the planning day 4D-CT. Then, the tumor movement field in each reconstructed treatment day 4D-CT can be obtained by integrating the deformed planning day tumor masks across all respiratory phases. The contours of tumor on the treatment day 3D-CT and the estimated tumor movement fields on the reconstructed 4D-CT are displayed in inner and outer contours in the middle of Figs. 12a, 12c, 12e, respectively. The anatomy inside yellow box is enlarged. It can be seen that the estimated tumor movement fields can always cover the entire tumor, which provides very useful tumor motion information for radiation therapy on the treatment day.

Figure 12.

Reconstructed 4D-CT from the single free-breathing 3D-CT in three treatment days. The tumors in the treatment-day free-breathing 3D-CT image are manually delineated by the inner contour. The estimated tumor movement fields in the treatment days are outlined by the outer contour.

Discussion

Although in the conventional method the bones between the free-breathing 3D-CT image of the planning day and the free-breathing 3D-CT images of the treatment days can be aligned automatically and also the soft tissues can be aligned manually, no tumor motion information on the treatment day is provided. Our method can automatically map the tumor movement from the planning day to the treatment days by also accommodating the new motion detected from the treatment day 3D-CT, and can thus precisely localize the moving tumor just prior to radiotherapy. In summary, our method will bring immediate improvement for lung tumor treatment in two aspects: (1) the reconstructed 4D-CT image will provide a complete description about lung/tumor motions on the treatment day, and thus the radiation fields can be more accurately aligned onto tumor for better treatment. (2) Our method is free of internal fiducial markers which could cause pneumothorax for many patients. With our method, the setup uncertainty used in the conventional PTV design can be potentially reduced.

Furthermore, we use a typical patient (given in Fig. 12) as an example to show that the margin in patient setup can be reduced by our method. In the planning day, it is straightforward to estimate tumor motion from the 4D-CT of the patient, which is about 5 mm. Based on this measurement, we usually expand clinical target volume (CTV) for 5 mm to form the internal target volume (ITV), in order to cover the whole tumor motion. In Fig. 12, each inner contour of the tumor outlines the CTV on the free-breathing 3D-CT of each treatment day. In the conventional patient setup based on only the free-breathing 3D-CT, we have to empirically expand ITV for another 7 mm in all directions to form the PTV for radiation treatment, in order to account for the setup uncertainty since it is difficult to obtain accurate tumor motion from the treatment day free-breathing 3D-CT. Thus, the overall dose margin is 12 mm (5 + 7 mm) for this particular patient. On the other hand, our method is able to provide the tumor movement field (i.e., the outer contours in Fig. 12) for each treatment day, which can be obtained by mapping the motion information encoded in the planning day 4D-CT to the treatment day by further considering the hidden motion information identified from the treatment day free-breathing 3D-CT. It is worth noting that the mean distance and standard deviation between the CTV and our estimated tumor movement field in the treatment day is 3.73 ± 1.32 mm, which is close to the 5 mm motion estimated in the planning day by considering also the standard deviation here. Recall that, using our method, the maximum registration error between two extreme phases is 3.67 mm upon 300 landmarks of ten 4D-CT cases. Thus, instead of using the empirical 7 mm expansion from ITV to PTV, we could use 3.67 mm only to account for the setup uncertainty. Then, the overall dose margin can be reduced to 5 + 3.67 mm = 8.67 mm [here, we still use 5 mm expansion from CTV to ITV, instead of 3.73 mm estimated by our method, due to the consideration of standard deviation (1.32 mm)], which implies 27.8% of margin reduction for the patient. It is worth noting that this is the result for one patient. To make more general conclusion on the amount of margin reduction by our method, we will test it on more patient data in our future work.

Most IGRT methods assume that the respiratory motion difference between the planning day and the treatment days is small, so that the respiratory motion obtained from the planning day 4D-CT can be directly used for the treatment dose management.³¹ In our method, we estimate the patient-specific respiratory motion on the treatment day, since our method is able to extract the motions hidden in the free-breathing 3D-CT. Note that the free-breathing 3D-CT does convey motion information, although it is mixed and incomplete. We have applied our method to ten cases and obtained significant improvement in patient setup over the conventional methods that generally use only the free-breathing 3D-CT, without guidance from the 4D-CT model built on the planning day. In our future work, we will further evaluate the performance of our method with respect to various factors, e.g., tumor size, tumor location, and patient breathing pattern.

CONCLUSIONS

We have proposed a novel two-step method to reconstruct a new 4D-CT from a single free-breathing 3D-CT on the treatment day, for possible improvement of lung cancer image-guided radiation therapy, which is currently often done by registration of two free-breathing 3D-CT images for patient setup. In our method, the 4D-CT model is first built on the planning day by a robust spatiotemporal registration method. Then, with the guidance of this 4D-CT model and the inclusion of newly detected motion from the free-breathing 3D-CT on the treatment day, a 4D-CT on the treatment day can be reconstructed for more accurate patient setup. We have extensively evaluated each step of our method with both real and simulated datasets, and obtained very promising results in building 4D-CT model and reconstructing new 4D-CT on the treatment day.