Abstract
Voltage-gated ion channels play a critical role in regulating neuronal intrinsic response dynamics (IRD). Here, we computationally analysed the roles of the two inactivating subthreshold conductances (A and T), individually and in various combinations with the non-inactivating h conductance, in regulating several physiological IRD measurements in the theta frequency range. We found that the independent presence of a T conductance, unlike that of an h conductance, was unable to sustain an inductive phase lead in the theta frequency range, despite its ability to mediate theta frequency resonance. The A conductance, on the other hand, when expressed independently, acted in a manner similar to a leak conductance with reference to most IRD measurements. Next, analysing the impact of pair-wise coexpression of these channels, we found that the coexpression of the h and T conductances augmented the range of parameters over which they sustained resonance and inductive phase lead. Additionally, coexpression of the A conductance with the h or the T conductance elicited changes in IRD measurements that were similar to those obtained with the expression of a leak conductance with a resonating conductance. Finally, to understand the global sensitivity of IRD measurements to all parameters associated with models expressing all three channels, we generated 100,000 neuronal models, each built with a unique set of parametric values. We categorized valid models among these by matching their IRD measurements with experimental counterparts, and found that functionally similar models could be achieved even when underlying parameters displayed tremendous variability and exhibited weak pair-wise correlations. Our results suggest that the three prominent subthreshold conductances contribute differently to intrinsic excitability and to phase coding. We postulate that the differential expression and activity-dependent plasticity of these conductances contribute to robustness of subthreshold IRD, whereby response homeostasis is achieved by recruiting several non-unique combinations of these channel parameters.
Key points
Voltage-gated ion channels (VGICs) play a critical role in determining how neurons respond to oscillatory inputs at various frequencies. How do inactivating VGICs regulate neuronal response properties to oscillatory inputs?
T-type Ca2+ channels mediate resonance in response to oscillatory inputs, without being accompanied by a lead in the intrinsic phase response, and A-type K+ channels act analogous to a leak channel with reference to many measurements characterizing intrinsic response dynamics (IRD).
Coexpression of these channels with a hyperpolarization-activated h channel augmented the range of parameters over which they sustained resonance and phase lead.
Global sensitivity analysis demonstrates that functionally similar models could be achieved even when underlying parameters displayed tremendous variability and exhibited weak pair-wise correlations.
A simplistic one-parameter-a-time analysis that does not account for the complex and non-linear interactions between channels would fail to provide a full understanding of subthreshold IRD.
Introduction
Hippocampal neurons reside within an oscillating neuronal network. These oscillations span multiple frequency ranges (from less than 1 Hz to hundreds of Hz), sometimes with each frequency range reflective of a specific behavioural state of the animal (Buzsaki, 2006). Given the crucial roles of multi-frequency oscillations in various behavioural states and information encoding, understanding neuronal responses to different stimulus frequencies spanning multiple durations forms an important step towards deciphering the neural code (Engel et al. 2001; Buzsaki, 2002, 2006; O’Keefe & Burgess, 2005; Wang, 2010). Intrinsic response dynamics (IRD) constitute the manner in which a single neuron intrinsically responds to time-varying stimulus with differential spatiotemporal patterns of activation. Whereas the spatial aspect is governed by the dendritic location of the input stimuli, the temporal aspect can be defined using the arrival times of synaptic inputs.
The passive properties of the dendritic tree in conjunction with the densities and characteristics of different ion channels located at various dendritic locations play critical roles in determining the IRD of a single neuron. Given the ability of ion channels to amplify or suppress specific inputs, it has been emerging from recent results that channels can sculpt IRD in a manner suitable for the neuron and its network, through their variable expression and/or activity-dependent plasticity (Johnston & Narayanan, 2008; Nelson & Turrigiano, 2008; Sjostrom et al. 2008; Spruston, 2008; Taylor et al. 2009; Wang, 2010; O’Donnell & Nolan, 2011; Magee, 2012). Hippocampal CA1 pyramidal neurons express various ion channels that are active at subthreshold voltage ranges with varying subcellular distributions. Whereas it is known that non-inactivating, resonating conductances (e.g. the h conductance) can intrinsically modulate the amplitude and phase of incoming oscillatory inputs, depending on their properties as well as expression profiles (Hutcheon & Yarom, 2000; Narayanan & Johnston, 2007, 2008; Hu et al. 2009; Marcelin et al. 2009; Zemankovics et al. 2010), the role of inactivating subthreshold conductances in modulating oscillatory inputs has not been studied in detail. Hippocampal CA1 pyramidal neurons are endowed with two prominent subthreshold inactivating channels: a fast-inactivating A-type K+ channel, and a fast-inactivating T-type Ca2+ channel (Magee & Johnston, 1995; Hoffman et al. 1997). Both the A current and the T current are known to express in the dendrites of CA1 pyramidal cells, with their densities increasing with distance from the soma (Magee & Johnston, 1995; Hoffman et al. 1997). Physiologically, both channels are known to be active in subthreshold voltage ranges (Magee & Johnston, 1995; Hoffman et al. 1997), and thus are capable of modulating the IRD and integrative properties of the neuron to incoming oscillatory inputs. Further, the A current has been shown to play crucial roles in modulating backpropagating action potentials, dendritic spikes (Hoffman et al. 1997; Gasparini et al. 2004) and certain rhythmic properties (Bourdeau et al. 2007); on the other hand, the T current is capable of initiating low-threshold calcium spikes (Tsay et al. 2007) and plays a role in the induction of certain forms of synaptic plasticity (Golding et al. 2002).
Given the prominent coexpression of h, A and T conductances in the dendrites of CA1 pyramidal neurons with overlapping subthreshold activation ranges, it is important to understand how these conductances and passive neuronal properties interact with each other to determine the IRD of the neuron for oscillatory inputs. In this study, we asked as to how h, A and T conductances interact with each other in regulating neuronal IRD, both in terms of the intrinsic amplitude and the phase responses of the neuron to incoming oscillatory inputs. In this process, we systematically analysed the interactions between these three channels, first considering combinations of two at a time, in regulating prominent measurements that characterize neuronal IRD to oscillatory inputs. Finally, we used a powerful global sensitivity analysis tool, which has been effectively used in understanding pyloric rhythms and their dependencies on underlying channels and receptors (Prinz et al. 2003, 2004; Taylor et al. 2009; Marder & Taylor, 2011), to analyse the sensitivities of these subthreshold measurements with respect to 17 active (with respect to all three channels) and passive model parameters that regulate the IRD measurements. Our results demonstrate that the neuronal IRD can remain robust to individual variability in underlying active and passive parameters, suggesting that a hippocampal neuron can recruit several non-unique mechanisms to maintain homeostasis in IRD, through the presence and plasticity of various subthreshold dendritic ion channels.
Methods
To reduce the computational cost and complexity of the model and to avoid the influences of morphology on the measurements, thereby focusing on ion channel kinetics and passive properties, a single compartment model was used for all simulations with dimensions 60 × 60 μm (Fig. 1A). Passive electrical parameters of the model were set as follows: specific membrane resistivity, Rm= 11 kΩ cm2; specific membrane capacitance, Cm= 1 μF cm−2. This gave rise to a baseline ‘passive’ input resistance of ∼97 MΩ, comparable to input resistance of hippocampal CA1 neurons in the absence of h conductance (Narayanan & Johnston, 2007).
Figure 1. Model and measurements used in this study.
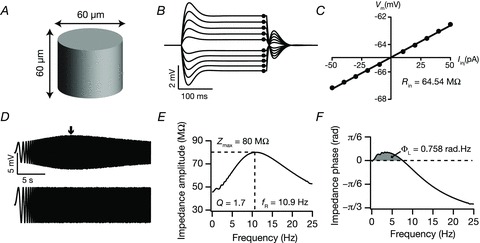
A, schematic diagram of the model used to study excitability and IRD of hippocampal pyramidal neurons. B, voltage traces in response to current injection from −50 to 50 pA in steps of 10 pA for 250 ms. C, steady state voltage response (black dots in B) plotted against the corresponding current amplitude to obtain V–I plot. Slope of the best linear fit to V–I was taken as input resistance (Rin). D, a chirp current stimulus, 50 pA in amplitude and frequency linearly increasing from 0.1 to 25 Hz in 25 s (lower trace) and corresponding voltage response in the presence of h conductance (upper trace). E and F, impedance amplitude profile (E) and impedance phase profile (F) obtained from the voltage response to the chirp stimulus, shown in D. Grey shaded area in F corresponds to the total inductive phase, ΦL.
Channel kinetics
Our study includes three different types of Hodgkin–Huxley (HH)-type voltage-gated ion channel (VGIC) models: T-type Ca2+, A-type K+ and hyperpolarization-activated h channels; and two different types of multi-state Markovian kinetic models: T-type Ca2+ and A-type K+. HH-type (all modelled from experimental measurements from CA1 pyramidal neurons) A-type K+ channels were adopted from Migliore et al. (1999), the h channel was modelled as in Poolos et al. (2002), and the T-type Ca2+ channel kinetics were taken from Shah et al. (2008). The current through the HH-type T-type Ca2+ channel was modelled using the Goldman–Hodgkin–Katz formulation (Goldman, 1943; Hodgkin & Katz, 1949), with the default values of external and internal Ca2+ concentrations set at 2 mm and 50 nm, respectively. The multi-state Markovian kinetic scheme for the A-type K+ channel was adopted from Amarillo et al. (2008), and for the T-type Ca2+ channel the kinetics were adapted from Serrano et al. (1999). The kinetics and voltage-dependent parameters associated with the multi-state Markovian kinetic schemes were modified to match their voltage dependence to that of HH-type counterparts. Calcium decay kinetics were modelled as in Narayanan & Johnston (2010). Reversal potentials for A-type K+ and h channels were set at −90 mV and −30 mV, respectively.
Measurements
The model's intrinsic subthreshold response dynamics and excitability were characterized using standard measurements described previously (Hu et al. 2002; Narayanan & Johnston, 2007, 2008). Specifically, input resistance (Rin) was measured by injecting subthreshold current pulses of amplitudes spanning −50 pA to +50 pA, in steps of 10 pA, and recording the steady state voltage responses to these current pulses (Fig. 1B). These steady state voltage responses were plotted against the corresponding current amplitude to obtain a V–I plot (Fig. 1C). The slope of a linear fit to this steady state V–I plot was taken as the input resistance (Rin) of the model. Subthreshold response dynamics of the model to oscillatory inputs was characterized by injecting a chirp stimulus: a sinusoidal current wave with constant amplitude (50 pA) with frequency linearly increasing from 0 to 25 Hz in 25 s (Fig. 1D). The Fourier transform of the voltage response was divided by the Fourier transform of the chirp stimulus to obtain the complex valued impedance Z(f), as a function of frequency f. The impedance amplitude profile (ZAP) was then estimated as the magnitude of this impedance (Fig. 1E):
where Re(Z(f)) and Im(Z(f)) are the real and imaginary parts of the impedance |Z(f)|, respectively. Three measurements associated with the impedance amplitude profile were employed for our analyses (Fig. 1E): resonance frequency (fR), resonance strength (Q) and maximum impedance amplitude (|Z|max). The frequency at which |Z(f)| reached its maximum value was measured as the resonance frequency (fR); |Z|max denotes the maximum value of the impedance, which by definition equals |Z(fR)| (Narayanan & Johnston, 2007). Resonance strength (Q) was measured as the ratio of |Z|max to the impedance amplitude at 0.5 Hz (Hu et al. 2002). The impedance phase profile (ZPP) was computed as (Fig. 1F):
Total inductive phase (ΦL) was defined as the area under the inductive part of the ZPP (Fig. 1F) as follows (Narayanan & Johnston, 2008):
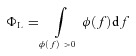 |
Generation of model population
To generate a population of models for performing global sensitivity analysis on our full model comprising all the three VGICs under consideration, we first generated the baseline model by inserting active conductances in the passive model described above. Then we randomized all the 17 passive and active model parameters (with respect to all three conductances and passive membrane parameters) such that they uniformly and independently span a neighbourhood around their default values (Table 1). With all parameters randomized, we generated 100,000 models, each built with a unique set of values for the 17 parameters. This approach is analogous to that taken in previous studies involving such global forms of sensitivity analysis (Foster et al. 1993; Goldman et al. 2001; Prinz et al. 2003, 2004; Achard & De Schutter, 2006; Tobin et al. 2006; Hobbs & Hooper, 2008; Weaver & Wearne, 2008; Taylor et al. 2009). The range of maximal conductance values was chosen such that they span the entire range of physiologically relevant measurements observed in CA1 neurons. For example, the range of h conductance was chosen such that resonance frequency reaches a maximum value of 10 Hz in the baseline model, a value observed physiologically (Narayanan & Johnston, 2007). Similarly, the maximum value of the A-type K+ conductance was chosen such that in the presence of fast sodium and delayed rectifier potassium conductances, action potential peak-to-peak amplitude decreases to 10 mV (Hoffman et al. 1997). The magnitude of T-type Ca2+ conductance was adjusted such that in the absence of the h conductance, the model does not elicit a calcium spike when injected with a 50 pA oscillatory current pulse for 25 s (Narayanan & Johnston, 2007; Tsay et al. 2007). All parameters and their ranges are given in Table 1. All measurements (see subsection on Measurements above) associated with each of these 100,000 models were used for further analyses of global sensitivities with respect to the 17 different parameters.
Table 1.
Range of parameters used in generating model population with random sampling of parameter space
| Parameter | Default value | Testing range |
|---|---|---|
| Rm (kΩ cm2) | 11 | 10–18 |
| Cm (μF cm−2) | 1 | 0.5–1.5 |
| Diameter (μm) | 60 | 40–80 |
 (S cm−2) (S cm−2) |
— | 0.02–0.1 |
 (μS cm−2) (μS cm−2) |
— | 100–500 |
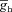 (μS cm−2) (μS cm−2) |
— | 30–150 |
| V1/2 activation of A channel (mV) | −1 | −20 to 20 |
| V1/2 inactivation of A channel (mV) | −56 | −80 to −40 |
| V1/2 activation of T channel (mV) | −60 | −75 to −35 |
| V1/2 inactivation of T channel (mV) | −85 | −105 to −65 |
| V1/2 activation of h channels (mV) | −82 | −100 to −60 |
| Activation time constant of A channel (ms) | 0.032 | 0.02–0.1 |
| Inactivation time constant of A channel (ms) | 2 | 1–5 |
| Activation time constant of T channel (ms) | 1.004 | 1–5 |
| Inactivation time constant of T channel (ms) | 31.012 | 10–50 |
| Activation time constant of h channel (ms) | 46.51 | 25–75 |
| Ca2+ decay time constant (ms) | 30 | 10–90 |
For each model, each parameter (first column) was drawn independently from a uniform distribution, generated around a large neighbourhood of their default values (second column), within set bounds (third column).
Experimental measurements
The validity of the measurements associated with the 100,000 generated models was tested against corresponding experimental measurement statistics from the soma (n= 121) and dendrites (200–300 μm from the soma, with mean ± SEM = 244.8 ± 4.76 μm; n= 52) of hippocampal CA1 pyramidal neurons pooled from previously published data (Narayanan & Johnston, 2007, 2008; Narayanan et al. 2010). All measurements correspond to baseline measurements at about the resting membrane potential of the cell, and was about −63 mV for the cells used for analysis.
Computational details
All simulations were performed using the NEURON simulation environment (Carnevale & Hines, 2006). Unless otherwise stated, simulations were performed with membrane potential set at −65 mV. Temperature was set at 34°C, and ion channel kinetics was adjusted appropriately accounting for their experimentally determined Q10 factors. The default integration time step was set at 25 μs. Calculation of all IRD measurements was performed using custom-built software written within the Igor Pro (WaveMetrics, Inc., Lake Oswego, OR, USA) programming environment. Correlation analysis and other statistical tests were done using the statistical computing language R (http://www.r-project.org/).
Results
Hippocampal neurons were modelled to study subthreshold IRD defined by five measurements: input resistance (Rin), resonance frequency (fR), resonance strength (Q), maximum impedance amplitude (|Z|max) and total inductive phase (ΦL), in the presence of a hyperpolarization-activated cation-non-specific h current (Ih), a T-type Ca2+ current (ICaT) and an A-type K+ current (IKA). In the sections that follow, we first explored the sensitivities of IRD measurements to the parameters of each of the T and A conductances, by inserting only these conductances into the model neuron. We did not analyse the h conductance separately because such sensitivity analyses for all these measurements have already been performed (Hutcheon et al. 1996; Narayanan & Johnston, 2007, 2008; Zemankovics et al. 2010). As far as the two other inactivating channels are concerned, existing sensitivity analysis for the T channel (Hutcheon et al. 1994) does not span all these measurements, and the A channel has not been analysed in detail. Although such single sensitivity analysis is useful to test the role of each channel and associated passive and active properties in regulating IRD, they do not help in understanding the interactions between these channels, which are typically coexpressed in the CA1 pyramidal neurons and their dendrites. To do this, we inserted combinations of only two of each of these three channels (h, A and T), and analysed the impact of each channel on how the other channel regulated IRD measurements. Finally, we used a powerful global sensitivity analysis methodology to explore the interactions among all three conductances, and analysed the sensitivities of these measurements to all the passive and active parameters that regulate subthreshold IRD of the model neuron.
Modulation of IRD by the individual presence of a regenerative or a restorative inactivating conductance
Although it is well established that ICaT can sustain resonance on its own and also mediate intrinsic membrane potential oscillations (Hutcheon et al. 1994; Hutcheon & Yarom, 2000), a detailed sensitivity analysis of its resonating properties and phase dynamics with respect to various active and passive parametric variability has not been performed. Therefore, we employed a model for an experimentally characterized T-type Ca2+ channel that is expressed in hippocampal pyramidal neurons, and studied the sensitivity of T-type Ca2+ conductance-mediated IRD to various active and passive parameters. First, we studied the role of ICaT in the regulation of membrane excitability by measuring input resistance (Rin) of the model neuron with various T-type Ca2+ conductance magnitudes. As ICaT is a regenerative current, Rin increased when T-type Ca2+ conductance magnitude was increased (Table 2). Rin measured at various membrane potentials in the presence of ICaT yielded a typical biphasic curve (Fig. S1B). This should be expected because ICaT is an inactivating current, thus constraining membrane excitability to be dependent on the balance between the activation and inactivation gating variables. Specifically, at depolarized potentials inactivation dominates, and at hyperpolarized potentials activation dominates for the window current and at the cross-over point, activation and inactivation completely balance each other, thus leading to the biphasic dependence of Rin on membrane potential. A similar explanation holds for the sensitivity of Rin to changes in V1/2 of activation and inactivation of the T channel (Fig. S1C and D). As Rin is a steady state measure, activation and inactivation time constants of the T channel did not modulate Rin, whereas passive electrical parameters had their expected effects (Narayanan & Johnston, 2008; Table 2; Fig. S1E and F).
Table 2.
Sensitivity analysis for IRD measurements corresponding to various passive and active parameters related to the T-type Ca2+ channel
| T-type Ca2+ channel | |||||
|---|---|---|---|---|---|
| Effect of increase in | Tested range | Rin | fR | Q | |Z|max |
| Rm (kΩ cm2) | 1–10 | Increases | Decreases | Increases | Increases |
| Cm (μF cm−2) | 0.5–2 | No effect | Decreases | Decreases | Decreases |
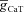 (mS cm−2) (mS cm−2) |
0–0.5 | Increases | Increases | Increases | Increases |
| Membrane potential (mV) | −150 to 30 | Biphasic | Bell shaped | Bell shaped | Biphasic |
| V1/2 activation of T channel (mV) | −150 to 0 | Increases | Decreases | Decreases | Increases |
| V1/2 inactivation of T channel (mV) | −100 to 0 | Increases | Bell shaped | Bell shaped | Increases |
| Activation time constant of T channel (ms) | 1–30 | No effect | Decreases | Decreases | Decreases |
| Inactivation time constant of T channel (ms) | 1–100 | No effect | Decreases* | Increases | Increases |
| Ca2+ decay time constant (ms) | 5–100 | No effect | No effect | No effect | No effect |
The model can sustain resonance only after crossing a certain threshold value of inactivation time constant of ICaT, beyond which there is a reduction in resonance frequency with increase in the inactivation time constant (Fig. S4E). Impedance phase does not exhibit inductive lead when the T-type Ca2+ channel is expressed alone, except for under cases where the inactivation time constant is large (Fig. 2); the sensitivity of total inductive area (ΦL) on the inactivation time constant is shown in Fig. S4F. Associated plots may be found in Figs 2 and S1–S5.
With respect to the other IRD measurements, an increase in maximal T-type Ca2+ conductance (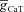 ) increased fR, Q and |Z|max (Fig. S2A–D), which is to be expected from a regenerative resonating conductance (Hutcheon et al. 1994, 1996; Hutcheon & Yarom, 2000; Narayanan & Johnston, 2008). Surprisingly, and in striking contrast to the h conductance (Narayanan & Johnston, 2008), the phase response dynamics of the model had no inductive part even when the model exhibited resonance in the impedance amplitude profile after the insertion of the T conductance. In other words, voltage phase was always lagging with respect to injected current in a resonating system mediated by the T conductance (Figs 2B and S2E).
) increased fR, Q and |Z|max (Fig. S2A–D), which is to be expected from a regenerative resonating conductance (Hutcheon et al. 1994, 1996; Hutcheon & Yarom, 2000; Narayanan & Johnston, 2008). Surprisingly, and in striking contrast to the h conductance (Narayanan & Johnston, 2008), the phase response dynamics of the model had no inductive part even when the model exhibited resonance in the impedance amplitude profile after the insertion of the T conductance. In other words, voltage phase was always lagging with respect to injected current in a resonating system mediated by the T conductance (Figs 2B and S2E).
Figure 2. T resonance did not contribute to an inductive lead in the impedance phase.
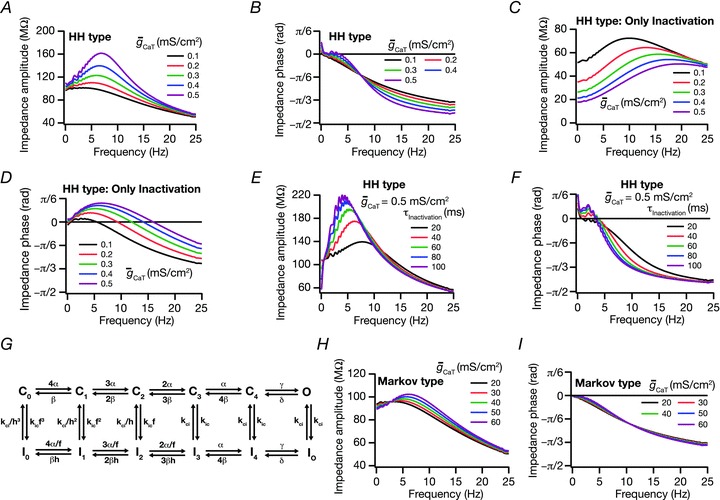
A, impedance amplitude traces for various values of maximal T conductance (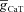 ) displaying characteristic resonance in the impedance amplitude. B, impedance phase traces for various values of maximal T conductance (
) displaying characteristic resonance in the impedance amplitude. B, impedance phase traces for various values of maximal T conductance (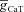 ). Note the absence of phase lead component in spite of resonance in impedance amplitude for the same conductance value (A). C and D, same as in A and B, but simulations were performed after removing the activation variable of the T conductance (
). Note the absence of phase lead component in spite of resonance in impedance amplitude for the same conductance value (A). C and D, same as in A and B, but simulations were performed after removing the activation variable of the T conductance (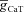 ) from the Hodgkin–Huxley (HH)-type model. Note the large phase lead component after removal of activation gate variable of T conductance (
) from the Hodgkin–Huxley (HH)-type model. Note the large phase lead component after removal of activation gate variable of T conductance (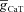 ). E and F, same as A and B, but simulations were run for various values of inactivation time constant. Note that the activation gate is intact. G, a 12-state Markovian kinetic scheme for gating of the T conductance. The model includes six rate constants with the following values: α= 8000 s−1, β= 0.04 s−1, γ= 16,000 s−1, δ= 32 s−1, kci= 80 s−1, kic= 0.01 s−1. Three of the rate constants (α, β and δ) depend exponentially on voltage, changing e-fold for 30, −50 and −11 mV depolarization (respectively). Allosteric factors were set as follows: f= 370 and h= 0.48. H and I, same as in A and B, but simulations were performed with the 12-state Markovian model of T conductance (G). Note the absence of phase lead in the phase profile despite the ability to sustain resonance in the amplitude profile.
). E and F, same as A and B, but simulations were run for various values of inactivation time constant. Note that the activation gate is intact. G, a 12-state Markovian kinetic scheme for gating of the T conductance. The model includes six rate constants with the following values: α= 8000 s−1, β= 0.04 s−1, γ= 16,000 s−1, δ= 32 s−1, kci= 80 s−1, kic= 0.01 s−1. Three of the rate constants (α, β and δ) depend exponentially on voltage, changing e-fold for 30, −50 and −11 mV depolarization (respectively). Allosteric factors were set as follows: f= 370 and h= 0.48. H and I, same as in A and B, but simulations were performed with the 12-state Markovian model of T conductance (G). Note the absence of phase lead in the phase profile despite the ability to sustain resonance in the amplitude profile.
To further explore the reasons behind this critical difference between the intrinsic phase responses associated with h and T resonance, we sought to dissect the biophysical mechanisms behind this phenomenon. The T current is an inactivating current, and previous studies have shown that the activation gate of this current acts as a low pass filter in conjunction with the membrane low pass filter (Hutcheon et al. 1994; Hutcheon & Yarom, 2000). We postulated that this additional low pass filter mediated by the activation gating variable could restrict the impedance phase from exhibiting a lead, as capacitive reactances contribute to a lag in impedance phase (Narayanan & Johnston, 2008). To test this hypothesis, we removed the activation variable from the modelled HH-type T current and repeated our simulations to measure impedance phase. In contrast to our previous observations where T current-mediated phase response dynamics had no inductive component (Fig. 2B), removal of the activation gate from the T current model resulted in a large inductive component (Fig. 2D), similar to those obtained with the h current (Narayanan & Johnston, 2008). Additionally, the removal of the activation gate also uncovered another similarity with the h current, where an increase in the magnitude of T current resulted in an increase in the inductive phase lead (Fig. 2D). Next, we reasoned that we could rescue phase lead in T resonance if the inactivation time constant was increased such that it nullifies the effect the additional low pass filter introduced by the activation gate, as the inactivation time constant of the T current, in conjunction with the leak channel, constitutes a high pass filter (Hutcheon & Yarom, 2000). To test this, we performed our simulations with larger values of inactivation time constants, and found that the phase lead was indeed restored when the inactivation time constant was larger than those for the T currents in hippocampal pyramidal neurons (Fig. 2F).
To further test this hypothesis and to especially rule out the possibility of dependence of this phenomenon on the specific HH-type model chosen for the T current, we employed a 12-state Markov-type kinetic model of the T current from a previous study (Serrano et al. 1999; Fig. 2G), and modified its rate constants to match the activation and inactivation profiles to that of the HH model of the T current. After adjusting the parameters, we performed simulations and, similar to our previous results (Fig. 2B), we found that T current-mediated phase response dynamics had no inductive lead (Fig. 2I), even when the Markovian multi-state channel model was employed. When we altered the parameters of the multi-state model such that it exhibited the same voltage-dependence properties, but slower inactivation kinetics (inactivation time constant at −65 mV of 200 ms), we found that the phase lead was restored similar to our results from the HH-type model (Fig. 2F; data not shown). Thus, our results suggest that resonance mediated by hippocampal T currents does not exhibit inductive phase lead, but could exhibit phase lead if the channel inactivation time constant was slower, and that these results were model independent. Finally, we performed a detailed sensitivity analysis of ICaT-mediated IRD with respect to various active and passive electrical parameters (Figs S2–S5), and the results are summarized in Table 2. Comparing our results (Figs S3 and S4) with sensitivity analyses on h resonance (Narayanan & Johnston, 2008; Zemankovics et al. 2010), we found that these results agree with earlier results that the inactivation gating variable in conjunction with passive membrane filter act together to form a band pass filter (Hutcheon et al. 1994; Hutcheon & Yarom, 2000).
We next turned our attention to a restorative inactivating conductance, and performed similar analyses with only the A-type K+ conductance inserted into the model. We found that increased A-type K+ conductance reduced Rin (Fig. S6A), owing to the presence of a significant amount of subthreshold window component in the activation–inactivation voltage dependencies of the A conductance (Hoffman et al. 1997; Migliore et al. 1999). Because the A conductance does not match the criteria for a resonating conductance (Hutcheon & Yarom, 2000), it cannot sustain resonance on its own (thus leaving fR, Q and ΦL unaltered with its individual presence), but affects |Z|max as a direct consequence of the large window component. Thus, of the chosen list of IRD measurements, we performed a sensitivity analysis with respect to Rin (Fig. S6) and |Z|max (Fig. S7) for various parametric changes in the A conductance, and the results are summarized in Table 3. We also tested model independence of these conclusions by repeating these simulations with a 13-state Markovian kinetic model of the A conductance, and found qualitatively similar results (Fig. S8).
Table 3.
Sensitivity analysis for IRD measurements corresponding to various active parameters related to the A-type K+ channel
| A-type K+ channel | |||
|---|---|---|---|
| Effect of increase in | Tested range | Rin | |Z|max |
| Rm (kΩ cm2) | 1–10 | Increases | Increases |
| Cm (μF cm−2) | 0.5–2 | No effect | Decreases* |
 (mS cm−2) (mS cm−2) |
0–0.5 | Decreases | Decreases |
| Membrane potential (mV) | −150 to 30 | Biphasic | Biphasic |
| V1/2 activation of A channel (mV) | −150 to 0 | Inverted bell | Inverted bell |
| V1/2 inactivation of A channel (mV) | −100 to 0 | Decreases | Decreases |
| Activation time constant of A channel (ms) | 1–30 | No effect | No effect |
| Inactivation time constant of A channel (ms) | 1–100 | No effect | No effect |
Resonance-related IRD measurements are not shown because A-type K+ channels are not resonating conductances. Associated plots may be found in Figs S6–S8.
A very small change.
In summary, the T conductance, a regenerative inactivating conductance, can sustain resonance on its own, with impedance amplitude profiles and their sensitivities similar to the h conductance (with an exception that the inactivation kinetics mediates resonance), but with a major difference in the temporal response where there is no inductive lead in phase profile in spite of resonance in the amplitude profile (Figs 2, and S1–S5; Table 2). The A conductance, a restorative inactivating conductance, alters Rin and impedance amplitudes owing to the large window component in the A conductance (Figs S6–S8; Table 3).
Coexpression of T and h conductances augmented resonance-related measurements through synergistic interactions between the two channels
Although the role of various VGICs and their active parameters in regulating various neurophysiological processes is well established (Migliore & Shepherd, 2002; London & Hausser, 2005; Johnston & Narayanan, 2008; Sjostrom et al. 2008; Spruston, 2008), systematic studies on the roles of interactions among ion channels in regulating specific neurophysiological processes have been few and far (Foster et al. 1993; Goldman et al. 2001; Prinz et al. 2003, 2004; Fransen et al. 2004, 2006; Achard & De Schutter, 2006; Tobin et al. 2006; Tsay et al. 2007; Hobbs & Hooper, 2008; Weaver & Wearne, 2008; George et al. 2009; Taylor et al. 2009; Marder & Taylor, 2011; Pavlov et al. 2011). Specifically, such cross-channel interactions have not been analysed with respect to the subthreshold response dynamics of hippocampal or other neurons to oscillatory inputs. Given the coexpression of h, A and T conductances in the dendrites of CA1 pyramidal neurons with overlapping subthreshold voltage-dependent activation ranges, and their roles in subthreshold integration (Magee et al. 1995; Hoffman et al. 1997; Magee, 2000; Spruston, 2008), it is reasonable to ask how the coexistence of these three channels alter the IRD of the system, specifically with reference to oscillatory inputs. In analysing these interactions systematically, we first picked sets of two of each of these conductances, and analysed the differences between single conductance sensitivity analyses of these channels (above) and their sensitivities in the presence of one other ion channel.
We first picked the interactions between the two resonating conductances: the T-type Ca2+ conductance and the h conductance. As they are resonating conductances, an increase in either conductance magnitude led to an increase in fR and Q (Figs 3A and B, and S9A). However, given that T is a regenerative conductance and h is a restorative conductance, increasing their conductance magnitude had opposite effects on |Z|max and Rin (Figs 3A and S9B; Table 4). In striking contrast to our previous observation where the phase response profile mediated by the T conductance had no inductive component (Fig. 2B), here we found a synergistic interaction between the two conductances, where increasing the magnitude of either conductance increased the inductive component and thus increased ΦL (Fig. 3C). This suggested that although the T conductance alone is insufficient to produce any phase lead, it augments the phase lead mediated by the h conductance. We performed detailed sensitivity analysis for this pair of conductances, and the results are summarized in Table 4 and Figs S9–S13. Most results were expected from our observations from single conductance sensitivity analyses (Table 2), but some results further confirmed the synergistic interactions between these two resonating conductances. For instance, in the case of h channel activation time constant (Fig. S10A), a threshold is known to exist on the time constant for sustenance of the resonance, where resonance is not sustained below a certain value for the activation time constant (Hutcheon & Yarom, 2000; Narayanan & Johnston, 2008). Here, we found that this threshold reduces when the T conductance was coexpressed with the h conductance, whereby, in the presence of the T conductance, resonance and phase lead were sustained for lower values of activation time constant of h channels (Fig. S10). Furthermore, given that the T conductance is a depolarization-activated resonating conductance, the co-presence of these two conductances enabled the model to sustain resonance at more depolarized membrane potentials where the presence of only the h conductance was insufficient to sustain resonance (Fig. S9C). Correspondingly, ΦL and Q also increased at more depolarized membrane potentials in the presence of the T conductance (Fig. S9D and E).
Figure 3. Coexpression of T and h conductances augmented several IRD-related measurements through synergistic interactions between the two channels.
A, voltage traces in response to chirp stimulus in the presence of h conductance alone (upper trace), and in the presence of both h and T conductances (lower trace). B and C, plots showing fR (B) and ΦL (C) as functions of maximal h conductance, for various values of maximal T conductance ( ). D and E, plots showing fR (D) and ΦL (E) as functions of half-maximal activation voltage of the T conductance, for various values of maximal T conductance (
). D and E, plots showing fR (D) and ΦL (E) as functions of half-maximal activation voltage of the T conductance, for various values of maximal T conductance ( ). F and G, plots showing fR (F) and ΦL (G) as functions of half-maximal inactivation voltage of the T conductance, for various values of
). F and G, plots showing fR (F) and ΦL (G) as functions of half-maximal inactivation voltage of the T conductance, for various values of 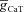 . H and I, plots showing fR (H) and ΦL (I) as functions of inactivation time constant of the T conductance, for various values of
. H and I, plots showing fR (H) and ΦL (I) as functions of inactivation time constant of the T conductance, for various values of 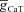 . The same maximal h conductance (
. The same maximal h conductance (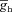 = 0.1 mS cm−2) was used for simulation results shown in D–I. Also see Figs S9–S13 and Table 4 for a complete analysis of the interactions of these two channels in determining neuronal IRD.
= 0.1 mS cm−2) was used for simulation results shown in D–I. Also see Figs S9–S13 and Table 4 for a complete analysis of the interactions of these two channels in determining neuronal IRD.
Table 4.
Sensitivity analysis for the IRD measurements corresponding to various active parameters related to T-type Ca2+ channel and h channel, when both channels were coexpressed in the model
| Coexpression of T and h channels | ||||||
|---|---|---|---|---|---|---|
| Effect of increase in | Tested range | Rin | fR | ΦL | Q | |Z|max |
| Rm (kΩ cm2) | 1–20 | Increases | Decreases | Increases | Increases | Increases |
| Cm (μF cm−2) | 0.5–2 | No effect | Decreases | Decreases | Decreases | Decreases |
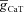 (mS cm−2) (mS cm−2) |
0–0.5 | Increases | Increases | Increases | Increases | Increases |
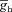 (mS cm−2) (mS cm−2) |
0–0.2 | Decreases | Increases | Increases | Increases | Decreases |
| V1/2 activation of T channel (mV) | −150 to 0 | Increases | Decreases | Decreases | Decreases | Increases |
| V1/2 inactivation of T channel (mV) | −100 to 0 | Increases | Decreases | Bell shaped | Bell shaped | Increases |
| V1/2 activation of h channel (mV) | −150 to 0 | Decreases | Bell shaped | Bell shaped | Bell shaped | Decreases |
| Activation time constant of T channel (ms) | 1–30 | No effect | Decreases | Decreases | Decreases | Decreases |
| Inactivation time constant of T channel (ms) | 1–100 | No effect | Decreases | Increases | Increases | Increases |
| Activation time constant of h channel (ms) | 5–500 | No effect | Decreases* | Decreases* | Decreases* | Increases |
| Ca2+ decay time constant (ms) | 5–100 | No effect | No effect | No effect | No effect | No effect |
To summarize, the two resonating conductances, h and T, synergistically interact with each other when they are expressed together, and augment resonance-related measurements by enhancing the dynamic range for sustaining resonance across various underlying parameters.
Coexpressing the A conductance with the resonating conductances was analogous to the presence of leak channels in modulating IRD
We next assessed the role of the restorative and inactivating A-type K+ conductance in modulating IRD measurements when coexpressed with the resonating h conductance. We found that increasing the magnitude of the A conductance led to an increase in fR while decreasing the Rin, ΦL, Q and |Z|max (Figs 4A–C, and S14A and B). This suggested that A-type K+ conductance acted analogous to a leak in determining IRD measurements of neuron (cf. effects of Rm on h conductance-mediated IRD measurements; Narayanan & Johnston, 2008; Zemankovics et al. 2010). We performed detailed sensitivity analyses with respect to various active parameters of the h and A conductances (Figs 4 and S14; Table 5). From these analyses, we found that the window current of the A current played a critical role in determining how IRD measurements mediated by the h conductance are modulated. Any parametric variation that enhanced the window current (e.g. depolarizing shift in inactivation voltage dependence) altered impedance-related measurements in a manner that was similar to increasing leak conductance.
Figure 4. Coexpressing the A conductance with the h conductance was analogous to the presence of leak channels in terms of modulating IRD measurements.
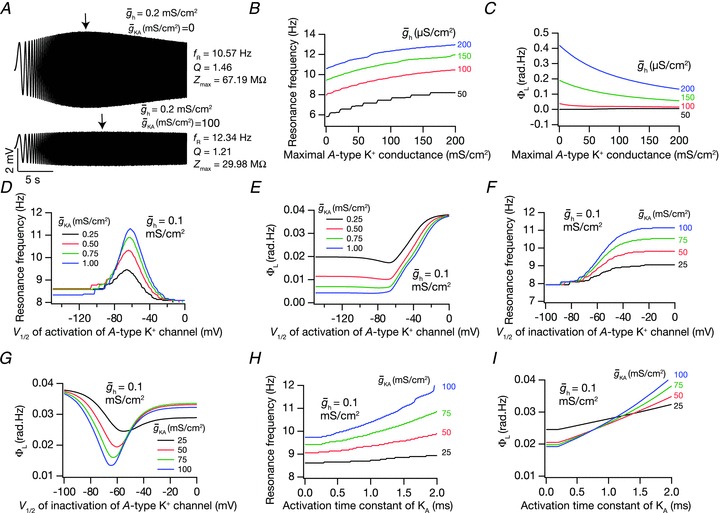
A, voltage traces in response to chirp stimulus in the presence of h conductance alone (upper trace), and in the presence of both h and A conductances (lower trace). B and C, plots showing fR (B) and ΦL (C) as functions of maximal A conductance (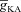 ), for various values of maximal h conductance (
), for various values of maximal h conductance (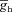 ). D and E, plots showing fR (D) and ΦL (E) as functions of half-maximal activation voltage of the A conductance, for various values of
). D and E, plots showing fR (D) and ΦL (E) as functions of half-maximal activation voltage of the A conductance, for various values of 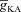 . F and G, plots showing fR (F) and ΦL (G) as functions of half-maximal inactivation voltage of the A conductance, for various values of
. F and G, plots showing fR (F) and ΦL (G) as functions of half-maximal inactivation voltage of the A conductance, for various values of 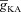 . H and I, plots showing fR (H) and ΦL (I) as functions of activation time constant of the A conductance, for various values of
. H and I, plots showing fR (H) and ΦL (I) as functions of activation time constant of the A conductance, for various values of 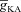 . The same maximal h conductance (
. The same maximal h conductance (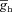 = 0.1 mS cm−2) was used for simulation results shown in D–I. Also see Fig. S14 and Table 5 for a complete analysis of the interactions of these two channels in determining neuronal IRD.
= 0.1 mS cm−2) was used for simulation results shown in D–I. Also see Fig. S14 and Table 5 for a complete analysis of the interactions of these two channels in determining neuronal IRD.
Table 5.
Sensitivity analysis for the IRD measurements corresponding to various active parameters related to A-type K+ channel and h channel, when both these channels were coexpressed in the model
| Coexpression of A and h channels | ||||||
|---|---|---|---|---|---|---|
| Effect of increase in | Tested range | Rin | fR | ΦL | Q | |Z|max |
| Rm (kΩ cm2) | 1–20 | Increases | Decreases | Increases | Increases | Increases |
| Cm (μF cm−2) | 0.5–2 | No effect | Decreases | Decreases | Decreases | Decreases |
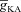 (mS cm−2) (mS cm−2) |
0–200 | Decreases | Increases | Decreases | Decreases | Decreases |
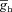 (mS cm−2) (mS cm−2) |
0–0.2 | Decreases | Increases | Increases | Increases | Decreases |
| V1/2 activation of A channel (mV) | −150 to 0 | Increases | Bell shaped | Increases | Increases | Increases |
| V1/2 inactivation of A channel (mV) | −100 to 0 | Decreases | Increases | Inverted Bell | Decreases | Decreases |
| V1/2 activation of h channel (mV) | −150 to 0 | Increases | Bell shaped | Increases | Decreases | Decreases |
| Activation time constant of A channel (ms) | 0.1–2 | No effect | Increases | Increases | Increases | No effect |
| Inactivation time constant of A channel (ms) | 1–200 | No effect | No effect | No effect | No effect | No effect |
| Activation time constant of h channel (ms) | 5–500 | No effect | Decreases* | Decreases* | Decreases* | Increases |
Similar analyses on interactions between the T and A conductances revealed, in most cases, that the A conductance modulated IRD measurements mediated by the T conductances in a manner analogous to its modulation of IRD measurements mediated by the h conductance (Figs 5A and B, and S15A and B; Table 6). Specifically, we found that parameters enhancing the window current magnitude of the A current altered impedance amplitude-related measurements in a manner that was similar to increasing leak conductance. However, in contrast to the interactions between A and h conductances (Fig. 4), we found that the presence of the A conductance did not significantly alter ΦL in spite of changing the phase response profile (Fig. 5E). This was to be expected, as the phase response profile mediated by the T conductance does not exhibit a significant inductive component (Fig. 2B).
Figure 5. Coexpressing the A conductance with the T conductance was analogous to the presence of leak channels in terms of modulating IRD measurements.
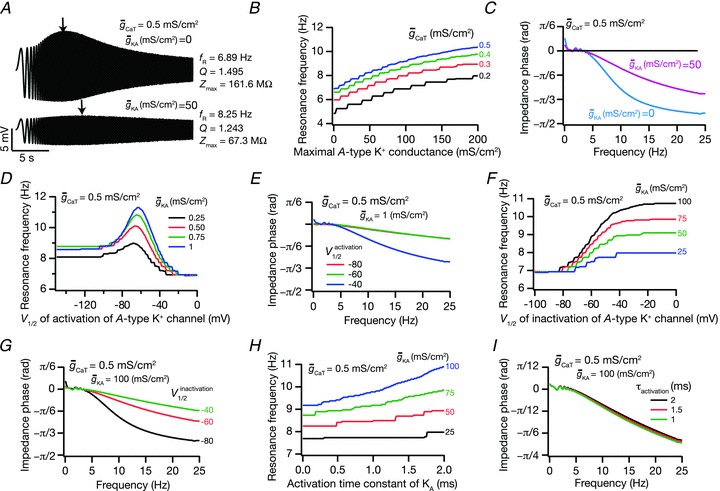
A, voltage traces in response to chirp stimulus in the presence of T conductance alone (upper trace), and in the presence of both T and A conductances (lower trace). B, plots showing fR as a function of maximal A conductance (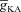 ), for various values of maximal T conductance (
), for various values of maximal T conductance (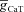 ). C, impedance phase profiles (ZPP), derived from traces in A, in the presence of T conductance alone (
). C, impedance phase profiles (ZPP), derived from traces in A, in the presence of T conductance alone (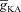 = 0), and in the presence of both T and A conductances (
= 0), and in the presence of both T and A conductances (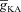 = 50 mS cm−2). D, plots showing fR as a function of half-maximal activation voltage of the A conductance, for various values of
= 50 mS cm−2). D, plots showing fR as a function of half-maximal activation voltage of the A conductance, for various values of 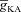 . E, ZPPs in the presence of both T and A conductances, for various values of the half-maximal activation voltage of the A conductance. F, plots showing fR as a function of half-maximal inactivation voltage of the A conductance, for various values of
. E, ZPPs in the presence of both T and A conductances, for various values of the half-maximal activation voltage of the A conductance. F, plots showing fR as a function of half-maximal inactivation voltage of the A conductance, for various values of 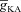 . G, ZPPs in the presence of both T and A conductances, for various values of the half-maximal inactivation voltage of the A conductance. H, plots showing fR as a function of the activation time constants of the A conductance, for various values of
. G, ZPPs in the presence of both T and A conductances, for various values of the half-maximal inactivation voltage of the A conductance. H, plots showing fR as a function of the activation time constants of the A conductance, for various values of 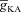 . I, ZPPs in the presence of both T and A conductances, for various values of the activation time constants of the A conductance. The same maximal T conductance (
. I, ZPPs in the presence of both T and A conductances, for various values of the activation time constants of the A conductance. The same maximal T conductance (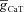 = 0.5 mS cm−2) was used for simulation results shown in D–I. Also see Fig. S15 and Table 6 for a complete analysis of the interactions of these two channels in determining neuronal IRD.
= 0.5 mS cm−2) was used for simulation results shown in D–I. Also see Fig. S15 and Table 6 for a complete analysis of the interactions of these two channels in determining neuronal IRD.
Table 6.
Sensitivity analysis for the IRD measurements corresponding to various active parameters related to T-type Ca2+ channel and A-type K+ channel, when both these channels were coexpressed in the model
| Coexpression of T and A channels | |||||
|---|---|---|---|---|---|
| Effect of increase in | Tested range | Rin | fR | Q | |Z|max |
| Rm (kΩ cm2) | 1–20 | Increases | Decreases | Increases | Increases |
| Cm (μF cm−2) | 0.5–2 | No effect | Decreases | Decreases | Decreases |
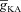 (mS cm−2) (mS cm−2) |
0–200 | Decreases | Increases | Decreases | Decreases |
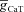 (mS cm−2) (mS cm−2) |
0–0.5 | Increases | Increases | Increases | Increases |
| V1/2 activation of A channel (mV) | −150 to 0 | Increases | Bell shaped | Increases | Increases |
| V1/2 inactivation of A channel (mV) | −100 to 0 | Decreases | Increases | Decreases | Decreases |
| V1/2 activation of T channel (mV) | −150 to 0 | Increases | Decreases | Decreases | Increases |
| V1/2 inactivation of T channel (mV) | −100 to 0 | Increases | Decreases | Bell shaped | Increases |
| Activation time constant of A channel (ms) | 0.1–2 | No effect | Increases | No effect | No effect |
| Inactivation time constant of A channel (ms) | 1–200 | No effect | No effect | No effect | No effect |
| Activation time constant of T channel (ms) | 1–30 | No effect | Decreases | Decreases | Decreases |
| Inactivation time constant of T channel (ms) | 1–100 | No effect | Decreases* | Increases* | Increases |
| Ca2+ decay time constant (ms) | 5–100 | No effect | No effect | No effect | No effect |
The model can sustain resonance only after crossing a certain threshold value of inactivation time constant of the T current. As the presence of T current did not elicit an inductive phase lead in the impedance phase profile, the sensitivity for ΦL is not presented here. Associated plots may be found in Figs 5 and S15.
To summarize, in terms of modulating Rin and various measurements related to impedance amplitude (fR, |Z|max and Q), the A conductance acted analogous to a leak conductance when coexpressed with any resonating conductance, and was dictated by its window magnitude. However, the phase response profile and related measurements were dependent on the specific resonating conductance and on the active and passive parameters in the underlying model.
Generation and validation of somatic and dendritic models for global sensitivity analysis
Thus far, we used single conductance sensitivity analyses and cross-channel interactions between pairs of ion channels to understand the modulation of IRD by the presence of three prominent subthreshold dendritic conductances expressed in CA1 pyramidal neuron dendrites. But, in reality, all these ion channels are expressed together in dendrites with variability in their parameters and expression levels (Magee & Johnston, 1995; Hoffman et al. 1997; Magee, 1998). How do various combinations of active properties of these channels and passive membrane parameters give rise to compartment-specific IRD profile? Are there constraints on these different parameters for compartments to have all IRD measurements to fall within experimentally observed ranges? Can compartments achieve experimentally observed IRD profiles through multiple means or is there only one way to have all measurements fall within experimental ranges?
To address these questions, we used the powerful global sensitivity analysis technique used in other systems for understanding other physiological properties (Foster et al. 1993; Goldman et al. 2001; Prinz et al. 2003, 2004; Achard & De Schutter, 2006; Tobin et al. 2006; Hobbs & Hooper, 2008; Weaver & Wearne, 2008; Taylor et al. 2009). To do this, we generated a population of 100,000 models with various combinations of active parameters of these three conductances in conjunction with passive membrane properties (a total of 17 parameters; see Methods, and Table 1). Then, we performed simulations on each of these models and computed the five subthreshold IRD measurements (Rin, fR, Q, |Z|max, and ΦL) for all of them. For all analyses below, we used these measurements and the underlying parameters from all the 100,000 models we generated.
As these measurements were obtained by randomly sampling the 17 parameters, the measurements from these 100,000 would not necessarily fall into their experimentally valid ranges. Therefore, we first classified these 100,000 models into two groups of ‘valid’ models: somatic and dendritic. This classification was arrived at by constraining all five IRD measurements from these model neurons with corresponding somatic or dendritic experimental measurements, which were obtained from the same cell bodies or dendrites, respectively (Fig. 6; also see Methods). Experimentally observed ranges employed as the basis for this classification are shown in Table 7. To arrive at these measurement bounds for valid models, we generated histograms for each experimental IRD measurement (Fig. 6A–J, upper rows), and set these bounds by ensuring that ∼80% of the central data points of each experimental measurement were covered within the bounds for that measurement (Taylor et al. 2009). Based on such analyses, independently for somatic and dendritic experimental measurements, and constraining the 100,000 models based on the bounds for each model measurement (Table 7), we obtained 662 valid somatic models (∼0.66% of the total model population) and 1006 valid dendritic models (∼1% of the total model population). In order to ensure the validity of the measurements corresponding to these somatic and dendritic valid models, we constructed histograms of IRD measurements corresponding to somatic and dendritic valid models (Fig. 6A–J, lower row), and found that these histograms were in the range of corresponding experimentally observed histograms (Fig. 6).
Figure 6. Distribution of IRD measurements associated with IRD in experiments and in valid model neurons.
A–E corresponds to somatic measurements, and F–J corresponds to dendritic measurements. A, histograms of experimentally determined somatic Rin (top) and Rin from valid somatic models (bottom). B, histograms of experimentally determined somatic fR (top) and fR from valid somatic models (bottom). C, histograms of experimentally determined somatic Q (top) and Q from valid somatic models (bottom). D, histograms of experimentally determined somatic ΦL (top) and ΦL from valid somatic models (bottom). E, histograms of experimentally determined somatic |Z|max (top) and |Z|max from valid somatic models (bottom). F–J, similar to A–E, but histograms correspond to dendritic measurements.
Table 7.
Bounds on measurements used to define somatic and dendritic valid model population
| For somatic valid models | For dendritic valid models | |||
|---|---|---|---|---|
| Measurement | Lower bound | Upper bound | Lower bound | Upper bound |
| Input resistance (MΩ) | 50 | 90 | 20 | 60 |
| Resonance frequency (Hz) | 2 | 5.5 | 4 | 8 |
| Resonance strength | 1.05 | 1.5 | 1.2 | 1.8 |
| Total inductive phase (rad Hz) | 0.005 | 0.15 | 0.1 | 0.6 |
| Maximum impedance amplitude (MΩ) | 70 | 110 | 40 | 70 |
The bounds were chosen such that ∼80% of experimental data points were included in the analysis (see Results).
Robustness of IRD measurements to individual variability in underlying parameters
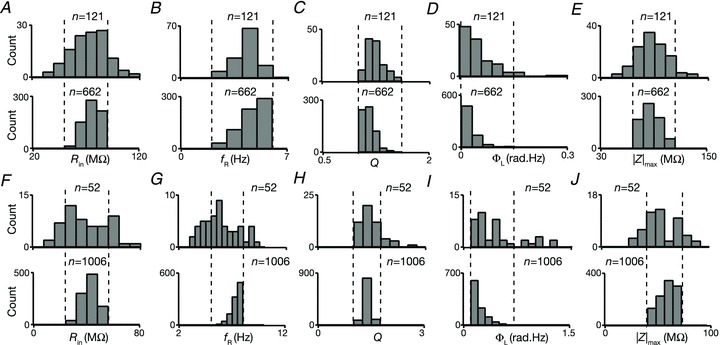
At the end of the above classification, we had all the 17 different parameters corresponding to all valid dendritic and somatic models whose measurements matched with experimental values. How do functionally similar model neurons compare with each other in this large parametric space? Are similar model neurons clustered together in parametric space, or are they distributed throughout? In other words, are the measurements severely constrained by cross-expression profiles or are they loosely coupled, with several parameters compensating for variability in one parameter? To answer these questions, we randomly picked six model neurons corresponding to somatic measurements with very narrow lower and upper bounds for the five IRD measurements and looked for variability in the underlying parameters of these models (Fig. 7). From analyses of the response traces, the impedance profiles and the IRD measurements from these six model neurons (Fig. 7A–D), it was evident that these neurons had very similar subthreshold IRD. However, the underlying model parameters that were the bases for these measurements were not clustered together, and exhibited large variability, almost spanning the entire range (Table 1) of the parametric space in most cases. This suggested that the IRD measurements were not constrained by changes in one parameter if other parameters were free to take any value in parametric space. Thus, from these results we concluded that changes in one or several parameter(s) could be compensated by changes in other parameters to produce similar subthreshold IRD measurements.
Figure 7. Six valid somatic model neurons with very similar IRD measurements illustrate robustness of measurements in spite of variability in underlying parameters.
A, voltage traces with corresponding values of fR, Q and |Z|max in response to chirp stimulus from six valid somatic model neurons. B and C, impedance amplitude (B) and phase (C) profiles for the six chosen model neurons, derived from traces in A. The values of ΦL for each of these traces may be noted. D, voltage traces in response to ±50 pA pulse current injections with corresponding values of Rin for the six model neurons. E, distribution of model parameters in the six chosen model neurons. Each coloured dot corresponds to parameters corresponding to the colour-matched model in A–D.
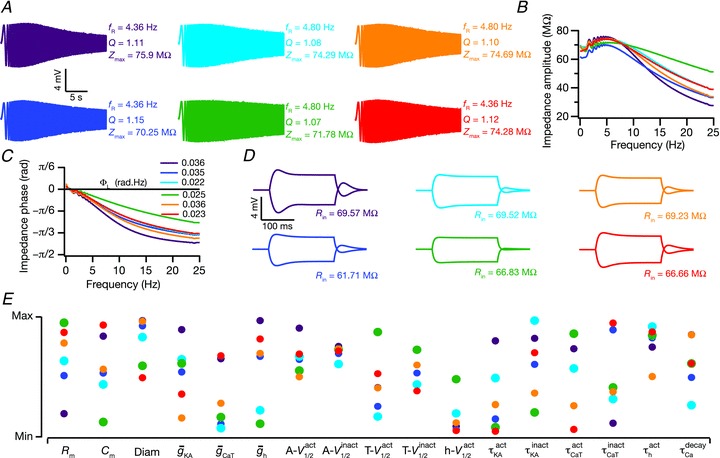
To further quantify these qualitative observations from these six handpicked models, and compare them with experimental measurements, we randomly picked five sets of 15 valid models each, and compared them with 15 randomly picked experimental values (Fig. 8). The rationale behind the choice of 15 models was from an experimental point of view, where the number of experiments performed is typically about 15 (Taylor et al. 2009). With such comparisons, we found that, in most cases, measurements derived from valid models and experimental observations were not significantly different from each other. This comparison was done several times, and five such comparisons are depicted in Fig. 8. From such analyses, it was evident that experimentally obtained IRD measurements were reproducible by our models, for both somatic and dendritic model populations (Fig. 8A and C). Similar to our earlier conclusions (Fig. 7), we found that these functionally similar models showed heavy variability in parametric space (Fig. 8), irrespective of whether they were sampled from the somatic or dendritic model populations. Specifically, each set of 15 random samples from valid population span almost the entire range of parametric space for most parameters (Fig. 8B and D), suggesting that various non-unique combinations of underlying parameters could lead to models with valid IRD measurements. Thus, the subthreshold IRD of model neurons was highly robust to individual variability in underlying parameters, suggesting that each model with a valid set of IRD measurements was maximally affected by a different set of underlying parameters.
Figure 8. Comparison of measurements related to IRD from various sets of 15 model neurons, chosen at random, with experimental data.
A, statistics (means ± SEM) of experimentally determined somatic measurements related to neuronal IRD of 15 neurons (first column) chosen at random. Other columns (labelled 1–5) correspond to the same IRD measurement statistics derived from 15 valid somatic model neurons, chosen at random, for each of the columns. B, distribution of parameters in each of the five sets of 15 model neurons employed in arriving at the statistics in A. Sets of 15 model neurons have been colour-matched with the statistics in A. C and D, same as A and B, but experimental data and model neurons correspond to dendritic measurements. Asterisks denote significant differences between experimental values and model values for that particular IRD measurement (P < 0.05; Mann–Whitney test).
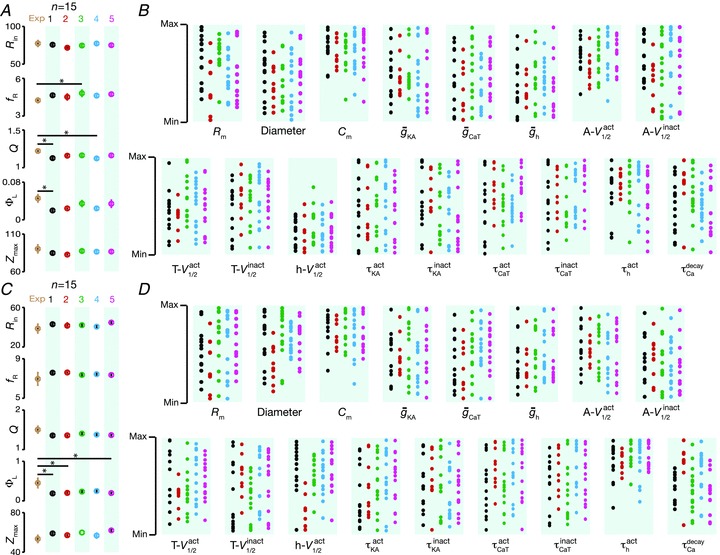
Weak pair-wise compensation among parameters for preserving validity of IRD measurements
The results above suggested that functionally similar model neurons could exhibit large parametric variability (Figs 7 and 8). To obtain a quantitative assessment of this parametric variability in valid model populations, we constructed histograms of all the parameters corresponding to somatic and dendritic valid model population (Fig. 9, bottom and top rows, respectively). From these histograms, we inferred that all parameters spanned almost the entire range chosen for the generation of these models (Table 1), and this was true for both somatic as well as dendritic valid model populations (Fig. 9). Whereas some of these parameters were distributed uniformly (e.g. Rm, 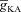 ,
, 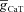 , etc.), others showed non-uniform distributions (e.g. activation time constant of Ih, Cm, inactivation time constant of ICaT) for somatic as well as dendritic valid model population. Furthermore, whereas the distributions were similar for most parameters (e.g. Cm, half-inactivation voltage of ICaT) across the dendritic and somatic valid models, some parameters (e.g. half-activation voltage of Ih, half-activation voltage of ICaT) showed significant differences in distribution across somatic and dendritic valid models (P < 0.05; Kolmogorov–Smirnov test).
, etc.), others showed non-uniform distributions (e.g. activation time constant of Ih, Cm, inactivation time constant of ICaT) for somatic as well as dendritic valid model population. Furthermore, whereas the distributions were similar for most parameters (e.g. Cm, half-inactivation voltage of ICaT) across the dendritic and somatic valid models, some parameters (e.g. half-activation voltage of Ih, half-activation voltage of ICaT) showed significant differences in distribution across somatic and dendritic valid models (P < 0.05; Kolmogorov–Smirnov test).
Figure 9. Weak pair-wise correlations between parameters in somatic and dendritic valid model populations.
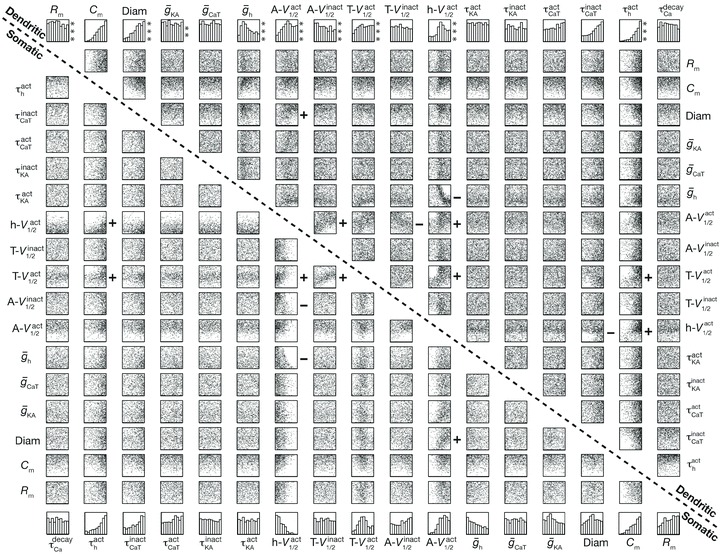
Lower-left triangle corresponds to the matrix depicting interactions among the 17 parameters for all somatic valid model population, and upper-right triangle corresponds to the same for dendritic valid model population. As both the matrices are symmetric, only the lower- (for somatic models) and upper-diagonals (for dendritic models) are shown. Bottom-most and top-most rows denote histograms of individual parameters in somatic and dendritic valid model populations, respectively. Asterisks accompanying histograms of individual parameters corresponding to dendritic valid models denote significant differences in their distribution relative to their counterpart for the somatic valid models (P < 0.05; Kolmogorov–Smirnov test). Each subpanel plots the values of the two chosen parameters (labels above/below and right/left) for all the valid somatic (below-left labels) and all valid dendritic models (above-right labels) as a scatter plot. It may be noted that the labels span the entire parametric space of 17 parameters for both dendritic and somatic models. Correlation coefficients were computed for each of the scatter plots; a ‘+’ to the right of the scatter plot denotes positive correlation with values greater than 0.3 and a ‘–’ to the right denotes negative correlation with values less than –0.3.
The power of global sensitivity analysis is its ability to tease apart the presence of strong correlations between underlying parameters when a certain set of measurements have to be constrained by experimental observations. Such analyses enable understanding of experimentally observed relationships in expression profiles in terms of how they regulate homeostasis in the experimental system under consideration (MacLean et al. 2005; Schulz et al. 2006, 2007; Taylor et al. 2009; Marder & Taylor, 2011; Amendola et al. 2012). To understand such correlations in underlying parameters of our model, with reference to the constraints on subthreshold IRD measurements, we analysed correlations among the parameters for somatic as well as dendritic valid model populations. Such analysis also allowed to test if, in achieving experimental constraints on model measurements, the effect of changes in one parameter was compensated by changes in any other single parameter or if several other parameters collectively compensated for the effect of changes in one parameter. Specifically, if the effect of change in one parameter was specifically compensated by a single other parameter, correlations among such coupled parameters would be strong when pair-wise correlations of these two parameters from all valid models were analysed. If, on the other hand, the effect of changes in one parameter were to be compensated by several parameters, then all parameters would exhibit weak pair-wise correlations among them (Taylor et al. 2009).
When we performed such pair-wise correlation analyses across all 17 parameters, separately for somatic and dendritic valid models, we found that the correlation coefficients for all pairs of parameters were generally low, irrespective of whether the chosen model population was somatic or dendritic. Specifically, 129 of the tested 136 pairs (upper or lower diagonal elements of the symmetric correlation matrix for 17 parameters) for somatic valid model population exhibited low correlation coefficients between −0.2 and +0.2, and only seven pairs had the absolute correlation coefficient values greater than 0.3. The strongest correlation for somatic valid model population still corresponded to a weak correlation, and was found to be 0.43 (R2= 0.185; Pearson's correlation), between V1/2 activation of ICaT and V1/2 activation of Ih. Similar weak correlations were obtained when similar analysis was repeated with the dendritic valid model population. Specifically, 127 of the 136 pairs for dendritic valid model population exhibited correlation coefficient values between −0.2 and +0.2, and only nine pairs had their absolute correlation coefficient values greater than 0.3. The strongest correlation for dendritic valid model population still corresponded to a weak correlation, and was again found between V1/2 activation of ICaT and V1/2 activation of Ih with a value of 0.4448 (R2= 0.197; Pearson's correlation). Together, these weak correlations suggested that the effect of changes in one parameter was compensated by collective changes in several other parameters, implying that a neuron can have distinct means to arrive at the same IRD measurements. In other words, the constraints imposed on the IRD measurements of the neurons in our model populations were insufficient to induce strong pair-wise correlations among the parameters that underlie these models (cf. conclusions in Taylor et al. 2009 for a different model system with different parameters).
Discussion
In this study, we analysed the roles of the three prominent subthreshold dendritic conductances (h, A and T), individually and in various combinations, in regulating several physiological measurements related to the IRD of hippocampal pyramidal neurons. The most intriguing result with the independent expression of the hippocampal T conductance was the absence of the inductive phase lead (Fig. 2), a prominent characteristic of the independent expression of the h conductance that led to the postulate of its involvement in phase coding (Narayanan & Johnston, 2008; Wang, 2010). Performing similar analyses with the A conductance, a restorative inactivating conductance, demonstrated that the A conductance acted in a manner similar to a leak conductance, either independently or in conjunction with the T or h conductances. Thus, two subthreshold inactivating conductances with very similar activation–inactivation kinetics behave very differently in terms of modulating IRD only based upon whether they are restorative or regenerative. We then analysed the behaviour of models when these conductances were coexpressed, and remarkably found augmentation of IRD measurements under such a scenario. Finally, when we subjected the model to the powerful global sensitivity analysis, the robustness of IRD measurements to widespread variability in underlying parameters was made distinctly evident (Figs 6–9), while also revealing weak pair-wise correlations among parameters of valid models (Fig. 9). In the sections that follow, we analyse the implications of our results to hippocampal neuronal physiology in the context of oscillatory inputs and dendritic integration.
Inactivating conductances and phase coding
The role of VGICs in regulating the phase of incoming oscillatory inputs is well established (Gutfreund et al. 1995; Narayanan & Johnston, 2008; Marcelin et al. 2009), and has been postulated to play a critical role in phase and temporal coding (Narayanan & Johnston, 2008; Wang, 2010). Specifically, such regulation of phase, especially in theta frequencies, could control the timing of action potential generation, as changes in subthreshold integration translate to changes in spike timing as well. These timing differences, in turn, form an important determinant of neuronal function, also acting as a behavioural correlate under many scenarios, especially with reference to oscillatory phase of the local field potential and/or intracellular oscillations (O’Keefe & Recce, 1993; Kamondi et al. 1998; Buzsaki, 2002, 2006; Mehta et al. 2002; Hasselmo, 2005; Lengyel et al. 2005; Lisman, 2005; O’Keefe & Burgess, 2005; Siapas et al. 2005; Fries et al. 2007; Huxter et al. 2008; Itskov et al. 2008; Harvey et al. 2009; van der Meer & Redish, 2011).
Our study elucidates the roles of restorative (A) and regenerative (T) inactivating subthreshold conductances, when expressed independently and in combinations among themselves and the h conductance, in altering the intrinsic response phase of neurons to oscillatory stimuli of various inputs (Figs 2–5). In this context, the most surprising result from our study was the absence of the inductive phase lead in the presence of the T channels, a resonating conductance, which is in striking contrast to the intrinsic phase response in the presence of h channels in hippocampal pyramidal neurons (Narayanan & Johnston, 2008). Demonstrating that this phenomenon is model-invariant using a Markovian kinetic model for the T conductance, we also traced the origins of the absence of such phase lead to the activation gate of the T conductance, and the fact that the T conductance is an amplifying conductance (Fig. 2). In contrast, the restorative A conductance altered the intrinsic phase response in a manner very similar to how leak conductances behave, irrespective of whether they were expressed independently or along with other resonating conductances. These results suggest that, unlike simple linear electric circuits, resonance in the impedance amplitude profile does not have to necessarily imply an inductive lead in the intrinsic phase response, but rather depends on the specific kinetics of the resonating conductance involved. Furthermore, given that these three subthreshold conductances alter the phase of the incoming signal differentially, future studies could focus on how these conductances could be involved in phase and temporal coding in the hippocampus and other regions of the brain, and how such codes translate to relevant behavioural correlates.
Neuronal plasticity and phase response dynamics
Synaptic plasticity has been demonstrated to be dependent on the timing of spikes with respect to the incoming stimuli, both in terms of the arrival time of the postsynaptic potential (Bi & Poo, 1998; Egger et al. 1999; Abbott & Nelson, 2000; Feldman, 2000; Sjostrom et al. 2001; Froemke & Dan, 2002; Caporale & Dan, 2008) and in terms of the phase at which spikes occur when spikes ride on an underlying oscillatory pattern (Huerta & Lisman, 1993, 1995, 1996). Several previous studies and our study clearly demonstrate the role of subthreshold VGICs in altering the phase of incoming stimuli, thus suggesting their roles in altering spike timing. Furthermore, as these subthreshold channels can either mediate (T) or modulate (A and h) cytosolic calcium influx (Hoffman et al. 1997; Frick et al. 2004; Tsay et al. 2007), a critical determinant of various forms of neural plasticity (Lisman, 1989, 2001; Frick et al. 2004; Fan et al. 2005; Lujan et al. 2009; Narayanan et al. 2010; Narayanan & Johnston, 2010), it stands to reason that the ability of these channels in modulating phase response dynamics (Figs 2–6) would translate to their ability in inducing metaplasticity in various forms of plasticity expressed in these neurons. Against this background, our study postulates a critical role of subthreshold ion channels in altering plasticity rules or in retaining ‘plasticity homeostasis’, through their ability to modulate phase response dynamics, in neurons where synchronous synaptically induced oscillations are present during behavioural states associated with learning (Sjostrom et al. 2008; Wang, 2010; Fell & Axmacher, 2011). Similar analyses with reference to the dependence of plasticity on spike timing or spike phase could also be extended to other forms of plasticity, such as those in VGICs, given that several forms of synaptic plasticity are accompanied by plasticity in VGICs (Johnston & Narayanan, 2008; Shah et al. 2010).
Augmentation of IRD measurements by coexpression of subthreshold ion channels
Our results suggest that the coexpression of subthreshold ion channels augment the range of parameters over which resonance and inductive phase lead can be sustained by model neurons. For instance, although the T channel cannot sustain inductive phase lead on its own, it increases the total inductive phase (a measure of both the magnitude of phase lead and the range over which phase lead is sustained) when coexpressed with the h conductance (Fig. 3C). As all three channels employed in this study have well-defined physiologically measured gradients associated with them, it is important to analyse the implications of such coexpression on neuronal measurements. In this context, the ability of a model neuron to sustain resonance at more depolarized voltages when the T and h conductances are coexpressed might explain the experimental observation that fR is higher at depolarized voltages in distal dendrites in comparison to the soma (Narayanan & Johnston, 2007), despite a hyperpolarizing shift in the half-maximal activation voltage of the h conductance in the dendrites (Magee, 1998). Although a hyperpolarized half-maximal activation voltage would reduce fR and ΦL at depolarized voltages (Narayanan & Johnston, 2007, 2008), experimental observations to the contrary hint at the postulate that this ability to resonate at depolarized voltages is mediated by the increased T conductance in the dendrites (Magee & Johnston, 1995). Furthermore, taking experimental observations on conductance properties and IRD measurements together, we note that the hyperpolarized shift in the V1/2 activation of the A conductance in distal dendrites of CA1 pyramidal neurons (Hoffman et al. 1997) coupled with increased conductances of the h, A and T conductances in distal dendrites should drive distal dendrites towards higher resonance frequency (Narayanan & Johnston, 2007; Hu et al. 2009; Marcelin et al. 2009). Thus, gradients and plasticity in channel densities and other properties at different dendrite locations could be constrained by the necessity to establish a well-defined IRD at these different locations to tune to the input patterns (Narayanan & Johnston, 2007; O’Donnell & Nolan, 2011; Magee, 2012). Future studies could focus on the roles of these channels and their coexpressions in encoding specific features associated with inputs, and the interactions among these ion channels across space in defining the response dynamics across the dendritic topograph (Rathour & Narayanan, 2012).
Global sensitivity analysis, correlations and IRD homeostasis
Sensitivity analysis by assessing physiological measurements against one of the underlying parameters while letting other parameters to be constant constitutes a very narrow treatise of the sensitivity of the system to its underlying parameters. This is especially true in cellular neurophysiological measurements because of the presence of non-linearities in VGIC properties that mediate them, and more importantly of the heavy interdependence of the underlying parameters. For instance, if a given VGIC conductance density was varied, it would alter the membrane voltage response to a given stimulus depending on the properties of the VGIC; this change in membrane voltage, in turn, would modulate the conductance properties of other VGICs present in the compartment, and the cycle would continue until a steady state is achieved. Thus, the measurement changes observed as a consequence of alterations to the VGIC conductance density are not just a consequence of that alone, but a result of all the changes that were initiated by that alteration.
In the context of subthreshold IRD measurements that we have considered, this cross-dependence on underlying parameters is starkly discernible. As an example, consider the case of experimentally blocking h channels and assessing the role of T channels in altering IRD measurements. Given the massive contribution of h channels to baseline conductance and resting membrane potential, this block in h channels increases input resistance, hyperpolarizes membrane potentials and increases membrane time constant of hippocampal pyramidal neurons (Magee, 1998; Fan et al. 2005; Narayanan & Johnston, 2007). In such an experimental setup, the absence of resonance in the absence of h channels cannot be construed as the inability of T channels in sustaining resonance, because resonance is dependent upon background conductance levels and on the membrane time constant, both of which have been altered by the h channel block (Hutcheon et al. 1996; Hutcheon & Yarom, 2000; Narayanan & Johnston, 2008). It is possible that T channels might sustain resonance under the normal, high background conductance state, where membrane time constants are lower, when h channels (or equivalent non-resonating leak channels) were not blocked. Thus, such differential contributions of various channels to IRD measurements would not be apparent by such one-parameter-at-a-time approach. Similar arguments would also hold for approaches that knock out specific genes that encode these ion channels and for approaches that use computational single sensitivity analyses (Taylor et al. 2009; Marder & Taylor, 2011).
To circumvent these problems, the global sensitivity analysis technique has been used by multiple studies to understand the differential contributions of various parameters to specific physiological measurements (for a recent review, see Marder & Taylor, 2011). We employed these techniques to understand the dependence of IRD measurements on various passive and active model parameters, and found that measurements that were experimentally valid could be achieved through multiple non-unique parametric combinations (Figs 7 and 8). We noted that there are variabilities in experimentally obtained IRD measurements (Fig. 6), and these measurement ranges were not restrictive enough to constrain underlying parameters to fall into specific clusters or to have strong pair-wise correlations among themselves (Fig. 9). Thus, our study suggests that the IRD of a neuron can be robust to large variabilities in underlying parameters, and the presence of subthreshold inactivating channels provides more non-unique ways to achieve such IRD homeostasis through augmentation of measurements when they are coexpressed (Figs 3–5). These conclusions have considerable implications to homeostasis of neuronal response properties, not just to steady state current injections, but also to time-varying and oscillatory inputs that they receive under in vivo conditions.
IRD homeostasis and VGIC plasticity
Plasticity in active membrane conductances has been implicated in maintaining firing rate homeostasis during altered neuronal/network dynamics (Johnston & Narayanan, 2008; Nelson & Turrigiano, 2008; Turrigiano, 2011). Our analyses suggest that such maintenance of homeostasis could be extended beyond firing rate homeostasis to maintaining homeostasis in IRD to time-varying inputs through plasticity in VGIC properties. Furthermore, as IRD homeostasis can be achieved through multiple non-unique means, a large class of biochemical pathways that modulate these channels could be recruited towards altering their properties, and maintaining IRD homeostasis in that process (Catterall, 2000; Sjostrom et al. 2008; Vacher et al. 2008; Shah et al. 2010), thus increasing the repertoire of mechanisms available to the neuron towards maintaining homeostasis.
Finally, in this study, as our focus was on subthreshold inactivating channels and their interactions with the h channel, we had focused only on the two channels: the A and the T channels, and their roles in regulating IRD to theta-frequency inputs. Our study suggests that the presence of these inactivating channels can enhance robustness in IRD measurements by providing several non-unique means to achieve the same response dynamics. Future studies could analyse interactions between other conductances that include the inward-rectifying and calcium-activated potassium channels, the persistent sodium channel, and their interactions with these and a range of suprathreshold conductances in regulating IRD measurements at other frequency ranges as well (Crawford & Fettiplace, 1981; Art & Fettiplace, 1987; Hutcheon et al. 1996; Kavalali et al. 1997; Hu et al. 2002, 2009; Wolfart & Roeper, 2002; Gu et al. 2005; Vervaeke et al. 2006; Higgs & Spain, 2009; Adelman et al. 2012). Inclusion of these channels and other IRD-related measurements would provide a broader analysis for how neurons and their dendrites could maintain their response properties across different frequency and voltage ranges, possibly through several non-unique combinations of parameters associated with these channels. Activity-dependent and activity-independent forms of plasticity in these VGICs could then be explored as the source of all associated parametric variability, executed with a goal of retaining IRD homeostasis across the dendritic topograph.
In summary, in this study, we explored the role of inactivating VGICs in regulating subthreshold IRD of a hippocampal pyramidal neuron. Emphasizing the necessity of a computational approach to this study, we demonstrated that neurons could robustly maintain their IRD measurements in spite of heavy variabilities across parameters that underlie these measurements. These results hold significant ramifications for how VGICs contribute to temporal as well as phase coding when they receive oscillatory inputs, and for how homeostasis in IRD could be maintained through plasticity in ion channel properties. They also clearly establish that computational and experimental approaches that employ a simplistic one-parameter-a-time analysis technique would fail in understanding subthreshold IRD, as the dependence of IRD measurements on underlying parameters is complex and non-linear, especially with heavy interdependencies on how changes in one parameter affect the impact of other parameters on the measurements.
Acknowledgments
The authors thank Dr Daniel Johnston and members of the cellular neurophysiology laboratory for helpful discussions and for critical comments on a draft of this manuscript. This work was supported by a career development award to R.N. by the International Human Frontier Science Program Organization, and by the Indian Institute of Science.
Glossary
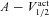
half-maximal activation voltage of the A conductance
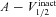
half-maximal inactivation voltage of the A conductance
- Cm
specific membrane capacitance
- Diam
diameter
- fR
resonance frequency
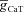
maximal T-type Ca2+ conductance
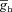
maximal h conductance
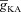
maximal A-type K+ conductance
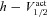
half-maximal activation voltage of the h conductance
- HH
Hodgkin–Huxley
- ICaT
T-type Ca2+ current
- Ih
hyperpolarization-activated cation-non-specific h current
- IKA
A-type K+ current
- IRD
intrinsic response dynamics
- Q
resonance strength
- Rin
input resistance
- Rm
specific membrane resistivity
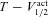
half-maximal activation voltage of the T conductance
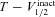
half-maximal inactivation voltage of the T conductance
- VGICs
voltage-gated ion channels
- |Z|max
maximum impedance amplitude
- ΦL
total inductive phase
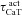
activation time constant of the T conductance
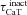
inactivation time constant of the T conductance
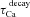
calcium decay time constant
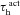
activation time constant of the h conductance
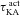
activation time constant of the A conductance
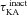
inactivation time constant of the A conductance
Author contributions
R.K.R. and R.N. conceived and designed the experiments; R.K.R. and R.N. performed simulations and their analyses, including interpretation of results; R.K.R. drafted the article; R.K.R. and R.N. revised it critically for important intellectual content; R.K.R. and R.N. approve the version to be published.
Supplementary material
Supplementary Figure S1
Supplementary Figure S2
Supplementary Figure S3
Supplementary Figure S4
Supplementary Figure S5
Supplementary Figure S6
Supplementary Figure S7
Supplementary Figure S8
Supplementary Figure S9
Supplementary Figure S10
Supplementary Figure S11
Supplementary Figure S12
Supplementary Figure S13
Supplementary Figure S14
Supplementary Figure S15
References
- Abbott LF, Nelson SB. Synaptic plasticity: taming the beast. Nat Neurosci. 2000;3(Suppl):1178–1183. doi: 10.1038/81453. [DOI] [PubMed] [Google Scholar]
- Achard P, De Schutter E. Complex parameter landscape for a complex neuron model. PLoS Comput Biol. 2006;2:e94. doi: 10.1371/journal.pcbi.0020094. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Adelman JP, Maylie J, Sah P. Small-conductance Ca2+-activated K+ channels: form and function. Annu Rev Physiol. 2012;74:245–269. doi: 10.1146/annurev-physiol-020911-153336. [DOI] [PubMed] [Google Scholar]
- Amarillo Y, De Santiago-Castillo JA, Dougherty K, Maffie J, Kwon E, Covarrubias M, Rudy B. Ternary Kv4.2 channels recapitulate voltage-dependent inactivation kinetics of A-type K+ channels in cerebellar granule neurons. J Physiol. 2008;586:2093–2106. doi: 10.1113/jphysiol.2007.150540. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Amendola J, Woodhouse A, Martin-Eauclaire MF, Goaillard JM. Ca(2)/cAMP-sensitive covariation of I(A) and I(H) voltage dependences tunes rebound firing in dopaminergic neurons. J Neurosci. 2012;32:2166–2181. doi: 10.1523/JNEUROSCI.5297-11.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Art JJ, Fettiplace R. Variation of membrane properties in hair cells isolated from the turtle cochlea. J Physiol. 1987;385:207–242. doi: 10.1113/jphysiol.1987.sp016492. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bi GQ, Poo MM. Synaptic modifications in cultured hippocampal neurons: dependence on spike timing, synaptic strength, and postsynaptic cell type. J Neurosci. 1998;18:10464–10472. doi: 10.1523/JNEUROSCI.18-24-10464.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bourdeau ML, Morin F, Laurent CE, Azzi M, Lacaille JC. Kv4.3-mediated A-type K+ currents underlie rhythmic activity in hippocampal interneurons. J Neurosci. 2007;27:1942–1953. doi: 10.1523/JNEUROSCI.3208-06.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buzsaki G. Theta oscillations in the hippocampus. Neuron. 2002;33:325–340. doi: 10.1016/s0896-6273(02)00586-x. [DOI] [PubMed] [Google Scholar]
- Buzsaki G. Rhythms of the Brain. New York: Oxford University Press; 2006. [Google Scholar]
- Caporale N, Dan Y. Spike timing-dependent plasticity: a Hebbian learning rule. Annu Rev Neurosci. 2008;31:25–46. doi: 10.1146/annurev.neuro.31.060407.125639. [DOI] [PubMed] [Google Scholar]
- Carnevale NT, Hines ML. The NEURON Book. Cambridge, UK: Cambridge University Press; 2006. [Google Scholar]
- Catterall WA. Structure and regulation of voltage-gated Ca2+ channels. Annu Rev Cell Dev Biol. 2000;16:521–555. doi: 10.1146/annurev.cellbio.16.1.521. [DOI] [PubMed] [Google Scholar]
- Crawford AC, Fettiplace R. An electrical tuning mechanism in turtle cochlear hair cells. J Physiol. 1981;312:377–412. doi: 10.1113/jphysiol.1981.sp013634. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Egger V, Feldmeyer D, Sakmann B. Coincidence detection and changes of synaptic efficacy in spiny stellate neurons in rat barrel cortex. Nat Neurosci. 1999;2:1098–1105. doi: 10.1038/16026. [DOI] [PubMed] [Google Scholar]
- Engel AK, Fries P, Singer W. Dynamic predictions: oscillations and synchrony in top-down processing. Nat Rev Neurosci. 2001;2:704–716. doi: 10.1038/35094565. [DOI] [PubMed] [Google Scholar]
- Fan Y, Fricker D, Brager DH, Chen X, Lu HC, Chitwood RA, Johnston D. Activity-dependent decrease of excitability in rat hippocampal neurons through increases in I(h) Nat Neurosci. 2005;8:1542–1551. doi: 10.1038/nn1568. [DOI] [PubMed] [Google Scholar]
- Feldman DE. Timing-based LTP and LTD at vertical inputs to layer II/III pyramidal cells in rat barrel cortex. Neuron. 2000;27:45–56. doi: 10.1016/s0896-6273(00)00008-8. [DOI] [PubMed] [Google Scholar]
- Fell J, Axmacher N. The role of phase synchronization in memory processes. Nat Rev Neurosci. 2011;12:105–118. doi: 10.1038/nrn2979. [DOI] [PubMed] [Google Scholar]
- Foster WR, Ungar LH, Schwaber JS. Significance of conductances in Hodgkin-Huxley models. J Neurophysiol. 1993;70:2502–2518. doi: 10.1152/jn.1993.70.6.2502. [DOI] [PubMed] [Google Scholar]
- Fransen E, Alonso AA, Dickson CT, Magistretti J, Hasselmo ME. Ionic mechanisms in the generation of subthreshold oscillations and action potential clustering in entorhinal layer II stellate neurons. Hippocampus. 2004;14:368–384. doi: 10.1002/hipo.10198. [DOI] [PubMed] [Google Scholar]
- Fransen E, Tahvildari B, Egorov AV, Hasselmo ME, Alonso AA. Mechanism of graded persistent cellular activity of entorhinal cortex layer v neurons. Neuron. 2006;49:735–746. doi: 10.1016/j.neuron.2006.01.036. [DOI] [PubMed] [Google Scholar]
- Frick A, Magee J, Johnston D. LTP is accompanied by an enhanced local excitability of pyramidal neuron dendrites. Nat Neurosci. 2004;7:126–135. doi: 10.1038/nn1178. [DOI] [PubMed] [Google Scholar]
- Fries P, Nikolic D, Singer W. The gamma cycle. Trends Neurosci. 2007;30:309–316. doi: 10.1016/j.tins.2007.05.005. [DOI] [PubMed] [Google Scholar]
- Froemke RC, Dan Y. Spike-timing-dependent synaptic modification induced by natural spike trains. Nature. 2002;416:433–438. doi: 10.1038/416433a. [DOI] [PubMed] [Google Scholar]
- Gasparini S, Migliore M, Magee JC. On the initiation and propagation of dendritic spikes in CA1 pyramidal neurons. J Neurosci. 2004;24:11046–11056. doi: 10.1523/JNEUROSCI.2520-04.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- George MS, Abbott LF, Siegelbaum SA. HCN hyperpolarization-activated cation channels inhibit EPSPs by interactions with M-type K(+) channels. Nat Neurosci. 2009;12:577–584. doi: 10.1038/nn.2307. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Golding NL, Staff NP, Spruston N. Dendritic spikes as a mechanism for cooperative long-term potentiation. Nature. 2002;418:326–331. doi: 10.1038/nature00854. [DOI] [PubMed] [Google Scholar]
- Goldman DE. Potential, impedance, and rectification in membranes. J Gen Physiol. 1943;27:37–60. doi: 10.1085/jgp.27.1.37. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goldman MS, Golowasch J, Marder E, Abbott LF. Global structure, robustness, and modulation of neuronal models. J Neurosci. 2001;21:5229–5238. doi: 10.1523/JNEUROSCI.21-14-05229.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gu N, Vervaeke K, Hu H, Storm JF. Kv7/KCNQ/M and HCN/h, but not KCa2/SK channels, contribute to the somatic medium after-hyperpolarization and excitability control in CA1 hippocampal pyramidal cells. J Physiol. 2005;566:689–715. doi: 10.1113/jphysiol.2005.086835. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gutfreund Y, Yarom Y, Segev I. Subthreshold oscillations and resonant frequency in guinea-pig cortical neurons: physiology and modelling. J Physiol. 1995;483(Pt 3):621–640. doi: 10.1113/jphysiol.1995.sp020611. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harvey CD, Collman F, Dombeck DA, Tank DW. Intracellular dynamics of hippocampal place cells during virtual navigation. Nature. 2009;461:941–946. doi: 10.1038/nature08499. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hasselmo ME. What is the function of hippocampal theta rhythm?– Linking behavioral data to phasic properties of field potential and unit recording data. Hippocampus. 2005;15:936–949. doi: 10.1002/hipo.20116. [DOI] [PubMed] [Google Scholar]
- Higgs MH, Spain WJ. Conditional bursting enhances resonant firing in neocortical layer 2–3 pyramidal neurons. J Neurosci. 2009;29:1285–1299. doi: 10.1523/JNEUROSCI.3728-08.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hobbs KH, Hooper SL. Using complicated, wide dynamic range driving to develop models of single neurons in single recording sessions. J Neurophysiol. 2008;99:1871–1883. doi: 10.1152/jn.00032.2008. [DOI] [PubMed] [Google Scholar]
- Hodgkin AL, Katz B. The effect of sodium ions on the electrical activity of giant axon of the squid. J Physiol. 1949;108:37–77. doi: 10.1113/jphysiol.1949.sp004310. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoffman DA, Magee JC, Colbert CM, Johnston D. K+ channel regulation of signal propagation in dendrites of hippocampal pyramidal neurons. Nature. 1997;387:869–875. doi: 10.1038/43119. [DOI] [PubMed] [Google Scholar]
- Hu H, Vervaeke K, Graham LJ, Storm JF. Complementary theta resonance filtering by two spatially segregated mechanisms in CA1 hippocampal pyramidal neurons. J Neurosci. 2009;29:14472–14483. doi: 10.1523/JNEUROSCI.0187-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hu H, Vervaeke K, Storm JF. Two forms of electrical resonance at theta frequencies, generated by M-current, h-current and persistent Na+ current in rat hippocampal pyramidal cells. J Physiol. 2002;545:783–805. doi: 10.1113/jphysiol.2002.029249. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huerta PT, Lisman JE. Heightened synaptic plasticity of hippocampal CA1 neurons during a cholinergically induced rhythmic state. Nature. 1993;364:723–725. doi: 10.1038/364723a0. [DOI] [PubMed] [Google Scholar]
- Huerta PT, Lisman JE. Bidirectional synaptic plasticity induced by a single burst during cholinergic theta oscillation in CA1 in vitro. Neuron. 1995;15:1053–1063. doi: 10.1016/0896-6273(95)90094-2. [DOI] [PubMed] [Google Scholar]
- Huerta PT, Lisman JE. Low-frequency stimulation at the troughs of theta-oscillation induces long-term depression of previously potentiated CA1 synapses. J Neurophysiol. 1996;75:877–884. doi: 10.1152/jn.1996.75.2.877. [DOI] [PubMed] [Google Scholar]
- Hutcheon B, Miura RM, Puil E. Models of subthreshold membrane resonance in neocortical neurons. J Neurophysiol. 1996;76:698–714. doi: 10.1152/jn.1996.76.2.698. [DOI] [PubMed] [Google Scholar]
- Hutcheon B, Miura RM, Yarom Y, Puil E. Low-threshold calcium current and resonance in thalamic neurons: a model of frequency preference. J Neurophysiol. 1994;71:583–594. doi: 10.1152/jn.1994.71.2.583. [DOI] [PubMed] [Google Scholar]
- Hutcheon B, Yarom Y. Resonance, oscillation and the intrinsic frequency preferences of neurons. Trends Neurosci. 2000;23:216–222. doi: 10.1016/s0166-2236(00)01547-2. [DOI] [PubMed] [Google Scholar]
- Huxter JR, Senior TJ, Allen K, Csicsvari J. Theta phase-specific codes for two-dimensional position, trajectory and heading in the hippocampus. Nat Neurosci. 2008;11:587–594. doi: 10.1038/nn.2106. [DOI] [PubMed] [Google Scholar]
- Itskov V, Pastalkova E, Mizuseki K, Buzsaki G, Harris KD. Theta-mediated dynamics of spatial information in hippocampus. J Neurosci. 2008;28:5959–5964. doi: 10.1523/JNEUROSCI.5262-07.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnston D, Narayanan R. Active dendrites: colorful wings of the mysterious butterflies. Trends Neurosci. 2008;31:309–316. doi: 10.1016/j.tins.2008.03.004. [DOI] [PubMed] [Google Scholar]
- Kamondi A, Acsady L, Wang XJ, Buzsaki G. Theta oscillations in somata and dendrites of hippocampal pyramidal cells in vivo: activity-dependent phase-precession of action potentials. Hippocampus. 1998;8:244–261. doi: 10.1002/(SICI)1098-1063(1998)8:3<244::AID-HIPO7>3.0.CO;2-J. [DOI] [PubMed] [Google Scholar]
- Kavalali ET, Zhuo M, Bito H, Tsien RW. Dendritic Ca2+ channels characterized by recordings from isolated hippocampal dendritic segments. Neuron. 1997;18:651–663. doi: 10.1016/s0896-6273(00)80305-0. [DOI] [PubMed] [Google Scholar]
- Lengyel M, Kwag J, Paulsen O, Dayan P. Matching storage and recall: hippocampal spike timing-dependent plasticity and phase response curves. Nat Neurosci. 2005;8:1677–1683. doi: 10.1038/nn1561. [DOI] [PubMed] [Google Scholar]
- Lisman J. A mechanism for the Hebb and the anti-Hebb processes underlying learning and memory. Proc Natl Acad Sci U S A. 1989;86:9574–9578. doi: 10.1073/pnas.86.23.9574. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lisman J. The theta/gamma discrete phase code occuring during the hippocampal phase precession may be a more general brain coding scheme. Hippocampus. 2005;15:913–922. doi: 10.1002/hipo.20121. [DOI] [PubMed] [Google Scholar]
- Lisman JE. Three Ca2+ levels affect plasticity differently: the LTP zone, the LTD zone and no man's land. J Physiol. 2001;532:285. doi: 10.1111/j.1469-7793.2001.0285f.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- London M, Hausser M. Dendritic computation. Annu Rev Neurosci. 2005;28:503–532. doi: 10.1146/annurev.neuro.28.061604.135703. [DOI] [PubMed] [Google Scholar]
- Lujan R, Maylie J, Adelman JP. New sites of action for GIRK and SK channels. Nat Rev Neurosci. 2009;10:475–480. doi: 10.1038/nrn2668. [DOI] [PubMed] [Google Scholar]
- MacLean JN, Zhang Y, Goeritz ML, Casey R, Oliva R, Guckenheimer J, Harris-Warrick RM. Activity-independent coregulation of IA and Ih in rhythmically active neurons. J Neurophysiol. 2005;94:3601–3617. doi: 10.1152/jn.00281.2005. [DOI] [PubMed] [Google Scholar]
- Magee JC. Dendritic hyperpolarization-activated currents modify the integrative properties of hippocampal CA1 pyramidal neurons. J Neurosci. 1998;18:7613–7624. doi: 10.1523/JNEUROSCI.18-19-07613.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Magee JC. Dendritic integration of excitatory synaptic input. Nat Rev Neurosci. 2000;1:181–190. doi: 10.1038/35044552. [DOI] [PubMed] [Google Scholar]
- Magee JC. Observations on clustered synaptic plasticity and highly structured input patterns. Neuron. 2012;72:887–888. doi: 10.1016/j.neuron.2011.12.009. [DOI] [PubMed] [Google Scholar]
- Magee JC, Christofi G, Miyakawa H, Christie B, Lasser-Ross N, Johnston D. Subthreshold synaptic activation of voltage-gated Ca2+ channels mediates a localized Ca2+ influx into the dendrites of hippocampal pyramidal neurons. J Neurophysiol. 1995;74:1335–1342. doi: 10.1152/jn.1995.74.3.1335. [DOI] [PubMed] [Google Scholar]
- Magee JC, Johnston D. Characterization of single voltage-gated Na+ and Ca2+ channels in apical dendrites of rat CA1 pyramidal neurons. J Physiol. 1995;487(Pt 1):67–90. doi: 10.1113/jphysiol.1995.sp020862. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marcelin B, Chauviere L, Becker A, Migliore M, Esclapez M, Bernard C. h channel-dependent deficit of theta oscillation resonance and phase shift in temporal lobe epilepsy. Neurobiol Dis. 2009;33:436–447. doi: 10.1016/j.nbd.2008.11.019. [DOI] [PubMed] [Google Scholar]
- Marder E, Taylor AL. Multiple models to capture the variability in biological neurons and networks. Nat Neurosci. 2011;14:133–138. doi: 10.1038/nn.2735. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mehta MR, Lee AK, Wilson MA. Role of experience and oscillations in transforming a rate code into a temporal code. Nature. 2002;417:741–746. doi: 10.1038/nature00807. [DOI] [PubMed] [Google Scholar]
- Migliore M, Hoffman DA, Magee JC, Johnston D. Role of an A-type K+ conductance in the back-propagation of action potentials in the dendrites of hippocampal pyramidal neurons. J Comput Neurosci. 1999;7:5–15. doi: 10.1023/a:1008906225285. [DOI] [PubMed] [Google Scholar]
- Migliore M, Shepherd GM. Emerging rules for the distributions of active dendritic conductances. Nat Rev Neurosci. 2002;3:362–370. doi: 10.1038/nrn810. [DOI] [PubMed] [Google Scholar]
- Narayanan R, Dougherty KJ, Johnston D. Calcium store depletion induces persistent perisomatic increases in the functional density of h channels in hippocampal pyramidal neurons. Neuron. 2010;68:921–935. doi: 10.1016/j.neuron.2010.11.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Narayanan R, Johnston D. Long-term potentiation in rat hippocampal neurons is accompanied by spatially widespread changes in intrinsic oscillatory dynamics and excitability. Neuron. 2007;56:1061–1075. doi: 10.1016/j.neuron.2007.10.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Narayanan R, Johnston D. The h channel mediates location dependence and plasticity of intrinsic phase response in rat hippocampal neurons. J Neurosci. 2008;28:5846–5860. doi: 10.1523/JNEUROSCI.0835-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Narayanan R, Johnston D. The h current is a candidate mechanism for regulating the sliding modification threshold in a BCM-like synaptic learning rule. J Neurophysiol. 2010;104:1020–1033. doi: 10.1152/jn.01129.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nelson SB, Turrigiano GG. Strength through diversity. Neuron. 2008;60:477–482. doi: 10.1016/j.neuron.2008.10.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- O’Donnell C, Nolan MF. Tuning of synaptic responses: an organizing principle for optimization of neural circuits. Trends Neurosci. 2011;34:51–60. doi: 10.1016/j.tins.2010.10.003. [DOI] [PubMed] [Google Scholar]
- O’Keefe J, Burgess N. Dual phase and rate coding in hippocampal place cells: theoretical significance and relationship to entorhinal grid cells. Hippocampus. 2005;15:853–866. doi: 10.1002/hipo.20115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- O’Keefe J, Recce ML. Phase relationship between hippocampal place units and the EEG theta rhythm. Hippocampus. 1993;3:317–330. doi: 10.1002/hipo.450030307. [DOI] [PubMed] [Google Scholar]
- Pavlov I, Scimemi A, Savtchenko L, Kullmann DM, Walker MC. I(h)-mediated depolarization enhances the temporal precision of neuronal integration. Nat Commun. 2011;2:199. doi: 10.1038/ncomms1202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Poolos NP, Migliore M, Johnston D. Pharmacological upregulation of h-channels reduces the excitability of pyramidal neuron dendrites. Nat Neurosci. 2002;5:767–774. doi: 10.1038/nn891. [DOI] [PubMed] [Google Scholar]
- Prinz AA, Billimoria CP, Marder E. Alternative to hand-tuning conductance-based models: construction and analysis of databases of model neurons. J Neurophysiol. 2003;90:3998–4015. doi: 10.1152/jn.00641.2003. [DOI] [PubMed] [Google Scholar]
- Prinz AA, Bucher D, Marder E. Similar network activity from disparate circuit parameters. Nat Neurosci. 2004;7:1345–1352. doi: 10.1038/nn1352. [DOI] [PubMed] [Google Scholar]
- Rathour RK, Narayanan R. Influence fields: a quantitative framework for representation and analysis of active dendrites. J Neurophysiol. 2012;107:2313–2334. doi: 10.1152/jn.00846.2011. [DOI] [PubMed] [Google Scholar]
- Schulz DJ, Goaillard JM, Marder E. Variable channel expression in identified single and electrically coupled neurons in different animals. Nat Neurosci. 2006;9:356–362. doi: 10.1038/nn1639. [DOI] [PubMed] [Google Scholar]
- Schulz DJ, Goaillard JM, Marder EE. Quantitative expression profiling of identified neurons reveals cell-specific constraints on highly variable levels of gene expression. Proc Natl Acad Sci U S A. 2007;104:13187–13191. doi: 10.1073/pnas.0705827104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Serrano JR, Perez-Reyes E, Jones SW. State-dependent inactivation of the alpha1G T-type calcium channel. J Gen Physiol. 1999;114:185–201. doi: 10.1085/jgp.114.2.185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shah MM, Hammond RS, Hoffman DA. Dendritic ion channel trafficking and plasticity. Trends Neurosci. 2010;33:307–316. doi: 10.1016/j.tins.2010.03.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shah MM, Migliore M, Valencia I, Cooper EC, Brown DA. Functional significance of axonal Kv7 channels in hippocampal pyramidal neurons. Proc Natl Acad Sci U S A. 2008;105:7869–7874. doi: 10.1073/pnas.0802805105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Siapas AG, Lubenov EV, Wilson MA. Prefrontal phase locking to hippocampal theta oscillations. Neuron. 2005;46:141–151. doi: 10.1016/j.neuron.2005.02.028. [DOI] [PubMed] [Google Scholar]
- Sjostrom PJ, Rancz EA, Roth A, Hausser M. Dendritic excitability and synaptic plasticity. Physiol Rev. 2008;88:769–840. doi: 10.1152/physrev.00016.2007. [DOI] [PubMed] [Google Scholar]
- Sjostrom PJ, Turrigiano GG, Nelson SB. Rate, timing, and cooperativity jointly determine cortical synaptic plasticity. Neuron. 2001;32:1149–1164. doi: 10.1016/s0896-6273(01)00542-6. [DOI] [PubMed] [Google Scholar]
- Spruston N. Pyramidal neurons: dendritic structure and synaptic integration. Nat Rev Neurosci. 2008;9:206–221. doi: 10.1038/nrn2286. [DOI] [PubMed] [Google Scholar]
- Taylor AL, Goaillard JM, Marder E. How multiple conductances determine electrophysiological properties in a multicompartment model. J Neurosci. 2009;29:5573–5586. doi: 10.1523/JNEUROSCI.4438-08.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tobin AE, Van Hooser SD, Calabrese RL. Creation and reduction of a morphologically detailed model of a leech heart interneuron. J Neurophysiol. 2006;96:2107–2120. doi: 10.1152/jn.00026.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tsay D, Dudman JT, Siegelbaum SA. HCN1 channels constrain synaptically evoked Ca2+ spikes in distal dendrites of CA1 pyramidal neurons. Neuron. 2007;56:1076–1089. doi: 10.1016/j.neuron.2007.11.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Turrigiano G. Too many cooks? Intrinsic and synaptic homeostatic mechanisms in cortical circuit refinement. Annu Rev Neurosci. 2011;34:89–103. doi: 10.1146/annurev-neuro-060909-153238. [DOI] [PubMed] [Google Scholar]
- Vacher H, Mohapatra DP, Trimmer JS. Localization and targeting of voltage-dependent ion channels in mammalian central neurons. Physiol Rev. 2008;88:1407–1447. doi: 10.1152/physrev.00002.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van der Meer MA, Redish AD. Theta phase precession in rat ventral striatum links place and reward information. J Neurosci. 2011;31:2843–2854. doi: 10.1523/JNEUROSCI.4869-10.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vervaeke K, Hu H, Graham LJ, Storm JF. Contrasting effects of the persistent Na+ current on neuronal excitability and spike timing. Neuron. 2006;49:257–270. doi: 10.1016/j.neuron.2005.12.022. [DOI] [PubMed] [Google Scholar]
- Wang XJ. Neurophysiological and computational principles of cortical rhythms in cognition. Physiol Rev. 2010;90:1195–1268. doi: 10.1152/physrev.00035.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weaver CM, Wearne SL. Neuronal firing sensitivity to morphologic and active membrane parameters. PLoS Comput Biol. 2008;4:e11. doi: 10.1371/journal.pcbi.0040011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wolfart J, Roeper J. Selective coupling of T-type calcium channels to SK potassium channels prevents intrinsic bursting in dopaminergic midbrain neurons. J Neurosci. 2002;22:3404–3413. doi: 10.1523/JNEUROSCI.22-09-03404.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zemankovics R, Kali S, Paulsen O, Freund TF, Hajos N. Differences in subthreshold resonance of hippocampal pyramidal cells and interneurons: the role of h-current and passive membrane characteristics. J Physiol. 2010;588:2109–2132. doi: 10.1113/jphysiol.2009.185975. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


