Vocal learning is constrained by the statistics of sensorimotor experience

Abstract

The brain uses sensory feedback to correct behavioral errors. Larger errors by definition require greater corrections, and many models of learning assume that larger sensory feedback errors drive larger motor changes. However, an alternative perspective is that larger errors drive learning less effectively because such errors fall outside the range of errors normally experienced and are therefore unlikely to reflect accurate feedback. This is especially crucial in vocal control because auditory feedback can be contaminated by environmental noise or sensory processing errors. A successful control strategy must therefore rely on feedback to correct errors while disregarding aberrant auditory signals that would lead to maladaptive vocal corrections. We hypothesized that these constraints result in compensation that is greatest for smaller imposed errors and least for larger errors. To test this hypothesis, we manipulated the pitch of auditory feedback in singing Bengalese finches. We found that learning driven by larger sensory errors was both slower than that resulting from smaller errors and showed less complete compensation for the imposed error. Additionally, we found that a simple principle could account for these data: the amount of compensation was proportional to the overlap between the baseline distribution of pitch production and the distribution experienced during the shift. Correspondingly, the fraction of compensation approached zero when pitch was shifted outside of the song’s baseline pitch distribution. Our data demonstrate that sensory errors drive learning best when they fall within the range of production variability, suggesting that learning is constrained by the statistics of sensorimotor experience.

Error correction based on sensory feedback is a ubiquitous mechanism for maintaining behavioral performance (1–4). However, sensory information is vulnerable to environmental noise and to errors in sensory encoding arising at the periphery or during central processing of the sensory signal (5). Such contamination can result in large mismatches between the actual and expected sensory feedback that do not necessarily reflect errors in performance. The brain must therefore decide whether to modify behavior based on sensory feedback (and risk “adapting” to signals that do not accurately reflect performance) or ignore sensory input (and risk leaving errors uncorrected). This problem is especially important in vocal behaviors, in which performance can have significant consequences for the success of an organism and auditory feedback is vulnerable to extrinsic acoustic signals and errors in auditory encoding.

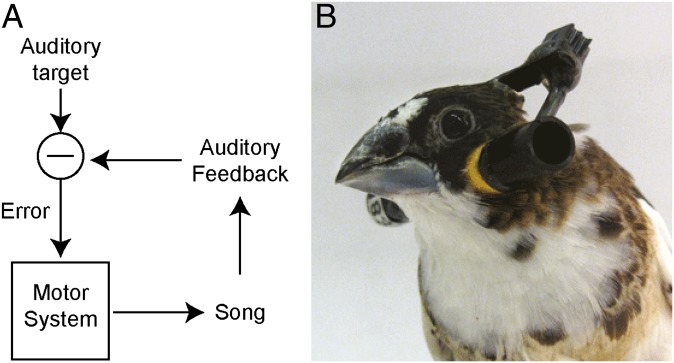
During development, both humans and songbirds learn by processes of vocal imitation that rely heavily on auditory feedback (2). Early vocalizations bear little resemblance to mature song or speech, resulting in large differences (errors) between experienced auditory feedback and the sensory goal. With practice, vocalizations become more similar to the “target,” reducing the size of the error. Based on these data, models of error correction often assume that the change in the motor program will be larger when the error in auditory feedback is larger, as shown in Fig. 1A.

Fig. 1.

(A) Schematic illustrating the hypothesis that, during vocal learning, auditory feedback is compared with a sensory target, and any mismatch (“Error”) is used to drive modifications of the vocal motor system. (B) Photograph showing headphones used to deliver manipulated auditory feedback in real time, as described previously (1).

In contrast, some studies of arm and eye movements have shown that as the size of an experimentally induced sensory error increases, the size of the behavioral response approaches an asymptote (3) or begins to decline (4, 6). Furthermore, when the magnitude of an auditory perturbation is gradually increased across a single training session, vocal compensation by human subjects can plateau or begin to decrease (7, 8), suggesting that larger errors are less effective at driving learning. Together with studies showing that a succession of small sensory perturbations is more effective at driving learning than a single large step (1, 9, 10), these experiments suggest that, contrary to the model in Fig. 1A, vocal adaptation may be better driven by smaller errors.

We exploited a learning paradigm in songbirds to investigate the computational rules underlying vocal error correction. We hypothesized that contrary to the model shown in Fig. 1A, larger auditory errors lead to smaller changes in vocal behavior. Adult Bengalese finches were fitted with miniaturized headphones (Fig. 1B) and online pitch perturbations were used to drive adaptive changes in vocal output. We examined the relationship between auditory errors and motor learning by varying the magnitude of the pitch shift and quantifying differences in the resulting changes in song.

Methods

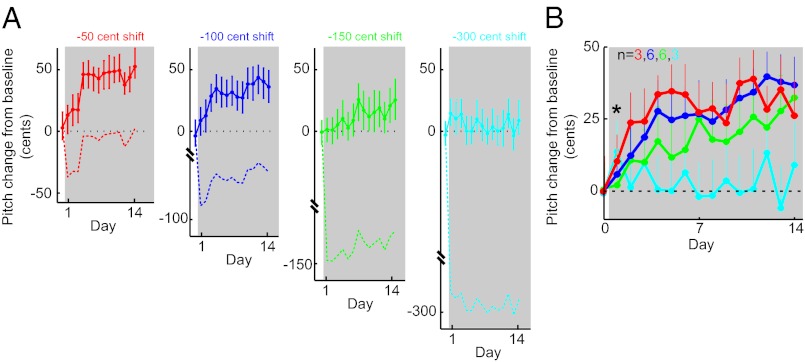
We used online perturbations of the pitch of auditory feedback to generate adaptive changes in the pitch of song. All procedures were approved by the University of California, San Francisco Institutional Animal Care and Use Committee. As described previously (1), lightweight headphones (Fig. 1B) were fit to each bird and online sound-processing hardware was used to shift the pitch of acoustic signals, which were then played back through the headphone speakers with a delay of 7–10 ms. After a baseline period (3–7 d) of singing with zero pitch shift, the pitch of auditory feedback was shifted upward or downward. Each experiment used a single shift size, and shift sizes were varied among eight values (±50, ±100, ±150, and ±300 cents, see below). In all cases, the pitch shift was constant in magnitude throughout the shift epoch. Therefore, changes in the vocal pitch in the direction opposite the feedback shift resulted in the bird receiving auditory feedback more similar to the pitch of baseline song (e.g., Fig. 2A, dashed red line).

Fig. 2.

Relationship between the size of sensory errors and vocal error correction. (A) Data from four separate experiments in which the same Bengalese finch experienced downward shifts in auditory feedback of four different magnitudes (−50, −100, −150, and −300 cents). The gray boxes indicate the 14 d during which the pitch shift was applied, and the solid lines show change in the mean pitch of song as a function of time (Methods). The solid lines indicate the median value of the (nonnormal) pitch distribution, and the error bars show the distributions’ 40th and 60th percentiles. The dashed lines in each plot indicate the pitch of auditory feedback played through the headphones (equal to the pitch of the song produced by the bird minus the appropriate downward pitch shift; note discontinuity on vertical axes). (B) Combined data from all experiments oriented so that adaptive changes are positive. The solid lines indicate median values, and the error bars show only the 60th percentile for visual clarity. Inset indicates the number of experiments for each shift size. The asterisk indicates the first day on which data differ significantly across the four shift size conditions (P < 0.05, Kruskal–Wallis test). Color conventions are as in A.

Individual adult male Bengalese finches (>190 d of age; n = 6) participated in multiple experiments with different shift sizes. The order of presentation of different shift sizes was varied pseudorandomly within each bird. Following 14- to 17-d exposure to each pitch shift, birds sang for at least 7 d with zero shift (still wearing the headphones apparatus) and then for at least 25 d without headphones before beginning the next experiment. Data from experiments using ±100-cent shifts have been presented previously (1).

Acoustic Analysis.

We quantified the average change in the pitch of song as a function of time by measuring changes in pitch at particular times (“spectral frames”) within individual song syllables (1). Individual birds produced a median of four (range, three to nine) syllables with quantifiable pitch. Individual iterations of each syllable were identified by visual inspection of song spectrograms. Pitch was quantified for all songs produced in a 2-h window between 10:00 AM and 12:00 PM. Birds sang many iterations of each syllable in their repertoire, producing a median of 528 (range, 31–1489) iterations of syllables with quantifiable pitch in each 2-h window. To measure the fractional change in the pitch of each syllable iteration relative to that syllable’s baseline pitch, we converted pitch measurements (in hertz) obtained throughout each experiment (i.e., from both the baseline and shift epochs) into units of cents as follows:

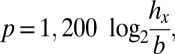where p is the change in pitch (in cents) of the syllable during the selected spectral frame, h_x is the pitch (in hertz) of the syllable during the selected spectral frame, and b is the average pitch of the syllable being analyzed (in hertz) during the baseline epoch. Note that 100 cents is the same pitch interval as a semitone, corresponding to a ∼6% change in absolute frequency. Note also that the change in frequency (in hertz) resulting from a given pitch shift (in cents) will depend on the frequency of the song syllable being shifted. In our dataset, the average frequency shifts (in hertz) for 50-, 100-, 150-, and 300-cent pitch shifts were 92.9, 215.9, 306.8, and 536.2 Hz, respectively.

To quantify the dynamics of learning and the fraction of error compensation at equilibrium, we fit the behavioral data with a simple exponential model as follows:

where p(t) is the change in the mean pitch of song on postshift day t and E is the experimentally imposed sensory (pitch) error. Free parameters c and τ describe the fraction of the imposed error that is corrected at equilibrium and the time constant of learning, respectively. This model was fit to group data in which each iteration of each syllable contributed a single data point. Furthermore, we fit the data with an alternate model in which the learning at equilibrium was quantified in units of cents, rather than as a fraction of the imposed pitch error:

Here, free parameter a describes the equilibrium level of pitch correction (in cents). All other model parameters and fitting procedures for Eq. 1′ are the same as those described for Eq. 1.

Overlap Calculations.

Our analysis considers the relationship between model parameter c and the overlap between the bird’s baseline distribution of pitches and the pitches experienced just after a pitch shift before any adaptive vocal changes occur. This overlap was calculated according to the following equation:

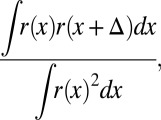where r(x) is the probability density function of pitches in the baseline condition and Δ is the applied pitch shift.

Permutation Tests for Significant Differences in c and τ.

To test the hypothesis that the value of c or τ differed between shift sizes, we used a permutation test (11) against the null hypothesis that the tested parameter was equal in the two conditions. For example, to test the hypothesis that c differs between 50- and 100-cent shift sizes, we tested against the null hypothesis H₀: c₅₀ = c₁₀₀, where c₅₀ is the value of c in the 50-cent shift condition and c₁₀₀ is the value of c in the 100-cent condition. This test is derived from the following generalization of Eq. 1:

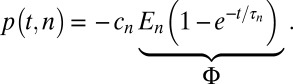Here, p(t,n) represents the change in the mean pitch of song on postshift day t for shift size n. This equation can be rewritten using the function δ_n=k, which equals 1 if the pitch value p was collected during exposure to shift size k and zero otherwise:

According to the null hypothesis of H₀: c₅₀ = c₁₀₀, the model will produce the same predictions if c₅₀ and c₁₀₀ are randomly interchanged across trials. This manipulation is implemented by permuting (randomly resorting) the values of n shown explicitly in Eq. 2, leaving the values of Φ unpermuted. To perform the permutation test, we created 1,000 artificial datasets in this manner, fit the model to each dataset, and computed the resulting R². If the R² value for the true dataset is greater than the 95th percentile of artificial R² values, then H₀ can be rejected. Null hypotheses for different pairs of shift sizes (e.g., H′₀: c₅₀ = c₁₅₀) and for parameter τ (e.g., H″₀: τ₅₀ = τ₁₀₀) were tested in a similar fashion.

Results

Shifting the pitch of auditory feedback consistently led to compensatory changes in the pitch of song, as shown for a representative bird in Fig. 2A. In all but one case, vocal changes induced by feedback shifts were confined to shifts in pitch, as reported previously (1). In one experiment (of 19 total) involving a +300-cent shift, we observed dramatic changes in syllable structure that made it difficult to measure the pitch of the syllable and bore a strong resemblance to spectral changes that precede song degradation in zebra finches (12). We therefore excluded data from this experiment from further analysis.

Comparing data from experiments involving different shift sizes revealed inverse relationships between pitch shift magnitude and both the speed and completeness of learning. First, as the size of the imposed pitch shift increased, the absolute pitch of song changed more slowly. As shown in data from four experiments in a single bird (Fig. 2A) and in data combined across all birds (Fig. 2B), smaller changes in the pitch of auditory feedback led to larger changes in the pitch of song in the first few days after pitch shifts began. As early as 24 h after the beginning of the feedback shift (Fig. 2B, asterisk), group data from the four shift size conditions differed significantly (P < 0.05, Kruskal–Wallis test).

Second, as size of the pitch shift increased, the fraction of error compensated at equilibrium decreased. For example, at the end of the shift epoch the adaptive change in the pitch of song in response to a 50-cent shift (Fig. 2B, red) was ∼30 cents, showing that birds compensated for ∼60% (30 of 50) of the imposed sensory error. Increasing the size of the pitch shift to 100 cents (Fig. 2B, blue) led to a mean adaptive change of ∼40 cents, corresponding to 40% compensation for the larger error. For 150- and 300-cent shifts, the fraction of compensation at the end of the shift epoch similarly decreased with shift size. Such incomplete learning could result from the bird’s relying in part on nonauditory inputs such as proprioceptive feedback or the output of an internal model used to predict sensory feedback (13–15). Furthermore, note that prior studies have demonstrated that Bengalese finches are able to produce changes in vocal pitches of 150 cents or greater (1, 10). It is therefore unlikely that the plateau in vocal learning shown in Fig. 2B reflects any mechanical constraint limiting pitch changes.

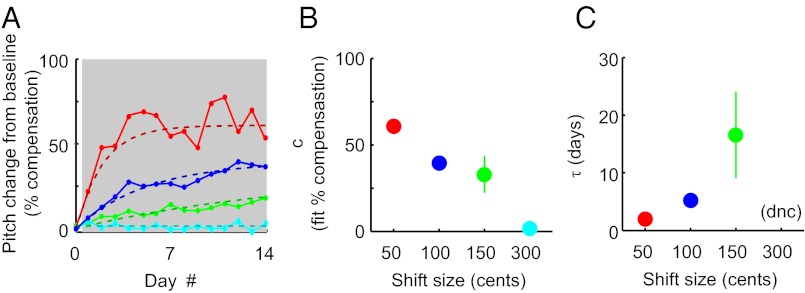
To allow quantitative comparisons of the time course of learning across shift sizes (even in cases in which learning may not have reached equilibrium by the end of the shift epoch), we fit our data with an exponential model of learning (Methods). The solid lines in Fig. 3A show group data plotted as the fraction of the total error compensated (rather than the absolute change in the pitch of song as in Fig. 2B), and the dashed lines show model fits for each shift size. Fit values of c show that as the size of sensory errors increases, the fraction of error correction decreases monotonically (Fig. 3B). As shown in Fig. 3C, the time constant of learning increased monotonically with shift size across shift magnitudes of 50, 100, and 150 cents. When fit to the 300-cent data, the model did not converge on a value of τ, presumably because the adaptive change being modeled was similar in magnitude to the day-to-day pitch fluctuations that occur even in the absence of experimental manipulations (1).

Fig. 3.

Inverse relationship between pitch shift magnitude and the completeness of error correction and results of model fitting. (A) Group data (median values), plotted in units of the percentage of the sensory error compensated (rather than absolute change in pitch). Other conventions are as in Fig. 2B. (B) Fit value of free parameter c, which quantifies the fraction of the sensory error compensated when learning has reached equilibrium. Permutation tests (Methods) revealed that all pairwise differences in c were significant (P < 0.03 in all cases) except for the difference between values fit to the 100- and 150-cent datasets (P = 0.34). (C) Fit values of free parameter τ, the time constant of learning. The model did not converge (dnc) on a value of τ for the 300-cent shift data (see text). All pairwise differences in τ between the 50-, 100-, and 150-cent datasets were significant (P < 0.001 in all cases). Error bars in B and C represent 95% confidence intervals and are obscured by symbols in some cases.

Fitting this model also allowed us to determine the statistical significance of behavioral changes in individual experiments and compare the dynamics of learning across shift sizes. In all but one experiment (which used a −300-cent shift), the fit value of c was significantly different from zero, indicating a significant adaptive change in the pitch of song. Therefore, as previously reported for ±100 cent shifts (1), ±50- and ±150-cent shifts reliably drive adaptive changes in song, and ±300-cent shifts do so in some cases. Permutation tests (Methods) were used to assess the significance of differences in the fit values of c and τ. All pairwise differences in c were significant (P < 0.03 in all cases) except for the difference between values fit to the 100- and 150-cent datasets (P = 0.34), as were all pairwise differences in τ between the 50-, 100-, and 150-cent datasets (P < 0.001 in all cases).

Furthermore, our data suggest that the fraction of error correction is limited by the statistics of birds’ prior sensorimotor experience. We observed that the fit value of c approaches zero when the pitch shift becomes sufficiently large (±300 cents) that the distribution of pitches heard by the bird no longer overlaps with the baseline (preshift) distribution. Fig. 4A shows the baseline distribution of pitches (black lines) and the same distribution translated by each shift size (colored lines). As the shift magnitude increases across experiments from ±50 to ±300 cents, the overlap between the distributions decreases. We computed the normalized overlap between the baseline and shifted distributions (Methods, Overlap calculations). Fig. 4B plots overlap against the fit value of c for each shift size, showing that both values decrease with increasing shift magnitude and approach zero together.

Fig. 4.

Completeness of error correction is predicted by the overlap between sensorimotor experience and sensory feedback. (A) Normalized probability density functions for all data recorded in the baseline epoch (black) before the introduction of ±50-, ±100-, ±150-, and ±300-cent shifts. The colored lines show the baseline probability distributions translated rightward by the corresponding shift size, representing the distribution of pitches that birds experience at the beginning of the shift epoch (distributions for experiments with negative shifts have been sign-reversed so that all shifts are shown as positive). Baseline pitch distributions are non-Gaussian (Jarque–Bera test, P < 0.001 in all cases). (B) Relationship between the overlap between the distributions shown in A (Methods) and the fit value of c. Data are combined across all experiments within each shift size. The dashed line shows unity. (C) Relationship between overlap and the fit value of c for 13 individual experiments. Fits to data from the other five experiments did not converge on a value of c (see Results). Shapes identify data from individual birds. Data identified with a circle and shown in Fig. 2A are from the same individual. The dotted line indicates a significant (P = 0.002) regression. Color conventions are as in Fig. 2.

To ask whether variability in overlap could predict variability in c, we fit Eq. 1 to data from each experiment, rather than combining data across birds within shift sizes, as in our other analyses. We were able to fit c to data from 13 of 18 experiments. In the other five experiments, the model did not converge on a value of c due to the day-to-day variability of the pitch data, which is substantially greater in data drawn from a single experiment compared with data combined across experiments using the same shift size (1). Cases in which the model did not converge on a value of c appeared in 100-cent (two cases), 150-cent (two cases), and 300-cent (one case) shift experiments and could represent either the greatest or smallest degree of learning (as measured by the change in song pitch on the last shift day) within each shift size. As shown in Fig. 4C, we found a significant correlation between overlap and the fit value of c (P = 0.002; note that the significance of this regression is due primarily to differences across shift sizes, rather than experiment-by-experiment variability within each shift size). The slope and intercept of this regression (Fig. 4C, dotted line) were not significantly different from unity and zero, respectively. As described below, this relationship between overlap and the extent of error correction suggests a simple strategy by which songbirds rely on the statistics of prior vocal motor experience to constrain sensorimotor learning.

Additionally, we fit our data with an alternate model (Eq. 1′) in which we quantified the absolute size of the error correction at equilibrium (in cents) rather than the fraction of the total imposed pitch error corrected at equilibrium, as in our primary analysis. Fit values of free parameter a in Eq. 1′ for 50-, 100-, 150-, and 300-cent shifts were 30.4, 39.5, 49.5, and 4.7 cents, respectively, and all pairwise differences were significant at P < 0.05 except for that between the 100- and 150-cent conditions. This nonmonotonic relationship between pitch shift size and absolute change in vocal pitch suggests a trade-off between the robustness of error correction (which decreases with error size) and the size of the sensory error itself, consistent with the primary analysis presented above.

Discussion

Our results demonstrate an inverse relationship between the magnitude of the pitch shift and both the completeness and speed of vocal error correction. Varying the shift size revealed that as the magnitude of auditory errors increases from ±50 cents to ±300 cents, the fraction of errors corrected when learning has reached equilibrium (c) (Fig. 3B) decreases and the time constant of learning (τ) (Fig. 3C) increases. Furthermore, the fraction of error correction (c) approaches zero when auditory errors become large enough to shift the distribution of pitches heard by the bird outside of the baseline distribution of pitches (Fig. 4).

Our results suggest a simple principle that predicts the extent to which auditory errors drive vocal learning. As shown in Fig. 4, the fraction of compensation approaches zero when (in the 300-cent shift experiments) sensory errors are large enough so that the distribution of pitch in the manipulated auditory feedback does not overlap with the baseline distribution of pitch. Such a finding suggests that learning in response to a sensory error is limited by the probability that the sensory signal could have come from the distribution of signals accumulated over past experience. This strategy represents a simple and robust solution to the problem of how much to rely on the inherently unreliable sensory signals needed to calibrate behavior (6) because it uses the statistics of the bird’s sensorimotor experience to determine whether to correct an apparent behavioral error.

Limiting learning in response to large sensory errors appears to be a principle common to many forms of complex behavior, suggesting that other systems might similarly constrain learning based on the expected distribution of sensory feedback. The inverse relationship between pitch error size and vocal learning reported here parallels similar findings in the response of the human arm movement system to visual (6) and force (3) perturbations and of the primate oculomotor system to visual errors during saccades (4). Similarly, in response to brief (200-500 ms) pitch perturbations during ongoing speech, transient compensatory vocal changes in human subjects occur on fewer trials (16) and correct a smaller fraction of the imposed error (17) for larger perturbations. Further analysis of these data from humans and nonhuman primates might reveal that the observed inverse relationships between error size and learning in fact reflect limitations imposed on learning based on the range of baseline feedback rather then on absolute error size per se.

Additionally, our results indicate that the vocal error correction model shown in Fig. 1A requires modification. Although future experiments will be needed to fully clarify the algorithm underlying vocal error correction in adulthood, at least two plausible (and nonexclusive) models could explain our findings. First, the reduced speed and completeness of learning in response to larger errors might reflect a change in multisensory integration. Psychophysical studies of human motor control have shown that when integrating sensory signals, subjects can flexibly weight sensory inputs (18, 19) and that such weighting appears to be based on the variability of the available sensory signals, as predicted by theories of optimal motor control (20). Such a flexible weighting strategy might account for the inverse relationship between the size of sensory pitch shifts and the magnitude of the behavioral responses. That is, when experiencing large errors, songbirds might reduce their reliance on auditory information and increase their reliance on proprioceptive signals (13, 14) or internal models of motor output (15) to estimate vocal pitch. The resulting integrated estimate might then be compared with an internal target to generate an error signal. Such a reweighting strategy might reflect an estimate that larger auditory errors reflect unreliable auditory signals (rather than motor errors) and are therefore less relevant to motor performance (6).

A second possibility is that the inverse relationship between pitch shift magnitude and learning reflects a reinforcement-based mechanism (21–23) in which plasticity is driven by the occurrence of “successful” trials rather than the magnitude of experienced errors. Internal reinforcement signals might reward trials in which the pitch of experienced auditory feedback falls within some acceptable range. Because the range of acceptable pitches would presumably be similar to the baseline pitch distribution (Fig. 4A, black), smaller pitch shifts would result in more reinforcement, as reflected by the larger amount of overlap between the baseline and shifted (Fig. 4A, red) distributions. Conversely, larger shifts might lead to less learning because the small amount of overlap between distributions (as in Fig. 4A, Right) results in less reinforcement. This account of our results is consistent with recent studies that use white noise-based negative reinforcement signals to drive adaptive changes in pitch (10, 24). These studies show that when a subset of pitches is punished by an aversive white noise stimulus, songbirds change their pitch distribution to avoid white noise. The common principle unifying these two sets of results might therefore be that birds will only adjust their vocal output when their current range of motor variation sometimes results in “successful” outcomes. In the present study, a successful outcome would be one in which auditory feedback falls within the bird’s baseline pitch distribution. In white noise experiments, a successful outcome would be an escape from negative reinforcement. Indeed, experimental conditions in which no trials are successful (very large pitch shifts in our study or previously published experiments in which white noise is provided on every trial) produce zero or near-zero learning (10, 24). Therefore, despite the methodological differences between shifting the pitch of feedback and differentially reinforcing some syllable variants with white noise, we believe that learning in both paradigms can be explained by birds evaluating the relative value of a range of vocal pitches.

Our results show that the adult song system corrects small errors more rapidly and robustly than large errors. This relationship is somewhat surprising given that song acquisition in juvenile birds is characterized by initially very large errors in vocal production, which are minimized during the dramatic changes to vocal output over a ∼6-wk-long period of sensorimotor learning. Although the mechanisms governing juvenile song acquisition and adult error correction might be distinct, it is possible that they rely on the same underlying computation. Although the absolute size of errors in young birds is very large, so is the variability of song itself (25–29). Constraining learning based on variability (Fig. 4) might therefore both allow the large changes necessary during song acquisition (when both error size and behavioral variability are high) and also provide the stability required during adult song maintenance (when both error size and behavioral variability are low). Our studies suggest that, for error correction in juvenile songbirds, and more broadly for error correction in other complex behaviors, the statistics of prior experience constrain the capacity for learning and adaptation.