Temperature Field Reconstruction for Minimally Invasive Cryosurgery With Application to Wireless Implantable Temperature Sensors and/or Medical Imaging

Abstract

There is an undisputed need for temperature-field reconstruction during minimally invasive cryosurgery. The current line of research focuses on developing miniature, wireless, implantable, temperature sensors to enable temperature-field reconstruction in real time. This project combines two parallel efforts: (i) to develop the hardware necessary for implantable sensors, and (ii) to develop mathematical techniques for temperature-field reconstruction in real time—the subject matter of the current study. In particular, this study proposes an approach for temperature-field reconstruction combining data obtained from medical imaging, cryoprobe-embedded sensors, and miniature, wireless, implantable sensors, the development of which is currently underway. This study discusses possible strategies for laying out implantable sensors and approaches for data integration. In particular, prostate cryosurgery is presented as a developmental model and a two-dimensional proof-of-concept is discussed. It is demonstrated that the lethal temperature can be predicted to a significant degree of certainty with implantable sensors and the technique proposed in the current study, a capability that is yet unavailable.

INTRODUCTION

Cryosurgery is the destruction of undesired tissues by freezing. It was introduced as an invasive procedure for the first time in 1961, with the development of the cryoprobe by Cooper and Lee [4]. As a minimally invasive procedure, cryosurgery experiments were conducted in the mid 1980’s, following technological developments in medical imaging. While cryosurgery has been applied to virtually any tissue of the body as a method of treatment, prostate cryosurgery was the first minimally invasive cryosurgical procedure to pass from the experimental stage to become a routine surgical treatment [13,4,15].

The minimally invasive approach created a new level of difficulty in cryosurgery, in which a well-defined 3D shape of tissue must be treated, while preserving the surrounding tissues. In an effort to gain better control over the cryosurgical procedure, the number of cryoprobes has been increased over the years so that more than a dozen cryoprobes can be applied simultaneously. If localized effectively, one of the potential benefits of the use of a large number of miniaturized cryoprobes is superior control over the freezing process [5,12,30,32,33].

With the dramatic increase in the number of cryoprobes, two new challenges in cryosurgery have arisen: (i) how to shape the frozen region and restrict the destructive freezing effect to the target area, and (ii) how to correlate the developing thermal field with established criteria for cryosurgery success. The current study is a part of an ongoing effort to address those challenges by developing means for real-time feedback to the cryosurgeon on the developing thermal field.

While the benefits of temperature measurements during cryosurgery are well documented and highly recommended in the literature [1, 2, 7, 9, 16, 28, 29, 35], and modern cryodevice setups often offer the feature of real-time temperature sensing, temperature sensors are often not integrated into the procedure for various reasons. At the current state of cryosurgery technology, two principle means have been developed for temperature sensing as a means of monitoring and control, the cryoprobe-embedded sensor and the so-called “needle sensor”. The cryoprobe-embedded sensor approach is as old as the first invasive cryoprobe, but with a diminishing use in recent years. It is the cooling capability and not the temperature that is often controlled in modern cryoprobe. For example, the surgeon would control the flow rate of the cryogen in order to control the rate of propagation of the freezing front, all in effort to match its final location with a predetermined contour (the organ contour for example). Here, a higher flow rate in a nearby cryoprobe will drive the freezing front propagation faster, and the entire process is performed in a trial-and-error fashion, while the freezing front contour is monitored by means of medical imaging. This mode of operation, combined with the everlasting effort to miniaturize cryoprobes, has led to abandoning temperature sensors in some modern cryoprobes altogether.

An example for the use of needle temperature sensors in cryosurgery is the placement of one or two such sensors near the rectal wall, as feedback to prevent freezing injury to it—one of the most severe complications in prostate cryosurgery [16,29,35]. The needle sensor is frequently a hypodermic needle in a diameter similar to that of the minimally invasive cryoprobe. The thermocouple is often the choice of practice as the measuring principle for hypodermic sensors. When incorporated, the needle sensor and the cryoprobe are localized using a similar methodology in prostate cryosurgery—inserting either into a predetermined depth through an x–y grid, which is aligned with the organ but placed outside of the body. Unfortunately, despite its advantages as a safety measure, and despite the capability of modern cryosurgical devices to integrate such temperature sensors, the needle sensor is not frequently used in cryosurgery in recent years.

The current study is a part of an ongoing effort to develop means to improve cryosurgery planning and control. The current project is focused on developing miniature, wireless, implantable temperature sensors to reconstruct the temperature field in real time—a capability which is yet unavailable for routine practice. This project combines two parallel efforts: (i) to develop the hardware necessary for implantable sensors [11,23], and (ii) to develop a method for temperature-field reconstruction in real time, which is the subject matter of the current study. This is a proof-of-concept level study, which uses prostate cryosurgery as a developmental model. For that purpose, the analysis presented in this study focuses on a two-dimensional target, representing the largest cross-section of the prostate, while using a proprietary computerized planning algorithm, known as “bubble-packing” [30,31,33]. Finally, this study investigates input from three potential sources, imaging, temperature sensor-embedded cryoprobes, and implantable sensors.

While hardware development is the subject matter of a parallel effort [11,23], its current state of development is overviewed here in brief, for the completeness of presentation only. Hardware development is aimed at an ultra-miniature, wireless, battery-less, implantable temperature-sensing device, having a diameter of 1.5 mm and a length of 3 mm to enable minimally invasive deployment through a hypodermic needle. The new device consists of three major subsystems: a sensing core, a wireless data-communication unit, and a wireless power reception and management unit. Power is delivered wirelessly to the implant from an external source using an inductive link. To meet size requirements while enhancing reliability and minimizing cost, the implant is fully integrated in a regular foundry CMOS technology (0.15 μm in the current phase of development), including the implant-side inductor of the power link.

MATHEMATICAL FORMULATION

It is customary to assume that heat transfer during cryosurgery can be modeled with the classical bioheat equation [12]:

$$C\frac{\partial T}{\partial t}=\nabla ·(k\nabla T)+w_b{C}_b(T_b-T)+q_{\mathit{met}}$$ (1)

where C is the volumetric specific heat of the tissue, T is the temperature, t is the time, k is the thermal conductivity of the tissue, w_b is the blood perfusion rate, C_b is the volumetric specific heat of the blood, T_b is the blood temperature entering the thermally treated area (typically the normal body temperature), and q_met is the metabolic heat generation.

The physical properties used for the current study are listed in Table 1. it is assumed in the current study that the specific heat is an effective property [34] within the phase-transition temperature range of −22°C to 0°C (the tissue is first-order approximated as an NaCl solution), where a detailed discussion about the application of the effective specific heat to phase change problems is given in [13]. The metabolic heat generation is typically negligible compared to the heating effect of blood perfusion [21], and is neglected in this study. While more advanced models of bioheat transfer are available in the literature [3,6], it is assumed in the current study that they would not guarantee greater accuracy in the cryosurgery simulation but will involve greater mathematical complications.

Table 1.

Representative thermophysical properties of soft biological tissue used in the current study [19]

Thermal property	Value
Thermal conductivity, k, W m−1 K−1	0.5	273K < T
	15.98 – 0.56T	251K< T< 273K
	1005T−1.15	T < 251K
Volumetric specific heat, C, kJ m−3 K−1	3,600	273K < T
	15,440	251K < T < 273K
	3.98 T	T < 251K
Blood perfusion rate, wb, W m−3	40,000	273K < T
	0	T < 273 K
Metabolic heat generation, qmet, W kg−1	0.67	273K< T
	0	T < 273K

The blood perfusion rate in the unfrozen region (Table 1) and the step-like change in the blood-perfusion rate upon the onset of freezing represent the worst-case scenario in terms of transient effects. In practice, one would expect a gradual decay in blood flow with the decreasing temperature, potentially leading to a complete stasis before the freezing temperature is achieved. To the best of knowledge of the authors, the actual temperature dependency of blood perfusion in the prostate is unknown. The uncertainty in blood perfusion rate may contribute a few percent to the uncertainty in predicting the freezing front location [21]; this uncertainty is not taken into account in the current study. A detailed discussion on the propagation of uncertainty in measurements into heat transfer simulations of cryosurgery is given in [22].

Quasi-Steady Approximation

At least two principal approaches are available in effort to provide the clinician with feedback on the developing temperature field: (i) prediction-based, by applying a real-time simulation of the procedure, and (ii) reconstruction-based, using measured data at multiple locations. In the first approach, the bioheat transfer process is simulated using Eq. (1), while temperature data obtained from the cryoprobes is used as internal boundary conditions.

The real-time simulation process is typically very computationally expensive [10,24] and rarely is it practical as a real-time feedback. While available data from implantable sensors can be used to verify the quality of a real-time simulation, such data cannot be straightforwardly implemented to correct the simulated temperature field once a deviation between predicted and measured values is observed. Since temperature sensors do not drive any thermal effect, merely correcting a predicted temperature field to specific values at the sensor locations has no physical meaning. More appropriately, this deviation can be used to correct the model properties (i.e, thermophysical properties) by employing a parametric estimation procedure [19], after which a computer simulation can be attempted again in effort to get a better match between computer results and experimental data. This prediction-correction process of model properties using a full-scale simulation, data measurements, and parametric estimation could continue until the convergence of property values. Obviously, this process is even more computationally expensive than the cost of a single simulation, and the cost only increases as the cryoprocedure progresses, since every simulation with corrected parameter values must restart from the same initial condition at the beginning of the cryosurgical procedure.

The proposed alternative approach of temperature-field reconstruction attempts to use all available data at any given instant in order to generate a current temperature field. In the absence of more detailed information, one could take all the available data at discrete points and approximate the temperature field in the domain by applying some method of interpolation. Here, the method of interpolation is the key to the quality of the reconstructed temperature field. A better-quality interpolation method means a better match between predicted and actual temperature field, while minimizing the number of required data points (i.e., sensors). A modified Laplacian interpolation is proposed in this study, where the modification is used to account for the blood perfusion term and temperature-dependent thermophysical properties. In practice, this interpolation method implies that the bioheat transfer process is modeled as a quasi-steady problem, where further justification for this modeling approach is provided in the literature [20].

The quasi-steady solution is based on the observation that the heat transfer process during cryosurgery is characterized by a low Stefan number:

$${St}_p=\frac{C_p\mathrm{\Delta }{T}_p}{H}$$ (2)

where ΔT_p is the maximum temperature difference in phase p (either frozen or unfrozen) and H is the latent heat of phase change. When the Stefan number is low, it means that the heat transfer process is dominated by the effect of latent heat rather than sensible heat and, hence, the transient term in Eq. (1) may be neglected [27]. It follows that the temperature distribution in the frozen region can be approximated as a steady solution at any instant, where the transient nature of the system comes about through boundary conditions—the rate of freezing front propagation is most significantly affected by the rate of latent heat absorption or release at the freezing front [20].

Numerical Solution

Taking the quasi-steady approach to solve Eq. (1), the temperature field in the frozen and unfrozen regions in the current study is approximated as:

$$0={\sum }_{l,m,n}\frac{T_{l,m,n}-T_{i,j,k}}{R_{l,m,n-i,j,k}}+{(w_b{C}_b)}_{i,j,k}(T_b-T_{i,j,k})$$ (3)

where i, j, k are spatial indices of the numerical grid representing the temperature field, l, m, n are spatial indices of the neighboring grid points, and R is the thermal resistance to heat transfer by conduction between node i, j, k and its neighbor l, m, n. For a regular Cartesian geometry, the thermal resistance to heat conduction can be presented as:

$$R_{l,m,n-i,j,k}={\left[\frac{\mathrm{\Delta }\eta }{2kA}\right]}_{l,m,n}+{\left[\frac{\mathrm{\Delta }\eta }{2kA}\right]}_{i,j,k}$$ (4)

where Δη is the space interval in the direction of interest, and A is the representative cross-sectional area perpendicular to the direction of heat flow. Equations (3)–(4) can be viewed as the steady-state version of the numerical scheme presented in [24]. Given the temperature dependency of the thermophysical properties (Table 1), Eq. (3) is solved simultaneously using an iterative predictor-corrector technique.

The simulated domain is assumed infinite from a heat transfer perspective, which means that a large enough domain is assumed, such that thermal information from the cryosurgically treated area would not reach the boundary of the domain during the simulated procedure. In mathematical terms, a core-body temperature (also the initial temperature) is assumed at the boundary of the numerical domain, and the solution is considered valid as long as the heat flux at the boundary remains negligible (unchanged temperature and no heat flex at the boundary of a finite domain make it indistinguishable from an infinite domain). In practice, a domain three-fold bigger than the target region can typically be considered infinite for that purpose.

RESULTS AND DISCUSSION

Five general cases are analyzed in this study, as listed in Table 2, with a variable number of temperature sensors up to 12, which led to over 200 special cases. Case A is a full-scale two-dimensional transient solution in a representative cross section of the prostate, which serves as a benchmark. This solution was generated using ANSYS on a prostate contour obtained from ultrasound imaging [33], subject to the following parameters and conditions: (1) eight cryoprobes are used simultaneously; (2) the cryoprobes are cooled from 37°C to −145°C in 30 sec, simulative of Argon-based cryoprobes; (3) the cryoprobe layout is computer generated, using a planning algorithm known as “bubble packing” [26], with the match between the 0°C isotherm and the organ contour as a planning criterion; and, (4) the urethra is maintained at 37°C throughout the procedure, simulative of the commonly applied urethral warmer. Depending upon the special case under investigation, the thermal history of the benchmark case has been used to extract the thermal history of implanted sensors at pre-selected locations.

Table 2.

A summary of five general cases explored in the current study, where Case A is a benchmark, and the location of the target isotherms for sensors placement is extracted from computerized planning of cryosurgery. Imaging of freezing front location is simulative of MRI, CT (complete contours), or ultrasound (a partial contour). The thermal history of the benchmark is used to simulate extraction of the freezing front location from medical imaging and temperature data obtained from implantable sensors

		Case Aa	Case B				Case C					Case D				Case E
			1b	2c	3	4	1d	2	3	4	5	1	2e	3	4	1	2	3	4
Target isotherm for sensors placement	Organ contour	N/A Benchmark									+					+	+	+	+
	Freezing front, 0°C						+	+	+	+		+		+	+
	Lower boundary of freezing, −22°C			+		+		+		+	+		+		+		+		+
	Lethal temperature, −45°C				+	+			+	+	+			+	+			+	+
Imaging of freezing front location			Complete Contour				Partial Contour					None				None
Method of Solution		Transient	Quasi-Steady				Quasi-Steady					Quasi-Steady				Quasi-Steady

^aBenchmark: Fig. 1

^bSpecial Case I: Figs. 2–3

^cSpecial Case II: Fig. 4

^dSpecial Case III: Figs. 5–6

^eSpecial Case VI: Fig. 7

Figure 1 displays results from the benchmark case, while highlighting the typical isotherms of interest: 0°C is the onset of freezing, −22°C is the lower boundary of phase transition, and −45°C is the lethal temperature—a temperature threshold below which maximum destruction is assumed. Reflective of the quality of the computer-generated planning (bubble packing) is the close match between the freezing front as would be viewed by medical imaging (0°C) and the organ contour. The gray area between the onset of freezing and the lethal temperature (−45°C) represents a region where cryodestruction is gradually achieved—the shape and dimensions of this region is critical in the evaluation of the outcome of cryosurgery.

Figure 1.

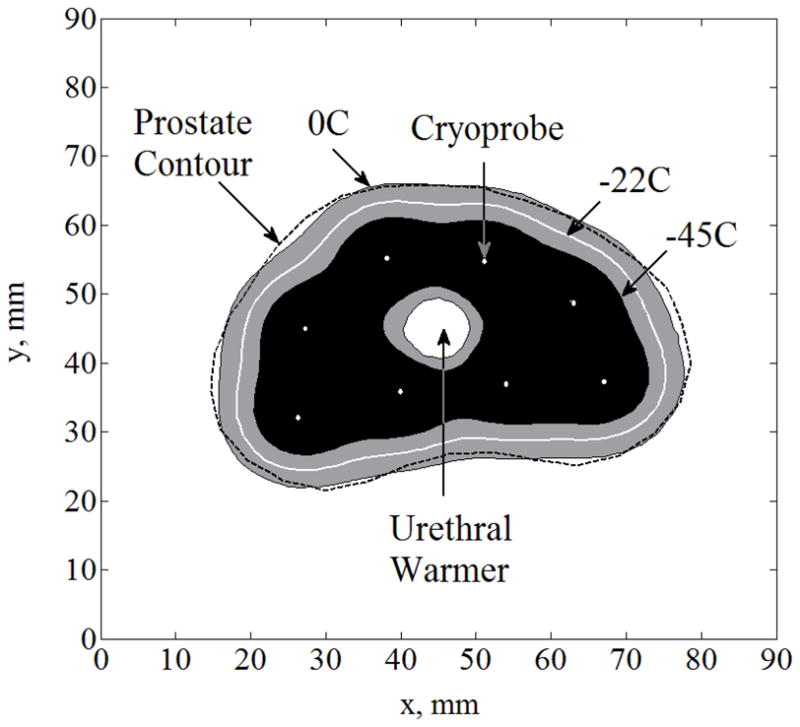
Temperature field regions resulted from the transient solution of Case A (the benchmark) at the point of optimal match between the freezing-front location and the prostate contour; cryoprobes are illustrated with white dots.

With reference to Table 2, solutions for the various special cases of the quasi-steady problem were obtained using MATLAB, by applying a sparse matrix format and internal solvers for efficiency in calculations. A typical quasi-steady solution was obtained within three seconds on an Intel® Quad Core^™ i7 machine with 9GB RAM, running at 3.07GHz. Case B is simulative of extraction of the freezing front location from medical imaging such as MRI or CT scanning (not routinely done in real time). In the current study, the benchmark case (Case A) is used to simulate freezing front reconstruction from medical imaging. Since the location of the freezing front is well established in Case B, the effects of implantable sensors are explored only on sensors embedded within the frozen region. It is noted that Rubinsky and co-workers [8,27] have already reported on a similar effort but without the application of implemented sensors (i.e., using only cryoprobe-embedded sensors and complete freezing-front location from MRI imaging).

Case C is similar to Case B with the exception that only a portion of the freezing front location can be extracted. Case C is simulative of freezing front extraction from ultrasound imaging, where only the portion of the freezing front close to the transducer can be imaged (a detailed example below). While medical imaging is a necessity in minimally invasive cryosurgery, it is conceivable that temperature-field reconstruction would be attempted without integration with imaging data, which is the investigated scenario in Cases D and E.

Strategies for implantable sensors placement are yet to be developed, where the investigation in current study is focused on four temperature contours relevant to cryosurgery: the target region contour (prostate contour), the freezing front (0°C), the lower boundary of phase transition (−22°C), and the lethal temperature (−45°C). While the target region contour can be identified a priori, the location of a particular isotherm for the purpose of sensor placement can only be predicted from bioheat simulations in the process of planning; those isotherms propagate during the cryoprocedure, and their location is evaluated in the current study at the point of cryoprobes deactivation. While computer simulations as a part of cryosurgery planning can be used to predict the location of those isotherms [25,26], the benchmark solution is used for this purpose in the current study.

For the purpose of discussion, letters are used to refer to general cases in the current study (A, B, C, D, and E), and Roman numerals are used to refer to special cases of investigation. The first special case analyzed (Case I) is Case B without the implementation of sensors. Figure 2 displays the temperature field regions as predicted by quasi-steady approximation. Figure 3 displays the difference between temperature fields predicted by quasi- steady approximation and the benchmark, where the maximum temperature difference, ΔT_max, is found to be less than 16°C. This difference is the direct result of neglecting the time-dependent term in the bioheat equation—making the governing equation quasi-steady. The same difference is also affected by the size of the space intervals selected for the numerical grid; however, the grid-size effect is at least one order of magnitude smaller than the effect of neglecting the time- dependent term in the governing equation. In the current study, a uniform grid of 90×90 was used, with a space interval of 1 mm, which is expected to contribute a numerical uncertainty of the order of 10⁻¹ °C—significantly smaller than the differences displayed in Fig. 3.

Figure 2.

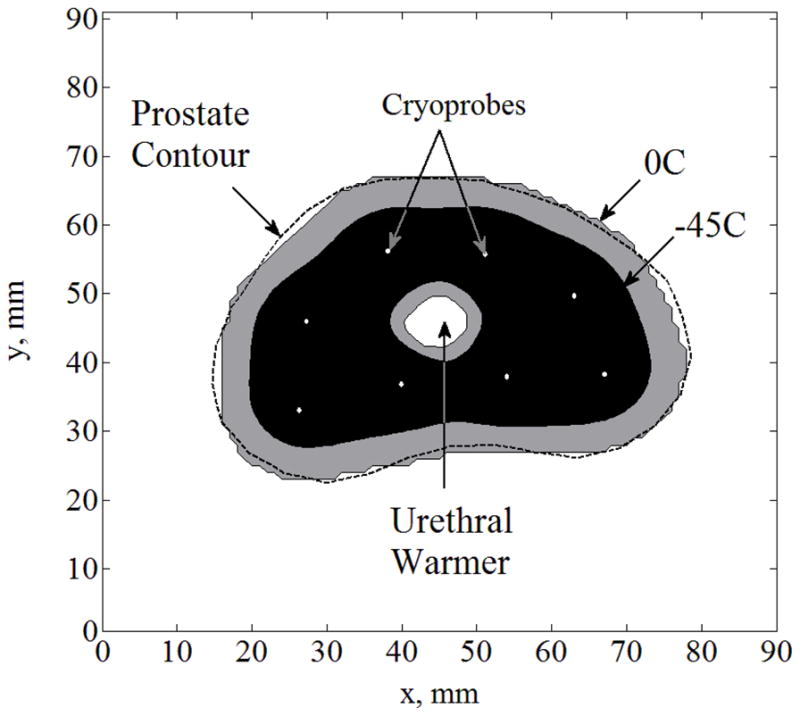
Temperature field regions for Case I: complete freezing front information from medical imaging (Case B) with no temperature sensors; cryoprobes are illustrated with white dots.

Figure 3.

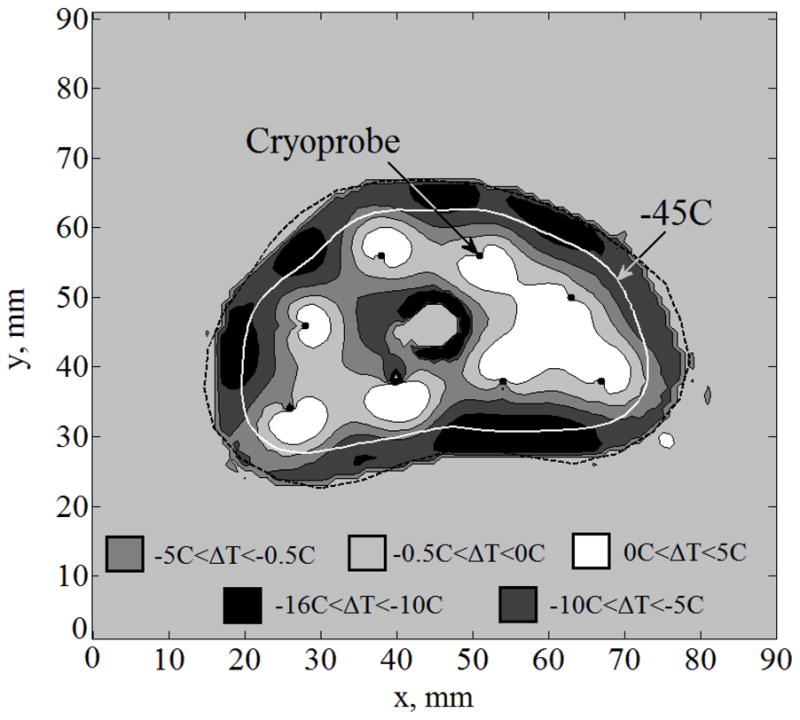
Temperature fields difference, ΔT, between the benchmark solution and the solution for Case I: complete freezing front information (Case B) with no temperature sensors; cryoprobes are illustrated with black dots.

The mismatch in the area bounded by the lethal isotherm (−45°C; urethral warmer area excluded), ΔA_lethal, is 9%. It is emphasized that despite its significance, the location of the lethal temperature isotherm can only be estimated using real-time temperature-field reconstruction, a capability that is yet to be available. Hence, clinicians often think of the lethal temperature but in practice attempt to control only the location of the freezing front. The average distance between those isotherms is defined in this study as:

$$B_{\mathit{avg},\mathit{lethal}}=\frac{A_{a,\mathit{lethal}}-A_{b,\mathit{lethal}}}{L_{a,\mathit{lethal}}}$$ (5)

where A_a,lethal and A_b,lethal are the areas bounded by the −45°C isotherm based on the approximated and benchmark solutions, respectively, and L_a,lethal is the length of the lethal temperature isotherm based on the approximated solution. B_ave,lethal in the Case I is found to be 0.8 mm.

In effort to improve temperature-field reconstruction, special Case II is now considered, integrating six temperature sensors at the points of maximum temperature differences along the isotherm of −22°C from Case I (can be identified in Fig. 3). It can be seen from Fig. 4 that ΔT_max is now reduced to less than 10°C. For Case II, ΔA_lethal is reduced to 6% and B_ave,lethal in reduced to 0.5 mm. A similar special case was considered where six sensors are placed along the lethal temperature instead of the −22°C isotherm but results were worse compared to Case II in terms of the maximum temperature difference, ΔT_max; further case studies showed consistent results. The reasons that the −22°C was originally chosen is that it serves as the lower boundary of phase transition. It can be concluded that the prediction of the phase-transition boundary contour is key to improve the quality of temperature-field reconstruction in terms of ΔT_max. However, in clinical practice, knowledge of location of the lethal isotherm (−45°C) is more important. Hence mismatch in the area bounded by the lethal isotherm, ΔA_lethal, is used as a metric for comparing the performance of various cases.

Figure 4.

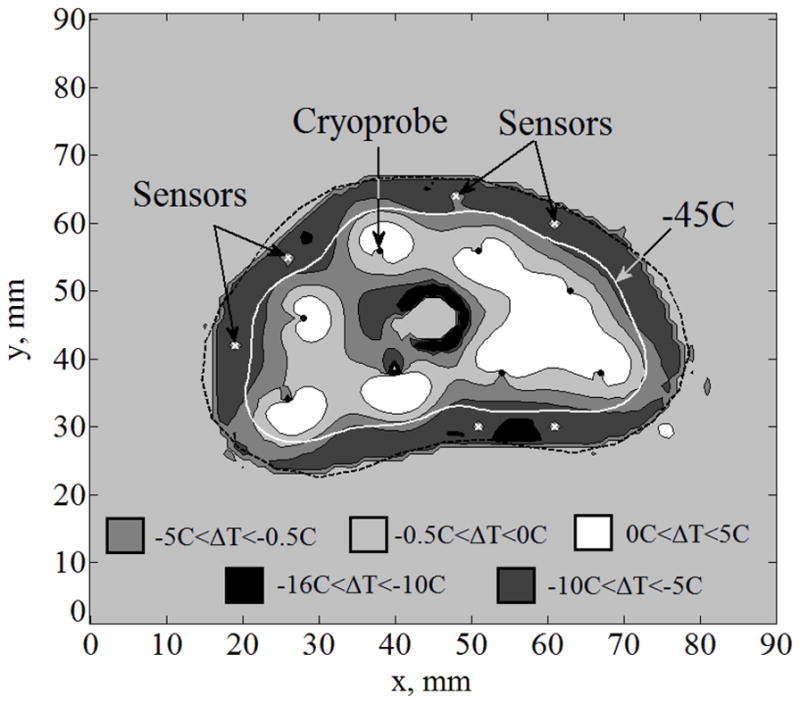
Temperature fields difference, ΔT, between the benchmark solution and the solution for Case II: complete freezing front information (Case B) with six sensors implanted along the −22°C isotherm at the locations of maximum temperature difference in Fig. 3; cryoprobes are illustrated with black dots and sensors with white “×”.

Case III is a special case of the more realistic scenario, where only a portion of the frozen region in the prostate is observable with a trans-rectal ultrasound transducer (TRUS, Case C). Typically, about one third of the frozen region can be identified, as shown in Fig. 5, where the frozen region is completely opaque to the ultrasound signals. The same six sensors used in Case II are also used in Case III. In addition, six sensors are distributed in equal distances along the unobservable portion of the prostate contour in Case III. Results in this case indicate ΔT_max=41°C, ΔA_lethal=14%, B_ave,lethal=1.4mm, and B_max,lethal=3.5 mm, where the distribution of the temperature difference between Case III and the benchmark solution is displayed in Fig. 6. While a temperature-difference of 41°C may be considered significant for some purposes, comparable data from current clinical practice is literally nonexistent. When taking into account the uncertainty in ultrasound imaging in the range of 1 to 2 mm, the error in predicting the lethal temperature location is quite remarkable, especially given the temperature gradients in the frozen region (of the order of 10°C/mm). While the optimal number and layout of sensors remain to be explored, Case III represents a scenario where implantable sensors could only improve the outcome of clinical practice.

Figure 5.

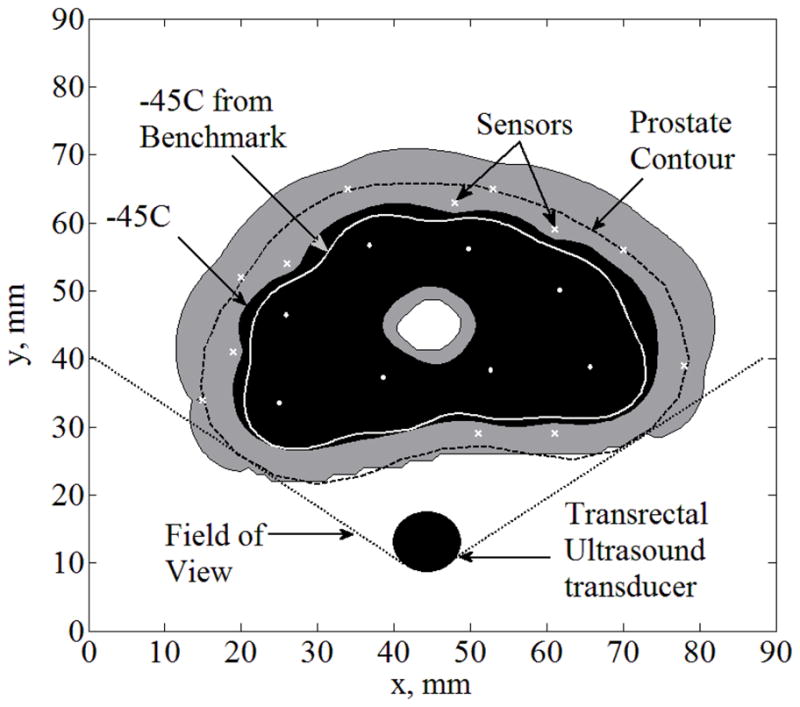
Temperature field regions for Case III: partial freezing front information obtained from a transrectal ultrasound transducer (Case C), combined with six sensors implanted along the −22°C isotherm, and six additional sensors equally distributed along the unobservable portion of the prostate contour (upper portion of the figure); α is the field of view of the trans-rectal ultrasound transducer; cryoprobes are illustrated with white dots and sensors with white “×”.

Figure 6.

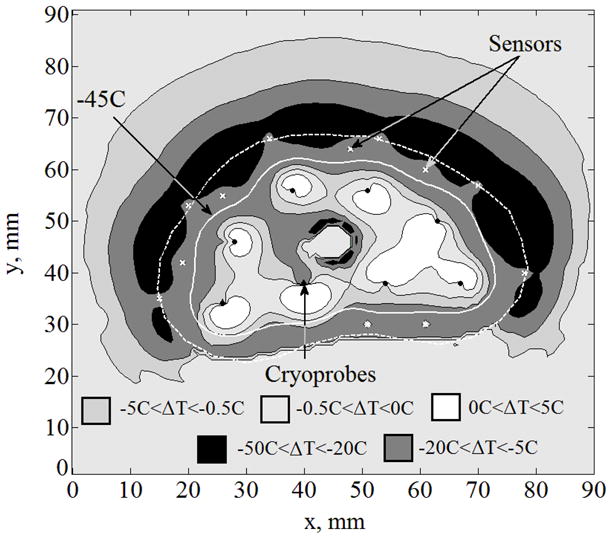
Temperature fields difference, ΔT, between the benchmark solution and the solution for Case III: partial freezing front information obtained from a trans-rectal ultrasound transducer (Case C) combined with six sensors implanted along the −22°C isotherm, and six additional sensors equally distributed along the unobservable portion of the prostate contour (upper portion of the figure); cryoprobes are illustrated with black dots and sensors with white “×”.

Case IV represents a practical case where freezing front data is not used for temperature-field reconstruction, where twelve temperature sensors are equally distributed along the −22°C isotherm. While special Case IV belongs to general Case D, if the cryoprobe layout is optimal, Case IV will essentially also be representative of general Case E (the quality of such a match is demonstrated in Fig. 1). The resulted temperature field for Case IV is shown in Fig. 7, where ΔT_max=47°C, ΔA_lethal=19%, B_ave,lethal=1.8 mm, and B_max,lethal= 4 mm. While the prediction of the location of the lethal temperature is off by 1.8 mm on average and approaches a value of 5 mm at the location of maximum disagreement, the predicted lethal temperature isotherm is still bounded by the organ contour. Hence, when the location of the lethal temperature is of high priority, the application of implantable sensors and the proposed reconstruction method can potentially improve real-time feedback on the procedure. Furthermore, the onset of freezing can be evaluated straightforwardly from medical imaging, and its integration with the information displayed here would improve the control over the destructive effects of freezing.

Figure 7.

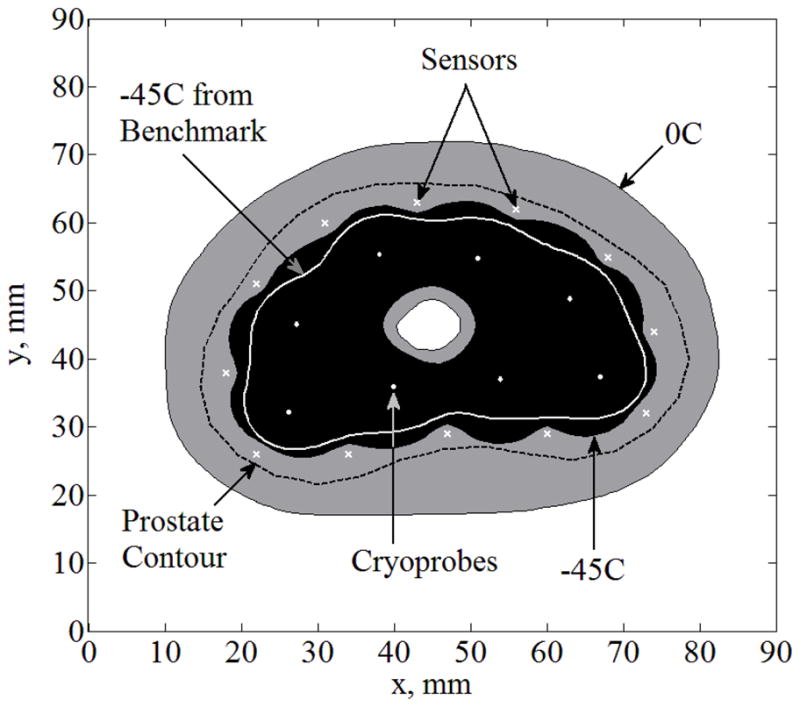
Temperature field reconstruction for Case IV (Case D—solely based on temperature sensors with no imaging data): twelve sensors equally distributed along the −22°C isotherm; cryoprobes are illustrated with white dots and sensors with white “×”.

The relationship between the number of sensors and mismatch in lethal area, ΔA_lethal, can be seen in Figs. 8, 9, and 10, for Cases B, C, and D, respectively. When sensors were equally distributed along more than one isotherm, the distance between sensors on the different isotherms was maximized. As could be expected, the increasing number of sensors always decreases ΔA_lethal, regardless of the particular sensor layout. For Case B (Fig. 8), the quality of lethal temperature reconstruction is less sensitive to the strategy of selecting the sensor layout, and ΔA_lethal is in the order of a percent. It is interesting to compare the results displayed in Fig. 8 with the results of Case II, which is based on Case B when six sensors are not equally distributed, but strategically placed in areas where the largest mismatch is expected along the −22°C isotherm (Fig. 4). Results of Case II suggest that the specific sensors layout would yield better results than placing them along the −45°C isotherm. While the results displayed in Figs. 4 and 8 may appear inconsistent at first glance, one should bear in mind that the cases are not identical, and that the results are influenced by different placement strategies. This comparison illustrates that the optimal sensor layout should be evaluated on a case-by-case basis.

Figure 8.

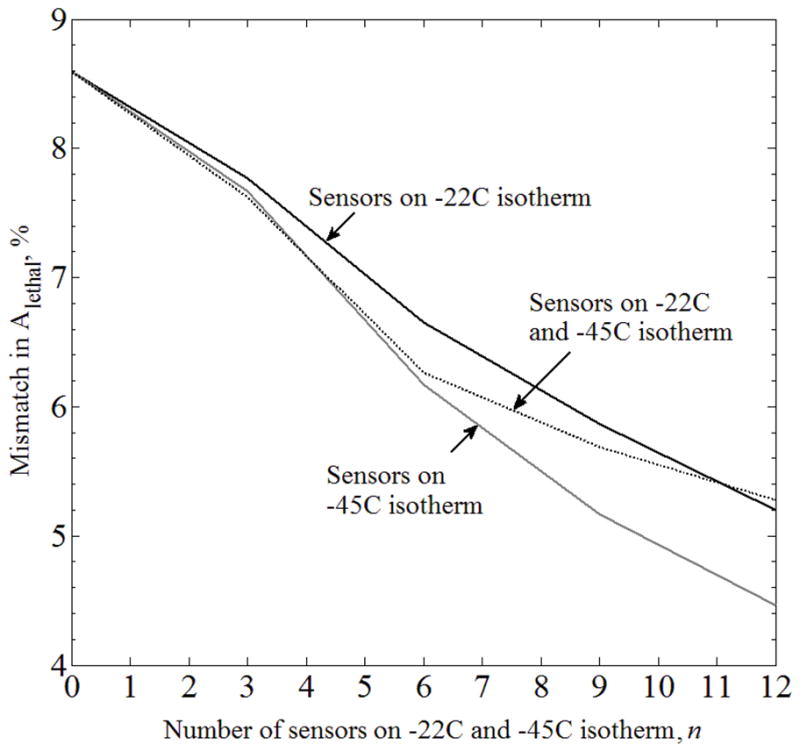
Mismatch in the areas bounded by the lethal isotherm, ΔA_lethal, between the benchmark (Case A) and the Case B, where complete freezing-front data is available from medical imaging, and the temperature sensor are equally distributed along predicted isotherms.

Figure 9.

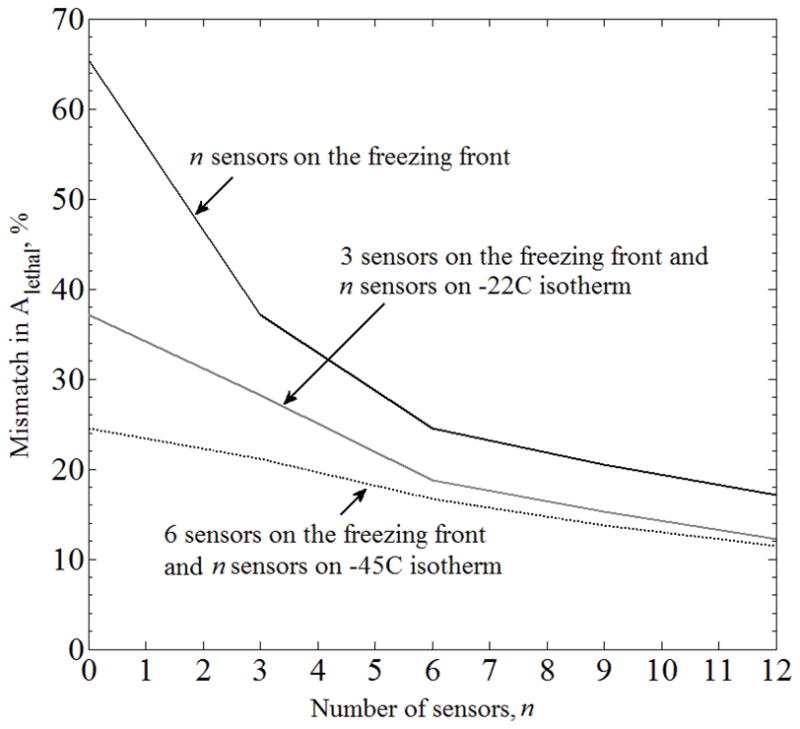
Mismatch in the areas bounded by the lethal isotherm, ΔA_lethal, between the benchmark (Case A) and the case of partial freezing-front data available from medical imaging (Case C), where the temperature sensors are equally distributed along the freezing front, and combined with temperature sensors distributed along the −22°C and −45°C isotherms.

Figure 10.

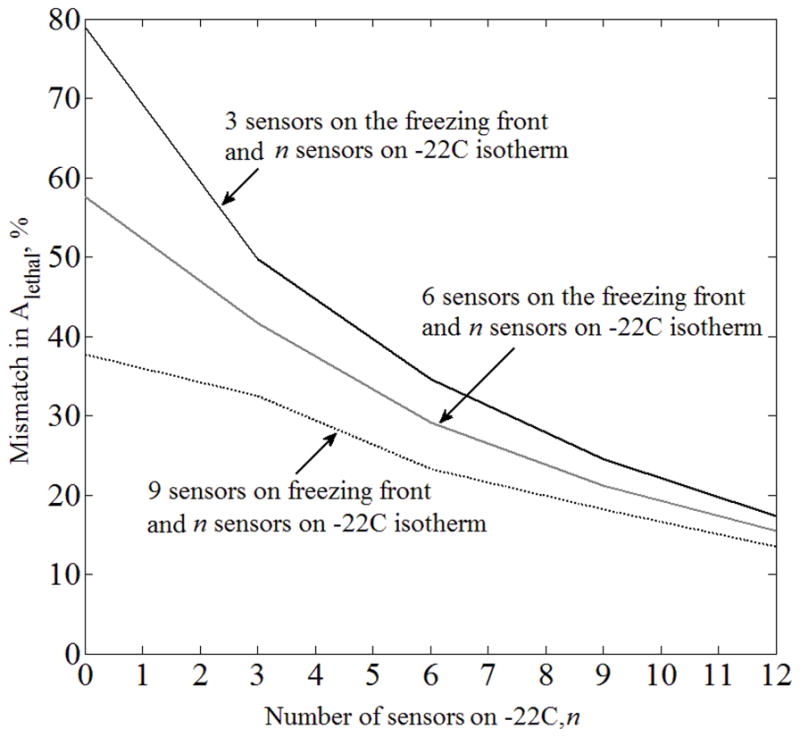
Mismatch in the area bounded by the lethal isotherm, ΔA_lethal, between the benchmark (Case A) and the case where no imaging data is available for the purpose of extracting the location of the freezing front (Case D), where temperature sensors are equally distributed along the −22°C and −45°C isotherms.

For Case C (Fig. 9), placing sensors at the predicted location of the freezing front is detrimental to the quality of lethal isotherm reconstruction. Interestingly, placing nine sensors on the freezing front, six sensors on the freezing front and three sensors on the −22°C isotherm, or three sensors on the freezing front and six sensors on the −22°C isotherm, all resulted in ΔA_lethal ≈21%, for the particular prostate model and cryoprobe layout under investigation. This observation was not repeated for a larger number of sensors. While Figs. 8–10 display an expected trend of improving the quality of temperature-field reconstruction with the increasing number of sensors, rules for the optimal strategy of sensor placement remain to be explored. Given the virtually infinite number of possibilities for sensor layout, computer planning has the potential of automatically and efficiently selecting a high quality sensor layout—a research effort currently underway

SUMMARY AND CONCLUSIONS

The current study is a part of an ongoing effort to develop means to improve cryosurgery planning and control, which combines the development of a wireless, implantable, temperature sensor with temperature-field reconstruction. This is a proof-of-concept level study uses cryosurgery prostate as a developmental model. Demonstrations are presented for a two-dimensional target, representative of the largest cross-section of the prostate.

This study investigates the integration of data from three potential sources for temperature-field reconstruction: implantable sensors, cryoprobe-embedded sensors, and medical imaging. The key modeling assumption for temperature-field reconstruction is that the cryosurgical process can be treated as quasi-steady, while the transient effects are introduced via internal boundary conditions at the cryoprobes and sensors. The justification for this assumption is that the Stefan number is typically small in cryosurgery problems, which means that the process of bioheat transfer is dominated by latent heat effects.

Results of this study indicate that temperature-field reconstruction in 2D can be achieved in the order of seconds using an available solver of the commercial code MATLAB. While temperature-field reconstruction in a time scale of seconds can be considered close-to-real-time, extension of the solution to 3D requires additional numerical formulation efforts, which is currently work in progress.

Emphasis in temperature-field analysis is given to the location of the so-called lethal temperature, which is of a clinical significance but typically not presented to the cryosurgeon in real time. The current analysis is focused on placing the sensors along the organ contour and along predicted locations of the isotherms: 0°C, −22°C, and −45°C. Those predictions make use of a proprietary cryosurgery planning code, which materializes the so-called bubble-packing planning technique.

When compared with a benchmark solution of a transient case, results of this study indicate that the quasi-steady scheme can provide a good approximation for the location of the lethal temperature in many scenarios. The mismatch between the benchmark and the approximated solutions is often comparable to the uncertainty inherent to medical imaging. Further sensitivity analysis and strategies for sensor placement are discussed in this study.

Temperature-field reconstruction using implantable sensors by no means is proposed to substitute any other modality of cryosurgery monitoring and control but to be complimentary. Combining image analysis in real time with data from cryoprobe-embedded temperature sensors can provide a comprehensive approach to temperature-field reconstruction in real time. In order to make the application of wireless implantable temperature sensors a practical reality, mathematical techniques and computer tools must be developed, to identify the minimum number of sensors and their optimal layout.