SUMMARY
The thrifty-gene hypothesis (TGH) posits that the modern genetic predisposition to obesity stems from a historical past where famine selected for genes that promote efficient fat deposition. It has been previously argued that such a scenario is unfeasible because under such strong selection any gene favouring fat deposition would rapidly move to fixation. Hence, we should all be predisposed to obesity: which we are not. The genetic architecture of obesity that has been revealed by genome-wide association studies (GWAS), however, calls into question such an argument. Obesity is caused by mutations in many hundreds (maybe thousands) of genes, each with a very minor, independent and additive impact. Selection on such genes would probably be very weak because the individual advantages they would confer would be very small. Hence, the genetic architecture of the epidemic may indeed be compatible with, and hence support, the TGH. To evaluate whether this is correct, it is necessary to know the likely effects of the identified GWAS alleles on survival during starvation. This would allow definition of their advantage in famine conditions, and hence the likely selection pressure for such alleles to have spread over the time course of human evolution. We constructed a mathematical model of weight loss under total starvation using the established principles of energy balance. Using the model, we found that fatter individuals would indeed survive longer and, at a given body weight, females would survive longer than males, when totally starved. An allele causing deposition of an extra 80 g of fat would result in an extension of life under total starvation by about 1.1–1.6% in an individual with 10 kg of fat and by 0.25–0.27% in an individual carrying 32 kg of fat. A mutation causing a per allele effect of 0.25% would become completely fixed in a population with an effective size of 5 million individuals in 6000 selection events. Because there have probably been about 24,000 famine events since the evolution of hominins 4 million years ago, there has been ample time even for genes with only very minor impacts on adiposity to move to fixation. The observed polymorphic variation in the genes causing the predisposition to obesity is incompatible with the TGH, unless all these single nucleotide polymorphisms (SNPs) arose in the last 900,000 years, a requirement we know is incorrect. The TGH is further weakened by the observation of no link between the effect size of these SNPs and their prevalence, which would be anticipated under the TGH model of selection if all the SNPs had arisen in the last 900,000 years.
INTRODUCTION
It has been established from a combination of twin studies and family association studies that the majority of the variance in obesity is genetic. Estimates vary between studies, but a consensus view is that genetic factors explain about 65% of the variance in body mass index (BMI) (Allison et al., 1996; Luke et al., 2001; Zhu et al., 2002; Wu et al., 2002; Segal and Allison, 2002), with most of the remaining variance being due to individual environmental rather than shared environmental effects. A major fundamental question is what evolutionary process led to this situation, because on the face of it there is a paradox. Obesity is well established to be associated with numerous negative health effects, including elevated risks of diabetes (Pi-Sunyer, 1991; Boffetta et al., 2011), non-alcoholic liver steatosis (Browning et al., 2004; Schwimmer et al., 2006), hypertension (Isomaa et al., 2001) and some cancers (Calle and Kaaks, 2004), which together lead to a positive curvilinear relationship between BMI and mortality risk for individuals with BMI above 25 (Prospective Studies Collaboration, 2009). How is it possible that natural selection could lead to such a high genetic susceptibility to develop such a disadvantageous trait?
A resolution to this paradox was proposed in the 1960s and has been called the ‘thrifty gene’ hypothesis (TGH), after the seminal paper on this topic by Neel (Neel, 1962). The TGH is beguilingly simple and hence extremely attractive. Consequently, it has been reiterated in basically the same form on numerous occasions since it was first formulated (Prentice et al., 2005; Prentice, 2001; Prentice, 2005; Chakravarthy and Booth, 2004; Eknoyan, 2006; Wells, 2006) and the hypothesis is mentioned in the introduction of many papers on obesity as the underlying cause of the genetic susceptibility to obesity.
The TGH states that, although obesity is disadvantageous in modern societies, in the past it was advantageous, primarily because stored body fat provided an energy buffer that allowed people to survive periods of food shortage. Individuals that had genetic mutations that favoured the deposition of fat during periods between famines would therefore be more likely on average to survive the period of famine and would hence be more likely to pass on their genes to future generations. When this genetic predisposition is embedded in modern society, where food is readily available, the result is widespread obesity. Obese people are simply those who in the past were the lucky ones who would survive famines, but in modern society are preparing for a famine that never comes. They consequently become so obese that the negative sequelae of obesity start to become apparent. Other examples of strong positive selection on genes in recent human history include the selection on the lactase gene in populations that developed milk drinking and dairying (Bersaglieri et al., 2004).
TRANSLATIONAL IMPACT.
Clinical issue
Obesity is one of the most significant health problems facing the world today. It is clear that obesity is a consequence of energy imbalance, but the reasons why some individuals store large amounts of fat, but others do not, are uncertain. Genetics plays a major role. One idea, called the thrifty-gene hypothesis (TGH), suggests that fat storage used to be important for survival in periods of famine. Hence, individuals with genes that predisposed them to deposit fat between famines would be positively selected. This interpretation has been questioned because, if it were correct, we would expect everyone to have inherited such a predisposition – yet clearly we have not. Recent studies using genome-wide association have shown that obesity depends on a large number of genes each with a small effect. This genetic structure might be compatible with the TGH because the selection on such small-effect genes would occur very slowly.
Results
The authors present a mathematical model of the process of starvation to predict the impact of genes with minor effects on survival during famines. This model shows that such genes would have effects in the range of 0.25 to 1.9% on famine survival. Taking the lowest value and modelling the spread of a mutant allele conferring a benefit on survival in this range shows that even such minor-effect alleles would move to fixation over the time course of human evolution. This suggests that the TGH is incorrect.
Implications and future directions
This study provides a context for understanding the evolutionary background of the predisposition of some individuals to obesity. The fact that the TGH is incompatible with the findings of recent genome-wide association studies suggests that other approaches to understand the evolutionary background of this condition are needed. Understanding why humans become obese might help to develop new ways to treat the condition. The mathematical model developed here might also be useful in predicting the responses of individuals and populations to starvation conditions.
The TGH has been criticised in part because of the term ‘thrifty’, which implies the dominant mechanism by which individuals are able to accumulate fat between famines is by reducing their metabolic rate so that they frugally utilise the available food which, while not in famine conditions, was assumed to be never very abundant (Campbell, 2008; Bouchard, 2008). More recent evidence tends to suggest that differences in metabolic rate do not underpin the obesity epidemic (Westerterp and Speakman, 2008; Luke et al., 2009; Swinburn et al., 2009) and that the major difference between obese and lean people in modern society is actually in their food intake (but see Church et al., 2011). However, this critique of the TGH rather misses the point. The crucial aspect of the hypothesis, despite its name, is not that the genes are thrifty, but that they confer on the holder the capacity to deposit fat that will enhance future survival when food becomes scarce or unavailable. Hence a ‘thrifty gene’, despite its name, could easily act by increasing the capacity to collect food, or efficiently digest it, and still perform its function as required by the hypothesis.
Nevertheless, there are some serious issues with the TGH (Speakman, 2007; Speakman, 2008; Benyshek and Watson, 2006). A major problem is that, if thrifty genes (or more correctly thrifty alleles) provide such a great advantage for people in times of famine, and famines have been an ‘ever present’ (Prentice, 2005) feature of the natural history of hominins, then we would expect that everyone in modern society would have inherited these alleles, and by implication then we should all be clinically obese. Yet clearly we are not. Surveys of the prevalence of obesity show that, even among the top ten most obese nations, the rate of obesity (using the WHO definition of obesity as individuals with a BMI >30) is seldom greater than 35% (Brewis, 2010). A pertinent question to ask therefore is: if thrifty alleles are really so advantageous for survival in famines, then how come so many of us did not inherit these alleles?
One of us has previously sought to illustrate this issue in a more quantitative manner (Speakman, 2006) by considering a ‘thrifty allele’ that confers a per allele survival advantage on its holder of 1.5%. Hence, heterozygous carriers of the ‘thrifty allele’ survive a famine on average 1.5% better than those individuals that are homozygous for the non-thrifty alleles, and a homozygous thrifty individual survives famines 3% better. A model of the spread of this allele from a single mutation in an effective population of 5 million individuals shows that it would move to complete fixation in only 600 famine events. Given a conservative estimate that famines with significant mortality occur once every 150 years or so (Speakman, 2007), it would only take 90,000 years for a thrifty allele to become completely fixed. This might seem a long time, but is only 2.2% of the available time since the emergence of Australopithecines 4 million years ago. By extension, any thrifty mutations, as long as they occurred during the first 97.2% of human history, would already be at complete fixation.
This scenario for the evolution of thrifty genes makes a critical assumption about the genetic architecture of the cause of obesity. This assumption is that obesity is caused by a relatively small number of genes, mutations in which cause relatively large differences in body weight that would translate to the 1.5% per allele differences in survival between individuals during a famine. This view was guided by the fact that, at the time the previous paper was written, the only examples we had of genes that caused obesity were mutations in single genes that had major impacts on body weight predominantly via disruption of food intake (O’Rahilly, 1998; O’Rahilly, 2009; Farooqi et al., 1999; Farooqi et al., 2001; Farooqi et al., 2002; Farooqi et al., 2007; Farooqi and O’Rahilly, 2008): so-called ‘monogenic’ obesities. At the time it was widely believed that the large genetic variation, which we knew from the twin and family studies underpins the majority of the variance in BMI, would be traced to mutations among a relatively small number of key genes.
Over the last 5 years there have been remarkable developments in our understanding of the genetic architecture of the obesity epidemic, owing in large part to genome wide association studies (GWAS) (Day and Loos, 2011), which have allowed us to probe in unprecedented detail the association between individual single nucleotide polymorphisms (SNPs) and BMI. The first common SNP associated with obesity in the general population identified in this manner was rs9099329, which lies in an untranscribed region adjacent to the FTO gene (Wellcome Trust Case Control Consortium, 2007). The ‘susceptible’ variant allele of FTO confers an effect on BMI that is equivalent to 1.5 kg in an average height person. This has been widely interpreted as a 1.5 kg effect on fatness but, given the imprecise linkage of BMI to body fatness (e.g. Ode et al., 2007; Okorodudu et al., 2010), this might be an overestimate. Nevertheless, the rs9939609 SNP, it turns out, has an exceptionally large effect relative to other SNPs identified by the GWAS approach. The largest study to date – the Genetic Investigation of Anthropometric Traits, or ‘GIANT’, consortium (Speliotes et al., 2010) has surveyed SNPs in 123,865 individuals and identified 32 important SNPs for obesity, but these confer much smaller effects averaging about 5–600 g of fat per allele. The effects of these SNPs were completely independent and additive. Perhaps most interestingly, these SNPs together explain only 7% of the variance in BMI. Yet we know that 65% of the variation in BMI is genetic (above). It has been extrapolated from these studies that there are probably another 200 or so SNPs with similar effect sizes and there are probably hundreds to thousands of other loci each contributing a per allele effect of less than 100 g/allele (Hebebrand et al., 2010).
This genetic architecture potentially causes a serious issue for the quantitative arguments we have made about the spread of thrifty alleles (Speakman, 2006), and it might well be that this structure identified by GWAS is compatible with, and hence indirectly supports, the TGH. The problem is that it seems very unlikely that an allele resulting in deposition of only 80–100 g of fat would lead to a 1.5% difference in survival under famine conditions. The spread of such an allele in the population would consequently be much slower than in the scenario presented in Speakman (Speakman, 2006). One might imagine, therefore, that if mutations affecting fat deposition had occurred at random over the past 4 million years, some of these older mutations might have moved to fixation, but that many mutations would still be under the process of selection and their fixation would be incomplete. We would then have a population embedded in modern society containing a random mix of about 1000 susceptibility genes each with a minor effect and most of these genes exhibiting a mix of zygosity at key SNPs: more ancient mutations being closer to fixation than more recent mutations.
In this paper we will evaluate whether this is indeed a credible scenario and hence whether the genetic architecture of the modern epidemic, as revealed by the GWAS studies, lends support to the TGH. The argument we will develop is as follows. We will first generate a mathematical model of the process of starvation based on our previous data concerning energy demands and body composition in a population of 592 adults (Speakman and Westerterp, 2010). This model allows prediction of the survival duration of individuals that vary in their levels of body fatness. We will use this model to predict the impact of a mutation that leads to deposition of small amounts of fat on survival time. The percentage difference in survival time with or without this small amount of fat is thus a measure of the selective advantage that this mutation would confer under famine conditions. We will then use this more realistic evaluation of the survival advantage conferred by ‘thrifty alleles’ to model the spread of such alleles over the period of human evolution.
METHODS AND RESULTS
A model of starvation
There have already been five models that have attempted to mathematically describe the process of starvation from a perspective of energy imbalance (Song and Thomas, 2007; Alpert, 2005; Caloin, 2004; Elia et al., 1999; Hall et al., 2002) and an output from three of these models is the effect of initial body composition on the time that an individual can survive in the absence of food. In addition, there have also been several previous models that have mathematically described the responses of individuals to energy imbalance, including weight loss (Westerterp et al., 1995; Speakman et al., 2002; Thomas et al., 2009; Thomas et al., 2010; Hall, 2006; Hall, 2010a; Hall, 2010b). Although it would be theoretically possible to model starvation using these latter models by setting the intake parameter to 0, they were not specifically formulated to deal with such large energy imbalances over the protracted periods concerned here. The models specifically dealing with starvation (above) differ in their underlying assumptions and in their details, and hence derive rather different quantitative outputs, while qualitatively agreeing on the expected finding that an individual that is fatter will survive longer than one who is thinner. There are also some less mathematical approaches that derive similar conclusions. Inadequacies in these previous models have led us to derive a new model that we will then parameterise using data from the literature.
The general equation for energy balance in humans (Hall et al., 2012) states that the amount of energy consumed Ein (food intake minus faecal production) must be equal to energy that is expended (Eout) plus or minus the energy that is stored (Estor), because energy can neither be created or destroyed (the first law of thermodynamics). Generally,
| (1) |
That is, the amount of energy stored is the difference between energy intake and expenditure. If expenditure exceeds intake then storage will be negative and vice versa. Note that, in this formulation, contrasting some other models, the units are energy and not the rates of energy utilisation (energy per unit time), although in practice the calculations of energy would be made over some fixed time period (e.g. a day). Energy expenditure (Eout) can be divided into four separate components. The energy required for basal energy expenditure (Ebee), the extra energy that is used following ingestion of a meal [called either diet induced thermogenesis (Edit), the thermic effect of food or the specific dynamic action], energy expended on physical activity (Epa) and energy used for thermoregulation (Et). Hence,
| (2) |
The energy stored in the body can be divided into three compartments: stored glycogen (Egly), stored fat (Efat) and protein that is a component of lean tissue (Eprot). Although the latter has primarily other functions, it represents a source of energy that can be utilised to prolong survival in the absence of intake (Forbes, 1987; Prentice et al., 1991; Caloin, 2004; Elia et al., 1999; Afolabi et al., 2007). It is primarily the compromised functions that occur when lean tissue is mobilised that ultimately leads to death when starving. Protein is found in the skeleton but we assume that this protein does not contribute to energy balance during starvation. Generally, therefore,
| (3) |
Substituting Eqn 2 and Eqn 3 into Eqn 1 gives:
| (4) |
During starvation, by definition, there is no food intake (Ein=0) and hence the diet-induced thermogenesis is also zero (Edit=0). For humans, we can also assume that they do not expend energy on thermoregulation, because they generally inhabit thermoneutral conditions (Et=0). We can also define the energy cost of physical activity as a function of basal energy expenditure. That is:
| (5) |
where λ is a constant. This greatly simplifies the situation and by substitution we can rewrite Eqn 4 as:
| (6) |
The minus in front of the storage terms reflects the fact the storage is being depleted. This is the fundamental equation describing energy balance in starvation. This equation is similar to previous treatments but differs in some key elements. Song and Thomas (Song and Thomas, 2007), for example, ignored the energy expended on physical activity (assumed λ=0) and the energy supplied by glycogen (Egly=0), but included an additional term, which was the conversion of fat into ketone bodies, which are a crucial component of brain metabolism. Alpert (Alpert, 2005) included glycogen with protein in a ‘lean tissue’ compartment and placed a constraint on the daily mobilisation of fat.
Given Eqn 6, there are two key issues that need to be resolved before a prediction can be made of the impact of variations of the different parameters on survival. The first is that Eqn 6 implies that the energy required for basal expenditure and physical activity is supplied by glycogen, fat and lean tissue (protein), but it does not indicate the ratios in which these different sources of energy are utilised (see also Yang and Van Itallie, 1976; Payne and Dugdale, 1977; Forbes, 1987; Prentice et al., 1991; Dulloo, 1998; Dulloo and Jacquet, 1999; Hall, 2010a; Hall, 2010b; Hall et al., 2011). The second issue is that Eqn 6 specifies a process of energy utilisation, but it does not indicate the conditions under which that process ends, i.e. the state in which the starving individual dies of starvation. We will now address these two issues.
Clearly, individuals start the process of starvation with a given level of each of the energy stores, i.e. ETOTgly, ETOTfat and ETOTprot. As time progresses these stores are depleted. Thus, after any given time interval (t), the level of storage of each of these compartments can be deduced from the amount available at the start of that time interval minus the amount that is utilised during that interval. Generally, the recurrence forms of the equations linking energy storage terms over time are:
| (7) |
| (8) |
| (9) |
The body weight (BW) of an individual at any given time (t) is the sum of the weights of the total storage compartments plus the skeleton (Wskel) at that time point. The weights of the individual compartments are defined by their energy density, which includes their water content when stored. Hence, the energy density (kJ/g) of glycogen is EDgly, of fat is EDfat and of protein is EDprot. Generally, the non-fat terms can be collected into a single term called ‘lean tissue’ or fat-free mass. Hence, lean tissue weight (LTW) at time t is defined as:
| (10) |
and fat tissue weight (FTW) at time t is defined as:
| (11) |
Total body weight can thus be defined as:
| (12) |
This formulation allows us to define the outstanding issues in a more tractable way. First, we will consider the issue of the point of death. Many empirical studies have observed the point of death of people from starvation and have concluded that once an individual reaches a BMI of 12 the probability of recovery, even if the subject is re-fed, is virtually zero (Leiter and Marliss, 1982; Owen et al., 1998; Henry, 1990; Rosling et al., 2011) [but see Collins (Collins, 1995) for a report on the survival of Somali famine victims at a BMI of 10, perhaps influenced by their unusual height].
We will therefore define the point of death as occurring when:
| (13) |
and
| (14) |
where h is the subjects height (m).
Second is the issue of utilisation of the different energy reserves. The source of energy used by the brain is usually glucose (Siesjo, 1978). When an individual starves, the glucose in the body is rapidly used up and the individual must then obtain glucose to sustain brain metabolic rates by a combination of gluconeogenesis from fat and glycogenolysis of the glycogen stores (Nilsson and Hultman, 1973; Rothman et al., 1991; Kreitzman et al., 1992). Once the glycogen stores are depleted, the glucose must be generated by gluconeogenesis alone, but generally this process is insufficient to meet the total energy demands of the brain. The shortfall can be initially made up by lactate (Boumezbeur et al., 2010), but the starving brain eventually switches to a mix of glucose and ketones that are derived from fat mobilisation. Hence, there is a hierarchy of energy utilisation in the initial phase of starvation that places use of the very small amounts of glucose in the body first, followed by depletion of the glycogen stores and then utilisation of fat and protein. Because the stores of glucose are very small, we will ignore their contribution and define two phases: the glycogen phase and the fat-protein phase. This separation is consistent with previous treatments of energy partitioning in starvation (Caloin, 2004). To simplify things further we will assume in the glycogen phase that no fat or protein is used, and then in the second phase when the glycogen stores are depleted that only fat and protein are used.
The sizes of the energy stores not only define the body weight, but are recognisable power functions of body weight. Glycogen is stored in both skeletal muscle and the liver. Hence, the total body glycogen consists of the sum of two terms: the concentration in the liver (Cliv) multiplied by the liver mass, and the concentration in the skeletal muscle (Csk) multiplied by the mass of skeletal muscle. Generally,
| (15) |
where weight of the liver is defined as Aliv × BWε and weight of skeletal muscle is defined as Ask × BWζ. On average, across a population, as individuals get heavier the proportion of fat they carry also gets larger. We can therefore define the proportion of the body that is fat (Pfat) as a power function of body weight:
| (16) |
where ξ is a fixed constant, η is a constant multiplied by age (years), θ is a constant multiplied by loge body weight (kg) and κ is a constant multiplied by a dummy variable reflecting sex (1=male and 2=female). This formulation assumes that individual variation in height does not explain any of the residual variance once the effects of body weight and sex are taken into account.
Having defined Pfat in this manner we can derive ETOTfat and ETOTprot as follows:
| (17) |
| (18) |
During phase 1 we will assume that the glycogen is depleted to 0.1-times its initial value. Thus, the duration of phase 1 is defined by the starting weight of the individual, which defines the sizes of these storage compartments. This formulation is also useful because basal energy expenditure (Ebee) can be defined as a power function of the fat and lean tissue weights plus the age and sex of the subject. Generally, logeEbee at time t is:
| (19) |
where Ξ, ψ, ω, χ and ε are constants, age(t) is the age at time t in years, and sex is a dummy variable where male is 1 and female is 2. Hence, although a larger individual has greater sizes of their glycogen stores, they also utilise these stores more rapidly. So the actual duration of phase 1 is a combination of the effects of initial body weight on storage and energy demands.
In general, phase 1 lasts for n days, where:
| (20) |
where all the terms are a function of body weight. Thus, substituting Eqns 15 and 19 into Eqn 20 gives:
| (21) |
once the first phase is over the individual starts to utilise stored fat and protein.
We can define the relative utilisation of fat and protein by a ratio (Rfat; the proportion of total energy utilisation that comes from fat):
| (22) |
Rfat varies with the amount of fat in the body relative to the amount of lean tissue. Hence, fatter individuals preferentially utilise fat, but use increasing amounts of protein as the fat compartment gets smaller, particularly as fat levels get very low (phase 3 of starvation) (Dulloo and Jacquet, 1999), so:
| (23) |
where Λ and Γ are constants not equal to 1.0 and 0, respectively. That is, the utilisation of fat and protein is not a simple linear reflection of their availability in the body. The physiological basis of Rfat remains unclear (Alpert, 2005), but we can define it empirically using the parameters Λ and Γ.
Having defined Rfat from the body composition, it is possible to model the sequential changes in body composition over time, which in turn affect the rate at which such resources are utilised via the effect of changing body weight on Ebee. Consequently, we can model the duration that an individual will survive under complete starvation if we know their initial body weight, their age and sex, and the values of all the unknown constants in the above equations. This is performed as a recurrent calculation over time intervals (t) using a day as the unit of time. Generally,
| (24) |
where ΔBW is the change in weight over the time interval and this is defined from the relative utilisation of fat and protein (Eqn 22) in combination with the demand function for Ebee (Eqn 19), both of which depend on BW(t).
Parameterising the model
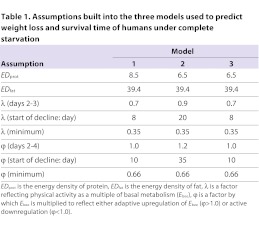
We searched the literature and utilised some data from a cohort that we have published on previously (Westerterp and Speakman, 2008; Speakman and Westerterp, 2010) to derive values of the constants in the above equations. The value of λ, in Eqn 5, which defines the amount of energy spent on physical activity in terms of Ebee has been measured on many occasions in fully fed individuals using the DLW method. λ seems to be independent of body weight but declines in relation to age once an individual passes the age of 55 (Speakman and Westerterp, 2010). The average value across many studies of individuals in western society is about 0.7 (e.g. Black et al., 1996; Speakman and Westerterp, 2010); estimates from developing countries are not significantly higher than this (Westerterp and Speakman, 2008). During complete starvation we can expect complex effects on λ, as are also observed during caloric restriction in humans (Martin et al., 2007) and rodents (reviewed by Speakman and Mitchell, 2011). Initially during complete starvation it would be adaptive to be more active and to seek food. However, if no food is available, continuing to be active would place an extra drain on stored resources; it would therefore be adaptive to return activity to normal levels and then progressively reduce activity to minimise energy utilisation. Hence, in the current model we have assumed that λ=0.7 on day 1, and then increases to 0.9 for 2 days before returning to 0.7 for an additional 2 days. We then modelled two scenarios. In the first we assumed that the level of λ would remain stable for a further 5 days before it started to decline at a rate of 0.005 per day until a baseline value of 0.35 is reached, reflecting virtually no physical activity in the latter stages of starvation. In the second scenario we assumed that the decline did not start until day 20 of starvation.
During starvation and severe food deprivation individuals respond by adaptive changes in their Ebee beyond that expected from the reductions due to reducing body size (Kleitman, 1926; Keys et al., 1950; Grande et al., 1958; Luke and Schoeller, 1992; Dulloo and Jacquet, 1998; Alpert, 2005; Alpert, 2007; Weyer et al., 2000; Prentice et al., 1991; Martin et al., 2007). Alpert (Alpert, 2007) suggested that by day 40 of severe restriction [data from the Keys et al. experiment (Keys et al., 1950)], Ebee was only 66% of the expected level. In contrast, Owen et al. (Owen et al., 1998) reported a decrease in Ebee of only 8% (not significant) after 18 days of complete starvation, and Yang and Van Itallie (Yang and Van Itallie, 1976) also reported no significant decrease after 10 days of starvation. Given the diversity of responses in the literature, we modelled two different scenarios. In both cases we multiplied Ebee resulting from Eqn 19 by an additional factor [φ where φ=f(t)]. In the first scenario it was assumed that Ebee was at the level expected from body composition defined in Eqn 19 for 10 days (φ=1) but then φ declined at a rate of 0.005 per day until it reached 0.66. In the second scenario the decline started at day 35 instead of day 8. It has been suggested that Ebee might actually increase in the very first few days of starvation (Mansell et al., 1990; Zauner et al., 2000), so we also included this scenario as well into the models, allowing φ to be 1.2 on days 2–4 of starvation. It has also been suggested that Ebee might also increase at the very end of starvation just prior to death (Rigaud et al., 2000), perhaps associated with almost exclusive protein catabolism, but we did not include this effect in the model. An additional possibility is that Ebee declines in relation to the initial adiposity (Luke and Schoeller, 1992; Dulloo and Jacquet, 1998), the reduction being less in more obese subjects. This effect was not taken into account but would tend to make the weight loss estimates we have made slightly too large.
Glycogen is a macromolecule comprising multiple glucose units, but the energy density of glycogen (EDgly) is much lower than that of glucose (14.2 MJ/kg) because glycogen is stored with 3×its own weight of water (Olsson and Saltin, 1970; Kreitzman et al., 1992). Protein energy content depends on its amino acid composition. This is generally assumed to be fixed with the average composition of amino acids and this leads to an energy density for protein (EDprot) of about 6.5 MJ/kg (McArdle et al., 2001) because it is also stored with attached water molecules. However, others have suggested that EDprot is higher, at 7.6 MJ/kg (Hall, 2008) or even 8.5 MJ/kg (Alpert, 2005). We used both 6.5 and 8.5 MJ/kg estimates in the models. The energy density of stored fat (triglycerides) is almost universally assumed to equal 39.4 MJ/kg (e.g. Leibel and Hirsch, 1984).
Glycogen is stored in the liver and in the skeletal muscle. Mass for mass the amount stored in the liver is higher, but because the liver is smaller the total store in the muscle is higher. In fed subjects the estimated glycogen concentrations of the liver (Cliv) (Nilsson, 1973; Rothman et al., 1991; Taylor et al., 1996; Petersen et al., 2004; Awad et al., 2010) approximate 500 mmol/kg dry weight and in muscle (Csk) 300 mmol/kg dry weight. Müller et al. (Müller et al., 2011) published scaling relationships for total muscle mass by DXA and liver mass from MRI scanning in 262 adult humans. These were muscle mass (kg) =0.93×BW0.76 and liver mass (g) =0.1×BW0.62. The values for ε and ζ in Eqn 15 were therefore set at 0.76 and 0.62, respectively. Assuming a water content of both the liver and skeletal muscle of 73%, the corresponding dry contents of these organs was 0.2511×BW0.76 and 0.027×BW0.62. Aliv and Ask in Eqn 15 were therefore set at 0.2511 and 0.027, respectively. The glycogen contents (mmol) would therefore be 75.33×BW0.76 and 13.5×BW0.62. Given a molecular mass of 180.16, one mmol of glycogen would weigh 0.1802 g; hence, substituting into Eqn 15, the total glycogen content (ETOTgly) was defined as:
| (25) |
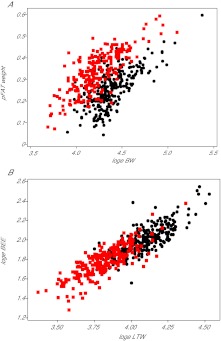
We have previously studied a cohort of 592 adults of both sexes ranging in age from 18 to 89 where we measured their body composition using DXA (Speakman and Westerterp, 2010). For that cohort we calculated the fat mass and then expressed it as a proportion of the total body weight (PFAT). The PFAT was dependent on body weight, sex and age (Fig. 1). The best-fit regression model explained 75% of the variance in PFAT:
| (26) |
where BW is in kg, age is in years and for sex males=1 and females=2.
Fig. 1.
Empirical relationships showing the proportion of body that is fat (pFAT) in relation to body weight (BW) and the relationship between basal energy expenditure (BEE) and lean tissue weight (LTW). (A) The proportion of fat in the body across a cohort of 592 individual adults aged between 18 and 93 years in relation to sex and body weight. Body composition was determined by DXA. The y-axis (pFAT weight) is the proportion of fat in the body by weight and the x-axis is the logn body weight in kg. Males are shown as black dots and females as red squares. (B) For the same individuals, the relationship between basal energy expenditure (Ebee) and loge lean tissue weight (LTW).
These data show that as individuals get heavier they get proportionately fatter. Moreover, at any given body weight females carry on average about 13.4% more body fat then males.
To explore the relationship between the proportion of the body that comprises fat (PFAT), and the utilisation of fat during weight loss (Rfat) we calculated the fat (FW1) and lean (LW1) contents of the body corresponding to a given body weight (BW1) using the data for the same cohort of 592 individuals (Speakman and Westerterp, 2010). We then calculated the same values (FW2 and LW2) for an individual that was 1 kg lighter (BW2=BW1–1). If an individual was to change body weight from BW1 to BW2 then it would utilise FW1–FW2 fat tissue and LW1–LW2 lean tissue. The Rfat ratio for this weight change could therefore be calculated knowing the energy densities of these tissues (above) and related to the proportion of fat in the body at the mid-point between BW1 and BW2. This procedure was iterated across the scale from high to low body mass in both males and females. The relationship between the Rfat and Pfat was described by the least squared regression:
| (27) |
which explained 98% of the variance in the fat utilisation ratio (Rfat). We therefore defined Γ and Λ from Eqn 22 as 0.489 and 0.547, respectively. This curve shows that when individuals are obese they preferentially burn fat but at lower body weights, as fat levels get very low, they increasingly burn protein (see also Forbes, 1987; Prentice et al., 1991; Dulloo and Jacquet, 1999; Alpert, 2007). This approach assumes that the cross-sectional differences in body composition are maintained longitudinally in individuals when starving, an assumption that has been previously questioned (Alpert, 2005; Alpert, 2007) and also assumes that there is no limit on the capacity to mobilise fat reserves, which has also been postulated (Alpert, 2005). The extent to which these two assumptions compromise the model is evaluated below, where we validate the model against actual data in starving individuals. We used the same data in Speakman and Westerterp (Speakman and Westerterp, 2010) to define the relationship between Ebee and LTW, FTW, age and sex (Fig. 1B). The least squares fit regression for these data gave values for the constants in Eqn 19 as Ξ=–0.7061, ψ=0.6241, ω=0.0907, χ=0.00125 and ε=0.0607.
Predicted effects on weight loss and survival time during total starvation
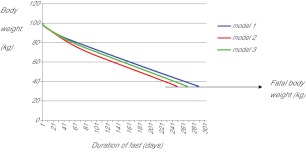
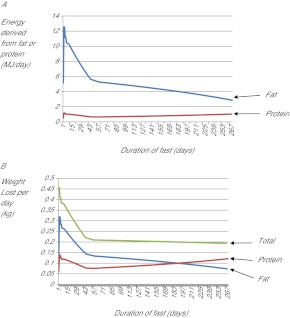
Because some of the parameters could not be defined exactly, we generated three different models. The details of the assumptions for values of the different parameters built into these models are summarised in Table 1. To show the different predictions from these models we predicted the change in body weight during total starvation for an obese 100 kg, 1.64 m tall female aged 35 (BMI=37.2). The results for the changes in body mass are shown in Fig. 2. During the early phase of weight loss the models were very similar but they started to diverge around day 35. Weight loss was initially more rapid in all three models. Beyond day 30 the rates of weight loss were virtually linear until the critical fatal BMI of 13 was reached. Empirically observed patterns of weight loss support this almost linear decline following a more rapid initial phase of weight loss (Heymsfield et al., 2011). Because the three different models resulted in different rates of weight loss they intercepted this critical low level at different times. Model 1 predicted a survival time of 289 days, model 2 of 249 days and model 3 of 268 days. Differences in the model assumptions therefore created a major impact on the final survival time and the level of weight loss expected at any given time from the start of the fast. For example, at day 150, model 1 predicted the body mass would be 62.5 kg, model 2 predicted 56.0 kg and model 3 predicted 59.8 kg. Although the predicted weight loss appeared to be almost linear throughout the period of starvation, these linear tracks were underpinned by a complex change in the pattern of utilisation of different body compartments. In all models glycogen utilisation lasted for less than 1 day. This is consistent with experimental data showing that oxidation of carbohydrate from glycogen was undetectable after 2–3 days of fasting (Owen et al., 1998). The contribution of fat and protein to energy demands over the remaining period of fasting for model 3 are shown in Fig. 3A. From this plot it can be seen that throughout the whole fast the contribution of fat to the total daily energy utilisation exceeded that of protein. There was a progressive drop in the fat contribution through time. In the first week it contributed about 11 MJ/day but by day 268 this had dropped to just 3.0 MJ/day. Protein in contrast contributed about 0.8 MJ/day in the first 150 days of the fast rising slowly to about 1.3 MJ/day at the very end. Contrasting the patterns of contribution to energy requirements, protein made a greater contribution to the total weight loss (Fig. 3B), reflecting its lower energy density. Until day 180 the fat also contributed more to the daily weight loss than protein did, but from day 180 onwards protein losses made an increasingly larger contribution until around the end of the fast (day 268), at which point the protein losses were contributing 1.5× more to weight loss than fat was. Similar patterns of protein and fat contributions to the total energy utilisation and weight loss were apparent for the other models. The predominance of fat over protein utilisation in the first few weeks of starvation is consistent with empirical measurements of substrate oxidation during starvation (Owen et al., 1998) and body composition measurements (reviewed by Heymsfield et al., 2011). One exception to this rule appears to be the fast by David Blaine, who lost predominantly protein over his 44 day fast (Jackson et al., 2006). The progressive shift from predominantly fat to predominantly protein utilisation in fasts has also been remarked on previously in many studies, some of which have defined the response to starvation as comprising three phases (phase 1 comprising mostly glycogen utilisation, phase 2 comprising predominantly fat and phase 3 protein oxidation) (e.g. Peret and Jacquot, 1972; Goodman et al., 1984; Forbes, 1987; Prentice et al., 1991; Caloin, 2004; Heymsfield et al., 2011), although the existence of a separate phase 3 has been questioned (Dulloo and Jacquet, 1999).
Table 1.
Assumptions built into the three models used to predict weight loss and survival time of humans under complete starvation
Fig. 2.
The trajectories of weight loss in a hypothetical 100 kg female subject starving to death, using three different models each with slightly different assumptions. See Table 1 for the model assumptions.
Fig. 3.
Energy utilisation from fat and protein, and weight loss during a hypothetical fast to death. (A) The modelled energy contributions by fat (blue) and protein (red) oxidation throughout a hypothetical 268-day fatal fast by a 100 kg female. Throughout the entire fast the majority of energy is supplied each day by fat oxidation, but this contribution by fat gets progressively smaller, whereas that from protein remains almost constant. (B) The modelled contributions to weight loss (green indicates total weight loss per day) by fat (blue) and protein (red) for the same fast. Until about half way through the fast, weight loss was predominantly fat, but in the second half of the fast it was predominantly protein.
Model validation
None of the previous models of weight loss or survival time during starvation have been validated against actual data beyond 30 days of starvation (Hall, 2006; Hall, 2011; Hall, 2012). We sought to validate the models we generated in two ways. During hunger strikes individuals deliberately refuse food, while sustaining water intake, generally to draw public attention to a political cause. Occasionally these hunger strikes are prolonged until the individuals die (Leiter and Marliss, 1982; Altun et al., 2004). We found records of the time taken to die for 20 political hunger strikers dating back to 1920, all except one of which were male. Among these individuals the average time to death was 62.5 days (range 11 to 115 days). From the model this corresponds to a predicted average starting body weight of 82 kg (predicted range of starting weights from 50 to 112 kg). Unfortunately, there are data for the body weight and height at the start of a fatal fast for only one individual: an American weighing 61.4 kg who starved himself to death in 1920 (Meyers, 1917; Elia, 2000). The models predicted that at this starting weight he would live for 63 days (model 1), 41 days (model 2) and 47 days (model 3). In fact he survived 63 days, the exact duration predicted by model 1.
In addition to people starving themselves to death, very often in the past people have starved themselves for protracted periods with the aim of losing weight (Johnstone, 2007). This ‘therapeutic fasting’ as a treatment for obesity was initially advocated by Folin and Denis (Folin and Denis, 1915) and Benedict (Benedict, 1915), but was not widely adopted until it and was picked up by Bloom (Bloom, 1959). During the early 1960s it was common for obese people to be placed on 12- to 16-day fasts to lose body weight (e.g. Drenick et al., 1964; Benoit et al., 1965; Harrison and Harden, 1966; Ball et al., 1967; Gilliland, 1967). Gradually, the durations of these fasts increased until fasts exceeding 100 days were relatively common (Thomson et al., 1966) culminating in a fast of 382 days by a grossly obese male patient from Dundee in Scotland (Stewart and Fleming, 1973). Therapeutic fasting, however, fell out of favour when it became apparent that it had a high incidental mortality rate mostly due to renal dysfunction and cardiac damage (Cubberley et al., 1965; Spencer, 1968; Runcie and Thomson, 1970). Fasting for protracted periods without the intention of dying remains occasionally practiced (Johnstone, 2007) for religious reasons, to gain public attention for a cause (e.g. Mia Farrow’s 12-day fast to draw attention to the crisis in Dafur) or as a publicity stunt (David Blaine’s 44-day fast in a perspex box suspended above the banks of the Thames in London, UK (Jackson et al., 2006; Korbonits et al., 2005; Korbonits et al., 2007).
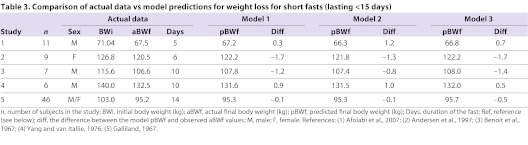
The extent of weight loss during prolonged fasts provides a second method to validate the model predictions. We collated data from the literature for 51 recorded fasts exceeding 15 days in duration where data were available for the starting and finishing weights of the subjects. We entered the starting weights into the three models to predict the finishing weight at the time when the fast was terminated (Table 1). In addition we compiled data on shorter fasts lasting 5–20 days (Table 2). In these shorter fasts the individual data were not available so we used the group means instead.
Table 2.
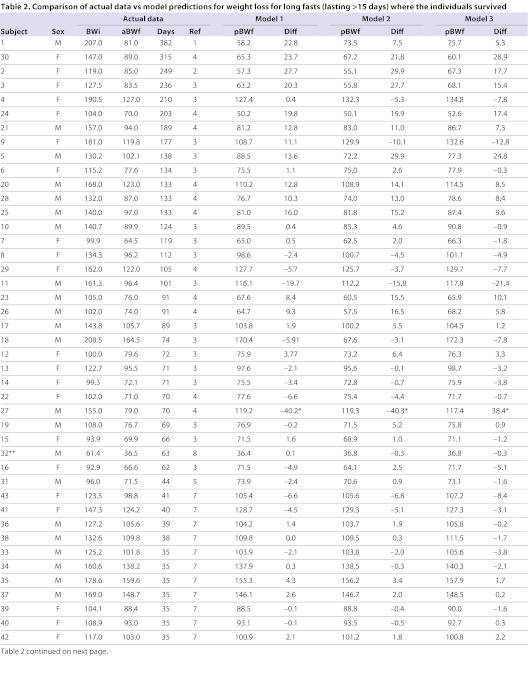
Comparison of actual data vs model predictions for weight loss for long fasts (lasting >15 days) where the individuals survived
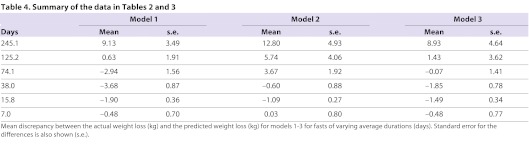
Combining the data from Tables 1 and 2 we grouped the fasting durations into classes and then compared the actual weight losses with those predicted from the three models. The differences between the model predictions and the actual weight losses in relation to fasting time are illustrated in Fig. 4 and tabulated in Table 4. At any particular duration there was a wide variation in the discrepancy between the actual and predicted weight losses. These discrepancies are at least in part because the model predictions depend on the age of the subject, yet the age was not specified for almost all the fasts reported in Tables 3 and 4 and hence we had to assume a fixed age (we used 35). Moreover, some weight loss must occur, and be variable between individuals, because of faecal losses – yet these were not accounted for in the model predictions. Ignoring the potential differences between longitudinal and cross-sectional responses (Alpert, 2007) and also ignoring a putative daily limit on fat oxidation (Alpert, 2005) did not appear to seriously compromise the predictive abilities of the models.
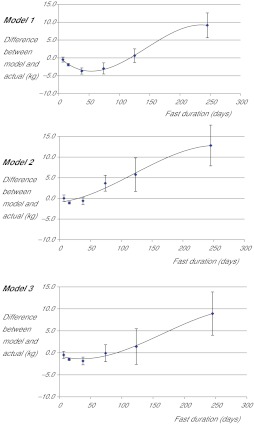
Fig. 4.
The differences between the predicted weight loss and the observed weight loss during complete starvation in humans. Predictions from three models are presented and compared with actual fasts. Points show the average discrepancies and the error bars show the standard deviations. The fitted lines show third-order polynomial best-fit regressions (r2>0.98 in all three cases).
Table 4.
Table 3.
Comparison of actual data vs model predictions for weight loss for short fasts (lasting <15 days)
The average differences between the models and the actual weight losses showed similar patterns as a function of the duration of the fasts for all three models. In particular the weight loss in the early phase of the fast was greater than the models predicted, but for very long fasts subjects lost less weight than predicted by the models. These patterns were best described by third-order polynomial equations. This discrepancy for very long fasts may mean that additional compensatory measures may be recruited when subjects fast for such protracted periods. For example, Ebee may continue to decline below the level reported in the Minnesota study (i.e. φ<0.66), and the level of physical activity relative to Ebee (λ) may also continue to decline below the value of 0.35 that we considered minimal. Nevertheless, it was impossible to eliminate the overestimated weight loss even by allowing the critical parameters to fall to φ=0.5 and λ=0.15. Because some of these individuals were being treated on an outpatient basis it is tempting to speculate that the failure of the models to accurately predict their weight loss was because they were not completely starving themselves in the latter phases of the fasts. For the early phase of the fasts, where we have more information on what responses individuals make, the discrepancies in the early phase of the fasts were greatest for model 1. Although model 2 had the lowest discrepancies for fasts up to 50 days, between 50 and 200 days it was more discrepant than model 3. On average, model 3 provided the least discrepant predictions over the widest duration of fasts. We therefore used model 3 to complete the analysis. Using models 1 and 2 did not change any of the conclusions that were ultimately drawn.
Using the model to predict the effect of fat content on survival time
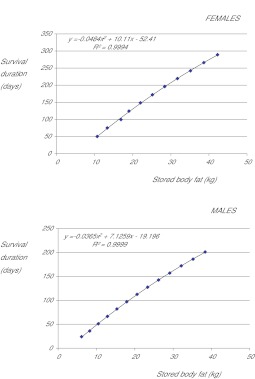
We used model 3 to predict the survival time of individual females that varied in total weight between 50 kg (BMI=18.6, fat content 10.66 kg) and 100 kg (BMI=37.2, fat content 32.3 kg) and for individual males that varied in body weight from 55 kg (BMI=16.97, fat content 6.1 kg) and 115 kg (BMI=35.5, fat content 38.4 kg). The BMI values stated above were estimated assuming average female height of 1.64 m and average male height of 1.8 m. The relationships between body fat content and survival time are shown in Fig. 5. In both males and females the relationships were positive and very slightly curved so hence best described by second-order polynomials. These plots show the expected result for both sexes, that if an individual stores more fat then, under complete starvation, they will live longer than someone who stores less fat. These differences in initial fat content are correlated with differences in protein stores, which are automatically adjusted in the model. They also show that at a given level of fat storage females will survive longer than males, although below a body fatness of 20 kg (BMI approx. 25) the difference between the sexes is minimal.
Fig. 5.
The predicted effect of body fatness on survival time under complete starvation for females and males carrying different amounts of body fat. The lines reflect the second-order polynomial equations that are shown in the plots.
Modelling the impact of alleles of small effect on survival time
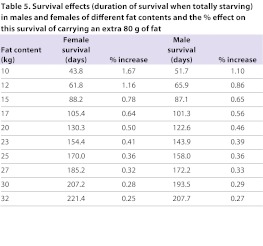
To explore the effect of alleles that have very minor effects on body fatness, which from the GWAS studies appears to be the majority of genetic variants in the human population, we used the relationships in Fig. 5 between fat content and survival. We considered individuals with fat contents up to 32 kg. We chose these limits because these are the fat masses that equate in the model to survival for about 150–200 days, which we considered to be the limits at which the model retained accuracy (Fig. 4). Moreover, individuals storing more fat than this were probably rare during the early period of our history. For each fat mass we predicted the survival time, and we then predicted the survival time if the individual stored 80 g more fat (Table 5). We then expressed the increase in survival time as a percentage of the survival time without the extra 80 g of fat. Having an extra 80 g of fat had only a minor effect on survival, as anticipated. Expressed relative to the starting amount of fat this generated an increase in survival time of 1.67% and 1.1% in females and males, respectively, when they had only 10 kg of body fat. However, at 32 kg of fat to start with, having an extra 80 g would only increase survival in females by 0.25% and in males by 0.27%. To take a conservative approach we assumed therefore that the smallest effect that an allele conferring deposition of an extra 80 g of fat would have would be about 0.25%. That is, a heterozygotic individual carrying one variant allele would have a 0.25% better survival chance in a famine than a wild-type homozygote, whereas the homozygotic individual with two alleles conferring deposition of 160 g of fat would survive 0.5% better. Using these values we modified our previous model (Speakman, 2006) to predict the number of famine events it would take for such a mutation to move to fixation under the pressure of natural selection as envisaged by the TGH.
Table 5.
Survival effects (duration of survival when totally starving) in males and females of different fat contents and the % effect on this survival of carrying an extra 80 g of fat
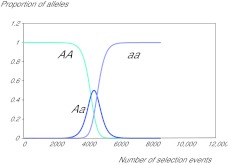
The model (Speakman, 2006) is a simple selection model based on differential expectations of survival of different genotypes in a series of selection events. The population is set at 5 million individuals and it is assumed that there is a single mutation event to generate a single heterozygous individual (Aa) at time 0. The abundance of each genotype is then calculated after a selection event resulting in differential mortality. That is, after event 1 the population abundance of the heterozygote Aa=(1/5,000,000)×pSurv(Aa), where pSurv(Aa) is the probability of the heterozygotic individual surviving, and the abundance of the homozygotic wild type (AA) is (4,999,999/5,000,000)×pSurv(AA), where pSurv(AA) is the probability of the wild-type surviving. The population is then assumed to expand back to 5 million individuals before the next selection event, under an assumption of random mating. That is, it is assumed the different alleles confer no reproductive advantages between selection events, and there is no assortative mating favouring the appearance of the homozygotic aa genotype. The model is then iterated through multiple selection events (up to 8500 events) to generate the time course of changes in the distribution of AA, Aa and aa genotypes.
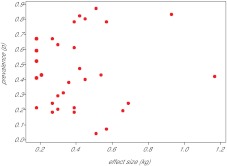
The results show that it would in fact take about 6000 famine events for such a mutation to become fixed (Fig. 6). Recall that this is a maximal estimate because (1) most identified and inferred mutations affecting fat storage have an effect size exceeding 80 g/allele, and (2) we modelled the effect of such an allele in individuals already storing large quantities of fat. In individuals storing lesser amounts the effect on survival would be greater (Table 5). If we use the estimated frequency of famine events as 1/150 years (Speakman, 2006; Speakman, 2007) then it would take about 900,000 years for such a mutation to spread through the entire population and become fixed. Given the 4-million-year timespan that hominins have existed, it is clear that this is easily enough time for putative mutations affecting obesity to become fixed, unless they had all occurred within the last million years or so. Given approximately 50% of the known SNPs linked to obesity identified to date are also found in chimpanzees (Pan troglodytes) (Southam et al., 2009), this requirement does not accord with the known facts. Let us imagine, however, that the SNPs causing obesity had all happened in the last 900,000 years as required by this model. If the SNPs occurred at random in time we would expect those having greater effects would move to fixation more rapidly than those having smaller effects if they were under selection. However, using the data from Speliotes et al. (Speliotes et al., 2010) for all the known SNPs affecting BMI, there is no significant relationship between the effect size of an SNP and its prevalence (Fig. 7).
Fig. 6.
The modelled spread of an allele due to a random mutation conferring an effect of storing an extra 80 g of fat on an individual already storing 30 kg of body fat. The allele is assumed to increase survival during famines by 0.25% [hence, survival during famine of AA (wild-type homozygote)=0.68, of Aa (heterozygote)=0.6825 and for aa (mutant homozygote)=0.685]. The allele moves from being a mutation in a single individual to complete fixation in the entire population after about 6000 selection events (famines).
Fig. 7.
The relationship between effect size and prevalence for 32 SNPs identified by Speliotes et al. as being significantly linked to BMI. r2=0.4, P=0.78 (Speliotes et al., 2010).
DISCUSSION
These data falsify the hypothesis that repeated catastrophic famine events provide the selection pressure that is responsible for the variety and prevalence of obesity gene variants identified in the GWAS studies. Because this was the original TGH proposed by Neel (Neel, 1962), we suggest that this is also a falsification of the TGH in its basic formulation. If the alleles in question also had positive effects on famine fertility as well as survival [as suggested by Prentice et al. (Prentice et al., 2008)] then they would go to fixation even more rapidly and hence this alternative adaptive scenario for the TGH is even less likely to be correct. Nevertheless, alternative selection models are possible – for example, the alleles may not be neutral in events between famines which may provide a counterbalancing selective pressure preventing the genes moving to fixation. These alternative selection models are fundamentally different from the TGH as envisaged by Neel (Neel, 1962) and subsequent iterations by many authors, and we suggest that they should be called ‘selection models for obesity’ or SMOs, to distinguish them from other models based on genetic drift (Speakman, 2007; Speakman, 2008).
The idea that the genetic basis of obesity may be a consequence of a process of genetic drift differs fundamentally from models based on selection. In the models suggested by Speakman (Speakman, 2007; Speakman, 2008) called the ‘drifty gene’ hypothesis, it is suggested that early in hominin evolution we probably had a very strictly controlled regulation of body weight and that excessive adiposity was selected against by the risk of predation [see also different models of weight regulation in Speakman et al. (Speakman et al., 2011)]. However, this selective cap on adiposity was effectively removed around 2 million years ago when we discovered fire, became social animals and invented weapons. These three factors were enough to almost eliminate the risk of predation. Under this scenario it is suggested that the genes regulating the upper cap on adiposity would be free from selection and would be susceptible to genetic drift.
Conclusion
Modelling the effects that an allele producing a minor effect on fat storage (80 g) has on survival during total starvation shows that such alleles would have an effect on famine survival greater than about 0.25%. A mutation with such a per allele effect on survival would still spread through the population to fixation in about 6000 selection (famine) events, which would take about 900,000 years of human history. Because human evolution spans a timescale about 4× longer than this, most mutations having an effect on fat storage would be predicted to move to fixation in the population if the TGH was correct – unless such mutations had all occurred in the past 900,000 years. Because we know that this is not the case, the genetic architecture of the modern susceptibility to obesity, revealed by the GWAS studies, is inconsistent with the TGH. Alternative ideas such as, but not restricted to, the ‘drifty gene’ hypothesis (Speakman, 2007; Speakman, 2008) are more consistent with the modern genetic data derived from GWAS, and may provide a better understanding of why some individuals are susceptible to obesity in modern society.
Acknowledgments
We are grateful to Jonathan Wells for interesting discussions of issues surrounding this topic, and to Tim Garvey and John Lazaro who independently raised questions at presentations about whether the GWAS data undermined the ‘drifty gene’ hypothesis.
Footnotes
COMPETING INTERESTS
The authors declare that they do not have any competing or financial interests.
AUTHOR CONTRIBUTIONS
J.R.S. developed the models and compiled the data for testing them. K.R.W. provided the database for model parameterisation. J.R.S. and K.R.W. wrote the paper.
FUNDING
J.R.S. was supported by a ‘1000 talents’ Professorship from the Ministry of Science and Technology, Peoples Republic of China, a Great Wall professorship from the Chinese Academy of Sciences–Novo-Nordisk Foundation and the Key State Laboratory of Molecular and Developmental Biology, Institute of Genetics and Developmental Biology, Chinese Academy of Sciences.
REFERENCES
- Afolabi P. R., Jahoor F., Jackson A. A., Subbs J., Johnstone A. M., Faber P., Lobley G., Gibney E., Elia M. (2007). The effect of total starvation and very low energy diet in lean men on kinetics of whole body protein and five hepatic secretry proteins. Am. J. Physiol. Endocrinol. Metab. 293, E1580–E1589 [DOI] [PubMed] [Google Scholar]
- Allison D. B., Kaprio J., Korkeila M., Koskenvuo M., Neale M. C., Hayakawa K. (1996). The heritability of BMI among an international sample of monozygotic twins reared apart. Int. J. Obes. Relat. Metab. Disord. 20, 501–506 [PubMed] [Google Scholar]
- Alpert S. S. (2005). A limit on the energy transfer rate from the human fat store in hypophagia. J. Theor. Biol. 233, 1–13 [DOI] [PubMed] [Google Scholar]
- Alpert S. S. (2007). The cross-sectional and longitudinal dependence of the resting metabolic rate on the fat-free mass. Metabolism 56, 363–372 [DOI] [PubMed] [Google Scholar]
- Altun G., Akansu B., Altun B. U., Azmak D., Yilmaz A. (2004). Deaths due to hunger strike: post-mortem findings. Forensic Sci. Int. 146, 35−38 [DOI] [PubMed] [Google Scholar]
- Andersen P. H., Kristensen K., Pedersen S. B., Hjøllund E., Schmitz O., Richelsen B. (1997). Effects of long-term total fasting and insulin on ob gene expression in obese patients. Eur. J. Endocrinol. 137, 229–233 [DOI] [PubMed] [Google Scholar]
- Awad S., Stephenson M. C., Placidi E., Marciani L., Constantin-Teodosiu D., Gowland P. A., Spiller R. C., Fearon K. C. H., Morris P. G., Macdonald I. A., et al. (2010). The effects of fasting and refeeding with a ‘metabolic preconditioning’ drink on substrate reserves and mononuclear cell mitochondrial function. Clin. Nutr. 29, 538–544 [DOI] [PubMed] [Google Scholar]
- Ball M. F., Canary J. J., Kyle L. H. (1967). Comparative effects of caloric restriction and total starvation on body composition in obesity. Ann. Intern. Med. 67, 60–67 [DOI] [PubMed] [Google Scholar]
- Benedict F. G. (1915). A Study of Prolonged Fasting, Vol. 203 Washington, DC: Carnegie Institute [Google Scholar]
- Benoit F. L. R., Martin R. L., Watten R. H. (1965). Changes in body composition during weight reduction in obesity. Balance studies comparing effects of fasting and a ketogenic diet. Ann. Intern. Med. 63, 604–612 [DOI] [PubMed] [Google Scholar]
- Benyshek D. C., Watson J. T. (2006). Exploring the thrifty genotype’s food-shortage assumptions: a cross-cultural comparison of ethnographic accounts of food security among foraging and agricultural societies. Am. J. Phys. Anthropol. 131, 120–126 [DOI] [PubMed] [Google Scholar]
- Bersaglieri T., Sabeti P. C., Patterson N., Vanderploeg T., Schaffner S. F., Drake J. A., Rhodes M., Reich D. E., Hirschhorn J. N. (2004). Genetic signatures of strong recent positive selection at the lactase gene. Am. J. Hum. Genet. 74, 1111–1120 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Black A. E., Coward W. A., Cole T. J., Prentice A. M. (1996). Human energy expenditure in affluent societies: an analysis of 574 doubly-labelled water measurements. Eur. J. Clin. Nutr. 50, 72–92 [PubMed] [Google Scholar]
- Bloom W. L. (1959). Fasting as an introduction to the treatment of obesity. Metabolism 8, 214–220 [PubMed] [Google Scholar]
- Boffetta P., McLerran D., Chen Y., Inoue M., Sinha R., He J., Gupta P. C., Tsugane S., Irie F., Tamakoshi A., et al. (2011). Body mass index and diabetes in Asia: a cross-sectional pooled analysis of 900,000 individuals in the Asia cohort consortium. PLoS ONE 6, e19930. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bouchard C. (2008). Response to ‘The thrifty gene hypothesis: maybe everyone is right?’. Int. J. Obes. 32, 725–726 [DOI] [PubMed] [Google Scholar]
- Boumezbeur F., Petersen K. F., Cline G. W., Mason G. F., Behar K. L., Shulman G. I., Rothman D. L. (2010). The contribution of blood lactate to brain energy metabolism in humans measured by dynamic 13C nuclear magnetic resonance spectroscopy. J. Neurosci. 30, 13983–13991 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brewis A. A. (2010). Obesity: Cultural and Biocultural Perspectives. New York, NY: Rutgers University Press [Google Scholar]
- Browning J. D., Szczepaniak L. S., Dobbins R., Nuremberg P., Horton J. D., Cohen J. C., Grundy S. M., Hobbs H. H. (2004). Prevalence of hepatic steatosis in an urban population in the United States: impact of ethnicity. Hepatology 40, 1387–1395 [DOI] [PubMed] [Google Scholar]
- Calle E. E., Kaaks R. (2004). Overweight, obesity and cancer: epidemiological evidence and proposed mechanisms. Nat. Rev. Cancer 4, 579–591 [DOI] [PubMed] [Google Scholar]
- Caloin M. (2004). Modelling lipid and protein depletion during total starvation. Am. J. Physiol. Endocrinol. Metab. 287, E790–E798 [DOI] [PubMed] [Google Scholar]
- Campbell L. V. (2008). The thrifty gene hypothesis: maybe everyone is right? Int. J. Obes. (Lond.) 32, 723–724 [DOI] [PubMed] [Google Scholar]
- Chakravarthy M. V., Booth F. W. (2004). Eating, exercise, and “thrifty” genotypes: connecting the dots toward an evolutionary understanding of modern chronic diseases. J. Appl. Physiol. 96, 3–10 [DOI] [PubMed] [Google Scholar]
- Church T. S., Thomas D. M., Tudor-Locke C., Katzmarzyk P. T., Earnest C. P., Rodarte R. Q., Martin C. K., Blair S. N., Bouchard C. (2011). Trends over 5 decades in U.S. occupation-related physical activity and their associations with obesity. PLoS ONE 6, e19657. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Collins S. (1995). The limit of human adaptation to starvation. Nat. Med. 1, 810–814 [DOI] [PubMed] [Google Scholar]
- Cubberley P. T., Polster S. A., Schulman C. L. (1965). Lactic acidosis and death after the treatment of obesity by fasting. N. Engl. J. Med. 272, 628–630 [DOI] [PubMed] [Google Scholar]
- Day F. R., Loos R. J. F. (2011). Developments in obesity genetics in the era of genome-wide association studies. J. Nutrigenet. Nutrigenomics 4, 222–238 [DOI] [PubMed] [Google Scholar]
- Drenick E. J., Swendseid M. E., Blahd W. H., Tuttle S. G. (1964). Prolonged starvation as treatment for severe obesity. JAMA 187, 100–105 [DOI] [PubMed] [Google Scholar]
- Dulloo A. G. (1998). Partitioning between protein and fat during starvation and refeeding: is the assumption of intra-individual constancy of P-ratio valid? Br. J. Nutr. 79, 107–113 [DOI] [PubMed] [Google Scholar]
- Dulloo A. G., Jacquet J. (1998). Adaptive reduction in basal metabolic rate in response to food deprivation in humans: a role for feedback signals from fat stores. Am. J. Clin. Nutr. 68, 599–606 [DOI] [PubMed] [Google Scholar]
- Dulloo A. G., Jacquet J. (1999). The control of partitioning between protein and fat during human starvation: its internal determinants and biological significance. Br. J. Nutr. 82, 339–356 [DOI] [PubMed] [Google Scholar]
- Eknoyan G. (2006). A history of obesity, or how what was good became ugly and then bad. Adv. Chronic Kidney Dis. 13, 421–427 [DOI] [PubMed] [Google Scholar]
- Elia M. (2000). Hunger disease. Clin. Nutr. 19, 379–386 [DOI] [PubMed] [Google Scholar]
- Elia M., Stubbs R. J., Henry C. J. K. (1999). Differences in fat, carbohydrate, and protein metabolism between lean and obese subjects undergoing total starvation. Obes. Res. 7, 597–604 [DOI] [PubMed] [Google Scholar]
- Farooqi I. S., O’Rahilly S. (2008). Mutations in ligands and receptors of the leptin-melanocortin pathway that lead to obesity. Nat. Clin. Pract. Endocrinol. Metab. 4, 569–577 [DOI] [PubMed] [Google Scholar]
- Farooqi I. S., Jebb S. A., Langmack G., Lawrence E., Cheetham C. H., Prentice A. M., Hughes I. A., McCamish M. A., O’Rahilly S. (1999). Effects of recombinant leptin therapy in a child with congenital leptin deficiency. N. Engl. J. Med. 341, 879–884 [DOI] [PubMed] [Google Scholar]
- Farooqi I. S., Keogh J. M., Kamath S., Jones S., Gibson W. T., Trussell R., Jebb S. A., Lip G. Y., O’Rahilly S. (2001). Partial leptin deficiency and human adiposity. Nature 414, 34–35 [DOI] [PubMed] [Google Scholar]
- Farooqi I. S., Matarese G., Lord G. M., Keogh J. M., Lawrence E., Agwu C., Sanna V., Jebb S. A., Perna F., Fontana S., et al. (2002). Beneficial effects of leptin on obesity, T cell hyporesponsiveness, and neuroendocrine/metabolic dysfunction of human congenital leptin deficiency. J. Clin. Invest. 110, 1093–1103 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Farooqi I. S., Bullmore E., Keogh J., Gillard J., O’Rahilly S., Fletcher P. C. (2007). Leptin regulates striatal regions and human eating behavior. Science 317, 1355–1355 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Folin O., Denis W. (1915). On starvation and obesity, with special reference to acidosis. J. Biol. Chem. 21, 183 [Google Scholar]
- Forbes G. B. (1987). Lean body mass-body fat interrelationships in humans. Nutr. Rev. 45, 225–231 [DOI] [PubMed] [Google Scholar]
- Gilliland I. C. (1967). Total fasting in the treatment of obesity. Postgrad. Med. J. 44, 58–61 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goodman M. N., Lowell B., Belur E., Ruderman N. B. (1984). Sites of protein conservation and loss during starvation: influence of adiposity. Am. J. Physiol. 246, E383–E390 [DOI] [PubMed] [Google Scholar]
- Grande F., Anderson J. T., Keys A. (1958). Changes of basal metabolic rate in man in semistarvation and refeeding. J. Appl. Physiol. 12, 230–238 [DOI] [PubMed] [Google Scholar]
- Hall K. D. (2006). Computational model of in vivo human energy metabolism during semi-starvation and refeeding. Am. J. Physiol. Endocrinol. Metab. 291, E23–E27 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hall K. D. (2008). What is the required energy deficit per unit weight loss? Int. J. Obes. (Lond.) 32, 573–576 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hall K. D. (2010a). Mathematical modelling of energy expenditure during tissue deposition. Br. J. Nutr. 104, 4–7 [DOI] [PubMed] [Google Scholar]
- Hall K. D. (2010b). Predicting metabolic adaptation, body weight change, and energy intake in humans. Am. J. Physiol. Endocrinol. Metab. 298, E449–E466 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hall K. D. (2012). Quantitative physiology of human starvation: Adaptations of energy expenditure, macronutrient metabolism and body composition. In Comparative Physiology of Fasting, Starvation and Food Limitation (ed. McCue M. D.), pp. 379–393 Berlin, Germany: Springer Verlag [Google Scholar]
- Hall K. D., Sacks G., Chandramohan D., Chow C. C., Wang Y. C., Gortmaker S. L., Swinburn B. A. (2011). Quantification of the effect of energy imbalance on bodyweight. Lancet 378, 826–837 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hall K. D., Heymsfield S. B., Kemnitz J. W., Klein S., Schoeller D. A., Speakman J. R. (2012). Energy balance and its components: implications for body weight regulation. Am. J. Clin. Nutr. 95, 989–994 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harrison M. T., Harden R. M. C. G. (1966). The long-term values of fasting in the treatment of obesity. Lancet 288, 1340–1342 [DOI] [PubMed] [Google Scholar]
- Hebebrand J., Volckmar A. L., Knoll N., Hinney A. (2010). Chipping away the ‘missing heritability’: GIANT steps forward in the molecular elucidation of obesity –but still lots to go. Obesity Facts 3, 294–303 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Henry C. J. K. (1990). Body mass index and the limits of human survival. Eur. J. Clin. Nutr. 44, 329–335 [PubMed] [Google Scholar]
- Heymsfield S. B., Thomas D., Nguyen A. M., Peng J. Z., Martin C., Shen W., Strauss B., Bosy-Westphal A., Muller M. J. (2011). Voluntary weight loss: systematic review of early phase body composition changes. Obes. Rev. 12, e348–e361 [DOI] [PubMed] [Google Scholar]
- Innes J. A., Campbell I. W., Campbell C. J., Needle A. L., Munro J. F. (1974). Long-term follow-up of therapeutic starvation. BMJ 2, 356–359 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Isomaa B., Almgren P., Tuomi T., Forsén B., Lahti K., Nissén M., Taskinen M. R., Groop L. (2001). Cardiovascular morbidity and mortality associated with the metabolic syndrome. Diabetes Care 24, 683–689 [DOI] [PubMed] [Google Scholar]
- Jackson J. M., Blaine D., Powell-Tuck J., Korbonits M., Carey A., Elia M. (2006). Macro- and micronutrient losses and nutritional status resulting from 44 days of total fasting in a non-obese man. Nutrition 22, 889–897 [DOI] [PubMed] [Google Scholar]
- Johnstone A. M. (2007). Fasting – the ultimate diet? Obes. Rev. 8, 211–222 [DOI] [PubMed] [Google Scholar]
- Keys A., Brozek J., Henschel A., Mickelsen O., Taylor H. L. (1950). The Biology of Starvation, Vol. 1, 2 Minneapolis, MN: University of Minnesota Press [Google Scholar]
- Kleitman N. (1926). Basal metabolism in prolonged fasting in man. Am. J. Physiol. 77, 33–44 [Google Scholar]
- Korbonits M., Blaine D., Elia M., Powell-Tuck J. (2005). Refeeding David Blaine – studies after a 44-day fast. N. Engl. J. Med. 353, 2306–2307 [DOI] [PubMed] [Google Scholar]
- Korbonits M., Blaine D., Elia M., Powell-Tuck J. (2007). Metabolic and hormonal changes during the refeeding period of prolonged fasting. Eur. J. Endocrinol. 157, 157–166 [DOI] [PubMed] [Google Scholar]
- Kreitzman S. N., Coxon A. Y., Szaz K. F. (1992). Glycogen storage: illusions of easy weight loss, excessive weight regain, and distortions in estimates of body composition. Am. J. Clin. Nutr. 56, 292S–293S [DOI] [PubMed] [Google Scholar]
- Leibel R. L., Hirsch J. (1984). Diminished energy requirements in reduced-obese patients. Metabolism 33, 164–170 [DOI] [PubMed] [Google Scholar]
- Leiter L. A., Marliss E. B. (1982). Survival during fasting may depend on fat as well as protein stores. JAMA 248, 2306–2307 [PubMed] [Google Scholar]
- Luke A., Schoeller D. A. (1992). Basal metabolic rate, fat-free mass, and body cell mass during energy restriction. Metabolism 41, 450–456 [DOI] [PubMed] [Google Scholar]
- Luke A., Guo X., Adeyemo A. A., Wilks R., Forrester T., Lowe W., Jr, Comuzzie A. G., Martin L. J., Zhu X., Rotimi C. N., et al. (2001). Heritability of obesity-related traits among Nigerians, Jamaicans and US black people. Int. J. Obes. Relat. Metab. Disord. 25, 1034–1041 [DOI] [PubMed] [Google Scholar]
- Luke A., Dugas L. R., Ebersole K., Durazo-Arvizu R. A., Cao G. C., Schoeller D. A., Adeyemo A., Brieger W. R., Cooper R. S. (2009). Energy expenditure does not predict weight change in either Nigerian or African American women. Am. J. Clin. Nutr. 89, 169–176 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mansell P. I., Fellows I. W., Macdonald I. A. (1990). Enhanced thermogenic response to epinephrine after 48-h starvation in humans. Am. J. Physiol. 258, R87–R93 [DOI] [PubMed] [Google Scholar]
- Martin C. K., Heilbronn L. K., de Jonge L., DeLany J. P., Volaufova J., Anton S. D., Redman L. M., Smith S. R., Ravussin E. (2007). Effect of calorie restriction on resting metabolic rate and spontaneous physical activity. Obesity (Silver Spring) 15, 2964–2973 [DOI] [PubMed] [Google Scholar]
- McArdle W. D., Katch F. I., Katch V. L. (2001). Exercise Physiology: Energy, Nutrition and Human Performance. Baltimore, MD: Lippincott, Williams and Wilkins [Google Scholar]
- Meyers A. W. (1917). Some morphological effects of prolonged inanitition. J. Med. Res. 36, 51. [PMC free article] [PubMed] [Google Scholar]
- Müller M. J., Langemann D., Gehrke I., Later W., Heller M., Glüer C. C., Heymsfield S. B., Bosy-Westphal A. (2011). Effect of constitution on mass of individual organs and their association with metabolic rate in humans – a detailed view on allometric scaling. PLoS ONE 6, e22732. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neel J. V. (1962). Diabetes mellitus a ‘thrifty’ genotype rendered detrimental by ‘progress’? Am. J. Hum. Genet. 14, 352–353 [PMC free article] [PubMed] [Google Scholar]
- Nilsson L. H. (1973). Liver glycogen content in man in the postabsorptive state. Scand. J. Clin. Lab. Invest. 32, 317–323 [DOI] [PubMed] [Google Scholar]
- Nilsson L. H., Hultman E. (1973). Liver glycogen in man – the effect of total starvation or a carbohydrate-poor diet followed by carbohydrate refeeding. Scand. J. Clin. Lab. Invest. 32, 325–330 [DOI] [PubMed] [Google Scholar]
- O’Rahilly S. (1998). Life without leptin. Nature 392, 330–331 [DOI] [PubMed] [Google Scholar]
- O’Rahilly S. (2009). Human genetics illuminates the paths to metabolic disease. Nature 462, 307–314 [DOI] [PubMed] [Google Scholar]
- Ode J. J., Pivarnik J. M., Reeves M. J., Knous J. L. (2007). Body mass index as a predictor of percent fat in college athletes and nonathletes. Med. Sci. Sports Exerc. 39, 403–409 [DOI] [PubMed] [Google Scholar]
- Okorodudu D. O., Jumean M. F., Montori V. M., Romero-Corral A., Somers V. K., Erwin P. J., Lopez-Jimenez F. (2010). Diagnostic performance of body mass index to identify obesity as defined by body adiposity: a systematic review and meta-analysis. Int. J. Obes. (Lond.) 34, 791–799 [DOI] [PubMed] [Google Scholar]
- Olsson K.-E., Saltin B. (1970). Variation in total body water with muscle glycogen changes in man. Acta Physiol. Scand. 80, 11–18 [DOI] [PubMed] [Google Scholar]
- Owen O. E., Felig P., Morgan A. P., Wahren J., Cahill G. F., Jr (1969). Liver and kidney metabolism during prolonged starvation. J. Clin. Invest. 48, 574–583 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Owen O. E., Smalley K. J., D’Alessio D. A., Mozzoli M. A., Dawson E. K. (1998). Protein, fat, and carbohydrate requirements during starvation: anaplerosis and cataplerosis. Am. J. Clin. Nutr. 68, 12–34 [DOI] [PubMed] [Google Scholar]
- Payne P. R., Dugdale A. E. (1977). A model for the prediction of energy balance and body weight. Ann. Hum. Biol. 4, 525–535 [DOI] [PubMed] [Google Scholar]
- Peret J., Jacquot R. (1972). Nitrogenous excretion on complete fasting and on a nitrogen free diet–endogenous nitrogen. In International Encyclopaedia of Food and Nutrition, Vol 11 (ed. Bigwood E. J.), pp. 73–118 Oxford, UK: Pergamon Press [Google Scholar]
- Petersen K. F., Dufour S., Befroy D., Garcia R., Shulman G. I. (2004). Impaired mitochondrial activity in the insulin-resistant offspring of patients with type 2 diabetes. N. Engl. J. Med. 350, 664–671 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pi-Sunyer F. X. (1991). Health implications of obesity. Am. J. Clin. Nutr. 53, 1595S–1603S [DOI] [PubMed] [Google Scholar]
- Prentice A. M. (2001). Obesity and its potential mechanistic basis. Br. Med. Bull. 60, 51–67 [DOI] [PubMed] [Google Scholar]
- Prentice A. M. (2005). Early influences on human energy regulation: thrifty genotypes and thrifty phenotypes. Physiol. Behav. 86, 640–645 [DOI] [PubMed] [Google Scholar]
- Prentice A. M., Goldberg G. R., Jebb S. A., Black A. E., Murgatroyd P. R., Diaz E. O. (1991). Physiological responses to slimming. Proc. Nutr. Soc. 50, 441–458 [DOI] [PubMed] [Google Scholar]
- Prentice A. M., Rayco-Solon P., Moore S. E. (2005). Insights from the developing world: thrifty genotypes and thrifty phenotypes. Proc. Nutr. Soc. 64, 153–161 [DOI] [PubMed] [Google Scholar]
- Prentice A. M., Hennig B. J., Fulford A. J. (2008). Evolutionary origins of the obesity epidemic: natural selection of thrifty genes or genetic drift following predation release? Int. J. Obes. (Lond.) 32, 1607–1610 [DOI] [PubMed] [Google Scholar]
- Prospective Studies Collaboration (2009). Body-mass index and cause-specific mortality in 900 000 adults: collaborative analyses of 57 prospective studies. Lancet 373, 1083–1096 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rigaud D., Hassid J., Meulemans A., Poupard A. T., Boulier A. (2000). A paradoxical increase in resting energy expenditure in malnourished patients near death: the king penguin syndrome. Am. J. Clin. Nutr. 72, 355–360 [DOI] [PubMed] [Google Scholar]
- Rosling A. M., Sparén P., Norring C., von Knorring A. L. (2011). Mortality of eating disorders: a follow-up study of treatment in a specialist unit 1974–2000. Int. J. Eat. Disord. 44, 304–310 [DOI] [PubMed] [Google Scholar]
- Rothman D. L., Magnusson I., Katz L. D., Shulman R. G., Shulman G. I. (1991). Quantitation of hepatic glycogenolysis and gluconeogenesis in fasting humans with 13C NMR. Science 254, 573–576 [DOI] [PubMed] [Google Scholar]
- Runcie J., Thomson T. J. (1970). Prolonged starvation – a dangerous procedure? BMJ 3, 432–435 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schwimmer J. B., Deutsch R., Kahen T., Lavine J. E., Stanley C., Behling C. (2006). Prevalence of fatty liver in children and adolescents. Pediatrics 118, 1388–1393 [DOI] [PubMed] [Google Scholar]
- Segal N. L., Allison D. B. (2002). Twins and virtual twins: bases of relative body weight revisited. Int. J. Obes. Relat. Metab. Disord. 26, 437–441 [DOI] [PubMed] [Google Scholar]
- Siesjo B. K. (1978). Brain Energy Metabolism. New York, NY: Wiley [Google Scholar]
- Song B., Thomas D. M. (2007). Dynamics of starvation in humans. J. Math. Biol. 54, 27–43 [DOI] [PubMed] [Google Scholar]
- Southam L., Soranzo N., Montgomery S. B., Frayling T. M., McCarthy M. I., Barroso I., Zeggini E. (2009). Is the thrifty genotype hypothesis supported by evidence based on confirmed type 2 diabetes- and obesity-susceptibility variants? Diabetologia 52, 1846–1851 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Speakman J. R. (2006). The genetics of obesity: five fundamental problems with the famine hypothesis. In Adipose Tissue and Adipokines in Health and Disease (ed. Fantuzzi G., Mazzone T.). New York, NY: Humana Press [Google Scholar]
- Speakman J. R. (2007). A nonadaptive scenario explaining the genetic predisposition to obesity: the “predation release” hypothesis. Cell Metab. 6, 5–12 [DOI] [PubMed] [Google Scholar]
- Speakman J. R. (2008). Thrifty genes for obesity, an attractive but flawed idea, and an alternative perspective: the ‘drifty gene’ hypothesis. Int. J. Obes. (Lond.) 32, 1611–1617 [DOI] [PubMed] [Google Scholar]
- Speakman J. R., Westerterp K. R. (2010). Associations between energy demands, physical activity, and body composition in adult humans between 18 and 96 y of age. Am. J. Clin. Nutr. 92, 826–834 [DOI] [PubMed] [Google Scholar]
- Speakman J. R., Mitchell S. E. (2011). Caloric restriction. Mol. Aspects Med. 32, 159–221 [DOI] [PubMed] [Google Scholar]
- Speakman J. R., Stubbs R. J., Mercer J. G. (2002). Does body mass play a role in the regulation of food intake? Proc. Nutr. Soc. 61, 473–487 [DOI] [PubMed] [Google Scholar]
- Speakman J. R., Levitsky D. A., Allison D. B., Bray M. S., de Castro J. M., Clegg D. J., Clapham J. C., Dulloo A. G., Gruer L., Haw S., et al. (2011). Set points, settling points and some alternative models: theoretical options to understand how genes and environments combine to regulate body adiposity. Dis. Model. Mech. 4, 733–745 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Speliotes E. K., Willer C. J., Berndt S. I., Monda K. L., Thorleifsson G., Jackson A. U., Lango Allen H., Lindgren C. M., Luan J., Mägi R., et al. (2010). Association analyses of 249,796 individuals reveal 18 new loci associated with body mass index. Nat. Genet. 42, 937–948 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spencer I. O. B. (1968). Death during therapeutic starvation for obesity. Lancet 291, 1288–1290 [DOI] [PubMed] [Google Scholar]
- Stewart W. K., Fleming L. W. (1973). Features of a successful therapeutic fast of 382 days’ duration. Postgrad. Med. J. 49, 203–209 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Swinburn B. A., Sacks G., Lo S. K., Westerterp K. R., Rush E. C., Rosenbaum M., Luke A., Schoeller D. A., DeLany J. P., Butte N. F., et al. (2009). Estimating the changes in energy flux that characterize the rise in obesity prevalence. Am. J. Clin. Nutr. 89, 1723–1728 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taylor R., Magnusson I., Rothman D. L., Cline G. W., Caumo A., Cobelli C., Shulman G. I. (1996). Direct assessment of liver glycogen storage by 13C nuclear magnetic resonance spectroscopy and regulation of glucose homeostasis after a mixed meal in normal subjects. J. Clin. Invest. 97, 126–132 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thomas D. M., Ciesla A., Levine J. A., Stevens J. G., Martin C. K. (2009). A mathematical model of weight change with adaptation. Math. Biosci. Eng. 6, 873–887 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thomas D. M., Schoeller D. A., Redman L. A., Martin C. K., Levine J. A., Heymsfield S. B. (2010). A computational model to determine energy intake during weight loss. Am. J. Clin. Nutr. 92, 1326–1331 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thomson T. J., Runcie J., Miller V. (1966). Treatment of obesity by total fasting for up to 249 days. Lancet 288, 992–996 [DOI] [PubMed] [Google Scholar]
- Wellcome Trust Case Control Consortium (2007). A common variant in the FTO gene is associated with body mass index and predisposes to childhood and adult obesity. Science 316, 889–894 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wells J. C. K. (2006). The evolution of human fatness and susceptibility to obesity: an ethological approach. Biol. Rev. Camb. Philos. Soc. 81, 183–205 [DOI] [PubMed] [Google Scholar]
- Westerterp K. R., Speakman J. R. (2008). Physical activity energy expenditure has not declined since the 1980s and matches energy expenditures of wild mammals. Int. J. Obes. (Lond.) 32, 1256–1263 [DOI] [PubMed] [Google Scholar]
- Westerterp K. R., Donkers J. H., Fredrix E. W., Boekhoudt P. (1995). Energy intake, physical activity and body weight: a simulation model. Br. J. Nutr. 73, 337–347 [DOI] [PubMed] [Google Scholar]
- Weyer C., Walford R. L., Harper I. T., Milner M., MacCallum T., Tataranni P. A., Ravussin E. (2000). Energy metabolism after 2 y of energy restriction: the biosphere 2 experiment. Am. J. Clin. Nutr. 72, 946–953 [DOI] [PubMed] [Google Scholar]
- Wu X., Cooper R. S., Borecki I., Hanis C., Bray M., Lewis C. E., Zhu X., Kan D., Luke A., Curb D. (2002). A combined analysis of genomewide linkage scans for body mass index from the National Heart, Lung, and Blood Institute Family Blood Pressure Program. Am. J. Hum. Genet. 70, 1247–1256 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang M. U., Van Itallie T. B. (1976). Composition of weight lost during short-term weight reduction. Metabolic responses of obese subjects to starvation and low-calorie ketogenic and nonketogenic diets. J. Clin. Invest. 58, 722–730 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zauner C., Schneeweiss B., Kranz A., Madl C., Ratheiser K., Kramer L., Roth E., Schneider B., Lenz K. (2000). Resting energy expenditure in short-term starvation is increased as a result of an increase in serum norepinephrine. Am. J. Clin. Nutr. 71, 1511–1515 [DOI] [PubMed] [Google Scholar]
- Zhu X., Cooper R. S., Luke A., Chen G., Wu X., Kan D., Chakravarti A., Weder A. (2002). A genome-wide scan for obesity in African-Americans. Diabetes 51, 541–544 [DOI] [PubMed] [Google Scholar]