Preconditioned Alternating Projection Algorithms for Maximum a Posteriori ECT Reconstruction

Abstract

We propose a preconditioned alternating projection algorithm (PAPA) for solving the maximum a posteriori (MAP) emission computed tomography (ECT) reconstruction problem. Specifically, we formulate the reconstruction problem as a constrained convex optimization problem with the total variation (TV) regularization. We then characterize the solution of the constrained convex optimization problem and show that it satisfies a system of fixed-point equations defined in terms of two proximity operators raised from the convex functions that define the TV-norm and the constrain involved in the problem. The characterization (of the solution) via the proximity operators that define two projection operators naturally leads to an alternating projection algorithm for finding the solution. For efficient numerical computation, we introduce to the alternating projection algorithm a preconditioning matrix (the EM-preconditioner) for the dense system matrix involved in the optimization problem. We prove theoretically convergence of the preconditioned alternating projection algorithm. In numerical experiments, performance of our algorithms, with an appropriately selected preconditioning matrix, is compared with performance of the conventional MAP expectation-maximization (MAP-EM) algorithm with TV regularizer (EM-TV) and that of the recently developed nested EM-TV algorithm for ECT reconstruction. Based on the numerical experiments performed in this work, we observe that the alternating projection algorithm with the EM-preconditioner outperforms significantly the EM-TV in all aspects including the convergence speed, the noise in the reconstructed images and the image quality. It also outperforms the nested EM-TV in the convergence speed while providing comparable image quality.

1 Introduction

Emission computed tomography (ECT) is a noninvasive molecular imaging method that requires administration of radioactive tracers to patients. It comprises of two branches: positron emission tomography (PET) and single-photon emission computed tomography (SPECT) [49, 60]. It might provide estimate of the spatial and/or temporal distribution of radioactive tracer inside a patient body through tomographic reconstruction from the detected emission events (typically in the form of projection images for SPECT and sinograms or list data for PET). ECT provides a three-dimensional (3D) functional rather than structural information provided by computed tomography (CT) or magnetic resonance imaging (MRI). In a SPECT imaging system, the detectors (detector units) record the number of single events due to gamma or x-ray photons emitted by SPECT radioactive tracer distributed inside a patient body. The photons are detected only if they travel along directions well defined by a collimator. The collection of such emission data can be sorted into a set of 2D projection images [60]. In PET systems, the pairs of detectors record the number of coincidence events due to two 511 keV gamma photons emitted in positron annihilation events. Positrons are emitted by PET radioactive tracer distributed inside a patient body. They travel certain randomly distributed distances in the tissue before they annihilate electrons and produce pairs of 511 keV photons emitted in random and approximately opposite directions. The collections of such emission data form list data and can be sorted into a set of sinograms [49]. Clinical applications of ECT include detection, staging and monitoring response to cancer therapy, detection and risk stratification of cardiovascular diseases, mapping of regional blood flow in the brain, bone scans, pulmonary ventilation/perfusion scans, and renal scans [63].

The aim of the reconstruction process is to obtain accurate estimation of the radiotracer distribution in a patient or a phantom from the detected emission photons. The most commonly used probability distribution for a description of raw ECT data is the Poisson model [35, 55, 60]. It states that the vector of the number of events recorded by the detector units during ECT scan is a Poisson distributed random vector with a mean equal to the sum of the system matrix multiplied by the mean radiotracer activity distribution vector within an object of interest and by the mean “background” counts vector. Sources of background counts include cosmic rays and terrestrial radioactive background. They are assumed to follow the Poisson distribution. For a given realization of the detected ECT data and for the known expected background counts, this model allows one to estimate the mean radiotracer activity distribution.

Finding numerical solutions of the model is a long-standing research problem. The iterative expectation-maximization (EM) algorithm is a frequently used reconstruction method for ECT imaging [35, 58]. Many reconstruction algorithms for the model are based on optimizing an objective function deduced in part from the statistical model of detection realization data. For example, the maximum-likelihood (ML) method is based on minimizing the negative log-likelihood of observed emission data conditional on radiotracer distribution. Under the Bayesian framework, the maximum a posteriori (MAP) estimator seeks minimizing the sum of the negative log-likelihood of observed emission data conditional on radiotracer distribution and a regularizing penalty function, which penalizes solutions that have low probability. With various considerations such as computational efficiency of the algorithm to be developed and the spatial resolution of the reconstructed images, many different types of penalty functions were proposed. The total-variation based penalty function introduced in [28, 48] is particularly interesting in the field of ECT image reconstruction because it preserves the high spatial frequencies components of the reconstructed radiopharmacuetical distribution including discontinuities and steep gradients. Many efficient algorithms for this model were proposed, including EM-based methods [28, 48, 54], projected quasi-Newton methods [1, 2, 3], and forward-backward approaches [7, 13, 56]. In particular, a nested EM-TV iterative scheme was proposed recently in [54] for reconstruction of PET data with low signal-to-noise ratio, while an alternating extragradient method was proposed in [7] for solving the primal-dual formulation of the Poisson ECT data model with the TV regularization.

In the present paper, we study the numerical solution of the model that optimizes the sum of the negative log-likelihood of observed emission data conditional on radiotracer distribution (i.e. the Kullbach-Leibler divergence) and a total-variation regularization term. The ECT detector physics requires that the solution of this model be nonnegative. Difficulties with the numerical solution of such a model stem from the nonlinearity due to the use of the Kullbach-Leibler divergence and the TV regularization, from the nonnegativity constraint on the solution, and from the dense and large sized system matrix necessary for realistic ECT models. Motivated by our previous work [39, 42, 43], we characterize the solutions of the model in terms of a fixed-point of the proximity operators with a precondition matrix. Numerical algorithms are then developed based on such a characterization. More precisely, by identifying the total-variation as a composition of the convex function, which defines the ‘ℓ¹-norm’ or the ‘ℓ²-norm’, and the first order difference operator, we formulate a characterization of the exact positive solutions to the optimization problem in terms of a system of fixed-point equations via the proximity operators of the convex function that defines the ‘ℓ¹-norm’ or the ‘ℓ²-norm’ and the one that defines the first quadrant of an Euclidean space. The proximity operators of these simple functions have closed forms, which provide great computational advantages. The nonlinearity is expressed in terms of a system of fixed-point equations, which naturally leads to an alternating projection algorithm. The dense system matrix of a large size is treated by preconditioning. Appropriate choices of the preconditioning matrices lead to efficient computational algorithms for solving the model.

This paper is divided into seven sections. In Section 2 we outline the Maximum a Posteriori ECT image reconstruction model in terms of a somewhat general constrained convex optimization problem. In Section 3, characterizations of the solution of the optimization problem are presented in terms of a system of fixed-point equations via proximity operators, and the iterative algorithms for finding the solution are developed based on the characterizations. Section 4 is devoted to convergence analysis of the algorithm. In Section 5, we specialize the general algorithm to the TV-regularized ECT image reconstruction problem. Numerical experiments are presented in Section 6 to test the approximation accuracy and computational efficiency of the proposed algorithm. The numerical results demonstrate that the alternating projection algorithm with the EM-preconditioner outperforms significantly the EM-TV in both the convergence speed and the image quality. We also observe that our algorithm performs favorably in comparison to the nested EM-TV in both the convergence speed and the image quality. We make concluding remarks in Section 7.

2 Maximum a Posteriori Estimation for ECT Reconstruction

In this section, we first present a mathematical model of a realistic ECT imaging system. We then find the unknown radioactive tracer distribution by maximizing the posterior probability distribution (the object function) using the observed emission data, known probability density function of the unknown radioactive tracer distribution, and the Bayes law. This approach is called the maximum a posteriori expectation-maximization (MAP-EM). Finally, the existence of a solution of the resulting variational problem is discussed.

We begin by introducing the notation to be used throughout this paper. Let ℕ_k := {1, 2, …, k}. We use the same notation “1” to represent both the scalar number 1 and the vector with all components equal to one. They can be distinguished by the context of their use. For x ∈ ℝ^k, the expression x ≥ 0 means that all components of x are no less than 0, and in this case, we say that x is a nonnegative vector. We denote by ${ℝ}_{+}^k$ the set {x : x ∈ ℝ^k and x ≥ 0}. For any vectors x and y in ℝ^k, we define

$$x\odot y≔(x_i{y}_i:i\in {\mathbb{N}}_k)\text{ and }\frac{x}{y}≔(\frac{x_i}{y_i}:i\in {\mathbb{N}}_k)$$

respectively, as the componentwise multiplication of x and y, and componentwise division of x by y. The logarithmic function at x ∈ ℝ^k is defined as

$$\text{ln }x≔(\text{ln }{x}_i:i\in {\mathbb{N}}_k),$$

while the expression “x + γ”, the sum of the vector x with a scalar γ ∈ ℝ, is understood as the vector

$$x+\gamma ≔(x_i+\gamma :i\in {\mathbb{N}}_k).$$

We use 〈·, ·〉 and ‖ · ‖, respectively, for the inner product and the corresponding ℓ²-norm in an Euclidean space, while we use ‖ · ‖₁ and ‖ · ‖_∞, respectively, for the ℓ¹-norm and ℓ^∞-norm.

It is well accepted that gamma and x-ray photons, as well as positrons emitted in radioactive decay follow a Poisson distribution. Assuming that the detection of photons by detector units are events independent of one another and can be described by a Bernoulli process, consequently the projection images are a collection of Poisson random variables. The Poisson distribution approximates the photon detection process only if one can neglect the detector dead-time i.e. count losses in the real detector systems, and no corrections are applied to the raw data. In addition to photons emitted from the patient, the detector bins (units) detect events due to ubiquitous radioactive terrestrial background and cosmic rays. It is assumed that they also follow the Poisson distribution.

Let f represent the expected radiotracer distribution within a patient or a phantom. Let g denote a vector with the i-th component being the number of single photons for SPECT or numbers of pairs of annihilation photons for PET originated from the radiotracer and recorded by the i-th detector unit or detector unit pair during the SPECT or PET scan, respectively. The dimension of the vector g is the number of detector units or detector unit pairs in the SPECT or PET imaging system, respectively. We assume that γ is a vector of the same size as g, with its i-th component being the mean number of “background” counts recorded by the i-th bin in SPECT or bin pair in PET. Under these assumptions, the observed emission data vector g related to the unknown radiotracer distribution f can be approximated by the following model [35, 55]

$$g=\text{Poisson }(\mathit{\text{Af}}+\gamma ),$$ (1)

where Poisson(α) denotes a Poisson distributed random vector with mean α and A is the ECT system matrix with its (ij)-th element equal to the probability of detection of the photon emitted from voxel j of image f by the i-th detector bin in SPECT or detector bin pair in PET.

The maximum a posteriori probability (MAP) EM estimate has been proven useful in ECT for estimating the unobservable radiotracer distribution f when prior knowledge on probability distribution function of f is available, especially when the observed emission data g are noisy or incomplete [10, 19, 20, 21, 22, 30, 45]. Specifically, we assume that g in (1) is a given random vector in ℝ^m and f is a random vector in ℝ^d. The MAP estimate f_⋆ is obtained by maximizing the conditional a posteriori probability p(f|g), the probability that f occurs when g is observed. This probability may be computed using the Bayes law

$$p(f|g)\propto p(g|f)p(f),$$ (2)

where α ∝ β means that the scalar α is proportional to the scalar β. By taking the logarithm of the both sides of equation (2), the MAP estimate can then be calculated using the formula

$$f_{\star }=\text{arg max }\{\text{ln }p(g|f)+\text{ln }p(f):f\in {ℝ}^d\}.$$ (3)

In other words, the MAP estimate f_⋆ is obtained by maximizing expectation, that is, by minimizing the sum of a negative log-likelihood of the observed emission data conditional on radiotracer distribution and a positive logarithm of the prior probability distribution. The first term can be considered as a fidelity term, a measure of the discrepancy between the estimated and the observed data. The second term is a regularization function, which penalizes solutions that have low probability. The Gibbs priors are commonly used in ECT reconstruction [18, 30, 36] in both convex [17, 20, 45, 47] and nonconvex [21, 31, 62] forms

$$p(f)\propto \text{exp}(-\lambda U(f))$$ (4)

with Gibbs real-valued energy function U(f) defined on ℝ^d, and a positive regularization parameter λ called hyperparameter.

We formulate our maximum a posteriori ECT reconstruction model from (3) and (4) by computing the likelihood objective p(g|f) using equation (1) and specifying the energy function U. According to equation (1), g follows the Poisson distribution having Af + γ as its mean. As a result, the probability density function p(g|f) of g conditioned on f can be computed by using the formula

$$p(g|f)={\displaystyle \prod _{i\in {\mathbb{N}}_m}}\frac{{({(\mathit{\text{Af}})}_i+{\gamma }_i)}^{g_i}\text{exp}(-({(\mathit{\text{Af}})}_i+{\gamma }_i))}{g_i!}.$$ (5)

We choose the energy function U in (4) as the total variation semi-norm. Accordingly, following the notation used in [42], we have that

$$U(f)≔(\phi ◦B)(f),$$ (6)

where B is an n × d first-order difference matrix and φ the ℓ¹-norm for the anisotropic total-variation or the ℓ²-norm for the isotropic total-variation on ℝⁿ. We shall provide more details of the total variation later in Section 5. Taking the logarithm of the both sides of equation (5) and incorporating identities

$${\displaystyle \sum _{i\in {\mathbb{N}}_m}}{g}_i\text{ ln}({(\mathit{\text{Af}})}_i+{\gamma }_i)=\langle \text{ln}(\mathit{\text{Af}}+\gamma ),g\rangle$$

and

$${\displaystyle \sum _{i\in {\mathbb{N}}_m}}{(\mathit{\text{Af}})}_i=\langle \mathit{\text{Af}},1\rangle$$

in the resulting equation, we obtain that

$$\text{ln }p(g|f)=\langle \text{ln}(\mathit{\text{Af}}+\gamma ),g\rangle -\langle \mathit{\text{Af}},1\rangle +{\text{const}}_1,$$

where const₁ is a constant independent of f. Moreover, from (4) and (6) we have that

$$\text{ln }p(f)=-\lambda (\phi ◦B)(f)+{\text{const}}_2,$$

where const₂ is again a constant independent of f. Substituting the above two equations into (3) leads to the following variational problem

$$\text{min }\{\langle \mathit{\text{Af}},1\rangle -\langle \text{ln}(\mathit{\text{Af}}+\gamma ),g\rangle +\lambda (\phi ◦B)(f):f\in {ℝ}_{+}^d\}.$$ (7)

Although the variational problem (7) is derived in the specific context of the ECT image reconstruction, in this paper, we shall consider solving the problem in the following somewhat more general setting. We assume that A is a matrix in ℝ^{m × d}, g is a given vector in ℝ^m, γ is a positive vector in ℝ^m, λ is a positive number, φ is a convex nonnegative function on ℝⁿ, and B is an n × d matrix. The ECT image reconstruction model is a special case of model (7) when φ ◦ B is chosen as the total-variation semi-norm. For this reason, we call the above variational problem the Poisson-TV model. In the remaining part of this section and Sections 3 and 4, we consider model (7) in the general setting described above while in Sections 5 and 6 we specify it for the ECT image reconstruction model. In model (7), the requirement of $f\in {ℝ}_{+}^d$ is feasible due to the fact that f represents the mean radiotracer activity distribution in the object in ECT.

In the remaining part of this section, we establish the existence of the solutions to the variational problem (7). Recall that for a lower semicontinuous and convex function F defined over ℝ^d, a sufficient condition for F to have a minimizer over a closed convex set C is that the intersection of C and a lower level set of F at some height ξ ∈ ℝ defined by

$${\text{lev}}_{\le \xi }F≔\{f:f\in {ℝ}^d,F(f)\le \xi \},$$

is nonempty and bounded (see, for example, [5]). We require some conditions on the system matrix A, motivated from the ECT imaging system. We denote by 𝔸 the collection of m × d matrices, each of whose columns is a nonzero vector in ${ℝ}_{+}^m$. Since photons emitted from each voxel of an object are detected by detector bins in the ECT imaging system, it is reasonable to assume that the general system matrix A in (1) is in 𝔸.

Proposition 2.1. If A ∈ 𝔸, $g\in {ℝ}_{+}^m$, γ is a positive vector in ℝ^m, λ is a positive number, φ is a convex nonnegative function on ℝⁿ, and B is an n × d matrix, then the solution set of model (7) is nonempty.

Proof. Let $F:{ℝ}_{+}^d\to ℝ$ be defined at any $f\in {ℝ}_{+}^d$ as

$$F(f)≔\langle \mathit{\text{Af}},1\rangle -\langle \text{ln}(\mathit{\text{Af}}+\gamma ),g\rangle +\lambda (\phi \circ B)(f).$$

Clearly, F is the objective function of the variational problem (7). It suffices to prove that F is convex and coercive on the unbounded convex domain ${ℝ}_{+}^d$.

Note that φ is a convex function. The convexity of F on ${ℝ}_{+}^d$ is equivalent to the convexity of the function

$$F_1≔\langle A·,1\rangle -\langle \text{ln}(A·+\gamma ),g\rangle$$

on ${ℝ}_{+}^d$. Since F₁ is twice continuously differentiable and the Hessian of F₁ at $f\in {ℝ}_{+}^d$

$${\nabla }^2{F}_1(f)≔A^{\top }\text{diag }\left(\frac{g}{{(\mathit{\text{Af}}+\gamma )}^2}\right)A,$$

is positive semi-definite due to $g\in {ℝ}_{+}^m$, the convexity of F follows.

Since φ is bounded below by 0, for any ξ ∈ ℝ we have that lev_≤ξF ⊂ lev_≤ξF₁. Hence, by Theorem 11.9 in [5], the existence of the minimizer of the objective function F over ${\mathrm{R}}_{+}^d$ follows from the boundedness of the lower level set lev_≤ξF₁ for some ξ ∈ ℝ. Recalling the exercise 14 of Section 1.2 in [8] and the conditions imposed on A, g and γ, we know that the function F₁ has compact lower level sets, which in turn completes the proof.

3 Characterizations and Algorithms

In this section, we first characterize solutions of the optimization problem (7) via the proximity operator. We then develop an alternating projection algorithm for solving the optimization problem based on the characterizations.

Let ℍ denote an Euclidean space. For a proper convex function ψ : ℍ → ℝ ∪ {+∞}, having a nonempty domain (the set on which ψ is finite), the proximity operator of ψ, denoted by prox_ψ, is a mapping from ℍ to itself, defined for a given vector x ∈ ℍ by

$${\text{prox}}_{\psi }(x)≔\text{arg min }\{\psi (u)+\frac{1}{2}{\Vert u-x\Vert }^2:u\in ℍ\}.$$ (8)

The subdifferential of a proper function ψ on ℍ at a given vector x ∈ ℍ is the set defined by

$$\partial \psi (x)≔\{y:y\in ℍ\text{ and }\psi (z)\ge \psi (x)+\langle y,z-x\rangle \text{ for all }z\in ℍ\}.$$

The subdifferential and the proximity operator of the function ψ are intimately related. Specifically, for x in the domain of ψ and y ∈ ℍ we have that

$$y\in \partial \psi (x)\text{ if and only if }x={\text{prox}}_{\psi }(x+y).$$ (9)

For a discussion of this relation, see, for example, [5, Proposition 16.34] and [42, 50].

The indicator function of a closed convex set C in ℍ is defined as

$${\iota }_C(u)≔\{\begin{array}{cc}0,\hfill & \text{if }u\in C,\hfill \\ +\mathrm{\infty },\hfill & \text{otherwise}.\hfill \end{array}$$

It can be observed that the proximity operator for the indicator function of a closed convex subset C in ℍ is the projection operator onto C. For notational simplicity, when the set C is ${ℝ}_{+}^d$, we let

$$\mathrm{\Upsilon }≔{\iota }_{{ℝ}_{+}^d}.$$

The subdifferential of ϒ can be explicitly given. To this end, for a given vector x = (x_i : i ∈ ℕ_d) in ${ℝ}_{+}^d$, we define a projection matrix P associated with x by:

$$P(x)≔\text{diag }(\delta (x_i):i\in {\mathbb{N}}_d),$$

where δ(x_i) equals to 1 if x_i = 0, and 0 otherwise. Then, by the definition of subdifferential, for a vector x in ${ℝ}_{+}^d$, we have that

$$\partial \mathrm{\Upsilon }(x)=-P(x){ℝ}_{+}^d.$$ (10)

Define

$$𝕊:=\{S:S\text{ is a }d\times d\text{ diagonal matrix with positive diagonal entries}\}.$$

For any S ∈ 𝕊 and $x\in {ℝ}_{+}^d$, from (10) together with the identity $S{ℝ}_{+}^d={ℝ}_{+}^d$, we have that

$$S\partial \mathrm{\Upsilon }(x)=-\mathit{\text{SP}}(x){ℝ}_{+}^d=-P(x)S{ℝ}_{+}^d=-P(x){ℝ}_{+}^d=\partial \mathrm{\Upsilon }(x).$$

Thus, we observe that

$$S◦\partial \mathrm{\Upsilon }=\partial \mathrm{\Upsilon }.$$ (11)

For given positive numbers λ and μ, a vector g in ${ℝ}_{+}^m$, an m × d matrix A ∈ 𝔸, an n × d matrix B, we define $H:{ℝ}_{+}^d\times {ℝ}^n\to ℝ$, at $(f,b)\in {ℝ}_{+}^d\times {ℝ}^n$, as

$$H(f,b)≔\langle \mathit{\text{Af}},1\rangle -\langle \text{ln}(\mathit{\text{Af}}+\gamma ),g\rangle +\lambda \mu \langle \mathit{\text{Bf}},b\rangle .$$ (12)

We use ∇_fH and ∇_bH to denote the gradient of H with respect to its first and the second variables, respectively. More precisely, we have for any point $(f,b)\in {ℝ}_{+}^d\times {ℝ}^n$ that

$${\nabla }_{f}H(f,b)=A^{\top }(1-\frac{g}{\mathit{\text{Af}}+\gamma })+\lambda \mu B^{\top }b,$$ (13)

$${\nabla }_{b}H(f,b)=\lambda \mu \mathit{\text{Bf}}.$$ (14)

Set

$$\tau ≔\frac{\beta }{\lambda }\text{ and }\sigma ≔\frac{1}{\lambda \mu }.$$ (15)

With this preparation, we present below a characterization of the solutions of model (7) via a coupled fixed-point equations.

Theorem 3.1. Let A ∈ 𝔸, $g\in {ℝ}_{+}^m$, γ and λ be two positive numbers, φ be a proper convex nonnegative function defined on ℝⁿ, and B be an n × d matrix. If $f\in {ℝ}_{+}^d$ is a solution of the minimization problem (7), then for any β, μ > 0, and S ∈ 𝕊, there exists b ∈ ℝⁿ such that the pair $(f,b)\in {ℝ}_{+}^d\times {ℝ}^n$ is a solution of the following coupled equations

$$b=(ℐ-{\text{prox}}_{{\mu }^{-1}\phi })(b+\sigma {\nabla }_{b}H(f,b)),$$ (16)

$$f={\text{prox}}_{\mathrm{\Upsilon }}(f-\tau S{\nabla }_{f}H(f,b)).$$ (17)

Conversely, if there exist β, μ > 0, S ∈ 𝕊, b ∈ ℝⁿ and $f\in {ℝ}_{+}^d$ such that the above equations hold, then f is a solution of the minimization problem (7).

Proof. Let f be a solution of the minimization problem (7). Applying Fermat’s rule to (7), we get the relation

$$0\in A^{\top }(1-\frac{g}{\mathit{\text{Af}}+\gamma })+\lambda B^{\top }\partial \phi (\mathit{\text{Bf}})+\partial \mathrm{\Upsilon }(f).$$ (18)

Hence, for arbitrary positive numbers β and μ, there exist $u\in \frac{\beta }{\lambda }\partial \mathrm{\Upsilon }(f)\text{ and }b\in \frac{1}{\mu }\partial \phi (\mathit{\text{Bf}})$ such that from (13) and (18), we have that

$$0={\nabla }_{f}H(f,b)+\frac{\lambda }{\beta }u.$$ (19)

By using relation (9), equation (16) is a direct consequence of $b\in \frac{1}{\mu }\partial \phi (\mathit{\text{Bf}})$ and (14). Multiplying the inclusion $u\in \frac{\beta }{\lambda }\partial \mathrm{\Upsilon }(f)$ by the diagonal matrix S and using (11) yield the relation Su ∈ ∂ϒ (f). Applying (9) to the above inclusion, we have that

$$f={\text{prox}}_{\mathrm{\Upsilon }}(f+\mathit{\text{Su}}).$$ (20)

Solving u from (19) and substituting it into (20) yield (17).

Conversely, if β, μ are given positive numbers and S is a matrix in 𝕊 such that (f, b) is a solution of (16)–(17), then all the arguments discussed above are reversible. This completes the proof.

The characterization of the solutions to the minimization problem (7) in Theorem 3.1 is essential for deriving other equivalent ones with the aim of developing efficient algorithms for finding the solutions of the variational problem. As an example, an alternative formulation for the minimization problem (7) based on Theorem 3.1 is presented below.

Proposition 3.2. Let A ∈ 𝔸, $g\in {ℝ}_{+}^m$, γ and λ be two positive numbers, φ be a proper convex nonnegative function defined on ℝⁿ, and B be an n × d matrix. If $f\in {ℝ}_{+}^d$ is a solution of the minimization problem (7), then for any β, μ > 0, and S ∈ 𝕊, there exists b ∈ ℝⁿ such that the pair $(f,b)\in {ℝ}_{+}^d\times {ℝ}^n$ is a solution of the coupled equations

$$b=(ℐ-{\text{prox}}_{{\mu }^{-1}\phi })(b+\sigma {\nabla }_{b}H({\text{prox}}_{\mathrm{\Upsilon }}(f-\tau S{\nabla }_{f}H(f,b)),b)),$$ (21)

$$f={\text{prox}}_{\mathrm{\Upsilon }}(f-\tau S{\nabla }_{f}H(f,b)).$$ (22)

Conversely, if there exist β, μ > 0, S ∈ 𝕊, b ∈ ℝⁿ and $f\in {ℝ}_{+}^d$ such that the above equations hold, then f is a solution of the minimization problem (7).

From the given assumptions, the existence of a fixed point (f_⋆, b_⋆) of the coupled equations (21)–(22) is a direct consequence of Proposition 2.1 and Theorem 3.1 together with Proposition 3.2.

Based on the above characterization, the following Picard iteration is adopted to find a solution of the equations (21)–(22): Given any initial $(f^{(0)},b^{(0)})\in {ℝ}_{+}^d\times {ℝ}^n$, for any k = 0, 1, …, we compute

$$\{\begin{array}{c}{b}^{(k+1)}=(ℐ-{\text{prox}}_{{\mu }^{-1}\phi })(b^{(k)}+\sigma {\nabla }_{b}H({\text{prox}}_{\mathrm{\Upsilon }}(f^{(k)}-\tau S{\nabla }_{f}H(f^{(k)},b^{(k)})),b^{(k)}))\hfill \\ f^{(k+1)}={\text{prox}}_{\mathrm{\Upsilon }}(f^{(k)}-\tau S{\nabla }_{f}H(f^{(k)},b^{(k+1)})).\hfill \end{array}$$ (23)

We show next that both ℐ − prox_μ⁻¹φ and prox_ϒ are projections. Since the iterative scheme (23) applies these two projections alternatingly, we shall call scheme (23) an alternating projection algorithm. It is of particularly interest that S in the characterization of Proposition 3.2 can be viewed as a preconditioner in our developed iterative scheme (23), therefore, it makes the algorithm practically tractable. For this reason, we call this matrix the preconditioning matrix.

To better prepare the convergence analysis of this algorithm which will be our focus of the next section, we present an equivalent form of (23). This new form is as follows:

$$\{\begin{array}{c}{h}^{(k)}≔{\text{prox}}_{\mathrm{\Upsilon }}(f^{(k)}-\tau S{\nabla }_{f}H(f^{(k)},b^{(k)})),\hfill \\ b^{(k+1)}=(ℐ-{\text{prox}}_{{\mu }^{-1}\phi })(b^{(k)}+\sigma {\nabla }_{b}H(h^{(k)},b^{(k)})),\hfill \\ f^{(k+1)}={\text{prox}}_{\mathrm{\Upsilon }}(f^{(k)}-\tau S{\nabla }_{f}H(f^{(k)},b^{(k+1)})).\hfill \end{array}$$ (24)

We now derive a technical lemma to show that the operator ℐ −prox_μ⁻¹φ in (24) is a projection operator on a closed convex set of ℝⁿ. To this end, we need to review the concept of the conjugate function and some related results. Let ψ : ℍ → ℝ ∪ {+∞} be a proper function. The function ψ* : ℍ → ℝ ∪ {+∞} defined, at u ∈ ℍ, by

$${\psi }^{*}(u)≔\text{sup}\{\langle x,u\rangle -\psi (x):x\in ℍ\}$$

is called the conjugate of ψ at u. For a proper lower semicontinuous convex function ψ on ℍ and any positive number α, the proximity operator of ψ and that of its conjugate ψ* satisfy the following relation ([5, Theorem 14.3 (ii)] and [44, Proposition 4.a])

$$ℐ={\text{prox}}_{\alpha \psi }+\alpha {\text{prox}}_{{\alpha }^{-1}{\psi }^{*}}◦{\alpha }^{-1}ℐ.$$ (25)

Next, we recall the notion of the positive homogeneous function. A function ψ : ℍ → {−∞} ∪ ℝ ∪ {+∞} is positive homogeneous if for any x ∈ ℍ and any positive number α,

$$\psi (\alpha x)=\alpha \psi (x).$$ (26)

Clearly, ψ(0) = 0. Furthermore, if ψ is a positive homogeneous and proper lower semicontinuous convex function on ℍ then the conjugate function ψ* is the indicator function on the set ∂ψ(0) (see, e.g., [5, 52]), that is,

$${\psi }^{*}={\iota }_{\partial \psi (0)}.$$ (27)

Lemma 3.3. If ψ is a positive homogeneous and proper lower semicontinuous convex function on ℍ and α is a positive number, then ℐ − prox_αψ is the projection operator on the set α∂ψ(0), that is,

$$ℐ-{\text{prox}}_{\alpha \psi }={\text{prox}}_{{\iota }_{\alpha \partial \psi (0)}}.$$ (28)

Proof. From (27), we know that α⁻¹ψ* = α⁻¹ι_∂ψ(0) = ι_∂ψ(0). Combining this relation with (25), we obtain that

$$ℐ-{\text{prox}}_{\alpha \psi }=\alpha {\text{prox}}_{{\iota }_{\partial \psi (0)}}○{\alpha }^{-1}ℐ={\text{prox}}_{{\iota }_{\alpha \partial \psi (0)}},$$

proving the desired formula.

By Lemma 3.3, we conclude that ℐ −prox_μ⁻¹φ in (24) is the same as prox_{ιμ⁻¹∂φ(0)}. Hence, each equation in the iterative algorithm (24) involves an operator of the form prox_ιC (· − T (∇G)(·)) for a convex set C in ℍ, a function G defined on ℍ and a symmetric positive definite matrix T mapping ℍ to itself.

We shall end this section by providing a more general characterization of the solutions of the minimization problem (7). To this end, for a proper convex nonnegative function φ on ℝⁿ, an n × d matrix B, a given h ∈ ℝ^d, a positive number μ, and a positive integer r, we define $Q_h^r:{ℝ}^n\to {ℝ}^n$, with

$$Q_h^0≔ℐ\text{ and }{Q}_h≔(ℐ-{\text{prox}}_{{\mu }^{-1}\phi })(·+\mathit{\text{Bh}}),$$

recursively, by:

$$Q_h^r≔Q_h◦Q_h^{r-1}.$$ (29)

By using equation (14) and the proof of Proposition 3.2, we may establish the following result.

Proposition 3.4. Let A ∈ 𝔸, $g\in {ℝ}_{+}^m$, γ and λ be two positive numbers, φ be a proper convex nonnegative function defined on ℝⁿ, and B be an n × d matrix. If $f\in {ℝ}_{+}^d$ is a solution of the minimization problem (7), then for any β, μ > 0, and S ∈ 𝕊, there exists b ∈ ℝⁿ such that the pair $(f,b)\in {ℝ}_{+}^d\times {ℝ}^n$ is a solution of the coupled equations

$$b={Q^r}_f(b)$$ (30)

$$f={\text{prox}}_{\mathrm{\Upsilon }}(f-\tau S{\nabla }_{f}H(f,b)).$$ (31)

Conversely, if there exist β, μ > 0, S ∈ 𝕊, b ∈ ℝⁿ and $f\in {ℝ}_{+}^d$ such that the above equations hold, then f is a solution of the minimization problem (7).

Essentially, both Theorem 3.1 and Proposition 3.2 can be viewed as special cases of Proposition 3.4 with r = 1. The purpose of introducing the operator Q^r_f with r greater than 1 is mainly from consideration of developing efficient algorithms in Sections 5 and 6.

4 Convergence Analysis

We analyze in this section convergence of the preconditioned alternating projection algorithm described in the last section.

The convergence consideration of the algorithm requires introducing the notion of the weighted norm. For a symmetric and positive definite matrix T : ℍ → ℍ, we define the weighted inner product by

$${\langle x,y\rangle }_T≔\langle T^{-1}x,y\rangle ,x,y\in ℍ.$$

The induced weighted norm is accordingly defined by

$${\Vert x\Vert }_T≔\sqrt{{\langle x,x\rangle }_T}.$$

Note that a symmetric positive definite matrix has precisely one symmetric positive definite square root. Hence, we can rewrite $\langle x,x\rangle T=\langle T^{-\frac{1}{2}}x,T^{-\frac{1}{2}}x\rangle$, which in turn implies that the above weighted norm is a norm on ℍ.

Next we present a lemma which provides a tool for the proof of the convergence of the sequence generated by the iterative scheme (23). For any initial pair $(f^{(0)},b^{(0)})\in {ℝ}_{+}^d\times {ℝ}^n$, we let

$$𝒰≔\{(f^{(k)},b^{(k)}):k\in \mathbb{N}\},\text{ where }\mathbb{N}≔\{1,2,\dots \}$$

be the sequence generated by the iterative scheme (23).

Lemma 4.1. Let σ and τ be the two positive numbers defined by (15), H be a function on ℝ^d × ℝⁿ defined by (12), S ∈ 𝕊 and φ be a positive homogeneous and convex function on ℝⁿ. If the following conditions hold

1. the sequence 𝒰 is bounded,

2. lim_k→∞‖f^(k+1) − f^(k)‖_S = lim_k→∞ ‖b^(k+1) − b^(k)‖ = 0,

then there exists a subsequence of 𝒰 that converges to a solution of the coupled equations (21)–(22).

Proof. Since by hypothesis 𝒰 is a bounded sequence in ${ℝ}_{+}^d\times {ℝ}^n$, there exists a subsequence {(f^(k_i), b^(k_i)) : i ∈ ℕ} that converges to a point (f̂, b̂) in ${ℝ}_{+}^d\times {ℝ}^n$. This together with Condition (ii) ensures that the subsequence {(f^(k_i+1), b^(k_i+1)) : i ∈ ℕ} converges to the same point. Therefore, in (23) by choosing k := k_i and letting i → ∞, we conclude that the point (f̂,b̂) satisfies the coupled equations (21)–(22).

The use of Lemma 4.1 in the proof of the convergence result requires that we verify the hypotheses of the lemma. This is fulfilled by establishing the following estimate on the quantities defined by

$$e^{(k)}≔\frac{1}{2\tau }{\Vert f^{(k)}-f_{\star }\Vert }_S^2+\frac{1}{2\sigma }{\Vert b^{(k)}-b_{\star }\Vert }^2$$

for a solution (f_⋆, b_⋆) of equations (21)–(22) that

$$e^{(k)}+\frac{1}{2\tau }{\displaystyle \sum _{j=0}^{k-1}}{\Vert f^{(j+1)}-h^{(j)}\Vert }_S^2+\frac{1}{2\tau }{\displaystyle \sum _{j=0}^{k-1}}{C}_j{\Vert h^{(j)}-f^{(j)}\Vert }_S^2+\frac{1}{2\sigma }{\displaystyle \sum _{j=0}^{k-1}}{D}_j{\Vert b^{(j+1)}-b^{(j)}\Vert }^2\le e^{(0)},$$ (32)

where h^(j) is defined as in (24), and C_j, D_j are some positive constants.

We now establish several results needed for proving estimate (32). For a proper convex function ψ : ℍ → ℝ ∪ {+∞} and a symmetric positive definite matrix T, the proximity operator of ψ with respect to T, denoted by ${\text{prox}}_{\psi }^T$, is defined for a given vector x ∈ ℍ by

$${\text{prox}}_{\psi }^T(x)≔\text{arg min }\{\psi (u)+\frac{1}{2}{\Vert u-x\Vert }_T^2:u\in ℍ\}.$$

Clearly, we have that ${\text{prox}}_{\psi }={\text{prox}}_{\psi }^I$. Moreover, for x in the domain of ψ and y ∈ ℍ, we have the following generalization of (9)

$$y\in T\partial \psi (x)\text{ if and only if }x={\text{prox}}_{\psi }^T(x+y).$$ (33)

We next present a reformulation of the proximity operator prox_ϒ.

Proposition 4.2. If S ∈ 𝕊, then

$${\text{prox}}_{\mathrm{\Upsilon }}={\text{prox}}_{\mathrm{\Upsilon }}^S.$$ (34)

Proof. Let x ∈ ℝ^d and p = prox_ϒ(x). By relation (9), we have the inclusion x − p ∈ ∂ϒ(p). Since $p\in {ℝ}_{+}^d$, using equation (11), we get that x − p ∈ S∂ϒ(p). By relation (33), it yields that $p={\text{prox}}_{\mathrm{\Upsilon }}^S(x)$, which completes the proof.

With Proposition 4.2 in mind, we next discuss several properties of the operator ${\text{prox}}_{{\iota }_C}^T(·-T(\nabla G)(·))$, which are crucial in our convergence analysis.

Lemma 4.3. Let C be a nonempty closed convex subset of ℍ, T be a symmetric positive definite matrix mapping ℍ to itself and G be a proper convex differentiable function on ℍ. Set

$$p:={\text{prox}}_{{\iota }_C}^T(x-T\nabla G(x)).$$ (35)

Then the following statements hold:

1. For any y ∈ C,

   $${\Vert p-y\Vert }_T^2\le {\Vert x-y\Vert }_T^2-{\Vert p-x\Vert }_T^2-2\langle \nabla G(x),p-y\rangle$$ (36)

   and

   $${\Vert p-y\Vert }_T^2\le {\Vert x-y\Vert }_T^2-{\Vert p-x\Vert }_T^2-2\langle \nabla G(x),p-x\rangle +2[G(y)-G(x)].$$ (37)
2. Furthermore, if G is also differentiable at p, then for any y ∈ C,

   $${\Vert p-y\Vert }_T^2\le {\Vert x-y\Vert }_T^2-{\Vert p-x\Vert }_T^2-2\langle \nabla G(x)-\nabla G(p),p-x\rangle +2[G(y)-G(p)].$$ (38)

Proof. We first prove the inequalities in Item (i). Note that for any y ∈ ℍ, we have that

$${\Vert p-y\Vert }_T^2={\Vert x-y\Vert }_T^2-{\Vert p-x\Vert }_T^2+2\langle T^{-1}(p-x),(p-y)\rangle .$$ (39)

By equations (35) and (9), we have the inclusion relation

$$x-T\nabla G(x)-p\in T\partial {\iota }_C(p).$$

Multiplying the above inclusion by the symmetric positive definite matrix T⁻¹ and recalling the definition of the subdifferential, we have for all y ∈ C that

$$\langle T^{-1}(x-T\nabla G(x)-p),y-p\rangle \le {\iota }_C(y)-{\iota }_C(p)=0.$$

By splitting the term 〈T⁻¹(p−x), p−y〉 as the sum of 〈T⁻¹(x−T∇G(x)−p), y−p〉 and 〈−∇G(x), p−y〉, and using the above inequality, from (39) we conclude that inequality (36) holds. Inequality (37) follows from (36) together with

$$\langle \nabla G(x),p-y\rangle =\langle \nabla G(x),p-x\rangle +\langle \nabla G(x),x-y\rangle$$

and the inequality

$$\langle \nabla G(x),x-y\rangle \ge G(x)-G(y)$$

ensured by the convexity of G.

Finally, since G is differentiable at p, again by the convexity of G, we have that

$$\langle \nabla G(p),p-x\rangle \ge G(p)-G(x).$$

This together with (37) leads to (38).

As a consequence of Lemma 4.3 with G being identical to zero, using (36) twice we derive for all x, y ∈ ℍ that

$${\Vert {\text{prox}}_{{\iota }_C}^T(x)-{\text{prox}}_{{\iota }_C}^T(y)\Vert }_T\le {\Vert x-y\Vert }_T.$$ (40)

We next show that a solution of the coupled equations (16)–(17) is a saddle point of the function H. This result is necessary for establishing inequality (32).

Lemma 4.4. Let H be a function on ℝ^d × ℝⁿ defined by (12). If $(f_{\star },b_{\star })\in {ℝ}_{+}^d\times {ℝ}^n$ is a solution of the coupled equations (16)–(17), then inequality

$$H(f_{\star ,}b)\le H(f_{\star ,}{b}_{\star })\le H(f,b_{\star })$$ (41)

holds for any point $(f,b)\in {ℝ}_{+}^d\times ({\mu }^{-1}\partial \phi (0))$.

Proof. We prove this lemma by showing the following two inequalities

$$H(f_{\star ,}b)\le H(f_{\star ,}{b}_{\star }),\text{ for all }b\in ({\mu }^{-1}\partial \phi (0))$$ (42)

and

$$H(f_{\star ,}{b}_{\star })\le H(f,b_{\star }),\text{ for all }f\in {ℝ}_{+}^d.$$ (43)

We first prove inequality (42). By the definition of b_⋆ and (28), we have that

$$b_{\star }={\text{prox}}_{{\iota }_{{\mu }^{-1}\partial \phi (0)}}(b_{\star }+{\mathit{\text{Bf}}}_{\star }).$$

Employing the characterization of the projection, we observe that

$$\langle {\mathit{\text{Bf}}}_{\star },b-b_{\star }\rangle =\langle (b_{\star }+{\mathit{\text{Bf}}}_{\star })-b_{\star },b-b_{\star }\rangle \le 0,\text{ for all }b\in ({\mu }^{-1}\partial \phi (0)),$$

which is equivalent to inequality (42).

It remains to show inequality (43). Using the relations (9) and (34), from (17) we get for any S ∈ 𝕊 that

$$0\in S{\nabla }_{f}H(f_{\star },b_{\star })+S{\partial }_{{\iota }_{{ℝ}_{+}^d}}(f_{\star }).$$

Multiplying the above inclusion by the matrix S⁻¹ guarantees that H(·, b_⋆) achieves its minimum value at the point f_⋆. Thus, inequality (43) is valid.

We next prove estimate (32) by employing Lemma 4.3 and Lemma 4.4. To this end, for an S ∈ 𝕊, we define the quantities

$$A_j≔\{\begin{array}{cc}\frac{{\Vert {\nabla }_{f}H(h^{(j)},b^{(j+1)})-{\nabla }_{f}H(f^{(j)},b^{(j+1)})\Vert }_{S-1}}{{\Vert h^{(j)}-f^{(j)}\Vert }_S},\hfill & \text{if }{\Vert h^{(j)}-f^{(j)}\Vert }_S\ne 0,\hfill \\ 0,\hfill & \text{otherwise},\hfill \end{array}$$

and

$$B_j≔\{\begin{array}{cc}\frac{\Vert {\nabla }_{f}H(f^{(j)},b^{(j+1)})-{\nabla }_{f}H(f^{(j)},b^{(j)})\Vert }{\Vert b^{(j+1)}-b^{(j)}\Vert },\hfill & \text{if }\Vert b^{(j+1)}-b^{(j)}\Vert \ne 0,\hfill \\ 0,\hfill & \text{otherwise}.\hfill \end{array}$$

Lemma 4.5. If (f_⋆, b_⋆) is a solution of the coupled equations (21)–(22), then the estimate (32) holds with C_j := 1 − 2τA_j and D_j := 1 − 2τ‖B‖₂‖S‖₂B_j.

Proof. Let j be a positive integer. Identifying x, y, p, T and G in (38), respectively, with b^(j), b_⋆, b^(j+1), I and −σH(h^(j), ·), and recalling b^(j+1) being defined by the projection (24), we have that

$$\frac{1}{2\sigma }{\Vert b^{(j+1)}-b_{\star }\Vert }^2\le \frac{1}{2\sigma }{\Vert b^{(j)}-b_{\star }\Vert }^2-\frac{1}{2\sigma }{\Vert b^{(j+1)}-b^{(j)}\Vert }^2+H(h^{(j)},b^{(j+1)})-H(h^{(j)},b_{\star }),$$ (44)

where we have used the fact that ∇_bH(f, ·) is a constant. Likewise, identifying x, y, p, T and G in (37), respectively, with f^(j), f_⋆, f^(j+1), S and τH(·, b^(j+1)), recalling f^(j+1) being defined by the projection (23) and applying Proposition 4.2, we observe that

$$\frac{1}{2\tau }{\Vert f^{(j+1)}-f_{\star }\Vert }_S^2\le \frac{1}{2\tau }{\Vert f^{(j)}-f_{\star }\Vert }_S^2-\frac{1}{2\tau }{\Vert f^{(j+1)}-f^{(j)}\Vert }_S^2+\langle {\nabla }_{f}H(f^{(j)},b^{(j+1)}),f^{(j)}-f^{(j+1)}\rangle +H(f_{\star },b^{(j+1)})-H(f^{(j)},b^{(j+1)}).$$ (45)

Using the inequality

$$H(f_{\star },b^{(j+1)})\le H(h^{(j)},b_{\star }),$$

which is ensured by Lemma 4.4, in the sum of the last two terms of (44) and (45) yields

$$H(h^{(j)},b^{(j+1)})-H(f^{(j)},b^{(j+1)})+H(f_{\star },b^{(j+1)})-H(h^{(j)},b_{\star })\le H(h^{(j)},b^{(j+1)})-H(f^{(j)},b^{(j+1)}).$$ (46)

The convexity of H(·, b^(j+1)) ensures that

$$\langle {\nabla }_{f}H(h^{(j)},b^{(j+1)}),f^{(j)}-h^{(j)}\rangle \le H(f^{(j)},b^{(j+1)})-H(h^{(j)},b^{(j+1)}),$$

which combined with (46) gives

$$H(h^{(j)},b^{(j+1)})-H(f^{(j)},b^{(j+1)})+H(f_{\star },b^{(j+1)})-H(h^{(j)},b_{\star })\le \langle {\nabla }_{f}H(h^{(j)},b^{(j+1)}),h^{(j)}-f^{(j)}\rangle .$$ (47)

Moreover, identifying x, y, p, T and G in (36), respectively, with f^(j), f^(j+1), h^(j), S and τH(·, b^(j)), and recalling the definition (24) of h^(j) in terms of the projection, we obtain that

$$\frac{1}{2\tau }{\Vert f^{(j+1)}-f^{(j)}\Vert }_S^2\ge \frac{1}{2\tau }{\Vert f^{(j+1)}-h^{(j)}\Vert }_S^2-\frac{1}{2\tau }{\Vert h^{(j)}-f^{(j)}\Vert }_S^2+\langle {\nabla }_{f}H(f^{(j)},b^{(j)}),h^{(j)}-f^{(j+1)}\rangle .$$ (48)

Recalling the definition of e^(j), summing (44) and (45), and using (48), (47) in the resulting sum yield

$$e^{(j+1)}-e^{(j)}\le -\frac{1}{2\tau }{\Vert f^{(j+1)}-h^{(j)}\Vert }_S^2-\frac{1}{2\tau }{\Vert h^{(j)}-f^{(j)}\Vert }_S^2-\frac{1}{2\sigma }{\Vert b^{(j+1)}-b^{(j)}\Vert }^2+I_1+I_2,$$ (49)

where

$$I_1≔\langle {\nabla }_{f}H(f^{(j)},b^{(j+1)})-{\nabla }_{f}H(h^{(j)},b^{(j+1)}),f^{(j)}-h^{(j)}\rangle ,$$

$$I_2≔\langle {\nabla }_{f}H(f^{(j)},b^{(j)})-{\nabla }_{f}H(f^{(j)},b^{(j+1)}),f^{(j+1)}-h^{(j)}\rangle .$$

Next we further estimate the last two inner products in (49). Note that S and S⁻¹ are diagonal and positive definite matrices, and hence they have unique diagonal positive definite square roots $S^{\frac{1}{2}}\text{ and }{S}^{-\frac{1}{2}}$, respectively. We then have that

$$I_1=\langle S^{\frac{1}{2}}({\nabla }_{f}H(f^{(j)},b^{(j+1)})-{\nabla }_{f}H(h^{(j)},b^{(j+1)})),S^{-\frac{1}{2}}(f^{(j)}-h^{(j)})\rangle \le {\Vert {\nabla }_{f}H(f^{(j)},b^{(j+1)})-{\nabla }_{f}H(h^{(j)},b^{(j+1)})\Vert }_{S-1}·{\Vert f^{(j)}-h^{(j)}\Vert }_S.$$ (50)

The last inequality follows from using the Cauchy-Schwartz inequality together with the definition of the weighted norm. Likewise, we can also get that

$$I_2\le {\Vert {\nabla }_{f}H(f^{(j)},b^{(j)})-{\nabla }_{f}H(f^{(j)},b^{(j+1)})\Vert }_{S-1}.{\Vert f^{(j+1)}-h^{(j)}\Vert }_S.$$ (51)

From the definitions of f^(j+1) in (23) and h^(j) in (24) and inequality (40), we get

$${\Vert f^{(j+1)}-h^{(j)}\Vert }_S\le \tau {\Vert S({\nabla }_{f}H(f^{(j)},b^{(j+1)})-{\nabla }_{f}H(f^{(j)},b^{(j)}))\Vert }_S=\tau \Vert S^{\frac{1}{2}}({\nabla }_{f}H(f^{(j)},b^{(j+1)})-{\nabla }_{f}H(f^{(j)},b^{(j)}))\Vert .$$ (52)

On the other hand, since

$${\nabla }_{f}H(f^{(j)},b^{(j)})-{\nabla }_{f}H(f^{(j)},b^{(j+1)})=\lambda \mu B^{\top }(b^{(j)}-b^{(j+1)}),$$

this equation with (52) yields that

$${\Vert f^{(j+1)}-h^{(j)}\Vert }_S\le \tau \lambda \mu {\Vert B\Vert }_2{\Vert S^{\frac{1}{2}}\Vert }_2\Vert b^{(j)}-b^{(j+1)}\Vert ,$$

which together with the estimate (51) implies that

$$I_2\le \lambda \mu \tau B_j{\Vert B\Vert }_2{\Vert S\Vert }_2{\Vert b^{(j+1)}-b^{(j)}\Vert }^2.$$ (53)

Combining inequalities (49), (50) and (53) together with using the definition of A_j gives the estimate

$$e^{(j+1)}-e^{(j)}\le -\frac{1}{2\tau }{\Vert f^{(j+1)}-h^{(j)}\Vert }_S^2-\frac{C_j}{2\tau }{\Vert h^{(j)}-f^{(j)}\Vert }_S^2-\frac{D_j}{2\sigma }{\Vert b^{(j+1)}-b^{(j)}\Vert }^2.$$ (54)

Summing the above inequality (54) for j running from 0 to k yields estimate (32).

In order to use the last lemma to show the validity of the hypotheses of Lemma 4.1, we bound the constants A_j and B_j that appear in the last lemma. To this end, we need the following lemma that pertains to the Lipschitz continuity of the gradient of H with respect to each of its variables.

Lemma 4.6. If H is a function on ℝ^d × ℝⁿ defined by (12) and S ∈ 𝕊, then for a fixed vector b in ℝⁿ, ∇_fH(·, b) is Lipschitz continuous with constant $\frac{{\Vert g\Vert }_{\mathrm{\infty }}{\Vert A\Vert }_2^2{\Vert S\Vert }_2}{{\gamma }^2}$ while for a fixed vector f in ℝ^d, ∇_fH(f, ·) is Lipschitz continuous with constant λμ‖B‖₂. That is, for any f₁, $f_2\in {ℝ}_{+}^d$ and b ∈ ℝⁿ

$${\Vert {\nabla }_{f}H(f_1,b)-{\nabla }_{f}H(f_2,b)\Vert }_{S^{-1}}\le \frac{{\Vert g\Vert }_{\mathrm{\infty }}{\Vert A\Vert }_2^2{\Vert S\Vert }_2}{{\gamma }^2}{\Vert f_1-f_2\Vert }_S$$ (55)

and for any b₁, b₂ ∈ ℝⁿ and $f\in {ℝ}_{+}^d$

$$\Vert {\nabla }_{f}H(f,b_1)-{\nabla }_{f}H(f,b_2)\Vert \le \lambda \mu {\Vert B\Vert }_2\Vert b_1-b_2\Vert .$$ (56)

Proof. Using (13) and the definition of the weighted norm, for any f₁, $f_2\in {ℝ}_{+}^d$ and b ∈ ℝⁿ, we have that

$${\Vert {\nabla }_{f}H(f_1,b)-{\nabla }_{f}H(f_2,b)\Vert }_{S^{-1}}=\Vert S^{\frac{1}{2}}{A}^{\top }\left(\frac{({\mathit{\text{AS}}}^{\frac{1}{2}}{S}^{-\frac{1}{2}}(f_2-f_1))\odot g}{({\mathit{\text{Af}}}_1+\gamma )\odot ({\mathit{\text{Af}}}_2+\gamma )}\right)\Vert .$$

It can be verified that

$${\Vert ({\mathit{\text{Af}}}_1+\gamma )\odot ({\mathit{\text{Af}}}_2+\gamma )\Vert }_{\mathrm{\infty }}\ge {\gamma }^2\text{ and }\Vert ({\mathit{\text{AS}}}^{\frac{1}{2}}{S}^{-\frac{1}{2}}(f_2-f_1))\odot g\Vert \le {\Vert A\Vert }_2{\Vert S^{\frac{1}{2}}\Vert }_2{\Vert g\Vert }_{\mathrm{\infty }}{\Vert f_1-f_2\Vert }_S,$$

from which inequality (55) follows.

Inequality (56) follows directly from the expression of ∇_fH given in (13).

Finally, we show the convergence of the sequence 𝒰 := {(f^(k), b^(k)) : k ∈ ℕ} generated by the preconditioned alternating projection algorithm (23).

Theorem 4.7. Let λ, μ, γ be positive numbers, σ and τ be the numbers defined by (15), S ∈ 𝕊, φ be a positive homogeneous convex function on ℝⁿ, and H be the function on ℝ^d × ℝⁿ defined by (12). If β and μ are chosen to satisfy the conditions

$$0<\beta \le \frac{(1-\epsilon )\lambda {\gamma }^2}{2{\Vert g\Vert }_{\mathrm{\infty }}{\Vert A\Vert }_2^2{\Vert S\Vert }_2},0<\beta \mu \le \frac{1-\epsilon }{2{\Vert B\Vert }_2^2{\Vert S\Vert }_2}$$

for some ε ∈ (0, 1), then for any initial pair $(f^{(0)},b^{(0)})\in {ℝ}_{+}^d\times {ℝ}^n$, the sequence 𝒰 converges to a solution of the coupled equations (21)–(22).

Proof. We prove this theorem by employing Lemma 4.1. The conditions imposed on β and μ together with Lemma 4.6 lead to that both 1 − 2τA_j and 1 − 2τ ‖B‖₂‖S‖₂B_j are bounded below by ε for all j. Hence, Lemma 4.5 implies that the sequence {(f^(j), b^(j)) : j ∈ ℕ} is bounded and sequence {‖b^(j+1) − b^(j)‖ : j ∈ ℕ} converges to 0 and moreover both the sequences {‖h^(j) − f^(j)‖_S : j ∈ ℕ}, {‖f^(j+1) − h^(j)‖_S : j ∈ ℕ} converge to 0, which implies the convergence of the sequence {‖f^(k+1) − f^(k)‖_S : k ∈ ℕ} to 0. Therefore, by Lemma 4.1, there exists a subsequence {(f^(k_i), b^(k_i)) : i ∈ ℕ} which converges to $(\mathrm{f̂},\mathrm{b̂})\in {ℝ}_{+}^d\times ({\mu }^{-1}\partial \phi (0))$, a solution of the equations (21)–(22). It remains to show that the sequence 𝒰 also converges to the same point (f̂,b̂). Indeed, inequality (54) ensures that

$$\frac{1}{2\tau }{\Vert f^{(j+1)}-f_{\star }\Vert }_S^2+\frac{1}{2\sigma }{\Vert b^{(j+1)}-b_{\star }\Vert }^2\le \frac{1}{2\tau }{\Vert f^{(j)}-f_{\star }\Vert }_S^2+\frac{1}{2\sigma }{\Vert b^{(j+1)}-b_{\star }\Vert }^2.$$ (57)

Replacing the point (f_⋆, b_⋆) in inequality (57) by the point (f̂,b̂) and summing the resulting inequality for j from k_i to k − 1 with k > k_i lead to the inequality

$$\frac{1}{2\tau }{\Vert f^{(k)}-\mathrm{f̂}\Vert }_S^2+\frac{1}{2\sigma }{\Vert b^{(k)}-\mathrm{b̂}\Vert }^2\le \frac{1}{2\tau }{\Vert f^{(k_i)}-\mathrm{f̂}\Vert }_S^2+\frac{1}{2\sigma }{\Vert b^{(k_i)}-\mathrm{b̂}\Vert }^2.$$

This clearly guarantees that the sequence 𝒰 converges to the point (f̂,b̂).

We remark that the conditions stated in the last theorem imposed on the parameter β and μ are rather restricted. We shall demonstrate in Section 6 by numerical examples that choices of significantly larger β and μ than those allowed by the theorem lead to convergence of the iteration.

5 TV-Regularized MAP ECT Reconstruction

In this section, we specialize the general preconditioned alternating projection algorithm developed in Section 3 to the MAP ECT reconstruction by specifying the function φ, the matrices B and the preconditioning matrix S in (23). In particular, we present explicit formulas of the proximity operators for the two special convex functions involved in the algorithm. We also discuss the importance of the inner iteration for efficient computation in the context of MAP ECT reconstruction. Finally, we compare differences and advantages of our proposed algorithm with those of several existing algorithms for the Poisson-TV model (7).

We first present explicit expressions of φ and B according to the definition of the total-variation [53]. The concrete expressions of φ and B depend on how three dimensional images are vectorized. A three-dimensional image is assembled by a stack of two-dimensional images. For convenience of exposition, we assume that an image considered in this paper has a size of p × p × q. The image is treated as a vector in ℝ^p2q in such a way that the ijk-th voxel of the image, where i, j ∈ ℕ_p and k ∈ ℕ_q, corresponds to the (i+(j − 1)p+(k − 1)p²)-th element of the vector in ℝ^p2q. In the current section, we set d := p²q. To define the matrix B, we define an α × α difference matrix D_α by

$$D_{\alpha }≔\left[\begin{array}{cccc}\hfill 0\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill -1\hfill & \hfill 1\hfill & \hfill \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \ddots \hfill & \hfill \ddots \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \hfill & \hfill -1\hfill & \hfill 1\hfill \end{array}\right].$$

In terms of the notion of the matrix Kronecker product ⊗, we define the 3d × d matrix B by

$$B≔\left[\begin{array}{c}\hfill I_q\otimes I_p\otimes D_p\hfill \\ \hfill I_q\otimes D_p\otimes I_p\hfill \\ \hfill D_q\otimes I_p\otimes I_p\hfill \end{array}\right].$$

The convex function φ : ℝ^3d → ℝ is defined at z ∈ ℝ^3d as

$$\phi (z):={\displaystyle \sum _{i=1}^d}\Vert {[z_i,z_{d+i},z_{2d+i}]}^{\top }\Vert .$$ (58)

The isotropic total-variation of a vector f is then expressed as φ(Bf).

Execution of the iterative scheme (23) requires the availability of explicit formulas for the proximity operators of functions φ defined in (58) and the indicator function $\mathrm{\Upsilon }≔{\iota }_{{ℝ}_{+}^d}$. For a positive number μ and a vector z ∈ ℝ^3d, the components of the vector

$$y≔{\text{prox}}_{{\mu }^{-1}\phi }(z)$$

can be computed by using the formula

$${[y_i,y_{d+i},y_{2d+i}]}^{\top }=\text{max }\{{\Vert [z_i,z_{d+i},z_{2d+i}]}^{\top }\Vert -\frac{1}{\mu },0\}\frac{{[z_i,z_{d+i},z_{2d+i}]}^{\top }}{\Vert {[z_i,z_{d+i},z_{2d+i}]}^{\top }\Vert },i\in {\mathbb{N}}_d.$$

With this formula, for any positive integer r and a vector h ∈ ℝ^d, the operator $Q_h^r$ defined by (29) can be explicitly computed. The proximity operator of the indicator function ϒ (the projection operator onto the first octant ${ℝ}_{+}^d$) also has an explicit expression. That is, for $x\in {ℝ}_{+}^d$,

$${({\text{prox}}_{\mathrm{\Upsilon }}(x))}_i=\text{max}\{x_i,0\},i\in {\mathbb{N}}_d.$$

Thus, both prox_μ⁻¹φ and prox_ϒ have closed forms in the current context. These closed forms are convenient for numerical evaluation of the proximity operators of the two specific functions in the sense that no further optimization problems are required to solve. These specific examples can be evaluated numerically within the machine precision. While in general, computing the proximity operator of a convex function requires solving an optimization problem by its definition. Even in the situation when closed forms of the proximity operators are available, some round-off errors may be introduced during computation. In such a case, one needs to consider the stability issue of computing the proximity operator.

Based on Proposition 3.4, we propose the following algorithm (Algorithm 1) for the MAP ECT reconstruction.

Algorithm 1.

(Alternating Projection Algorithm for MAP ECT Reconstruction with a Fixed Matrix S)

1: Preparation: ∇fH, ∇bH, τ are defined in (13), (14) and (15), respectively. The parameter r is a positive integer.

2: Initialization: f(0) = 1, b(0) = 0.

3: repeat

4:      Step 1: h(k) ← proxΥ(f(k) − τS∇fH(f(k), b(k)))

5:      Step 2: $b^{(k+1)}\leftarrow Q_{h^{(k)}}^r(b^{(k)})$

6:      Step 3: f(k+1) ← proxΥ (f(k) − τS∇fH(f(k), b(k+1)))

7: until “convergence”

The parameter r in Algorithm 1 is the iteration number for the inner iteration. When r is chosen to be 1, three steps in Algorithm 1 correspond to the three equations in (24), respectively. In Algorithm 1, both Steps 1 and 3 involve the matrices A and A^⊤ while Step 2 involves matrix B. In the context of the MAP ECT reconstruction, matrix A is a dense matrix of a large size and matrix B is a sparse matrix of a relatively small size. As a result, computation with the matrix A or A^⊤ is more costly than computation with the matrix B. To reduce the overall computational cost, we suggest that the inner iteration be carried out with an appropriate choice of iteration number r. By paying less computational effort with an appropriate r we could obtain a more accurate estimate f^(k+1) at the k-th outer iterate. We shall study in the next section by numerical examples the choices of the iteration number r.

The preconditioning matrix S is not specified in Algorithm 1. The choice of the preconditioning matrix is crucial in designing computationally efficient algorithms. One may choose the preconditioning matrix S as the identity matrix, which corresponds to the trivial case without preconditioning. More interesting cases are the nontrivial choices. The choice of the preconditioning matrix S may be motivated from different ways with the same purpose of speeding up the convergence of the algorithm. A possible nontrivial choice is motivated by the idea of the projected Newton method. For more details of the projected Newton method, see [3, 6]. In passing, we point it out that preconditioning techniques were used in the context of emission computed tomography for other algorithms (see, for example, [15, 32, 34, 45]).

We propose a choice of the preconditioner S based on the classical expectation-maximization (EM). Recall that EM is an iterative scheme for computing the maximum likelihood estimate. According to [35], when the EM algorithm is applied to (1), we have for any $f^{(0)}\in {ℝ}_{+}^d$ that

$$f^{(k+1)}=E^{(k)}{A}^{\top }\left(\frac{g}{{\mathit{\text{Af}}}^{(k)}+\gamma }\right),$$ (59)

where E^(k) is a diagonal matrix defined by

$$E^{(k)}≔\text{diag }\left(\frac{f^{(k)}}{A^{\top }1}\right).$$ (60)

In the EM algorithm, the matrix E^(k) determines the direction for the next step of a search for the minimizer, for the purpose of finding the maximum likelihood estimate. By comparing (59) with the form of ∇_fH given in (13), motivated by the matrix E^(k) having the form (60) we suggest that we choose the matrix S in Algorithm 1 as the diagonal matrix E^(k) at the k-th iteration. This choice of the preconditioning matrix allows the search of the minimizer to follow the direction of the search in the classical EM algorithm for finding the maximum likelihood estimate while preserving the advantage of the alternating projection nature in the proposed algorithm. In this way, the preconditioning matrix is updated at every iterate step when a new value f^(k) is available. This leads to the following algorithm (Algorithm 2) for the MAP ECT reconstruction.

Since the choice of S is motivated from the EM algorithm (59), we shall call Algorithm 2 the EM preconditioned alternating projection algorithm (PAPA) for MAP ECT reconstruction and call the matrix E the EM-preconditioner. A numerical comparison of the proposed Algorithm 1 and Algorithm 2 will be presented in the next section. The numerical study shows that the EM-preconditioner speeds up significantly the convergence of the alternating projection algorithm.

We further comment on the dynamics of the EM-preconditioner. The PAPA algorithm which we described in Section 3 and for which we proved convergence in Section 4 has a fixed preconditioning matrix S. The preconditioner in Algorithm 2 changes dynamically from step to step. In the next section, we shall study the dynamics of the EM-preconditioner numerically and shall see that after some iteration steps, the change in the EM-preconditioner is so small that it can be neglected. In other wards, the EM-preconditioner tends to a fixed preconditioning matrix as the iteration number increases. Therefore, in practise, we may fix the preconditioning matrix after some iteration steps and propose the following semi-dynamic PAPA (Algorithm 3). In this way, the convergence theorem established in Section 4 is still applicable.

Algorithm 2.

(Preconditioned Alternating Projection Algorithm for MAP ECT Reconstruction)

Preparation: ∇fH, ∇bH, τ are defined in (13), (14) and (15), respectively. The parameter r is a positive integer.

Initialization: f(0) = 1, b(0) = 0.

repeat

Step 1: $S^{(k)}\leftarrow \text{diag }\left(\frac{f^{(k)}}{A^{\top }1}\right)$

Step 2: $h^{(k)}\leftarrow P_{{ℝ}_{+}^d}(f^{(k)}-\tau S^{(k)}{\nabla }_{f}H(f^{(k)},b^{(k)}))$

Step 3: $b^{(k+1)}\leftarrow Q_{h^{(k)}}^r(b^{(k)})$

Step 4: $f^{(k+1)}\leftarrow P_{{ℝ}_{+}^d}(f^{(k)}-\tau S^{(k)}{\nabla }_{f}H(f^{(k)},b^{(k+1)}))$

until “convergence”

Algorithm 3.

(Semi-Dynamic PAPA for MAP ECT Reconstruction)

Preparation: ∇fH, ∇bH, τ are defined in (13), (14) and (15), respectively. The parameters r and l are positive integers.

Initialization: f(0) = 1, b(0) = 0.

Run Algorithm 2 until k > l.

Set $S^{(l)}\leftarrow \text{diag }\left(\frac{f^{(l)}}{A^{\top }1}\right)$.

repeat

Step 1: $h^{(k)}\leftarrow P_{{ℝ}_{+}^d}(f^{(k)}-\tau S^{(l)}{\nabla }_{f}H(f^{(k)},b^{(k)}))$

Step 2: $b^{(k+1)}\leftarrow Q_{h^{(k)}}^r(b^{(k)})$

Step 3: $f^{(k+1)}\leftarrow P_{{ℝ}_{+}^d}(f^{(k)}-\tau S^{(l)}{\nabla }_{f}H(f^{(k)},b^{(k+1)}))$

until “convergence”

To close this section we compare PAPA with four existing algorithms, namely, the alternating extragradient method (AEM) [7], the nested EM-TV algorithm [54], the nested iterative algorithm for convex constrained problem [13], and the preconditioned primal-dual algorithm (P-PD) [50, 56].

The AEM algorithm, which is a variant of the extragradient method, was developed to solve the saddle-point formulation of the Poisson-TV model (7). We point out that the AEM appears to be a special case of the proposed Algorithm 1 with the trivial preconditioner S = I and inner iteration number r = 1, but it was developed based on a different principle. The introduction of inner iteration number r and a nontrivial preconditioner S in PAPA allows us to develop more efficient reconstruction algorithms.

We now compare PAPA with the nested EM-TV algorithm. Actually, the nested EM-TV requires to solve an optimization problem of the form

$$\text{argmin }\{\frac{1}{2}\langle f-f^{(k+\frac{1}{2})},\frac{A^{\top }1}{f^{(k)}}\odot (f-f^{(k+\frac{1}{2})})\rangle +\lambda \phi (\mathit{\text{Bf}}):f\in {ℝ}_{+}^d\}$$

exactly in each outer iteration. While PAPA does not need to do this and it leads to a more efficient algorithm. This will be demonstrated by numerical examples in the next section.

Next we compare PAPA with the nested iterative algorithm proposed in [13] for solving convex constrained problems. The paper combined the forward-backward and the Douglas-Rachford iterations together to minimize the sum of two functions over a convex set. The validity of the resulting algorithm requires at least one of the two functions differentiable. While PAPA is developed based on a fixed-point characterization (in terms of the proximity operator) of the solutions of the Poisson-TV model (7), which does not necessarily require any term of the objective function to be differentiable.

Finally, we compare PAPA with the P-PD algorithm developed in [56], which prototyped several convex optimization problems for computed tomography (CT) image reconstruction with the primal-dual (PD) algorithm, proposed earlier in [12]. Within each complete iterate step, the PD algorithm introduces an extrapolation step based on the current and previous iterates, which can be seen as an approximate extragradient step. In contrast, PAPA computes the primal leading point h^(k) by taking an extragradient step based on the current iterate only. Besides, PAPA made good use of the sparsity of the difference matrix B by carrying out the inner iteration to reduce the overall computational cost, while reference [56] did not. Indeed, matrix A is much denser than matrix B, and hence computation with A or A^⊤ is more costly than that with B. As we have pointed out earlier, by carrying out the inner iteration with an appropriate iteration number r we could greatly accelerate the whole iterative scheme. Moreover, following the idea in [50], paper [56] developed a P-PD algorithm for model (7) using fixed diagonal preconditioners. While in PAPA, we proposed a dynamic preconditioner motivated from the EM algorithm, which proves to be more efficient and converging faster in the numerical experiments presented in the next section.

6 Numerical Experiments

In this section, we report numerical results obtained from computational experiments for the proposed algorithms. We compare our algorithms with the conventional EM-TV algorithm [48] and the nested EM-TV algorithm [54] in terms of the reconstruction quality and computational performance. We also compare the convergence speed of our proposed algorithms with that of the P-PD algorithm developed in [56].

6.1 Simulated SPECT Projection Data

We created a digital cylindrical emission phantom with uniform mean background activity distribution (that is, with uniform mean number of nuclear disintegrations per time unit and per unit volume) and sets of 7 hot spheres and 7 cold spheres embedded in the cylinder. The hot and cold spheres simulate hyperperfused and hypoperfused defects, respectively. Such defects are of interest in nuclear medicine and one of the main tasks of ECT is detection of such defects. Mean activities across all spheres are uniform. The mean activity ratios of hot:background:cold areas are 40:10:1, respectively. The pixel size used is 0.172 cm. The phantom dimensions are: base radius 84 pixels and length 128 pixels. The spheres radii are 3, 4, 5, 6, 7, 9 and 14 pixels. Their centers are in slices 33 and 97. The locations of spheres in transaxial and sagittal planes are shown in Figure 1. The spheres are separated by a uniform region located between slices 47 and 82. The mean activity distribution in the phantom represents the mean radiotracer distribution, that is, the image f in (1). The parallel-collimator SPECT projection data for our experiments consist of 120 views in 256 × 128 matrix with pixel size 1.78 mm and were generated using analytical pixel-wise discretized projector A in (1) with 20 rays per detector bin [59]. The generated data follow Poisson probability distribution created by a random number generator and the total number of detector counts in 120 views equal to 1.79 × 10⁶ and 1.947 × 10⁷ corresponding to approximately 10 : 1 total activities ratio. Neither attenuation nor scatter was modeled and an ideal detector was assumed. Each image in these projection sets was then downsampled to a 128 × 64 matrix with pixel size 3.56 mm. The coefficient of variation (CV) defined as the ratio of the standard deviation to the mean in the projection image of a sufficiently large uniform region away from edges is used as a measure of Poisson noise in the noisy projection data. Using such a definition, our projection sets are characterized at 56% and 15% noise levels, respectively (Figure 2). For the sake of convenience, the phantom with higher (less noisy) and lower total activity (more noisy) is called“low-noise phantom” and “high-noise phantom”, respectively. The low-noise phantom corresponds to clinically realistic SPECT data, while the high-noise phantom SPECT data would result in clinically unacceptable high noise in the reconstructed images if treated with conventional reconstruction techniques.

Figure 1.

Morphology of numerical phantom used: (a) Transaxial cross-section (slice 17) through the centers of all hot spheres; (b)Transaxial cross-section (slice 49) through the centers of all cold spheres; (c) Sagittal cross-section through the centers of the two largest spheres. The mean activity ratios of hot:background:cold areas are 40:10:1, respectively. The spheres radii are counterclockwise: 3, 6, 4, 5, 7, 9 and 14 (center) pixels, respectively. The pixel size used is 0.172 cm.

Figure 2.

Example of one parallel-beam collimator SPECT projection view, out of 120 views in the projection set, simulated for one noise realization for a digital phantom shown in Figure 1: (a) 15% Poisson noise, 1.62 × 10⁵ counts per view; (b) 56% Poisson noise, 1.49 × 10⁴ counts per view.

Examples of one noise realization for one projection view are shown in Figure 2.

6.2 Numerical Studies of the Proposed Algorithms

In this subsection, we assess the numerical performance of the proposed algorithms: Algorithms 1, 2 and 3 in image reconstruction for the SPECT projection data generated from the low-noise and high-noise phantoms. Specifically, we consider three issues related to the proposed algorithms: the necessity of the preconditioning, the convergence of the proposed preconditioner (60) and the role of the multiple iteration steps in the inner iteration.

In our numerical experiments, the regularization parameter λ in the Poisson-TV model (7) is chosen by adopting the Bias-Noise curve method. Specifically, we calculated bias and the coefficient of variation (CV) in a reconstructed background region of interest for candidate regularization parameters (ranging from 1 × 10⁻⁴ to 1), and obtained the bias-CV curve. When choosing the optimal parameters, we consider the best trade-off between bias and CV. Furthermore, in order to improve the statistical accuracy, we generated three SPECT projection data sets with different noise realizations from the low-noise and the high-noise phantom, respectively, and evaluated the mean values of bias and CV with respect to the three different noise realizations. In particular, in our numerical experiments, the regularization parameter λ in the Poisson-TV model (7) is chosen to be 0.1 and 0.2 for the SPECT projection data sets generated from low-noise and high-noise phantom, respectively. The constant γ in the model is set to be 0.01 for both phantoms. Let {f^(k) : k ∈ ℕ} be a sequence generated by either Algorithm 1, 2 or 3. For a pre-given tolerance tol, the iterative process of an algorithm is terminated if the following requirement is satisfied

$$\Vert f^{(k)}-f^{(k+1)}\Vert /\Vert f^{(k+1)}\Vert \le \text{tol}.$$ (61)

The parameters in Algorithms 1, 2 and 3 are specified as follows. For Algorithm 1 without preconditioning (S = I) we choose β to be 10⁷ times of the upper bound suggested by Theorem 4.7, and $\mu ≔1/(2\beta {\Vert B\Vert }_2^2)$. For Algorithm 1 with the fixed diagonal preconditioner $\text{diag }\left(\frac{1}{A^{\top }1}\right)$, we set β = λ, and $\mu =1/(2\lambda {\Vert B\Vert }_2^2{\Vert \frac{1}{A^{\top }1}\Vert }_{\mathrm{\infty }})$. For Algorithms 2 and 3 we set β = λ, and $\mu =1/(2\lambda {\Vert B\Vert }_2^2{\Vert \frac{f^{(k)}}{A^{\top }1}\Vert }_{\mathrm{\infty }})$ in their k-th iterations.

In the first experiment, we compare the performance of Algorithm 1 without preconditioning (S = I) with that of Algorithm 1 with the fixed diagonal preconditioner $\text{diag }\left(\frac{1}{A^{\top }1}\right)$ and that of Algorithms 2 and 3. The parameter r for all the algorithms is fixed at 10 and the other parameters for each algorithm are chosen as discussed above. When implementing Algorithm 3, in the first 100 iterations, we use the dynamic preconditioner and after 100 iterations, we fix the preconditioner. Table 1 gives a summary of the CPU times (process times) and numbers of the complete iterations for reconstructing images from the noisy SPECT projection data set generated from low-noise phantom. It clearly shows that Algorithms 2 and 3, which have dynamic and semi-dynamic EM-preconditioners respectively, converge significantly faster than Algorithm 1 with either preconditioner. We remark that Algorithm 1 with either preconditioner cannot meet the stopping criteria for the last tolerance level. This phenomenon is marked by (−,−) in the table. Therefore, in the remaining part of this section, only Algorithm 3 will be used to compare with other existing algorithms for the Poisson-TV model (7). For comparison, we include in Table 1 the numerical results for the P-PD algorithm [56] which also uses a fixed preconditioner. Its performance is even worse than that of Algorithm 1 with the fixed diagonal preconditioner $\text{diag }\left(\frac{1}{A^{\top }1}\right)$.

Table 1.

The pair (·, ·) represents the CPU time and the number of the complete iterations used in Algorithms 1, 2, 3 and P-PD algorithm with different choices of tol for the noisy SPECT projection data set generated from low-noise phantom. T represents the diagonal matrix diag $(\frac{1}{A^{\top }1})$.

	tol	10−1	10−2	10−3	10−4	10−5	10−6	10−7
Alg.
Alg. 1 (S = I)		(5.4, 2)	(70.2, 27)	(250.9, 99)	(1359.6, 525)	(4300.9, 1653)	(10241.8, 3940)	(−, −)
Alg. 1 (S = T)		(5.4, 2)	(57.5, 23)	(210.5, 85)	(1088.5, 445)	(3204.9, 1301)	(7383.4, 3000)	(−, −)
Alg. 2		(12.6, 5)	(35.0, 14)	(109.6, 44)	(291.1, 117)	(768.6, 309)	(1915.6, 770)	(5435.0, 2109)
Alg. 3		(12.3, 5)	(34.8, 14)	(109.6, 44)	(305.7, 123)	(759.5, 307)	(1464.3, 592)	(3954.8, 1599)
P-PD Alg.		(6.6, 2)	(75.9, 23)	(292.7, 89)	(1569.1, 479)	(4357.6, 1331)	(9885.1, 3024)	(−, −)

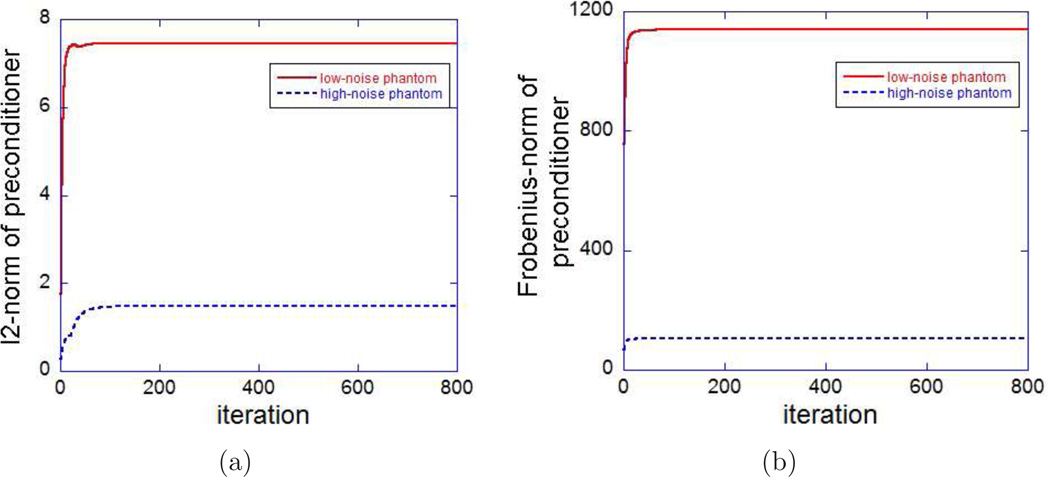
The proposed preconditioner (60) depends on the current iterate and is updated at each iterate step. The second experiment explores numerically how the preconditioner (60) changes in iterations in terms of its ℓ²-norm and Frobenius-norm. Figure 3 presents the curves of both norms versus iteration numbers for the low-noise and high-noise phantoms. From the figure we conclude that after a few iterations, the change of the preconditioner (60) is neglectable. This suggests that except for the first few iterations, the preconditioner may be chosen to be the same. In this regard, the convergence result (Theorem 4.7) that we establish for the fixed preconditioner is applicable to the practical situation.

Figure 3.

Curves of (a) ℓ²-norm and (b) Frobenius-norm of the preconditioner (60) versus iteration numbers for low-noise and high-noise phantoms.

The third experiment tests numerically the choice of the parameter r in the inner iteration for Algorithm 3 (PAPA) in terms of the CPU time that the algorithm requires to reach the stopping criteria (61) for different tolerances. We perform PAPA with r from 6 to 15 for the noisy SPECT projection data sets generated from low-noise and high-noise phantoms with the tolerance tol = 10⁻⁶. The numerical results for the noisy SPECT projection data set generated from the low-noise phantom show that the algorithms with the parameter r ranging from 7 to 11 perform comparably and are better than those with other ranges of r. The numerical results for the noisy SPECT projection data set generated from the high-noise phantom indicate that the algorithms with the parameter r ranging from 10 to 12 perform comparably and are better than those with other ranges of r. According to this numerical observation, in the remaining part of this section, we fix the parameter r for PAPA at 10.

6.3 Comparison of PAPA with the EM-TV Algorithm

We now compare performance of the proposed PAPA with that of the conventional EM-TV [48], in terms of the CPU time, local image quality metrics: the coefficient-of-variation (CV) measured within the uniform region of interest, contrast-to-noise ratio (CNR), and a global image quality metric: the normalized mean-squared error (NMSE).

We first recall the conventional EM-TV algorithm. For a given positive number δ, the smoothed version of the total variation is a function R : ℝ^d → ℝ defined at u ∈ ℝ^d as

$$R(u)≔{\displaystyle \sum _{i=1}^d}\Vert {[{(\mathit{\text{Bu}})}_i,{(\mathit{\text{Bu}})}_{d+i},{(\mathit{\text{Bu}})}_{2d+i},\delta ]}^{\top }\Vert .$$ (62)

With this function R, the conventional EM-TV algorithm [48] is described in Algorithm 4.

Algorithm 4.

(Conventional EM-TV Algorithm for MAP ECT Reconstruction)

Initialization: f(0) = 1.

repeat

$f^{(k+1)}\leftarrow \text{diag }\left(\frac{f^{(k)}}{A^{\top }1+\lambda \nabla R(f^{(k)})}\right)A^{\top }\left(\frac{g}{{\mathit{\text{Af}}}^{(k)}+\gamma }\right)$.

until “convergence”

For reconstructions with the conventional EM-TV algorithm, following [48] we choose δ = 0.001 which is less than 1% of the maximum value of the phantom. Moreover, we note that when λ vanishes the conventional EM-TV algorithm reduces to the EM algorithm (59).

We now evaluate the quality of the reconstructed images. First, we compare noise in the reconstructed images. We use the coefficient of variation (CV) within a uniform region of interest as a surrogate of noise measure in the reconstructed images obtained using Algorithm 2 and the conventional EM-TV. The CV of an image f^∞ reconstructed by an algorithm is defined by

$$\text{CV}≔\frac{{\text{SD}}_{\mathrm{\Omega }}(f^{\mathrm{\infty }})}{{𝔼}_{\mathrm{\Omega }}(f^{\mathrm{\infty }})},$$

where SD_Ω(·) and 𝔼_Ω(·) denote the standard deviation and the mean of the reconstructed activities over a region. In our case, the region is a cylinder with the radius of base and the height equal to 25 and 8 pixels, respectively. This cylindrical region lies between the hot spheres and the cold spheres (please refer to Figure 1 (c)) and does not intersect with any hot or cold spheres. Under these circumstances, the means of CVs (with respect to 5 different noise realizations) for PAPA and the conventional EM-TV are 0.12% and 3.81%, respectively, for the low-noise phantom, and are 4.09% and 13.15%, respectively, for the high-noise phantom. From these numerical results, we find out that PAPA performs considerably (factor of 31 for low-noise phantom data and factor of 3 for high-noise phantom data) better than the conventional EM-TV in terms of the noise.

Next, a local quality metric, contrast-to-noise ratio (CNR), of images will be used to measure the quality of the reconstructed hot or cold spheres. Too low CNR might result in inability to detect the lesion by an observer. The contrast-to-noise ratio (CNR) for a reconstructed image f^∞ is defined as a ratio of a lesion contrast to the background noise [4, 40, 51]

$$\text{CNR}≔\frac{|{𝔼}_{{\mathrm{\Omega }}_T}(f^{\mathrm{\infty }})-{𝔼}_{{\mathrm{\Omega }}_B}(f^{\mathrm{\infty }})|}{{\text{SD}}_{{\mathrm{\Omega }}_B}(f^{\mathrm{\infty }})}.$$

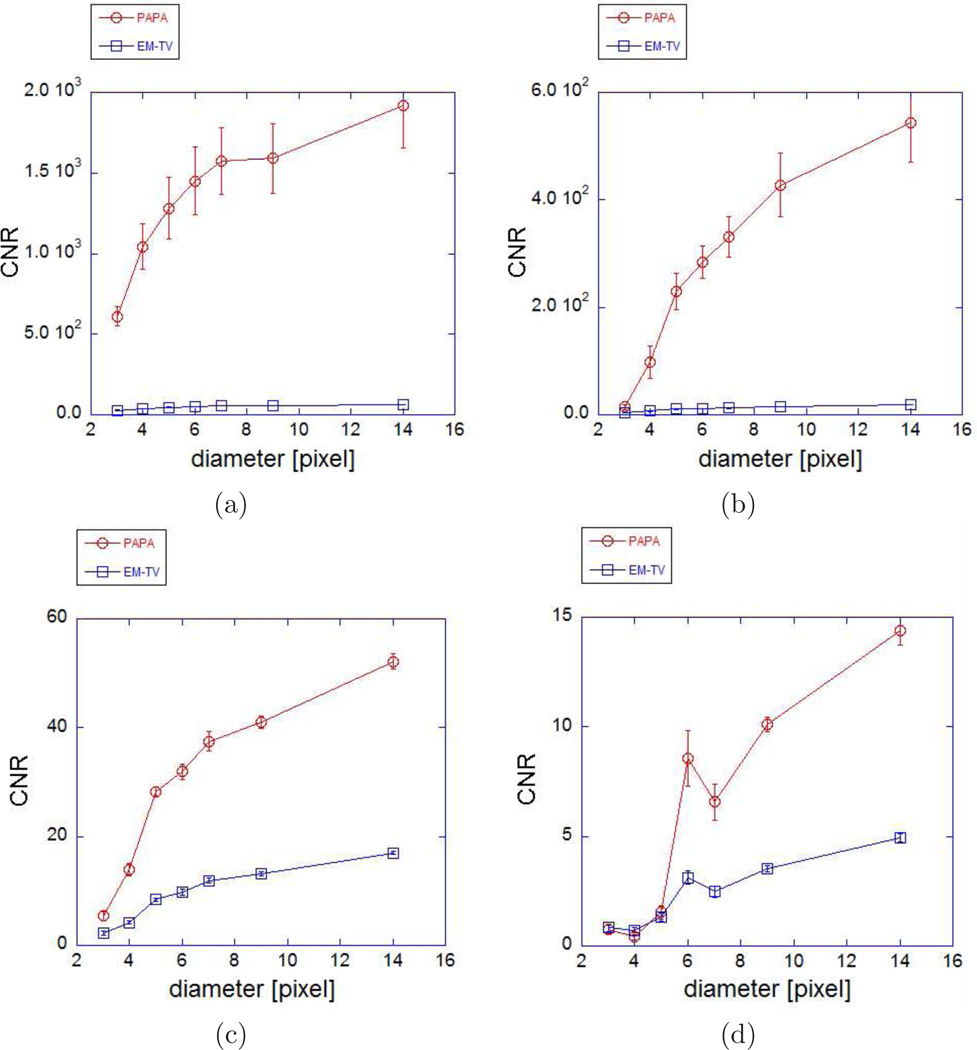
Here 𝔼_ΩT (f^∞) is the mean reconstructed activity in the region Ω_T where a specific hot (resp. cold) sphere is located, while Ω_B is a spherical region with the same diameter as the hot (resp. cold) sphere but located within the uniform region of the cylindrical phantom that does not intersect with any hot or cold sphere. The CNR metric is important in Radiology because it allows to asses detectability of a lesion that is one of the main tasks of ECT. It is well established by human observer studies that the lesion contrast and the background noise influence lesion detectability [40]. We note that even when the signal-to-noise ratio is high, the presence of a significant bias in the reconstructed image might result in the lesion contrast being too low for a lesion to be detected. Very high noise or correlation of the noise will contribute to low detectability of the lesion even if the lesion contrast is high [46]. The curves of the means of CNRs (with respect to 5 different noise realizations again) versus diameters of spheres are plotted in Figure 4. Again, we observe that PAPA very significantly (factor of 7–14 for high-noise phantom) outperforms the conventional EM-TV in terms of the CNR values.

Figure 4.

Reconstructed image quality assessment for hot and cold spheres: Plots of mean (with respect to 5 different noise realizations) contrast-to-noise ratio (CNR) vs. diameter of sphere. The vertical error bars denote the calculated standard deviation of the mean. For the EM-TV the error bars are smaller than the symbols used: (a) hot spheres in low-noise phantom; (b) cold spheres in low-noise phantom; (c) hot spheres in high-noise phantom; (d) cold spheres in high-noise phantom. Open squares - the conventional EM-TV. Open circles - PAPA.

We use the normalized mean-squared error (NMSE) to assess accuracy of reconstructions. The NMSE is a global image quality metric. It quantifies the difference between the activity reconstruction f^∞ and the true mean activity f in the whole object. It is defined by

$$\text{NMSE}≔\frac{\Vert f-f^{\mathrm{\infty }}\Vert }{{\Vert f\Vert }^2}.$$

The mean values of NMSE (with respect to 5 different noise realizations) for the images reconstructed by PAPA and the conventional EM-TV are 0.485 and 0.787, respectively, for the low-noise phantom, and 2.55 and 3.93, respectively, for the high-noise phantom. Once again, PAPA significantly outperforms the conventional EM-TV in terms of the NMSE values.

6.4 Comparison of PAPA with the Nested EM-TV Algorithm

In this subsection, we compare performance of PAPA with the nested EM-TV algorithm, the algorithm recently described in [54].

In Algorithm 5, we describe the nested EM-TV algorithm for ECT reconstruction. This algorithm has two major steps: the EM step and the TV correction step, and they are performed alternatively. The EM step is identical to (59). The TV correction step is a modified version of the Rudin-Osher-Fatemi (ROF) model and was implemented by exploiting an existing scheme for the ROF model. In fact, it was stated in [54] that the TV correction step in Algorithm 5 was carried out by adopting Chambolle’s method originally reported in [11]. We shall follow the suggestion made in [54] to apply Chambolle’s method with 10 iterations for each TV correction step to achieve an approximate solution.

Algorithm 5.

(Nested EM-TV Algorithm for MAP ECT Reconstruction)

Initialization: f(0) = 1.

repeat

EM Step: $f^{(k+\frac{1}{2})}\leftarrow \text{diag }\left(\frac{f^{(k)}}{A^{\top }1}\right)A^{\top }\left(\frac{g}{{\mathit{\text{Af}}}^{(k)}+\gamma }\right)$.

TV Step: $f^{(k+1)}\leftarrow \text{argmin }\{\frac{1}{2}\langle f-f^{(k+\frac{1}{2})},\frac{A^{\top }1}{f^{(k)}}\odot (f-f^{(k+\frac{1}{2})})\rangle +\lambda \phi (\mathit{\text{Bf}}):f\in {ℝ}_{+}^d\}$.

until “convergence”

In Table 2, we list the CPU time expended and the number of the complete iterations used by PAPA, the nested EM-TV and the conventional EM-TV, for the two SPECT projection data sets. After examining the table, we conclude that under the same stopping criteria PAPA is better than the nested EM-TV, and significantly better than the conventional EM-TV in terms of the convergence speed. We remark that the conventional EM-TV algorithm cannot even meet the stopping criteria for most of the given tolerance levels.

Table 2.

Comparison of performance of PAPA, the conventional EM-TV and the nested EM-TV for the test data. The pair (·, ·) represents the CPU time and the number of the complete iterations used.

	tol	10−1	10−2	10−3	10−4	10−5	10−6	10−7
Alg.
				low-noise phantom
PAPA		(12.3, 5)	(34.8, 14)	(109.6, 44)	(305.7, 123)	(759.5, 307)	(1464.3, 592)	(3954.8, 1599)
Nested EM-TV		(14.1, 5)	(40.0, 14)	(122.8, 43)	(333.1, 117)	(872.4, 307)	(2207.3, 777)	(6184.5, 2179)
EM-TV		(7.15, 4)	(−, −)	(−, −)	(−, −)	(−, −)	(−, −)	(−, −)
				high-noise phantom
PAPA		(12.4, 5)	(35.3, 14)	(106.2, 42)	(295.3, 117)	(724.7, 289)	(1451.6, 580)	(4349.4, 1741)
Nested EM-TV		(13.2, 5)	(38.1, 14)	(115.2, 42)	(304.5, 111)	(798.8, 291)	(2024.3, 737)	(5593.6, 2045)
EM-TV		(9.01, 5)	(−, −)	(−, −)	(−, −)	(−, −)	(−, −)	(−, −)

In addition to the CPU time and the number of complete iterations, we further estimate the number of arithmetic operations for PAPA and the nested EM-TV algorithm. We list in Table 3 the number of total arithmetic operations required by PAPA and the nested EM-TV, under various stopping criteria.

Table 3.

Comparison of arithmetic operations of semi-dynamic PAPA and the nested EM-TV for the test data. The number · represents · × 2²⁰ arithmetic operations required.

	tol	10−1	10−2	10−3	10−4	10−5	10−6	10−7
Alg.
			low-noise phantom
PAPA		3380	9464	29744	83148	207532	400192	1080924
Nested EM-TV		3795	10626	32637	88803	233013	589743	1653861
			high-noise phantom
PAPA		3380	9464	28392	79092	195364	392080	1176916
Nested EM-TV		3795	10626	31878	84249	220869	559383	1552155

Furthermore, we compare the image quality metrics of the reconstructed images obtained by using PAPA and by the nested EM-TV. The means of CVs for the reconstructions by PAPA and the conventional EM-TV are reported in Table 4. The means of CNRs with respect to 5 different noise realizations versus the diameters of the hot spheres (resp. cold spheres) for PAPA, the nested EM-TV, and the conventional EM-TV are listed in Table 5 (resp. 6). Moreover, the means of NMSEs with respect to 5 different noise realizations for the images of the low-noise phantom and the high-noise phantom are presented in Table 7. We conclude from these tables that both PAPA and the nested EM-TV outperform the conventional EM-TV in terms of the values of CV, CNR and NMSE while PAPA performs comparably with the nested EM-TV.

Table 4.

Means of CVs for the reconstructions by PAPA, the nested EM-TV and the conventional EM-TV.

Phantom	low-noise phantom	high-noise phantom
PAPA	0.12%	4.09%
nested EM-TV	0.14%	4.54%
EM-TV	3.81%	13.15%

Table 5.

Means of CNRs for 7 hot spheres reconstructed using PAPA, the nested EM-TV and the conventional EM-TV.

Diameters of Spheres	14	9	7	6	5	4	3
		low-noise phantom
PAPA	1915.768	1590.557	1574.134	1451.297	1280.732	1043.835	611.271
nested EM-TV	1912.141	1587.496	1571.388	1448.454	1277.969	1041.962	610.677
EM-TV	65.801	55.159	56.717	51.872	47.284	40.451	28.124
		high-noise phantom
PAPA	52.171	41.019	37.525	31.919	28.247	13.939	5.448
nested EM-TV	52.149	41.002	37.510	31.905	28.234	13.932	5.445
EM-TV	17.007	13.116	11.885	9.815	8.389	4.237	2.232

Table 7.

Means of NMSEs for the reconstructions by PAPA, the nested EM-TV and the conventional EM-TV.

Phantom	low-noise phantom	high-noise phantom
PAPA	0.48469	2.54701
nested EM-TV	0.48481	2.54794
EM-TV	0.78670	3.92571

In order to qualitatively compare the image reconstruction quality, in Figures 5 and 6 we present selected transaxial cross-sections through the reconstructed images of the hot and cold spheres, respectively. Images reconstructed by PAPA, the nested EM-TV, and the conventional EM-TV for two noise levels (56% and 15%) are shown. We observe much higher background noise in the images reconstructed by the conventional EM-TV, as compared to PAPA and the nested EM-TV. The quality of images reconstructed by PAPA and the nested EM-TV is similar. The hot sphere with 4-pixel radius cannot be detected in the images reconstructed from high-noise data by the conventional EM-TV. But, it is detectable in the reconstructions performed using PAPA and the nested EM-TV. The cold spheres with 6 and 7-pixel radii are poorly visible in the images reconstructed from high-noise data by the conventional EM-TV. However, they are easily detectable in the reconstructions performed using PAPA and the nested EM-TV.

Figure 5.

Transaxial cross-sections through the centers of the hot spheres (slice 17) in images reconstructed for low-noise phantom: (a) PAPA; (b) the nested EM-TV; and (c) the conventional EM-TV. Transaxial cross-sections through the centers of the hot spheres (slice 17) in images reconstructed for high-noise phantom: (d) PAPA; (e) the nested EM-TV; and (f) the conventional EM-TV. The calibration bars indicates the linear mapping between reconstructed activity and the gray scale used.

Figure 6.

Transaxial cross-sections through the centers of the cold spheres (slice 49) in images reconstructed for low-noise phantom: (a) PAPA; (b) the nested EM-TV; and (c) the conventional EM-TV. Transaxial cross-sections through the centers of the cold spheres (slice 49) in images reconstructed for high-noise phantom: (d) PAPA; (e) the nested EM-TV; and (f) the conventional EM-TV. The calibration bars indicates the linear mapping between reconstructed activity and the gray scale used.

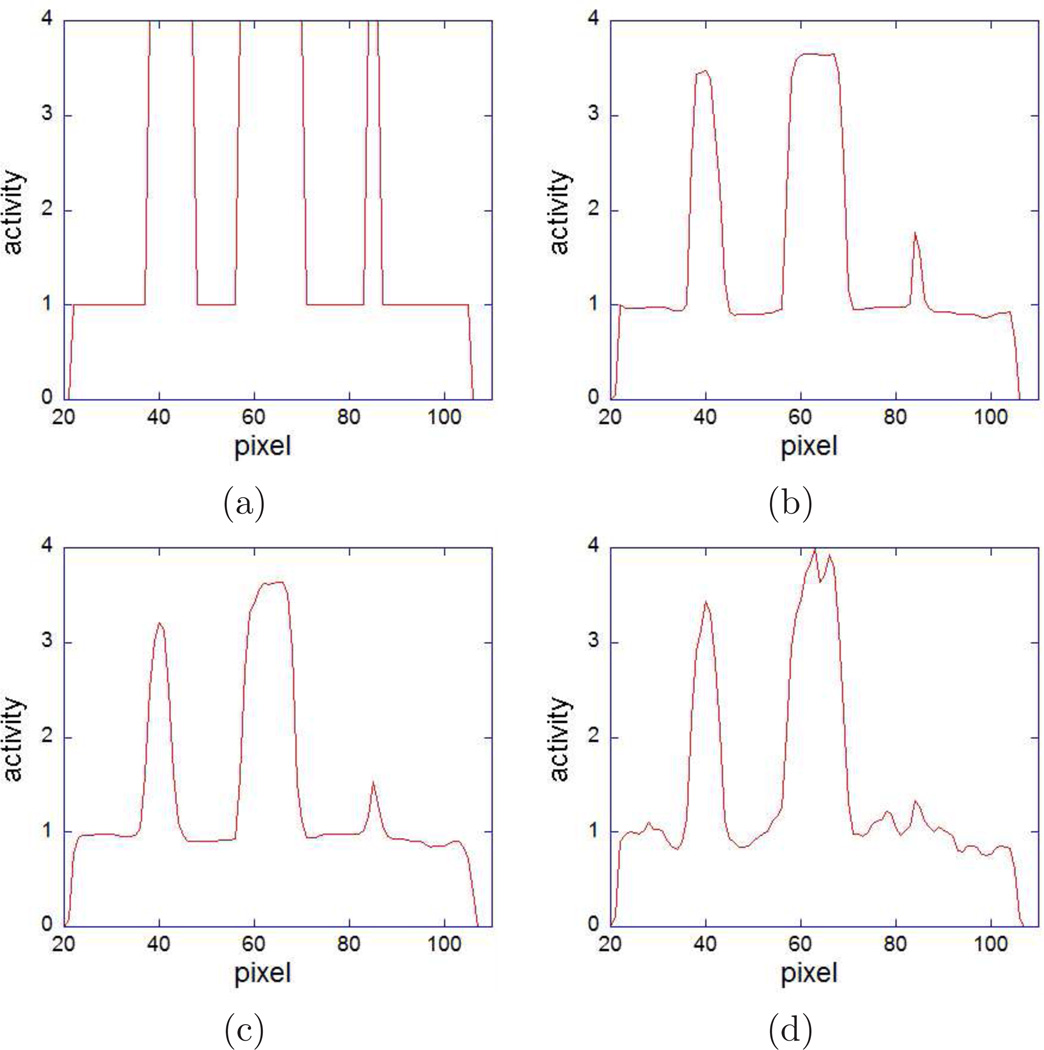
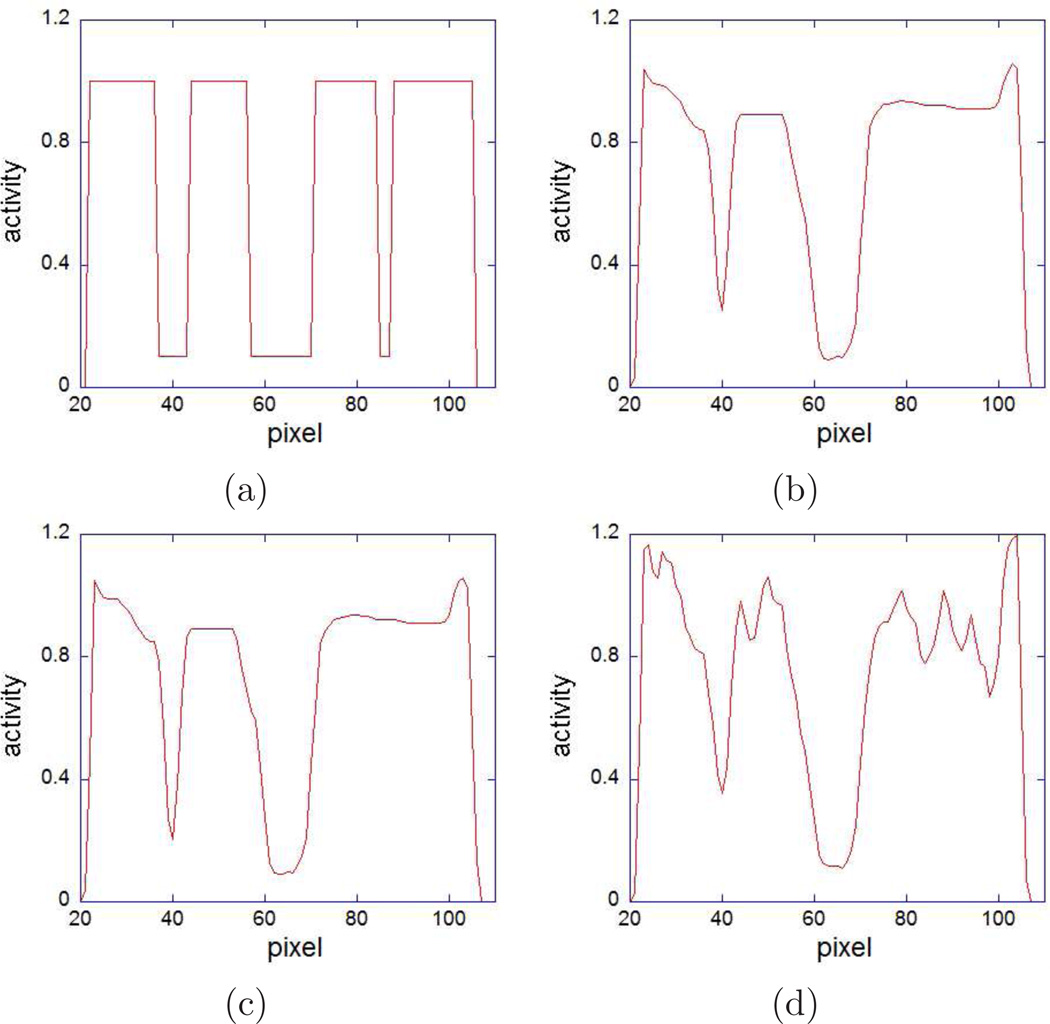
To better access the differences between images reconstructed using PAPA and the nested EM-TV, we obtain line profiles through selected transaxial cross-sections of the reconstructed images containing the hot and cold spheres. They are shown in Figures 7 and 8 for hot and cold spheres, respectively. We observe that for hot spheres reconstructions PAPA provides images with slightly better contrast and spatial resolution, as compared to the nested EM-TV. For cold spheres reconstructions both algorithms perform similarly. The conventional EM-TV reconstructions are inferior in any case.

Figure 7.

One-pixel wide line profiles through the centers of hot spheres with 7, 14 and 3-pixel radii in transaxial cross-sections (slice 17) of: (a) the high-noise phantom; (b) image reconstructed using PAPA from the high-noise phantom data; (c) image reconstructed using the nested EM-TV from the high-noise phantom data; and (d) image reconstructed using conventional EM-TV from the high-noise phantom data.

Figure 8.

One-pixel wide line profiles through the centers of cold spheres with 7, 14 and 3-pixel radii in transaxial cross-sections (slice 49) of: (a) the high-noise phantom; (b) image reconstructed using PAPA from the high-noise phantom data; (c) image reconstructed using the nested EM-TV from the high-noise phantom data; and (d) image reconstructed using conventional EM-TV from the high-noise phantom data.

7 Concluding Remarks

There is a great need to reduce radiation dose to the patients undergoing ECT examinations. This could be accomplished by lowering the total amount of activity in the radiotracer administered. However, it would lead to very high Poisson noise in the raw ECT data. In turn, such very noisy data if treated by conventional techniques, such as EM-TV or OSEM, would lead to very noisy and clinically unacceptable reconstructed images. To attain good quality ECT reconstructions from low-dose ECT examinations, we propose a preconditioned alternating projection algorithm (PAPA) for solving the maximum a posteriori (MAP) ECT reconstruction problem. We prove that the algorithm enjoys nice theoretical convergence results in the case that the preconditioner is fixed. Motivated by the classical EM algorithm, we propose dynamic and semi-dynamic EM-preconditioners for PAPA to accelerate convergence of the original iterative scheme, which is the main contribution of this work. We demonstrate in the numerical experiments that the EM-preconditioner converges fast to a fixed preconditioning matrix, which in turn confirms the applicability of the convergence result to the practical situation. Since the total-variation (TV) based penalty function can well preserve the edges and details of the reconstructed object, we particularly concentrate on the example with TV regularization. Based on the numerical experiments performed in this work, we observe that the alternating projection algorithm with the EM-preconditioner significantly outperforms the conventional EM-TV in all aspects including the convergence speed, the noise in the reconstructed images and the image quality. It also outperforms the recently developed algorithm - the nested EM-TV - in the convergence speed while having a comparable image quality.

We conclude that the developed alternating projection algorithm with dynamic or semi-dynamic EM-preconditioner might allow very significant reduction in the radiation dose to the patients imaged using ECT by providing the same contrast-to-noise ratio for hot and cold lesions as conventional EM-TV, but with the total administered radiotracer activity 2 to 6 times lower than presently used in ECT examinations reconstructed using the conventional EM-TV.

Table 6.

Means of CNRs for 7 cold spheres reconstructed using PAPA, the nested EM-TV and the conventional EM-TV.

Diameters of Spheres	14	9	7	6	5	4	3
		low-noise phantom
PAPA	543.563	427.444	330.512	283.982	229.776	97.887	14.505
nested EM-TV	542.524	426.538	330.087	283.587	229.380	97.331	14.437
EM-TV	18.721	15.195	12.599	11.744	10.610	6.785	3.993
		high-noise phantom
PAPA	14.378	10.106	6.577	8.570	1.543	0.424	0.764
nested EM-TV	14.373	10.105	6.576	8.568	1.542	0.424	0.762
EM-TV	4.929	3.544	2.484	3.128	1.310	0.724	0.839