THE PEAKS AND GEOMETRY OF FITNESS LANDSCAPES

Abstract

Fitness landscapes are central in the theory of adaptation. Recent work compares global and local properties of fitness landscapes. It has been shown that multi-peaked fitness landscapes have a local property called reciprocal sign epistasis interactions. The converse is not true. We show that no condition phrased in terms of reciprocal sign epistasis interactions only, implies multiple peaks. We give a sufficient condition for multiple peaks phrased in terms of two-way interactions. This result is surprising since it has been claimed that no sufficient local condition for multiple peaks exist. We show that our result cannot be generalized to sufficient conditions for three or more peaks. Our proof depends on fitness graphs, where nodes represent genotypes and where arrows point toward more fit genotypes. We also use fitness graphs in order to give a new brief proof of the equivalent characterizations of fitness landscapes lacking genetic constraints on accessible mutational trajectories. We compare a recent geometric classification of fitness landscape based on triangulations of polytopes with qualitative aspects of gene interactions. One observation is that fitness graphs provide information not contained in the geometric classification. We argue that a qualitative perspective may help relating theory of fitness landscapes and empirical observations.

1. Introduction

We will study qualitative aspects of gene interactions. In particular, it is of interest to what extent beneficial mutations combine well. This question relates to the concept epistasis. Absence of epistasis means that the fitness effects of mutations sum, where fitness is defined as the expected reproductive success (different definitions of these concepts occur in the literature (Mani et. al, 2008)). It is immediate that beneficial mutations combine well if there is no epistasis. However, it is well known that double mutants which combine beneficial single mutations may have very low fitness. Several examples from different species are given in Weinreich et al. (2005). Put briefly, “good+good=better” if there is no epistasis, but sometimes “good+good=not good” in nature. By a qualitative perspective we understand that one considers fitness ranks of genotypes, but not necessarily more fine scaled information such as relative fitness values.

Fitness landscapes are central in the theory of adaptation and we will focus on the qualitative perspective. The fitness landscape was initially introduced as a metaphor for adaptation (Wright, 1931). Informally, the surface of the landscape consists of genotypes, where similar genotypes are close to each other, and the fitness of a genotype is represented as a height coordinate. Adaptation can then be pictured as an uphill walk in the fitness landscape.

A qualitative analysis is sufficient for several theoretical aspects of fitness landscapes. Coarse properties of fitness landscapes, such as the number of peaks, depend on fitness ranks of genotypes only. The relation between global and local properties can be analyzed from a qualitative perspective as well. From a more practical point of view, the qualitative perspective has several advantages. Fitness ranks are usually easier to determine as compared to relative fitness values. Fitness ranks tend to be stable under small variations in the environment. Moreover, fitness data of qualitative nature are already available. In particular, medical records on HIV drug resistance and antibiotic resistance provides indirect information about fitness ranks (see Section 5). It is frequently claimed that we know virtually nothing about fitness landscapes in nature. In our view, better methods for interpretation of fitness data are at least as important as new fitness measurements.

The concept of a fitness landscapes has been formalized in different ways. Conventionally, as a string in the 20, 4 or 2 letter alphabet, depending on if one considers the amino acids, the base pairs or biallelic system. In many real systems at most two alternative alleles occur at each position (or locus), resulting in a biallelic system. Alternatively, a biallelic assumption may be a reasonable simplification. For simplicity, we will consider biallelic populations throughout the paper. Let Σ = {0, 1} and let Σ^L denote bit strings of length L. The zero-string denotes the string with zero in all L positions, and the 1-string denotes the string with 1 in all L positions. We define the fitness landscape as a function w: Σ^L ↦ ℝ, which assigns a fitness value to each genotype. The metric we use is the Hamming distance, meaning that the distance between two genotypes equals the number of positions where the genotypes differ. In particular, two genotypes are adjacent, or mutational neighbors, if they differ at exactly one position.

A walk in the fitness landscape has a precise interpretation. Consider a population after a recent change in the environment. Assume that the wild-type no longer has optimal fitness. If we assume the strong-selection weak-mutation (SSWM) regime, then a beneficial mutation is assumed to go to fixation in the population before the next mutation occurs (Gilliespie, 1983, 1984). The population is monomorphic for most of the time, so that one genotype dominates the population at a particular point in time. It follows that we can think of a Darwinian process as an adaptive walk in the fitness landscape, where each step represents that a beneficial mutation goes to fixation in the population. The described model of adaptation has been widely used and relies on work by Gilliespie (1983, 1984). The sequence-based model of adaptation was introduced by Maynard Smith (1970). For more background and references, see also Orr (2002, 2006).

For the qualitative perspective on fitness landscapes, one needs a refined version of the concept epistasis. According to our definition, fitness is additive or non-epistatic if fitness effects of mutations sum. (In the literature non-epistatic fitness is sometimes defined as multiplicative fitness.) Suppose that

$$w(00)=1,w(10)=1.04,w(01)=\mathrm{1.02.}$$

If one considers 00 as a starting point, then the fitness effect of a mutation at the first locus is +0.04, and at the second +0.02. If fitness is additive, then w(11) = 1.06 since 0.04 + 0.02 = 0.06, meaning that the fitness effects sum. Epistasis exists if w(11) ≠ 1.06. Sign epistasis means that a particular mutation is beneficial or deleterious depending on genetic background. For example, if w(11) = 1.03, then there is sign epistasis. Indeed, in this case a mutation at the second locus is beneficial for the genotype 00 since w(01) > w(00), and deleterious for the genotype 10 since w(11) < w(10). In contrast, if w(11) = 1.05 there is epistasis, but no sign epistasis since fitness increases whenever a 0 at some locus is replaced by 1. For more background about epistasis, see e.g. Weinreich et al. (2005); Beerenwinkel et al. (2007 b); Poelwijk et al. (2007, 2011); Kryazhimskiy et al. (2011). Recent work that considers qualitative properties of fitness landscapes includes Weinreich et al. (2005); Poelwijk et al. (2007, 2011). A central theme is how global properties of the fitness landscape, such as the number of peaks, relate to local properties, such as sign epistasis (see Section 2 and 3). A related field is the study of constraints for orders in which mutations accumulate (see e.g. Desper et al., 1999; Beerenwinkel et al., 2007 a). It is well known that a drug resistance mutation is sometimes selected for, only if a different mutation has already occurred. Such a phenomenon requires sign epistasis. Indeed, if a particular mutation is beneficial regardless of background, then it can occur before or after other mutations.

We will give an overview of classical models of fitness landscapes, and then compare with recent approaches and the qualitative perspective.

1.1. Classical models of fitness landscapes

Several models of fitness landscapes have had a broad influence in evolutionary biology, primarily additive fitness landscapes, random fitness landscapes, the block model and Kaufman’s NK model. Additive fitness landscapes are single peaked. In contrast, for a random (uncorrelated or rugged) fitness landscape (see e.g. Kingman, 1978; Kauffman and Levin, 1987; Flyvberg and Lautrup, 1992; Rokyta et al., 2006; Park and Krug, 2008) there is no correlation between the fit-nesses of mutational neighbors, or genotypes that differ at one locus only. Random fitness landscapes tend to have many peaks. Random fitness and additivity can be considered as two extremes with regard to the amount of structure in the fitness landscapes.

For the block model (Macken and Perelson, 1995; Orr, 2006) the string representing a genotype can be subdivided into blocks, where each block makes an independent contribution to the fitness of the string. Each block has random fitness, and the fitness of the string is the sum of contributions from each block. In particular, if there is only one block, then the block model coincides with a a random fitness landscape.

Kaufmann’s NK model (see e.g. Kauffman and Weinberger, 1989) is defined so that the epistatic effects are random, whereas the fitness of a genotype is the average of the “contributions” from each locus. More precisely, for the NK model the genotypes have length N (in our notation L = N), and the parameter K, where 0 ≤ K ≤ N − 1, reflects interactions between loci. The fitness contribution from a locus is determined by its state and the states at exactly K other loci. The key assumption is that this contribution, determined by the 2^K+1 states (since we assume biallelic systems), is assigned at random from some distribution. The fact that the fitness of the genotype is the average of these N contributions, means that fitness effects of non-interacting mutations sum. Several important properties of NK landscapes depend mainly on N and K, rather than the exact structure of the epistatic interactions.

Notice that the NK model as well as the block model includes additive landscapes and random landscapes as special cases. More importantly, the models are similar in that there is a sharp division between effects which are completely random and effects which are additive.

In contrast to the models discussed, the Orr-Gillespie theory (e.g. Orr, 2002) depends on the strategy to make minimal assumptions about the underlying fitness landscape, motivated by the fact that our knowledge about fitness landscapes is limited. The theory focuses on properties that hold for a broad category of fitness landscapes. Most results depend on extreme value theory. For more background and references on fitness landscapes in evolutionary biology, see e.g. Weinreich et al. (2005); Beerenwinkel et al. (2007 b); Kryazhimskiy et al. (2009). Fitness landscapes have been used in chemistry, physics and computer science, in addition to evolutionary biology. For a survey on combinatorial landscapes in general see Reidys and Stadler (2002). In combinatorial optimization the fitness function is referred to as the cost function.

1.2. New approaches to the theory of fitness landscapes

The classical theory of fitness landscapes has been critizised for the lack of contact with empirical data (Kryazhimskiy et al., 2009). One sometimes encounters the misunderstanding that the block model, or Kaufmanns NK models, would include almost all [theoretically possible] fitness landscapes since they include the two extremes. According to this view, the goal of empirical work would be to determine parameters; the block length in the first case, or the “K” value in the NK model. On the contrary, these two models are equipped with very special structures. Additive fitness and random fitness are of course even more special. The Orr-Gillespie theory on the other hand focuses on general properties of adaptation for a broad category of landscapes, rather than relating properties of fitness landscapes and fitness data.

Put briefly, the theory of fitness landscapes has been developed in isolation from data, and available fitness data have been left without systematic interpretations. We argue that qualitative methods could be of some help. Practical methods for checking if some of the standard models of fitness landscapes are compatible with fitness data are indicated in Section 5, along with concepts for interpretations of fitness data (see also Crona et al., 2012).

In general, methods for revealing and interpreting properties of fitness landscapes from data, without assumptions about the underlying fitness landscape are especially valuable in our view. A recent contribution in this category is the geometric theory of gene interactions (Beerenwinkel et al., 2007 b). Conventionally, the study of epistasis is restricted to two-way interactions or average effects of mutations. A full description of the gene interactions for multiple loci requires an entirely different theory. The geometric classification in Beerenwinkel et al. (2007 b) uses triangulations of polytopes. For mathematical background we refer to De Loera et al. (2010), see also Ziegler (1995) for general theory about polytopes. Briefly, a square is an example of a polytope, and the two triangles obtained by cutting the square along a diagonal constitute a triangulation of the square (see Section 4). The geometric approach has revealed previously unappreciated gene interactions (Beerenwinkel et al., 2007 b,c). This approach is relevant for the theory of recombination. Geometric and qualitative information is compared in Section 4.

The paper is structured as follows. Section 2 and 3 consider the relation between global and local properties of fitness landscapes. We prove our main results in Section 2, and introduce fitness graphs. We give a new proof of the main result in Weinreich et al. (2005) using fitness graphs in Section 3. In Section 4 we compare qualitative aspects of gene interactions with the geometric classification of fitness landscapes in terms of triangulations of polytopes. Section 5 is about applications, mainly the relation between models and fitness data.

2. A sufficient local condition for multiple peaks

2.1. A counterexample

As before, Σ = {0, 1} and w: Σ^L ↦ ℝ is the fitness landscape. For simplicity we assume that w(s) ≠ w(s′) for any two strings s and s′ which differ in one position only in this section, in addition to the assumptions stated in the introduction.

An adaptive step in the fitness landscape corresponds to a change in exactly one position of a string so that the fitness increases strictly. An adaptive walk is a sequence of adaptive steps. A peak in the fitness landscape has the property that there are no adaptive steps away from it, i.e., a genotype is at a peak if all mutational neighbors have lower fitness as compared to the genotype.

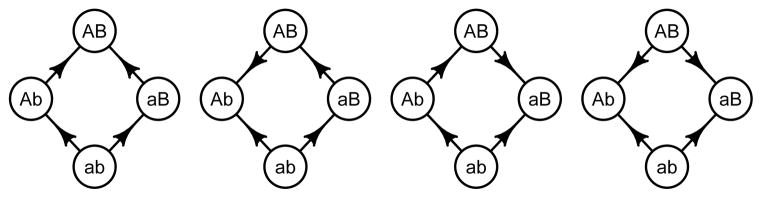
For L ≥ 2, given a string and two positions, exactly four strings can be obtained wich coincide with the string except at the two positions (an example of four such strings would be 1100, 1110, 1101, 1111). Denote such a set of four strings

$$ab,Ab,aB,AB,$$

according to the two positions of interest, and assume that w(ab) is minimal. Sign epistasis means that

$$w(AB)<w(Ab)\text{or}w(AB)<w(aB).$$

Reciprocal sign epistasis interactions means that

$$w(AB)<w(Ab)\text{and}w(AB)<w(aB).$$

See Fig. 1 for the four possibilities under our assumption that w(ab) is minimal.

Figure 1.

The arrows point toward the more fit genotype. The graphs represent no sign epistasis (a type 0 system), two cases with sign epistasis but not reciprocal sign epistasis (type 1 systems), and one case with reciprocal sign epistasis (a type 2 system).

For example, w′ (00) = 1, w′ (10) = 0.8, w′ (01) = 0.9, w′ (11) = 1.2 is a case of reciprocal sign epistasis. Notice that 00 and 11 are at peaks. On the other hand, w″ (00) = 1, w″ (10) = 0.8, w″ (01) = 1.1, w″ (11) = 1.2 is a case of sign epistasis, but not reciprocal sign epistasis. Notice that only 11 is at a peak. For more background about sign epistasis and reciprocal sign epistasis, see Weinreich et al. (2005); Poelwijk et al. (2007, 2011).

For L ≥ 2, given a string and two positions, consider the four strings wich coincide with the string except at the two positions. We call the strings a type 2 system if there is reciprocal sign epistasis, a type 1 system if there is sign epistasis, but not reciprocal sign epistasis, and a type 0 system if there is no sign epistasis. Notice that an additive fitness landscape, i.e., a landscape where the fitness effect of changes of strings at single positions sum, has no type 1 or 2 systems.

It was shown in Poelwijk et al. (2011) that multiple fitness peaks implies that there are type 2 systems. The converse is not true, a counterexample was given in the same paper. In order to show a stronger negative result we will define a fitness landscape f in terms of w.

Define f_w: Σ^L+1 ↦ ℝ as

$$f_w(s)=\{\begin{array}{l}w(s_1,\dots ,s_L)\text{if}{s}_{L+1}=0,\hfill \\ M+\sum s_i\text{where}M=maxw,\text{if}{s}_{L+1}=1.\hfill \end{array}$$

Lemma 1

The fitness landscape defined by the function f_w is single peaked.

Proof

The 1-string is at the global maximum. For any string s where s_L+1 = 0, we can increase the fitness by changing the last position. Next the fitness increases if we keep the 1 in the last position and change any other position from 0 to 1. This is repeated until we arrive at the 1-string.

Lemma 2

The type 2 systems for f are exactly the sets of the form

$$c(s^1),c(s^2),c(s^3),c(s^4),$$

where s¹, s², s³, s⁴ is a type 2 system for w, and where c(s) = s0 denotes the concatenation with zero.

Proof

If s¹, s², s³, s⁴ are a type 2 system, obviously the same is true for

$$c(s^1),c(s^2),c(s^3),c(s^4).$$

Consider the set of strings with last position 1. Replacing 0 by 1 at any position increases the fitness. From this property, it is easy to verify that there exist no type 2 systems where all four strings have last position 1.

It remains to consider sets of four strings where the last positions are not all the same. For such a system, two strings end with zero. Denote the strings a0, a1, b0, b1, where a0 and b0 end with 0, and the others with 1. We may assume that a0 has minimal fitness. By assumption, f(b1) > f(b0) > f(a0). It follows that a0, a1, b0, b1 are not a type 2 system.

The next result follows from Lemma 1.1 and 1.2.

Theorem 1

For any fitness landscape, a single peaked landscape can be constructed from it with exactly the corresponding type 2 systems.

2.2. Fitness graphs and the main result

Fitness graphs have been use in empirical work, in particular they are used extensively in Goulart et al. (2012). We will use fitness graphs in some proofs, and to our knowledge fitness graphs have not been used for theoretical purposes in biology before.

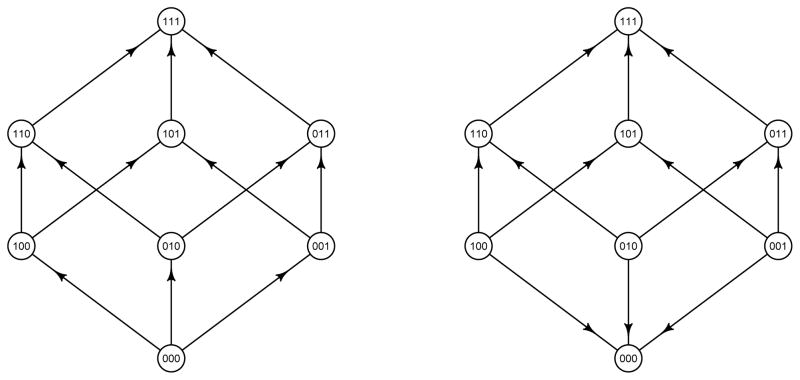
In empirical work, the wild-type is typically represented by the zero-string and then each non-zero position of a string corresponds to an event, i.e., that a mutation has occurred. Roughly, under these assumptions the fitness graph for Σ^L, coincides with the Hasse-diagram of the power set of events, except that each edge in the Hasse-diagram is replaced with an arrow toward the string with greater fitness. For a formal definition, a fitness graph is a directed graph where each node corresponds to a string of Σ^L. The fitness graphs has L + 1 levels. Each string such that Σ s_i = l corresponds to a node on level l in the fitness graph. In particular, the node representing the zero-string is at the bottom, the nodes representing strings with exactly one non-zero position, including 10 · · · 0, are one level above, the nodes representing strings with exactly two non-zero positions, including 110 · · · 0, are on the next level, and the 1-string is at the top. Moreover, the nodes are ordered from left to right according to the lexicographic order of the strings (see e.g. Fig. 3). A directed edge connects each pair of nodes such that the corresponding strings differ in exactly one position. The edge is directed toward the node representing the more fit of the two genotypes.

Figure 3.

The fitness graph on the left has type 0 systems only and the corresponding fitness landscape is single peaked. The fitness graph on the right has 3 type 0 system, 3 type 2 systems and no type 1 systems. The corresponding fitness landscape has two peaks.

The fact that the zero-string is at the bottom is natural since the zero-string corresponds to “no events”, meaning no mutations, in the empirical context discussed. In general, notice that the choice of which genotype corresponds to the zero-string in principle determines the fitness graph. Indeed, the level of a particular node coincides with the number of loci where the corresponding genotype differs from the genotype which is represented by the zero-string.

Remark 1

Unless otherwise states, the words “level”, “up”, “down” “above” and “below” refer to fitness graphs in the proofs. In particular, notice that a higher level does not imply greater fitness.

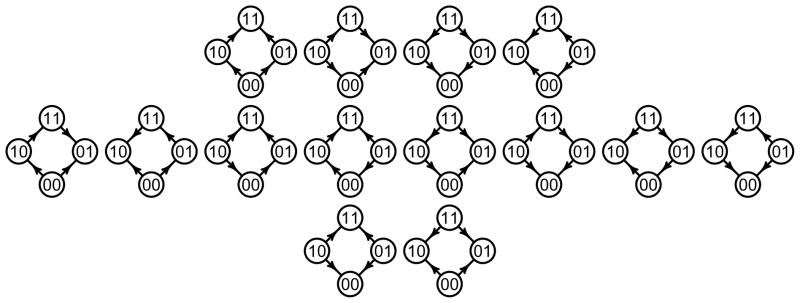
For interpretations of general fitness graphs, it may be helpful to first analyze the two-loci case in some detail. There exist exactly 14 fitness graphs for biallelic two-loci systems (see Fig. 2), where 4 are type 0 systems, 8 type 1 systems, and 2 type 2 systems. One verifies the following result.

Figure 2.

There exist exactly 14 fitness graphs for biallelic two-loci systems, where the type 0 systems are on the first row, the type 1 systems on the second row, and the type 2 systems on the third row.

Remark 2

For two-loci, type 0, 1, and 2 systems have the following properties.

1. A type 0 system can be rotated so that all arrows point up.

2. A type 1 system differs from a cycle by exactly one arrow.

3. A type 2 system have two nodes such that all edges are directed toward them, and two nodes such that no edges are directed toward them.

These observations can be used for identifying type 0, 1 and 2 systems in any fitness graph. In particular, it is immediate that the graph on the left in Fig. 3 has type 0 systems only, whereas the graph on the right has type 0 and 2 systems, but no type 1 systems.

Theorem 1 shows that no local property phrased in terms of type 2 systems (reciprocal sign epistasis) only, implies multiple peaks. However, we will phrase a condition in terms of type 1 and 2 systems, which is our main result.

Theorem 2

If a fitness landscape has type 2 systems and no type 1 systems, then it has multiple peaks.

Proof

Assume that the landscape is single peaked and that there exists a type 2 system in the landscape. It is sufficient to show that there exists a type 1 system. We may assume that the 1-string has optimal fitness, and this choice determines the levels of the fitness graph. If all arrows would point up, there would be no type 2 (or type 1) systems. Consequently some arrows point down. It follows that there exist adaptive walks which start with one step down and where the remaining steps to the 1-string are up, since the fitness landscape is single peaked.

Among such walks, pick one so that the step down starts from a level which is as high as possible. We will refer to the string corresponding to the starting point as the initial string. Consider the first two steps of the walk.

• Step 1The step corresponds to that the 1 at some position of the initial string is replaced by 0, since the step is down.
• Step 2The step corresponds to that the 0 at some position of the new string is replaced by 1, since the step is up.

There are exactly four strings which coincide with the initial string in all positions except the two mentioned in Step 1 and 2. Denote the strings 10, 00, 01, 11, where 10 is the initial string, 00 the string obtained after Step 1 and 01 the string obtained after Step 2 (formally the labels of the strings have no meaning, but one should associate to the two positions where the strings differ). Notice that the fourth string 11 is one level above 10 and 01 in the fitness graph.

By assumption,

$$w(10)<w(00)<w(01),$$

since fitness increases by each step of the walk. It is not possible that w(11) < w(01), since then there would exist a walk where the step down (from 11 to 01) was from a higher level as compared to the walk we picked. Consequently, w(01) < w(11) and we conclude that

$$w(10)<w(00)<w(01)<w(11).$$

Moreover, it is not possible that w(11) < w(10) since then one would get a cycle. It follows that

$$10,00,01,11$$

is a type 1 system.

Remark 3

This result is surprising since Poelwijk et al. (2011) claims that no sufficient local condition for multiple peaks exist. However, the discussion related to this claim in Poelwijk et al. (2011) is somewhat unclear to us.

One can ask if a lower bound for the number of peaks of a fitness landscape can be expressed in terms of type 2 and 1 systems. The next example shows that no such generalization of the previous result is possible.

Example 1

The fitness landscapes w̃ has exactly two peaks, 2^L−2 type 2 systems and no type 1 systems, where

$$\stackrel{\sim }{w}(11s)=4+\sum s_i,\stackrel{\sim }{w}(10s)=1+\sum s_i,\stackrel{\sim }{w}(01s)=2+\sum s_i,\stackrel{\sim }{w}(00s)=3+\sum s_i,$$

for s ∈ Σ^L−2. One verifies that 11s, 10s, 01s, 00s are a type 2 system for any s ∈ Σ^L−2 and that there are no type 1 systems. The fitness landscape has exactly two peaks, at the 1-string and the string 001 · · · 1.

3. Fitness landscapes with no constraints

We will demonstrate the efficiency of fitness graphs by providing a brief proof of a result from Weinreich et al. (2005). For simplicity we assume that w(s) ≠ w(s′) if s ≠ s′ in this section, in addition to the assumptions stated in the introduction. We refer to the global maximum of the landscape as “the fitness peak”. Moreover, define a general step similar to “adaptive step”, except that the fitness may decrease. A general walk, as opposed to “adaptive walk” is a sequence of general steps. If a general walk between two nodes has minimal length, we call it a shortest walk.

We can now state the main result in Weinreich et al. (2005) and give a new brief proof.

1. (Weinreich et al., 2005)

1. The following conditions are equivalent for a fitness landscape.

   1. Each general step toward the fitness peak, i.e., a step that decreases the graph distance to the peak, is an adaptive step.

   2. Each shortest general walk to the fitness peak is an adpative walk.

   3. The fitness landscape has no type 1 or 2 systems.

2. If the equivalent conditions in (1) are satisfied, then each adaptive walk to the fitness peak is a shortest general walk.

New proof

Proof

Represent the fitness landscape with a fitness graph where the 1-string corresponds to maximal fitness. Notice that a general walk from any node to the 1-string is a shortest general walk if and only if each step is up. From this observation we will verify that each condition (i)–(iii) is equivalent to all arrows in the fitness graph pointing up. It is immediate that (i)–(iii) hold if all arrows in the fitness graph point up. Assume (i). For any arrow, a general step through the arrow toward the fitness peak is a step up. By assumption, such a step is adaptive, so that the arrow points up. It follows that all arrows in the fitness graph point up. Assume (ii). A shortest general walk consists of general steps toward the fitness peak, so that the argument for (i) gives the result. Assume (iii). Since the 1-string (at level L in the fitness graph) is at the peak, all arrows starting from the nodes on level L − 1 point up. Then condition (iii) implies that all arrows from nodes on level L − 2 point up, and so forth.

Part 2 is immediate, since we may assume that all arrows in the fitness graph point up.

A fitness landscape satisfying the equivalent conditions (i)–(iii) above is referred to as a fitness landscape lacking genetic constraints on accessible mutational trajectories in Weinreich et al. (2005). It is important to notice that this concept is biologically meaningful. Type 1 systems may cause the adaptation process to be slower since not all shortest general walks to the peak are adaptive walks, even if the landscape is single peaked.

4. Fitness graphs and the shapes of fitness landscapes

We will compare information derived from fitness graphs with the geometric classification of fitness landscapes. For the reader’s convenience, we will give a brief description of the geometric theory of gene interactions introduced in Beerenwinkel et al. (2007 b). Our discussion is somewhat informal, and we refer to the original article for concepts and theory about the geometric classification of fitness landscapes, and to De Loera et al. (2010) for theory about polytopes and triangulations.

As before, we restrict to biallelic systems in our presentation. We will use some concepts which are defined in terms of populations. If one groups individuals into classes of identical genotypes, a population can be described as the frequencies of the genotypes. The fitness of a population is defined as the average fitness of all individuals.

We first describe the geometric classification in the case L = 2. Then the genotope is the square with vertices 00, 01, 10, 11. We denote this genotope [0, 1]², and interpret a point v = (v₁, v₂) ∈ [0, 1]² as the allele frequencies of the population, where v₁ denotes the frequency of 1’s at the first locus, and v₂ the frequency of 1’s at the second locus.

Let

$$\mathrm{\Delta }=\{(p_{00},p_{01},p_{10},p_{11})\in {[0,1]}^4:p_{00}+p_{01}+p_{10}+p_{11}=1\}$$

denote the population simplex. A population is given as a point in Δ.

Example 2

Consider v = (0.4, 0.8) ∈ [0, 1]². The populations p¹ = (0.2, 0.4, 0, 0.4) ∈ Δ and p² = (0, 0.6, 0.2, 0.2) ∈ Δ both have the allele frequencies described by v.

In general, a triangulation of a polygon is a subdivision of the polygon into triangles. A fitness landscape w will almost always induce a triangulation of the genotope [0, 1]². We will first describe the triangulations, and then provide some explanation. Notice that fitness is additive exactly if

$$w(11)-w(10)-w(01)+w(00)=0.$$

Case 1

If

$$w(11)-w(10)-w(01)+w(00)>0,$$

then the triangulation induced by the fitness landscape has 00 − 11 diagonal, meaning that the triangles are {00, 01, 11} and {00, 10, 11} (Fig. 3).

Case 2

If

$$w(11)-w(10)-w(01)+w(00)<0,$$

then the induced triangulation of the genotope has 10 − 01 diagonal meaning that the triangles are {00, 01, 10} and {01, 10, 11} (Fig. 3).

Having described the two possible triangulations (Case 1 and 2) we will explain how w induces a triangulation in some detail. Let ρ denote the map from the population simplex Δ to the genotope [0, 1]².

$$\rho (p_{00},p_{01},p_{10},p_{11})=(p_{10}+p_{11},p_{01}+p_{11}).$$

Notice that ρ maps a point of the population simplex to the allele frequencies. Indeed, p₁₀ + p₁₁ equals the frequency of 1’s at the first locus and p₀₁ + p₁₁ equals the frequency of 1’s at the second locus. (Notice that ρ (p¹) = ρ(p²) = v in Example 2.) For a fixed v ∈ [0, 1]², consider the linear programming problem

$$max\{p·w:\rho (p)=v\}.$$

A solution gives the maximal population fitness, i.e., the maximum of p · w, given the allele frequency vector v (since ρ (p) = v). If we let v vary, we get the following parametric linear programming problem

$$\stackrel{\sim }{w}(v)=max\{p·w:\rho (p)=(v)\text{for}\text{all}v\in {[0,1]}^2\}.$$

From the theory of triangulations (De Loera et al., 2010, chap. 2), the domains of linearity of w̃ are exactly the triangles of the triangulation induced by w (Case 1 or 2 depending on w), which completes the explanation. We will refer to Case 1 as “positive epistasis”, and Case 2 as “negative epistasis”.

For a geometric interpretation, consider the genotope [0, 1]² and the four points above the vertices of [0, 1]², such that the height coordinates corresponds to fitness. The four points are vertices of a tetrahedron (Fig. 3). The upper sides of the tetrahedron (marked with different patterns) project onto two triangles of [0, 1]². The projections describe the triangulation induced by w. The left picture corresponds to positive epistasis, and the right to negative epistasis.

Notice that for any v ∈ [0, 1]², there is a unique fittest population p with ρ (p) = v. The genotypes that occur in the fittest population are the vertices of the triangle which contains v. For positive epistasis (Case 1), notice that p¹ in Example 2 is a fittest population.

In general, the genotope of a biallelic L-loci system is the L-cube, where the vertices represent the genotypes. The fitness landscape will almost always induce a triangulation of the genotope. A triangulation of the L-cube is a subdivision of the cube into simplices (triangles if L = 2, tetrahedra if L =3, pentachora for L = 4, and so on). The shape of the fitness landscape is the triangulation induced by w. Moreover, in general there is a unique fittest population, as in the case L = 2. For a fittest population, one cannot increase the fitness by shuffling around alleles. The biological significance is immediate, since such allele shuffling relates to recombination.

In the case with positive epistasis for L = 2, the genotypes 10 and 01 are not on the same triangle. A recombination of 10 and 01 resulting in the genotypes 00 and 11, implies increased average fitness of the population.

Remark 4

Our description was restricted to the case where the genotope is an L-cube. The theory in Beerenwinkel et al. (2007 b) defines the genotope for any set of genotypes found in the population under consideration, and the shape is defined accordingly. The authors stress that the genotope is never an L-cube for binary data and many loci (≥ 20). This observation is important for complexity reasons.

We will compare the geometric classification with fitness graphs. Consider the case with positive epistasis where the 1-string has optimal fitness. This case is compatible with three different fitness graphs (no arrows down, exactly one arrow down, or two arrows down). This example shows that fitness graphs provide some information that cannot be obtained from the geometric classification. On the other hand, consider the fitness graphs with all arrows up. It is easily seen that there exist fitness landscapes having this fitness graph with positive, negative and no epistasis.

Since the case L = 2 is rather special, we will proceed with L =3. The 3-cube has 74 triangulations. For a complete list, see Beerenwinkel et al. (2007 b, Table 5.1), where each shape has a number between 1 and 74. Shapes of the same interaction types, differ only in the labeling of the vertices of the cube. There are six interaction types for the 3-cube in total.

Shape 74 is defined by the following inequalities:

$$\begin{array}{l}{w}_{000}-w_{010}-w_{100}+w_{110}>0\\ w_{001}-w_{011}-w_{101}+w_{111}>0\\ w_{000}-w_{001}-w_{100}+w_{101}>0\\ w_{010}-w_{011}-w_{110}+w_{111}>0\\ w_{000}-w_{001}-w_{010}+w_{011}>0\\ w_{100}-w_{101}-w_{110}+w_{111}>0.\end{array}$$

The six tetrahedra of the induced triangulation are:

$$\begin{array}{l}\{000,010,110,111\},\{000,010,011,111\},\{000,100,110,111\},\\ \{000,100,101,111\},\{000,010,110,111\},\{000,010,011,111\}.\end{array}$$

Shape 2 is defined by the following inequalities:

$$\begin{array}{l}{w}_{011}+w_{101}+w_{110}-w_{000}-2w_{111}>0\\ w_{000}+w_{011}+w_{101}-w_{110}-2w_{001}>0\\ w_{000}+w_{011}+w_{110}-w_{101}-2w_{010}>0\\ w_{000}+w_{101}+w_{110}-w_{011}-2w_{100}>0.\end{array}$$

Each inequality of Shape 74 can be described in terms of epistasis (in the usual sense), since each inequality keeps one locus fixed. In contrast, the inequalities of Shape 2 considers three-way interactions. For Shape 74, notice that 100 and 010 are not on the same tetrahedron. The recombination of 100 and 010 resulting in 110 and 000, implies increased average fitness. This observation is analogous to what we found for the square, and a similar result holds in any dimension.

Example 3

The following fitness landscape is of shape 74.

$$w_{000}=1,w_{100}=w_{010}=w_{001}=2,w_{110}=w_{101}=w_{011}=4,w_{111}=7.$$

For the corresponding fitness graph, all arrows point up.

Example 4

The following fitness landscape is of shape 74.

$$w_{000}=2,w_{100}=w_{010}=w_{001}=1,w_{110}=w_{101}=w_{011}=4,w_{111}=8.$$

Notice that the corresponding fitness graph has exactly 3 arrows down, and that 000 and 111 are at peaks.

It is easily seen that there exist fitness landscapes of shape 74 with several different fitness graphs, in addition to our two examples. Consider shapes for a fixed fitness graph. For each interaction type, Table 1 gives a shape specified by its number in Beerenwinkel et al. (2007 b, Table 5.1), as well as an example of a fitness landscape of this shape. Notice that the corresponding fitness graphs are the same in all 6 cases (all arrows point up).

Table 1.

Interaction types, shape numbers and fitness landscapes

	w000	w100	w010	w001	w110	w101	w011	w111
Type 1, no 2:	1	2	2	2	4	4	4	5
Type 2, no 10:	1	2	2	2	6	6	6	9
Type 3, no 34:	1	2	2	2	10	6	5	12
Type 4, no 46:	1	2	5	5	8	8	8	13
Type 5, no 70:	1	2	5	5	9	9	10	15
Type 6, no 74:	1	2	2	2	4	4	4	7

Summarizing, the fitness graph provides information about the adaptive potential, and the shape of a landscape reflects all gene interactions. Graphs and shapes provide complementary information about fitness landscapes. We will compare information from fitness graphs and the geometric theory for empirical data as well. For a detailed understanding of the next example, as well as terminology, the reader may consult Beerenwinkel et al. (2007 b). Alternatively, one can proceed to the next section without consequences for the further reading.

Using standard notation, consider the three-loci biallelic system with the HIV-1 mutations PRO L90M, RT M184V and RT T215Y (Segal et al., 2004). This system associated with HIV drug resistance was analyzed in Beerenwinkel et al. (2007 b), see also Bonhoeffer et al. (2004). We determined the fitness graph, as well as the shape from the mean fitness values (Beerenwinkel et al., 2007 b, Table 6.2) of the genotypes, since these data are sufficient for comparing geometric and qualitative information. From the fitness graph, one concludes that there are two peaks, 3 type 2 systems, 2 type 1 systems, and 1 type 0 system. Moreover, 010 and 001 have lower fitness as compared to their mutational neighbors. Notice that 4 out of 12 arrows point up, which shows that we are far from the most simple pattern one could expect from combinations of three deleterious mutations, i.e., that all arrows point down. The geometric classification for biallelic three-loci systems depends on the signs of in total 20 circuits. (Briefly, the circuits are linear forms including the 10 which occur in the description of Shapes 2 and 74.) The fitness graph provides some information about the circuits. For example, from the fitness graph, one can conclude that

$$w_{000}-w_{010}-w_{100}+w_{110}>0,$$

since w₀₀₀ > w₁₀₀ and w₁₁₀ > w₀₁₀. This is an example of conditional epistasis, since the last position is zero for all strings. However, from the fitness graph one cannot determine the sign of the following circuit which considers three-way interactions:

$$w_{001}+w_{010}+w_{001}-w_{111}-2w_{000}.$$

The fitness landscape is of shape 7 (Beerenwinkel et al., 2007 b, Table 5.1), and this shape slices off the genotypes 010 and 001. The interpretation is that the two genotypes have low fitness values. Compare with the two-loci case where the shape slices off the 11 genotype in Case 2, since this genotype has lower fitness as compared to an additive expectation (see Fig. 4). We conclude that the shape and the fitness graph agree that 010 and 001 have low fitness. Clearly there is some overlap in information from the fitness graph and the geometric theory. However, the geometric theory is more fine-scaled since it takes 20 circuits into consideration.

Figure 4.

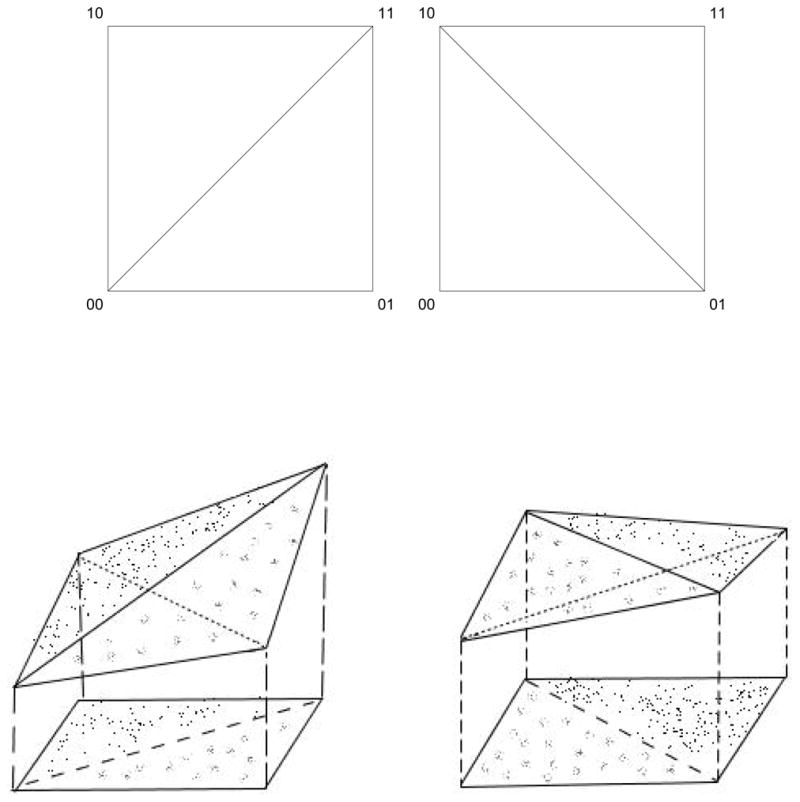
The upper pictures shows the triangulations of the genotopes (the squares) in Case 1 and 2, corresponding to positive and negative epistasis. The lower left picture shows the tetrahedron above the genotope in Case 1, where the height coordinates correspond to the fitness of the four genotypes under consideration. The projections of the upper sides of the tetrahedron describe the triangulations. The lower right picture shows how the triangulation is induced in Case 2.

5. Applications

Qualitative aspects of gene interactions are interesting for practical reasons. Suppose that two single mutants which confer resistance to a particular drug have been found frequently, but never the corresponding double mutant. From this observation one concludes that there is sign epistasis. Indeed, “good+good=not good”, since the combination of two beneficial single mutations was never found. This information is intrinsic, whereas fitness measurements tend to be sensitive to the environment or laboratory conditions. Qualitative observations of the type described are central for understanding adaptation in nature. We will indicate how one can check if qualitative data are compatible with standard models of fitness landscapes such as additive landscapes, random landscapes and the block model.

Recall that for the block model, the fitness of a genotype is the sum of contributions from each block. The rationale behind this assumption is that the effect of two changes in different blocks should be independent if the blocks have completely different functions. A falcon benefits from a strong heart and good vision. Most likely these factors are independent, so that simultaneous adaptation of heart and eyes are not problematic. We will consider block independence, or rather candidates for independent blocks. Block independence relates to the problem of finding “units of evolution”. From a conceptual and computational point of view, it is of interest to what extent nature can be subdivided into parts that act as independent units of evolution. A systematic approach to the topic of finding units of evolution is given in Shpak et al. (2004). In principle, one can model evolution of a population as a dynamical system determined by the fitness landscape and the mutation rates, provided that the population is asexual. The authors analyze aggregation of variables and decomposability of dynamical systems with applications to units of evolution. Different approaches to the problem of finding units of evolution above or below the genotype level are discussed. Following our philosophy, we will focus on qualitative aspects. The next two examples compare block independence and fitness graphs.

Example 5

Let L = 3 and assume that fitness differences

$$w_{1ij}-w_{0ij}>0$$

is the same for all i, j. For the corresponding fitness graphs there are 4 arrows up, from any node 0* * to the node 1 * *.

Example 6

Assume that

$$w_{1ij}-w_{0ij}>0$$

but that the difference depends on the background. For the corresponding fitness graphs there are 4 arrows up, from any node 0 * * to 1 * *, as in the previous example.

Notice that the first locus constitutes an independent block in the first example, but not in the second example. However, the fitness graphs in the two examples may coincide. Fitness graphs cannot detect independence, but they reveal if the sign of the effect of a particular locus, or a particular block, is independent of background. We suggest as a definition that a block is sign independent if each state of the block determines if the fitness contribution is positive or negative. However, the magnitude of the effect may depend on the background. Sign independence of fitness effects could be used for finding candidates for independent blocks.

We will introduce some concepts of relevance for mutation records. The main application is drug resistance mutations. From a record of clinically found mutants one wants to draw conclusion about the fitness landscape. The presence of the drug constitutes a new environment where the wild-type is no longer of optimal fitness. However, it is realistic to assume that the wild-type is much more fit in the new environment as compared to a randomly chosen string. *

It follows that most single and double mutants are not more fit than the wild type. However, if the fitness landscape is additive, then the double mutant corresponding to two beneficial single mutations is more fit than the single mutants. It is thus of interest whether beneficial single mutations tend to combine well or not for a fitness landscape. We define B and B_p as follows.

The set B_p consist of all double mutants such that both corresponding single mutations are beneficial.

The set B ⊆ B_p consists of all double mutants in B_p which are more fit than at least one of the corresponding single mutants.

Notice that $\frac{\mid B\mid }{\mid B_p\mid }=1$ for a landscape lacking genetic constraints on accessible mutational trajectories, in particular for an additive landscape. In contrast, one expects $\frac{\mid B\mid }{\mid B_p\mid }$ to be very small for a random landscape under the assumption *. The value one would expect for a random landscape depends on the circumstances, but 1% could be a realistic value.

For a quantitative measure of the degree of additivity, we refer to the concept “roughness” (Carnerio and Hartl, 2010; Aita et al., 2001). We suggest using $\frac{\mid B\mid }{\mid B_p\mid }$ as a qualitative measure of the degree of additivity for a fitness landscape. This measure is coarse. However, we have all reason to believe that a fitness landscape where $\frac{\mid B\mid }{\mid B_p\mid }=4\%$ differs from a landscape where the ratio is 96% in biologically interesting ways. For example, one could ask if there is a relation between this ratio and recombination strategies. The condition that double mutants in B ⊆ B_p are more fit than at least one of the corresponding single mutants is practical. Indeed, if the double mutant is more fit than at least one of the corresponding single mutants, then we have a good chance to find the double mutant in nature.

For an empirical example, consider the TEM family of beta-lactamases associated with antibiotic resistance, where the TEM-1 enzyme is considered the wild-type. The 4-loci biallelic system with the mutations L21F, R164S, T265M and E240K were studied in Goulart et al. (2012). Fitness ranks were determined for the genotypes in 15 selective environments corresponding to different antibiotics. However, fitness was not measured, so that only qualitative information is available. The mean value of $\frac{\mid B\mid }{\mid B_p\mid }$ for the 15 fitness landscapes was 0.61. Briefly, from knowledge about the TEM family, the expected $\frac{\mid B\mid }{\mid B_p\mid }$ value for a random fitness landscape in this context is less than 1% (Goulart et al., 2012; Crona et al., 2012). The value 0.61 indicates substantially more additivity as compared to random fitness, and at the same time the landscapes deviates considerably from additive fitness landscapes.

In general, if $\frac{\mid B\mid }{\mid B_p\mid }<1$ it is of interest if the block model or some related condition holds. In particular, one can ask if it is possible to partition the single mutations so that members of different subsets in the partition combine well. This question motivates us to suggest the next concept.

The qualitative decomposition property holds if there exists a partition of the beneficial single mutations satisfying the condition: For each double mutant in B_p such that the corresponding single mutations belongs to different subsets of the partition, the double mutant is a member of B.

Notice that a fitness landscape satisfying the block model has the qualitative decomposition property. Moreover, the qualitative decomposition property holds also for a generalized block model, where the fitness contributions of blocks sum (but where block fitness need not be random). The next example illustrates the qualitative decomposition property.

Example 7

Assume that the qualitative decomposition property holds and that the partition is as follows.

$$\{m_1,m_2,m_3\}\cup \{m_4,m_5,m_6,m_7,m_8,m_9,m_{10}\}.$$

In this case m₁ combines well with at least 7 elements, whereas m₄ combines well with at least 3 elements.

If we assume the block model, then very few pairs from the same set in the partition will combine well under the assumption *. The following observations are immediate from our definitions and from considering Example 7.

Remark 5

Assume that a fitness landscape has the qualitative decomposition property. Let B be the set of beneficial single mutations. Assume that no member of B combines well with all other members of B. Consider the set of the greatest combiners in B. One expects such great combiners not to combine well with each other, in comparison with randomly chosen pairs of single beneficial mutations.

Remark 6

Sign independence of blocks implies the qualitative decomposition property.

Remark 5 and 6 were used in an empirical study of antibiotic resistance (Crona et al., 2012). The conclusion was that the fitness data under consideration were not compatible with the block model. For real fitness data, one needs to consider complications such as incomplete records and multiple environments. However, in principle one can use $\frac{\mid B\mid }{\mid B_p\mid }$, Remark 6 and other patterns indicated here, for checking if fitness data are compatible with additive, random or block models of fitness landscapes. This theme is developed in Crona et al. (2012).

6. Discussion

Fitness landscapes are central in the theory of adaptation, and we have studied them from a qualitative perspective. Our main result relates global and local properties of fitness landscapes. The qualitative perspective has contributed to our understanding of coarse properties of fitness landscapes. Moreover, there are practical reasons for the qualitative perspective. We have indicated simple tests for checking if fitness data are compatible with some of the classical models of fitness landscapes, along with concepts for interpretations of fitness data.

It goes without saying that relative fitness values are more interesting than fitness ranks of genotypes. However, most of the available fitness data are qualitative, especially if one considers data of central relevance for adaptation in nature. It is equally obvious that one needs more than fitness ranks for a complete understanding of adaptation. In particular, the theory of recombination depends on quantitative aspects of gene interactions (Otto and Lenormand, 2002). The most fine-scaled theory of gene interactions is the geometric theory. However, as we have seen the shape alone does not provide all information of relevance for adaptation. A qualitative analysis could serve as a complement.

Classical theory of fitness landscapes has been developed without much contact with empirical results. In general, it would be valuable with methods for revealing and interpreting properties of fitness landscapes from fitness data without assumptions, or with minimal assumptions, about the underlying fitness landscapes. Sufficiently independent methods for analyzing data may be as important as new fitness measurements. The geometric classification of fitness landscapes, which falls under non-parametric statistics, as well as some of the qualitative approaches discussed here, are contributions in this category.

6.1. Conclusions

If a fitness landscape has type 2 systems but no type 1 systems, then the landscape has multiple peaks. Moreover, one cannot find a sufficient local condition for multiple peaks expressed in terms of type 2 systems only. (Recall that a type 2 system corresponds to reciprocal sign epistasis, whereas a type 1 system corresponds to sign epistasis but not reciprocal sign epistasis.)

Fitness graphs provide information not contained in the geometric classification of fitness landscapes. (Recall that fitness graphs are determined by fitness ranks of genotypes.)

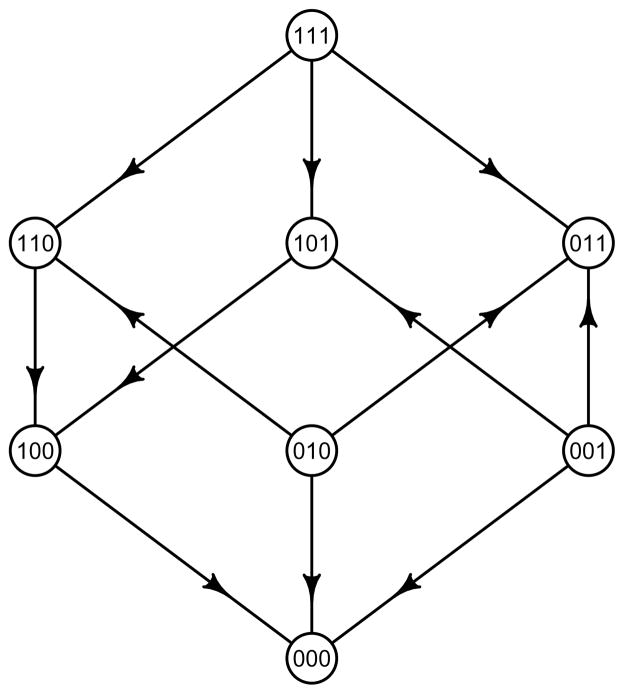
Figure 5.

From HIV data we obtained this fitness graph with 3 type 2 systems, 2 type 1 systems and 1 type 0 system. There are exactly two peaks.

• We study qualitative aspects of gene interactions and fitness landscapes.

• A sufficient local condition for multiple peaks is given.

• The fitness graph reveals sign epistasis and other coarse properties.

• The shape, as defined in the geometric theory, reveals all gene interactions.

• Fitness graphs and shapes provide complementary information.