Summary
Secretory phospholipase A2 exhibits much greater activity toward apoptotic versus healthy cells. Various plasma membrane changes responsible for this phenomenon have been proposed, including biophysical alterations described as “membrane fluidity” and “order.” Understanding of these membrane perturbations was refined by applying studies with model membranes to fluorescence measurements during thapsigargin-induced apoptosis of S49 cells using probes specific for the plasma membrane: Patman and trimethylammonium-diphenylhexatriene. Alterations in emission properties of these probes corresponded with enhanced susceptibility of the cells to hydrolysis by secretory phospholipase A2. By applying a quantitative model, additional information was extracted from the kinetics of Patman equilibration with the membrane. Taken together, these data suggested that the phospholipids of apoptotic membranes display greater spacing between adjacent headgroups, reduced interactions between neighboring lipid tails, and increased penetration of water among the heads. The phase transition of artificial bilayers was used to calibrate quantitatively the relationship between probe fluorescence and the energy of interlipid interactions. This analysis was applied to results from apoptotic cells to estimate the frequency with which phospholipids protrude sufficiently at the membrane surface to enter the enzyme’s active site. The data suggested that this frequency increases 50–100-fold as membranes become susceptible to hydrolysis during apoptosis.
Keywords: two-photon microscopy, merocyanine 540, Laurdan, hydrolysis kinetics, Patman, diphenylhexatriene
1. Introduction
Secretory phospholipase A2 (sPLA2) is an enzyme which adsorbs to the cell surface and hydrolyzes phospholipid acyl chains in the sn-2 position, yielding lysophospholipid and fatty acid (often arachidonic acid). Moreover, sPLA2 is a model protein for studying enzymatic activity at a lipid-water interface. Interestingly, all cell membranes are not equally susceptible to hydrolysis by sPLA2. Healthy cells resist hydrolysis by this enzyme whereas apoptotic or damaged cells become susceptible [1–4]. Studies have suggested that perturbations to the bilayer cause changes in the physical properties of the membrane, allowing individual lipids to migrate into the enzyme’s active site and become hydrolyzed [2, 5–9].
Attempts to understand this differential susceptibility have emphasized changes that occur in the plasma membrane during apoptosis. Three relevant changes have been described, but all are not equally understood. The most well-defined change is externalization of phosphatidylserine (PS), which is sequestered in the inner leaflet of the lipid bilayer in healthy cells. The thought is that the negative charge of exposed PS facilitates adsorption of sPLA2 to the membrane surface [5, 10, 11]. Accordingly, many studies have demonstrated that sPLA2 has higher activity toward anionic compared to zwitterionic synthetic membranes [12–17]. A second property correlating with sPLA2 activity is increased membrane permeability [18]. The mechanistic basis of this relationship is not yet understood and will not be addressed in this paper. The third alteration has been suggested by studies utilizing fluorescent membrane probes such as merocyanine 540 (MC540), Laurdan, and diphenylhexatriene (DPH) [2, 5, 6, 9]. These modifications appear necessary for membrane susceptibility to sPLA2, but they are vaguely defined as changes in “membrane fluidity” and “order.” In addition, there have been challenges in interpreting the results to focus solely on the plasma membrane because Laurdan and DPH freely enter the cell and interact with intracellular membranes.
These biophysical changes are more specifically defined in this study by assaying Patman spectral shifts and equilibration kinetics as well as trimethylammonium-DPH (TMA-DPH) anisotropy during thapsigargin-induced apoptosis. Thapsigargin (TG) produces endoplasmic reticulum stress by inhibiting the Ca2+ ATPase, and was chosen because it initiates synchronized cell death on a time scale amenable to the experiments required for this study. Patman and TMA-DPH are cationic versions of Laurdan and DPH that have been reported to reside primarily in the plasma membrane [19–21] and therefore eliminate the ambiguities of probe entering the cell. The experiments with Patman apply work done in model membranes by Franchino et al. [22]. Using vesicles of different compositions and a quantitative model, they determined that the pattern of equilibration of Patman reflects different configurations of the probe in the bilayer. They also concluded that the kinetics reveal dynamic changes in the molecular environment around the probe and can be used to infer additional biophysical detail beyond what can be gleaned from steady-state observations. Data from TMA-DPH and Patman during the main phase transition of artificial bilayers with different compositions are also used to correlate fluorescence observations with the interaction energy among adjacent phospholipids. The resulting calibration coefficients are then applied to data from living cells to estimate increases in the probability of lipid protrusions that promote hydrolysis during apoptosis [23, 24].
2. Materials and methods
2.1 Reagents
The monomeric aspartate-49 sPLA2 was isolated from the venom of Agkistrodon piscivorus piscivorus as described [25]. Snake venom sPLA2 was used because of its availability and sensitivity to biophysical changes in the plasma membrane. Results similar to those shown here have been demonstrated with TG-induced susceptibility to human sPLA2 isoforms [18].
Ionomycin, DPH, TMA-DPH, MC540, acrylodan-labeled fatty acid-binding protein (ADIFAB), propidium iodide, Laurdan, Patman, and annexin V Alexa Fluor® 488 conjugate were all purchased from subsidiaries of Life Technologies (Grand Island, NY). The carboxyfluorescein-labeled peptide (Val-Ala-Asp) fluoromethylketone caspase inhibitor (FAM-VAD-fmk) was acquired from Cell Technology (Mountain View, CA). Thapsigarin and Z-Val-Ala-Asp(OMe)-Fluoromethylketone (Z-VAD-fmk) were both acquired from Enzo Life Sciences (Plymouth Meeting, PA). These agents were dissolved in N,N-dimethylformamide, dimethylsulfoxide (DMSO), or aqueous buffer as appropriate. Lipids were purchased from Avanti Polar Lipids (Birmingham, AL). All other reagents were obtained from standard suppliers.
2.2 General
S49 lymphoma cells were grown in Dulbecco’s Modified Eagle Medium containing 10% heat-inactivated horse serum at 10% CO2 and 37°C as described [26]. Cells in culture medium were treated with TG (5 µM final) or equivalent volumes of the solvent (DMSO) and incubated for the indicated times. When applicable, Z-VAD-fmk (50 µM) was added in culture 30 min before TG or DMSO. Cells were harvested by centrifugation, washed, and resuspended in a balanced salt buffer (134 mM NaCl, 6.2 mM KCl, 1.6 mM CaCl2, 1.2 mM MgCl2, 18 mM HEPES, 13.6 mM glucose, pH 7.4 at 37° C) to a final density of about 0.25–3 × 106 cells/ml for experiments. Sample viability was assessed by trypan blue exclusion. All cell experiments were performed at 37 °C. Unless stated otherwise, all error representations are SE.
Multilamellar vesicles were made using 1,2-dipalmitoyl-sn-glycero-3-phosphocholine (DPPC), 1,2-dimyristoyl-sn-glycero-3-phosphocholine (DMPC), or 1,2-distearoyl-sn-glycero-3-phosphocholine (DSPC). Samples (0.1 µmole phospholipid dissolved in chloroform) were dispersed with TMA-DPH (1:200 probe:lipid), dried under a N2 gas stream, and suspended in 2 mL citrate buffer (20 mM sodium citrate/citric acid, 150 mM KCl, pH 7). Suspensions were incubated 1 h in a shaking water bath at ≥ 50 °C (or ≥ 60 °C for all samples containing DSPC) with intermittent vortex mixing at 10-min intervals.
2.3 Fluorescence Spectroscopy
Time-based fluorescence intensities and emission spectra were collected with a Fluoromax (Horiba Jobin Yvon, Edison, NJ) photon-counting spectrofluorometer. Anisotropy measurements were taken with a PC-1 (ISS, Champaign, IL) photon-counting spectrofluorometer. Continuous gentle stirring with a magnetic stir bar ensured sample homogeneity, and temperature was maintained by a jacketed sample chamber fed by a circulating water bath. Bandpass was set at 16 nm for anisotropy measurements and 4 nm for all other experiments. Cell samples were treated and prepared as described above and equilibrated in the fluorometer sample chamber for at least 5 min before initiating data acquisition.
Membrane hydrolysis catalyzed by sPLA2 was assayed by ADIFAB fluorescence and by propidium iodide uptake in the presence of the enzyme. The amount of fatty acid released was quantified by comparing ADIFAB fluorescence emission (65 nM final; excitation = 390 nm) at 432 and 505 nm (I432 and I505) and calculating the generalized polarization as described [26, 27]:
| (1) |
Propidium iodide fluorescence was collected over time (excitation = 537 nm, emission = 617 nm) as propidium iodide (37 µM final), sPLA2 (70 nM final), and triton X-100 were added sequentially. Triton X-100 permeabilizes all cells and provides the maximal fluorescence. The proportional rise in propidium iodide fluorescence after the addition of both propidium iodide and sPLA2 was quantified by fitting fluorescence intensity time courses with an arbitrary function by nonlinear regression. The subpopulation of cells that were alive but susceptible to sPLA2 was quantified as the fraction of total propidium uptake that occurred after sPLA2 addition. The data were adjusted to account for cells with degraded DNA (invisible in this assay) using data obtained from flow cytometery (see below). Details of these calculations have been reported previously [11].
Merocyanine 540 (170 nM final) spectra (excitation: 540 nm, emission: 550 to 700 nm) were collected before probe addition (to assess stray light background), after 5 min equilibration with MC540, and after 10 min treatment with 300 nM ionomycin (a calcium ionophore which quickly initiates a maximal MC540 response Ref. [2]). Intensity values from 565 to 615 nm were summed to quantify the overall intensity for each spectrum. The intensity of the first spectrum was subtracted from the second, and the difference was divided by the intensity of the third spectrum (also corrected for background) to standardize for cell number. To quantify shifts in the spectral peak, spectra were fit by nonlinear regression to an arbitrary function (sum of Gaussian curves). The peak wavelength was then calculated as the point at which the first derivative of the generated curve was equal to zero. The magnitude of spectral shifts was calculated by subtracting the peak wavelength of the second spectrum from the third (ionomycin). The data are expressed as the average change in peak wavelength after ionomycin addition for the control group minus the change observed for each individual sample.
Measurements of DPH and TMA-DPH (2.5 µM final) fluorescence were collected with different configurations of excitation (350 nm) and emission (452 nm) polarizers in the vertical and horizontal positions after 10 min equilibration of cells with the probe. The anisotropy (r) was then calculated from the fluorescence intensity when both polarizers were vertical (I‖) and when the excitation was vertical and the emission horizontal (I⊥). Correction for differential transmission and detection at the two polarizer positions was included (G) according to convention:
| (2) |
Anisotropy measurements were also made with DMPC, DPPC, or DSPC multilamellar vesicles equilibrated with TMA-DPH during vesicle preparation as described above. Samples were equilibrated first with the probe and then 5 min at each temperature in 1–2 °C increments spanning the main phase transition for each lipid (DMPC: 15–35 °C; DPPC: 18–50 °C; DSPC: 18–60 °C). The change in anisotropy associated with the phase transition was calculated as the difference in limiting anisotropy values at the two ends of the transition (rlow and rhigh) obtained by nonlinear regression using the following:
| (3) |
where n is the cooperativity of the transition, and Tm is the melting temperature.
Both Laurdan and Patman (250 nM final) fluorescence intensity measurements were acquired as a function of time with excitation at 350 nm and emission collected at 435 and 500 nm (I435 and I500). Spectral changes were quantified by calculating the generalized polarization (GP) as follows [28]:
| (4) |
For Patman equilibration analyses, time courses of probe intensity were smoothed by nonlinear regression to an arbitrary function (analogous to Eq. 5) and normalized to the intensity at 435 nm at 400 s to aggregate data from multiple replicate samples. These pooled data were then fit by nonlinear regression to the following:
| (5) |
where A and C are arbitrary scalars, b and d are rate constants, and F is the intercept intensity. Intensities at both wavelengths were fit together with b and d constrained as shared parameters. These fitting parameters were then used to calculate model parameter values according to Eqs. 11–14 in the accompanying paper [22]. Error was estimated by using the extreme values of the 95% confidence intervals for each fitting parameter generated by nonlinear regression. Every permutation of these fitting parameters was inputted into Eqs. 11–14 to determine the range of possible model parameter values. This range is illustrated as error bars in the relevant figure.
2.4 Flow Cytometry
Cells were treated and prepared as described above. For caspase assays, FAM-VAD-fmk was added in culture 30 min before cell harvesting according to instructions provided with the vendor’s kit. Because peaks were not easily distinguishable for analysis by gating, histograms of FAM-VAD-fmk intensity were fit with a sum of Gaussian curves. The area under the curves composing the more positive peak was used to represent the percent of the population staining positive for caspase activation. Probes for all other flow cytometry assays (MC540 (250 nM), propidium iodide (10 µM), annexin V) were added after cells were resuspended in buffer and incubated for 10 – 15 min before data acquisition. Merocyanine 540 data were analyzed in the same way as for the caspase assay. The annexin V Alexa Fluor® 488 conjugate was used to assay PS externalization according to manufacturer’s instructions (Life Technologies, Grand Island, NY). A gate representing positive staining was determined from samples containing no probe. Propidium iodide and triton X-100 were used in conjuction to quantify the number of cells containing hypodiploid-staining DNA due to fragmentation as described [29]. This was determined by setting a gate below the peak representing G1-phase DNA staining. All flow cytometry samples were processed in a BD FACSCanto flow cytometer (BD Biosciences, San Jose, CA) with an argon excitation laser (488 nm). Emission was assessed using a bandpass filter at 515–545 nm for FAM-VAD-fmk and annexin V or 564–606 nm for propidium iodide and MC540.
2.5 Two-Photon Microscopy
Two-photon excitation microscopy was performed at the Laboratory for Fluorescence Dynamics (Irvine, CA) using an Axiovert 35 inverted microscope (Zeiss, Thornwood, NY). S49 cells were prepared for experiments as described above, treated with Laurdan, Patman, DPH, or TMA-DPH (250 nM final), and equilibrated for 10 min before data acquisition. Excitation was usually set at 753 nm, but when experiments involved only Laurdan or Patman, 780 nm was used because of more efficient excitation. Using software obtained from the Laboratory for Fluorescence Dynamics, histograms of Laurdan GP were created for both the whole cell and the middle of each cell (54 ± 5% (SD) of image pixels). The average GP for the perimeter of the cell was calculated as the difference between the average GP of the whole cell and its middle.
3. Results
3.1 Death
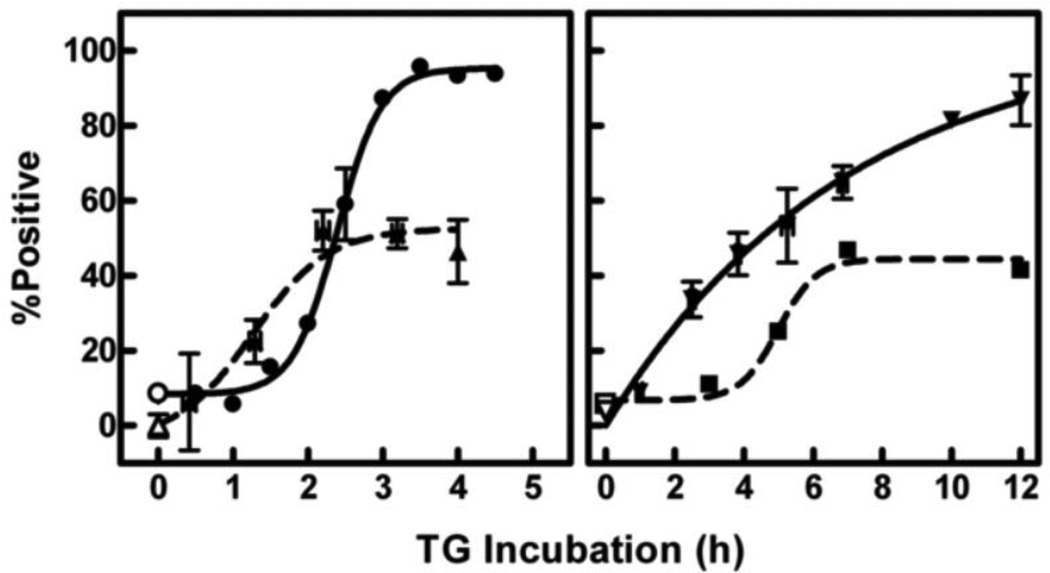
A timeline of major apoptotic markers during TG-induced death is shown in Fig. 1. Caspase activation was assessed using the fluorescent pan-caspase inhibitor FAM-VAD-fmk which enters the cell and irreversibly binds activated caspases. The caspase cascade was activated in half of the cells (triangles, dashed curve, left panel) and preceded externalization of PS (circles, solid curve, left panel), trypan blue uptake (inverted triangles, solid curve, right panel; note the different time scale on the right panel), and DNA fragmentation (squares, dashed curve, right panel). Likewise, DNA fragmentation was observed in 50% of the cells, although it was not complete until 7 h after addition of TG. In contrast, 100% of the cells exposed PS in the outer leaflet of the cell membrane. This exposure was complete after 3 h with TG. However, only half of the gain in PS exposed in response to TG was preventable by the general caspase inhibitor, Z-VAD-fmk (42.3 ± 9.2% reduction; p < 0.05; effect of Z-VAD-fmk on control cells was insignificant; analysis of variance with Bonferroni post-test, n = 5 for all groups). The proportion of the cell population that was permeable to trypan blue gradually increased, reaching ~85% at 12 h of TG treatment. These results suggested that about half of the cells died by classical apoptosis although the rest eventually died by another mechanism.
Fig. 1.
Timing of apoptotic events during TG-induced death. Cells were treated in culture with either DMSO (vehicle control; open symbols) or TG (solid symbols) for various times as indicated on the x-axis. Caspase activation (triangles, n = 6–13 in TG groups, 47 in control group), PS externalization (circles, each time point is a separate experiment), and DNA degradation (squares, each time point is a separate experiment) were assessed via flow cytometry after incubation with FAM-VAD-fmk (30 min), AlexaFluor-labeled Annexin-V (15 min), or propidium iodide with Triton X-100 (10 min) respectively. Death (inverted triangles, n = 1–31 in TG groups, 72 in control group) was determined by cell permeability to trypan blue. Data are represented as the percentage of the population positive for each response. Nonspecific binding of FAM-VAD-fmk [44] was subtracted from all time points.
3.2 Susceptibility to sPLA2
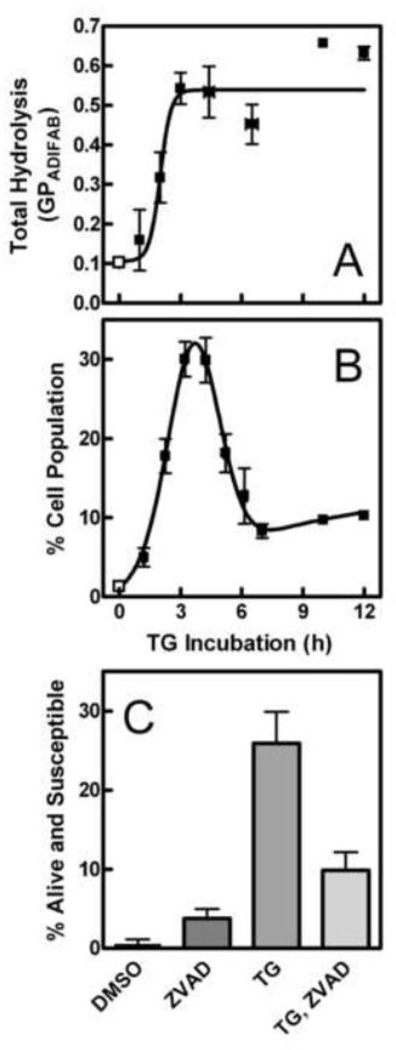
Figure 2 illustrates that treatment with TG rendered S49 cells susceptible to hydrolysis by sPLA2. Fig. 2A is a summary of the total amount of membrane hydrolysis after different incubation times with the apoptotic inducer. Maximal hydrolysis was observed after 3 h with TG. When the vital stain propidium iodide is included to assess viability concurrently, it is possible to quantify the subpopulation of cells that is still alive but has progressed far enough into the death process to be susceptible to sPLA2. As demonstrated previously, these cells exclude the dye until their membranes are damaged by hydrolysis [4, 9]. Figure 2B shows that this alive and susceptible subpopulation reached a maximum of about 30% of the total cell population around 3.5 h. As shown in Fig. 2C, about half of this subpopulation was apoptotic (based on inhibition by Z-VAD-fmk). This proportion of alive but susceptible cells was large compared to the ~5–8% seen previously with dexamethasone [4, 9], indicating that TG-induced apoptosis is a good model for exploring membrane changes responsible for susceptibility. At longer time points, this alive but susceptible subpopulation diminished in size because a larger proportion of the cells were now already permeable to propidium iodide in the absence of sPLA2. Comparing the shapes of the time profiles in Figs. 2A and B demonstrates that the cells continued to be good substrates for sPLA2 after they become permeable to propidium iodide. Interestingly, the subpopulation of alive and susceptible cells never reached zero at long incubation times even though all other markers of apoptotic progression indicate completion of the process for vulnerable cells by ~7 h. This result suggests that about 10% of the cells progress far enough to become susceptible to hydrolysis but remain static in that state without completing the death process. The ~10% discrepancy between PS exposure and trypan blue uptake shown in Fig. 1 supports this conclusion as it illustrates that there are cells with altered membranes that remain alive up to 12 h.
Fig. 2.
Susceptibility of TG-treated cells to sPLA2. Cells were treated for various times with DMSO (vehicle control; open squares) or TG (solid squares) in cell culture. (A) Fatty acid release was measured using ADIFAB. The total amount of hydrolysis was calculated as the maximal change in ADIFAB GP after addition of sPLA2 (n = 1–6 in TG groups, 20 in control group). (B) The percentage of the cell population that was both alive and susceptible to sPLA2 was assessed using propidium iodide (n = 1–18 in TG groups, 63 in control group) as described in Materials and Methods. (C) Cells were incubated with Z-VAD-fmk or control solvent (DMSO) for 30 min before TG or DMSO treatment. The percentage of cells alive and susceptible to hydrolysis by sPLA2 was assayed as in Panel B. Groups differed significantly by one-way analysis of variance (p < 0.0001, n = 4–8 per group). A post-test (Bonferroni) demonstrated that the TG group differed from all others (p < 0.01) and that cells treated with ZVAD-fmk alone or before TG were indistinguishable from control cells.
3.3 Probes of membrane biophysics
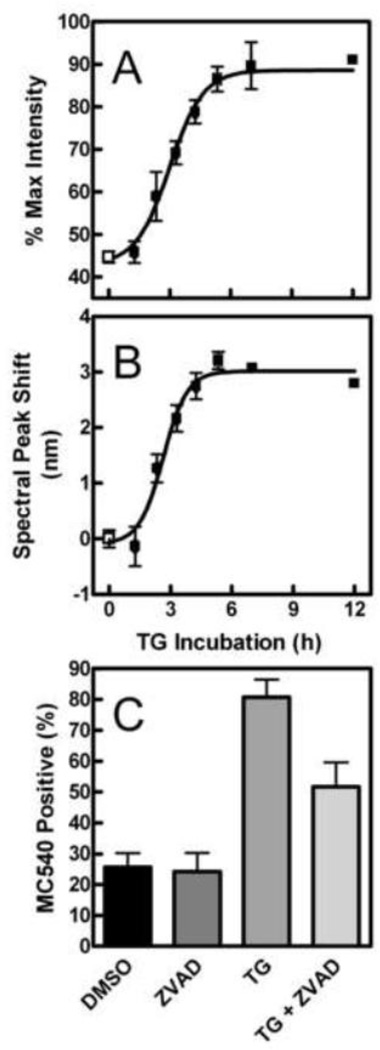
The strategy we employed to identify the nature of biophysical changes in the cell membrane associated with enhanced hydrolysis by sPLA2 was to use information from several membrane probes sensitive to the level of lipid order in the membrane (MC540, Laurdan, Patman, TMA-DPH and DPH). Figure 3 illustrates that TG treatment caused both an increase in the intensity (Panel A) and red-shift in the peak (Panel B) of the MC540 emission spectrum compared to vehicle controls (DMSO). These two effects appeared to follow a similar time course and were maximal by about 5 h. Figure 3C indicates that about half of the response was prevented by treatment with Z-VAD-fmk. Therefore, the cells displaying changes in membrane physical properties included both apoptotic and non-apoptotic subpopulations, as was observed in Fig. 2 C for sPLA2 vulnerability.
Fig. 3.
Effect of TG treatment on MC540 fluorescence. The effect of DMSO (open squares) or TG (solid squares) on MC540 emission intensity (A) or spectral maximum (B, expressed as shift compared to that induced by ionomycin) was obtained and calculated as explained in Materials and Methods (n = 1–13 in TG groups, 45 in control group). (C) Cells were pretreated with Z-VAD-fmk or control solvent (DMSO), equilibrated with MC540, and analyzed by flow cytometry. Data represent the percentage of the cell population staining positive for MC540. Groups differed significantly by one-way analysis of variance (p < 0.0001, n = 5 per group). A Bonferroni post-test revealed that TG significantly increased MC540 fluorescence (p < 0.001). Treatment with Z-VAD-fmk alone was not distinguishable from control cells (p > 0.05). Addition of Z-VAD-fmk before TG treatment was significantly different from both control cells and cells incubated with TG alone (p < 0.05 in both cases).
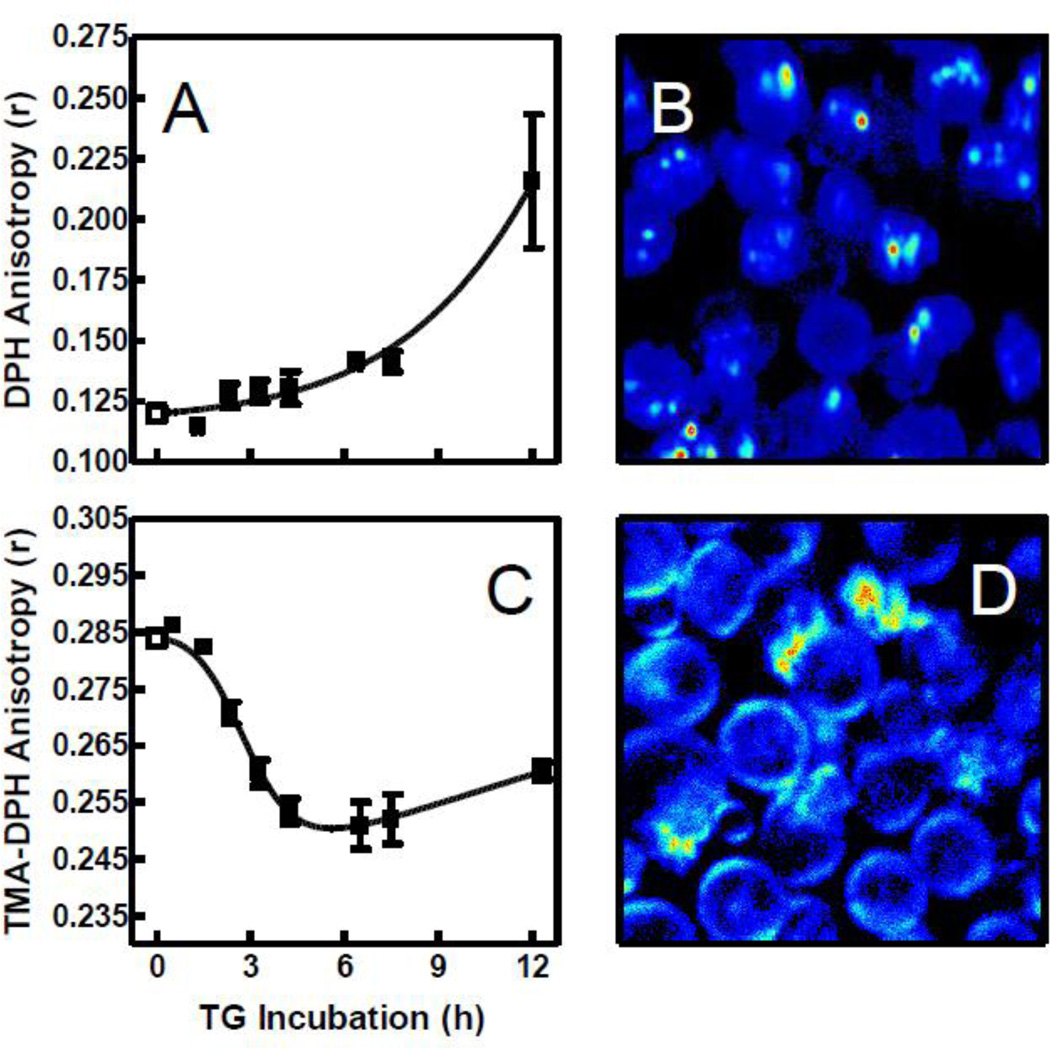
Figure 4A illustrates that DPH anisotropy increased gradually with TG treatment. As shown by two-photon microscopy in Fig. 4B, DPH distributes rapidly among all membranes in the cell, thus reporting an average for probe mobility throughout the cell. To isolate effects at the plasma membrane, we repeated the experiment of Fig. 4A with a charged analog of DPH, TMA-DPH. The trimethylammonium moiety on TMA-DPH is reported to retard diffusion of the probe into the cells so that it is enriched in the plasma membrane [21]. This assertion was verified for S49 cells by two-photon microscopy as shown in Fig. 4D. Figure 4C demonstrates two major differences between TMA-DPH and DPH anisotropy. First, the baseline anisotropy differed by 0.16 anisotropy units suggesting a very different mobility in the plasma membrane compared to the cell interior, a result reminiscent of the higher GP value reported for Laurdan at the plasma membrane compared to internal membranes [9]. Second, the temporal trend during TG treatment was sharper and in the opposite direction compared to DPH. The time scale for the changes in TMA-DPH anisotropy was comparable to that observed for MC540.
Fig. 4.
DPH and TMA-DPH anisotropy and localization in TG-treated cells. After incubation with DMSO (open squares) or TG (solid squares) for the indicated times, DPH (A and B) or TMA-DPH (C and D) was added to cell samples. Panels A and C show anisotropy measurements (DPH: n = 2–5 in TG groups, 26 in control group; TMA-DPH: n = 2–6 in TG groups, 30 in control group). Panels B and D are representative two-photon images showing localization of probe intensity after 2 h TG treatment and 12 min equilibration with the probe. Fluorescence intensity is represented by a relative false color scale (blue, low; red, high).
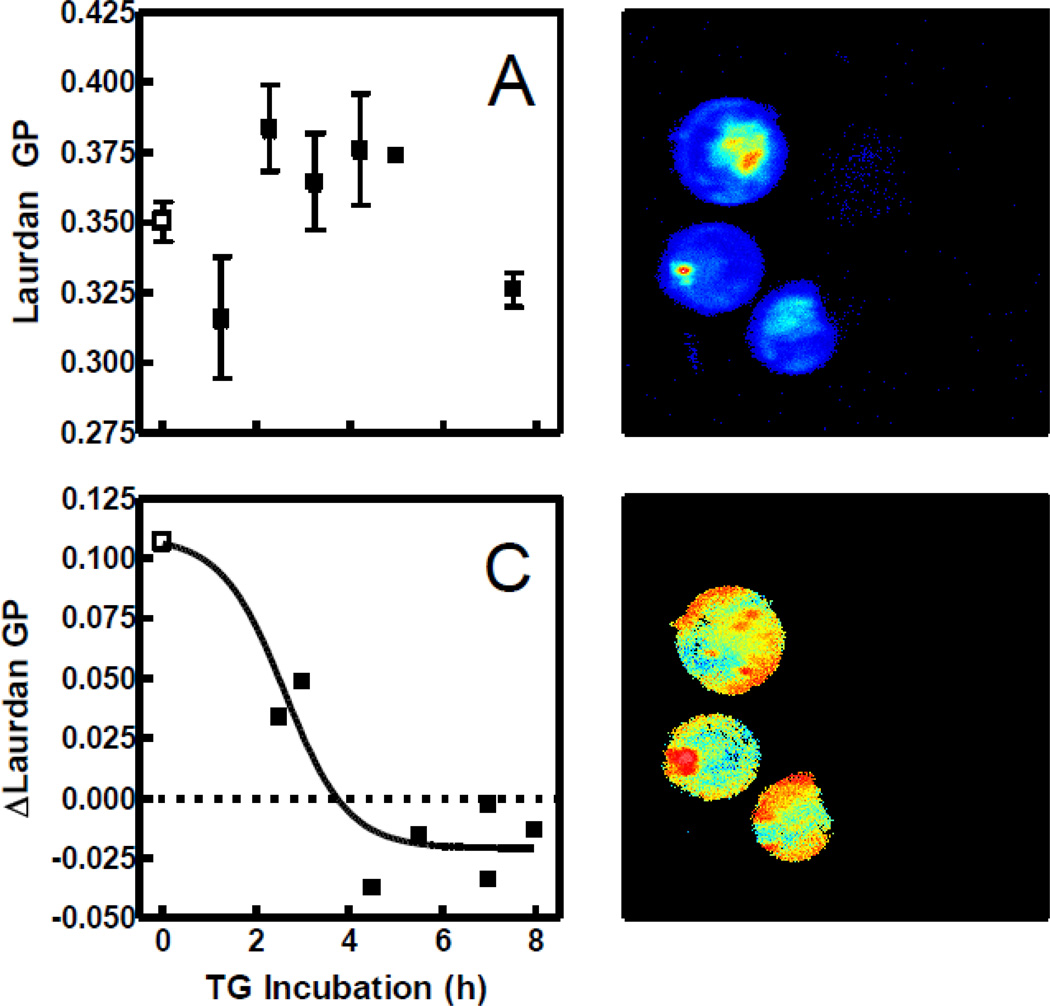
Figure 5A illustrates the absence of any distinct pattern in Laurdan fluorescence assessed spectroscopically in bulk samples with increasing TG incubation time. As explained previously, interpretation of Laurdan data with cells is confounded by the fact that the probe rapidly penetrates the plasma membrane and stains the interior as well as the exterior of the cell (Fig. 5B). The problem is mitigated by analyzing images of the fluorescence staining. Two-photon images (Fig. 5D) suggested that the average Laurdan GP of the cell perimeter was different from that of the interior. Figure 5C is a quantification of this observation, confirming the difference between plasma membrane and internal membrane staining and that this difference changes with TG treatment. Nevertheless, these images cannot distinguish fluorescence originating from the internal leaflet of the cell membrane versus the external, which is the site of action of sPLA2.
Fig. 5.
Effect of TG incubation on Laurdan intensity and GP. (A) Laurdan GP of cells treated with DMSO (open squares) or TG (solid squares) for various times was assessed via fluorescence spectroscopy (n = 1–8 in TG groups, 31 in control group). Values of GP were calculated from the intensities measured 600 s after probe addition. (B) Laurdan intensity was visualized by two-photon microscopy after a 3 h incubation with TG and 12 min with probe. Fluorescence intensity is represented by a relative false color scale (blue, low; red, high). (C) Images such as that in Panel D were quantified (n = 151 cells) by calculating the difference in GP between pixels corresponding to the cell perimeter and those in the middle (see Materials and Methods) for control (open squares) and TG-treated cells (solid squares). (D) The image from Panel B is shown with false coloring representing Laurdan GP (blue = −0.25 GP units; red = 0.75 GP units).
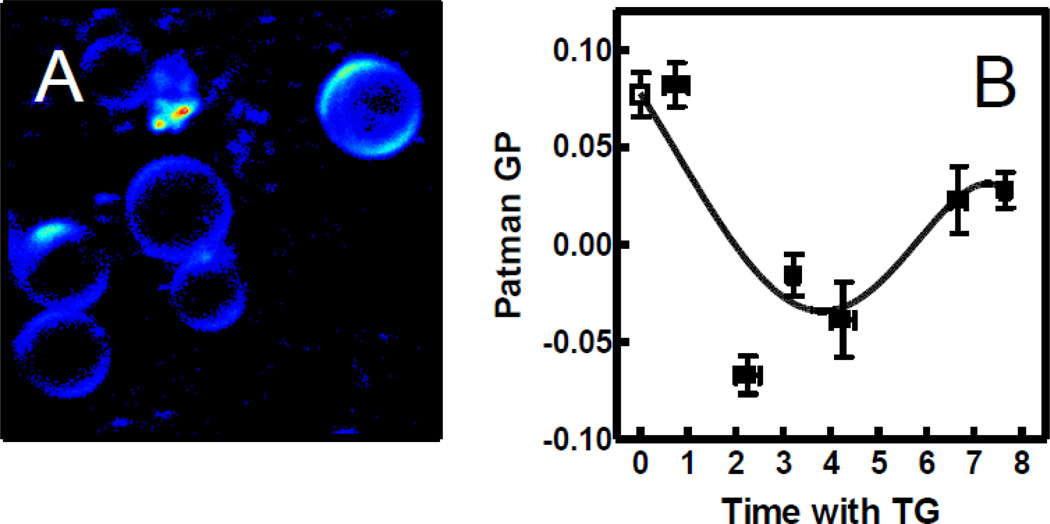
Patman has essentially the same structure as Laurdan except for a charged moiety attached to its head [30]. This modification appears to provide the same advantage as TMA-DPH, i.e., retaining the probe in the outer leaflet of the cell membrane [19, 20]. We verified this expectation for S49 cells with two-photon microscopy as shown in Fig. 6A. Figure 6B illustrates that Patman GP decreased with increasing TG incubation time, starting between 1 and 2 h, similar to the time scale observed with MC540 and TMA-DPH. The data suggest that the maximum response may occur sooner with Patman compared to the other probes, raising the possibility that the details sensed by this probe are especially early in the time course of TG-induced apoptosis. In any case, the Patman result suggests greater water penetration into the plasma membrane [28]. At later time points, when the membranes begin to become permeable, the reduction in Patman GP appeared to partially reverse, perhaps due to probe entering the cell interior.
Fig. 6.
Patman localization and GP after TG treatment. (A) Patman intensity was visualized by two-photon excitation microscopy after 3 h TG treatment plus 12 min with probe. Fluorescence intensity is represented by a relative false color scale (blue, low; red, high). (B) Patman GP of cell samples treated with DMSO (open square) or TG (solid squares) was assessed by fluorescence spectroscopy. GP was assessed 400 s after probe addition (n = 2–7 in TG groups, 25 in control group) The curve was generated by nonlinear regression using an arbitrary function.
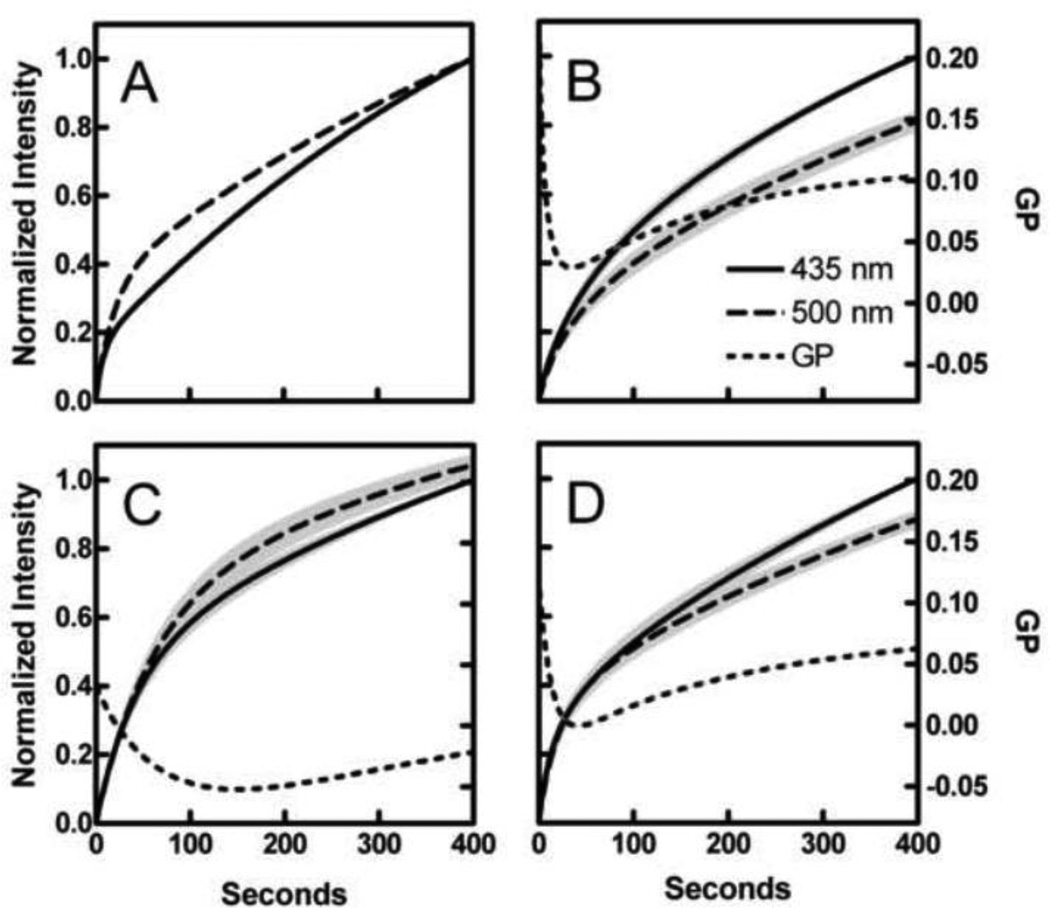
During Patman data acquisition, an interesting phenomenon was observed; the probe appeared to equilibrate at different rates when emission was measured at 435 nm compared to 500 nm. These differences are most easily seen by normalizing the data at the two wavelengths to their own values at 400 s (Fig. 7A). As shown in the accompanying paper [22], this phenomenon also occurs in artificial membranes and may provide additional information regarding the properties of the bilayer beyond that revealed by the GP alone. Extraction of that information requires analysis with a quantitative model such as the one developed in the companion paper [22]. That model is employed here.
Fig. 7.
Effect of TG on Patman equilibration kinetics. (A) Patman was added to control cells and intensity measured for 400 s. Normalized intensity at both 435 nm (solid curves) and 500 nm (dashed curves) is shown to illustrate differences in equilibration kinetics. (B, C, and D) Equilibration time profiles of intensity at 435 nm, intensity at 500 nm, and GP (dotted curves) from control samples (B), samples treated with TG from 2–5 h (C), and samples treated for over 6.5 h (D). Data from both wavelengths were normalized to that measured at 435 nm at 400 s and aggregated (n = 10–25 per group). Gray shading represents ± SE.
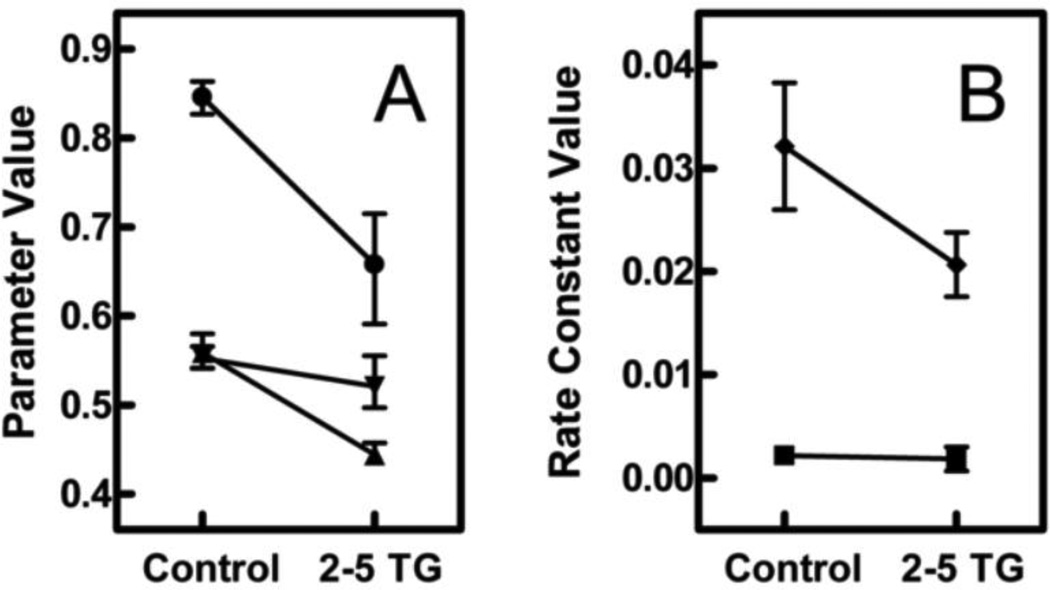
Accordingly, Patman time courses were smoothed by nonlinear regression using Eq. 5. The regression curves at 435 (solid) and 500 nm (dashed) were normalized to the intensity of the 435 nm curve at 400 s. This normalization made it possible to aggregate results from multiple experiments to examine general patterns in shape. Averages of controls, samples treated for 2–5 h with TG, and those treated for 6.5–8 h are shown in Figs. 7B, C, and D respectively. The pattern of Patman equilibration in living cells resembles that observed with vesicles in that they both represent a sum of two kinetic processes distinguished by rate constants that differ by at least a factor of 10 [22]. Figure 8 displays the effects of TG treatment on the parameters associated with the model (discussed below).
Fig. 8.
Effect of TG on membrane properties and Patman distribution. (A) The effect of TG on the fraction of the probe in the “slow” environment (circles), the polarity of “slow” environment (inverted triangles), and the polarity of the “fast” environment (triangles) were estimated using the model developed in [22]. (B) The same model was used to estimate the change in the equilibrations rates of the “slow” environment (squares) and the “fast” environment (diamonds). Model parameters and error estimates were obtained from nonlinear regressions of the data shown in Figs. 7 B and C as explained in Materials and Methods.
4. Discussion
As expected, TG induced apoptosis in S49 cells as seen by caspase activation, PS exposure, DNA fragmentation, and cell death. These classical events were accompanied by a previously reported biophysical change in the plasma membrane that correlates with susceptibility to sPLA2 and precedes cell death. Consistent with other studies of apoptosis, MC540 emission spectra became red shifted and increased in intensity during TG treatment, suggesting a reduction in lipid packing [9, 31].
DPH and Laurdan have previously been used to investigate changes in membrane fluidity and order. As a lipid bilayer becomes less fluid and more ordered, movement of DPH becomes more restricted and its anisotropy increases [32, 33]. Laurdan is sensitive to the presence and mobility of water molecules near the phospholipid glycerol backbone [28]. Alignment of water dipoles with that of the excited probe shifts the emission spectrum (quantified by calculating the GP) to longer wavelengths indicating greater water penetration into the membrane, presumably allowed by a reduction in phospholipid order and packing [34]. As shown in Figs. 4B and 5B, these two probes quickly cross the plasma membrane to stain the cell interior, making interpretation difficult. In addition, their fluorescence properties did not change in a pattern reproducible enough to defend statistically during the time range when membranes became susceptible to hydrolysis. When the cell perimeter and interior of two-photon Laurdan images were examined separately, however, an early trend of decreasing GP was observed. This trend suggested that alterations of the plasma membrane detected by Laurdan on a time scale relevant to sPLA2 activity do occur (Fig. 5C).
To more fully define this biophysical change in the membrane, charged analogues of DPH and Laurdan, TMA-DPH and Patman respectively, were utilized. As shown in Figs. 4D and 6A, diffusion of these two probes into the cell interior is reduced, validating their direct use for assessment of plasma membrane properties. The trend in TMA-DPH anisotropy after TG treatment was substantially different from that of DPH, showing instead a decrease (Fig. 4C) at the same time that membranes were becoming vulnerable to sPLA2 (Figs. 2A and B). This diminished anisotropy implied a reduction in stereo-constraints imposed by neighboring membrane lipids during early apoptosis, a result consistent with the MC540 data. The concurrent drop in Patman GP displayed in Fig. 6B substantiated this interpretation since a loosening of neighbor-neighbor interactions would allow increased water penetration into the membrane. The data at long time points (> 6 h) for Patman suggest that this reduction in lipid order is reversed as the apoptotic process progresses. The data with TMA-DPH hinted at the same effect, although the late trend was much smaller than observed with Patman. These results suggest that this phenomenon is either complex in nature or confounded by membrane blebbing and differential distribution of these probes during that late time frame. Therefore, at these later time points, Patman and, to a lesser degree, TMA-DPH could also be staining internal membranes and reflect the increased order seen with DPH and reported previously for glucocorticoid-induced apoptosis [9]. Moreover, the focus of this study is to understand the nature of membrane changes facilitating hydrolysis by sPLA2 early in apoptosis before membrane integrity is compromised. Thus, the remainder of the discussion will focus on changes during the 2–5 h interval after TG addition.
Further information can be obtained from Patman if equilibration kinetics are examined in addition to the endpoint GP [22]. The same phenomenon shown in Fig. 7 was observed in artificial vesicles, and suggested that the probe exists in multiple configurations in the membrane. One possibility is that the configurations correspond to probe localized in different bilayer domains. This possibility was considered and rejected in the accompanying study [22] for artificial membranes. Molecular dynamics simulations of other probes with structure related to Patman suggest a second possibility that these configurations represent different stereo-conformations of the probe [35]. Experimental measurements of Patman fluorescence quenching indicate that they may refer to different depths in the membrane [36]. For parsimony, only two configurations were considered here (referred to as “fast” and “slow”, see Ref. [22]) even though data such as those shown in Ref. [36] indicated a possible continuum of Patman locations. With the data gathered thus far, a continuous model cannot be distinguished from a two-state model in which the observable properties of the states overlap as a function of the independent variable, in this case wavelength. Regardless of the molecular details of the configurations, the data in Ref. [22] argue that equilibration of Patman’s fluorescence represents the local microenvironment relaxing around newly-inserted probe.
By applying the specific model described in the accompanying paper [22], it was possible to determine which specific parameters were altered with TG treatment. Figure 8 illustrates that TG treatment produced three detectable effects. First, a smaller proportion of Patman molecules populated the “slow” configuration compared to control cells (66% compared to 85%, circles, Panel A). To the extent that the “slow” configuration represents a deeper location in the membrane, the vertical distribution of Patman molecules was skewed toward shallower depths after TG treatment. Second, the “fast” configuration became more polar, presumably reflecting the invasion of water molecules into the membrane (triangles, Panel A). Third, the rate of equilibration slowed for probes in this more polar microenvironment (diamonds, Panel B).
The positioning of Patman in the membrane is probably determined by two factors: the ability to form a salt bridge between its trimethylammonium and the phosphate of a neighboring lipid, and the strength of the interactions between Patman’s 16-carbon chain and the surrounding fatty-acid tails. In the accompanying paper, it was proposed that the “fast” configuration applies to Patman molecules bonded electrostatically to phospholipid heads and the “slow” configuration connotes Patman molecules with weaker interactions with the heads and therefore anchored predominately through the 16-carbon tail [22]. The increase of Patman molecules in the “fast” configuration, then, suggests a weakening of the interactions between the probe’s hydrophobic tail and neighboring lipids with, perhaps, a net movement of the probe toward shallower depths.
It was interesting that only the “fast” configuration experienced a change in polarity after TG treatment. We assume that this polarity increase reflected enhanced water penetration, an assumption that is well supported [28]. If the two configurations represent different depths, then only the shallow configuration was influenced by this additional water penetration. However, fluorescence quenching measurements indicate that the expected difference in depth is less than an angstrom [36], smaller than the size of a water molecule. Thus, if depth is the distinction of the configurations, then the change in polarity must be localized superficially to both depths so that water’s influence on both configurations is long-range. The sub-angstrom distinction between configurations must then rely on the sensitive distance dependency of solvent dipole influences on the fluorophore’s excited state (i.e., d−6), which would produce large changes in solvent effects with small adjustments to probe location.
The slower equilibration of the “fast” (presumably shallower) configuration implies a greater diversity of metastable conformations of Patman relative to the molecules comprising its local microenvironment such that fluctuations among these conformations delays achievement of steady state. The presence of that diversity further suggests a lessening of constraints imposed on the probe by neighboring molecules, allowing greater freedom to sample conformations as equilibrium is approached. This interpretation is also consistent with the idea that the anchoring of Patman’s tail among the phospholipid chains has been weakened.
Taken together, the TMA-DPH and Patman results complement the findings with MC540 and suggest that early events in apoptosis produce a membrane that now possesses three new characteristics. Lipid headgroups are more spaced. The amount and/or depth of water located among the heads has/have increased. Interactions among lipids in the phospholipid tail region are reduced so that molecules such as Patman are less tightly anchored to the deep part of the bilayer and constraints on TMA-DPH motion are lessened.
Based on these interpretations, we are able to explain the increase in phospholipase activity on the molecular level quantitatively. In order for hydrolysis to occur, a single lipid must protrude 1.5 nm from the lipid bilayer up into the active site of sPLA2 adsorbed to the membrane surface [37]. Normally the frequency of such phospholipid protrusions is very low because of the “friction” opposing this movement created by favorable interactions between neighboring fatty acid tails. Hence, healthy cells show minimal susceptibility to hydrolysis by sPLA2. A reduction of these associations between carbon chains, and thus a decrease in that “friction,” will increase the likelihood of a single lipid migrating from the membrane to be cleaved. Here we assume that this reduction in lipid interactions is analogous to the phase transition of artificial membranes, which is known to greatly enhance sPLA2 activity [38–42]. Therefore, data from vesicles were used to estimate the magnitude of energy reduction between neighboring lipids during apoptosis and the consequential change in the density of lipid protrusions. Patman GP and TMA-DPH anisotropy were measured across the main phase transition of vesicles (pure DMPC, DPPC, or DSPC) to obtain the total change in anisotropy or GP in each system. The average change in enthalpy for these phase transitions was used to determine a coefficient relating TMA-DPH and Patman measurements to energy changes (Table 1). Linear regression of the enthalpy and probe fluorescence in Table 1 yielded coefficients of 3.00 × 10−6 TMA-DPH anisotropy units/J and 1.12 × 10−5 Patman GP units/J. These coefficients were then applied to the change in TMA-DPH anisotropy and Patman GP after about 3 h of TG treatment (Figs. 4C and 6B), the time at which the alive and susceptible subpopulation was the largest (Fig. 2B). As shown in Table 2, TMA-DPH and Patman measurements predicted a −1.31 × 10−20 J and −1.38 × 10−20 J change in interaction energy per phospholipid after TG treatment respectively. The change in density of lipid protrusions after TG treatment was calculated from an adaptation of the theory presented by Mouritsen and co-workers [23, 24].
| (6) |
where p(z) is the probability or frequency of protrusions of distance z and y is the energy cost of a protrusion of distance z. Some of the parameters, p(z), p(0) and y, are not known for a cell membrane. However, the proportional change in protrusion frequency (Δp(z)) upon discounting the energy cost due to reduced lipid-lipid interactions can be calculated without explicit knowledge of the basal condition as follows:
| (7) |
where Δyapp is the apparent change in interaction energy estimated from the TMA-DPH or Patman data and z = 1.5 nm. As indicated in Table 2, TMA-DPH and Patman predicted a 50–100-fold increase in the protrusion frequency after 3 h treatment with TG. We note that this analysis assumes that the membrane environments detected by these probes are generally synonymous with those hydrolyzed by sPLA2. The diversity of structure within cell membranes surely implies that the numbers calculated here are averages for the overall system. Our calculations also assume that all of the phospholipids “seen” by TMA-DPH and Patman have experienced similar physical alterations. If this assumption is not true, then a smaller proportion of lipids is experiencing a greater change in protrusion probability than we have estimated here.
Table 1.
Changes in TMA-DPH anisotropy and Patman GP during main phase transitions of DMPC, DPPC, or DSPC vesicles
Table 2.
Change in frequency of lipid protrusions during TG-induced apoptosis
| Δr or ΔGPa | Δyapp (J)b | fold increase in p(z)c | ||
|---|---|---|---|---|
| TMA-DPH | −0.0237 | −1.31 × 10−20 | 99.2 | |
| Patman | −0.0931 | −1.38 × 10−20 | 48.9 | |
The changes in TMA-DPH anisotropy and Patman GP after 3.25 h TG treatment (the time at which the subpopulation of alive and susceptible cells is at a maximum) are from Figs. 4 C and 6 B respectively.
The coefficients calculated from Table 1 were used to determine Δyapp, the apparent change in interaction energy estimated from the TMA-DPH or Patman data.
Calculated according to Eq. 7.
One of the challenges of detailed biophysical studies on simple artificial membranes is applying the results and conclusions to complex biological systems. In this paper, we have demonstrated a combined application involving a membrane-binding enzyme (sPLA2) and two fluorescent membrane probes. In one case, the supporting work with artificial bilayers included thermodynamic analysis relating kinetic and structural data for sPLA2 to create a molecular model relating lipid dynamics (protrusion fluctuations) to enzyme activity [23, 24]. In the other, we assessed the behavior of TMA-DPH and Patman with artificial membranes quantitatively to provide a frame of reference for interpretation of data with cells (Table 1 and Ref. [22]). These quantitative approaches were then used together here to interpret biological phenomena at a level of detail greater than generally achieved in the discipline of cell membrane biology. In particular, this study demonstrates a new level of real time application of fluorescence spectroscopy to bulk samples of living cells.
Highlights.
Reduced membrane order during apoptosis enhances secretory phospholipase A2 activity.
Patman equilibration kinetics differ between healthy cells and apopotic cells.
The probability of a lipid protruding from the membrane increases 100-fold during apoptosis.
Acknowledgements
The authors thank the staff of the Laboratory for Fluorescence Dynamics for providing facilities and guidance in acquiring the two-photon images.
This work was supported by grant GM073997 from the National Institutes of Health.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Wilson HA, Waldrip JB, Nielson KH, Judd AM, Han SK, Cho W, Sims PJ, Bell JD. Mechanisms by which elevated intracellular calcium induces S49 cell membranes to become susceptible to the action of secretory phospholipase A2. J.Biol.Chem. 1999;274:11494–11504. doi: 10.1074/jbc.274.17.11494. [DOI] [PubMed] [Google Scholar]
- 2.Bailey RW, Olson ED, Vu MP, Brueseke TJ, Robertson L, Christensen RE, Parker KH, Judd AM, Bell JD. Relationship between Membrane Physical Properties and Secretory Phospholipase A2 Hydrolysis Kinetics in S49 Cells during Ionophore-Induced Apoptosis. Biophys.J. 2007;93:2350–2362. doi: 10.1529/biophysj.107.104679. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Atsumi G, Murakami M, Tajima M, Shimbara S, Hara N, Kudo I. The perturbed membrane of cells undergoing apoptosis is susceptible to type II secretory phospholipase A2 to liberate arachidonic acid. Biochim.Biophys.Acta. 1997;1349:43–54. doi: 10.1016/s0005-2760(97)00082-9. [DOI] [PubMed] [Google Scholar]
- 4.Nielson KH, Olsen CA, Allred DV, O'Neill KL, Burton GF, Bell JD. Susceptibility of S49 lymphoma cell membranes to hydrolysis by secretory phospholipase A(2) during early phase of apoptosis. Biochim.Biophys.Acta. 2000;1484:163–174. doi: 10.1016/s1388-1981(00)00004-4. [DOI] [PubMed] [Google Scholar]
- 5.Harris FM, Smith SK, Bell JD. Physical properties of erythrocyte ghosts that determine susceptibility to secretory phospholipase A2. J.Biol.Chem. 2001;276:22722–22731. doi: 10.1074/jbc.M010879200. [DOI] [PubMed] [Google Scholar]
- 6.Smith SK, Farnbach AR, Harris FM, Hawes AC, Jackson LR, Judd AM, Vest RS, Sanchez S, Bell JD. Mechanisms by which intracellular calcium induces susceptibility to secretory phospholipase A2 in human erythrocytes. J.Biol.Chem. 2001;276:22732–22741. doi: 10.1074/jbc.M010880200. [DOI] [PubMed] [Google Scholar]
- 7.Best KB, Ohran AJ, Hawes AC, Hazlett TL, Gratton E, Judd AM, Bell JD. Relationship between erythrocyte membrane phase properties and susceptibility to secretory phospholipase A2. Biochemistry. 2002;41:13982–13988. doi: 10.1021/bi026796r. [DOI] [PubMed] [Google Scholar]
- 8.Jensen LB, Burgess NK, Gonda DD, Spencer E, Wilson-Ashworth HA, Driscoll E, Vu MP, Fairbourn JL, Judd AM, Bell JD. Mechanisms governing the level of susceptibility of erythrocyte membranes to secretory phospholipase A2. Biophys.J. 2005;88:2692–2705. doi: 10.1529/biophysj.104.056457. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Bailey RW, Nguyen T, Robertson L, Gibbons E, Nelson J, Christensen RE, Bell JP, Judd AM, Bell JD. Sequence of physical changes to the cell membrane during glucocorticoid-induced apoptosis in S49 lymphoma cells. Biophys.J. 2009;96:2709–2718. doi: 10.1016/j.bpj.2008.12.3925. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Murakami M, Kambe T, Shimbara S, Higashino K, Hanasaki K, Arita H, Horiguchi M, Arita M, Arai H, Inoue K, Kudo I. Different functional aspects of the group II subfamily (Types IIA and V) and type X secretory phospholipase A(2)s in regulating arachidonic acid release and prostaglandin generation. Implications of cyclooxygenase-2 induction and phospholipid scramblase-mediated cellular membrane perturbation. J.Biol.Chem. 1999;274:31435–31444. doi: 10.1074/jbc.274.44.31435. [DOI] [PubMed] [Google Scholar]
- 11.Olson ED, Nelson J, Griffith K, Nguyen T, Streeter M, Wilson-Ashworth HA, Gelb MH, Judd AM, Bell JD. Kinetic evaluation of cell membrane hydrolysis during apoptosis by human isoforms of secretory phospholipase A2. J.Biol.Chem. 2010;285:10993–11002. doi: 10.1074/jbc.M109.070797. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Jain MK, Yu BZ, Kozubek A. Binding of phospholipase A2 to zwitterionic bilayers is promoted by lateral segregation of anionic amphiphiles. Biochim.Biophys.Acta. 1989;980:23–32. doi: 10.1016/0005-2736(89)90195-8. [DOI] [PubMed] [Google Scholar]
- 13.Yu BZ, Poi MJ, Ramagopal UA, Jain R, Ramakumar S, Berg OG, Tsai MD, Sekar K, Jain MK. Structural basis of the anionic interface preference and kcat* activation of pancreatic phospholipase A2. Biochemistry. 2000;39:12312–12323. doi: 10.1021/bi000740k. [DOI] [PubMed] [Google Scholar]
- 14.Scott DL, White SP, Otwinowski Z, Yuan W, Gelb MH, Sigler PB. Interfacial catalysis: the mechanism of phospholipase A2. Science. 1990;250:1541–1546. doi: 10.1126/science.2274785. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Kinkaid AR, Wilton DC. The effect of anions on interfacial binding and activation of secretory phospholipase A2. Biochem.Soc.Trans. 1995;23:556S. doi: 10.1042/bst023556s. [DOI] [PubMed] [Google Scholar]
- 16.Diraviyam K, Murray D. Computational analysis of the membrane association of group IIA secreted phospholipases A2: a differential role for electrostatics. Biochemistry. 2006;45:2584–2598. doi: 10.1021/bi051901t. [DOI] [PubMed] [Google Scholar]
- 17.Bezzine S, Bollinger JG, Singer AG, Veatch SL, Keller SL, Gelb MH. On the binding preference of human groups IIA and X phospholipases A2 for membranes with anionic phospholipids. J.Biol.Chem. 2002;277:48523–48534. doi: 10.1074/jbc.M203137200. [DOI] [PubMed] [Google Scholar]
- 18.Nelson J, Gibbons E, Pickett KR, Streeter M, Warcup AO, Yeung CH, Judd AM, Bell JD. Relationship between membrane permeability and specificity of human secretory phospholipase A(2) isoforms during cell death. Biochim.Biophys.Acta. 2011;1808:1913–1920. doi: 10.1016/j.bbamem.2011.04.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Williams RM, Webb WW. Single granule pH cycling in antigen-induced mast cell secretion. Journal of cell science. 2000;113(Pt 21):3839–3850. doi: 10.1242/jcs.113.21.3839. [DOI] [PubMed] [Google Scholar]
- 20.Zipfel WR, Williams RM, Webb WW. Nonlinear magic: multiphoton microscopy in the biosciences. Nat.Biotechnol. 2003;21:1369–1377. doi: 10.1038/nbt899. [DOI] [PubMed] [Google Scholar]
- 21.Kuhry JG, Fonteneau P, Duportail G, Maechling C, Laustriat G. TMA-DPH: a suitable fluorescence polarization probe for specific plasma membrane fluidity studies in intact living cells. Cell Biophys. 1983;5:129–140. doi: 10.1007/BF02796139. [DOI] [PubMed] [Google Scholar]
- 22.H.S. Franchino E, Nelson J, Bell TA, Bell JD. Wavelength dependence of patman equilibration dynamics in phosphatidylcholine bilayers. Biochim.Biophys.Acta. doi: 10.1016/j.bbamem.2012.08.025. (submitted) [DOI] [PubMed] [Google Scholar]
- 23.Hoyrup P, Callisen TH, Jensen MO, Halperin A, Mouritsen OG. Lipid protrusions, membrane softness, and enzymatic activity. Phys.Chem.Chem.Phys. 2004;6:1608–1615. [Google Scholar]
- 24.Halperin A, Mouritsen OG. Role of lipid protrusions in the function of interfacial enzymes. Eur.Biophys.J. 2005;34:967–971. doi: 10.1007/s00249-005-0466-z. [DOI] [PubMed] [Google Scholar]
- 25.Maraganore JM, Merutka G, Cho W, Welches W, Kezdy FJ, Heinrikson RL. A new class of phospholipases A2 with lysine in place of aspartate 49. Functional consequences for calcium and substrate binding. J.Biol.Chem. 1984;259:13839–13843. [PubMed] [Google Scholar]
- 26.Wilson HA, Huang W, Waldrip JB, Judd AM, Vernon LP, Bell JD. Mechanisms by which thionin induces susceptibility of S49 cell membranes to extracellular phospholipase A2. Biochim.Biophys.Acta. 1997;1349:142–156. doi: 10.1016/s0005-2760(97)00089-1. [DOI] [PubMed] [Google Scholar]
- 27.Richieri GV, Kleinfeld AM. Continuous measurement of phospholipase A2 activity using the fluorescent probe ADIFAB. Anal.Biochem. 1995;229:256–263. doi: 10.1006/abio.1995.1410. [DOI] [PubMed] [Google Scholar]
- 28.Parasassi T, De Stasio G, Ravagnan G, Rusch RM, Gratton E. Quantitation of lipid phases in phospholipid vesicles by the generalized polarization of Laurdan fluorescence. Biophys.J. 1991;60:179–189. doi: 10.1016/S0006-3495(91)82041-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Riccardi C, Nicoletti I. Analysis of apoptosis by propidium iodide staining and flow cytometry. Nat.Protoc. 2006;1:1458–1461. doi: 10.1038/nprot.2006.238. [DOI] [PubMed] [Google Scholar]
- 30.Lakowicz JR, Bevan DR, Maliwal BP, Cherek H, Balter A. Synthesis and characterization of a fluorescence probe of the phase transition and dynamic properties of membranes. Biochemistry. 1983;22:5714–5722. doi: 10.1021/bi00294a006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Williamson P, Mattocks K, Schlegel RA. Merocyanine 540, a fluorescent probe sensitive to lipid packing. Biochim.Biophys.Acta. 1983;732:387–393. doi: 10.1016/0005-2736(83)90055-x. [DOI] [PubMed] [Google Scholar]
- 32.Dale RE, Chen LA, Brand L. Rotational relaxation of the "microviscosity" probe diphenylhexatriene in paraffin oil and egg lecithin vesicles. J.Biol.Chem. 1977;252:7500–7510. [PubMed] [Google Scholar]
- 33.Veatch WR, Stryer L. Effect of cholesterol on the rotational mobility of diphenylhexatriene in liposomes: a nanosecond fluorescence anisotrophy study. J.Mol.Biol. 1977;117:1109–1113. doi: 10.1016/s0022-2836(77)80017-x. [DOI] [PubMed] [Google Scholar]
- 34.Harris FM, Best KB, Bell JD. Use of laurdan fluorescence intensity and polarization to distinguish between changes in membrane fluidity and phospholipid order. Biochim.Biophys.Acta. 2002;1565:123–128. doi: 10.1016/s0005-2736(02)00514-x. [DOI] [PubMed] [Google Scholar]
- 35.Parisio G, Marini A, Biancardi A, Ferrarini A, Mennucci B. Polarity-sensitive fluorescent probes in lipid bilayers: bridging spectroscopic behavior and microenvironment properties. J.Phys.Chem.B. 2011;115:9980–9989. doi: 10.1021/jp205163w. [DOI] [PubMed] [Google Scholar]
- 36.Jurkiewicz P, Olzynska A, Langner M, Hof M. Headgroup hydration and mobility of DOTAP/DOPC bilayers: a fluorescence solvent relaxation study. Langmuir. 2006;22:8741–8749. doi: 10.1021/la061597k. [DOI] [PubMed] [Google Scholar]
- 37.Berg OG, Gelb MH, Tsai MD, Jain MK. Interfacial enzymology: the secreted phospholipase A(2)-paradigm. Chemical reviews. 2001;101:2613–2654. doi: 10.1021/cr990139w. [DOI] [PubMed] [Google Scholar]
- 38.Bell JD, Biltonen RL. The temporal sequence of events in the activation of phospholipase A2 by lipid vesicles. Studies with the monomeric enzyme from Agkistrodon piscivorus piscivorus. J.Biol.Chem. 1989;264:12194–12200. [PubMed] [Google Scholar]
- 39.Lichtenberg D, Romero G, Menashe M, Biltonen RL. Hydrolysis of dipalmitoylphosphatidylcholine large unilamellar vesicles by porcine pancreatic phospholipase A2. J.Biol.Chem. 1986;261:5334–5340. [PubMed] [Google Scholar]
- 40.Menashe M, Lichtenberg D, Gutierrez-Merino C, Biltonen RL. Relationship between the activity of pancreatic phospholipase A2 and the physical state of the phospholipid substrate. J.Biol.Chem. 1981;256:4541–4543. [PubMed] [Google Scholar]
- 41.Honger T, Jorgensen K, Biltonen RL, Mouritsen OG. Systematic relationship between phospholipase A2 activity and dynamic lipid bilayer microheterogeneity. Biochemistry. 1996;35:9003–9006. doi: 10.1021/bi960866a. [DOI] [PubMed] [Google Scholar]
- 42.Bell JD, Baker ML, Bent ED, Ashton RW, Hemming DJ, Hansen LD. Effects of temperature and glycerides on the enhancement of Agkistrodon piscivorus piscivorus phospholipase A2 activity by lysolecithin and palmitic acid. Biochemistry. 1995;34:11551–11560. doi: 10.1021/bi00036a031. [DOI] [PubMed] [Google Scholar]
- 43.Caffrey M. Lipidat: A database of thermodynamic data and associated information on lipid mesomorphic and polymorphic transitions. Boca Raton: CRC Press, Inc.; 1993. [Google Scholar]
- 44.Pozarowski P, Huang X, Halicka DH, Lee B, Johnson G, Darzynkiewicz Z. Interactions of fluorochrome-labeled caspase inhibitors with apoptotic cells: a caution in data interpretation. Cytometry A. 2003;55:50–60. doi: 10.1002/cyto.a.10074. [DOI] [PubMed] [Google Scholar]