Abstract
Rodents are commonly used as test subjects in research on traumatic brain injury and stroke. However, study of rat cerebral vessel properties has largely been limited to pressure-diameter response within the physiological loading range. A more complete, multiaxial description is needed to guide experiments on rats and rat vessels and to appropriately translate findings to humans. Accordingly, we dissected twelve rat middle cerebral arteries (MCAs) and subjected them to combined inflation and axial stretch tests around physiological loading conditions while in a passive state. The MCAs were finally stretched axially to failure. Results showed that MCAs under physiological conditions were stiffer in the axial than circumferential direction by a mean (± standard deviation) factor of 1.72 (± 0.73), similar to previously reported behavior of human cerebral arteries. However, the stiffness for both directions was lower in rat MCA than in human cerebral arteries (p<0.01). Failure stretch values were higher in rat MCA (1.35 ± 0.08) than in human vessels (1.24 ± 0.09) (p=0.003), but corresponding 1st Piola Kirchhoff stress values for rats (0.42 ± 0.09 MPa) were considerably lower than those for humans (3.29 ± 0.64 MPa) (p<0.001). These differences between human and rat vessel properties should be considered in rat models of human cerebrovascular injury and disease.
Keywords: traumatic brain injury, rat cerebral arteries, passive biaxial mechanical properties
INTRODUCTION
Disruption of cerebral blood vessel function leads to stroke and is a common outcome of traumatic brain injury (TBI). In the United States, 52,000 deaths result from over 1.7 million cases of TBI annually (Faul et al., 2010); the number of deaths is over 140,000 per year for stroke (Lloyd-Jones et al., 2010). Total annual costs associated with TBI and stroke have been estimated at 60 (Faul et al., 2010) and 65.5 (Rosamond et al., 2008) billion dollars, respectively.
Efforts to better prevent and treat cerebrovascular injury and disease are, in part, dependent upon a more complete understanding of vessel mechanics. This includes definition of blood vessel injury thresholds as well as characterization of relationships between applied forces and vessel function. Experiments on human cerebral vessels have revealed some characteristics of these tissues (Busby and Burton, 1965; Hayashi et al., 1980; Monson et al., 2008; Scott et al., 1972), but the limited availability of human specimens is a barrier to additional research.
Rodents are commonly used as models for both TBI and stroke (Coulson et al., 2002; Coulson et al., 2004; Gonzalez et al., 2005; Hajdu and Baumbach, 1994; Hogestatt et al., 1983). Rodent cerebral vessels have also been studied in isolation, but the mechanical properties of these vessels have not been fully characterized. Emphasis has mainly been on circumferential behavior within the physiological loading range (Coulson et al., 2002; Coulson et al., 2004; Hajdu and Baumbach, 1994). A more complete definition of these properties is an important step toward addressing questions more specific to cerebral vessel injury and disease. Accordingly, the aim of this research was to define the biaxial and failure properties of passive rat middle cerebral arteries (MCAs) and to compare these characteristics to those of previously studied human cerebral vessels.
METHODS
Vessel Dissection and Cannulation
The MCA was dissected from 12 male Sprague Dawley rats (389 ± 41 grams). All procedures met requirements established by the Institutional Animal Use and Care Committee at the University of Utah. Rats were anesthetized with isoflurane and exsanguinated via cardiac perfusion using Hank’s Buffered Saline Solution (HBSS; KCl 5.37, KH2PO4 0.44, NaCl 136.9, Na2HPO4 0.34, D-Glucose 5.55, NaHC03 4.17; concentrations in mM), followed by a 1% nigrosin dye (Sigma-Aldrich, St. Louis, MO) HBSS solution. The dye enhanced visibility of the artery and its branches during dissection. MCA side branches were ligated with individual fibrils from unwound 6-0 silk suture, and the vessel was cannulated with glass tip needles and secured with 6-0 silk suture and cyanoacrylate glue. Lack of calcium in the HBSS ensured a passive response.
Experimental Apparatus and Methodology
Mechanical testing methodology was similar to that described previously (Monson et al., 2008). Briefly, the needles on which the MCA were mounted, and the associated fixtures, were attached to a custom vertical linear stage (Parker Automation, Cleveland, OH). The upper fixture was suspended from a 250 gram capacity load cell (Model 31 Low, Honeywell, Golden Valley, MN) through an X-Y stage (MS-125-XY, Newport, Irvine, CA) that allowed for correction of any needle misalignment. The lower fixture was mounted to the stage via a vertical, low friction sled supported by a voice coil actuator (MGV52-25-1.0, Akribis, Singapore). Displacement of this actuator moved the lower fixture vertically along the sled track, axially stretching the MCA. A narrow, glass water bath, filled with HBSS and surrounding the MCA and needles, was attached to the lower fixture. Specimens were viewed via a digital video camera (PL-A641, Pixelink, Ottawa, Canada) equipped with a zoom lens (VZM 450i, Edmund Optics, Barrington, NJ). Vessels were perfused with HBSS originating from a syringe attached to a computer-controlled linear actuator (D-A0.25-AB-HT17075-4-P, Ultra Motion, Cutchogue, NY) and passing through the lower fixture, the mounted MCA, and the upper fixture. Pressure was determined by averaging the signals of pressure transducers (26PCDFM6G, Honeywell, Golden Valley, MN) located at each end of the vessel. Test control, as well as data and video acquisition, were accomplished using a custom LabVIEW program (National Instruments, Austin, TX). Actuator positions were given by digital encoders (resolution 1.0 μm).
Following mounting of the MCA, it was preconditioned by oscillating the luminal pressure (6.7–20 kPa; 50–150 mmHg) for five cycles while length was held constant at various sub-failure axial stretch values up to λz ≈ 1.2. The zero-load length (corresponding with λz = 1.0) of each MCA was then estimated as that length where the measured axial load began to increase during an unpressurized (0.25 kPa to maintain an open lumen) axial stretch test. This was followed by a series of six sub-failure, quasi-static, biaxial sequences, consisting of three inflation tests at constant axial stretch (λz ≈ 1.1, 1.15, 1.2) and three axial stretch tests at constant luminal pressure (20, 13.3, and 6.7 kPa). Finally, the vessel was stretched axially to failure, at a pressure of 13.3 kPa, to study deformations relevant to TBI.
Data Analysis
Data from the encoders, load cell, and pressure transducers were recorded at 100 Hz. Noise observed in the load cell readings was smoothed using the SAE J211 filter (SAE, 1995). Images were acquired at 3 Hz, and current outer diameter (de) was measured via image analysis software (Vision Assistant; National Instruments, Austin, TX). Similarly, the reference diameter (De) was measured from an image taken from the zero load length test at λz = 1.0. Since images were obtained at a lower rate than the other signals, additional diameter data were defined using interpolation to allow one-to-one correspondence. Following the method defined by Wicker et al. (Wicker et al., 2008), wall volume was determined at six different configurations (each combination of λz ≈ 1.1, 1.15, 1.2 and pressure pi = 0.25,10.6 kPa) by measuring inner diameter (di), de, and vessel length (l) in the images and calculating the associated wall volume of a tube. The average wall volume (V), along with the incompressibility assumption, was used to calculate di from the measured de in subsequent analysis, including the reference inner diameter (Di) from De (Eq. 1).
| (1) |
Vessels were assumed to be homogeneous circular cylinders, with mid-wall stretch defined by Eqs. 2
| (2a) |
| (2b) |
where the subscripts θ and z refer to the local cylindrical coordinates in the circumferential and axial directions respectively. Enforcing equilibrium in the two directions results in the mean Cauchy stresses defined in Eqs. 3
| (3a) |
| (3b) |
where Fz represents the experimental axial force. Residual stresses were not considered due to large variations in measured opening angle.
As a first step in characterizing response in the axial and circumferential directions, stress–stretch data around approximate in vivo conditions were examined. Axial in vivo length was determined for each sample by observing the pressure-axial force response during preconditioning tests (Van Loon, 1977). Circumferential in vivo stiffness was defined as the slope of the stress-stretch curve in the inflation test with an axial stretch value closest to the axial in vivo stretch. An exponential function was fit through the data around the point corresponding to a pressure of 13.3 kPa (100 mmHg), and the value of the function’s derivative at 13 kPa was taken as circumferential stiffness. Axial in vivo stiffness was defined in a similar manner from the axial stretch test conducted at a luminal pressure of 13.3 kPa, with the location where stiffness was calculated corresponding to the in vivo length. Note that stiffness is used here as a measure of the resistance of the vessel structure to deformation, rather than as an intrinsic tissue property.
A hyperelastic constitutive model, based on a phenomenological approach, was additionally applied to parameterize the biaxial response of the vessels based on the data from inflation tests. Data from axial stretch tests were not included since they resulted in slight unloading in the circumferential direction during axial stretch, inconsistent with requirements of pseudoelasticity (Humphrey et al., 1990). We applied the Fung-type strain energy function with the zero-load state as the reference configuration shown in Eq. 4 (Fung, 1993)
| (4) |
where , W represents the strain energy per unit mass of the material, Eθθ and Ezz refer to the Green strains in the circumferential and axial directions, and c (units kPa), c1, c2 and c3 are material parameters. Shear strains were ignored owing to the axisymmetric loading conditions and observed response. Incompressibility was enforced directly (Humphrey, 2002). The associated mean Cauchy stress values are shown in Eq. 5
| (5a) |
| (5b) |
where tθθ and tzz correspond to the theoretical Cauchy stress values in the circumferential and axial directions respectively. Radial stresses were assumed to be small based on findings from our previous work on human arteries (Monson et al., 2008). Mean values of tθθ and tzz were calculated for comparison to experimentally derived stresses (Eq. 3). Material parameters c, c1, c2 and c3 that best fit the experimental data were computed by employing a nonlinear regression routine (fminsearch) in MATLAB (Mathworks, Natick, MA) to minimize the objective function f (Eq. 8)
| (8) |
where N represents the total number of data points, and the stresses are defined in Eqs. 3, and 5. Previously collected data from human cerebral arteries were similarly fit for comparison.
Two-tailed, unpaired t-tests were used to determine the significance of any differences between determined values, with p < 0.01 indicating statistical significance.
RESULTS
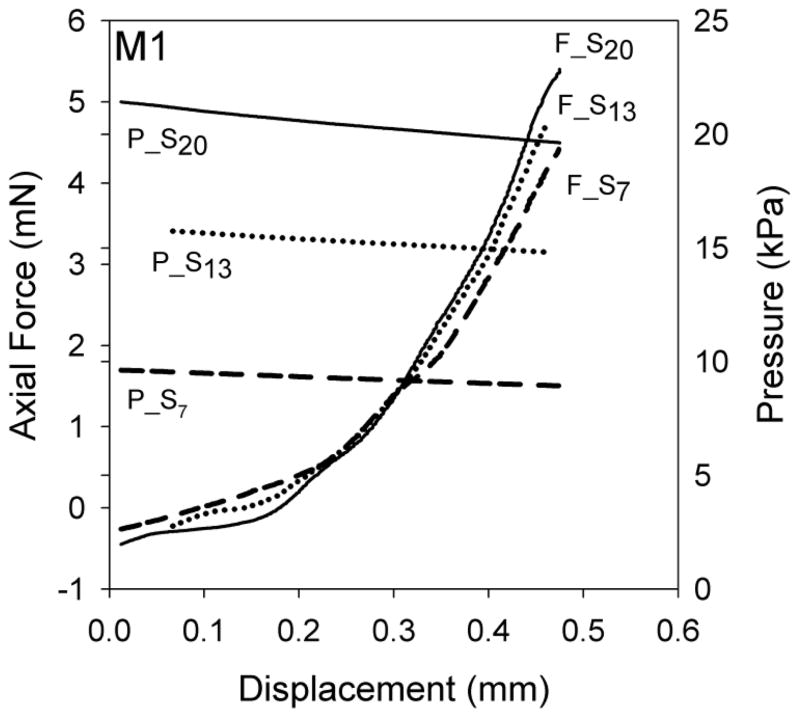
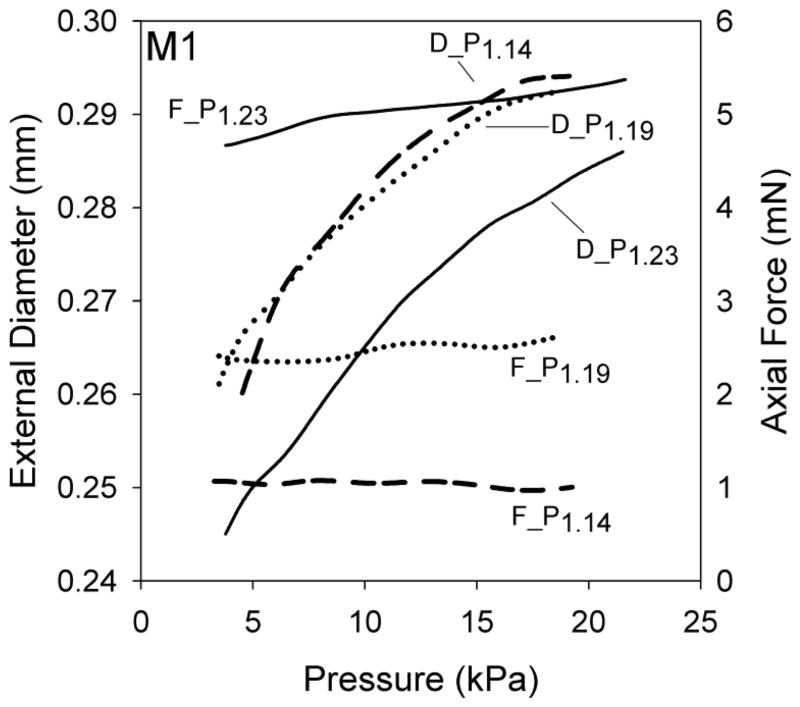
Twelve arteries were successfully tested. Mean (± standard deviation) unloaded outer diameter and length of these specimens were 0.25 (± 0.02) mm and 2.11 (± 0.51) mm respectively. Typical response is shown in Figures 1 and 2 and is qualitatively similar to what we have previously reported for biaxial behavior of human cerebral arteries.
Figure 1.
Axial force (F_Sm) and luminal pressure (P_Sm) for a representative MCA sample (M1) during axial stretch tests. Label subscript m indicates the approximate luminal pressure for these axial stretch tests.
Figure 2.
Outer diameter (D_Pn) and axial force (F_Pn) responses for a representative MCA sample (M1) during inflation tests. Label subscript n indicates the axial stretch for these inflation tests.
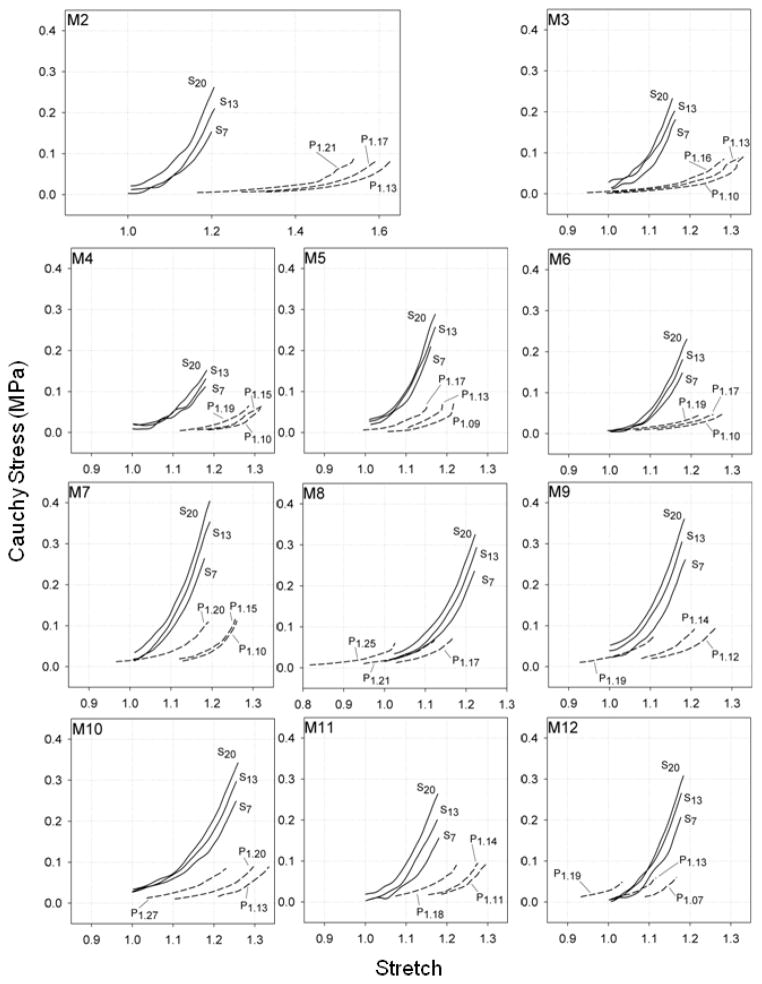
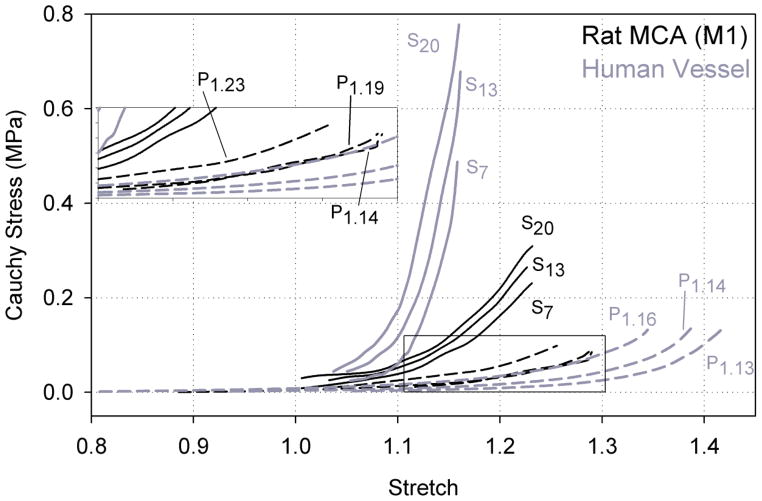
Rat MCA in vivo stretch was 1.10 (± 0.03) and 1.27 (± 0.11) for the axial and circumferential directions, respectively. At these stretch levels, axial stiffness was 1.14 (± 0.37) MPa and circumferential stiffness was 0.73 (± 0.29) MPa (p=0.006), resulting in a ratio of 1.72 (± 0.73) between the two directions; the ratio ranged from 1.05 (M5, Fig. 4) to 3.30 (M6, Fig. 4). For clarity, the rat data used to determine the axial and circumferential in vivo stiffnesses are identified as S13 and the inflation test having the lowest value of axial stretch, respectively, in Figures 3 and 4. The inflation test having the lowest value of axial stretch was selected as it was consistently closest to the in vivo stretch. However, in most cases it was not exactly at the in vivo axial stretch since this value could only be precisely determined during post-processing.
Figure 4.
Cauchy stress-stretch response curves for remaining rat MCAs in the axial (Sm) and circumferential (Pn) directions. Label subscript m indicates the luminal pressure during axial stretch tests while subscript n indicates the axial stretch during inflation tests.
Figure 3.
Cauchy stress-stretch response curves for representative rat MCA (M1) and human cerebral artery (Monson et al., 2008) samples in the axial (Sm) and circumferential (Pn) directions. Label subscript m indicates the luminal pressure during axial stretch tests while subscript n indicates the axial stretch during inflation tests.
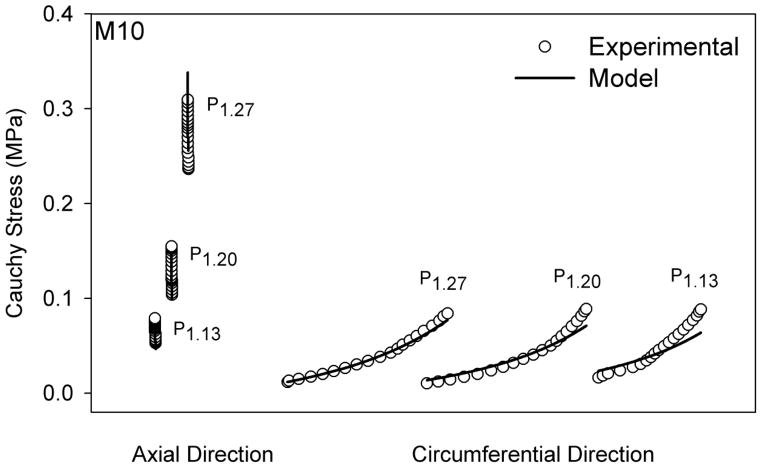
The Fung-type constitutive model fit the rat MCA data well, as shown for a representative data set in Figure 5. Further, best-fit material parameters showed that c2 was consistently larger than c1 (p < 0.001) (Table 1). These best fit parameters, along with the in vivo stiffness measurements, indicate that the mechanical behavior in the axial direction was consistently stiffer than in the circumferential direction in the rat MCA. Requirements imposed by energy conservation for orthotropic symmetry (c1, c2, c3 > 0 and ) were met by the determined material parameters (excepting M2 and M4) (Holzapfel et al., 2000); it is unclear why c3 was negative for M2 and M4.
Figure 5.
Experimental and predicted axial and circumferential stress values from inflation tests only (Pn) for a representative rat MCA (M10). M10 was selected here since it has a fit parameter closest to that of the mean fit for all the samples, without violating the pseudoelasticity assumption. Predicted values are derived from best-fit parameters from the Fung-type constitutive model. Label subscript n indicates the axial stretch during inflation tests. Datasets having the same label are from the same test.
Table 1.
Rat MCA best-fit material parameters computed for inflation tests (Eq. 4), with mean and standard deviation shown for each. Corresponding summary of human cerebral artery inflation tests also shown (Monson et al., 2008).
| Sample No. | Rat MCAs Fung-type Material Parameters | ||||
|---|---|---|---|---|---|
| c (kPa) | c1 | c2 | c3 | f | |
| M1 | 14.98 | 1.87 | 12.60 | 1.56 | 5.74 |
| M2 | 5.95 | 1.34 | 25.33 | −0.55 | 3.00 |
| M3 | 8.79 | 3.46 | 27.47 | 1.44 | 1.62 |
| M4 | 6.58 | 4.37 | 25.29 | −1.65 | 5.67 |
| M5 | 4.94 | 8.71 | 40.78 | 0.85 | 5.75 |
| M6 | 12.71 | 3.06 | 18.08 | 0.75 | 1.34 |
| M7 | 21.13 | 3.02 | 19.30 | 1.22 | 4.21 |
| M8 | 13.32 | 3.93 | 16.93 | 2.86 | 1.43 |
| M9 | 6.26 | 5.85 | 33.95 | 4.23 | 1.28 |
| M10 | 13.19 | 3.12 | 12.47 | 0.48 | 2.14 |
| M11 | 3.59 | 8.58 | 37.39 | 0.14 | 0.63 |
| M12 | 5.59 | 12.25 | 37.03 | 6.16 | 1.97 |
| Summary | |||||
| Mean | 9.75 | 4.96 | 25.55 | 1.46 | 2.90 |
| Std. Dev. | 5.28 | 3.28 | 9.94 | 2.11 | 1.93 |
|
| |||||
| Human Cerebral Arteries Summary | |||||
| Mean | 2.88 | 5.14 | 179.29 | 2.66 | 19.17 |
| Std. Dev. | 2.63 | 3.35 | 199.63 | 14.59 | 18.20 |
The responses of rat MCA and human cerebral arteries were qualitatively similar. The ratio of in vivo stiffness values, with means (± standard deviation) 1.72 (± 0.73) for rat MCA and 1.87 (± 0.84) from human pial arteries (Monson et al., 2008), were not statistically different (p=0.67), indicating that the difference between the stiffness in the axial and circumferential directions in the rat MCA (Fig. 3) is proportional to the difference in human pial arteries. However, the magnitude of the in vivo stiffness was lower for both directions in rat MCAs compared to human cerebral arteries, with axial stiffnesses of 1.1 (± 0.4) and 2.9 (± 1.4) MPa for rat and human arteries, respectively (p=0.005), and circumferential stiffnesses of 0.7 (± 0.3) and 1.6 (± 0.5) MPa for the two tissues (p<0.001) (Fig. 3). This trend is also supported by best fit values for c1 and c2 reported in Table 1, but since the fit of the Fung-type model was poor for the human cerebral arteries, a statistical comparison of these fitted parameters between the vessel types was not considered to be meaningful. Additionally, the mean axial in vivo stretch for the rat MCAs, 1.10 (± 0.03), was larger than that for human arteries, 1.07 (± 0.04). This difference approached statistical significance (p=0.04) but was above our threshold of p<0.01. The circumferential in vivo stretch was not statistically different between rat MCAs, 1.27 (± 0.11), and human arteries, 1.33 (± 0.17) (p=0.37).
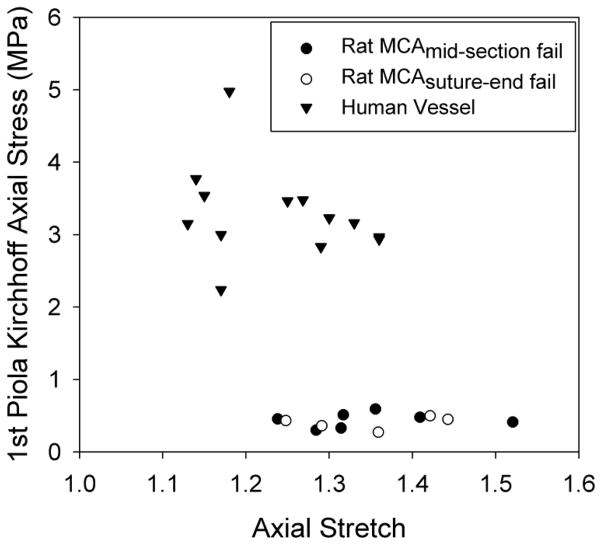
Failure values for the twelve tested MCA samples, along with those from human cerebral arteries tested in our laboratory, are plotted in Figure 6. For rat MCAs, the mean axial stretch at failure was 1.35 (± 0.08) and the corresponding axial 1st Piola-Kirchhoff stress ( Fz/A) was 0.42 (± 0.09) MPa. These two values for human vessels were 1.24 (± 0.09) and 3.29 (± 0.64) MPa, respectively, indicating that the rat MCAs had a lower failure stress (p<0.001) but a higher failure stretch (p=0.003) as compared to human cerebral arteries. Five rat vessels failed near a suture tie-off, while seven failed in mid-section. Failure values were not a function of failure location (p>0.50) (Fig. 6). Stress values are reported in 1st Piola-Kirchhoff form because the incompressibility assumption commonly yielded a complex number for inner diameter in the current configuration, suggesting that large vessel deformations are not isochoric.
Figure 6.
1st Piola-Kirchhoff ultimate failure stress-stretch values for rat MCAs and human cerebral vessels.
DISCUSSION
The present study aimed to characterize the biaxial mechanical properties of passive rat MCAs and to compare them to those of human cerebral arteries. Qualitatively, rat MCA response was similar to that of the human vessels. Stiffness around the in vivo configuration was also found to be higher axially than circumferentially, as in human arteries, but the human vessels were stiffer in both directions compared to rat arteries. Additionally, failure stretch values were slightly higher and failure stresses were considerably lower for rat arteries. These similarities and differences should be considered in the translation of knowledge gained from rat models of TBI and stroke to the human system.
Based on the observed rat MCA stress-stretch response and the corresponding material parameter values, it is clear that axial and circumferential responses are statistically different. This agrees with our previous work showing that behavior is considerably stiffer axially than circumferentially in human cerebral arteries (Monson et al., 2008). Reasons for the observed differences between rat and human arteries are unknown, but it is important to note that rat data were obtained from MCAs while human data were collected from pial arteries on the surface of the temporal lobe, two different locations in the cerebral circulation. Our previous work comparing these two sites in humans (Monson et al., 2005) indicated that differences between them were not significant, but any similarity between rat MCA and pial artery is currently undefined. Dissimilarities in the general structure of rat and human cerebral arteries may also contribute to the observed differences (Lee, 1995) and should be further investigated through histological studies.
It is interesting to note the good quality of fit obtained here for the rat MCAs using the Fung-type strain energy function, in contrast to our previous efforts to fit this function to human data (Monson et al., 2008). It should be emphasized that the function was here fitted to data from inflation tests only, whereas the previous effort also included data from axial stretch tests. Initial efforts to fit Eq. 4 to the rat MCA data included results from both types of test, and the quality of that combined fit was also poor, consistent with our previous experience. This was also the case for a more complex, microstructure-based strain energy function (Baek et al., 2007; Wagner and Humphrey, 2011; Wicker et al., 2008) that we initially fitted to both the human and rat MCA data. This more complex model did not provide a substantial increase in the quality of fit to either data set so its performance is not reported here. The decision to limit the data used for fitting was based on the recognition that the circumferential direction unloads slightly during axial stretch tests, inconsistent with requirements of pseudoelasticity (Humphrey et al., 1990). Despite the use of this limited data set, it is interesting that the resulting fit of the human data was still poor.
The primary challenge with conducting the current experiments, relative to previous work on human vessels, was the small size of the specimens, and errors related to size could lead to some of the differences observed here. Forces measured were not far above the specified error of the load cell in some tests, but results for axial stretch tests at different pressures were discernible from one another and were consistent with the multi-axial behavior observed in other vessels. Also, filtered force traces were always compared to raw data to ensure fidelity.
Despite the significance of the stress-strain relationship in cerebrovascular mechanics, previous studies on rat cerebral vessels have mostly focused on analyzing the pressure-diameter response for different purposes (Coulson et al., 2002; Coulson et al., 2004; Hajdu and Baumbach, 1994). Coulson et al. have examined the rat MCA mechanical behavior in both a myogenically active state and a drug-induced passive state, but they limited their study to uniaxial circumferential testing only (Coulson et al., 2004). Our circumferential findings compare well with theirs, i.e. the pressure-diameter relationship is non-linear and lies within a similar range. Apart from that, other related studies have either examined rat cerebral arteries in a different state or have focused on a different aspect. As far as we know, no researchers have conducted multiaxial testing and analysis of rat middle cerebral arteries.
While our findings shed light on the mechanical behavior of rat cerebral arteries and their relationship to those of human cerebral arteries, further work is needed to more completely define both types of vessels. In particular, the use of the zero-load state as the reference configuration ignores contributions from residual stresses (Chuong and Fung, 1986). Further investigation including through-wall stress distribution is needed to better identify conditions associated with disease development and injury, and should utilize the zero-stress state as reference. Future work should also address the multiple layers present in any vessel and how specific components of these layers are loaded, especially during injury. Based on preliminary fits of the current data to more advanced models that incorporate arterial microstructure (Baek et al., 2007; Holzapfel et al., 2000; Wagner and Humphrey, 2011; Wicker et al., 2008), the more complex functions do not currently provide substantial fitting advantages over the simpler Fung-type model, but functions that accurately simulate microstructure have intrinsically greater potential to capture the complex behavior of these tissues and should continue to be developed. Additionally, cerebral artery response varies with smooth muscle tone (Coulson et al., 2004; Wagner and Humphrey, 2011), and our study focused only on passive properties. The nature of this contribution needs further attention, as do other questions related to tethering (Steelman et al., 2010) and the influence of fluid flow, in order to more completely define cerebrovasculature function in health and disease.
Acknowledgments
This work was supported by grants from the National Institutes of Health (5K25HD048643) and the Department of Defense (W81XWH-08-1-0295).
Footnotes
CONFLICT OF INTEREST STATEMENT
The authors have no conflict of interest.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Baek S, Gleason RL, Rajagopal KR, Humphrey JD. Theory of small on large: Potential utility in computations of fluid-solid interactions in arteries. Computer Methods in Applied Mechanics and Engineering. 2007;196:3070–3078. [Google Scholar]
- Busby DE, Burton AC. The Effect of Age on the Elasticity of the Major Brain Arteries. Can J Physiol Pharmacol. 1965;43:185–202. doi: 10.1139/y65-018. [DOI] [PubMed] [Google Scholar]
- Chuong CJ, Fung YC. On residual stresses in arteries. J Biomech Eng. 1986;108:189–192. doi: 10.1115/1.3138600. [DOI] [PubMed] [Google Scholar]
- Coulson RJ, Chesler NC, Vitullo L, Cipolla MJ. Effects of ischemia and myogenic activity on active and passive mechanical properties of rat cerebral arteries. Am J Physiol Heart Circ Physiol. 2002;283:H2268–2275. doi: 10.1152/ajpheart.00542.2002. [DOI] [PubMed] [Google Scholar]
- Coulson RJ, Cipolla MJ, Vitullo L, Chesler NC. Mechanical properties of rat middle cerebral arteries with and without myogenic tone. J Biomech Eng. 2004;126:76–81. doi: 10.1115/1.1645525. [DOI] [PubMed] [Google Scholar]
- Faul M, Xu L, Wald MM, Coronado VG. Traumatic Brain Injury in the United States: Emergency Department Visits, Hospitalizations and Deaths 2002–2006. Centers for Disease Control and Prevention, National Center for Injury Prevention and Control; Atlanta, GA: 2010. [Google Scholar]
- Fung YC. Biomechanics: Mechanical Properties of Living Tissues. 2. Springer; New York: 1993. [Google Scholar]
- Gonzalez JM, Briones AM, Starcher B, Conde MV, Somoza B, Daly C, Vila E, McGrath I, Gonzalez MC, Arribas SM. Influence of elastin on rat small artery mechanical properties. Exp Physiol. 2005;90:463–468. doi: 10.1113/expphysiol.2005.030056. [DOI] [PubMed] [Google Scholar]
- Hajdu MA, Baumbach GL. Mechanics of large and small cerebral arteries in chronic hypertension. Am J Physiol. 1994;266:H1027–1033. doi: 10.1152/ajpheart.1994.266.3.H1027. [DOI] [PubMed] [Google Scholar]
- Hayashi K, Nagasawa S, Naruo Y, Okumura A, Moritake K, Handa H. Mechanical properties of human cerebral arteries. Biorheology. 1980;17:211–218. [PubMed] [Google Scholar]
- Hogestatt ED, Andersson KE, Edvinsson L. Mechanical properties of rat cerebral arteries as studied by a sensitive device for recording of mechanical activity in isolated small blood vessels. Acta Physiol Scand. 1983;117:49–61. doi: 10.1111/j.1748-1716.1983.tb07178.x. [DOI] [PubMed] [Google Scholar]
- Holzapfel G, Gasser T, Ogden R. A New Constitutive Framework for Arterial Wall Mechanics and a Comparative Study of Material Models. Journal of Elasticity. 2000;61:1–48. [Google Scholar]
- Humphrey JD. Cardiovascular Solid Mechanics: Cells, Tissues, and Organs. Springer; New York: 2002. [Google Scholar]
- Humphrey JD, Strumpf RK, Yin FC. Determination of a constitutive relation for passive myocardium: II. Parameter estimation. J Biomech Eng. 1990;112:340–346. doi: 10.1115/1.2891194. [DOI] [PubMed] [Google Scholar]
- Lee RM. Morphology of cerebral arteries. Pharmacology & Therapeutics. 1995;66:149–173. doi: 10.1016/0163-7258(94)00071-a. [DOI] [PubMed] [Google Scholar]
- Lloyd-Jones D, Adams RJ, Brown TM, Carnethon M, Dai S, De Simone G, Ferguson TB, Ford E, Furie K, Gillespie C, Go A, Greenlund K, Haase N, Hailpern S, Ho PM, Howard V, Kissela B, Kittner S, Lackland D, Lisabeth L, Marelli A, McDermott MM, Meigs J, Mozaffarian D, Mussolino M, Nichol G, Roger VL, Rosamond W, Sacco R, Sorlie P, Roger VL, Thom T, Wasserthiel-Smoller S, Wong ND, Wylie-Rosett J. Heart disease and stroke statistics--2010 update: a report from the American Heart Association. Circulation. 2010;121:e46–e215. doi: 10.1161/CIRCULATIONAHA.109.192667. [DOI] [PubMed] [Google Scholar]
- Monson KL, Barbaro NM, Manley GT. Biaxial response of passive human cerebral arteries. Ann Biomed Eng. 2008;36:2028–2041. doi: 10.1007/s10439-008-9578-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Monson KL, Goldsmith W, Barbaro NM, Manley GT. Significance of source and size in the mechanical response of human cerebral blood vessels. J Biomech. 2005;38:737–744. doi: 10.1016/j.jbiomech.2004.05.004. [DOI] [PubMed] [Google Scholar]
- Rosamond W, Flegal K, Furie K, Go A, Greenlund K, Haase N, Hailpern SM, Ho M, Howard V, Kissela B, Kittner S, Lloyd-Jones D, McDermott M, Meigs J, Moy C, Nichol G, O’Donnell C, Roger V, Sorlie P, Steinberger J, Thom T, Wilson M, Hong Y. Heart disease and stroke statistics--2008 update: a report from the American Heart Association Statistics Committee and Stroke Statistics Subcommittee. Circulation. 2008:e25–146. doi: 10.1161/CIRCULATIONAHA.107.187998. [DOI] [PubMed] [Google Scholar]
- SAE. Part 1: electronic instrumentation, SAE J211-1. Society of Automotive Engineers; Warrendale, PA: 1995. S.A.E. Instrumentation for impact test. [Google Scholar]
- Scott S, Ferguson GG, Roach MR. Comparison of the elastic properties of human intracranial arteries and aneurysms. Can J Physiol Pharmacol. 1972;50:328–332. doi: 10.1139/y72-049. [DOI] [PubMed] [Google Scholar]
- Steelman SM, Wu Q, Wagner HP, Yeh AT, Humphrey JD. Perivascular tethering modulates the geometry and biomechanics of cerebral arterioles. Journal of Biomechanics. 2010;43:2717–2721. doi: 10.1016/j.jbiomech.2010.06.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Loon P. Length-force and volume-pressure relationships of arteries. Biorheology. 1977;14:181–201. [PubMed] [Google Scholar]
- Wagner HP, Humphrey JD. Differential passive and active biaxial mechanical behaviors of muscular and elastic arteries: basilar versus common carotid. J Biomech Eng. 2011;133:051009. doi: 10.1115/1.4003873. [DOI] [PubMed] [Google Scholar]
- Wicker BK, Hutchens HP, Wu Q, Yeh AT, Humphrey JD. Normal basilar artery structure and biaxial mechanical behaviour. Comput Methods Biomech Biomed Engin. 2008;11:539–551. doi: 10.1080/10255840801949793. [DOI] [PubMed] [Google Scholar]