Solid state nuclear magnetic resonance with magic-angle spinning and dynamic nuclear polarization below 25 K

Abstract

We describe an apparatus for solid state nuclear magnetic resonance (NMR) with dynamic nuclear polarization (DNP) and magic-angle spinning (MAS) at 20–25 K and 9.4 Tesla. The MAS NMR probe uses helium to cool the sample space and nitrogen gas for MAS drive and bearings, as described earlier (Thurber et al., J. Magn. Reson. 2008) [1], but also includes a corrugated waveguide for transmission of microwaves from below the probe to the sample. With a 30 mW circularly polarized microwave source at 264 GHz, MAS at 6.8 kHz, and 21 K sample temperature, greater than 25-fold enhancements of cross-polarized ¹³C NMR signals are observed in spectra of frozen glycerol/water solutions containing the triradical dopant DOTOPA-TEMPO when microwaves are applied. As demonstrations, we present DNP-enhanced one-dimensional and two-dimensional ¹³C MAS NMR spectra of frozen solutions of uniformly ¹³C-labeled L-alanine and melittin, a 26-residue helical peptide that we have synthesized with four uniformly ¹³C-labeled amino acids.

I. Introduction

Demonstrations by Griffin and coworkers [2] of large nuclear magnetic resonance (NMR) signal enhancements in frozen solutions at high magnetic fields and under magic-angle spinning (MAS) through dynamic nuclear polarization (DNP) have stimulated much interest in DNP for solid state NMR studies of biological [3–9] and non-biological [10–14] systems in recent years. A popular approach is to use continuous-wave gyrotron microwave sources, capable of producing many watts at frequencies above 200 GHz [15–18], and to operate at sample temperatures in the 80–100 K range [19, 20]. In these studies, samples are typically doped with nitroxide-based biradical dopants in frozen solutions [21, 22], although other dopants have also been described [23–25].

Our laboratory has shown that double- and triple-resonance MAS NMR can be performed at sample temperatures below 30 K (which we call “ultra-low” temperatures, in contrast to more conventional low-temperature MAS NMR experiments that use liquid nitrogen for cooling) using a novel probe design in which the sample space is cooled with helium, but nitrogen gas is used for MAS drive and bearings [1]. This design permits stable, long-term operation without excessive consumption of liquid helium. As we have demonstrated, this design can also provide the radio-frequency (rf) power-handling capabilities, NMR signal detection efficiencies, NMR linewidths (i.e, field homogeneity), and MAS frequencies that are required for many common solid state NMR measurements on biomolecular systems. After developing this probe design, we decided to investigate its utility in DNP experiments, motivated by the idea that operation at very low sample temperatures might permit large absolute NMR signals to be obtained with relatively low microwave powers, principally because the partial saturation of electron spin transitions required for DNP [26] can be achieved with lower microwave fields at lower temperatures due to the smaller nitroxide electron spin-lattice relaxation rates [27]. In subsequent ¹H NMR and cross-polarized ¹³C NMR experiments on nitroxide-doped frozen solutions without MAS [28–30], we have shown that large DNP effects can indeed be observed at temperatures below 30 K. In this paper, we describe our initial results from the combination of ultra-low-temperature MAS NMR with microwave irradiation for DNP.

II. Ultra-low-temperature MAS DNP apparatus

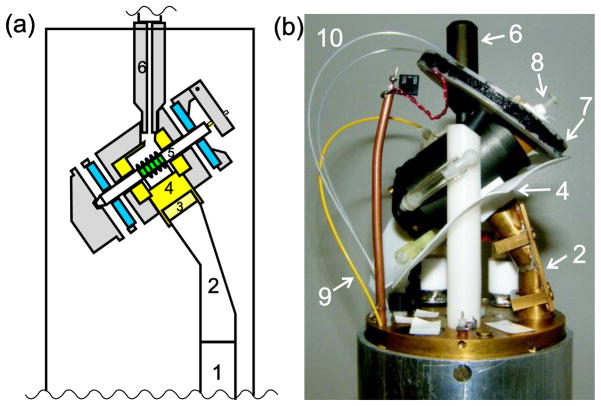
Fig. 1 shows the principal components of the ultra-low-temperature DNP MAS probe. As in the earlier version [1], cold helium is supplied from a pressurized liquid helium tank (typically 6–8 psi) through a vacuum-insulated stainless steel transfer line that includes a manually adjusted needle valve to control helium flow (Janis model FHT-ST). The transfer line threads into a 5 cm long Torlon fitting that inserts into the Torlon MAS housing. Within the housing, a Teflon insert encloses the sample space and acts as a baffle to separate this space from the MAS bearings, as previously described [1]. Hipped (hot isostatic pressed) zirconia MAS rotors (O’Keefe Ceramics) have a 4.0 mm outer diameter and are 4.6 cm in length. Rotor wall thickness is discussed below. Nitrogen gas for MAS drive and bearings travels from the base of the probe in vacuum-insulated glass lines, allowing cooled gas to be used in certain experiments (see below). The drive and bearing gases are carried by Delrin support posts for the MAS assembly, and enter the assembly near the ends of the rotor through Tygon tubes in an “outrigger” arrangement (rather than traveling through channels within the MAS housing, which would increase the heat load). optical fiber temperature sensor (Neoptix model T1) is inserted into the sample space to provide an approximate indication of sample temperatures. More accurate sample temperatures are determined from ⁷⁹Br spin-lattice relaxation rates in KBr powder as previously described [31]. To prevent axial vibration of the rotor during MAS, the tip of a plastic screw wrapped with Teflon tape rests on the end cap during operation. The drive and bearing configuration and other aspects of the MAS housing are identical to the design described previously [1].

Figure 1.

He-cooled DNP MAS probe: (a) Cross-section view of probe head. The sample is shown in green, the bearings in blue, Teflon parts in yellow, and other plastic parts in grey. (b) Photograph of the probe head. Microwaves enter the bottom of the probe by reflection from a mirror on the optical table [30] into a corrugated waveguide (1), which leads to a miter bend (2) to direct the microwaves towards the MAS assembly. To reach the sample, the microwaves pass through a Teflon lens (3), a Teflon coil holder (4), the RF coil, and the zirconia rotor (5). Cold helium from a vacuum-insulated stainless steel transfer line enters the MAS assembly through a Torlon tip (6). Also visible are the shim coil (7), hinged pointer for stabilizing spinning (8), fiber optic temperature sensor (9), and optical fibers for detection of MAS rate (10).

The outer diameter of the probe body is 88.3 mm, requiring that room temperature shims be removed from our 89 mm bore superconducting magnet when this probe is used. The large diameter of the probe body was chosen to easily provide space for the components of a triple-resonance rf circuit (currently setup as double-resonance ¹³C-¹H) plus a microwave waveguide. A smaller diameter probe could accommodate our long MAS rotor, and allow the use of external room temperature shim coils. However, a single internal shim coil provides adequate cancellation of field gradients along the MAS axis, which is the most significant gradient direction under MAS. The rf coil within the MAS housing is a 10 mm long 6-turn solenoid, constructed from 0.64 mm diameter copper wire. The wire diameter was chosen smaller than the earlier version [1], to reduce microwave reflections from the coil. The rf coil is soldered to threaded brass rods that pass through threaded holes in a Teflon platform. Connections to the coil are made at the external ends of these threaded rods. Use of brass presumably reduces heat transmission from outside the MAS housing to the sample space at low temperatures. However, the rf leads could still be a significant source of heat into the sample space. Threading through the Teflon platform minimizes leakage of helium into the rf circuitry below the MAS housing, which might otherwise lead to arcing during high-power rf pulses, and prevents the rf coil from shifting its position at low temperatures or during adjustment of the sample rotation angle. Besides the rf leads, other parts of the probe provide thermal paths that can warm the sample space. Rough, order-of-magnitude estimates of thermal losses through various paths are presented in the Supplementary Information. The current liquid helium usage for this probe is slightly less than 4 L/h for a sample temperature of 25 K, actually slightly worse than the previous version [1], perhaps because a different helium transfer tube was used. The Teflon and plastic housing of the spinner may provide a significant thermal path into the sample space, because of the large surface area with regions kept warm by the constant flow of nitrogen gas. Experiments on the earlier version showed that the Torlon tip used on the end of the transfer tube also uses some of the cooling power of the liquid helium flow. The rotor and the Teflon spacers it contains are not expected to be significant thermal paths, due to their small cross section and low thermal conductivity. In addition, the helium gas exits the sample space around the circumference of the rotor, which should help cool the rotor. Forcing the helium gas to exit around the rotor is deliberate, because the outward flow of helium gas is necessary to prevent the nitrogen gas from entering and warming the sample space.

Temperature gradients along the length of the sample were estimated from the dependence of the ⁷⁹Br spin-lattice relaxation rate on axial position, using the internal shim coil to create an axial field gradient that produced a one-dimensional image of the KBr sample. The ⁷⁹Br relaxation rate could be measured for roughly 1 mm slices of the 10 mm long sample. With room-temperature bearing (22 psi) and drive gas, 7.0 kHz MAS, and an overall average temperature of 25 K, the slice temperatures varied from 23 K to a maximum of 30 K at the edge of the sample nearest the drive tip of the rotor. With the bearing gas (28 psi) cooled by a dry ice/ethanol bath and room-temperature drive gas, 6.65 kHz MAS, and an average temperature of 25 K, the slice temperatures varied from 24 K to 28.5 K. With cooled bearing gas (24 psi), room-temperature drive gas, 6.7 kHz MAS, and an average temperature of 22.5 K, the slice temperatures varied from 22 K to 24 K.

Microwaves are supplied from beneath the probe by the solid state source (Virginia Diodes) and quasi-optical system (Thomas Keating, Ltd.) described previously [30]. The microwave frequency is controlled with a LabVIEW (National Instruments Corp.) program that sets the frequency of the initial ~11 GHz synthesizer. The final output of the solid state source is 24 times this initial frequency. The power output is controlled by an external analog voltage, and the power can be monitored, relative to the specified 30 mW maximum, by a thermal power sensor (Thorlabs model S302C) or diode detector (Pacific Millimeter Products model YD). Microwaves travel through a vertical corrugated waveguide within the probe body, then enter a miter bend [19] that reflects them by the complement of the magic angle, so that the microwaves are aimed perpendicular to the surface of the MAS housing. A Teflon lens at the end of the brass miter bend is designed to focus the microwaves in the radial direction (i.e., perpendicular to the rotor axis) [32]. No focusing in the axial direction (i.e., parallel to the rotor axis) is attempted in the current design. The Teflon lens is designed to irradiate an area that is roughly 2.2 mm in the radial direction and 5 mm in the axial direction (full width at half maximum microwave power density). Measurements of the microwave power distribution including the rf coil and rotor were made using the temperature change of a T1 optical fiber temperature sensor. These measurements suggest that inside a rotor with 0.381 mm wall thickness, the peak microwave power is approximately half of the peak power at the entrance to the corrugated waveguide of the probe. The measured width of the microwave power distribution inside the rotor in the axial direction is roughly 8.5 mm. The extra apparent spread of the microwaves may arise from the fact that the temperature sensor is sensitive to microwave heating not just at its tip, or from the influence of the coil and rotor on the microwave beam.

The rf circuit in our DNP MAS probe is currently double-tuned, to ¹H (400.9 MHz) and ¹³C (100.8 MHz), but the probe has provisions for a third rf channel. We achieve ¹H nutation frequencies of 90 kHz with 110 watts of rf power and ¹³C nutation frequencies of 45 kHz with 120 watts of rf power. Rf power levels are determined from peak-to-peak voltages on a Tektronix model DPO4104 oscilloscope, through directional couplers with nominal 50 dB attenuation. Experiments described below were performed with a Varian Infinity spectrometer console.

III. Experimental results

A. L-alanine

Initial tests were performed on a 48 μl frozen solution of uniformly ¹³C-labeled L-alanine (50 mM) in glycerol/water, using perdeuterated glycerol and partially deuterated water (25:58:17 mol% d₈-glycerol:D₂O:H₂O) with 165 mM acetate buffer, pH 3. As the paramagnetic dopant, we use the tri-nitroxide compound DOTOPA-TEMPO described in our earlier publications about ultra-low-temperature DNP without MAS [30], at 10 mM concentration. As previously shown in experiments at higher temperatures [33], deuteration of the solvent leads to more rapid build-up of DNP-enhanced, cross-polarized ¹³C NMR signals and larger signal enhancements, presumably due to the smaller number of ¹H spins that need to be polarized for each dopant molecule. Data in Fig. 2 were acquired at 6.7 kHz MAS frequency and an average sample temperature of 20 K, determined from the ⁷⁹Br spin-lattice relaxation rate of KBr powder [31] contained within the same rotor as the L-alanine solution. ¹H-¹³C cross-polarization (CP) periods were 0.6 ms, with 47 kHz and 40 kHz ¹H and ¹³C rf fields, respectively. ¹H decoupling fields were 90 kHz, with two-pulse phase modulation (TPPM) [34].

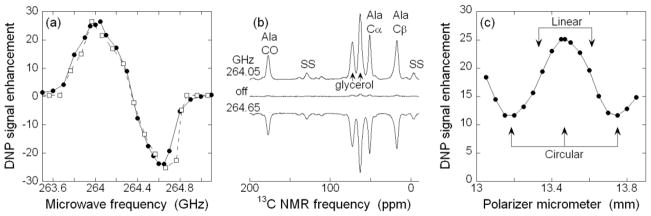
Figure 2.

(a) DNP enhancement as a function of microwave frequency, experimental (●) and calculated (□). The sample is 50 mM uniformly ¹³C-labeled L-alanine in partially deuterated glycerol/water, with 10 mM DOTOPA-TEMPO dopant. Data were acquired at 20 K sample temperature with 6.7 kHz MAS. Calculated enhancements are based on numerical simulations for a three-spin system (one ¹H, two nitroxide electron spins) as described [26], and are normalized to match the maximum positive enhancement in experiments. Lines are guides to the eye. (b) ¹³C CP NMR spectra at 264.05 GHz (4 scans), 264.65 GHz (4 scans), and with microwaves off (32 scans, vertical scale divided by 8). (c) Experimental DNP enhancement as a function of microwave polarization. Lines are guides to the eye.

Fig. 2a shows the dependence of the ¹³C CP NMR signal enhancement from DNP (ratio of integrated ¹³C signals from the alanine Cα and glycerol peaks, with and without microwave irradiation at 30 mW) on microwave frequency. The DNP signal enhancement is the same within error (~10%) for all the alanine and glycerol ¹³C peaks. Fig. 2a shows that the experimental frequency dependence is very similar to the calculated frequency dependence from a three-spin model for cross effect DNP with MAS [26]. The frequency dependence is also similar to results observed without MAS at 16 K [30] and with MAS at higher temperatures [20]. Enhancements greater than 25-fold are observed at the optimal microwave frequencies. In these experiments, the DNP build-up time (from fitting to a single-exponential function) was 4.4 ± 0.2 s for all of the alanine and glycerol ¹³C peaks, equal within error to the ¹H spin-lattice relaxation time measured by ¹³C CP without microwave irradiation. Fig. 2b shows examples of ¹³C NMR spectra without microwaves and with microwaves at the positive and negative extrema of the frequency dependence.

Our quasi-optical system includes a Martin-Puplett interferometer for controlling the microwave polarization [35, 36]. Fig. 2c shows the dependence of the DNP enhancement on the micrometer setting of the interferometer. An oscillatory dependence is observed, with a period of 0.57 mm that equals half the wavelength at 264 GHz as expected. All other data presented were acquired with the micrometer adjusted to give maximum enhancements. In principle, the minimum enhancement in Fig. 2c should be unity (i.e., equal signals with and without microwave irradiation), when the microwaves are circularly polarized in the direction opposite to the direction that drives electron spin transitions in our magnet. Our tests of microwave polarization (using a wire-grid polarizer and thermal power sensor to evaluate the linear polarization and microwave power from the two legs of the interferometer) indicate that nearly pure circular polarization is present at the entrance to the corrugated waveguide of the DNP MAS probe. However, from the results in Fig. 2c, it appears that pure circular polarization is not achieved at the sample. Contributing factors may include unequal reflections of linear polarizations parallel and perpendicular to the rotor axis by the rf coil or by the rotor itself, multiple reflections within the combined probe and quasi-optical system, or other imperfections.

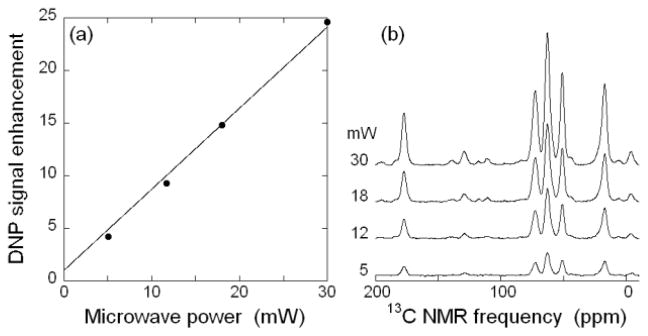
Fig. 3 shows the dependence of DNP enhancement on microwave power. A linear dependence is observed, indicating that our maximum power is well below the limit at which saturation of DNP enhancements occurs. Thus, higher microwave powers are expected to produce even greater DNP enhancements. It is worth noting that, in simplistic terms, an enhancement factor of 25 at 20 K corresponds to the same absolute NMR signal amplitude as an enhancement factor of 100–125 at 80–100 K, where most DNP-enhanced ¹³C MAS NMR data have been obtained to date [19, 20]. Of course, the absolute signal-to-noise ratio for a given sample in a given measurement time also depends on signal losses due to paramagnetic doping, DNP build-up rates, intrinsic (i.e., independent of paramagnetic doping) nuclear spin-lattice relaxation rates, transverse relaxation rates (T₂ and T_1ρ), probe efficiency, noise levels, and possibly other factors, all of which can be temperature-dependent.

Figure 3.

(a) DNP enhancement as a function of microwave power, under the same experimental conditions as in Fig. 2. The line is a linear fit to the data, constrained to an enhancement of one at zero microwave power. (b) DNP-enhanced ¹³C CP NMR spectra at the indicated microwave powers.

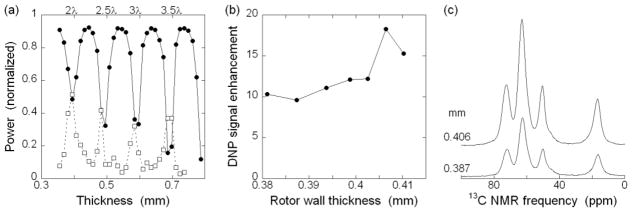
Given the limited microwave power currently available to us, it is important to optimize power density at the sample. We use zirconia MAS rotors in part because of their low thermal conductivity, which allows us to achieve low sample temperatures in the center of the rotor while using nitrogen gas for MAS drive and bearings at the ends of the rotor. However, the high dielectric constant for zirconia at microwave frequencies implies that most of the microwave power could be reflected at the rotor surfaces before reaching the sample. Sapphire has a lower dielectric constant, but the high thermal conductivity is very unfavorable for thermal separation of helium sample cooling from the nitrogen MAS bearings. Rosay, et al. [20], compared sapphire and zirconia rotors (3.2 mm OD, 2.2 mm ID) at ~97 K with enough microwave power to saturate the DNP enhancement, resulting in 18–20% lower maximum enhancement for the zirconia rotor. Another alternative design that we considered is to irradiate the sample from the end of the rotor to avoid reflection at the zirconia surfaces and rf coil wires [5]. However, for our long rotors, the microwave beam would tend to diverge significantly during the transmission from the end of the rotor to the sample near the center of the rotor [37], unless some type of waveguide is used in or around the rotor to maintain a focused beam. Metal waveguide structures, if spun with the rotor, can create significant drag on the spinning, through eddy currents in the large magnetic field. Ultimately, microwave irradiation through the side of the rotor was chosen as a simple, low-risk microwave design, which also allows easy magic angle adjustment [32]. In principle, microwave reflection from the zirconia surfaces can be minimized by adjusting the rotor wall thickness to a multiple of half the wavelength in zirconia, so that reflections from the inner and outer surface of the rotor nearly cancel. To investigate this issue, we used our quasioptical system to measure the microwave reflection and transmission of a series of hipped zirconia plates, with thicknesses between 0.36 mm and 0.79 mm, for microwaves at 264 GHz. Data in Fig. 4a show pronounced minima in reflection and maxima in transmission for thicknesses that are multiples of 0.099 mm, which is then half of the wavelength within hipped zirconia, implying a room-temperature dielectric constant equal to 33.2 ± 0.2, or an index of refraction equal to 5.76 ± 0.02. Measurements at 77 K indicated that the ideal thickness increases by 2–3% at low temperatures. Computer simulations of microwave transmission suggested that the curved surfaces of the rotor and sample would be expected to still have significant reflection minima at roughly the same positions as the flat plates experimentally tested (see Supplementary Information). We then tested MAS rotors with wall thicknesses in a small range around an expected optimal value of 0.403 mm. Data in Figs. 4b and 4c show that there is a significant dependence of the DNP enhancement on rotor wall thickness, with a maximum at 0.406 mm. Notably, for rotors with nearly optimal wall thickness, the reflected microwave power, measured by the diode detector of our quasi-optical system, oscillates at the MAS frequency, presumably caused by small variations in the wall thickness around the circumference of the rotor. The quoted tolerance on the wall thickness of the rotors is 0.005 mm.

Figure 4.

(a) Reflected (●) and transmitted (□) microwave power as a function of the thickness of a flat hipped zirconia plate, normalized for reflectance from a copper plate and for transmission without any zirconia. Lines are guides to the eye. Reflectance minima are marked with the derived number of wavelengths in the zirconia. Data were taken with 264.0 GHz circularly polarized microwaves at room temperature. (b) Experimental DNP enhancement as a function of rotor wall thickness. Outer diameter of rotors is 3.988 mm, with variable inner diameter. Lines are guides to the eye. (c) ¹³C CP NMR spectra from rotors with 0.406 mm and 0.387 mm wall thickness. Samples contained 54 μl of 95 mM uniformly ¹³C- labeled L-alanine and 20 mM DOTOPA in 25:75 mol% glycerol:H₂O, with 210 mM acetate buffer, pH 3. Data were acquired at 6.6–6.9 kHz MAS, with 20 ρ 2 K sample temperature.

B. Melittin

As an initial test of applications to peptides and proteins, we prepared a ¹³C-labeled sample of melittin, a 26-residue peptide from bee venom with a known helical structure [38–42], using standard solid-phase synthesis and high-performance liquid chromatography purification. Uniformly ¹³C-labeled amino acids were included at four positions, namely Pro14, Ala15, Leu16, and Ile17. The sample was prepared by dissolving the peptide in 100 mM phosphate buffer, pH 7.4, to a concentration of 14 mM. A 21 μl aliquot of the buffered solution was then mixed with 44 μl of D₂O and 88 μl of perdeuterated, ¹³C-depleted glycerol (¹²C,D₈-glycerol). DOTOPA-TEMPO was dissolved in perdeuterated dimethyl sulfoxide (D₆-DMSO) to a concentration of 253 mM (optical absorbance = 0.80 at 460 nm). A 6.4 μl aliquot of the DOTOPA-TEMPO solution was mixed with the peptide solution immediately before measurements, producing a final sample containing 1.9 mM melittin, 9.9 mM DOTOPA-TEMPO (nominal concentration, as the solubility limit of DOTOPA-TEMPO in glycerol/water at pH 7.4 is roughly 7 mM), and 14% v/v H₂O. Experiments were performed on 82 μl of this solution, frozen in an MAS rotor with 0.406 mm wall thickness. Fig. 5 shows ¹³C CP NMR spectra, obtained at 6.5 kHz MAS frequency and 25 K. ¹H-¹³C CP periods were 0.6 ms, with 52 kHz and 45 kHz ¹H and ¹³C rf fields, respectively. ¹H TPPM decoupling fields were 90 kHz. Melittin ¹³C NMR signals are enhanced by a factor of 17 by microwave irradiation. In this case, the DNP build-up time was 8 s, and a 12 s recycle delay was used.

Figure 5.

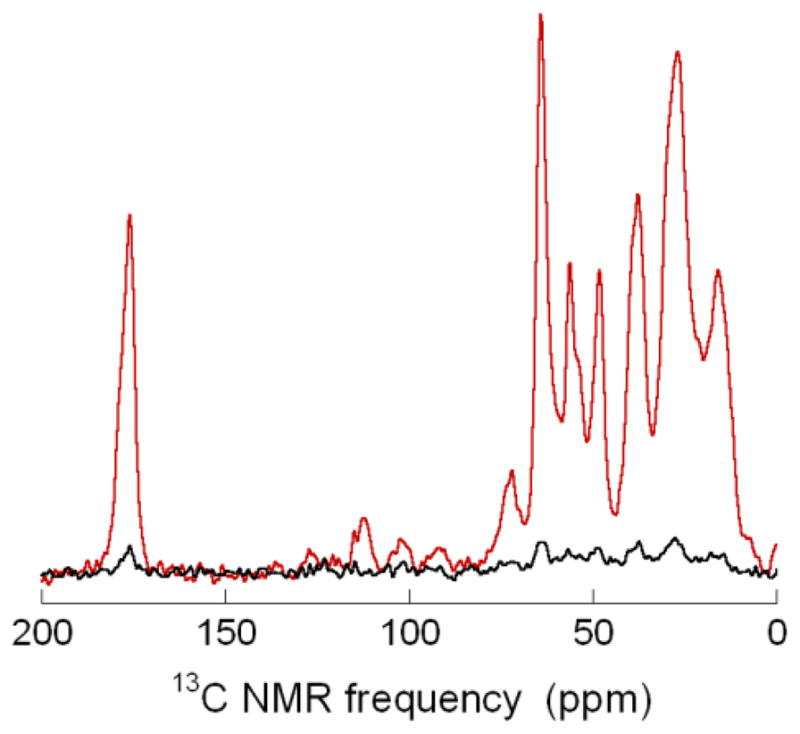
¹³C CP NMR spectra of 1.9 mM melittin in partially deuterated water/glycerol/DMSO, with (red, 16 scans) and without (black, 32 scans, vertical scale divided by two) microwaves. Melittin was prepared with uniform ¹³C labeling of Pro14, Ala15, Leu16, and Ile17. See text for other details of sample conditions. Spectra were acquired at 25 K sample temperature with 6.5 kHz MAS and processed with 100 Hz Gaussian line broadening

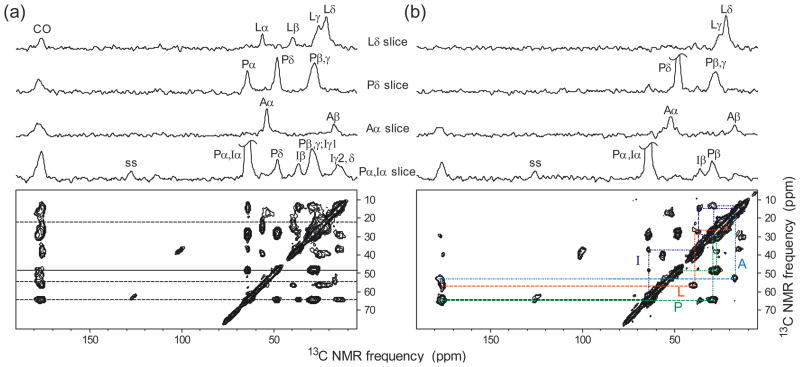
Fig. 6 shows two DNP-enhanced 2D ¹³C-¹³C NMR spectra of the same melittin sample, obtained at 6.4 kHz MAS frequency and 25 K, using either a 25.1 ms spin diffusion mixing period (Fig. 6a), or a 2.5 ms fpRFDR [43, 44] mixing period (Fig. 6b), with 35 μs ¹³C π pulses at a carrier frequency of 45.7 ppm for fpRFDR. The fpRFDR spectrum emphasizes single-bond cross peaks, while the spin diffusion spectrum shows cross peaks among all ¹³C sites in each labeled residue. Both spectra were acquired with 100 complex t₁ points and a 31.5 μs t₁ increment and with four scans per free-induction decay. The recycle delay was 10 s for the fpRFDR spectrum (2.2 hr total experiment time) and 12 s for the spin diffusion spectrum (2.7 hr total experiment time). Residual glycerol ¹³C signals at 62.9 ppm and 72.7 ppm were used for chemical shift referencing [1]. CP contact times were 1.0 ms, with 45 kHz and 51 kHz RF fields on ¹³C and ¹H spins, respectively. TPPM decoupling fields were 90 kHz.

Figure 6.

DNP-enhanced 2D ¹³C-¹³C NMR spectra of melittin in frozen glycerol/water. (a) Spin diffusion spectrum with a 25.1 ms mixing period, acquired in 2.7 hr. (b) fpRFDR spectrum with a 2.5 ms exchange period, acquired in 2.2 hr. The sample is the same as in Fig. 5. 1D slices above each spectrum are taken at the dashed line positions in the 2D spin diffusion spectrum. Cross peak assignment paths in the 2D fpRFDR spectrum are based on the chemical structures and typical ¹³C chemical shift ranges of the labeled residues. Spectra were acquired at a 25 K sample temperature with 6.4 kHz MAS and processed with 100 Hz Gaussian line broadening in both dimensions.

IV. Discussion

Experimental results presented above demonstrate the feasibility and utility of DNP MAS NMR at sample temperatures below 25 K, using the ultra-low-temperature MAS probe design described previously [1] together with a low-power microwave source. ¹³C NMR signal enhancement factors greater than 25 are achieved without excessively long recycle delays for DNP build-up. The system is sufficiently stable that 2D experiments lasting many hours can be performed. In frozen solutions, concentrations of ¹³C-labeled molecules below 1 mM (80 nmole or less) are feasible with the current experimental conditions. Although in the past we have successfully performed solid state ¹³C NMR experiments on biologically significant, ¹³C-labeled peptides and proteins in frozen solutions at concentrations in the 1–5 mM range without DNP, at sample temperatures around 120 K and using CuNa₂EDTA to reduce ¹H spin-lattice relaxation times and thereby accelerate data acquisition, those experiments required larger sample volumes (200–240 μl) and measurement times ranging from several days to several weeks [45–48].

In earlier work without MAS, using the same microwave source, we obtained DNP enhancements of ¹H NMR signals by factors of 40–50 near 25 K (but at higher DOTOPA-TEMPO concentrations) [29, 30], and DNP enhancements of cross-polarized ¹³C NMR signals by factors of 20–40 at lower temperatures [28]. Results presented above show that the net DNP enhancement (averaged over the sample volume) under MAS are not greatly reduced by the problem of microwave reflection from the walls of our zirconia MAS rotors, especially when the wall thickness is optimized to minimize reflections.

Our results show that DNP systems that combine ultra-low-temperature MAS with relatively low microwave power can be competitive with systems that use higher sample temperatures and higher microwave power. Nonetheless, as shown in Fig. 3, microwave power above 30 mW should be beneficial at 25 K sample temperatures, because there is no sign of saturation of the DNP enhancement at 30 mW. Figure 3 shows a linear dependence of the DNP enhancement on microwave power, with an increase of ~0.8 in enhancement per mW. Extrapolating from these results, we can speculate that microwave power in the 0.3–1.0 W range could produce ¹³C NMR signal enhancements at 25 K equal to the highest enhancements (230) reported at 80–100 K [49], and larger absolute ¹³C NMR signals. We should emphasize that the utility of DNP for NMR experiments will rely not just on the signal enhancement, but also other factors such as the absolute NMR signal, relaxation rates, and resolution, which may all depend on the particular sample, radical dopant, and NMR experiment, in addition to temperature.

In addition to somewhat higher microwave powers, several other factors may lead to improved performance in future applications of our DNP MAS system: (i) We have not fully optimized the focusing of microwaves into the NMR sample. Since the DNP-enhanced signals are proportional to microwave power, it may be advantageous to focus the microwave beam more tightly into the center of the sample; (ii) We have not fully optimized the geometry of the RF coil, which may affect both the reflection of microwaves away from the sample and the polarization of microwaves within the sample; (iii) It would be advantageous to reduce the liquid helium consumption at low sample temperatures, which may be possible with better insulation of the MAS assembly and the connection from our stainless steel transfer line to the MAS assembly; (iv) Cooling of the entire RF circuit within the probe, as well as the RF preamplifier, may reduce the noise levels in our measurements; (v) New multi-radical molecules may increase DNP efficiency.

Highlights.

• Probe for solid state NMR with dynamic nuclear polarization (DNP) and magic-angle spinning (MAS) at 20 K and 9.4 Tesla.

• Signal enhancement greater than 25 fold (microwaves on versus microwaves off) using 30 mW of microwaves.

• 2D ¹³C-¹³C spectra for 160 nanomoles of the 26 residue peptide melittin in frozen solution, taken in ~2½ hr.