Abstract
In the multiple object tracking task, participants are asked to keep targets separate from identical distractors as all items move randomly. It is well known that simple manipulations such as object speed and number of distractors dramatically alter the number of targets that are successfully tracked, but very little is known about what causes this variation in performance. One possibility is that participants tend to lose track of objects (dropping) more frequently under these conditions. Another is that the tendency to confuse a target with a distractor increases (swapping). These two mechanisms have very different implications for the attentional architecture underlying tracking. However, behavioral data alone cannot differentiate between these possibilities. In the current study, we used an electrophysiological marker of the number of items being actively tracked to assess which type of errors tended to occur during speed and distractor load manipulations. Our neural measures suggest that increased distractor load led to an increased likelihood of confusing targets with distractors while increased speed led to an increased chance of a target item being dropped. Behavioral experiments designed to test this novel prediction support this assertion.
1. Introduction
The ability to keep track of the location of multiple items simultaneously is a valuable skill for modern life; from tracking multiple cars on the highway while driving to appreciating the complexity of perfectly executed pick-and-roll in basketball. This skill has been explored experimentally using the multiple object tracking task (MOT: for reviews see Cavanagh & Alvarez, 2005; Scholl, 2009), where participants are asked to keep multiple targets distinct from identical distractors as they move randomly about a screen. Over the course of several seconds of movement, participants must mentally track the location of each target so that they can distinguish between targets and distractors at the end of each trial.
There have been over a hundred papers published using the MOT paradigm in the 23 years since Pylyshyn & Storm (1988) introduced the task (http://www.yale.edu/perception/Brian/refGuides/MOT.html). Three general findings can be abstracted from these studies. First, participants can track more than one object at a time, a finding which may come as a surprise to a reader new to the field. Second, there is typically a limit on the number of items which can be tracked (typically ≈ 4). Finally, the number of items that can be tracked varies not only from person to person (Oksama & Hyönä, 2004) but as a function of many different independent variables (Bettencourt & Somers, 2009).
Performance on the MOT task (and its real world counterparts) addresses fundamental questions about the architecture of selective attention. Can we simultaneously attend to multiple foci? If so, are these foci regions of space or objects? What is the relationship between attention and memory? A satisfying theoretical account of MOT performance would be a fundamental component of an account of selective attention.
For example, let’s take a very naïve view of the seminal account of MOT performance, Pylyshyn’s FINST (“Fingers of INSTantiation”) model. In this model, there is a set of preattentive spatial indexes or pointers which refer to objects in the visual world. FINST’ed objects may have priority access to attention, but are not in fact attended (Pylyshyn, 1989); the FINST is a pointer that can only be used for spatial computations (e.g., “this object is above that object”). To know anything non-spatial about the object, your must direct a (presumably unitary) focus of attention to it. Critically, there is a limited number of FINSTs. Although the number of FINSTs is variable between individuals, each individual’s capacity (and therefore performance) will be fixed.
In contrast, Alvarez and Franconeri (2007) proposed a more flexible system (called, appropriately, FLEXs) which could be concentrated on a single item when tracking was difficult or spread among many items when tracking was easy. In support of this proposal, they demonstrated that capacity decreases with the log of the speed of the targets: at very slow speeds, their participants could track up to eight objects, whereas at high speeds, only one target could be tracked. This is strong evidence against Pylyshyn’s (1989; 2006) account, which predicts that capacity should be constant.
More generally, the primary source of evidence for or against various accounts of MOT is tracking accuracy, compared across various conditions (Alvarez & Franconeri, 2007; Bettencourt & Somers, 2009; Franconeri, Jonathan, & Scimeca, 2010; Franconeri, Lin, Pylyshyn, Fisher, & Enns, 2008; Horowitz, Birnkrant, Fencsik, Tran, & Wolfe, 2006; Horowitz, Place, Van Wert, & Fencsik, 2007; Keane & Pylyshyn, 2006; Scholl & Pylyshyn, 1999; Shim, Alvarez, & Jiang, 2008). Accuracy is then converted into capacity by some transformation (Horowitz, Klieger, et al., 2007; Hulleman, 2005; Scholl, Pylyshyn, & Feldman, 2001), allowing some inference about the number of objects tracked.
The problem with this logic is that incorrect responses may be caused by a number of different types of errors. If we ignore simple response errors, there are two major error types that have very different implications for capacity, but which are difficult to distinguish in a purely behavioral experiment. We call these two error types dropping and swapping. Dropping corresponds to simply losing track of a target. At time t1 the participant is tracking four targets, and at t2 she is tracking three targets; in the interval t1-t2, she dropped a target. In a swap error, on the other hand, the participant confuses a target for a non-target. At t1 she is tracking four targets, and at t2 she is tracking three targets and one non-target; in the interval t1-t2, she confused a non-target for a target. The key difference between the two errors is the number of items tracked. Drops lead to the participant tracking fewer items, while swaps keep the number of items tracked constant.
The two error types obviously have different implications for the outcome of an experiment. Some manipulations may reduce the number of items that participants can track, while other manipulations may simply make targets and non-targets more confusable. For example, if we introduce featural differences between targets and distractors, performance will improve (Bae & Flombaum, 2012; Makovski & Jiang, 2009; Ren, Chen, Liu, & Fu, 2009). It seems unlikely that changing the stimulus allowed participants to grow an extra FINST, or amplify their store of FLEXs. Instead, this manipulation makes swaps less likely. For example, by manipulating the onset of unique color onsets during tracking, Bae & Flombaum found that the benefit of for unique colors was only observed when the uniquely colored distractors were within close proximity of the targets. However, although increasing the perceptual space between targets and distractors typically improves performance, it does not eliminate all errors, suggesting that errors must be taking place for reasons other than swapping.
Unfortunately, swaps and drops are indistinguishable in the standard MOT methodology. One of two response methods is typically used in MOT experiments: mark all or probe one (Hulleman, 2005). In the mark all technique, the participant has to indicate all of the targets that he was tracking, usually by pointing to them with a computer mouse (e.g. Makovski, Vazquez, & Jiang, 2008). In the probe one technique, one item is highlighted and the participant has to indicate whether or not that item is a target (this seems to be the most popular method e.g. Bettencourt & Somers, 2009; Thomas & Seiffert, 2010; Zelinsky & Todor, 2010). In either technique, both drops and swaps will lead to decreased accuracy, but there is no way to tell which kind of error is occurring.
In the current study, we devise what we believe is a more direct method to determine whether changes in error rates are due to swaps or drops. Rather than rely on inference from performance, we used a neural index of the number of items being actively tracked. In previous work, our group demonstrated that MOT evokes a sustained, lateralized ERP component, referred to as Contralateral Delay Activity, or CDA (Drew, Horowitz, Wolfe, & Vogel, 2011; Drew & Vogel, 2008), related to a similar component observed in visual working memory tasks (Vogel & Machizawa, 2004; Vogel, McCollough, & Machizawa, 2005). We propose that the CDA amplitude can be used as a measure of how many objects are being tracked at a given moment in time. This proposal is based on three lines of evidence. First, across several studies, the amplitude of the CDA scales with the number of objects being actively tracked in the contralateral hemifield, and asymptotes when the number of tracked objects exceeds tracking capacity (Drew et al., 2011; Drew & Vogel, 2008). Second, the CDA is sensitive to online manipulations of target load within a trial, such that amplitude declines when participants are asked to drop targets and increases when they add more targets (Drew, Horowitz, Wolfe, & Vogel, 2012). Third, the CDA can be dissociated from simple tracking difficulty. If we hold target load constant while increasing display density, difficulty increases (as indexed by behavioral performance, e.g. Bettencourt & Somers, 2009) without changing CDA amplitude (Drew & Vogel, 2008). Based on these studies, the CDA responds to manipulations which change tracking load, and not to those which do not necessarily change tracking load.
If we assume, then, that CDA amplitude is a dynamic measure of how many objects are being tracked at a given time, then by combining the CDA with behavioral performance measures, we should be able to differentiate between swapping and dropping, something that is impossible given behavioral data alone. Recall that swap errors do not change the number of items tracked. Thus, swap errors should lead to a decrease in accuracy without a corresponding decrease in the CDA. Drop errors, in contrast, reduce the number of tracked items and thus should lead to a decrease in amplitude.
In the current study, we apply this approach to two factors known to modulate MOT performance: distractor load (Bettencourt & Somers, 2009; Horowitz, et al., 2007) and speed (Alvarez & Franconeri, 2007; Bettencourt & Somers, 2009). In Experiment 1 CDA amplitude suggested that errors associated with increased distractor load are primarily associated with an increased rate of confusing targets with distractors whereas Experiment 2 CDA amplitude suggested that errors associated with increased speed were primarily associated with dropping the targets as the trial progressed. Ultimately, analyzing CDA amplitude in Experiments 1 & 2 led us to make a novel prediction regarding the types of errors responsible for decreased performance, which we then confirmed in two behavioral experiments by manipulating object distinctiveness.
2. Experiment 1: Distractor manipulation
Previous work has shown that increasing the number of distractors while holding the number of targets constant decreases tracking performance (Bettencourt & Somers, 2009). One intuitively appealing explanation for this effect is that it is simply a byproduct of the coarse grain of attentional selection (Intriligator & Cavanagh, 2001). A more recent theory has extended this logic, suggesting that object spacing is the root cause of limits on MOT performance (Franconeri et al., 2010). When a distractor and target come in close proximity, it increases the likelihood that the visual system can no longer distinguish the two. After such a close encounter, the participant is more likely to track the wrong item: a swapping error. Close encounters become will occur more frequently as we add more distractors.
Bettencourt and Somers (2009) proposed a different explanation. In their view, distractors require active suppression (Pylyshyn, 2006), and this process draws on the same resource used to track targets. More distractors lead to fewer resources available for target tracking, which would lead to fewer targets tracked. This explanation predicts that increasing distractors would lead to drop errors.
In Experiment 1 we manipulated the number of distractors and the number of targets orthogonally, and measured the electrophysiological response. We expect that accuracy will decline as we increase both target and distractor number. In the ERP domain, CDA amplitude will increase with the number of targets, as observed in previous studies (Drew et al., 2011). The key question is how amplitude changes with the number of distractors. There are three possibilities. First, if the CDA simply responds to task difficulty (as opposed to Drew & Vogel, 2008), amplitude might increase with the number of distractors. Second, assuming amplitude reflects the number of targets tracked, then if distractors interfere by causing participants to drop targets, then amplitude might decrease with number of distractors. Finally, if the increased errors with distractor load predominately reflect swapping targets with distractors, then amplitude should remain constant with distractor number.
2.2. Procedure
2.2.1 Participants
Twenty-nine neurologically normal participants (average age: 22.4) from the Eugene, OR community gave informed consent according to procedures approved by the University of Oregon institutional review board.
2.2.2 Stimulus displays and procedure
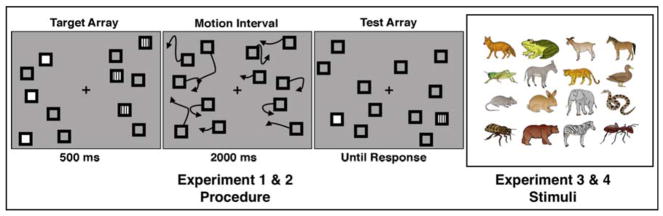
The procedure for Experiment 1 and 2 was adapted from the experimental design previously used by our group (Drew & Vogel, 2008). There were four conditions in each experiment and participants completed 10 blocks of 64 trials, yielding 160 trials per condition. Participants were asked to perform a lateralized tracking task while maintaining central fixation. Trials where horizontal eye-movement or blinks were detected were excluded from further analysis. Stimuli were boxes subtending 0.6° on each side. Each trial began with a selection screen showing an array of stationary boxes. In the attended hemifield (which varied randomly from trial to trial), one or three boxes were colored red, while three or six boxes were colored black. In this experiment and all experiments reported here, all condition types were interleaved within each block of the experiment. Participants were instructed that the red boxes were targets that they would be asked to track through the movement phase. In order to perceptually equate the two hemifields, an equal number of boxes was presented in the unattended hemifield, with photometrically equiluminant green boxes substituting for the red boxes. After 500 ms, all red and green boxes were changed to black, rendering all objects visually identical. During the 2 s movement phase, all objects moved randomly at a rate of 2.2°/s. Objects bounced off one another and invisible walls that enclosed the 5.9° × 8.1° lateralized movement area. These areas were lateralized 0.8° from the central fixation point to ensure that small eye-movement would not allow participants to fixate objects during tracking. When motion stopped, one item in the attended hemifield became red while another became green in the opposite hemifield. Participants were instructed to categorize the red object as either a target or a distractor. The red item was a target on 50% of trials (see Figure 1). Accuracy scores were converted to the signal detection theory sensitivity parameter d′.
Figure 1.
Experimental procedure and stimuli. A) Procedure for Experiments 1 & 2. Objects on the attended and unattended side of the screen were photometrically equiluminant and are displayed as white and striped for illustrative purposes here. Participants were instructed to hold fixation while tracking attended objects. Trials where eye-movements were detected were discarded. B) Experimental stimuli used in Experiments 3 & 4.
2.2.3 Electrophysiological recording and analysis
ERPs were recorded in each experiment using our standard recording and analysis procedures (Drew & Vogel, 2008; McCollough, Machizawa, & Vogel, 2007). Participants were asked to hold central fixation throughout each trial, and we rejected all trials that were contaminated by blocking, blinks or large (>1 degree) eye movements. We applied a stringent rejection criteria to participants who were unable to hold rigid fixation, rejecting all participants where the percentage of rejected trials exceeded 25%. On the basis of these criteria, we rejected 6 of the 29 participants in Experiment 1 and 7 of the 36 participants in Experiment 2.
We recorded from 22 tin electrodes mounted in an elastic cap (Electrocap International, Eaton, OH) using the International 10/20 System. 10/20 sites F3, FZ, F4, T3, C3, CZ, C4, T4, P3, PZ, P4, T5, T6, O1 and O2 were used along with 5 non-standard sites: OL midway between T5 and O1; OR midway between T6 and O2; PO3 midway between P3 and OL; PO4 midway between P4 and OR; POz midway between PO3 and PO4. All sites were recorded with a left-mastoid reference, and the data were re- referenced offline to the algebraic average of the left and right mastoids. Horizontal electrooculogram (EOG) was recorded from electrodes placed approximately 1 cm to the left and right of the external canthi of each eye to measure horizontal eye movements. To detect blinks, vertical EOG was recorded from an electrode mounted beneath the left eye and referenced to the left mastoid. The EEG and EOG were amplified with a SA Instrumentation amplifier with a bandpass of 0.01–80Hz and were digitized at 250 Hz in LabView 6.1 running on a Macintosh. Contralateral and ipsilateral waveforms were defined based on the side of screen the participant attended on each trial. In this paper, as in previous work, we will focus on lateralized components by defining electrode pairs as either contralateral or ipsilateral with respect to the side of the screen the participants were asked to covertly attend on a given trial. Finally, we averaged the response across a set of 5 electrodes (P3/4, PO3/4, OL/OR, O1/O2 and T5/6) and the side of the screen that was attended on a given trial and subtracted ipsilateral from contralateral activity. The dependent variable for the ERP analyses is the amplitude of the resultant difference waves.
In previous work, we restricted our electrophysiological analyses to correct trials (Drew, Horowitz, Wolfe, & Vogel, 2011; Drew & Vogel, 2008). In the current set of studies, we are specifically interested in trials when errors are made. Therefore, all analyses in Experiments 1 & 2 include all trials. If increasing task difficulty increases the likelihood of dropping targets, then including incorrect trials should give us a better chance of finding an observable decrease in CDA amplitude.
2.3 Results
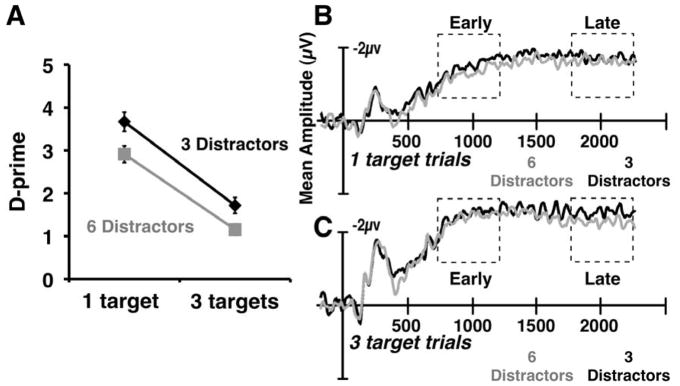
D′ is plotted in Figure 2A as a function of number of targets and number of distractors. To assess the effect of our task manipulations on performance, we computed a 2 (Target Load) X 2 (Distractor Load) repeated measures ANOVA. As predicted, we observed significant main effects of both Target (F(1,22)= 212.2, p<.001, η2= .90) and Distractor load (F(1,22)= 85.02, p<.001, η2= .79), replicating previous findings that increasing either distractor load or stimulus density decreases tracking performance (Bettencourt & Somers, 2009; Intriligator & Cavanagh, 2001). There was no significant evidence for an interaction between the two factors (F(1,22)= 2.41, p = .135, η2= .21), which may mean that they exert independent influences on tracking ability, though our experiment may simply have lacked he power to detect such an interaction.
Figure 2.
Experiment 1 results. A) Behavioral performance (d′) for Experiment 1. Error bars here and throughout the paper represent standard error of the mean. B) CDA amplitude for 1 target trials in Experiment 1. CDA amplitude is computed by taking the difference of contralateral and ipsilateral activity over an average of 5 posterior-occipital electrodes. See methods for additional details. C): CDA amplitude for 3 target trials in Experiment 1.
Turning to the ERP data, we measured mean amplitude of the difference waves for each of the four conditions during two 400 ms time windows: an early window beginning 300 ms after motion onset (800–1200 ms), and a late window near the end of the trial (1800–2200 ms). The logic of our analysis was that if distractor load caused participants to lose track of targets, losses are likely to accumulate over the tracking duration, so that we are more likely to observe a difference in the late window than the early window.
As with the behavioral data, we analyzed CDA amplitude with 2 2×2 repeated measures ANOVAs on each time window. Analysis of the early time window yielded a significant main effect for Target load (F(1,22)=49.97, p<.001, η2=.69), but not Distractor load (F(1,22)=1.35, p=.25, η2=.06), and the factors did not interact (F(1,22)=. 28, p=.59, η2=.01). Analysis of the late time window yielded the same pattern: a significant main effect of target load (F(1,22)=21.99, p<.001, η2=.5), there was no effect of distractor load (F(1,22)=1.79, p=.2, η2=.08) and the two factors did not interact (F (1,22)=.22, p=.64, η2=.01)
2.4 Discussion
These data are inconsistent with the hypothesis that the CDA reflects task difficulty. Both target load and distractor load have significant effects on performance, but only target load affects amplitude to a detectable degree. This finding is in agreement with the conclusions of Drew and Vogel (2008).
Our second hypothesis, that distractor load might reduce the resources available for tracking and lead to lost targets, was also not supported. That hypothesis predicts that we should have observed overall lower amplitudes in the high distractor load conditions, as fewer targets were being tracked. Furthermore, this effect should be cumulative: there should be more trials with lost targets toward the end of the trial then at the beginning, with is not consistent with the fact that we obtained the same findings in both early and late time windows. Thus, it seems likely that errors due to increased distractor load reflect swaps, where participants inadvertently end up tracking the wrong item by mistake.
However, one might conclude that this is the only possible outcome we could have observed. Perhaps even if participants were actually losing targets, they would latch on to the nearest item in hope that it was a target. Thus any manipulation that produces tracking errors will fail to alter CDA amplitude. On the other hand, perhaps the rate of swapping and dropping errors varies as a function of the factor being used to modulate difficulty. In the Experiment 2, we manipulated object speed: another classic method to manipulate MOT difficulty.
3. Experiment 2: Speed manipulation
In Experiment 2, we manipulated target load and object speed. Previous studies have demonstrated that MOT performance decreases with increasing speed (Alvarez & Franconeri, 2007; Bettencourt & Somers, 2009; Cohen, Pinto, Howe, & Horowitz, 2011). One explanation of this effect is that faster targets require increased attentional resources, drawn from a limited pool. Thus, fewer targets can be attended at greater speeds (Alvarez & Franconeri, 2007; Bettencourt & Somers, 2009). On this account, speed induces participants to drop targets, and should result in a decrease in CDA amplitude for fast trials relative to trials where the objects move more slowly. Alternatively, if the CDA is sensitive to the difficulty of tracking a target set, CDA amplitude should increase with increased speed.
3.2 Procedure
3.2.1 Participants
Twenty-nine neurologically normal participants (average age: 23.7) from the Eugene, OR community gave informed consent according to procedures approved by the University of Oregon institutional review board.
3.2.2 Stimulus displays and procedure
Unless otherwise noted, the procedures in Experiment 2 followed procedures from Experiment 1. There were two key differences. First, in this experiment, we held the total number of objects constant at eight across target load. Thus, the number of distractors is inversely related to the number of targets. However, since Experiment 1 showed that the number of distractors does not have a detectable effect on CDA amplitude, we can attribute any difference between target load conditions to the number of targets being tracked. Second, we varied item speed. In the slow speed condition, all objects moved at a rate of 2.2°/s whereas in the fast condition, object speed increased to a rate of 3.8°/s
3.3 Results
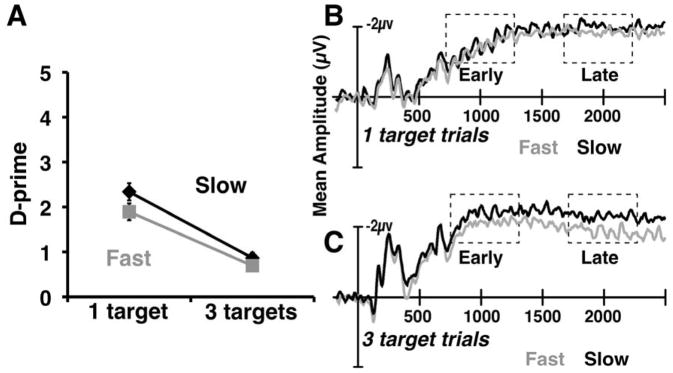
Analysis of behavioral results (d′) revealed main effects of both target load (F (1,28)= 162.7, p<.001, η2=.85) and object speed (F(1,28)= 21.96, p<.001, η2=.44), and the factors interacted significantly (F(1,28)= 6.04, p<.05, η2=.18; see Figure 3). Increased object speed led to a large, reliable cost in behavioral performance.
Figure 3.
Experiment 2 results. A) Behavioral performance (d′) for Experiment 2. B) CDA amplitude for 1 target trials in Experiment 2. C): CDA amplitude for 3 target trials in Experiment 2.
As before, we analyzed mean amplitude of the CDA during two critical time windows, early (800–1200 ms) and late (1800–2200 ms). The early window yielded a result similar to Experiment 1. There was a significant main effect of target load (F(1,28) = 21.89, p<.001 η2=.44), but no effect of object speed (F(1,28)= 2.33, p=.14, η2=.08) and no interaction (F(1,28)= 2.48, p=.13, η2=.08).
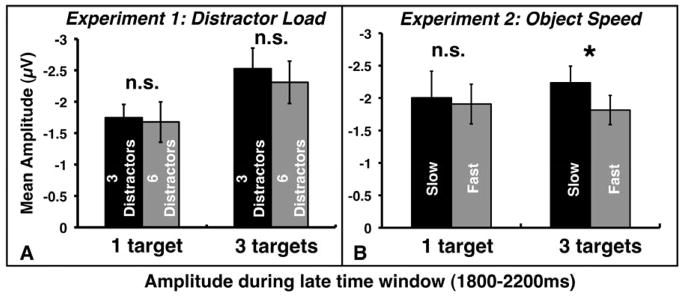
Recall that when reporting the results of Experiment 1, we argued that the effect of drops should be cumulative with time. On trials where the participant loses a target early, amplitude would be depressed throughout the trial, whereas on trials where the participant loses a target late, amplitude would only be depressed toward the end of the trial. Thus, the late time window is the critical test for the drop hypothesis. In the late time window, in contrast to Experiment 1, we observed a significant main effect of object speed (F(1,28)= 8.32, p<.01, η2=.23), but not target load (F(1,28)= 0.14, p=.60, η2=.01). In this experiment, the interaction was marginally significant (F(1,28)=3.33, p=.08, η2=.11). We used paired t-tests to further probe this finding. There was no difference in amplitude for the low target load condition (t(28)=0.96, p=.34, η2=.03). This may be due to fact that participants are unlikely to drop the only target that they are tracking regardless of object speed because doing so would leave the participant with no task for the remainder of the trial. However, in the high target load condition, mean amplitude in the fast object speed condition was significantly lower than slow amplitude (t(28)=2.89, p<.01, η2=.23). To highlight the different pattern of results evoked by modulating distractor load, we then computed post-hoc t-tests in the same late (1800–2200ms) period in Experiment 1 (see Figure 4). We found no evidence of an influence of distractor load on CDA amplitude (Set size 1 (t(22)=.38, p=.71, η2=.01); Set size 3 (t (22)=1.57, p=.13, η2=.1)). We performed a post-hoc power analysis (reference) in order to ensure that our experimental design was adequately powered to detect an effect of a similar magnitude to the one found in Experiment 1. Our analysis suggests that the design was adequately powered: π (1-beta error probability) = .81 given our alpha level of .05.
Figure 4.
Mean CDA amplitude during the late time window (1880–2200ms) for Experiment 1 (A) and Experiment 2 (B).
3.4 Discussion
There were three unambiguous findings from this experiment. First, in the early time window, we replicated the finding from Experiment 1 and Drew and Vogel (2008): increasing difficulty per se does not result in significantly increased CDA amplitude. This reinforces the conclusion that the CDA is initially measuring the number of items indexed, not the difficulty or amount of effort required. Second, there are conditions (here increased speed) under which increased difficulty decreases CDA amplitude.
The third major finding is the striking differences in the pattern of results under distractor load and object speed manipulations in the late time window. In this window, we found that there was a significant effect of object speed (Experiment 2), but not distractor load (Experiment 1). We also found a significant effect of target load in Experiment 1, but not in Experiment 2. The lack of a target load effect in the late time window is just as striking as the emergence of the speed effect. We have replicated the typical target load effect in a variety of contexts across three published papers (Drew, et al., 2011; Drew & Vogel, 2008) and a number of unpublished experiments, as well as Experiment 1 of the current paper and even the early time window of the present experiment. Why did it disappear in the late time window with fast moving objects?
One hypothesis would be that both distractor load and speed equally lead to drop errors, but that our ERP measures were not sensitive enough to pick up the effect in Experiment 1, because distractor load is a weaker manipulation than speed. The performance data do not support this story, however; the effect of distractor load on d′ is actually greater than the effect of speed, yet only speed produced a significant drop in CDA amplitude.
We argue that the most parsimonious explanation is that greater target speeds induce participants to drop targets. The drop hypothesis predicts lower amplitude with increased speed, because fewer targets are indexed. It specifically predicts that this effect should be larger in the late as opposed to the early time window, since losses are cumulative. It does not require that the target load effect disappear in the late time window. However, if we additionally stipulate that participants will almost always be able to track a single target, as long as speeds are slow enough to preclude data limitations (Verstraten, Cavanagh, & Labianca, 2000), then this finding begins to make sense. In the fast condition, participants may only be tracking one target on a majority of trials by the late time window. While the interaction was only marginally significant, post-hoc t-tests show that while there was a significant effect of object speed with three targets, the effect was not significant with only one target.
It is important to note that the decreased amplitude in the high load, fast trials does not mean all errors associated with increased object speed are due to dropping targets during the trial. Conversely not all errors associated with increased distractor load were necessarily due to swapping targets and distractors; indeed, there was a small (albeit not statistically significant) decrease in amplitude in the six distractor condition of Experiment 1, suggesting a small increase in drops. Nevertheless, the data overall suggest that the speed manipulation led participants to drop targets more often than the distractor load manipulation in Experiment 1. If we accept the premise that the CDA is an accurate representation of the number objects that are currently indexed, then the data from Experiments 1 & 2 clearly predict that errors associated with increased object speed tend to be due to dropping target items whereas increasing distractor load tends to lead to swapping errors where distractors are inappropriately tracked. We tested these predictions in Experiments 3 & 4.
4. Experiments 3&4: Distractor and speed manipulation with unique objects
Using behavioral data alone, it is difficult to ascertain the cause of errors during MOT. Our electrophysiological data suggest that distractor load tends to influence the rate of swapping errors while speed manipulations influence the rate of dropping errors. To test this prediction behaviorally, we manipulated object feature variability. Instead of tracking identical squares, here we asked participants to track cartoon animals. In the low variability condition, all of the animals were identical, while in the high variability condition, all of the animals were unique. We propose that rate of swapping and dropping errors should be differentially affected by this manipulation. Relative to tracking identical objects, the rate of swapping targets for distractors should decrease when tracking unique objects. As we noted in Experiment 1, swapping errors presumably come about because a target and a distractor approach within the width of the attentional window. When the two items separate, the visual system cannot decide which item to follow on the basis of location information alone. When all items are identical, this may lead to inappropriately tracking a distractor. However, this should be less likely when the items are unique. If you are tracking a monkey who crosses paths with a goat, it should be easier to keep tracking the monkey than in a situation where the monkey you are tracking crosses paths with another monkey.
In Experiment 3 we manipulated both distractor load and object variability (either Unique or Identical). Based on the logic above and our findings in Experiment 1, we predicted that the benefit of unique items would be larger when the distractor load increased because distractor load should lead to a higher rate of swapping. In Experiment 4 we manipulated object speed and object variability. Here, we predicted that the unique benefit should be unaffected by object speed because data from the preceding experiments suggests that the increased difficulty associated with increased object speed is primarily associated with dropping targets.
To our knowledge, this is the first experiment to suggest that specific circumstances lead to an increased likelihood of dropping a target rather than confusing it with another item. We must therefore consider the possibility that these results were a product of our specific experimental conditions. In the vast majority of MOT experiments, stimuli are presented in the central visual field, rather than lateralized, and observers are allowed free eye movements. Dropped targets might only occur in the unique situation where a lateralized target interacts with a distractor and the participant is not allowed to make a rescue saccade (Zelinsky & Todor, 2010) to disambiguate the collision. In order to test whether our results would generalize to more conventional MOT paradigms, in the final two experiments we used a non-lateralized design where participants were allowed to move their eyes freely. As a result, object speed was substantially faster (8.5–11.6 °/s) than in the electrophysiological experiments (2.2–3.8 °/s). Despite the large speed difference, the approximate behavioral performance was equivalent across all 4 experiments. The discrepancy in speed is due to the fact that participants in Experiments 1 & 2 had to track objects in the periphery while rigidly holding central fixation. When eye-movements are not prohibited, participants tend to either fixate the objects themselves or the centroid of the group of targets they are tracking (Fehd & Seiffert, 2008; Zelinsky & Neider, 2008). Not surprisingly, tracking in the periphery while maintaining fixation is difficult and we adjusted object speed accordingly.
4.2 Procedure
4.2.1 Participants
Twenty-seven neurologically normal participants (average age: 19.9; 13 in Experiment 3) from the Eugene, OR community gave informed consent according to procedures approved by the University of Oregon institutional review board.
4.2.2 Stimulus displays and procedure
Unless otherwise noted, the procedures for Experiments 3 and 4 were identical. Note that since we were not collecting ERP data in this experiment, stimuli were not lateralized. Instead, stimuli were contained within a square 17.5° on each side, centered in the screen. Sixteen cartoon animal stimuli were obtained from Michael J. Tarr’s website: http://www.tarrlab.org (Figure 4). Each animal occupied a square subtending roughly 1° of visual angle. At the beginning of the experiment, each participant was given a set of five random animals to track throughout the experiment. On identical trials, all objects (targets and distractors) had the same identity, chosen randomly from the subset of target animals. On unique trials, the targets comprised all five animals in the participant’s target set, while the distractors were sampled without replacement from the remaining animals outside the target set. Unique and identical trials were equally probable. Each trial began with a red target box flashing on and off on top of five target animals for 1500 ms. All objects then moved unpredictably for a variable interval of time, bouncing off one another and off the invisible borders of a the movement area. The movement interval was 500, 2000, 3500 or 5000 ms, after which all animals simultaneously stopped and turned into empty black boxes. One item turned into a red box and participants were asked to categorize this item as either a target or a distractor. The red item was a target on 50% of trials.
In Experiment 3, we manipulated distractor load in addition to the identity (unique or identical). There were five distractors in the low distractor load condition and ten distractors in the high load condition. All the objects in this experiment moved at a rate of 8.5 °/s. In Experiment 4, we manipulated object speed rather than distractor load. Distractor load was held constant at five objects. Object speed was 8.5 °/s on slow trials and 11.6 °/s on fast trials. In both experiments, participants completed 224 trials after a short block of practice trials.
4.3 Results
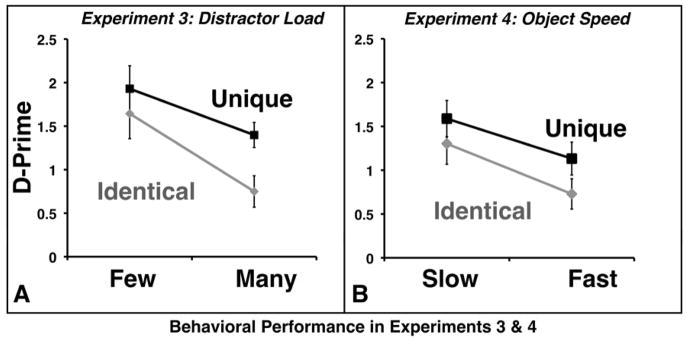
Behavioral performance (d′) for Experiment 3 is plotted in Figure 5A as a function of distractor load and object identity. We computed a 2 X 2 ANOVA on the average accuracy, excluding trials when the tracking duration was 500 ms. These trials were included as catch trials in case the participants tried to select target items near the end of the trial rather than tracking throughout the duration of the trial. We used the same approach in the analysis of Experiment 4. In both cases, inclusion or exclusion of the data from the catch trials does not change the outcome of the test (the presence or absence of an interaction). In Experiment 3 there was a large main effect for both object variability (F(1,12)=14.29, p<.005, η2=.54) and distractor load (F(1,12)=31.83, p<.001, η2=.73). The effect of object variability replicates the benefit for tracking unique objects observed in previous studies (Horowitz, et al., 2007; Makovski & Jiang, 2009). Critically, we obtained the significant interaction (F(1,12)=7.00, p<.05, η2=.37) predicted by our hypothesis: the benefit of object variability was larger when there were more distractors.
Figure 5.
Behavioral performance (d′) for Experiment 3 (A) and Experiment 4 (B).
In Experiment 4, there was a significant effect of both object speed (F(1,13) =17.1, p<.005, η2=.57) and object variability (F(1,13)=9.93, p<.01, η2=.43). Unlike Experiment 3, the two factors did not interact (F(1,13)=0.44, p= .51, η2=.03). These results support our hypotheses, lending credence to the idea that distractor load and object speed influence behavioral tracking performance for different reasons: increasing distractor load tends to increase the rate of inadvertently swapping targets and distractors while increasing object speed increases the rate of dropping items.
5. General Discussion
When difficulty is increased, estimates of tracking capacity go down. People are capable of tracking fewer fast moving objects than slow moving objects, and track fewer targets in the presence of more distractors than fewer. However, based on behavioral data alone it has never been clear why this is the case. Do participants truly track fewer objects when the task is more difficult, or are they simply more likely to track the wrong objects as difficulty increases? By employing CDA amplitude as an online index of the number of items being tracked, we can better understand how object speed and distractor load influence behavioral tracking ability. In the case of distractor load, we found that doubling the number of distractors significantly impaired tracking performance, but resulted in no discernible effect on CDA amplitude. We argue that this result indicates that participants tracked the same number of targets irrespective of distractor load; the increased errors at high distractor load were due to tracking the wrong items, rather than tracking fewer items. In contrast, we found that an increase in speed did lead to fewer items being tracked by the end of the tracking interval. This decrease may have been due to participants voluntarily dropping some fast targets so that they were better able to track the remaining targets, or targets may have been lost involuntarily. On the basis of these data, we hypothesized that the distractor load manipulation resulted in more swapping errors whereas the object speed manipulation led to more dropping errors.
We then tested these hypotheses in a pair of behavioral experiments comparing performance with unique items and with identical items. We reasoned that if additional errors are due to swapping, there should be a larger unique item advantage, because unique items should reduce the ambiguity that leads to swap errors. In contrast, object uniqueness should not have any effect on drop errors. In line with these predictions, we found that the cost of increased distractors was reduced for unique objects, while the cost of faster targets was not. In addition to providing converging evidence for our hypotheses, these results generalize our conclusions beyond the slow moving, lateralized stimuli required by the constraints of our ERP experiments.
To summarize, we have provided evidence to support the claim that CDA amplitude reflects the number of items tracked, irrespective of task difficulty. Here, as in previous studies (Drew & Vogel, 2008; Drew, et al., 2011), CDA amplitude faithfully increases in response to target load, but does not increase in response to other difficulty manipulations. Furthermore, our data suggest that while some difficulty manipulations (e.g., speed) increase the likelihood of dropping targets thereby changing the number of targets actually tracked, others (e.g. distractor load) increase the likelihood of confusing targets and distractors, ultimately resulting in decreased performance despite no change in the total number of items tracked.
5.2 Models of Multiple Object Tracking
Capacity estimates for a number of attentionally demanding tasks including MOT, visual working memory and enumeration are strikingly similar, leading to the proposal that there may be a “magical number 4” that serves as an architecturally constrained limit for the number of items that can be attended at any given moment (Cowan, 2001; Pylyshyn, 1989; Pylyshyn & Storm, 1988). A straightforward interpretation of these fixed architecture models would predict that the number of items that could be tracked might vary between individuals, but would be constant across stimulus conditions (though subject to data limitations). If an individual can track four targets because she has four visual indexes, for example, then she should be able to track four targets regardless of how fast they move or how many distractors there are.
This simple model was always unlikely to be true. Early in the study of MOT, Yantis (1992) pointed out that grouping targets could improve tracking, while Viswanathan and Mingolla (2002) demonstrated that performance improved when stimuli were distributed over more than one depth plane. Neither of these findings is compatible with a simple fixed architecture theory. More recently however, a number of researchers have shown that simple task manipulations such as, object spacing (Franconeri, et al., 2008), speed (Liu, et al., 2005; Alvarez & Franconeri, 2007; Bettencourt & Somers, 2009), number of distractors (Bettencourt & Somers, 2009), or even duration (Oksama & Hyönä, 2004; Pylyshyn, 2004), can drastically alter capacity estimates. To explain these results, Alvarez and Franconeri (2007) proposed that MOT relies on a flexible resource that can be reallocated in accordance with the amount of resources necessary to track each individual item (see also Cohen et al., 2011; Iordanescu, Grabowecky, & Suzuki, 2009). The flexible resource model predicts that capacity will vary inversely with the difficulty of tracking each individual item.
If there is a flexible attentional resource which is redeployed to fewer items when tracking is more difficult, it is fair to ask why the CDA should ever change at all. If there is a fixed pool of attentional resources in the brain available for tracking, why should it matter whether the resource is divided among one, two, three, or twenty items? If the total resource is fixed, then surely the neural response should be constant. The answer must be that there is more to tracking than the total amount of resources used.
To understand this distinction, consider Zhang and Luck’s (2008) “juice box” model of visual working memory capacity. In this model, there is a fixed number of structures (the juice boxes), as well as a limited resource (the juice), which can be flexibly allocated among the boxes. If you only need to remember one item, all the juice can go into one box, and the memorial precision for this item will be very high. As you add memoranda, the juice is divided into smaller portions among the available juice boxes, until the limit is reached. Once all of your juice boxes have an item, you cannot add more.
So there is a fixed limit, but under that limit, there is flexibility. We can apply a similar model to MOT performance (e.g. Horowitz & Cohen, 2010). As item speed increases, more resources are needed to track a target (Alvarez & Franconeri, 2007), and as the amount of juice required per box increases, fewer boxes can be tracked. In this analogy, the CDA amplitude corresponds to the number of boxes in play, but not the total amount of juice. If we minimize the distinctions between swapping and dropping by focusing on single target trials, CDA amplitude was unaffected by both a distractor load manipulation (Experiment 1) and an object speed manipulation (Experiment 2). In other words, two strong behavioral manipulations of MOT difficulty led to no difference in CDA amplitude. While we have shown here and in previous studies (Drew et al., 2011, 2012; Drew & Vogel, 2008) that the CDA is acutely sensitive to the number of objects being tracked at a given point in time, the current data show that CDA amplitude does not reflect the amount of resources that are devoted to tracking a static number of objects. We take this as converging evidence towards an important distinction between attentional resources devoted to the number of items and the fidelity of the representation for each item.
Our aim was to further delineate the mechanisms that underlie MOT by distinguishing between these two types of errors, and by developing methods to discriminate between them. While most recent models of MOT consider confusion between targets and distractors the primary cause of errors in MOT, this is the first paper to demonstrate strong evidence that targets can also be dropped. While we have shown that different difficulty manipulations tend to lead to different types of errors, it is not currently clear why this is the case. Specifically, we do not yet know what causes fast moving objects to be dropped. We can use the CDA to generate a rough estimate of when the dropping occurs, and the late timing of drop suggests that dropping is not a strategic decision made at the beginning of the trial to track a subset of items (Drew, Horowitz, Wolfe, & Vogel, 2011). Still, more works needs to be done to understand why objects are sometimes dropped during MOT. The manipulation of target-distractor relationships introduced in Experiments 3 & 4 appears to be a promising method for moving forward on this question.
We are not aware of any models of MOT that explicitly predict that targets will be dropped under specific circumstances. One recent computational model emphasizes the role of target and distractor confusion (what we have termed swaps), but does not address situations where a target may be dropped without concomitant pickup of another item (Vul, Frank, Tennebaum, & Alvarez, 2009). From a computational perspective, there must certainly be situations where it is logical to drop an uncertain target rather than continuing the expend resources tracking an item that has a low probability of being a target. Given the evidence of target drops provided here, we hope that future models will take this possibility into account. A recent model from Franconeri and colleagues (Franconeri, Jonathan, & Scimeca, 2010) has suggested that tracking is limited by object spacing and the number of close interactions between objects rather than other factors such as object speed, or even number of items. Although controversial (Holcombe & Chen, 2012), the model does an admirable job accounting for many of the results in the MOT literature (Franconeri et al., 2010). According to this account, targets that pass within the suppressive surround of other items should inhibit one another, creating noise in the target selection process. This situation may lead to dropping at target item, but it remains unclear why a speed increase should lead to more dropping than an increase in number of distractors.
6. Conclusions
One of the appeals of studying the neural underpinnings of a given task is that this approach allows researchers to draw inferences about the mechanisms that underlie these tasks which could not be gained through behavior alone. In some cases, these inferences can lead to novel predictions that would never have been made without an appreciation of the mechanisms that underlie behavior. In the current study, increasing either object speed or number of distractors led to behavioral costs. However, the electrophysiological data show that the increased difficulty manifest in fundamentally different ways: increasing speed appears to increase the rate of dropping targets whereas increasing distractor load seems to increase inadvertent swapping between targets and distractors. We found clear evidence in favor this very specific set of predictions in a behavioral MOT task. Our data also corroborate previously reported fMRI evidence (Shim et al., 2010) that there are neural mechanisms that underlie MOT which appear to index the number of items being attended and are insensitive to task difficulty. While the CDA appears to be finely sensitive the necessity to update target information (Drew et al., 2011), it is also insensitive to difficulty manipulations that tax the tracking stage, unless the manipulation leads a target being dropped, which decreases the CDA accordingly.
Highlights.
Errors in MOT are due to swapping targets with distractors or dropping targets.
Behavior cannot distinguish between these error types, CDA amplitude can.
CDA amplitude appears to decrease when objects are dropped.
Increasing distractor load led to swapping. Increasing speed led to dropping.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Alvarez GA, Franconeri S. How many objects can you track?: Evidence for a resource-limited attentive tracking mechanism. Journal of Vision. 2007;7(13):1–10. doi: 10.1167/7.13.14. [DOI] [PubMed] [Google Scholar]
- Bettencourt KC, Somers DC. Effects of target enhancement and distractor suppression on multiple object tracking capacity. Journal of Vision. 2009;9(7) doi: 10.1167/9.7.9. [DOI] [PubMed] [Google Scholar]
- Bae GY, Flombaum JI. Close encounters of the distracting kind: identifying the cause of visual tracking errors. Atten Percept Psychophys. 2012;74(4):703–715. doi: 10.3758/s13414-011-0260-1. [DOI] [PubMed] [Google Scholar]
- Cavanagh P, Alvarez GA. Tracking multiple targets with multifocal attention. Trends in Cognitive Sciences. 2005;9(7):349–354. doi: 10.1016/j.tics.2005.05.009. [DOI] [PubMed] [Google Scholar]
- Cohen MA, Pinto Y, Howe PDL, Horowitz TS. The what-where trade-off in multiple-identity tracking. Attention Perception & Psychophysics. 2011;73(5):1422–1434. doi: 10.3758/s13414-011-0089-7. [DOI] [PubMed] [Google Scholar]
- Cowan N. The magical number 4 in short-term memory: A reconsideration of mental storage capacity. Behavioral and Brain Sciences. 2001;24:87–185. doi: 10.1017/s0140525x01003922. [DOI] [PubMed] [Google Scholar]
- Drew T, Horowitz TS, Wolfe JM, Vogel EK. Delineating the neural signatures of tracking spatial position and working memory during attentive tracking. Journal of Neuroscience. 2011;31(2):659–668. doi: 10.1523/JNEUROSCI.1339-10.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Drew T, Horowitz TS, Wolfe JM, Vogel EK. Neural Measures of Dynamic Changes in Attentive Tracking Load. Journal of Cognitive Neuroscience. 2012;24(2):440–450. doi: 10.1162/jocn_a_00107. [DOI] [PubMed] [Google Scholar]
- Drew T, Vogel EK. Neural measures of individual differences in selecting and tracking multiple moving objects. Journal of Neuroscience. 2008;28(16):4183–4191. doi: 10.1523/JNEUROSCI.0556-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fehd HM, Seiffert AE. Eye movements during multiple object tracking: Where do participants look? Cognition. 2008;108(1):201–209. doi: 10.1016/j.cognition.2007.11.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Franconeri SL, Jonathan SV, Scimeca JM. Tracking multiple objects is limited only by object spacing, not by speed, time, or capacity. Psychological Science. 2010;21(7):920–925. doi: 10.1177/0956797610373935. [DOI] [PubMed] [Google Scholar]
- Franconeri SL, Lin JY, Pylyshyn ZW, Fisher B, Enns JT. Evidence against a speed limit in multiple-object tracking. Psychonomic Bulletin & Review. 2008;15(4):802–808. doi: 10.3758/pbr.15.4.802. [DOI] [PubMed] [Google Scholar]
- Horowitz TS, Birnkrant RS, Fencsik DE, Tran L, Wolfe JM. How do we track invisible objects? Psychonomic Bulletin & Review. 2006 Jun;13(3):516–523. doi: 10.3758/bf03193879. [DOI] [PubMed] [Google Scholar]
- Horowitz TS, Cohen MA. Direction information in multiple object tracking is limited by a graded resource. Attention Perception & Psychophysics. 2010;72(7):1765–1775. doi: 10.3758/APP.72.7.1765. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Horowitz TS, Klieger SB, Fencsik DE, Yang KK, Alvarez GA, Wolfe JM. Tracking unique objects. Perception & Psychophysics. 2007;69(2):172–184. doi: 10.3758/bf03193740. [DOI] [PubMed] [Google Scholar]
- Horowitz TS, Place SS, Van Wert MJ, Fencsik DE. The nature of capacity limits in multiple object tracking. Perception. 2007;36:9–9. [Google Scholar]
- Holcombe AO, Chen WY. Exhausting attentional tracking resources with a single fast-moving object. Cognition. 2012;123(2):218–228. doi: 10.1016/j.cognition.2011.10.003. [DOI] [PubMed] [Google Scholar]
- Hulleman J. The mathematics of multiple object tracking: From proportions correct to number of objects tracked. Vision Research. 2005;45(17):2298–2309. doi: 10.1016/j.visres.2005.02.016. [DOI] [PubMed] [Google Scholar]
- Intriligator J, Cavanagh P. The spatial resolution of visual attention. Cognitive Psychology. 2001;43:171–216. doi: 10.1006/cogp.2001.0755. [DOI] [PubMed] [Google Scholar]
- Iordanescu L, Grabowecky M, Suzuki S. Demand-based dynamic distribution of attention and monitoring of velocities during multiple-object tracking. Journal of Vision. 2009;9(4) doi: 10.1167/9.4.1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keane BP, Pylyshyn ZW. Is motion extrapolation employed in multiple object tracking? Tracking as a low-level, non-predictive function. Cognitive Psychology. 2006;52(4):346–368. doi: 10.1016/j.cogpsych.2005.12.001. [DOI] [PubMed] [Google Scholar]
- Makovski T, Jiang YV. Feature binding in attentive tracking of distinct objects. Visual Cognition. 2009;17(1–2):180–194. doi: 10.1080/13506280802211334. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Makovski T, Vazquez GA, Jiang YV. Visual Learning in Multiple-Object Tracking. Plos One. 2008;3(5):e2228. doi: 10.1371/journal.pone.0002228. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCollough AW, Machizawa MG, Vogel EK. Electrophysiological measures of maintaining representations in visual working memory. Cortex. 2007;43(1):77–94. doi: 10.1016/s0010-9452(08)70447-7. [DOI] [PubMed] [Google Scholar]
- Oksama L, Hyönä J. Is multiple object tracking carried out automatically by an early vision mechanism independent of higher-order cognition? An individual difference approach. Visual Cognition. 2004;11(5):631–671. [Google Scholar]
- Pylyshyn Z. The role of location indexes in spatial perception: A sketch of the FINST spatial-index model. Cognition. 1989 Jun;32(1):65–97. doi: 10.1016/0010-0277(89)90014-0. [DOI] [PubMed] [Google Scholar]
- Pylyshyn Z, Storm RW. Tracking multiple independent targets: Evidence for a parallel tracking mechanism. Spatial Vision. 1988;3(3):179–197. doi: 10.1163/156856888x00122. [DOI] [PubMed] [Google Scholar]
- Pylyshyn ZW. Some puzzling findings in multiple object tracking: I. Tracking without keeping track of object identities. Visual Cognition. 2004;11(7):801–822. [Google Scholar]
- Pylyshyn ZW. Some puzzling findings in multiple object tracking (MOT): II. Inhibition of moving nontargets. Visual Cognition. 2006;14(2):175–198. [Google Scholar]
- Ren DG, Chen WF, Liu CH, Fu XL. Identity processing in multiple-face tracking. Journal of Vision. 2009;9(5) doi: 10.1167/9.5.18. [DOI] [PubMed] [Google Scholar]
- Scholl BJ. What have we learned about attention from multiple object tracking (and vice versa)? In: Dedrick D, Trick L, editors. Computation, cognition, and Pylyshyn. Cambridge, MA: MIT Press; 2009. [Google Scholar]
- Scholl BJ, Pylyshyn ZW. Tracking multiple items through occlusion: Clues to visual objecthood. Cognitive Psychology. 1999 Mar;38(2):259–290. doi: 10.1006/cogp.1998.0698. [DOI] [PubMed] [Google Scholar]
- Scholl BJ, Pylyshyn ZW, Feldman J. What is a visual object? Evidence from target merging in multiple object tracking. Cognition. 2001 Jun;80(1–2):159–177. doi: 10.1016/s0010-0277(00)00157-8. [DOI] [PubMed] [Google Scholar]
- Shim WM, Alvarez GA, Jiang YV. Spatial separation between targets constrains maintenance of attention on multiple objects. Psychonomic Bulletin & Review. 2008;15(2):390–397. doi: 10.3758/PBR.15.2.390. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thomas LE, Seiffert AE. Self-motion impairs multiple-object tracking. Cognition. 2010;117(1):80–86. doi: 10.1016/j.cognition.2010.07.002. [DOI] [PubMed] [Google Scholar]
- Verstraten FAJ, Cavanagh P, Labianca AT. Limits of attentive tracking reveal temporal properties of attention. Vision Research. 2000;40(26):3651–3664. doi: 10.1016/s0042-6989(00)00213-3. [DOI] [PubMed] [Google Scholar]
- Viswanathan L, Mingolla E. Dynamics of attention in depth: Evidence from multi-element tracking. Perception. 2002;31(12):1415–1437. doi: 10.1068/p3432. [DOI] [PubMed] [Google Scholar]
- Vogel EK, Machizawa M. Neural activity predicts individual differences in visual working memory capacity. Nature. 2004;428:748–751. doi: 10.1038/nature02447. [DOI] [PubMed] [Google Scholar]
- Vogel EK, McCollough AW, Machizawa MG. Neural measures reveal individual differences in controlling access to working memory. Nature. 2005;438(7067):500–503. doi: 10.1038/nature04171. [DOI] [PubMed] [Google Scholar]
- Vul E, Frank MC, Tennebaum JB, Alvarez GA. Explaining human multiple object tracking as a resource-constrained approximate inference in a dynamic probabilistic model. In: Bengio Y, Shuurmans D, Lafferty J, Williams CK, Culotta A, editors. Advances in neural information processing systems. Vol. 22. La Jolla, CA: Neural Information Processing System Foundation; 2009. pp. 1955–1963. [Google Scholar]
- Yantis S. Multi-Element visual tracking - attention and perceptual organization. Cognitive Psychology. 1992;24(3):295–340. doi: 10.1016/0010-0285(92)90010-y. [DOI] [PubMed] [Google Scholar]
- Zelinsky GJ, Neider MB. An eye movement analysis of multiple object tracking in a realistic environment. Visual Cognition. 2008;16(5):553–566. [Google Scholar]
- Zelinsky GJ, Todor A. The role of “rescue saccades” in tracking objects through occlusions. Journal of Vision. 2010;10(14) doi: 10.1167/10.14.29. [DOI] [PubMed] [Google Scholar]
- Zhang WW, Luck SJ. Discrete fixed-resolution representations in visual working memory. Nature. 2008;453(7192):233–U213. doi: 10.1038/nature06860. [DOI] [PMC free article] [PubMed] [Google Scholar]