Haplotype-based profiling of subtle allelic imbalance with SNP arrays

Abstract

Due to limitations of surgical dissection and tumor heterogeneity, tumor samples collected for cancer genomics studies are often heavily diluted with normal tissue or contain subpopulations of cells harboring important aberrations. Methods for profiling tumor-associated allelic imbalance in such scenarios break down at aberrant cell proportions of 10%–15% and below. Here, we present an approach that offers a vast improvement for detection of subtle allelic imbalance, or low proportions of cells harboring aberrant allelic ratio among nonaberrant cells, in unpaired tumor samples using SNP microarrays. We leverage the expected pattern of allele-specific intensity ratios determined by an individual's germline haplotypes, information that has been ignored in existing approaches. We demonstrate our method on real and simulated data from the CRL-2324 breast cancer cell line genotyped on the Illumina 370K array. Assuming a 5 million SNP array, we can detect the presence of aberrant cells in proportions lower than 0.25% in the breast cancer sample, approaching the sensitivity of some minimal residual disease assays. Further, we apply a hidden Markov model to identify copy-neutral LOH (loss of heterozygosity) events as short as 11 Mb in mixtures of only 4% tumor using 370K data. We anticipate our approach will offer a new paradigm for genomic profiling of heterogeneous samples.

Genetic instability is a hallmark of tumors and results in a high prevalence of aneuploidy and copy-neutral loss of heterozygosity (cn-LOH) events. Since these events typically impact many bases in a single hit, they are important players in the accumulation of mutations that lead to cell dysregulation and tumor progression (Knudson 1971). Characterization of these mutations has myriad applications in cancer studies. For example, the presence of specific aberrations may allow classification of patients into risk or therapeutic sensitivity categories. In addition, characterization across samples will help to elucidate the basic dynamics of tumor-associated mutations.

One of the challenges in identifying mutations in a tumor sample comes from the presence of normal cell contamination within the sample, which dilutes the signal from the aberrant cells. Recently, specialized methods have been developed to characterize aneuploidy and cn-LOH occurring in a fraction of a sample using data from single nucleotide polymorphism (SNP) genotyping arrays. Here, we present methods that lower the boundary of sample purity at which aberrant events may be robustly estimated.

Our method relies on allelic imbalance (AI), or the alteration from the normal one-to-one allele ratio at markers heterozygous in the germline. For example, consider a heterozygous marker with alleles arbitrarily labeled as A and B. A duplication covering the marker results in either an AAB or ABB genotype with a corresponding allele ratio of 2:1 or 1:2; cn-LOH results in an AA or BB genotype with a more severe distortion (2:0 or 0:2). At high sample purity, the observed genotypes will reflect the tumor genome, and copy number changes can be inferred directly with standard software designed originally for germline data (Wang et al. 2007; Korn et al. 2008); cn-LOH can be inferred via comparison to paired normal tissue. However, when the sample is a mixture of mostly normal cells with a small number of tumor cells, the called genotypes will reflect the germline genotypes only. Thus, inferences of aberrations in the tumor must be made by detecting more subtle signals of allelic imbalance using additional data from the SNP microarrays.

These data include the B allele frequency (BAF) and the log R ratio (logRR). The BAF is derived from the ratio of the allele-specific signal intensities observed at the marker and may be interpreted as the proportion of chromosomes carrying the B allele; in a normal diploid sample, the expected BAF values are 0, ½, and 1, corresponding to the three possible diploid genotypes AA, AB, and BB. The logRR is a function of the sum of the allele-specific signal intensities at a marker and informs the total copy number. The logRRs are informative for mutation detection as long as the mutation creates a change in total copy number, and the BAFs are informative as long as the mutation creates allelic imbalance.

In a mixture sample, the BAF and logRR at each marker is an average of the signals from each of the cell populations, i.e., the tumor cells and the normal cells. Multiple segmentation-based methods exist to detect allelic imbalance and copy number changes in DNA from heterogeneous tumor samples (Beroukhim et al. 2006; Assié et al. 2008; Staaf et al. 2008a; Popova et al. 2009; Sun et al. 2009; Yau et al. 2010; Li et al. 2011). Each method attempts to detect heterogeneity by detecting increased dispersion or multimodality of BAFs at heterozygous loci. For example, BAFsegmentation (Staaf et al. 2008a) folds the BAFs over the expected value of 0.5 to create a “mirrored BAF,” the mean value of which can then be modeled using circular binary segmentation to detect a difference relative to adjacent regions. Along with the other aforementioned methods, the assumption is made that consecutive markers affected by the same aberration will exhibit consistent evidence of sample heterogeneity. At low tumor proportions, the effect of AI on the BAFs is so small that it is difficult to distinguish from the inherent stochastic deviation present in all array data. As a consequence, current SNP array-based methods have limited sensitivity for identifying specific events; a typical limit occurs at sample purities of 10%–15% for an unpaired sample.

Homer et al. (2008) overcame a similar problem, in a setting of forensics. They determined whether specific individuals had contributed to a pooled DNA sample by comparing the pooled sample allele frequencies to frequencies from a population reference sample. Although the allele frequency deviations attributable to any one individual are small, they may still be anticipated using the individual's genotypes. Our approach is reminiscent of this method. Here, we know the “individuals” in the pool are the two germline chromosomes and instead attempt to detect whether they have made differential contributions to the pool as a result of allele-specific loss or gain. We use a key feature of the data ignored by other methods, which is the correlation among BAFs within an allelic imbalance region created by the underlying molecular event.

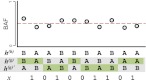
In Figure 1, we illustrate the input data and intermediate output of the method. Briefly, we first determine what the BAF data indicate to be the “excess haplotype” by applying a threshold at each marker independently. If no imbalance exists, this BAF-based haplotype reflects only stochastic deviation and may as well have been generated from a series of independent coin flips. Otherwise, if there is even a trace level of cells with AI, the BAF deviations reflect true underlying molecular imbalance, and the BAF-based haplotype should bear at least a subtle resemblance to one of the germline haplotypes. The germline haplotypes may be obtained via statistical estimation using the observed genotype calls, a matched reference sample, and principles of population genetics (Templeton et al. 1988; Clark 1990; Excoffier and Slatkin 1995; Stephens et al. 2001). We then quantify phase concordance between the BAF-based and statistical haplotypes using a local metric, switch consistency, which accommodates errors in the statistical reconstructions.

Figure 1.

Quantification of phase concordance. We illustrate the determination of local switch consistency using a hypothetical data set from 10 heterozygous loci. The plotted circles represent the BAFs at each marker. The shaded haplotypes, h^(g) and 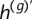, represent the germline haplotypes, obtained by statistical estimation using the called genotypes. We call each allele in haplotype h^(b) by comparing each BAF to a threshold (depicted as a dotted line). Then we assess local switch consistency, indicated in vector x, between the two haplotype reconstructions at each pair of consecutive heterozygous markers by looking for a match between h^(b) and either h^(g) or .

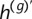We draw a parallel between our approach and two existing methods for slightly different settings. One is the trio-based algorithm of PennCNV (Wang et al. 2007), which uses parental genotypes to validate de novo copy-number variants (CNVs)—within a putative de novo CNV region, it identifies sites at which the maternal and paternal genotypes allow unambiguous determination of the chromosome on which the mutation occurred and then tests for consistency with a single chromosomal event by counting the number of sites that implicate the same chromosome. Another method with similarities to one of our specific applications is HATS (Dewal et al. 2012), which applies to data from next-generation sequencing. It uses a set of reference haplotypes to inform which haplotype has been deleted, demonstrating strong sensitivity for detecting deletion in a 10% tumor sample at moderate sequencing depths. To do so, they construct a hidden Markov model (HMM) to search reference haplotypes for likely sequences of nondeleted alleles that are consistent with the observed sample data.

Below, we demonstrate three applications of our method, which we call hapLOH, on real and simulated data. First, we attempt to detect the presence of aberrant cells in a sample by formally testing the phase concordance for deviations from the value expected in normal samples. This approach is analogous to testing for an unfair coin (subtle AI) with a large number of flips (many heterozygous markers). We then apply an HMM to identify specific regions harboring subtle levels of AI. Finally, given a region of AI, we call the specific alleles that are overrepresented. Although we focus on LOH (hemizygosity and cn-LOH), hapLOH captures AI resulting from any chromosomal mechanism that would affect consecutive markers and result in a haplotype imbalance, including duplications and more severe aneuploidies.

Results

Detection of tumor cells in highly diluted samples

We applied our method to Illumina 370K data from 10 lab dilution samples of the CRL-2324 breast cancer cell line and the matched lymphoblastoid (normal) cell line, ranging from 10% to 79% tumor. The cancer cell line genome is severely aneuploid, with over three-fourths of the genome having cn-LOH or aberrant copy number. We applied tQN (Staaf et al. 2008b) to the BAFs and logRRs to reduce allele-specific biases and also masked some sites that were aberrant in the normal sample (see Methods).

Application of the method to the 10% tumor sample data (103,556 heterozygous sites) results in a phase concordance of 0.65, which differs significantly from the expected null concordance of 0.5 (P-value = 10⁻²¹⁴⁰). Eager to query the limits of detection in this data set using our method, we created computational dilutions, literal averages of the BAFs, at much lower proportions of tumor, as well as at the proportions targeted in the lab dilutions. We also extrapolated the results from the observed 370K data to predict the results that would be observed from application of 1M and 5M SNP chips with 30% and 25% heterozygous markers, respectively.

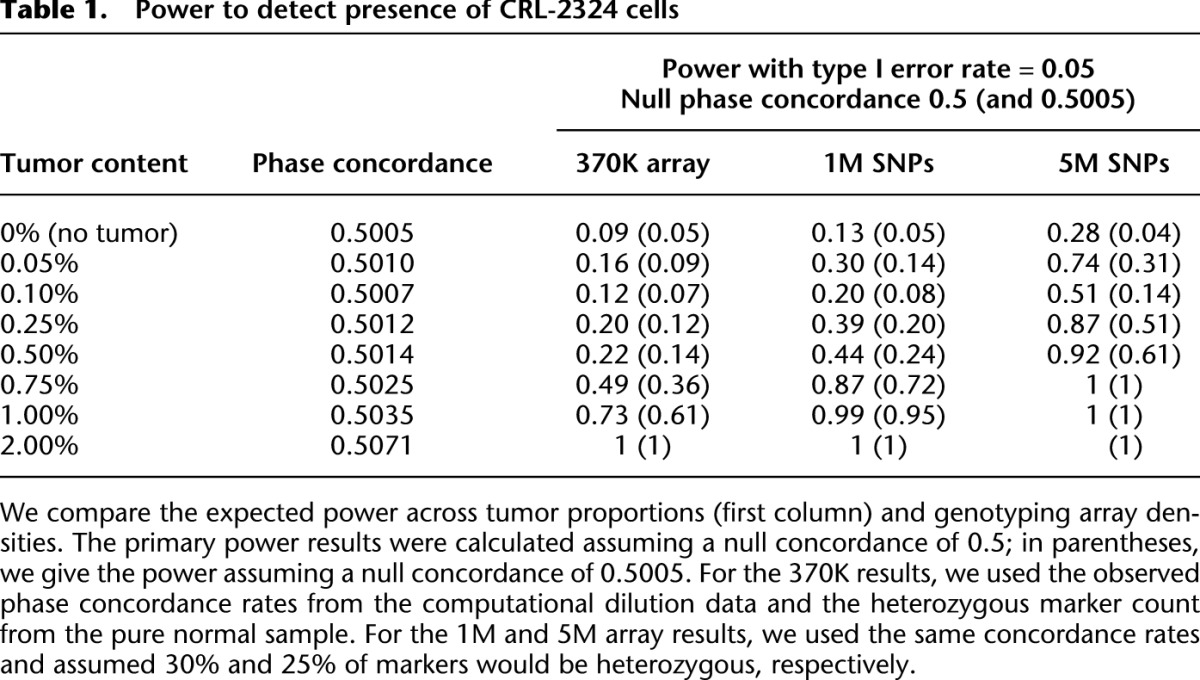
We present these results in Table 1. We observe that, in the pure normal sample, the phase concordance is 0.5005, which is slightly higher than the expected null concordance rate of 0.5. This deviation could be due to somatic nontumor-associated events in the individual or mutation during the growth of the cell line. To obtain the correct type I error rate for detecting tumor cells, we show power results using both the expected normal phase concordance rate of 0.5 and the observed “normal” rate of 0.5005. Our results indicate potential to detect aberrant cells for this particular breast cancer genome at concentrations on the order of two or three in 1000 using a hypothetical 5M SNP array (power > 50%). These levels may be close to a lower bound for this data set with our method, since at these levels we start to observe slightly erratic measures (phase concordance at 0.05% tumor is higher than at 0.10% tumor).

Table 1.

Power to detect presence of CRL-2324 cells

To further investigate the sensitivity of our method to somatic variation in normal tissue, we applied the method to 86 normal liver samples taken from patients who had liver cancer. We observed a slightly increased phase concordance relative to the expected null rate of 0.5 in many samples (Supplemental Fig. S1). This deviation may be due to slight contamination from nearby cancerous cells or to benign somatic variation. We applied our method to 12 control samples from a GWA study of lung cancer (Amos et al. 2008), conducted with an Illumina 317K SNP array. As expected, these data showed negligible signals of AI, with an average phase concordance of 0.501.

Instead of testing all markers genome-wide, one could test specific loci, such as gene regions or chromosome arms, to detect tumor cells with mutations at these regions. The power of the method depends on the number of observed heterozygous markers in the test region and the magnitude of the phase concordance for the region, which, in turn, depends on the type of imbalance event, the proportion of tumor cells in the sample, and the size of the aberration. In Supplemental Figure S2, we present the power to detect events across different values of these characteristics.

Identification of specific regions of allelic imbalance

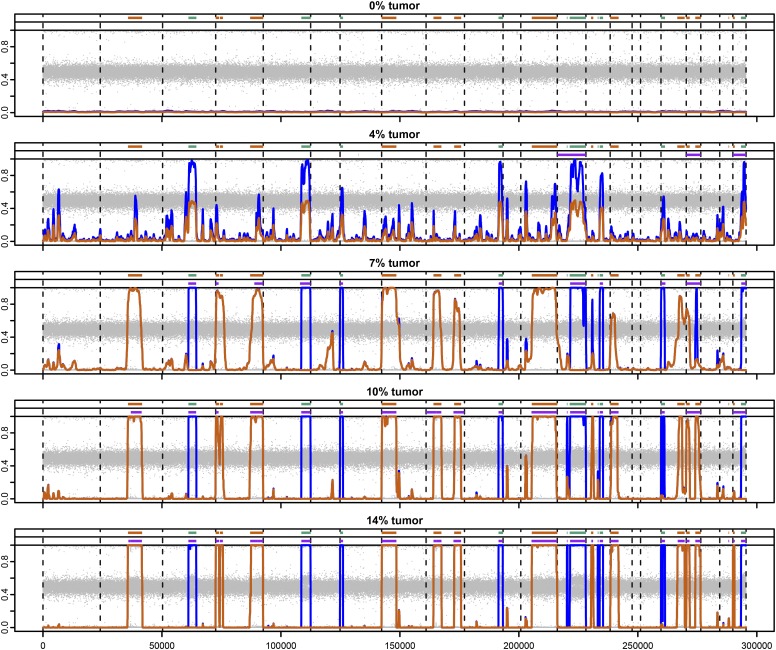
In the manner above, our method can aid in the detection of very low levels of tumor cells. However, this approach is naive because it ignores spatial clustering of the signal, which we would expect, given the underlying mechanisms of chromosomal loss or cn-LOH. Further, it is naturally of interest to identify specific regions of the genome exhibiting aberrations to look for known or potential tumor suppressor genes or oncogenes. To address this, we implemented a simple hidden Markov model with a latent process for two types of allelic imbalance, one for AI arising from deletions (lower imbalance) and one for AI from cn-LOH (higher imbalance). The HMM is applied to the switch consistency observations from a curated data set described in Methods. The curated data set includes 15 deletions and 10 cn-LOH events ranging in size from 2.39 Mb to 95 Mb. At each marker, the pointwise evidence of imbalance is summarized by the conditional probability of being in an AI state, given the data and parameters (“posterior probabilities”) (Fig. 2). We also applied BAFsegmentation with the mBAF threshold set to 0.526, which corresponds to deletion events occurring in at least 10% of the sampled cells; at thresholds corresponding to 9% tumor and below, the calls are highly unlocalized, usually covering entire chromosomes (data not shown).

Figure 2.

Local posterior probabilities of allelic imbalance at various dilutions. These whole-genome results are from a three-state HMM, accommodating two levels of imbalance. Horizontal lines at the top of each plot show the locations of simulated deletions (orange) and cn-LOH (green). Below these, purple bars show the regions identified by BAFsegmentation to contain AI. Vertical axes range from 0 to 1 for both the BAFs (gray points) and posterior probabilities (orange for deletions, blue for deletions and cn-LOH combined).

In the 4% tumor sample, the phase concordance rates for the deletions and cn-LOH events are not differentiated enough to classify the two types of events into different states with our current implementation. Still, even at this low tumor proportion, signal is obvious at the cn-LOH events. At 7% tumor, hapLOH discriminates between regions with different levels of imbalance. BAFsegmentation begins to identify the stronger (cn-LOH) signals at this tumor proportion; however, we have specified an approximate value of the true mixture proportion, a parameter of the algorithm for that method, which confers some advantage and in practice would not be known. At 14% tumor, virtually all events are picked up by both methods, although hapLOH produces only modest signal for at least one true event (1.52 Mb on chromosome 21) that was picked up by BAFsegmentation. At higher concentrations of tumor (>21%), the BAFs diverge so strongly from the expected normal value that the phase concordance reaches the upper limit; at these proportions, hapLOH no longer separates deletions and cn-LOH. We compare hapLOH and BAFsegmentation at multiple levels of sensitivity and specificity in Supplemental Figure S3.

Estimation of alleles overrepresented in the tumor genome

The tumor genotype profile can be inferred from the allele-specific counts at loci that have become imbalanced. Existing methods provide some knowledge of total copy number, and several attempt to provide allele-specific (or “parent of origin”) tabulation of copy number (Sun et al. 2009; Chen et al. 2011). Here, we assess the ability of hapLOH to provide this information. We developed an HMM to infer the over- and underrepresented haplotypes in AI regions, assuming a dominant tumor clone. In order to assess our allele calls, we used the BAFs for the pure tumor sample that was used in the creation of the dilution samples to get what we believed would be a highly accurate representation of the overrepresented haplotype. For each marker within the simulated event regions of our curated data set, we called a “B” if the pure tumor BAF was greater than 0.8 and an “A” if the BAF was less than 0.2.

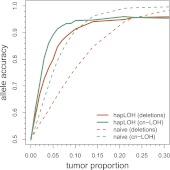
We then compared the overrepresented haplotype constructed using our HMM to these calls at a range of tumor proportions (Fig. 3). For comparison, we also constructed a naive estimate of the overrepresented haplotype by simply taking the allele with the highest frequency at each site. Integrating the statistical phase estimates with the BAF information using the HMM improves accuracy over the naive calls at the lower tumor proportions. For example, at 5% tumor content and within our simulated events, hapLOH achieved accuracies of 80% and 89% for deletions and cn-LOH, respectively, compared to 64% and 75% using the naive method. Our method may thus facilitate association studies of abundant or deficient haplotypes in diluted tumor samples using an allelic disequilibrium test (Dewal et al. 2010).

Figure 3.

Identification of the overrepresented haplotype. Solid lines indicate the accuracy of hapLOH's haplotype calls at deletions (orange) and cn-LOH (green) in the curated data set at various tumor proportions. Dotted lines indicate accuracy of the naive BAF-based calls. Accuracy was calculated as the proportion of correct calls at sites where we could confidently call LOH using the BAFs from the 100% tumor sample—about 18,000 markers for deletions and 8000 markers for cn-LOH.

Discussion

While surgical microdissection may yield greater tumor purity for studies of cancer genomics, in reality the available sample may be a significant admixture of tumor and normal cells. We have presented a new method, hapLOH, for the detection and profiling of allelic imbalance in tumor samples heavily diluted with cells from normal tissue. hapLOH may also be useful for studying samples with tumor heterogeneity, where aberrant events exist in a fraction of the tumor cells. Within an AI event that covers multiple heterozygous markers, at some markers the BAF will shift toward 1 and at others toward 0, creating a two-component mixture distribution. Existing SNP array-based methods interpret the detection of a two-component mixture as evidence of AI. When the AI event is subtle and the shifts thus small, determining whether there exist two distributions instead of one becomes a challenge, since the shifts produce an increased dispersion of the BAFs rather than an obvious change in the density. We use estimates of the germline haplotypes to capitalize on an alternative hypothesis of reduced dimension—the deviations of the BAFs will follow a very specific pattern determined by the molecular allele configuration. We essentially deconvolute a mixture by “imputing” jointly the component memberships of the BAF at each marker. We avoid the need to label lost or gained haplotypes by using phase concordance, which compares unordered haplotypes. The strength of the method comes from the highly specific alternative hypothesis, which allows even subtle imbalance to create a significant signal. We note that our method may also be applied to data from Affymetrix genotyping arrays; in Supplemental Table S1, Supplemental Figure S4, and the Supplemental Note, we describe an analysis using our method of normal-karyotype acute myeloid leukemia samples genotyped on the Affymetrix SNP 6.0 array.

Several aspects of our procedure are suboptimal and may be improved. For one, we do not consider the magnitude, per se, of the BAFs and ignore the total intensities; that is, we may do better by modeling more explicitly the distribution of the BAF signals and incorporating the logRR values into the method. In addition, more flexible modeling of the germline haplotypes may improve the sensitivity of our method, although the use of local switch consistency provides robustness to germline phasing errors (Supplemental Fig. S5). In ongoing work, we are addressing these issues.

The sensitivity and resolution of the method depends in part on the number of heterozygous markers in the germline DNA. Data from next-generation sequencing (NGS) may enable arbitrarily precise assessments of allelic imbalance, and we are adapting our methods to these data for studies of whole genomes and exomes. Due in part to the popularity of large population genetic surveys using NGS, such as The 1000 Genomes Project (The 1000 Genomes Project Consortium 2010), commercially available microarrays are available in increasing marker densities and offer the potential for highly sensitive yet affordable diagnostics. For example, we estimate that a 5M marker array would allow detection of tumor cells at very low concentrations, on the order of 0.25%, which may approach the sensitivity of some minimal residual disease (MRD) assays. More generally, application of hapLOH in this manner facilitates treatment of aberrant genomes as biomarkers. We note that low levels of nonmalignant somatic variation will also create a signal in our method and may not be uncommon in some tissue types such as epithelial tissue. When attempting to detect very subtle tumor aberrations in these tissues, a paired sample will be useful to determine an appropriate null phase concordance rate.

hapLOH also includes methods to locate allelic imbalance regions and to call the lost or gained haplotype within these regions, both of which employ HMMs. The profiling HMM imposes a geometric size distribution on mutations, though we provide options for flexible estimation of the parameters governing mutation size and genome-wide rate. We have shown that, in our curated data set, we are able to identify specific regions of cn-LOH at tumor proportions of about 4% and discern deletions from cn-LOH at 6%–7% tumor. Our HMM for identifying haplotypes gained or lost incorporates information about the confidence of the haplotype reconstructions.

In addition to the applications considered here, hapLOH may be utilized in other settings, such as for time-course monitoring of subtle changes in tumor genome profiles and cell concentrations or for monitoring response to therapy. We hope it may also aid in studies of cancers that require complicated filtration steps to enrich for tumor cells, such as myelomas. Finally, we note that nothing inherent in our method restricts its application to cancer genomics. Indeed, our method may be used to elucidate subtle somatic copy number variation or gene conversion in healthy individuals, such as in studies of twins or across tissue types.

Methods

Our method leverages the expectation that when imbalance exists in haplotypes rather than merely single-nucleotide alleles, a haplotype signal will be captured, however noisily, in the BAFs. We assess haplotypic imbalance by comparing crude haplotype reconstructions based on the BAFs with highly accurate statistical haplotype estimates. Since our method is designed for mixtures with a high proportion of normal cells, we use genotype calls obtained from the mixed sample and assume they are representative of the germline. For convenience, we assume the two alleles at a heterozygous site are arbitrarily labeled as A and B. Sites that are homozygous in the germline are ignored since the genotypes are uninformative with respect to phase and the BAFs are uninformative for AI (assuming no somatic point mutations at the typed SNPs).

Phase concordance

To provide further details, we will introduce the following notation for data from M heterozygous loci from a single individual. Let b_m denote the BAF at heterozygous marker m (m = 1, …, M), and let 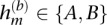represent the BAF-based estimate of the allele on the overrepresented haplotype. Our algorithm for calling alleles using the BAFs is simply the following:

where 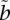is some threshold. When 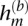is equal to 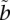, the alleles are assigned with equal probability. In principle, this threshold should be the median BAF for a diploid heterozygous genotype at marker m; in practice, we use the median of observed BAFs at all heterozygous loci. For convenience, at sites where the BAF is missing, we randomly assigned an allele. Let h^(b) denote the haplotype defined by the set of 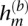alleles at all m. Similarly, let h^(g) denote one of the two germline haplotypes at heterozygous loci estimated statistically using homozygous genotypes as well (see below for details).

We assess phase concordance between h^(b) and h^(g) with switch accuracy (Lin et al. 2002), or more aptly “switch consistency,” since, in our setting, phase is not known but estimated. Formally, let x_i be an indicator of consistency between the two sets of two-site haplotypes defined by 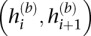and 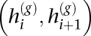(i = 1, …, M − 1), i.e.,

Across a set of consecutive heterozygous markers (j, …, k),

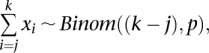where p is the true concordance rate in the marker region. From this distribution, it is straightforward to test for imbalance at arbitrary regions by testing p > 0.5 against the null hypothesis, p = 0.5. Implicitly above, we are assuming no marker-specific bias in the BAFs toward alleles that tend to cosegregate in the population, which could possibly arise if “B” allele designations were made based on population frequencies or in order of discovery, intentionally or otherwise, and there existed some biased intensity for alleles of the same label.

A hidden Markov model to identify regions of imbalance

Due to the segmental nature of AI events, signal in the data would not be distributed uniformly across the genome, but rather in clusters of phase-concordant heterozygotes (subsets of x where 1s are observed at a frequency higher than 0.5). To use this pattern to discover regions of LOH or other sources of AI, we implemented a simple HMM. Let L_i be an indicator for whether the interval between heterozygous loci i and i + 1 (i = 1, …, M − 1) is contained within a region of LOH (or aberration leading to AI) in the tumor genome and also what type of aberration. We assume L₁, …, L_M−1 form a Markov chain on three states, but this could be generalized further. The states are defined as follows: 0, no AI; 1, low level of AI; 2, higher level of AI. Each nonzero state may represent a different copy number in the aberrant cells or may capture one event type occurring in different proportions of the sample; that is, they are defined in terms of imbalance level, not explicitly in terms of underlying mutation characteristics. The transition probability matrix is constructed as

where λ₀ and λ₁ are assumed to be constant across marker intervals. This assumption could be relaxed or replaced by different modeling assumptions on mitotic processes underlying LOH, for example. Here, we have made the assumption that events consistent with states 1 and 2 have the same distribution for their tract lengths. Further, states 1 and 2 cannot directly communicate; the process must pass through the non-AI state to go between deletion and cn-LOH events. These assumptions are made mainly for reasons of parsimony but seem prudent based on presumed underlying mechanisms. Regardless, they may be generalized, and hapLOH accommodates such flexibility.

We let α_l (l = 0,1,2) denote the emission probability Pr(x_i = 1 | L_i = l). The emission probability α₀ for the non-AI state is set to 0.5. For the other states, the parameter is estimated from the data using an EM algorithm. At each iteration, the parameter α_l is updated to

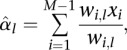where w_i,l is the marginal conditional probability that the process is in state l at marker interval i and is calculated using standard forward and backward algorithms (Rabiner 1989).

While it is reasonable to fix the transition probabilities λ₀ and λ₁, for the results presented here we estimate them from the data using pseudocounts for a combination of flexibility and stability. We obtain maximum a posteriori estimates by combining terms in the maximum likelihood estimator with pseudocounts in a “maximization” step of a stochastic-EM algorithm (first sampling L given the data and current values of parameters, then reestimating λ₀, λ₁, α₁, and α₂). Specifically, we assume λ₁ ∼ Beta(2.5, 999.5), motivated by a mode of 20 Mb for the average tract length of an AI event and ∼5% mass on average lengths <5 Mb. For λ₀, we chose parameters corresponding to a genome-wide rate of 10% for AI and such that the sums of the parameters of the two beta distributions were equal (so that total pseudocounts were equal). We found that fewer than 25 iterations of the EM algorithm were sufficient to achieve reasonable parameter estimates for these data.

Identifying alleles imbalanced in the tumor genome

Here, we present an approach to calling the over- and underrepresented SNP alleles in regions of AI, assuming a dominant clone. Our goal is to estimate the haplotype of the overrepresented chromosome, which we denote by h*. Note, to motivate our technique, that statistical estimation provides an unordered pair of haplotypes (represented by h^(g) and its complement 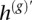) with a low but nonzero switch error rate. Thus, h* is a mosaic of h^(g) and 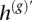, switching between the two when there has been a phasing error. Also note that, in AI regions, the haplotype h^(b) represents a guess at the allele in excess at each marker, although with low accuracy at the tumor proportions we consider. Nevertheless, when there is at least subtle imbalance, h^(b) contains information useful for determining which of the two haplotypes h^(g) and 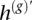is the source for h* at each marker.

To utilize this information, we assume a series of hidden states at M heterozygous loci, denoted by H₁, …, H_M, form a two-state Markov chain on {0,1} with transition probabilities specified by the switch accuracy estimates for h^(g) from fastPHASE. In this way, “prior” information from the statistical phasing can be propagated to inform distributions of the size and locations of “chunks” of h^(g) and 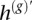that likely represent the actual excess chromosome. We let the observed data for our HMM consist of a series of indicators y₁, …, y_M, where

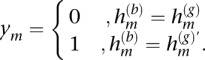Finally, the emission probabilities are specified as

where I_{C} is 1 if C is true and 0 otherwise, and a may be estimated from the data but has a natural relationship with the emission probabilities α specified above. In practice, we simply substitute 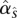, where 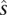is the maximum a posteriori estimate of the imbalance state for the interval to the right of the marker (or to the left for the last marker). The final step in our algorithm is to summarize the evidence that a particular allele is in excess by making maximum a posteriori probability estimates of H_m, (m = 1, …, M), which yields an estimate of h*. We can combine this with information about ploidy so that, at cn-LOH events, the estimates of genotypes in the tumor are the homozygotes of alleles in h*; at a deletion, the genotypes would be specified by a single copy of h*, etc. We note a more sophisticated approach to this problem would be to directly model the chromosome in putative excess in the HMM introduced above, and we are pursuing this in concurrent work.

SNP array data and haplotype estimation

Breast cancer cell line data

We downloaded genotypes, BAFs, and logRRs for 11 samples processed on the Illumina HumanCNV370-Duov1 BeadChip array (GEO accession GSE11976). These consisted of a breast cancer cell line with a paired normal (lymphoblastoid) cell line, and nine heterogeneous samples created from serial dilutions of these (in tumor proportions of 10%, 14%, 21%, 23%, 30%, 34%, 45%, 47%, and 50%). We ignored the 79% dilution, since most genotype calls did not reflect the germline genotypes. A more complete description of the data set is given in Staaf et al. (2008a). We applied tQN (Staaf et al. 2008b) to the BAFs and logRRs to reduce probe-specific biases so that the data more accurately reflected the true allele ratios and copy numbers. In an attempt to exclude regions that may indicate false positives, we removed some marker data from analysis (see Supplemental Table S2 and Supplemental Fig. S6 for details). After making these exclusions and taking the intersection with the HapMap samples that were used for phasing (see next section), the data set included 295,548 markers.

To investigate the performance of our method on samples with more subtle amounts of tumor cells, we created “computational dilutions” using the pure normal and pure tumor sample data. To remain consistent with real phenomena, we first visually inspected the BAFs and logRRs of the pure tumor sample and identified regions that had undergone complete cn-LOH or deletion. At each marker in these regions, we computed weighted averages of the normal and tumor BAFs and replaced the normal BAFs with these averaged BAFs. The weights reflect the proportion of tumor cells and the copy number of the LOH event. For tumor proportions below 10%, we assumed the genotypes would be the same as the normal genotypes. For the higher proportions, we assembled the set of genotypes for each curated sample by replacing the normal genotypes in the AI regions with the genotypes from the lab sample with matching tumor proportion. This gave us a “curated data set” with known event boundaries and tumor proportions (see Supplemental Table S3 for a complete list of events). Regions of AI covered 25% of the markers in the curated data set.

We note that these simulations are based on the observed BAFs themselves. To generate the test data for the detection of the presence of the tumor genome, we averaged the normal and tumor BAFs assuming hemizygosity for the odd chromosomes and cn-LOH for the even chromosomes to reflect our observation that these two event types constituted the majority of events and occurred in roughly equal proportions. Empirical comparisons with the laboratory-based dilution series indicate this procedure is well calibrated (Supplemental Fig. S7) and may be more accurate at very low levels of tumor than laboratory-based dilutions, where physically mixing such proportions is difficult.

Statistical estimation of haplotypes

To estimate the haplotypes from the observed (presumably germline) genotypes, we applied fastPHASE (Scheet and Stephens 2006) with default settings. For each data set, we extracted the SNPs in common with the HapMap (International HapMap Consortium 2005) CEU analysis panel, fit the model to the 120 CEU haplotypes, and then applied this fitted model to the unphased sample genotypes to infer haplotypes. From fastPHASE, we also obtained “switch probabilities” (the estimated “confidence” in two-marker haplotype reconstructions).

Software

The hapLOH software is available for academic, noncommercial use at scheet.org/software.