P-value-based regulatory motif discovery using positional weight matrices

Abstract

To analyze gene regulatory networks, the sequence-dependent DNA/RNA binding affinities of proteins and noncoding RNAs are crucial. Often, these are deduced from sets of sequences enriched in factor binding sites. Two classes of computational approaches exist. The first describe binding motifs by sequence patterns and search the patterns with highest statistical significance for enrichment. The second class uses the more powerful position weight matrices (PWMs). Instead of maximizing the statistical significance of enrichment, they maximize a likelihood. Here we present XXmotif (eXhaustive evaluation of matriX motifs), the first PWM-based motif discovery method that can optimize PWMs by directly minimizing their P-values of enrichment. Optimization requires computing millions of enrichment P-values for thousands of PWMs. For a given PWM, the enrichment P-value is calculated efficiently from the match P-values of all possible motif placements in the input sequences using order statistics. The approach can naturally combine P-values for motif enrichment, conservation, and localization. On ChIP-chip/seq, miRNA knock-down, and coexpression data sets from yeast and metazoans, XXmotif outperformed state-of-the-art tools, both in numbers of correctly identified motifs and in the quality of PWMs. In segmentation modules of D. melanogaster, we detect the known key regulators and several new motifs. In human core promoters, XXmotif reports most previously described and eight novel motifs sharply peaked around the transcription start site, among them an Initiator motif similar to the fly and yeast versions. XXmotif's sensitivity, reliability, and usability will help to leverage the quickly accumulating wealth of functional genomics data.

The rapid progress in high-throughput sequencing is transforming the way in which we study genomes and their role in regulating cellular and developmental processes. Increasingly, single-locus and single-gene approaches are replaced by genome-wide measurements. Whether it be ChIP-seq (Johnson et al. 2006), DamID mapping (van Steensel et al. 2001), CLIP-seq/PAR-CLIP (Hafner et al. 2010), ribosome profiling (Ingolia et al. 2011), DNase-seq (Crawford et al. 2006), FAIRE-seq (Giresi et al. 2007), HiTS-FLIP (Nutiu et al. 2011), RNA-seq (Garber et al. 2011), or chromosome conformation capture and its variants (Lieberman-Aiden et al. 2009), most of these experiments need to be analyzed with respect to protein and noncoding RNA (ncRNA) factors that bind to specific sequences in the genome or transcriptome. These binding events are the key to understanding regulatory processes because, unlike epigenetic marks, only the genomic sequence carries information at a density that is sufficient to target factors unambiguously to specific loci or transcripts.

Therefore, finding binding motifs for regulatory factors that are expected to be enriched in certain sequences is of central importance in the analysis of most of these types of experiments. This has led to a growing interest in tools for de novo motif finding (Tompa et al. 2005; Sandve et al. 2007). De novo motif discovery methods search for motifs of binding sites that are enriched in a positive sequence set in comparison to a negative sequence set or to a statistical background model derived from such sequences. Despite increases in experimental resolution, motif finding remains challenging: Motifs are typically short (about 6 to 15 bp), the binding sites are mostly only weakly conserved between related species (Borneman et al. 2007; Odom et al. 2007), and weak, statistically insignificant sites contribute a considerable portion to the overall factor occupancy (Segal et al. 2008; Kim et al. 2009). Last, binding sites often occur in only a small subset of input sequences.

Classical motif finding tools can be categorized as pattern based or PWM based. Pattern-based methods describe binding-site motifs by a consensus sequence, some methods allowing IUPAC characters that represent degenerate positions (e.g., W for A/T, S for C/G) (ERMIT) (Georgiev et al. 2010) and others allowing for a maximum number of mismatches to the consensus sequence (Weeder) (Pavesi and Pesole 2006). Pattern-based methods usually exhaustively evaluate the P-value of enrichment for thousands of seed nucleotide patterns of a given length. The enrichment P-value is the probability to obtain at least as many motif matches in the positive sequences by chance, that is, assuming that matches occur with the same probability as in the negative set or in the background model. Enrichment P-values for patterns are simple and fast to calculate using the hypergeometric or binomial distributions. The pattern methods then extend and refine the best seed patterns with the goal of finding the pattern with the most significant enrichment P-value. Most of the methods can report final PWMs by simply calculating the frequencies of the four bases in the matched subsequences.

PWM-based methods represent the motifs by PWMs. A PWM of length l is a 4 × l matrix that contains for each of the l motif positions the probabilities of the four bases. This representation gives a much more nuanced description of binding preferences than patterns. First, candidate PWMs are generated, for instance, by using the PWMs from an upstream, pattern-based motif discovery algorithm (AMADEUS) (Linhart et al. 2008), or using each l-mer occurring in the positive sequence to initialize a PWM (MEME) (Bailey and Elkan 1994). These PWMs are iteratively optimized using either Gibbs sampling (PRIORITY) (Narlikar et al. 2006) or the expectation maximization (EM) algorithm (MEME) (Bailey and Elkan 1994). As a heuristic measure of enrichment, these algorithms compute the statistical likelihood that a weighted mixture of the PWM and the background model generated the set of input sequences. Although optimizing the likelihood amounts to optimizing the fit of the PWM to the predicted motif occurrences, it is unclear how suitable the likelihood is for ranking motifs. Typically, PWM-based methods do calculate enrichment P-values, but since this usually involves time-consuming random sampling approaches (Knijnenburg et al. 2009) it is only done at the very end to rank the PWMs. A few methods for the exact or approximate computation of PWM P-values have been developed (Touzet and Varre 2007; Zhang et al. 2007), but they are much too slow for being used to iteratively optimize the PWMs (Supplemental Methods, section 3.4).

Here, we present XXmotif, an all-purpose de novo motif discovery tool that can directly optimize the enrichment P-values of motif PWMs. XXmotif combines a pattern-based enumerative approach with an iterative PWM refinement during which the PWM length and quality are improved by minimizing the enrichment P-value. When motif occurrences are expected to be positioned, XXmotif is able to calculate localization P-values and to combine them with the enrichment P-value in an exact, nonheuristic manner. We compared XXmotif with four state-of-the-art general-purpose motif discovery tools and their variants, each of which had recently been reported to be among the best-performing motif discovery methods. We also included a tool specialized to motif discovery in ChIP-chip/seq data sets that needs ChIP enrichment P-values as input (ERMIT) (Georgiev et al. 2010). ERMIT is representative of a class of more specialized methods that need sequence ranks or other information for each measured sequence (Foat et al. 2006; Eden et al. 2007; Georgiev et al. 2010). We then applied XXmotif to early embryo segmentation modules from D. melanogaster and to a large set of human core promoter sequences. We find most previously described and several novel motifs in these data sets. Intriguingly, among the eight newly discovered human core promoter elements is a motif that is sharply peaked around the transcription start sites, which resembles the canonical Initiator elements from other species.

Results

Overview of XXmotif

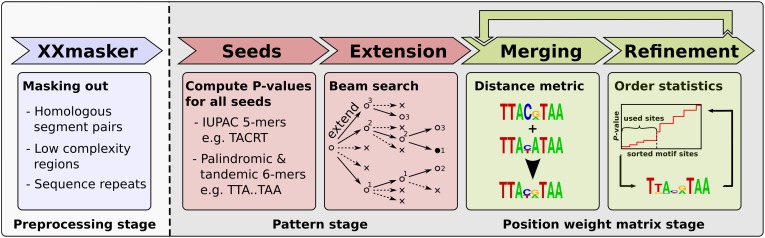
We now briefly describe how XXmotif works (Fig. 1). Please refer to the Methods and Supplemental Methods sections for details.

Figure 1.

Overview of XXmotif with its three main stages. After an optional step to mask confounding sequence regions (blue), enrichment P-values of all 5-mers and gapped palindromic and tandemic 6-mer seed patterns are evaluated, and the best seeds are recursively extended by an optional gap and a motif position (red). Patterns are converted to PWMs and fed to the PWM stage (green). Here, similar PWMs are merged and then iteratively refined by optimizing the motif enrichment E-value. Finally, merging and refinement stages are iterated until convergence.

Masking stage

When the input sequences contain homologous segments, repeat regions, or low complexity regions, parts of these may be reported as false motifs. In this study, we therefore masked out these regions using XXmotif's “XXmasker” option (Methods).

Seed stage

XXmotif starts by enumerating all 5-mer seed sequences with at most two degenerate IUPAC characters (S, W, R, Y, M, K). It also enumerates palindromic and tandemic (3 + 3)-mer seeds with central gaps up to size 11 and, at most, one degenerate IUPAC character per half (Fig. 1, Seeds). For each of these seed patterns, an enrichment P-value is calculated using a binomial distribution. In order to compare patterns of differing lengths, we transform P-values to expect values (E-values) using a length- and gap-dependent Bonferroni correction factor (Methods). For each nondegenerate seed (i.e., without IUPAC characters), the five most significant matching IUPAC seed patterns are subjected to length optimization (Fig. 1, Extension). This results in 5 × 4⁵ = 5120 5-mer seeds, 5 × 12 × 4³ = 3840 palindromic and 3840 tandemic 6-mer seeds. For each of the 12,800 seeds, the three patterns with the best E-values are further extended. The extension proceeds for all seeds and partially extended patterns, whether significant or not, until their enrichment E-values cannot be improved any further. All 80 possible extensions by an additional IUPAC character on either side of the pattern with a maximum gap size of three are assessed. After the extension, IUPAC strings are converted to PWMs by counting the nucleotides over all matched subsequences.

Merging stage

Similar PWMs are merged together if their Euclidean distance is below a certain threshold and the two patterns have at least 40% of their matches in common (Methods). The merging reduces the redundancy in the reported list of motifs, decreases run time, and may increase the sensitivity by aggregating information over binding sites that are likely to belong to the same factor.

Refinement stage

The PWMs are then refined and their lengths optimized by optimizing their statistical significance as measured by their enrichment E-value (explained below). The iterative step in the refinement consists of selecting the best motif occurrences in the positive sequences from which the updated PWM is computed. For this purpose, we first calculate match P-values for each possible motif placement, i.e., for each position in each of the input sequences. The match P-values quantify how well the potential binding site sequence matches the PWM. It is computed using a very fast branch-and-bound algorithm (Methods). To decide where to set the threshold between accepted motif occurrences (corresponding to factor binding sites) and nonfunctional sites, we sort the list of potential motif occurrences by their match P-values and test each possible index K ≥ 2 to split the list. For each K, we calculate the enrichment P-value, which is the probability for observing such a degree of enrichment by chance in a sequence set distributed according to the background model. More precisely, the enrichment P-value is the probability to observe by chance at least K nonoverlapping motif occurrences with a match P-value equal to or better than the K'th best (order statistic). The K that optimizes this enrichment P-value is used to select the sites contributing to the refined PWM. The same procedure of calculating match P-values and selecting the best score cut-off is then repeated using the updated PWM. To optimize the PWM length, PWMs are extended or shortened by up to two positions at both ends and their enrichment P-values are computed. As with patterns, the PWMs' enrichment P-values are transformed to E-values using a Bonferroni correction factor (Methods), and the refinement and extension steps are repeated as long as the E-value improves. Since merging PWMs may only become possible after PWM refinement and extension, the merging and refinement/extension steps are repeated together until the E-value cannot be improved any further. As an alternative to the “multiple occurrences per sequence” model just described, XXmotif can also be run with slightly different statistics to compute the enrichment P-values: a “zero or one occurrence per sequence” model or a “one occurrence per sequence” model (Supplemental Methods), which may be more sensitive to detect motifs that occur only once per sequence.

Negative sequence set

When a negative sequence set is given, the background distribution is modeled up to eighth-order using an interpolated Markov model (Salzberg et al. 1998). Otherwise, a background model of order 2 is learned from the positive sequence set. The choice of a good negative set is critical, as choosing an unsuitable negative set may result in seemingly significant false-positive motifs and long runtimes. A set is unsuitable if it has a significantly different trinucleotide composition from the positive set. Therefore, XXmotif compares the trinucleotide frequencies in the positive and negative sets and issues a warning when the root mean square deviation is above a trusted threshold.

Localization and conservation P-values

Motifs whose occurrences cluster at a fixed distance from a specified anchor point can be detected particularly well with XXmotif by combining the enrichment P-values of motif occurrences with their localization P-values. The localization P-value of each motif is on the order of d/L, where d is the distance from the cluster center and L is the length of the sequences in the positive set (exact calculation in Supplemental Methods, section 3.8). These P-values are combined with the match P-values for each potential motif occurrence before using the order statistic to compute enrichment P-values. When multiple sequence alignments over orthologous sequences from related species are given as positive set, XXmotif can compute conservation P-values for each potential motif occurrence (Supplemental Methods, section 3.6). Briefly, we count the number of mutations between the motif sequence in the main species and the aligned orthologous sequences and calculate the conservation P-value as the probability of observing that many or fewer mutations by chance given the frequency of each nucleotide within the motif sequence in the main species.

Sensitivity of motif detection methods

Benchmarks based on artificially created test sequences containing randomly placed occurrences of known motifs (Tompa et al. 2005; Sandve et al. 2007) have the advantage of being easy to evaluate since the true sites are known, but it has been questioned how transferable the results are to real biological data. For our first two benchmark tests we therefore use the most widely employed biological test set for motif discovery tools, which consists of lists of S. cerevisiae intergenic regions that were significantly enriched in 352 ChIP-chip experiments using 203 tagged transcription factors, 82 of which where assayed under several conditions (Harbison et al. 2004). For a subset of 80 transcription factors and 156 experiments, Harbison and colleagues found a published motif as a gold-standard reference. We gave the general-purpose motif discovery tools the positive and negative sets of intergenic sequences, as described in Harbison et al. (2004) (ChIP-chip P-values < 1 × 10⁻³ and > 0.5, respectively), while ERMIT (Georgiev et al. 2010) was supplied with all intergenic sequences and with the set of published ChIP-chip enrichment P-values for each sequence and each experiment. As in Harbison et al. (2004), only experiments having at least 10 sequences with a ChIP-chip P-value < 0.001 were considered.

In addition to the gold standard set of literature motifs described by Harbison et al. (2004) (“Harbison set”) we used two more recent data sets of literature motifs obtained by protein-binding microarray (PBM) experiments: the “Bulyk set,” 56 motifs matching to 101 experiments (Zhu et al. 2009), and the “Hughes set,” 72 motifs matching to 126 experiments (Badis et al. 2008). We defined a correctly detected motif as having a normalized Euclidean distance smaller than a given threshold, as in Harbison et al. (2004). But when working with the “Bulyk set” it became obvious that we also needed a condition of minimum entropy in the overlapping part of both matrices, as was done by Gordân et al. (2010). This precludes counting motifs as correct that look similar only in noninformative regions (Methods).

We measured the sensitivity of the motif discovery tools in the same way as was done previously (Harbison et al. 2004; Linhart et al. 2008; Georgiev et al. 2010; Gordân et al. 2010). For each tool, we counted the number of successfully identified motifs within the top 1 and top 4 predictions (Fig. 2; Supplemental Table S1). Tools that can include conservation information were tested in both versions. When including conservation, the four yeast species in the sensu strictu Saccharomyces clade were used for comparison (Methods).

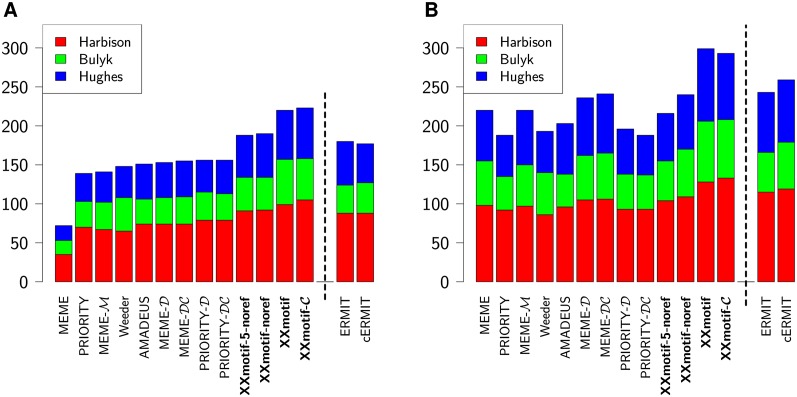
Figure 2.

Sensitivity of motif discovery tools on yeast ChIP-chip data. Shown is the number of correctly predicted transcription factor binding motifs within the top 1 (A) or top 4 predictions (B). Predictions are based on ChIP-enriched intergenic regions from 352 ChIP-chip experiments (Harbison et al. 2004). Three experimental reference sets are used to judge the correctness of motifs (red, green, blue). The dashed line separates the general-purpose motif discovery tools from ERMIT, which needs ChIP enrichment P-values. In the tool names, M indicates a fifth-order Markov model, C the use of conservation, and D the discriminative prior from the Hartemink lab (Gordân et al. 2010). XXmotif-noref and XXmotif-5-noref omit the PWM refinement and the latter version uses only 5-mer seeds.

XXmotif without conservation information found 220 correct motifs cumulated over all three data sets, 41% more than PRIORITY-D (Gordân et al. 2010) with 156, the next best general-purpose tool, and 22% more than ERMIT (Georgiev et al. 2010), which is specialized for ChIP-chip/seq data. With conservation, XXmotif-C detected 223 correct motifs, 43% more than PRIORITY-DC (Gordân et al. 2010). Interestingly, the background model is important to avoid ranking false motifs as top candidates. The standard version of MEME (Bailey and Elkan 1994) uses a zeroth-order background model trained on the input set and scores only 72 correct motifs among its top predictions. Replacing its zeroth-order background model with a fifth-order Markov model learned from the negative set (MEME-M) raises this number to 141. This can be further increased to 153 by using the discriminative prior from the Hartemink lab (MEME-D) (Bailey et al. 2010). We analyzed the influence of the background model by running XXmotif with interpolated Markov models of order 0 to 9 (Supplemental Fig. S1). The sensitivity improved quite dramatically from order 0 (with 77 correctly detected motifs) to order 2 (190 correct motifs), and further improvements were seen up to order 8 (220 correct motifs).

When considering the best prediction out of the top 4 (Fig. 2B), MEME with a zeroth-order model achieved results nearly as good as the tools using higher-order background models. Hence, the higher-order background model and discriminative prior mainly help to rank down false motifs, which are often repetitive or have a biased nucleotide composition. The sensitivity of Weeder (Pavesi and Pesole 2006), AMADEUS (Linhart et al. 2008), and PRIORITY on the top 4 motifs is lower than that of MEME, as these tools often report different variants of the same motif.

In order to understand the origin of XXmotif's high sensitivity, we built a simplified version that omits the PWM-based merging, refinement, and ranking stage (XXmotif-noref). This purely pattern-based version simply reports the PWMs calculated from the matched sites in the positive sequence set. These are the same PWMs that are merged and refined in the full XXmotif method. The PWMs are ranked by the enrichment E-values of the patterns. Figure 2A shows that, of the 43% improvement of XXmotif over the best general motif discovery tool PRIORITY-D, about half (34 motifs) are explained by our effective, pattern-based search stage. Three percent of this improvement (two motifs) is due to using tandemic and palindromic 6-mer seeds in addition to all 5-mers, as can be seen from the results of running XXmotif-noref with the 5-mer seeds-only option (XXmotif-5-noref).

The other half (33 motifs) are owed to the PWM stage with its PWM refinement by E-value minimization and the E-value-based ranking of PWMs. Within the top 4 ranked predictions, XXmotif-noref finds 240 correct motifs, while the full XXmotif discovers 299, or 25% more (Fig. 2B). This improvement is higher than for the top-ranked predictions in Figure 2A, which shows that the positive effect of the PWM stage is not simply due to providing a better ranking of motifs, but that it leads to improved predictions at all ranks.

Surprisingly, none of the tested tools—including our own—could gain significantly on this data set by using conservation information. MEME-D/DC improved from 153 to 155, PRIORITY-D/DC stayed constant at 156, and ERMIT/cERMIT even decreased from 180 to 177. These sobering results might be due to only weak cross-species conservation of functional binding sites (Borneman et al. 2007; Odom et al. 2007), but they may also point to limitations of how conservation is evaluated and integrated into the motif search (see Discussion).

We investigated the impact of the masking stage by testing the performance of the other tools on the masked sequence data. We observed minor improvements between 0% and 7% (Supplemental Table S1). We also studied the influence of how greedily PWMs are merged during the PWM refinement stage. The greediness of merging controls the redundancy in the list of predicted motifs. Changing the merging threshold from its standard setting “high” to “medium” (Methods) resulted in insignificant changes in sensitivity, both for the top motif and for the best four motifs, whereas a “low” threshold resulted in slight losses in sensitivity.

Reference-free quality assessment of detected motifs

To assess the quality of the predicted motifs quantitatively, we could simply evaluate the similarity of the predicted motif PWMs to the reference motifs. However, since some of the reference motifs themselves may be inaccurate, we used a reference-free quality assessment similar to the one in Zhu et al. (2009). We analyzed how well the ChIP-enriched regions of Harbison et al. (2004) are predicted using the motif PWMs reported by the tools. Of the 352 ChIP-chip data sets from Harbinson and colleagues we selected the 247 data sets that have at least 10 significantly ChIP-enriched regions (ChIP P-value < 0.001), as described by Harbison et al. (2004). The negative sequence sets were generated as in the previous section. We selected the best from each breed of tools, ran these six tools on the 247 sequence sets, and analyzed the PWMs they reported. For this purpose, we ranked all intergenic regions by the score of the best match to the reported PWM. Regions that were significantly ChIP-enriched (P-value < 0.001) were counted as correct predictions, all others as false predictions. A receiver-operating characteristic (ROC) curve plots the number of correct predictions over the number of false predictions (Supplemental Fig. S2). Usually, only a small fraction of all intergenic regions contain a binding site for a transcription factor. We therefore calculated the partial area under the ROC curve (pAUC) within the best-ranked 5% false predictions. Here, pAUC = 1 corresponds to a perfect PWM that scores all significantly ChIP-enriched regions above all other regions. A PWM whose correct predictions are distributed uniformly among the 5% false predictions would achieve a pAUC ≈ 0.5. To avoid rewarding methods that tended to report overly specific motifs, we used fivefold cross-validation, ensuring that PWMs are assessed on a part of the data that was not used to predict these PWMs.

Figure 3 shows the cumulated distribution of pAUC values, for the 247 PWMs (Fig. 3A,B), and for each of 151 PWMs on a collection of 151 high-quality ChIP-chip data sets (explained below) (Fig. 3C,D). In A and C, the pAUC values of all top-ranked PWMs are plotted (no matter whether these motifs were reported as significant or not). The average pAUC values are listed in the legend. For the best of the top 4 PWMs, XXmotif attains an average pAUC value 26%–34% higher than MEME-DC and 45% higher than PRIORITY-DC, the next best tools (Fig. 3B,D). Similar results are obtained on the top-ranked PWMs (Fig. 3A,C).

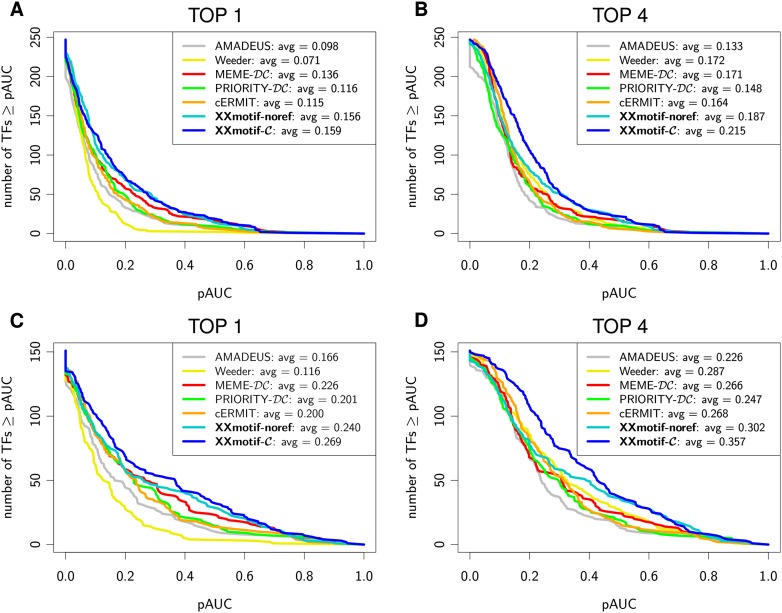
Figure 3.

Reference-free PWM quality assessment on yeast ChIP-chip data. The curves quantify how well the scores of the reported PWMs can predict the ChIP enrichment of the sequences. Intergenic regions are ranked by their maximum PWM score. For each predicted PWM, a ROC curve with the number of correct predictions over the number of false predictions is computed, and the partial area under the 5% best-ranked false predictions of the ROC curve (pAUC) is calculated. The plots show the cumulative distributions of pAUC values (A,B) for all 247 ChIP-chip data sets that had at least 10 significantly enriched regions (P-value < 0.001). Regions with a ChIP enrichment P-value of <0.001 are defined as correct predictions, all other regions as false predictions. (C,D) Same as A and B but using a subset of 151 high-quality data sets. For “TOP 4,” the best of the top 4 reported motifs is evaluated. The average pAUC scores are listed in the figure legends.

The biggest differences between top 1 and top 4 predictions are observed for Weeder, scoring 0.071 and 0.172, respectively, although top 1 and top 4 predictions are comparable in the sensitivity benchmark (Fig. 2). Weeder has the tendency to report short motifs as the top 1 prediction. These PWMs are too unspecific to achieve good pAUC values, although they are counted as correct in the sensitivity benchmark. The improvement for the top 4 predictions mainly originates from longer versions of the same motif at lower ranks. In contrast, PRIORITY and AMADEUS have a predefined motif length (eight by default). Since many regulatory elements have more than eight informative positions, their motifs are often less specific than those of tools that optimize the motif length. cERMIT incorporates conservation information into the algorithm by filtering out all nonconserved binding sites. This strategy leads to very specific PWMs that cannot generalize well to weak, but functional sites, and, hence, to relatively low pAUC scores (Fig. 2). ERMIT, the version without conservation scoring, obtained significantly better average pAUC values (Supplemental Fig. S3). XXmotif incorporates conservation information by combining P-values for conservation and motif enrichment (Supplemental Methods). Therefore, conserved and nonconserved sites can contribute to the resulting motif, leading to good motif qualities for both the top 1 and top 4 predictions.

No tool achieved a pAUC value of larger than 0.7 on any of the data sets, although ∼50% of the PWMs are expected to be correct according to Figure 2. This low correlation of binding sites predicted using PWMs and in vivo binding sites as measured by ChIP-chip/seq and related techniques is well known, and various causes have been implicated, such as chromatin accessibility (Li et al. 2011), binding competition with nucleosomes (Segal and Widom 2009) and with other transcription factors (Zhou and O'Shea 2011), and indirect binding to DNA.

We observed that quite often, long CA- and TG-repeats were predicted irrespective of the immunoprecipitated transcription factor. These unspecific motifs are over-represented in the ChIP-enriched regions of the Harbison data set, and therefore obtained high pAUC scores (Eden et al. 2007). To reduce these and other potential sources of discrepancies between ChIP-enrichment and binding sites, we defined a collection of 151 high-quality data sets that have at least five significantly ChIP-enriched sequences (P-value < 0.001) with matches to one of the reference motifs in the “Harbison set,” the “Bulyk set,” or the “Hughes set.” Here, we defined a match to a reference motif by a log-odds score of at least 70% of the maximum attainable log-odds score for the PWM. For the ROC analysis, we also ignored ChIP-enriched regions without a match to one of the transcription factor's reference motifs. Figure 3, C and D show the resulting pAUC distributions. Around 50% of all top-ranked PWMs reported by XXmotif achieved pAUC values of at least 0.2, compared with 30% in Figure 3A. XXmotif improved most on this stricter set since its masking stage tended to suppress the low-complexity CA- and TG-repeats.

Sensitivity of motif discovery in metazoan and mammalian sequences

The great majority of motif discovery tools have been tested on artificial data sets or on the yeast ChIP-chip data sets of Harbison et al. (2004). Shamir and coworkers therefore assembled a benchmark set (“metazoan target set compendium”) with sequences mainly from human and mouse (Linhart et al. 2008): 32 target sets contain enriched transcription factor binding sites from human, mouse, fly (Drosophila melanogaster), and worm (Caenorhabditis elegans), which are based on ChIP-chip experiments, coexpressed genes, and other data sources. Ten target sets from human and mouse contain genes that are coregulated under microRNA (miRNA) knock-downs.

The 8-mer miRNA seeds were imported from miRBase 16.0 (Griffiths-Jones et al. 2006). While Linhart et al. (2008) used experimentally validated transcription factor PWMs from release 8.0 of the TRANSFAC database (Wingender et al. 1996), we could only access the latest public release (7.0) and therefore had to remove eight transcription factors from the analysis. We used the benchmark set-up and motif divergence metric as described in Linhart et al. (2008). We evaluated the sensitivity of XXmotif and the best versions of the previously tested tools without sequence conservation scoring. ERMIT could not be evaluated, since for many target sets no P-values existed. We used the same metric as before to calculate the distance of a predicted motif from a literature motif. If multiple validated motifs were listed in TRANSFAC or miRBase, we took the motif that had the lowest distance to the predicted motif.

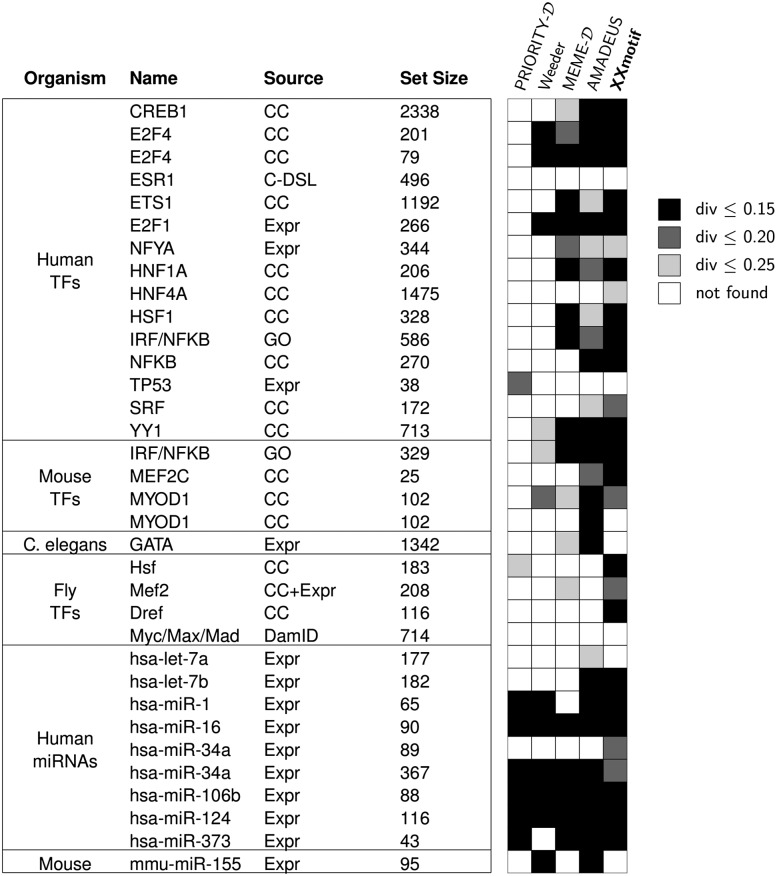
Figure 4 displays the results of the top 4 predictions in the same way as in Linhart et al. (2008). On the transcription factor target sets, PRIORITY-D finds only two correct motifs, Weeder, MEME-D, AMADEUS, and XXmotif find 6, 14, 17, and 19, respectively (light-gray boxes). When counting only predictions with a Euclidean distance ≤0.15 (black boxes), PRIORITY-D achieves 0, Weeder 3, MEME-D 8, AMADEUS 10, and XXmotif 14 correct predictions. On the miRNA target sets, PRIORITY-D and AMADEUS, whose fixed motif length of eight coincides with the length of the miRNA seeds, are able to detect six and nine miRNA seeds, respectively. Weeder and MEME-D find six and five, respectively, whereas XXmotif finds eight correct miRNA seeds. The results for the top 1 predictions show the same trend (Supplemental Fig. S4).

Figure 4.

Top 4 benchmark results on 24 target sets for transcription factors from human, mouse, worm, and fly, as well as 10 target sets for microRNAs from human, and mouse from the metazoan target set compendium (Linhart et al. 2008). The plot is adapted from Linhart et al. (2008): The “Source” column indicates the experimental procedure or database from which the target set was derived: Gene-expression microarrays (Expr), ChIP-chip (CC), ChIP-DSL (C-DSL), DamID (van Steensel et al. 2001), or Gene Ontology (GO) database (Ashburner et al. 2000). The black and gray boxes indicate the similarity of the predicted PWM to the reference motif in TRANSFAC or miRBase. Darker shades indicate closer similarity. “Set Size”: number of sequences within the input set.

We compared the run times of the five tools on the metazoan target set compendium for a single core Xeon 2.9 GHz CPU (Supplemental Fig. S5). AMADEUS is the fastest tool, with an average run time per target set of 1m57s. XXmotif comes in second with an average run time of 5m48s, whereas PRIORITY-D needs, on average, 13m23s. Neither AMADEUS nor PRIORITY-D optimizes the motif length, which is the most time-consuming step within XXmotif. Weeder and MEME do optimize the motif length and are, on average, 15 and 536 times slower than XXmotif, respectively.

Accuracy of E-values

We conducted extensive tests to validate the accuracy of the E-values reported by XXmotif for different input set sizes (N = 10, 100, and 1000 sequences), sequence lengths (L = 100, 300, and 1000), background model orders (2 and 8), and motif model (“zero or one occurrence” and “multiple occurrences per sequence”). For each combination, we generated 100 sets of random sequences with the corresponding background model. We then started XXmotif with default parameters on each of these input sets, learning the background model from the input sequences. For each combination, we recorded the cumulative distribution of motif E-values reported by XXmotif (Supplemental Figures S6A–D). The results show that XXmotif's E-values vary between being precise to being too conservative by a factor up to 100, depending on N, L, and the background model order.

Regulatory motifs for early embryo segmentation in flies

One of the most studied model systems of transcription regulatory networks is the network that lays down the segmentation pattern along the anterior-posterior axis in the early Drosophila embryo (Jaeger et al. 2004; Zinzen et al. 2009; Li and Arnosti 2011; Perry et al. 2011). Various transcription factors are known to participate in this network, but also other as yet unidentified factors are believed to be involved (Segal et al. 2008; He et al. 2010). The identification of these “missing nodes” in the network would set the stage for more accurate, quantitative models for this network paradigm.

We obtained the sequences of 54 hand-curated cis-regulatory modules for segmentation in the early D. melanogaster embryo (Methods) that are all primarily targeted by maternal and gap genes (Schroeder et al. 2004, 2011). Since we expect functional binding sites to be more conserved than background, we used the 13 most related species of the UCSC 15-way multiple sequence alignments (Blanchette et al. 2004) consisting of the Drosophila group and Anopheles gambiae as outgroup. We did not supply a negative sequence set, and XXmotif automatically constructed a second-order background model from the sequences in the positive set.

Figure 5 lists all motifs reported by XXmotif up to an E-value of 0.5. In the previous section, we showed that XXmotif's E-values are rather conservative, and therefore most of the listed motifs are likely to represent real binding motifs. To keep the results list as short and nonredundant as possible, we changed XXmotif's threshold for merging similar PWMs from “high” to “medium” (Methods). Of the 28 predicted motifs, 18 were similar to motifs known to organize segmentation in the early embryo according to assignments to literature motifs by TOMTOM (Gupta et al. 2007), or if the motif could not be assigned by TOMTOM, by our own assignment. Nicely, the list of motifs includes representatives of most classes of the transcription factors that are known to be involved in the segmentation. Factors missing are Forkhead, which is under-represented in the considered sequences, and Hunchback, for which an unusual motif with consensus “TTTTTT” was reported in the literature (Gallo et al. 2011). As Hunchback has many binding sites in the segmentation modules, we surmise that P(T|TT) received a high probabilities with our second-order background model, rendering matches to poly-Ts insignificant.

Figure 5.

Motifs discovered in cis-regulatory modules for fly segmentation. The table lists all motifs that XXmotif reports up to an E-value of 0.5 on 54 segmentation modules responsible for patterning the anterior-posterior (AP) axis during early embryogenesis. To score conservation, multiple sequence alignments of D. melanogaster, 11 other Drosophila species, and Anopheles gambiae were supplied as input. For 18 of the 28 predicted motifs, similar literature motifs of transcription factors known to be involved in AP axis segmentation were assigned by TOMTOM (Gupta et al. 2007) or by visual inspection. Nine of the predicted motifs may describe transcription factors representing missing nodes in the transcriptional network.

Ten of the predicted motifs cannot be matched to known factors. Their E-values are of comparable significance as the known motifs. We therefore speculate that many of these novel motifs belong to transcription factors that represent missing nodes in the network. It will be interesting to determine experimentally what factors bind to these motifs; for example, using one-hybrid screens (Deplancke et al. 2006; Hens et al. 2011) or mass spectrometry techniques (Mittler et al. 2009).

Human core promoter motifs

Core promoters are the regions around transcription start sites (TSS) to which the general transcription machinery consisting of RNA polymerase and general transcription factors bind. In recent years it has become clear that the motif architecture of core promoters can influence the regulatory behavior of the promoter (Juven-Gershon and Kadonaga 2010). Around 15 motifs have been discovered that are enriched around human TSSs (Gershenzon and Ioshikhes 2005; FitzGerald et al. 2006; Gershenzon et al. 2006; Xi et al. 2007), the most frequently occurring ones being the TATA box (∼10% occurrence) and the SP1 motif (∼11%). Most of the elements are rare and not generally conserved within Animalia. For example, the human Initiator motif reported by Xi et al. (2007) with consensus GCCATTTTG occurs in only ∼1% of the core promoters analyzed here (see below), and bears little resemblance to the Initiator found in D. melanogaster (consensus TCAGT) (Ohler et al. 2002).

We extracted the sequences of the 1871 core promoters contained in the eukaryotic genome database (Schmid et al. 2006) from −300 bp to +100 bp around human transcription start sites, and ran XXmotif using the “zero or one occurrence per sequence” option. As we expect core promoter elements to have a defined distance to the TSS, we used the “localization” option of XXmotif, which combines P-values for positioning of motif occurrences with match P-values. A second-order background model was learned from the core promoter sequences. The similarity score for merging PWMs was set to “medium.”

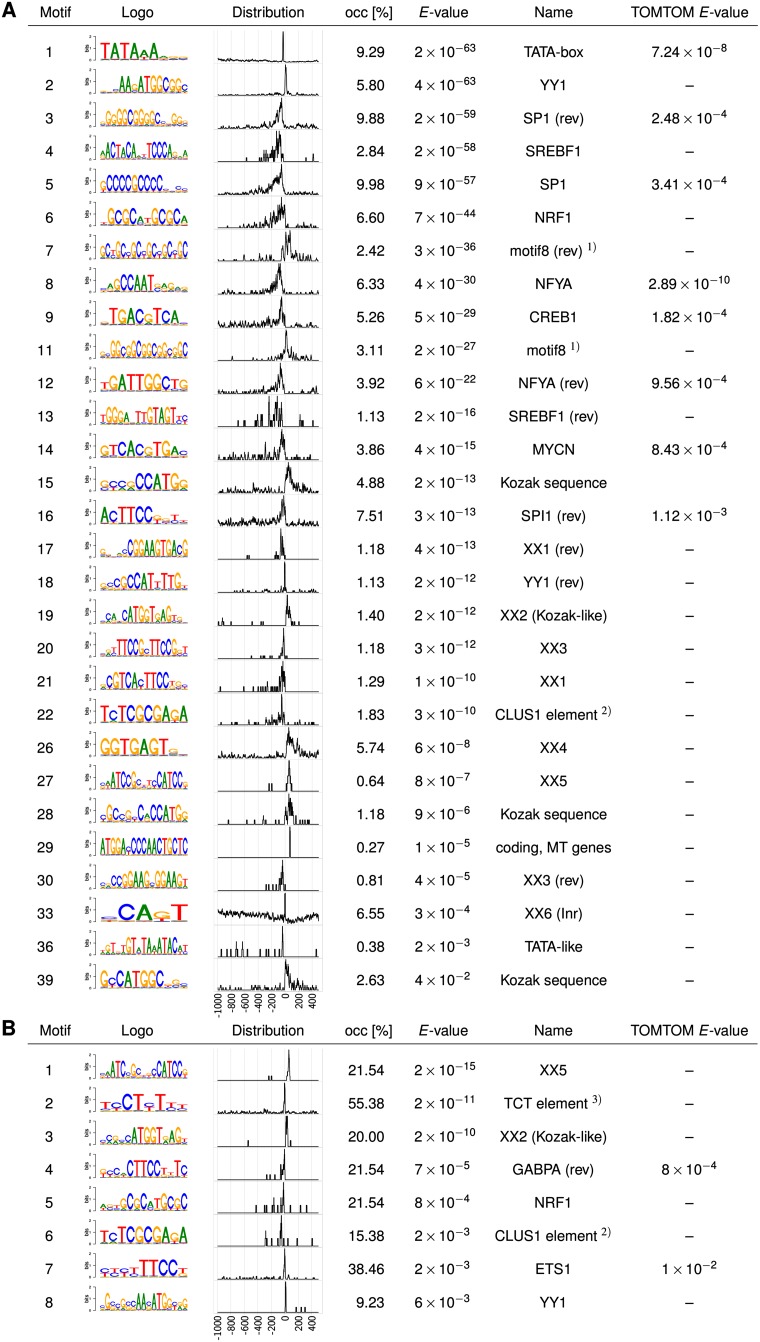
Figure 6A shows all enriched PWMs with an E-value up to 0.1. Of the 39 motifs, 20 are similar to previously described motifs (last column), assigned either by TOMTOM or, if this did not yield a significant match, by visually matching the obtained PWM logos with literature PWM logos. These 20 motifs are indeed enriched within the core promoter region, as shown by their positional distribution in a region from −1000 bp to +500 bp around the TSS.

Figure 6.

Human core promoter motifs discovered by XXmotif. (A) List of motifs up to an E-value of 0.1 in a set of 1871 human core promoter regions (−300 bp to +100 bp around TSS) from the eukaryotic promoter database (EPD) (Schmid et al. 2006). For 20 of the 39 predicted motifs, similar literature motifs were assigned by TOMTOM (Gupta et al. 2007) or us (last two columns). The motif at position 18, which was originally named Initiator (Xi et al. 2007), is actually the reverse complement of YY1. Eight novel, highly significant motifs, designated XX1 to XX6, XX1(rev), and XX3(rev), show positional distribution peaks near the TSS. XX6 is the canonical Initiator motif similar to elements found in D. melanogaster and S. cerevisiae. Ten motifs with a broad positional distribution are not shown. The positional distributions of the PWMs were obtained by scanning the PWMs over a larger region (−1000 bp to +500 bp) around the TSS. (B) Top eight motifs obtained with the core promoter sequences of the 65 genes annotated as coding for ribosomal proteins in EPD (Xi et al. 2007; FitzGerald et al. 2006; Parry et al. 2010).

Ten mostly repetitive, rather uniformly distributed motifs of low-compositional complexity are not shown (see Supplemental Fig. S7A for a complete list). We believe that they do not represent functional promoter motifs. Possibly these low complexity regions serve to modulate the physical properties of the DNA double helix near the core promoter; for example, in order to attract or repel nucleosomes. When preprocessing the input sequences with RepeatMasker (www.repeatmasker.org) (Supplemental Fig. S7B), some of these low-complexity motifs disappeared from the results list and the rest received less significant E-values, indicating that they most probably do not constitute factor-binding motifs. Motif 29 in Figure 6A is a false motif that XXmasker failed to repress. It represents the first 17 nucleotides of the coding regions of five recently duplicated Metallothioneine genes (MT-IA, MT-IB, MT-IF, MT-IL, MT-IIA).

XXmotif further detected eight sharply peaked motifs with E-values comparable to those of previously described motifs (XX1 to XX6, XX1(rev), XX3(rev)). The bipartite motifs XX1 and XX3 share a 3′ TTCC G/T submotif. XX1 further contains the AYTTCC(G/T) motif characteristic for the ETS transcription factor family (SPI1, GABPA, ETS1, and others), and looks like a significantly extended version of these. Both X1 and X3 are well positioned within 50 nt upstream of the TSS. XX2 is similar to the classical Kozak sequence (consensus: RCCATGG) (Kozak 1999; Nakagawa et al. 2008), but has an atypical, conserved T after this core motif and five other partly conserved positions downstream. XX4 is relatively frequent (5.7%) and has a distribution peaked within the first 150 bp after the TSS. XX5 is sharply peaked around 60 bp downstream from the TSS. Since XX4 and XX5 occur downstream from the TSS, it is possible that these motifs are in fact motifs bound on the RNA that are involved in efficient mRNA export or translation, as is likely for XX2, or that they have dual roles as DNA and RNA motifs. Motifs XX1(rev) and XX3(rev) are almost exact reverse complements of XX1 and XX3. Since this is extremely unlikely to happen by chance, we conclude that these motifs belong to transcription factors that bind in two opposing orientations.

We performed a Gene Ontology (GO) analysis (Huang et al. 2009) on genes carrying the novel motifs (Supplemental Table S2). Motifs XX1 to XX5 all have significant correlations (Bonferroni-corrected P-value < 0.05) with GO categories “translational elongation” or “structural constituent of ribosome.” Genes with an Initiator motif (XX6) are overrepresented in the “RNA-splicing” category (Bonferroni-corrected P-value = 7 × 10⁻⁵). The reverse complements of XX1 and XX3 have no significant GO-enrichments. Not surprisingly, genes with motifs having the highest overlap with “translation elongation,” XX2, XX3, and XX5, show the strongest expression in RNA-seq measurements in three human cell lines (Lundberg et al. 2010): Their 90% quantiles of expression levels are between two- and threefold higher than for all genes in the EPD (Supplemental Table S3). In contrast, genes possessing XX1 or the Initiator (XX6) have approximately normal expression levels. Interestingly, genes with XX1(rev) and XX3(rev) motifs have a much lower expression than their reverse complements. This indicates that the binding orientation of the associated, unknown factors is important for an efficient assembly of the transcription initiation complex.

YY1 (rev) was called Initiator element in Xi et al. (2007) due to its precise localization at the TSS. But, in contrast to the very specific YY1 (rev) motif, which we find in only 1.2% of EPD core promoter sequences, motif XX6 occurs in 6.6% and is equally well positioned at the TSS. This Initiator element is also similar to the much less informative Initiator motif YYANWYY that was defined based on in-vitro transcription assays (Corden et al. 1980; Lo and Smale 1996; Smale and Kadonaga 2003) and the motif CAN(T/C/A) detected by computational analysis (Bucher 1990). We therefore suggest that XX6 is the canonical human Initiator motif.

To further analyze the ribosomal system of transcription initiation, we searched for motifs in the subset of 65 promoter regions of genes annotated to code for ribosomal proteins (Fig. 6B). We found eight motifs, six of which we had already identified on the large set of core promoters, and their PWMs look almost identical. All eight are strongly enriched at ribosomal protein core promoters. In 55% of the ribosomal genes we find a second Initiator element, called the “TCT element,” which was discovered in fly promoters of ribosomal protein genes and was shown to also be enriched around human TSSs (Parry et al. 2010). Motif XX2 (Kozak-like) is present in 13 (20%) and XX5 in 14 (21.5%) of these 65 promoters in comparison to 26 (1.4%) and 12 (0.64%) in the entire set of EPD promoters, respectively. Hence, approximately half of the XX2 motifs and all of the XX5 motifs in the full EPD data set occur in genes annotated as ribosomal protein genes.

In summary, in addition to finding almost all motifs known to be enriched in human core promoters, we discovered eight new motifs that are strongly peaked around TSSs, and three of which are associated with strong expression. Whereas six of these motifs are rather rare (frequency <2%) and probably represent binding motifs for sequence-specific transcription factors, we also identified a motif similar to the canonical initiator motif known in other species and a motif (XX4) that occurs with similar frequency (6%) as the canonical initiator. The quest is now to identify the transcription factors that bind these motifs, and to investigate the association of these motifs with regulatory properties of core promoters, such as stress inducibility, degree of tissue- and time-dependent regulation, maximum and basal transcription rates (Valen and Sandelin 2011).

Discussion

We compared XXmotif's sensitivity and the quality of its reported PWMs with five other state-of-the-art motif discovery tools and found it to perform strongly in this comparison. What are the methodological improvments that can explain XXmotif's success?

Optimization of PWM by statistical significance of enrichment

XXmotif's PWM stage refines motif PWMs by optimizing their enrichment E-values. It thus combines the solid statistical estimates of pattern-based algorithms with the more powerful representation of motifs by PWMs. In contrast to patterns, PWMs can describe weak and strong binding. In a thermodynamic treatment of factor binding, PWMs emerge naturally, representing the independent energetic contributions of the binding-site nucleotides to the binding energy.

To analyze the causes of XXmotif's good performance, we benchmarked a version of XXmotif in which the PWM-based refinement stage was omitted. About one-half of the improvement in the sensitivity of motif discovery of ∼43% over the best competing general motif discovery methods was owed to XXmotif's pattern stage, whereas the other half was contributed by the E-value-based PWM refinement (Fig. 2). Similarly, both stages contributed roughly equally to the improvements in the quality of PWMs, as measured by how well the reported PWMs could predict the ChIP enrichment on hold-out sequence data not used for discovering the motif (Fig. 3). Thus, the PWM-refinement stage could substantially improve the quality of the PWMs. Better PWMs also improved the sensitivity of motif discovery by bringing the top-ranked motif nearer to the “true” PWM and by better ranking of the motif PWMs.

In order to optimize the enrichment P-values of PWMs, we need to compute P-values for all relevant score thresholds extremely fast, as millions of enrichment P-values for thousands of alternative PWMs need to be computed during the extension, PWM merging, and refinement stage. Most motif discovery programs calculate enrichment P-values for a PMW using a time-consuming sampling approach, generating a large number of random input sets and scoring these with the PWMs. While a few methods have been described that can calculate P-values for PWMs directly without sampling (Touzet and Varre 2007; Zhang et al. 2007; Bailey et al. 2010), they are still much too slow for our purposes (Supplemental Methods, section 3.4).

We solved the speed challenge with three ideas: First, we developed a fast branch-and-bound algorithm to compute match P-values for every possible site in the input sequences. This is done in a time proportional to the number of l-mers having a log-odds score of at least zero bits. Second, as this number grows exponentially with the PWM length l, we sped this calculation up for l > 8 with an approximation in which we split the l-mers into an 8-mer and an l−8-mer part. Third, we apply order statistics to combine the match P-values for all sites to yield a motif enrichment P-value. We optimize the score threshold above which the potential sites are counted as matches. This procedure can be interpreted from a thermodynamic viewpoint. It is equivalent to the zero-temperature approximation of factor binding, in which sites are either not bound or fully occupied (Homsi et al. 2009). The optimization of K (and hence of the match P-value threshold) corresponds to finding the factor concentration at which the total occupancy on the positive sequences differs most significantly from that on the background sequences.

Nongreedy pattern search

Almost half of XXmotif's improvement over the best alternative method is due to our strategy to follow up not only a subset of seed patterns with the highest significance, but to extend a large and representative set of 5120 IUPAC 5-mer seeds, irrespective of how insignificant their initial E-values may be. A similar strategy is used in ERMIT, which extends all 512 5-mers (Georgiev et al. 2010). In this way, XXmotif can discover enriched motifs that do not contain even a single marginally significantly enriched 5-mer. During the extension stage, we follow up to three different extensions per seed pattern as long as the E-value is improved by the extension. Using the best three instead of only the best extension reduces the risk of getting trapped in local optima that often plague greedy searches. By allowing up to three gap positions when extending patterns by an additional position, XXmotif can jump across regions in the motif with low selective constraints. A further strength of the pattern-based stage is that it extends thousands of palindromic and tandemic 6-mer seed patterns containing gap positions in the middle. Thus, even motifs with widely spaced regions of conservation, such as Gal4's CGG-N(11)-CCG motif, for example, are found without difficulty as long as they are either palindromic or tandemic. The palindromic and tandemic seeds contribute ∼6% to the performance gain of the pattern stage (Fig. 2, XXmotif-5-noref).

Background model

Many methods use a second-order background model to describe the properties of reference sequences. We obtained improvements of around 16% by using an order 8 instead of an order 2 background model (Supplemental Fig. S1). To train such high orders with limited data, we made use of an interpolated Markov model (Salzberg et al. 1998). Higher-order models help to distinguish true motifs, which appear enriched only in the positive set, from sequences with relatively low complexity, such as (imperfect) trinucleotide repeats that are over-represented in the entire genome, and that will look enriched in comparison to a first-order background model in any subset of genomic sequences. Some tools, such as AMADEUS, do not train a statistical background model, but instead use the negative set directly to determine the enrichment P-values of patterns. Therefore, no patterns of any length that are enriched uniformly in the entire genome can become significant. However, this approach has the disadvantage of limiting the significance of enrichment P-values that can be calculated. If a pattern does not have a single match in the negative set, it is not possible to decide whether it can be improved by extending it. This limits the pattern length for these tools to around eight positions in practice.

Sequence masking

A further improvement has been realized by masking homologous sequence segments using the XXmasker procedure. Supplemental Table S1 shows that other tools can also slightly improve their performance when running on sequence sets that were preprocessed using XXmasker. The goal of XXmasker is somewhat different from standard RepeatMaskers such as RepeatMasker (www.repeatmasker.org), which scan the input sequences against a database of known repeats. XXmasker mainly serves to mask duplicated, homologous sequence stretches. These would otherwise be reported as false-positive motifs. This is important for XXmotif, since its nongreedy motif extension strategy has proved more sensitive than alternative tools to detect duplicated sequence stretches as “motifs” even if they occur in only two sequences—if the motif is long enough to become statistically significant. The XXmotif filtering strategy is more general than using a standard RepeatMasker, as it does not assume any knowledge about the type of duplicated or repetitive elements. In fact, XXmasker can be used in combination with a RepeatMasker, and comparing Figure 6 with Supplemental Figure S7 demonstrates that this may indeed improve results slightly.

Positional clustering of motifs

When the motif occurrences are spatially clustered relative to anchor points such as transcription start sites, splice sites, or other motifs, the sensitivity can be improved considerably (Kim et al. 2008; Keilwagen et al. 2011). A few studies have shown that including a positional prior probability distribution can increase the sensitivity of motif discovery (MEME-D) (Bailey et al. 2010). For example, transcription factors compete with nucleosomes for DNA; hence, a positional prior that relies on predicted or actual nucleosome positions can improve motif discovery (Narlikar et al. 2007). XXmotif has the option to calculate localization P-values describing the positional clustering of motif occurrences. These positional P-values quantify how unlikely it would be to observe the actually observed positional clustering by chance. Although we did not find a good data set to benchmark the impact of scoring localization, XXmotif's localization P-values have been important for finding the weak and rare human core promoter elements.

Negligible improvement through sequence conservation

Functional motifs are generally conserved above average, since mutations that abrogate their function are negatively selected (Kheradpour et al. 2007; Stark et al. 2007; Margulies and Birney 2008; Roy et al. 2010). We tried several versions of alignment-free and alignment-based conservation scores in XXmotif. The alignment-based conservation P-values turned out to perform best on our test cases (Sandve et al. 2007), but even with these we failed to obtain clear improvements on the large yeast benchmark. Actually, none of the tested methods for scoring conservation could improve the sensitivity significantly. This may seem surprising, since it is well established that conservation information helps to uncover functional genomic elements (Meireles-Filho and Stark 2009; Lindblad-Toh et al. 2011). However, these successful studies looked at the most conserved genomic elements, which are probably almost always functional. The reverse is not necessarily true: The majority of functional genomic elements seem to show only a weak degree of conservation, too low to contribute positively to their identification with present approaches. One of the reasons for this failure might be that most methods score the number of mutations instead of the conservation of binding affinity of a site, as suggested by recent work (Mustonen and Lässig 2005; Kim et al. 2009; Shultzaberger et al. 2010).

Motifs in human core promoters

We analyzed human core promoter sequences with XXmotif and found most previously described motifs as well as eight novel motifs that have sharply peaked positional distributions around the TSS. One of the novel motifs is localized to within ±10 bp of the TSS and is similar to the Initiator motif in fly and yeast, which identifies it as the canonical human Initiator motif. We did not find the BRE, DPE, and MTE elements. However, these were never found by a de novo search on human core promoter sequences. The BRE element was deduced from crystal structures of TFIIB and TBP bound to the DNA (Nikolov et al. 1995) and later shown to be weakly positioned, but enriched around TSSs of several species (Gershenzon et al. 2006; Sandelin et al. 2007). The MTE and DPE elements were discovered in D. melanogaster (Ohler et al. 2002), and by scanning their PWMs over human core promoter sequences the DPE element was then found to be slightly enriched around human TSSs (FitzGerald et al. 2006). However, their positioning and signal over background is much weaker than what we observed for the novel motifs reported here. Eight motifs, two of them discovered in this study, are found to be strongly enriched in human core promoters of ribosomal protein genes. It is an intriguing possibility to try to combine these motifs into a ‘super core promoter’ that would support extremely high levels of transcription for applications in basic research and biotechnology (Juven-Gershon et al. 2006)

In conclusion, XXmotif is a general-purpose method for the discovery of enriched motifs in nucleotide sequences that is based on optimizing the enrichment P-values of motif PWMs. In several benchmarks on yeast and metazoan sequences, XXmotif compared favorably with some of the best state-of-the-art motif discovery tools. We hope that in this era of functional genomics and high-throughput, data-driven biology, XXmotif will contribute toward understanding the regulation of our genomes by the sequence-specific binding of protein and ncRNA factors.

Methods

Data sets

The 352 ChIP-chip S. cerevisiae data sets were taken from Harbison et al. (2004). The positive and negative sets of intergenic sequences are as described in Harbison et al. (2004) (ChIP-chip P-values < 1 × 10⁻³ and > 0.5, respectively). Sequence alignments to the four yeast species in the sensu strictu Saccharomyces clade were extracted from the UCSC 7-way yeast alignment (sacCer2). Sequences for the metazoan benchmark set were taken from Linhart et al. (2008). Eight transcription factors for which no literature motif was available in the latest public version of the TRANSFAC (Release 7.0) (Wingender et al. 1996) were removed. We used the same sequence regions as suggested by Linhart et al. (2008). For transcription factor target sets, the positive set consisted of promoter regions between −1000 bp and +200 bp relative to the transcription start site (TSS), and for the miRNA target sets it comprised the whole 3′ UTR of each transcript. As negative sequence sets we used all other promoter sequences or 3′ UTRs, respectively, in the given organism. The hand-curated set of 54 cis-regulatory modules was provided by Mark Schroeder (Supplemental Material) and comprises sequences that are primarily targeted by maternal and gap genes and exclude some of the pair rule elements that are primarily targeted by pair rule genes. Alignments for these sequences were generated using the UCSC 14-way multiple sequence alignments (dm3). The sequences of human core promoters were extracted from the web interface of the eukaryotic promoter database (EPD, Schmid et al. 2006). The subset of ribosomal proteins was filtered by the term “Hs RP” within the identifier of each sequence.

Definition of correct motifs

A predicted motif is considered correct if two criteria are fulfilled: (1) As in Georgiev et al. (2010) and Gordân et al. (2010), the normalized Euclidian distance is <0.25 in an overlapping region of length , and similar to Gordân et al. (2010), (2) the average relative entropy per position over the six positions with highest information content in the overlapping region is at least 0.5 for both PWMs. This ensures that the overlap is within informative parts of the PWMs, while not penalizing uninformative positions that can occur within motifs.

Merging similar PWMs

Two PWMs are merged into one (Fig. 1, Merging) if in addition to the two above criteria, a sufficient number of motif occurrences of the two PWMs overlap. More precisely, at the default “high” setting of the merging threshold, the binding sites of both motifs have to overlap at least 40% of the binding sites of the other motif. At medium merging threshold, the binding sites of the motif with fewer sites have to overlap with at least 40% of the binding sites of the other motif. At low threshold, this fraction must be at least 20%. The merged PWM is built from all binding sites of both PWMs and 10% pseudocounts (Durbin et al. 2006). If the length of both motifs is not the same, the length of the motif with the better E-value is chosen. Afterward, an E-value is calculated for the merged motif. If this E-value is better than the E-values of both unmerged motifs, only the merged motif is kept. Otherwise, only the better of the original motifs is kept.

Calculating match P-values

A match P-value for an l-mer x is the probability of obtaining the same or better log-odds score S(x) with the PWM on a random sequence, i.e., on a sequence generated according to the background model: P-value(x) = ∑_{z:S(z)≥S(x)} P_bg(z), where P_bg(z) denotes the probability to observe z according to the background model. To evaluate this sum, we enumerate all l-mers with a log-odds score larger than 0 bits using a fast branch-and-bound algorithm (Supplemental Methods), sort them according to their log-odds score, and calculate the probabilities P_bg(z) for each. We then calculate the P-value for each l-mer x in this list by cumulating the background probabilities down to x, since for all l-mers z with higher rank than x we have S(z) ≥ S(x). To speed up the calculation for PWMs with length l > 8, they are split into two parts of length 8 and l-8. Separate lists are created for the two parts and higher-order dependencies between them are efficiently approximated (Supplemental Methods, section 3.2).

Calculating E-values

We transform the motif enrichment P-values to E-values by multiplying the P-value by a Bonferroni factor of 6^l for IUPAC patterns of length l and by 10^l for PWMs of length l. For gapped IUPAC patterns, an additional Bonferroni factor of 2 per gap position is used. We scale down the log E-value by 2 to improve the agreement between reported and empirical E-values (Supplemental Fig. S6).

XXmasker

A nucleotide is masked if one of three conditions is fulfilled: (1) The nucleotide is within a homologous region detected by an all-against-all BLAST search with E-value cut-off of 1 × 10⁻¹⁰ and soft masking option. (2) The nucleotide is within a low complexity region defined as a stretch of length 50, consisting of not more than two different nucleotides. (3) The nucleotide is within a repeat, defined as a stretch of length 50, consisting only of perfect repeats with a length of three to 10.

Data access

The XXmotif web server, binaries, and the source code is available at http://xxmotif.genzentrum.lmu.de.